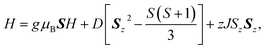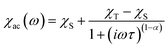Zero-field slow relaxation of magnetization in cobalt(II) single-ion magnets: suppression of quantum tunneling of magnetization by tailoring the intermolecular magnetic coupling

Abstract

The correlation between magnetic relaxation dynamics and the alignment of single-ion magnets (SIMs) in a crystal was investigated using four analogous cobalt(II) complexes with unique hydrogen-bond networks. The hydrogen-bonding interactions in the crystals resulted in a relatively short intermolecular Co⋯Co distance, which led to non-zero intermolecular magnetic coupling. All the complexes with a Co⋯Co distance shorter than 6.5 Å exhibited zero-field slow magnetic relaxation as weak magnetic interactions split the ground ±M_s levels and suppressed quantum tunneling of magnetization (QTM). In particular, antiferromagnetically coupled one-dimensional chain SIM networks effectively suppressed QTM when the two intrachain Co⋯Co distances were non-equivalent. However, when the two distances in a chain were equivalent and each molecular symmetry axis aligned parallell within the chain, QTM suppression was insufficient because magnetic coupling from the adjacent molecules was virtually cancelled. Partial substitution of the Co^II ion with the diamagnetic Zn^II ion up to 33% for this complex resulted in complete QTM suppression in the absence of an external field. These results show that the manipulation of intermolecular distances and alignments is effective for suppressing undesired QTM events in SIMs.

---

Introduction

Single-molecule magnets (SMMs) are individual molecules that display a bistable spin ground state.^1–3 Since their first discovery, substantial effort has been devoted to this research field owing to the potential application in areas such as high-density information storage, spintronics, and quantum computing.^4–6 The magnetic bistability of SMMs arises from the negative axial zero-field splitting (ZFS) and the spin reversal-barrier (U). The U can be described as |D|S² for an integer spin system and |D|(S² − 1/4) for a half-integer spin system, where D denotes the axial ZFS parameter and S is the spin of the ground state of the molecule. In the early days of SMM studies, many polynuclear clusters were synthesized and characterized to achieve a large U.^1–3,7–11 However, this task appears to be difficult because the D value is inversely proportional to S.¹²

Single-ion magnets (SIMs) are a subclass of SMMs with a single magnetic center. Since the first discovery of a lanthanide-based SIM,¹³ SIMs have taken the place of polynuclear cluster-based SMMs because of their simplicity and facile synthesis in controlling and enhancing the axial magnetic anisotropy. Mononuclear complexes with first-row transition metal are also good candidates for SIMs.^14–28 Within the 3d SIMs, particular attention has been paid to the pseudo-tetrahedral cobalt(II) complexes because of their strong magnetic anisotropy. The strong magnetic anisotropy is originated from a second order spin–orbit coupling interaction between ground and excited electronic states that yields a large ZFS.²⁵

Although a number of 3d SIMs with metals, such as Mn, Fe, Co, and Ni, have been reported, most of these do not show slow magnetic relaxation in the absence of an external direct current (dc) field because of fast relaxation via quantum tunneling of magnetization (QTM).^29–32 Therefore, for future SMM applications, QTM suppression is one of the most important topics that needs to be addressed.

QTM arises from the mixing of ±M_s levels through hyperfine interactions, transverse ZFS or dipolar interactions.³¹ The Kramers theorem predicts that the mixing of the ground ±M_s levels by transverse ZFS for half-integer spin system is forbidden.³³ To avoid QTM induced by dipolar interactions, SMMs have to be discrete and kept separated by a long distance in the crystal. By contrast, Christou and co-workers reported that a weak intermolecular magnetic coupling can suppress QTM in a hydrogen-bonded dimer of Mn₄ clusters in the absence of a dc field.³⁴ Such a weak coupling between SMMs can work as a bias to split the ground ±M_s levels. Since the first report of such an exchange-biased SMM, several supramolecular dimers, chains, and three-dimensional networks of weakly coupled SMMs connected by hydrogen bonds have been reported.^35–39 However, most such supramolecular aggregates of SMMs have been unintentional discoveries. To control and design such a SMM aggregate by hydrogen bonds, a mononuclear SIM is more advantageous than with polynuclear clusters because of its simplicity.

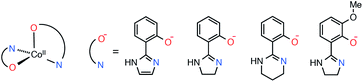
With the above in mind, we recently reported on hydrogen-bonded supramolecular aggregates of pseudo-tetrahedral cobalt(II) SIMs with three bidentate ligands, [Co(Himl)₂]·CH₃OH (1·CH₃OH), [Co(Himn)₂] (2), and [Co(Hthp)₂] (3), where Himl⁻, Himn⁻, and Hthp⁻ are 2-(2-imidazolyl)phenolate, 2-(2-imidazolinyl)phenolate, and 2-(1,4,5,6-tetrahydropyrimidin-2-yl)phenolate, respectively (Scheme 1).⁴⁰ It was indicated that one-dimensional (1-D) chain structures with intrachain Co⋯Co distances of 6.0–6.3 Å suppress the QTM of the SIMs by intermolecular magnetic coupling. However, the correlation between the SIM alignments in the chain and the quenching of QTM remained unclear. In this study, we prepared a new complex with a dimeric hydrogen-bond structure to elucidate the magnetic relaxation dynamics of the SIMs in supramolecular hydrogen-bonded structures. The magnetic relaxation dynamics in Co^II SIMs with hydrogen-bond networks were considerably varied depending on the intrachain Co⋯Co distances. Furthermore, we succeeded in tailoring the magnetic coupling by a partial substitution of Co^II ions with Zn^II, which resulted in complete suppression of QTM in 3.

Scheme 1 Chemical structures of the Co^II complex and the ligands Himl⁻, Himn⁻, Hthp⁻, and Hmimn⁻.

Results and discussion

Synthesis

The cobalt(II) complexes, 1·CH₃OH, 2, and 3, were synthesized according to previously reported methods.⁴⁰ An analogous complex, [Co(Hmimn)₂]·CH₃OH (4·CH₃OH), was obtained as red crystals by a reaction of CoCl₂·6H₂O and the ligand in a 1 : 2 ratio in methanol under an Ar atmosphere (Hmimn⁻ = 2-(2-imidazolinyl)-6-methoxyphenolate).

The isomorphous zinc(II) complexes for 1–3 were reported by He and by our group.^41–43 The synthesis of the Hthp⁻ analogue, [Zn(Hthp)₂], using the BF₄⁻ salt resulted in precipitation because the formation of the product was too fast. Alternatively, the desired crystals were obtained from a reaction with ZnCl₂, in which the coordination of Cl⁻ ions may hinder the fast formation of [Zn(Hthp)₂].

The Zn^II-doped samples for 1–3 were prepared by mixing the chloride or tetrafluorobarate salt of Co^II and Zn^II ion in the starting material under an Ar atmosphere. The identity of the crystals was confirmed by powder X-ray diffraction (PXRD) measurements (Fig. S32–S34†). As the Co : Zn ratio (x = molar fraction of Co^II ion) of mixed crystals may deviate from the expected value, the accurate molar fractions of the crystals were determined by inductively-coupled plasma atomic emission spectroscopy (ICP-AES). The composition of [Co_xZn_(1−x)(Himn)₂] (2′_x) was consistent with the expected value. The molar fractions of the Co^II ion in the [Co_xZn_(1−x)(Himl)₂]·CH₃OH (1′_x·CH₃OH) compounds were smaller than expected, presumably because of the more facile formation of the Zn complex. By contrast, for [Co_xZn_(1−x)(Hthp)₂] (3′_x), the molar fraction of Co ion was higher than expected. Upon reaction of the metal salts mixture and the Hthp⁻ ligand, a colorless precipitate of [Zn(Hthp)₂] was immediately formed.⁴³ Thirty minutes later, pale red crystals of 3′_x started to form. As the colorless [Zn(Hthp)₂] precipitate was removed upon purification, it resulted in a larger Co^II ion composition than expected (x_expected = 0.49 and x_actual = 0.67). An attempt to prepare 3′_x with x < 0.5 was unsuccessful, and only a colorless precipitate was obtained as solid.

Crystal structures

Single-crystal X-ray analysis of the Co^II complexes indicated the formation of bis-bidentate complexes with O–N chelate. The molecular structures and bonding parameters of the complexes are shown in Fig. 1 and Tables S1, S2.† In the Co^II complexes with Himl⁻ and Hmimn⁻, a methanol molecule of crystallization was contained in the crystal, whereas the others contained no solvent molecule. The bond distances around the Co^II ion were comparable among the series. The bite angle in 3 was larger by ca. 3° than the others because of the steric restriction of the ligand.

Fig. 1 Molecular structures of (a) 1·CH₃OH, (b) 2, (c) 3, (d) 4·CH₃OH (50% probability levels).

Owing to the non-coordinating N–H bond in the ligands, all the complexes formed supramolecular structures by intermolecular hydrogen bonds (Fig. 2). In the crystal, 1 formed hydrogen-bond networks via a methanol molecule of crystallization to construct a two-dimensional sheet structure. The shortest intrasheet Co⋯Co distance was 7.03 Å, and the intersheet distance was 7.51 Å.

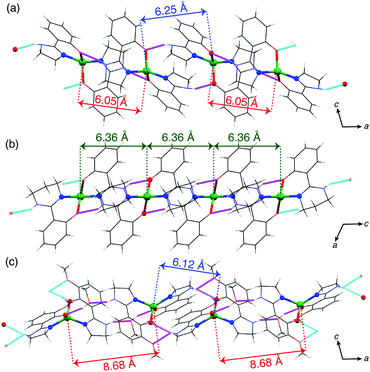Fig. 2 1-D hydrogen-bonded chain structures of (a) 2 along the a axis, (b) 3 along the c axis and (c) 4·CH₃OH along the a axis. The magenta and cyan dashed lines indicate the hydrogen bonds.

By contrast, the other complexes formed 1-D chain structures in the crystals. In the crystal of 2, the Co⋯Co distances between two adjacent molecules in the chain were 6.05 and 6.25 Å, which are significantly shorter than the Co⋯Co distances in 1·CH₃OH. The shortest interchain distance of 7.67 Å was considerably longer than the intrachain distance, which suggests that the intermolecular magnetic coupling in 2 is dominated by the intrachain interactions.

In the case of 3, the intrachain distances were crystallographically equivalent, 6.36 Å, and the shortest interchain distance was 7.93 Å. As the interchain Co⋯Co distance is ca. 8 Å, the interchain magnetic interactions must be negligible, like in 2.

In 4·CH₃OH, the two intrachain Co⋯Co distances were differed by over 2.5 Å (6.15 and 8.68 Å). In the chain, two discrete 4 molecules were directly connected by a double hydrogen bond to form a dimeric structure. The dimers were connected by hydrogen bonds via two methanol molecules of crystallization unlike in 2 and 3. The shortest interchain distance was 7.55 Å, also much longer than that in the dimer. Thus, the supramolecular structure in 4·CH₃OH can be regarded as a dimer structure in terms of intermolecular magnetic interactions.

Static magnetic properties

The temperature and field dependent magnetic data of 4·CH₃OH is depicted in Fig. 3. The features of χ_MT vs. T and M vs. H plots were similar to those of 1·CH₃OH, 2 and 3 (Fig. S1†).⁴⁰ The effective χ_MT product at room temperature were ca. 2.5 cm³ mol⁻¹ K, which coincides to previously reported values for tetrahedral Co^II complexes.^44–47 The χ_MT product remained approximately constant upon lowering the temperature down to ca. 70 K, and it decreased abruptly below that, which is suggestive of non-zero ZFS. In the field-dependent measurements, the magnetization values did not saturate at 5 T and the isothermal magnetization curves at different temperatures did not coincide. To determine the g-factors and the axial ZFS parameter (D), the temperature dependence of the χ_MT data and the field dependence of the magnetization were simultaneously fitted to the following spin Hamiltonian:
where D and zJ are axial ZFS parameter and the intermolecular magnetic interaction, respectively. The transversal ZFS parameter E was not considered in the spin Hamiltonian because it is difficult to determine only from magnetic data. The obtained parameters are summarized in Table 1. The data could not be fitted without considering the intermolecular interactions. For all the compounds, the determined zJ values for all compounds imply the existence of intermolecular antiferromagnetic interactions. Furthermore, negative D values were obtained although both negative and positive signs are possible for a pseudo-tetrahedral Co^II complex.²² The large negative axial ZFS parameters are suggestive of SIM behavior with a spin-reversal barrier of ca. 60–80 cm⁻¹ (U = 2|D|).

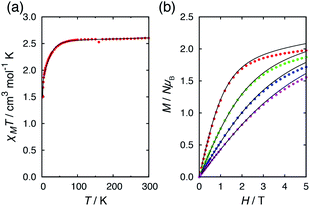Fig. 3 (a) Temperature dependence of the χ_MT product for 4·CH₃OH in an applied field of 5.0 kOe, and (b) field dependence of the magnetization for 4·CH₃OH at 2, 4, 6, and 8 K (red, green, blue, and magenta points, respectively). The solid lines correspond to the fit using the MagSakiTetra W0913 program.⁶⁰

Table 1 Experimental g-factors (g_x, g_y, and g_z) and axial ZFS parameters (D), and intermolecular magnetic interactions (zJ) with standard errors^a

	1·CH3OH^b	2^b	3^b	4·CH3OH
a The temperature-independent paramagnetism for all fits was fixed at 0.0003 cm^−1 mol^−1.b The experimental parameters for 1·CH3OH, 2, and 3 were obtained by fitting the previously reported data with the latest fitting program MagSakiTetra W0913.^40,60
gx, gy	2.11(1)	2.19(1)	2.18(1)	2.18(1)
gz	2.48(1)	2.52(1)	2.48(1)	2.55(1)
D/cm^−1	−41(1)	−32(1)	−30(4)	−30(1)
zJ/cm^−1	−0.15(3)	−0.19(1)	−1.5(3)	−0.25(8)

---

Dynamic magnetic properties

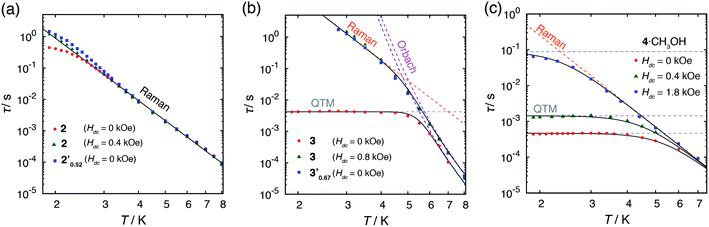
Alternating current (ac) magnetic susceptibility measurements for 1·CH₃OH, 2 and 3 have previously reported.⁴⁰ 1·CH₃OH did not exhibit a slow magnetic relaxation behavior in the absence of an external field presumably due to the fast relaxation via QTM. In the presence of an external field, a slow relaxation behavior was observed in 1·CH₃OH (Fig. S2†). The relaxation dynamics was reported to be predominated by the combination of a phonon-bottleneck-limited direct process (1.9–2.5 K) and a Raman process (4.0–6.5 K): τ⁻¹ = A_pbT² + CTⁿ (A_pb = 1.96 s⁻¹ K⁻², C = 1.35 × 10⁻³ s⁻¹ K^−8.0 and n = 8.0).^48,51 For a Kramers ion, the n value should be ≤9 when both an acoustic and an optical phonon are considered.^52,53 The obtained n value is consistent with the expected value.

In contrast to 1·CH₃OH, compounds 2, 3, and 4·CH₃OH, which form 1-D chain structures, exhibited slow relaxation of the magnetization in the absence of an external dc field (Fig. 4a, S4 and S7†). It should be noted that zero-field 3d SIMs are still rare. The τ vs. T plot of 2 in the absence of an external field was nicely overlapped with the one under 0.4 kOe.⁴⁰ Both plots were well-fitted with the Raman process: τ⁻¹ = CTⁿ (C = 1.18 × 10⁻² s⁻¹ K^−6.6, n = 6.6, Table S21†). Thus, in the relaxation dynamics of 2, the Raman relaxation process is predominant.

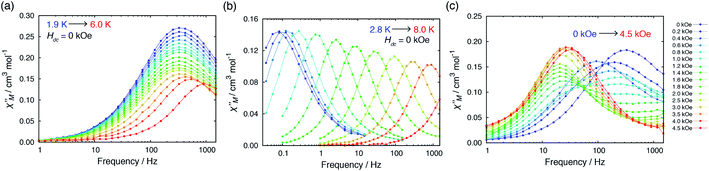Fig. 4 Temperature dependence of out-of-phase susceptibilities for (a) 4·CH₃OH and (b) 3′_0.67 in the absence of the dc field. (c) Dc field-dependence of 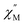for 4·CH₃OH with an dc field of 0–4.5 kOe.

In 3, by contrast, the τ vs. T plot under 0 kOe was independent of temperature between 1.9 and 5 K, which is a characteristic feature of QTM (Fig. 5b).⁴⁰ This temperature independent feature was completely removed upon application of an external field. The τ vs. T plot under 0.8 kOe fit well with the combination of two relaxation processes, Raman (≤4 K) and Orbach (>4 K) with τ⁻¹ = CTⁿ + τ₀⁻¹ exp(−Δ_Orbach/k_BT) (C = 4.69 × 10⁻⁴ s⁻¹ K^−6.7, n = 6.7, τ₀ = 4.77 × 10⁻¹⁰ s, Δ_Orbach = 63.9 cm⁻¹, Table S22†). The relaxation dynamics under zero field were reproduced by the combination of the QTM and with Orbach process with the same Δ_Orbach and with a τ₀ value (τ₀ = 2.40 × 10⁻¹⁰ s) similar to that under 0.8 kOe. It should be noted that the obtained Δ_Orbach value was consistent with the expected spin-reversal barrier for 3 (U = 2|D| = 60 cm⁻¹). Thus, slow magnetic relaxation was observed for 3 under a zero dc field, although the relaxation via QTM remained at low temperature.

Fig. 5 Temperature dependence of relaxation time τ. (a) 2 under fields of 0 and 0.4 kOe, and 2′_0.52 under 0 kOe. (b) 3 under fields of 0 and 0.8 kOe, and 3′_0.67 under 0 kOe. (c) 4·CH₃OH under fields of 0, 0.4, and 1.8 kOe. The dashed lines indicate fitted lines for a single relaxation process of Raman τ⁻¹ = CTⁿ, Orbach τ⁻¹ = τ₀⁻¹ exp(−Δ_Orbach/k_BT) and QTM τ⁻¹ = τ_QTM⁻¹. The solid black lines indicate the sum of the relaxation processes.

In the absence of a dc field, 4·CH₃OH also exhibited slow magnetic relaxation (Fig. 4a and c). Upon application of a dc field, the relaxation pathway started to shift to a lower frequency, reaching minimum frequency at 0.4 kOe. With further increase of the applied field, another relaxation pathway appeared at a lower frequency, reaching minimum frequency at 1.8 kOe. The τ vs. T plots under 0, 0.4, and 1.8 kOe are shown in Fig. 5c. The measurements under these fields exhibited similar relaxation features: temperature independence, which is a characteristic of QTM at low temperature, and the power law of τ ∝ T⁻ⁿ at higher temperature. The relaxation dynamics under all the fields fit well with a combination of QTM and the Raman process with the same C and n values (τ⁻¹ = τ_QTM⁻¹ + CTⁿ; C = 4.68 × 10⁻² s⁻¹ K^−6.4, n = 6.4; τ_QTM = 4.67 × 10⁻⁴, 1.43 × 10⁻³, and 8.82 × 10⁻² s for H_dc = 0, 0.4, and 1.8 kOe, respectively).

Magnetic relaxation dynamics and intermolecular interactions

As described above, in the absence of an external field, superparamagnet-like slow magnetic relaxation was observed in 2, 3, and 4·CH₃OH. One of the possible reasons for the zero-field SIM behavior in these complexes is the short intermolecular Co⋯Co distance. In some hydrogen-bonded structures of SMM, QTM is suppressed because a static exchange bias field splits the ground ±M_s levels.^34–39 The shortest Co⋯Co distance in 2, 3, and 4·CH₃OH was 6.0–6.4 Å, whereas the distance in 1·CH₃OH was ≥7 Å. In general, the strength of a magnetic coupling depends on the distance between the magnetic centers. To suppress QTM by a dipolar field, a weak but a certain degree of intermolecular magnetic interaction is necessary. Hence, the individual dipolar field from the neighboring SIMs might be too weak in 1·CH₃OH.⁴⁰

QTM at ≥2.5 K was completely suppressed in 2, but a significant QTM contribution was observed in the relaxation dynamics of 3. Unlike the other complexes, 3 molecule is C₂ symmetric in the crystal. In the hydrogen-bonded chain, each molecule is equally spaced along the c-axis and the molecular C₂ axis oriented along the b-axis. As each molecular symmetry axis is parallelly aligned in a chain, the dipolar field and magnetic anisotropy axis can be mutually oriented and the bias field from adjacent molecule in the chain is canceled. Consequently, the weakly coupled 1-D networks in 3 suppress QTM only partially. By contrast, in the 1-D networks of 2, the dipolar field from the adjacent molecule is not canceled because the magnetic anisotropy axis is not mutually oriented and the two intrachain Co⋯Co distances differ by ca. 0.2 Å. Thus, QTM in 2 is completely suppressed even in the absence of an external field.

Considering the intrachain Co⋯Co distances, the intermolecular magnetic interaction in 4·CH₃OH should be originated from the dimeric structure. In the magnetic relaxation dynamics, two relaxation pathways were observed. At H_dc = 0 kOe, each molecule of 4 was under the magnetic perturbation (±H_dip) of the other molecule in the dimer. This H_dip splits the ±M_s levels that results in partial QTM suppression. In the presence of a dc field, this H_dip is stochastically directed to be either parallel or antiparallel to the field (H = H_dc + H_dip or H_dc − H_dip). When H_dc = H_dip, H_dip in the parallel state suppresses QTM by magnetic perturbation, whereas H_dip in the antiparallel state is virtually canceled by H_dc, which results in the occurrence of QTM. Under H_dc ≫ H_dip, QTM is suppressed irrespective of the direction of H_dc and H_dip. Consequently, the field dependence of the 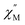vs. frequency plot showed two peaks when H_dc was between 0.4 and 1.8 kOe because the relaxation process of 4·CH₃OH should be influenced by both parallel and antiparallel states (Fig. 4c).

Magnetic relaxation dynamics in magnetically diluted crystals

As discussed above, it is suggested that a weak magnetic coupling between SIMs induces a zero-field slow relaxation of the magnetization. To elucidate the effect of the intermolecular coupling in more detail, we conducted partial magnetic dilution experiments. In a common magnetic dilution experiment, the concentration of a paramagnetic ion is diluted down to ca. 5% to remove the dipolar interaction.^54–56 In our experiment, we first aimed to prepare the sample with a Co^II ion concentration of ca. 50%. However, control of the molar fractions of the Co^II ion in 1′_x·CH₃OH and 3′_x was difficult, and 1′_0.33·CH₃OH and 3′_0.67 were obtained from the 1 : 1 mixture of Co and Zn salts (see above).

Upon magnetic dilution of 1·CH₃OH, frequency dependence of the 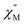was observed under 0 kOe, and the peak of the 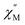vs. frequency plots was shifted to a low frequency, although the temperature independence of the peak was still apparent (Fig. S19 and S22†). This suggests that the relaxation time was prolonged through reduced dipolar interactions by extension of the average Co⋯Co distances in 1′_0.33·CH₃OH and 1′_0.12·CH₃OH. However, temperature independence was observed for both 1′_0.33·CH₃OH and 1′_0.12·CH₃OH. As the relaxation time reached a plateau with the application of an external field, a significant contribution of QTM remained in 1′_x·CH₃OH (Fig. S21 and S24†). Thus, the partial substitution of the paramagnetic Co^II center only reduced the influence of the weak dipolar interactions, and QTM was not completely suppressed. This suggests that a relatively short Co⋯Co distance is important for effective QTM suppression.

The τ vs. T plot of 2′_0.52 measured under zero field overlapped well with that of 2 under both 0 and 0.4 kOe (Fig. 5a). Below 2.3 K, the value of τ in 2 under 0 kOe was slightly smaller than the expected value for the Raman process, but the τ vs. T plot of 2′_0.52 under 0 kOe obeyed the model in the whole temperature range. Thus, the magnetic dilution down to ca. 50% in 2 afforded almost no change in the relaxation dynamics under zero field.

By contrast, the magnetic dilution of 3 drastically changed the magnetic relaxation dynamics (Fig. 4b). The temperature independence observed below 5 K in 3 disappeared completely in 3′_0.67 under a zero dc field. The τ vs. T plot of 3′_0.67 under 0 kOe perfectly overlaps with that of 3 under 0.8 kOe (Fig. 5b). Substitution of the Co^II ion with a diamagnetic Zn^II ion up to ca. 30% breaks the mutual orientation of the dipolar field and the magnetic anisotropy in the hydrogen-bonded chain. As a result, the dipolar field is not canceled within the chain, and QTM was effectively quenched. These results indicate that a relatively short distances between SIMs and a non-symmetric alignment of them are important for achieving a zero-field SIM behavior.

Conclusions

Static and dynamic magnetic properties of four structurally analogous bis-bidentate cobalt(II) complexes were analyzed. In all the complexes in which the intermolecular distances were less than 6.5 Å, QTM was either partially or completely suppressed because of intermolecular magnetic coupling in the absence of an external field. In 4·CH₃OH, the hydrogen-bonded dimer structure of SIMs resulted in the partial suppression of QTM. Upon application of an external field, QTM was suppressed in two steps because the magnetic perturbation is canceled when the direction of the external field and the perturbation are antiparallel. QTM was suppressed more effectively in the 1-D chain network, as the lowest-energy state is the alternating alignment of ±M_s levels. The non-symmetric alignment of SIMs in the chain in 2 led to a complete suppression of QTM. However, the symmetric alignment of SIMs in 3 caused cancelation of the magnetic perturbation, which resulted in partial occurrence of the QTM event. A partial substitution of the Co^II ion in 3 with the diamagnetic Zn^II ion (3′_0.67) resulted in complete suppression of QTM in the absence of an external field. This is a clear evidence that tailoring the intermolecular distances of SIMs and symmetry of the alignments can prevent the occurrence of QTM.

Experimental

General considerations

All chemicals were used as purchased without further purification. The ligand precursors H₂iml, H₂imn and H₂thp were prepared according to previously reported methods.⁵⁷ 1·CH₃OH, 2 and 3 were prepared according to a previously reported method.⁴⁰ The Co : Zn ratio of the magnetically diluted samples was determined by ICP-AES using a Shimadzu ICPE-9000. The 5 mg samples were digested in 60 μL of concentrated HNO₃, and then diluted to 10 mL using ca. 1.2% HNO₃ solution. The solution underwent a further 50 times dilution by ca. 1.2% HNO₃ solution to obtain the desired sample solution. The standard solutions were prepared using Co(NO₃)₂·6H₂O and Zn(NO₃)₂·6H₂O.

Syntheses

2-(2-Imidazilinyl)-6-methoxyphenol (H₂mimn). This compound was prepared by a similar method to that reported in the literature.⁵⁷ A mixture of methyl 3-methoxysalicylate (9.10 g, mmol) and ethylenediamine (10 mL) was refluxed overnight. The unreacted ethylenediamine was evaporated off under ambient pressure, followed by the addition of 10 mL ethanol. After cooling, the pale-yellow residue was collected by filtration and washed with methanol. Yield: 7.24 g, 75%.

[Co(Hmimn)₂]·CH₃OH (4·CH₃OH). A methanol solution (5 mL) of CoCl₂·6H₂O (24.9 mg, 0.10 mmol) was slowly added to a mixture of methanol (5 mL), H₂mimn (39.1 mg, 0.20 mmol) and triethylamine (30 μL) in a Schlenk flask under Ar atmosphere. The reaction mixture was allowed to stand at room temperature under Ar for a few weeks, and red crystals were obtained. Although H₂mimn hardly dissolves in methanol, slow formation of 4·CH₃OH crystals promoted dissolution. Yield: 22.0 mg, 46%. Anal. calcd for [Co(Hmimn)₂]·CH₃OH = C₂₁H₂₆CoN₄O₅: C, 53.28; H, 5.54; N, 11.84%. Found: C, 53.17; H, 5.46; N, 11.67%.

[Co_0.33Zn_0.67(Himl)₂]·CH₃OH (1′_0.33·CH₃OH). A methanol solution (10 mL) of CoCl₂·6H₂O (47.7 mg, 0.20 mmol) and ZnCl₂ (30.3 mg, 0.22 mmol) was slowly added to a methanol solution (10 mL) of H₂iml (129.6 mg, 0.81 mmol) and KO^tBu (86.7 mg, 0.77 mmol) in a Schlenk flask under Ar atmosphere. The reaction mixture was allowed to stand at room temperature under Ar for a few days, and red crystals were obtained. Yield: 102.1 mg, 61%. ICP analysis yielded that the molar fraction of Co in the sample was 32.71%, which is smaller than the 48% Co employed for the synthesis.

[Co_0.12Zn_0.88(Himl)₂]·CH₃OH (1′_0.12·CH₃OH). A methanol solution (5 mL) of CoCl₂·6H₂O (11.5 mg, 0.05 mmol) and ZnCl₂ (21.8 mg, 0.16 mmol) was slowly added to a methanol solution (5 mL) of H₂iml (64.0 mg, 0.40 mmol) and KO^tBu (42.7 mg, 0.38 mmol) in a Schlenk flask under Ar atmosphere. The reaction mixture was allowed to stand at room temperature under Ar for a few days, and red crystals were obtained. Yield: 55.7 mg, 65%. ICP analysis yielded that the molar fraction of Co in the sample was 12.03%, which is smaller than the 23% Co employed for the synthesis.

[Co_0.52Zn_0.48(Himn)₂] (2′_0.52). A methanol solution (8 mL) of CoCl₂·6H₂O (25.4 mg, 0.11 mmol) and ZnCl₂ (14.0 mg, 0.10 mmol) was slowly added to a methanol solution (8 mL) of H₂imn (65.9 mg, 0.41 mmol) and KO^tBu (44.6 mg, 0.40 mmol) in a Schlenk flask under Ar atmosphere. The reaction mixture was allowed to stand at room temperature under Ar for a few days, and red crystals were obtained. Yield: 46.5 mg, 59%. ICP analysis yielded that the molar fraction of Co in the sample was 51.52%, in accordance with the 52% Co employed for the synthesis.

[Co_0.67Zn_0.33(Hthp)₂] (3′_0.67). An ethanol solution (12 mL) of Co(BF₄)₂·6H₂O (68.3 mg, 0.20 mmol) and Zn(BF₄)₂·nH₂O (50.3 mg, 0.21 mmol (anhydrous basis)) was slowly added to an ethanol solution (12 mL) of H₂thp (141.3 mg, 0.80 mmol) and KO^tBu (88.9 mg, 0.79 mmol) in a Schlenk flask under Ar atmosphere. The reaction mixture was allowed to stand at room temperature under Ar for a few days, and red crystals were obtained together with a colorless precipitate. The precipitate was removed by washing with methanol and diethyl ether. Yield: 93.3 mg, 57%. ICP analysis yielded that the molar fraction of Co in the sample was 66.88%, which is larger than the 49% Co employed for the synthesis.

X-ray crystallography

X-ray diffraction data were obtained at 90(2) K with a Bruker SMART APEX equipped with CCD detector with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å). A single crystal was mounted with a glass capillary and flash-cooled with a cold N₂ gas stream. Data were processed using the SMART software packages. Structures were solved using the intrinsic phasing methods employing the SHELXT software packages and refined on F² (with all independent reflections).^58,59 The non-hydrogen atoms were refined anisotropically. All H atoms at C–H bonds were located using a riding model, and H atoms at N–H bonds were located from the electron-density difference maps and refined isotropically.

PXRD measurement

PXRD data were collected at room temperature on a Rigaku RINT 2100 powder diffractometer using Cu Kα radiation (λ = 1.5418 Å). The sample was ground in an agate mortar and placed on a silicon sample holder. The simulated diffraction pattern was calculated from the CIF using Mercury 3.8 software.

Magnetic measurement

Magnetic susceptibility measurements were performed with a MPMS-XL7 or MPMS-7 SQUID magnetometer. Susceptibility data were obtained in the temperature range from 1.9 to 300 K with a static field of 0.5 T. The polycrystalline samples were ground into fine powders in an agate mortar. The samples were then loaded into a gelatin capsule and covered in liquid paraffin to prevent field-induced orientation of crystals. All data were corrected for the diamagnetism of the sample by means of Pascal's constants. The temperature and field-dependent magnetic data were fitted using the MagSakiTetra W0913 program.⁶⁰ Dynamic susceptibility was measured with ac fields of 3 Oe magnitude and a constant dc field of 0–5000 Oe in the frequency range from 0.03 to 1500 Hz.

Analysis of ac susceptibility measurements

The relaxation time τ was extracted from fitting to the following generalized Debye model:
where χ_T and χ_S are the isothermal and adiabatic susceptibilities, ω is the angular frequency, and α indicates the deviation from a pure Debye model.^49,50 The fit was performed using the CC-Fit program.⁶¹ The best fit parameters are summarized in Tables S7–S19.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr Takahiro Iwai (Kwansei Gakuin University) for the help with the ICP-AES measurements. A part of the magnetic measurements was conducted at the Institute of Molecular Science, supported by the Nanotechnology Platform Program (Molecule and Material Synthesis). This work was supported by a Grant-in-Aid for Scientific Research No. 19K15525 from MEXT, Japan.

Notes and references

1. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
2. H. J. Eppley, H.-L. Tsai, N. de Vries, K. Folting, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1995, 117, 301–317.
3. G. Arom, S. M. J. Aubin, M. A. Bolcar, G. Christou, H. J. Eppley, K. Folting, D. N. Hendrickson, J. C. Huffman, R. C. Squire, H.-L. Tsai, S. Wang and M. W. Wemple, Polyhedron, 1998, 17, 3005–3020.
4. M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197.
5. A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201.
6. P. C. E. Stamp and A. Gaita-Ariño, J. Mater. Chem., 2009, 19, 1718–1730.
7. A. L. Barra, A. Caneschi, A. Cornia, F. Fabrizi de Biani, D. Gatteschi, C. Sangregorio, R. Sessoli and L. Sorace, J. Am. Chem. Soc., 1999, 121, 5302–5310.
8. D. Gatteschi, R. Sessoli and A. Cornia, Chem. Commun., 2000, 725–732.
9. H. Oshio, N. Hoshino and T. Ito, J. Am. Chem. Soc., 2000, 122, 12602–12603.
10. C. Boskovic, H. U. Güdel, G. Labat, A. Neels, W. Wernsdorfer, B. Moubaraki and K. S. Murray, Inorg. Chem., 2005, 44, 3181–3189.
11. T. Glaser, M. Heidemeier, T. Weyhermüller, R. Hoffmann, H. Rupp and P. Müller, Angew. Chem., Int. Ed., 2006, 45, 6033–6037.
12. O. Waldmann, Inorg. Chem., 2007, 46, 10035–10037.
13. N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
14. J. Vallejo, A. Pascual-Álvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079.
15. R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 8300–8302.
16. W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126.
17. A. K. Bar, C. Pichon, N. Gogoi, C. Duhayon, S. Ramasesha and J.-P. Sutter, Chem. Commun., 2015, 51, 3616–3619.
18. S. Mossin, B. L. Tran, D. Adhikari, M. Pink, F. W. Heinemann, J. Sutter, R. K. Szilagyi, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2012, 134, 13651–13661.
19. Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467.
20. V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M.-E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792–9795.
21. J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734.
22. S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018.
23. Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Guo, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802–1806.
24. M. S. Fataftah, J. M. Zadrozny, D. M. Rogers and D. E. Freedman, Inorg. Chem., 2014, 53, 10716–10721.
25. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491.
26. T. J. Ozumerzifon, I. Bhowmick, W. C. Spaller, A. K. Rappé and M. P. Shores, Chem. Commun., 2017, 53, 4211–4214.
27. Y. Peng, V. Mereacre, C. E. Anson, Y. Zhang, T. Bodenstein, K. Fink and A. K. Powell, Inorg. Chem., 2017, 56, 6056–6066.
28. R. Mitsuhashi, K. S. Pedersen, T. Ueda, T. Suzuki, J. Bendix and M. Mikuriya, Chem. Commun., 2018, 54, 8869–8872.
29. P. Politi, A. Rettori, F. Hartmann-Boutron and J. Villain, Phys. Rev. Lett., 1995, 75, 537–540.
30. B. Barbara, W. Wernsdorfer, L. C. Sampaio, J. G. Park, C. Paulsen, M. A. Novak, R. Ferré, D. Mailly, R. Sessoli, A. Caneschi, K. Hasselbach, A. Benoit and L. Thomas, J. Magn. Magn. Mater., 1995, 140–144, 1825–1828.
31. D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297.
32. M. A. Sørensen, U. B. Hansen, M. Perfetti, K. S. Pedersen, E. Bartolomé, G. G. Simeoni, H. Mutka, S. Rols, M. Jeong, I. Zivkovic, M. Retuerto, A. Arauzo, J. Bartolomé, S. Piligkos, H. Weihe, L. H. Doerrer, J. van Slageren, H. M. Rønnow, K. Lefmann and J. Bendix, Nat. Commun., 2018, 9, 1292.
33. H. A. Kramers, Proc. Amsterdam Akad., 1930, 33, 959–972.
34. W. Wernsdorfer, N. Aliaga-Alcalde, D. N. Hendrickson and G. Christou, Nature, 2002, 416, 406–409.
35. R. Tiron, W. Wernsdorfer, N. Aliaga-Alcalde and G. Christou, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 1–4.
36. L. M. Wittick, K. S. Murray, B. Moubaraki, S. R. Batten, L. Spiccia and K. J. Berry, J. Chem. Soc., Dalton Trans., 2004, 4, 1003–1011.
37. R. Bagai, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2007, 129, 12918–12919.
38. R. Inglis, G. S. Papaefstathiou, W. Wernsdorfer and E. K. Brechin, Aust. J. Chem., 2009, 62, 1108–1118.
39. A. Das, K. Gieb, Y. Krupskaya, S. Demeshko, S. Dechert, R. Klingeler, V. Kataev, B. Büchner, P. Müller and F. Meyer, J. Am. Chem. Soc., 2011, 133, 3433–3443.
40. R. Mitsuhashi, S. Hosoya, T. Suzuki, Y. Sunatsuki, H. Sakiyama and M. Mikuriya, Dalton Trans., 2019, 48, 395–399.
41. H.-S. He, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m3042–m3043.
42. R. Mitsuhashi and M. Mikuriya, X-Ray Struct. Anal. Online, 2019, 35, 15–16.
43. R. MitsuhashiI and M. Mikuriya, X-Ray Struct. Anal. Online, 2019, 35, 37–38.
44. S. Sottini, G. Poneti, S. Ciattini, N. Levesanos, E. Ferentinos, J. Krzystek, L. Sorace and P. Kyritsis, Inorg. Chem., 2016, 55, 9537–9548.
45. S. Vaidya, S. K. Singh, P. Shukla, K. Ansari, G. Rajaraman and M. Shanmugam, Chem.–Eur. J., 2017, 23, 9546–9559.
46. R. C. Yang, D. R. Wang, J. L. Liu, Y. F. Wang, W. Q. Lin, J. D. Leng and A. J. Zhou, Chem.–Asian J., 2019, 14, 1467–1471.
47. T. Ishizaki, T. Fukuda, M. Akaki, A. Fuyuhiro, M. Hagiwara and N. Ishikawa, Inorg. Chem., 2019, 58, 5211–5220.
48. The relaxation time τ was extracted from the generalized Debye model fit of the ac susceptibility data at various temperatures.^49,50.
49. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351.
50. Y.-N. Guo, G.-F. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953–9963.
51. R. Orbach, Proc. R. Soc. A, 1961, 264, 458–484.
52. P. L. Scott and C. D. Jeffries, Phys. Rev., 1962, 127, 32–51.
53. K. N. Shrivastava, Phys. Status Solidi B, 1983, 117, 437–458.
54. J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209–217.
55. S. Vaidya, S. Tewary, S. K. Singh, S. K. Langley, K. S. Murray, Y. Lan, W. Wernsdorfer, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2016, 55, 9564–9578.
56. N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931–2935.
57. R. Mitsuhashi, T. Suzuki and Y. Sunatsuki, Inorg. Chem., 2013, 52, 10183–10190.
58. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
59. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
60. H. Sakiyama, J. Comput. Chem., 2016, 2, 1–4.
61. N. F. Chilton, CC-Fit, The University of Manchester, Manchester, U.K., 2014, http://www.nfchilton.com/cc-fit.html.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1986712. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ra08286d

---