Open Access Article
Open Access ArticleProbing the high performance of photoinduced birefringence in V-shaped azo/PMMA guest–host films†
Lidiana M. Silvaa,
Daniel L. Silvab,
Mariana V. Boasa,
Yann Bretonniere c,
Chantal Andraudc and
Marcelo G. Vivas
c,
Chantal Andraudc and
Marcelo G. Vivas *a
*a
aLaboratório de Espectroscopia Óptica e Fotônica, Universidade Federal de Alfenas, Poços de Caldas, MG, Brazil. E-mail: mavivas82@gmail.com
bDepartamento de Ciências da Natureza, Matemática e Educação, Universidade Federal de São Carlos, Rod. Anhanguera – Km 174, 13600-970 Araras, SP, Brazil
cUniv. Lyon, ENS de Lyon, CNRS UMR 5182, Université Claude Bernard Lyon 1, Laboratoire de Chimie, F69342, Lyon, France
First published on 9th November 2020
Abstract
Optical birefringence in polymeric films containing azo-chromophores is an important feature related to the development of several technologies such as electro-optic modulators, optical switching, and optical gates, to cite a few. Therefore, it is essential to understand the main underlying mechanisms describing dynamic switching. In this context, we have investigated the optical birefringence performance of a guest–host film produced from a poly(methyl methacrylate) (PMMA) matrix containing a V-shaped azo-chromophore, which exhibited a larger optical response in comparison to the linear chromophores. The optical birefringence was induced by a linearly polarized diode laser (532 nm, writing laser), while a low-intensity HeNe (632.8 nm) laser and a tungsten-halogen lamp are employed, respectively, to monitor the optical storage and the absorption change during the photoinduced birefringence. Our results pointed out that the guest–host film presents maximum residual optical memory at around 50% and local optical birefringence at around 3.3 × 10−4 in the low concentration and intensity regimes. The high optical birefringence obtained in guest–host films was attributed to the considerable photoisomerization quantum yield in the solid-state (0.15 ± 0.02 for 532 nm). Besides, we have shown that the switching mechanism is driven by angular hole-burning during the first seconds after excitation, and, subsequently, molecular reorientation quickly rises, dominating the photochemical process. The latter mechanism is highly efficient in converting cis to trans molecules (100%), which is responsible for the high residual optical memory obtained. In order to better understand the isomerization mechanism of the azo-chromophore/PMMA film, we performed quantum chemical calculations within the DFT framework. The electronic transitions of the azo-chromophore isomers were determined using the TD-DFT method and potential energy curves (PECs) were constructed to investigate the possibility of the thermal-isomerization process of the V-shaped azo-chromophore through both rotation and inversion mechanisms. For both mechanisms, the amplitude of the energy barrier and activation energy for thermal isomerization are determined and the results are discussed.
1. Introduction
Due to their ultrafast and efficient photoisomerization process, azo-chromophores have been widely studied for the development of several photonic devices such as surface-relief gratings, nanodevices for electro-optical modulators, all-optical switching, micro-resonators, logic gates, 3D optical storage and so on.1–20 Moreover, azo-chromophores have presented high nonlinear optical responses such as two-photon absorption, second harmonic generation, and first-order hyperpolarizability.21–24Azoaromatic compounds can be found in two configurations, trans and cis isomers, in which the cis is more unstable due to closer aromatic rings, causing a stronger electronic repulsion. The switching mechanism (trans–cis and cis–trans) can be triggered by light from UV-visible to near-infrared region, and it is called photoisomerization. This photochemical process plays a central role in the photoinduced optical birefringence in polymers containing azo-chromophores. According to ref. 25, such a goal is achieved due to two main mechanisms. The first one is called the angular hole burning (AHB), in which the light isomerizes chromophores initially in the trans configuration, having an electric dipole moment component projected on the light polarization. Subsequently, there is relaxation from cis to trans configuration caused by molecular reorientation (MRO),25 and when there is no excitation arises randomly. Thus, combining these two mechanisms, for a linearly polarized excitation, a set of several trans–cis–trans cycles tends to align the chromophores perpendicularly to the light polarization because they are no longer isomerized by the excitation beam.
In general, to obtain an efficient device based on optical switching in azo-chromophores, four different parameters are essential: (i) high electronic transition rate (related to the molar absorptivity), (ii) high photoisomerization quantum yield, (iii) a steady-state relative abundance of trans and cis isomers at room temperature and (iv) the reproducibility of photochemical switching over time.1,26,27 Hence, these parameters need to be available.
In the last decades, the linear azo-chromophore dyes such as the disperse red (DR) family have been widely studied for optical storage applications. However, this class of organic molecules presents low optical birefringence and residual optical memory due to the small photoisomerization quantum yield and optical absorption.28–30 Otherwise, azo-chromophores with branched structures such as V-shaped, Y-shaped, and multi-branched (dendrimers) have emerged as an alternative synthesis route to tune and enhance the optical response of organic materials.31,32 For example, ref. 33 and 34 have shown that the V-shaped molecules may present higher linear and nonlinear optical responses than linear molecules. In this context, we have investigated optical storage performance based on photoinduced birefringence of guest–host films containing V-shaped azo-chromophores in the poly(methyl methacrylate) (PMMA) matrix. The molecular structure of the V-shaped azo-chromophore is illustrated in Fig. 1(a).
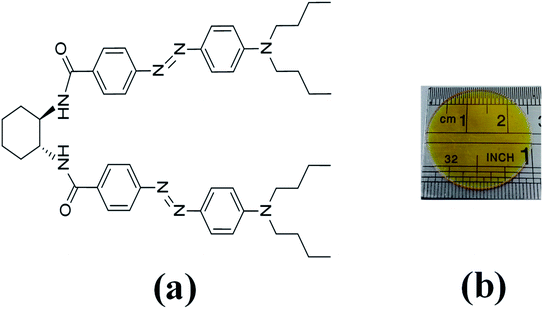 | ||
| Fig. 1 (a) Molecular structure of V-shaped azo-chromophore. (b) V-shape azo-chromophore/PMMA guest–host film. | ||
This study aims to understand the underlying mechanism that rules the high performance of optical birefringence obtained in this present work. For that, we have performed several experiments in which we observed the formation and relaxation times and residual optical memory for optical birefringence as a function of the power laser. The ground-state transient absorption also was monitored to aid understanding of the photoisomerization process. These results were explained based on the photoisomerization quantum yield and the AHB and MRO contributions obtained for the switching mechanism based on the Kawabe et al.29 approach. Moreover, we have studied the nature of the isomerization mechanism for the V-shaped azo-chromophore by employing quantum chemical calculations.
2. Experimental
We have studied two films with different dye concentrations. The films were prepared from a mixture of PMMA/chloroform solution (160 mg ml−1) with a solution of 2.0 mg ml−1 (1.25 w/w%, Film 1) or 0.09 mg ml−1 (0.056 w/w%, Film 2, see Fig. 1(b)) of azo-chromophore/chloroform. The azo-chromophore/PMMA solution (400 μl) was cast onto a circular glass substrate (diameter of 2.54 cm). The glass substrate was placed on a Petri plate and left in a chloroform-rich environment. The films were left to dry slowly at room temperature for 6 hours. Details about the synthesis of the azo-chromophore can be found in ref. 32. The PMMA (average Mw ∼ 120.000, Tg = 105 °C (midpoint)) was purchased from Sigma-Aldrich. The film thickness was measured from optical microscopy, according to ref. 35, and values 120 ± 15 μm were found.The first experiment performed was to measure the induced optical birefringence. In this experiment, the optical birefringence is induced by a cw diode laser (writing laser) at 532 nm with vertical polarization (0.2–10 mW). For the reading laser, we employed a low-intensity HeNe laser (<0.1 mW, at 632.8 nm) with a polarization angle of 45° with respect to the polarization of the writing beam. The reading laser passes through the sample, and by a crossed polarizer (−45°) positioned after the sample that acts as an analyzer. The writing laser induces birefringence such that a fraction of the reading laser beam passes through the analyzer, and it is detected by the silicon photodetector. Thus, the reading laser transmittance is used to monitor photoinduced birefringence over time, which requires a precise superposition of both beams in the sample. The diameter of the reading (green laser and white-light) and writing (HeNe) laser were of 2 mm and 3 mm, respectively, which were measured through the knife-edge technique. In the second experiment, we have changed the reading laser by a stabilized tungsten-halogen lamp and the photodetector by an optical fiber coupled to the spectrometer to measure in real-time the absorption change during the photoinduced birefringence. Such a procedure was performed for the white-light with parallel and perpendicular polarization with respect to the writing laser. In both experiments, we have used a shutter to switch on and off the writing laser. The experiments were automatically controlled by dedicated software. In all measurements, the wait time for the formation and relaxation of the optical birefringence was of 200 s and 100 s, respectively.
3. Theoretical calculations
Quantum chemical (QC) calculations were performed using Gaussian 09 package.36 All QC calculations were conducted at the density functional theory (DFT) level37,38 using the hybrid B3LYP functional39,40 and the 6-31G(d,p) basis set for H and C atoms and 6-31+G(d,p) basis set for N and O atoms. The geometry optimization calculations were performed with the molecule isolated (gas-phase) and in the CHCl3 solvent. In the solvated case, the self-consistent reaction field (SCRF) method based on the polarizable continuum model using the integral equation formalism variant (IEF-PCM),41 as implemented in Gaussian 09 package, was employed. The geometry optimization calculations were performed free of constraints.We also have calculated the ground-state potential energy curves (PEC) starting from either the trans or cis optimized geometry to investigate the thermal isomerization process of V-shaped azo-chromophore. By constraining the C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C dihedral angle or one of the C–N
N–C dihedral angle or one of the C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond angles, while optimizing all the other structural parameters, the rotation and inversion mechanisms of the isomerization were respectively investigated. The constrained angle was incremented in 10° steps, between the cis and trans isomer structures, and the energy of the optimized structure with zero-point energy corrections obtained at each point.
N bond angles, while optimizing all the other structural parameters, the rotation and inversion mechanisms of the isomerization were respectively investigated. The constrained angle was incremented in 10° steps, between the cis and trans isomer structures, and the energy of the optimized structure with zero-point energy corrections obtained at each point.
The energy barrier of the thermal trans–cis isomerization process was computed as the difference between the DFT energies with zero-point energy corrections of the trans isomer and the one of the transition state (TS). Moreover, the activation energy (Ea) of the kinetics of the thermal cis–trans isomerization was computed as the difference between the DFT energies with zero-point energy corrections of the cis isomer and the one of the transition state (TS). The nature of the two isomers stationary points and the transition state were confirmed by vibrational frequency analysis.
Time-Dependent Density Functional Theory (TD-DFT)42 was employed for computing the UV/vis spectra of the V-shaped azo-chromophore in gas-phase and CHCl3 solvent. Indeed, TD-DFT is often found robust and efficient for evaluating the low-lying excited spectra of organic and inorganic conjugated molecules and has been the subject of numerous applications aiming at providing a rationalization of experimental absorption spectra. In addition, the most appealing characteristic of TD-DFT is its ability to produce at a relatively small computational cost accurate electronic transition energies and intensities. The ten singlet lowest-energy of the two isomers of V-shaped azo-chromophore were determined and using the eight lowest-energy ones their absorption spectrum was simulated by the superposition of individual Lorentzian lines with a full width at half-maximum (FWHM) of 0.40 eV.
4. Results and discussions
The ground-state absorption spectrum for the V-shaped azo-chromophores/PMMA in solution (solid line) and film (dashed line) is shown in Fig. 2(a). As noted, for both solution and film forms, the azo-chromophore presents a wide absorption band located at 448 nm, which is related to the π–π* transition. It is also observed that the film is completely transparent for the reading laser wavelength (632.8 nm). Details about the electronic and optical features for this molecule can be found in ref. 32.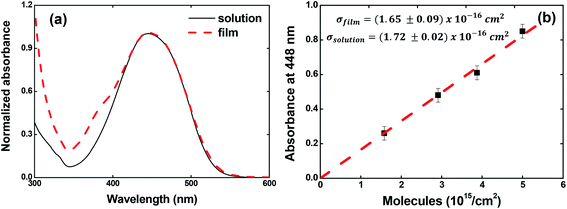 | ||
| Fig. 2 (a) Absorption spectrum for V-shaped azo-chromophores/PMMA in chloroform solution (solid line) and guest–host film (dash line). (b) Absorbance at 448 nm as a function of the concentration. | ||
In Fig. 2(b), we illustrated the results obtained for the calculations of the absorption cross-section (or molar absorptivity) for the guest–host films, which is very important to calculate the photoisomerization quantum yield. For that, we measured the absorption spectrum for four films containing different concentrations of azo-chromophores. The absorption spectrum for the films containing different chromophores concentrations can be found in Fig. SI.1 (see ESI).† Our results pointed out that the absorption cross-section value to the film is the same observed in solution within the experimental error (σfilm (448 nm) = (1.65 ± 0.09) × 10−16 cm2 and σsolution (448 nm) = (1.72 ± 0.02) × 10−16 cm2 or equivalently ε (448 nm) = 4.31 × 104 M−1 cm−1). These results confirm the high optical quality of the guest–host films.
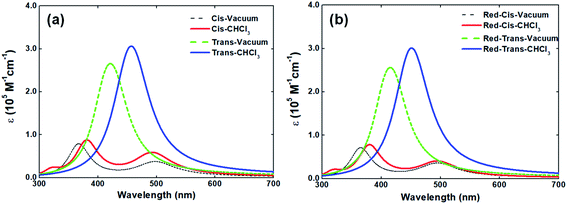
In solid-state, the V-shaped azo-chromophore exhibits a shoulder at 380 nm as compared to the solution. In order to gain a deeper understanding of the azo-chromophore/PMMA film optical features, we have performed quantum chemical calculations within the DFT framework. The simulated absorption spectrum of the V-shaped molecule in gas-phase and CHCl3 is presented in Fig. 3(a). It is worth mentioning that the implicit solvation PCM, as implemented in the Gaussian package, adopts a dielectric constant (or refractive index) for chloroform solvent very similar to the one of the PMMA matrix. Moreover, the absorption spectrum of a reduced version of V-shaped azo-chromophore was also simulated. Such a reduced version was obtained by substituting the four saturated chains of the molecules to ethyl groups. Since the main role of such chains is to increase the solubility of the molecule, being in principle secondary their contribution for the V-shaped electronic structure, it was expected that the effects of such substitutions on the absorption spectrum would be small. The simulated absorption spectra of the reduced V-shaped azo-chromophore molecule in gas-phase and CHCl3 are presented in Fig. 3(b) and, as it was expected, the effects of the substitutions on the absorption spectrum were confirmed to be small.
From Fig. 3, it is observed that the simulated absorption spectrum of trans-isomer presents a single peak, centered at 460 nm. This feature is in agreement with the experimental absorption spectrum of trans-isomer, in which the absorption band peak is located at 448 nm. However, the results of the TD-DFT/PCM calculations point out that such absorption band should be ascribed to two electronic transitions of similar intensities (f = 1.381 and f = 1.384), separated by only 0.07 eV in energy, and both described by the HOMO−1 → LUMO and HOMO → LUMO+1 excitations. It is also observed that the simulated absorption spectrum of trans-isomer has a tail that extends to the red region (up to 600 nm). Such a feature is not observed in the experimental spectrum of the molecule in solution, which after 560 nm no longer shows any absorption. Such divergence from the theoretical description in relation to experimental observation may be related to the choice adopted in this work, for the sake of simplicity, of adopting a single Lorentzian linewidth value (0.40 eV) for all electronic transitions taken into consideration to simulate the spectrum.
As can be observed in Fig. 3, the absorption spectrum of cis-isomer presents two peaks, lowest-energy one located at 500 nm and the higher-energy one around 360–380 nm. In CHCl3 solvent, the higher-energy peak of both the isomers and its reduced version is localized at 380 nm. Such observation sheds light on the issue of the shoulder observed in the absorption spectrum of the molecule in solid-state and confirms that such a shoulder should be ascribed to the contribution of the cis-isomer for the final absorption spectrum of the molecule in solid-state. The experimental absorption spectrum of V-shaped azo-chromophore in solution also shows some absorption in the region energetically above 350 nm (ultraviolet region). However, because only the eight lowest-energy transitions of the isomers were taken into account to simulate the absorption spectrum, such experimental information is not reproduced by the simulated spectra here presented.
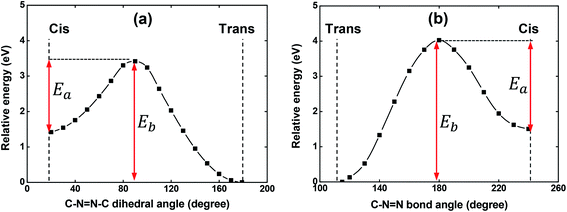
As it is well-known, the isomerization process of azobenzene chromophores in rigid media depends strongly on the local environment and free volume distribution around the chromophores.43–45 Thus, the appearance of a more significant contribution of the cis-isomers to the absorption in solid-state could, in principle, be understood in this way. Since a shoulder in the film absorption spectrum is observed just after the casting procedure onto a glass substrate, i.e., before the film to be irradiated with laser light, the possibility of the isomerization process having a thermal origin was theoretically investigated. Potential energy curves (PECs) were constructed starting from either the trans or cis optimized geometry to investigate the possibility of the thermal-isomerization process through both the rotation and inversion mechanisms. These computations were performed with the V-shaped molecule in gas-phase.
The PECs obtained for the rotation and inversion mechanisms are shown in Fig. 4(a) and (b), respectively. For both mechanisms, the amplitude of the energy barrier (Eb) of the thermal trans–cis isomerization and the activation energy (Ea) for the thermal cis–trans isomerization are illustrated in Fig. 4. As can be observed, Eb = 3.42 eV (362 nm) and Eb = 4.02 eV (308 nm) for the mechanism of the rotation and inversion, respectively. For such high energies, the thermal contribution for the isomerization process of the V-shaped azo-chromophore can be basically discarded. Therefore, we are led to conclude that the observed isomerization process is photo-induced by the laboratory ambient light.
Concerting the activation energy of the thermal cis–trans isomerization kinetics, the values Ea = 2.00 eV and Ea = 2.50 eV were obtained for the mechanism of the rotation and inversion, respectively. Such values indicated that from the energetic point of view, the thermal cis–trans isomerization process would happen more easily through the rotation mechanism. However, some studies on the literature evidence that the rotation mechanism requires more space (free volume) to isomerize, while the inversion mechanism takes up less space when transitioning between the isomers.43,46 Thus, for the results obtained here, a difference of only 0.50 eV between the activation energies, we believe that structural restrictions imposed by the polymeric matrix significantly hinder the isomerization process from evolving through the rotational pathway and, therefore, it is not possible to point out a predominant mechanism in the thermal cis–trans isomerization kinetics. Since the photoisomerization pathways were elucidated, we have performed photoinduced birefringence measurements.
Fig. 5 depicts the optical birefringence curves as a function of the laser power for Film 1 (Fig. 5(a)) and Film 2 (Fig. 5(b)). To calculate the photoinduced optical birefringence, we have used the following equation (valid for thick sample):
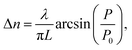 | (1) |
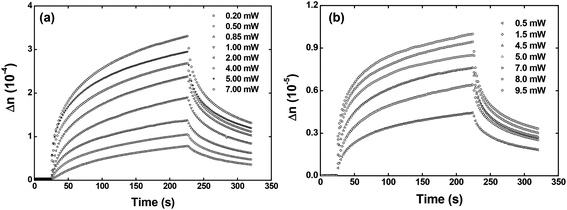 | ||
| Fig. 5 Optical birefringence curves as a function of the writing laser power for the (a) Film 1 and (b) Film 2. | ||
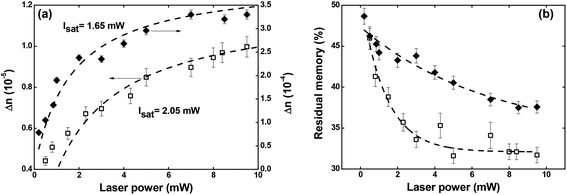 | ||
| Fig. 6 (a) Maximum optical birefringence and (b) residual memory as a function of the writing laser power. Full diamonds and empty squares correspond, respectively, to Film 1 and Film 2. | ||
Regarding the residual optical memory (Fig. 6(b)), we have observed a similar behavior, i.e., Film 1 presents a higher performance. Besides, a residual optical memory decrease is noticed as the laser power increase. It happens because of the higher laser power to generate larger thermal agitation, which increases the angular diffusion effect that tends to restore the isotropic thermodynamic equilibrium.25 It is important to emphasize that in guest–host films, the chromophores are not covalently bonded to the polymer, and, therefore, there is great freedom for angular diffusion. In such a system, the van der Waals forces are predominantly responsible for the interaction between the chromophores and the host matrix.49
Concerning the temporal evolution of the optical birefringence mechanism, we have employed the bi-exponential model to obtain the formation and relaxation times.50 Our results show that the slow (τ1 and τ3) and fast (τ2 and τ4) characteristic times for the formation and relaxation optical birefringence decrease as a function of the laser power (see Fig. SI.2 of the ESI†). Such behavior is characteristic of optical storage in guest–host films.51 Moreover, all the times found are higher for Film 1 due to the higher chromophores density, which decreases the free volume to occur trans → cis → trans photoisomerization cycle (details on the formation and relaxation times can be found in ESI†).
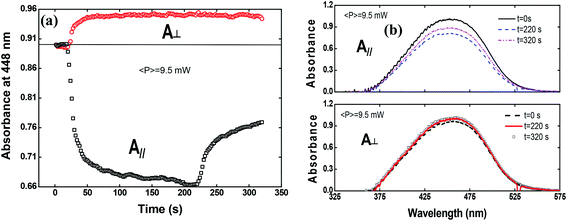
To shed more light on the photoinduced birefringence mechanism, we have analyzed the absorption change for the guest–host films during the formation of optical birefringence. For this study, we have measured the absorption change only for Film 2, because Film 1 presents a very high absorption. This experiment was performed in two configurations using the white light with parallel and perpendicular polarization to the writing laser. Fig. 7(a) shows the absorption change at 448 nm (related to the peak of π–π* transition) as a function of the time for the perpendicular (circles) and parallel (squares) polarization in respect to the writing laser.
The absorption spectra for the three different times along the temporal window of the experiment (at the first reading, when the writing laser is switched off and at the last reading) are illustrated in Fig. 7(b). For the white light polarization parallel to the writing laser, we observed a great reduction in the absorption during the first 15 seconds after the excitation. This behavior can be explained by the increase of chromophores aligned perpendicularly to the excitation laser, and, consequently, to the white light polarization, decreasing its absorption. After switching off the writing laser, the absorbance increase by only 45%. On the other hand, when the white light is perpendicularly polarized to the writing laser, the absorbance increases quickly and maintain such value during all time even after removing the excitation. Now, due to the AHB and MRO mechanisms, we have the polarization of white light in the same direction of the chromophores alignment. Thus, the projection of the radiation electric field is maximum on the dipole moment of the chromophores and, therefore, we observed an increase in the absorption. These two interesting outcomes suggested that the main photoinduced birefringence mechanism is related to the molecular reorientation. The absorption change for perpendicularly polarized white light is 1/3 compared to the parallel polarization. Therefore, we observed that, at the end of the experiment (t = 320 s), the average absorption (Ā = (A∥(t) + 2A⊥(t))/3, as defined in ref. 25) to the π–π* transition returns to the initial value (Ai = 0.89), indicating that there was a complete conversion of the cis to trans isomers, corroborating the high contribution of the MRO mechanism. To stress such a result, in Fig. 8, we show the ground-state transient absorption spectra for the (Fig. 8(a)) perpendicular and (Fig. 8(b)) parallel polarization and (Fig. 8(c)) average absorption. As can be seen in Fig. 8, the behavior previously mentioned happens for all wavelengths (380–530 nm). Thus, we can conclude that, indeed, the MRO mechanism is responsible for returning the cis to trans molecules with 100% efficiency.
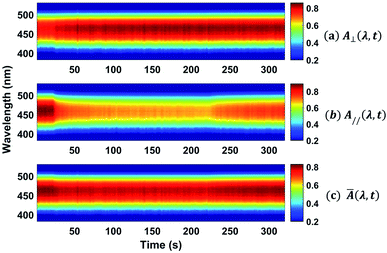 | ||
| Fig. 8 Colormap representing the ground-state transient absorption for the (a) perpendicular and (b) parallel polarization and the (c) average absorption. | ||
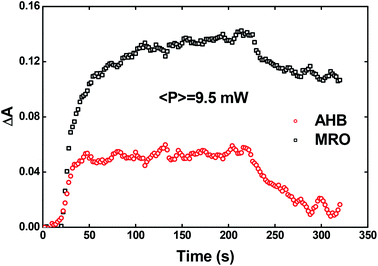
Recently, Kawabe et al.29 have formulated a simple model to discriminate the contributions of the AHB due to photoisomerization and MRO on the optical switching mechanism for DR1 in PMMA. According to that model, the contributions of the AHB and MRO mechanism can be evaluated as:
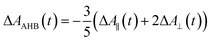 | (2) |
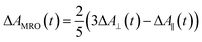 | (3) |
As noted, after switching on the writing laser during the first seconds, the AHB dominates the process. However, after that, a quick rise of MRO mechanism achieved values 250% higher than the AHB for 9.5 mW. Similar behavior also was observed for lower laser power. When the results are compared to ones published in ref. 50 for PMMA/DR1, we observed that the dominant mechanism for the chromophores DR1 and V-shaped (this work) is distinct. For instance, we found the MRO, while the AHB was the dominant mechanism observed by them. This can explain the great difference obtained for residual optical memory as we compared the V-shaped molecule with the DR family.
We have also calculated the quantum yield of photoisomerization (trans–cis) for the V-shaped chromophores. For that, we applied the model described in detail in ref. 52 for sample in film form that describes the absorbance change over time due to the trans to cis photoisomerization. Such a model can be given by:
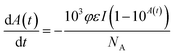 | (4) |
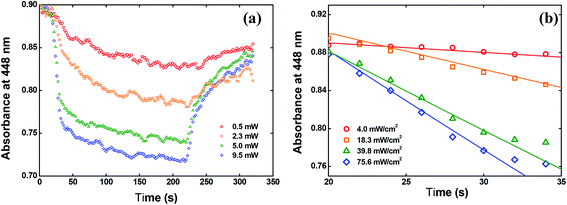 | ||
| Fig. 10 (a) Absorbance change at 448 nm over time. (b) Fitting the data by using the eqn (4). | ||
In Fig. 10(b), we showed the same results but only for the first 15 seconds after switching on the writing laser, because in this time interval the trans to cis isomerization occurs strongly. The solid lines in Fig. 10(b) are the fitting obtained by solving the eqn (4) numerically. From these fitting, we found φ = 0.15 ± 0.02 at 532 nm for the solid-state sample. This value is almost twice the value reported for the red disperse family, for example.29
5. Final remarks
We have investigated the photoinduced birefringence in a V-shaped azo-chromophore/PMMA guest–host film. Our result pointed out a maximum optical birefringence of 3.3 × 10−4 along with the large residual optical memory (50%) in the low-concentration regime. The high performance for the optical birefringence observed in guest–host films can be explained as follows. The significant photoisomerization quantum yield (trans–cis) found for this material in solid-state (15%) is responsible for the high optical birefringence, which is preferentially related to the AHB mechanism. On the other hand, the large residual optical memory can be attributed to cis–trans MRO, in which our results have shown to be highly efficient (100%). Moreover, we have employed a simple model recently developed that corroborated these results, indicating that the MRO mechanism dominates the optical birefringence. Employing TD-DFT calculations, the contribution of the cis-isomers of the V-shaped azo-chromophore to the absorption spectrum of the guest–host film was confirmed. Moreover, potential energy curves (PECs) were constructed to investigate the possibility of the isomerization occur through thermal processes. Based on the values obtained for the energy barriers of the thermal trans–cis isomerization, Eb = 3.42 eV and Eb = 4.02 eV, for the mechanism of the rotation and inversion, respectively, we were led to conclude that the observed isomerization process is basically photoinduced. Finally, our outcomes indicate the V-shaped azo-chromophore as an interesting material for the development of photonic devices based on optical birefringence.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from FAPEMIG (Fundação de Amparo à Pesquisa do Estado de Minas Gerais, APQ-01469-18), CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico, 425180/2018-2), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) are acknowledged.References
- S. Crespi, N. A. Simeth and B. Koinig, Nat. Rev. Chem., 2019, 3, 133–146 CrossRef CAS.
- R. Petruskevicius, D. Urbonas, M. Gabalis, A. Balcytis, G. Seniutinas, R. Tomasiunas, V. Getautis and IEEE, in 2013 15th International Conference on Transparent Optical Networks, 2013 Search PubMed.
- P. Gopalan, H. E. Katz, D. J. McGee, C. Erben, T. Zielinski, D. Bousquet, D. Muller, J. Grazul and Y. Olsson, J. Am. Chem. Soc., 2004, 126, 1741–1747 CrossRef CAS.
- M. R. Cardoso, U. M. Neves, L. Misoguti, Z. H. Ye, X. R. Bu and C. R. Mendonca, Opt. Mater., 2006, 28, 1118–1122 CrossRef CAS.
- S. Hvilsted, C. Sanchez and R. Alcala, J. Mater. Chem., 2009, 19, 6641–6648 RSC.
- A. H. Gelebart, D. J. Mulder, M. Varga, A. Konya, G. Vantomme, E. W. Meijer, R. L. B. Selinger and D. J. Broer, Nature, 2017, 546, 632–636 CrossRef CAS.
- W. M. Gibbons, P. J. Shannon, S. T. Sun and B. J. Swetlin, Nature, 1991, 351, 49–50 CrossRef CAS.
- C. Jones and S. Day, Nature, 1991, 351, 15 CrossRef.
- M. S. Ho, A. Natansohn and P. Rochon, Macromolecules, 1996, 29, 44–49 CrossRef CAS.
- X. Meng, A. Natansohn and P. Rochon, Polymer, 1997, 38, 2677–2682 CrossRef CAS.
- J. C. Liang, Opt. Lett., 2010, 35, 4081–4083 CrossRef CAS.
- D. S. dos Santos, A. Bassi, J. J. Rodrigues, L. Misoguti, O. N. Oliveira and C. R. Mendonca, Biomacromolecules, 2003, 4, 1502–1505 CrossRef CAS.
- T. X. Gao, Y. J. Xue, Z. Zhang and W. X. Que, Opt. Express, 2018, 26, 4309–4317 CrossRef CAS.
- M. Poprawa-Smoluch, J. Baggerman, H. Zhang, H. P. A. Maas, L. De Cola and A. M. Brouwer, J. Phys. Chem. A, 2006, 110, 11926–11937 CrossRef CAS.
- T. Chida and Y. Kawabe, Opt. Mater., 2014, 36, 778–781 CrossRef CAS.
- L. Mazaheri, R. G. Sabat, O. Lebel and J. M. Nunzi, Opt. Mater., 2016, 62, 378–391 CrossRef CAS.
- F. Pirani, A. Angelini, F. Frascella, R. Rizzo, S. Ricciardi and E. Descrovi, Sci. Rep., 2016, 6, 31702 CrossRef CAS.
- A. Kovach, J. H. He, P. J. G. Saris, D. Y. Chen and A. M. Armani, AIP Adv., 2020, 10, 045117 CrossRef CAS.
- M. Sailer, R. Fernandez, X. Y. Lu and C. J. Barrett, Phys. Chem. Chem. Phys., 2013, 15, 19985–19989 RSC.
- J. T. Huang, S. Beckemper, S. Wu, J. Shen, Q. J. Zhang, K. Y. Wang and A. Gillner, Phys. Chem. Chem. Phys., 2011, 13, 16150–16158 RSC.
- B. Kulyk, D. Guichaoua, A. Ayadi, A. El-Ghayoury and B. Sahraoui, Dyes Pigm., 2017, 145, 256–262 CrossRef CAS.
- L. De Boni, L. Misoguti, S. C. Zilio and C. R. Mendonca, ChemPhysChem, 2005, 6, 1121–1125 CrossRef CAS.
- U. M. Neves, L. De Boni, Z. H. Ye, X. R. Bu and C. R. Mendonca, Chem. Phys. Lett., 2007, 441, 221–225 CrossRef CAS.
- B. Jedrzejewska, M. Gordel, J. Szeremeta, M. A. Kaczorowska, M. Jozefowicz and M. Samoc, Dyes Pigm., 2016, 132, 237–247 CrossRef CAS.
- P. A. Blanche, P. C. Lemaire, M. Dumont and M. Fischer, Opt. Lett., 1999, 24, 1349–1351 CrossRef CAS.
- A. R. M. Timoteo, J. H. F. Ribeiro, P. A. Ribeiro and M. Raposo, Opt. Mater., 2016, 51, 18–23 CrossRef CAS.
- A. Stoilova, A. Georgiev, L. Nedelchev, D. Nazarova and D. Dimov, Opt. Mater., 2019, 87, 16–23 CrossRef CAS.
- C. R. Mendonca, U. M. Neves, L. De Boni, A. A. Andrade, D. S. dos Santos, F. J. Pavinatto, S. C. Zilio, L. Misoguti and O. N. Oliveira, Opt. Commun., 2007, 273, 435–440 CrossRef CAS.
- Y. Kawabe and K. Okoshi, Opt. Mater. Express, 2018, 8, 332–341 CrossRef CAS.
- A. Goulet-Hanssens, T. C. Corkery, A. Priimagi and C. J. Barrett, J. Mater. Chem. C, 2014, 2, 7505–7512 RSC.
- D. M. Junge and D. V. McGrath, J. Am. Chem. Soc., 1999, 121, 4912–4913 CrossRef CAS.
- M. G. Vivas, D. L. Silva, L. De Boni, Y. Bretonniere, C. Andraud, F. Laibe-Darbour, J. C. Mulatier, R. Zalesny, W. Bartkowiak, S. Canuto and C. R. Mendonca, J. Phys. Chem. B, 2012, 116, 14677–14688 CrossRef CAS.
- R. D. Fonseca, M. G. Vivas, D. L. Silva, G. Eucat, Y. Bretonniere, C. Andraud, L. De Boni and C. R. Mendonca, J. Phys. Chem. C, 2018, 122, 1770–1778 CrossRef CAS.
- R. D. Fonseca, M. G. Vivas, D. L. Silva, G. Eucat, Y. Bretonniere, C. Andraud, C. R. Mendonca and L. De Boni, J. Phys. Chem. Lett., 2019, 10, 2214–2219 CrossRef CAS.
- R. Bakke and P. Q. Olsson, J. Microbiol. Methods, 1986, 5, 93–98 CrossRef.
- M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, G. Cheeseman, J. R. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, R. Staroverov, V. N. Kobayashi, K. Normand, J. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, S. Dannenberg, J. J. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- W. K. P. Hohenberg, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- J. Tomasi, B. Mennucci and E. Cances, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- M. S. Ho, A. Natansohn and P. Rochon, Macromolecules, 1995, 28, 6124–6127 CrossRef CAS.
- C. H. Wang and R. G. Weiss, Macromolecules, 2003, 36, 3833–3840 CrossRef CAS.
- M. Ueda, H. B. Kim, T. Ikeda and K. Ichimura, Chem. Mater., 1992, 4, 1229–1233 CrossRef CAS.
- S. Shinkai, Y. Kusano, K. Shigematsu and O. Manabe, Chem. Lett., 1980, 1303–1306 CrossRef CAS.
- I. G. Marino, D. Bersani and P. P. Lottici, Opt. Mater., 2000, 15, 175–180 CrossRef CAS.
- A. Natansohn, P. Rochon, C. Barrett and A. Hay, Chem. Mater., 1995, 7, 1612–1615 CrossRef CAS.
- Y. Shuto, M. Amano and T. Kaino, Electro-optical light modulation in novel azo-dye-substituted poled polymers, 1991 Search PubMed.
- S. Elhani, I. Maouli, S. Refki, M. Halim, S. Hayashi and Z. Sekkat, J. Opt., 2019, 21, 115401 CrossRef CAS.
- S. Janssens, R. Breukers, A. Swanson and S. Raymond, J. Appl. Phys., 2017, 122, 023107 CrossRef.
- K. Stranius and K. Borjesson, Sci. Rep., 2017, 7, 41145 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08379h |
| This journal is © The Royal Society of Chemistry 2020 |