Open Access Article
Open Access ArticleSemi-empirical and ab initio calculations for crystals under pressure at fixed temperatures: the case of guanidinium perchlorate
Dmitry V. Korabel'nikov * and
Yuriy N. Zhuravlev
* and
Yuriy N. Zhuravlev
Institute of Fundamental Sciences, Kemerovo State University, Krasnaya 6, 650043, Kemerovo, Russia. E-mail: dkorabelnikov@yandex.ru
First published on 19th November 2020
Abstract
A simple semi-empirical approach is proposed to calculate structure and properties of crystals under pressure at fixed temperatures. The computed semi-empirical pressure dependencies for guanidinium perchlorate are in good agreement with available experimental data. Ab initio results within quasi-harmonic approximation for guanidinium perchlorate are also presented.
1. Introduction
The effect of external factors, such as pressure (P) and temperature (T), on crystal structure and properties has been of great interest in recent years.1–10 Studies of the behavior of solids under pressure are very promising as it is one of the effective methods for studying intermolecular interactions.11Quantum chemical ab initio computations within density functional theory (DFT) allow modelling crystal structure and properties, which are in good agreement with experimental results.12 Moreover, computer modeling is used to predict and design new materials.13 Standard ab initio calculations correspond to a static lattice (ground state) and do not take into account thermal effects caused by atomic thermal vibrations. Anharmonicity in interactions and thermal expansion for crystals can be considered within so-called quasi-harmonic approximation (QHA),14 which takes into account dependence of harmonic phonon frequencies ω on the volume V. Dispersion-corrected quasi-harmonic ab initio computations perform well in describing thermal properties of molecular crystals.2 The main problem within quasi-harmonic ab initio calculations is to determine the phonon frequency distribution g(ω, V). This is due to the fact that phonon density of states calculations are very computationally demanding tasks. The relatively simple method is quasi-harmonic Debye–Einstein (DE) approximation.15
The crystal structure at ambient pressure is usually known from X-ray or neutron diffraction measurements. It's well known that there is “structure–properties” relationship.16 It's interesting to know how we can to account thermal expansion for structure of compressed crystal (thus, for its properties under pressure) based on simple standard ab initio calculations for static lattice and structural experimental data at ambient pressure. Therefore, it is significant to find simple semi-empirical approach to compute equation of state P (V, T) and its equivalent V (P, T).
Perchlorates have been widely used in explosive compositions, propellant mixtures and pyrotechnics. Guanidinium perchlorate (GP) is semi-organic nonlinear optical (NLO) and ferroelectric material.17,18 Ferroelectric materials are widely used in many applications.19 Besides, GP is quite attractive to be used in solid-state coolers and can provide temperature control.18 Guanidinium perchlorate is ionic-molecular oxyanionic crystal which has layered supramolecular structure with molecular organic guanidinium cations, C(NH2)3+, and molecular perchlorate anions, ClO4−. Under ambient conditions, it has trigonal structure (space group symmetry R3m).20 The experimental ambient lattice constants a and c for its hexagonal unit cell (with 3 formula units) are equal to 7.606 Å and 9.121 Å, respectively.20 Perchlorate anions in guanidinium perchlorate contain two nonequivalent oxygen atoms O1 and O2. The knowledge of the behavior of GP and similar supramolecular structures under external pressure is important both for fundamental and applied research.21,22 The pressure effect on the guanidinium perchlorate structure was experimentally studied using Raman spectroscopy and X-ray diffraction at room temperature.21,22 Strong anisotropy of GP linear compressibility was shown. GP is stable up to 4.5 GPa, after that it undergoes a phase transition. The GP structural data at various fixed temperatures (T ∼ 100–400 K) were studied in ref. 18. Thermal measurements for GP show that it undergoes a phase transition at T ∼450 K.18,23 The results of optical and nonlinear optical studies for GP were reported in ref. 17. As we know, data on pressure dependencies of structure at low temperatures (below room temperature), band gap, elastic constants and electron density topological properties were not reported for GP. In the present work we studied GP under pressure with account of thermal effects based on semi-empirical and ab initio calculations.
2. Computational details
Ab initio calculations were performed using CRYSTAL program.24 Basis sets of atomic orbitals25–28 and dispersion-corrected generalized-gradient PBE DFT functional29,30 were used in our calculations. Grimme's dispersion correction30 was used in order to include the long-range intermolecular interactions. Structural parameters for static lattice were calculated by geometry optimization (all atoms positions and cell lengths) in accordance with BFGS algorithm.31 Energy convergence was better than at 10−8 a.u. Chemical bond was studied based on Bader's quantum theory of atoms in molecules (QTAIM).32 Energies of hydrogen bonds were evaluated using potential energy density at bond critical points.33 The TOPOND code34 was used for QTAIM electron density topological analysis. We used quasi-harmonic DE approximation15 to include thermal effects based on ab initio calculations. Ab initio frequencies were computed using diagonalization of the mass-weighted Hessian matrix of second energy derivatives with respect to atomic displacements.24 Vinet universal equation of state35 (EOS) was fitted to pressure-volume data. Three parameters determine this EOS: equilibrium volume (V0), bulk modulus (B0) and its pressure derivative (∂B0/∂P).It's known36 that pressure can be expressed as P (V, T) = PST (V) + PTH (V, T), where PST (V) = −∂EST (V)/∂V is static pressure (EST (V) is ab initio static energy) and PTH (V, T) = −∂Fvib (V, T)/∂V is thermal pressure (Fvib (V, T) is vibrational part of the Helmholtz free energy). Within the framework of the quasi-harmonic approximation the thermal pressure PTH (V, T) can be expressed as 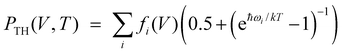 , where fi(V) = ħωiγi/V (ωi and γi are the frequency and Gruneisen's parameter of i-th vibrational mode, respectively).14 The functions fi (V) are equal to constants ħ·bi within the frequency linear approximation (ωi = ai − bi·V). Thermal pressure is weakly dependent on V and, therefore, PTH (V, T) ≈ PTH (T).37 So, volume-pressure dependencies at fixed temperatures T0 (isotherms P (V, T0)) can be obtained through shift of static pressure function PST (V) by PTH (T0). Thermal pressure PTH (T0) should correspond to equilibrium volume V0 at fixed temperature T0.
, where fi(V) = ħωiγi/V (ωi and γi are the frequency and Gruneisen's parameter of i-th vibrational mode, respectively).14 The functions fi (V) are equal to constants ħ·bi within the frequency linear approximation (ωi = ai − bi·V). Thermal pressure is weakly dependent on V and, therefore, PTH (V, T) ≈ PTH (T).37 So, volume-pressure dependencies at fixed temperatures T0 (isotherms P (V, T0)) can be obtained through shift of static pressure function PST (V) by PTH (T0). Thermal pressure PTH (T0) should correspond to equilibrium volume V0 at fixed temperature T0.
Ab initio thermal pressures were found based on ab initio calculations of frequencies ωi within quasi-harmonic approximation. In contrast to ab initio method, we used experimental equilibrium volumes in semi-empirical approach to find thermal pressures PTH without ab initio calculations of frequencies. In the present work we propose to set the equilibrium volumes V0 for isotherms P(V, T0) as equal to experimental ones V0 (T0)expt (Scheme 1). So, PTH (T0) = −PST (Vexpt0).
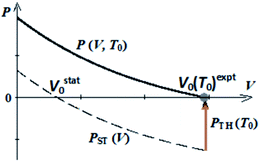 | ||
| Scheme 1 Pressure–volume dependencies for static lattice (PST (V)) and for crystal at fixed temperature (P (V, T0)) according to semi-empirical approach (V0 = V0 (T0)expt). | ||
Thermal pressure for guanidinium perchlorate at room temperature obtained in our work within semi-empirical approach (0.68 GPa) is comparable with its ab initio value (0.78 GPa).
3. Results and discussion
Fig. 1 presents our calculated semi-empirical and ab initio pressure dependencies of lattice parameters and volume for guanidinium perchlorate at T = 295 K (solid lines), 210 K (dashed lines), 100 K (dash-dotted lines) and at static lattice (dotted lines). Calculated equation of state parameters (V0, B0, ∂B0/∂P) for GP at different temperatures are presented in Table 1. Experimental data are given for T = 295 K.22 It can be seen that ab initio method within quasi-harmonic Debye–Einstein approximation overestimated structural parameters in comparison with experimental data. It should be noted that ab initio equilibrium volumes (V0) at room temperature are also overestimated (∼1%) for RDX and TATB crystals.2 More powerful and time-consuming ab initio methods need to be used for stricter account of anharmonicity effects in GP, RDX and TATB. On the other hand, the results obtained, using simple semi-empirical method, agree well with experiment (Fig. 1).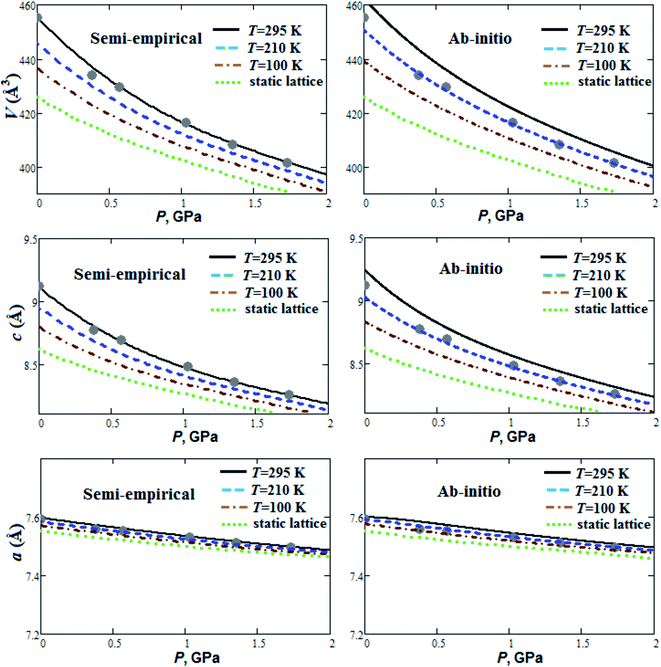 | ||
| Fig. 1 Calculated semi-empirical and ab initio pressure dependencies of lattice parameters and volume for guanidinium perchlorate at T = 295 K (solid lines), 210 K (dashed lines), 100 K (dash-dotted lines) and at static lattice (dotted lines). Experimental points correspond to T = 295 K.22 | ||
| Temperature | Method | V0 | B0 | ∂B0/∂P |
|---|---|---|---|---|
| T = 295 K | Expt.22 | 455 | 6.93 | 11.4 |
| Semi-empirical | 455 | 7.35 | 10.0 | |
| Ab initio | 462 | 7.43 | 8.83 | |
| T = 210 K | Semi-empirical | 446 | 9.14 | 9.51 |
| Ab initio | 451 | 9.10 | 8.66 | |
| T = 100 K | Semi-empirical | 437 | 11.1 | 9.06 |
| Ab initio | 439 | 11.2 | 8.49 | |
| Static lattice | Semi-empirical | 426 | 13.7 | 8.55 |
| Ab initio | 426 | 13.7 | 8.55 |
The GP compressibility along a-axis is much less than along c-axis (Fig. 1). So, there is strong compressibility anisotropy for GP. This can occur due to layered structure of GP with strong covalent and hydrogen bonds in ab plane (Fig. 3). GP is highly compressible material (Fig. 1) with relatively small bulk modulus ∼7 GPa at T = 295 K (Table 1), which is even smaller than room temperature bulk moduli for some molecular crystals reported in ref. 2. It is interesting to note that our calculated semi-empirical bulk moduli are in good agreement with ab initio moduli (Table 1). Fig. 1 demonstrates nonlinearity of pressure dependencies for c parameter and volume of GP. Such pressure behavior results in relatively high pressure derivative of B0 (Table 1). With temperature increase from 100 K up to 295 K equilibrium volume V0 increases by 4.1 and 5.2% within semi-empirical and ab initio approaches, respectively (Table 1). At the same time, this thermal volume expansion results in considerable decrease of B0 (∼33%). So, it is important to take into account thermal effects for behavior under pressure and mechanical properties of GP.
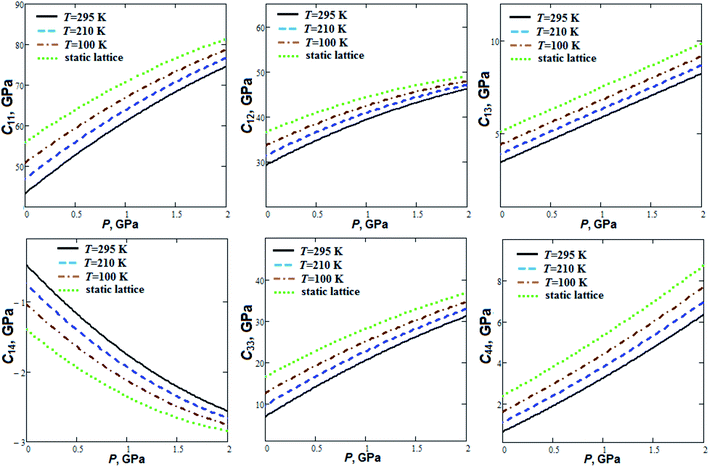
Pressure dependencies of GP elastic constants at fixed temperatures (Fig. 2) were computed according to quasi-static approach38 and semi-empirical volume–pressure–temperature dependencies.
The elastic stability conditions39 (the Born criteria) are fulfilled for GP. C11 elastic constant is considerably greater (∼4 to 6 times) than C33. This is due to the layered structure of GP (Fig. 3) with strong intralayer interactions (covalent and hydrogen bonds) in ab plane. C44 elastic constant has a relatively small value at room temperature (0.63 GPa). C11 and C12 elastic constants increase by 72 and 58% at room temperature whereas C13, C14, C33 and C44 increase by a factor of 1.4, 4.4, 3.5 and 9.1, respectively, when the pressure increases up to 2 GPa. On the other hand, elastic constants C11 and C12 at ambient pressure decrease by 15 and 13%, whereas C13, C14, C33 and C44 by 22, 54, 45 and 61%, respectively, when the temperature increases from T = 100 K up to T = 295 K.
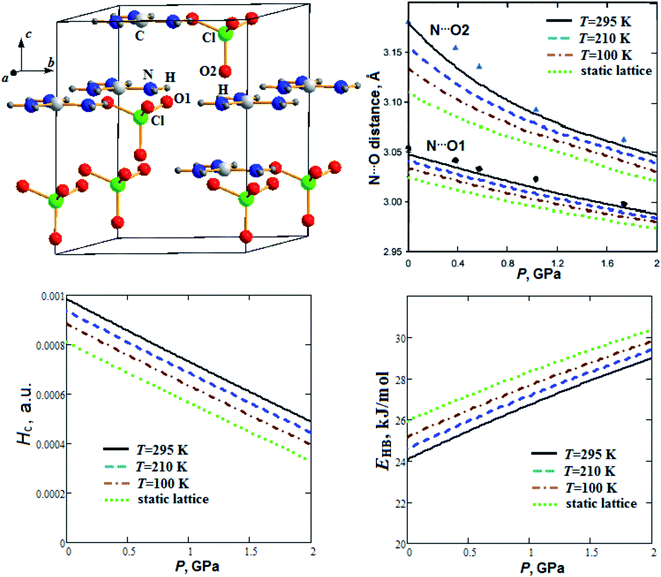 | ||
| Fig. 3 Calculated semi-empirical pressure dependencies of N⋯O distances, energy density Hc at H⋯O1 critical points and hydrogen bond energy EHB for guanidinium perchlorate at T = 295 K (solid lines), 210 K (dashed lines), 100 K (dash-dotted lines) and at static lattice (dotted lines). Experimental points and triangles correspond to T = 295 K.22 | ||
Fig. 3 presents our calculated semi-empirical pressure dependencies of N⋯O distances, energy density at hydrogen bond critical points (Hc) and hydrogen bond energy (EHB) for guanidinium perchlorate at T = 295 K (solid lines), 210 K (dashed lines), 100 K (dash-dotted lines) and at static lattice (dotted lines). Experimental points and triangles are given for T = 295 K.22 Fig. 3 reveals that interlayer N⋯O2 distance decreases with pressure more significantly than intralayer N⋯O1 distance, similar to c and a parameters, respectively (Fig. 1). It can also be seen that GP cooling down to T = 100 K leads to reduction of N⋯O2 distance by 1.5%.
The electron density topological analysis, in the framework of the QTAIM, is a powerful chemical bond study method.40 The condition for chemical bond formation is the presence of so-called bond critical point (BCP).32 Electron density (ρc) and energy density at the bond critical point (Hc) are important characteristics. Hc > 0 corresponds to non-covalent closed shell interactions (electrostatic or dispersion), while at Hc < 0 (ρc is stabilizing) the bond has a covalent component (covalent or partly covalent interactions).41 One of the superiority of Bader QTAIM approach is the possibility to reveal even weak bonding interatomic interactions and calculate their energies.42
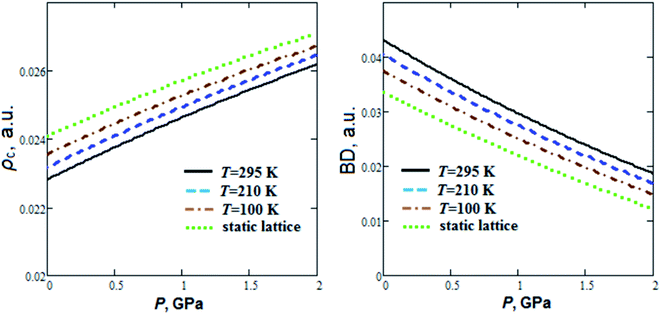
As can be seen from Fig. 3, energy density Hc nearly linearly decreases with pressure increase. At the same time hydrogen bond energy (EHB ∼ 24–26 kJ mol−1) increases by ∼20% when the pressure increases up to 2 GPa. EHB at ambient pressure decreases by 4.5% when the temperature increases from T = 100 K up to T = 295 K. Extrapolations for pressure dependencies of energy density give negative values of Hc at pressures more than 4.2, 3.8 and 3.5 GPa for 295 K, 210 K and 100 K, respectively. So, the GP hydrogen bonds at pressure ∼4 GPa become partially covalent in nature. Electrostatic and partially covalent nature of hydrogen bonds for other crystals and molecular complexes was studied earlier in ref. 43. It is interesting to note that GP at P ∼4 GPa undergoes a phase transition.21 The electron density at BCP (ρc ∼ 0.023 a.u.) increases by ∼15%, whereas bond degree parameter44 (BD = Hc/ρc) decreases ∼2 times as the pressure rises to 2 GPa (Fig. 4). On the other hand, when the temperature increases from T = 100 K up to T = 295 K, ρc at ambient pressure decreases and BD increases by 3.2% and 15%, respectively.
Our calculated Raman spectrum of GP for NH2 stretch modes in comparison with experimental spectrum21 is given in Fig. 5. It shows three maximums at 3371, 3419 and 3493 cm−1, which are in agreement with experimental ones within 2%. In general, blue or red shift can occur when hydrogen bond length decreases.45 Our calculated frequencies of NH2 stretch modes increase with pressure increase up to 2 GPa (blue shift ∼10 cm−1) in accordance with experimental data reported in ref. 21. As it was pointed out in ref. 21, this reflects the strengthening of hydrogen bonds in GP with increasing pressure. When the temperature increases from T = 100 K up to T = 295 K, our calculated frequencies ω of NH2 stretch modes at ambient pressure decreases by ∼2 cm−1 (Fig. 5).
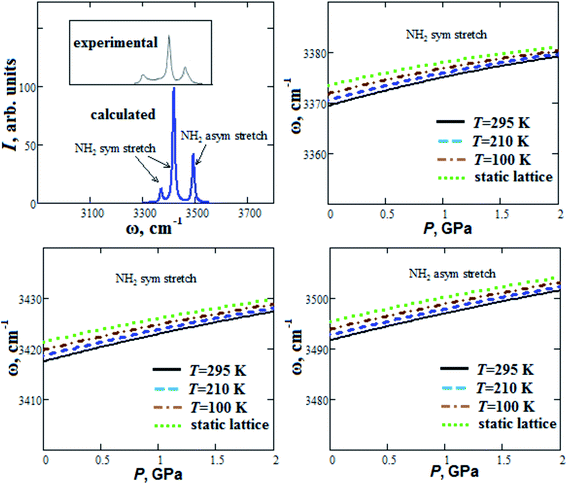 | ||
| Fig. 5 Calculated Raman spectrum and semi-empirical pressure dependencies of frequencies ω of NH2 stretch modes for guanidinium perchlorate at T = 295 K (solid lines), 210 K (dashed lines), 100 K (dash-dotted lines) and at static lattice (dotted lines). Experimental Raman spectrum corresponds to ambient conditions.21 | ||
In our previous works we reported ab initio investigations of thermal properties for alkali metal nitrates, chlorates and perchlorates.46 In the present work we performed ab initio calculations of GP thermal properties (thermal expansion, entropy and heat capacity) as functions of temperature for pressures P = 0, 1, 2 GPa (Fig. 6). The computed volume thermal expansion is in reasonable agreement with experimental data reported in ref. 18. The calculated volume thermal expansion coefficient is ∼3 × 10−4 K−1 (at room temperature) and it decreases ∼3 times when the pressure increases up to 2 GPa. The computed room temperature entropy is 241 J mol−1 K−1 and it decreases by 12.5% with pressure increase up to 2 GPa. Heat capacity almost linearly increases with temperature increase from 50 K and it has value of ∼200 J mol−1 K−1 at room temperature, this is in reasonable agreement with experimental data (ref. 18). It decreases by 7.8% as the pressure grows up to 2 GPa. On the other hand, volume thermal expansion coefficient αV, entropy S and heat capacity Cp at ambient pressure increase by a factor of 1.5, 2.7 and 2.2, respectively, when the temperature increases from T = 100 K up to T = 295 K. It should be noted that thermal expansion, entropy and heat capacity for GP are much higher (∼1.5 to 2 times) than the ones for alkali metal perchlorates.46 This can occur due to large molecular polyatomic guanidinium cations in GP.
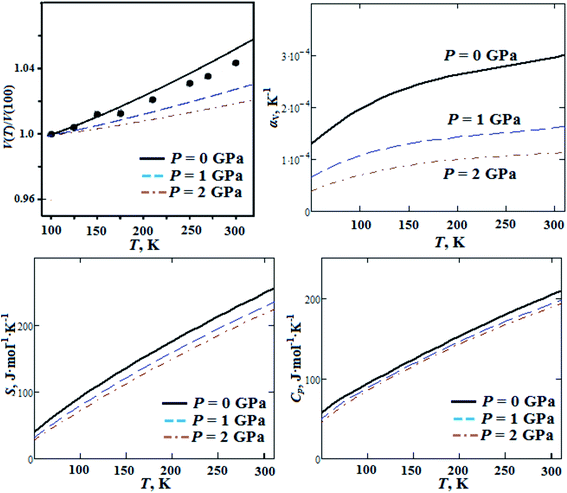 | ||
| Fig. 6 Calculated temperature dependencies of relative volume, volume thermal expansion coefficient, entropy S and heat capacity Cp for guanidinium perchlorate at ambient pressure (solid lines), P = 1 GPa (dashed lines) and P = 2 GPa (dash-dotted lines). Experimental points correspond to ambient pressure.18 | ||
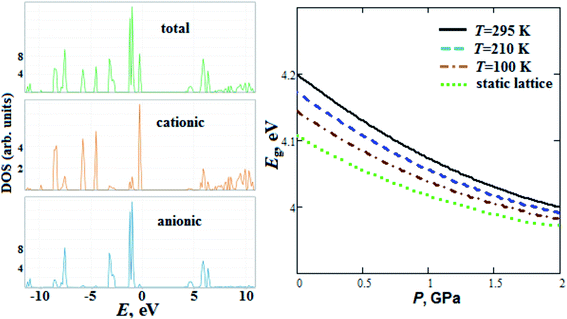
We have also calculated GP total and partial (anionic and cationic) densities of electronic states (Fig. 7). The GP lower unoccupied states have anionic nature, whereas upper valence states for GP, in contrast to alkali metal perchlorates,47 mainly corresponds to cationic states. Our calculated GP band gap energy Eg (4.2 eV) at room temperature is comparable with experimental one (4.9 eV) reported in ref. 17. We should note that the calculated Eg for perchlorate with organic guanidinium cation is smaller (by ∼10%) than Eg for alkali metal perchlorates reported in ref. 47. The band gap of GP, in contrast to alkali metal perchlorates,47 decreases with pressure (Fig. 7).
So, Eg at room temperature decreases by ∼5 and 1.4% when the pressure increases up to 2 GPa and the temperature decreases down to T = 100 K, respectively.
4. Conclusions
Thus, in this work we proposed simple semi-empirical method to calculate structure and properties of crystals under pressure at fixed temperatures. Only one experimental parameter (equilibrium volume) is used in this approach for isothermal pressure dependencies. We performed semi-empirical and ab initio calculations for guanidinium perchlorate, which allowed us to find pressure dependencies for its structure and properties (electronic, elastic, vibrational, thermal). We showed high compressibility and importance of taking into account of thermal effects for GP pressure behavior and mechanical properties. Pressure dependencies for interlayer and intralayer N⋯O distances correlate with c and a parameters, respectively. Moreover, we showed that hydrogen bond energy increases when the pressure increases. We revealed that GP hydrogen bonds become partially covalent in nature near the phase transition pressure. We also established that GP volume thermal expansion coefficient significantly decreases while the pressure increases. It was found out that the band gap of GP, in contrast to alkali metal perchlorates, decreases with pressure.Conflicts of interest
There are no conflicts to declare.References
- E. Zurek and W. Grochala, Phys. Chem. Chem. Phys., 2015, 17, 2917 RSC.
- (a) A. Erba, J. Maul and B. Civalleri, Chem. Commun., 2016, 52, 1820–1823 RSC; (b) A. C. Landerville, M. W. Conroy, M. M. Budzevich, Y. Lin, C. T. White and I. I. Oleynik, Appl. Phys. Lett., 2010, 97, 251908 CrossRef.
- (a) B. A. Zakharov and E. V. Boldyreva, CrystEngComm, 2019, 21, 10 RSC; (b) A. Y. Fedorov, D. A. Rychkov, E. A. Losev, T. N. Drebushchak and E. V. Boldyreva, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2019, 75, 598–608 CrossRef CAS; (c) A. A. Sidelnikov, S. A. Chizhik, B. A. Zakharov, A. P. Chupakhin and E. V. Boldyreva, CrystEngComm, 2016, 18, 7276 RSC.
- A. D. Fortes, E. Suard and K. S. Knight, Science, 2011, 331, 742 CrossRef CAS.
- (a) F. Colmenero, Mater. Adv., 2020, 1, 1399–1426 RSC; (b) F. Colmenero, J. Plasil, V. Timon and J. Cejka, RSC Adv., 2020, 10, 31947 RSC.
- (a) B. M. Abraham, B. Adivaiah and G. Vaitheeswaran, Phys. Chem. Chem. Phys., 2019, 21, 884–900 RSC; (b) N. Yedukondalu and G. Vaitheeswaran, J. Phys. Chem. C, 2019, 123, 2114–2126 CrossRef CAS.
- (a) C. J. McMonagle, P. Comar, G. S. Nichol, D. R. Allan, J. Gonzalez, J. A. Barreda-Argueso, F. Rodriguez, R. Valiente, G. F. Turner, E. K. Brechin and S. A. Moggach, Chem. Sci., 2020, 11, 8793–8799 RSC; (b) S. K. Filatov, M. G. Krzhizhanovskaya, R. S. Bubnova, A. P. Shablinskii, O. L. Belousova and V. A. Firsova, Struct. Chem., 2016, 27, 1663 CrossRef CAS.
- (a) S. G. Kozlova and S. P. Gabuda, Sci. Rep., 2017, 7, 11505 CrossRef; (b) A. R. Aliev, M. M. Gafurov, I. R. Akhmedov, M. G. Kakagasanov and Z. A. Aliev, Phys. Solid State, 2018, 60, 1203 CrossRef CAS; (c) A. R. Aliev, I. R. Akhmedov, M. G. Kakagasanov and Z. A. Aliev, Phys. Solid State, 2020, 62, 998 CrossRef CAS.
- (a) D. V. Korabel’nikov and Yu. N. Zhuravlev, Phys. Chem. Chem. Phys., 2016, 18, 33126 RSC; (b) D. V. Korabel’nikov and Yu. N. Zhuravlev, J. Phys. Chem. A, 2017, 121, 6481 CrossRef; (c) I. A. Fedorov, Comput. Mater. Sci., 2017, 139, 252–259 CrossRef CAS.
- (a) R. A. Evarestov and A. Kuzmin, J. Comput. Chem., 2020, 41, 1337–1344 CrossRef CAS; (b) I. S. Lyubutin, A. G. Gavriliuk, N. D. Andryushin, M. S. Pavlovskiy, V. I. Zinenko, M. V. Lyubutina, I. A. Troyan and E. S. Smirnova, Cryst. Growth Des., 2019, 19, 6935–6944 CrossRef CAS.
- (a) E. V. Boldyreva, J. Mol. Struct., 2004, 700, 151 CrossRef CAS; (b) V. V. Boldyrev, Russ. Chem. Rev., 2006, 75, 177 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 2014, 140, 18A301 CrossRef.
- A. R. Oganov and C. W. Glass, J. Phys.: Condens. Matter, 2008, 20, 064210 CrossRef.
- S. Baroni, P. Giannozzi and E. Isaev, Rev. Mineral. Geochem., 2010, 71, 39–57 CrossRef CAS.
- A. Otero-de-la-Roza, D. Abbasi-Perez and V. Luana, Comput. Phys. Commun., 2011, 182, 2232–2248 CrossRef CAS.
- D. A. Druzhbin, T. N. Drebushchak, V. S. Min’kov and E. V. Boldyreva, J. Struct. Chem., 2015, 56, 317–323 CrossRef CAS.
- S. Sivashankar, R. Siddheswaran and P. Murugakoothan, Mater. Chem. Phys., 2011, 130, 323–326 CrossRef.
- M. Szafranski, J. Phys. Chem. B, 2011, 115, 8755–8762 CrossRef CAS.
- J. F. Scott, Science, 2007, 315, 954–959 CrossRef CAS.
- A. E. Koziol, Z. Kristallogr., 1984, 168, 313–315 CrossRef CAS.
- (a) S. Li, Q. Li, K. Wang, X. Tan, M. Zhou, B. Li, B. Liu, G. Zou and B. Zou, J. Phys. Chem. B, 2011, 115, 11816–11822 CrossRef CAS; (b) K. Wang, S. Li, X. Tan, G. Xiao, B. Liu and B. Zou, Chin. Sci. Bull., 2014, 59, 5258 CrossRef CAS.
- M. Szafranski, CrystEngComm, 2014, 16, 6250–6256 RSC.
- M. R. Udupa, Propellants, Explos., Pyrotech., 1983, 8, 109 CrossRef CAS.
- (a) R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Z. Kristallogr., 2005, 220, 571–573 CAS; (b) R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre and Ph D'Arco, Int. J. Quantum Chem., 2014, 114, 1287 CrossRef CAS.
- F. Cora, Mol. Phys., 2005, 103, 2483–2496 CrossRef CAS.
- C. Gatti, V. R. Saunders and C. Roetti, J. Chem. Phys., 1994, 101, 10686 CrossRef CAS.
- R. Dovesi, E. Ermondi, E. Ferrero, C. Pisani and C. Roetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 3591 CrossRef CAS.
- M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS.
- C. G. Broyden, J. Inst. Math. Its Appl., 1970, 6, 222 CrossRef.
- (a) R. F. W. Bader, Atoms in Molecules - A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170 CrossRef CAS.
- C. Gatti and S. Casassa, TOPOND14 User's Manual, CNR-ISTM Milano, Milano, 2014 Search PubMed.
- (a) P. Vinet, J. Ferrante, J. R. Smith and J. H. Rose, J. Phys. C: Solid State Phys., 1986, 19, L467–L473 CrossRef CAS; (b) R. E. Cohen, O. Gulseren and R. J. Hemley, Am. Mineral., 2000, 85, 338–344 CrossRef CAS.
- C. G. Ungureanu, R. Cossio and M. Prencipe, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2012, 37, 25–33 CrossRef CAS.
- (a) P. Vinet, J. R. Smith, J. Ferrante and J. H. Rose, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 1945–1953 CrossRef CAS; (b) Y. Wang, D. J. Weidner and F. Guyot, J. Geophys. Res., 1996, 101, 661–672 CrossRef CAS.
- (a) Y. Wang, J. J. Wang, H. Zhang, V. R. Manga, S. L. Shang, L. Q. Chen and Z. K. Liu, J. Phys.: Condens. Matter, 2010, 22, 225404 CrossRef CAS; (b) S. L. Shang, H. Zhang, Y. Wang and Z. K. Liu, J. Phys.: Condens. Matter, 2010, 22, 375403 CrossRef.
- (a) F. Mouhat and F. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef; (b) O. Gomis, H. M. Ortiz, J. A. Sans, F. J. Manjon, D. Santamaria-Perez, P. Rodriguez-Hernandez and A. Munoz, J. Phys. Chem. Solids, 2016, 98, 198–208 CrossRef CAS.
- (a) C. F. Matta and R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, Wiley-VCH Verlag GmbH & Co. KgaA, Weinheim, 2007 CrossRef; (b) S. G. Kozlova, M. R. Ryzhikov and D. G. Samsonenko, J. Mol. Struct., 2017, 1150, 268 CrossRef CAS.
- (a) D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627 CrossRef; (b) E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529 CrossRef CAS.
- (a) Yu. V. Nelyubina, M. Yu. Antipin and K. A. Lyssenko, Russ. Chem. Rev., 2010, 79, 167 CrossRef CAS; (b) E. A. Zhurova, A. I. Stash, V. G. Tsirelson, V. V. Zhurov, E. V. Bartashevich, V. A. Potemkin and A. A. Pinkerton, J. Am. Chem. Soc., 2006, 128, 14728 CrossRef CAS.
- (a) S. J. Grabowski, Chem. Rev., 2011, 111, 2597 CrossRef CAS; (b) D. V. Korabel’nikov and Yu. N. Zhuravlev, RSC Adv., 2019, 9, 12020–12033 RSC.
- C. Gatti, Z. Kristallogr., 2005, 220, 399–457 CAS.
- (a) J. Joseph and E. D. Jemmis, J. Am. Chem. Soc., 2007, 129, 4620–4632 CrossRef CAS; (b) E. S. Kryachko and T. Zeegers-Huyskens, J. Phys. Chem. A, 2001, 105, 7118–7125 CrossRef CAS.
- (a) D. V. Korabel’nikov, Phys. Solid State, 2018, 60, 571 CrossRef; (b) D. V. Korabel’nikov and Yu. N. Zhuravlev, Phys. Solid State, 2013, 55, 1765 CrossRef.
- (a) Yu. N. Zhuravlev and D. V. Korabel’nikov, J. Struct. Chem., 2009, 50, 1021–1028 CrossRef CAS; (b) D. V. Korabel’nikov and Yu. N. Zhuravlev, Phys. Solid State, 2017, 59, 254–261 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |