 Open Access Article
Open Access ArticleIrregular solution thermodynamics of wood pulp in the superbase ionic liquid [m-TBDH][AcO]†
Gordon W. Driver * and
Ilkka A. Kilpeläinen
* and
Ilkka A. Kilpeläinen
Materials Chemistry Division, Department of Chemistry, University of Helsinki, P. O. Box 55, FI-00014, Finland. E-mail: gordon.driver@helsinki.fi; gordon.driver@gmail.com; Tel: +358 50 593 9238
First published on 19th November 2020
Abstract
Knowledge of solution thermodynamics is fundamental for solution control and solvent selection processes. Herein, experimentally determined thermodynamic quantities for solutions of wood pulp (hardwood dissolving pulp, i.e. cellulose) in [m-TBDH][AcO] are presented. Model-free activities (ai,j) and associated mass fraction (wi,j) activity coefficients (Ωi,j), are determined to quantify inherent solution non-ideality. Access to the Gibbs energy of mixing, Gmix, in combination with associated partial molar thermodynamic quantities, reveal strong enthalpically favourable (exothermic) interactions due to solvent-j and solute-i contact-encounters. Onset of an entropy driven phase instability appears at increased temperatures as excess entropic contributions dominate solvation character of the irregular solutions formed.
Investigations concerning dissolution of carbon-neutral biomass components in varieties of ionic liquids (ILs) have increasingly populated the literature since the turn of the century.1 From this renewed interest in the discovery and development of powerful new solvents for difficult to dissolve polymeric bio-solutes, protic “superbase” ILs have emerged as promising candidates for cellulose dissolution and upstream processing related to a variety of materials.2–8 To date, focus in the literature has largely been bounded by efforts to identify liquid salts with qualitative dissolution utility for biomass components, among various contributions detailing new developments in synthetic carbohydrate derivatisation chemistry.9,10 Much less attention has been given towards gaining a detailed understanding of the energetics governing solvent–solute contact-encounters in such mixtures, using robust thermodynamic methods.11
Knowledge gained from such approaches reveal available composition- and temperature-dependent solvation character of both solvent-j and solute-i, which in turn provides the fundamental basis upon which the solvent selection process may be anchored, and furthermore, the means to identify a given solvent's utility in terms of true task specificity. Herein, we report thermodynamic solution behaviour of cellulose dissolved in the superbase comprised IL, [m-TBDH][AcO] (7-methyl-1,5,7-triazabicyclo[4.4.0]dec-5-enium acetate). Employing a minimal experimental data set, we present the subsequent processing and interpretation of results obtained directly from fundamental thermodynamic relationships, thereby avoiding various well-known limitations introduced by numerous thermodynamic polymer models available (e.g. Flory–Huggins and associated theoretical developments).12–17
This investigation relies on the well-known colligative property defined by the freezing point depression of the solvent-j, in the presence of solute-i, at low mass fractions, wi. In combination with the Gibbs–Duhem relation for a 2 component system, widln(ai) + wjdln(aj) = 0, this permits the realisation of solute-i activities (ai) based on those experimentally determined for the solvent-j (aj). In essence, freezing point depressions for the binary solutions, recorded experimentally using modulated differential scanning calorimetry (MDSC), reveal changes to aj using the variant of Kirchhoff's law given in eqn (1)., imposed by the presence of solute-i (i.e. enocell-i)‡, which perturbs the chemical potential of the solvent-j, [m-TBDH][AcO]-j, to a measurable extent.
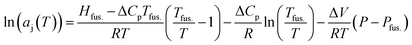 | (1) |
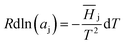 | (2) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) j represents the relative partial molar enthalpy of solvent-j. The Gibbs–Duhem relation, utilised on the basis of the form given in eqn (3),
j represents the relative partial molar enthalpy of solvent-j. The Gibbs–Duhem relation, utilised on the basis of the form given in eqn (3),
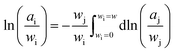 | (3) |
Freezing point depressions recorded during the independently run triplicate MDSC experiments produced standard deviations for a given composition on the order of ± < 0.18 K. Solute-i activity coefficients, Ωi, determined from experimentally recorded solvent-j activity coefficients, 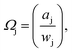 via eqn (3), were subsequently employed to back-calculate experimentally determined values, again using eqn (3). The closeness of computed Ωj, obtained using Ωi, to the experimental values, serves as a consistency check, to validate and verify the Ωi obtained. We observed very satisfactory consistency by this method, where differences between experimental and calculated Ωj were generally ≪1% for dilute solutions, and up to ∼5% for certain wj, at the highest temperature investigated (see the ESI†).
via eqn (3), were subsequently employed to back-calculate experimentally determined values, again using eqn (3). The closeness of computed Ωj, obtained using Ωi, to the experimental values, serves as a consistency check, to validate and verify the Ωi obtained. We observed very satisfactory consistency by this method, where differences between experimental and calculated Ωj were generally ≪1% for dilute solutions, and up to ∼5% for certain wj, at the highest temperature investigated (see the ESI†).
Selected thermodynamic results presented in Tables 1 and 2 are discussed below in terms of the thermodynamic suitability of [m-TBDH][AcO] for the task of dissolving cellulose, based on the molar Gibbs mixing energies, in relation to associated partial molar enthalpic and entropic contributions.§
| T/K | Gmixa/kJ mol−1 | Gideali/kJ mol−1 | Gidealj/kJ mol−1 | GEi/kJ mol−1 | GEj/kJ mol−1 | Ωi | Ωj |
|---|---|---|---|---|---|---|---|
| a Gmix = Gideal + GE.b LCST = 363.127 K. | |||||||
| 357.15 | −0.527 | −0.737 | −0.320 | 0.296 | 0.234 | 2.39 | 1.09 |
| 358.15 | −0.457 | −0.739 | −0.321 | 0.351 | 0.252 | 2.80 | 1.10 |
| 359.15 | −0.369 | −0.742 | −0.322 | 0.425 | 0.269 | 3.46 | 1.11 |
| 360.15 | −0.258 | −0.744 | −0.323 | 0.521 | 0.286 | 4.57 | 1.11 |
| 363.07b | 8.82 × 10−4 | −0.750 | −0.325 | 0.742 | 0.334 | 8.53 | 1.13 |
| 373.15 | 0.898 | −0.770 | −0.334 | 1.52 × 103 | 0.480 | 72.3 | 1.19 |
| Sideali/J K−1 mol−1 | Sidealj/J K−1 mol−1 | SEi/J K−1 mol−1 | SEj/J K−1 mol−1 |
|---|---|---|---|
| 2.07 | 0.896 | −77.5 | −15.2 |
Results presented in Table 1 indicate the presence of enocell-i in the dilute mixtures appears to impart a weak destabilising influence on the solvent-j where aj > 1 although this reverses with aj < 1 for the largest wi, where ai becomes substantial. Mixing becomes increasingly favourable with increases in wi, where associated relative incremental changes to Gmix are observed to approach 0 kJ mol−1 from the positive side, crossing over to negative values for the 11.5 wt% enocell-i composition, where Hmix + −TSmix < 0. As wi increases from conditions of infinite-dilution, with maximum non-ideality due the absence of solute–solute contact-encounters, it becomes clear that such interactions, being attractive in nature, impart a favourable influence towards dissolution. Exclusion volumes, initially maintained via random polymer coiling (e.g. chain twisting and kinking) at the lower mass fractions, reduce proportionally with subsequent increases in wi, which serves to progressively stabilise the mixture. This effect materialises from an increase in permitted non-random (directional) contacts whereby solvent ions progressively access the polymer's coiled domain, as de-coiling proceeds due to polymer chain elongation.19 Polymer de-coiling is further evidenced by conformational changes resulting in loss of degrees of freedom according to SEi = −77.5 J K−1 mol−1.20 Such an effect also influences the solvent-j albeit to a smaller extent with SEj = −15.2 J K−1 mol−1, suggesting a lowering of solvent density (c.f. Table 2).21 Such entropic contributions indicate directly the solvation character of enocell dissolved in [m-TBDH][AcO] and are expected to correlate with possible property enhancements observed with chemical modification chemistries, as well as with regeneration processes for different materials.22,23 Polymer swelling, an unavoidable consequence of increased solvent penetration into the coiled domain, is rationalised here as serving to promote increased linearity of solvated polymer units, in proportion to degrees of freedom lost, enabling enhancement of their ability towards independent solution behaviour.
Across solute-i mass fractions, wi, enthalpic stabilisation occurs, promoting dissolution, where Hmix, already strongly negative at the highly diluted compositions, more than doubles in the most concentrated composition. The magnitude of wiHEi, at the investigated compositions, indicate attractive interactions of solute-i, with solvent-j, are strong and directional (e.g. ij ≠ ji and with opposing composition dependence), revealing specific attractive solute–solvent contact-encounters driving dissolution, exceed contributions expected from random statistical solute–solvent contact-encounters characterised by −TSmix. Simultaneous and progressive loss of wjHEj, over the same composition range, indicate specific, directional solvent–solute contact configurations, that provide excellent stabilisation of the solute, are weakly less energetically favourable for the solvent. This opposing behaviour is facilitated by the large negative molar enthalpy of mixing at wi = 0.115, Hmix = −32.6 kJ mol−1, comprised of contributions due to enthalpic gains of wiHEi that far outweigh contributions resultant from enthalpic losses exhibited by wjHEj.
With the operative temperature range employed in this study being necessarily narrow, from ∼7° above the melting point of the solvent (mp = 350.34 K ± 1.44 K) to 373.15 K, we observe a near doubling of +GEi over the interval 357.15 K to 360.15 K at wi = 0.115, to a value of 0.521 kJ mol−1, a 43% increase, as repulsive forces increasingly dominate. Over the same temperature range, +GEj increases by 18%. At yet higher temperatures, solute–solvent de-mixing becomes feasible as Gmix > 0, a result of the increasing magnitude of repulsive forces characterised by GE as it effectively dominates the −TSideal term, for both solute-j and solvent-i. Enthalpic gains contributing to solvation are all but completely cancelled by the −TSmix term, due to SEi being large and negative, signifying a loss of disorder that serves to disfavour dissolution, as indicated above. Such high temperature de-mixing behaviour is due to a type-V lower critical solution temperature (LCST), according to the classification scheme of Scott and van Konynenburg.24 This result in an ionic liquid is bound to originate as a consequence of the increased ionicity of solvent ions, proportional to increased temperatures, where stabilising configurations for anion-solute, cation-solute and cation–anion interactions are lost due to thermal scattering and breaking of hydrogen bond interactions.25 This expected behaviour is known to be controlled by oppositely charged ion dynamics as ions escape the potential energy wells of their nearest ionic neighbours, resulting in concomitant losses of the binding coulombic energy.26
Thermodynamic analyses presented indicate enocell-i solutions in [m-TBDH][AcO]-j are non-ideal, exhibiting positive deviations from Raoult's law, as observed by the sign of GEi,j. These solutions classify as irregular, with strong negative enthalpic contributions driving dissolution. Evolution of an increasingly large and positive −TSmix term, due to polymer chain deformation of the Gaussian random coil and subsequent solvent ordering through the direct solute-ion contacts, induce a type-V LCST.20 Accordingly, [m-TBDH][AcO] is well suited for the task of wood pulp dissolution, driven by strongly negative directional enthalpic contributions to solvation in the available temperature range below the LCST. Above T = 363.127 K (for wi = 0.115), repulsive interactions between solute and solvent dominate to the extent that de-mixing instability is expected in the liquid phase, where increased temperatures will cease to benefit solution character. In this way, location of a LCST phase region must clearly be identified to ensure polymer dissolution is profitably carried out at appropriate temperatures. The Flory–Huggins model is, through its fundamental premise, inappropriate for modelling of the title systems, in which the requirement for Smix > 0 is not met. Entropic effects leading to the expectation of a LCST may correlate with reported enhancement of material properties from use of ionic liquid solutions, suggesting dissolution temperatures in close proximity, yet below the LCST, are beneficial for chemical modification chemistries and regeneration processes.
Conflicts of interest
There are no conflicts to declare.Notes and references
- R. P. Swatloski, S. K. Spear, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2002, 124, 4974–4975 CrossRef CAS.
- A. M. Stepan, A. Michud, S. Hellstén, M. Hummel and H. Sixta, Ind. Eng. Chem. Res., 2016, 55, 8225–8233 CrossRef CAS.
- L. K. J. Hauru, M. Hummel, K. Nieminen, A. Michud and H. Sixta, Soft Matter, 2016, 12, 1487–1495 RSC.
- X. Li, H. Li, Z. Ling, D. Xu, T. You, Y.-Y. Wu and F. Xu, Macromolecules, 2020, 53, 3284–3295 CrossRef CAS.
- X. Niu, S. Huan, H. Li, H. Pan and O. J. Rojas, J. Hazard. Mater., 2021, 402, 124073 CrossRef CAS.
- L. Jin, J. Gan, L. Cai, Z. Li, L. Zhang, Q. Zheng and H. Xie, Polymers, 2019, 11, 994 CrossRef.
- T. Kakko, A. W. T. King and I. Kilpeläinen, Cellulose, 2017, 24, 5341–5354 CrossRef CAS.
- S. Elsayed, S. Hellsten, C. Guizani, J. Witos, M. Rissanen, A. H. Rantamäki, P. Varis, S. K. Wiedmer and H. Sixta, ACS Sustain. Chem. Eng., 2020, 8, 14217–14227 CrossRef CAS.
- D. R. del Cerro, T. V. Koso, T. Kakko, A. W. T. King and I. Kilpeläinen, Cellulose, 2020, 27, 5545–5562 CrossRef CAS.
- S. Asaadi, T. Kakko, A. W. King, I. Kilpeläinen, M. Hummel and H. Sixta, ACS Sustain. Chem. Eng., 2018, 6, 9418–9426 CrossRef CAS.
- J.-M. Andanson, A. A. H. Pádua and M. F. Costa Gomes, ChemComm, 2015, 51, 4485–4487 RSC.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- M. L. Huggins, J. Chem. Phys., 1941, 9, 440 CrossRef CAS.
- J. M. Prausnitz, R. N. Lichtenthaler and E. Gomes de Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria, Prentice Hall, New Jersey, 3rd edn., 1999 Search PubMed.
- J. Gmehling, B. Kolbe, M. Kleiber and J. Rarey, Chemical Thermodynamics for Process Simulation, Wiley-VCH, Weinheim, 2012 Search PubMed.
- S. I. Sandler, Chemical, Biochemical, and Engineering Thermodynamics, John Wiley & Sons, New Jersey, 4th edn., 2006 Search PubMed.
- J. M. G. Cowie and V. Arrighi, Polymers: Chemistry and Physics of Modern Materials, Taylor & Francis, Boca Raton, 3rd edn., 2007 Search PubMed.
- M. L. Lakhanpal and B. E. Conway, Can. J. Chem., 1960, 38, 199–203 CrossRef CAS.
- P. C. Hiemenz, Polymer Chemistry: The Basic Concepts, Marcel Dekker, New York, 1984 Search PubMed.
- S. Seiffert, Physical Chemistry of Polymers: A Conceptual Introduction, De Gruyter, Berlin, 2020 Search PubMed.
- P. Paricaud, A. Galindo and G. Jackson, Mol. Phys., 2003, 101, 2575–2600 CrossRef CAS.
- H. Sixta, A. Michud, L. Hauru, S. Asaadi, Y. ma, A. King, I. Kilpeläinen and M. Hummel, Nord. Pulp Pap Res. J., 2015, 30, 43–57 CAS.
- B. Kosan, C. Michels and F. Meister, Cellulose, 2008, 15, 59–66 CrossRef CAS.
- P. H. van Konynenburg, R. L. Scott and J. S. Rowlinson, Philos. Trans. Royal Soc. A, 1980, 298, 495–540 CAS.
- G. W. Driver, Y. Huang, A. Laaksonen, T. Sparrman, Y.-L. Wang and P.-O. Westlund, Phys. Chem. Chem. Phys., 2017, 19, 4975–4988 RSC.
- G. W. Driver, PhD thesis, The Queen’s University of Belfast, 2007.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental data are reported along with the methods employed. See DOI: 10.1039/d0ra08892g |
| ‡ Enocell starting material: DPn = 333 and DPw = 13339 |
| § Further details of this method are provided in the available ESI. |
| This journal is © The Royal Society of Chemistry 2020 |
