 Open Access Article
Open Access ArticleEquilibrium swelling of thermo-responsive copolymer microgels†
A. D. Drozdov * and
J. deClaville Christiansen
* and
J. deClaville Christiansen
Department of Materials and Production, Aalborg University, Fibigerstraede 16, Aalborg 9220, Denmark. E-mail: aleksey@m-tech.aau.dk
First published on 24th November 2020
Abstract
Thermo-responsive (TR) hydrogels with a lower critical solution temperature swell strongly at temperatures below their volume phase transition temperature Tc and collapse above Tc. Biomedical application of these materials requires tuning the critical temperature in a rather wide interval. A facile method for modulation of Tc is to polymerize the basic monomers with hydrophilic or hydrophobic comonomers. Although the effectiveness of this method has been confirmed by experimental data, molar fractions of comonomers necessary for fine tuning of Tc in macroscopic gels and microgels are unknown. A simple model is developed for the equilibrium swelling of TR copolymer gels. Its adjustable parameters are found by fitting swelling diagrams on several macro- and microgels with N-isopropylacrylamide as a basic monomer. Good agreement is demonstrated between the experimental swelling curves and results of numerical analysis. An explicit expression is derived for the volume phase transition temperature as a function of molar fraction of comonomers. The ability of this relation to predict the critical temperature is confirmed by comparison with observations.
1 Introduction
Thermo-responsive (TR) gels form a special class of hydrogels whose equilibrium degree of swelling is strongly affected by temperature. TR gels of the LCST (lower critical solution temperature)-type swell pronouncedly at temperatures T below their volume phase transition temperature Tc and collapse when T exceeds Tc. Preparation of TR gels and analysis of their properties have recently attracted substantial attention due to a wide range of biomedical and biotechnological applications of these materials.1,2 Covalently cross-linked poly(N-isopropylacrylamide) (PNIPAm) gel is the most extensively studied TR gel.3,4 It exhibits a sharp volume phase transition at Tc = 32 °C and demonstrates good mechanical properties below and above Tc.As swelling of a gel is driven by diffusion of water molecules, the rate of its response to external stimuli is determined by the characteristic size: the smaller a sample is, the faster it swells or collapses. Equilibrium and transient swelling of TR microgels (spherical particles with radii ranging from 10 to 1000 nm) has become a hot topic in the past decade.5 This interest is driven by applications of these materials as carriers for targeted delivery of drugs and genes,6 scaffolds for tissue regeneration,7 systems for biosensing and bioimaging,8 and nanoreactors with high catalytic activity,9 to mention a few.
Biomedical applications of microgels (for electrophoretic separation of DNA and proteins,10 targeted delivery of drugs and genes,11 storage and transportation of vaccines,12 and as temperature-triggered actuators13) require modulation of their volume phase transition temperature Tc in a rather wide interval.1 Several methods for tuning Tc of TR gels have been proposed.14–17 It is found that (i) Tc is practically unaffected by molar fractions of monomers and cross-linkers, as well as by the polymerization temperature and solvent for synthesis, (ii) it is weakly affected by the presence of polymer chains immersed into a pre-gel solution to prepare gels with inter-penetrating networks, and (iii) Tc changes significantly when TR monomers are polymerized with neutral or ionic comonomers whose hydrophilicity differs from that of the basic monomers. Although the trend in alteration of Tc is clear: the volume phase transition temperature decreases due to the presence of hydrophobic comonomers and increases when hydrophilic comonomers are incorporated, no explicit relations have been developed for the quantitative prediction of these changes.
Macroscopic TR gels are conventionally prepared by free-radical cross-linking polymerization of an aqueous solution of monomers and cross-linker at temperatures T below Tc.18 On the contrary, TR microgels are synthesized by precipitation or emulsion polymerization (with or without surfactants) under stirring at temperatures far above their volume phase transition temperature.19 As the mechanical response of TR gels is strongly affected by polymerization conditions,20–22 equilibrium swelling diagrams of macro- and microgels distinguish substantially.23
The objective of this work is three-fold: (i) to develop a model for the equilibrium swelling of TR macro- and microgels with a relatively small number of material constants, (ii) to determine adjustable parameters by fitting experimental swelling diagram on copolymer gels with NIPAm as basic monomers and non-ionic comonomers whose hydrophilicity is lower and higher than that of NIPAm, (iii) to derive a analytical formula that expresses the volume phase transition temperature of a copolymer gel Tc by means of the molar fraction of comonomers in a pre-gel solution cco and to examine its ability to predict observations.
The novelty of this study consists in the following. (I) The polymer network in a TR gel is treated as a superposition of two networks: the first is formed under preparation when chains are covalently cross-linked, and the other is developed at T > Tc when new physical bonds between chains are formed due to aggregation of hydrophobic segments. This approach allows us to describe a strong increase in the elastic modulus of TR gels above their volume-phase transition temperature Tc, on the one hand, and to avoid introduction of nonlinear dependencies of the Flory–Huggins parameter on volume fraction of polymer network, on the other. (II) A simple equation (see eqn (27) below) is derived that connects the volume phase transition temperature of a copolymer gel with the molar fraction of comonomers. The ability of this relation to predict Tc is confirmed by comparison with experimental data. It is shown, in particular, that eqn (27) predicts accurately Tc of microgels when its only coefficient a is found by matching experimental data on macroscopic gels, and vise versa. (III) A phenomenological relation (32) is established between the modified Flory–Huggins parameter of comonomers and their Hildebrand solubility parameter. Based on this approach, the volume phase transition temperature of copolymer gels is predicted for several copolymer gels and a reasonable agreement is demonstrated between results of numerical analysis and experimental data.
2 Model
2.1 Swelling of homopolymer gels
A TR gel is modeled as a two-phase medium composed of solid (an equivalent polymer network) and fluid (water) constituents. The solid and fluid phases are treated as immiscible interpenetrating continua.The initial state of a gel coincides with that of an undeformed dry specimen at some temperature T0 < Tc. According to the affinity hypothesis, deformation of the gel coincides with deformation of its polymer network. Transformation of the initial state into the actual state at temperature T is described by the deformation gradient F. We disregard thermally induced volume expansion and write the molecular incompressibility condition in the form
det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F = 1 + Cv, F = 1 + Cv,
| (1) |
To describe abrupt changes in the equilibrium degree of swelling of TR gels above their volume phase transition temperature Tc, we follow the approach proposed in ref. 24 and 25, see also recent reviews.26,27 Polymer chains in a network are presumed to consist of hydrophilic and hydrophobic segments. At temperatures T < Tc, each hydrophobic segment is surrounded by a cage-like structure formed by water molecules bridged by hydrogen bonds. An increase in temperature results in the growth of intensity of thermal fluctuations that destabilize these bonds. Breakage of cage-like structures surrounding hydrophobic segments induces their agglomeration and formation of aggregates from which water molecules are expelled. At temperatures above Tc, all cage-like structures are broken, and a gel consists of a number of deswollen hydrophobic aggregates bridged by hydrophilic segments and separated by nano-channels in which water molecules are located.28
According to this scenario, the polymer network in a TR gel involves two components. The first network with covalent bonds is formed under cross-linking polymerization of a pre-gel solution. The other network is built at temperatures T > Tc due to aggregation of hydrophobic segments into clusters that serve as physical bonds between chains. For simplicity, both networks are treated as permanent. This picture is confirmed by observations on TR macroscopic gels29,30 and microgels31 that show a pronounced (by an order of magnitude) increase in their elastic moduli when temperature T exceeds Tc.
The deformation gradient for macro-deformation F is connected with the deformation gradient for elastic deformation of the mth network Fe(m) by the multiplicative decomposition formula
| F = Fe(m)·fm (m = 1, 2), | (2) |
Homogeneous transformation of the initial configuration into the reference configuration of a covalently cross-linked network is described by the deformation gradient
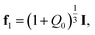 | (3) |
Keeping in mind that all water molecules are expelled from hydrophobic aggregates, we presume the reference state of the network with physical bonds to coincide with the initial (dry) state of the gel,
| f2 = I. | (4) |
The Helmholtz free energy of the gel (per unit volume in the initial state) Ψ equals the sum of the specific energies of fluid and solid components not interacting with each other and the energy of their interaction,
| Ψ = Ψ1 + Ψ2 + Ψint, | (5) |
The specific energy of water molecules is given by
| Ψ1 = μ0C, | (6) |
The specific energy of the network (consisting of two parts with chemical and physical bonds) reads
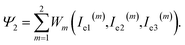 | (7) |
The specific mechanical energy Wm stored in chains of the mth network depends on the principal invariants Ie1(m), Ie2(m), Ie3(m) of the corresponding Cauchy–Green tensor for elastic deformation
| Be(m) = Fe(m)·Fe(m)⊤, | (8) |
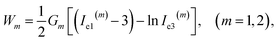 | (9) |
We disregard the effect of temperature on the elastic modulus of the covalently cross-linked network and treat G1 as a constant. The modulus G2 of the network with physical bonds vanishes below Tc and grows with the difference T − Tc above the volume phase transition temperature. The following expression is adopted for this function:
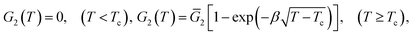 | (10) |
The specific energy of mixing of water molecules with segments of chains is adopted in the conventional form36
Ψint = kBT0(C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕw + χCϕn), ϕw + χCϕn),
| (11) |
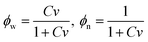 | (12) |
Unlike the conventional approach to the analysis of swelling of TR gels,37,38 we treat the FH parameter as a function of temperature T only. The following expression is accepted for χ:
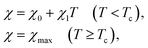 | (13) |
| χmax = χ0 + χ1Tc. | (14) |
Eqn (13) means that breakage of cage-like structures formed by water molecules around hydrophobic segments induces the growth of the effective hydrophobicity of chains (characterized by χ) at temperatures T below Tc. When T exceeds Tc, the increase in χ is prohibited due to formation of aggregates of hydrophobic segments. This condition ensures that material parameters do not accept anomalously high values mentioned in ref. 39. It has been demonstrated in ref. 40 that replacement of the first equality in eqn (13) with a nonlinear dependence of χ on temperature does not improve the quality of fitting (as T varies in a rather narrow interval between 0 °C and Tc).
Under unconstrained equilibrium swelling of a TR gel at an arbitrary temperature T, its degree of swelling
| Q = Cv | (15) |
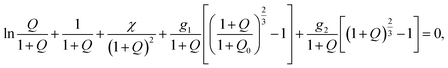 | (16) |
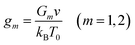 | (17) |
Eqn (16) together with eqn (13) for the FH parameter χ and eqn (10) and (17) for the dimensionless moduli provide governing equations for the equilibrium degree of swelling Q. These relations involve 7 adjustable parameters: (i) coefficients χ0 and χ1 describe how hydrophilicity of chains is affected by temperature below the critical temperature Tc, (ii) parameter χmax characterizes their hydrophilicity above the volume phase transition temperature, (iii) g1 and Q0 stand for the dimensionless shear modulus of the covalently cross-linked network and its degree of swelling in the reference state, and (iv) coefficients ḡ2 and β describe an increase in the dimensionless shear modulus of the network with physical bonds above Tc. Given χ0, χ1 and χmax, the volume phase transition temperature Tc is calculated from eqn (14).
Unlike macroscopic gels, whose degrees of swelling in the as-prepared and fully swollen states can be measured directly, the equilibrium degree of swelling of microgels Q is recalculated from their hydrodynamic radii rh, which, in turn, are found from observations in dynamic light scattering, small-angle X-ray scattering or small-angle neutron scattering tests on diluted microgel colloids.41 Under homogeneous swelling of a microgel, Q(T) is connected with the hydrodynamic radius rh(T) by the equation
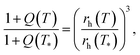 | (18) |
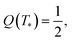 | (19) |
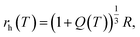 | (20) |
2.2 Swelling of copolymer gels
We consider equilibrium swelling of binary copolymer gels prepared by cross-linking polymerization of thermo-responsive monomers (NIPAm) with non-ionic temperature-insensitive comonomers. Although some comonomers used in the analysis of experimental data demonstrate weak sensitivity to changes in temperature,45 this effect is disregarded. Molar fraction of comonomers equals cco, and molar fraction of NIPAm monomers equals 1 − cco, where cco is presumed to be small compared with unity.Eqn (10), (13) and (16) describe equilibrium swelling of homopolymer and copolymer gels. Our aim is to establish correlations between material constants of PNIPAm gel and its copolymer gels to be confirmed by fitting observations in Sect. 3.
The coefficients β and ḡ2 = Ḡ2v/(kBT0) are presumed to be independent of cco. These parameters describe the kinetics of aggregation of hydrophobic segments of NIPAm monomers above the volume phase transition temperature Tc. We suppose that the presence of comonomers does not affect the aggregation process when cco ≪ 1.
With reference to the conventional scaling rules for hydrogels,46 we presume g1 to be independent of cco, as this quantity characterizes concentration of cross-links in a gel. It will be shown in what follows that this assumption is fulfilled for macroscopic gels, but it can be violated for microgels with strongly hydrophobic comonomers (these entities aggregate into hydrophobic clusters that serve as extra permanent cross-links between chains even at temperatures T below Tc). At small cco, changes in g1 with molar fraction of comonomers are described by the linear equation
| g1 = g01(1 − cco) + g11cco, | (21) |
The volume fraction of polymer network in the reference (stress-free) state ϕn0 (this quantity is determined by eqn (12) where C is replaced with C0) obeys the equation
| ϕn0 = ϕ0n0(1 − cco) + ϕn01cco, | (22) |
As an analog of eqn (21) and (22) for the FH parameter of a copolymer gel (the so-called two-parameter model47) is overly simplified to describe equilibrium swelling diagrams, we use the three-parameter model,48,49
| χ = χPNIPAm(1 − cco) + χcocco − χintcco(1 − cco), | (23) |
χ = χPNIPAm(1 − cco) + ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) cocco, cocco,
| (24) |
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co = χco − χint co = χco − χint |
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co to be independent of temperature and arrive at the analog of eqn (13) for TR copolymer gels below their volume phase transition temperature
co to be independent of temperature and arrive at the analog of eqn (13) for TR copolymer gels below their volume phase transition temperature
χ = [χ0(1 − cco) + ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) cocco] + χ1(1 − cco)T (T < Tc). cocco] + χ1(1 − cco)T (T < Tc).
| (25) |
Above the critical temperature Tc, the FH parameter of the copolymer network obeys eqn (13) with χmax independent of concentration of comonomers,
| χ = χmax (T ≥ Tc). | (26) |
Eqn (26) means that the presence of a small molar fraction of comonomers in the pre-gel solution does not affect aggregation of hydrophobic segments of PNIPAm chains.
Substitution of eqn (25) and (26) into continuity condition (14) results in the formula for the volume phase transition of a copolymer gel
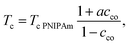 | (27) |
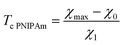 | (28) |
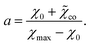 | (29) |
Given Tc PNIPAm, eqn (27) involves the only material constant a that characterizes interactions of comonomers with NIPAm monomers and water molecules. It follows from eqn (27) that Tc increases with cco when a > −1(![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co > −χmax), decreases when a < −1(
co > −χmax), decreases when a < −1(![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co < −χmax), and remains unchanged when a = −1. These inequalities can serve as explicit conditions of hydrophilicity and hydrophobicity of comonomers.
co < −χmax), and remains unchanged when a = −1. These inequalities can serve as explicit conditions of hydrophilicity and hydrophobicity of comonomers.
To reduce the number of material constants in the model, we treat the coefficients χ0 and χ1 as universal (which means that their values are independent of preparation conditions and molar fraction of a cross-linker, and are determined by properties of NIPAm monomers exclusively). These parameters were found in ref. 50 by approximation of observations on PNIPAm gel prepared by irradiation cross-linking of an aqueous solution of PNIPAm chains,51
| χ0 = −2.0980, χ1 = 7.908 × 10−2. | (30) |
Given χ0 and χ1, the coefficient χmax (this quantity is weakly affected by preparation conditions for a copolymer gel) is calculated from eqn (28). The coefficient a in eqn (27) is determined by fitting an experimental dependence of Tc on cco. Finally, the coefficient ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co is found from eqn (29).
co is found from eqn (29).
3 Comparison with experimental data
Our aim now is threefold: (i) to examine the ability of the model (10), (16), (25) and (26) to describe experimental swelling diagrams on PNIPAm microgels synthesized with various comonomers, (ii) to verify its ability to predict the influence of comonomers on the volume phase transition temperature, and (iii) to assess a difference between the thermo-mechanical responses of microgels and their macroscopic analogs.When the coefficients χ0 and χ1 are given by eqn (30) and the coefficient χmax is determined from eqn (28), the governing equations for a copolymer gel involve only five adjustable parameters. This number is substantially (by twice) lower than that in conventional models for copolymer gels.52,53 For each set of observations, three coefficients (g1, Q0, ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co) are found by fitting experimental data below Tc, and the remaining two coefficients (ḡ2, β) are determined by matching observations above Tc. Adjustable parameters are calculated by the nonlinear regression method to minimize the expression
co) are found by fitting experimental data below Tc, and the remaining two coefficients (ḡ2, β) are determined by matching observations above Tc. Adjustable parameters are calculated by the nonlinear regression method to minimize the expression
| ∑(Qexp − Qsim)2, |
3.1 P(NIPAm–tBA) microgels
We begin with the study of swelling diagrams on poly(N-isopropylacrylamide-co-tert-butyl acrylate) (P(NIPAm–tBA)) microgels prepared by surfactant-free radical emulsion polymerization (6 h at 70 °C) of an aqueous solution of NIPAm (82.7 mM) and tBA (various amounts) monomers by using N,N′-methylene-bis(acrylamide) (BIS, 5.6 mol% with respect to NIPAm monomers) as a cross-linker and ammonium persulfate (APS) as an initiator.54 Experimental data on microgels with cco = 0 and 0.28 are reported in Fig. 1A and those on microgels with cco = 0.11, 0.16 and 0.21 are presented in Fig. S-1A–C.† In these figures, the hydrodynamic radius rh is plotted versus temperature T together with results of numerical simulation with the material parameters listed in Table S-1.†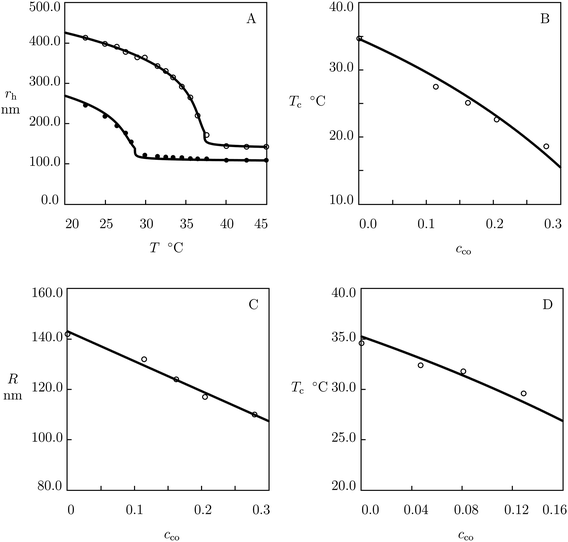 | ||
| Fig. 1 (A) Hydrodynamic radius rh of microgel particles versus temperature T. Symbols: experimental data54 on P(NIPAm–tBA) microgels with molar fractions of comonomers cco = 0 (○) and cco = 0.28 (●). Solid lines: results of simulation. (B) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data. Solid line: results of simulation. (C) Radius R of microgel particles versus molar fraction of comonomers cco. Circles: treatment of observations. Solid line: results of simulation. (D) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data55 on P(NIPAm–tBA) gels. Solid line: predictions of the model. | ||
Observations on homopolymer PNIPAm microgel (Fig. 1A) are fitted by using the following algorithm. Given a set of experimental data rh(T), the swelling curve Q(T) is calculated from eqn (18) and (19), and the dependence χ(T) (below Tc) is found from eqn (16) with g2 = 0. For χ0 and χ1 given by eqn (30), this dependence is matched by eqn (13), and parameters g1 and Q0 are found from the best-fit condition. The coefficients ḡ2 and β are determined by fitting the swelling diagram Q(T) above Tc. Parameters χmax and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co are found by fitting the experimental dependence of Tc on molar fraction of comonomers cco (Fig. 1B) by means of eqn (27)–(29). After finding all material parameters, radius of a microgel particle in the initial state R is calculated by approximating the dependence rh(T) with the help of eqn (20).
co are found by fitting the experimental dependence of Tc on molar fraction of comonomers cco (Fig. 1B) by means of eqn (27)–(29). After finding all material parameters, radius of a microgel particle in the initial state R is calculated by approximating the dependence rh(T) with the help of eqn (20).
Observations show that parameters g1, Q0, ḡ2 and β are unaffected by cco. The effect of molar fraction of comonomers on radius of microgel particles R is illustrated in Fig. 1C, where the data are approximated by the linear equation
| R = R0(1 − cco) + R1cco | (31) |
To validate our results, we use observations of macroscopic P(NIPAm–tBA) gels prepared by means of a two-step process.55 First, tBA monomers were dissolved in an aqueous solution of sodium dodecyl sulfate (SDS) at 80 °C. Afterwards, cross-linking polymerization was performed at room temperature of NIPAm monomers in an emulsion of tBA by using BIS as a cross-linker, APS as an initiator and N,N,N′,N′-tetramethylethylenediamine (TEMED) as an accelerator. The effect of molar fraction of comonomers cco on the volume phase transition temperature Tc is illustrated in Fig. 1D, where experimental data are plotted together with predictions of eqn (27) and (29) (without fitting parameters).
3.2 P(NIPAm–NtBAm) microgels
We analyze observations on poly(N-isopropylacrylamide-co-N-tert-butylacrylamide) (P(NIPAm–NtBAm)) microgels synthesized by surfactant-free radical emulsion polymerization (4 h at 70 °C) of an aqueous solution of NIPAm and NtBAm monomers by using BIS (5 mol% with respect to monomers) as a cross-linker and potassium peroxodisulfate (KPS) as an initiator.56 Experimental swelling curves on microgels with cco = 0 and 0.15 are reported in Fig. 2A and those on microgels with cco = 0.05 and 0.10 are depicted in Fig. S-2A and B† together with results of simulation with the material constants collected in Table S-1.†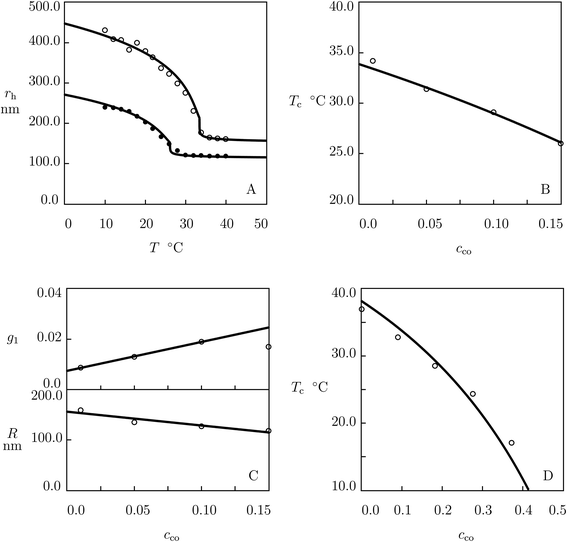 | ||
| Fig. 2 (A) Hydrodynamic radius rh of microgel particles versus temperature T. Symbols: experimental data56 on P(NIPAm–NtBAm) microgels with molar fractions of comonomers cco = 0 (○) and cco = 0.15 (●). Solid lines: results of simulation. (B) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data. Solid line: results of simulation. (C) Dimensionless modulus g1 and radius R versus molar fraction of comonomers cco. Circles: treatment of observations. Solid lines: results of simulation. (D) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data57 on P(NIPAm–NtBAm) microgels. Solid line: predictions of the model. | ||
Adjustable parameters are determined by the same method that was applied to fit observations in Fig. 1. The only difference is that the dimensionless modulus g1 is presumed to be affected by molar fraction of comonomers. For each cco, this quantity is calculated by matching the swelling diagram Q(T) below the critical temperature Tc. The coefficient ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co is found by fitting the experimental dependence Tc(cco) reported in Fig. 2B.
co is found by fitting the experimental dependence Tc(cco) reported in Fig. 2B.
The effect of molar fraction of comonomers on the elastic modulus g1 and radius of microgel particles R is demonstrated in Fig. 2C, where the data are approximated by eqn (21) and (31). This figure shows that g1 increases and R decreases with cco for a strongly hydrophobic comonomer NtBAm.
To verify our findings, we use experimental data on P(NIPAm–NtBAm) microgels synthesized by precipitation polymerization (4 h at 70 °C) of an aqueous solution of NIPAm and NtBAm monomers by using BIS (molar fraction is not provided) as a cross-linker, APS as an initiator, and TWEEN-20 as a non-ionic surfactant.57 The experimental dependence of the volume phase transition temperature Tc on molar fraction of comonomers cco is reported in Fig. 2D together with predictions of the model.
3.3 P(NIPAm–HEMA) gels
We now approximate experimental swelling diagrams on poly(N-isopropylacrylamide-co-2-hydroxyethyl methacrylate) (P(NIPAm–HEMA)) hydrogels. The gels were prepared by free radical cross-linking polymerization (1 day at room temperature) of a solution of NIPAm and HEMA monomers in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of water and acetone by using BIS (3 mol% with respect to monomers) as a cross-linker, APS as an initiator, and TEMED as an accelerator.58 Experimental swelling diagrams on gels with cco = 0, 0.1 and 0.3 are presented in Fig. 3A together with results of simulation with the material parameters listed in Table S-1.† The effect of molar fraction of HEMA monomers cco on the volume phase transition temperature Tc is illustrated in Fig. 3B, where the data are approximated by means of eqn (27)–(29).
1 mixture of water and acetone by using BIS (3 mol% with respect to monomers) as a cross-linker, APS as an initiator, and TEMED as an accelerator.58 Experimental swelling diagrams on gels with cco = 0, 0.1 and 0.3 are presented in Fig. 3A together with results of simulation with the material parameters listed in Table S-1.† The effect of molar fraction of HEMA monomers cco on the volume phase transition temperature Tc is illustrated in Fig. 3B, where the data are approximated by means of eqn (27)–(29).
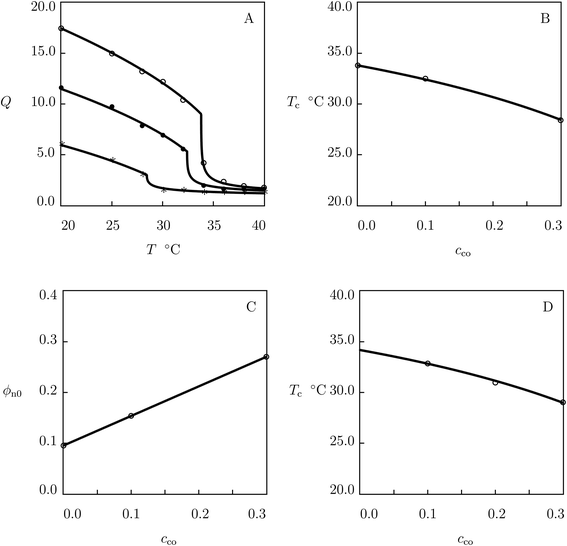 | ||
| Fig. 3 (A) Degree of swelling Q versus temperature T. Symbols: experimental data58 on P(NIPAm–HEMA) gels with molar fractions of comonomers cco = 0 (○), cco = 0.1 (●) and cco = 0.3 (*). Solid lines: results of simulation. (B) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data. Solid line: results of simulation. (C) Parameter ϕn0 versus molar fraction of comonomers cco. Circles: treatment of observations. Solid line: results of simulation. (D) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data59 on P(NIPAm–HEMA) microgels. Solid line: predictions of the model. | ||
Each swelling curve in Fig. 3A is fitted separately with the help of the only parameter: volume fraction of polymer network in the reference state ϕn0. This quantity is found by approximation of observations below Tc. Evolution of ϕn0 with cco is demonstrated in Fig. 3C, where the data are approximated by eqn (22).
To confirm that ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co is determined correctly, we study observations on P(NIPAm–HEMA) microgels synthesized by surfactant-free radical polymerization (4 h at 90 °C) of an aqueous solution of NIPAm and NEMA monomers by using BIS (2 mol% with respect to NIPAm monomers) as a cross-linker and APS as an initiator.59 The effect of comonomers on the volume phase transition temperature is reported in Fig. 3D, where experimental data are plotted together with predictions of the model.
co is determined correctly, we study observations on P(NIPAm–HEMA) microgels synthesized by surfactant-free radical polymerization (4 h at 90 °C) of an aqueous solution of NIPAm and NEMA monomers by using BIS (2 mol% with respect to NIPAm monomers) as a cross-linker and APS as an initiator.59 The effect of comonomers on the volume phase transition temperature is reported in Fig. 3D, where experimental data are plotted together with predictions of the model.
To demonstrate that the value of ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co found by matching experimental data in Fig. 3A can be used not only in prediction of Tc, but also in the analysis of swelling diagrams, we focus on observations on P(NIPAm–HEMA) gels prepared by free-radical cross-linking polymerization (1 day at 4 °C) in an aqueous solution of NIPAm and HEMA monomers (0.74 M) by using BIS (2.4 mol% with respect to monomers) as a cross-linker, KPS as an initiator, and TEMED as an accelerator.60 Equilibrium swelling curves on the copolymer gels with cco ranging from 0 to 0.47 immersed into phosphate buffer solution (with pH = 7 and ionic strength 0.1) are reported in Fig. S-3A† together with results of numerical analysis with the material parameters collected in Table S-1.† Each set of data in Fig. S-3A† is determined by the only parameter ϕn0. The effect of molar fraction of comonomers on this quantity is illustrated in Fig. S-3B,† where the data are approximated by eqn (22).
co found by matching experimental data in Fig. 3A can be used not only in prediction of Tc, but also in the analysis of swelling diagrams, we focus on observations on P(NIPAm–HEMA) gels prepared by free-radical cross-linking polymerization (1 day at 4 °C) in an aqueous solution of NIPAm and HEMA monomers (0.74 M) by using BIS (2.4 mol% with respect to monomers) as a cross-linker, KPS as an initiator, and TEMED as an accelerator.60 Equilibrium swelling curves on the copolymer gels with cco ranging from 0 to 0.47 immersed into phosphate buffer solution (with pH = 7 and ionic strength 0.1) are reported in Fig. S-3A† together with results of numerical analysis with the material parameters collected in Table S-1.† Each set of data in Fig. S-3A† is determined by the only parameter ϕn0. The effect of molar fraction of comonomers on this quantity is illustrated in Fig. S-3B,† where the data are approximated by eqn (22).
3.4 P(NIPAm–TREGMA) microgels
We match experimental data on poly(N-isopropylacrylamide-co-triethyleneglycol methacrylate) P(NIPAm–TREGMA) microgels prepared by surfactant-free precipitation polymerization (6 h at 75 °C) of an aqueous solution on NIPAm and TREGMA monomers by using BIS (5 mol% with respect to monomers) as a cross-linker and KPS as an initiator.61 Equilibrium swelling diagrams on microgels with cco = 0 and 0.12 are reported in Fig. 4A and those on microgels with cco = 0.04 and 0.08 are presented in Fig. S-4A and B† together with results of simulation with the materials constants collected in Table S-1.† The effect of molar fraction of TREGMA comonomers on the critical temperature Tc is illustrated in Fig. 4B, where the data are approximated by eqn (27)–(29).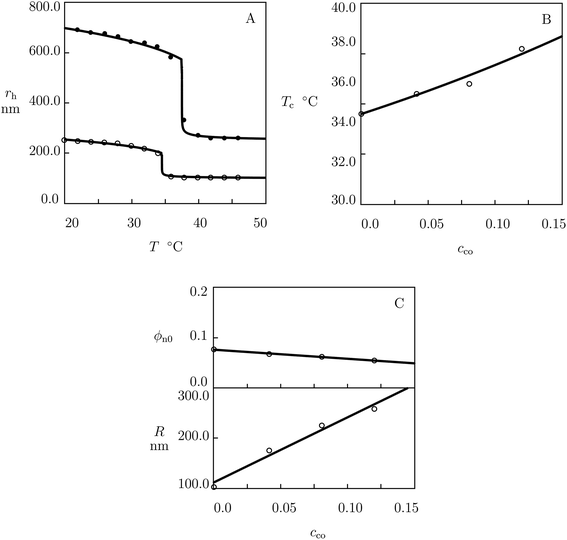 | ||
| Fig. 4 (A) Hydrodynamic radius rh of microgel particles versus temperature T. Symbols: experimental data61 on P(NIPAm–TREGMA) microgels with molar fractions of comonomers cco = 0 (○) and cco = 0.12 (●). Solid lines: results of simulation. (B) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data. Solid line: results of simulation. (C) Parameters ϕn0 and R versus molar fraction of comonomers cco. Circles: treatment of observations. Solid lines: results of simulation. | ||
Each swelling diagram in Fig. 4A and S-4† is fitted by means of two parameters: volume fraction of polymer network in the reference state ϕn0 (this coefficient is determined by matching experimental data below Tc) and radius R of microgel particles in the initial state (this quantity is calculated by fitting the dependence rh(T) with the help of eqn (20)). Changes in ϕn0 and R with cco are demonstrated in Fig. 4C, where the data are approximated by eqn (22) and (31).
3.5 P(NIPAm–DMAAm) gels and microgels
We begin with fitting swelling diagrams on poly(N-isopropylacrylamide-co-N,N-dimethylacrylamide) (P(NIPAm–DMAAm)) gels prepared by free-radical polymerization (1 day at 55 °C) of a solution on NIPAm and DMAAm monomers in methanol by using BIS (3.3 mol% with respect to monomers) as a cross-linker and azobisisobutyronitrile (AIBN) as an initiator.62 Experimental data in equilibrium water uptake tests on gels with molar fractions of comonomers cco = 0 and 0.3 are reported in Fig. 5A, where degree of swelling Q is plotted versus temperature T together with results of simulation with the material parameters listed in Table S-1.† The effect of molar fraction of DMAAm comonomers on the volume phase transition temperature Tc is illustrated in Fig. 5B, where the data are approximated by eqn (27)–(29).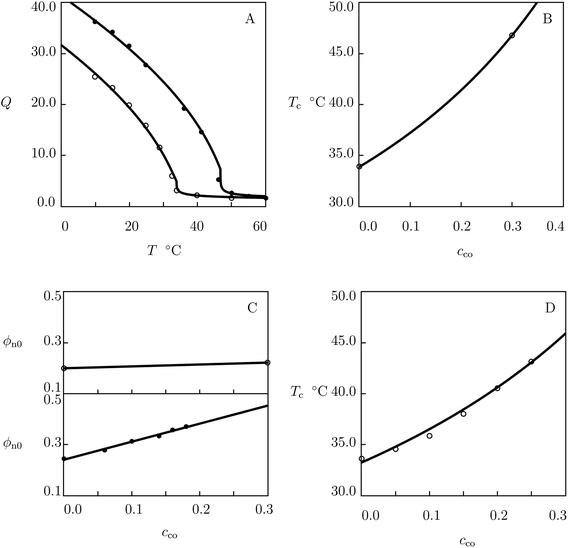 | ||
| Fig. 5 (A) Degree of swelling Q versus temperature T. Symbols: experimental data62 on P(NIPAm–DMAAm) gels with molar fractions of comonomers cco = 0 (○) and cco = 0.3 (●). Solid lines: results of simulation. (B) Volume phase transition temperature Tc versus molar fraction cco of comonomers. Circles: experimental data. Solid line: results of simulation. (C) Parameter ϕn0 versus molar fraction of comonomers cco. Symbols: treatment of observations on P(NIPAm–DMAAm) gels (○) and microgels (●). Solid lines: results of simulation. (D) Volume phase transition temperature Tc versus molar fraction of DMAAm comonomers cco. Circles: experimental data63 on P(NIPAm–DMAAm) gels. Solid line: predictions of the model. | ||
Each set of observations in Fig. 5A is determined by the only parameter ϕn0. Evolution of this quantity with cco is shown in Fig. 5C, where the data are matched by means of eqn (22).
The modified FH parameter ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co is calculated by using only two data points in Fig. 5B. To show that even a small number of observations ensures sufficient accuracy in determination of this parameter, we study experimental data on P(NIPAm–DMAAm) gels prepared by free-radical polymerization at room temperature of an aqueous solution of monomers (0.7 M) by using BIS (3.2 mol% with respect to monomers) as a cross-linker, APS as an initiator, and TEMED as an accelerator.63 Fig. 5D demonstrates good agreement between predictions of the model and experimental volume phase transition temperatures Tc of copolymer gels with cco ranging from 0.0 to 0.25.
co is calculated by using only two data points in Fig. 5B. To show that even a small number of observations ensures sufficient accuracy in determination of this parameter, we study experimental data on P(NIPAm–DMAAm) gels prepared by free-radical polymerization at room temperature of an aqueous solution of monomers (0.7 M) by using BIS (3.2 mol% with respect to monomers) as a cross-linker, APS as an initiator, and TEMED as an accelerator.63 Fig. 5D demonstrates good agreement between predictions of the model and experimental volume phase transition temperatures Tc of copolymer gels with cco ranging from 0.0 to 0.25.
To compare the thermo-mechanical responses of macroscopic gels and microgels, we analyze observations on P(NIPAm–DMAAm) microgels synthesized by free-radical polymerization (6 h at 75 °C) of an aqueous solution of NIPAm and DMAAm monomers (170 mM) by using BIS (1.4 mol% with respect to monomers) as a cross-linker, SDS (0.75 mol% with respect to monomers) as a surfactant, and KPS as an initiator.64 Experimental data on microgels with cco = 0 and 0.18 are plotted in Fig. 6A and those on microgels with cco = 0.06, 0.10, 0.14 and 0.16 are depicted in Fig. S-5A–D.† In these figures, experimental dependencies of the hydrodynamic radius rh on temperature T are reported together with results of simulation with the material parameters collected in Table S-1.†
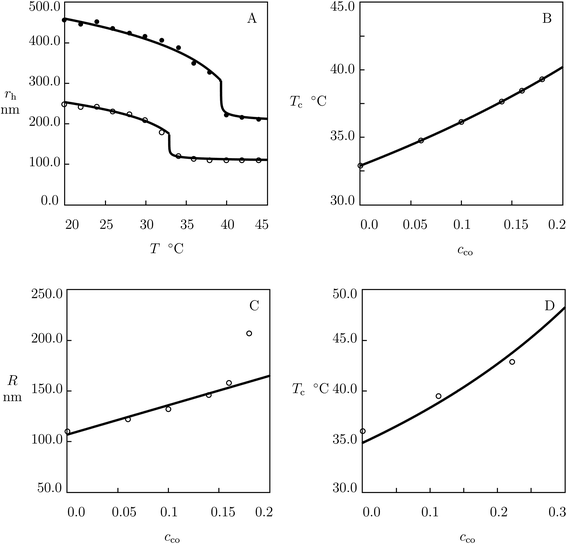 | ||
| Fig. 6 (A) Hydrodynamic radius rh of microgel particles versus temperature T. Symbols: experimental data64 on P(NIPAm–DMAAm) microgels with molar fractions of comonomers cco = 0 (○) and cco = 0.18 (●). Solid lines: results of simulation. (B) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data. Solid line: predictions of the model. (C) Radius R versus molar fraction of comonomers cco. Circles: treatment of observations. Solid line: results of simulation. (D) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data57 on P(NIPAm–DMAAm) microgels. Solid line: predictions of the model. | ||
The effect of molar fraction of comonomers on the volume phase transition temperature Tc is illustrated in Fig. 6B, where experimental data are reported together with predictions of the model (the parameter ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co is found by fitting observations in Fig. 5B).
co is found by fitting observations in Fig. 5B).
Each set of observations in Fig. 6A and S-5† is matched by means of two parameters: ϕn0 (which is found by fitting swelling curves below Tc) and R (which is calculated by matching the experimental dependence rh(T) with the help of eqn (20)). The influence of cco on ϕn0 is illustrated in Fig. 5C, where the data are fitted by eqn (22). Changes in radius R with cco are demonstrated in Fig. 6C, where the data are approximated by eqn (31).
To confirm that the volume phase transition temperature of P(NIPAm–DMAAm) microgels can be predicted correctly by using ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co determined by fitting observations on macroscopic gels, we study experimental data on microgels synthesized by precipitation polymerization (4 h at 70 °C) of an aqueous solution of monomers by using BIS (4 mol% with respect to monomers) as a cross-linker, APS as an initiator, and TWEEN-20 as a non-ionic surfactant.57 Fig. 6D reveals an acceptable agreement between predictions of the model and experimental data on microgels with cco ranging from 0.0 to 0.22.
co determined by fitting observations on macroscopic gels, we study experimental data on microgels synthesized by precipitation polymerization (4 h at 70 °C) of an aqueous solution of monomers by using BIS (4 mol% with respect to monomers) as a cross-linker, APS as an initiator, and TWEEN-20 as a non-ionic surfactant.57 Fig. 6D reveals an acceptable agreement between predictions of the model and experimental data on microgels with cco ranging from 0.0 to 0.22.
3.6 P(NIPAm–AAm) microgels
Finally, we analyze observations on poly(N-isopropylacrylamide-co-acrylamide) (P(NIPAm–AAm)) microgels prepared by precipitation polymerization (4.5 h at 70 °C) of an aqueous solution of monomers (0.12 M) by using BIS (1 mol% with respect to monomers) as a cross-linker, KPS as an initiator, and SDS (0.5 mol% with respect to monomers) as a surfactant.65 The experimental dependencies of the hydrodynamic radius rh on temperature T for microgels with cco = 0 and 0.05 and 0.10 are reported in Fig. 7A together with results of simulation with the material parameters collected in Table S-1.† The effect of molar fraction of comonomers on the volume phase transition temperature Tc is demonstrated in Fig. 7B, where the data are approximated by eqn (27)–(29).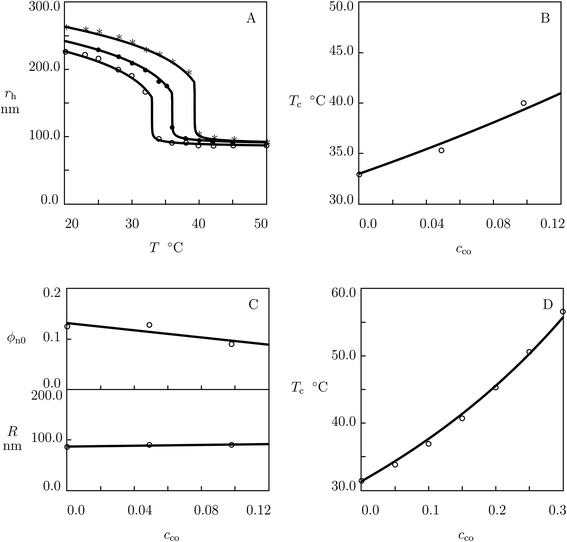 | ||
| Fig. 7 (A) Hydrodynamic radius rh of microgel particles versus temperature T. Symbols: experimental data65 on P(NIPAm–AAm) microgels with molar fractions of comonomers cco = 0 (○), cco = 0.05 (●) and cco = 0.10 (*). Solid lines: results of simulation. (B) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data. Solid line: results of simulation. (C) Parameters ϕn0 and R versus molar fraction of comonomers cco. Circles: treatment of observations. Solid lines: results of simulation. (D) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data66 on PVA/P(NIPAm–AAm) gels with interpenetrating network. Solid line: predictions of the model. | ||
Each set of observations in Fig. 7A is determined by two parameters: volume fraction of polymer network in the reference state ϕn0 (this coefficient is determined by matching experimental data below Tc) and radius R of microgel particles in the initial state (which is calculated by matching the dependence rh(T) by eqn (20)). Changes in ϕn0 and R with cco are illustrated in Fig. 7C, where the data are approximated by eqn (22) and (31). This figure shows that ϕn0 and R remain practically independent of cco.
To examine the ability of the model to predict the volume phase transition temperature of P(NIPAm–AAm) macroscopic gels based on observations on microgels, we analyze observations on gels with interpenetrating polymer network (IPN) formed by poly(vinyl alcohol) (PVA) and P(NIPAm–AAm) chains.66 The gels were prepared by polymerization of NIPAm and AAm monomers in a 15 wt% aqueous solution of PVA chains. First, PVA chains were cross-linked (6 h at room temperature) by using glutaraldehyde (GDA, 0.5 mol% with respect to PVA). Afterwards, cross-linking photo-polymerization (12 h at room temperature) of NIPAM and AAm monomers was conducted by using BIS (0.2 mol% with respect to monomers) as a cross-linker and 2-ketoglutaric acid (KGA) as an initiator. The growth of Tc with molar fraction of AAm comonomers cco is demonstrated in Fig. 7D, where experimental data are presented together with predictions of the model.
4 Discussion
Fig. 1–7 confirm the ability of the model to describe experimental swelling diagrams on thermo-responsive copolymer microgels and macroscopic gels. The entire set of equilibrium swelling curves for gels with a particular comonomer is determined by one (Fig. 1, 3 and 6) or two (Fig. 2, 4, 5 and 7) adjustable parameters. The effect of molar fraction of comonomers on these quantities is described by eqn (21), (22) and (31).The influence of comonomers on the volume phase transition temperature Tc is determined by eqn (27) and (29). These relations involve the only adjustable parameter ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co. Fig. 1–7 reveal that the coefficient
co. Fig. 1–7 reveal that the coefficient ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co is practically independent of preparation conditions and concentrations of monomers and cross-linker. This allows the effect of molar fraction of comonomers on the critical temperature of microgels to be predicted when this effect is known for macroscopic gels (Fig. 1 and 7) and vice versa (Fig. 3, 5 and 6).
co is practically independent of preparation conditions and concentrations of monomers and cross-linker. This allows the effect of molar fraction of comonomers on the critical temperature of microgels to be predicted when this effect is known for macroscopic gels (Fig. 1 and 7) and vice versa (Fig. 3, 5 and 6).
Comparison of material parameters in Table S-1† demonstrates that g1, ḡ2, χmax and β adopt similar values that are weakly affected by the size (micro- versus macro-) and conditions of synthesis for the gels. In particular, χmax (this quantity characterizes the volume phase transition temperature for homopolymer PNIPAm gels) varies in a narrow interval between 0.51 and 0.64, which corresponds to small (about 4 K) variations in Tc driven by the temperature and solvent used in preparation of hydrogels. Changes in Q0 induced the presence of comonomers are more pronounced: from 0.1 for strongly hydrophobic comonomers (tBA and NtBAm) up to more than 10 for hydrophilic comonomers (AAm). It is worth noting that these changes are not caused by molar fractions of monomers in pre-gel solutions: for all microgels under consideration, these fractions vary in the interval between 0.08 and 0.17 M.
Comonomers can be roughly split into two groups: (i) more hydrophobic than NIPAm (tBA, NIBAm, HEMA; their incorporation causes a reduction in the volume phase transition temperature) and (ii) more hydrophilic than NIPAm (PREGMA, DMAAm, AAm; copolymerization with these moieties leads to an increase in Tc). Fig. 1–7 show that the presence of hydrophobic comonomers results in a decrease in radius R (that characterizes the size of microgels in the dry state), while incorporation of hydrophilic monomers induces an increase in R.67 Evolution of the volume fraction of polymer network in the reference (stress-free) state ϕn0 obeys more sophisticated dependencies, as this parameter is strongly affected by hydrogen bonds between segments of chains. Concentration of these bonds depends not only on the hydrophilicity of comonomers, but on the presence of surfactant, temperature of polymerization, and composition of solvents used in preparation.68
Bearing in mind that the critical temperature Tc is determined uniquely by the modified FH parameter ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co, see eqn (27) and (29), which, in turn, serves as a measure of hydrophilicity of chains, it is tempting to connect this quantity with the Hildebrand solubility parameter of comonomers δH. Several attempts have previously been undertaken to establish correlations between the FH parameter of homopolymer and copolymer gels with the Hildebrand and Hansen solubility parameters, see ref. 69–72, to mention a few. An advantage of this approach is that the Hildebrand solubility parameter of comonomers can be evaluated straightforwardly by means of the group contribution method,73 whereas the accuracy of this method for calculation of the FH parameter (by using the UNIQUAC equation or its modifications74,75) is rather modest.76–78 Possible reasons for such an inaccuracy are discussed in ref. 79. The most important of them is that the group contribution method estimates the energy contribution to the FH parameter, but it disregards the contribution of entropy.
co, see eqn (27) and (29), which, in turn, serves as a measure of hydrophilicity of chains, it is tempting to connect this quantity with the Hildebrand solubility parameter of comonomers δH. Several attempts have previously been undertaken to establish correlations between the FH parameter of homopolymer and copolymer gels with the Hildebrand and Hansen solubility parameters, see ref. 69–72, to mention a few. An advantage of this approach is that the Hildebrand solubility parameter of comonomers can be evaluated straightforwardly by means of the group contribution method,73 whereas the accuracy of this method for calculation of the FH parameter (by using the UNIQUAC equation or its modifications74,75) is rather modest.76–78 Possible reasons for such an inaccuracy are discussed in ref. 79. The most important of them is that the group contribution method estimates the energy contribution to the FH parameter, but it disregards the contribution of entropy.
For the comonomers used in the analysis of swelling of macro- and microgels, the modified FH parameter ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co is reported in Table S-2† together with the Hildebrand solubility parameter δH calculated by means of the Hoftyzer–van Krevelen method (Table 7.10 in ref. 73). Table S-2† shows that
co is reported in Table S-2† together with the Hildebrand solubility parameter δH calculated by means of the Hoftyzer–van Krevelen method (Table 7.10 in ref. 73). Table S-2† shows that ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co is reduced with δH. The data are reported in Fig. 8A, where they are approximated by the linear equation
co is reduced with δH. The data are reported in Fig. 8A, where they are approximated by the linear equation
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co = c0 − c1δH co = c0 − c1δH
| (32) |
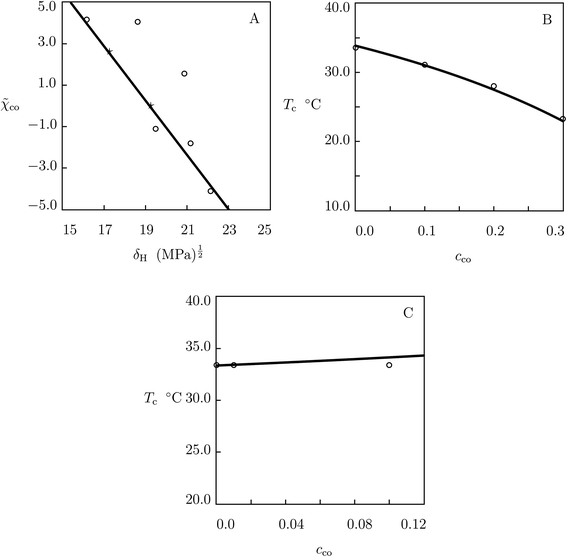 | ||
Fig. 8 (A) The modified Flory–Huggins parameter ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co versus the Hildebrand solubility of comonomers δH. Circles: treatment of observations. Solid line: results of simulation. Stars: predictions for EA and AAc comonomers. (B and C) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data on P(NIPAm–EA) microgels59 (B) and P(NIPAm–AAc) gels in water with pH = 1 (ref. 82) (C). Solid lines: predictions of the model. co versus the Hildebrand solubility of comonomers δH. Circles: treatment of observations. Solid line: results of simulation. Stars: predictions for EA and AAc comonomers. (B and C) Volume phase transition temperature Tc versus molar fraction of comonomers cco. Circles: experimental data on P(NIPAm–EA) microgels59 (B) and P(NIPAm–AAc) gels in water with pH = 1 (ref. 82) (C). Solid lines: predictions of the model. | ||
Fig. 8A reveals an acceptable agreement between the data and their description by eqn (32) for all comonomers except for NtBAm and HEMA (for which noticeable deviations are observed between results of simulation and predictions of eqn (32)). These deviations for P(NIPAm–NtBAm) microgels can be ascribed to built-up of aggregates formed by NtBAm monomers and hydrophobic segments of NIPAm monomers under preparation conditions. The fact that these aggregates remain sufficiently stable and they are not broken when temperature decreases below Tc is confirmed by Fig. 2C, which shows an increase in g1 with cco. For P(NIPAm–HEMA) gels, these deviations are ascribed to formation of hydrogen bonds between water molecules and HEMA segments,80 which cause an “unusual” thermo-mechanical behavior of these gels.81
To demonstrate the ability of eqn (27), (29) and (32) to predict the effect of molar fraction of comonomers on the volume phase transition temperature Tc, we study two sets of observations on copolymer gels not included into Table S-2.†
We begin with the analysis of poly(N-isopropylacrylamide-co-ethylacrylate) (P(NIPAm–EA)) microgels prepared by precipitation polymerization (4 h at 90 °C) of an aqueous solution of PNIPAm and EA monomers (0.32 M) by using BIS (2 mol% with respect to monomers) as a cross-linker and APS as an initiator.59 In simulation, we find δH = 18.32 (MPa)1/2 by means of the Hoftyzer–van Krevelen method for EA, determine ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co = 2.595 from eqn (32) and Fig. 8A, calculate the dependence Tc(cco) from eqn (27) and (29), and present results of numerical analysis in Fig. 8B together with experimental values of Tc for microgels with cco = 0.1, 0.2 and 0.3.
co = 2.595 from eqn (32) and Fig. 8A, calculate the dependence Tc(cco) from eqn (27) and (29), and present results of numerical analysis in Fig. 8B together with experimental values of Tc for microgels with cco = 0.1, 0.2 and 0.3.
We proceed with prediction of the volume phase transition temperature for poly(N-isopropylacrylamide-co-acrylic acid) (P(NIPAm–AAc)) gels synthesized by free-radical cross-linking copolymerization (6 h at 25 °C) of an aqueous solution of NIPAm (1.55 M) and AAc monomers by using BIS (0.5 mol% with respect to monomers) as a cross-linker, APS as an initiator, and TEMED as an accelerator.82 Following the above procedure, we find δH = 21.31 (MPa)1/2 by the Hoftyzer–van Krevelen method for AAc, determine ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co = −0.0183 from eqn (32) and Fig. 8A, and calculate the dependence Tc(cco) from eqn (27) and (29). Bearing in mind that AAc is an ionic monomer with pKa close to 4.2, we report results of simulation in Fig. 8C together with experimental values of Tc for gels with cco = 0.01 and 0.1 in water with pH = 1 (under this condition, ionization of comonomers can be disregarded).
co = −0.0183 from eqn (32) and Fig. 8A, and calculate the dependence Tc(cco) from eqn (27) and (29). Bearing in mind that AAc is an ionic monomer with pKa close to 4.2, we report results of simulation in Fig. 8C together with experimental values of Tc for gels with cco = 0.01 and 0.1 in water with pH = 1 (under this condition, ionization of comonomers can be disregarded).
Fig. 8B and C show an acceptable agreement between the observations on Tc and predictions of the model. This implies that eqn (27), (29) and (32) can be used for “quick-and-dirty” evaluation of the effect of molar fraction of comonomers on the volume phase transition temperature of macro- and microgels.
5 Conclusions
A model is developed for equilibrium swelling of thermo-responsive copolymer gels. Following,25,27 we presume chains in the polymer network to involve hydrophilic and hydrophobic segments. Below the volume phase transition temperature Tc, each hydrophobic segment is surrounded by a cage-like structure formed by water molecules bridged by hydrogen bonds. An increase in temperature induces breakage of these structures driven by thermal fluctuations. This process is accompanied by aggregation of hydrophobic segments and formation of clusters from which water molecules are expelled. These clusters serve as extra physical bonds between chains in the collapsed state of a gel. This scenario allows a pronounced increase in the elastic modulus of macroscopic gels30 and microgels31 above Tc to be described, on the one hand, and unrealistic values of the Flory–Huggins parameter39 to be excluded from consideration, on the other.Unlike the conventional approach grounded on the Flory–Rehner concept,36 where the FH parameter χ is modeled as a nonlinear function of temperature and volume fraction of the polymer network, we treat χ as a linear function of temperature T only. Presuming the volume phase transition to occur in a homopolymer gel when χ reaches its maximum value χmax, a simple relation, eqn (14), is derived for the critical temperature Tc. With the help of the three-parameter model for the FH parameter of copolymer gels,47 this formula is extended to gels prepared by copolymerization of thermo-responsive and temperature-insensitive nonionic monomers, see eqn (27) and (29).
An advantage of the model is that it involves a relatively small number of material constant. According to eqn (30), for copolymer gels with NIPAm monomers as the main component of the network and an arbitrary molar fraction cco of comonomers, the entire set of equilibrium swelling diagrams Q(T) is described by six parameters with transparent physical meaning: g1 and ḡ2 are the dimensionless elastic moduli in the swollen and collapsed states, ϕn0 denotes volume fraction of the polymer network in the stress-free state, χmax and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co stand for the FH parameters of NIPAm monomers and comonomers, and β characterizes the rate of aggregation of hydrophobic segments above Tc. To describe the equilibrium water uptake by a microgel (characterized by the dependence of its hydrodynamic radius rh on temperature T), an extra parameter R (the radius of a microgel particle in the dry state) is added. Analysis of observations on copolymer gels and microgels reveals that only g1, ϕn0 and R may be affected by cco. The other material parameters found by matching observations on homopolymer gels can be used for copolymer gels without modification.
co stand for the FH parameters of NIPAm monomers and comonomers, and β characterizes the rate of aggregation of hydrophobic segments above Tc. To describe the equilibrium water uptake by a microgel (characterized by the dependence of its hydrodynamic radius rh on temperature T), an extra parameter R (the radius of a microgel particle in the dry state) is added. Analysis of observations on copolymer gels and microgels reveals that only g1, ϕn0 and R may be affected by cco. The other material parameters found by matching observations on homopolymer gels can be used for copolymer gels without modification.
The model is applied to fit experimental data on macroscopic gels and microgels prepared by copolymerization of NIPAm monomers with hydrophobic (tBA, NtBAm, HEMA) and hydrophilic (TREGMA, DMAAm, AAm) comonomers. The criteria of hydrophobicity and hydrophilicity of comonomers read ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co > −χmax and
co > −χmax and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co < −χmax, respectively. Fig. 1–7 demonstrate good agreement between observations and results of numerical simulation. An important conclusion of the analysis is that the effect of comonomers on the volume phase transition temperature Tc is independent of preparation conditions for macro- and microgels.
co < −χmax, respectively. Fig. 1–7 demonstrate good agreement between observations and results of numerical simulation. An important conclusion of the analysis is that the effect of comonomers on the volume phase transition temperature Tc is independent of preparation conditions for macro- and microgels.
To establish correlations between the modified FH parameter of comonomers ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) co and their Hildebrand solubility parameter δH, phenomenological eqn (32) is suggested. This relation together with eqn (27) and (29) predicts changes in the critical temperature of copolymer gels by using an estimate of δH developed with the help of the group contribution method. Application of this method to P(NIPAm–EA) and P(NIPAm–AAc) copolymer gels reveals reasonable agreement between experimental data and results of simulation. This agreement confirms that the simplified approach can be used for a “quick-and-dirty” prediction of the volume phase transition temperature of copolymer gels.
co and their Hildebrand solubility parameter δH, phenomenological eqn (32) is suggested. This relation together with eqn (27) and (29) predicts changes in the critical temperature of copolymer gels by using an estimate of δH developed with the help of the group contribution method. Application of this method to P(NIPAm–EA) and P(NIPAm–AAc) copolymer gels reveals reasonable agreement between experimental data and results of simulation. This agreement confirms that the simplified approach can be used for a “quick-and-dirty” prediction of the volume phase transition temperature of copolymer gels.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support by Innovationsfonden (Innovation Fund Denmark, project 9091-00010B) is gratefully acknowledged.References
- Y. J. Kim and Y. T. Matsunaga, J. Mater. Chem. B, 2017, 5, 4307–4321 RSC.
- P. Zarrintaj, M. Jouyandeh, M. R. Ganjali, B. S. Hadavand, M. Mozafari, S. S. Sheiko, M. Vatankhah-Varnoosfaderani, T. J. Gutierrez and M. R. Saeb, Eur. Polym. J., 2019, 117, 402–423 CrossRef CAS.
- M. A. Haq, Y. Su and D. Wang, Mater. Sci. Eng., C, 2017, 70, 842–855 CrossRef.
- L. Tang, L. Wang, X. Yang, Y. Feng, Y. Li and W. Feng, Prog. Mater. Sci., 2021, 115, 100702 CrossRef CAS.
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231–6255 CrossRef CAS.
- D. G. He, S. Wang, L. Lei, Z. Hou, P. Shang, X. He and H. Nie, Chem. Eng. Sci., 2015, 125, 108–120 CrossRef CAS.
- L. Kumar Meena, H. Rather, D. Kedaria and R. Vasita, Int. J. Polym. Mater. Polym. Biomater., 2020, 69, 381–397 CrossRef CAS.
- T. Shu, L. Hu, Q. Shen, L. Jiang, Q. Zhang and M. J. Serpe, J. Mater. Chem. B, 2020, 8, 7042–7061 RSC.
- Y. Lua and M. Ballauff, Prog. Polym. Sci., 2011, 36, 767–792 CrossRef.
- M. Zarei, TrAC, Trends Anal. Chem., 2017, 93, 7–22 CrossRef CAS.
- L. E. Theune, R. Charbaji, M. Kar, S. Wedepohl, S. Hedtrich and M. Calderon, Mater. Sci. Eng., C, 2019, 100, 141–151 CrossRef CAS.
- L. Tang, L. Gong, G. Zhou, L. Liu, D. Zhang, J. Tang and J. Zheng, Polymer, 2019, 173, 182–189 CrossRef CAS.
- Q. Shi, H. Liu, D. Tang, Y. Li, X.-J. Li and F. Xu, NPG Asia Mater., 2019, 11, 64 CrossRef.
- A. Gutowska, Y. H. Bae, H. Jacobs, S. W. Kim and J. Feijen, Macromolecules, 1994, 27, 4167–4175 CrossRef CAS.
- R. Y. O. Yoshida, T. Okano, Y. Sakurai and K. Sakai, J. Biomater. Sci., Polym. Ed., 1995, 6, 585–598 CrossRef.
- S. Ida, T. Kawahara, Y. Fujita, S. Tanimoto and Y. Hirokawa, Macromol. Symp., 2015, 350, 14–21 CrossRef CAS.
- H. Guo, N. Sanson, A. Marcellan and D. Hourdet, Macromolecules, 2016, 49, 9568–9577 CrossRef CAS.
- Y. Hirokawa and T. Tanaka, J. Chem. Phys., 1984, 81, 6379–6380 CrossRef.
- R. Pelton, Adv. Colloid Interface Sci., 2000, 85, 1–33 CrossRef CAS.
- W.-F. Lee and S.-H. Yen, J. Appl. Polym. Sci., 2000, 78, 1604–1611 CrossRef CAS.
- X.-J. Ju, L.-Y. Chu, X.-L. Zhu, L. Hu, H. Song and W.-M. Chen, Smart Mater. Struct., 2006, 15, 1767–1774 CrossRef CAS.
- A. D. Drozdov and J. deClaville Christiansen, J. Appl. Polym. Sci., 2018, 135, 46353 CrossRef.
- C. Wu, Polymer, 1998, 39, 4609–4619 CrossRef CAS.
- V. Aseyev, H. Tenhu and F. M. Winnik, Adv. Polym. Sci., 2011, 242, 29–89 CrossRef CAS.
- A. Halperin, M. Kroger and F. M. Winnik, Angew. Chem., Int. Ed., 2015, 54, 15342–15367 CrossRef CAS.
- H. Kojima, Polym. J., 2018, 50, 411–418 CrossRef CAS.
- D. Mukherji, C. M. Marques and K. Kremer, Annu. Rev. Condens. Matter Phys., 2020, 11, 271–299 CrossRef CAS.
- D. Kurzbach, M. J. N. Junk and D. Hinderberger, Macromol. Rapid Commun., 2013, 34, 119–134 CrossRef CAS.
- G. L. Puleo, F. Zulli, M. Piovanelli, M. Giordano, B. Mazzolai, L. Beccai and L. Andreozzi, React. Funct. Polym., 2013, 73, 1306–1318 CrossRef CAS.
- M. Lehmann, P. Krause, V. Miruchna and R. von Klitzing, Colloid Polym. Sci., 2019, 297, 633–640 CrossRef CAS.
- A. Aufderhorst-Roberts, D. Baker, R. J. Foster, O. Cayre, J. Mattsson and S. D. Connell, Nanoscale, 2018, 10, 16050–16061 RSC.
- A. D. Drozdov, Int. J. Appl. Mech., 2014, 6, 1450023 CrossRef.
- A. D. Drozdov and J. d. C. Christiansen, Int. J. Solids Struct., 2013, 50, 3570–3585 CrossRef CAS.
- A. D. Drozdov and J. deClaville Christiansen, Acta Mech., 2018, 229, 5067–5092 CrossRef.
- A. D. Drozdov and J. deClaville Christiansen, Polym. Int., 2020, 69, 974–984 CrossRef CAS.
- P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11, 521–526 CrossRef CAS.
- M. Quesada-Perez, J. A. Maroto-Centeno, J. Forcada and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 10536–10547 RSC.
- K. Dusek and M. Duskova-Smrckova, Gels, 2020, 6, 22 CrossRef.
- C. G. Lopez and W. Richtering, Soft Matter, 2017, 13, 8271–8280 RSC.
- A. D. Drozdov and J. deClaville Christiansen, Eur. Polym. J., 2017, 94, 56–67 CrossRef CAS.
- S. Seelenmeyer, I. Deike, S. Rosenfeldt, C. Norhausen, N. Dingenouts, M. Ballauff, T. Narayanan and P. Lindner, J. Chem. Phys., 2001, 114, 10471–10478 CrossRef CAS.
- Y. Suzuki, K. Tomonaga, M. Kumazaki and I. Nishio, Polym. Gels Networks, 1996, 4, 129–142 CrossRef CAS.
- T. Okajima, I. Harada, K. Nishio and S. Hirotsu, J. Chem. Phys., 2002, 116, 9068–9077 CrossRef CAS.
- W. McPhee, K. C. Tam and R. Pelton, J. Colloid Interface Sci., 1993, 156, 24–30 CrossRef CAS.
- Y. H. Bae, T. Okano and S. W. Kim, J. Polym. Sci., Part B: Polym. Phys., 1990, 28, 923–936 CrossRef CAS.
- M. Shibayama, Y. Shirotani, H. Hirose and S. Nomura, Macromolecules, 1997, 30, 7307–7312 CrossRef CAS.
- Z. S. Petrovic, W. J. MacKnight, R. Koningsveld and K. Dusek, Macromolecules, 1987, 20, 1088–1096 CrossRef CAS.
- W. H. Stockmayer, L. D. Moore, M. Fixman and B. N. Epstein, J. Polym. Sci., 1955, 16, 517–530 CrossRef CAS.
- T. K. Kwei, T. Nishi and R. F. Roberts, Macromolecules, 1974, 7, 667–674 CrossRef CAS.
- A. D. Drozdov and J. deClaville Christiansen, Polymer, 2017, 132, 164–173 CrossRef CAS.
- T. Norisuye, Y. Kida, N. Masui, Q. Tran-Cong-Miyata, Y. Maekawa, M. Yoshida and M. Shibayama, Macromolecules, 2003, 36, 6202–6212 CrossRef CAS.
- A. K. Lele, I. Devotta and R. A. Mashelkar, J. Chem. Phys., 1997, 106, 4768–4772 CrossRef CAS.
- H. S. Choi, J. M. Kim, K.-J. Lee and Y. C. Bae, J. Appl. Polym. Sci., 1999, 72, 1091–1099 CrossRef CAS.
- Q.-S. Zhang, L.-S. Zha, J.-H. Ma and B.-R. Liang, J. Appl. Polym. Sci., 2007, 103, 2962–2967 CrossRef CAS.
- J.-H. Park, J.-W. Jang, J.-H. Sim, I.-J. Kim, D.-J. Lee, Y.-H. Lee, S.-H. Park and H.-D. Kim, Int. J. Polym. Sci., 2019, 2019, 3824207 Search PubMed.
- Y. Hertle, M. Zeiser, C. Hasenohrl, P. Busch and T. Hellweg, Colloid Polym. Sci., 2010, 288, 1047–1059 CrossRef CAS.
- Y. D. Yi, K. S. Oh and Y. C. Bae, Polymer, 1997, 38, 3471–3476 CrossRef CAS.
- W.-F. Lee and Y.-L. Huang, J. Appl. Polym. Sci., 2000, 77, 1769–1781 CrossRef CAS.
- Y. G. Kim, C. H. Lee and Y. C. Bae, Fluid Phase Equilib., 2014, 361, 200–207 CrossRef CAS.
- H. Cicek and A. Tuncel, J. Polym. Sci., Part A: Polym. Chem., 1998, 36, 527–541 CrossRef CAS.
- X. Ma, J. Xi, X. Zhao and X. Tang, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 3575–3583 CrossRef CAS.
- S. Ida, T. Kawahara, H. Kawabata, T. Ishikawa and Y. Hirokawa, Gels, 2018, 4, 22 CrossRef.
- M. Shibayama, S.-y. Mizutani and S. Nomura, Macromolecules, 1996, 29, 2019–2024 CrossRef CAS.
- D. Zehm, A. Lieske and A. Stoll, Macromol. Chem. Phys., 2020, 221, 2000018 CrossRef CAS.
- Q. Wang, Y. Zhao, H. Xu, X. Yang and Y. Yang, J. Appl. Polym. Sci., 2009, 113, 321–326 CrossRef CAS.
- A. Szilagyi and M. Zrinyi, Polymer, 2005, 46, 10011–10016 CrossRef CAS.
- J. Gao and B. J. Frisken, Langmuir, 2005, 21, 545–551 CrossRef CAS.
- Q. Wang, C. S. Biswas, M. Galluzzi, Y. Wu, B. Du and F. J. Stadler, RSC Adv., 2017, 7, 9381–9392 RSC.
- K. Choi and W. H. Jo, Macromolecules, 1997, 30, 1509–1514 CrossRef CAS.
- T. Lindvig, M. L. Michelsen and G. M. Kontogeorgis, Fluid Phase Equilib., 2002, 203, 247–260 CrossRef CAS.
- S. Wu, H. Li, J. P. Chen and K. Y. Lam, Macromol. Theory Simul., 2004, 13, 13–29 CrossRef CAS.
- D. L. Olynick, P. D. Ashby, M. D. Lewis, T. Jen, H. Lu, J. A. Liddle and W. Chao, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 2091–2105 CrossRef CAS.
- D. W. van Krevelen and K. te Nijenhuis, Properties of Polymers, Elsevier, 4th edn, 2009 Search PubMed.
- D. S. Abrams and J. M. Prausnitz, AIChE J., 1975, 21, 116–128 CrossRef CAS.
- T. Oishi and J. M. Prausnitz, Ind. Eng. Chem. Process Des. Dev., 1978, 17, 333–339 CrossRef CAS.
- K. Poschlad and S. Enders, J. Chem. Thermodyn., 2011, 43, 262–269 CrossRef CAS.
- L. Ninni, V. Ermatchkov, H. Hasse and G. Maurer, Fluid Phase Equilib., 2014, 382, 235–243 CrossRef CAS.
- H. E. Yang and Y. C. Bae, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 455–463 CrossRef CAS.
- G. Y. Gor, J. Cannarella, C. Z. Leng, A. Vishnyakov and C. B. Arnold, J. Power Sources, 2015, 294, 167–172 CrossRef CAS.
- G. Su, T. Zhou, X. Liu and Y. Ma, Polym. Chem., 2017, 8, 865–878 RSC.
- B. Zhang, H. Tang and P. Wu, Polym. Chem., 2014, 5, 5967–5977 RSC.
- J. L. Velada, Y. Liu and M. B. Huglin, Macromol. Chem. Phys., 1998, 199, 1127–1134 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08619c |
| This journal is © The Royal Society of Chemistry 2020 |
