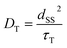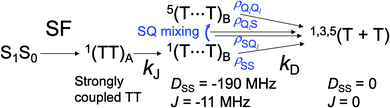DOI:
10.1039/C9SC04949E
(Edge Article)
Chem. Sci., 2020,
11, 2934-2942
Electron spin polarization generated by transport of singlet and quintet multiexcitons to spin-correlated triplet pairs during singlet fissions†
Received
1st October 2019
, Accepted 30th December 2019
First published on 21st February 2020
Abstract
Singlet fission (SF) is expected to exceed the Shockley–Queisser theoretical limit of efficiency of organic solar cells. Transport of spin-entanglement in the triplet–triplet pair state via one singlet exciton is a promising phenomenon for several energy conversion applications including quantum information science. However, direct observation of electron spin polarization by transport of entangled spin-states has not been presented. In this study, time-resolved electron paramagnetic resonance has been utilized to observe the transportation of singlet and quintet characters generating correlated triplet–triplet (T + T) exciton-pair states by probing the electron spin polarization (ESP) generated in thin films of 6,13-bis(triisopropylsilylethynyl)pentacene. We have clearly demonstrated that the ESP detected at the resonance field positions of individual triplet excitons is dependent on the morphology and on the detection delay time after laser flash to cause SF. ESP was clearly explained by quantum superposition of singlet–triplet–quintet wavefunctions via picosecond triplet-exciton dissociation as the electron spin polarization transfer from strongly exchange-coupled singlet and quintet TT states to weakly-coupled spin-correlated triplet pair states. Although the coherent superposition of spin eigenstates was not directly detected, the present interpretation of the spin correlation of the separated T + T exciton pair may pave new avenues not only for elucidating the vibronic role in the de-coupling between two excitons but also for scalable quantum information processing using quick T + T dissociation via one-photon excitation.
Introduction
Recent remarkable advances in organic materials of organic semiconductors have achieved power conversion efficiencies (PCE) close to 17% (ref. 1–3) for single junction organic solar cells (OSCs), although the PCE is still lower than the recent developments of 22–23% in solar cells employing organolead halide perovskites.4 Solid-state organic thin films composed of electron donor (D) and acceptor (A) organic materials have been utilized for generating photocarriers from the photoactive layer of OSCs.5 Singlet fission (SF)6 is expected to exceed the Shockley–Queisser theoretical limit7 with PCE ∼ 33% because two separated triplet excitons (T + T) can be produced from one excited singlet state (S1S0) sharing its excitation energy with a neighboring ground-state chromophore.8 Subsequent two charge-separation (CS) processes9 at the D:A domain interface after individual triplet-exciton diffusion may boost the photocurrent density of OSCs in the solid state. Application of SF-induced triplet generation is also promising for boosting the organic light emitting diode (OLED) efficiency.10 Several studies clarified the initial multiexciton (TT in Fig. 1) generation mechanism from the S1S0 state.8,11–17 More importantly, elucidation of the TT → T + T dissociation mechanism is highly desired. Dissociation time constants ranging from sub-picosecond to microsecond regions are reported.16–25 However little is known about how the T + T dissociation or the decoupling12,16,24 occurs from the strongly coupled TT state.
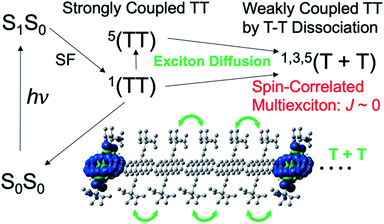 |
| | Fig. 1 Schematic representation of the spin-correlated triplet pair (SCTP) state of 1,3,5(T + T) generated by the SF in thin films of TIPS-Pn by the triplet energy transfer via the TT state. | |
In Fig. 1, the strongly coupled singlet TT state is known to be initially generated from the S1S0 state. Generation of the quintet state in the triplet–triplet pair17,22,23,25–28 has been reported and is thought to be essential for preventing the loss of the SF-born multiexciton through the singlet channels. Using the time-resolved electron paramagnetic resonance (TREPR) method for TIPS-tetracene thin films, Weiss et al.26 characterized the SF-induced strongly-coupled quintet of 5(TT) in Fig. 1. Quintet electron spin polarization (ESP) was detected as the microwave absorption (A) and emission (E) in 5(TT) for frozen aggregates of SF-materials.25 ESP was interpreted using the sublevel-selective quintet conversion by the zero-field splitting (ZFS) interaction at the singlet–quintet level-crossing in the presence of negative exchange coupling (J) during triplet exciton-diffusion and subsequent re-encounter in the highly disordered region, causing modulation of the J-coupling to result in spontaneous 5(TT) generation.25 Interestingly, transport of spin-entangled multiexcitons20,29–31 by the dissociative exciton diffusion has been observed using ultrafast transient absorption imaging of pentacene crystals32 and by the magnetic field effect on the fluorescence time-profiles. Although such transportation of spin-entanglements is key to elucidate the dissociation mechanism and to apply in quantum information science,33–35 no direct evidence for the transportation of spin-entanglements has been found in the separated T + T state with the singlet and quintet characters.
The present study thus focuses on how spin-entanglements develop and affect the direct TREPR detection of the T + T state. As shown in Fig. 1, when the triplet excitons are separated from each other to result in a negligible magnitude of exchange coupling (J ≈ 0), spin correlations in the triplet–triplet pair may occur to induce diagonalized nine spin-states as the quantum superpositions of the singlet–triplet–quintet character through the spin–spin dipolar couplings of individual triplet species. This is quite similar to the spin-correlated radical pair (SCRP) model33,34,36–42 in the photoinduced long-range charge-separation system generated by singlet or triplet precursors, causing the superpositions of the singlet–triplet characters when the J-coupling is small in the radical pairs. We herein demonstrate that the transportations of the SF-induced 5(TT) and 1(TT) characters can be distinguished on the T + T dissociation using the ESP of the correlated T–T state by applying TREPR spectroscopy to thin films of 6,13-bis(triisopropylsilylethynyl)pentacene (TIPS-Pn).
Methods
Chemicals and sample preparation
TIPS-Pn (Sigma-Aldrich) was used as received without further purification. 60 μL of 60 mM TIPS-Pn solution in chloroform was spin-coated on thin cover-glasses of 1 cm2 size using a spin coater (Mikasa MS-A100) with two different spinning rates of 300 rpm and 2000 rpm for 120 and 30 seconds, respectively. Each fabricated thin film was manually cut within a medicine paper to produce many small films of ca. 0.3 mm3 and they were placed in EPR sample tubes with a 5 mm diameter. EPR tubes containing small pieces of films produced with different spinning rates are shown in Fig. S1 of the ESI.†41 This quantity of powder-like samples ensured an optical density of ca. 1 by the 532 nm laser and powder-pattern EPR analyses for the fabricated thin films, because the laser irradiation spot area was ca. 10 mm2 which is much larger than one cut piece of the film. The films were then deaerated using a vacuum line under a vacuum pressure of 10−3 Pa to remove solvent and oxygen in the films. Nitrogen gas was then introduced into the tube through the vacuum line to ensure the film temperature for the EPR measurements.
Time-resolved EPR measurements
The X-band TREPR measurements were carried out using a Bruker EMX Plus system without using field modulation, as reported previously.41 The microwave power was 1.0 mW. Light excitations were performed by the second harmonic (532 nm) of a Nd:YAG laser (Continuum, Minilite II, fwhm ∼5 ns with 0.5 mJ mm−2). A laser de-polarizer (SIGMA KOKI, DEQ 1N) was placed between the laser exit and the microwave cavity. Temperature (80 K) was controlled by a cryostat system (Oxford, ESR900) using liquid nitrogen as the cryogen with a temperature controller (Oxford, ITC5035S).
Results and discussion
TIPS-Pn film morphology
Fig. 2 shows ground-state absorption spectra of the as-spun blend films. The absorbance obtained for each film was normalized by the strongest band intensity in the spectrum. When the spinning rate was high at 2000 rpm, the spectrum shape was similar to a TIPS-Pn solution spectrum, although the band widths were slightly broader in the film than in solution, indicating a weak chromophore interaction to form disordered morphology. On the other hand, the 300 rpm film (red line in Fig. 2) exhibits broader band shapes with an additional 700 nm band. This was explained by a strong chromophore coupling originating between the TIPS-Pn molecules indicating that the self-organized crystalline phase of TIPS-Pn is predominant, as reported previously.25,43–45
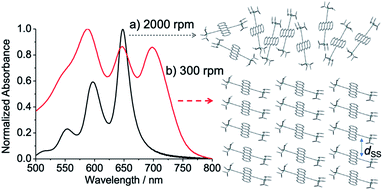 |
| | Fig. 2 Ground-state absorption spectra of as-spun TIPS-Pn thin films prepared with the spinning rates of (a) 2000 rpm (black) and (b) 300 rpm (red), representing that disordered and self-organized morphologies are dominant, respectively. dSS represents site-to-site separation for the stepwise energy transfer. | |
TREPR spectra
Fig. 3 shows the TREPR data obtained by the 532 nm-laser excitation of the TIPS-Pc films at T = 80 K. At 0.2 μs after the laser irradiation, an A/E/A/E spin polarization was detected at the resonance field positions from the fine structures for the isolated triplet excitons of TIPS-Pn in Fig. 3a and b. As for the film spun at 2000 rpm, an additional E/A polarized splitting was imposed on the broad A/E/A/E pattern, as marked by asterisks and is explained by the strongly exchange-coupled 5(TT) signals, as reported previously25–27 (vide infra).
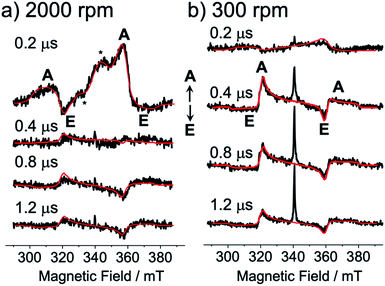 |
| | Fig. 3 Delay time dependence of the TREPR spectra after the 532 nm laser irradiation of the as-spun TIPS-Pn thin films prepared with the spinning rates of (a) 2000 rpm and (b) 300 rpm. Detection temperature was 80 K. Computed EPR spectra (red lines) were obtained by spin polarization calculations of the correlated T + T (Fig. 4 and 5) by the electron spin polarization transfer with the quintet and singlet precursors causing A/E/A/E and E/A/E/A patterns (Fig. S2†), respectively. | |
The broad A/E/A/E pattern was explained along with the T + T separation25,46 from 5(TT) in Fig. 1 to cause a dominant sublevel population at ms = 0 among ms = +1, 0 and −1 sublevels in the isolated triplet exciton. This is probably because 5(TT)ms=0 may initially be populated during the modulation of the J-coupling; the initial geminate triplet-dissociation to J = 0 in T + T and the subsequent re-encounter to a large J with the spin decoherence by the exciton migration result in the 5(TT)ms=0 populations.25,26 However, the A/E/A/E signals immediately disappeared, while the inverted ESP pattern of E/A/E/A polarization emerged after delay times larger than 0.4 μs in Fig. 3. Notably, the contribution from the E/A/E/A polarization in Fig. 3b is stronger when the self-organized crystalline phase is predominant for the film spun at 300 rpm (Fig. 2b) than in the disordered film in Fig. 3a. In our previous report, the absorptive ESP in the strongly exchange-coupled 5(TT) state was explained by sublevel-selective quintet populations and decoherences at 5(TT)−2, 5(TT)−1 and 5(TT)0 by the singlet–quintet mixing through the zero-field splitting interaction (HTTzfs) in the presence of the negative J during triplet exciton-diffusion and subsequent re-encounter in highly disordered regions.25,28 Thus, the strong absorptive feature in the initial A/E/A/E signals in Fig. 3a is consistent with T + T dissociation from 5(TT)−2 and 5(TT)−1 in the disordered film spun at 2000 rpm, because these sublevels possess the ββ-spin characters while the αα-characters are absent (see eqn (4) and (5) below). The minor initial A/E/A/E contribution in Fig. 3b denotes the existence of such a disordered area in the as-spun sample for the high crystalline film. It is reported that the triplet exciton migration is significantly quick after the SF in pentacene crystals,32 suggesting that 1(T + T) dissociation may occur before the 1(TT) → 5(TT)ms decoherences in the crystalline film. Thus, the singlet character would be preserved as the transport of the spin-entanglement of the 1(TT) in the high crystallinity sample (Fig. 2b), while 5(T + T) characteristics may also be transported from 5(TT) in the disordered film (Fig. 2a). Therefore, in the following, we consider the spin correlation in the (T + T) state, as the spin-correlated triplet pair (SCTP).
Modeling electron spin polarization of the T + T state
To interpret the ESP (A/E/A/E and E/A/E/A polarizations) in the T + T dissociated character, spin eigenfunctions were obtained. The quintet, triplet and singlet basis functions of the triplet–triplet states are represented, as follows at the high field limit,47| | 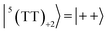 | (1) |
| | 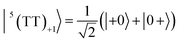 | (2) |
| | 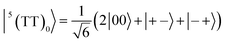 | (3) |
| | 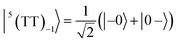 | (4) |
| | 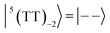 | (5) |
| | 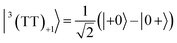 | (6) |
| | 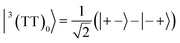 | (7) |
| | 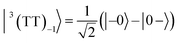 | (8) |
| | 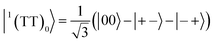 | (9) |
where |+〉, |0〉, and |−〉 are the triplet basis spins of |αα〉, 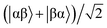 , and |ββ〉, respectively.
, and |ββ〉, respectively.
Under a very strong magnetic field, the energy levels of these wavefunctions are depicted as shown in Fig. 4a in the absence of zero-field splitting (ZFS) interactions of triplet excitons. As was previously performed to obtain the eigenfunctions for strongly J-coupled multiexcitons,25 the nine spin eigenvalues can be computed in the presence of the Zeeman interaction and of the ZFS interactions of triplet excitons to obtain the quintet, triplet and singlet TT states. Concerning the T + T dissociation, one may also obtain the nine eigen energies and corresponding eigenfunctions as shown by |1〉, |2〉, …, |9〉, in Fig. 4b.
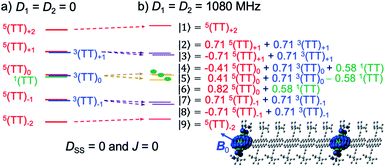 |
| | Fig. 4 Schematic representation of the sublevels of SCTP, as the weakly coupled multiexciton in (b) caused by the ZFS interactions (D1 = D2 = 1080 MHz) of 3TIPS-Pn. The energy shifts in the SCTP levels in (b) are shown with respect to the levels in (a) with D1 = D2 = 0 in the presence of the external magnetic field (340 mT) for highly separated T + T (DSS = 0 and J = 0). The wavefunctions were computed for the field direction (B0) parallel to the out-of-plane axes of the aromatic rings. | |
The numerical computations of the nine eigenvalues were performed by diagonalizing25 the spin Hamiltonian (HTT) composed of the Zeeman interaction (HTTZ), the spin–spin dipolar couplings (HTTzfs) in the individual triplets, the spin–spin dipolar coupling between the triplets represented by HTTss = DSS(cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θD − 1/3)(3S1ZS2Z − S1S2),48 and the exchange interaction (HTTee = −2JS1S2). In HTTzfs (=S1D1S1 + S2D2S2), Si is the i-th (i = 1, 2) triplet spin operator in T + T and in TT, and Di represents the zero-field splitting tensor of the individual triplet. Because the matrix of the HTTzfs tensor is dependent on the orientation of the principal axes in the D2 tensor (X2, Y2, Z2) with respect to the principal axes in the D1 tensor (X1, Y1, Z1), the geometries of the second TIPS-Pn groups were generated by using Euler rotation angles (α, β, γ) with respect to the principal axes in Di. The D2 principal axes were set to be collinear; i.e. (α, β, γ) = (0°, 0°, 0°) with respect to (X1, Y1, Z1). Direction (dS–S) for the second triplet-state position in TT was set by the polar angles (θ2 = 40°, ϕ2 = 30°) with respect to the (X1, Y1, Z1) principal axes. The direction of the external magnetic field (B0) was set by the polar angles (θ, ϕ).25 Thus, cos2
θD − 1/3)(3S1ZS2Z − S1S2),48 and the exchange interaction (HTTee = −2JS1S2). In HTTzfs (=S1D1S1 + S2D2S2), Si is the i-th (i = 1, 2) triplet spin operator in T + T and in TT, and Di represents the zero-field splitting tensor of the individual triplet. Because the matrix of the HTTzfs tensor is dependent on the orientation of the principal axes in the D2 tensor (X2, Y2, Z2) with respect to the principal axes in the D1 tensor (X1, Y1, Z1), the geometries of the second TIPS-Pn groups were generated by using Euler rotation angles (α, β, γ) with respect to the principal axes in Di. The D2 principal axes were set to be collinear; i.e. (α, β, γ) = (0°, 0°, 0°) with respect to (X1, Y1, Z1). Direction (dS–S) for the second triplet-state position in TT was set by the polar angles (θ2 = 40°, ϕ2 = 30°) with respect to the (X1, Y1, Z1) principal axes. The direction of the external magnetic field (B0) was set by the polar angles (θ, ϕ).25 Thus, cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θD in HTTss is defined for each B0 direction, as reported previously.49 Because the anisotropy in HTTZ is much smaller, we assumed isotropic g-tensors (g = 2.002) for an external magnetic field strength around 340 mT in Fig. 3. When the B0 direction is set to be parallel to both the Z1 and Z2 principal axes for the collinear T + T (Z1∥Z2), the nine eigenvalues were obtained together with the wavefunctions, as shown in Fig. 4b. These levels are influenced by the anisotropic HTTzfs causing energy shifts depending on the field direction (dotted arrows), and thus may produce the fine structure by the EPR transitions. For small J, sixteen of the allowed EPR transitions (|1〉 ↔ |2〉, |1〉 ↔ |3〉, |2〉 ↔ |4〉, |2〉 ↔ |5〉, |2〉 ↔ |6〉, |3〉 ↔ |4〉, |3〉 ↔ |5〉, |3〉 ↔ |6〉, |4〉 ↔ |7〉, |4〉 ↔ |8〉, |5〉 ↔ |7〉, |5〉 ↔ |8〉, |6〉 ↔ |7〉, |6〉 ↔ |8〉, |7〉 ↔ |9〉, and |8〉 ↔ |9〉 in Fig. 4b and 5e) may contribute to the TREPR spectrum.
θD in HTTss is defined for each B0 direction, as reported previously.49 Because the anisotropy in HTTZ is much smaller, we assumed isotropic g-tensors (g = 2.002) for an external magnetic field strength around 340 mT in Fig. 3. When the B0 direction is set to be parallel to both the Z1 and Z2 principal axes for the collinear T + T (Z1∥Z2), the nine eigenvalues were obtained together with the wavefunctions, as shown in Fig. 4b. These levels are influenced by the anisotropic HTTzfs causing energy shifts depending on the field direction (dotted arrows), and thus may produce the fine structure by the EPR transitions. For small J, sixteen of the allowed EPR transitions (|1〉 ↔ |2〉, |1〉 ↔ |3〉, |2〉 ↔ |4〉, |2〉 ↔ |5〉, |2〉 ↔ |6〉, |3〉 ↔ |4〉, |3〉 ↔ |5〉, |3〉 ↔ |6〉, |4〉 ↔ |7〉, |4〉 ↔ |8〉, |5〉 ↔ |7〉, |5〉 ↔ |8〉, |6〉 ↔ |7〉, |6〉 ↔ |8〉, |7〉 ↔ |9〉, and |8〉 ↔ |9〉 in Fig. 4b and 5e) may contribute to the TREPR spectrum.
EPR line-shape analysis using the TT → T + T jump dissociation model
Details on the computation method of the 9 × 9 matrices of the spin Hamiltonians were reported previously.25 The wavefunction |i〉 (i = 1, 2, …, 9) of the diagonalized T + T state (J = 0) is represented as follows,| | 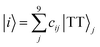 | (10) |
In eqn (10), j (=1, 2, …, 9) represents an eigenstate in the presence of the strong J coupling shown in eqn (1)–(9) where each equation number corresponds to the number of j. The transformation matrix can be described as,| | 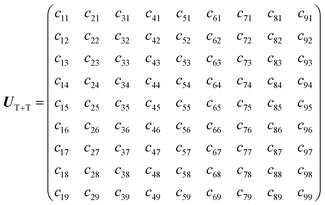 | (11) |
The EPR transverse magnetizations represented by Tr(Syρ)49,50 are proportional to factors determined by S(S + 1) ± mS (mS ∓ 1). Thus, the EPR intensities are proportional to 4, 6, and 2 for the transitions of 5TT±2 ↔ 5TT±1, 5TT0 ↔ 5TT±1, and 3TT±1 ↔ 3TT0, respectively. Additionally, the transverse magnetizations are proportional to probabilities of finding the corresponding allowed transition characters36 of 5TT±2 ↔ 5TT±1, 5TT0 ↔ 5TT±1, and 3TT±1 ↔ 3TT0 in the mixed wavefunctions of eqn (10). Therefore, the EPR-transition intensity of Int(i,k) between the |i〉 ↔ |k〉 eigenstates (Fig. 5e) is formulated as follows:
| | | Int(i,k) = 4|ci1|2|ck2|2 + 4|ci2|2|ck1|2 + 6|ci2|2|ck3|2 + 6|ci3|2|ck2|2 + 6|ci3|2|ck4|2 + 6|ci4|2|ck3|2 + 4|ci4|2|ck5|2 + 4|ci5|2|ck4|2 + 2|ci6|2|ck7|2 + 2|ci7|2|ck6|2 + 2|ci7|2|ck8|2 + 2|ci8|2|ck7|2 | (12) |
Consequently, the EPR line-shape (SP) of the SCTP is computed as a function of the external magnetic field strength, as,
| | 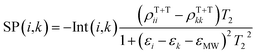 | (13) |
where
T2 represents the phase memory time.
εMW denotes the angular frequency of the microwaves. The density matrix (
ρT+T) of the T + T state will be detailed below. The spectrum computations can be performed by the powder pattern integration of
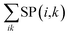
from all possible field directions (
θ,
ϕ) to obtain the EPR spectra of T + T in
Fig. 5.
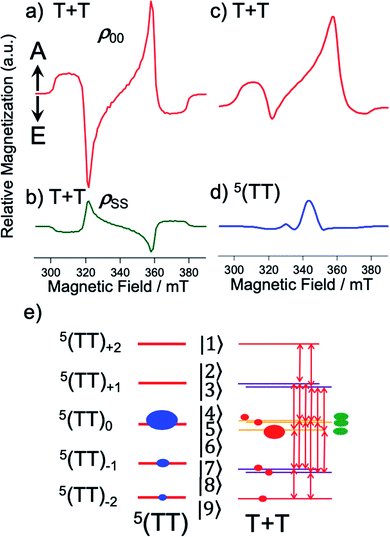 |
| | Fig. 5 Computed EPR spectra after the powder-pattern integrations of the T + T states (Fig. 4b) with DSS = 0 and J = 0 in (a–c) and of the strongly-coupled 5(TT) in (d) using the ZFS interaction of 3TIPS-Pn. (a) 5(TT)0-precursor SCTP showing the A/E/A/E pattern and (b) 1(TT)-precursor case (Fig. 4b) resulting in the E/A/E/A pattern by the sequential ESPT model (green line in Fig. 7). (c and d) SCTP and strongly coupled 5(TT) polarization computed with eqn (13) from the spin-state populations ρTT00 = 0.75, ρTT−1−1 = 0.19, and ρTT−2−2 = 0.07 in 5(TT) in (e). (e) Computed T + T populations by eqn (15) are shown by red circles to explain the absorptive ESP in (c) and (d) corresponding to the 0.2 μs-spectrum in Fig. 3a. Sixteen allowed EPR transitions are shown to obtain the T + T spectra in (b) and (c) with the sublevel populations by the 1(TT) precursor (green) and by the 5(TT) precursor (red) from the blue circles, respectively. | |
When the spin-entangled 1(TT) character is immediately transported to 1(T + T) in Fig. 1 by the dissociation, one can expect that the populations occur in |4〉, |5〉, and |6〉 with ρ44 = ρ55 = ρ66 = 0.33 (green populations in Fig. 4b) as the singlet characters from the corresponding coefficients of the wavefunctions. Therefore, the state mixings in Fig. 4b would enable the ESP detection as SCTP polarization even if the EPR-silent singlet TT is the precursor, as was observed in the singlet-precursor SCRP after the photoinduced charge-separation.36 When the 5(TT)0 state dissociates to form 5(T + T) in Fig. 1, on the other hand, one expects overpopulation in ρ66 = 0.66 while ρ44 = ρ55 = 0.17 in Fig. 4b, resulting in different ESP from the singlet-precursor polarization.
We performed powder pattern integrations of the polarized EPR transitions to obtain the EPR spectra with the 5(TT)0 precursor. For this, the density matrix (ρT+T) of the multiexciton was computed for the T + T system (Fig. 4b), as follows. HTT (=HTTZ + HTTzfs + HTTee + HTTss) was first diagonalized to obtain the nine eigenfunctions of the strongly-coupled TT using J = −60 GHz, the ZFS parameters22 of D = +1080 MHz with E = −18 MHz for TIPS-Pn molecules with the collinear TT conformation, and DSS = −280 MHz from an inferred contact T–T separation51 of 0.6 nm for the disordered regions (Fig. 2a). J = −60 GHz is one assumed value to compute the EPR spectrum for the strongly coupled TT state. Another input parameter of J = −30 GHz, as an example, will not affect the computation results. On the basis of the diagonalized quintets (|TT〉j=1 = 5TT+2, |TT〉j=2 = 5TT+1, |TT〉j=3 = 5TT0, |TT〉j=4 = 5TT−1, |TT〉j=5 = 5TT−2), triplets (|TT〉j=6 = 3TT+1, |TT〉j=7 = 3TT0, |TT〉j=8 = 3TT−1) and singlet (|TT〉j=9 = 1TT), the density matrix ρTT was considered, as the initial conditions. Using this basis system, HT+T = HTTZ + HTTzfs was then diagonalized to obtain the 9 × 9 diagonal eigenvalues matrix and the eigenvectors matrix (UT+T) in the absence of J, so that the following relation is satisfied:
| | 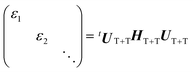 | (14) |
For the diagonal system in Fig. 4b, the following density matrix is thus obtained as
| | ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a6.gif) T+T = kESPTtUT+TρTTUT+T T+T = kESPTtUT+TρTTUT+T | (15) |
and is thus used to describe the spin-state populations (
ρT+Tii) in
eqn (13) where
i = 1, 2, …, 9 in the dissociated multiexciton, when the TT → T + T dissociation is treated to be a jump with rate constant represented by
kESPT from
J = −60 GHz to
J = 0. This treatment is the same as the model of electron spin polarization transfer (ESPT).
40 In
ρTT,
ρTTSS = 1 (where S represents
1TT in Fig. 6) can be set as the singlet population while the other 80 elements were set to be zero for the singlet-dissociation. In the
5(TT)
0-precursor case,
ρTT00 = 1 was considered where subscript 0 represents
5TT
0. In the previous report, the quintet-state EPR spectrum was explained by isotropic sublevel populations at
5TT
0,
5TT
−1, and
5TT
−2 in the disordered TIPS-Pn aggregates.
25 Thus, we also computed the quintet EPR spectrum of
5TT and the spectrum of the T + T state by using common quintet populations of
ρTT00 = 0.75,
ρTT−1−1 = 0.19, and
ρTT−2−2 = 0.07 (blue populations in
Fig. 5e) generated by the spin-conversion by the exciton-diffusion and the subsequent TT re-encounter.
Fig. 5a–c show the calculated SCTP polarization spectra obtained by the powder-pattern integration for the field directions in Fig. 4b. In Fig. 5a and b, β = 0° was assumed, while β = 82° is set in Fig. 5c. β = 82° reflects that the molecular conformation of the second triplet exciton (D2 tensor in HTTzfs) is changed by the T + T dissociation after SF because of the disordered morphology in Fig. 2a, while D1 = D2 is preserved upon the T + T dissociation in the crystalline region when β = 0°. Thus, Fig. 5c is applicable for the 2000 rpm film (Fig. 3a). When the T + T dissociation mainly occurs from 5(TT)0, the A/E/A/E pattern is obtained in Fig. 5c and coincides with the initial ESP spectra at 0.2 μs in Fig. 3. It is noteworthy that the inverted E/A/E/A pattern (Fig. 5b) is obtained when the T + T dissociation is considered from 1(TT) and that this ESP is consistent with the experimental results for the delay times larger than 0.2 μs in Fig. 3 as detailed below. On the quintet-precursor computations, the absorptive ESPs were obtained both for T + T and for 5(TT) in Fig. 5c and d, respectively when the additional populations were considered in 5TT−1 and 5TT−2. These are well explained by the spin-state populations in Fig. 5e in which the ESPT by eqn (15) also creates ρT+T44 = ρT+T55 = 0.15, ρT+T66 = 0.30, ρT+T77 = ρT+T88 = 0.08, and ρT+T99 = 0.06 in the SCTP levels for B0 parallel to the Z axis.
Spin correlated triplet pair polarization via SF
A sum of the spectra of Fig. 5c and d was obtained as shown by the red line in the initial TREPR spectrum at 0.2 μs in Fig. 3a observed for the disordered morphology film (Fig. 2a) spun at 2000 rpm. Even though several parameters are used to compute the quintet precursor EPR spectra, all parameters are justifiable and invoke reasonable values: ρTT00 = 0.75, ρTT−1−1 = 0.19, and ρTT−2−2 = 0.07 in 5(TT) are explained by the dominant singlet–quintet mixing26 with ms = 0 for J = 0 during the geminate exciton diffusion together with the minor mixings at ms = −1 and at −2 by the level-crossing for J < 0.25 The ZFS parameters (D and E) were taken from the reported values in TIPS-Pn.22θ2 = 40° and ϕ2 = 30° were taken as final adjustable parameters to fit the line-shape at 0.2 μs at the asterisk signals (Fig. 3a), because the quintet EPR spectrum shape (Fig. 5d) became narrower for θ2 = 0° while the spectrum was too broad for θ2 = 90°. Although a unique fit using inexact parameters would be very difficult, θ2 = 40° and ϕ2 = 30° also represent a reasonable parameter set for the disordered film. From all utilized parameters above, the agreement of the computed spectrum at 0.2 μs in Fig. 3a strongly indicates that the T + T dissociation occurs by electron spin polarization transfer (eqn (15)) to the spin correlated triplet pair from the quintet TT state. The quick decays of these quintet-induced signals in Fig. 3a denote that the spin–lattice relaxation time (T1) is short due to the fluctuations in the HTTzfs during the exciton diffusion. This easily coincides with the dominant disordered morphology in Fig. 2a because the anisotropic spin dipolar coupling may be modulated via the exciton diffusion to cause molecular conformation changes. Such an initial A/E/A/E polarization is also detected in Fig. 3b for the high crystallinity film (Fig. 2b). The very weak A/E/A/E signal intensity contribution at 0.2 μs in this film denotes that such a disordered region is minor in the 300 rpm film. We also confirmed that non-zero J-couplings with |J| > 10 MHz produced highly deviated peak positions and polarization patterns in the T + T spectrum. Also, |DSS| > 50 MHz for the T + T state produced a stronger A/E/A/E symmetric polarization effect rather than the net absorptive effect, suggesting that the inter-spin separation is larger than 1.2 nm estimated from the point-dipole approximation.
After the quick decays of the A/E/A/E polarization in Fig. 3, inverted E/A/E/A polarizations were detected. The E/A/E/A contribution is significantly higher in the 300 rpm film than in the 2000 rpm film. This strongly supports the singlet-precursor SCTP scheme in Fig. 4; the dominant crystalline phase causes immediate T + T dissociation from the 1(TT) initially populated by SF in Fig. 1 before the interconversion dominated in the disordered region.25 Furthermore, the long-lived E/A/E/A signals indicate that T1s are significantly large. This is rationalized by the scheme that 1(TT) → T + T dissociations preferentially occur in the ordered crystalline region as shown in Fig. 1, because the fluctuations in HTTzfs are highly restricted even if the triplet exciton diffusion is fast compared to primary T + T dissociation. The slower rise in the E/A/E/A polarizations than those of the A/E/A/E is also explained by the above slow spin-relaxation characteristics resulting in large phase memory time (T2).41 For the delay times larger than 0.4 μs, the TREPR spectra were reproduced (the red lines in Fig. 3a and b) by using combinations of the green spectrum component in Fig. 5b and minor red spectrum components in Fig. 5c with different intensity ratios, supporting the jump T + T dissociation mechanism. Decomposed contributions of the quintet- and singlet-precursor SCTP spectra are presented in Fig. S2 of the ESI.† Highly sharp signal contributions were also observed in the center regions in Fig. 3b. This would be caused by the motional narrowing effect due to inter-microcrystalline domain triplet-diffusion for the 300 rpm as-spun film.
Sequential electron spin polarization transfer model by stepwise singlet dissociation
In eqn (15), the 1(TT) → T + T dissociation is treated to be an immediate jump to J = 0. It is not likely that the singlet–quintet (SQ) coherences 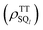 are initially generated because of the strong J-coupling at the initial event. Here, S and Ql represent 1(TT) and 5(TT)l where l = +2, +1, 0, −1, −2 in the presence of the strong J. On the other hand, when the stepwise exciton diffusion (Fig. 1) occurs slower than the 10 ps time scale, the SQ coherences are allowed to develop at the T–T separation where the J-coupling is comparable to the ZFS interaction. Thus, a modified stepwise model was examined to highlight how the T + T dissociation affects the SQ0 coherences and resultant ESP during the SF-induced triplet exciton diffusion, as shown in Fig. 6.
are initially generated because of the strong J-coupling at the initial event. Here, S and Ql represent 1(TT) and 5(TT)l where l = +2, +1, 0, −1, −2 in the presence of the strong J. On the other hand, when the stepwise exciton diffusion (Fig. 1) occurs slower than the 10 ps time scale, the SQ coherences are allowed to develop at the T–T separation where the J-coupling is comparable to the ZFS interaction. Thus, a modified stepwise model was examined to highlight how the T + T dissociation affects the SQ0 coherences and resultant ESP during the SF-induced triplet exciton diffusion, as shown in Fig. 6.
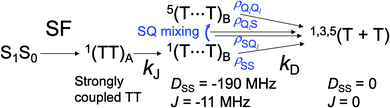 |
| | Fig. 6 Sequential ESPT model for generation of the SCTP via the intermediate T⋯T state at site B followed by the T + T dissociation by the exciton diffusion. Note that 1(TT) → 3(TT) conversion is not caused by the ZFS interaction and thus is neglected when kD is large. | |
From the scheme in Fig. 6, the elements of the density matrix in the T⋯T state were computed on the basis spin system of 5TT+2, 5TT+1, 5TT0, 5TT−1, 5TT−2, 3TT+1, 3TT0, 3TT−1, 1TT including the SQi coherences by numerically solving coupled stochastic-Liouville equations (SLE) to obtain the populations for the nine diagonalized eigenstates in Fig. 4e. We thus finally computed the diagonal elements ρT+Tii as the populations in the SCTP levels by ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a6.gif) T+T= kDtUT+TρTTBUT+T.52,53θ2 = 90° and ϕ2 = −5° were considered in the intermediate T⋯T as shown by geometry in Fig. S3† based upon the crystal structure.58J = −11 MHz was assumed for the T⋯T state. See ESI† for more details. Fig. 7 shows the dependence of the sequential triplet energy transfer rate constant (kD) on the SCTP polarization by the triplet diffusion. Since D and J are both in the range of 1010 rad s−1 in the intermediate T⋯T in Fig. 6, it is anticipated that the SQ0 coherences can be generated when the residence lifetime of the T⋯T state is larger than 10 ps and thus be transferred to the sublevel populations in the SCTP levels by the unitary transform of tUT+TρTTBUT+T. As expected, the ESP is stronger when the residence time (τT = 1/kD) becomes longer in Fig. 7. This E/A/E/A effect is relevant to the ESP by the chemically induced dynamic electron polarization54,55 in radical pairs creating the multiplet patterns (A/E and E/A, depending on J and DSS)56 by the development of the S–T0 coherences (ρST0 and ρT0S) in the singlet–triplet radical-pair system.59
T+T= kDtUT+TρTTBUT+T.52,53θ2 = 90° and ϕ2 = −5° were considered in the intermediate T⋯T as shown by geometry in Fig. S3† based upon the crystal structure.58J = −11 MHz was assumed for the T⋯T state. See ESI† for more details. Fig. 7 shows the dependence of the sequential triplet energy transfer rate constant (kD) on the SCTP polarization by the triplet diffusion. Since D and J are both in the range of 1010 rad s−1 in the intermediate T⋯T in Fig. 6, it is anticipated that the SQ0 coherences can be generated when the residence lifetime of the T⋯T state is larger than 10 ps and thus be transferred to the sublevel populations in the SCTP levels by the unitary transform of tUT+TρTTBUT+T. As expected, the ESP is stronger when the residence time (τT = 1/kD) becomes longer in Fig. 7. This E/A/E/A effect is relevant to the ESP by the chemically induced dynamic electron polarization54,55 in radical pairs creating the multiplet patterns (A/E and E/A, depending on J and DSS)56 by the development of the S–T0 coherences (ρST0 and ρT0S) in the singlet–triplet radical-pair system.59
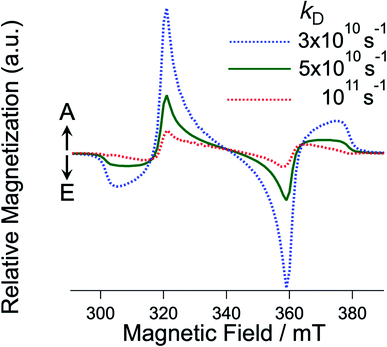 |
| | Fig. 7
k
D dependence of the EPR spectra for the T + T state with J = 0 computed by the sequential ESPT model (Fig. 6) via the intermediate T⋯T state. kJ was fixed to be 1011 s−1. | |
The experimental E/A/E/A antiphase spectra in Fig. 3 agreed with the sequential model as shown in Fig. S2.† Because the green spectrum (Fig. 7) computed with kD = 5 × 1010 s−1 only explains the experimental results τT of the T⋯T state is concluded to be short (1/kD = 20 ps). In the crystalline phase of the TIPS-Pn film, the site-to-site separation (dSS) between the TIPS-Pn molecules was estimated to be 0.4 nm from the crystal structure in Fig. 2a. The one-step site-to-site energy transfer rate constant may correspond to kD (=1/τT) in Fig. 6. Thus, τT can be related to the diffusion constant (DT) assuming that one-dimension diffusion57 through the π-stacking interaction is dominated by the Dexter-type energy transfer in Fig. 1, as follows,58
| | 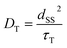 | (16) |
From eqn (16), DT ≈ 10−4 cm2 s−1 is estimated from τT = 20 ps to explain the antiphase ESP in Fig. 3b at 80 K. In a previous report, the triplet diffusion motion was investigated in the TIPS-Pn films by monitoring the triplet–triplet annihilation (TTA) kinetics.19 In this, DT = 2.7 × 10−5 cm2 s−1 was obtained for a high crystallinity film at room temperature. The TTA rate constant may become smaller at 80 K to result in DT < 10−5 cm2 s−1.57 One should note however that the geminate T + T dissociative diffusion (Fig. 1) via the SF is quicker than the diffusion for the encounter of the free excitons in the TTA process. This is because, for the TTA, the exciton migration occurs via three-dimensional motion and thus is hindered in the minor disordered area during the long-distance diffusion (LD > 30 nm, as the diffusion length).19 In contrast, the exciton–exciton separation (ca. 1 nm) in the primary T⋯T state (Fig. 6) is much shorter than LD and thus exciton migration is free from the exciton-trapping31 in the crystalline phase. The above SF-induced 1T⋯T → T + T spin-transportation with τT = 20 ps is compatible with the previous reports of the corresponding dissociation dynamics (3.2 ps) in the crystalline TIPS-Pn film observed by the ultrafast spectroscopic measurements18,19 and with a recent magnetic field effect studied by Yago and co-workers20 on SF-induced geminate triplet hopping kinetics (9 ps) in the fluorinated diphenyl-hexatriene crystals that form parallel stacking structures. From these reported picosecond dissociations at room temperature and from the present ps-dissociation at 80 K, the SF-induced geminate hopping dynamics is roughly temperature independent.32 Note that the hopping dynamics does not correspond to the initial dissociation kinetics kJ but kD in Fig. 6.
Conclusion
We have established SF-induced electron spin polarization models for the weakly-coupled T + T state as the quantum superposition (Fig. 4) of singlet–triplet–quintet wavefunctions by ZFS via the jump from the strongly coupled TT and via the sequential ESPT through the intermediate T⋯T state (Fig. 6) in TIPS-Pn thin films. From the ESP analysis, it is concluded that the SF-induced singlet TT character is transferred to the separated T + T spin-state as quick transport of spin-entanglements with preserving the S-Q0 coherence by picosecond jumps in the crystalline TIPS-Pn film, generating the E/A/E/A antiphase EPR spectra. Both of the singlet and quintet entanglements are revealed to be transported even in the amorphous film denoting the coexistence of ordered and disordered regions. This result is in line with the detection of the SF-induced quintet EPR signal at 0.2 μs in Fig. 3a, because a minor crystalline region is required to generate quintet multiexcitons in amorphous aggregates, as reported in our previous study.25
From the present data and the reported optical studies,18,19,32 the primary T + T hopping dynamics (kD in Fig. 6) is suggested to be temperature independent. The picosecond-dynamics in the respective 1T⋯T → T + T step in Fig. 6 strongly indicates that de-coupling of the J in the 1T⋯T state (Fig. S3)† plays a role in the T + T separation. From the temperature-independent dissociation kinetics,22 it is found that quick nuclear reorganization in T⋯T by high-frequency vibration motions24 may play a role in the de-coupling, as previously proposed for pentacene dimers,12 resulting in significant reduction of the orbital overlap between the triplet chromophores. This mechanism is also relevant to our recent low-temperature TREPR study for charge-separation geometries (distance ≈ 3 nm) in the bulk-heterojunction interfaces of organic solar cells; it was concluded that the high-frequency in-plane stretching reorganization within aromatic polymer backbones promoted 1D charge-dissociation at the D:A domain interfaces.41 The present SCTP spin polarization mechanism may thus pave new avenues to understand the nature of ultimate de-coupling and dissociation of two excitons for energy conversion. Although the coherent superposition of spin eigenstates was not directly detected, the present SCTP may be applicable to scalable quantum information processing via one-photon excitation because the sixteen possible EPR transitions from the nine sublevels (Fig. 5e) can be taken into account, which is significantly more scalable than the four EPR transitions34 in SCRP.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The work was supported by a Grant-in-Aid for Scientific Research (No. JP19H00888 and JP17K19105) from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. We appreciate the support by Dr Hiroki Nagashima (Saitama University) in the TREPR measurements using the cryostat system. YK thanks Professor Tomoaki Yago (Saitama University) and Professor Tadaaki Ikoma (Niigata University) for fruitful discussions on the triplet diffusion dynamics.
References
- S. Zhang, Y. Qin, J. Zhu and J. Hou, Adv. Mater., 2018, 30, 1800868 CrossRef PubMed.
- S. Li, L. Ye, W. Zhao, H. Yan, B. Yang, D. Liu, W. Li, H. Ade and J. Hou, J. Am. Chem. Soc., 2018, 140, 7159–7167 CrossRef CAS PubMed.
- Y. Cui, H. Yao, J. Zhang, T. Zhang, Y. Wang, L. Hong, K. Xian, B. Xu, S. Zhang, J. Peng, Z. Wei, F. Gao and J. Hou, Nat. Commun., 2019, 10, 2515 CrossRef PubMed.
- H.-S. Kim, A. Hagfeldt and N.-G. Park, Chem. Commun., 2019, 55, 1192–1200 RSC.
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CrossRef CAS.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- H. Zang, Y. Zhao and W. Z. Liang, J. Phys. Chem. Lett., 2017, 8, 5105–5112 CrossRef CAS PubMed.
- A. Rao, M. W. B. Wilson, J. M. Hodgkiss, S. Albert-Seifried, H. Bassler and R. H. Friend, J. Am. Chem. Soc., 2010, 132, 12698–12703 CrossRef CAS PubMed.
- R. Nagata, H. Nakanotani, W. J. Potscavage and C. Adachi, Adv. Mater., 2018, 30, 01484 CrossRef PubMed.
- D. H. Arias, J. L. Ryerson, J. D. Cook, N. H. Damrauer and J. C. Johnson, Chem. Sci., 2016, 7, 1185–1191 RSC.
- E. G. Fuemmeler, S. N. Sanders, A. B. Pun, E. Kumarasamy, T. Zeng, K. Miyata, M. L. Steigerwald, X. Y. Zhu, M. Y. Sfeir, L. M. Campos and N. Ananth, ACS Cent. Sci., 2016, 2, 316–324 CrossRef CAS PubMed.
- A. T. Gilligan, E. G. Miller, T. Sammakia and N. H. Damrauer, J. Am. Chem. Soc., 2019, 141, 5961–5971 CrossRef CAS PubMed.
- K. Miyata, Y. Kurashige, K. Watanabe, T. Sugimoto, S. Takahashi, S. Tanaka, J. Takeya, T. Yanai and Y. Matsumoto, Nat. Chem., 2017, 9, 983–989 CrossRef CAS PubMed.
- S. W. Eaton, L. E. Shoer, S. D. Karlen, S. M. Dyar, E. A. Margulies, B. S. Veldkamp, C. Ramanan, D. A. Hartzler, S. Savikhin, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2013, 135, 14701–14712 CrossRef CAS PubMed.
- C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Beljonne, J. E. Anthony, J. Clark and H. Sirringhaus, Nat. Commun., 2017, 8, 15953 CrossRef CAS PubMed.
- H. Sakai, R. Inaya, H. Nagashima, S. Nakamura, Y. Kobori, N. V. Tkachenko and T. Hasobe, J. Phys. Chem. Lett., 2018, 9, 3354–3360 CrossRef CAS PubMed.
- J. Herz, T. Buckup, F. Paulus, J. U. Engelhart, U. H. F. Bunz and M. Motzkus, J. Phys. Chem. A, 2015, 119, 6602–6610 CrossRef CAS PubMed.
- C. Grieco, E. R. Kennehan, H. Kim, R. D. Pensack, A. N. Brigeman, A. Rimshaw, M. M. Payne, J. E. Anthony, N. C. Giebink, G. D. Scholes and J. B. Asbury, J. Phys. Chem. C, 2018, 122, 2012–2022 CrossRef CAS.
- M. Wakasa, T. Yago, Y. Sonoda and R. Katoh, Commun. Chem., 2018, 1, 9 CrossRef.
- C. Grieco, E. R. Kennehan, A. Rimshaw, M. M. Payne, J. E. Anthony and J. B. Asbury, J. Phys. Chem. Lett., 2017, 8, 5700–5706 CrossRef CAS PubMed.
- M. J. Y. Tayebjee, S. N. Sanders, E. Kumarasamy, L. M. Campos, M. Y. Sfeir and D. R. McCamey, Nat. Phys., 2017, 13, 182–188 Search PubMed.
- Y. Matsui, S. Kawaoka, H. Nagashima, T. Nakagawa, N. Okamura, T. Ogaki, E. Ohta, S. Akimoto, A. Sato-Tomita, S. Yagi, Y. Kobori and H. Ikeda, J. Phys. Chem. C, 2019, 123, 18813–18823 CrossRef CAS.
- K. Miyata, F. S. Conrad-Burton, F. L. Geyer and X. Y. Zhu, Chem. Rev., 2019, 119, 4261–4292 CrossRef CAS PubMed.
- H. Nagashima, S. Kawaoka, S. Akimoto, T. Tachikawa, Y. Matsui, H. Ikeda and Y. Kobori, J. Phys. Chem. Lett., 2018, 9, 5855–5861 CrossRef CAS PubMed.
- L. R. Weiss, S. L. Bayliss, F. Kraffert, K. J. Thorley, J. E. Anthony, R. Bittl, R. H. Friend, A. Rao, N. C. Greenham and J. Behrends, Nat. Phys., 2017, 13, 176–181 Search PubMed.
- D. Lubert-Perquel, E. Salvadori, M. Dyson, P. N. Stavrinou, R. Montis, H. Nagashima, Y. Kobori, S. Heutz and C. W. M. Kay, Nat. Commun., 2018, 9, 4222 Search PubMed.
- T. Saegusa, H. Sakai, H. Nagashima, Y. Kobori, N. V. Tkachenko and T. Hasobe, J. Am. Chem. Soc., 2019, 141, 14720–14727 CrossRef CAS PubMed.
- A. J. Musser and J. Clark, Annu. Rev. Phys. Chem., 2019, 70, 323–351 CrossRef CAS PubMed.
- C. J. Bardeen, Annu. Rev. Phys. Chem., 2014, 65, 127–148 CrossRef CAS PubMed.
- T. Yago, K. Ishikawa, R. Katoh and M. Wakasa, J. Phys. Chem. C, 2016, 120, 27858–27870 CrossRef CAS.
- Y. Wan, G. P. Wiederrecht, R. D. Schaller, J. C. Johnson and L. Huang, J. Phys. Chem. Lett., 2018, 9, 6731–6738 CrossRef CAS PubMed.
- B. K. Rugg, M. D. Krzyaniak, B. T. Phelan, M. A. Ratner, R. M. Young and M. R. Wasielewski, Nat. Chem., 2019, 11, 981–986 CrossRef CAS PubMed.
- J. H. Olshansky, M. D. Krzyaniak, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2019, 141, 2152–2160 CrossRef CAS PubMed.
- H. Atsumi, S. Nakazawa, C. Dohno, K. Sato, T. Takui and K. Nakatani, Chem. Commun., 2013, 49, 6370–6372 RSC.
- P. J. Hore, D. A. Hunter, C. D. McKie and A. J. Hoff, Chem. Phys. Lett., 1987, 137, 495–500 CrossRef CAS.
- G. L. Closs, M. D. E. Forbes and J. R. Norris, J. Phys. Chem., 1987, 91, 3592–3599 CrossRef CAS.
- G. Kothe, S. Weber, R. Bittl, E. Ohmes, M. C. Thurnauer and J. R. Norris, Chem. Phys. Lett., 1991, 186, 474–480 CrossRef CAS.
- S. Weber, T. Biskup, A. Okafuji, A. R. Marino, T. Berthold, G. Link, K. Hitomi, E. D. Getzoff, E. Schleicher and J. R. Norris, J. Phys. Chem. B, 2010, 114, 14745–14754 CrossRef CAS PubMed.
- Y. Kobori, M. Fuki and H. Murai, J. Phys. Chem. B, 2010, 114, 14621–14630 CrossRef CAS PubMed.
- Y. Kobori, T. Ako, S. Oyama, T. Tachikawa and K. Marumoto, J. Phys. Chem. C, 2019, 123, 13472–13481 CrossRef CAS.
- M. Hasegawa, H. Nagashima, R. Minobe, T. Tachikawa, H. Mino and Y. Kobori, J. Phys. Chem. Lett., 2017, 8, 1179–1184 CrossRef CAS PubMed.
- R. D. Pensack, A. J. Tilley, S. R. Parkin, T. S. Lee, M. M. Payne, D. Gao, A. A. Jahnke, D. G. Oblinsky, P.-F. Li, J. E. Anthony, D. S. Seferos and G. D. Scholes, J. Am. Chem. Soc., 2015, 137, 6790–6803 CrossRef CAS PubMed.
- M. J. Y. Tayebjee, K. N. Schwarz, R. W. MacQueen, M. Dvořák, A. W. C. Lam, K. P. Ghiggino, D. R. McCamey, T. W. Schmidt and G. J. Conibeer, J. Phys. Chem. C, 2016, 120, 157–165 CrossRef CAS.
- C. Grieco, G. S. Doucette, R. D. Pensack, M. M. Payne, A. Rimshaw, G. D. Scholes, J. E. Anthony and J. B. Asbury, J. Am. Chem. Soc., 2016, 138, 16069–16080 CrossRef CAS PubMed.
- S. L. Bayliss, F. Kraffert, R. Wang, C. Zhang, R. Bittl and J. Behrends, J. Phys. Chem. Lett., 2019, 10, 1908–1913 CrossRef CAS PubMed.
- H. Benk and H. Sixl, Mol. Phys., 1981, 42, 779–801 CrossRef CAS.
- S. Weber, G. Kothe and J. R. Norris, J. Chem. Phys., 1997, 106, 6248–6261 CrossRef CAS.
- Y. Kobori, N. Ponomarenko and J. R. Norris, J. Phys. Chem. C, 2015, 119, 8078–8088 CrossRef CAS.
- T. Miura, M. Aikawa and Y. Kobori, J. Phys. Chem. Lett., 2014, 5, 30–35 CrossRef CAS PubMed.
- Y. Kobori and M. Fuki, J. Am. Chem. Soc., 2011, 133, 16770–16773 CrossRef CAS PubMed.
- Y. Kobori, S. Yamauchi, K. Akiyama, S. Tero-Kubota, H. Imahori, S. Fukuzumi and J. R. Norris, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10017–10022 CrossRef CAS PubMed.
- A. L. Morris, S. W. Snyder, Y. N. Zhang, J. Tang, M. C. Thurnauer, P. L. Dutton, D. E. Robertson and M. R. Gunner, J. Phys. Chem., 1995, 99, 3854–3866 CrossRef CAS.
- J. B. Pedersen and J. H. Freed, J. Chem. Phys., 1973, 58, 2746–2761 CrossRef.
-
L. T. Muss, P. W. Atkins, K. A. McLauchlan and J. B. Pedersen, Chemically Induced Magnetic Polarization, Reidel, Dordrecht, The Netherlands, 1977 Search PubMed.
- Y. Kobori, S. Sekiguchi, K. Akiyama and S. Tero-Kubota, J. Phys. Chem. A, 1999, 103, 5416–5424 CrossRef CAS.
- O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888 RSC.
- J. E. Anthony, J. S. Brooks, D. L. Eaton and S. R. Parkin, J. Am. Chem. Soc., 2001, 123, 9482–9483 CrossRef CAS PubMed.
- I. A. Shkrob, Chem. Phys. Lett., 1997, 264, 417–423 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details on the simulations of time-dependent EPR data and on the modeling of sequential ESPT analysis based upon the SLE. See DOI: 10.1039/c9sc04949e |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab
*ab


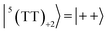
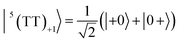
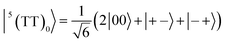
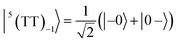
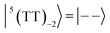
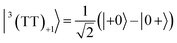
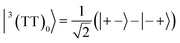
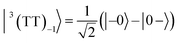
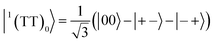
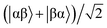 , and |ββ〉, respectively.
, and |ββ〉, respectively.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θD − 1/3)(3S1ZS2Z − S1S2),48 and the exchange interaction (HTTee = −2JS1S2). In HTTzfs (=S1D1S1 + S2D2S2), Si is the i-th (i = 1, 2) triplet spin operator in T + T and in TT, and Di represents the zero-field splitting tensor of the individual triplet. Because the matrix of the HTTzfs tensor is dependent on the orientation of the principal axes in the D2 tensor (X2, Y2, Z2) with respect to the principal axes in the D1 tensor (X1, Y1, Z1), the geometries of the second TIPS-Pn groups were generated by using Euler rotation angles (α, β, γ) with respect to the principal axes in Di. The D2 principal axes were set to be collinear; i.e. (α, β, γ) = (0°, 0°, 0°) with respect to (X1, Y1, Z1). Direction (dS–S) for the second triplet-state position in TT was set by the polar angles (θ2 = 40°, ϕ2 = 30°) with respect to the (X1, Y1, Z1) principal axes. The direction of the external magnetic field (B0) was set by the polar angles (θ, ϕ).25 Thus, cos2
θD − 1/3)(3S1ZS2Z − S1S2),48 and the exchange interaction (HTTee = −2JS1S2). In HTTzfs (=S1D1S1 + S2D2S2), Si is the i-th (i = 1, 2) triplet spin operator in T + T and in TT, and Di represents the zero-field splitting tensor of the individual triplet. Because the matrix of the HTTzfs tensor is dependent on the orientation of the principal axes in the D2 tensor (X2, Y2, Z2) with respect to the principal axes in the D1 tensor (X1, Y1, Z1), the geometries of the second TIPS-Pn groups were generated by using Euler rotation angles (α, β, γ) with respect to the principal axes in Di. The D2 principal axes were set to be collinear; i.e. (α, β, γ) = (0°, 0°, 0°) with respect to (X1, Y1, Z1). Direction (dS–S) for the second triplet-state position in TT was set by the polar angles (θ2 = 40°, ϕ2 = 30°) with respect to the (X1, Y1, Z1) principal axes. The direction of the external magnetic field (B0) was set by the polar angles (θ, ϕ).25 Thus, cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θD in HTTss is defined for each B0 direction, as reported previously.49 Because the anisotropy in HTTZ is much smaller, we assumed isotropic g-tensors (g = 2.002) for an external magnetic field strength around 340 mT in Fig. 3. When the B0 direction is set to be parallel to both the Z1 and Z2 principal axes for the collinear T + T (Z1∥Z2), the nine eigenvalues were obtained together with the wavefunctions, as shown in Fig. 4b. These levels are influenced by the anisotropic HTTzfs causing energy shifts depending on the field direction (dotted arrows), and thus may produce the fine structure by the EPR transitions. For small J, sixteen of the allowed EPR transitions (|1〉 ↔ |2〉, |1〉 ↔ |3〉, |2〉 ↔ |4〉, |2〉 ↔ |5〉, |2〉 ↔ |6〉, |3〉 ↔ |4〉, |3〉 ↔ |5〉, |3〉 ↔ |6〉, |4〉 ↔ |7〉, |4〉 ↔ |8〉, |5〉 ↔ |7〉, |5〉 ↔ |8〉, |6〉 ↔ |7〉, |6〉 ↔ |8〉, |7〉 ↔ |9〉, and |8〉 ↔ |9〉 in Fig. 4b and 5e) may contribute to the TREPR spectrum.
θD in HTTss is defined for each B0 direction, as reported previously.49 Because the anisotropy in HTTZ is much smaller, we assumed isotropic g-tensors (g = 2.002) for an external magnetic field strength around 340 mT in Fig. 3. When the B0 direction is set to be parallel to both the Z1 and Z2 principal axes for the collinear T + T (Z1∥Z2), the nine eigenvalues were obtained together with the wavefunctions, as shown in Fig. 4b. These levels are influenced by the anisotropic HTTzfs causing energy shifts depending on the field direction (dotted arrows), and thus may produce the fine structure by the EPR transitions. For small J, sixteen of the allowed EPR transitions (|1〉 ↔ |2〉, |1〉 ↔ |3〉, |2〉 ↔ |4〉, |2〉 ↔ |5〉, |2〉 ↔ |6〉, |3〉 ↔ |4〉, |3〉 ↔ |5〉, |3〉 ↔ |6〉, |4〉 ↔ |7〉, |4〉 ↔ |8〉, |5〉 ↔ |7〉, |5〉 ↔ |8〉, |6〉 ↔ |7〉, |6〉 ↔ |8〉, |7〉 ↔ |9〉, and |8〉 ↔ |9〉 in Fig. 4b and 5e) may contribute to the TREPR spectrum.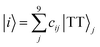
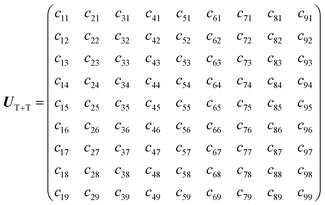
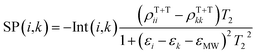
 from all possible field directions (θ, ϕ) to obtain the EPR spectra of T + T in Fig. 5.
from all possible field directions (θ, ϕ) to obtain the EPR spectra of T + T in Fig. 5.

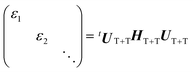
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a6.gif) T+T = kESPTtUT+TρTTUT+T
T+T = kESPTtUT+TρTTUT+T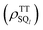 are initially generated because of the strong J-coupling at the initial event. Here, S and Ql represent 1(TT) and 5(TT)l where l = +2, +1, 0, −1, −2 in the presence of the strong J. On the other hand, when the stepwise exciton diffusion (Fig. 1) occurs slower than the 10 ps time scale, the SQ coherences are allowed to develop at the T–T separation where the J-coupling is comparable to the ZFS interaction. Thus, a modified stepwise model was examined to highlight how the T + T dissociation affects the SQ0 coherences and resultant ESP during the SF-induced triplet exciton diffusion, as shown in Fig. 6.
are initially generated because of the strong J-coupling at the initial event. Here, S and Ql represent 1(TT) and 5(TT)l where l = +2, +1, 0, −1, −2 in the presence of the strong J. On the other hand, when the stepwise exciton diffusion (Fig. 1) occurs slower than the 10 ps time scale, the SQ coherences are allowed to develop at the T–T separation where the J-coupling is comparable to the ZFS interaction. Thus, a modified stepwise model was examined to highlight how the T + T dissociation affects the SQ0 coherences and resultant ESP during the SF-induced triplet exciton diffusion, as shown in Fig. 6.
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a6.gif) T+T= kDtUT+TρTTBUT+T.52,53θ2 = 90° and ϕ2 = −5° were considered in the intermediate T⋯T as shown by geometry in Fig. S3† based upon the crystal structure.58J = −11 MHz was assumed for the T⋯T state. See ESI† for more details. Fig. 7 shows the dependence of the sequential triplet energy transfer rate constant (kD) on the SCTP polarization by the triplet diffusion. Since D and J are both in the range of 1010 rad s−1 in the intermediate T⋯T in Fig. 6, it is anticipated that the SQ0 coherences can be generated when the residence lifetime of the T⋯T state is larger than 10 ps and thus be transferred to the sublevel populations in the SCTP levels by the unitary transform of tUT+TρTTBUT+T. As expected, the ESP is stronger when the residence time (τT = 1/kD) becomes longer in Fig. 7. This E/A/E/A effect is relevant to the ESP by the chemically induced dynamic electron polarization54,55 in radical pairs creating the multiplet patterns (A/E and E/A, depending on J and DSS)56 by the development of the S–T0 coherences (ρST0 and ρT0S) in the singlet–triplet radical-pair system.59
T+T= kDtUT+TρTTBUT+T.52,53θ2 = 90° and ϕ2 = −5° were considered in the intermediate T⋯T as shown by geometry in Fig. S3† based upon the crystal structure.58J = −11 MHz was assumed for the T⋯T state. See ESI† for more details. Fig. 7 shows the dependence of the sequential triplet energy transfer rate constant (kD) on the SCTP polarization by the triplet diffusion. Since D and J are both in the range of 1010 rad s−1 in the intermediate T⋯T in Fig. 6, it is anticipated that the SQ0 coherences can be generated when the residence lifetime of the T⋯T state is larger than 10 ps and thus be transferred to the sublevel populations in the SCTP levels by the unitary transform of tUT+TρTTBUT+T. As expected, the ESP is stronger when the residence time (τT = 1/kD) becomes longer in Fig. 7. This E/A/E/A effect is relevant to the ESP by the chemically induced dynamic electron polarization54,55 in radical pairs creating the multiplet patterns (A/E and E/A, depending on J and DSS)56 by the development of the S–T0 coherences (ρST0 and ρT0S) in the singlet–triplet radical-pair system.59