Monoaurated vs. diaurated intermediates: causality or independence?

Abstract

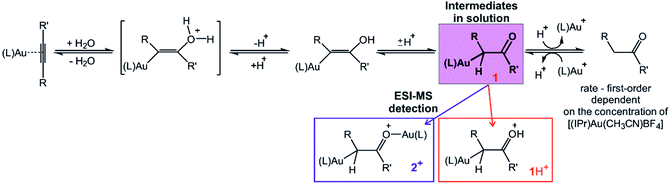
Diaurated intermediates of gold-catalysed reactions have been a long-standing subject of debate. Although diaurated complexes were regarded as a drain of active monoaurated intermediates in catalytic cycles, they were also identified as the products of gold–gold cooperation in dual–activation reactions. This study shows investigation of intermediates in water addition to alkynes catalysed by [(IPr)Au(CH₃CN)(BF₄)]. Electrospray ionisation mass spectrometry (ESI-MS) allowed us to detect both monoaurated and diaurated complexes in this reaction. Infrared photodissociation spectra of the trapped complexes show that the structure of the intermediates corresponds to α-gold ketone intermediates protonated or aurated at the oxygen atom. Delayed reactant labelling experiments provided the half life of the intermediates in reaction of 1-phenylpropyne (∼7 min) and the kinetic isotope effects for hydrogen introduction to the carbon atom (KIE ∼ 4–6) and for the protodeauration (KIE ∼ 2). The results suggest that the ESI-MS detected monoaurated and diaurated complexes report on species with a very similar or the same kinetics in solution. Kinetic analysis of the overall reaction showed that the reaction rate is first-order dependent on the concentration of the gold catalyst. Finally, all results are consistent with the reaction mechanism proceeding via monoaurated neutral α-gold ketone intermediates only.

---

Introduction

Gold cations have unique properties. They can act as large protons, they can form strong bonds with carbon atoms, and they strongly interact among themselves.^1,2 All these properties led to the current boom in the field of gold catalysis.³ Mechanisms of gold-catalysed reactions have been extensively addressed.⁴ Gold-containing reaction intermediates have often been detected and characterised using several methods, such as NMR, MS, or X-ray crystallography.⁵ However, the initial studies indicated that some detected organogold complexes are not necessarily the reactive intermediates, but rather off-cycle species that react either sluggishly or not at all.⁶

Gold-catalysed nucleophile addition to alkynes was initially postulated to proceed via monoaurated intermediates A that can be trapped with another gold cation and form non-reactive, geminally diaurated complexes X⁺ (Scheme 1).⁶ Conversely, a subsequent study suggested that complexes X⁺ are not formed by trapping A but rather in a dual activation pathway leading to the primary diaurated intermediates B⁺, which can rearrange to the geminal isomers X⁺.^7,8 In fact, the analysis of these reaction pathways is complicated by a possible causality problem: diaurated complexes B⁺ and X⁺ may be formed by a gold attachment to the primary intermediates A, while the monoaurated intermediates can be simultaneously formed by gold detachment from either B⁺ or X⁺. Hence, the detection of either species does not necessarily exclude alternative pathways.

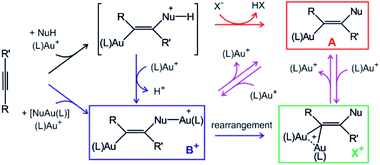Scheme 1 Intermediates in gold(I)-mediated nucleophile addition to an alkyne. Red and blue code independent pathways to monoaurated and diaurated intermediates, respectively.

We have developed a method for following the kinetics of reaction intermediates in solution using mass spectrometry – Delayed Reactant Labelling.⁹ This approach combines the power of mass-spectrometry, in detecting minor species and in analysing them individually, with the advantage of collecting information on their solution kinetics. We used this method here to monitor intermediates in a gold(I)-catalysed addition of water to alkynes. This reaction was selected because both monoaurated and diaurated complexes can be detected by electrospray ionisation mass spectrometry. We have supplemented the obtained kinetic information on the intermediates with overall reaction kinetics measurements using gas chromatography approach. The obtained data give an answer to the title dilemma for gold-catalysed water addition to alkynes.

Results and discussion

One of the efficient gold catalysts for water addition to alkynes is [Au(IPr)(CH₃CN)(BF₄)] (IPr = 1,3-bis(2,6-diisopropylphenyl)imidazol-2-ylidene).¹⁰ This catalyst forms digold hydroxide ([Au₂(IPr)₂(OH)]) in water (reaction (1)) which can be even isolated upon addition of a base.¹¹ Hence, next to the classical activation of a substrate by cationic gold, we could expect involvement of digold hydroxide.

We have studied water addition to 3-hexyne and to 1-phenylpropyne. Water addition to 3-hexyne yields only one product, 3-hexanone. 1-Phenylpropyne is transformed to either benzylmethylketone or ethylphenylketone in a 6 : 1 ratio (Fig. S1, S2 and Scheme S1 in the ESI†). Under our conditions (see below), the reaction of 3-hexyne is rather fast – we can reach almost complete conversion in about 1 hour. This is not convenient for ESI-MS study, because the rapidly formed products interact with the gold catalyst and form complexes with the same m/z ratio as the monitored reaction intermediates. The reaction with 1-phenylpropyne has suitable kinetics. Under our typical conditions, we had about 10% conversion after one hour at room temperature (see the NMR kinetics in Fig. S2 in the ESI†). Therefore, the reaction with 1-phenylpropyne is ideally suited for monitoring reaction intermediates in a time span up to one hour. We have also tested diphenylacetylene in the same reaction. The hydration reaction was extremely slow and ESI-MS detected only negligible signals of the aurated intermediates (Fig. S12†). Hence, we continued the ESI-MS investigation with 1-phenylpropyne acknowledging the problem of dealing with a mixture of regioisomers of the intermediates. For the measurements of infrared spectra of the reaction intermediates, we cooled the reaction down to −30 °C in order to further suppress the conversion to products.

Structure of the detected intermediates

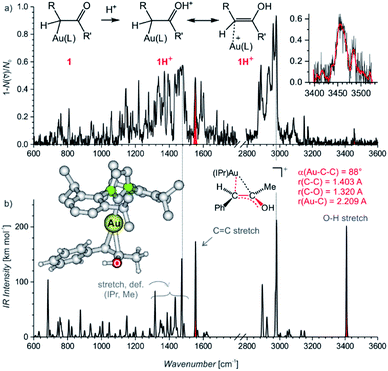
Electrospray ionization mass spectra of the reaction mixture with 1-phenylpropyne show signals corresponding to the mono- and diaurated intermediates (Fig. S5†). The monoaurated intermediate [Au(IPr)(PhCCCH₃,OH)] (1) is detected in its protonated form, i.e., 1H⁺ (m/z 719). This ion is isomeric with a gold complex of the ketone product. The diaurated complex ([Au₂(IPr)₂(PhCCCH₃,OH)]⁺, 2⁺) can have a structure of isomers B⁺ or X⁺ in Scheme 1 (Nu = OH), or it could be an isomer of B⁺ in which a hydrogen atom migrated from the oxygen atom to the carbon atom (all m/z 1303). To assign the correct structures to the ions detected by ESI-MS, we measured their helium tagging infrared photodissociation (IRPD) spectra.¹²

The IRPD spectrum of monoaurated ions with m/z 719 shows the O–H stretching vibrations slightly above 3450 cm⁻¹ (Fig. 1). The inset shows a detail of the O–H stretching bands measured with a maximum photon flux. We observe two O–H stretching bands, and the sum of their heights is higher than 0.9 that is, more than 90% of the trapped ions have an OH group. These ions are present as a mixture of isomers/conformers. The position of the OH bands is consistent with the theoretically predicted spectra of protonated α-gold ketones with R and R′ being methyl and phenyl or vice versa. The remaining <10% of ions are probably gold complexes of the ketone products.

Fig. 1 (a) IRPD spectrum of [Au(IPr)(PhCCCH₃,OH)]H⁺ (m/z 719). The insert shows the O–H stretching IR range measured with a high photon flux. (b) Theoretical IR spectrum of the most stable isomer of 1H⁺ and its geometry parameters. Red colour highlights the important bands corresponding to the characteristic bands found in the experimental spectrum.

The lower wavenumber, finger-print region of the IRPD spectrum is also consistent with the assignment of the detected ions as protonated α-gold ketone intermediates. Especially, the band at about 1560 cm⁻¹ (highlighted in red, in Fig. 1a) corresponds to the C–C stretch of the central C=C bond. The C–O stretching band should be found below 1400 cm⁻¹ among peaks that mostly correspond to the vibrations of the IPr ligand. The spectrum agrees well with the predicted IR spectrum of protonated α-gold ketones, but it is not possible to distinguish between the regioisomers of the intermediates (R and R′ being methyl and phenyl or vice versa; see Fig. S25 in the ESI†).

The alternative assignment of the detected ions to the gold-tagged ketone products can be excluded. The C=O stretching of these ions would be expected in the range 1650–1700 cm⁻¹ and the CO stretching band should have a large intensity (see the spectrum of gold-tagged acetone in ref. 9c, in which the C=O stretch is the dominant band at ∼1660 cm⁻¹). Probably, the small peak at about 1680 cm⁻¹ indicates a minor abundance of these gold-tagged products among the detected ions. However, their co-detection should have only a negligible effect on the kinetics associated with the intermediates which represent more than 90% of the detected ions as the OH stretching bands suggest (see above).

The DFT calculated structures of the protonated α-gold ketone intermediates (1H⁺) suggest that the (Au–C–C) bonding angle ranges between 82° and 90°, and the Au–C bonding length ranges from 2.21 to 2.24 Å for different conformers and regioisomers (Table S10, Fig. S23†). Hence, the detected ions have a structure characterized by two mesomeric extremes: (1) a gold complex of an enol and (2) protonated α-gold ketone. In comparison to these ions, the (Au–C–C) angle in neutral intermediate 1 is predicted to range from 102° to 106°, and the Au–C length is expected to range from 2.10 to 2.12 Å (Table S10, Fig. S23†). The values of the neutral intermediates imply that the gold atom binds to an sp³ carbon atom and thus the neutral intermediates can be assigned as α-gold ketones. We can conclude that protonation occurring during electrospray ionization (see below) substantially weakens the Au–C bond and drives the geometry of the complex towards the enol form, as shown in Fig. 1a.¹³ In principle, this protonation mimics the mechanism of protodeauration leading to the enol product of the overall reaction.

An alternative explanation could involve 2-gold vinyl alcohol intermediates (A in Scheme 1 with Nu = OH). These intermediates could be protonated during electrospray ionization at the carbon atom yielding also monourated protonated complexes 1H⁺. However, DFT calculations suggest that the enol form of the intermediates is 74 kJ mol⁻¹ higher in energy than the suggested α-gold keto-form (R = R′ = CH₃, see Fig. S24 in the ESI†). Hence, a fast tautomerization of the initially formed enol-intermediates to the keto-intermediates is expected. The suggested α-gold keto-form of the intermediates is also fully consistent with all other finding in this work (see below).

The IRPD spectrum of the diaurated complexes (m/z 1303) shows no O–H stretching band (Fig. 2) which means that neither geminally diaurated complexes of the type X⁺, nor the intermediates of the type B⁺ (Nu = OH in Scheme 1) are detected. Instead, the detected ions correspond to the intermediates 2⁺ with one gold atom bonded to the carbon atom and with the other gold atom bonded to the oxygen atom shown in Fig. 2. The C–O stretching band is highlighted in blue. This part of the composite band around 1500 cm⁻¹ does not overlap with the vibrational bands originating from the IPr ligand (compare with Fig. 1) and thus must correspond to the C–O bond. The large red shift of the carbonyl vibration is in agreement with DFT calculations. These calculations predict that the Au–C–C bonding angle ranges from 99° to 101° and a Au–C bonding distance is about ∼2.16 Å (Table S10, Fig. S23†). Hence, these geometry parameters fall between those found for the neutral monoaurated intermediate 1 and for its protonated ion 1H⁺ suggesting a substantial delocalisation of the π electrons, as shown by the mesomeric structures in Fig. 2a.

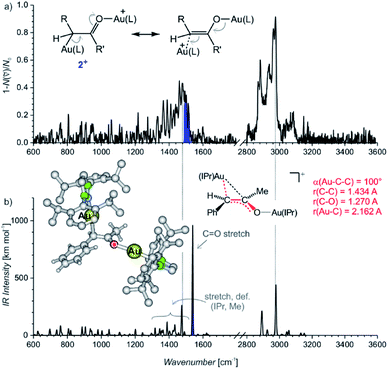Fig. 2 (a) IRPD spectrum of [Au₂(IPr)₂(PhCCCH₃,OH)]⁺ (m/z 1303). The blue colour highlights the additional band next to the bands originating from vibration of the IPr ligand (compare with Fig. 1a). (b) Theoretical IR spectrum of the most stable isomer of 2⁺ and its geometry parameters.

Degradation of the intermediates in solution

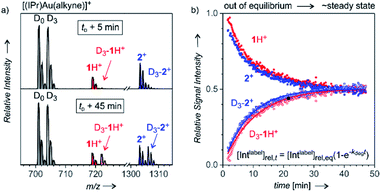
After analysing the structure of the detected ions, we shifted our focus to the reaction kinetics associated with these intermediates in solution. The solution kinetics of the ESI-MS detected species can be investigated by Delayed Reactant Labelling.⁹ Peak heights in an MS spectrum are unrelated to the concentrations of the given species in a solution. The concentrations can be determined only by using internal isotopically labelled standards. Obviously, such standards are unavailable for reaction intermediates. Therefore, we formed the isotopically labelled intermediates in situ with a time delay in relation to the unlabelled intermediates, and we evaluated the relative evolution of the corresponding signals. The typical experiment began by starting a reaction with unlabelled reactants (here: H₂O, Ph–CC–CH₃, catalyst, solvent), which leads to a build-up of a specific concentration of the unlabelled intermediates 1 and 2⁺. After a t_D delay, an isotopically labelled reactant (here: Ph–CC–CD₃) was added to the reaction mixture. ESI-MS spectra of this reaction mixture show the progression of the signals of the unlabelled (1H⁺ and 2⁺) and labelled (D₃-1H⁺ and D₃-2⁺) reaction intermediates reflecting the relative changes in the concentration of the intermediates in solution (Fig. 3).

Fig. 3 Delayed reactant labelling method. (a) ESI-MS spectrum recorded 5 and 45 min after adding PhCCCD₃ to the reaction mixture of PhCCCH₃ with 5.4 mol% [Au(IPr)(CH₃CN)(BF₄)] in acetone/water (5 : 1); the time-delay was 30 min. (b) Mutual time progression of the integrated MS peak intensities of 1H⁺ and D₃-1H⁺ (in red) and of 2⁺ and D₃-2⁺ (in blue). The solid lines are exponential fits of the relative growth of the D₃-1H⁺ and D₃-2⁺ signals.

The concentrations of intermediates in the steady state equilibrium depend on the concentrations of the reactants. For the conditions here, the equilibrium is reached after about 40 min (the concentrations of the labelled and unlabelled intermediates are about equal as the concentrations of Ph–CC–CH₃ and Ph–CC–CD₃ are). The relative progression of the MS signals of the labelled and unlabelled intermediates can be fitted using an exponential function derived from the steady-state approximation for the intermediates (see the equation in Fig. 3). The fits provide rate constants for the degradation (k_deg) and the half-life t_1/2 = ln(2)/k_deg of the intermediates in solution (details can be found in the ESI† and in the ref. 9).

It should be noted that kinetics of complexes formed in a fast equilibrium (t_1/2 < 1 min), such as [(IPr)Au(PhCCCH₃)]⁺ and [(IPr)Au(PhCCCD₃)]⁺ (in gray denoted by D₀ and D₃ in Fig. 3) cannot be monitored by ESI-MS, because the equilibrium is reached faster than the response of ESI-MS is. Hence, the signal intensities show no mutual evolution. The same observation is expected for complexes/ions formed as artefacts during the electrospray ionisation. On contrary, the signals of product complexes do show the evolution of the intensities, but they never reach the steady-state concentrations in equilibrium with the reactants (details are in the ref. 9). Therefore, we can exclude that the signals of 1H⁺ and 2⁺ would originate from gold-tagging of reaction products.

The half-life of the intermediate detected as 1H⁺ was determined as (8.7 ± 1.6) min, and the half-life of the intermediate detected as diaurated 2⁺ was (6.9 ± 1.0) min (Table 1). The addition of an acid usually accelerates the degradation of the organogold intermediates.¹⁴ Therefore, we have assessed the effect of p-toluenesulfonic acid (TsOH) on the half-lives of the intermediates detected here. The results showed that 10.8 mol% TsOH in the reaction mixture shortens the half-lives of the detected intermediates to approximately 3 min.

Table 1 Half-lives of the intermediates detected as [Au(IPr)(PhCCCH₃,OH)]H⁺ (1H⁺), [Au₂(IPr)₂(PhCCCH₃,HO)]⁺ (2⁺) and [Au(IPr)(PhCCCH₃,OH)(acetone)]Na⁺ ([1(acetone)Na]⁺) determined from Delayed Reactant Labelling experiments (the labelled reactant was PhCCCD₃, and the time delay was 30 min)

Nucleophile	Additive/sheath liquid	1H^+t1/2 [min]	2 ^+ t 1/2 [min]	[1(acetone)Na]^+t1/2 [min]
a The solution of PhCCCD3 in acetone was added to the reaction mixture of 1-phenylpropyne with 5.4 mol% [Au(IPr)(CH3CN)(BF4)] in acetone/H2O (5 : 1). b 10.8 mol% p-toluenesulfonic acid was added to the reaction mixture. c 0.12 mmol solution of NaSbF6 in 3 ml of acetone was infused as a sheath liquid in the reaction mixture to trap neutral complexes in sodium cations. d The solution of PhCCCD3 in acetone was added to the reaction mixture of 1-phenylpropyne with 5.4 mol% [Au(IPr)(CH3CN)(BF4)] in acetone/D2O (5 : 1).
H2O^a		8.7 ± 1.6	6.9 ± 1.0	—
H2O^a	TsOH^b	2.9 ± 0.4	2.8 ± 0.2	—
H2O^a	NaSbF6^c	7.6 ± 0.5	6.6 ± 0.3	7.0 ± 0.4
D2O^d	NaSbF6^c	16.2 ± 1.2	14.9 ± 1.8	15.5 ± 2.0

---

We have also tried to detect the neutral monoaurated intermediates 1 as adducts with sodium cations. Therefore, we infused an acetone solution of NaSbF₆ as a sheath liquid into the ion source. Indeed, we detected [1(acetone)Na]⁺ ions, and we were again able to follow the kinetics associated with 1 from the unlabelled and labelled signals of the sodium complexes. The [1(acetone)Na]⁺ signals were weak and only observable under slightly harder ionisation conditions (Fig. S9†). The half-lives determined from these experiments are: 1H⁺ (7.6 ± 0.5) min, [1(acetone)Na]⁺ (7.0 ± 0.4) min, and 2⁺ (6.6 ± 0.3) min (Table 1).

In addition, we have studied the reaction with D₂O because we wanted to assess possible kinetic isotope effects on the degradation of the intermediates. The half-lives of the intermediates detected as 1D⁺, [1(acetone)Na]⁺, and 2⁺ more than doubled in the reaction with D₂O, compared to the reaction with H₂O (Table 1). The corresponding kinetic isotope effects are thus slightly above 2 (see Table 2). The values of the kinetic isotope effects suggest that the degradations of the intermediates are connected to hydrogen/proton transfer and that the mechanism is likely very similar or the same for all detected species.

Table 2 Kinetic isotope effects in the formation and degradation of the intermediates detected as [Au(IPr)(PhCCCH₃,OH)]H⁺ (1H⁺), [Au₂(IPr)₂(PhCCCH₃,HO)]⁺ (2⁺) and [Au(IPr)(acetone)(PhCCCH₃,OH)]Na⁺ ([1(acetone)Na]⁺)

Kinetic isotope effect	1H^+		2 ^+	[1(acetone)Na]^+
a The solution of PhCCCD3 in acetone was added to the reaction mixture of 1-phenylpropyne with 5.4 mol% [Au(IPr)(CH3CN)(BF4)] in acetone/H2O (5 : 1) and in acetone/D2O (5 : 1). b H2O and D2O were simultaneously added to the reaction mixture of 1-phenylpropyne with 5.4 mol% gold catalyst in acetone/(H2O + D2O) (5 : 1) (0.12 mmol solution of NaSbF6 in 3 ml of acetone was infused as a sheath liquid in the reaction mixture to trap neutral complexes in sodium cations).
Degradation^a	2.1 ± 0.2		2.3 ± 0.4	2.2 ± 0.3
Formation^b	5.8 ± 0.2	1.0 ± 0.2	4.1 ± 0.3	6.6 ± 0.5

---

Formation of the intermediates in solution

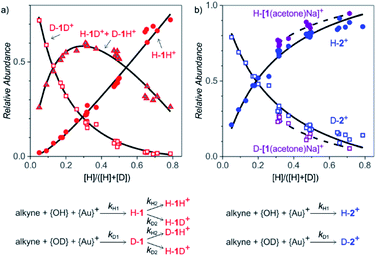
After collecting the data on the degradation of the intermediates, we gathered kinetic information on their formation. For this purpose, we started the reactions in a mixture of H₂O and D₂O (without any delay) and studied the ratios of H and D incorporation into the intermediates detected as 1H⁺ and 2⁺ (Fig. 4). We performed the experiments with different ratios of H₂O vs. D₂O to enable kinetic modelling and to improve the accuracy of our results. The exact H : D ratio was determined from the ratio of the [(IPr)₂Au₂(OH)]⁺ and [(IPr)₂Au₂(OD)]⁺ signals in the spectra.

Fig. 4 Formation of intermediates detected as monoaurated and diaurated complexes in the reaction of 1-phenylpropyne with a mixture of H₂O and D₂O with variable H : D ratios (catalyst: 5.4 mol% [Au(IPr)(CH₃CN)(BF₄)]). The ratio of “acidic” H and D (x-axis) was determined from the ratio of [Au₂(IPr)₂(OH)]⁺ and [Au₂(IPr)₂(OD)]⁺ in each experiment. The graphs show the relative abundances of (a) H-AH⁺ (circles) vs. D-AH⁺ + H-AD⁺ (triangles), and vs. D-AD⁺ (squares) and (b) H-B⁺ (blue circles) vs. D-B⁺ (blue squares) and H-[A(acetone)Na]⁺ (violet circles) vs. D-[A(acetone)Na]⁺ (violet squares). The experimental results were fitted with kinetic equations shown below the graphs.

The relative signal intensities of monoaurated complexes (protonated α-gold ketones) depend on H : D ratios of the hydrogen atoms at the α-carbon atom and at the oxygen atom. This situation can be described by a simple kinetic scheme with two rate constants k₁ and k₂ describing the introduction of each hydrogen atom (Fig. 4, details of the model are in the ESI†). Quantitatively, we can fit only ratios of the isotopic mass-spectrometry signals. It means that we fitted k_H1/k_D1 and k_H2/k_D2; i.e., kinetic isotope effects for the introduction of the hydrogen atoms to the α-carbon atom and to the oxygen atom, respectively. An unconstrained fit of the signal intensities of H-1H⁺, (H-1D⁺ + D-1H⁺) and D-1D⁺ in dependence of the H : D ratio provided the kinetic isotope effects KIE₁ = 5.8 ± 0.2 and KIE₂ = 1.0 ± 0.2 (Fig. 4, see also Fig. S11 in ESI†).

Protonation/deprotonation reactions (or exchange of acidic hydrogen atoms) are fast processes, therefore mass spectrometry detects protonated ions in equilibrium with the concentrations of H⁺ and D⁺ in the solution. This is consistent with the determination of the apparent kinetic isotope effect KIE₂ = 1.0 ± 0.2 for the protonation of the monoaurated intermediates at the oxygen atom. Accordingly, KIE₁ = 5.8 ± 0.2 corresponds to the reaction pathway that leads to the introduction of H to the carbon-atom.

The sodium-tagged monoaurated complexes and the diaurated complexes have only one added hydrogen atom; therefore, the dependence of H-2⁺/D-2⁺ and H-[1(acetone)Na]⁺/D-[1(acetone)Na]⁺ on the H : D ratio can be fitted using only one KIE. The resulting kinetic isotope effects are 4.1 ± 0.3 for the formation of the diaurated complexes and 6.6 ± 0.5 for the formation of the sodiated monoaurated complexes.

The results again show that the kinetics associated with the intermediates detected as diaurated complexes is slightly different than that associated with the formation of the monoaurated complexes. The values of the kinetic isotope effects corresponds to the values expected for general-acid catalysed processes in a mixture of H₂O and D₂O (KIE ∼ 5).¹⁵ Hence, it is consistent with concerted protonation/deprotonation of the initially formed 2-gold vinyl alcohol intermediates (A or B⁺ in Scheme 1 with Nu = OH) to form the detected α-gold ketones.

In summary, the experiments with 1-phenylpropyne showed that we can detect monoaurated and diaurated complexes by ESI-MS with structures derived from neutral α-gold ketones protonated or aurated at the oxygen atom. The kinetics associated with the formation and degradation of the intermediates in solution detected as 1H⁺ or 2⁺ slightly differ and suggest that the intermediates detected as 2⁺ have probably a higher turn-over frequency. However, the results for the intermediates detected as 1H⁺ and 2⁺ are not fundamentally different. The small differences between the detected 1H⁺ and 2⁺ can be well explained by other scenarios.¹⁶ Most relevantly, two possible isomers (depending on R and R′) of only one type of the intermediate might be present in solution and the detected differences might result from different capabilities of the isomers to attach or detach the gold cation bound at the oxygen atom. Hence, the results showed that the kinetics of the intermediates in solution are very similar, but further experiments are necessary to resolve whether only one type of the intermediates is relevant in this reaction and which one it is.

Experiments with a symmetric alkyne

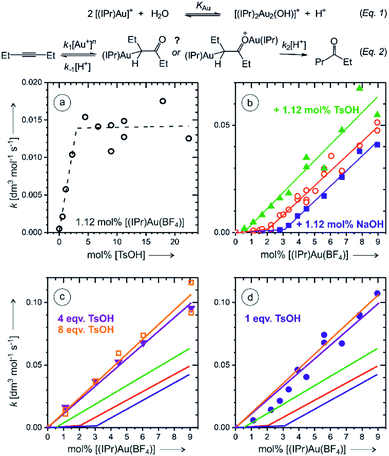
In order to remove the ambiguity of working with isomers, we have repeated the experiments with symmetric 3-hexyne. The NMR experiments showed that the reaction is much faster than that with 1-phenylpropyne (Fig. S3 and S4†). The ESI-MS experiments detected monoaurated as well as diaurated complexes. The kinetic profiles of the complexes determined by delayed reactant labelling experiments show that the detected complexes are a mixture of intermediates and product complexes (see the analysis in Fig. S14–S16†). More importantly, however, the kinetics associated with both types of the complexes is identical within the experimental noise. This implies that the monoaurated and diaurated ions detected by ESI-MS report on only one species present in solution. We have further investigated the kinetics of the overall reaction by gas chromatography.

Firstly, we have determined rate constants for the product formation in dependence of the p-toluenesulfonic acid (TsOH) concentration. Indeed, we observed that the rate linearly increases up to the concentration of TsOH being double of the concentration of the gold catalyst. Further increase of the TsOH concentration did not increase the overall rate (Fig. 5a). The rate constant increased three-fold which is in a very good agreement with a three-fold increase of the degradation rate of monoaurated as well as diaurated intermediates in the reaction of 1-phenylpropyne described above (Table 1). Hence, we have concluded that the addition of 4 or more equivalents of the acid with respect to the concentration of the gold catalyst results in a situation that protodeauration step is not anymore the rate determining step.

Fig. 5 Rate of the ketone product formation in the reaction of 3-hexyne (27.6 mM in 5 : 1 mixture of THF and H₂O, respectively) with water catalysed by [Au(IPr)(CH₃CN)(BF₄)]. (a) Dependence of the rate on the concentration of p-toluenesulfonic acid (TsOH). The experiment was done with 1.12 mol% of the catalyst. (b) Dependence of the reaction rate on the concentration of the catalyst under the standard conditions (in red) and with addition of 1.12 mol% of NaOH (blue) or 1.12 mol% TsOH (green). The lines are bimodal linear fits of the data. (c) Dependence of the reaction rate on the concentration of the catalyst under the standard conditions with addition of 4 equiv. (purple) and 8 equiv. (yellow) of TsOH with respect to the concentration of the catalyst. The red, blue, and green lines are fits from (b). (d) Dependence of the reaction rate on the concentration of the catalyst under the standard conditions with addition of 1 equiv. of TsOH (blue solid circles). The other solid lines are experiments from (b) and (c).

Next, we have investigated the dependence of the kinetics of the product formation on the concentration of the gold catalyst. In the regime with a large excess of the TsOH acid, the rate depended linearly on the concentration of [Au(IPr)(CH₃CN)(BF₄)] (Fig. 5c). This clearly suggests that the product is formed in the reaction mechanism involving a single gold cation. The negligible role of (di)gold hydroxide in the reaction under these conditions is also expected from the effect of the acid on the eqn (1).

Without the addition of TsOH, the rate dependence on the concentration of the gold catalyst shows an initial phase with very small rates, but with the concentration of the gold catalyst above 2 mol%, the rate started to increase linearly (Fig. 5b). We have tested this linear dependence by a small addition of sodium hydroxide (1.12 mol%) and of TsOH (1.12 mol%), respectively. The rate dependence on the concentration of the gold catalyst was almost exactly the same as without the additives, but the lag phase was larger when NaOH was added and smaller when TsOH was added (compare red, blue, and green data in Fig. 5b). These results suggest that the lag phase is associated with the lack of available protons in the reaction mixture. We suspected that a glassware, silica capillary or other experimental circumstances might affect the reaction rate at small concentrations of the catalyst. To test this hypothesis, we repeated the experiment in a plastic vial and the lag phase was indeed somewhat smaller (Fig. S22 and details in the ESI†).

The results clearly show that the basic conditions suspend the overall reaction rate (eqn (2)).¹⁷ Firstly, a base shifts the equilibrium of the reaction (1) to the right converting the gold catalyst to the digold hydroxide complex that most probably does not catalyse this reaction. Secondly, a base impairs the protodeauration step. The accounting of this “background base” effect at low concentrations of the catalyst is important, because the rate dependence on the gold catalyst concentration could be incorrectly denoted as quadratic, especially if a smaller range of concentrations is explored (see Fig. 5b) or when the reaction is conducted in an intermediate regime e.g., with 1 equiv. of added acid (Fig. 5d).

In summary, the kinetic experiments suggest that the reaction rate is first-order dependent on the gold catalyst concentration. Adding of a base and thus promoting of the formation of digold hydroxide leads to suspending of the reaction rate. On the other hand, adding of an acid increases the reaction rate, because it accelerates the rate-determining step – protodeauration. However, for the acid concentrations exceeding the concentration of the gold catalyst, the reaction rate is not anymore dependent of the concentration of the acid. This suggests that protodeauration is not the rate-determining step under these acidic conditions, but instead the deprotonation of the initial adduct between the gold-activated alkyne and water becomes the rate-determining step. All these results are consistent with the reaction mechanism involving just a single gold-cation as an active catalyst and the reaction pathway shown in Scheme 2.

Scheme 2 Reaction pathway for [(IPr)Au]⁺ mediated hydration of alkynes. The ESI-MS experiments revealed that the detected monoaurated and diaurated complexes report on the identical intermediate in solution, α-gold ketone. Small differences in the measured kinetics are most probably associated R and R′. The GC kinetic experiments showed that the rate of the formation of the product depends on the first order of the gold catalyst concentration.

Conclusions

Gold(I) ([Au(IPr)(CH₃CN)(BF₄)]) catalysed water addition to alkynes proceeds most likely via monoaurated intermediates. We have shown that these intermediates are neutral in solution and can be detected by electrospray ionization mass spectrometry either as protonated complexes or tagged with another gold cation. The structures of the detected complexes correspond to α-gold ketones protonated or aurated at the oxygen atom. Exploratory DFT calculations suggest the α-gold ketone intermediates are more than 70 kJ mol⁻¹ more stable than the alternative, probably primarily formed 2-gold vinyl alcohol intermediates.¹⁸

Kinetic experiments with the intermediates in the water addition to 1-phenylpropyne showed differences in the formation and the degradation of the ESI-MS detected monoaurated and diaurated complexes. However, these differences are most likely caused by different selectivities in protonation and auration of the two possible isomers of the neutral α-gold ketone intermediates. In agreement, the differences in kinetics vanished, when we did the experiments with symmetric 3-hexyne reactant. The results for the reaction involving 1-phenylpropyne showed that the half-life of the neutral monoaurated intermediates in solution is on the order of 7 min. The protodeauration of the α-gold ketone intermediates is associated with the kinetic isotope effect of about 2. The kinetic isotope effect for the hydrogen introduction to the gold-bonded carbon atom is isomer-dependent and is in the range of 4–6. These values are consistent with kinetic isotope effects expected for general-acid mediated reactions in H₂O/D₂O.¹⁵ Hence, it is in accordance with the scenario of keto–enol tautomerisation of the initially formed 2-gold vinyl alcohol intermediates.

The overall reaction kinetics of water addition to symmetric 3-hexyne revealed that the reaction is first-order dependent on the concentration of the gold catalyst. The reaction is accelerated by addition of an acid which correlates with the observed acceleration of degradation (protodeauration) of the ESI-MS detected intermediates. In the absence of an acid, we observed a lag in reactivity at small catalyst concentrations, but at larger concentrations the rate dependence on the catalyst concentration was again linear. All these kinetic data clearly point towards reaction mechanism involving only monoaurated intermediates.

Experimental

The electrospray ionization mass spectra were measured with a TSQ 7000 mass spectrometer or an LTQ linear ion trap instruments.¹⁹ The ions were generated from reaction mixtures of 1-phenylpropyne with 5.4 mol% [Au(IPr)(CH₃CN)(BF₄)] in acetone/water (5 : 1) at soft ionization (low potentials on the entrance ion optics and the temperature of the capillary was 200 °C). Compositions of all investigated reaction mixtures and MS/MS analysis of the selected ions can be found in the ESI.† Details of kinetic analysis as well as derivation of the kinetic equations used can be also found in the ESI.†

The infrared photodissociation spectra were measured with the ISORI instrument.²⁰ ISORI is based on the combination of a low-temperature ion trap with a commercial TSQ 7000 instrument. It preserves the same ionization chamber (here the electrospray ionization is used in exactly the same way as for the other MS experiments). The generated ions are mass-selected by quadrupole and guided by a quadrupole bender and octopole to an ion trap. The trap has a linear quadrupole geometry and operates at 3.4–3.6 K and at 1 Hz. Trapping and cooling of the ions is achieved by collisions with a helium buffer gas (first 300 ms of the trapping cycle). About 1–3% of the ions form helium-tagged complexes. The ions were irradiated during the 300–990 ms time interval (10 Hz repetition rate, OPO/OPA system from LaserVision pumped by Nd:YAG laser Surelite EX from Continuum, tuning range 700–4700 cm⁻¹, FWHM ∼ 1.5 cm⁻¹, 10 ns pulse length). At 990 ms, the ions were extracted, mass-analyzed by a second quadrupole and detected by a Daly type detector operated in the ion-counting mode. The IRPD spectrum is constructed as wavenumber-dependent (1 − N(ν_i)/N₀), where N(ν_i) is the number of helium complexes surviving irradiation at the ν_i wavenumber and N₀ is the total number of helium complexes (obtained in the alternative cycles with a photon beam blocked by a mechanical shutter).

Gas chromatography was performed with a Shimadzu GC-2010 Plus instrument with split/splitless injection and a flame-ionization detector. H₂ was used as carrier gas at a constant linear velocity of 40 cm s⁻¹. The total flow was 38.4 mL min⁻¹ and the column flow 1.42 mL min⁻¹. Compounds were separated on a 30 m × 0.25 mm AB-5MS capillary column (5% phenyl/95% dimethyl polysiloxane). The injection port was held at 300 °C and used in split mode with a split ratio of 25. The oven temperature started at 50 °C, increasing 10 °C min⁻¹ up to 100 °C. The temperature was then set to increase 80 °C min⁻¹ up to 250 °C. The total time for one GC run was 6.88 min. The FID temperature was 300 °C. The exact reaction mixtures compositions and all measure data can be found in the ESI (Tables S5–S9 and Fig. S17–S22†).

Density functional theory (DFT) calculations have been performed with the mPW1PW91 density functional²¹ and with the LanL2DZ basis set for the gold atoms and the cc-pVDZ basis set for the remaining elements as implemented in Gaussian 09.²² The geometries were fully optimized and the results were controlled by Hessian matrix calculations. The computed vibrational frequencies were scaled by 0.97 in the finger-print region and by 0.945 above 2000 cm⁻¹.^9,23,24 The final IR spectra were convoluted with a Gaussian function with a full width at half maximum of 3 cm⁻¹. The optimized geometries, energies, and IR spectra are in the ESI (Tables S10 and S11, Fig. S23–S26†).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The project was funded by the European Research Council (ERC CoG No. 682275).

Notes and references

1. D. Weber and M. R. Gagne, in Homogeneous Gold Catalysis, Book Series: Topics in Current Chemistry-Series, ed. L. M. Slaughter, Springer-Verlag, Berling, 2015, vol. 357,p. 167.
2. (a) D. J. Gorin and F. D. Toste, Nature, 2007, 446, 395; (b) M. Anania, L. Jasikova, J. Jasik and J. Roithova, Org. Biomol. Chem., 2017, 15, 7841; (c) E. Andris, P. C. Andrikopoulos, J. Schulz, J. Turek, A. Ruzicka, J. Roithova and L. Rulisek, J. Am. Chem. Soc., 2018, 140, 2316.
3. (a) A. Corma, A. Leyva-Perez and M. J. Sabater, Chem. Rev., 2011, 111, 1657; (b) M. N. Hopkinson, A. Tlahuext-Aca and F. Glorius, Acc. Chem. Res., 2016, 49, 2261; (c) Z. T. Zheng, Z. X. Wang, Y. L. Wang and L. M. Zhang, Chem. Soc. Rev., 2016, 45, 4448; (d) W. W. Zi and F. D. Toste, Chem. Soc. Rev., 2016, 45, 4467; (e) A. M. Asiri and A. S. K. Hashmi, Chem. Soc. Rev., 2016, 45, 4471; (f) A. Furstner, Angew. Chem., Int. Ed., 2018, 57, 4215.
4. (a) A. S. K. Hashmi, Angew. Chem., Int. Ed., 2008, 47, 6754; (b) M. Bandini, A. Bottoni, M. Chiarucci, G. Cera and G. P. Miscione, J. Am. Chem. Soc., 2012, 134, 20690; (c) M. M. Hansmann, M. Rudolph, F. Rominger and A. S. K. Hashmi, Angew. Chem., Int. Ed., 2013, 52, 2593; (d) A. Zhdanko and M. E. Maier, Angew. Chem., Int. Ed., 2014, 53, 7760; (e) M. Q. Jia and M. Bandini, ACS Catal., 2015, 5, 1638; (f) M. Trinchillo, P. Belanzoni, L. Belpassi, L. Biasiolo, V. Busico, A. D'Arnora, L. D'Amore, A. Del Zotto, F. Tarantelli, A. Tuzi and D. Zuccaccia, Organometallics, 2016, 35, 641; (g) J. E. M. N. Klein, G. Knizia, L. Nunes dos Santos Comprido, J. Kästner and A. S. K. Hashmi, Chem.–Eur. J., 2017, 23, 16097–16103; (h) M. E. de Orbe, L. Amenos, M. S. Kirillova, Y. H. Wang, V. Lopez-Carrillo, F. Maseras and A. M. Echavarren, J. Am. Chem. Soc., 2017, 139, 10302; (i) M. Lu, Y. Su, P. Zhao, X. Ye, Y. Cai, X. Shi, E. Masson, F. Li, J. L. Campbell and H. Chen, Chem.–Eur. J., 2018, 24, 2144.
5. (a) A. S. K. Hashmi, I. Braun, P. Nösel, J. Schädlich, M. Wieteck, M. Rudolph and F. Rominger, Angew. Chem., Int. Ed., 2012, 51, 4456; (b) A. S. K. Hashmi, M. Wieteck, I. Braun, P. Nösel, L. Jongbloed, M. Rudolph and F. Rominger, Adv. Synth. Catal., 2012, 354, 555; (c) A. Gómez-Suárez and S. P. Nolan, Angew. Chem., Int. Ed., 2012, 51, 8156; (d) V. Vreeken, D. L. J. Broere, A. C. H. Jans, M. Lankelma, J. N. H. Reek, M. A. Siegler and J. I. van der Vlugt, Angew. Chem., Int. Ed., 2016, 55, 10042; (e) S. Ferrer and A. M. Echavarren, Organometallics, 2018, 37, 781.
6. (a) G. Seidel, C. W. Lehmann and A. Fürstner, Angew. Chem., Int. Ed., 2010, 49, 8466 and references therein; (b) T. J. Brown, D. Weber, M. R. Gagne and R. A. Widenhoefer, J. Am. Chem. Soc., 2012, 134, 9134; (c) A. Zhdanko and M. E. Maier, Organometallics, 2013, 32, 2000; (d) A. Zhdanko and M. E. Maier, Chem.–Eur. J., 2014, 20, 1918.
7. (a) J. Roithova, S. Jankova, L. Jasikova, J. Vana and S. Hybelbauerova, Angew. Chem., Int. Ed., 2012, 51, 8378; (b) Y. Oonishi, A. Gomez-Suarez, A. R. Martin and S. P. Nolan, Angew. Chem., Int. Ed., 2013, 52, 9767; (c) A. Gómez-Suárez, Y. Oonishi, A. R. Martin, S. V. C. Vummaleti, D. J. Nelson, D. B. Cordes, A. M. Z. Slawin, L. Cavallo, S. P. Nolan and A. Poater, Chem.–Eur. J., 2016, 22, 1125.
8. The dual activation pathway was recently supported by examples of cooperation of different metals: (a) F. Lazreg, S. Guidone, A. Gómez-Herrera, F. Nahrab and C. S. J. Cazin, Dalton Trans., 2017, 46, 2439; (b) O. F. González-Belman, J. O. C. Jiménez-Halla, F. Nahra, C. S. J. Cazin and A. Poater, Catal. Sci. Technol., 2018, 8, 3638.
9. (a) L. Jašíková, M. Anania, S. Hybelbauerová and J. Roithová, J. Am. Chem. Soc., 2015, 137, 13647; (b) J. Schulz, J. Jašík, A. Gray and J. Roithová, Chem.–Eur. J., 2016, 22, 9827; (c) M. Anania, L. Jasikova, J. Jasik and J. Roithova, Org. Biomol. Chem., 2017, 15, 7841.
10. (a) S. P. Nolan, Acc. Chem. Res., 2011, 44, 91; (b) N. Marion, R. S. Ramon and S. P. Nolan, J. Am. Chem. Soc., 2009, 131, 448.
11. A. Gomez-Suarez, R. S. Ramon, A. M. Z. Slawin and S. P. Nolan, Dalton Trans., 2012, 41, 5461.
12. J. Roithová, A. Gray, E. Andris, J. Jašík and D. Gerlich, Acc. Chem. Res., 2016, 49, 223.
13. For comparison, see a study of gold complexes with enolethers: Y. Zhu, C. S. Day and A. C. Jones, Organometallics, 2012, 31, 7332.
14. E. Mizushima, K. Sato, T. Hayashi and M. Tanaka, Angew. Chem., Int. Ed., 2002, 41, 4563.
15. T. Riley and F. A. Long, J. Am. Chem. Soc., 1962, 84, 522.
16. (a) H. Kurouchi and D. A. Singleton, Nat. Chem., 2018, 10, 237; (b) H. R. Aziz and D. A. Singleton, J. Am. Chem. Soc., 2017, 139, 5965D. A. Singleton and A. A. Thomas, J. Am. Chem. Soc., 1995, 117, 9357.
17. M. Kumar, G. B. Hammond and B. Xu, Org. Lett., 2014, 16, 3452.
18. (a) G. Mazzone, N. Russo and E. Sicilia, J. Chem. Theory Comput., 2010, 6, 2782; (b) G. Mazzone, N. Russo and E. Sicilia, Organometallics, 2012, 31, 3074; (c) L. Jin, Y. Wu and X. Zhao, RSC Adv., 2016, 6, 89836.
19. L. Ducháčková and J. Roithová, Chem.–Eur. J., 2009, 15, 13399.
20. (a) J. Jašík, J. Žabka, J. Roithová and D. Gerlich, Int. J. Mass Spectrom., 2013, 354–355, 204; (b) D. Gerlich, J. Jašík, E. Andris, R. Navrátil and J. Roithová, ChemPhysChem, 2016, 17, 3723; (c) J. Jašík, D. Gerlich and J. Roithová, J. Phys. Chem. A, 2015, 119, 2532.
21. (a) J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671; (b) J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978; (c) J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533; (d) C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664.
22. M. J. Frisch, et al., Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009.
23. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502.
24. A. Škríba, L. Jašíková and J. Roithová, Int. J. Mass Spectrom., 2012, 330, 226.

---

Footnote

† Electronic supplementary information (ESI) available: Supporting results obtained by NMR, MS and DFT calculations. See DOI: 10.1039/c9sc05662a

---