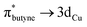Isomerism and dynamic behavior of bridging phosphaalkynes bound to a dicopper complex

Abstract

A dicopper complex featuring a symmetrically bridging nitrile ligand and supported by a binucleating naphthyridine-based ligand, [Cu₂(μ-η¹:η¹-MeCN)DPFN](NTf₂)₂, was treated with phosphaalkynes (RC≡P, isoelectronic analogues of nitriles) to yield dicopper complexes that exhibit phosphaalkynes in rare μ-η²:η² binding coordination modes. X-ray crystallography revealed that these unusual “tilted” structures exist in two isomeric forms (R “up” vs. R “sideways”), depending on the steric profile of the phosphaalkyne's alkyl group (R = Me, Ad, or ^tBu). Only one isomer is observed in both solution and the solid state for R = Me (sideways) and ^tBu (up). With intermediate steric bulk (R = Ad), the energy difference between the two geometries is small enough that both are observed in solution, and NMR spectroscopy and computations indicate that the solid-state structure corresponds to the minor isomer observed in solution. Meanwhile, treatment of [Cu₂(μ-η¹:η¹-MeCN)DPFN](NTf₂)₂ with 2-butyne affords [Cu₂(μ-η²:η²-(MeC≡CMe))DPFN](NTf₂)₂: its similar ligand geometry demonstrates that the tilted μ-η²:η² binding mode is not limited to phosphaalkynes but reflects a more general trend, which can be rationalized via an NBO analysis showing maximization of π-backbonding.

---

Introduction

In recent years, the demand for efficient, inexpensive, and environmentally sustainable catalysts has inspired the study of homogeneous, heterogeneous, and biological systems containing copper active sites that enable a range of small molecule transformations, including nitrous oxide and nitrogen dioxide reduction, water oxidation, and selective hydrocarbon oxidation.^1–6 The implicated copper active sites are often multimetallic, raising fundamental questions concerning the extent of metal–metal interaction during catalysis, and the nature of cooperative electronic effects on the binding and activation of substrates.^7–9 Indeed, sterically accessible multimetallic cores can support a wide variety of binding modes, including bridging ones that may enable reactivity not observed in monometallic systems.^10,11 Unsaturated substrates such as alkenes, alkynes, and nitriles, provide interesting cases as they can interact in an end-on (η¹) or side-on (η²) fashion with each metal center (Fig. 1).¹² Many multicopper assemblies bind substrates through a combination of these modes, and unsaturated molecules more often bind in a canted μ-η¹:η¹ or μ-η¹:η² fashion, rather than in a symmetrical mode through one bridging atom (μ-η¹:η¹).^10,13–20 Moreover, the observed binding modes are often found to be substrate-specific rather than examples of a broader structural class.^21–23 One system that notably exhibits a high tendency toward symmetrical μ-η¹:η¹ binding is the naphthyridine-supported dicopper(I) core reported by this laboratory, which binds nitriles, isonitriles, carbon monoxide, as well as phenyl and terminal alkynyl anions exclusively in a symmetrical μ-η¹:η¹ fashion.^24–26 However, these earlier studies primarily focused on the coordination of C- and N-donating unsaturated bridging fragments, and reactions with heavier, softer donors like phosphorus-based ones have not been investigated.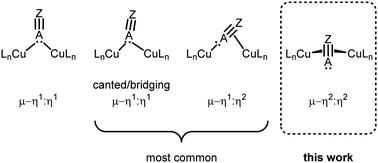

Fig. 1 Possible bridging binding modes for unsaturated substituents bearing a terminal lone pair of electrons in dicopper complexes.

Here we describe the coordination of phosphaalkynes, a relatively understudied class of reactive compounds that are useful building blocks for complex phosphorus-containing assemblies.²⁷ They are analogous to nitriles but possess a much more diffuse terminal lone pair of electrons that, unlike nitriles, is lower in energy than the triple bond's π-system; overall this makes phosphaalkynes less suitable for end-on binding.^27,28 Phosphaalkynes bind in a μ-η²:η² fashion to the dicopper core, which is unprecedented for unsaturated bridging ligands featuring a terminal lone electron pair. Study of a series of phosphaalkyne ligands with varied steric profiles reveals the occurrence of various side-on coordination modes, whose relative energies are studied spectroscopically and computationally. Moreover, comparison with a symmetrical internal alkyne reveals that the unusual binding modes exhibited by phosphaalkynes do not arise solely from the unsymmetrical triple bond substituents but result from a fundamental characteristic of π-systems bound to these naphthyridine-supported dicopper(I) cores.

Results and discussion

Synthesis and structure of bridging RCP complexes

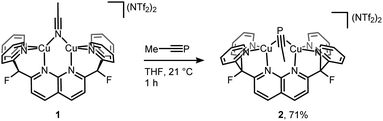
Initial synthetic efforts focused on displacement of the bridging acetonitrile ligand in [Cu₂(μ-η¹:η¹-MeCN)DPFN](NTf₂)₂ (1) with methylphosphaalkyne (MeCP).^24,25 Addition of 3 equivalents of MeCP to a solution of 1 in THF quantitatively afforded the corresponding [Cu₂(μ-η²:η²-MeCP)DPFN](NTf₂)₂ complex 2, isolated in high yield by removing volatile compounds in vacuo and triturating the resulting powder with diethyl ether to afford an analytically pure yellow powder (Scheme 1).

Scheme 1 Synthesis of [Cu₂(μ-η²:η²-MeCP)DPFN][NTf₂]₂ (2).

The X-ray structure of 2 revealed that MeCP binds to the dicopper unit in a side-on, side-on fashion (Fig. 2 and SC1), resulting in an expanded dicopper core with a Cu1⋯Cu2 distance of 2.6548(5) Å compared to that of 2.4781(6) in 1.²⁵ This complex has a lower symmetry than 1, since μ-η²:η² binding disrupts the mirror plane containing the ligand's naphthyridine core. However, the mirror plane perpendicular to the naphthyridine is preserved, and MeCP binds symmetrically to both copper centers; the two Cu–P1 distances are equivalent, as are the Cu–C31 distances. The bound phosphaalkyne is slightly activated, as evidenced by an elongated triple bond distance (P1–C31: 1.631(2) Å, compared to 1.544 Å in free MeCP as determined by microwave spectroscopy²⁹) and a bending at C31 (∠P1–C31–C32: 154.5(1)°).

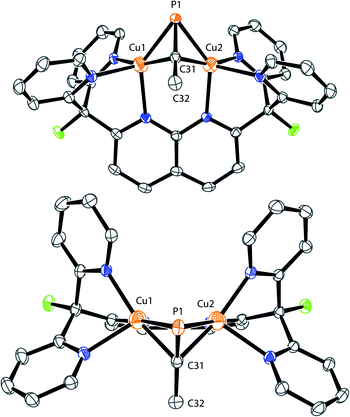Fig. 2 Front (top) and top (bottom) view of the solid-state structure of 2. The two triflimide anions and hydrogen atoms are omitted for clarity. Thermal ellipsoids are set at 50% probability.

To the best of our knowledge, this is the first example of a phosphaalkyne–copper complex, and one of only a few bimetallic complexes containing a phosphaalkyne fragment bound in a μ-η²:η² fashion, without coordination of the phosphorus lone pair of electrons to an additional acceptor.^30–35 Of these other bimetallic complexes, only three feature first-row transition metals, namely iron,³¹ cobalt,³² and nickel,³⁵ all supported at least partially by carbonyl ligands, and only the dicobalt one was isolated without observation of further phosphaalkyne-based reactivity. These complexes exhibit a more activated C≡P triple bond, as determined by longer C–P distances (1.687(7),1.702(6) and 1.7087(17) Å, respectively) and less obtuse ∠P–C–C angles (139.0(5), 135.1(4) and 135.17(14)° respectively) than are found in 2. To our knowledge, 2 is the first structurally characterized dicopper complex with a μ-η²:η²-coordinated triple bond featuring a non-coordinated terminal lone-pair of electrons. While the dramatic difference in binding geometries between 1 and 2 was initially unexpected, computational studies suggest that for MeCP a μ-η²:η² binding mode is significantly more stable than the μ-η¹:η¹ structure. DFT geometry optimizations for [Cu₂(μ-MeCP)DPFN]²⁺ featuring either a side-on or an end-on bridging MeCP fragment indicate that the μ-η²:η² geometry is stable, while the μ-η¹:η¹ geometry describes a transition state rather than a minimum on the potential surface (see ESI); the end-on structure is 14.0 kcal mol⁻¹ higher in energy than the μ-η²:η² geometry (Fig. S10 and Table S2†). Additionally, the different coordination behavior observed for nitriles vs. phosphaalkynes is in line with the relative energies for the frontier orbitals of each molecule. Both bind through their highest occupied molecular orbital (HOMO): for nitriles, it corresponds to the terminal lone pair while the HOMO for a phosphaalkyne corresponds to the π system.²⁸

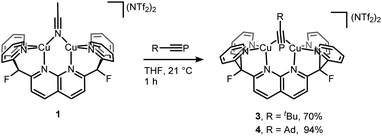
Interestingly, the solid-state structure of 2 reveals strain in the DPFN backbone, which lies flat in 1, but bends 20° out of plane in 2 to accommodate the bridging substituent (Fig. 2 and SC1†).²⁵ Thus, it seemed that other bridging geometries, including possibly an end-on, end-on linkage, could be accessed by increasing the steric strain caused by the phosphaalkyne substituent. To test this, two additional dicopper complexes were synthesized following the same procedure used for 2, with the electronically similar but sterically more demanding phosphaalkyne ligands ^tBuCP and AdCP. This led to isolations of [Cu₂(μ-η²:η^2-tBuCP)DPFN](NTf₂)₂ (3) and [Cu₂(μ-η²:η²-AdCP)DPFN](NTf₂)₂ (4), respectively (Scheme 2).

Scheme 2 Synthesis of [Cu₂(μ-η²:η^2-tBuCP)DPFN][NTf₂]₂ (3) and [Cu₂(μ-η²:η²-AdCP)DPFN][NTf₂]₂ (4).

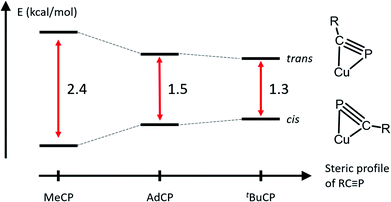
The solid-state structures of 3 and 4 reveal that the bulkier phosphaalkyne fragments bind to the dicopper core in a different μ-η²:η² fashion (Fig. 3 for 4, Fig. SC2† for 3). In complex 2, the alkyl group (Me) and the naphthyridine backbone are cis to one another, i.e. on the same sides of the plane defined by the two Cu centers and the four pyridine N atoms (Cu₂N₄ plane), and opposite to the phosphorus atom. In 3 and 4, the phosphorus atom and naphthyridine moieties lie on the same side of the Cu₂N₄ plane, opposite to the ^tBu and Ad groups, respectively, presumably minimizing steric repulsion between the phosphaalkynes' bulky hydrocarbon moieties and the DPFN pyridine rings (trans geometry). Further comparisons between the solid-state structures of 2 and 4 reveal that the phosphaalkyne is similarly activated in both, with a P–C bond length of 1.628(4) Å in 4 (compared to 1.631(2) Å in 2) and an only slightly more pronounced P1–C31–C32 deviation from linearity (143.1(3)° in 4 compared to 154.5(1)° in 2). Moreover, a slightly shorter Cu1⋯Cu2 distance (2.6177(8) Å) is observed in 4 as compared to 2 (2.6548(5) Å), and the out-of-plane bending of its naphthyridine backbone, 20°, is identical to the 20° deformation observed in 2.

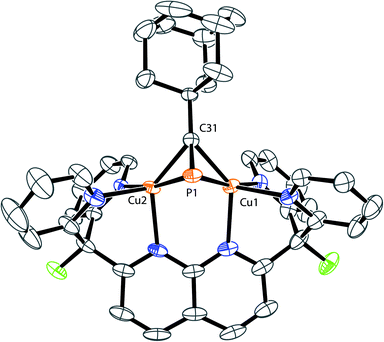Fig. 3 Solid-state structure of 4. Two triflimide anions and hydrogen atoms are omitted for clarity. Thermal ellipsoids are set at 50% probability.

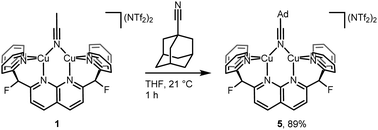
To probe possible effects of the bulky adamantyl group on the binding of the AdCP moiety to the dicopper core in 4, the coordination of 1-adamantanecarbonitrile (AdCN) to [Cu₂(DPFN)]²⁺ was studied for comparison. The bridging acetonitrile in 1 was readily exchanged for AdCN in THF to afford the analogous complex [Cu₂(μ-η¹:η¹-AdCN)DPFN](NTf₂)₂ (5, Scheme 3). Its solid-state structure (Fig. SC4†) reveals that AdCN adopts a μ-η¹:η¹ binding mode similar to that observed in 1; among other structural parameters, the Cu1⋯Cu2 distances in 1 and 5 are within error of one another, as are the Cu–N_nitrile distances. This adds support to the idea that side-on coordination of AdCP in 4 is driven by the C≡P moiety, rather than by the bulky adamantyl group. Also, this further indicates that μ-η¹:η¹ binding of phosphaalkyne ligands to the dicopper core is inherently disfavored with respect to μ-η²:η² binding.

Scheme 3 Synthesis of [Cu₂(μ-η²:η²-AdCN)DPFN][NTf₂]₂ (5).

Solution dynamics for RCP complexes

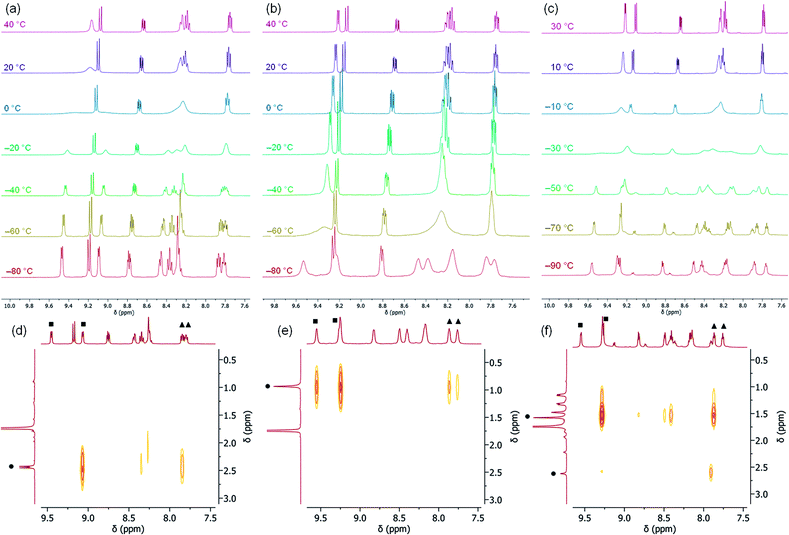
The occurrence of two different μ-η²:η² binding modes of RCP in the solid state, apparently determined by the nature of the R group, prompted an NMR study of the solution structures of complexes 2–4. All three complexes exhibit dynamic behavior in solution at ambient temperatures, and their ¹H NMR spectra acquired at 20 °C in THF exhibit only 6 resonances in the aromatic region (Fig. 4 and S2–S4†), corresponding to four equivalent pyridine rings. However, slight broadening of the signals corresponding to the 5- and 6-positions on the pyridine rings is observed for 2 and 4, while sharper spectra are obtained at higher temperatures, and the spectra of 2–4 between 20 °C and −80 °C exhibit decoalescence of the NMR resonances corresponding to the DPFN pyridine side-arms (Fig. 4). Specifically, the aromatic ¹H NMR resonances of 2 and 3 decoalesce to two sets of inequivalent pyridine resonances while the two naphthyridine resonances remain intact (Fig. 4a and b). These results suggest the presence of a single species possessing a mirror plane perpendicular to the naphthyridine rings, in accordance with the geometries observed in the solid state. The high symmetry observed at ambient temperatures thus arises from the averaging of the pyridine resonances through a rapid interconversion between the side-on geometries observed in the solid-state, rather than the presence of a highly symmetrical species. Accordingly, no temperature dependence is observed in the NMR spectrum of 5 between 20 °C and −60 °C (Fig. S5†). In addition, for 2 and 3, low temperature NOESY experiments (−60 °C and −90 °C, respectively) are consistent with solution state μ-η²:η² binding geometries that are the same as those observed in the solid state (Fig. 3d and e). In 2, only one 6-pyridyl position exhibits a strong correlation to the bridging MeCP ¹H NMR resonance, while in 3, both 6-pyridyl positions correlate significantly with the ^tBu signal (Fig. 4d, e and S7†). These results match well the similar ^tBu⋯6-pyridyl distances observed in the solid state and the very different Me⋯6-pyridyl distances (Tables S9 and S10†).

Fig. 4 Excerpts of the NMR spectra in THF-d₈ of complexes 2-4. Top: aromatic region of the variable-temperature ¹H NMR spectra of: (a) 2, (b) 3 and (c) 4. Bottom: low temperature NOESY NMR spectra, highlighting H atoms belonging to 6-pyridyl (■), 5-pyridyl (▲) and RC≡P alkyl group positions (●) of: (d) 2 at −60 °C, (e) 3 at −90 °C and (f) 4 at −90 °C.

The solution-state behavior of 4 is more complex. Indeed, below −60 °C, the 6 aromatic ¹H NMR resonances of 4 decoalesce to two sets of resonances in a 3 : 1 ratio (Fig. 4c), suggesting the presence of two solution state species that are very similar in energy; observation of this ratio at −60 °C corresponds to a ca. 0.4 kcal mol⁻¹ difference in energy between the two species. The major species observed is characterized by 10 aromatic ¹H NMR resonances, suggesting disruption of the mirror plane corresponding to the ligand's naphthyridine core but conservation of a mirror plane in the perpendicular direction. Low-temperature NOESY correlations (−90 °C) indicate close contacts between the phosphaalkyne's alkyl moiety and only one 6-pyridyl position, as was observed in 2 (Fig. 4f), which is inconsistent with the solid-state structure of 4. Indeed, the solid-state geometry of 4 more closely resembles that of 3, so a closer resemblance between their NOESY spectra would be expected as well (Tables S9–S11†). Unfortunately, these ¹H and NOESY NMR experiments did not allow for conclusive statements of the minor isomer's symmetry in solution, since many aromatic resonances of the major and minor isomers overlap and therefore limit the possibility of an accurate resonance count or conclusive NOESY correlation determination for the minor isomer. Additional insights were instead gained by performing low temperature (−60 °C) DOSY NMR experiments to rule out the possibility of aggregation. They revealed that the two observed species have similar hydrodynamic radii, suggesting that they are both monomeric (Fig. S8†).

Computational investigation of RCP binding modes

Computational methods were used to gain additional structural insights into the isomers of 4. Given the X-ray diffraction data and NMR spectra, three possible structures for the [Cu₂(μ-AdCP)DPFN]²⁺ dication were explored computationally: 4-trans, the cationic part of the solid-state structure of 4, characterized by having the adamantyl group and the naphthyridine backbone on opposite sides of the Cu₂N₄ plane; 4-end, with the phosphaalkyne bound end-on, as in 5; and 4-cis, where AdCP binds with the alkyl moiety and naphthyridine backbone on the same side of the Cu₂N₄ plane, as in 2 (Fig. 5). The minimum-energy structures were calculated using density functional theory (see Computational Methods section and ESI† for more details). The final energies suggest that 4-trans, the isomer most closely resembling the crystal structure of 4, is not the most stable isomer of the three. Rather, 4-cis is slightly (1.5 kcal mol⁻¹) more stable than 4-trans, despite a significantly larger out-of-plane deformation of the naphthyridine backbone: 29° for 4-cis compared to 20° for 4-trans (Table S4†). This suggests that deformation of the naphthyridine backbone is not very energetically costly, while the final energies further indicate that an end-on geometry is possible but disfavored. Indeed, 4-end is a stable intermediate but is 10.8 kcal mol⁻¹ higher in energy than 4-trans, and therefore unlikely to be present in solution in observable quantities. This is consistent with the energies computed for [Cu₂(μ-η²:η²-MeCP)DPFN]²⁺, for which the end-on structure is 14.0 kcal mol⁻¹ higher in energy than the geometry observed crystallographically.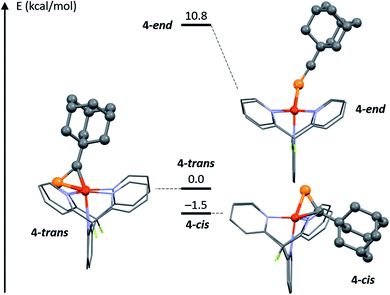

Fig. 5 DFT-optimized potential geometries 4-trans, 4-end and 4-cis for 4 in solution at low temperature, and relative energies.

These computed relative energies are in good agreement with the low temperature NOESY NMR data, since they suggest that 4-cis corresponds to the major isomer observed in solution. However, a 1.5 kcal mol⁻¹ difference in energy is close to the limits of accuracy in DFT computations, and these optimized geometries do not take into account potentially strong interactions with solvent molecules or triflimide counterions.³⁶ Such interactions could influence the relative stabilities of 4-trans and 4-cis in solution, and especially in the solid state, causing 4 to crystallize in the 4-trans geometry despite computations suggesting that 4-cis is more stable.

To corroborate the hypothesis that 4-cis and 4-trans are the major and minor isomers, respectively, observed in solution, NMR parameters of both complexes were computed and compared to experimental values. Both the ¹³C NMR chemical shift (δ) and ¹³C–³¹P coupling constant (¹J_CP) of the quaternary carbon atom directly bound to phosphorus (labeled C31 on Fig. 3) depend on its chemical environment. At −60 °C, the ¹³C{¹H} NMR spectrum of 4 reveals decoalescence of the C31 ¹³C NMR signal into two signals characterized by distinct chemical shifts (174.8 ppm and 175.8 ppm, respectively) and ¹J_CP values (83.3 and 76.8 Hz, respectively), with a 3 : 1 intensity ratio (Fig. S9†). The chemical shift difference between these two resonances is smaller than the typical accuracy of ¹³C NMR spectrum predictions (>2 ppm), but the difference in J_CP could be significant.^37,38 To the best of our knowledge, no systematic computational investigation of J_CP values has been performed. However, considering the percent error obtained from systematic studies of computed J_HH values (<5%, depending on method), the observed Δ¹J_CP between the isomers (6.5 Hz, Δ¹J_CP/¹J_CP = 8%) should be large enough to reasonably compare experimental values with computed estimates.^39,40 Systematic deviations from experimental J_XY values are often encountered when computing coupling constants and can be addressed by the application of an empirical correction factor (α) based on a linear regression using a training dataset.⁴¹ With an appropriate training set comprised of molecules featuring a variety of C–P bonds (see details in Computational Methods section and ESI†), an optimal value of 0.7949 for the empirical correction factor α was determined. Then, the coupling constant ¹J_CP,calcd was calculated for isomers 4-trans, 4-end, and 4-cis, as well as the corrected coupling constant ¹J_CP,corr = α¹J_CP,calcd (Table 1). The good agreement between the computed values for 4-cis and 4-trans and the experimental values for the major and minor isomers, respectively, as well as the poor agreement between computed values for 4-end and either experimental value further support our initial assignment of 4-cis as the major isomer observed in solution and 4-trans as the minor one.

Table 1 Computed ¹³C NMR coupling constants of 4-trans, 4-end and 4-cis, either performed in the gas phase (4-trans, 4-cis) or using a THF solvation model (4-end), and corrected coupling constants after applying a 0.7949 empirical correction factor

Structure	J CP,calcd (Hz)	J CP,corr (Hz)
4-trans	92.6	73.6
4-end	191.9	152.5
4-cis	106.7	84.8

---

To better understand the observation of both binding geometries in solutions of 4, the relative energies of both side-on geometries of 2 and 3 were also computed (Fig. 6, S10, S11, Tables S2 and S3†). These geometries are labeled 2-trans and 3-trans, where the naphthyridine backbone and phosphorus atom are on the same side of the Cu₂N₄ plane, opposite to the alkyl chain, and 2-cis and 3-cis, where the naphthyridine backbone and alkyl chain are on the same side of the Cu₂N₄ plane, opposite to the phosphorus atom. As with 4, optimized structures 2-cis and 3-cis are lower in energy than those for 2-trans and 3-trans. The computed energies of 2 show the most stabilization of the cis geometry relative to the trans one, consistent with it having the smallest R group. Meanwhile, 3 features the smallest stabilization of the cis geometry, consistent with it having the most sterically demanding R group. The lower final energy of isomer 3-cis with respect to that for 3-trans is especially unexpected, as there is no experimental evidence for the presence of the cis geometry in solution or the solid state of 3. However, in the case of 4, the final energies obtained for 4-trans and 4-cis overestimate the stabilization of 4-cis by 1.1 kcal mol⁻¹ compared to experimental evidence (1.5 kcal mol⁻¹ computationally compared to 0.4 kcal mol⁻¹ experimentally), possibly due to a systematic error in the DFT-computed energy differences caused by additional interactions that are not modeled well computationally (for example with solvent molecules and/or triflimide counterions). As the energy difference between 3-trans and 3-cis is even smaller than that between 4-trans and 4-cis, a similar DFT overestimate of the stabilization of 3-cis over 3-trans could correspond to both isomers having the same energy or even to 3-trans being more stable, which is consistent with observation of the trans isomer in solution. Moreover, a similar overestimate of the stabilization of 2-cis over 2-trans would still correspond to an experimental energy difference of 1.3 kcal mol⁻¹, which is consistent with the observation of only the cis isomer in solution at low temperatures.

Fig. 6 Relative energies of DFT-optimized P-up or R-up side-on geometries for complexes 2–4. The schematic representation of the dicopper core is viewed along the Cu⋯Cu axis to best illustrate the difference between the two binding geometries.

Generalization to other multiply bonded bridging ligands

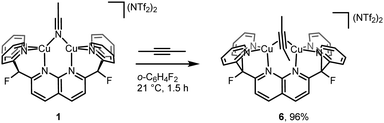
Despite the small energy differences between binding modes, one striking characteristic common to the solid-state and solution geometries of 2–4 is the tilt of the phosphaalkyne bridging fragment away from a central position between the copper atoms. In the X-ray and computationally suggested solution-state structures, one of the atoms (P1 in 2, C31 in 3 and 4) binds roughly in the plane defined by the naphthyridine backbone, while the other (C31 in 2, P1 in 3 and 4) lies significantly out of this plane and closer to the Cu₂N₄ plane, defined by the two copper and four pyridine nitrogen atoms. Significantly, this tilted binding mode is not limited to phosphaalkyne bridging fragments. For example, 1 also reacts with 2-butyne to afford [Cu₂(μ-η²:η²-(MeC≡CMe))DPFN](NTf₂)₂ (6, Scheme 4) in near-quantitative yield. Single-crystal X-ray diffraction reveals that despite its symmetry, the butyne ligand in 6 bridges in a tilted fashion (Fig. 7) similar to that observed in the solid-state structure of 2: the Cu1⋯Cu2 distance in 6 is 2.6687(4) Å, compared to 2.6548(5) Å in 2. In addition, the butyne ligand is bent, with an average H₃C–C≡C angle of 154°, very close to the 155° P–C≡C angle observed in 2, and the naphthyridine backbone is bent by 16° out of plane, which is only slightly less than the 20° bending observed for 2.

Scheme 4 Synthesis of [Cu₂(μ-η²:η²-2-butyne)DPFN][NTf₂]₂(6).

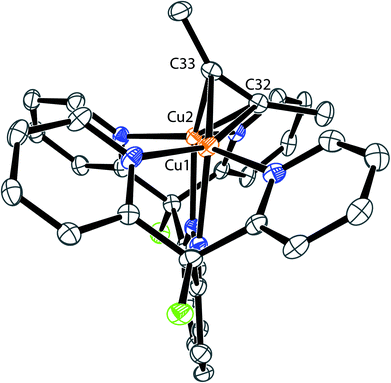Fig. 7 Solid-state structure of 6. Two triflimide anions and hydrogen atoms are omitted for clarity. Thermal ellipsoids are set at 50% probability.

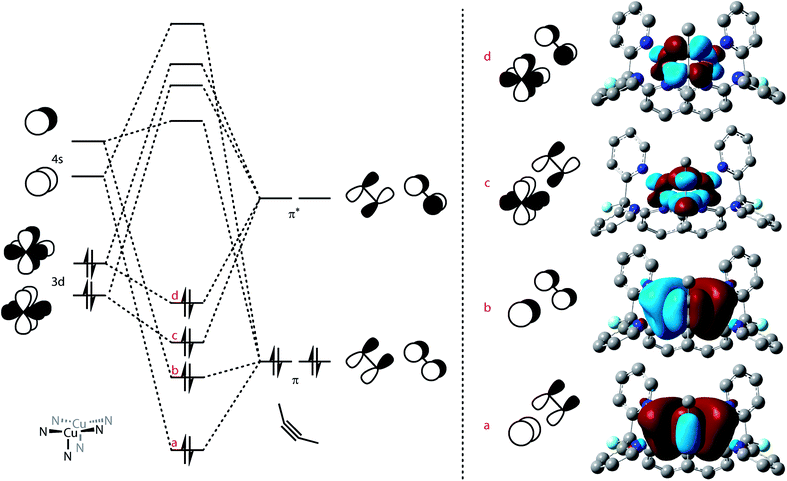
This tilted binding of alkynes is uncommon for dicopper cores: most structurally characterized alkyne-bound dicopper complexes possess a mirror plane defined by both copper centers and the center of the alkyne triple-bond.^42–47 To elucidate this system's preference for tilted binding, we employed natural bond orbital analysis (NBO) on a DFT-optimized structure of [Cu₂(μ-η²:η²-(H₃CC≡CCH₃)₂)DPFN]²⁺ (Fig. 8, S12 and Table S8†).⁴⁸ The calculations suggest that two major contributions determine the dicopper–butyne interaction. One of these bonding interactions involves donation of the filled π orbitals of the butyne fragment into empty 4s orbitals of the two copper centers. The other is the π-back-donation that occurs from filled 3d orbitals on the metals into the empty π* orbitals of the butyne fragment. Both the donation and the back-donation weaken the butyne's internal C≡C bond, as evidenced by the elongated C≡C distance observed in the crystal structure of 6 (1.261(4) Å compared to 1.207 Å for free 2-butyne).⁴⁹ In addition, the Cu⋯Cu interaction (cuprophilicity) is manifested in s–s and d–d overlaps, leading to bonding and antibonding combinations (Fig. 8); bonding to the bridging alkyne is dominated by the in-phase orbitals.^50,51

Fig. 8 MO diagram depicting the orbital interactions between the butyne fragment and the dicopper core of 6 (left) and major contributions to that binding determined by NBO analysis (right): π_butyne → 4s_Cu donation (a and b) and: back-donation (c and d) contributions. All schematic MOs are depicted along the dicopper axis, while the NBO interactions are depicted in a top-down view. NBO orbital contributions to NLMOs and relative magnitude of stabilization interactions (averaged for both Cu centers): (a) 91.1% π, 7.7% 4s, 22.2 kcal mol; (b) 97.4% π, 1.2% 4s, 3.7 kcal mol; (c and d) 90.5% 3d, 8.4% π*, 12.0 and 8.6 kcal mol⁻¹ for (c) and (d), respectively.

As the donation contributions involve the butyne π orbitals and the Cu 4s orbitals, the magnitude of the bonding interaction between the butyne fragment and the dicopper core should not depend on the tilt of the alkyne fragment. Conversely, the orbital interactions for back-donation are highly directional due to involvement of π* and 3d orbitals. NBO analysis reveals that only one 3d orbital on each copper center significantly interacts with the butyne fragment. The orientation of these 3d orbitals is conveniently viewed with respect a pseudo-C₃ axis defined at each copper center by the three N atoms on the ligand (one belonging to the naphthyridine backbone, the two others to one dipyridyl side-arm, Fig. 8, left). This 3d orbital possesses one lobe oriented along a Cu–N_pyridine bond (Cu1–N4 and Cu2–N6, Fig. SC5 and S12†) and the other out of the Cu₂N₄ plane. This preferred orientation of the 3d orbital of interest means it achieves optimal overlap with the π* orbitals of the alkyne with one of the triply bonded carbon atoms in the Cu₂N₄ plane (to maximize overlap with the component along the Cu–N_pyridine axis) and the other out of the Cu₂N₄ plane, which is close to the experimental solid-state geometry of 6 (Fig. 7).

Conclusions

Phosphaalkynes are an interesting class of building blocks in organophosphorus chemistry. Identification of these molecules' binding modes can help elucidate their reactivity profiles and aid in their application to new chemical processes. Leveraging the rigid [Cu₂(DPFN)]²⁺ platform, we synthesized and characterized, to our knowledge, the first reported examples of copper-bound phosphaalkyne complexes and bimetallic first-row transition metal phosphaalkyne complexes in carbonyl-free systems.

Despite the presence of a terminal lone pair of electrons, phosphaalkynes bind to the dicopper core in a tilted μ-η²:η² fashion that resembles the binding of internal alkynes more than the binding of nitriles and terminal alkynyl anions. This is notable since bimetallic platforms often promote further phosphaalkyne-based reactivity rather than providing a simple RCP complex. In addition, two distinct μ-η²:η² binding modes were observed even though the three phosphaalkynes of interest (MeCP, ^tBuCP and AdCP) have similar electronic properties and only differ by the steric profile of their substituents. As variable temperature NMR studies suggest little energetic preference for one structure over the other, often leading to significant amounts of both in solution, they can both be targeted for reactivity.

Carbon–phosphorus (¹J_CP) coupling constants were found to be a reliable parameter that can be estimated computationally and compared to experimental values to support assignment of phosphaalkynes' binding modes in solution. This approach can be applied beyond the specific systems studied herein and will provide a valuable probe for solution- and solid-state structure agreement in a wide variety of metal-containing assemblies.

This study furthers our understanding of the variety of binding modes occurring in multimetallic assemblies and highlights how subtle changes in steric and electronic factors can favor one over the other. These trends will allow us to elucidate activation pathways and new transformations involving phosphaalkynes and other unsaturated molecules. Applying these principles of unsaturated substrate binding to multimetallic complexes and materials can enable finer structural and electronic tuning of such systems to rationally improve reactivity and catalysis.

Computational methods

For all geometry optimizations, NMR parameters computations, and NBO analysis, atoms were modelled using the parameter free, dispersion-corrected density functional model PBE0-D3(BJ),^52,53 chosen for its good performance on numerous organometallic closed-shell systems,⁵⁴ and a combination of all-electron def2SVP, def2TZVP, def2TZVPD and def2QZVPPD basis sets (see ESI† for more details).⁵⁵ The more comprehensive def2QZVPPD basis set was systematically used to model atoms for which NMR coupling constants were calculated, in the training dataset and in the dicopper complexes of interest. The geometry optimizations prior to NMR parameters determination and J_CP computations were performed in the gas phase. Indeed, unphysical dependence of the J_CP values on solvent choice using implicit solvation was observed for these computations, as well as decreased linearity of the solvation J_CP data (see ESI†). This approach is further rationalized by the typically low dependence of experimentally measured coupling constants on experimental NMR solvent.

The training set used in this study is composed of 21 molecules containing C–P bonds for which experimental ¹J_CP values have been reported: 5 with a C–P single bond,^56,57 6 with a double bond,^57–62 and 10 with a triple bond (see ESI† for more details).^63–69 Originally, exploring empirical corrections for a broader dataset of ¹J_XY coupling-constant data, where X and Y are C, N, or P, was intended. However, unlike the coupled cluster data reported by Del Bene and coworkers,⁴¹ experimental and computed DFT data for this level of atom generality were too poorly correlated for meaningful linear regression. Similar inconsistencies leading to poor correlation were observed when including data of molecules with and without H-atoms bound to the C and P atoms of interest. Therefore, the training set was restricted to C–P bonds where the atoms of interest are not H-substituted. An important conclusion of the present work is that chemical specificity is required for linear regression to be applicable to coupling constant prediction using DFT.

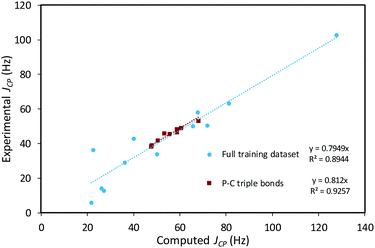
The empirical correction factor α = 0.7949 used in this study was determined by linear regression using the experimental and calculated coupling constant data of this training set (Fig. 9). As the sign of the experimental coupling constant was unreported in several of the experimental reference papers, the absolute values of all J_CP data were used. In order to avoid introducing additional systematic error by using absolute values, the fit was constrained to a 0-intercept. The triple-bond-subset data is particularly linear and performing the linear regression with only this subset produces a very similar slope of 0.812. This supports the application of this model to the formal C–P triple bonds of structures of 4-trans and 4-cis. Multiple linear regression using the standard contributions to the calculated J_CP can also be performed and leads to very similar corrected coupling constants (see ESI†).

Fig. 9 Scatter plot of computed and experimental coupling constants of the training dataset comprised of 21 molecules containing P–C bonds, and linear regression to determine the empirical correction factor α.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was primarily funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division under Contract No. DE-AC02-05CH11231. We acknowledge the National Institutes of Health (NIH) for funding the UC Berkeley CheXray X-ray crystallographic facility under grant no. S10-RR027172, the UC Berkeley College of Chemistry and QB3 NMR facilities under grant no. SRR023679A, 1S10RR016634-01 and GM68933, and the UC Berkeley Molecular Graphics and Computation Facility under grant no. S10OD023532. We also acknowledge Beamline 12.2.1 of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. Phosphaalkynes were synthesized at the University of Regensburg by Dr Eva-Maria Rummel. Part of the dynamic NMR work was performed by Amélie Nicolay at the University of Regensburg with the support of the international PhD Program at Universität Regensburg (iPUR) and the UC Berkeley Institute of European Studies. Additional travel facilitating this collaboration was funded by the Alexander von Humboldt Foundation and a joint US/German DAAD project. In addition, Amélie Nicolay was supported by a Fulbright Fellowship and a Link Foundation Fellowship and Dr Micah S. Ziegler was supported by a National Science Foundation (NSF) Graduate Research Fellowship (grant no.: DGE 1106400). We thank Dr Addison N. Desnoyer, Henry Z. Xu, Helena Brake, Dr Gábor Balázs, Jaruwan Amtawong, and Nicolle A. Doering for helpful discussions. We also thank Dr Hasan Celik and Dr Jeffrey G. Pelton for NMR spectroscopy advice, and Dr Simon J. Teat for X-ray crystallography advice.

Notes and references

1. Catalysis without precious metals, ed. R.Bullock, 2010.
2. S. E. Allen, R. R. Walvoord, R. Padilla-Salinas and M. C. Kozlowski, Chem. Rev., 2014, 114, 899.
3. E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659–3853.
4. F. Lazreg, F. Nahra and C. S. J. Cazin, Coord. Chem. Rev., 2015, 293–294, 48–79.
5. C. E. Elwell, N. L. Gagnon, B. D. Neisen, D. Dhar, A. D. Spaeth, G. M. Yee and W. B. Tolman, Chem. Rev., 2017, 117, 2059–2107.
6. S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672.
7. J. I. Van Der Vlugt, Eur. J. Inorg. Chem., 2012, 3, 363–375.
8. P. Buchwalter, J. Rosé and P. Braunstein, Chem. Rev., 2015, 115, 28–126.
9. I. G. Powers and C. Uyeda, ACS Catal., 2017, 7, 936–958.
10. G. van Koten and J. T. B. H. Jastrzebski, Structural Organocopper Chemistry, 2011.
11. I. G. Powers, J. M. Andjaba, X. Luo, J. Mei and C. Uyeda, J. Am. Chem. Soc., 2018, 140, 4110–4118.
12. H. Lang, D. S. A. George and G. Rheinwald, Coord. Chem. Rev., 2000, 206–207, 101–197.
13. B. N. Storhoff and H. C. Lewis Jr, Coord. Chem. Rev., 1977, 23, 1–29.
14. M. F. Lappert, P. I. W. Yarrow, J. Holton and R. Pearce, Chem. Rev., 1983, 83, 135–201.
15. J. Díez, M. P. Gamasa, J. Gimeno, A. Aguirre, S. García-Granda, J. Holubova and L. R. Falvello, Organometallics, 2002, 18, 662–669.
16. É. Fournier, F. Lebrun, M. Drouin, A. Decken and P. D. Harvey, Inorg. Chem., 2004, 43, 3127–3135.
17. M. Ito, D. Hashizume, T. Fukunaga, T. Matsuo and K. Tamao, J. Am. Chem. Soc., 2009, 18024–18025.
18. A. M. Lilio, K. A. Grice and C. P. Kubiak, Eur. J. Inorg. Chem., 2013, 4016–4023.
19. B. Liu, C. Chen, Y. Zhang, X. Liu and W. Chen, Organometallics, 2013, 32, 5451–5460.
20. L. Jin, D. R. Tolentino, M. Melaimi and G. Bertrand, Sci. Adv., 2015, 1, e1500304.
21. R. W. M. ten Hoedt, J. G. Noltes, G. van Koten and A. L. Spek, J. Chem. Soc., Dalton Trans., 1978, 1800–1806.
22. S. Kuang, Z. Zhang, Q. Wang and T. C. W. Mak, J. Chem. Soc., Dalton Trans., 1998, 1115–1119.
23. N. Martínez-Espada, M. Mena, M. E. G. Mosquera, A. Pérez-Redondo and C. Yélamos, Organometallics, 2010, 29, 6732–6738.
24. T. C. Davenport and T. D. Tilley, Angew. Chem., Int. Ed. Engl., 2011, 50, 12205–12208.
25. M. S. Ziegler, D. S. Levine, K. V. Lakshmi and T. D. Tilley, J. Am. Chem. Soc., 2016, 138, 6484–6491.
26. M. S. Ziegler, K. V Lakshmi and T. D. Tilley, J. Am. Chem. Soc., 2017, 139, 5378–5386.
27. A. Chirila, R. Wolf, J. Chris Slootweg and K. Lammertsma, Coord. Chem. Rev., 2014, 270–271, 57–74.
28. J. C. T. R. B.-S. Laurent, M. A. King, H. W. Kroto, J. F. Nixon and R. J. Suffolk, J. Chem. Soc., Dalton Trans., 1983, 755–759.
29. H. W. Kroto, J. F. Nixon and N. P. C. Simmons, J. Mol. Spectrosc., 1979, 77, 270–285.
30. G. Becker, W. A. Herrmann, W. Kalcher, G. W. Kriechbaum, C. Pahl, C. T. Wagner and M. L. Ziegler, Angew. Chem., Int. Ed. Engl., 1983, 22, 413–414.
31. P. B. Hitchcock, T. J. Madden and J. F. Nixon, J. Organomet. Chem., 1993, 463, 155–162.
32. D. Pohl, J. Ellermann, M. Moll, F. A. Knoch and W. Bauer, Z. Anorg. Allg. Chem., 1996, 622, 283–291.
33. M. Nowotny, B. F. G. Johnson, J. F. Nixon and S. Parsons, Chem. Commun., 1998, 3, 2223–2224.
34. C. Jones, C. Schulten and A. Stasch, J. Chem. Soc., Dalton Trans., 2006, 3733–3735.
35. G. Hierlmeier, P. Coburger, M. Bodensteiner and R. Wolf, Angew. Chem., Int. Ed., 2019, 58, 16918–16922.
36. S. R. Jensen, S. Saha, J. A. Flores-Livas, W. Huhn, V. Blum, S. Goedecker and L. Frediani, J. Phys. Chem. Lett., 2017, 8, 1449–1457.
37. K. G. Andrews and A. C. Spivey, J. Org. Chem., 2013, 78, 11302–11317.
38. M. G. Chini, R. Riccio and G. Bifulco, Eur. J. Org. Chem., 2015, 2015, 1320–1324.
39. A. G. Kutateladze and O. A. Mukhina, J. Org. Chem., 2014, 79, 8397–8406.
40. A. G. Kutateladze and D. S. Reddy, J. Org. Chem., 2017, 82, 3368–3381.
41. J. E. Del Bene, J. Elguero and I. Alkorta, J. Phys. Chem. A, 2004, 108, 3662–3667.
42. G. M. Villacorta, D. Gibson, I. D. Williams and S. J. Lippard, J. Am. Chem. Soc., 1985, 107, 6732–6734.
43. D. L. Reger, M. F. Huff, T. A. Wolfe and R. D. Adams, Organometallics, 1989, 8, 848–850.
44. H. L. Aalten, G. van Koten, E. Riethorst and C. H. Stam, Inorg. Chem., 1989, 28, 4140–4146.
45. P. O. Oguadinma and F. Schaper, Organometallics, 2009, 28, 6721–6731.
46. D. Parasar, R. M. Almotawa, N. B. Jayaratna, Y. S. Ceylan, T. R. Cundari, M. A. Omary and H. V. R. Dias, Organometallics, 2018, 37, 4105–4118.
47. W. Tao, J. K. Bower, C. E. Moore and S. Zhang, J. Am. Chem. Soc., 2019, 141, 10159–10164.
48. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
49. J. L. Duncan, Spectrochim. Acta, 1964, 20, 1197–1221.
50. T. C. Davenport and T. D. Tilley, Angew. Chem., Int. Ed. Engl., 2011, 50, 12205–12208.
51. N. V. S. Harisomayajula, S. Makovetskyi and Y. C. Tsai, Chem. - Eur. J., 2019, 8936–8954.
52. C. Adamo and V. Barone, Chem. Phys., 1999, 110, 6158–6170.
53. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
54. S. Dohm, A. Hansen, M. Steinmetz, S. Grimme and M. P. Checinski, J. Chem. Theory Comput., 2018, 14, 2596–2608.
55. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
56. T. Allman and R. G. Goel, Can. J. Chem., 1982, 60, 716–722.
57. E. P. O. Fuchs, H. Heydt, M. Regitz, W. W. Schoeller and T. Busch, Tetrahedron Lett., 1989, 30, 5111–5114.
58. T. A. van der Knaap and F. Bickelhaupt, Chem. Ber., 1984, 117, 915–924.
59. M. Yoshifuji, K. Toyota and N. Inamoto, J. Chem. Soc., Chem. Commun., 1984, 689–690.
60. J. Heinicke, Tetrahedron Lett., 1986, 27, 5699–5702.
61. K. Paasch, M. Nieger and E. Niecke, Angew. Chem., Int. Ed. Engl., 1995, 34, 2369–2371.
62. E. Öberg, X. L. Geng, M. P. Santoni and S. Ott, Org. Biomol. Chem., 2011, 9, 6246–6255.
63. R. Appel and A. Westerhaus, Tetrahedron Lett., 1981, 22, 2159–2160.
64. R. Appel, G. Maier, H. P. Reisenauer and A. Westerhaus, Angew. Chem., Int. Ed. Engl., 1981, 20, 197.
65. T. Allspach and M. Regitz, Synthesis, 1986, 31–36.
66. B. Pellerin, J. M. Denis, J. Perrocheau and R. Carrie, Tetrahedron Lett., 1986, 27, 5723–5726.
67. M. Regitz and P. Binger, Angew. Chem., Int. Ed., 1988, 27, 1484–1508.
68. J. C. Guillemin, T. Janati and J. M. Denis, J. Org. Chem., 2001, 66, 7864–7868.
69. W. Liang, K. Nakajima, K. Sakata and Y. Nishibayashi, Angew. Chem., Int. Ed., 2019, 58, 1168–1173.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1966159–1966163. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc05835d

---