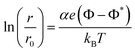Open Access Article
Open Access ArticlePromoting heterogeneous catalysis beyond catalyst design
Max J.
Hülsey
 ,
Chia Wei
Lim
,
Chia Wei
Lim
 and
Ning
Yan
and
Ning
Yan
 *
*
Department of Chemical and Biomolecular Engineering, National University of Singapore, 4 Engineering Drive 4, 117585 Singapore, Singapore. E-mail: ning.yan@nus.edu.sg
First published on 14th January 2020
Abstract
Despite the indisputable success of conventional approaches to manipulate the performance of heterogeneous catalysts by tuning the composition and structure of active sites, future research on catalysis engineering will likely go beyond the catalyst itself. Recently, several auxiliary promotion methods, either promoting the activity of reagents or enabling optimized adsorbate–catalyst interactions, have been proven as viable strategies to enhance catalytic reactions. Those auxiliary promotion methods range from electric/magnetic fields and electric potentials to mechanic stress, significantly altering the properties of reagent molecules and/or the surface characteristics of nanostructured catalysts. Apart from static enhancement effects, they in principle also allow for spatially and temporally variable modifications of catalyst surfaces. While some of those methods have been demonstrated, some are only theoretically predicted, opening exciting avenues for future experimental advances. Besides fundamental descriptions and comparisons of each activation method, in this perspective we plan to provide examples for the applications of those techniques for a variety of catalytic reactions as diverse as N2 and CO2 hydrogenation as well as electrochemical water splitting. Finally, we provide a unifying view and guidelines for future research into the use of promotion methods, generating deeper understanding of the complex dynamics on the nanoparticle surface under auxiliary promotion and the expansion of auxiliary techniques to different sustainability-related reactions.
1. Introduction & overview
Heterogeneous catalysis remains at the core of chemical manufacturing with approximately 80–90% of chemical processes relying on the use of catalysts, generating global sales of around 1.5 trillion US $.1 Improvements for catalytic processes heavily rely on finding better catalysts, but significant progress seems to have stalled in the past two decades and most industrially relevant processes are performed in the same or a similar manner as at the end of the last century. Innovations should go beyond improving catalyst synthesis recipes. In this regard, auxiliary promotion where the effectiveness of a process is altered by exploiting various physical phenomena is attracting increasing attention. They can be loosely divided into two categories – the activation of reagent molecules before catalytic reactions and the modification of the catalyst surface to exhibit higher reactivity. For the former, plasma- and electromagnetic activation of molecules in the liquid and gas phases have potential, especially in accelerating the reactions of notoriously inert molecules like N2, CH4 and CO2 (Fig. 1, top). For the latter, the electronic structure of catalyst surfaces is altered either by applying an electric potential on the catalyst surface, placing the catalyst into an external electric field or using electromagnetic waves to induce charge fluctuations. In addition, magnetic fields as well as mechanic strain applied to metallic surfaces have been shown to effectively modify heterogeneous catalysis (Fig. 1, bottom). In this perspective, the physical background of each promotion technique will be briefly introduced with specific examples where enhanced activity or selectivity has been reported before. Similarities and differences between those methods will be highlighted and future prospects will be provided for each method as well as general aspects of auxiliary promotion. Although the value of heating catalyst particles locally by e.g. plasmonic or induction heating has been demonstrated before, those effects will not be considered in this perspective. Dynamic field promotion – a concept only recently proposed – will be discussed and put into context with existing methods.2 Despite the existence of more detailed and comprehensive reviews on specific promotion methods,3–8 this perspective to our knowledge represents the first attempt to unify auxiliary promotion in heterogeneous catalysis.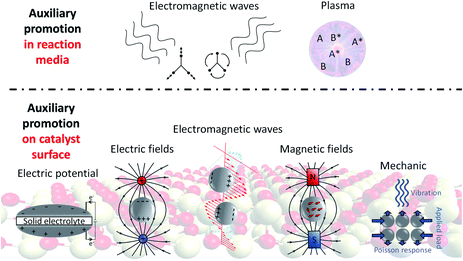 | ||
| Fig. 1 An overview of different auxiliary promotion methods in the reaction media and on the catalyst surface. | ||
2. Activation of reagents in reaction media
2.1 Activation of reagents by electromagnetic waves
Various interactions of electromagnetic waves with chemical compounds range from the specific excitation of rotational states by low energy waves to changes of electronic states by high energy waves. In principle, many promotion methods can be envisioned where those excited gas phase species are used for heterogeneous catalytic processes.9 It is therefore rather surprising that in fact those techniques have been explored to a small extent. One effect highlighting the strong capabilities of electromagnetic waves in promoting catalysis is vibrational strong coupling (VSC). Coupling molecular transitions to the vacuum field of a cavity mode leads to Rabi splitting of vibrational states into vibro-polaritonic states (P+ and P−). The Rabi splitting energy is given as:with d as the transition dipole moment of the material, ħω as the resonant energy, ε0 as the vacuum permittivity, v as the volume of the electromagnetic mode, and nph as the number of photons involved in the coupling process (Fig. 2A). This splitting is only observable when resonant components exchange faster than any decay process occurs. One amplitude of the electromagnetic wave covers around 105 molecules which can then have N + 1 collective states (N… number of molecules) with N − 1 transitions (only P+ and P− are visible; others are forbidden and thus dark). The strength of the collective coupling may reach 1 eV and thus, this effect is called strong coupling.4
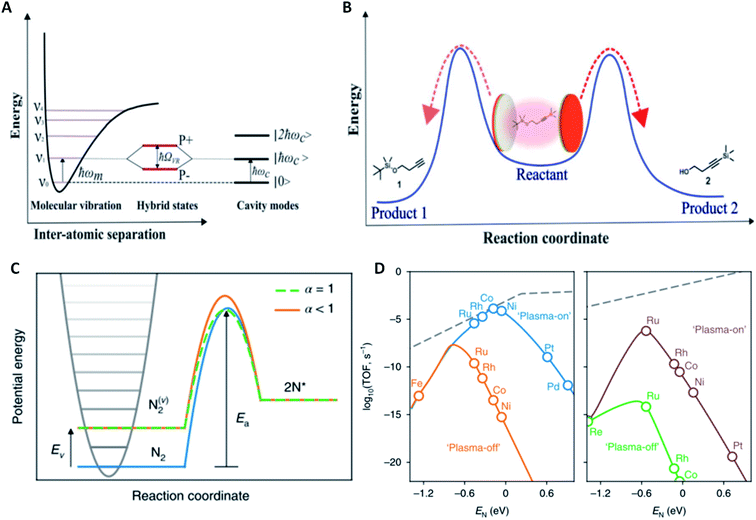 | ||
| Fig. 2 Auxiliary promotion methods in the reaction media; (A) schematic representation of the strong coupling of light and matter in resonance with a Fabry–Pérot cavity mode resulting in the splitting of polaritonic states with the Rabi splitting energy ħΩR; (B) depiction of the competing site–selective reaction pathways when substrates are in a vibrational strong coupling environment, reproduced from ref. 11 with permission from the American Association for the Advancement of Science, copyright 2019; (C) schematic for the plasma-assisted activation of N2 in the gas phase resulting on a decrease in activation energy dependent on the Fridman α factor; (D) prediction of the rate-enhancement under plasma-on versus plasma-off conditions estimated by microkinetic modelling for (left) step and (right) terrace sites under the following reaction conditions: Tgas = 473 K, Tvib = 3000 K, and conversion = 1%, reproduced from ref. 23 with permission from Springer Nature, copyright 2018. | ||
Experimentally, this has been realized by using a Fabry–Pérot cavity with an appropriate distance of two reflective surfaces. The effect of VSC was investigated for the cleavage of silanes by a fluoride salt. It was observed that upon placing the reaction mixture into a cavity with the cavity mode in resonance with the substrate Si–C bonds, the reaction rate decreased by a factor of 5.5. Furthermore, the activation enthalpy and entropy changed significantly under the effect of VSC indicating a change in the reaction mechanism.10 This approach was recently extended to the chemoselective silyl bond cleavage reaction of a molecule with one C–Si and one O–Si bond (Fig. 2B). By choosing a cavity in resonance with either of the bonds, the reaction rate drastically reduced and thus, the silyl bond cleavage reaction became more selective for the bond out of resonance.11 In the aforementioned two examples, the chemical reactivity was selectively reduced but recently, the promotion of reactivity has been achieved by coupling the resonance of a solvent with a substrate both of which contain a 12C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. When the Fabry–Pérot cavity resonance matched the resonance of the 12C
O bond. When the Fabry–Pérot cavity resonance matched the resonance of the 12C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, a reaction rate enhancement of almost 11 times was achieved. Kinetic isotope effects with 13C
O bond, a reaction rate enhancement of almost 11 times was achieved. Kinetic isotope effects with 13C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O labelled solvent revealed that the reaction rate was indeed decreased by almost an order of magnitude even when the cavity size was adjusted to the new resonance frequency of the 13C
O labelled solvent revealed that the reaction rate was indeed decreased by almost an order of magnitude even when the cavity size was adjusted to the new resonance frequency of the 13C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O labelled solvent.12 More recently, this approach was used for the enhancement of enzymatic catalysis by matching the cavity mode with the stretching vibration of water enhancing the apparent second order rate constant by a factor of 4.5. Thus, VSC could be potentially used to clarify the contribution of the modes of certain molecules in (bio)chemical reactions.13 Although the VSC effect has so far not been used to promote heterogeneous catalytic reactions, device geometries allowing for this possibility to be explored should be developed. Furthermore, the above example demonstrates the enormous potential of electromagnetic waves in altering and promoting chemical reactions with transition dipole moments.
O labelled solvent.12 More recently, this approach was used for the enhancement of enzymatic catalysis by matching the cavity mode with the stretching vibration of water enhancing the apparent second order rate constant by a factor of 4.5. Thus, VSC could be potentially used to clarify the contribution of the modes of certain molecules in (bio)chemical reactions.13 Although the VSC effect has so far not been used to promote heterogeneous catalytic reactions, device geometries allowing for this possibility to be explored should be developed. Furthermore, the above example demonstrates the enormous potential of electromagnetic waves in altering and promoting chemical reactions with transition dipole moments.
Microwaves (MWs) as a form of electromagnetic radiation with wavelengths ranging from about one meter to one millimeter are commonly employed for accelerating gas and liquid phase catalysis. Although resonant (non-thermal) promotion mechanisms have been proposed previously, no conclusive evidence for such an effect was shown. In fact, the energy of MWs is too low to excite even vibrations of molecules but merely achieves rotational excitation of reactants. According to the Debye model, molecules experience frictional damping in a condensed phase, making the direct absorption of radiation by resonant processes unlikely. Therefore, it should be assumed that MWs do not specifically excite molecules into more ‘reactive’ rotational states but solely heat up the reaction mixture.14,15 Although MWs are praised for their ability to rapidly and selectively heat mixtures based on the dielectric loss of their components,16 they do not fall into the category of catalytic promotion as defined here.
2.2 Activation of reagents by plasma
Another technique for the activation of reactant species in the reaction medium is plasma, the state where nuclei are stripped of some of their surrounding electrons generating an electrically conductive gas of highly excited molecules. Although this sounds like an ideal environment to force normally inert molecules into rearranging their chemical bonds, applying heterogeneous catalysis in a plasma is not straightforward. Dating back to the very beginning of chemical nitrogen fixation, the Birkeland–Eyde process included the direct oxidation of N2 to nitrogen oxides using an electrical arc generating a plasma at 3000 °C.17 Although this process has not proven economically competitive with the Haber–Bosch process, plasma catalytic processes have been under development since then. Roughly there are two types of plasma relevant for catalysis, thermal and non-thermal. When free electrons and heavy particles are in thermal equilibrium with each other, the plasma can reach temperatures of a few thousand degrees Celsius whereas the plasma temperature is normally within 300–1000 K in case hot electrons are not in equilibrium with heavier components. A strong synergy between heterogeneous catalysis and plasma is reported for example related to the in situ photon generation and catalyst morphology or oxidation state changes, some of which go beyond the scope of this perspective.5,18 Non-thermal plasmas are particularly suitable to generate vibrationally excited gas molecules. Considering Polanyi's transition state theory which stated that late transition states (TSs) occurring for endothermic processes are more dependent on vibrational energy contributions,19 most plasmas used for catalysis target reactions with late TSs such as ammonia synthesis and methane dry reforming. Even though a large body of literature exists on plasma promoted catalysis,5,18,20–22 we will here focus on one recent study exemplifying its key differences to thermal catalysis.For the thermal hydrogenation of N2, scaling relationships have been well established, identifying step sites on monometallic Ru as most active. Metals with a strong N binding energy tend to activate N2 efficiently but have trade-offs in the subsequent hydrogenation and ammonia desorption steps. On the other side, metals with a lower affinity to N are efficient in hydrogenation and product desorption but lack N2 activation capabilities. Microkinetic models have been used to elucidate the effect of plasma activation of N2 in ammonia synthesis. By including a parameter called the Fridman factor α to link the vibrationally excited reactant energy state with the change in transition state energy, the impact of plasma activation becomes quantifiable. For metals with low α, the activation energy remains unchanged with vibrational excitation of nitrogen molecules thus reducing the overall apparent activation energy of N2 dissociation (Fig. 2C). When further considering the non-Boltzmann distributed population of highly excited vibrational states by non-resonant vibrational–vibrational energy transfer within the microkinetic model for ammonia synthesis, new scaling relationships specific to plasma catalysis can be developed. On step sites, it is apparent that in a plasma Ru is no longer the metal with the highest predicted TOF but metals that previously exhibited high N2 activation barriers (like Co and Ni) feature predicted TOFs a few orders of magnitude above that of Ru. Furthermore, terrace sites on Ru metal exhibit TOFs similar to those of step sites when catalysis is done in a plasma indicating that plasma significantly affects active site requirements for catalytic reactions (Fig. 2D). Encouragingly, it has been experimentally demonstrated that in plasma Co nanoparticles are more active for ammonia synthesis than Ru and Fe.23 This example highlights the usefulness of plasma promotion for achieving chemical reactivity that is unprecedented for thermal catalysis. However, common reaction rate enhancements due to the addition of catalysts in the plasma process are rather low and the current relatively high energy requirements for plasma generation and the troublesome scalability of plasma processes hinder their implementation in chemical industries.24,25
3. Catalyst surface activation
Significant efforts have been devoted to promoting the catalytic properties of metallic nanostructures by means of electric polarization and induction of strain or external magnetic fields. In contrast to promotion processes in reaction media introduced in the last section, modifications of the catalyst surface are often relatively better developed and understood. It is well known that surface charges affect the activity of catalysts for various chemical transformations and the design of catalyst materials has relied on this principle by employing bimetallic alloys, the support of transition metal particles on electron-donating or withdrawing supports, interfacing with semiconductors and strain effects to name a few. It may be more desirable, however, to be able to tune the surface polarization of a catalyst dynamically during the catalytic reactions. Many methods have been developed for achieving this, the most prominent of which are summarized below.3.1 Electromagnetic waves
Interactions of light with solid materials are complex, depending significantly on the choice of metal as well as the size and shape of inorganic nano-objects. In traditional photocatalysis, photons with sufficient energy excite electrons from the valence band into the conduction band of semiconductors. This separated electron–hole pair then drive the chemical reaction. Those advances will not be discussed here in detail as they do not represent an auxiliary promotion method. When incident light falls on the metal–dielectric interface of nano-objects of an appropriate element, size and shape, a surface wave from oscillations of conduction electrons is formed leading to pronounced surface polarization. This effect is called surface plasmon resonance and has been investigated predominantly for spectroscopy, imaging and sensing applications. More recently, this effect was also explored for promoting heterogeneous catalysis. Indeed, shining visible light on small metal nanoparticles enhances their activity in oxidation reactions26–28 and the hydrogenation of unsaturated bonds.29For the epoxidation of ethylene over Ag nanoparticles, the activity increased by a factor of 4 upon visible light irradiation at 450 K. The rate-determining step is believed to be O2 activation. By polarizing the Ag surface, transient negative ions (TNIs) are formed, e.g. O2−. These TNIs have a different equilibrium bond distance than O2 in the ground state and thus, the ions reorganize if the lifetime of the TNIs is sufficiently high. During the process of TNIs falling back into their electronic ground state, the reformed O2 will not fall back into the vibrational ground state but stay in an excited state according to the Franck–Condon principle (Fig. 3A). This resulting vibrational excitation is then responsible for the enhanced O2 dissociation activity of plasmonic particles.26
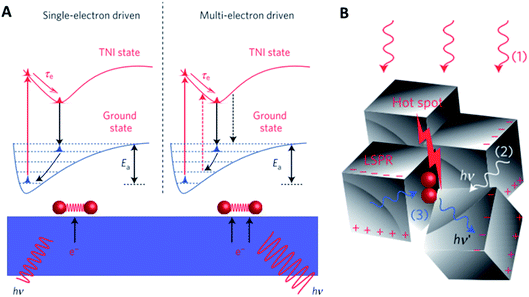 | ||
| Fig. 3 (A) Different reaction pathways driven by plasmonically excited electrons; (B) creation of hotspots by an interaction of photons (1) from a source, (2) scattered elastically from other plasmonic nanoparticles or (3) scattered inelastically from adsorbates, reproduced from ref. 27 with permission from Springer Nature, copyright 2012. | ||
A multi-electron excitation model was developed based on the finding that the quantum efficiency scales super-linearly with the light intensity above a certain threshold light intensity. This threshold is determined by the frequency of vibrational excitation which depends on the electron flux compared to the thermal dissipation of excited state energy. Photons elastically scattered from adjacent Ag nanoparticles as well as inelastically scattered from O2 enhance the photon intensity within certain hotspots where multiple electron excitation may occur (Fig. 3B).27
Plasmonic bimetallic Cu–Ru alloys were recently investigated for a hot electron mediated ammonia decomposition reaction. Light illumination at the surface plasmon resonance frequency (550 nm) of the material enhanced the H2 production rate by a factor of 12–13 and remarkably decreased the apparent reaction energy barrier from 117 kJ mol−1 without light irradiation to 34 kJ mol−1. Based on kinetic measurements, the rate-determining step was changed from associative desorption of N2 for the thermocatalytic process to N–H bond scission under light illumination. This was rationalized by transfer of hot electrons to adsorbed N and the subsequent electronically excited Ru–N species then undergoing associative desorption with a lower activation barrier.30 Overall, the interaction between electromagnetic waves and matter needs to be understood better and plasmonic heating effects need to be clearly differentiated from hot electron-driven chemistry31 to allow the design of better plasmonic catalysts and processes.
3.2 Electric potential and electric field
The direct application of an electric potential to the catalyst surface has been developed and explored widely throughout the past few decades. Significant improvements for non-faradaic electrocatalysis have been demonstrated for a variety of reactions. The efficiency at which charge is transferred to promote an electrochemical reaction is termed the faradaic efficiency. When an electric potential is applied to a metal surface, a small current flows to or from the metal surface. The value of the faradaic efficiency is given by the ratio of the increase in the catalytic rate to the magnitude of the current required to produce the applied potential. If the faradaic efficiency is greater than one, the reaction system under the applied potential is considered “non-Faradaic”,7 meaning the current does not simply act as a charge provider but instead modifies the system energetically, for example by altering the work function of the catalyst surface. This was demonstrated experimentally by applying an electric potential to a catalyst surface, increasing the steady-state catalytic rate of the reaction by up to several orders of magnitude higher than the current flow to or from the catalyst surface, an effect called the non-faradaic electrochemical modification of catalytic activity (NEMCA). The NEMCA effect stemmed from the alteration of the catalyst work function due to polarisation of the catalyst surface caused by a spillover of charges, and the rate of the catalysed reaction had been shown to vary exponentially with the average catalyst work function.32 The electric potential applied to the catalyst electrode is equal to ΔΦ, where eΔΦ is the change in the work function of the catalyst surface. The variation of the catalytic rate, r, is given by:where r0 is the open-circuit catalytic rate, α and Φ* are constants that depend on the reaction and catalyst, e is the elementary charge, kB is the Boltzmann constant and T is the temperature. The value of the constant α is normally between 1 and −1. As eΦ increases, the catalytic rate increases exponentially for electrophobic (or nucleophilic) reactions, in which the rate-determining step involves the breaking of a bond between the metal catalyst and an electron-acceptor adsorbate. On the other hand, the catalytic rate decreases with increasing eΦ for electrophilic reactions, whose rate is limited by the cleavage of a bond within an electron-acceptor adsorbate.
The NEMCA effect was demonstrated by supplying or removing oxide anions, O2−, at the metal catalyst through the use of an O2− conductor such as the gas impervious zirconia solid electrolyte under an applied electric potential.32–36 A metal counter electrode was used to supply O2− to the catalyst surface, inducing a spillover of O2− and thus altering the catalyst work function (Fig. 4A). A linear correlation was found between the applied potential, the change in the catalyst work function and the reaction rate enhancement for the combustion of ethylene (Fig. 4B). Similarly, for 12 gas phase reactions occurring on Pt, Pd or Ag surfaces and involving the oxidation of hydrocarbons, methanol or carbon monoxide, the increase in the catalytic rate ranged from 5 to 3 × 105 times of the rate of supply or removal of O2− while the ratio 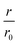 ranged from 1.5 to 55, for values of eΔΦ between 0.3 and 1 eV.37 The NEMCA effect is hence not restricted to a specific metal catalyst or reaction and forms the basis in modelling the relationship between the catalyst work function and catalytic rate in heterogeneous catalysis. The reversible migration of electrolyte components on metal surfaces has been unambiguously demonstrated by atomically resolved Scanning Tunnelling Microscopy.38
ranged from 1.5 to 55, for values of eΔΦ between 0.3 and 1 eV.37 The NEMCA effect is hence not restricted to a specific metal catalyst or reaction and forms the basis in modelling the relationship between the catalyst work function and catalytic rate in heterogeneous catalysis. The reversible migration of electrolyte components on metal surfaces has been unambiguously demonstrated by atomically resolved Scanning Tunnelling Microscopy.38
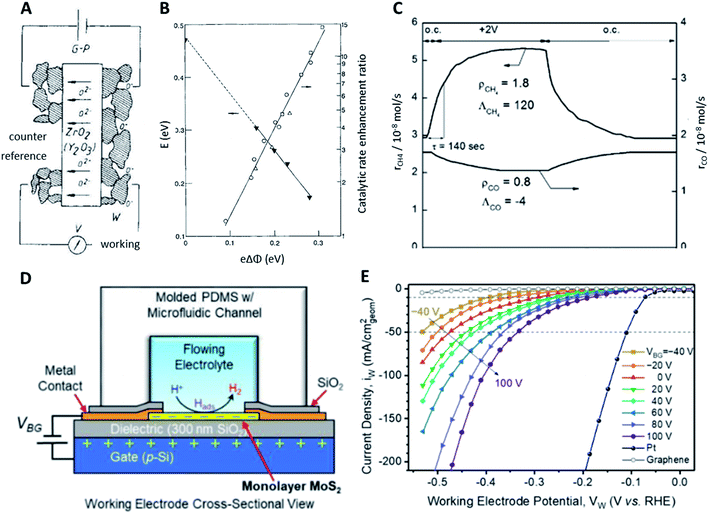 | ||
| Fig. 4 (A) In principle catalyst bed setup for electrochemical promotion reactions; (B) effect of the work function on the activation energy and catalytic enhancement ratio under constant adsorbate coverage, reproduced from ref. 32 with permission from Springer Nature, copyright 1990; (C) transient effect of a constant applied potential of +2 V on the catalytic rates of CH4 and CO formation from CO2 on Ru/YSZ, reproduced from ref. 41 with permission from ChemPubSoc Europe, copyright 2014; (D) cross-sectional view of the electrochemical/electrical MoS2 HER cell; (E) polarisation curves of the HER in 0.5 M H2SO4 depending on the back-gated bias VBG, reproduced from ref. 42 with permission from the American Chemical Society, copyright 2019. | ||
In addition to electrochemical reactions using solid electrolytes, the NEMCA effect was also shown for reactions using aqueous electrolytes, specifically the oxidation of H2 to H2O on a platinum electrode in aqueous KOH.39 Using 20 wt% finely dispersed Pt supported on graphite, it was observed that an applied electric potential of 1 to 2 V enhanced the overall catalytic rate by up to 5 times. Under the applied potential, the rate of O2 consumption increased to 310% while the rate of H2 consumption increased to 344% compared to their respective open-circuit values, giving a faradaic efficiency of up to 20. The catalytic rate depended exponentially on the applied potential, similar to the trend observed for reactions using solid electrolytes. Furthermore, experiments conducted at different partial pressures of O2 and H2 confirmed that a higher applied potential increased the catalyst work function, weakening the Pt![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O chemisorptive bond and strengthening the Pt–H bond as expected (here, O2 is the electron acceptor while H2 is the electron donor). Therefore, an applied electric potential influences both the adsorption energies and the surface reaction kinetics.
O chemisorptive bond and strengthening the Pt–H bond as expected (here, O2 is the electron acceptor while H2 is the electron donor). Therefore, an applied electric potential influences both the adsorption energies and the surface reaction kinetics.
More recently, the oxidation of H2 in aqueous alkaline media was investigated using carbon-supported Pt, Rh and Pd catalysts.40 Under alkaline conditions and with a positive potential applied, OH− ions are attracted to and subsequently adsorbed on the surface, inducing a strong polarisation and altering the work function of the catalyst as well as the adsorption energies. For the Pt electrode, it was shown that small positive currents enhanced the catalytic rate by up to 3 times and the maximum faradaic efficiency observed was 24. For both the Rh and Pd electrodes, positive currents similarly enhanced the catalytic rate, but the rate enhancement seemed to be irreversible, unlike most other systems investigated. In the case of the Rh electrode, the NEMCA effect was only observed under reducing conditions, i.e. when the partial pressure of H2 was about 2.5 times that of O2, and the maximum faradaic efficiency was 20. For the Pd electrode, a faradaic efficiency of up to 11 was observed under strongly oxidising conditions. Those results indicate that NEMCA occurs on different metal surfaces, but the extent varies significantly.
Electrochemical promotion using an applied electric potential was also demonstrated for reactions related to environmental concerns like the hydrogenation of CO2 to CH4 and CO on a nanodispersed Ru–Co catalyst (2% and 15% respectively) deposited on a proton-conducting solid electrolyte.43,44 As the applied potential was varied between 0 and 1.5 V, a faradaic efficiency of up to 60 was achieved while the selectivity of CH4 ranged between 16% and 41%. The production of CH4 was electrophobic while the production of CO was electrophilic. The rates of these two reactions always changed in opposite directions, implying that they were parallel instead of consecutive. The hydrogenation of CO2 was also studied using β′′-Al2O3, a Na+-conducting solid electrolyte.41,45 Applying a constant potential of +2 V to the Ru-catalyst film deposited on YSZ could have drastically different effects on the catalytic rates of formations of CH4 and CO under certain conditions. Specifically, the rate of CH4 formation was increased by 80% with a large positive faradaic efficiency of +120 while the rate of CO formation was decreased by 20% with a small negative faradaic efficiency of −4 (Fig. 4C). Through a series of experiments using the Ru/β′′-Al2O3 catalyst, it was found that the methanation reaction exhibited a positive order with respect to H2 and a positive-to-zero order with respect to CO2, while CO formation displayed a negative order in H2 and a positive order in CO2. Under a negative potential applied, methane formation was promoted while CO production exhibited electrophilic behaviour. A more positive applied potential led to a higher Na coverage, with full Na coverage achieved at around 1 V. At a higher applied potential and hence Na coverage, electrophobic behaviour was observed for CO formation and there was a maximum in the rate as the applied potential was increased. A similar reaction, the reduction of CO2 to formate using Pd nanoparticles in KHCO3 aqueous solution, was also investigated.46 A negative applied potential of −0.2 V enhanced the catalytic rate up to 143 times for 2.4 nm Pd. The maximum rate enhancement ratios for 3.7 nm and 7.8 nm Pd were 119 and 23 respectively, both also at an applied potential of −0.2 V, because the optimal adsorption strength of H2 for the reaction occurred at −0.2 V. Despite the maturity of this promotional method, more efforts need to be undertaken to combine catalyst materials design with NEMCA and to prove the scalability and economic feasibility for industrial applications.
While it is common to apply electric potentials to catalyst surfaces for promotion purposes, external electric fields have been used significantly less frequently. Inspired by MoS2-based transistors, where applying an electric field reduces contact and sheet resistance, using an electric field was developed to be a viable method to enhance electrocatalytic activity. The enhancement of the hydrogen evolution reaction (HER) has been realised using a back-gated electrode setup where an electric field normal to the electrode surface is generated by applying a back-gate voltage (Fig. 4D). Electrode materials based on transition metal dichalcogenides like MoS2 or VSe2 are widely employed for the HER and are also used to investigate field modulation. Using MoS2 nanosheets and voltages up to ±5 V, the overpotential for achieving current densities of 100 mA cm−2 was reduced from 240 mV without an external electric field to 38 mV under 5 V gate bias in 0.5 M H2SO4 which was very close to 25 mV of Pt without field enhancement. Decreasing Tafel slopes from 200 mV dec−1 without an external field to 110 mV dec−1 with 5 V gate voltage further confirmed the significantly enhanced catalytic activity. The channel conductivity increased from 0.0073 S m−1 (−5 V) to 0.1776 S m−1 (5 V) which was assumed to be the main reason for the gate bias enhanced activity.47
Similarly, electric fields were reported to reduce overpotentials for the HER on VSe2 nanosheets from 126 to 70 mV between 0 and −1 V almost comparable with that of Pt (54 mV) at 10 mA cm−2. Tafel slopes decreased from 70 to 59 mV dec−1 with a 0.5 M H2SO4 solution. This pronounced enhancement effect was ascribed to the optimization of adsorption/desorption processes demonstrated by charge transfer resistance which changed from 1.03 to 0.15 MΩ similar to what was reported in a previous study. Furthermore, the time constant of the adsorption process decreased from 2.5 × 10−3 to 5.0 × 10−4 s indicating enhanced adsorption upon applying a gate voltage as low as −1 V.48 Based on theoretical calculations, both facilitated charge injection and changes in the adsorption energy of atomic hydrogen on different MoS2 sites have been predicted upon application of electric fields as strong as ±0.8 V Å−1.49 Sulphur vacancies were not affected by external electric fields as strongly as other sites.50 In contrast to this, a recent study on MoS2 monolayer electrodes correlated the electric field enhancement to increased Mo–H bond strengths. Overpotentials for achieving current densities of 10 mA cm−2 were reduced from 388 ± 9 to 176 ± 27 mV with gate voltages between −40 and 100 V (Fig. 4E) with a decrease of the corresponding slopes from 164 (−40 V) to 100 mV dec−1 (100 V). DFT calculations suggested that the hydrogen adsorption energy correlated well with the experimental activity enhancement due to electric fields. The lack of conductivity enhancement observed previously was ascribed to the use of MoS2 monolayers instead of nanosheets consisting of multiple layers.42
Although conclusive experimental and theoretical evidence is presented for different hypotheses, a unifying picture is still missing. Besides the size and dimensions of the electrode material used, the device geometry and dimensions seem to govern the activity and the enhancement effect by electric fields significantly. Vastly different reported Tafel slopes even for the same material indicate that even the rate-determining step might be different and the extent of enhancement with different applied gate voltages is dissimilar among different studies. This possibly makes the comparison of field enhancement effects between the different studies meaningless. Careful comparison of different catalyst materials in the same back-gated electrochemical device should yield clear answers to many of those remaining questions. Scanning Tunnelling Microscopy on organic molecules has been employed previously to investigate the effects of electric fields for simple chemical reactions51,52 – a method that should be explored as well for heterogeneous catalysis research. Moreover, DFT calculations have suggested that electric fields can enhance a range of different reactions such as CO oxidation, methane steam reforming, the oxygen reduction reaction or even enzyme-catalysed reactions3,53–57 but conclusive experimental studies are still required to prove the wider applicability of electric fields in heterogeneous catalytic reactions.
3.3 Strain effects
Strain effects, referring to the contraction or expansion of a metal structure beyond its common lattice parameters, are commonly used to alter the catalytic activity of metal surfaces. This can be achieved by coating a host metal with layers of a catalytically active metal where the lattice mismatch leads to strain on the surface. This strain modifies the electronic properties like the d band centre of materials and thus the activity and/or selectivity for electrocatalytic CO2 reduction, the HER and the oxygen reduction reaction among others.58–62 A rigorous analysis of the mechanic implications of strain effects revealed that they offer one explanation how scaling relationships in heterogeneous catalysis can be overcome by mechanic stress. Binding of adsorbates on metal surfaces will inevitably lead to eigenstress – a deformation caused by adsorbate–metal interactions. Depending on whether this is compressive or expansive stress, an additional external stress will make the binding either stronger or weaker. It was shown that although overall adsorption energy differences are in the range of 0.1–0.2 eV different intermediates for the same reaction exhibit different kinds of eigenstress and thus will be affected by isotropic external strain in varied ways resulting in a loss of linear correlation between adsorption strengths. The application of uniaxial, anisotropic strain on the surface leads to compression or extension in one direction but also will cause a Poisson response which is orthogonal and usually opposite in sign to the initial strain (Fig. 5A). Since for most associative and dissociative reactions, the adsorbates are at different locations during the initial and transition states, the energies of both states are affected dissimilarly by anisotropic stress. In the extreme case with opposite eigenstress of initial and transition states, anisotropic strain increases the energy of one state while lowering the energy of the other (Fig. 5B). It was shown specifically for the self-diffusion of Pt atoms on a Pt(100) surface that upon application of uniaxial strain transverse diffusion follows scaling relationships while the initial and transition states for inline diffusion exhibit opposite effects with regard to the application of strain (Fig. 5C).63 Although this was independent of facets on ideal flat surfaces, most active sites are believed to be non-terrace sites – a situation where the anisotropic strain effect prediction may no longer hold true. This proposed effect was shown experimentally for the dissociation of N2 where the catalytic cycle was closed by cyclic strain engineering.64 However, further experimental evidence for the violation of scaling relationships due to anisotropic strain should be provided to clarify the effects of eigenstress compared to more conventionally accepted electronic effects. Recent studies also suggested that applying a dynamic strain to a gold surface affected the induced electrochemical current significantly indicating that strain can modify charge carrier diffusion across electrochemical interfaces.65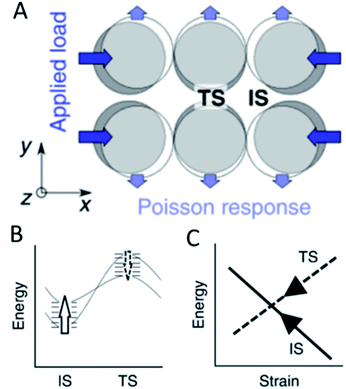 | ||
| Fig. 5 The application of uniaxial compression on a surface (A) leads to a change in the energy levels (B) between the initial (IS) and the transition state (TS) resulting in the breaking of traditional scaling relationships (C), reproduced from ref. 63 with permission from Springer Nature, copyright 2018. | ||
3.4 Magnetic field
It is known that electronically conducting materials are heated up by rapidly changing magnetic fields. This local heating effect has been used for water electrolysis66 and hydrodeoxygenation of aromatic ketones.67 Magnetic field effects on the chemical kinetics of fundamental reactions have been extensively studied68 but most reports on catalytic activity promotion due to magnetic fields beyond pure thermal effects have only emerged relatively recently. Earlier studies on the promotion of chemical and biocatalytic reactions under a permanent magnetic field focused on the mass transfer enhancement across the catalyst–electrolyte interface. In the case of a magnetic field parallel to the planar electrode surface, the magnetohydrodynamic effect accounts for a decrease in the diffusion boundary layer thickness at the working electrode caused by the flow tangential to the electrode surface by Lorentz forces on moving ions. The diffusion coefficients of electroactive species have been determined to remain unchanged and thus overall electrode performance was enhanced when operating in a mass-transfer limited regime.69,70 Meanwhile, magnetic fields also induce the preference of one particular spin state over the other called the Zeeman effect, which is of use for analytical techniques like NMR, MRI, EPR and Mössbauer spectroscopy. In reactions in which the angular momentum is not conserved, that is, reactions where the total spin of the substrates and products is different, large activation barriers are observed. This applies not only for simple processes like sorption and dissociation71 but also is the case for processes as complex as the electrocatalytic splitting of water, where most of the energy input is required for the generation of magnetic 3O2 from nonmagnetic water. Based on DFT calculations, the RuO2 (110) surface – a particularly active catalyst for water splitting – carries magnetic moments which enable angular momentum conservation during O2 evolution so that 3O2 is produced with an energy of around 116 kJ mol−1 lower than what would be required for the generation of 1O2. This hints at a wider range of magnetic materials applicable for reactions which would otherwise violate angular momentum conservation.72Applying a permanent magnetic field in different positions relative to a water splitting electrode based on various magnetic metal oxide materials enhances the current density up to ∼100% (Fig. 6A). A strong correlation between the magnetic current and the bulk magnetization was found and thus it was assumed that local spin polarization is the main reason for the enhanced water electrolysis activity. Experiments revealed that the enhancement effect was immediate and fully reversible upon adding or removing the magnet indicating that no permanent changes in the catalyst structure occurred in a permanent magnetic field. Based on DFT calculations on different antiferromagnetic (antiparallel spin of two adjacent Ni ions) and ferromagnetic (parallel spin) domains of NiO, the magnetic field was assumed to be favouring the local spin alignment. After the oxidation of two OH−, the product O2 is produced in the significantly more stable triplet state (Fig. 6B).73 Considering the simplicity and the essentially net zero additional energy input, static magnetic fields have a great future in enhancing catalytic activities. From the materials science perspective, coating a chiral dye sensitizer on a graphite electrode was sufficient to suppress the formation of H2O2 during photoelectrochemical water splitting. This was ascribed to the generation of OH radicals with parallel spin when chiral instead of racemic sensitizers were used which will make the direct coupling of OH radicals impossible. This approach – although not promotional (by our definition) in nature – could open interesting avenues towards modifying the reactivity and selectivity of electrode surfaces.74
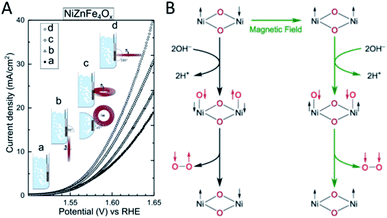 | ||
| Fig. 6 (A) Application of a static external magnetic field enhances the water splitting activity of a NiZnFe4Ox electrode significantly with a dependence on the location and direction of the magnetic field relative to the electrode; (B) simplified mechanism of the water splitting reaction and the assumed effect of an external magnetic field on the spin-switch of adjacent nickel atoms, reproduced from ref. 73 with permission from Springer Nature, copyright 2019. | ||
Despite the promising initial studies, key questions remain about the nature of magnetic promotion in heterogeneous catalysis. Studies have so far focused on electrochemical reactions where the transfer of single electrons and radical coupling reactions are common but similar effects may occur for thermal reactions when organic or metal-centred radicals are involved. Thorough analyses of the effect of the magnetic field direction and field strength are vastly missing although the position of magnetic field lines relative to the catalyst is reported to be relevant.73 Studies on model catalysts or ideal surfaces will shed light on both the effects governing the activity enhancement caused by magnetic fields and the effects on the level of elementary steps. The possibility of directly favouring certain spin orientations in adsorbates should also be explored. Furthermore, the reaction should include unpaired fermions (e.g. electrons or protons) whose spin can be directed by external magnetic fields if the overall kinetics are not dominated by mass transfer effects.
4. Dynamic catalyst activation
Heterogeneous catalysis is conventionally limited by what is described by the Sabatier principle, where it is stated that an adsorbate must neither bind too strongly nor too weakly on an active site. This implies that a single static catalytic site cannot exceed a maximum rate. In theory, an active site that is oscillating between two different electronic states with a sufficiently high frequency and amplitude should be able to overcome the maximum activity commonly referred to as the Sabatier maximum, as has been recently proposed by Dauenhauer and co-workers as dynamic heterogeneous catalysis.2 When considering a simple reaction of A being converted into B on a catalyst surface, only two adsorbates A* and B* and the transition state between those two exist. According to the Brønsted–Evans–Polanyi (BEP) principle, changing the adsorption energy of A* should also affect the energy barrier between A* and B*, as described by the linear-scaling parameter α between the enthalpy of the surface reaction and the activation energy. When this is done statically, the desorption of B* will eventually become the rate-limiting step and thus the total turnover frequency (TOF) is not enhanced. If, after the conversion of A* into B* over a low energy barrier, the energy of B* is elevated again, the desorption becomes more favourable. With the repetition of this cycle (Fig. 7A) at a certain suitable resonance frequency, the overall catalytic activity can be elevated above the Sabatier maximum. The enhancement of this generic chemical reaction has been shown by kinetic modelling to be in the range of a few orders of magnitude. When applying dynamic electronic catalyst modifications with a frequency below the average TOF, the reaction rate is in fact lower compared to the static optimum. At higher frequencies, however, the TOF is predicted to increase significantly up to a threshold frequency upon which the reaction rate is predicted to return to the static optimum value (Fig. 7B).2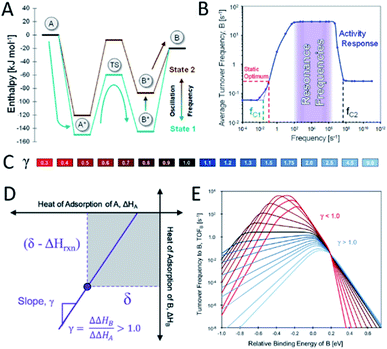 | ||
| Fig. 7 (A) Schematic description of dynamic heterogeneous catalysis in the A-to-B reaction where the adsorption energies of A* and B* can oscillate between state 1 and state 2; (B) average turnover frequency of a catalytic reaction exposed to a dynamic field with a given frequency and a waveform amplitude of 0.6 eV at 150 °C and 100 bar, reproduced from ref. 2 with permission from the American Chemical Society, copyright 2019; (C) colour scale of different γ values related to (E); (D) linear scaling between the binding energies of A* and B* with slope γ and common point δ; (E) turnover frequency to produce B depending on the relative binding energy of B at different γ values (conditions: YB ∼1%, P ∼100 bar, T ∼150 °C, α ∼0.6, β ∼102 kJ mol−1, and δ ∼1.4 eV), reproduced from ref. 75 with permission from the Royal Society of Chemistry, copyright 2019. | ||
In a non-generic reaction system, the binding energies of two adsorbates A* and B* will not exhibit the same variation in binding energies upon introducing an electronic catalyst modification. Therefore, the kinetic model must be extended to account for additional reaction parameters to include the ratio between the relative binding energies of A* and B*, γ, under dynamic field variation. β indicates the intercept of the BEP curve and δ defines the point of electronic variation of the catalytic site where the binding energies of A* and B* are identical (Fig. 7D). Balandin–Sabatier volcano plots with varying γ values (Fig. 7C) are depicted in Fig. 7E, illustrating a pronounced effect of this parameter on the TOF to produce B. For γ > 1, the energy of B* decreases faster than that of A*, accompanied by a decrease in activation energy. The increased binding energy of B* thus results in an increased TOF. The effects of the adsorption energy of B on the TOF are more intricate for γ < 1 where for binding energies of B below −0.4 eV, the reaction becomes adsorption-controlled. Higher binding energies of B of −0.4 to 0.2 eV and above 0.2 eV make the reaction desorption- and surface reaction-controlled respectively (Fig. 7E).75 Although this proposed strategy for enhancing the reaction rate of catalytic sites may open exciting new avenues in heterogeneous catalysis research, experimental validation for the predicted enhancements is urgently required.
5. Conclusion and outlook
Advances in the field of promotion methods for heterogeneous catalysis are promising. Nonetheless, more efforts are required to gather understanding about the underlying physics and chemistry of the processes. In an attempt to provide a unified view on those distinct promotion strategies, we have compared the methods described above in Table 1 regarding the achieved reaction rate and selectivity enhancements as well as the predicted adsorption energy differences for molecules on the catalyst surface. The rate enhancements for most auxiliary methods are around one order of magnitude except for the electrical potential method which has been proven to accelerate reaction rates by up to two orders of magnitude. Applying an electrical potential also seems to be the most effective way to alter the adsorption energy of a substrate by up to 1 eV, while electric field and mechanic stress-induced adsorption energy changes are often within 0.2 eV. With regard to recently proposed dynamic heterogeneous catalytic enhancement, we estimated the time scale on which those methods can potentially work. Combining requirements for adsorption energy differences and the frequency at which the electronic structure of the catalyst can be switched based on previous reports, mostly three, namely electric field, potential and mechanic promotion, should be considered.| Common reaction rate enhancements | Achieved selectivity enhancement | Adsorption energy difference [eV] | Possible time scale [s] | Possible spatial resolution [m] | |
|---|---|---|---|---|---|
| EM waves | Up to 11 (ref. 12) | Change in silyl bond cleavage regioselectivity (ref. 11) | N.A. | N.A. for VSC | ∼10−5 VSC (ref. 11) |
| 10−12 to 10−15 for EM waves in general | 100–10−15 for EM waves | ||||
| Plasma | 1–2* (ref. 5) | Selectivity profiles severely affected in plasma processes | N.A. | N.D. For thermal plasmas | Up to 10−4 (ref. 79) |
| Electric potential | Up to 150 (ref. 46) | Massive changes for many electrophobic and electrophilic reactions (ref. 7) | 0.5–1 (ref. 80 and 81) | Up to 10−10 (ref. 82 and 83) | Up to 10−10 (ref. 84) |
| Electric field | 5 (ref. 42) | N.D. | 0.1–0.2 (ref. 42) | Up to 10−11 (ref. 85) | 10−7-10−6 (ref. 86) |
| EM waves | 10–12 (ref. 30) | Preferential oxidation of CO over H2 (ref. 87) | N.D. | Up to 10−14 (ref. 88) | 100–10−15 |
| Magnetic field | 2–3 (ref. 73) | H2O2 formation suppression for electrochemical water splitting (ref. 74) | N.D. | Up to 10−10 (ref. 89) | Up to 10−6 (ref. 89) |
| Mechanic | 6–10 (ref. 90) | Higher C-number products from CO2RR on Cu electrodes (ref. 91 and 92) | 0.1–0.2 (ref. 63) | 10−4–10−3 (ref. 93) | 10−5–10−4 (ref. 94) |
Beyond offering additional avenues to enhance catalytic activity, the effects of promotional methods enable us to learn more about structure–activity relationships, providing insights into enhanced materials design. Being able to promote catalytic activity on a very small area of the catalyst surface would be beneficial for systematic fundamental studies and thus, potential spatial resolution achievable with various promotional methods is also summarized. It becomes obvious that current research on these methods is far away from the reported physical time and length scales, indicating huge potential for future research. Care must be taken, however, to avoid the so common over-promise and under-deliver pitfall, especially regarding the scalability and economic viability of those approaches. As far as we are aware, only for plasma and electric potential promotion, scalability to some extent has been demonstrated.5,76 Promotional methods based on other phenomena, in particular waves such as electromagnetic and sound waves, deserve more research.77,78 With continuing efforts in improving fundamental understanding, we should strive to include promotional methods into the common repertoire of catalysis research.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National University of Singapore Flagship Green Energy Program (R-279-000-553-646 and R-279-000-553-731) for financial support.References
-
Z. Ma and F. Zaera, in Encyclopedia of Inorganic and Bioinorganic Chemistry, ed. R. A. Scott, John Wiley & Sons, Ltd., 2014 Search PubMed
.
- M. A. Ardagh, O. A. Abdelrahman and P. J. Dauenhauer, ACS Catal., 2019, 9, 6929–6937 CrossRef CAS
.
- F. Che, J. T. Gray, S. Ha, N. Kruse, S. L. Scott and J.-S. McEwen, ACS Catal., 2018, 8, 5153–5174 CrossRef CAS
.
- T. W. Ebbesen, Acc. Chem. Res., 2016, 49, 2403–2412 CrossRef CAS PubMed
.
- E. C. Neyts, K. Ostrikov, M. K. Sunkara and A. Bogaerts, Chem. Rev., 2015, 115, 13408–13446 CrossRef CAS PubMed
.
- U. Aslam, V. G. Rao, S. Chavez and S. Linic, Nat. Catal., 2018, 1, 656–665 CrossRef
.
- C. G. Vayenas and S. Brosda, Top. Catal., 2014, 57, 1287–1301 CrossRef CAS
.
- M. Luo and S. Guo, Nat. Rev. Mater., 2017, 2, 17059 CrossRef CAS
.
- R. R. Smith, D. R. Killelea, D. F. DelSesto and A. L. Utz, Science, 2004, 304, 992–995 CrossRef CAS PubMed
.
- A. Thomas, J. George, A. Shalabney, M. Dryzhakov, S. J. Varma, J. Moran, T. Chervy, X. Zhong, E. Devaux, C. Genet, J. A. Hutchison and T. W. Ebbesen, Angew. Chem., Int. Ed., 2016, 55, 11462–11466 CrossRef CAS PubMed
.
- A. Thomas, L. Lethuillier-Karl, K. Nagarajan, R. M. A. Vergauwe, J. George, T. Chervy, A. Shalabney, E. Devaux, C. Genet, J. Moran and T. W. Ebbesen, Science, 2019, 363, 615–619 CrossRef CAS PubMed
.
- J. Lather, P. Bhatt, A. Thomas, T. W. Ebbesen and J. George, Angew. Chem., Int. Ed., 2019, 58, 10635–10638 CrossRef CAS PubMed
.
- R. Vergauwe, A. Thomas, K. Nagarajan, J. George, T. Chervy, M. Seidel, E. Devaux, V. Torbeev and T. W. Ebbesen, Angew. Chem., Int. Ed., 2019, 58, 15324–15328 CrossRef CAS PubMed
.
- G. B. Dudley, R. Richert and A. E. Stiegman, Chem. Sci., 2015, 6, 2144–2152 RSC
.
- C. O. Kappe, B. Pieber and D. Dallinger, Angew. Chem., Int. Ed., 2013, 52, 1088–1094 CrossRef CAS PubMed
.
- T. Durka, T. Van Gerven and A. Stankiewicz, Chem. Eng. Technol., 2009, 32, 1301–1312 CrossRef CAS
.
- H. S. Eyde, J. R. Soc. Arts, 1909, 57, 568–576 Search PubMed
.
- J. C. Whitehead, J. Phys. D: Appl. Phys., 2016, 49, 243001 CrossRef
.
- J. C. Polanyi, Acc. Chem. Res., 1972, 5, 161–168 CrossRef CAS
.
- T. Nozaki and K. Okazaki, Catal. Today, 2013, 211, 29–38 CrossRef CAS
.
- J. Hong, S. Prawer and A. B. Murphy, ACS Sustainable Chem. Eng., 2018, 6, 15–31 CrossRef CAS
.
- P. Mehta, P. Barboun, D. B. Go, J. C. Hicks and W. F. Schneider, ACS Energy Lett., 2019, 4, 1115–1133 CrossRef CAS
.
- P. Mehta, P. Barboun, F. A. Herrera, J. Kim, P. Rumbach, D. B. Go, J. C. Hicks and W. F. Schneider, Nat. Catal., 2018, 1, 269–275 CrossRef
.
- R. Snoeckx, Y. X. Zeng, X. Tu and A. Bogaerts, RSC Adv., 2015, 5, 29799–29808 RSC
.
- J. C. Whitehead, Front. Chem. Sci. Eng., 2019, 13, 264–273 CrossRef
.
- P. Christopher, H. Xin and S. Linic, Nat. Chem., 2011, 3, 467–472 CrossRef CAS PubMed
.
- P. Christopher, H. Xin, A. Marimuthu and S. Linic, Nat. Mater., 2012, 11, 1044–1050 CrossRef CAS PubMed
.
- U. Aslam, S. Chavez and S. Linic, Nat. Nanotechnol., 2017, 12, 1000–1006 CrossRef CAS PubMed
.
- M. J. Landry, A. Gellé, B. Y. Meng, C. J. Barrett and A. Moores, ACS Catal., 2017, 7, 6128–6133 CrossRef CAS
.
- L. Zhou, D. F. Swearer, C. Zhang, H. Robatjazi, H. Zhao, L. Henderson, L. Dong, P. Christopher, E. A. Carter, P. Nordlander and N. J. Halas, Science, 2018, 362, 69–72 CrossRef CAS PubMed
.
- J. Y. Park, S. M. Kim, H. Lee and I. I. Nedrygailov, Acc. Chem. Res., 2015, 48, 2475–2483 CrossRef CAS PubMed
.
- C. G. Vayenas, S. Bebelis and S. Ladas, Nature, 1990, 343, 625–627 CrossRef CAS
.
- D. Theleritis, S. Souentie, A. Siokou, A. Katsaounis and C. G. Vayenas, ACS Catal., 2012, 2, 770–780 CrossRef CAS
.
- F. Matei, D. Ciuparu, C. Jiménez-Borja, F. Dorado, J. L. Valverde and S. Brosda, Appl. Catal., B, 2012, 127, 18–27 CrossRef CAS
.
- V. Jiménez, C. Jiménez-Borja, P. Sánchez, A. Romero, E. I. Papaioannou, D. Theleritis, S. Souentie, S. Brosda and J. L. Valverde, Appl. Catal., B, 2011, 107, 210–220 CrossRef
.
- A. Nakos, S. Souentie and A. Katsaounis, Appl. Catal., B, 2010, 101, 31–37 CrossRef CAS
.
- F. Matei, C. Jiménez-Borja, J. Canales-Vázquez, S. Brosda, F. Dorado, J. L. Valverde and D. Ciuparu, Appl. Catal., B, 2013, 132–133, 80–89 CrossRef CAS
.
- M. Makri, C. G. Vayenas, S. Bebelis, K. H. Besocke and C. Cavalca, Ionics, 1996, 2, 248–253 CrossRef CAS
.
- S. G. Neophytides, D. Tsiplakides, P. Stonehart, M. M. Jaksic and C. G. Vayenas, Nature, 1994, 370, 45–47 CrossRef CAS
.
- M. Athanasiou, B. Hasa, J. Vakros, L. Sygellou and A. Katsaounis, J. Chem. Technol. Biotechnol., 2018, 93, 1542–1548 CrossRef CAS
.
- D. Theleritis, M. Makri, S. Souentie, A. Caravaca, A. Katsaounis and C. G. Vayenas, ChemElectroChem, 2014, 1, 254–262 CrossRef
.
- Y. Wang, S. Udyavara, M. Neurock and C. D. Frisbie, Nano Lett., 2019, 19, 6118–6123 CrossRef CAS PubMed
.
- A. Kotsiras, I. Kalaitzidou, D. Grigoriou, A. Symillidis, M. Makri, A. Katsaounis and C. G. Vayenas, Appl. Catal., B, 2018, 232, 60–68 CrossRef CAS
.
- I. Kalaitzidou, A. Katsaounis, T. Norby and C. G. Vayenas, J. Catal., 2015, 331, 98–109 CrossRef CAS
.
- I. Kalaitzidou, M. Makri, D. Theleritis, A. Katsaounis and C. G. Vayenas, Surf. Sci., 2016, 646, 194–203 CrossRef CAS
.
- F. Cai, D. Gao, H. Zhou, G. Wang, T. He, H. Gong, S. Miao, F. Yang, J. Wang and X. Bao, Chem. Sci., 2017, 8, 2569–2573 RSC
.
- J. Wang, M. Yan, K. Zhao, X. Liao, P. Wang, X. Pan, W. Yang and L. Mai, Adv. Mater., 2017, 29, 1604464 CrossRef PubMed
.
- M. Yan, X. Pan, P. Wang, F. Chen, L. He, G. Jiang, J. Wang, J. Z. Liu, X. Xu, X. Liao, J. Yang and L. Mai, Nano Lett., 2017, 17, 4109–4115 CrossRef CAS PubMed
.
- F. L. Ling, T. W. Zhou, X. Q. Liu, W. Kang, W. Zeng, Y. X. Zhang, L. Fang, Y. Lu and M. Zhou, Nanotechnol, 2017, 29, 03LT01 CrossRef PubMed
.
- F. Ling, X. Liu, H. Jing, Y. Chen, W. Zeng, Y. Zhang, W. Kang, J. Liu, L. Fang and M. Zhou, Phys. Chem. Chem. Phys., 2018, 20, 26083–26090 RSC
.
- M. Alemani, M. V. Peters, S. Hecht, K.-H. Rieder, F. Moresco and L. Grill, J. Am. Chem. Soc., 2006, 128, 14446–14447 CrossRef CAS PubMed
.
- S. Fatayer, F. Albrecht, Y. Zhang, D. Urbonas, D. Peña, N. Moll and L. Gross, Science, 2019, 365, 142–145 CAS
.
- F. Che, J. T. Gray, S. Ha and J.-S. McEwen, J. Catal., 2015, 332, 187–200 CrossRef CAS
.
- F. Che, S. Ha and J.-S. McEwen, Appl. Catal., B, 2016, 195, 77–89 CrossRef CAS
.
- P. Deshlahra, E. E. Wolf and W. F. Schneider, J. Phys. Chem. A, 2009, 113, 4125–4133 CrossRef CAS PubMed
.
- G. S. Karlberg, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 5158–5161 RSC
.
- S. D. Fried, S. Bagchi and S. G. Boxer, Science, 2014, 346, 1510–1514 CrossRef CAS
.
- P. Strasser, S. Koh, T. Anniyev, J. Greeley, K. More, C. Yu, Z. Liu, S. Kaya, D. Nordlund, H. Ogasawara, M. F. Toney and A. Nilsson, Nat. Chem., 2010, 2, 454–460 CrossRef CAS PubMed
.
- R. P. Jansonius, L. M. Reid, C. N. Virca and C. P. Berlinguette, ACS Energy Lett., 2019, 4, 980–986 CrossRef CAS
.
- K. Yan, T. A. Maark, A. Khorshidi, V. A. Sethuraman, A. A. Peterson and P. R. Guduru, Angew. Chem., Int. Ed., 2016, 55, 6175–6181 CrossRef CAS PubMed
.
- V. A. Sethuraman, D. Vairavapandian, M. C. Lafouresse, T. Adit Maark, N. Karan, S. Sun, U. Bertocci, A. A. Peterson, G. R. Stafford and P. R. Guduru, J. Phys. Chem. C, 2015, 119, 19042–19052 CrossRef CAS
.
- L. A. Kibler, A. M. El-Aziz, R. Hoyer and D. M. Kolb, Angew. Chem., Int. Ed., 2005, 44, 2080–2084 CrossRef CAS PubMed
.
- A. Khorshidi, J. Violet, J. Hashemi and A. A. Peterson, Nat. Catal., 2018, 1, 263–268 CrossRef
.
- G.-F. Han, X.-M. Shi, S.-J. Kim, J. Kim, J.-P. Jeon, H.-J. Noh, Y.-K. Im, F. Li, Y. R. Uhm, C. S. Kim, Q. Jiang and J.-B. Baek, Sci. Adv., 2019, 5, eaax8275 CrossRef
.
- Q. Deng and A. Yuan, J. Electrochem. Soc., 2019, 166, 480–484 CrossRef
.
- C. Niether, S. Faure, A. Bordet, J. Deseure, M. Chatenet, J. Carrey, B. Chaudret and A. Rouet, Nat. Energy, 2018, 3, 476–483 CrossRef CAS
.
- J. M. Asensio, A. B. Miguel, P.-F. Fazzini, P. W. N. M. van Leeuwen and B. Chaudret, Angew. Chem., Int. Ed., 2019, 58, 11306–11310 CrossRef CAS PubMed
.
- U. E. Steiner and T. Ulrich, Chem. Rev., 1989, 89, 51–147 CrossRef CAS
.
- O. Lioubashevski, E. Katz and I. Willner, J. Phys. Chem. B, 2004, 108, 5778–5784 CrossRef CAS
.
- E. Katz, O. Lioubashevski and I. Willner, J. Am. Chem. Soc., 2004, 126, 11088–11092 CrossRef CAS PubMed
.
- J. Behler, B. Delley, S. Lorenz, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2005, 94, 036104 CrossRef PubMed
.
- E. Torun, C. M. Fang, G. A. de Wijs and R. A. de Groot, J. Phys. Chem. C, 2013, 117, 6353–6357 CrossRef CAS
.
- F. A. Garcés-Pineda, M. Blasco-Ahicart, D. Nieto-Castro, N. López and J. R. Galán-Mascarós, Nat. Energy, 2019, 4, 519–525 CrossRef
.
- W. Mtangi, F. Tassinari, K. Vankayala, A. Vargas Jentzsch, B. Adelizzi, A. R. A. Palmans, C. Fontanesi, E. W. Meijer and R. Naaman, J. Am. Chem. Soc., 2017, 139, 2794–2798 CrossRef CAS
.
- A. M. Alexander, B. Turan, Z. Qi, A. Omar and D. Paul, Catal. Sci. Technol., 2019, 9, 5058–5076 RSC
.
- S. Balomenou, D. Tsiplakides, A. Katsaounis, S. Thiemann-Handler, B. Cramer, G. Foti, C. Comninellis and C. G. Vayenas, Appl. Catal., B, 2004, 52, 181–196 CrossRef CAS
.
- P. N. Amaniampong, A. Karam, Q. T. Trinh, K. Xu, H. Hirao, F. Jérôme and G. Chatel, Sci. Rep., 2017, 7, 40650 CrossRef PubMed
.
- P. N. Amaniampong, Q. T. Trinh, K. De Oliveira Vigier, D. Q. Dao, N. H. Tran, Y. Wang, M. P. Sherburne and F. Jérôme, J. Am. Chem. Soc., 2019, 141, 14772–14779 CrossRef CAS PubMed
.
- M. J. E. Manuel, A. B. Sefkow, C. C. Kuranz, A. M. Rasmus, S. R. Klein, M. J. MacDonald, M. R. Trantham, J. R. Fein, P.
X. Belancourt, R. P. Young, P. A. Keiter, B. B. Pollock, J. Park, A. U. Hazi, G. J. Williams, H. Chen and R. P. Drake, Phys. Rev. Lett., 2019, 122, 225001 CrossRef CAS PubMed
.
- F. Che, J. T. Gray, S. Ha and J.-S. McEwen, ACS Catal., 2017, 7, 551–562 CrossRef CAS
.
- M. P. Hyman and J. W. Medlin, J. Phys. Chem. B, 2005, 109, 6304–6310 CrossRef CAS PubMed
.
- S. Bhattacharjee, D. Rahmedov, D. Wang, J. Íñiguez and L. Bellaiche, Phys. Rev. Lett., 2014, 112, 147601 CrossRef PubMed
.
- J. Li, B. Nagaraj, H. Liang, W. Cao, C. H. Lee and R. Ramesh, Appl. Phys. Lett., 2004, 84, 1174–1176 CrossRef CAS
.
- C. Hauf, A.-A. H. Salvador, M. Holtz, M. Woerner and T. Elsaesser, Struct. Dyn., 2018, 5, 024501 CrossRef PubMed
.
- V. Lopez-Dominguez, H. Almasi and P. K. Amiri, Phys. Rev. Appl., 2019, 11, 024019 CrossRef CAS
.
- F. Wu, Appl. Opt., 2017, 56, 8866–8870 CrossRef
.
- M. J. Kale, T. Avanesian, H. Xin, J. Yan and P. Christopher, Nano Lett., 2014, 14, 5405–5412 CrossRef CAS
.
- H. Shan, Y. Yu, X. Wang, Y. Luo, S. Zu, B. Du, T. Han, B. Li, Y. Li, J. Wu, F. Lin, K. Shi, B. K. Tay, Z. Liu, X. Zhu and Z. Fang, Light: Sci. Appl., 2019, 8, 9 CrossRef
.
- K. Vahaplar, A. M. Kalashnikova, A. V. Kimel, D. Hinzke, U. Nowak, R. Chantrell, A. Tsukamoto, A. Itoh, A. Kirilyuk and T. Rasing, Phys. Rev. Lett., 2009, 103, 117201 CrossRef CAS PubMed
.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed
.
- C. W. Li, J. Ciston and M. W. Kanan, Nature, 2014, 508, 504 CrossRef CAS PubMed
.
- E. L. Clark, C. Hahn, T. F. Jaramillo and A. T. Bell, J. Am. Chem. Soc., 2017, 139, 15848–15857 CrossRef CAS PubMed
.
- G. K. Lopp, C. R. Kelley and J. L. Kauffman, Appl. Phys. Lett., 2018, 112, 054102 CrossRef
.
- T. Nan, H. Lin, Y. Gao, A. Matyushov, G. Yu, H. Chen, N. Sun, S. Wei, Z. Wang, M. Li, X. Wang, A. Belkessam, R. Guo, B. Chen, J. Zhou, Z. Qian, Y. Hui, M. Rinaldi, M. E. McConney, B. M. Howe, Z. Hu, J. G. Jones, G. J. Brown and N. X. Sun, Nat. Commun., 2017, 8, 296 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2020 |