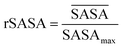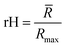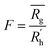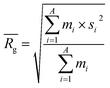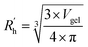Open Access Article
Open Access ArticleMolecular dynamics based descriptors for predicting supramolecular gelation†
Ruben
Van Lommel
 ab,
Jianyu
Zhao
b,
Wim M.
De Borggraeve
ab,
Jianyu
Zhao
b,
Wim M.
De Borggraeve
 a,
Frank
De Proft
b and
Mercedes
Alonso
a,
Frank
De Proft
b and
Mercedes
Alonso
 *b
*b
aMolecular Design and Synthesis, Department of Chemistry, KU Leuven, Celestijnenlaan 200F Leuven Chem&Tech, box 2404, 3001 Leuven, Belgium
bEenheid Algemene Chemie (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium. E-mail: mercedes.alonso.giner@vub.be
First published on 3rd April 2020
Abstract
Whilst the field of supramolecular gels is rapidly moving towards complex materials and applications, their design is still an effortful and laborious trial-and-error process. Herein, we introduce four new descriptors that can be derived from all-atom molecular dynamics simulations and which are able to predict supramolecular gelation in both water and organic solvents. Their predictive ability was demonstrated via two separate machine learning techniques, a decision tree and an artificial neural network, with a dataset composed of urea-based gelators. Owing to the physical relevance of these descriptors to the supramolecular gelation process, their use could be conceptualized to other classes of supramolecular gelators and hence steer their design.
Introduction
In recent years, Low Molecular Weight Gelators (LMWGs) have attracted significant attention. Currently, the field is focussed on developing efficient supramolecular gels for various specialized applications, ranging from drug delivery systems to catalyst templates or even optoelectronic applications.1–3 Despite two decades of intense research on supramolecular gelators, their discovery remains surprisingly reliant on serendipity, due to the sensitivity of the supramolecular gelation process towards small molecular changes of the LMWG.4–6 In this context, multiscale computational methodologies have the potential to provide a better understanding of the underlying relationship between the molecular structure and the gelation ability.7 However, besides post-rationalization, the ability to predict supramolecular gelation by means of computational methods has been scarcely explored.The first predictive tool for organogel formation was reported in 2011 by Raynal and Bouteiller.8 In their pioneering work, Hansen Solubility Parameters (HSPs) were employed to define solubility and gelation spheres in Hansen space by means of an elaborate assessment of the behaviour of a known Low Molecular Weight Gelator (LMWG) in several solvents. Based on these spheres, the gelation performance of the LMWG in an untested solvent could then be predicted using the HSPs of this new solvent. If the HSP values fall inside the solubility sphere or the gelation sphere, it is likely that the LMWG will, respectively, be soluble or form a gel in the solvent. Follow-up works from the group of Bouteiller further improved the quality and scope of this method to determine the gelation domain from the solubility data of LMWGs.9,10 This approach, however, still requires the synthesis of the molecule and an extensive gelation screening beforehand, as for each new LMWG, solubility data needs to be gathered to define the gelation domain. Furthermore, the reliability of the prediction depends on the quality of the initial solubility data set.8
The combined effort of the Tuttle and Ulijn groups resulted in the development of a predictive method for the self-assembly properties of tripeptides in water based solely on computations.11,12 Using high throughput coarse-grained molecular dynamics simulations, a hydrophobicity-corrected aggregation propensity score (APH) could be obtained, which originates from the solvent accessible surface area of the aggregate as well as the partitioning coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) of the gelator.13 By screening the APH score of 8000 tripeptides in water, they were able to bring forth a set of design rules to promote aggregation and supramolecular hydrogelation. As their method focuses on the hydrogelation of tripeptide gelators, the applicability to non-peptide gelators requires a specialized coarse-grained model. Recently, Adams and Berry developed a machine learning model to successfully predict the hydrogelation propensity of functionalised amino acids and dipeptides using physicochemical properties and molecular fingerprints.14 Descriptors such as the number of rings, polar surface area, solvent accessible surface area and log
P) of the gelator.13 By screening the APH score of 8000 tripeptides in water, they were able to bring forth a set of design rules to promote aggregation and supramolecular hydrogelation. As their method focuses on the hydrogelation of tripeptide gelators, the applicability to non-peptide gelators requires a specialized coarse-grained model. Recently, Adams and Berry developed a machine learning model to successfully predict the hydrogelation propensity of functionalised amino acids and dipeptides using physicochemical properties and molecular fingerprints.14 Descriptors such as the number of rings, polar surface area, solvent accessible surface area and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P emerged as key parameters for predicting gelation, together with a number of molecular fingerprint descriptors, which are abstract and difficult to interpret. An added value of such approach is that it can be offered via an online interface, since only a SMILES code is needed as input to obtain a prediction of the hydrogelation properties of the molecule. Moreover, next to the prediction itself, the relevancy of the prediction is indicated. The predictions are accurate as long as the molecule falls within the applicability domain of the model, defined by the properties of the amino acids and dipeptides present in the training set. To recreate a similar predictive model for non-peptide gelators that currently fall outside the applicability domain of their prediction model, a significant amount of new data is required.
P emerged as key parameters for predicting gelation, together with a number of molecular fingerprint descriptors, which are abstract and difficult to interpret. An added value of such approach is that it can be offered via an online interface, since only a SMILES code is needed as input to obtain a prediction of the hydrogelation properties of the molecule. Moreover, next to the prediction itself, the relevancy of the prediction is indicated. The predictions are accurate as long as the molecule falls within the applicability domain of the model, defined by the properties of the amino acids and dipeptides present in the training set. To recreate a similar predictive model for non-peptide gelators that currently fall outside the applicability domain of their prediction model, a significant amount of new data is required.
Among the different types of LMWGs, peptide-based hydrogelators belong to one of the best represented classes of gelators due to their potency in several biomedical applications.15,16 While they benefit from biocompatibility, their synthesis is often costly and time consuming. In contrast, the class of urea-based gelators enjoy a cheap and straightforward synthesis allowing easy derivatization. Recently, we reported on a thixotropic and cytocompatible bis-urea derivative with potential in biomedical applications.17 In this work, we set out to develop a conceptual molecular dynamics guided predictive model for urea-based supramolecular gelation to improve their current empirical design strategy. In essence, we aim for an approach fulfilling the following four criteria: (i) the method should be able to correctly predict supramolecular gelation of urea-based molecules by means of computations exclusively. (ii) Instead of a binary yes/no answer, the outcome of the predictions should be a three-level categorical response: gel, precipitate and solution. (iii) Only descriptors with a physical relevance towards supramolecular gelation should be used to build the model, in order to provide chemical insights into the structure–gelation relationships. With suitable descriptors, the approach could be conceptualized to other supramolecular gelator classes. (iv) And finally, the predictions should be accurate in both water (hydrogelation) and organic solvents (organogelation) (Fig. 1).
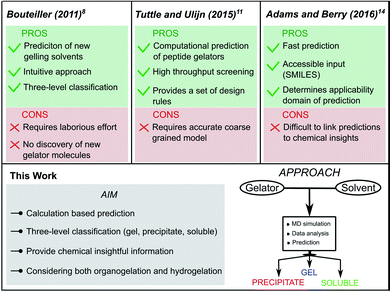 | ||
| Fig. 1 Comparison of reported supramolecular gelation predictive models with the approach followed in this work. | ||
Methodology
The dataset
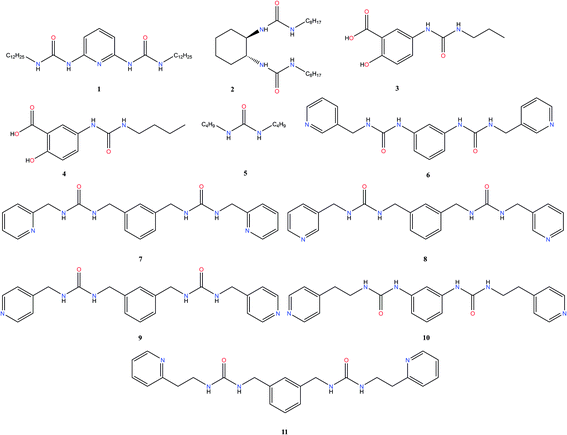
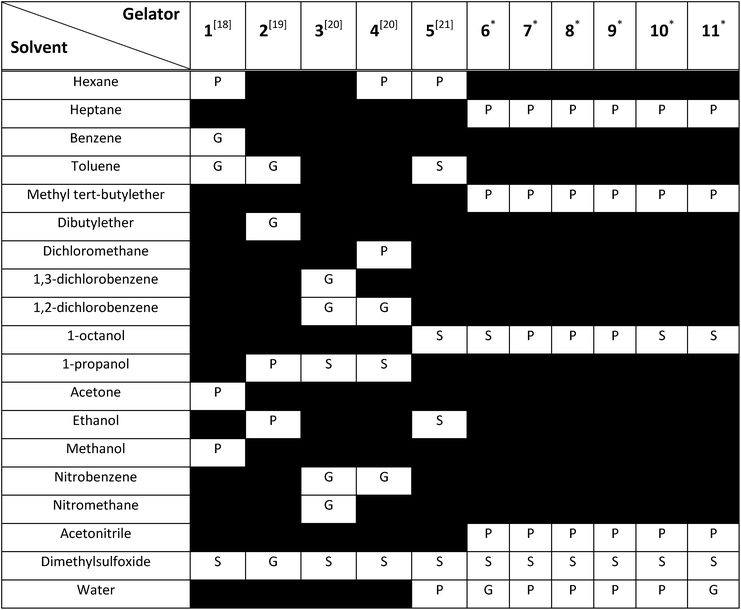
To construct the model and test the predictive ability of our approach, a library of urea-based LMWGs was generated, which is shown in Fig. 2. Some LMWGs were previously reported by other research groups (1, 2, 3, 4 and 5), while other compounds were recently synthesized by our group (6, 7, 8, 9, 10 and 11).7,17–21 The compounds were selected on the basis of two criteria. First, the molecule should contain at least one urea moiety. Second, the experimental protocol to assess the gelation performance in a certain solvent should be exactly the same for all compounds. It is crucial to fulfil the latter criteria in order for the data to be consistent, since the gelation procedure significantly affects the gelation propensity.22 This imposes serious restrictions on the data available in literature on urea-based LMWGs that can be used in this study, as gelation procedures often vary or are ill-defined. Herein, all compounds have been screened for their gelation ability based on the same procedure, involving a heating and cooling cycle to obtain the gel at a concentration of LMWG smaller or equal than 1.0% w/v. The full library contains non-gelators, organogelators as well as hydrogelators. A total of 65 data points has been obtained by screening the gelation performance in different solvents. For compound 1–5, gelator–solvent combinations were selected based on available literature data keeping diversity in gelation properties in mind.17–21 Whilst data on compound 6–11 was generated by our own experiments, with solvents being selected based on their difference in polarity and hydrogen bonding capabilities. Although the size of this dataset is modest, previous studies in different fields have shown to deliver a promising predictive model with similar dataset sizes, by using models with a low complexity or by means of chemically relevant descriptors.14,23,24Molecular dynamics
In our previous work on the rationalization of supramolecular hydrogelation through a multiscale computational approach, we have showed that all-atom molecular dynamics simulations, emerge as a unique tool to provide insight into the aggregation phase during supramolecular gelation.7 Similarly, in the pioneering work of Tuttle and Ulijn,11 coarse grained molecular dynamics was applied to obtain their APH score and predict the hydrogelation performance of tripeptides. Herein, molecular dynamics simulations are performed to obtain a set of descriptors, which we envisioned to have predictive ability value in supramolecular gelation. The MD simulations were performed by placing 5 gelator molecules in a periodic cubic box filled with solvent molecules to reach a concentration of 1.0% w/v. The same concentration is used in the experimental determination of the gelation performance. A trajectory of 50 ns with a timestep of 0.5 fs was gathered using the CHARMM27 force field, with the parameters retrieved from the Swissparam service.25,26 This force field was already shown to accurately describe urea based interactions, which are key during the supramolecular gelation of urea containing compounds.7,27 Before production, an energy minimization and temperature/pressure equilibration step was performed to ensure steric clashes or inadequate equilibration of the NPT-ensemble would not affect the production simulation. The V-rescale thermostat and Parrinello–Rahman barostat were used with the temperature set at 300 K and the pressure at 1.0 bar.28 All molecules were randomly placed inside the simulation box with the gelator molecules separately being dispersed in the solvent, using the Packmol software, while simulations were run with the Gromacs software version 2018.3.29,30 All descriptors were obtained as a time average over the 50 ns simulation, with a snapshot taken every 2.5 ps. A detailed description of the methodology can be found in the ESI (S3†).Descriptors for supramolecular gelation
For a molecule to act as an efficient low molecular weight gelator, a number of criteria needs to be met: (i) the molecule should have a suitable solvophobic balance, (ii) it should contain sites for non-covalent interactions allowing the formation of a reversible network and (iii) these non-covalent interactions should promote the anisotropic growth of a Self-Assembled Fibrillar Network (SAFiN) that immobilizes the solvent and causes the distinct supramolecular gel features.31 Four MD generated descriptors are introduced in this work that quantify one or more of these criteria and thus could have the ability to predict supramolecular gelation.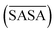 of the gelator molecules during the 50 ns simulations with a maximum SASA (SASAmax). The latter is obtained by multiplying the SASA of a single fully extended gelator molecule (i.e. all dihedral angles of the backbone are set to 180°) with the number of gelator molecules present in the simulation box.
of the gelator molecules during the 50 ns simulations with a maximum SASA (SASAmax). The latter is obtained by multiplying the SASA of a single fully extended gelator molecule (i.e. all dihedral angles of the backbone are set to 180°) with the number of gelator molecules present in the simulation box.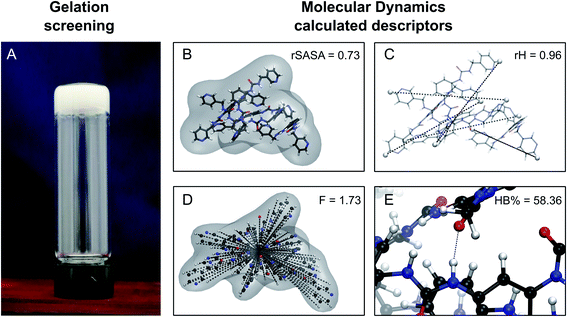 | ||
| Fig. 3 Schematic representation of the experimental gelation screening (A) and the computation of the four descriptors rSASA, rH, F and HB% from a molecular dynamics simulation (B–E). | ||
By taking the time-averaged value of the SASA instead of the SASA of the final frame of the simulation, a robust score is obtained important for small scale all-atom simulations. The 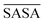 and SASAmax are computed by the double cubic lattice method with the radius of the solvent probe set at 1.4 Å.32 Values close to 1 of the rSASA descriptor indicate absence of aggregation, while values significantly smaller than 1 indicate solvophobic interactions triggering aggregation.
and SASAmax are computed by the double cubic lattice method with the radius of the solvent probe set at 1.4 Å.32 Values close to 1 of the rSASA descriptor indicate absence of aggregation, while values significantly smaller than 1 indicate solvophobic interactions triggering aggregation.
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ) and dividing this value with the maximum end-to-end distance, obtained by measuring the distance between the respective atoms of a corresponding fully extended molecule (Rmax) (Fig. 3C).
) and dividing this value with the maximum end-to-end distance, obtained by measuring the distance between the respective atoms of a corresponding fully extended molecule (Rmax) (Fig. 3C).Similarly, it is rationalized that, if sufficient rotatable bonds are present in the molecule, the rH descriptor evaluates the interactions between the gelator molecule and the environment. If the molecule has pronounced solvophobic interactions, it will decrease its contact with the solvent resulting in a collapsed shape and a decreased value of rH. Therefore, rH can be regarded as a measure for intramolecular aggregation. Nevertheless, it is important to note that, next to gelator/solvent interactions, intramolecular and intermolecular gelator/gelator interactions could also have a pronounced effect on the value of rH. Indeed, upon self-assembly of the gelator molecules to a nanofiber, one can assume that in the centre of the fiber, the gelator molecules are mainly surrounded by other gelator molecules. While at the surface, the gelator molecules are in contact with solvent molecules and here solvent–gelator interactions need to be taken into consideration. As molecules are constantly moving during the simulation, it is not straightforward to make a clear differentiation between molecules located in the centre of the aggregate or at the surface. For this reason, the average is taken over all gelator molecules in the simulation. Additionally, the flexibility of the gelator molecule will have an effect on the value of this descriptor, as molecules with no or little rotatable bonds in their structure will have an almost constant value of rH irrespective of the solvent.
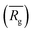 to a pseudo hydrodynamic radius
to a pseudo hydrodynamic radius 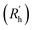 , similar to the particle shape factor used in the field of proteins and polymers (Fig. 3D).37
, similar to the particle shape factor used in the field of proteins and polymers (Fig. 3D).37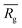 is calculated as the square root of the mass averaged distance of all gelator atoms (A) to the centre of mass of all gelator atoms in the simulation. Classically, the hydrodynamic radius Rh of a particle is measured by dynamic light scattering experiments and is defined as the radius of a hypothetical hard sphere that will diffuse with the same speed as the solvated particle under investigation.37 Based on this, a computable pseudo hydrodynamic radius
is calculated as the square root of the mass averaged distance of all gelator atoms (A) to the centre of mass of all gelator atoms in the simulation. Classically, the hydrodynamic radius Rh of a particle is measured by dynamic light scattering experiments and is defined as the radius of a hypothetical hard sphere that will diffuse with the same speed as the solvated particle under investigation.37 Based on this, a computable pseudo hydrodynamic radius 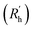 is suggested as the radius of a hypothetical hard sphere that has the same volume as the combined molecular volume of all gelator molecules (Vgel). The latter can be approximated by calculating the volume of a single extended gelator molecule using the double cubic lattice method with the probe radius set to 1.4 Å and multiplying this value with the total number of gelator molecules present in the simulation. The purpose of the shape factor F lies in the description of the shape of the aggregate that is observed during the molecular dynamics simulation. When the aggregate has a spherical shape a low value of F is computed, when the aggregate adopts a more fibrous shape, F increases.
is suggested as the radius of a hypothetical hard sphere that has the same volume as the combined molecular volume of all gelator molecules (Vgel). The latter can be approximated by calculating the volume of a single extended gelator molecule using the double cubic lattice method with the probe radius set to 1.4 Å and multiplying this value with the total number of gelator molecules present in the simulation. The purpose of the shape factor F lies in the description of the shape of the aggregate that is observed during the molecular dynamics simulation. When the aggregate has a spherical shape a low value of F is computed, when the aggregate adopts a more fibrous shape, F increases.The descriptors defined above can all be calculated based on data generated in a molecular dynamics simulation and by employing the open-source GROMACS software (version 2018.3) together with its implementations.29 A detailed explanation on the practical aspects to obtain the descriptors is provided in the ESI (S4–S7†).
Results and discussion
Gelation results
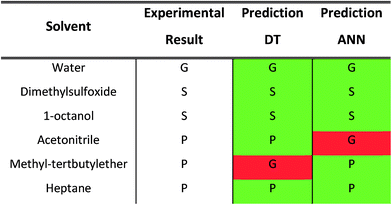
A thorough gelation screening in multiple solvents was already performed on some of the urea-based compounds in our library (1, 2, 3, 4 and 5), making the classification of data associated with these compounds straightforward (Fig. 2).18–21 In order to get a meaningful and consistent three-level classification of the gelator–solvent combinations as precipitate (P), solution (S) or gel (G), a fixed gelation procedure and minimum gelation concentration (MGC) need to be defined. The gelation procedure consisted of heating the sample to dissolve the gelator followed by cooling to room temperature. The sample is deemed to be a gel if the material does not flow upon vial inversion. When the material does flow upon inversion, it is classified as a precipitate if solid particles are observed, or as soluble when the sample is a clear solution. All gels that are formed have an MGC no higher than 1.0% w/v. From the results gathered in Table 1, it is clear that our dataset comprises urea-based non-gelators (5, 7, 8, 9, 10), organogelators (1, 2, 3, 4) and hydrogelators (6, 11) under the experimental conditions specified above.Molecular dynamics derived descriptors
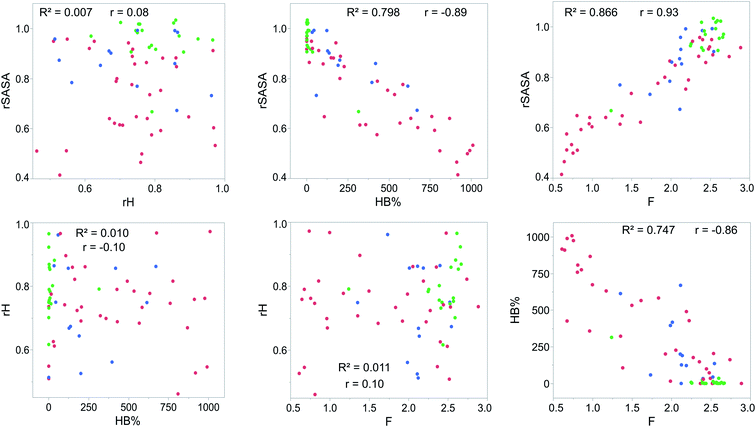
For each gelator–solvent combination, a 50 ns molecular dynamics simulation was performed to obtain a time averaged value for the descriptors (Fig. 3). All possible 2D plots between the four molecular descriptors (rSASA, HB%, rH and F) are presented in Fig. 4, together with their respective linear regression R2 value and Pearson correlation coefficient (r). From these graphs, it can be seen that the molecular descriptors rSASA, HB% and F have an R2 value between themselves ranging from 0.747 to 0.866. Additionally, their corresponding correlation coefficient is either higher than 0.85 or lower than −0.85 suggesting a linear trend between these descriptors. The negative linear trend between rSASA and HB% and between HB% and F might be expected. Indeed, as the gelator molecules in the simulation tend to aggregate in a solvent, the values of rSASA and F decrease as they quantify respectively the aggregation tendency and shape of the aggregate being formed by the gelator molecules. The HB%, on the other hand, will increase as more intermolecular hydrogen bonds are being formed between the gelator molecules in the aggregated state compared to the soluble state. With the same reasoning, the positive linear trend between rSASA and F can be rationalized. One might argue that because of the apparent linear relationship between rSASA, HB% and F, the aforementioned descriptors provide the same information and hence could be reduced to a single property. However, the following thought experiment demonstrates their unique intrinsic value and their independency from one another. Imagine a class of gelators consisting solely out of carbon and hydrogen atoms. The HB% descriptor will be equal to 0, regardless of the solvent and the gelator molecule as there are no hydrogen bond donor or acceptor atoms present. However, in this case rSASA and F will still vary upon changing the solvent as the solubility of the molecule and the aggregates shape of the aggregates can be influenced by other gelator–solvent interactions such as van der Waals interactions. In this case, no linear trend would be observed between HB% and rSASA or between HB% and F. Note, that this statement is supported by the 2-dimensional plots of rSASA vs. HB% and HB% vs. F in Fig. 4. In these plots, systems that are characterized by a value of HB% close to 0 still differ significantly in their values of rSASA (ranging from approximately 0.85 to 1.00) and F (ranging from approximately 2.00 to 3.00). Otherwise, the independency between rSASA and F can be demonstrated by imagining a set of gelator molecules that do not self-aggregate in a range of solvents. Here the rSASA will always be valued close to 1. Nevertheless, the value of F can still vary depending on the placement of the gelator molecules in the solvent. For example, a 1-dimensional alignment of the gelator molecules connected to each other through a solvent molecule will have a substantially larger value of F compared to a disperse placement of the gelator molecules, while both cases have an rSASA value close to 1. Although to a lesser extent, this is observable in the 2-dimensional plot of rSASA vs. F for values of rSASA close to 1. As such, while the descriptors rSASA, HB% and F might seem to be linearly correlated for the systems under investigation, they are independent from each other and provide their own unique information. rH shows no apparent linear trend with any of the molecular descriptors. This is because rH is highly dependent on the structure and flexibility of the gelator molecule and only mildly dependent on the aggregation behaviour. Compound 6, for example, has only two free rotatable bonds in its backbone, resulting in an rH value larger than 0.9, independent of the solvent. In contrast, compound 11 contains a large amount of rotatable bonds in its backbone, resulting in an rH value ranging from 0.55 to 0.78 (Table S2†). With this in mind, rH is a descriptor of the flexibility of the molecule under study.When allocating the data points in the graph to the respective experimental result of the gelation test (green = soluble, blue = gel, red = precipitate), it is clear that soluble samples are characterized by a high value of rSASA and F and a low value of HB%, whereas a gel material is characterized by intermediate values of rSASA, F and HB%. Following this reasoning, samples resulting in a precipitate should be characterized by a low value of rSASA and F and a high value of HB% (Fig. 5). While a majority of the data agrees with this trend, there remain several outliers, especially when the sample forms a precipitate. For example, compound 8 in 1-octanol is experimentally classified as a precipitate (Table 1). Nevertheless, from the respective molecular dynamics simulations, relatively high values of rSASA (0.8818) and F (2.74) and a low value of HB% (162.40%) were obtained (Table S2†). This makes prediction of supramolecular gelation by visually inspecting the 2D-plots of the molecular descriptors challenging. However, we believe that the latter can be achieved by increasing the size of the simulation box, increasing the total simulation time and/or using more accurate sampling techniques such as ab initio molecular dynamics. At present, these methods would render the simulation computationally intractable.
Prediction using machine learning methods
In recent years, several machine learning (ML) methods have established themselves in different areas of chemical research.38 For example in targeted drug discovery, where ML can be used to model quantitative structure–activity relationships (QSAR).39,40 Also in theoretical chemistry these methods have shown to assist the interpretation of complex calculations, replace otherwise computationally demanding methods, develop new accurate density functionals or force fields and even predict the electronic charge density and density of states within the framework of density functional theory (DFT).41–45 Moreover, in the field of materials discovery, ML methods have shown their usefulness as evidenced by the earlier referred work of Gupta et al.14,46,47 In this work, two separate ML methods, a decision tree and an artificial neural network (ANN), are used to showcase the ability to predict supramolecular gelation by the proposed molecular descriptors.48 To achieve this challenging goal, the data is partitioned as follows: all data points coming from compound 11 will be used for testing, while the rest is used for training and validating the models (Table S3†). As such, the classification ability of the models will be tested on an unseen compound that can show any of the three responses (gel, soluble, precipitate) depending on the solvent. The models were constructed using JMP Pro version 14.49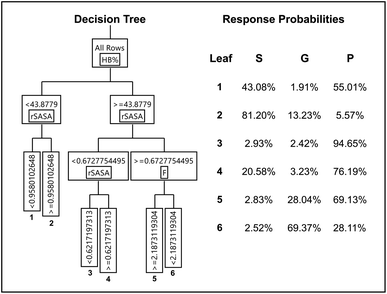 | ||
| Fig. 6 Diagram of the optimized decision tree having 5 nodes (left) and gelation outcome probability reported for the six resulting leaves (right). | ||
A subset of 14 data points, which was randomly stratified according to the gelation response, was used as validation to assess the quality of the DT model and avoid over fitting. The remaining data was used for training (Table S3† specifies which data is used during training, validation and final testing). Multiple measures of fit, such as the balanced accuracy (BA), entropy R2, the misclassification rate (MR), Cohen's kappa (K) and the area under the receiver operating characteristics curve for the three responses (AUROC (S), AUROC (G), AUROC (P)) are summarized for the training set (T), validation set (V) and a hypothetical perfect model (P) and random model (R) in Table 2. A definition for each of these statistical evaluation metrics is provided in the ESI (S23†). From Table 2, we observe that the DT model is adequately fitted as the training and validation data show similar values for all measures. Models that are over fitted are characterized by large discrepancies between the measures of fit obtained from training data and validation data (i.e. excellent measures of fit are obtained on the training set, but poor measures of fit are obtained on the validation set). Additionally, the DT exhibits substantial predictive behaviour, when comparing the measures of fit of the validation set to a perfect and random model.
| Measure | T | V | P | R |
|---|---|---|---|---|
| BA | 0.72 | 0.68 | 1 | 0.33 |
| Entropy R2 | 0.50 | 0.48 | 1 | 0 |
| MR | 0.23 | 0.27 | 0 | 0.67 |
| K | 0.67 | 0.61 | 1 | 0 |
| AUROC (S) | 0.93 | 0.91 | 1 | 0.50 |
| AUROC (G) | 0.92 | 0.86 | 1 | 0.50 |
| AUROC (P) | 0.88 | 0.93 | 1 | 0.50 |
 | ||
| Fig. 7 Optimized artificial neural network consisting out of the input layer, a hidden layer having 5 sigmoid neurons and the output layer. | ||
| Measure | T | V | P | R |
|---|---|---|---|---|
| BA | 0.97 | 1 | 1 | 0.33 |
| Entropy R2 | 0.82 | 0.93 | 1 | 0 |
| MR | 0.03 | 0 | 0 | 0.67 |
| K | 0.96 | 1 | 1 | 0 |
| AUROC (S) | 0.98 | 1 | 1 | 0.50 |
| AUROC (G) | 1 | 1 | 1 | 0.50 |
| AUROC (P) | 0.98 | 1 | 1 | 0.50 |
Upon closer inspection of the gelator molecules that are present in the dataset, it can be observed that compound 6–11 have a more similar molecular structure compared to compound 1–5 (Fig. 2). Therefore, the quality of prediction of the gelation performance of compound 11 with models where compound 1–10 were used during training and validation, might be explained by the high resemblance of 11 with 6–10. To further investigate this, several neural networks were optimized, with the same architecture as the neural network described above, i.e. 1 hidden layer and 5 hyperbolic tangent neurons with the weight of each neuron optimized through a weight decay procedure. But in each neural network all data associated with a certain gelator molecule from the data set was subsequently left out during the training of the model and used for validation, similar to a leave-one-out cross validation approach. Validation statistics of each molecule separately together with the average measures of fit across molecules 1–10 are provided in Table 5. The results of this analysis establish that the models provide the best predictive qualities for compound 6–10, as the lowest observed entropy R2 for these molecules is equal to 0.99 (compound 6). Nevertheless, substantial predictive power is also observed for compound 1–4, with the lowest observed entropy R2 for this set being equal to 0.5 (compound 3). Only the model where compound 5 was left out for validation, shows significantly less predictive prowess with a misclassification rate of 0.20 and an entropy R2 value of 0.09. All-in-all, the validation data on each molecule separately and the average measures of fit across the different neural networks indicate the ability of the descriptors to predict supramolecular gelation of an unknown compound. We should, however, highlight that 5 to 6 data points are associated with each gelator molecule and hence the validation statistics presented in Table 5 are taken over a low amount of data. Additionally, we want to acknowledge that both the decision tree and neural network models validate the predictive ability of the derived molecular descriptors over supramolecular gelation, however for practical purposes, these models would benefit greatly from a substantial increase in training data.
| Molecule | BA | Entropy R2 | MR | K | AUROC (S) | AUROC (G) | AUROC (P) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.96 | 0 | 1 | 1 | 1 | 1 |
| 2 | 1 | 0.90 | 0 | 1 | N.A. | 1 | 1 |
| 3 | 1 | 0.50 | 0 | 1 | 1 | 1 | N.A. |
| 4 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 5 | 0.50 | 0.09 | 0.20 | 0.44 | 0.88 | N.A. | 0.88 |
| 6 | 1 | 0.99 | 0 | 1 | 1 | 1 | 1 |
| 7 | 1 | 1 | 0 | 1 | 1 | N.A. | 1 |
| 8 | 1 | 1 | 0 | 1 | 1 | N.A. | 1 |
| 9 | 1 | 1 | 0 | 1 | 1 | N.A. | 1 |
| 10 | 1 | 1 | 0 | 1 | 1 | N.A. | 1 |
| Average | 0.95 | 0.85 | 0.02 | 0.94 | 0.99 | 1 | 0.99 |
Outlook
While this work showcases that predicting supramolecular gelation based on descriptors derived from molecular dynamics simulations is feasible, there are still a number of factors limiting their applicability. Here, an overview of these factors is given and we discuss how they might be mitigated or overcome in the near future.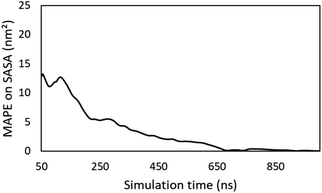 | ||
| Fig. 8 Evolution of the MAPE on the time averaged SASA during the simulation. The average SASA obtained after 1 microsecond is regarded as the true value. | ||
To further increase the reproducibility of the computed values of the descriptors, initial topologies of the simulation were ensured to have the gelator molecules completely dispersed in the solvent, i.e. no atoms of the gelator molecules are closer than 3.0 Å from each other at the start of the simulation. To demonstrate the robustness of this method, simulations of compound 2, 5 and 6 in DMSO, ethanol and acetonitrile respectively, were performed in triplicate. From Table 6 it is concluded that this method provides highly repeatable values for each descriptor, as the deviation between the three simulations for each descriptor is relatively small for all systems that were considered. Especially when comparing the standard errors on the averages with the full range of values that were obtained in this study, the reliability of this method is shown.
| System | Entry | rSASA [0.4–1.0] | rH [0.5–1.0] | HB% [0–1010] | F [0.6–2.9] |
|---|---|---|---|---|---|
| Compound 2 in DMSO | 1 | 0.958 | 0.510 | 0.030 | 2.1 |
| 2 | 0.965 | 0.526 | 0.020 | 2.8 | |
| 3 | 0.963 | 0.535 | 0.000 | 2.7 | |
| Average | 0.962 ± 0.004 | 0.524 ± 0.013 | 0.017 ± 0.015 | 2.6 ± 0.4 | |
| Compound 5 in ethanol | 1 | 0.933 | 0.790 | 2 | 2.26 |
| 2 | 0.928 | 0.787 | 8 | 2.55 | |
| 3 | 0.927 | 0.786 | 7 | 2.54 | |
| Average | 0.929 ± 0.003 | 0.788 ± 0.002 | 6 ± 3 | 2.45 ± 0.16 | |
| Compound 6 in acetonitrile | 1 | 0.912 | 0.970 | 73 | 2.5 |
| 2 | 0.922 | 0.969 | 74 | 2.8 | |
| 3 | 0.907 | 0.970 | 104 | 2.9 | |
| Average | 0.913 ± 0.007 | 0.9698 ± 0.0007 | 84 ± 18 | 2.7 ± 0.2 |
Conclusion
Predicting supramolecular gelation on the basis of computations is regarded as a challenging task. In this study, four molecular dynamic based descriptors with physical relevance to supramolecular gelation are introduced: the relative solvent accessible surface area (rSASA) to evaluate aggregation, the relative end-to-end distance (rH) describing the flexibility and conformational preferences of the molecules, the hydrogen bonding percentage (HB%) to quantify the non-covalent linkage of the gelator molecules, and the shape factor (F) which is a measure for the aggregate's shape. Via two separate machine learning techniques, it was demonstrated that these descriptors can accurately differentiate the gelation response of a set of urea-based gelators as a precipitate, a gel or a fully solubilised sample. To the best of our knowledge, this is the first computational method that addresses the prediction of urea-based supramolecular gelation in both organic solvents as well as in water. We hope that the proposed descriptors can be conceptualized for other types of gelators and will steer the field to discover potential new low molecular weight gelators in the near future.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Tier2 computational resources and services were provided by the Shared ICT Services Centre Funded by the Vrije Universiteit Brussel, the Flemish Supercomputer Center (VSC) and FWO. The Strategic Research Program funding of the VUB is thanked for financial support. F. D. P. also acknowledges the Francqui foundation for a position as “Francqui research professor”. R. V. L. thanks FWO for the PhD fellowship received (1185219N) and Jos L. Teunissen for valuable discussions. M. A. thanks the FWO for a postdoctoral fellowship (12F4416N) and the VUB for financial support.Notes and references
- K. J. Skilling, F. Citossi, T. D. Bradshaw, M. Ashford, B. Kellam and M. Marlow, Soft Matter, 2014, 10, 237–256 RSC.
- B. Escuder, F. Rodríguez-Llansola and J. F. Miravet, New J. Chem., 2010, 34, 1044–1054 RSC.
- S. Ghosh, V. K. Praveen and A. Ajayaghosh, Annu. Rev. Mater. Res., 2016, 46, 235–262 CrossRef CAS.
- E. R. Draper and D. J. Adams, Chem, 2017, 3, 390–410 CAS.
- P. Dastidar, Chem. Soc. Rev., 2008, 37, 2699–2715 RSC.
- A. R. Hirst, I. A. Coates, T. R. Boucheteau, J. F. Miravet, B. Escuder, V. Castelletto, I. W. Hamley and D. K. Smith, J. Am. Chem. Soc., 2008, 130, 9113–9121 CrossRef CAS PubMed.
- R. Van Lommel, L. A. J. Rutgeerts, W. M. De Borggraeve, F. De Proft and M. Alonso, ChemPlusChem, 2020, 85, 267–276 CrossRef CAS.
- M. Raynal and L. Bouteiller, Chem. Commun., 2011, 47, 8271–8273 RSC.
- J. Bonnet, G. Suissa, M. Raynal and L. Bouteiller, Soft Matter, 2015, 11, 2308–2312 RSC.
- D. Rosa Nunes, M. Raynal, B. Isare, P.-A. Albouy and L. Bouteiller, Soft Matter, 2018, 14, 4805–4809 RSC.
- P. Frederix, G. G. Scott, Y. M. Abul-Haija, D. Kalafatovic, C. G. Pappas, N. Javid, N. T. Hunt, R. V. Ulijn and T. Tuttle, Nat. Chem., 2015, 7, 30–37 CrossRef CAS.
- I. P. Moreira, G. G. Scott, R. V. Ulijn and T. Tuttle, Mol. Phys., 2019, 117, 1151–1163 CrossRef CAS.
- P. W. J. M. Frederix, R. V. Ulijn, N. T. Hunt and T. Tuttle, J. Phys. Chem. Lett., 2011, 2, 2380–2384 CrossRef CAS.
- J. K. Gupta, D. J. Adams and N. G. Berry, Chem. Sci., 2016, 7, 4713–4719 RSC.
- D. J. Adams and P. D. Topham, Soft Matter, 2010, 6, 3707–3721 RSC.
- E. Ye, P. L. Chee, A. Prasad, X. Fang, C. Owh, V. J. J. Yeo and X. J. Loh, Mater. Today, 2014, 17, 194–202 CrossRef CAS.
- L. A. J. Rutgeerts, A. H. Soultan, R. Subramani, B. Toprakhisar, H. Ramon, M. C. Paderes, W. M. De Borggraeve and J. Patterson, Chem. Commun., 2019, 55, 7323–7326 RSC.
- K. Yabuuchi, E. Marfo-Owusu and T. Kato, Org. Biomol. Chem., 2003, 1, 3464–3469 RSC.
- N. Zweep, A. Hopkinson, A. Meetsma, W. R. Browne, B. L. Feringa and J. H. van Esch, Langmuir, 2009, 25, 8802–8809 CrossRef CAS PubMed.
- M. George, G. Tan, V. T. John and R. G. Weiss, Chem.–Eur. J., 2005, 11, 3243–3254 CrossRef CAS PubMed.
- A. E. Hooper, S. R. Kennedy, C. D. Jones and J. W. Steed, Chem. Commun., 2016, 52, 198–201 RSC.
- Y. Sang and M. Liu, Mol. Syst. Des. Eng., 2019, 4, 11–28 RSC.
- C. Fang, M. Fantin, X. Pan, K. de Fiebre, M. L. Coote, K. Matyjaszewski and P. Liu, J. Am. Chem. Soc., 2019, 141, 7486–7497 CrossRef CAS.
- S. G. Robinson, Y. Yan, K. H. Hendriks, M. S. Sanford and M. S. Sigman, J. Am. Chem. Soc., 2019, 141, 10171–10176 CrossRef CAS.
- N. Foloppe and J. A. D. MacKerell, J. Comput. Chem., 2000, 21, 86–104 CrossRef CAS.
- V. Zoete, M. A. Cuendet, A. Grosdidier and O. Michielin, J. Comput. Chem., 2011, 32, 2359–2368 CrossRef CAS PubMed.
- M. H. Mamme, S. L. C. Moors, E. A. Mernissi Cherigui, H. Terryn, J. Deconinck, J. Ustarroz and F. De Proft, Nanoscale Adv., 2019, 1, 2847–2856 RSC.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS.
- J. H. van Esch, Langmuir, 2009, 25, 8392–8394 CrossRef CAS PubMed.
- F. Eisenhaber, P. Lijnzaad, P. Argos, C. Sander and M. Scharf, J. Comput. Chem., 1995, 16, 273–284 CrossRef CAS.
- J. van Esch, F. Schoonbeek, M. de Loos, H. Kooijman, A. L. Spek, R. M. Kellogg and B. L. Feringa, Chem.–Eur. J., 1999, 5, 937–950 CrossRef CAS.
- P. Byrne, D. R. Turner, G. O. Lloyd, N. Clarke and J. W. Steed, Cryst. Growth Des., 2008, 8, 3335–3344 CrossRef CAS.
- K. Pandurangan, J. A. Kitchen, S. Blasco, F. Paradisi and T. Gunnlaugsson, Chem. Commun., 2014, 50, 10819–10822 RSC.
- R. B. Best, G. Hummer and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17874 CrossRef CAS.
- W. Burchard, Light Scattering from Polymers, Springer Berlin, Heidelberg, Berlin, Heidelberg, 1983, pp. 1–124 Search PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- Y.-C. Lo, S. E. Rensi, W. Torng and R. B. Altman, Drug Discovery Today, 2018, 23, 1538–1546 CrossRef CAS.
- X. Yang, Y. Wang, R. Byrne, G. Schneider and S. Yang, Chem. Rev., 2019, 119, 10520–10595 CrossRef CAS.
- F. Häse, I. F. Galván, A. Aspuru-Guzik, R. Lindh and M. Vacher, Chem. Sci., 2019, 10, 2298–2307 RSC.
- J. C. Snyder, M. Rupp, K. Hansen, K.-R. Müller and K. Burke, Phys. Rev. Lett., 2012, 108, 253002 CrossRef.
- V. Botu, R. Batra, J. Chapman and R. Ramprasad, J. Phys. Chem. C, 2017, 121, 511–522 CrossRef CAS.
- A. Chandrasekaran, D. Kamal, R. Batra, C. Kim, L. Chen and R. Ramprasad, npj Comput. Mater., 2019, 5, 22 CrossRef.
- O. A. von Lilienfeld, Angew. Chem., Int. Ed., 2018, 57, 4164–4169 CrossRef CAS.
- Y. Liu, T. Zhao, W. Ju and S. Shi, J. Materiomics, 2017, 3, 159–177 CrossRef.
- A. Mansouri Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, J. Am. Chem. Soc., 2018, 140, 9844–9853 CrossRef CAS PubMed.
- E. Alpaydin, Introduction to Machine Learning, MIT Press, Cambridge, 2010 Search PubMed.
- JMP®, Version Pro 14, SAS Institute Inc., Cary, NC, 1989–2019 Search PubMed.
- G. B. Goh, N. O. Hodas and A. Vishnu, J. Comput. Chem., 2017, 38, 1291–1307 CrossRef CAS PubMed.
- Classically, in a k-fold cross validation the data set is randomly divided into k-subsets. Next, for each subset a model is made where the kth subset is used for validation and the rest of the data as training data. As such k models are built. The validation performance statistics are then determined by averaging over the k models. In the JMP software, however, the model that shows the best performance for a certain fold k is chosen as the final model upon which the validation metrics are based.
- S. Grimme and P. R. Schreiner, Angew. Chem., Int. Ed., 2018, 57, 4170–4176 CrossRef CAS PubMed.
- C. Kutzner, S. Páll, M. Fechner, A. Esztermann, B. L. de Groot and H. Grubmüller, J. Comput. Chem., 2019, 40, 2418–2431 CrossRef CAS PubMed.
- K. Sugisaki, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, ACS Cent. Sci., 2019, 5, 167–175 CrossRef CAS PubMed.
- A. Tropsha, Mol. Inf., 2010, 29, 476–488 CrossRef CAS PubMed.
- J. Jaworska, N. Nikolova-Jeliazkova and T. Aldenberg, Altern. Lab. Anim., 2005, 33, 445–459 CrossRef CAS.
- R. P. Sheridan, B. P. Feuston, V. N. Maiorov and S. K. Kearsley, J. Chem. Inf. Comput. Sci., 2004, 44, 1912–1928 CrossRef CAS.
- I. Sushko, S. Novotarskyi, R. Körner, A. K. Pandey, V. V. Kovalishyn, V. V. Prokopenko and I. V. Tetko, J. Chemom., 2010, 24, 202–208 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc00129e |
| This journal is © The Royal Society of Chemistry 2020 |