Mildly regulated intrinsic faradaic layer at the oxide/water interface for improved photoelectrochemical performance

Abstract

Metal oxides are widely used in different fields, including photoelectrocatalysis, photocatalysis, dye-sensitized solar cells, photoinduced superhydrophilicity and so on. It is well-known that there are intrinsic hydrated layers on the surfaces of metal oxides in ambient air or the electrolyte. Generally, interface layers between metal oxides and solutions have significant effects on the performances in these applications. However, the exact roles of the intrinsic hydrated layers are still unclear. In this study, taking TiO₂ and Fe₂O₃ as model materials, we propose a mild heat treatment to increase the hydroxyl concentration in the hydrated surface layers of the oxides, which improves their photoelectrochemical performance remarkably. Moreover, we find that the heat-regulated hydrated layer plays the role of a hole transfer mediator between oxides and the electrolyte, which can accelerate both interface charge collection and oxygen evolution reaction kinetics in acidic solution. The new insights into the intrinsic hydrated interface layer on oxides can offer guidance not only in photoelectrocatalysis, but also in the other applications mentioned above.

---

1 Introduction

Metal oxides are widely used in different fields, including photoelectrocatalysis,¹ photocatalysis,² dye-sensitized solar cells,³ photoinduced superhydrophilicity⁴ and so on. In these applications, the interface charge transfer between metal oxides/solution has significant effects on the performance.^5–7 For example, in previous studies, some intermediate layers, such as Ni(OH)₂ and CoPi, were introduced at the interface between oxides and the electrolyte to improve the photoelectrocatalytic performance.^8,9 These intermediate layers include variable valence metal ions. When the semiconductor photoanodes are excited under illumination, the metal ions in the intermediate layers will be oxidized by photo-generated holes very fast, and simultaneously release protons into the electrolyte to maintain electrical neutrality. This process is also reversible by controlling the applied potential, which is a faradaic reaction.¹⁰ Therefore, the intermediate layers can be considered as extrinsic faradaic layers.¹¹ The faradaic layers can accelerate both interface charge collection and oxygen evolution reaction (OER) kinetics and improve the performance of a photoelectrode.^12–15

Moreover, some recent studies have suggested that there is an intrinsic hydrated layer on the surface of metal oxide in ambient air or an electrolyte,^6,16–19 which also has significant effects on interface charge separation and transfer.^20–22 Is it possible that the intrinsic hydrated layer plays the same role with an extrinsic faradaic layer? In fact, the effects of the intrinsic hydrated layer on photoelectrochemical performance are controversial. Some results suggest that the hydrated interface layer passivates the surface states or provides a new charge transfer pathway to improve the performance.^20,22 However, other studies argue that the hydrated layer acts as recombination centers, which decreases the photoelectrochemical performance.^23–25 These inconsistent results possibly come from harsh post-treatment methods on photoelectrodes used in previous studies, which change not only the hydrated interface layer but also the bulk of photoelectrodes. In order to understand the real role of a hydrated interface layer, it is desirable to develop a new method that only changes the intrinsic hydrated interface layer of metal oxide.

In this work, taking TiO₂ and Fe₂O₃ as model materials, we proposed a facile low-temperature heat treatment (200 °C) to regulate the hydrated surface layers of the two metal oxides. The low-temperature heat treatment only changed the hydrated surface layer, not the bulk, because the heat treatment conditions were much milder than the previous ones.²⁰ Moreover, TiO₂ and Fe₂O₃ were used as photoanodes for solar water splitting and their performance increased significantly after the heat treatment. Our study suggests that the regulated hydrated layer played the same role as the extrinsic faradaic layer mentioned above. Therefore, the hydrated interface layer can also be considered an intrinsic faradaic layer. Different from previous studies, we propose new insights into the role of a hydrated interface layer, which are significant for mechanistic study and performance improvement. Moreover, many reports suggest that there are also (hydro)oxide surface layers on non-oxides in ambient air or aqueous solution.^26,27 Therefore, this study can also offer guidance to improve the performance of a non-oxide photoelectrode.

2 Results and discussion

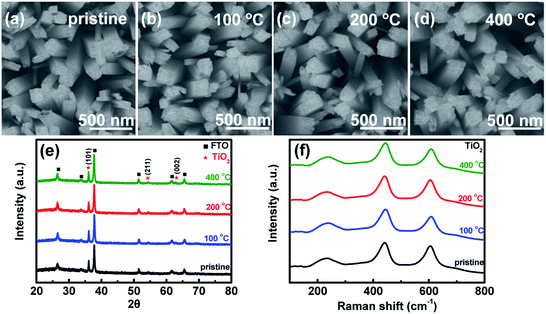
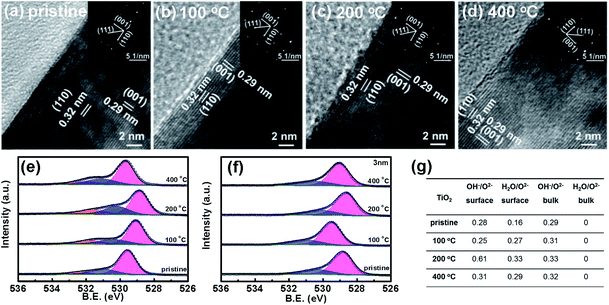
TiO₂ and Fe₂O₃ films were deposited on FTO substrates, prepared by the hydrothermal method and calcined at 450 °C and 675 °C in air, respectively.^28,29 In order to investigate the effect of heat-treatment temperatures on the surface layer, the samples were further calcined in air at different temperatures (100 °C, 200 °C and 400 °C) for 30 min. The SEM images of TiO₂ samples before and after the heat treatment are shown in Fig. 1a–d, respectively. A sample before heat treatment is denoted as pristine. The SEM images of Fe₂O₃ are also shown in Fig. S1.† TiO₂ shows a dispersed nanorod array with an average diameter of about 150 nm. After the heat treatment, the morphologies of TiO₂ and Fe₂O₃ do not change obviously. Fig. 1e indicates the XRD patterns of the TiO₂ samples. The strongest peak corresponds to the (101) plane of rutile TiO₂ (JCPDS 21-1276). From the XRD patterns, no phase changes or other new phases are observed after the heat treatment. Raman spectroscopy is more sensitive to the surface of materials. Therefore, Raman spectroscopy is also used to investigate the samples and the results are shown in Fig. 1f. The characteristic peaks of rutile TiO₂ (236, 444 and 610 cm⁻¹) are observed.³⁰ The Raman peaks do not change after the heat treatment, which is in good agreement with the XRD results. The SEM (Fig. S1†), XRD and Raman results (Fig. S2†) of Fe₂O₃ also suggest that the morphologies and phases of Fe₂O₃ do not change after the heat treatment either.

Fig. 1 Scanning electron microscopy (SEM) images of TiO₂ before (a) and after heat treatment in air at 100 °C (b), 200 °C (c) and 400 °C (d); X-ray diffraction (XRD) patterns (e) and Raman spectra (f) of TiO₂ before and after heat treatment at different temperatures.

A transmission electron microscope (TEM) can be used to investigate microcosmic changes of materials. Therefore, a TEM is also used to further characterize the TiO₂ samples before and after the heat treatment and the results are shown in Fig. 2. Lattice spacings of 0.32 nm and 0.29 nm are assigned to the (110) and (001) of rutile TiO₂, respectively. Clear electron diffraction (ED) patterns are observed for the sample before and after heat treatment, which suggests that TiO₂ samples are single crystal nanorods. A second ED pattern is observed in the sample before the heat treatment, which possibly comes from some overlapping grains. The ED patterns of all the samples after heat treatment are the same, which further confirms that the bulk of TiO₂ does not change after the heat treatment. From the TEM images, the surface of TiO₂ nanorods does not change obviously after the heat treatment at different temperatures. Irregular morphologies and agglomerated grains are observed on the Fe₂O₃ samples (see Fig. S3†). It is difficult to obtain useful information by comparing the TEM images of the Fe₂O₃ before and after the heat treatment. Therefore, the TEM images of Fe₂O₃ calcined at different temperatures are not shown. According to the above results and analysis, the bulk properties of TiO₂ and Fe₂O₃ samples do not change after the heat treatment.

Fig. 2 Transmission electron microscope (TEM) images of TiO₂ before (a) and after heat treatment in air at 100 °C (b), 200 °C (c), and 400 °C (d) and the corresponding electron diffraction (ED) patterns (inset); X-ray photoelectron spectroscopy (XPS) results of O 1s on the surface (e) and in the bulk (3 nm depth) (f) of TiO₂ before and after heat treatment at different temperatures. The red, blue and yellow peaks are assigned to lattice O²⁻, lattice OH⁻ and adsorbed H₂O molecules, respectively; a table of the XPS ratio of lattice OH⁻ and chemically adsorbed H₂O to lattice O²⁻ on the surface and in the bulk (3 nm depth) of TiO₂ (g).

In order to analyze the composition of the surface layer, X-ray photoelectron spectroscopy (XPS) is used to characterize the TiO₂ and Fe₂O₃ thin films before and after the heat treatment. Fig. 2e and S4† indicate the binding energies of O 1s and Ti 2p of the surface of TiO₂, respectively. Only Ti⁴⁺ and not Ti³⁺ peaks are observed on the surfaces of the samples after the heat treatment. Three binding energies of O 1s (529.6 eV, 530.9 and 532.1 eV) are observed on the surfaces of TiO₂ samples before heat treatment (see Fig. 2e), which are assigned to the lattice O²⁻, lattice OH⁻ and adsorbed H₂O molecules, respectively.^31–33 A partially hydrated surface layer is observed, which is in good agreement with some previous studies.³⁴ The surface layer is hydroxylated, which comes from the reaction between the surface of oxides and water in ambient air. Moreover, some H₂O molecules are chemically adsorbed on the hydroxylated surface layer. The binding energies of bulk O 1s are also measured for the samples at a depth of 3 nm by Ar⁺ etching and the results are shown in Fig. 2f; no adsorbed H₂O molecules are observed in the bulk of TiO₂.

The ratios of the three O species on the surface change remarkably after the heat treatment, but do not in the bulk. The quantitative ratios of lattice OH⁻ and adsorbed H₂O molecules to lattice O²⁻ on the surface and in the bulk of TiO₂ are calculated and the results are shown in Fig. 2g. After the heat treatment at 100 °C, the ratio of OH⁻ to O²⁻ on the surface of the TiO₂ sample decreases from 0.28 to 0.25, but remarkably increases to 0.61 on the sample at 200 °C, and then decreases to 0.31 when the temperature is further increased to 400 °C. The ratio of adsorbed H₂O to O²⁻ on the surface increases from 0.16 to 0.33 when increasing the heat-treatment temperature to 200 °C and then decreases to 0.29 when further increasing the temperature to 400 °C. However, the ratio of OH⁻ to O²⁻ in the bulk TiO₂ increases from 0.29 to 0.33 after the treatment. The contents of surface OH⁻ and adsorbed H₂O are the highest on the sample at 200 °C. The bulk shows much less change than the surface. The XPS peak of O 1s in carbonate is usually near that of lattice OH⁻, which would affect the hydroxylation coverage analysis. In order to exclude the effects of carbonate, the XPS spectrum of C 1s in TiO₂ is shown in Fig. S5.† The results suggest that the C 1s peak (288.5 eV) for carbonate does not change obviously after the heat treatment at 200 °C.^35,36 Therefore, the change of the O 1s peak comes from OH⁻ concentration variation in the surface hydrated layer, and not from the carbonate. The binding energy shift of the samples after heat treatment is not discussed here since the calibration method of binding energy is controversial.³⁷ The heat-treatment process is also examined by TGA analysis (Fig. S6†). The first mass loss stage of TiO₂ that extends from room temperature to 300 °C can be ascribed to the desorption of physically and chemically adsorbed water. The second distinct mass loss from 300 °C to 350 °C possibly comes from the removal of surface hydroxyl groups.^38–40 For Fe₂O₃, the three mass loss stages are ascribed to the desorption of physically and chemically adsorbed water and hydroxyl, respectively.⁴¹ From the TGA results of TiO₂ and Fe₂O₃, the desorption of hydroxyl occurs at a temperature over 200 °C, and the OH⁻ content decreases after heat treatment at higher temperature (400 °C). Therefore, it is reasonable that the sample after heat treatment at 200 °C has the highest OH⁻ content. Both the XPS and TGA results suggest that the surface changes come from the reaction of the oxide samples with water. Therefore, the heat treatment leads to the increase of lattice OH⁻ and adsorbed H₂O in the hydrated surface layer of TiO_2. Moreover, we also characterize the surface changes of TiO₂ by the contact angle method and the results are shown in Fig. S7.† After the heat treatment at 200 °C, the contact angle of TiO₂ decreases, which further supports the increase of the surface hydroxyl concentration after 200 °C heat treatment.^42,43 Moreover, the ratios of OH⁻ to O²⁻ on the surface and in the bulk of Fe₂O₃ indicate similar changes to those in TiO₂ after heat treatment (see Fig. S8†). Therefore, the heat treatment increases the hydration degree of the surface layer on the metal oxides.

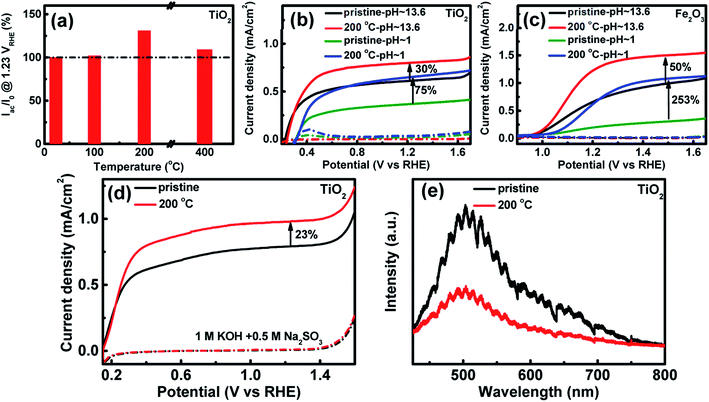
In order to investigate the effects of the heat-treated hydrated layer of TiO₂ and Fe₂O₃ on the photoelectrochemical performance, TiO₂ and Fe₂O₃ before and after heat treatment at different temperatures are used as photoanodes and the photocurrents @1.23 V_RHE are measured in 1 M KOH (pH ∼ 13.6). The ratios of the photocurrent of TiO₂ after to before the heat treatment are calculated and shown in Fig. 3a. The sample at 100 °C indicates similar photocurrent to that of the pristine sample. The photocurrent increases by 30% at 200 °C, but the increase is only 9% at 400 °C. The TiO₂ sample at 200 °C shows the highest photocurrent among these samples. Fig. S9† indicates the photocurrent stability of the sample at 200 °C at 1.23 V_RHE, which suggests that the photocurrent increase is stable after the heat treatment. A similar photocurrent variation trend is observed on an Fe₂O₃ photoanode (see Fig. S10a†). The heat treatment changes both lattice OH⁻ and adsorbed H₂O molecules on the surface (see Fig. S8a†). However, the photocurrent only shows a similar variation trend for OH⁻, and not the adsorbed H₂O molecules on the surface of Fe₂O₃. Therefore, the change of the surface OH⁻ and not the adsorbed H₂O molecules contributes to the improved photoelectrochemical performance. The surface OH⁻ concentration is higher, and the photocurrent density is higher. Fig. 3b displays the CV curves of TiO₂ at 200 °C in aqueous solution with different pHs in the dark and under illumination. The sample exhibits a much lower photocurrent and more positive onset potential in the acidic electrolyte than in the basic electrolyte. Similar results have also been reported in previous studies.²⁵ After the heat treatment at 200 °C, the photocurrent of TiO₂ increases by 75% in the acidic solution, much higher than the increase in the basic solution (30%). The results are further verified from the incident-photon-to-current-conversion efficiency (IPCE) spectra (Fig. S11†). A more obvious effect of pH on the photocurrent increase is observed on Fe₂O₃ (see Fig. 3c): the photocurrent at 1.5 V_RHE increases by 253% in the acidic solution, which is also much higher than that in the basic solution (50%).

Fig. 3 Photocurrent ratio of TiO₂ at different heat-treatment temperatures to a pristine sample at 1.23 V_RHE (a); I_ac is the photocurrent of the samples after heat treatment and I₀ is the photocurrent of the pristine sample; photocurrent–potential curves of TiO₂ (b) and Fe₂O₃ (c) before and after heat treatment at 200 °C in electrolytes with different pHs, 1 M KOH (pH ∼ 13.6) and 0.1 M HClO₄ (pH ∼ 1), respectively; the solid line and dashed line correspond to the photocurrent and dark current, respectively; photocurrent–potential curves of TiO₂ before and after the heat treatment at 200 °C in 1 M KOH with 0.5 M Na₂SO₃ as the hole sacrificial agent (d); photoluminescence (PL) spectra of the TiO₂ before and after the heat treatment at 200 °C (e).

In order to investigate the mechanism of the improved performance after the heat treatment, the CV curves for the electrolyte with the hole sacrificial agent Na₂SO₃ were measured and the results are shown in Fig. 3d. The photocurrent at 1.23 V_RHE on TiO₂ in the electrolyte with the hole sacrificial agent increases by 23% after the heat treatment at 200 °C. The SO₃²⁻ ions can consume photo-generated holes very fast, which suggests that all the holes that reach the hydrated interface layer can be injected into the electrolyte to oxidize SO₃²⁻.⁴⁴ Therefore, the photocurrent in the hole sacrificial agent only depends on the density and separation efficiency of photo-generated carriers.^45,46 The optical absorption spectra (Fig. S12†) of TiO₂ samples before and after the heat treatment at 200 °C were measured. The absorption at 300–400 nm contributes to the photocurrent of TiO₂, which does not change obviously after the heat treatment at 200 °C. The effect of the heat treatment on the density of photo-generated carriers is negligible. Therefore, the higher photocurrent of TiO₂ after treatment in the electrolyte with Na₂SO₃ mainly comes from the improved separation efficiency, which is further confirmed using the PL spectra (Fig. 3e). The PL decreases after the heat treatment at 200 °C. The XPS data (Fig. S4†) suggest that there are no oxygen vacancies on the surface. According to the literature, it is possible that the PL peak comes from carrier recombination in the bulk or subsurface oxygen vacancies.^34,47,48 The surface hydrated layer decreases carrier recombination in the bulk/subsurface by transferring the carriers from the bulk to the hydrated interface layer very fast. The photocurrent increase (23%) in the electrolyte with the hole sacrificial agent is similar to that (30%) in the basic solution, so the photocurrent increase in the basic solution mainly comes from improved interface charge collection by decreasing carrier recombination. Moreover, the photocurrent increase in the acidic solution is 75% at 1.23 V_RHE, much higher than the increase in the basic solution. It is likely that the photocurrent increase in the acidic solution does not arise only from the improved interface charge collection. There are still other reasons for the improved performance in the acidic electrolyte. Some previous studies suggested that the pH of the electrolyte can influence the oxygen evolution reaction kinetics.⁴⁹ Therefore, it is possible that the surface hydroxylation can also promote OER kinetics in the acidic solution.

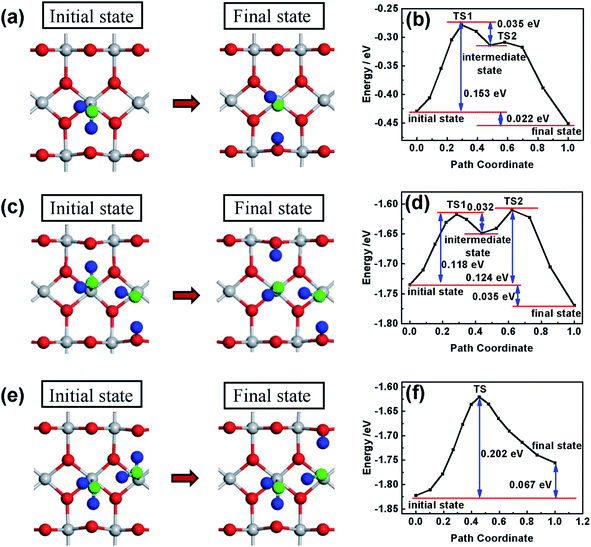
Different from that in the basic solution, H₂O molecules and not OH⁻ are adsorbed on the surface of the oxides in the acidic solution. In order to investigate the effect of the surface hydroxylation on OER kinetics in the acidic solution, the water molecule dissociation process on the surface of TiO₂ is simulated by DFT calculation and the results are shown in Fig. 4. H₂O molecules are chemically adsorbed on the surface of bare TiO₂ as the initial state, with water dissociation as the final state (see Fig. 4a and b). Though the water dissociation reaction is exothermic, there is an energy barrier height of about 0.153 eV, which suggests that activation energy is necessary to dissociate H₂O molecules on the surface of TiO₂. The results can explain the OH⁻ content increase after heat treatment only at temperatures higher than 100 °C (see Fig. 2). The reaction of water and the TiO₂ surface occurs following the equation TiO₂ + xH₂O → TiO_2−x(OH)_2x. The low-temperature heat treatment can increase the content of OH⁻ in the hydrated surface layer by activating the water dissociation reaction. In previous studies, an electrochemical method (treatment energy of about 1 eV) was usually used to treat a TiO₂ photoelectrode to achieve surface hydroxylation,^20,22 which caused decreased photocurrent near the onset potential. However, no decreased photocurrent near the onset potential is observed after the heat treatment, possibly because the heat treatment is mild and does not change the bulk. On the surface with the first water dissociation, the dissociation of the second adsorbed water molecule is also exothermic (see Fig. 4c and d). There are two important variations in this case: the first is a decrease in the largest energy barrier from 0.153 to 0.118 eV, indicating that water molecules dissociate more easily; the second is that the reaction energy increases from 0.022 to 0.035 eV, indicating that the dissociation state is more stable and the reverse reaction of water decomposition occurs with more difficulty. However, if the first adsorbed water molecule on the surface of TiO₂ is not dissociated, the dissociation of the second adsorbed water molecule is more difficult, because of the higher energy barrier (0.202 eV) (see Fig. 4e and f). Most importantly, the dissociation of the second water molecule turns into an endothermic reaction, indicating that the dissociation state is relatively unstable and the reverse reaction of water decomposition easily occurs. In the acidic solution, H₂O reacting with the surface of oxides is the first step of water oxidation, which is significant for OER kinetics.⁵⁰ Therefore, the heat treatment can dissociate water molecules and accelerate OER kinetics.

Fig. 4 A slab model of the rutile TiO₂ (110) surface with H₂O adsorbed on Ti atoms. Grey and red spheres represent the oxygen and titanium atoms from TiO₂, respectively. Blue and green spheres represent hydrogen and oxygen from H₂O, respectively. The initial and final states of the first H₂O molecule dissociated on the TiO₂ (110) surface (a) and the corresponding reaction path (b); the initial and final states of the second H₂O molecule dissociated on the TiO₂ (110) surface with the dissociated H₂O molecule (c) and the corresponding reaction path (d); the initial and final states of the second H₂O molecule dissociated on the TiO₂ (110) surface with non-dissociated H₂O (e) and the corresponding reaction path (f).

According to the above results and analysis, a possible mechanism for the improved performance after the heat treatment is proposed in Fig. 5. After the heat treatment, some H₂O molecules are dissociated on the surface of TiO₂, which leads to a higher OH⁻ content in the hydrated surface layer. When TiO₂ is immersed into the electrolyte for photoelectrocatalytic water splitting, a two-step successive interface charge transfer process will occur (see Fig. 5). The first step is the collection of photo-generated holes by the hydrated interface layer from the bulk of TiO₂, according to the following reaction:^50–52 Ti⁺⁴O_2−x(OH)2x + h⁺ + H₂O ⇌ Ti⁺⁴O⁻¹O_1−x(OH)_2x+1 + H⁺. The second step is the transfer of holes from the oxidized hydrated interface layer to H₂O or OH⁻ to produce oxygen. In the first step, when the hydrated interface layer is oxidized by the photo-generated holes, it simultaneously releases H⁺ into the electrolyte to maintain the electrical neutrality. The coupled electron and ion transfer process is fast and reversible and is called a faradaic reaction.¹⁰ For an extrinsic faradaic layer (Ni(OH)₂ or CoPi) on a photoanode, metal ions are usually oxidized and their valence states become higher under illumination.⁵³ However, herein, the valence state of Ti⁴⁺ in the hydrated interface layer does not change, but the valence state of O²⁻ becomes higher (Ti⁺⁴–O⁻¹˙ species). And for Fe₂O₃, a faradaic reaction, Fe⁺³OOH + h⁺ ⇌ Fe⁺⁴O₂ + H⁺, occurs through the oxidation of Fe³⁺ in the hydrated layer to Fe⁴⁺.^54,55 In the faradaic reaction, the transfer rate of ions is much slower than that of electrons. Therefore, the ion transfer is a rate-limiting step in the faradaic reaction.⁵⁶ After the heat treatment, the OH⁻ in the hydrated interface layer becomes higher, which can make ions permeate more easily and improve the collection efficiency of photo-generated holes from the bulk of TiO₂.^14,57 Therefore, the heat-regulated interface layer can improve the first step of interface charge transfer, which is independent of the pH of the electrolyte. For the second step of interface charge transfer, different OER kinetics processes occur in the basic and acidic solutions, respectively. In the basic solution, OH⁻ is oxidized (see Fig. 5a), which is favorable kinetically.⁵⁸ Therefore, the heat treatment mainly improves the first and not the second step of interface charge transfer in the basic solution. However, in the acidic solution, the H₂O molecule is oxidized (see Fig. 5b), which is slow and should be initiated by water dissociation (see Fig. 4). The heat-treated interface layer with higher OH⁻ can lower the activation energy of water dissociation and accelerate OER kinetics. Therefore, the heat treatment enhances both the first (interface charge separation) and the second step (OER kinetics) of the interface charge transfer in the acidic solution, just like the role of an extrinsic faradaic layer.¹² Therefore, the photocurrent increase in the acidic solution is much higher than that in the basic solution.

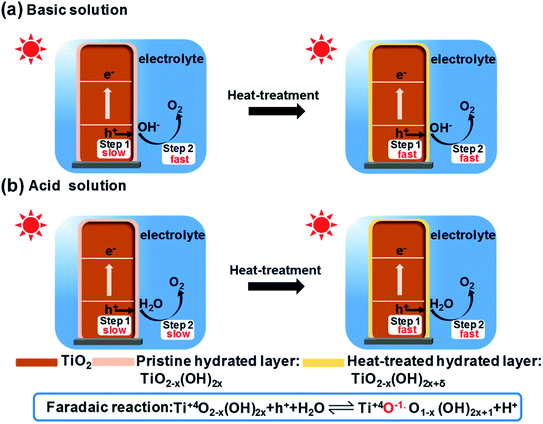Fig. 5 A possible mechanism of improved performance of an oxide photoelectrode after the heat treatment in basic (a) and acidic solutions (b), respectively.

3 Conclusions

We propose a mild heat-treatment method to regulate the intrinsic hydrated layer of TiO₂ and Fe₂O₃ and improve their photoelectrochemical performance remarkably. The heat treatment does not change the bulk, but increases the OH⁻ content in the hydrated layer on the surface of the oxide samples. Moreover, the effects of the intrinsic hydrated layer on the photoelectrochemical properties are investigated in basic and acidic solutions. In the basic solution, the regulated hydrated layer only increases the interface charge collection. However, in the acidic solution, the regulated hydrated layer improves both interface charge collection and OER kinetics. The regulated hydrated layer plays a role as a hole mediator between the oxide and electrolyte, just like an extrinsic faradaic layer. Therefore, we propose a new concept of an intrinsic faradaic layer on the surface of oxides. The hydrated layers exist on the surfaces of not only oxides, but also non-oxides. Therefore, the new insights into the intrinsic faradaic layer can also offer guidance to improve the performance of non-oxide photoelectrodes. Moreover, the concept of the intrinsic hydrated layer possibly has significant effects on interface charge transfer in other fields, such as photocatalysis, dye-sensitized solar cells, photoinduced superhydrophilicity and so on.

Author contributions

W. L. supervised the project, proposed the concept and designed the experiments. Z. Y. carried out sample preparation, characterization and electrochemical measurements; Z. Z. carried out the DFT calculation. W. L. and Z. Y. analyzed the data and wrote the paper. All the authors discussed the results and gave comments on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Prof. Bin Liu and Ms. Yimeng Sang at Nanjing University for their help in photoluminescence (PL) spectroscopy characterization of samples. This work was supported by the National Key R&D Program of China (2017YFE0120700), the National Natural Science Foundation of China (21875105), the National Scientific Instrument Development Major Project of the National Natural Science Foundation of China (51627810), and the Fundamental Research Funds for the Central Universities (021314380139 and 021014380115).

References

1. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
2. X. Chen, L. Liu, P. Y. Yu and S. S. Mao, Science, 2011, 331, 746–750.
3. B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740.
4. R. Wang, K. Hashimoto, A. Fujishima, M. Chikuni, E. Kojima, A. Kitamura, M. Shimohigoshi and T. Watanabe, Nature, 1997, 338, 431–432.
5. D. Wang, F. Niu, M. J. Mortelliti, M. V. Sheridan, B. D. Sherman, Y. Zhu, J. R. McBride, J. L. Dempsey, S. Shen, C. J. Dares, F. Li and T. J. Meyer, Proc. Natl. Acad. Sci. U. S. A., 2019, 201821687.
6. K. Onda, B. Li, J. Zhao, K. D. Jordan, J. Yang and H. Petek, Science, 2005, 308, 1154–1158.
7. A. Fujishima, X. Zhang and D. Tryk, Surf. Sci. Rep., 2008, 63, 515–582.
8. K. Nie, S. Kashtanov, Y. Wei, Y. S. Liu, H. Zhang, M. Kapilashrami, Y. Ye, P. A. Glans, J. Zhong, L. Vayssieres, X. Sun and J. Guo, Nano Energy, 2018, 53, 483–491.
9. L. Han, S. Dong and E. Wang, Adv. Mater., 2016, 28, 9266–9291.
10. Y. Shao, M. F. El-Kady, J. Sun, Y. Li, Q. Zhang, M. Zhu, H. Wang, B. Dunn and R. B. Kaner, Chem. Rev., 2018, 118, 9233–9280.
11. X. Chen, K. Zhu, P. Wang, G. Sun, Y. Yao, W. Luo and Z. Zou, iScience, 2020, 23, 100949.
12. F. A. L. Laskowski, M. R. Nellist, J. Qiu and S. W. Boettcher, J. Am. Chem. Soc., 2019, 141, 1394–1405.
13. T. W. Kim and K. S. Choi, Science, 2014, 343, 990–994.
14. F. Lin and S. W. Boettcher, Nat. Mater., 2014, 13, 81–86.
15. J. Y. Kim, D. H. Youn, K. Kang and J. S. Lee, Angew. Chem., Int. Ed., 2016, 55, 10854–10858.
16. H. Tamura, A. Tanaka, K. Mita and R. Furuichi, J. Colloid Interface Sci., 1999, 209, 225–231.
17. Z. T. Wang, J. C. Garcia, N. A. Deskins and I. Lyubinetsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 081402.
18. Z. Jakub, F. Kraushofer, M. Bichler, J. Balajka, J. Hulva, J. Pavelec, I. Sokolović, M. Müllner, M. Setvin, M. Schmid, U. Diebold, P. Blaha and G. S. Parkinson, ACS Energy Lett., 2019, 4, 390–396.
19. R. Martinez-Casado, G. Mallia, N. M. Harrison and R. Pérez, J. Phys. Chem. C, 2018, 122, 20736–20744.
20. H. Zhu, M. Zhao, J. Zhou, W. Li, H. Wang, Z. Xu, L. Lu, L. Pei, Z. Shi, S. Yan, Z. Li and Z. Zou, Appl. Catal., B, 2018, 234, 100–108.
21. D. Zhang, M. Yang and S. Dong, J. Phys. Chem. C, 2015, 119, 1451–1456.
22. B. H. Meekins and P. V. Kamat, ACS Nano, 2009, 3, 3437–3446.
23. Y. Li and H. Chen, J. Mater. Chem. A, 2016, 4, 14974–14977.
24. S. Jiang, Y. Li, X. Zhang and Y. Li, Catal. Today, 2016, 259, 360–367.
25. M. Pyeon, T.-P. Ruoko, J. Leduc, Y. Gönüllü, M. Deo, N. V. Tkachenko and S. Mathur, J. Mater. Res., 2018, 33, 455–466.
26. D. J. Michalak, S. R. Amy, D. Aureau, M. Dai, A. Estève and Y. J. Chabal, Nat. Mater., 2010, 9, 266–271.
27. M. Sato, Y. Imazeki, K. Fujii, Y. Nakano and M. Sugiyama, J. Chem. Phys., 2019, 150, 154703.
28. X. Xia, J. Luo, Z. Zeng, C. Guan, Y. Zhang, J. Tu, H. Zhang and H. J. Fan, Sci. Rep., 2012, 2, 981.
29. T. Wang, W. Luo, X. Wen, Z. Zou and W. Huang, ChemNanoMat, 2016, 2, 652–655.
30. D. A. H. Hanaor and C. C. Sorrell, J. Mater. Sci., 2011, 46, 855–874.
31. X. Lu, G. Wang, T. Zhai, M. Yu, J. Gan, Y. Tong and Y. Li, Nano Lett., 2012, 12, 1690–1696.
32. J. G. Yu, H. G. Yu, B. Cheng, X. J. Zhao, J. C. Yu and W. K. Ho, J. Phys. Chem. B, 2003, 107, 13871–13879.
33. W. Luo, C. Jiang, Y. Li, S. A. Shevlin, X. Han, K. Qiu, Y. Cheng, Z. Guo, W. Huang and J. Tang, J. Mater. Chem. A, 2017, 5, 2021–2028.
34. Y. Zhang, Z. Xu, G. Li, X. Huang, W. Hao and Y. Bi, Angew. Chem., Int. Ed., 2019, 58, 14229–14233.
35. F. Dong, Q. Li, Y. Sun and W. K. Ho, ACS Catal., 2014, 4, 4341–4350.
36. M. Kang, E. D. Park, J. M. Kim and J. E. Yie, Appl. Catal., A, 2007, 327, 261–269.
37. G. Greczynski and L. Hultman, Angew. Chem., Int. Ed., 2020, 59, 5002–5006.
38. G. Li, L. Li, J. Boerio-Goates and B. F. Woodfield, J. Am. Chem. Soc., 2005, 127, 8659–8666.
39. N. G. Petrik and G. A. Kimmel, J. Phys. Chem. C, 2009, 113, 4451–4460.
40. M. I. Said, J. Alloys Compd., 2020, 819, 152976.
41. D. Walter, Thermochim. Acta, 2006, 445, 195–199.
42. K. Liu, M. Cao, A. Fujishima and L. Jiang, Chem. Rev., 2014, 114, 10044–10094.
43. Z. Luo, H. Zhang, Y. Yang, X. Wang, Y. Li, Z. Jin, Z. Jiang, C. Liu, W. Xing and J. Ge, Nat. Commun., 2020, 11, 1116.
44. Y. Kuang, Q. Jia, H. Nishiyama, T. Yamada, A. Kudo and K. Domen, Adv. Energy Mater., 2016, 6, 1501645.
45. H. Dotan, K. Sivula, M. Grätzel, A. Rothschild and S. C. Warren, Energy Environ. Sci., 2011, 4, 958–964.
46. Q. Meng, B. Zhang, L. Fan, H. Liu, M. Valvo, K. Edström, M. Cuartero, R. Marco, G. A. Crespo and L. Sun, Angew. Chem., Int. Ed., 2019, 131, 19203–19209.
47. A. Samokhvalov, J. Phys. Chem. C, 2017, 121, 21985–21994.
48. B. Santara, P. K. Giri, K. Imakita and M. Fujii, J. Phys. D: Appl. Phys., 2014, 47, 215302.
49. Y. Liu, F. Le Formal, F. Boudoire and N. Guijarro, ACS Appl. Energy Mater., 2019, 2, 6825–6833.
50. R. Nakamura and Y. Nakato, J. Am. Chem. Soc., 2007, 129, 11569–11579.
51. R. Nakamura and Y. Nakato, J. Am. Chem. Soc., 2004, 126, 1290–1298.
52. P. Salvador, Prog. Surf. Sci., 2011, 86, 41–58.
53. G. Wang, Y. Ling, X. Lu, T. Zhai, F. Qian, Y. Tong and Y. Li, Nanoscale, 2013, 5, 4129.
54. T. Takashima, K. Ishikawa and H. Irie, J. Phys. Chem. C, 2016, 120, 24827–24834.
55. B. Klahr and T. Hamann, J. Phys. Chem. C, 2014, 118, 10393–10399.
56. Y. S. Kim, S. Kriegel, K. D. Harris, C. Costentin, B. Limoges and V. Balland, J. Phys. Chem. C, 2017, 121, 10325–10335.
57. G. Tocci and A. Michaelides, J. Phys. Chem. Lett., 2014, 5, 474–480.
58. F. Ambrosio, J. Wiktor and A. Pasquarello, ACS Energy Lett., 2018, 3, 829–834.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01052a

---