Open Access Article
Open Access ArticleDNA scaffold supports long-lived vibronic coherence in an indodicarbocyanine (Cy5) dimer†
Sara H.
Sohail
a,
John P.
Otto
 a,
Paul D.
Cunningham
a,
Paul D.
Cunningham
 b,
Young C.
Kim
b,
Ryan E.
Wood
a,
Marco A.
Allodi
b,
Young C.
Kim
b,
Ryan E.
Wood
a,
Marco A.
Allodi
 a,
Jacob S.
Higgins
a,
Joseph S.
Melinger
b and
Gregory S.
Engel
a,
Jacob S.
Higgins
a,
Joseph S.
Melinger
b and
Gregory S.
Engel
 *a
*a
aDepartment of Chemistry, The Institute for Biophysical Dynamics, The James Franck Institute, The University of Chicago, Chicago, IL 60637, USA. E-mail: gsengel@uchicago.edu; Tel: +1-773-834-0818
bU.S. Naval Research Laboratory, 4555 Overlook Avenue SW, Washington, DC 20375, USA
First published on 22nd July 2020
Abstract
Vibronic coupling between pigment molecules is believed to prolong coherences in photosynthetic pigment–protein complexes. Reproducing long-lived coherences using vibronically coupled chromophores in synthetic DNA constructs presents a biomimetic route to efficient artificial light harvesting. Here, we present two-dimensional (2D) electronic spectra of one monomeric Cy5 construct and two dimeric Cy5 constructs (0 bp and 1 bp between dyes) on a DNA scaffold and perform beating frequency analysis to interpret observed coherences. Power spectra of quantum beating signals of the dimers reveal high frequency oscillations that correspond to coherences between vibronic exciton states. Beating frequency maps confirm that these oscillations, 1270 cm−1 and 1545 cm−1 for the 0-bp dimer and 1100 cm−1 for the 1-bp dimer, are coherences between vibronic exciton states and that these coherences persist for ∼300 fs. Our observations are well described by a vibronic exciton model, which predicts the excitonic coupling strength in the dimers and the resulting molecular exciton states. The energy spacing between those states closely corresponds to the observed beat frequencies. MD simulations indicate that the dyes in our constructs lie largely internal to the DNA base stacking region, similar to the native design of biological light harvesting complexes. Observed coherences persist on the timescale of photosynthetic energy transfer yielding further parallels to observed biological coherences, establishing DNA as an attractive scaffold for synthetic light harvesting applications.
Introduction
Prolonged quantum coherences of vibronic (mixed electronic and vibrational) origin have been observed in pigment–protein complexes from multiple photosynthetic organisms,1–8 suggesting that these long-lived coherences may be a universal design principle for effective photosynthesis. Vibronic coupling, coupling between an underdamped vibrational mode and the electronic excited state, is believed to be responsible not only for this longer coherence lifetime,3,9–11 but also for the high fidelity energy transfer seen in natural light harvesting systems.10,11 The mechanisms through which molecular systems sustain vibronic coherences could offer synthetic strategies for light harvesting.In photosynthetic pigment–protein complexes, the decay, or dephasing, of quantum coherences is dependent on the coupling between the chromophores and on the surrounding protein scaffold.12 This chromophore–protein interaction is also integral to exciton energy transfer.13 When designing biomimetic molecular systems with light harvesting abilities, developing long-range molecular architecture that can mimic the role of the protein in native systems is of utmost importance. Molecular systems may exhibit steady-state spectroscopic signatures of mixing between vibrational and electronic states, but coherent superpositions between these states may dephase within 10 s of femtoseconds. Dephasing on this timescale would not promote energy transfer occurring on the hundreds of femtosecond to picosecond timescale. In previous studies on vibronic coherences in molecular systems, prolonged vibronic coherences were only observed when strict order was imposed on the chromophores, either through molecular design14 or an external scaffold.15 These studies point to the importance of macroscopic structure in sustaining coherences.
From a synthetic standpoint, DNA is an attractive scaffold for biomimetic light harvesting. Unlike the complex folding mechanisms exhibited by proteins, DNA assembly is predictable and programmable. Organic dyes constrained by DNA scaffolds in multiple geometries have been used to create controllable energy transfer pathways16–23 but designing vibronic coherence into these structures has not yet been explored. To excite quantum superpositions of states with the potential for slow dephasing, exciton delocalization (observable in spectroscopic signatures) is required. A recent study24 reported that the absorption spectra of organic dyes at single digit base pair separations along a DNA scaffold show marked differences compared with the spectra of the constituent monomer due to exciton delocalization, indicating that the multiple-dye constructs are molecular aggregates.25–28 Aggregate constructs in different geometries have been shown to support long-lived vibronic coherence.14,29 Conversely, covalent dimers of organic dyes with no macroscopic scaffold analogous to a protein have only been able to support vibronic coherences on timescales much faster than the timescale of energy transfer for light harvesting.9,30 If a DNA scaffold can sustain vibronic coherence, dye-DNA constructs may provide a path to highly efficient artificial light harvesting.
To investigate if DNA scaffolds can prolong vibronic coherence, we use ultrafast two-dimensional electronic spectroscopy (2DES). 2DES can elucidate energy transfer pathways and dynamics and couplings between chromophores.4,8,31–34 The femtosecond resolution of this technique enables the visualization of excited superpositions of quantum states as time-dependent spectral oscillations. These quantum coherences can arise from any pair of non-degenerate electronic, vibrational, or vibronic states, and pinpointing the precise physical origin of the coherence is non-trivial.35–37 Careful design of molecular constructs and knowledge of their electronic, vibrational, and vibronic structure can facilitate identification of the origin of observed spectral oscillations.
In the current study, we use three dye-DNA constructs to determine whether DNA can support long-lived coherence between the vibronic states of indodicarbocyanine (Cy5) dimers. We explore the role of excitonic coupling between the dyes in supporting coherence by varying their relative spacing along the DNA scaffold. We use 2DES to examine how quantum beating signals (vibrational and vibronic coherences) change with excitonic coupling strength and how long they persist before dephasing. We pair our ultrafast spectroscopic studies with a vibronic exciton model to better assign the origin of the observed coherences.
Results and discussion
Design of dye-DNA constructs and their linear spectral signatures
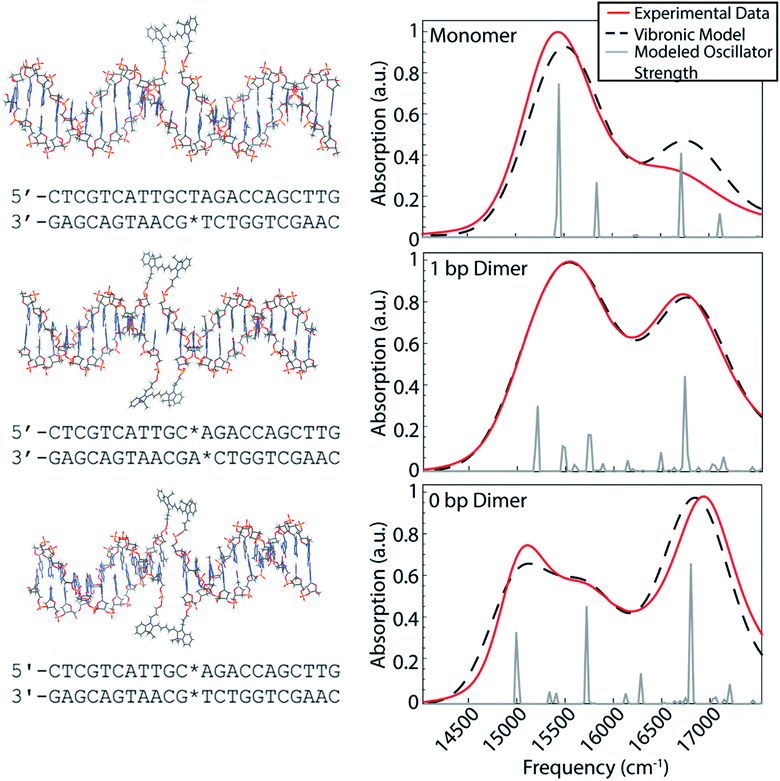
Our dye-DNA constructs were designed such that the only difference between our monomer control sample and two dimer samples is the excitonic coupling strength between the dyes (Fig. 1). The organic cyanine5 (Cy5) dye is used for all constructs; therefore, the vibrational and electronic states are universal. By varying the excitonic coupling strength between the dyes through control of inter-dye separation, the mixing between the electronic and vibrational states changes and gives rise to different vibronic states and different degrees of vibronic exciton delocalization. Unlike proteins in photosynthetic pigment–protein complexes that hold chromophores in a fixed spatial configuration non-covalently, the coupled Cy5 dyes were covalently attached to the DNA scaffold through a double phosphodiester attachment. This attachment chemistry, achieved during DNA synthesis, promotes dye localization and greater certainty of absolute dye position compared to single attachment chemistry.17,38 The monomer construct consists of a Cy5 dye replacing a single adenine in the middle of an 18 base pair double-stranded DNA (dsDNA) segment. Note, the replacement of the adenine leaves the opposite thymine unpaired. The dimeric constructs consist of the same dsDNA segment but with two nucleobases replaced with Cy5 dyes on opposite backbones of the double helix. The 1 bp dimer has the Cy5 dyes attached to each backbone chain at a vertical separation of one base pair. The 0 bp dimer has the Cy5 dyes attached to each backbone chain replacing a complete pair of nucleotides. This zero base pair separation represents the closest dye proximity, and therefore the strongest excitonic coupling, for the chosen attachment chemistry. Fig. 1 shows model structures that depict the chemical attachment of the Cy5 dye to the DNA backbone, as well as the positioning of the Cy5 dyes along the double helix. These structures are non-physical, but are intended to illustrate the dye attachment to the scaffold. All Cy5 dyes are flanked by either an adenine or thymine on one side and by a guanine or cytosine on the other. Hydrogen bonding strength of the flanking base pairs affects the nature of the molecular dimer formed (relative weighting of H- and J-like components).24 Keeping the DNA sequence as conserved as possible across the constructs mitigates the influence of the flanking base pairs on our results. The role of the DNA sequence in vibronic coherence is another interesting area to explore but is outside the scope of this work.To gain insight into the positioning of the Cy5 dyes on the DNA duplex we performed molecular dynamics simulations. Fig. S1 and S2† summarize the dye positioning and orientation of the 0 bp and 1 bp dimers. For the 0 bp dimer, the MD simulation shows that the Cy5 dyes form an approximately oblique dimer with an average center–center distance of 7.6 Å. While there are fluctuations in the center–center distance and relative orientation, the overall configuration remains stable throughout the MD simulation. Representative snapshots from the MD simulation show that the 0 bp dimer is positioned within the DNA base stacking region. The strongly interacting dyes tend to affect the local structure of the DNA. Most noticeably, the DNA duplex tends to bend slightly at the dye insertion region. However, the DNA structure is preserved outside the dye region. This is consistent with circular dichroism measurements of similar cyanine dimers attached to dsDNA, which show a bisignate feature near 260 nm that is indicative of the B-form of DNA.26 In contrast, the structure of the 1 bp dimer shows much greater fluctuations in the Cy5 center–center distance and relative orientation, which is likely due to a weakening of the duplex caused by the two adjacent unpaired nucleobases. The MD simulation shows a broad range of dimer structures, including strongly interacting dyes positioned in the base stacking regions and weakly interacting dyes that reside in the DNA backbone region.
The room temperature UV/vis absorption spectra for the monomer, 1 bp dimer, and 0 bp dimer constructs are presented in Fig. 1 (red curves) and provide insight into the vibronic structures. All samples were prepared in 1× TAE buffer, pH 8.3 to an optical density of ∼0.3 (0.5 mm pathlength) for the strongest absorbing feature. As expected for molecular aggregates, the spectra of the dimeric constructs show large deviations from the monomeric spectral signature. The linear absorption spectrum for the Cy5 monomer construct exhibits a prominent absorption feature around 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1, which we will refer to as the 0–0 transition. The 0–0 transition is a transition that occurs between ground and excited states that possess zero quanta of vibrational energy. The higher energy absorption band, around 16
300 cm−1, which we will refer to as the 0–0 transition. The 0–0 transition is a transition that occurs between ground and excited states that possess zero quanta of vibrational energy. The higher energy absorption band, around 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, which will be referred to as the 0–1 transition, is a vibronic sub-band typical of cyanine dyes corresponding to a transition between the ground state and an excited state possessing one quanta of vibrational energy.39 The higher energy vibronic sub-band arises due to an active ∼1200 cm−1 vibrational mode on the electronic excited state which has been previously assigned to a C–C stretch of the polymethine backbone of the Cy5 dye.39
500 cm−1, which will be referred to as the 0–1 transition, is a vibronic sub-band typical of cyanine dyes corresponding to a transition between the ground state and an excited state possessing one quanta of vibrational energy.39 The higher energy vibronic sub-band arises due to an active ∼1200 cm−1 vibrational mode on the electronic excited state which has been previously assigned to a C–C stretch of the polymethine backbone of the Cy5 dye.39
The 1 bp dimer absorption spectrum shows little shift in the 0–0 peak maximum compared with the monomer spectrum, though the lineshape is considerably broadened and there is a significant enhancement in the oscillator strength of the 0–1 feature. This redistribution of oscillator strength into the vibronic progression is typical of vibronic coupling and the enhancement of the 0–1 feature is proportional to how H-like the dye geometry is.24–26,28 The 0–1 feature is also slightly blue shifted in the 1 bp dimer spectrum, with a central frequency near 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1. The absence of a clear excitonic splitting of the 0–0 feature indicates that the electronic coupling is not larger than the line broadening for the 1 bp dimer. The broad 0–0 feature for the 1 bp dimer is also consistent with the large distribution of dye–dye distances and orientations suggested by the MD simulation (Fig. S2†). The 0 bp dimer absorption spectrum shows further deviation from the monomer spectral signature. The maximum absorption of the 0–0 transition feature is red shifted considerably compared to the monomer and 1 bp dimer spectra. Additionally, the 0–0 feature in the 0 bp dimer spectrum is bi-modal with a slightly more intense peak centered around 15
700 cm−1. The absence of a clear excitonic splitting of the 0–0 feature indicates that the electronic coupling is not larger than the line broadening for the 1 bp dimer. The broad 0–0 feature for the 1 bp dimer is also consistent with the large distribution of dye–dye distances and orientations suggested by the MD simulation (Fig. S2†). The 0 bp dimer absorption spectrum shows further deviation from the monomer spectral signature. The maximum absorption of the 0–0 transition feature is red shifted considerably compared to the monomer and 1 bp dimer spectra. Additionally, the 0–0 feature in the 0 bp dimer spectrum is bi-modal with a slightly more intense peak centered around 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and a slightly less intense peak around 15
000 cm−1 and a slightly less intense peak around 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. The 0–1 feature in the 0 bp dimer spectrum is more blue shifted and more intense than that in the 1 bp dimer spectrum.
500 cm−1. The 0–1 feature in the 0 bp dimer spectrum is more blue shifted and more intense than that in the 1 bp dimer spectrum.
This red shift of the 0–0 transition in the 0 bp dimer spectrum and coincident blue shift and intensity enhancement in 0–1 absorption has been reported previously in homo- and hetero-dimers of cyanine dyes.9,17,26–28,40,41 Neither H- nor J-like coupling can fully explain these spectral changes as a function of dye separation. H-type coupling occurs when the transition dipoles of the dyes are oriented parallel to each other while J-type coupling occurs when the transition dipoles of the dyes are oriented head-to-tail.42 The splitting seen in the 0–0 peak of the 0 bp dimer spectrum is due to Davydov splitting, a mixing of H- and J-like optical properties that is typical of oblique dye orientations. Similar to H- and J-like spectral signatures, Davydov splitting is another optical manifestation of exciton delocalization.28 We observe increased Davydov splitting when the dyes are held in closest proximity, indicative of significant delocalization between the dyes. The higher energy feature in the 0 bp dimer 0–0 transition is due to H-like coupling between the dyes and the lower energy 0–0 feature is due to J-like coupling. These steady-state spectral deviations from the monomeric spectral signature are a result of strong excitonic interactions between vibronic states.
While formation efficiency of the dye-DNA duplexes is typically greater than 90%, we note that minor imperfections in the formation efficiency can lead to Cy5 monomers that contribute to the dimer absorption spectra. However, the fluorescence from the 0 bp dimer was observed to be weak (below a few percent) due strong fluorescence quenching.43 This indicates that the concentration of monomeric DNA strands is below 10%.
Vibronic exciton model
Vibronic-exciton theory can explain the Davydov splitting of the 0–0 feature and the enhanced intensity of the 0–1 feature seen in the linear absorption spectra of the 1 bp and 0 bp dimers.25,44 Calculating the vibronic states in our dye-DNA constructs will help enable interpretation of the physical origin of any observed spectral oscillations in our upcoming 2DES experiments. If observed spectral oscillations do not match the energetic gap between vibronic states, they are more likely of vibrational origin. Our calculations follow the theoretical framework set forth by Kühn, Renger, and May25,44,45 and the details of the model are reported in the ESI.† The model includes two vibrational modes with three vibrational quanta in both the ground and excited electronic state for the lower frequency mode and two vibrational quanta in the both the ground and excited electronic state for the higher frequency mode. The number of vibrational quanta were chosen to ensure coverage of the bandwidth of absorption for these constructs. Eqn S8† was used to simulate the absorption spectra for the monomer, 1 bp dimer, and 0 bp dimer constructs. Fig. 1 (dashed black) shows the resultant calculated linear absorption spectra.Spectra were calculated by optimizing the fit produced by the model to the experimental linear absorption spectra. The 0–0 transition energy, the frequencies of the two incorporated vibrational modes and their corresponding Huang–Rhys factors are parameters that should be shared across the monomer and dimer constructs and as such were applied to all three constructs. One of the included vibrational modes (1270 cm−1) was held as a fixed variable during our modeling. This frequency was chosen based on the energy gap between the 0–0 and 0–1 features in the monomer construct as seen in the linear absorption spectra. The frequency of the second vibrational mode, the Huang–Rhys factors for both modes and the 0–0 transition energy were optimized by our fitting procedure. This global minimization assures values that simultaneously best reproduce the absorption spectra for all three constructs. The electronic coupling strength, J, and phase factor, ϕ, related to the relative orientation between the dyes, were set to zero for the monomer but were optimized independently for each of the dimers.
Each vibronic state carrying oscillator strength for a given construct was fit with a single Gaussian linewidth. While the linewidths of these states are likely different from each other, using a single linewidth prevents our optimization algorithm from using widely varying linewidths to produce slightly better fits to the experimental absorption data, which can result in unphysical linewidth values. All parameters were optimized simultaneously for the three constructs to produce the best overall fit to the three experimental linear absorption spectra. Table 1 contains the values of all the parameters calculated using the vibronic exciton model. The fit phase factor, ϕ, values of 1.16 and 1.24 for the 1 bp dimer and 0 bp dimer, respectively, give dihedral angles of 66 and 71 degrees, corresponding to ∼70% and ∼66% H-like character for these constructs. These dihedral angles are comparable to highly sampled dye configurations from the results of our MD simulations for the dimeric constructs (Fig. S1 and S2†).
| E 0–0 (cm−1) | E ω1 (cm−1) | E ω2 (cm−1) | S 1 | S 2 | J (cm−1) | γ (cm−1) | A | ϕ | |
|---|---|---|---|---|---|---|---|---|---|
| Monomer | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 401 |
1270 | 397 | 0.447 | 0.251 | 0 | 350 | 0.046 | N/A |
| 1 bp dimer | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 401 |
1270 | 397 | 0.447 | 0.251 | 356 | 357 | 0.068 | 1.16 |
| 0 bp dimer | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 401 |
1270 | 397 | 0.447 | 0.251 | 611 | 301 | 0.064 | 1.24 |
The calculated stick spectra (gray lines in Fig. 1) show the energies of the mixed electronic-vibrational states in the dye-DNA constructs. The vibronic states calculated for the constructs result from nonadiabatic mixing between their electronic and vibrational energy levels. We calculate multiple vibronic states under the 0–0 transition features for both dimeric constructs, indicating that the model captures the splitting of the 0–0 feature as a result of the coupling between the dyes in the 0 bp dimer spectrum.
Two-dimensional electronic spectra
We use 2DES to interrogate whether the DNA scaffold can support coherent superpositions between the vibronic states calculated by the vibronic exciton model. 2DES is a four wave mixing technique that probes frequency–frequency correlations as a function time and in doing so can report on electronic coupling between chromophores, energy transfer pathways, and ultrafast coherent dynamics (see Experimental methods).31,46,47 Picosecond transient absorption spectroscopy experiments were also performed for all three dye-DNA constructs to determine the ultimate fate of the excited states (Fig. S13†). Details on the long-time excited state behavior can be found in the ESI.†An absorptive 2D spectra for each of the three dye-DNA constructs at T = 250 fs is presented in Fig. 2. The spectra for all three constructs show a prominent positive diagonal feature near 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and above and below diagonal cross peaks (both positive) corresponding to coupling between the 0–0 (∼15
000 cm−1 and above and below diagonal cross peaks (both positive) corresponding to coupling between the 0–0 (∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) and 0–1 (∼16
000 cm−1) and 0–1 (∼16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1) transitions. Positive features in our 2DES spectra correspond to ground state bleach (GSB) or stimulated emission (SE) signals. An upper diagonal feature near 16
600 cm−1) transitions. Positive features in our 2DES spectra correspond to ground state bleach (GSB) or stimulated emission (SE) signals. An upper diagonal feature near 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 from the 0–1 transition appears in the spectra for the dimeric constructs but is absent in the monomer spectra. The 0–1 transition carries less oscillator strength than the 0–0 and is excited and detected by significantly less intense light (Fig. S1†) which explains the absence of an upper diagonal feature in the monomer spectra.
700 cm−1 from the 0–1 transition appears in the spectra for the dimeric constructs but is absent in the monomer spectra. The 0–1 transition carries less oscillator strength than the 0–0 and is excited and detected by significantly less intense light (Fig. S1†) which explains the absence of an upper diagonal feature in the monomer spectra.
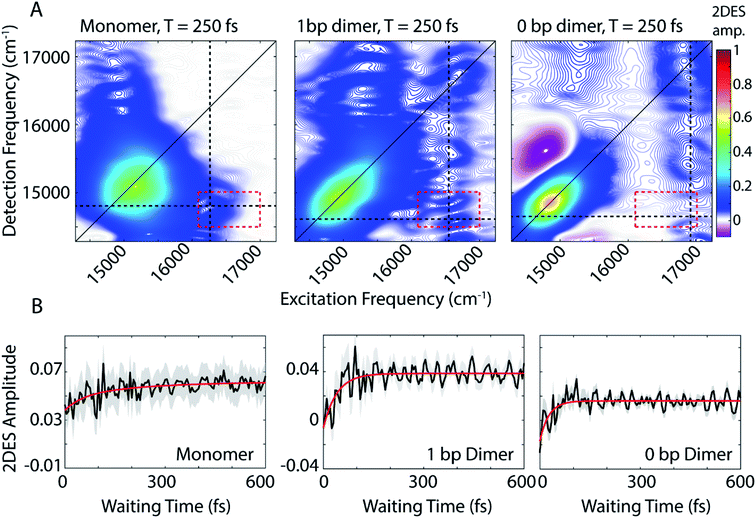 | ||
| Fig. 2 (A) Absorptive 2DES spectra of monomer (left), 1 bp dimer (center), and 0 bp dimer (right) constructs at a waiting time of 250 fs. All presented spectra are the average of 16 individual data runs. The black dashed lines indicate the approximate spectral location of the 0–0 transition in detection frequency and 0–1 transition in excitation frequency. All points contained within the dashed red box are used to generate the power spectra in Fig. 4(B) 2DES signal as a function of waiting time (T) from the below diagonal cross peak location at the intersection of the dashed lines in (A). Monoexponential fits to the time traces are shown in red. Shaded gray region shows the standard error of the mean for the 16 data runs averaged to produce the mean waiting time trace (black). | ||
The 0 bp dimer spectrum has an intense negative feature slightly above the diagonal at excitation frequency 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1, detection frequency 15
900 cm−1, detection frequency 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, corresponding to an excited state absorption (ESA) signal. There is likely an ESA signal at this above diagonal location in the 1 bp dimer spectra, but due to cancellation with stronger positive signals, it is obscured. With increasing coupling strength in the 0 bp dimer, the ESA pathway at this spectral location dominates because the change in electronic coupling alters the oscillator strength of different transitions.
500 cm−1, corresponding to an excited state absorption (ESA) signal. There is likely an ESA signal at this above diagonal location in the 1 bp dimer spectra, but due to cancellation with stronger positive signals, it is obscured. With increasing coupling strength in the 0 bp dimer, the ESA pathway at this spectral location dominates because the change in electronic coupling alters the oscillator strength of different transitions.
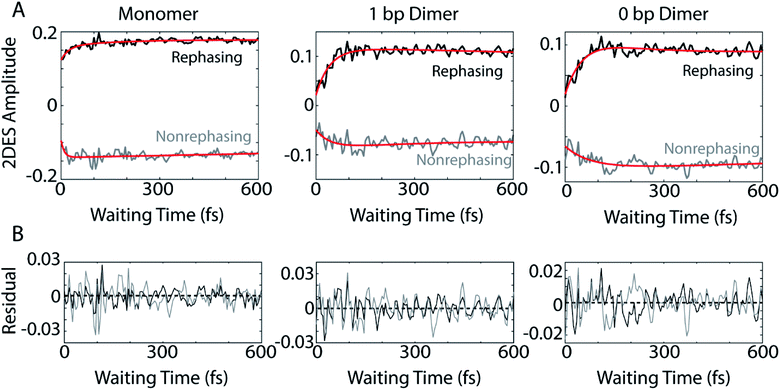
The dynamics of the below diagonal cross peak provides insight into the nature of the coupling and energy transfer between the higher and lower energy states in the three constructs. We fit the growth of the below diagonal cross peak signal to monoexponential functions (Fig. 2B). In all three constructs, the below diagonal cross peak grows in on a timescale of 100 fs or faster (τmonomer = 116 fs, τ1bp = 40 fs, τ0bp = 26 fs). The fast time constants associated with these signals suggest an ultrafast delocalization of an initially more localized excitation. The correlation between delocalization dynamics and excitonic coupling strength follows from the degree of Davydov splitting in the linear absorption spectra. That is, we see the fastest delocalization (growth of the below diagonal cross peak) in the 0 bp dimer spectra which shows the most Davydov splitting. A small amount of ultrafast solvation dynamics is seen even in the monomer, indicating that these slight polarization changes in the environment are what drive the delocalization in the vibronically coupled system.
The location of the below diagonal cross peak for all three constructs appears at a lower detection frequency (<15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) than would be expected based on the linear absorption. We attribute the location of this feature to our laser spectrum (which is much more intense at redder wavelengths, see Fig. S1†) and relaxation to a Stokes-shifted fluorescence state. Previous 2DES experiments on cyanine dimers show this below diagonal cross peak in a similarly red-shifted spectral location.9
000 cm−1) than would be expected based on the linear absorption. We attribute the location of this feature to our laser spectrum (which is much more intense at redder wavelengths, see Fig. S1†) and relaxation to a Stokes-shifted fluorescence state. Previous 2DES experiments on cyanine dimers show this below diagonal cross peak in a similarly red-shifted spectral location.9
In addition to the population dynamics contained in the time traces in Fig. 2B, the time traces all show significant oscillations. We use the oscillations to report on coherence evolution during the waiting time and assign observed frequencies to physical mechanisms. Differences in observed coherent oscillations at this spectral location may contribute to the increasingly fast growth of the cross peak as a function of excitonic coupling between the dyes.
Beating frequency analysis of dye-DNA constructs
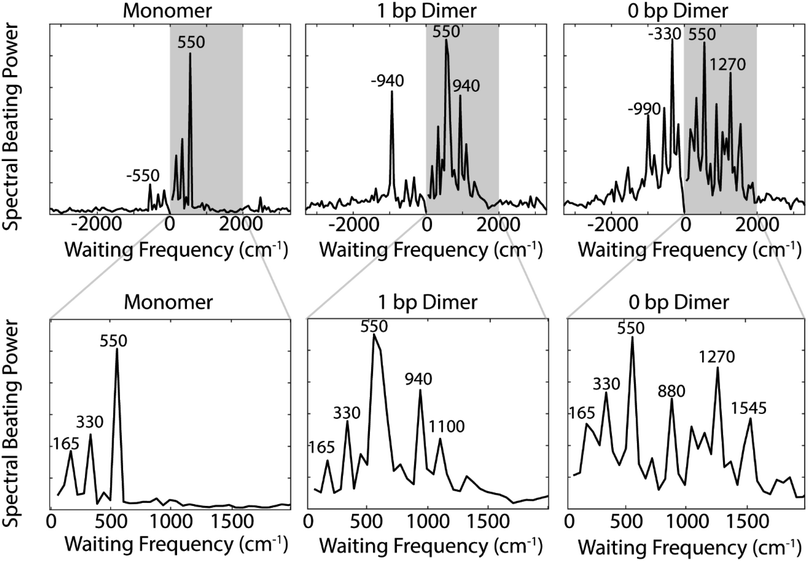
The coherences in our 2D spectra are either superpositions between vibrational levels or vibronic exciton states. Our constructs do not possess any purely electronic coherences since the electronic excited states are all non-trivially mixed with vibrational modes. Fourier transforming over the waiting time tells us the frequencies and intensities of the oscillations. In photosynthetic systems, preservation of vibronic coherences is optimized when the vibrational quantum mixed with the electronic excited state is resonant with the splitting between electronic energies.3 This resonance criterion complicates the distinction between vibrational and vibronic coherences as there can be intense quantum beating signals from vibrational wavepackets on the ground electronic state. These oscillations may be widespread in the 2D spectrum.9 By breaking down our absorptive 2DES spectra into their rephasing and nonrephasing components, we can more easily distinguish between ground state vibrational and vibronic beating signals.37,47–49 Rephasing and nonrephasing 2DES signals differ in the relative direction of their phase evolution during the first and second laser pulses and the third laser pulse and the emission of the nonlinear signal. The sum of the real components of the rephasing and nonrephasing signals gives the fully absorptive spectra presented in Fig. 2A. Rephasing and nonrephasing 2D spectra are shown in Fig. S2.† The nonrephasing spectra for all three constructs contain a strong ESA feature (negative) at the below diagonal cross peak location. Because the nonrephasing signal is dominated by ESA, it is most likely that observed coherences are on the excited state, though they may be vibrational or vibronic in origin. Previous calculations performed for a molecular biscyanine dimer9 determined that nonrephasing pathways predominantly support ground state coherences on or near the diagonal for a similar construct, indicating that nonrephasing coherences at cross peak locations likely involve vibronic exciton (excited) states.Fig. 3A shows the below diagonal cross peak dynamics of the rephasing and nonrephasing signals for the three constructs. Fig. 3B shows the residual beating as a function of waiting time after subtraction of bi-exponential fits. Bi-exponential fits were used to ensure complete removal of population dynamics before beating frequency analysis. Nonrephasing power spectra (Fig. 4) of observed beating are generated by Fourier transforming over the waiting time at each point in the 2D spectrum corresponding to the below diagonal cross peak and summing the results. The power spectra were generated by summing the nonrephasing signal across the region denoted by the dashed red box in Fig. 2. Summing over this region, as opposed to looking at the Fourier transform of the signal at a single point in the spectrum, increases the signal-to-noise of the power spectrum.
Comparing the nonrephasing power spectra for the three constructs provides insight into how increasing excitonic coupling modulates the frequency of observed coherences. The power spectra in Fig. 4 show the frequency and power of spectral beating. All three constructs show beating signals at ±165 cm−1, ±330 cm−1, and ±550 cm−1. In the monomer nonrephasing signal, these are the only detectable beating signals. We can determine that they arise from ground or excited states vibrational coherences because they do not match the energy gap between the 0–0 and 0–1 vibronic exciton states (∼1270 cm−1). The presence of positive and negative beating signals at the same three frequencies in the 1 bp dimer and 0 bp dimer indicate that the excitonic coupling between the dyes does not disrupt the underlying vibrational structure of the monomeric Cy5. We had made this assumption when executing the vibronic exciton model by using the same Huang–Rhys factors for all three constructs. Our 2D data now confirms this assumption was valid. In order to verify further that these coherences can be assigned as purely vibrational we measured the Raman spectrum for the monomer construct. The Raman spectrum (Fig. S12†) shows a prominent mode at ∼560 cm−1, indicating that this coherence is, indeed, purely vibrational.
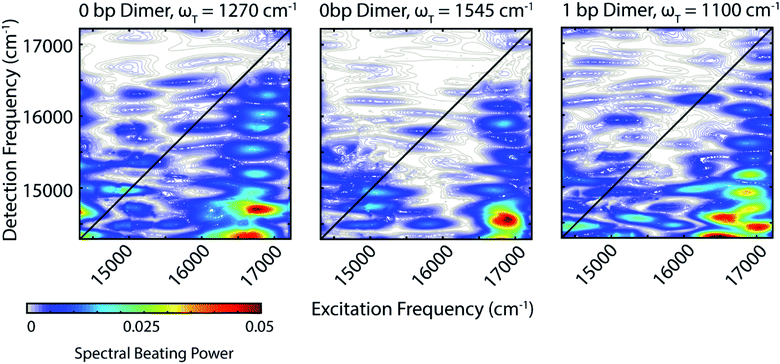
Zooming in on a region of the power spectra (Fig. 4, lower panel), we see that both of the dimeric constructs have high frequency quantum beating signals that are not observed in the monomer. The 1 bp dimer has oscillations at ±940 and 1100 cm−1. The 0 bp dimer has oscillations at −990 cm−1, 880 cm−1, 1270 cm−1, and 1545 cm−1. These higher frequency beating signals are either coherent superpositions between vibronic exciton states or vibrational coherences with enhanced transition dipole strength relative to the monomer due to resonance with vibronic transitions. Placing these beating signals in the greater context of the 2D spectrum can point to the most likely origin of the observed coherences. We generate 2D frequency beating maps by taking the Fourier transform over the residual waiting time traces after subtraction of bi-exponential fits to the real and imaginary components of the 2DES signal at every point in the 2D spectrum. Although these bi-exponential fits may not be the most physical representation of the population dynamics, this fitting strategy enables us to remove population dynamics even in extremely noisy regions of the 2D spectrum.50 A single beating map is generated for each waiting frequency. The nonrephasing 1270 cm−1 and 1545 cm−1 beating maps for the 0 bp dimer and the 1100 cm−1 beating map for the 1 bp dimer are shown in Fig. 5.
The localization of beating power for these frequencies at the below diagonal cross peak, with little intensity on the diagonal, indicates that these quantum beats are coherences between the 0–0 and 0–1 vibronic states. The frequencies, 1270 cm−1 and 1545 cm−1, roughly match the separations between the vibronic states calculated by our vibronic exciton model (Fig. 1, bottom) for the 0 bp dimer. The 1100 cm−1 mode observed in the nonrephasing power spectrum for the 1 bp dimer also matches the energy gap between vibronic exciton states for that construct (Fig. 1, middle). The spectral location and frequency of these coherences support that these are superpositions between the 0–0 and 0–1 vibronic exciton states. Recent SERS studies of Cy5 attached to ssDNA adsorbed to metal nanoparticles,51 show several high frequency Raman shifts that went undetected in our Raman measurements. Two of these high frequency Raman modes are near 1100 cm−1 and 1270 cm−1, which supports our assignment of these oscillatory signals as vibronic coherences. Vibronic coherences in vibronically coupled dimers are preserved when the electronic energy gap is resonant with an existing vibrational mode on one of the monomers.3 Beating frequency maps for the 940 cm−1 oscillation (Fig. S3†) shows that the beating signals are widespread throughout the 2D spectrum. The mirrored beating at positive and negative frequency for the 940 cm−1 oscillation suggests a vibrational origin for this coherence. The beating frequency map for the −940 cm−1 mode also show beating signals that are not predominantly localized to the below diagonal cross peak location (Fig. S3†). For the 880 cm−1 and -990 cm−1 modes in the 0 bp dimer power spectra, beating frequency maps show that the beating signals are not localized to the below diagonal cross peak region, therefore we attribute these oscillations to be vibrational coherences (Fig. S3†). Beating frequency maps for all prominent beating modes observed in Fig. 4 are presented in the ESI (Fig. S3–S6†).
Analyzing possible Feynman pathways supports the conclusion that there is vibronic coherence between the 0–0 and 0–1 states. Double-sided Feynman diagrams depicting possible pathways with oscillations of >1000 cm−1 are presented in Fig. S7.† The three nonrephasing Feynman pathways corresponding to oscillatory ESA, SE, and GSB signals all contain one light–matter interaction that induces a transition that is slightly red of our laser bandwidth. The peak energy of this transition may be just outside our experimental bandwidth; however, if the transition from the 0–1 vibronic state (represented as e2 in Fig. S7†) to a higher-lying excited state f that we see in the nonrephasing ESA pathway is broad and carries a large transition dipole moment, it could be accessed with our laser spectrum. This vibrational structure can both explain the observed vertical pattern of beating and would indicate that the e2 to f transition is not necessarily out of our bandwidth.
There are competing explanations as to the microscopic origins of observed coherences in the presence of vibronic coupling. Jonas and co-workers8 proposed that observed coherences are ground-state vibrational coherences that are enhanced due to vibronic coupling and thus report on the electronic excited state. Mančal and co-workers3 propose that vibronic coupling induces beating on both the ground and excited states when the electronic transition on one monomer is resonant with a vibrational mode on the excited state of the other monomer. We believe that the latter more fully explains our observations as we see beating localized to a region of the nonrephasing spectrum where ESA signal dominates.
DNA scaffold supports long-lived vibronic coherence at small base pair separations
To assess whether using a DNA scaffold to hold the dyes in close proximity more successfully replicates the vibronic coherences seen in photosynthetic pigment–protein complexes, we examined how long our observed coherences persist. By eliminating the first 100 fs of waiting time dynamics and then remaking the beating frequency maps, we can assess how these beating signals persist throughout the 2D spectrum beyond 100 fs. Fig. S8† shows that 1270 cm−1 and 1545 cm−1 beating frequency maps still show strong beating at the below diagonal cross peak position even if we omit the first 100 fs of waiting time from the Fourier transform.To gain a quantitative estimate of the coherence lifetime, we compare the amplitude of peaks of interest from the below diagonal cross peak power spectra (Fig. 4) as a function of the length of the waiting time window used for the Fourier transform. Fig. S11† shows the power spectra from the below diagonal cross peak region calculated with three different portions of the waiting time signal, 0 to 600 fs, 100 to 600 fs, and 300 to 600 fs. Eliminating early waiting times will decrease the amplitude of the beating signals in the power spectra and the percentage of coherence amplitude lost based on the reduction of waiting time points used offers a good estimation of the coherence lifetime. Based on the power spectra in Fig. S11,† we calculate coherence lifetimes of 300 fs for the 1100 cm−1 vibronic coherence in the 1 bp dimer and 325 fs and 270 fs for the 1270 cm−1 and 1545 cm−1 vibronic coherences, respectively, in the 0 bp dimer. For reference, we performed the same calculation on the 550 cm−1 mode in the monomer which resulted in a coherence lifetime of 160 fs. Further details on how these decay times were computed can be found in the ESI.†
Our estimated decay lifetimes for the vibronic coherences in the dye-DNA constructs exceed previously reported lifetimes for covalent and scaffolded dimers of dyes, indicating that DNA, like the protein scaffold in photosynthetic pigment–protein complexes can preserve vibronic coherence. Halpin et al.9 have previously reported on the effect of strong vibronic coupling on coherence between vibronic excitons in a molecular biscyanine dimer in a combined experimental and numerical study. In their work, the authors reported oscillations in the waiting time of the nonrephasing ESA signal with a beat frequency consistent with the energy gap between the two strongest absorbing excitons; however the chosen molecular construct in those experiments could only sustain the vibronic coherence for 80 fs (1/e decay time).9 Our results indicate that the DNA scaffold can prolong this vibronic coherence relative to covalent linkage between the dyes.9 Even previous reports of dye-DNA dimeric constructs,52 have reported vibronic coherence lifetimes of ∼100 fs. Our data suggest significantly longer dephasing times. Our MD simulations indicate that, in contrast to previously studied constructs,52 for our given DNA scaffold and dye attachment chemistry the Cy5 dyes lay in the base-stacking region of the DNA helix in the 0 bp dimer. The MD simulation for the 1 bp dimer yielded a much larger range of dye orientations, but did result in structures in which the dyes were also internal to the scaffold. This dye orientation relative to the scaffold is similar to the way photosynthetic pigments are embedded within their protein scaffolds. The studies presented here offer a promising synthetic route to engineering long-lived vibronic coherence using a DNA scaffold.
The structural fluctuations of the DNA scaffold at room temperature also cause fluctuations in the electronic coupling between the dyes (off-diagonal disorder), which are quasi-static on the timescale of the experiment, leading to inhomogeneously broadened lineshapes in both the linear and nonlinear spectra. Previous theoretical work by Chenu and colleagues,3 concluded that vibronic coherences occurring at energy gaps resonant with the vibration involved in vibronic coupling experience enhances amplitudes and long dephasing times even over energetic disorder (∼100 cm−1 of bandwidth). While the current experiments cannot directly identify the specific mechanisms by which the nuclear or electronic degrees of freedom in the DNA scaffold preserve these vibronic, room temperature fluctuations in the structure of the DNA duplex also cause fluctuations in the transition energies of the dyes (diagonal disorder). These fluctuations may act to either preserve or disrupt observed coherences. Preservation of coherence in the Fenna–Matthews–Olson (FMO) complex has been attributed to synchronized and correlated spectral dynamics that result from the motions of the protein scaffold.53 The key elements of the chromophore arrangement in this complex are rigid relationships between the chromophores that enforce narrow ensemble distributions of site energies, of distance between chromophores, and of coupling angle. Further, the structure of the chlorophyll itself limits reorganization via isomerization. These design elements have each been explored in prior studies and found to be critical to prolonging observed coherence signals.15,54 It is plausible that our DNA scaffold acts in a similar manner to preserve vibronic coherence in dye-DNA constructs because we have a bi-dentate binding scheme that forces the dyes into the pi-stacking region of the DNA in contrast to prior studies.52 This approach effectively dictates the spacing between chromophores, limits the rotation of the chromophores, and restricts movement of the chromophore affecting both site energies and isomerization.
Conclusion
Strong excitonic coupling between closely spaced dyes on DNA induces exciton delocalization. Increased Davydov splitting and redistribution of oscillator strength into higher energy vibronic bands have been reported at separations under 2 base pairs in vibronically coupled dyes.24 Our 2DES beating frequency analysis shows that the large changes in linear spectral signatures at small dye separations correspond to detectable coherences between vibronic exciton states delocalized across the dyes. Further analysis of the 2D data reveal that these vibronic exciton coherences that persist for ∼300 fs MD simulations reveal that for both the 1 bp dimer and the 0 bp dimer the Cy5 dyes are internal to the base stacking region of the DNA scaffold. This dye orientation relative to the scaffold creates a strong parallel to the orientation of photosynthetic pigments within the protein scaffold of light harvesting complexes in photosynthetic pigment–protein complexes. Our results indicate that organic dyes on a DNA scaffold offer an avenue for building tunable excitonic networks that can support coherent phenomena, an important design principle for building biomimetic light harvesting networks.Experimental methods
Sample preparation
DNA oligomers were purchased from Integrated DNA Technologies (Coralville, IA). DNA duplexes containing Cy5 monomers and homodimers were prepared in 1× TAE buffer (tris acetate EDTA; 40 mM tris base, 20 mM acetic acid, 50 mM EDTA sodium salt dehydrate) by combining stoichiometric equivalent amounts of each complementary strand and then thermal cycling to 90 °C. The samples were subsequently cooled slowly to 4 °C over an hour. Initial stock solutions were made at a concentration of 50 μM in dsDNA.UV/vis absorption spectroscopy
UV/vis spectra were acquired using a Shimadzu UV-1700 spectrometer. Spectra were measured using a 1 mm quartz cuvette (Starna).Gradient assisted photon echo spectroscopy (GRAPES)
2DES is a four wave mixing technique that probes frequency–frequency correlations as a function of time and in doing so can report on electronic coupling between chromophores, energy transfer pathways, and ultrafast coherent dynamics.31,46,47 In a 2DES experiment, three ultrafast laser pulses interact with the sample to generate a macroscopic oscillating polarization which generates a signal in a defined, phase-matched direction. The first two pulses are separated by coherence time, τ, and produce either a population or a coherence between excited electronic states, vibronic states, or vibrational states. During the waiting time (T), the time delay between the second and third pulses, the system undergoes a combination of coherent oscillation and incoherent relaxation. The arrival of the third pulse initiates the emission of the third-order signal which is a function of the detection time, t. The emitted signal is captured and resolved by a spectrometer and sCMOS camera. Fourier transforms over the coherence time and the detection time give a two-dimensional frequency–frequency correlation map for every waiting time that contain positive signals from stimulated emission (SE) and ground state bleach (GSB) pathways and negative signals from excited state absorption (ESA) pathways.The pulses used in these 2DES experiments were produced by focusing the output of a 5 kHz Coherent Legend Elite USP regenerative amplifier seeded by a coherent Micra Ti:Sapph oscillator through 2.25 m argon gas held 4 psi above atmospheric pressure. The broadened output was recompressed via a pair of negative GVD mirrors (Layertec) and then refocused through the argon tube. The resulting supercontinuum white light pulse was compressed using another pair of negative GVD mirrors (Layertec) and a multiphoton intrapulse interference phase scan compressor (Biophotonics Solutions, Inc.). The compressed pulse was 15 fs FWHM, with a spectrum spanning 580–720 nm. The compressed pulse was divided into two using a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 beamsplitter (Layertec), with one pulse sent to a retroflecting delay line (Aerotech) to control the waiting time, T. Each pulse was directed to a 40 percent reflective beamsplitter (Chroma) in front of a silver mirror angled at ∼1.5 degrees, replacing the wedged glass beamsplitters used in a previous iteration of GRAPES. The beamsplitter-silver mirror pairs create a set of four pulses in a modified BOXCAR geometry, which are overlapped vertically using flat mirrors and focused to vertical lines (1 cm by 60 μm) with a cylindrical mirror. The angle with which pulses 1 and 2 pass through the sample creates a gradient of coherence times (τ), which include negative and positive coherence times. For details on using both negative and positive coherence times in GRAPES to obtain fully absorptive spectra see ref. 55.
50 beamsplitter (Layertec), with one pulse sent to a retroflecting delay line (Aerotech) to control the waiting time, T. Each pulse was directed to a 40 percent reflective beamsplitter (Chroma) in front of a silver mirror angled at ∼1.5 degrees, replacing the wedged glass beamsplitters used in a previous iteration of GRAPES. The beamsplitter-silver mirror pairs create a set of four pulses in a modified BOXCAR geometry, which are overlapped vertically using flat mirrors and focused to vertical lines (1 cm by 60 μm) with a cylindrical mirror. The angle with which pulses 1 and 2 pass through the sample creates a gradient of coherence times (τ), which include negative and positive coherence times. For details on using both negative and positive coherence times in GRAPES to obtain fully absorptive spectra see ref. 55.
The resulting third-order signal co-propagates with pulse 4 (local oscillator, L.O.) which has been attenuated by two orders of magnitude before passing through the sample and is set to arrive 2 ps before the other pulses. Both the sample and the L.O. are focused through an imaging spectrometer (Andor Shamrock 303i) onto a 2D CMOS array (Andor Neo 5.5) running at 20 Hz. Neighboring pixels were binned in both dimensions of the detector such that a 2560 × 2160 array acts as 1280 × 1080 array with four times the pixel area. After binning, the τ spacing on the vertical dimension of the detector was 0.53 fs per pixel (original pixel size 6.5 μm). A chopper is used such that the camera collects the heterodyned signal (signal plus L.O.) every second frame. The chopped frames contain only L.O. and pulse 3 scatter, which is subtracted in the data processing. After chopping, signal acquisition speed is 10 Hz. Fast acquisition enables fine sampling of the waiting time, every 0.5 fs. The use of fine waiting time sampling to remove contamination from scattered light has been described in detail elsewhere.56,57 During the measurement, solutions of dye-DNA constructs were contained within a 500 μm flow cell (Starna). The samples were not flowing during the measurement but were flowed in and out of the sample cell using a peristaltic pump in between each of the 16 independent runs to minimize photobleaching.
Vibronic exciton model
The vibronic exciton model used to reproduce linear absorption spectra is described in detail in the ESI.†Raman spectroscopy
A Raman spectrum was acquired for the Cy5 monomer construct. Experimental details are provided in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Vannevar Bush Faculty Fellowship Program (Grant No. N00014-16-1-2513 and N00014-15-1-0048), Air Force Office of Scientific Research (AFOSR) (FA9550-18-1-0099) and the NSF (under grant no. 1900359). This work was also supported in part by the NSF MRSEC grant programs at the University of Chicago (DMR-1420709). S. H. S. and R. E. W. individually acknowledge support from the Department of Defense (DoD), AFOSR, through the National Defense Science and Engineering Graduate (NDSEG) Fellowship Program, 32 CFR 168a. M. A. A. acknowledges support from the Arnold O. Beckman Postdoctoral Fellowship funded by the Arnold and Mabel Beckman Foundation. J. S. H. acknowledges support from the NSF-GRFP program. The authors thank Dr Karen Watters for scientific editing of the manuscript. J. S. M. acknowledges support from the Laboratory-University Research Initiative (LUCI) and the Office of Naval Research as administered through the Nanoscience Institute at the Naval Research Laboratory.References
- F. D. Fuller, J. Pan, A. Gelzinis, V. Butkus, S. S. Senlik, D. E. Wilcox, C. F. Yocum, L. Valkunas, D. Abramavicius and J. P. Ogilvie, Nat. Chem., 2014, 6, 706–711 CrossRef CAS PubMed.
- P. D. Dahlberg, G. J. Norris, C. Wang, S. Viswanathan, V. P. Singh and G. S. Engel, J. Chem. Phys., 2015, 143, 101101 CrossRef PubMed.
- A. Chenu, N. Christensson, H. F. Kauffmann and T. Mančal, Sci. Rep., 2013, 3, 2029 CrossRef PubMed.
- E. Collini, C. Y. Wong, K. E. Wilk, P. M. Curmi, P. Brumer and G. D. Scholes, Nature, 2010, 463, 644–647 CrossRef CAS PubMed.
- M. Ferretti, V. I. Novoderezhkin, E. Romero, R. Augulis, A. Pandit, D. Zigmantas and R. v. Grondelle, Phys. Chem. Chem. Phys., 2014, 16, 9930–9939 RSC.
- M. L. Flanagan, P. D. Long, P. D. Dahlberg, B. S. Rolczynski, S. C. Massey and G. S. Engel, J. Phys. Chem. A, 2016, 120, 1479–1487 CrossRef CAS PubMed.
- G. S. Schlau-Cohen, A. Ishizaki, T. R. Calhoun, N. S. Ginsberg, M. Ballottari, R. Bassi and G. R. Fleming, Nat. Chem., 2012, 4, 389–395 CrossRef CAS PubMed.
- V. Tiwari, W. K. Peters and D. M. Jonas, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203–1208 CrossRef CAS PubMed.
- A. Halpin, P. J. M. Johnson, R. Tempelaar, R. S. Murphy, J. Knoester, T. L. C. Jansen and R. J. D. Miller, Nat. Chem., 2014, 6, 196–201 CrossRef CAS PubMed.
- A. W. Chin, J. Prior, R. Rosenbach, F. Caycedo-Soler, S. F. Huelga and M. B. Plenio, Nat. Phys., 2013, 9, 113–118 Search PubMed.
- V. Tiwari, W. K. Peters and D. M. Jonas, Nat. Chem., 2014, 6, 173–175 CrossRef CAS PubMed.
- M. Schlosshauer, Rev. Mod. Phys., 2005, 76, 1267–1305 CrossRef.
- R. Shankar, Principles of Quantum Mechanics, Springer US, 2nd edn, 1994 Search PubMed.
- J. Lim, D. Paleček, F. Caycedo-Soler, C. N. Lincoln, J. Prior, H. von Berlepsch, S. F. Huelga, M. B. Plenio, D. Zigmantas and J. Hauer, Nat. Commun., 2015, 6, 7755 CrossRef PubMed.
- L. Wang, G. B. Griffin, A. Zhang, F. Zhai, N. E. Williams, R. F. Jordan and G. S. Engel, Nat. Chem., 2017, 9, 219–225 CrossRef CAS PubMed.
- S. Buckhout-White, C. M. Spillmann, W. R. Algar, A. Khachatrian, J. S. Melinger, E. R. Goldman, M. G. Ancona and I. L. Medintz, Nat. Commun., 2014, 5, 5615 CrossRef CAS PubMed.
- P. D. Cunningham, A. Khachatrian, S. Buckhout-White, J. R. Deschamps, E. R. Goldman, I. L. Medintz and J. S. Melinger, J. Phys. Chem. B, 2014, 118, 14555–14565 CrossRef CAS PubMed.
- J. S. Melinger, A. Khachatrian, M. G. Ancona, S. Buckhout-White, E. R. Goldman, C. M. Spillmann, I. L. Medintz and P. D. Cunningham, ACS Photonics, 2016, 3, 659–669 CrossRef CAS.
- A. Dietrich, V. Buschmann, C. Müller and M. Sauer, Rev. Mol. Biotechnol., 2002, 82, 211–231 CrossRef CAS PubMed.
- T. Kato, H. Kashida, H. Kishida, H. Yada, H. Okamoto and H. Asanuma, J. Am. Chem. Soc., 2013, 135, 741–750 CrossRef CAS PubMed.
- É. Boulais, N. P. D. Sawaya, R. Veneziano, A. Andreoni, J. L. Banal, T. Kondo, S. Mandal, S. Lin, G. S. Schlau-Cohen, N. W. Woodbury, H. Yan, A. Aspuru-Guzik and M. Bathe, Nat. Mater., 2018, 17, 159–166 CrossRef PubMed.
- J. L. Banal, T. Kondo, R. Veneziano, M. Bathe and G. S. Schlau-Cohen, J. Phys. Chem. Lett., 2017, 8, 5827–5833 CrossRef CAS PubMed.
- P. K. Dutta, R. Varghese, J. Nangreave, S. Lin, H. Yan and Y. Liu, J. Am. Chem. Soc., 2011, 133, 11985–11993 CrossRef CAS PubMed.
- P. D. Cunningham, Y. C. Kim, S. A. Díaz, S. Buckhout-White, D. Mathur, I. L. Medintz and J. S. Melinger, J. Phys. Chem. B, 2018, 122, 5020–5029 CrossRef CAS PubMed.
- S. Polyutov, O. Kühn and T. Pullerits, Chem. Phys., 2012, 394, 21–28 CrossRef CAS.
- L. I. Markova, V. L. Malinovskii, L. D. Patsenker and R. Häner, Chem. Commun., 2013, 49, 5298–5300 RSC.
- L. Kringle, N. P. D. Sawaya, J. Widom, C. Adams, M. G. Raymer, A. Aspuru-Guzik and A. H. Marcus, J. Chem. Phys., 2018, 148, 085101 CrossRef PubMed.
- B. L. Cannon, L. K. Patten, D. L. Kellis, P. H. Davis, J. Lee, E. Graugnard, B. Yurke and W. B. Knowlton, J. Phys. Chem. A, 2018, 122, 2086–2095 CrossRef CAS PubMed.
- F. Milota, V. I. Prokhorenko, T. Mancal, H. von Berlepsch, O. Bixner, H. F. Kauffmann and J. Hauer, J. Phys. Chem. A, 2013, 117, 6007–6014 CrossRef CAS PubMed.
- C. C. Jumper, J. M. Anna, A. Stradomska, J. Schins, M. Myahkostupov, V. Prusakova, D. G. Oblinsky, F. N. Castellano, J. Knoester and G. D. Scholes, Chem. Phys. Lett., 2014, 599, 23–33 CrossRef CAS.
- T. Brixner, J. Stenger, H. M. Vaswani, M. Cho, R. E. Blankenship and G. R. Fleming, Nature, 2005, 434, 625–628 CrossRef CAS PubMed.
- M. Cho, H. M. Vaswani, T. Brixner, J. Stenger and G. R. Fleming, J. Phys. Chem. B, 2005, 109, 10542–10556 CrossRef CAS PubMed.
- M. L. Cowan, J. P. Ogilvie and R. J. D. Miller, Chem. Phys. Lett., 2004, 386, 184–189 CrossRef CAS.
- T. Brixner, T. Mancal, I. V. Stiopkin and G. R. Fleming, J. Chem. Phys., 2004, 121, 4221–4236 CrossRef CAS PubMed.
- V. Butkus, D. Zigmantas, L. Valkunas and D. Abramavicius, Chem. Phys. Lett., 2012, 545, 40–43 CrossRef CAS.
- C. Kreisbeck, T. Kramer and A. Aspuru-Guzik, J. Phys. Chem. B, 2013, 117, 9380–9385 CrossRef CAS PubMed.
- D. B. Turner, K. E. Wilk, P. M. G. Curmi and G. D. Scholes, J. Phys. Chem. Lett., 2011, 2, 1904–1911 CrossRef CAS.
- E. M. S. Stennett, N. Ma, A. van der Vaart and M. Levitus, J. Phys. Chem. B, 2014, 118, 152–163 CrossRef CAS PubMed.
- H. Mustroph, K. Reiner, J. Mistol, S. Ernst, D. Keil and L. Hennig, ChemPhysChem, 2009, 10, 835–840 CrossRef CAS PubMed.
- V. Sundström and T. Gillbro, J. Chem. Phys., 1985, 83, 2733–2743 CrossRef.
- F. Nicoli, M. K. Roos, E. A. Hemmig, M. Di Antonio, R. de Vivie-Riedle and T. Liedl, J. Phys. Chem. A, 2016, 120, 9941–9947 CrossRef CAS PubMed.
- M. Kasha, Radiat. Res., 1963, 20, 55–70 CrossRef CAS PubMed.
- J. S. Huff, P. H. Davis, A. Christy, D. L. Kellis, N. Kandadai, Z. S. D. Toa, G. D. Scholes, B. Yurke, W. B. Knowlton and R. D. Pensack, J. Phys. Chem. Lett., 2019, 10, 2386–2392 CrossRef CAS PubMed.
- M. Schröter, S. D. Ivanov, J. Schulze, S. P. Polyutov, Y. Yan, T. Pullerits and O. Kühn, Phys. Rep., 2015, 567, 1–78 CrossRef.
- O. Kühn, T. Renger and V. May, Chem. Phys., 1996, 204, 99–114 CrossRef.
- Y. C. Cheng and G. R. Fleming, Annu. Rev. Phys. Chem., 2009, 60, 241–262 CrossRef CAS PubMed.
- Y.-C. Cheng, G. S. Engel and G. R. Fleming, Chem. Phys., 2007, 341, 285–295 CrossRef CAS.
- D. B. Turner, R. Dinshaw, K. K. Lee, M. S. Belsley, K. E. Wilk, P. M. Curmi and G. D. Scholes, Phys. Chem. Chem. Phys., 2012, 14, 4857–4874 RSC.
- A. Volpato, L. Bolzonello, E. Meneghin and E. Collini, Opt. Express, 2016, 24, 24773–24785 CrossRef PubMed.
- E. Thyrhaug, R. Tempelaar, M. J. P. Alcocer, K. Žídek, D. Bína, J. Knoester, T. L. C. Jansen and D. Zigmantas, Nat. Chem., 2018, 10, 780–786 CrossRef CAS PubMed.
- A. Jaworska, E. Pyrak and A. Kudelski, Vib. Spectrosc., 2019, 101, 34–39 CrossRef CAS.
- M. Cipolloni, B. Fresch, I. Occhiuto, P. Rukin, K. G. Komarova, A. Cecconello, I. Willner, R. D. Levine, F. Remacle and E. Collini, Phys. Chem. Chem. Phys., 2017, 19, 23043–23051 RSC.
- B. S. Rolczynski, H. Zheng, V. P. Singh, P. Navotnaya, A. R. Ginzburg, J. R. Caram, K. Ashraf, A. T. Gardiner, S.-H. Yeh, S. Kais, R. J. Cogdell and G. S. Engel, Chem, 2018, 4, 138–149 CAS.
- D. Hayes, G. B. Griffin and G. S. Engel, Science, 2013, 340, 1431–1434 CrossRef CAS PubMed.
- S. H. Sohail, P. D. Dahlberg, M. A. Allodi, S. C. Massey, P. C. Ting, E. C. Martin, C. N. Hunter and G. S. Engel, J. Chem. Phys., 2017, 147, 131101 CrossRef PubMed.
- E. Harel, A. F. Fidler and G. S. Engel, J. Phys. Chem. A, 2011, 115, 3787–3796 CrossRef CAS PubMed.
- E. Harel, A. F. Fidler and G. S. Engel, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16444–16447 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01127d |
| This journal is © The Royal Society of Chemistry 2020 |