Open Access Article
Open Access ArticleA kinetic description of how interfaces accelerate reactions in micro-compartments †
Kevin R.
Wilson
 *a,
Alexander M.
Prophet
ab,
Grazia
Rovelli
a,
Megan D.
Willis
a,
Rebecca J.
Rapf
a and
Michael I.
Jacobs
c
*a,
Alexander M.
Prophet
ab,
Grazia
Rovelli
a,
Megan D.
Willis
a,
Rebecca J.
Rapf
a and
Michael I.
Jacobs
c
aChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: krwilson@lbl.gov
bDepartment of Chemistry, University of California, Berkeley, CA 94720, USA
cBeckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA
First published on 27th July 2020
Abstract
A kinetic expression is derived to explain how interfaces alter bulk chemical equilibria and accelerate reactions in micro-compartments. This description, aided by the development of a stochastic model, quantitatively predicts previous experimental observations of accelerated imine synthesis in micron-sized emulsions. The expression accounts for how reactant concentration and compartment size together lead to accelerated reaction rates under micro-confinement. These rates do not depend solely on concentration, but rather the fraction of total molecules in the compartment that are at the interface. Although there are ∼107 to 1013 solute molecules in a typical micro-compartment, a kind of “stochasticity” appears when compartment size and reagent concentration yield nearly equal numbers of bulk and interfacial molecules. Although this is distinct from the stochasticity produced by nano-confinement, these results show how interfaces can govern chemical transformations in larger atmospheric, geologic and biological compartments.
I. Introduction
Complex reaction networks, important for the chemistry of biological (cells), environmental (mineral pores), and atmospheric (aerosols and cloud droplets) systems, often occur in micron-sized compartments. Measurements of reaction rates and mechanisms required to understand the evolution of these systems are often broken into elementary steps and measured in the laboratory using macroscopic reaction vessels. However, as reviewed in a number of studies,1–7 there is emerging evidence that when chemical reactions are confined in micro-droplets, Leidenfrost droplets, thin films and emulsions, they are accelerated by many orders of magnitude (10 to 106) relative to large reaction vessels. These results have potentially important ramifications for understanding chemical reactivity in atmospheric and industrial aerosols, the biochemistry within liquid–liquid phase-separated8 and other cellular compartments and the development of more efficient synthetic methods.9Despite extensive observations, the molecular origin of these enhanced rates, in many cases, remains unclear. Factors that likely contribute to observed accelerated rates in droplets, such as those formed in electrospray ionization (ESI) sources, include the concentration of reagents due to solvent evaporation,10 electrochemistry,11,12 interference from gas phase reactions,13,14 surface charge,15,16 enrichment17 and acidity2 as well as surface reactions.1,18 that become more pronounced in small droplets or thin films.17,19 These factors likely all contribute to varying extents when ESI droplets are used for both compartmentalization and detection of reactants and products. The multiphase processes inherent in ESI mass spectrometry make it extremely difficult to design control experiments13 needed to isolate the exact mechanism(s) responsible for observed reaction acceleration in droplets.
Alternatively, emulsions have smaller surficial charge, lack solvent evaporation and interferences from competing gas phase reactions. As a result, emulsions can be used to isolate the relative importance of interfacial reactions in the observed acceleration factors. For example, Fallah-Araghi et al.1 studied a condensation reaction in monodisperse emulsions: the synthesis of an imine from the reaction of an amine with an aldehyde. Although unfavorable in bulk aqueous solutions due to the elimination of H2O, the apparent equilibrium constant for this reaction is observed to be enhanced 29-fold in an 8.4 μm radius (R) emulsion. Both the equilibrium and the forward rate constant for imine synthesis increase linearly with 1/R; a clear signature of surface effects. To explain their results, Fallah-Araghi et al.1 proposed a reaction-adsorption mechanism to show how surface adsorption, desorption and reaction couple with bulk reactions to produce the observed size-dependent kinetics. For a set of limiting cases, an analytical expression was derived to describe how the effective equilibrium constant depends upon radius, adsorption length, surface reaction and desorption rates.
Motivated to further generalize the results reported in ref. 1, we have developed a new stochastic model of compartmentalized chemistry. The simulations are parameterized using literature rate coefficients, which makes them physically realistic. The simulation results are first benchmarked against the size dependent kinetic data reported by Fallah-Araghi et al.,1 providing additional molecular insights into the coupling of surface and bulk reactivity, interfacial propensity and bulk phase depletion. Next, the simulations are expanded to a larger range of compartment sizes and concentrations than were originally considered in ref. 1. Together, the simulation results and the prior experimental data are then used to develop and validate a theoretical description, beyond the limiting cases considered in ref. 1, which allows for more general predictions of how surface reactions modify equilibria and lead to accelerated reaction kinetics in micro-compartments.
This work is organized as follows: Section II outlines some general considerations for understanding chemistry in micro-compartments, which guide the development of the stochastic model detailed in Section III. In Section IV, the simulation results are benchmarked against the data reported in ref. 1 and then extended over a much larger range of compartment sizes and concentrations. Finally, in Section V a general kinetic expression is derived that correctly predicts the scaling of the apparent equilibrium constant in micro-compartments observed both in the numerical simulations developed here and in the previous dataset reported by Fallah-Araghi et al.1
II. Compartment dimensions, concentrations and characteristic lengths for reactions in micro-compartments
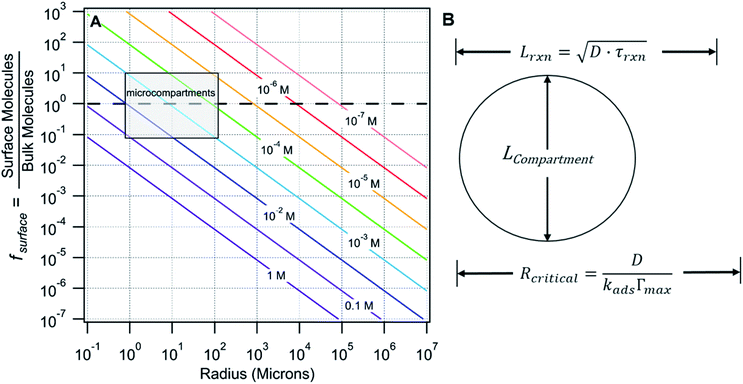
There are many examples where nano-confinement20 of a small number of molecules or atoms has a profound influence on physical and chemical properties; including the electronic structure of quantum dots and the transport and reactivity in carbon nanotubes,21 zeolites, nanovessels,22 metal organic frameworks, cells, etc. For these cases, compartmentalization produces properties and behavior not observed in their macroscopic analogs or described by continuum theories because confinement is on the order of molecular/atomic dimensions, solvent correlation lengths23,24 and/or is governed by stochastic fluctuations of small numbers of molecules.25–29In contrast, it is not immediately obvious why confinement of many, many millions of solute molecules in a micron-sized droplet or emulsion would produce behavior substantially different from what is observed in a beaker. One difference between macro- and microscale environments is illustrated in Fig. 1A where the ratio of surface to bulk molecules (fs) in a spherical aqueous compartment is shown as a function of radius and solute concentration ([solute]). Here, the ratio fs is,
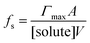 | (1) |
For large compartments (e.g. R = 105 microns = 10 cm), fs is much less than 1 for the concentrations shown. At mM concentrations, ∼1 in every 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules is, on average, at the surface and it is only under the most dilute conditions (e.g. 10−7 M) that the number of molecules at the surface and in the bulk are equivalent (fs = 1, dashed line Fig. 1A). For reactions in macroscale compartments conducted under typical laboratory concentrations (10−4 to 1 M), processes that occur at the interface would involve, on average, only a small fraction of the total number of molecules in the system and therefore remain invisible, except to the most interface sensitive analytical techniques.
000 molecules is, on average, at the surface and it is only under the most dilute conditions (e.g. 10−7 M) that the number of molecules at the surface and in the bulk are equivalent (fs = 1, dashed line Fig. 1A). For reactions in macroscale compartments conducted under typical laboratory concentrations (10−4 to 1 M), processes that occur at the interface would involve, on average, only a small fraction of the total number of molecules in the system and therefore remain invisible, except to the most interface sensitive analytical techniques.
This is in contrast to micro-compartments (R = 1–100 microns), where a substantial number (fs > 0.1) of molecules in the concentration range of (0.1 to 10−4 M) reside at the interface (shaded region, Fig. 1A). Many of the reports of accelerated reactions in ESI micro-droplets are in fact conducted within this shaded region. At these sizes and concentrations (as will be shown below) there is strong coupling between surface and bulk kinetics, which cannot be neglected. Generally, these simple observations suggest that dividing a bulk mM solution into a large number of micron-sized compartments (e.g. in sprays or emulsions) might be an effective way to study surface reaction kinetics that would otherwise be difficult to observe in a single large reaction vessel.
There are a number of characteristic lengths relative to compartment size that likely impact whether a reaction is “chemically confined” (Fig. 1B). The reacto-diffusive length (Lrxn) is the distance, on average, a reagent travels prior to a reaction. This length is related to the Kuramoto Length30 and the Damköhler number, or reaction diffusion index.31Lrxn depends upon the square root of diffusion coefficient (D) and the chemical lifetime (τrxn). For a bimolecular reaction, τrxn, and therefore Lrxn, can be changed via reactant concentration. When reactions are slow and diffusion is fast, Lrxn> Lcompartment (as shown in Fig. 1B), reagents can sample the surface region of the compartment repeatedly before reacting. For this case, the chemical evolution of the compartment will be governed both by reactions occurring in the compartment interior as well as at its surface. For the opposite case (i.e. fast reaction rates and slow diffusion) where Lrxn< Lcompartment, the surface will play a more minor role as reagents, on average, will be consumed prior to encountering the interface. For the imine synthesis reaction considered here Lrxn ∼400 μm.1
In the surfactant literature a critical radius (Rcritical) is used to describe mass transfer to a curved interface (i.e. bubble or droplet, Fig. 1B).32 For compartment sizes larger than Rcritical, diffusion limits transport timescales to the interface. For compartments smaller than Rcritical, energetic barriers for surface adsorption are kinetically limiting. It is expected that the overall rate of a chemical transformation in a compartment might depend sensitively upon the mode of mass transfer (i.e. diffusion vs. adsorption). For the synthesis reaction considered here, Rcritical ∼200–300 cm, indicating that the flux of reactants to the surface is kinetically limited.
III. Model formulation
Kinetiscope©33 is used to numerically simulate the chemistry as a function of compartment size. This open access software package uses a stochastic algorithm to propagate the chemical evolution of a system by randomly selecting among probability-weighted elementary reaction and diffusion steps.34,35 The rate law is used to compute the probability for each elementary step. Stochastic methods differ from the more common approach of constructing and solving sets of deterministic coupled ordinary differential equations, which provide a reasonable description of kinetics at the macroscale. As physical dimensions are reduced and the number of molecules become small, discreteness is likely to have a larger influence on overall system behavior. Models built in Kinetiscope© have been used extensively to predict multiphase transformations in submicron aerosols,31,36–41 where quantitative descriptions of surface and bulk reactions, diffusion, and evaporation are required.Simulation geometry
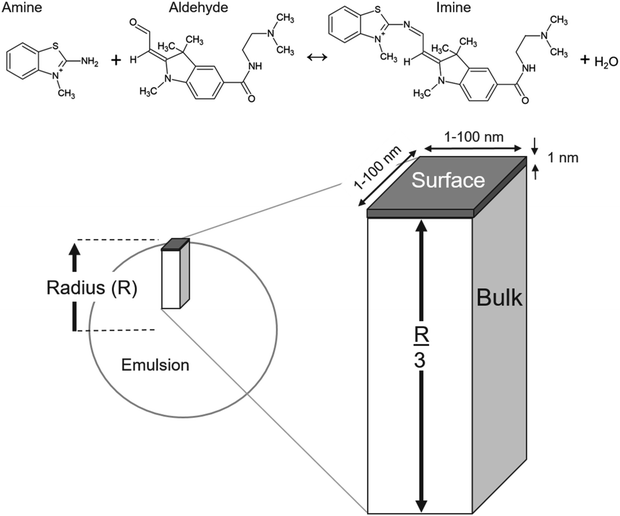
To model the data reported in Fallah-Araghi et al.1 the emulsions are assumed to be spherical. Houle and coworkers40,41 showed that to model a spherical aerosol, with radius = R, the simulation geometry could be simplified to a rectangular prism with a height of R/3, as shown in Fig. 2. Here, the prism is divided into two sub-volumes: a surface (located at the top, Fig. 2) with a bulk region below. The rectangular prism with surface and bulk sub-volumes preserves the correct scaling between surface and bulk processes and is computationally more efficient than simulating an entire sphere. Molecules move between these volumes by Fickian diffusion.The length and width of the prism are 1 × 1 nm (Fig. 2). The simulation results presented below are found to be insensitive to these dimensions and were checked by using larger 10 × 10 × R/3 nm and 100 × 100 × R/3 nm simulation volumes. These expanded dimensions correspond to a 4 orders of magnitude change in the total number of molecules in the simulation. An additional parameter is required to define the surface volume—the interface thickness. A thickness of 1 nm is used and is consistent with Molecular Dynamics simulations of the density profile across an oil/water interface.42
Bulk and surface concentrations
For the imine synthesis reaction reported in ref. 1, stoichiometric amounts of reactant amine and aldehyde (i.e. [amine] = [aldehyde] = 15 mM) are used. Molecular structures of the reactants and products are shown in Fig. 2. In the simulation, the compartment volume and reactant concentration are specified separately. This means that in order to maintain the same concentrations for different emulsion sizes, the total number of molecules in the simulation volume must naturally change as is shown in Table S1.†A Langmuir43 framework (detailed below) is used to describe the kinetics of the adsorption and desorption of molecules at the interface. This is implemented in the simulation by defining the concentration of available adsorption sites in the surface volume.38 It is assumed that a site is occupied by a single species and that reactants and products compete for the same set of adsorption sites. In the absence of measurements, the surface excess concentration is assumed, since to our knowledge neither of reactants are not commercially available and were synthesized by Fallah-Araghi et al.1 It is assumed that a site corresponds to a mean molecular area of 60 Å2. This corresponds to a surface excess of 1.67 × 1014 molecules per cm2 and a volumetric concentration in the 1 nm thick surface compartment of 1.67 × 1021 molecules per cm3. The estimated44 pure liquid densities of the amine and aldehyde are 4.39 × 1021 and 2.09 × 1021 molecules per cm3, which correspond to mean molecular areas of 23 Å2 and 48 Å2, respectively. A larger average value of 60 Å2 for a surface site appears to be reasonable, since it is generally observed that the molecular footprint derived from experiments often exceeds geometric estimates of molecular area. The simulation results depend on the assumed molecular area, which governs, together with the surface reaction rate coefficient, the overall rate of the interfacial reaction.
Table S1† shows the computed number of available surface sites and bulk molecules as a function of size for the rectangular prism simulation geometry for [reactant] = 15 mM and Γ∞ = 1.67 × 1014 molecules per cm2. This is compared with the numbers of bulk and surface molecules in a sphere using the same reagent concentration and surface excess. It can be seen that fs for the rectangular prism and sphere exhibit identical scaling with size. This scaling accurately weights bulk vs. surface processes (described below) and is important for accurately capturing the differences one might expect between micro- vs. macro-scale systems discussed above and shown in Fig. 1A.
Reaction mechanism
Shown in Table S2† is the list of elementary reaction and diffusion steps used in the simulation. There are two elementary steps in the bulk compartment, corresponding to the forward bimolecular synthesis of the imine and its backward unimolecular decomposition. As shown in Fig. S1† the rate coefficients for these two steps are determined using a single reactor simulation (i.e. no compartmentalization) where only reagent concentrations are specified ([amine] = [aldehyde] = 15 mM). To replicate the observed bulk kinetics, a forward rate coefficient for step 12 (Table S2†) of 2.60 × 10−5 M−1 s−1 is used; consistent with the value (2.85 × 10−5 M−1 s−1) reported in Table S3 of the ESI in ref. 1. The reverse rate coefficient for step 13 (1.52 × 10−3 s−1, Table S2†) is slightly larger than the range previously reported ref. 1 (0.68–1.06 × 10−3 s−1), but nevertheless replicates the bulk kinetics shown in Fig. S1.† The diffusion coefficients for the amine, aldehyde and imine (steps 9–11, Table S2†) are fixed at the values determined by Fallah-Araghi et al.1The elementary steps in the surface compartment comprise both adsorption/desorption (steps 1–6, Table S2†) and reaction (steps 7 and 8, Table S2†) steps. It is assumed that the amine and aldehyde react in the surface compartment only after they adsorb; consistent with a Langmuir–Hinshelwood mechanism. Adsorption/desorption rate constants (kads and kdes) for the aldehyde and amine synthesized by Fallah-Araghi et al.1 are not available, so rate coefficients are used that are consistent with, though not identical to, those reported by Tomoaia et al.45 for structurally similar molecules adsorbing to the benzene/water interface. For the three molecules in that study,45 dibucaine, tetracaine, and stearic acid, kads is measured to be 0.1204, 0.0831 and 0.0035 M−1 s−1, respectively. The corresponding values for kdes are 2.65 × 10−3, 2.48 × 10−3 and 6.53 × 10−4 s−1. Of the three molecules, dibucaine and tetracaine are the most structurally similar (structure and charge) to the molecules considered here and thus provide a reasonable constraint for the values of kads and kdes used in the simulation and shown in Table S2.†
If kdes (step 6, Table S2†) for the imine is set to values similar to those used for the amine and aldehyde, large surface-to-bulk gradients form in the simulations, which are inconsistent with observations.1 Therefore, kdes for the imine is selected to be larger in order to yield simulation results that are consistent with the observation that the product is uniformly distributed in the emulsion. The underlying physical reason why the imine desorption rate is so much faster than the amine/aldehyde is unclear, but likely related to its enhanced solubility in the oil phase of the emulsion as discussed below and in Fallah-Araghi et al.1
Steps 7 and 8 in Table S2† describe the forward rate of imine formation and its dissociation at the surface. Fallah-Araghi et al.1 concluded that the dissociation of the imine back to reactants occurred roughly with the same rate coefficient as in the bulk and furthermore found it to be independent of emulsion size. So the dissociation rate constant at the surface (step 8) is set to be equivalent to the bulk value (step 13).
The forward bimolecular rate constant for imine synthesis (Table S2† simulation 1, step 7) at the surface is selected to be 1.54 × 10−3 M−1 s−1. This is the value previously measured by Meguellati et al.46 for the same reaction conducted in an aqueous solution containing sodium dodecyl sulfate micelles at 3× the critical micelle concentration. In that study,46 the presence of the micelle phase favorably alters the free energy for the reaction over the bulk aqueous solution—leading to faster imine formation rates in the presence of micelles. It seems plausible that the emulsion surface, considered here, could play a similar role as small micellar structures; serving as a hydrophobic environment of higher local concentration leading to more favorable interactions between reactants.46 These observations are also consistent with the observation that imine synthesis is more efficient in organic solvents since the reaction requires the elimination of H2O.1 Finally, a second simulation (simulation 2, Table S2†) is developed, which uses all of the same rate coefficients as simulation 1 except step 7. This value is increased slightly in order to provide the best representation of the observed 1/R dependence of the equilibrium constant as will be described in detail below.
IV. Results: simulation vs. experiment
Shown in Fig. 3 are the experimentally observed [imine] as a function of reaction time for the bulk solution and a R = 8.4 μm emulsion. At steady state, the [imine] is 43× larger in the 8.4 μm emulsion than the bulk (inset, Fig. 3). The observed kinetic rise in the 8.4 μm emulsion is markedly sigmoidal compared to the near exponential rise observed for the bulk. Also shown in Fig. 3 are the results from simulation 1. The agreement between the simulation and the 8.4 μm emulsion is reasonable with some differences apparent at early reaction times (∼500 s). The bulk is simulated as a R = 10 cm sphere and is similarly consistent with the observed bulk kinetics. The model replicates both the steady state [imine] as well as the change from sigmoidal to exponential kinetics observed in 8.4 μm emulsion and bulk, respectively.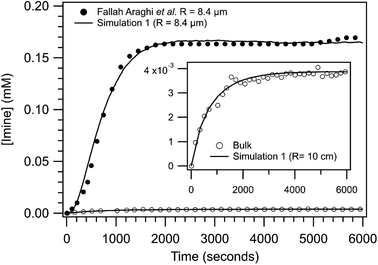 | ||
| Fig. 3 Imine concentration as a function of reaction time for a R = 8.4 μm emulsion and a bulk solution (inset). Lines are results from simulation 1 for R = 8.4 μm and 10 cm and points are data reproduced from ref. 1. To compare with simulations, the non-zero [imine] at time = 0, likely arising from the weakly fluorescent aldehyde, has been subtracted from experimental data. | ||
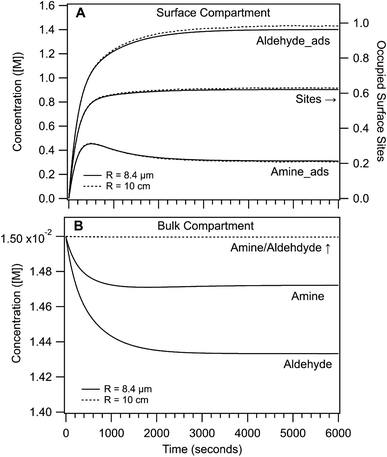
Shown in Fig. 4 are the simulated time dependent concentrations of the aldehyde, amine and imine in the surface and bulk compartments for R = 8.4 μm and 10 cm. As expected for both cases, the steady state concentration of adsorbed reactants at the interface is much higher than in the bulk compartment (i.e. M vs. mM). This surface enrichment (e.g. ∼100 × for the aldehyde) is a consequence of the relative magnitude of adsorption and desorption rate coefficients and the surface excess concentration (i.e. available sites). From the difference in surface and bulk concentrations alone, we would expect that the rate of imine formation to be faster at the interface.
In the surface compartment (Fig. 4A), reactants adsorb to the interface over the first 1000 seconds. The relatively slow adsorption timescales compete with reaction and govern the sigmoidal shaped rise in imine formation observed for R = 8.4 μm and as discussed in ref. 1. Also shown is the fraction of occupied sites, which reaches only 60% at steady state; indicating a sub-saturated surface in the linear region of the Langmuir isotherm. In the simulation, the aldehyde is more surface active than the amine and its interfacial concentration throughout the reaction is ∼2× larger (cf. adsorption/desorption rate coefficients, Table S2†). Notably, the surface kinetics and concentrations in the R = 8.4 μm and 10 cm simulations are nearly indistinguishable. This suggests that the overall enhancement in imine formation in small compartments is not due to substantial differences in surface chemistry as a function of size as will be discussed below.
The largest difference between the R = 8.4 μm and 10 cm actually appears in the bulk compartment (Fig. 4B). For R = 10 cm, the amine and aldehyde concentrations (on the scale shown) remain nearly invariant over the course of the reaction, in contrast to the R = 8.4 μm case where bulk depletion is observed. Although the depletion is small (2% for the amine and 5% for the aldehyde), it nevertheless reflects the 104 difference in the relative numbers of surface and bulk molecules in the micro-compartment. fs for R = 10 cm is 5.5 × 10−6 compared with 0.07 for R = 8.4 μm.
Additional differences between R = 8.4 μm and 10 cm are observed by examining the event fraction vs. reaction step number (Table S2†) as shown in Fig. S2.† Since the probability for an event is computed using the rate law, the event fraction reflects the relative importance of a particular step for the overall chemical evolution of the system. For R = 10 cm, 98% of the events occur in the bulk compartment, corresponding to the forward (step 12, Table S2†) synthesis and backward (step 13, Table S2†) decomposition of the imine.
This is in contrast to R = 8.4 μm, where reactions in the bulk compartment account for only 12% of the total events, with the largest event fractions corresponding to the surface (88%). It is clear from Fig. S2† that for the R = 8.4 μm compartment imine synthesis occurs at the interface (step 7) while its decomposition happens in the bulk (step 13). This is consistent with the difference in magnitude of imine dissociation vs. desorption rate coefficients (steps 8 vs. 6) as well as the conclusions drawn by Fallah-Araghi et al.1 It is expected that the large differences in the bulk and surface event fractions observed for these extreme cases (R = 8.4 μm and 10 cm) will evolve as a function of fs (i.e. emulsion size).
As reported previously,1 the steady state [imine] is observed to increase with decreasing droplet size, with the most dramatic change observed in going from R = 8.4 to 13.4 μm. This is shown in Fig. 5A where the imine formation kinetics as a function of emulsion size are reproduced from ref. 1. The kinetics observed for the R = 33.7 μm are nearly identical to the bulk solution (as is shown in Fig. 3, inset). For all sizes, the kinetic rise in the [imine] is sigmoidal. Shown in Fig. 5B are the results from simulation 1. The shape of the simulated kinetics as a function of size are reasonably consistent with the data shown in Fig. 5A. The most notable difference between simulation and experiment is the steady state [imine], which in the simulations, shows a more modest decrease in going from R = 8.4 to 13.4 μm. There is a ∼2× difference in simulated vs. observed [imine] for R = 13.4, 21.2 and 33.7 μm.
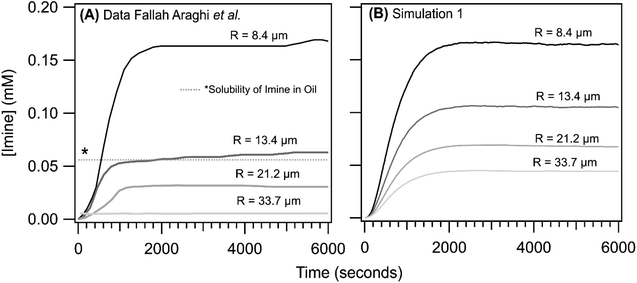 | ||
| Fig. 5 Imine concentration as a function of reaction time for R = 8.4, 13.4, 21.2 and 33.7 μm. (A) data reproduced from ref. 1. To compare with simulations, the non-zero [imine] at time = 0, likely arising from an interference from the weakly fluorescent aldehyde, has been subtracted from experimental data. (B) Simulation 1 results. The dotted line (denoted with a *) reflects the concentration of non-fluorescent product sequestered in the oil phase of the emulsion; see ref. 1 and text for details. | ||
Unfortunately, after exploring a range of parameters in simulation 1 we were unable to replicate the exact size dependence observed in the experiment. This difference, however, likely originates from the partitioning of the imine product into the oil fraction of the emulsion, which quenches its fluorescence as discussed by Fallah-Araghi et al.1 The solubility of the product in the oil phase is not explicitly included in the simulation. Fallah-Araghi et al.1 estimated the imine solubility in the oil phase to be ∼0.056 mM (shown as a dotted line in Fig. 5A), which likely explains the factor of ∼2 difference between simulation and experiment.
Shown in Fig. 6A is the observed equilibrium constant (Kobseq) vs. 1/R reported in ref. 1Kobseq is computed using the [imine] at equilibrium and the concentrations of amine and aldehyde. In the experiment, Kobseq increases linearly with 1/R, with a 29× enhancement of Kobseq for R = 8.4 μm relative to the bulk. A linear fit to the data exhibits a negative y-intercept and reflects the solubility of the imine product in the oil phase as described above and discussed in Fallah-Araghi et al.1 Results from simulation 1 are shown for comparison. Although, simulation 1 (Fig. 6A) exhibits a linear 1/R dependence, the slope is smaller than what is observed experimentally (dashed line Fig. 6A). Simulation 1 over-predicts Kobseq for the intermediate emulsion sizes (R = 13.4, 21.2, 33.7 μm), which is anticipated given the comparison of simulation with experiment shown in Fig. 5.
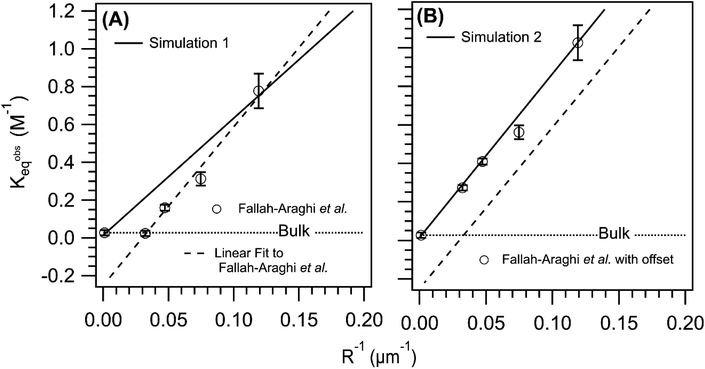 | ||
| Fig. 6 Comparison of the simulated and observed1 equilibrium constant vs. 1/R. (A) Experimental results reproduced from ref. 1 and compared to simulation 1 (solid line). (B) A constant offset (+0.25) applied to the experimental Kobseq to account of imine solubility in the oil phase of the emulsion compared with simulation 2 (solid line). The dashed line in both panels is a linear fit to the data. The dotted line in both panels indicates the value of the equilibrium constant measured in a bulk solution. | ||
Without sufficient kinetic information to explicitly simulate the solubility of the imine in the oil phase, a constant offset is applied to the experimental data as shown in Fig. 6B. This offset eliminates the negative y-intercept shown in Fig. 6 and facilitates a closer comparison of the experimental and simulated Kobseq. To best replicate the slope of Kobseqvs. 1/R in the corrected data set, (see solid line in Fig. 6B), requires a surface forward rate coefficient (step 7, Table S2†) that is 2× larger than the one used in simulation 1. This larger rate coefficient, used in simulation 2 (3.22 × 10−3 M−1 s−1, step 7, Table S2†) produces a slope of 8.5 M−1 μm and is consistent with the experiment (8.3 M−1 μm). Although this rate coefficient is 124× larger than the bulk value (see step 12, Table S2†) it appears consistent with the previous micelle studies46 of the same reaction, in which a similar order of magnitude increase over the bulk is observed when increasing the micelle concentration. For reference, Fig. S3† shows the sensitivity of the simulated results to the magnitude of this surface rate coefficient. This figure shows only a minimal increase of Kobseq for the case where the forward surface rate coefficient for imine synthesis is equal to the bulk value (i.e. step 12, Table S2†).
To gain additional insights into the origin of the size dependence of Kobseq, the total surface (steps 1–8, Table S2†) and bulk (steps 12–13) event fractions ([amine] = [aldehyde] = 15 mM) from simulation 2 are computed and plotted as a function of size in Fig. S4.† For values of R larger than ∼104 microns (i.e. 1 cm) > 90% of the reactive events occur in the bulk compartment, consistent with only a modest increase in Kobseq above its bulk macroscopic value. As size decreases, the relative fraction of surface events increase; accounting for ∼50% of the total events at R ∼ 1500 microns (1.5 mm). Below 100 microns, surface events dominate (>80%).
Although the simulation results in Fig. S4† show the increasing importance of the surface with decreasing compartment size, large changes in the event fraction occur only after correspondingly large changes in compartment size (i.e. note log x-axis in Fig. S4†). For the narrow range of emulsion sizes, R = 8.4, 13.4, 21.2, 33.7 μm, the relative event fractions are nearly indistinguishable, suggesting that surface event fraction alone is not sufficient to explain the scaling behavior of Kobseq with 1/R observed in Fig. 6.
Since the simulations are constrained by physically realistic rate coefficients and provide a reasonable description of the experimental data, we have some confidence that they can be reliably extended over a larger range of size and reactant concentrations. This allows a more comprehensive view of the factors that govern reactivity in micro-compartments. Although simulations 1 and 2 both capture the key features of imine synthesis in small emulsions, simulation 2 is used in the following sections since it provides a slightly better representation of the observed scaling of Kobseq with micro-compartment size (Fig. 6).
Shown in Fig. S5† are results from simulation 2 as a function of concentration for a stoichiometric mixture of reactants. For each concentration, linear scaling of Kobseq with 1/R is observed, with the absolute value of the slope increasing with decreasing concentration. A factor of ∼7 change from the concentrations used in Fallah-Araghi et al.1 (15 mM to 100 mM) produces only a modest difference in Kobseq from what is observed in the bulk solution. In contrast, for the R = 8.4 micron compartment (1/R = 0.12 μm−1) a factor of 3 decrease in concentration (30 mM to 10 mM) produces a factor of 5 increase in Kobseq. These results point to additional scaling relationships that depend sensitively on concentration.
Shown in Fig. 7 are simulated Kobseqvs. reactant concentration and size, again assuming a stoichiometric mixture of reactants. At large reactant concentrations (>0.1 M) all compartment sizes asymptotically approach Kobseq = 0.017 M−1; the bulk macroscopic value. As concentration decreases there is an overall increase in Kobseq, the magnitude of which depends on compartment size. As expected, in large compartments (R = 10 cm) there is only a modest increase in Kobseq with decreasing concentration. This is in contrast to micro-compartments, where at low concentration (10−5 to 10−4 M), Kobseq approaches much larger asymptotic values. For example, for R = 8.4 microns (at 10−5 M) Kobseq ∼ 50 M−1, which is ∼3000 times larger than the bulk value.
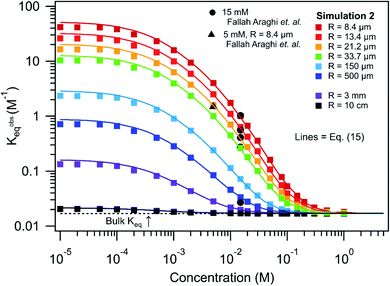 | ||
| Fig. 7 K obseq vs. concentration and radius for [amine] = [aldehyde]. Comparison of experimental data (5 and 15 mM) from ref. 1, results from simulation 2 and predictions from eqn (15). KBeq = 0.017 M−1 as indicated with a dashed line. | ||
Also included in Fig. 7 is a single measurement1 of Kobseq (1.24 M−1) for R = 8.5 micron at [amine] = [aldehyde] = 5 mM. Although, Kobseq is larger relative to the 15 mM case, which is generally consistent with the simulated trends, the simulated value is a factor of ∼3 larger. The reason for this difference is unclear and difficult to evaluate in the absence of a complete set of size dependent measurements at 5 mM. As discussed above, this difference could originate from the unknown amounts of the imine product partitioning to the oil phase of the emulsion. Nevertheless, it would be highly desirable to compare these simulation results, and the derivation that follows, to larger experimental data sets that systemically measure how observed rate or equilibrium constants depend both on compartment size and concentration.
Discussion
Together, the experimental data reported by Fallah-Araghi et al.1 and the results of simulation 2 provide a self-consistent set of observations that reveal how microdroplet reactivity depends both on concentration and compartment size. Below, we derive a set of governing kinetic equations and predictions that can be directly evaluated against these observations.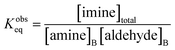 | (2) |
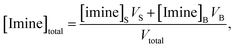 | (3) |
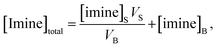 | (4) |
| [Imine]S = KSeq[amine]S[aldehyde]S | (5) |
| [Imine]B = KBeq[amine]B[aldehyde]B. | (6) |
As noted above, both KSeq and KBeq have units of inverse concentration (i.e. M−1). Substituting eqn (5) and (6) into eqn (4) yields,
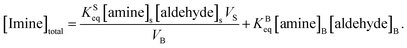 | (7) |
Eqn (7) is then substituted into eqn (2) to yield,
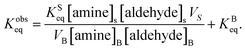 | (8) |
The surface and bulk concentrations in eqn (8) are recast as numbers of molecules (n),
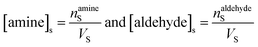 | (9) |
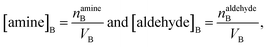 | (10) |
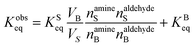 | (11) |
f s is the ratio of surface to bulk molecules,
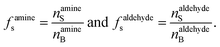 | (12) |
Eqn (12) is an equivalent way of expressing fs as in eqn (1), which computes fs using compartment area and surface excess in units of cm2 per molec. 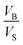 can be computed for any compartment geometry; for a sphere VS and VB are,
can be computed for any compartment geometry; for a sphere VS and VB are,
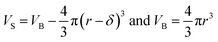 | (13) |
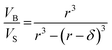 | (14) |
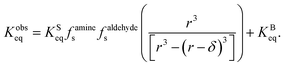 | (15) |
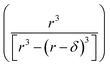 term is the ratio of the total compartment volume to surface volume and increases linearly with increasing compartment size. fs is a nonlinear function that increases with both decreasing radius and decreasing concentration as shown in Fig. 1. Together
term is the ratio of the total compartment volume to surface volume and increases linearly with increasing compartment size. fs is a nonlinear function that increases with both decreasing radius and decreasing concentration as shown in Fig. 1. Together  is a function that increases linearly with 1/R, consistent with the scaling of Kobseq observed in the experiments and simulations described above.
is a function that increases linearly with 1/R, consistent with the scaling of Kobseq observed in the experiments and simulations described above.
For large compartment sizes and/or reactant concentrations, the first term on the RHS of eqn (15) approaches zero and the system exhibits the expected macroscopic behavior (i.e. Kobseq = KBeq). For small compartments under dilute conditions this term becomes sizable leading to Kobseq ≫ KBeq. It should be noted that eqn (15) is a different expression than was derived by Fallah-Araghi et al.1 Although their expression for Kobseq (eqn (8) in ref. 1) exhibits linear 1/R scaling, it does not explicitly account for the concentration dependence in eqn (15), which is needed to explain what is observed in the experiments and simulations shown above.
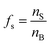 . Here, fs depends upon adsorption/desorption and reaction rates as well as bulk concentration. These factors were explicitly neglected, for discussion purposes, in the idealized expression in eqn (1). nB is straightforward to compute using compartment volume and bulk concentration. However, for a system undergoing reaction, nS cannot be simply computed from the Langmuir equation, the equilibrium constant for adsorption
. Here, fs depends upon adsorption/desorption and reaction rates as well as bulk concentration. These factors were explicitly neglected, for discussion purposes, in the idealized expression in eqn (1). nB is straightforward to compute using compartment volume and bulk concentration. However, for a system undergoing reaction, nS cannot be simply computed from the Langmuir equation, the equilibrium constant for adsorption 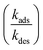 and the bulk concentrations. This is because nS will depend upon both the rates of reaction and the rates of adsorption/desorption to and from the interface. The following kinetic expressions are used to derive fs for this more complex case. Eqn (16) and (17) describe the time dependent concentrations of species (denoted x and y) at the surface,
and the bulk concentrations. This is because nS will depend upon both the rates of reaction and the rates of adsorption/desorption to and from the interface. The following kinetic expressions are used to derive fs for this more complex case. Eqn (16) and (17) describe the time dependent concentrations of species (denoted x and y) at the surface,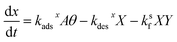 | (16) |
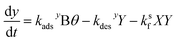 | (17) |
| [amine]s = X and [aldehyde]s = Y | (18) |
| [amine]B = A and [aldehyde]B = B | (19) |
| θtotal = [total surface sites] | (20) |
| θ = [unoccupied surface sites] | (21) |
| θ = θtotal − X − Y | (22) |
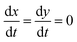 , so eqn (16) and (17) become,
, so eqn (16) and (17) become,| 0 = kadsxAθ − kdesxX − ksfXY | (23) |
| 0 = kadsyBθ − kdesyY − ksfXY | (24) |
Substituting the expression for θ in eqn (22) into eqn (23) and solving for X and Y yields the following two expressions,
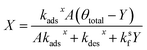 | (25) |
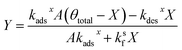 | (26) |
Similarly, substituting θ in eqn (22) into eqn (24) and rearranging yields two additional expressions for X and Y:
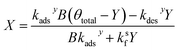 | (28) |
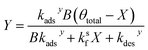 | (29) |
Setting the two expressions for X in eqn (25) and (28) to be equal yields,
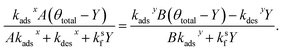 | (30) |
Eqn (30) can be solved for Y (using Mathematica48) yielding,
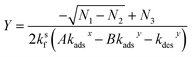 | (31) |
| N1 = (−AθTkadsxksf − Akadsxkdesy + BθTkadsyksf − Bkdesxkadsy − kdesxkdesy)2 | (31a) |
| N2 = 4BθTkdesxkadsy(Akadsxksf − Bkadsyksf − kdesyksf) | (31b) |
| N3 = AθTkadsxksf + Akadsxkdesy − BθTkadsyksf + Bkdesxkadsy + kdesxkdesy | (31c) |
X is computed by substituting the expression for Y in eqn (31) into eqn (25). It should be noted that the equations above are a general solution for a bimolecular reaction occurring via the Langmuir–Hinshelwood mechanism. Both X and Y are concentrations and can be converted to numbers of molecules (nXS and nYS) using eqn (9) (where X = [amine]s and Y = [aldehyde]s). Eqn (31), although somewhat lengthy, is straightforward to compute using the adsorption, desorption, and reaction rate coefficients and bulk concentrations of reactants, A and B. As an internal check of this derivation, eqn (31) and (25) are used to compute the concentration of [amine]s and [aldehyde]s as well as θ (the fraction of occupied sites), which are compared to the numerical results of simulation 2. As is shown in Fig. S6,† these equations quantitatively predict the surface concentrations and sites as a function of bulk concentration that are observed in the simulation.
To make global predictions of how Kobseq depends upon compartment size and reactant concentration, eqn (31) and (25) are used to compute famines and faldehydes in eqn (15). Rate coefficients needed for eqn (31) and (25), for the specific system considered here, are found in Table S2.† The predictions are shown as a function of size and concentration in Fig. S5 and S7.†Eqn (15) quantitatively predicts the linear scaling of Kobseq with 1/R observed by Fallah-Araghi et al.1 and in simulation 2 (Fig. S5†). Eqn (15) also correctly predicts the asymptotic approach of Kobseq → KBeq with increasing concentration shown in Fig. 7. Eqn (15) accounts for the increase in Kobseq with decreasing concentration (and its dependence on size) as well as the eventual plateau of Kobseq at low concentrations (10−4 to 10−5 M). This plateau is a natural consequence of the small surface occupancy at low bulk concentrations (cf. Langmuir Equation). We have further verified the predictions of eqn (15) against simulation results for the case of non-stoichiometric reactant concentrations as is shown in Fig. S7.†
At low concentrations (10−4 to 10−5 M), eqn (15) over-predicts Kobseq by ∼10–20% from what is observed in simulation 2. Although the number of interface molecules at 10−4 to 10−5 M is small they are still factors of 10 larger (Fig. 1) than the number in the bulk, suggesting that more complex phenomena may emerge when the system is very dilute. Nevertheless, the near quantitative agreement between eqn (15) and both the experimental and simulated observations suggest that the majority of the underlying kinetic behavior is correctly predicted by eqn (15).
V. Conclusions
Using a combination of new stochastic simulations and previous experimental data, a general kinetic expression is derived that connects Kobseq with KSeq and KBeq. The relative contribution of KSeq to the observed equilibrium is found to be governed by the ratio of molecules at the surface, which becomes more pronounced when compartment sizes are small and concentrations are dilute. fs in turn depends upon the relative adsorption, desorption and surface reaction rates—all features of the reaction-adsorption mechanism proposed by Fallah-Araghi et al.1 Unlike prior work,1 however, eqn (15) provides a more general prediction of how Kobseq scales with compartment size and concentration. These results also highlight the importance and experimental need to make measurements as a function of concentration and well-defined compartment size or film thickness,19,49 which together are needed to assess the role that surface chemistry (e.g. rather than evaporative concentration of reactants, etc.) plays in accelerating reactions in micro-droplets.It is clear to fully understand the chemistry occurring inside of micro-compartments, detailed insights (and new measurements) into adsorption/desorption dynamics of reactants, intermediates, and products are needed, since these steps kinetically link the surface with bulk reactivity and together ultimately determine the magnitude of the acceleration. Although, these linkages are present in macroscale systems, since surface partitioning is governed by thermodynamics and not by compartment size at these scales, the role of the surface remains obscured due to the relatively small number of surface molecules participating in the overall chemical transformation. For micro-compartments or thin films,19 however, the finite system size enhances the overall importance of interfacial phenomena, where reaction rates and mechanisms can be modified due to partial solvation, stabilization of unique transition states and by molecular alignment and enrichment. For gas-surface reactions, it has been observed that diffusive confinement at semi-solid and glassy interfaces can alter product distributions50 and enhance reaction pathways31,51 that would normally be too slow in well-mixed liquids or at aqueous interfaces.
The magnitude of the observed rate acceleration in micron-sized spaces will depend on the enhancement of the surface reaction rate constant (relative to the bulk) and the adsorption/desorption rate coefficients embedded in eqn (15). These rate coefficients will be sensitive to the molecular structure of the reactants, intermediates and products as well as additional compartment features such as solvent, electric fields and pH gradients that can alter reaction energetics and transition states at the interface.23,52,53 Rate coefficients for adsorption and desorption, which also control surface reaction rates via interfacial concentration, will be similarly sensitive to the exact nature of the interface (i.e. liquid/vapor vs. oil/aqueous) as well as the solvent environment of the compartment. The kinetic framework and simulation methods described here can be adapted to account for these different environments.
Liquid/vapor interfaces are regions in which hydrophobic reactants concentrate and orient, providing unique environments for the acceleration of those reactions that are unfavorable in water (e.g. condensation reactions, peptide bond formation,54etc.). Thus, micro-compartment interfaces appear to behave somewhat analogously to micelles55 and aqueous suspensions,56 and, perhaps, nanovessels for catalytic reactions, in that molecules can sample and react in two rather different solvent environments (bulk aqueous vs. surface hydrophobic).
Whether a reaction is accelerated in a micro-compartment depends not only on the interfacial reaction rate but also on the surface concentration as well as the timescales for adsorption/desorption. For example, the adsorption kinetics at the oil–aqueous interface45 examined here, are ∼103 to 104 times slower than the observed kinetics of surfactants and other small molecules to the air–water interface (e.g. ESI droplets).57 For these faster systems, the interface reaches its equilibrium enriched concentration on ∼10 to 100 ms timescales. Many of the previous reports of accelerated reactions in ESI droplets operate under conditions, (Lcompartment ≪ Rcritical, Fig. 1), where adsorption kinetics rather than diffusion is likely limiting mass transfer to the interface. In order for surface reactions to contribute substantially to the observed rate acceleration, the droplet interface would thus require millisecond timescales to fully relax. It appears likely that some other acceleration mechanism is operative for those experiments that report product formation at microsecond timescales.
Yet there is no reason a priori to expect that all reactions are accelerated at micro-compartment interfaces since this will depend upon the fine details of how surface solvation structure, molecular orientation, acidity, and electric fields alter reaction energetics58,59 and transition states; topics that can be addressed theoretically by quantum chemistry and/or statistical mechanics. Rather, the kinetic framework presented here provides a way of using these theoretical determinations to predict the overall chemical kinetics in a micro-compartment or thin film.19Eqn (15) also provides a way of extrapolating beaker scale kinetic measurements in the laboratory to transformations for example in atmospheric compartments such as cloud droplets60 and aerosols, provided that adsorption and desorption kinetics are known.
The expression for Kobseq shown in eqn (15) is not simply related to concentration, but instead depends upon the ratio of molecules at the micro-compartment interface. This suggests a kind of “stochasticity” in micro-compartments despite the total number of molecules being rather large. In a 10 mM, R = 5 μm droplet there are ∼109 solute molecules, but unlike its macroscale analog, ∼17% of these molecules, on average, reside at the interface. This is distinct from the stochasticity that governs reaction rates under nano-confinement28,29 or in subcellular biological structures61,62 where the average concentrations of proteins or other small molecules corresponds to less than 1 molecule/compartment.25 Nevertheless, given the widespread occurrence of micro-confinement in environmental, atmospheric and biological settings, these results suggest that surfaces likely play a central role in governing the overall reaction rates and mechanisms observed in these systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Condensed Phase and Interfacial Molecular Science Program (CPIMS), in the Chemical Sciences Geosciences and Biosciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. MDW acknowledges support from a Natural Sciences and Engineering Research Council of Canada (NSERC) postdoctoral fellowship. We thank Dr Frances Houle (LBNL) and Dr Meirong Zeng (LBNL) for helpful insights and Dr William D. Hinsberg (Columbia Hill Technical Consulting) for technical assistance with Kinetiscope.References
- A. Fallah-Araghi, K. Meguellati, J.-C. Baret, A. E. Harrak, T. Mangeat, M. Karplus, S. Ladame, C. M. Marques and A. D. Griffiths, Enhanced Chemical Synthesis at Soft Interfaces: A Universal Reaction-Adsorption Mechanism in Microcompartments, Phys. Rev. Lett., 2014, 112(2), 028301 CrossRef.
- S. Banerjee, E. Gnanamani, X. Yan and R. N. Zare, Can all bulk-phase reactions be accelerated in microdroplets?, Analyst, 2017, 142(9), 1399–1402 RSC.
- M. Girod, E. Moyano, D. I. Campbell and R. G. Cooks, Accelerated bimolecular reactions in microdroplets studied by desorption electrospray ionization mass spectrometry, Chem. Sci., 2011, 2(3), 501–510 RSC.
- J. K. Lee, S. Banerjee, H. G. Nam and R. N. Zare, Acceleration of reaction in charged microdroplets, Q. Rev. Biophys., 2015, 48(4), 437–444 CrossRef CAS PubMed.
- Z. Wei, Y. Li, R. G. Cooks and X. Yan, Accelerated Reaction Kinetics in Microdroplets: Overview and Recent Developments, Annu. Rev. Phys. Chem., 2020, 71(1), 31–51 CrossRef CAS.
- X. Yan, R. M. Bain and R. G. Cooks, Organic Reactions in Microdroplets: Reaction Acceleration Revealed by Mass Spectrometry, Angew. Chem., Int. Ed., 2016, 55(42), 12960–12972 CrossRef CAS PubMed.
- S. Kwak, J. Yeo, S. Jung and I. Nam, Microdroplet Chemistry: Difference of Organic Reactions between Bulk Solution and Aqueous Microdroplets, Academic Journal of Polymer science, 2018, 1(1), 555551 Search PubMed.
- K. K. Nakashima, M. A. Vibhute and E. Spruijt, Biomolecular Chemistry in Liquid Phase Separated Compartments, Front. Mol. Biosci., 2019, 6, 21 CrossRef CAS PubMed.
- R. J. R. W. Peters, M. Marguet, S. Marais, M. W. Fraaije, J. C. M. van Hest and S. Lecommandoux, Cascade Reactions in Multicompartmentalized Polymersomes, Angew. Chem., Int. Ed., 2014, 53(1), 146–150 CrossRef CAS PubMed.
- A. K. Badu-Tawiah, D. I. Campbell and R. G. Cooks, Accelerated C–N Bond Formation in Dropcast Thin Films on Ambient Surfaces, J. Am. Soc. Mass Spectrom., 2012, 23(9), 1461–1468 CrossRef CAS.
- P. Liu, M. Lu, Q. Zheng, Y. Zhang, H. D. Dewald and H. Chen, Recent advances of electrochemical mass spectrometry, Analyst, 2013, 138(19), 5519–5539 RSC.
- G. J. Van Berkel and V. Kertesz, Using the Electrochemistry of the Electrospray Ion Source, Anal. Chem., 2007, 79(15), 5510–5520 CrossRef CAS PubMed.
- M. I. Jacobs, R. D. Davis, R. J. Rapf and K. R. Wilson, Studying Chemistry in Micro-compartments by Separating Droplet Generation from Ionization, J. Am. Soc. Mass Spectrom., 2019, 30(2), 339–343 CrossRef CAS PubMed.
- A. Gallo, A. S. F. Farinha, M. Dinis, A.-H. Emwas, A. Santana, R. J. Nielsen, W. A. Goddard and H. Mishra, The chemical reactions in electrosprays of water do not always correspond to those at the pristine air–water interface, Chem. Sci., 2019, 10(9), 2566–2577 RSC.
- J. K. Lee, K. L. Walker, H. S. Han, J. Kang, F. B. Prinz, R. M. Waymouth, H. G. Nam and R. N. Zare, Spontaneous generation of hydrogen peroxide from aqueous microdroplets, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(39), 19294–19298 CrossRef CAS PubMed.
- H. J. Sterling, M. P. Daly, G. K. Feld, K. L. Thoren, A. F. Kintzer, B. A. Krantz and E. R. Williams, Effects of supercharging reagents on noncovalent complex structure in electrospray ionization from aqueous solutions, J. Am. Soc. Mass Spectrom., 2010, 21(10), 1762–1774 CrossRef CAS PubMed.
- Z. Zhou, X. Yan, Y.-H. Lai and R. N. Zare, Fluorescence Polarization Anisotropy in Microdroplets, J. Phys. Chem. Lett., 2018, 9(11), 2928–2932 CrossRef CAS PubMed.
- Y. Li, X. Yan and R. G. Cooks, The Role of the Interface in Thin Film and Droplet Accelerated Reactions Studied by Competitive Substituent Effects, Angew. Chem., Int. Ed., 2016, 55(10), 3433–3437 CrossRef CAS PubMed.
- A. A. Heath and K. T. Valsaraj, Effects of Temperature, Oxygen Level, Ionic Strength, and pH on the Reaction of Benzene with Hydroxyl Radicals at the Air–Water Interface in Comparison to the Bulk Aqueous Phase, J. Phys. Chem. A, 2015, 119(31), 8527–8536 CrossRef CAS PubMed.
- A. B. Grommet, M. Feller and R. Klajn, Chemical reactivity under nanoconfinement, Nat. Nanotechnol., 2020, 15(4), 256–271 CrossRef CAS PubMed.
- H. G. Park and Y. Jung, Carbon nanofluidics of rapid water transport for energy applications, Chem. Soc. Rev., 2014, 43(2), 565–576 RSC.
- M. Mastalerz, Porous Shape-Persistent Organic Cage Compounds of Different Size, Geometry, and Function, Acc. Chem. Res., 2018, 51(10), 2411–2422 CrossRef CAS PubMed.
- L. R. Pestana, H. Hao and T. Head-Gordon, Diels–Alder Reactions in Water Are Determined by Microsolvation, Nano Lett., 2020, 20(1), 606–611 CrossRef CAS PubMed.
- D. Muñoz-Santiburcio and D. Marx, Chemistry in nanoconfined water, Chem. Sci., 2017, 8(5), 3444–3452 RSC.
- W. Goch and W. Bal, Stochastic or Not? Method To Predict and Quantify the Stochastic Effects on the Association Reaction Equilibria in Nanoscopic Systems, J. Phys. Chem. A, 2020, 124(7), 1421–1428 CrossRef CAS PubMed.
- M. J. Shon and A. E. Cohen, Mass Action at the Single-Molecule Level, J. Am. Chem. Soc., 2012, 134(35), 14618–14623 CrossRef CAS PubMed.
- M. Maioli, G. Varadi, R. Kurdi, L. Caglioti and G. Pályi, Limits of the Classical Concept of Concentration, J. Phys. Chem. B, 2016, 120(30), 7438–7445 CrossRef CAS PubMed.
- R. Szymanski, S. Sosnowski and Ł. Maślanka, Statistical effects related to low numbers of reacting molecules analyzed for a reversible association reaction A + B = C in ideally dispersed systems: An apparent violation of the law of mass action, J. Chem. Phys., 2016, 144(12), 124112 CrossRef CAS PubMed.
- Y. Khodorkovsky, L. Rubinovich and M. Polak, Stochastic Kinetics and Equilibrium of Nanoconfined Reactions, J. Phys. Chem. C, 2019, 123(40), 24949–24956 CrossRef CAS.
- Y. Kuramoto, Effects of Diffusion on the Fluctuations in Open Chemical Systems, Prog. Theor. Phys., 1974, 52(2), 711–713 CrossRef CAS.
- F. A. Houle, A. A. Wiegel and K. R. Wilson, Changes in Reactivity as Chemistry Becomes Confined to an Interface. The Case of Free Radical Oxidation of C30H62 Alkane by OH, J. Phys. Chem. Lett., 2018, 9(5), 1053–1057 CrossRef CAS PubMed.
- F. Jin, R. Balasubramaniam and K. J. Stebe, Surfactant adsorption to spherical particles: the intrinsic length scale governing the shift from diffusion to kinetic-controlled mass transfer, J. Adhes., 2004, 80(9), 773–796 CrossRef CAS.
- W. D. Hinsberg, F. A. Houle, Kinetiscope©, http://hinsberg.net/kinetiscope/, 2020.
- D. L. Bunker, B. Garrett, T. Kleindienst and G. S. Long, Discrete simulation methods in combustion kinetics, Combust. Flame, 1974, 23(3), 373–379 CrossRef CAS.
- D. T. Gillespie, General method for numerically simulating stochastic time evolution of coupled chemical reactions, J. Comput. Phys., 1976, 22(4), 403–434 CrossRef CAS.
- N. Heine, C. Arata, A. H. Goldstein, F. A. Houle and K. R. Wilson, Multiphase Mechanism for the Production of Sulfuric Acid from SO2 by Criegee Intermediates Formed During the Heterogeneous Reaction of Ozone with Squalene, J. Phys. Chem. Lett., 2018, 9(12), 3504–3510 CrossRef CAS PubMed.
- N. Heine, F. A. Houle and K. R. Wilson, Connecting the Elementary Reaction Pathways of Criegee Intermediates to the Chemical Erosion of Squalene Interfaces during Ozonolysis, Environ. Sci. Technol., 2017, 51(23), 13740–13748 CrossRef CAS PubMed.
- F. A. Houle, W. D. Hinsberg and K. R. Wilson, Oxidation of a model alkane aerosol by OH radical: the emergent nature of reactive uptake, Phys. Chem. Chem. Phys., 2015, 17(6), 4412–4423 RSC.
- F. A. Houle, A. A. Wiegel and K. R. Wilson, Predicting Aerosol Reactivity Across Scales: from the Laboratory to the Atmosphere, Environ. Sci. Technol., 2018, 52(23), 13774–13781 CrossRef CAS PubMed.
- M. J. Liu, A. A. Wiegel, K. R. Wilson and F. A. Houle, Aerosol Fragmentation Driven by Coupling of Acid–Base and Free-Radical Chemistry in the Heterogeneous Oxidation of Aqueous Citric Acid by OH Radicals, J. Phys. Chem. A, 2017, 121(31), 5856–5870 CrossRef CAS PubMed.
- A. A. Wiegel, K. R. Wilson, W. D. Hinsberg and F. A. Houle, Stochastic methods for aerosol chemistry: a compact molecular description of functionalization and fragmentation in the heterogeneous oxidation of squalane aerosol by OH radicals, Phys. Chem. Chem. Phys., 2015, 17(6), 4398–4411 RSC.
- C. Herdes, Å. Ervik, A. Mejía and E. A. Müller, Prediction of the water/oil interfacial tension from molecular simulations using the coarse-grained SAFT-γ Mie force field, Fluid Phase Equilibria, 2018, 476, 9–15 CrossRef CAS.
- I. Langmuir, The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 1918, 40(9), 1361–1403 CrossRef CAS.
- G. S. Girolami, A Simple "Back of the Envelope" Method for Estimating the Densities and Molecular Volumes of Liquids and Solids, J. Chem. Educ., 1994, 71(11), 962 CrossRef CAS.
- G. Tomoaia, A. Tomoaia-Cotisel, M. Tomoaia-Cotisel and A. Mocanu, Kinetic study of adsorption of some biocompounds at the oil/water interface, Cent. Eur. J. Chem., 2005, 3(2), 347–360 CAS.
- K. Meguellati, A. Fallah-Araghi, J.-C. Baret, A. El Harrak, T. Mangeat, C. M. Marques, A. D. Griffiths and S. Ladame, Enhanced imine synthesis in water: from surfactant-mediated catalysis to host–guest mechanisms, Chem. Commun., 2013, 49(96), 11332–11334 RSC.
- K. T. Valsaraj, Trace gas adsorption thermodynamics at the air−water interface: Implications in atmospheric chemistry, Pure Appl. Chem., 2009, 81(10), 1889 CAS.
- Wolfram Research, Inc., Mathematica, Version 12.1, Champaign, Illinois, 2020 Search PubMed.
- J. Chen, F. S. Ehrenhauser, K. T. Valsaraj and M. J. Wornat, Uptake and UV-Photooxidation of Gas-Phase PAHs on the Surface of Atmospheric Water Films. 1. Naphthalene, J. Phys. Chem. A, 2006, 110(29), 9161–9168 CrossRef CAS PubMed.
- J. F. Davies and K. R. Wilson, Nanoscale interfacial gradients formed by the reactive uptake of OH radicals onto viscous aerosol surfaces, Chem. Sci., 2015, 6(12), 7020–7027 RSC.
- A. A. Wiegel, M. J. Liu, W. D. Hinsberg, K. R. Wilson and F. A. Houle, Diffusive confinement of free radical intermediates in the OH radical oxidation of semisolid aerosols, Phys. Chem. Chem. Phys., 2017, 19(9), 6814–6830 RSC.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic catalysis of a Diels–Alder reaction, Nature, 2016, 531(7592), 88–91 CrossRef PubMed.
- N. Narendra, X. Chen, J. Wang, J. Charles, R. G. Cooks and T. Kubis, Quantum Mechanical Modeling of Reaction Rate Acceleration in Microdroplets, J. Phys. Chem. A, 2020, 124(24), 4984–4989 CrossRef CAS PubMed.
- E. C. Griffith and V. Vaida, In situ observation of peptide bond formation at the water–air interface, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(39), 15697–15701 CrossRef CAS PubMed.
- G. La Sorella, G. Strukul and A. Scarso, Recent advances in catalysis in micellar media, Green Chem., 2015, 17(2), 644–683 RSC.
- S. Narayan, J. Muldoon, M. G. Finn, V. V. Fokin, H. C. Kolb and K. B. Sharpless, “On Water”: Unique Reactivity of Organic Compounds in Aqueous Suspension, Angew. Chem., Int. Ed., 2005, 44(21), 3275–3279 CrossRef CAS PubMed.
- G. Bleys and P. Joos, Adsorption kinetics of bolaform surfactants at the air/water interface, J. Phys. Chem., 1985, 89(6), 1027–1032 CrossRef CAS.
- A. F. Tuck, Gibbs Free Energy and Reaction Rate Acceleration in and on Microdroplets, Entropy, 2019, 21(11), 1044 CrossRef CAS.
- A. Sanfeld and A. Steinchen, Chemical reactions in microdroplets and microbubbles. Thermodynamic approach, C. R. Chim., 1999, 2(14), 697–700 CAS.
- D. J. Donaldson and K. T. Valsaraj, Adsorption and Reaction of Trace Gas-Phase Organic Compounds on Atmospheric Water Film Surfaces: A Critical Review, Environ. Sci. Technol., 2010, 44(3), 865–873 CrossRef CAS PubMed.
- D. J. Wilkinson, Stochastic modelling for quantitative description of heterogeneous biological systems, Nat. Rev. Genet., 2009, 10(2), 122–133 CrossRef CAS PubMed.
- H. H. McAdams and A. Arkin, It's a noisy business! Genetic regulation at the nanomolar scale, Trends Genet., 1999, 15(2), 65–69 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc03189e |
| This journal is © The Royal Society of Chemistry 2020 |