Open Access Article
Open Access ArticleRationalizing the diverse reactivity of [1.1.1]propellane through σ–π-delocalization†
Alistair J.
Sterling
 a,
Alexander B.
Dürr
a,
Alexander B.
Dürr
 a,
Russell C.
Smith‡
b,
Edward A.
Anderson
a,
Russell C.
Smith‡
b,
Edward A.
Anderson
 *a and
Fernanda
Duarte
*a and
Fernanda
Duarte
 *a
*a
aChemistry Research Laboratory, 12 Mansfield Road, Oxford, OX1 3TA, UK. E-mail: edward.anderson@chem.ox.ac.uk; fernanda.duartegonzalez@chem.ox.ac.uk
bJanssen P.R.D., 3210 Merryfield Row, San Diego, California CA 92121, USA
First published on 13th April 2020
Abstract
[1.1.1]Propellane is the ubiquitous precursor to bicyclo[1.1.1]pentanes (BCPs), motifs of high value in pharmaceutical and materials research. The classical Lewis representation of this molecule places an inter-bridgehead C–C bond along its central axis; ‘strain relief’-driven cleavage of this bond is commonly thought to enable reactions with nucleophiles, radicals and electrophiles. We propose that this broad reactivity profile instead derives from σ–π-delocalization of electron density in [1.1.1]propellane. Using ab initio and DFT calculations, we show that its reactions with anions and radicals are facilitated by increased delocalization of electron density over the propellane cage during addition, while reactions with cations involve charge transfer that relieves repulsion inside the cage. These results provide a unified framework to rationalize experimental observations of propellane reactivity, opening up opportunities for the exploration of new chemistry of [1.1.1]propellane and related strained systems that are useful building blocks in organic synthesis.
Introduction
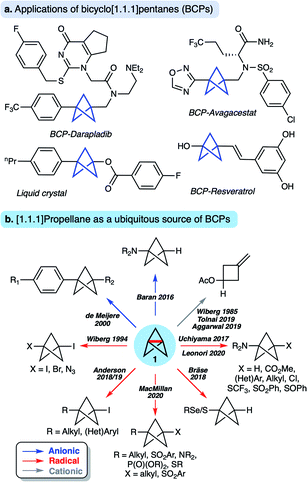
[1.1.1]Propellane (tricyclo[1.1.1.01,3]pentane 1, Fig. 1) is a molecule that has long fascinated organic and theoretical chemists due to its unique structure and intriguing reactivity. In recent years, 1 has also become established as a key precursor to bicyclo[1.1.1]pentanes (BCPs),1,2 motifs that are attractive bioisosteres for aryl,3–8 alkynyl9 and tert-butyl10 groups in drug design due to the enhanced pharmacokinetic profile of the BCP spacer unit compared to the parent functional group (Fig. 1a). BCPs are also useful motifs for organic materials, including rod-like one-dimensional polymers,11 supramolecular spacer units,12 liquid crystals13 and FRET sensors.14 Such applications have stimulated the development of a number of methods to access BCPs in a single step from 1via radical15–24 and anionic25–29 intermediates (Fig. 1b). Limitations nonetheless remain, in particular due to the harsh reaction conditions often associated with many of these processes, which can restrict functional group tolerance. A third reactivity mode of 1 involves facile cationic addition, a process that fragments the cage to an exo-methylene cyclobutane.30–32This diverse ‘omniphilic’ reactivity has traditionally been ascribed to the high strain energy of [1.1.1]propellane (total strain energy ∼100 kcal mol−1),33 albeit only ∼30 kcal mol−1 of this strain is thought to be released on cleavage of the inter-bridgehead C1–C3 bond.2,34 Nonetheless, this omniphilicity is not generally observed with other ring-opening reactions where relief of ring strain is a driving force (such as in cyclopropane, Estrain = ∼28 kcal mol−1),35 which could suggest other factors govern the reactivity of 1.36
To date, a handful of experimental studies have employed density functional theory (DFT) to investigate the pathways of addition of radicals and anions to [1.1.1]propellane, offering useful insight to support reaction development.17,18,20,28,29 However, no in-depth theoretical analysis has tackled the origin of the omniphilic reactivity of 1. Here we combine ab initio approaches with electron density difference analysis and Distortion/Interaction Analysis (DIA)37–39 to develop a unified model for the reactivity of [1.1.1]propellane. Contrary to classical explanations, we demonstrate that its chemistry is not determined simply by geometric ‘strain relief’; instead, it is the change in electron delocalization over the cage that defines the observed activation profiles. These results bridge the gap between the theoretical understanding of [1.1.1]propellane as a ‘scientific curiosity’ to its applications in real-life settings.2
Results and discussion
The structure of [1.1.1]propellane
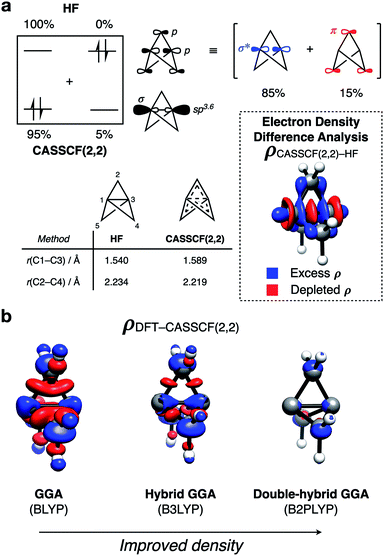
Before considering the reactivity of [1.1.1]propellane, we first sought to characterize the nature of its inter-bridgehead C1– C3 bond in the ground state (Fig. 2a). The geometry of 1 has been determined experimentally by low-temperature X-ray diffraction40 and gas-phase electron diffraction;41 from the latter, the C1–C3 distance was found to be 1.594 Å which, being similar to the C–C bond length in ethane (1.524 Å),42 is suggestive of a C1–C3 bonding interaction. The nature of this bond has been much debated over the past 30 years, with theoretical43–55 and experimental30,41,43,56–59 studies offering contrasting evidence. For example, despite a closed-shell singlet ground state and a calculated bond energy of ∼65 kcal mol−1,43 photoelectron spectroscopy reveals the HOMO (C1–C3 σ MO) to be non-bonding due to poor overlap of atomic orbitals between the ‘inverted’ carbon atoms.59 This result is corroborated by synchrotron experiments that reveal depletion of electron density at the bond critical point.57Such studies led to the proposal that the inverted C1–C3 bond in 1 should be best described as a charge-shift bond, with its stability attributed to resonance stabilization between the covalent ([C1˙⋯˙C3], repulsive) and ionic ([C1(−)⋯(+)C3] and [C1(+)⋯(−):C3], attractive) structures.47,60 This type of bonding arises through significant Pauli repulsion pressure between each of the C1/3–C2 ‘wing’ bonds and the C1–C3 bond,61,62 and accounts for both the observed closed-shell singlet ground state and the unusual positive sign of the Laplacian of the electron density at the critical point of the C1–C3 bond. However, the consequences of the unique electronic configuration of 1 on its reactivity remains an unanswered question.
To further quantify the effects of the electronic repulsion within the propellane cage, we employed the complete active space (CASSCF) method (with a (2,2) active space) for the formal inclusion of static correlation. This allows electrons to populate both the C1–C3 σ and σ* orbitals (Fig. 2a). In ‘normal’ closed-shell organic molecules, >1.98 electrons populate the occupied molecular orbitals (MOs), however in 1 we found this value to be 1.91 electrons, indicating that static correlation effects are important. Such behavior is typically only seen in systems with near-degenerate frontier orbitals, which is certainly not the case here (Egap = 13.0 eV, HF/def2-QZVPP). We propose that delocalization of electron density from the C1–C3 σ to σ* reduces the unusually high electronic repulsion inside the propellane cage; the effect of this delocalization can be seen in the stabilization of the structure of 1 by 19.2 kcal mol−1.
An electron density difference plot (Fig. 2a, inset) comparing the Hartree–Fock and CASSCF(2,2) densities reveals that, using CASSCF(2,2), charge is depleted from the center of the cage (red lobes), and is instead delocalized onto the bridge carbon atoms (blue lobes). This is consistent with the depleted electron density that is observed at the critical point of the C1–C3 bond.
This electronic reorganization can be considered as ‘σ–π-delocalization’ (σ → [σ* + π]), where electrons from the C1–C3 σ MO partially populate the C1–C3 σ* orbital, which is of the correct symmetry to overlap with the π system formed from p orbitals on the bridge carbon atoms (Fig. 2a, top).63 This effect can be observed through lateral compression of the cage to maximize this ‘side-on’ orbital overlap, decreasing the C2–C4 distance from 2.234 to 2.219 Å and increasing the C1–C3 distance from 1.540 to 1.589 Å, which is in excellent agreement with experiment (Fig. 2a, bottom left).
Overall, this description of the electronic structure of 1 is equivalent to the charge-shift bonding model introduced by Shaik and co-workers with a localized representation of the orbitals (see ESI Fig. S4†).47 Moreover, the use of electron density difference plots provides an intuitive pictorial representation of the role of delocalization in 1. It reveals that electron density is not only expelled from the cage along the C1–C3 axis, as was previously thought, but is also delocalized onto the bridge carbon atoms. This delocalization mechanism both reduces Pauli repulsion between the C1–C3 and C1–C2 bonding electrons, and stabilizes the cage towards fragmentation of the C1–C2 bond.
To reduce the cost and complexity of the calculations, we also sought a suitable DFT method to accurately model these delocalization effects and the reactivity of 1. The performance of DFT depends directly on the electron density, and the challenge in describing 1 arises from low density in the C1–C3 region.57 This problem can be qualitatively depicted using density difference plots (Fig. 2b), which were calculated for a range of DFT functionals and compared to those obtained with CASSCF(2,2). While the inexpensive GGA functional (BLYP)64,65 accurately predicts the C1–C3 bond length to <0.01 Å, it poorly reproduces the CASSCF(2,2) density, and substantially over-delocalizes electron density across the cage. The incorporation of some exact exchange into the functional (B3LYP)66 over-localizes electron density along the C1–C3 axis, resulting in a bond that is too short, and likely too strong. However, further augmentation to a double-hybrid GGA functional through the inclusion of MP2-like correlation (B2PLYP)67 results in a lengthened C1–C3 bond, and a better match with the CASSCF(2,2) electron density. Further analysis of the singlet-triplet gap and vertical ionization potential for each of these functionals reveals double-hybrid GGA functionals to give the best performance of those tested (see ESI Fig. S13†). These results highlight how accuracy in geometries and energetics are not necessarily linked to accuracy in electronic structure.
A benchmark study on the reactivity of [1.1.1]propellane with anions, radicals and cations reactions also revealed that double-hybrid DFT was required to accurately describe the geometric and electronic features of this system (see ESI Fig. S17–S22†). Among them, B2GP-PLYP-D3BJ with the triple-ζ quality basis set def2-TZVP was found to afford good geometries and energies within 1 kcal mol−1 of the reference coupled-cluster method DLPNO-CCSD(T).68–70 Solvent effects, accounted with the SMD implicit model,71 were found to be particularly important for anionic and cationic reactions, but have a much smaller effect on radical reactivity.72
The reactivity of [1.1.1]propellane with anions
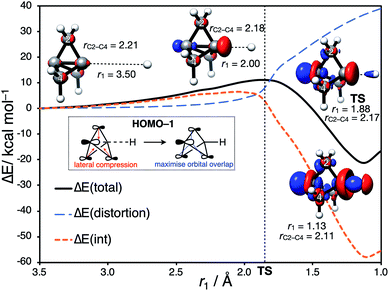
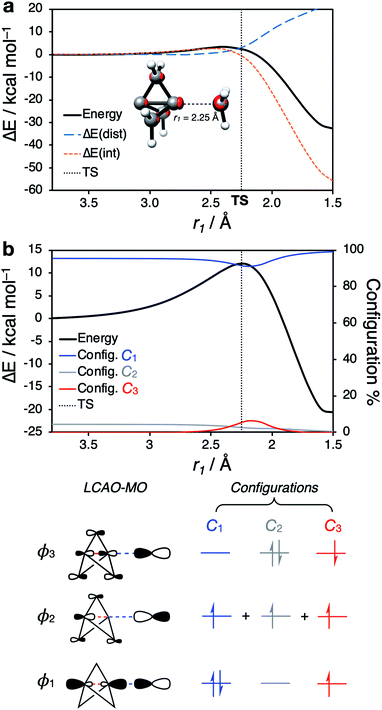
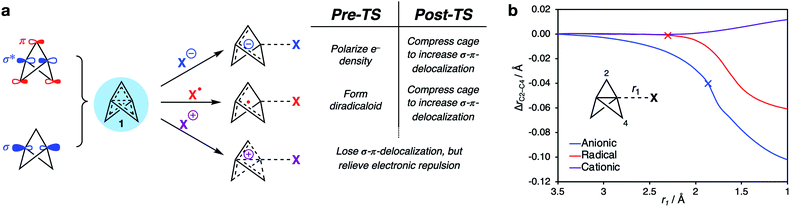
Having identified the beneficial role of σ–π-delocalization and a suitable computational methodology, we set out to explore the reactivity of 1 under a variety of conditions, and compare theoretical predictions with experimental reality. This began with a study of anionic addition, for which a number of examples of have been described that access aryl-, alkyl- and amino-substituted BCPs.25–29 Given the apparent strain relief associated with this chemistry, it is perhaps surprising that extended reaction times (∼16 h) and elevated temperatures (>50 °C) are often required for successful addition. Walsh et al. have studied the related addition of dithiane anions,29 complementing their synthetic work with DFT calculations at the M06-2X level of theory,73 which revealed carbanion addition to be highly endergonic. These examples led us to question the role of strain relief in the reaction of anions with 1, and in particular how a thermodynamically disfavored process could occur in a system thought to be primed to react.Addition of an anion to 1 is analogous to a standard SN2 reaction, where the leaving group in this case is the distal C3 atom in the cage. However, the inverted geometry of the bridgehead carbon atom in 1 uniquely circumvents the need for planarization in the transition state,39 which might suggest that the activation barrier has a greater contribution from a change in electronic structure than from geometric distortion.23,26,27,33 To investigate the origin of this barrier to addition, a Distortion/Interaction Analysis (DIA) was performed on a model hydride addition to 1.37–39 This approach separates the overall energy of the addition [ΔE(total)] into geometric distortion [ΔE(dist)] and electronic interactions [ΔE(int)] of the approaching species. On going from the reactant state to the transition state (TS), ΔE(int) was found to be positive, and to dominate over ΔE(dist) (70% contribution of ΔE(int) up to the TS) (Fig. 3). This is highly unusual: to our knowledge, ΔE(int) has not been observed to be positive and greater than ΔE(dist) for any other system.39 Prior to the TS, the population of the σ and [σ* + π] MOs remains constant while electron density is polarized by the approaching anion (Fig. 3, blue lobes, and ESI Fig. S7 and S8†), suggesting that electrostatic repulsion between the anion and 1 is the dominant factor causing the barrier to addition.
Significant structural distortion only occurs after the transition state, which suggests that geometric strain relief is not responsible for the reactivity of 1. In fact, to maximize σ–π-delocalization, the cage is laterally compressed to increase the overlap of each bridge carbon p orbital with the C3 p orbital in the HOMO−1 (Fig. 3, inset), which is a strain-increasing process.
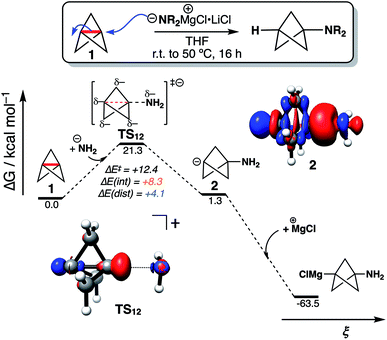
To explore the implications of these findings in a chemically established setting, we modelled the addition of turbo-Hauser amides (R2NMgCl·LiCl, R = alkyl) to form 1-amino-BCPs (Fig. 4).26 The reaction of 1 with amide anions was computed using NH2−; the formation of the BCP anion adduct 2 was found to be reversible and endergonic (ΔG‡ = 21.3 kcal mol−1, ΔG° = +1.3 kcal mol−1), despite the formation of C–N in place of the weaker C1–C3 bond (balanced with the formation of a C-centered anion). DIA at the transition state (TS12) reveals ΔE(dist) and ΔE(int) are both positive, with ΔE(int) around twice the magnitude of ΔE(dist) (+8.3 and +4.1 kcal mol−1 respectively). Only on complexation of the bicyclo[1.1.1]pentyl anion to a MgCl+ ion does the overall reaction become highly exergonic (ΔG° = −64.8 kcal mol−1). This description appears consistent with the relatively harsh reaction conditions often required for anionic additions, as significant electronic repulsion must be overcome prior to the development of the stabilizing σ–π-delocalization.
The reactivity of [1.1.1]propellane with radicals
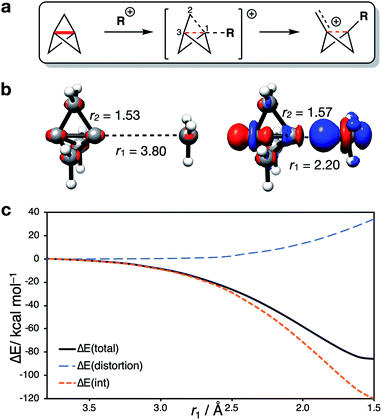
Our attention next turned to the reactivity of 1 with radicals, chemistry that is of much utility in the synthesis of highly-functionalized BCPs.15–21,23,24 Such reactions proceed through addition of a radical to the C1–C3 bond to give a bridgehead BCP radical that subsequently reacts either via atom transfer, or addition to a radical trap (such as an azodicarboxylate, a further molecule of 1, or an organometallic species). Alkoxycarbonyl, alkyl and aryl radical additions have been studied using DFT (B3LYP, M06-2X, ωB97X-D, B2PLYP)66,67,73,74 by the Uchiyama group17 and ourselves,18,20 where the focus has lain on the fate of the bicyclo[1.1.1]pentyl radical.We instead sought to study the initial radical addition to 1, where a similar reactivity mode to the anionic addition was anticipated (Fig. 5). As in the anionic regime, the barrier for the addition of ˙CH3 is dominated by the positive ΔE(int) term (66% contribution up to the TS, Fig. 5a). ΔE(dist) again increases most significantly after the TS, showing that this reactivity profile cannot be explained by simple geometric distortion. However, compared with the anionic addition, radical addition features a decreased electrostatic penalty in bringing two neutral species together; as a result, the additional electron density from approach of the radical species is incorporated inside the cage, rather than expelled from the back of the cage (Fig. 5a, r1 = 2.25 Å).
To understand how the repulsion from the injection of an additional electron is overcome during the reaction, we examined the change in CASSCF(3,3) MO coefficients along the reaction coordinate (Fig. 5b). At large separation, the orbitals resemble those of the isolated species; ϕ1 and ϕ3 correspond to the C1–C3 σ and [σ* + π] orbitals of 1 respectively (vide supra), and ϕ2 corresponding to the p orbital of the radical species. As the two species approach one another, the MOs mix such that ϕ1 is the bonding combination, ϕ2 is non-bonding, and ϕ3 is the antibonding combination of the σ orbitals in the forming and breaking bonds (Fig. 5b, bottom). The populations of these MOs are described by the coefficients Ci (i = 1, 2, 3), which change over the course of the reaction. C1 [(ϕ1)2(ϕ2)1(ϕ3)0] (blue) and C2 [(ϕ1)0(ϕ2)1(ϕ3)2] (grey), which correspond to the σ → [σ* + π] delocalization in 1 itself, dominate at large separations, but decrease approaching the TS, where a new configuration C3 [(ϕ1)1(ϕ2)1(ϕ3)1] (red) emerges (Fig. 5c). This corresponds to the singlet diradical state of 1 interacting with the approaching radical species.
These results indicate that cleavage of the C1–C3 bond by a radical species requires access to an open-shell doublet electronic configuration. 1 itself is not diradicaloid in nature,54 and as such perturbation of the electronic structure of 1 by an approaching radical necessarily results in a ‘more diradical’ configuration, which minimizes electronic repulsion inside the cage at the TS (Fig. 5c). This description is consistent with the equivalent charge-shift representation of the C1–C3 bond, where the covalent-ionic resonance interaction decreases upon interaction with a radical species, causing an increase in ΔE(int) prior to the TS.
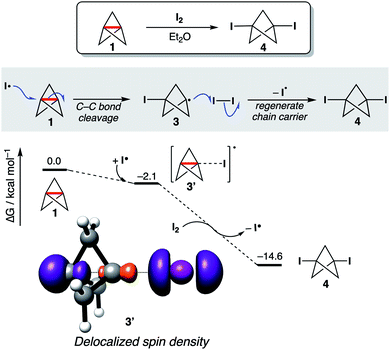
To test the consequences of this proposal in a chemically established setting, the addition of I2 to 1 was selected as a model reaction, not least given its utility as a method for the titration of solutions of 1 (Fig. 6).75 This reaction is presumed to occur via addition of I˙ to 1 to form an iodobicyclo[1.1.1] pentyl radical 3, which is trapped by I2 to afford 1,3-diiodoBCP 4, regenerating I˙ as a chain carrier. However, computational study of this reaction revealed that the initial addition of I˙ does not proceed to the expected carbon-centered radical; remarkably, barrierless exergonic association (ΔG° = −2.1 kcal mol−1) of the iodine radical to 1 is favored over full C1–C3 bond cleavage, with only a slight increase in the C1–C3 bond length observed in 3′ compared with 1 (Δr2 = 0.02 Å). Spin density is delocalized in the radical adduct 3′ (Fig. 6), despite the lack of distortion of the geometry of 1; this causes C1–C3 bond weakening in order to accommodate the unpaired electron, resulting in facile iodine atom abstraction from I2 through the distal carbon atom, to form 4 and an iodine radical. We propose that full C1–C3 cleavage during radical addition can only occur if the formation of the new C–X bond is sufficiently strong to outweigh the loss of σ–π-delocalization energy; in this example, the formation of a weak C–I bond results in the C1–C3 bond remaining intact. Should a strong C–X bond be formed upon addition, full cleavage of the inter-bridgehead C–C bond is seen (see ESI Fig. S29† for addition of halide and chalcogen hydride radicals to [1.1.1]propellane). These results suggest that 1 can undergo reversible radical reactions, which again challenges the role of strain relief as a reaction driving force.
The reactivity of [1.1.1]propellane with cations
In both radical and anionic reactions, the propellane cage must accommodate an increase in electron density (Fig. 7). This raised the question of the consequence of removing electrons from the cage, as would be expected in cationic activation. The reactions of 1 with cations is an underexplored field; despite the observation of rapid protonation by acetic acid,30 few cation-promoted reactions have been reported.31,32 Cationic bicyclo[1.1.1]pentyl adducts are known to rapidly fragment to bicyclo[1.1.0]butyl-1-carbinyl cations (Fig. 7a),76 which suggests that a significant change in the electronics of the cage occurs as addition takes place.Analysis of the electron density distribution on a model system (methyl cation addition to 1) revealed contrasting behavior to that seen with anions and radicals. While in the latter cases transition state barriers arise from the increase in electron repulsion during the approach of the two species, for cation addition, electron density is lost from the cage (Fig. 7b). In this case, charge transfer from 1 to the cation was found to be barrierless (Fig. 7c), and accompanied by a large negative ΔE(int).
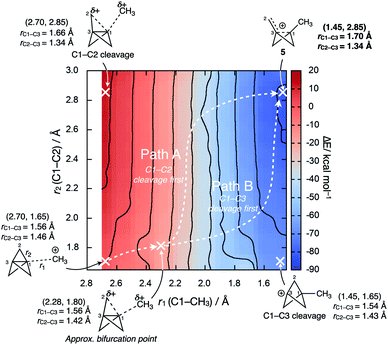
Intriguingly, the C1–C3 bond was found to decrease in length over the course of the addition, which contrasts with the instinctive expectation that bond cleavage should be accompanied by bond lengthening. Upon reaction at C1, the frontside C1–C2 bonds lengthen, while the backside C3–C2 bonds shorten. A More O'Ferrall–Jencks plot for the addition process as a function of the forming C1–CH3 length (r1) and the breaking C1–C2 length (r2) reveals a relatively flat bifurcated potential energy surface, where initial charge transfer that cleaves the C1–C3 bond is accompanied by either delayed donation of electron density from the C1–C2 bond to stabilize the forming cation through cage fragmentation (Fig. 8, path A), or the formation of a bicyclo[1.1.1]pentyl cation that then spontaneously fragments (path B). Both paths lead to a non-classical bicyclo[1.1.0]butyl-1-carbinyl cation 5 with a partially-formed C1–C3 bond.77 No local minimum or shoulder was observed for the bicyclo[1.1.1]pentyl cation, suggesting that this species is not a viable intermediate in the cationic reactivity of 1.
We suggest that, ironically, C1–C2 fragmentation occurs due to the loss of Pauli repulsion inside the cage, as the resultant decreased population of the [σ* + π] MO (σ–π delocalization) weakens the C1–C2 bonds; the C1–C3 bond is also weakened and decreases in length as electron density is donated to the cation. This observation contrasts with analogous results from Jemmis and co-workers in calculations of halogen-bonded complexes of 1, where the removal of electron density from the cage was suggested to strengthen the C1–C3 bond (B3LYP-D3BJ/QZ4P).45
A unified model for [1.1.1]propellane reactivity
The above results provide a unified framework that explains the omniphilic reactivity of [1.1.1]propellane with anions, radicals and cations. Two distinct modes of reactivity are defined, with the main features summarized as follows:(1) The ground state structure of 1 is stabilized by partial population of the C1–C3 σ-antibonding/bridge π-bonding orbitals. The resultant σ–π-delocalization relieves Pauli repulsion inside the cage (Fig. 9a). This leads to a moldable electron density that allows 1 to engage with electron-rich, electron-deficient and open-shell species.
(2) Anionic and radical additions to 1 involve an increase in electronic repulsion inside an already electron-rich cage, causing a barrier to addition. To offset this effect, stabilization after the transition state occurs through σ–π-delocalization of electron density over the cage, which is maximized through compression of the cage (Fig. 9b, blue [anion] and red [radical] lines).
(3) Cationic additions are dominated by loss of electron density from the electron-rich cage through charge transfer to the cation. This process is barrierless due to the reduction of Pauli repulsion. However, as the σ–π-delocalization that results from this repulsion is itself responsible for the structural integrity of the propellane cage (Fig. 9b, purple line), this loss of stabilization can result in spontaneous fragmentation to form a bicyclo[1.1.0]butyl-1-carbinyl cation.
These results provide a basis to develop new reactions of 1, such as processes that capitalize on the unique structural distortion of the cage upon loss of electronic repulsion. We also predict that ‘reversible addition’ reactivity could feature in the formation of radical-pair complexes with species incapable of overcoming the delocalization energy of 1. Moreover, we suggest that substitution of the bridge carbon atoms, either as heteroatoms or with carbon-based substituents, will modify the degree of σ–π-delocalization both in the ground state and during reactions. The consequences of substitution on strain and electronic structure in [1.1.1]propellanes have been suggested to derive from changes in electronegativity; however, the ability of substituents to engage in σ–π-delocalization is an alternative effect to consider,37,78,79 for example stabilizing addition pathways by increased delocalization.
Conclusions
The classical Lewis representation of [1.1.1]propellane places an inter-bridgehead bond along its central axis, which is thought to enable reactions through ‘rapid strain relief’. Here, we have developed a unified framework that challenges this view, and explains the omniphilic reactivity profile of 1. We show that the ground state electronic structure of 1 is best described as a delocalized electron density spanning the entire cage. The result is a moldable electron density that imparts a broad reactivity profile on 1: anionic and radical additions are favored by stabilization of adducts through increased σ–π-delocalization, while reactions with cationic species are driven by charge transfer that relieves Pauli repulsion. We anticipate that this understanding will open up possibilities for the exploration of new reactivity of [1.1.1]propellane and related systems, and will provide a general framework to understand the behavior of strained cage-like molecules, which continue to be of both fascination and utility in organic synthesis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Sason Shaik and Prof. Philippe C. Hiberty for comments on the manuscript, and Dr Alex J. W. Thom, Harry W. T. Morgan and Tom A. Young for insightful discussions. A. J. S. thanks the EPSRC Centre for Doctoral Training in Synthesis for Biology and Medicine for a studentship (EP/L015838/1), generously supported by AstraZeneca, Diamond Light Source, Defence Science and Technology Laboratory, Evotec, GlaxoSmithKline, Janssen, Novartis, Pfizer, Syngenta, Takeda, UCB and Vertex. A. J. S. also thanks the Oxford-Radcliffe Scholarship for a studentship. A. B. D. thanks the Heinrich Hertz Foundation for a fellowship. This work used the Cirrus UK National Tier-2 HPC Service at EPCC (http://www.cirrus.ac.uk) funded by the University of Edinburgh and EPSRC (EP/P020267/1) and the EPSRC Centre for Doctoral Training for Theory and Modelling in Chemical Sciences (EP/L015722/1) for providing access to the Dirac cluster at Oxford. E. A. A. thanks the EPSRC for support (EP/S013172/1).Notes and references
- M. D. Levin, P. Kaszynski and J. Michl, Chem. Rev., 2000, 100, 169–234 CrossRef CAS PubMed.
- A. M. Dilmaç, E. Spuling, A. de Meijere and S. Bräse, Angew. Chem., Int. Ed., 2017, 56, 5684–5718 CrossRef PubMed.
- A. F. Stepan, C. Subramanyam, I. V. Efremov, J. K. Dutra, T. J. O'Sullivan, K. J. Dirico, W. S. McDonald, A. Won, P. H. Dorff, C. E. Nolan, S. L. Becker, L. R. Pustilnik, D. R. Riddell, G. W. Kauffman, B. L. Kormos, L. Zhang, Y. Lu, S. H. Capetta, M. E. Green, K. Karki, E. Sibley, K. P. Atchison, A. J. Hallgren, C. E. Oborski, A. E. Robshaw, B. Sneed and C. J. O'Donnell, J. Med. Chem., 2012, 55, 3414–3424 CrossRef CAS PubMed.
- N. D. Measom, K. D. Down, D. J. Hirst, C. Jamieson, E. S. Manas, V. K. Patel and D. O. Somers, ACS Med. Chem. Lett., 2017, 8, 43–48 CrossRef CAS PubMed.
- Y. P. Auberson, C. E. Brocklehurst, M. Furegati, T. C. Fessard, G. Koch, A. Decker, L. La Vecchia and E. Briard, ChemMedChem, 2017, 12, 590–598 CrossRef CAS PubMed.
- Y. L. Goh, Y. T. Cui, V. Pendharkar and V. A. Adsool, ACS Med. Chem. Lett., 2017, 8, 516–520 CrossRef CAS PubMed.
- K. C. Nicolaou, D. Vourloumis, S. Totokotsopoulos, A. Papakyriakou, H. Karsunky, H. Fernando, J. Gavrilyuk, D. Webb and A. F. Stepan, ChemMedChem, 2016, 11, 31–37 CrossRef CAS PubMed.
- J. Wang, H. Lundberg, S. Asai, P. Martín-Acosta, J. S. Chen, S. Brown, W. Farrell, R. G. Dushin, C. J. O'Donnell, A. S. Ratnayake, P. Richardson, Z. Liu, T. Qin, D. G. Blackmond and P. S. Baran, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6404–E6410 CrossRef CAS PubMed.
- I. S. Makarov, C. E. Brocklehurst, K. Karaghiosoff, G. Koch and P. Knochel, Angew. Chem., Int. Ed., 2017, 56, 12774–12777 CrossRef CAS PubMed.
- M. V. Westphal, B. T. Wolfstädter, J. M. Plancher, J. Gatfield and E. M. Carreira, ChemMedChem, 2015, 10, 461–469 CrossRef CAS PubMed.
- L. Itzhaki, E. Altus, H. Basch and S. Hoz, Angew. Chem., Int. Ed., 2005, 44, 7432–7435 CrossRef CAS PubMed.
- P. F. H. Schwab, B. C. Noll and J. Michl, J. Org. Chem., 2002, 67, 5476–5485 CrossRef CAS PubMed.
- A. De Meijere and M. Messner, Mol. Cryst. Liq. Cryst., 1994, 257, 161–167 CrossRef CAS.
- A. De Meijere, Z. Ligang, V. N. Belov, M. Bossi, M. Noltemeyer and S. W. Hell, Chem.–Eur. J., 2007, 13, 2503–2516 CrossRef CAS PubMed.
- P. Kaszynski, A. C. Friedli and J. Michl, J. Am. Chem. Soc., 1992, 114, 601–620 CrossRef CAS.
- K. D. Bunker, US Pat., 2017081295, 2015.
- J. Kanazawa, K. Maeda and M. Uchiyama, J. Am. Chem. Soc., 2017, 139, 17791–17794 CrossRef CAS PubMed.
- D. F. J. Caputo, C. Arroniz, A. Dürr, J. J. Mousseau, A. F. Stepan, S. J. Mansfield and E. A. Anderson, Chem. Sci., 2018, 9, 5295–5300 RSC.
- R. M. Bär, S. Kirschner, M. Nieger and S. Bräse, Chem.–Eur. J., 2018, 24, 1373–1382 CrossRef PubMed.
- J. Nugent, C. Arroniz, B. R. Shire, A. J. Sterling, H. D. Pickford, M. L. J. Wong, S. J. Mansfield, D. F. J. Caputo, B. Owen, J. J. Mousseau, F. Duarte and E. A. Anderson, ACS Catal., 2019, 9, 9568–9574 CrossRef CAS.
- M. L. J. Wong, J. J. Mousseau, S. J. Mansfield and E. A. Anderson, Org. Lett., 2019, 21, 2408–2411 CrossRef CAS PubMed.
- M. Kondo, J. Kanazawa, T. Ichikawa, T. Shimokawa, Y. Nagashimi, K. Miyamoto and M. Uchiyama, Angew. Chem., Int. Ed., 2020, 59, 1970–1974 CrossRef CAS PubMed.
- J. H. Kim, A. Ruffoni, Y. Al-Faiyz, N. S. Sheikh and D. Leonori, Angew. Chem., Int. Ed. DOI:10.1002/anie.202000140.
- X. Zhang, R. T. Smith, C. Le, S. J. McCarver, B. T. Shireman, N. I. Carruthers and D. W. C. MacMillan, Nature, 2020, 580, 220–226 CrossRef CAS PubMed.
- M. Messner, S. I. Kozhushkov and A. De Meijere, Eur. J. Org. Chem., 2000, 1137–1155 CrossRef CAS.
- R. Gianatassio, J. M. Lopchuk, J. Wang, C.-M. Pan, L. R. Malins, L. Prieto, T. A. Brandt, M. R. Collins, G. M. Gallego, N. W. Sach, J. E. Spangler, H. Zhu, J. Zhu and P. S. Baran, Science, 2016, 351, 241–246 CrossRef CAS PubMed.
- J. M. Lopchuk, K. Fjelbye, Y. Kawamata, L. R. Malins, C. M. Pan, R. Gianatassio, J. Wang, L. Prieto, J. Bradow, T. A. Brandt, M. R. Collins, J. Elleraas, J. Ewanicki, W. Farrell, O. O. Fadeyi, G. M. Gallego, J. J. Mousseau, R. Oliver, N. W. Sach, J. K. Smith, J. E. Spangler, H. Zhu, J. Zhu and P. S. Baran, J. Am. Chem. Soc., 2017, 139, 3209–3226 CrossRef CAS PubMed.
- R. A. Shelp and P. J. Walsh, Angew. Chem., Int. Ed., 2018, 57, 15857–15861 CrossRef CAS PubMed.
- N. Trongsiriwat, Y. Pu, Y. Nieves-Quinones, R. A. Shelp, M. C. Kozlowski and P. J. Walsh, Angew. Chem., Int. Ed., 2019, 58, 12416–13420 CrossRef PubMed.
- K. B. Wiberg, W. P. Dailey, F. H. Walker, S. T. Waddell, L. S. Crocker and M. D. Newton, J. Am. Chem. Soc., 1985, 107, 7247–7257 CrossRef CAS.
- D. Lasányi and G. L. Tolnai, Org. Lett., 2019, 21, 10057–10062 CrossRef PubMed.
- S. Yu, A. Noble, R. B. Bedford and V. K. Aggarwal, J. Am. Chem. Soc., 2019, 141, 20325–20334 CrossRef CAS PubMed.
- J. A. Milligan and P. Wipf, Nat. Chem., 2016, 8, 296–297 CrossRef CAS PubMed.
- K. B. Wiberg and S. T. Waddell, J. Am. Chem. Soc., 1990, 112, 2194–2216 CrossRef CAS.
- K. B. Wiberg, Angew. Chem., Int. Ed., 1986, 25, 312–322 CrossRef.
- For an example where stereoelectronic effects govern reactivity in strained systems, see: B. Gold, G. B. Dudley and I. V. Alabugin, J. Am. Chem. Soc., 2013, 135, 1558–1569 CrossRef CAS PubMed.
- F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198 CrossRef CAS PubMed.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- P. Seiler, Helv. Chim. Acta, 1990, 73, 1574–1585 CrossRef CAS.
- L. Hedberg and K. Hedberg, J. Am. Chem. Soc., 1985, 107, 7257–7260 CrossRef CAS.
- M. D. Harmony, J. Chem. Phys., 1990, 93, 7522–7523 CrossRef CAS.
- K. B. Wiberg and F. H. Walker, J. Am. Chem. Soc., 1982, 104, 5239–5240 CrossRef CAS.
- K. B. Wiberg, R. F. Bader and C. D. Lau, J. Am. Chem. Soc., 1987, 109, 985–1001 CrossRef CAS.
- J. Joy, E. Akhil and E. D. Jemmis, Phys. Chem. Chem. Phys., 2018, 20, 25792–25798 RSC.
- R. Laplaza, J. Contreras-garcia and F. Fuster, Chem.–Eur. J. DOI:10.1002/chem.201904910.
- W. Wu, J. Gu, J. Song, S. Shaik and P. C. Hiberty, Angew. Chem., Int. Ed., 2009, 48, 1407–1410 CrossRef CAS PubMed.
- J. E. Jackson and L. C. Allen, J. Am. Chem. Soc., 1984, 106, 591–599 CrossRef CAS.
- D. Feller and E. R. Davidson, J. Am. Chem. Soc., 1987, 109, 4133–4139 CrossRef CAS.
- T. Kar and K. Jug, Chem. Phys. Lett., 1996, 256, 201–206 CrossRef CAS.
- J. O. Jensen, J. Mol. Struct.: THEOCHEM, 2004, 673, 51–58 CrossRef CAS.
- V. Polo, J. Andres and B. Silvi, J. Comput. Chem., 2007, 28, 857–864 CrossRef CAS PubMed.
- Y. Yang, J. Phys. Chem. A, 2012, 116, 10150–10159 CrossRef CAS PubMed.
- E. Ramos-Cordoba and P. Salvador, Phys. Chem. Chem. Phys., 2014, 16, 9565–9571 RSC.
- M. Bremer, H. Untenecker, P. A. Gunchenko, A. A. Fokin and P. R. Schreiner, J. Org. Chem., 2015, 80, 6520–6524 CrossRef CAS PubMed.
- P. Seiler, J. Belzner, U. Bunz and G. Szeimies, Helv. Chim. Acta, 1988, 71, 2100–2110 CrossRef CAS.
- M. Messerschmidt, S. Scheins, L. Grubert, M. Pätzel, G. Szeimies, C. Paulmann and P. Luger, Angew. Chem., Int. Ed., 2005, 44, 3925–3928 CrossRef CAS PubMed.
- B. Müller, T. Bally, R. Pappas and F. Williams, J. Am. Chem. Soc., 2010, 132, 14649–14660 CrossRef PubMed.
- E. Honegger, H. Huber, E. Heilbronner, W. P. Dailey and K. B. Wiberg, J. Am. Chem. Soc., 1985, 107, 7172–7174 CrossRef CAS.
- S. Shaik, Z. Chen, W. Wu, A. Stanger, D. Danovich and P. Hiberty, ChemPhysChem, 2009, 10, 2658–2669 CrossRef CAS PubMed.
- Head-Gordon defines Pauli repulsion as “the marked increase in energy when two non-bonded atoms are forced to occupy the same space”. P. R. Horn, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2016, 144, 114107 CrossRef PubMed . In the case of [1.1.1]propellane, the total kinetic energy of the electrons inside the cage increases as a result.
- S. Shaik, D. Danovich, J. M. Galbraith, B. Braida, W. Wu and P. C. Hiberty, Angew. Chem., Int. Ed., 2019, 75252, 2–20 Search PubMed.
- This effect can also be represented in terms of resonance forms, where the C1–C3 bond breaks to form six degenerate alkene/carbene pairs (see ESI Fig. S4†). To our knowledge, this is the only example of stabilization of a neutral hydrocarbon through such ‘sacrificial hyperconjugation’, where the resonance structure contains one two-electron bond less than the Lewis representation, D. McNaught and A. Wilkinson, IUPAC Compendium of Chemical Terminology, The Gold Book, 2nd edn, Blackwell Science, 1997 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- S. Kozuch, D. Gruzman and J. M. L. Martin, J. Phys. Chem. C, 2010, 114, 20801–20808 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 4054–4063 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- We note that some single-hybrid functionals performed adequately to describe the kinetics of anionic addition; however, this occurs through fortuitous error cancellation, where small errors are observed in the activation barriers despite large errors in the density.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- K. R. Mondanaro and W. P. Dailey, Org. Synth., 1998, 75, 98 CrossRef CAS.
- K. B. Wiberg and N. McMurdie, J. Am. Chem. Soc., 1994, 116, 11990–11998 CrossRef CAS.
- R. A. More O'Ferrall, J. Chem. Soc. B, 1970, 274 RSC.
- H. Xu, S. Saebo and C. U. Pittman, Mol. Phys., 2012, 110, 2349–2357 CrossRef CAS.
- J. Belzner and G. Szeimies, Tetrahedron Lett., 1986, 27, 5839–5842 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Computational methods and data including benchmarking studies, Fig. S1–S29 and Tables S1–S48, Cartesian coordinates (PDF); Cartesian coordinates (ZIP). See DOI: 10.1039/d0sc01386b |
| ‡ Current address: Abbvie Drug Discovery Science & Technology (DDST), 1 North Waukegan Road, North Chicago, IL 60064, USA. |
| This journal is © The Royal Society of Chemistry 2020 |