Open Access Article
Open Access ArticleInterpretable molecular models for molybdenum disulfide and insight into selective peptide recognition†
Juan
Liu
 a,
Jin
Zeng
a,
Cheng
Zhu
a,
Jianwei
Miao
bc,
Yu
Huang
a,
Jin
Zeng
a,
Cheng
Zhu
a,
Jianwei
Miao
bc,
Yu
Huang
 cd and
Hendrik
Heinz
cd and
Hendrik
Heinz
 *a
*a
aDepartment of Chemical and Biological Engineering, University of Colorado- Boulder, Boulder, CO 80309, USA. E-mail: hendrik.heinz@colorado.edu
bDepartment of Physics and Astronomy, University of California Los Angeles, California 90095, USA
cCalifornia NanoSystems Institute, University of California, Los Angeles, CA 90095, USA
dDepartment of Materials Science and Engineering, University of California, Los Angeles, 90095, USA
First published on 21st July 2020
Abstract
Molybdenum disulfide (MoS2) is a layered material with outstanding electrical and optical properties. Numerous studies evaluate the performance in sensors, catalysts, batteries, and composites that can benefit from guidance by simulations in all-atom resolution. However, molecular simulations remain difficult due to lack of reliable models. We introduce an interpretable force field for MoS2 with record performance that reproduces structural, interfacial, and mechanical properties in 0.1% to 5% agreement with experiments. The model overcomes structural instability, deviations in interfacial and mechanical properties by several 100%, and empirical fitting protocols in earlier models. It is compatible with several force fields for molecular dynamics simulation, including the interface force field (IFF), CVFF, DREIDING, PCFF, COMPASS, CHARMM, AMBER, and OPLS-AA. The parameters capture polar covalent bonding, X-ray structure, cleavage energy, infrared spectra, bending stability, bulk modulus, Young's modulus, and contact angles with polar and nonpolar solvents. We utilized the models to uncover the binding mechanism of peptides to the MoS2 basal plane. The binding strength of several 7mer and 8mer peptides scales linearly with surface contact and replacement of surface-bound water molecules, and is tunable in a wide range from −86 to −6 kcal mol−1. The binding selectivity is multifactorial, including major contributions by van-der-Waals coordination and charge matching of certain side groups, orientation of hydrophilic side chains towards water, and conformation flexibility. We explain the relative attraction and role of the 20 amino acids using computational and experimental data. The force field can be used to screen and interpret the assembly of MoS2-based nanomaterials and electrolyte interfaces up to a billion atoms with high accuracy, including multiscale simulations from the quantum scale to the microscale.
Introduction
Two-dimensional (2D) materials, including graphene, hexagonal boron nitride, and transition metal dichalcogenides (TMDs or TMDCs) such as molybdenum disulfide (MoS2) have received widespread attention in recent years due to their unique structural, electronic, and conductive properties.1–3 The compounds have strong polar covalent bonds within the layers and weaker inter-layer interaction. Specifically, MoS2 is widely used in electrochemical catalysts,4,5 sensors,6 composites,7,8 and photovoltaics.9,10 The surface, interfacial, and mechanical properties are important for the design of functional materials and increased control over performance. For example, the surface properties of MoS2 influence the performance as a catalyst in the hydrogen evolution reaction,11 the conductivity upon specific binding of analytes,12 as well as the performance in electrode materials and polymer/MoS2 composites.13,14To-date, however, it has remained challenging to understand and predict interfacial and mechanical properties of MoS2 and related 2D materials to support the rational synthesis and performance in applications. Electronic structure calculations such as density functional theory (DFT), coupled with experimental data, have yielded critical information on the electron density and band structures.15 However, DFT calculations are limited to small scales of hundreds of atoms, insignificant dynamics, and the uncertainties in property predictions for transition metals and their compounds such as MoS2 are high.16–18 For example, computed surface energies19–21 and elastic constants deviate more than 50% relative to experiment (Table 1).22 Binding energies of small molecules on heavy metal surfaces can have several 100% error depending on the density functional and available corrections.16–18
| Method | Lattice parameter | r 0 (Å) | E cleav (mJ m−2) | IR/Ramana (cm−1) | Y (GPa) | B (GPa) | Contact angle (°) | All atoms mobile | Applicable potentials and compatibilityb | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a (Å) | c (Å) | H2O | CH2I2 | ||||||||
| a Major IR and Raman peak (Fig. 3c). b Details of the potential function are given in Table S1 in the ESI. c We estimate the cleavage energy (surface energy) as 150 ± 10 mJ m−2, close to the experimental value 121 mJ m−2 for natural bulk MoS2 samples (ref. 54) and to the lower end of values from DFT calculations of 160 mJ m−2 (ref. 19). d Reactive empirical bond-order (REBO) potential. e The energy function comprises multiple exponential terms. | |||||||||||
| Expt | 3.16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55 |
12.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55 |
2.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55 |
45–121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 57 |
384![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
170–300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59–62 59–62 |
43 ± 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63 63 |
69 ± 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 52 |
15 ± 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 52 |
Yes | NA |
| This work | 3.16 | 12.25 | 2.38 | 150 ± 2c | 360 ± 5 | 175 ± 2 | 41.7 ± 1 | 69 ± 2 | 15 ± 2 | Yes | IFF, CVFF, PCFF, OPLS-AA, Dreiding, CHARMM, AMBER |
| DFT | 3.19 | 12.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 64 |
2.43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 64 |
160–284![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19–21 19–21 |
387![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 65 |
220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66 66 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 22 |
NA | NA | Yes | NA |
| SR(2017)49 | 3.16 | 12.16 | NA | 241 | 160 | 226 | 43.7 | 69.6 | 0 | Yes | OPLS |
| LU(2016)50 | NA | NA | NA | NA | NA | NA | NA | 86–90 | NA | Yes | OPLS |
| JI(2013)47 | 3.21 | 11.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | 229 | NA | NA | NA | Yes | Stillinger–Weber (SW) |
| DA(2012)46 | 3.20 | 11.59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | NA | NA | NA | NA | Yes | QEq |
| VA9(2010)45 | 3.25 | 12.23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | 404 | NA | NA | 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
NA | No | CVFF |
| VA8(2010)45 | 3.21 | 12.27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | 584 | NA | NA | 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
NA | No | CVFF |
| LI(2009)48 | 3.16 | 12.31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | NA | NA | 97.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
NA | Yes | REBOd |
| ON(2009)44 | 3.16 | 12.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | NA | NA | NA | NA | No | Buckingham |
| MO(2008)43 | 3.05 | 13.89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | NA | NA | 69.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
NA | No | Buckingham |
| BE(2003)42 | 3.16 | 12.31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | NA | NA | 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 49 |
NA | No | Embeddede |
| FA(1996)41 | 3.16 | 12.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | NA | NA | NA | NA | Yes | Embedded empiricale |
| BR(1992)40 | 3.17 | 12.28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | NA | NA | NA | NA | No | Empirical without Coulombe |
| DR(1988)39 | 3.19 | 11.74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
2.42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 67 |
NA | NA | NA | NA | NA | NA | Yes | Empirical without Coulombe |
Molecular dynamics (MD) simulation has become a reliable tool to gain insight into the details of molecular motion, nanoscale assembly, crystal growth, and catalysis. Examples include peptide–metal binding,23–26 silica–electrolyte interactions,27,28 mineralization of apatite,29 nanoscale forces in building materials30 and polymer–carbon nanomaterials composites.31–34 Interpretability of the force field parameters is hereby essential to explain and predict the physical and chemical behavior. Parameters that are consistently derived and explained, rather than numerically fitted, achieve multiple times increased reliability and compatibility as shown by the interface force field (IFF) and its surface model database.35–38
In this study, we introduce parameters for MoS2 with record accuracy (Fig. 1) including validation and application to explain specific binding of peptides and amino acid residues. Interestingly, a number of modeling studies since the 1980s have attempted to characterize the interfacial and surface properties of 2H-MoS2 (Table 1).39–50 However, the results are poor since earlier force fields consist of empirical fitting parameters that are missing a chemical interpretation. Available potentials neglect the polarity of Mo–S bonds and use energy expressions other than harmonic, Coulomb, and Lennard-Jones, that are difficult to use with common models for water, minerals, organic compounds, and biomolecules.51 Due to the lack of interpretability and rationale, the parameters by DR (1988),39 BR (1992),40 FA (1996),41 BE (2003),42 MO (2008),43 LI (2009),48 VA9 (2010),45 DA (2012),46 and JI (2013)47 have considerable deviations (>2%) in Mo–S bond length and lattice parameters in comparison to X-ray diffraction data for 2H-MoS2 (Table 1). VA8 (2010)45 and VA9 (2010)45 parameters were tested to calculate vibration spectra, whereby VA9 (2010)45 achieves good agreement in vibration frequencies. Nevertheless, a discussion of the polarity of chemical bonding and polarizability was not included, leading to a computed water contact angle of 0° that deviates 100% from measurements of 69° on freshly cleaved MoS2 surfaces.52 Similar difficulties to reproduce surface and interfacial energies, or contact angles, are seen for LI (2009),48 BE (2003),42 and LU (2016).50 The SR (2017)49 parameters for 2H-MoS2 report better performance in lattice parameters, surface wetting, and some mechanical properties. However, bond angles are oversimplified to be octahedral and deviate more than 30° from X-ray data. Vibration constants lack a justification and are over 50% (200 cm−1) redshifted relative to the experimental IR spectrum, allowing lipid-like buckling of the 2D MoS2 layers, which are known to be stiff structural reinforcements in experiments (Fig. 2). Lennard-Jones parameters have likewise no documentation and include well-depths for sulfur that are about twice as high as typical values in similar chemical environments such as sulfides or sulfoxides. As a result, the parameters offset the cleavage energy more than +60% from a realistic value and yield a contact angle of diiodomethane of 0° in simulations, which differs 100% from the value of 15° obtained in experiments (Table 1). In summary, lack of chemical understanding and interpretation of prior potentials cause multiple discrepancies, disables compatibility and meaningful property predictions.
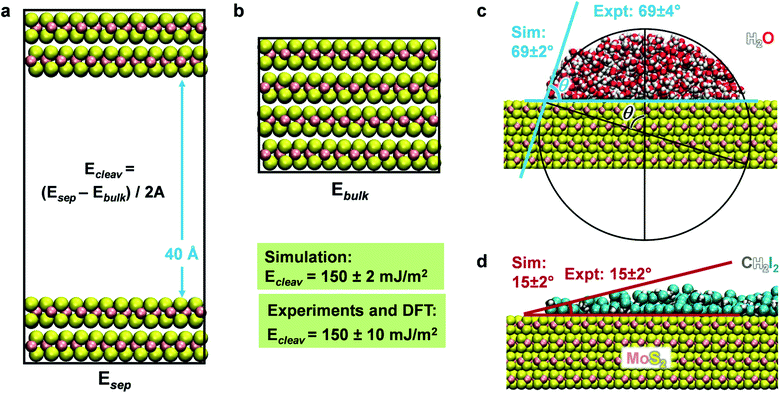
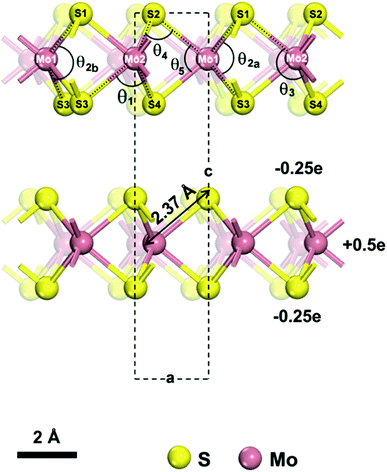 | ||
| Fig. 1 Model of a 2H-MoS2 unit cell (from ref. 55). The lattice parameters are a = b = 3.16 Å and c = 12.295 Å under standard conditions. The atomic charges for Mo and S are +0.5e and −0.25e, respectively. We describe the structure using two atom types for Mo and 4 atom types for S, which are necessary to identify unique bonds and angles. We distinguish one Mo–S bond of 2.37 Å length and five bond angles θ1, θ2, θ3, θ4, θ5, of which the θ2 angle (∠S1–Mo1–S3) can assume two values θ2a = 78.38° and θ2b = 134.4° and has no constraints in the model. | ||
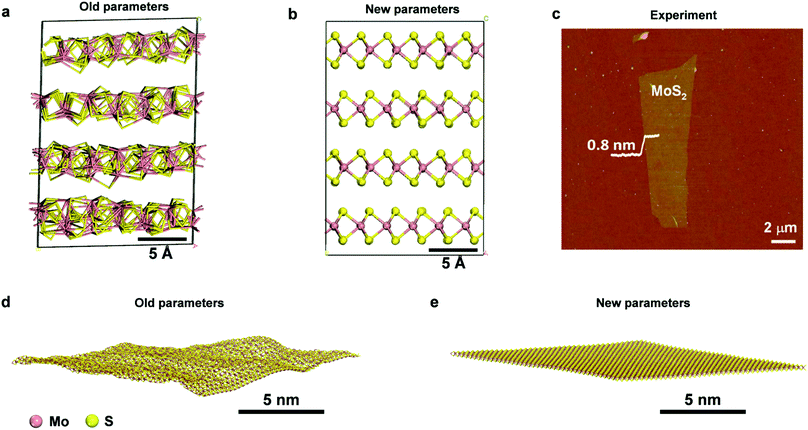 | ||
| Fig. 2 Comparison of the performance of prior parameters and new parameters for the structure of bulk and single-layer MoS2. 3D structure of MoS2 after 50 ns NPT simulation at 298.15 K and 1.013 MPa with (a) prior parameters (SR 2017, ref. 49) and (b) new parameters. The internal structure of the prior model collapses while it is maintained very close to X-ray data in the new model. (c) An AFM image of single-layer MoS2 with a thickness of ∼0.8 nm, showing a planar stiff geometry (reproduced with permission from ref. 56). (d and e) Snapshots of an MoS2 layer after 0.5 ns NVT simulation at 298.15 K in vacuum with prior parameters (SR 2017, ref. 49) and new parameters, respectively. The old parameters lead to unphysical lipid-like buckling, whereas the new model preserves the shape and allows minor undulations. | ||
Step-by-step, we resolved these shortcomings by the logical development and explanation of a Hamiltonian, applicable to other 2D materials, and demonstrate improvements in reliability by more than 10 times compared to earlier models for multiple properties.37,53,54 Our focus is on reproducing chemical bonding, lattice parameters, surface energies for 2H-MoS2, as well as mechanical properties with a minimum of random parameter search and fitting. We explain compatibility with at least 7 force fields including the interface force field (IFF), Consistent Valence Force Field (CVFF), Dreiding, the Polymer Consistent Force Field (PCFF), COMPASS, Chemistry of Harvard Macromolecular Mechanics (CHARMM), Assisted Model Building with Energy Refinement (AMBER), All-Atom Optimized Potentials for Liquid Simulations (OPLS-AA), and others.37 As an example of an application, we explain the affinity of various peptides to the basal MoS2 surface in agreement with experimental observations and elucidate molecular controls for tuning the binding strength.
The outline of this paper is as follows. Following a brief introduction of the interatomic potential in different formats (IFF, CVFF, PCFF, Dreiding, CHARMM, AMBER and OPLS-AA), we describe the chemistry of MoS2 and the transcription into interpretable force field parameters. We discuss, step-by-step, critical information about bonding, structure, vibrations, and interatomic interactions to derive a consistent classical Hamiltonian that reproduces structures and energies. We identify the origin of errors in prior models and explain how limitations are overcome, extensible to any other layered materials. Then, we discuss the validation of structural, vibration, interfacial, and mechanical properties. As an application, we elucidate selective peptide binding mechanisms to 2H-MoS2. The manuscript ends with conclusions. The ESI† provides computational details, force field files, and molecular models ready to use.
Results and discussion
Chemical features and their translation into force field parameters
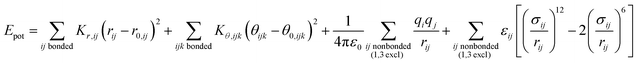 | (1) |
The energy expressions employ a 12-6 Lennard-Jones potential, including small differences in combination rules and more notable differences in the scaling of nonbonded interactions between 1,4 bonded atoms.29,30 In addition, we report force field parameters for the IFF, CFF,73 PCFF,74 and COMPASS75 energy expressions that employ a 9-6 Lennard-Jones potential, Waldmann-Hagler combination rules, and include nonbonded interactions between all 1,4 bonded atoms:
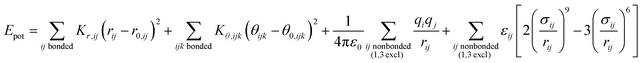 | (2) |
The force field parameters in eqn (1) and (2) include equilibrium bond lengths r0,ij, harmonic bond stretching constants Kr,ij, equilibrium bond angles θ0,ijk, angle bending constants Kθ,ijk, atomic charges qi, as well as the equilibrium nonbond diameters σ0,ii and the nonbond well depth ε0,ii. The latter two parameters are specific to the respective LJ potentials. The bonded parameters r0,ij, θ0,ijk, Kr,ij, and Kθ,ijk are used for atoms that are part of predominantly covalent bonds (bonds with less than half ionic character). The nonbonded parameters qi, σ0,ii and ε0,ii apply to all pairs of atoms, except bonded atoms with 1,2 and 1,3 covalent connections. Further additive terms for torsions, out-of-plane, higher order (cubic, quartic) and cross-terms are not required for MoS2 and have no impact on compatibility with existing parameters for biomolecules and inorganic compounds (see Section S2 in the ESI† for more details).37
We further utilized equilibrium bond lengths and bond angles from reproducible X-ray data. Minor adjustments within few percent were permitted to account for small superimposed contributions by the nonbond interactions (last two terms in eqn (1) and (2)). Prior methods have similarly relied on X-ray data for the bond length. However, bond angles were oversimplified or included as empirical fit parameters, disregarding existing experimental knowledge. The parameters for bonds and angles, for physical reasons, are furthermore about the same for all energy expressions regardless of 12-6 or 9-6 Lennard-Jones potentials. A small adjustment is recommended for OPLS-AA, related to different scaling of nonbond interactions between 1, 4 bonded atoms in OPLS-AA (0.5 vdW, 0.5 Coulomb) relative to AMBER (0.5 vdW, 5/6th Coulomb) and other force fields (1.0 for vdW and Coulomb).37 Differences in combination rules for 12-6 LJ parameters have negligible influence for MoS2 (arithmetic mean of ε0,ii in CHARMM and AMBER versus geometric mean in CVFF and OPLS-AA). Our force field considers details of compatibility and portability of chemical features and parameters for 2D materials for the first time.
We assigned vibration constants for bonds and angles to qualitatively reproduce Infrared and Raman frequencies and obtain reliable mechanical properties. Most earlier models do not consider realistic vibration frequencies and encounter stability problems, such as unphysical buckling, detrimental for the function of the model (Fig. 3). Another critical contribution are the Lennard-Jones parameters that represent relative atomic radii, short-range repulsion between atoms, and van-der-Waals attraction. Earlier studies include no interpretation and validation for LJ parameters while we discuss and assign the values consistent with nearby elements in the periodic table and with cleavage energies. The nonbond diameters σ0,ii correlate with van-der-Waals diameters of Mo and S. The well depths ε0,ii play a critical role to reproduce atomic polarizability, cleavage energies and, as a result, interactions with solvents, organic molecules, and other compounds, as verified by contact angles. The downside of neglecting such balances can be seen in the work of (SR2017).49 Random (and inconsistent) fitting to several properties including water contact angles was performed, arriving at a well depth of sulfur that is about 100% too large relative to similar sulfides. For another solvent, diiodomethane, a 100% mismatch of the contact angle relative to experiment was then reported, as well as other coarse deviations in surface energy by +60% and in energy derivatives.
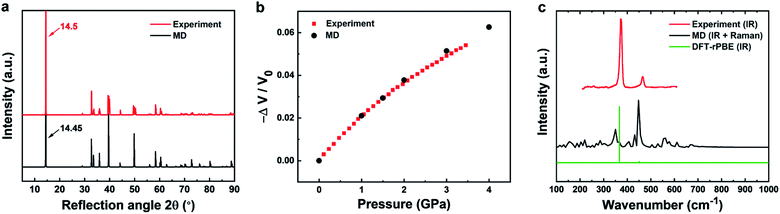 | ||
| Fig. 3 Comparison of experimental data (red) and results from molecular dynamics simulation (black) for structural, mechanical, and vibrational properties of 2H-MoS2. (a) XRD patterns show a good match (experimental data from ref. 80). (b) The compressibility of bulk MoS2 is nearly identical in experiment and simulation (experimental data from ref. 63). (c) Experimental infrared data (from ref. 58 and 82) are reasonably approximated by MD simulation, although the intensities are difficult to reproduce in MD. MD simulation also captures additional Raman peaks (see experimental details in ref. 65). A simulated IR spectrum from DFT calculations with the rPBE functional (green) approximately reproduces the wavenumbers and relative intensities of the experimental data. | ||
2H-MoS2 has only one Mo–S bond type and more than five types of bond angles. For simplicity, we can work with two atom types of Mo and four atom types of S. The model can then be designed with five types of bond angles θ1, θ2, θ3, θ4, θ5,39,40 whereby angle θ2 can assume two possible values (78.38° and 134.4°) and an angle bending constant Kθ,ijk of zero (Table 2). When one θ2 angle (S1–Mo–S3 angle) would change, the other θ2 angle on the same Mo atom would change by the same amount (Fig. 1). Our chosen assignment avoids the definition of further atom types, which is possible but would increase the complexity of the model. The five angles help reproduce the lattice parameters of MoS2, and the force constants were chosen to reproduce approximate IR/Raman vibration frequencies from experiments. Bond rotation and out-of-plane force constants are zero due to the absence of such deformations among bonded atoms in MoS2. In some prior models,43,49 only two types of angles, Mo–S–Mo and S–Mo–S, were included, then resulting in failure to capture the geometry and bonding environment (Fig. 2a and b), as well as in bending artifacts and unphysical crumpling of larger layers (Fig. 2c–e). The new models replicate bending stability consistent with the flat geometry and uniform height of MoS2 layers seen in AFM images, analogous to earlier IFF models for clay minerals (Fig. 2c–e).53,78
| I. Nonbond | Atomic charge (e) | σ (pm) | ε (kcal mol−1) | ||
|---|---|---|---|---|---|
| CVFF, CHARMM, AMBER, DREIDING, OPLS-AA (12-6 LJ) | PCFF, COMPASS (9-6 LJ) | CVFF, CHARMM, AMBER, DREIDING, OPLS-AA (12-6 LJ) | PCFF, COMPASS (9-6 LJ) | ||
| a The equilibrium bond length (r0,ij) and bond stretching constant (Kr) are the same for all force fields. b The equilibrium bond angles (θ0,ijk) and angle bending constants (Kθ) are the same for all the force fields. The values for θ0,ijk are equal to data from X-ray diffraction (Fig. 1). We recommend a minor modification of angles θ1 and θ4 for OPLS-AA, which uses significantly different scaling rules for nonbond interactions between 1, 4 bonded atoms. A complete list of individual angles and angle bending constants is given in Table S2 in the ESI. c The value in brackets is recommended for OPLS-AA to best reproduce bond length and lattice parameters. The default angle of 84.32° still facilitates good performance. d Two values are possible for θ2: θ2a and θ2b. The values are represented using an angle bending constant of zero without loss of accuracy (see Table S2 in the ESI for details). | |||||
| Mo | +0.5 | 480 | 501 | 0.07 | 0.054 |
| S | −0.25 | 384 | 398 | 0.30 | 0.26 |
| II. Bonda | r 0,ij (pm) | K r (kcal mol−1 Å−2) |
|---|---|---|
| Mo–S | 239 | 118 |
The assignment of Lennard-Jones equilibrium nonbond diameters σ0,ii was guided by known crystallographic radii,79 according to which Mo is somewhat larger than S, followed by numerical refinement (Table 1). σ0,ii assumes a 4% larger value in the 9-6 LJ potential versus the 12-6 LJ potential to compensate decreased repulsion.28,30,53 The exact magnitude of the equilibrium nonbond diameters σ0,ii was determined so that lattice parameters closely agree with experimental data, and refined in combination with ε0,ii to reproduce the cleavage energy and contact angles. The nonbond well depths ε0,ii represent atomic polarizabilities and assume a minor repulsive role to counterbalance internal Coulomb attraction. The ε0,ii value for Mo is lower than for S since the positively charged metal atom is less polarizable than the negatively charged S atom. The well depth of S atoms in MoS2 (−0.30 or −0.26 kcal mol−1) is about the same as that of S atoms in thiols and in similar chemical environments.37 In contrast, well depths in SR (2017) were fitted to about twice this value without explanation.49 We obtain mechanical properties in the correct range without further parameter adjustments.
Validation of structural, vibrational, and mechanical properties
Lattice parameters were tested on a supercell constructed from multiples of the unit cell (Table 3). The deviation from experiment is consistently <0.5% and the density agrees better than 1% with available measurements. The use of different energy expressions with minor changes in combination rules causes only minor changes (Table 3). The accuracy is better than with DFT and indicates that the force field mimics the real lattice configuration with minor discrepancies (Table 1).| Method | a (Å) | b (Å) | c (Å) | α = β (°) | γ (°) | r 0 (Å) | ρ (g cm−3) |
|---|---|---|---|---|---|---|---|
| Expt (XRD) | 56.89 | 56.89 | 24.59 | 90 | 120 | 2.38 | 5.00 |
| CVFF, Dreiding | 56.89 | 56.89 | 24.50 | 90 | 120 | 2.36 | 5.03 |
| PCFF, COMPASS | 56.92 | 56.92 | 24.58 | 90 | 120 | 2.36 | 5.00 |
| CHARMM | 56.92 | 56.92 | 24.50 | 90 | 120 | 2.36 | 4.99 |
| AMBER | 57.11 | 57.20 | 24.51 | 90 | 120 | 2.37 | 4.97 |
| OPLS-AA | 57.23 | 57.19 | 24.57 | 90 | 120 | 2.37 | 4.96 |
Accordingly, the computed XRD pattern is in good agreement with experimental data (JCPDS # 37-1492) (Fig. 3a).80 Likewise, computed mechanical properties show an impressive match to experiments (Fig. 3b). The compressibility was calculated under different pressures (0.001, 1, 1.5, 2, 3, 4 kbar) in NPT molecular dynamics simulations by recording the volume change in comparison to experimental data.63 The two curves are essentially identical up to about 2 kbar. Even when the pressure exceeds 2 kbar, the difference between computation and experimental data remains under 2%. Further mechanical properties include the Young's modulus in-plane, computed as 175 ± 2 GPa and measured in a range from 170 to 400 GPa.59–62 The agreement is very good and the computed value is similar to the in-plane modulus of 160 ± 10 GPa of clay minerals.81 Elastic properties help to validate the consistency of the force field parameters, along with the cleavage energy and hydration energy, as they represent the second derivatives of the energy with respect to coordinates. The original energy landscape and the derivatives agree with experimental data within few %. In contrast, earlier models feature over 50% deviation of the original energy (cleavage energy), having no compatibility with other inorganic and organic compounds.49
The experimental vibration spectrum shows two characteristic adsorption peaks at 384 and 470 cm−1 that belong to the infrared-active E11u and A12u modes of MoS2 (Fig. 3c).58,82 The simple classical model with only three bond stretching and angle bending constants (Table 2) reproduces the frequencies with a 20–30 cm−1 blue shift (360 and 450 cm−1). In experiment, also a major A1g Raman band is observed at 409 cm−1. This band is not visible in the IR spectrum, however, MD simulations reveal all vibrations regardless of selection rules and the Raman band can be seen near 410 cm−1 (Fig. 3c). DFT calculations of the IR spectrum with the rPBE functional are close to experimental wavenumbers and qualitatively reproduce the intensities.65 An excellent review of vibrational and optical properties is given in ref. 65. The performance of the classical model relative to earlier force fields is excellent while, as a limitation, intensities cannot be reproduced without quantum mechanical details (Table 1).
Surface and interfacial properties
Molecular dynamics simulations of the cleavage energy, MoS2–water, and MoS2–diiodomethane interactions were carried out using the NAMD program in comparison to experimental data and to cleavage energies computed by DFT calculations (Fig. 4 and Section S1 in the ESI†). The cleavage energy of the basal plane of a layered material is a key material parameter for its application in devices and for the validation of the model Hamiltonian. Unfortunately, the quantitative analysis of the cleavage energy can be challenging in experiments and a wide range of values from 40 to 121 mJ m−2 has been reported for MoS2.54,57,83 The differences are related to the surface quality (well-ordered and clean) and the analysis method. Tang et al. measured the surface tension of MoS2 basal plane as 110 ± 10 mJ m−2 using an in situ transmission electron microscopy probing technique.84 In 2017, Otyepková et al. used inverse gas chromatography (IGC) to measure and analyze the surface properties of MoS2.54 For a natural MoS2 sample, the surface energy was determined in the range from 99 mJ m−2 at a higher surface coverage of 20% gas probe to 121 mJ m−2 at a low surface coverage of 1% gas probe.54 The higher values are likely closer to the pure system. Separately, we considered data from quantum mechanics at the DFT level for further reference. These data tend to be less reliable and show considerable scatter between 160 and 284 mJ m−2 (Table 1).19–21 On balance, we consider the data at the lower end for further reference,19 arriving at a best estimate of 150 ± 10 mJ m−2 for the cleavage energy as a reference value. The cleavage energy was computed with the force field using molecular dynamics simulations in the NVT ensemble at 298 K as an energy difference using two boxes (Fig. 4). One box contained a surface slab of greater than 2 nm thickness separated with a 40 Å vacuum layer (Fig. 4a), and the other box a combined 3D periodic model of the same number of atoms without vacuum (Fig. 4b). The results agree with the target data of 150 mJ m−2 for IFF-CHARMM. The use of different energy expressions consistently yields 148 ± 2 mJ m−2 (Table S4 in the ESI†).The wetting behavior of MoS2 was studied for two solvents, polar and hydrogen-bonded water as well as somewhat less polar diiodomethane (CH2I2), similar to previous studies on silica surfaces, graphite, and clays.28,34,51 An artificial cubic-shaped cluster of solvent molecules was located on an extended MoS2 surface and subjected to MD simulations for equilibration into a continuous semi-cylindrical liquid continuous in one dimension (Fig. S1 in the ESI†). We used the convergence of the total energy versus time to determine the equilibrium state (Fig. S3 in the ESI†). After several nanoseconds, the change in amplitude was less than 0.01% of the total energy. The contact angle was measured using a new circle-based method as an average over 100 snapshots in equilibrium for each simulation (Fig. 4c and S2 in the ESI†). The circle-based method reduces biases and uncertainties on the order of ±5° associated with individual readings in earlier studies28,49,50 to a small uncertainty of ±2° or only ±1°. We obtained a contact angle of water of 69 ± 2° (Fig. 4c) and a contact angle of 15 ± 2° for CH2I2 (Fig. 4d) using the MoS2 parameters in IFF-CHARMM format. The two values closely match data from laboratory measurements on freshly cleaved MoS2 surfaces, which are 69 ± 3.8° and 15 ± 2°, respectively.52 The uncertainty in experimental measurements arises from differences in advancing contact angles versus receding contact angles and is included to characterize the overall reproducibility. Quantitative agreement of computed cleavage energies, contact angles, and mechanical properties with experimental data without further adjustable parameters documents an unprecedented level of internal consistency of the force field for MoS2 and its suitability for property predictions of other mixed-phase systems.
For the computation of the contact angles, we used the TIP3P water model and further tests with the flexible SPC water model yield nearly identical results within ±1°. A similarly small dependence on the water model was found earlier on silica,28 metal,85 and graphite surfaces34 using chemically consistent, interpretable parameters in IFF.37 Deviations may be larger if other, chemically inconsistent and non-interpretable force field parameters are used. The CVFF parameters of CH2I2 were updated to reproduce dipole moment, density at 298 K, and vaporization energy at the boiling point 480 K in agreement with experimental data (Table S3 in the ESI†).
Earlier computational studies of the contact angle also involved tuned interaction parameters to match contact angles of fresh and aged MoS2 surfaces,86 however, in this approach the chemical changes to the surface such as contamination by airborne hydrocarbons or oxidation are not considered.65 In our approach, the interaction parameters have a clear rationale, do not require customized fits to reproduce contact angles, and changes in surface chemistry can be explicitly included.
Peptide recognition on MoS2 surfaces and identification of binding residues
Functionalization of MoS2 with peptides and other functional ligands finds promising applications in sensing, catalysis, hierarchical assembly, and 3D-printed biomaterials.4–10 Several studies on the adsorption of peptide molecules on the MoS2 surface have been reported and indicate that the hydrophobicity, aromatic structure and electrostatic properties of amino acids are important factors affecting adsorption and surface assembly.87–92 However, experimental data remain qualitative in nature, including AFM, TEM imaging, binding information from concentration measurements, QCM, XPS, CD, Raman shifts, and relative ranking from washing cycles in phage display. Quantitative binding energies and conformations in solutions are not accessible. As an example application of this model, we determine the binding strength and conformations of eight different peptides on the MoS2 surface in aqueous solution at pH 7 (Fig. 5 and 6). We discuss the results in the context of experimental findings and develop criteria for selective peptide design. This analysis is not part of our model derivation.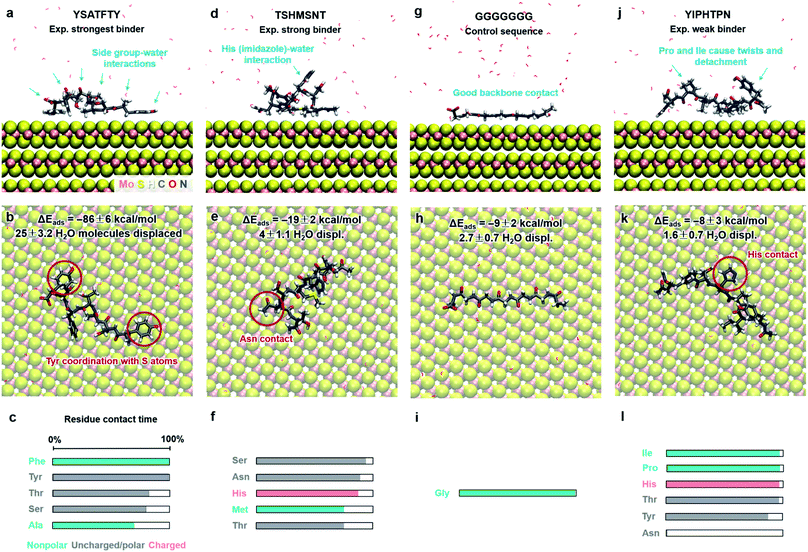 | ||
| Fig. 5 Adsorption characteristics of three peptides identified by phage display and a control sequence on 2H-MoS2 surfaces in aqueous solution at 298.15 K and 101.3 kPa from molecular dynamics simulation. Side and top views of adsorbed conformations in equilibrium are shown, including highlights of specific binding features. Adsorption energies, the average number of displaced water molecules on the surface, and the percentage of contact time for each residue (within 3.5 Å from the MoS2 surface) are identified. The color code in the bar charts (c, f, i, l) represents the hydrophobicity according to the Eisenberg and Weiss scale (ref. 98). | ||
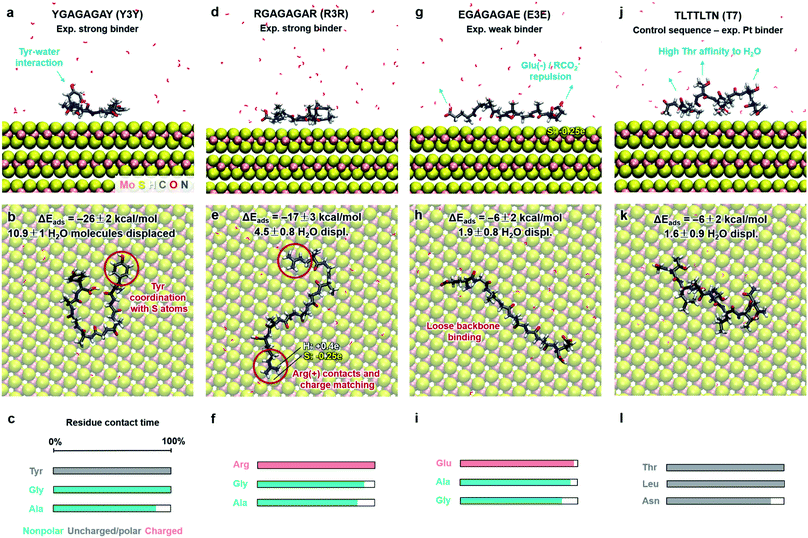 | ||
| Fig. 6 Adsorption characteristics of three peptide mutants (from ref. 89) and a control sequence (from ref. 93) on 2H-MoS2 surfaces in aqueous solution at 298.15 K and 101.3 kPa from molecular dynamics simulations. Side and top views of adsorbed conformations in equilibrium are shown, including highlights of specific binding features. Adsorption energies, the average number of displaced water molecules on the surface, and the percentage of contact time for each residue (within 3.5 Å from the MoS2 surface) are indicated. The color code in the bar charts (c, f, i, l) represents the hydrophobicity according to the Eisenberg and Weiss scale (ref. 98). | ||
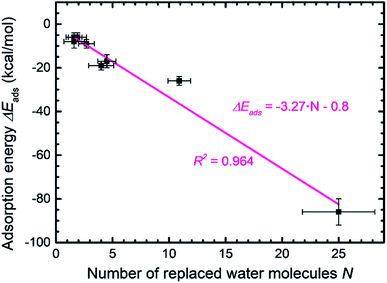
Peptide GGGGGGG was tested as a control sequence to examine the contribution of the backbone to adsorption (Fig. 5g–i). The computed binding energy of −9 ± 2 kcal mol−1 concurs with no specific binding expectations, although it is quite significant given the absence of side groups. GGGGGGG displaced 2.7 water molecules and aliphatic hydrogen atoms of the Gly backbone were found closest to the surface. The linear conformation, related to the absence of intramolecular hydrogen bonds, shows that flexible backbone contact alone does not lead to strong binding. A similarly small binding energy of −8 ± 3 kcal mol−1 was observed for the peptide YIPHTPN (Fig. 5j–l). YIPHTPN was identified as a weak binder in phage display and contains the potentially strongly binding Tyr. However, two Pro residues introduce local helicity in the backbone and drastically reduce effective surface contact (highlights in Fig. 5j).97 Steric hindrance also originates from bulky Ile. Hydrophobic side groups, such as –CH3 in Ala (Fig. 5a–c) and butyl groups in Ile (and Leu) seek surface contact with MoS2 to avoid contact with water. Similarly, aliphatic hydrogen atoms in Pro and Thr had van-der-Waals interactions with the MoS2 surface with limited contact area. Thereby, large Pro, Ile, and Leu groups diminish potential binding of neighbor groups through steric demand. In YIPHTPN, His maintained contact with the surface due to conformation constraints from neighboring Pro residues.
The order of computed adsorption energies for these four 7-mer peptides agrees with the relative binding affinity according to experimental data from phage display. Adsorption energies vary widely from −86 to −8 kcal mol−1 and the data clearly show that side groups have a greater influence on the adsorption than the backbone.
Furthermore, we examined three 8-mer peptide mutants with differently charged end groups YGAGAGAY (±0), RGAGAGAR (+2)·2Cl− and EGAGAGAE (−2)·2Na+, which have been characterized in experiments by Hayamizu's team (Fig. 6).89 The computed adsorption energies are −26 ± 2 kcal mol−1, −17 ± 3 kcal mol−1, and −6 ± 2 kcal mol−1, respectively, and match the order of the experimental binding affinity. The neutral peptide YGAGAGAY was most attracted to the MoS2 surface, whereby the aromatic ring in Tyr undergoes coordination with polarizable sulfur atoms on the surface, and the phenolic OH group maintains favorable contact with water (Fig. 6a–c). The GAGAGA backbone, however, does not leverage binding. In comparison, the peptide YSATFTY with the strongest adsorption (−86 kcal mol−1) also contains two Tyr residues located at the ends with similar coordination on the surface, plus additional binding residues in a suitable sequence (Fig. 5a–c). We also noted that Tyr in a terminal position, such as in YIPHTPN, can result in marginal adsorption strength (−8 ± 2 kcal mol−1 in Fig. 5j–l). Then, the 2 Pro residues induce 2× local helical twists that disrupt contact with the surface and make binding of Tyr and Asn ineffective (Fig. 5j–l). Therefore, the effect of individual residues is not the only reason for the high binding affinity, but also the sequence along the backbone. Among the charged mutants, the positively charged peptide RGAGAGAR (+2) clearly prefers the MoS2 surface (−17 kcal mol−1) over the negatively charged peptide EGAGAGAE (−2) (−6 kcal mol−1). Hereby, multiple positively charged H atoms at the N atoms in the guanidinium group (+0.4e) coordinate in a well-matched geometry at least three negatively charged sulfur atoms (−0.25e) exposed on the MoS2 surface (Fig. 6d–f). Therefore, Arg significantly binds to the MoS2 surface. In contrast, the peptide EGAGAGAE with negatively charged carboxylate groups does not coordinate well with the MoS2 surface, which consists of negatively charged sulfur atoms while the positively charged Mo atoms (+0.5e) are tucked away underneath the surface (Fig. 6g–i). Weak backbone contact (1.9 water molecules replaced) plus some repulsion of Glu lower the binding energy to −6 kcal mol−1, consistent with lowest binding strength and instability of EGAGAGAE peptide films on MoS2 surfaces in experiments.89
A small binding energy of −6 ± 2 kcal mol−1 was also observed for a Pt-binding peptide TLTTLTN (T7)93 (Fig. 6j–l). This control sequence, identified by phage display against a different material, was also expected of random affinity to MoS2. The simulation predicts, in agreement, no specific attraction towards the MoS2 surface and only 1.6 displaced water molecules. Leu diminishes binding, like Ile in YIPHTPN (Fig. 5j–l), for steric reasons and lack of strong affinity. The high Thr content in TLTTLTN allows conformational flexibility and favorable interaction with supernatant water, which, in the absence of strongly binding residues, lowers attraction to the MoS2 surface (highlights in Fig. 6j). We therefore recognize that several neutral polar groups in TLTTLTN, without other residues that induce a specific geometry match to the MoS2 surface (e.g., Tyr) or a match in polarity (Arg), tend to be more attracted to water and result in weak adsorption. In comparison, GGGGGGG without any specific side groups shows slightly better adsorption (−9 kcal mol−1) (Fig. 5g–i).
Surface interactions can also be further characterized by free energy calculations. However, the computational expense is high and we consider the average contact time of individual residues as a comparable measure.
The wide range of possible binding energies thus arises from concerted interactions of multiple amino acids with the surface. Strongly binding residues include Tyr due to epitaxial fit and a polar OH group that enhances contact with water, as well as Phe (and likely Trp). Binding is also enhanced by Arg due to a good epitaxial fit of the guanidinium group to the MoS2 surface and matching of positive atomic charges to opposite MoS2 surface charges. Some electrostatic binding may occur for Lys, although without the geometry advantage of Arg. Asn, Gln, and Met tend to somewhat support binding. His, in the nonprotonated state, has reduced surface attraction due to negative charges on the nitrogen atoms. Ser and Thr allow backbone flexibility and interactions with water. Gly and Ala (and likely Cys) also support flexible conformations and are weak binders themselves. Val has unfavorable effects on adsorption due to steric hindrance. Leu and Ile are sterically demanding and tend to reduce adsorption even further. Negatively charged residues such as Asp and Glu diminish adsorption due to unfavorable electrostatic interactions. Pro induces helicity in a peptide and strongly disfavors binding by lowering the number of displaced water molecules.
These trends are largely supported by further experimental observations. A study of two amyloid peptides in contact with MoS2 (SNNFGAILSS and GLMVGGVVIA) reported stronger binding of Ser, Asn, and Phe to MoS2 than binding of Met, Val, and Leu.87 Investigations of the binding of a dodecapeptide (HLLQPTQNPFRN) to MoS2 suggested significant binding of Phe and His to MoS2, as well as some binding of Arg, and no binding of Leu.90 These data, however, are at least partly based on simulations and have some uncertainty. Other reported peptides with high binding constants in experiments include GVIHRNDQWTAPGGG and DRWVARDPASIFGGG, as well as a weakly binding/non-binding peptide SVMNTSTKDAIEGGG.88 The interpretation of binding residues in ref. 88 relied exclusively on MD simulation with a misleading force field, indicating Val, Pro, and Trp as binding residues, whereas Val and Pro are expected to bind weakly according to other studies. A more likely interpretation of the experimental data in ref. 88 is to consider Trp, Phe, Arg, Asn, Gln, and perhaps His as significantly binding residues in the first two peptides, with Ser and Thr serving as linkers for conformational flexibility. These binding residues, except 1 Asn, are missing in the 3rd nonbinding peptide, and only 1 intermediately binding Met is present, explaining the difference in relative binding strength and far lower adsorbed amount in experiment. Tyr was clearly the strongest binder in the series of X-(GA)n-X peptides, followed by Arg, as analyzed in detail here.89 Studies of the self-assembly of two other peptides on MoS2, LEY (LEYLLEYLL) and LKY (LKYLLKYLL) show strong binding of Tyr and a trend towards more adsorption of LKY than LEY at low peptide concentration (comparable to single peptide adsorption considered here).91 Preferred adsorption of the positively charged, Lys-containing peptide LKY over the negatively charged Glu-containing peptide LEY agrees with our interpretation.89 At the same time, very different assembly patterns were observed for multiple LKY and LEY peptides.91 LKY showed higher affinity to MoS2 and larger film thickness at low peptide concentration in contrast to higher stability of LEY at high peptide concentration. The major driver for binding was clearly Tyr in both cases.89,91
In summary, simulations and available experimental data enable a consistent interpretation of peptide binding to MoS2 and design rules for MoS2-binding single peptides. Computational screening allows quantitative forecasts of peptide affinity for new amino acid sequences in atomic detail, many times better than with existing force fields. Our analysis further shows that traditional descriptors such as amino acid polarity, hydrophilicity, aromaticity, and charge are not sufficient to identify the multifactorial rules of binding. The reason is that such identifiers only characterize the peptides and neglect the unique surface chemistry and geometry of the substrate. For example, there is no direct correspondence between the contact time of the peptides and the number of hydrophobic groups or the sum of hydrophobicity indices. Design rules are uncovered when considering the chemistry of both the substrate and the peptides, as previously shown for metals and oxides.95,97,99–102 The binding strength also further depends on surface coverage, pH, and ionic strength.103 The assembly of multiple peptides and films across large areas remains challenging to predict, however, computational screening and experimental studies can take these conditions into account and be used in tandem to accelerate progress.
Potential broader uses and applications
The models can be applied to study protein-, DNA-, lipid-, and polymer-MoS2 nanomaterials in 4D resolution, MoS2 electrode–electrolyte interfaces, as well as mixed MoS2 materials with graphene, metals, and minerals in composites and capacitors. Molecular dynamics simulations allow the quantitative, dynamic analysis at the level of individual atoms and functional groups up to the 1000 nm scale and support the discovery of specific materials formulations and properties. Substitutions by dopant elements can be implemented by changes in atomic charges and LJ parameters (similar to clay minerals, see ref. 53). The reliability of the simulations relative to experimental data is multiple times higher than prior force fields and clearly better than DFT, opening up interesting perspectives for computation-driven discoveries. The consistent representation of chemical bonding, structure, and energies allows coupling with quantum-mechanical methods at the local scale to analyze the complete electronic structure, as well as integration with coarse-grain and continuum models towards the micrometer scale. Stress–strain curves including failure can be computed by replacing the harmonic bonded potential for Mo–S bonds with a Morse potential (IFF-R).Conclusions
We present interpretable force field parameters for atomistic simulations of MoS2 and related nanomaterials and biomaterials, compatible with major force fields and programs for molecular simulations (IFF, CVFF, PCFF, DREIDING, CHARMM, AMBER, and OPLS-AA). The models reproduce lattice parameters, infrared frequencies, surface and interfacial properties, as well as mechanical properties relative to experiments in multiple times higher accuracy compared to prior models. Prior force fields for MoS2 fail to reproduce the physical structure and energies relative to experimental data due to lack of a rationale for parameters and severe internal inconsistencies. The model overcomes these limitations and bypasses questionable assumptions in DFT by reliance on reproducible experimental data and established theory, performing clearly better than current density functionals in interfacial and mechanical properties.We utilized the models to analyze the binding mechanism of 8 different peptides on the MoS2 surface in aqueous solution. Specific amino acid sequences lead to a wide range of adsorption energies from −6 to −86 kcal mol−1. More surface contact and release of surface-bound water increase the negative binding energy. We ranked all 20 amino acids in relative binding strength, consistent with the interpretation of extensive experimental data and insight from simulation. Strong binding is mediated by aromatic amino acids via favorable epitaxial coordination to superficial sulfur atoms (e.g., Tyr, Phe), by positively charged Arg through complementary charge distribution and geometry of guanidinium groups to the superficial sulfur lattice. Conformationally flexible, weakly polar residues with side chains can support binding and simultaneously contribute favorable hydrogen bonding to water molecules in the solution phase. Negatively charged residues diminish binding due to mild electrostatic repulsion, and bulky hydrophobic residues (Pro, Ile, Leu) strongly diminish binding and surface contact. The binding selectivity arises from unique properties of the peptides and of the surface, and is not possible to derive using traditional criteria such as hydrophobicity that only focus on the organic molecules and neglect the substrate.
The models explore the performance limit of current energy expressions and can be used for property predictions of MoS2-containing nanomaterials and biomaterials, as well as in-depth, full atomic-scale characterization of assemblies up to a billion atoms. Full electrolyte conditions, realistic dynamics, and combinations with electronic structure calculations at the local scale may be used to assess band gaps, conductivity, and catalytic activity. Potential uses include electrocatalysts, supercapacitors, polymer composites, biosensors, and mixed layered materials containing MoS2. Coupling with atomic electron tomography measurements can further correlate crystal defects with the physical and chemical properties of 2D materials.104,105 Extensions to other 2D chalcogenides are in progress.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation (DMREF-1623947, CBET-1530790, OAC 1931587), and the University of Colorado-Boulder. J. M. acknowledges the support by STROBE: A National Science Foundation Science & Technology Center (DMR-1548924). We acknowledge computing resources at the Summit supercomputer, a joint effort of the University of Colorado Boulder and Colorado State University, which is supported by the National Science Foundation (ACI-1532235 and ACI-1532236), as well as resources at the Argonne Leadership Computing Facility, which is a DoE Office of Science User Facility supported under Contract DE-AC02-06CH11357.References
- Z. Wang and B. Mi, Environ. Sci. Technol., 2017, 51, 8229–8244 CrossRef CAS PubMed.
- H. Wang, C. Li, P. Fang, Z. Zhang and J. Z. Zhang, Chem. Soc. Rev., 2018, 47, 6101–6127 RSC.
- Z. Li, X. Meng and Z. Zhang, J. Photochem. Photobiol., C, 2018, 35, 39–55 CrossRef CAS.
- Z. Wu, B. Fang, Z. Wang, C. Wang, Z. Liu, F. Liu, W. Wang, A. Alfantazi, D. Wang and D. P. Wilkinson, ACS Catal., 2013, 3, 2101–2107 CrossRef CAS.
- L. B. Huang, L. Zhao, Y. Zhang, Y. Y. Chen, Q. H. Zhang, H. Luo, X. Zhang, T. Tang, L. Gu and J. S. Hu, Adv. Energy Mater., 2018, 1800734 CrossRef.
- S. Barua, H. S. Dutta, S. Gogoi, R. Devi and R. Khan, ACS Appl. Nano Mater., 2018, 1, 2–25 CrossRef CAS.
- S. Wu, J. Wang, L. Jin, Y. Li and Z. Wang, ACS Appl. Nano Mater., 2018, 1, 337–343 CrossRef CAS.
- B. Dou, J. Yang, R. Yuan and Y. Xiang, Anal. Chem., 2018, 90, 5945–5950 CrossRef CAS PubMed.
- Z. Guan, C.-S. Lian, S. Hu, S. Ni, J. Li and W. Duan, J. Phys. Chem. C, 2017, 121, 3654–3660 CrossRef CAS.
- Y. Almadori, N. Bendiab and B. Grévin, ACS Appl. Mater. Interfaces, 2017, 10, 1363–1373 CrossRef PubMed.
- G. R. Bhimanapati, T. Hankins, Y. Lei, R. A. Vilá, I. Fuller, M. Terrones and J. A. Robinson, ACS Appl. Mater. Interfaces, 2016, 8, 22190–22195 CrossRef CAS PubMed.
- T. H. Kim, Y. H. Kim, S. Y. Park, S. Y. Kim and H. W. Jang, Chemosensors, 2017, 5, 15 CrossRef.
- K.-K. Liu, W. Zhang, Y.-H. Lee, Y.-C. Lin, M.-T. Chang, C.-Y. Su, C.-S. Chang, H. Li, Y. Shi and H. Zhang, Nano Lett., 2012, 12, 1538–1544 CrossRef CAS.
- K. Liu, Q. Yan, M. Chen, W. Fan, Y. Sun, J. Suh, D. Fu, S. Lee, J. Zhou and S. Tongay, Nano Lett., 2014, 14, 5097–5103 CrossRef CAS.
- X. Tian, D. S. Kim, S. Yang, C. J. Ciccarino, Y. Gong, Y. Yang, Y. Yang, B. Duschatko, Y. Yuan and P. M. Ajayan, Nat. Mater., 2020, 1–7 CAS.
- V. G. Ruiz, W. Liu and A. Tkatchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035118 CrossRef.
- P. L. Silvestrelli and A. Ambrosetti, J. Low Temp. Phys., 2016, 185, 183–197 CrossRef CAS.
- W. Liu, A. Tkatchenko and M. Scheffler, Acc. Chem. Res., 2014, 47, 3369–3377 CrossRef CAS PubMed.
- T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502 CrossRef PubMed.
- J. Fuhr, J. Sofo and A. Saúl, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 8343–8347 CrossRef CAS.
- K. Weiss and J. M. Phillips, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 14, 5392 CrossRef CAS.
- V. Alexiev, R. Prins and T. Weber, Phys. Chem. Chem. Phys., 2000, 2, 1815–1827 RSC.
- H. Heinz, K. C. Jha, J. Luettmer-Strathmann, B. L. Farmer and R. R. Naik, J. R. Soc., Interface, 2011, 8, 220–232 CrossRef CAS PubMed.
- I. L. Geada, H. Ramezani-Dakhel, T. Jamil, M. Sulpizi and H. Heinz, Nat. Commun., 2018, 9, 716 CrossRef PubMed.
- H. Ramezani-Dakhel, P. A. Mirau, R. R. Naik, M. R. Knecht and H. Heinz, Phys. Chem. Chem. Phys., 2013, 15, 5488–5492 RSC.
- H. Ramezani-Dakhel, L. Y. Ruan, Y. Huang and H. Heinz, Adv. Funct. Mater., 2015, 25, 1374–1384 CrossRef CAS.
- T. V. Ndoro, E. Voyiatzis, A. Ghanbari, D. N. Theodorou, M. C. Böhm and F. Müller-Plathe, Macromolecules, 2011, 44, 2316–2327 CrossRef CAS.
- F. S. Emami, V. Puddu, R. J. Berry, V. Varshney, S. V. Patwardhan, C. C. Perry and H. Heinz, Chem. Mater., 2014, 26, 2647–2658 CrossRef CAS.
- T. Z. Lin and H. Heinz, J. Phys. Chem. C, 2016, 120, 4975–4992 CrossRef CAS.
- R. K. Mishra, L. Fernández-Carrasco, R. J. Flatt and H. Heinz, Dalton Trans., 2014, 43, 10602–10616 RSC.
- D. Roccatano, E. Sarukhanyan and R. Zangi, J. Chem. Phys., 2017, 146, 074703 CrossRef PubMed.
- S. Frankland, A. Caglar, D. Brenner and M. Griebel, J. Phys. Chem. B, 2002, 106, 3046–3048 CrossRef CAS.
- J. R. Gissinger, C. Pramanik, B. Newcomb, S. Kumar and H. Heinz, ACS Appl. Mater. Interfaces, 2018, 10, 1017–1027 CrossRef CAS PubMed.
- C. Pramanik, J. R. Gissinger, S. Kumar and H. Heinz, ACS Nano, 2017, 11, 12805–12816 CrossRef CAS PubMed.
- H. Heinz, H. J. Castelijns and U. W. Suter, J. Am. Chem. Soc., 2003, 125, 9500–9510 CrossRef CAS PubMed.
- H. Heinz and U. W. Suter, J. Phys. Chem. B, 2004, 108, 18341–18352 CrossRef CAS.
- H. Heinz, T.-J. Lin, R. K. Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765 CrossRef CAS PubMed.
- J. Liu, E. Tennessen, J. Miao, Y. Huang, J. M. Rondinelli and H. Heinz, J. Phys. Chem. C, 2018, 122, 14996–15009 CrossRef CAS.
- M. Drew, S. Edmondson, G. Forsyth, R. Hobson and P. Mitchell, Catal. Today, 1988, 2, 633–641 CrossRef CAS.
- T. M. Brunier, M. G. Drew and P. C. Mitchell, Mol. Simul., 1992, 9, 143–159 CrossRef CAS.
- P. Faye, E. Payen and D. Bougeard, J. Chem. Soc., Faraday Trans., 1996, 92, 2437–2443 RSC.
- U. Becker, K. M. Rosso, R. Weaver, M. Warren and M. F. Hochella Jr, Geochim. Cosmochim. Acta, 2003, 67, 923–934 CrossRef CAS.
- Y. Morita, T. Onodera, A. Suzuki, R. Sahnoun, M. Koyama, H. Tsuboi, N. Hatakeyama, A. Endou, H. Takaba and M. Kubo, Appl. Surf. Sci., 2008, 254, 7618–7621 CrossRef CAS.
- T. Onodera, Y. Morita, A. Suzuki, M. Koyama, H. Tsuboi, N. Hatakeyama, A. Endou, H. Takaba, M. Kubo and F. Dassenoy, J. Phys. Chem. B, 2009, 113, 16526–16536 CrossRef CAS PubMed.
- V. Varshney, S. S. Patnaik, C. Muratore, A. K. Roy, A. A. Voevodin and B. L. Farmer, Comput. Mater. Sci., 2010, 48, 101–108 CrossRef CAS.
- M. Dallavalle, N. Sändig and F. Zerbetto, Langmuir, 2012, 28, 7393–7400 CrossRef CAS.
- J.-W. Jiang, H. S. Park and T. Rabczuk, J. Appl. Phys., 2013, 114, 064307 CrossRef.
- T. Liang, S. R. Phillpot and S. B. Sinnott, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245110 CrossRef.
- V. Sresht, A. Govind Rajan, E. Bordes, M. S. Strano, A. A. Padua and D. Blankschtein, J. Phys. Chem. C, 2017, 121, 9022–9031 CrossRef CAS.
- B. Luan and R. Zhou, Appl. Phys. Lett., 2016, 108, 131601 CrossRef.
- H. Heinz and H. Ramezani-Dakhel, Chem. Soc. Rev., 2016, 45, 412–448 RSC.
- A. Kozbial, X. Gong, H. Liu and L. Li, Langmuir, 2015, 31, 8429–8435 CrossRef CAS.
- H. Heinz, H. Koerner, K. L. Anderson, R. A. Vaia and B. L. Farmer, Chem. Mater., 2005, 17, 5658–5669 CrossRef CAS.
- E. Otyepková, P. Lazar, J. Luxa, K. Berka, K. Čépe, Z. Sofer, M. Pumera and M. Otyepka, Nanoscale, 2017, 9, 19236–19244 RSC.
- B. Schönfeld, J. Huang and S. Moss, Acta Crystallogr., Sect. B: Struct. Sci., 1983, 39, 404–407 CrossRef.
- Z. Yin, H. Li, H. Li, L. Jiang, Y. Shi, Y. Sun, G. Lu, Q. Zhang, X. Chen and H. Zhang, ACS Nano, 2011, 6, 74–80 CrossRef PubMed.
- G. Cunningham, M. Lotya, C. S. Cucinotta, S. Sanvito, S. D. Bergin, R. Menzel, M. S. Shaffer and J. N. Coleman, ACS Nano, 2012, 6, 3468–3480 CrossRef CAS PubMed.
- T. Wieting and J. Verble, Phys. Rev. B: Solid State, 1971, 3, 4286–4292 CrossRef.
- R. C. Cooper, C. Lee, C. A. Marianetti, X. Wei, J. Hone and J. W. Kysar, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035423 CrossRef.
- S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703–9709 CrossRef CAS PubMed.
- P. Li, Z. You and T. Cui, J. Micromech. Microeng., 2013, 23, 045026 CrossRef.
- J. Feldman, J. Phys. Chem. Solids, 1976, 37, 1141–1144 CrossRef CAS.
- A. Webb, J. Feldman, E. Skelton, L. Towle, C. Liu and I. Spain, J. Phys. Chem. Solids, 1976, 37, 329–335 CrossRef CAS.
- G. Levita, A. Cavaleiro, E. Molinari, T. Polcar and M. C. Righi, J. Phys. Chem. C, 2014, 118, 13809–13816 CrossRef CAS.
- A. Molina-Sanchez, K. Hummer and L. Wirtz, Surf. Sci. Rep., 2015, 70, 554–586 CrossRef CAS.
- J. Li, N. V. Medhekar and V. B. Shenoy, J. Phys. Chem. C, 2013, 117, 15842–15848 CrossRef CAS.
- P. Nicolini and T. Polcar, Comput. Mater. Sci., 2016, 115, 158–169 CrossRef CAS.
- P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Proteins: Struct., Funct., Genet., 1988, 4, 31–47 CrossRef CAS PubMed.
- J. Huang and A. D. MacKerell, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987 CrossRef CAS.
- H. Sun, Macromolecules, 1995, 28, 701–712 CrossRef CAS.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- C. C. Dharmawardhana, K. Kanhaiya, T.-J. Lin, A. Garley, M. R. Knecht, J. Zhou, J. Miao and H. Heinz, Mol. Simul., 2017, 43, 1394–1405 CrossRef CAS.
- K. C. Gross, P. G. Seybold and C. M. Hadad, Int. J. Quantum Chem., 2002, 90, 445–458 CrossRef CAS.
- Y. T. Fu, G. D. Zartman, M. Yoonessi, L. F. Drummy and H. Heinz, J. Phys. Chem. C, 2011, 115, 22292–22300 CrossRef CAS.
- S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885 CrossRef CAS.
- R. Zhang, W. Wan, L. Qiu and Y. Zhou, Mater. Lett., 2016, 181, 321–324 CrossRef CAS.
- G. D. Zartman, H. Liu, B. Akdim, R. Pachter and H. Heinz, J. Phys. Chem. C, 2010, 114, 1763–1772 CrossRef CAS.
- T. Livneh and J. E. Spanier, 2D Mater., 2015, 2, 035003 CrossRef.
- A. P. Gaur, S. Sahoo, M. Ahmadi, S. P. Dash, M. J.-F. Guinel and R. S. Katiyar, Nano Lett., 2014, 14, 4314–4321 CrossRef CAS PubMed.
- D.-M. Tang, D. G. Kvashnin, S. Najmaei, Y. Bando, K. Kimoto, P. Koskinen, P. M. Ajayan, B. I. Yakobson, P. B. Sorokin and J. Lou, Nat. Commun., 2014, 5, 3631 CrossRef PubMed.
- H. Heinz, R. A. Vaia, B. L. Farmer and R. R. Naik, J. Phys. Chem. C, 2008, 112, 17281–17290 CrossRef CAS.
- L. L. Zhang, B. Q. Luang and R. H. Zhou, J. Phys. Chem. B, 2019, 123, 7243–7252 CrossRef CAS PubMed.
- J. Wang, L. Liu, D. Ge, H. Zhang, Y. Feng, Y. Zhang, M. Chen and M. Dong, Chem. –Eur. J., 2018, 24, 3397–3402 CrossRef CAS PubMed.
- S. Cetinel, W.-Z. Shen, M. Aminpour, P. Bhomkar, F. Wang, E. R. Borujeny, K. Sharma, N. Nayebi and C. Montemagno, Sci. Rep., 2018, 8, 1–12 CrossRef CAS PubMed.
- P. Li, K. Sakuma, S. Tsuchiya, L. Sun and Y. Hayamizu, ACS Appl. Mater. Interfaces, 2019, 11, 20670–20677 CrossRef CAS PubMed.
- C. Muratore, A. Juhl, A. Stroud, D. Wenbi Lai, A. Jawaid, K. Burzynski, J. Dagher, G. Leuty, C. Harsch and S. Kim, Appl. Phys. Lett., 2018, 112, 233704 CrossRef.
- L. Sun, T. Narimatsu, S. Tsuchiya, T. Tanaka, P. Li and Y. Hayamizu, RSC Adv., 2016, 6, 96889–96897 RSC.
- J. Chen, E. Zhu, J. Liu, S. Zhang, Z. Lin, X. Duan, H. Heinz, Y. Huang and J. J. De Yoreo, Science, 2018, 362, 1135–1139 CrossRef CAS PubMed.
- C. Y. Chiu, Y. J. Li, L. Y. Ruan, X. C. Ye, C. B. Murray and Y. Huang, Nat. Chem., 2011, 3, 393–399 CrossRef CAS PubMed.
- E. Zhu, S. Wang, X. Yan, M. Sobani, L. Ruan, C. Wang, Y. Liu, X. Duan, H. Heinz and Y. Huang, J. Am. Chem. Soc., 2019, 141, 1498–1505 CrossRef CAS PubMed.
- F. S. Emami, V. Puddu, R. J. Berry, V. Varshney, S. V. Patwardhan, C. C. Perry and H. Heinz, Chem. Mater., 2014, 26, 5725–5734 CrossRef CAS.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- H. Heinz, B. L. Farmer, R. B. Pandey, J. M. Slocik, S. S. Patnaik, R. Pachter and R. R. Naik, J. Am. Chem. Soc., 2009, 131, 9704–9714 CrossRef CAS PubMed.
- D. Eisenberg, R. M. Weiss, T. C. Terwilliger and W. Wilcox, Faraday Symp. Chem. Soc., 1982, 17, 109–120 RSC.
- E. Pustovgar, R. K. Mishra, M. Palacios, J.-B. d. E. de Lacaillerie, T. Matschei, A. S. Andreev, H. Heinz, R. Verel and R. J. Flatt, Cem. Concr. Res., 2017, 100, 245–262 CrossRef CAS.
- F. S. Emami, V. Puddu, R. J. Berry, V. Varshney, S. V. Patwardhan, C. C. Perry and H. Heinz, Chem. Mater., 2014, 26, 2647–2658 CrossRef CAS.
- S. V. Patwardhan, F. S. Emami, R. J. Berry, S. E. Jones, R. R. Naik, O. Deschaume, H. Heinz and C. C. Perry, J. Am. Chem. Soc., 2012, 134, 6244–6256 CrossRef CAS PubMed.
- T. Jamil, A. Javadi and H. Heinz, Green Chem., 2020, 22, 1577–1593 RSC.
- H. Ramezani-Dakhel, N. M. Bedford, T. J. Woehl, M. R. Knecht, R. R. Naik and H. Heinz, Nanoscale, 2017, 9, 8401–8409 RSC.
- J. Zhou, Y. Yang, Y. Yang, D. S. Kim, A. Yuan, X. Tian, C. Ophus, F. Sun, A. K. Schmid, M. Nathanson, H. Heinz, Q. An, H. Zeng, P. Ercius and J. Miao, Nature, 2019, 570, 500–503 CrossRef CAS.
- R. Xu, C.-C. Chen, L. Wu, M. C. Scott, W. Theis, C. Ophus, M. Bartels, Y. Yang, H. Ramezani-Dakhel, M. R. Sawaya, H. Heinz, L. D. Marks, P. Ercius and J. Miao, Nat. Mater., 2015, 14, 1099–1103 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01443e |
| This journal is © The Royal Society of Chemistry 2020 |