Chiral cyclic [n]spirobifluorenylenes: carbon nanorings consisting of helically arranged quaterphenyl rods illustrating partial units of woven patterns

Abstract

Chiral cyclic [n]spirobifluorenylenes consisting of helically arranged quaterphenyl rods, illustrating partial units of woven patterns, were designed and synthesized as a new family of carbon nanorings. The synthesis was accomplished by the Ni(0)-mediated Yamamoto-coupling of chiral spirobifluorene building blocks. The structures of the cyclic 3-, 4-, and 5-mers were determined by X-ray crystallographic analysis. These carbon nanorings exhibited a strong violet colored emission with high quantum yields in solution (95%, 93%, and 94% for 3-, 4-, and 5-mer, respectively). Other spectroscopic properties, including their chiroptical properties, were also investigated. The g-values for circularly polarized luminescence were found to be in the order of 10⁻³. Characteristic spiroconjugation induced by multiple (≧3) bifluorenyl units, for example the even-odd effect of the number of units in the matching of the signs of the orbitals, was also indicated by DFT calculations.

---

Introduction

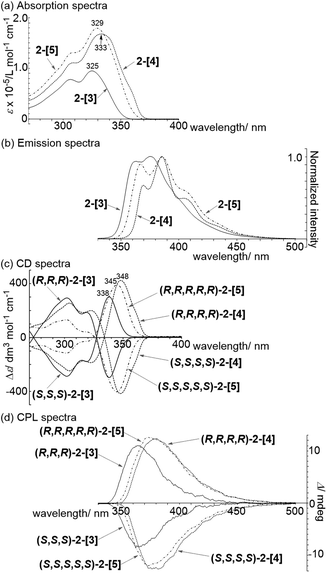
Synthesis of shape-persistent carbon nanorings or carbon-based macrocycles containing extended conjugated π-electron systems has fascinated chemists due to their unique molecular geometry and the associated characteristic properties.¹ The increasing importance of carbon-rich compounds as materials has caused this area to grow and expand into an interdisciplinary area.² Among the synthetic studies of such compounds, the synthesis of p-phenylene compounds with various geometries has attracted attention, as represented by the chemistry of cycloparaphenylene molecules.³ Recent examples of such compounds with a unique geometry include molecules with motifs including spoked wheels,⁴ cages,⁵ tri-helicates,⁶ lemniscates,⁷ Möbius loops,⁸ catenanes and trefoil knots.⁹ We also reported a p-phenylene molecule with an S-shaped geometry, as demonstrated by the synthesis of the linear [3]spirobifluorenylene 1 consisting of three spirobifluorene units, where the stereochemistry of 1 is RMR/SPS (Fig. 1a).¹⁰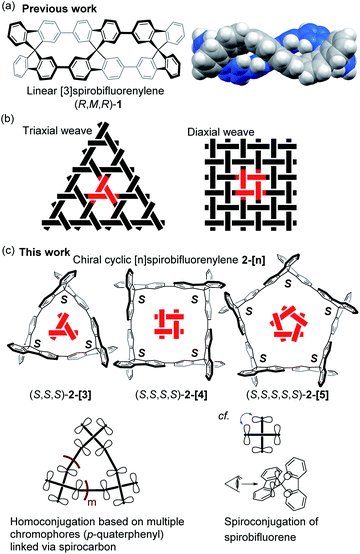

Fig. 1 (a) Previous work. (b) Schematic illustration of triaxial and diaxial weave patterns. (c) This work.

In the present study, we focused on the structural motif of the woven pattern found in textiles.¹¹Fig. 1b shows typical examples of triaxial and diaxial weave patterns. The designed chiral carbon nanorings 2-[n] are constructed by the cyclic connection of spirobifluorene with the same chirality, i.e., RRR or SSS (Fig. 1c). The structures also can be viewed as macrocycles with helically arranged p-quaterphenyl rods. The carbon nanorings 2-[3] and 2-[4] have the same geometric arrangements as units of triaxial and diaxial weave patterns, respectively, in which the spirobifluorene corresponds to the crossing in these weaves. The pentagonal molecule 2-[5] represents a geometrical partial unit with a more elaborate weave involving five sets of threads. Although many unique p-phenylene molecules have been synthesized to date, those based on a weave-motif have not yet been studied, to the best of our knowledge.¹² Moreover, these types of molecules 2-[n] are expected to possess a unique type of spiroconjugation as well as characteristic chiroptical properties. More specifically, multiple orbital interactions in this system will lead to an electronic configuration that is distinct from that of a simple spirobifluorene (Fig. 1c). Such homoconjugation based on multiple π-conjugated units arranged cyclically via spirocarbons has not been investigated.¹³ In addition, a three-dimensional π-conjugation based on spiroconjugation is expected to contribute to the development of charge carrier transport materials.¹⁴ Here, we report the synthesis, structure, spectroscopic properties and spiroconjugation of chiral cyclic [n]spirobifluorenylenes 2-[3], 2-[4], and 2-[5] with the helically-arranged p-quaterphenyl rods illustrating partial units of woven patterns.

Results and discussion

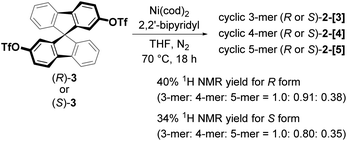
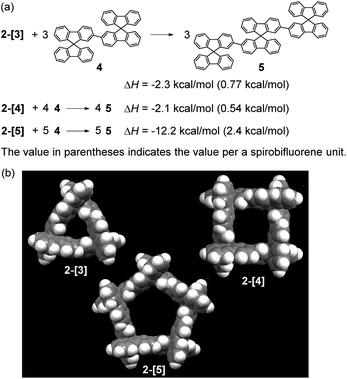
The chiral cyclic [n]spirobifluorenylenes 2-[n] were synthesized by the Ni(0)-mediated Yamamoto coupling of chiral triflates (R or S)-3 (Scheme 1). After filtering through a short silica-gel column, the MALDI-TOF mass analysis of the product showed the formation of a mixture of cyclic oligomers up to a 9-mer (Fig. S1†), although the dimer 2-[2] was not observed. The combined yield of 2-[3], 2-[4], and 2-[5] for the R isomer was 40% with the ratio of 1.0, 0.91, and 0.38, respectively. S-isomers of 2-[n] were also obtained. Pure 2-[3], 2-[4], and 2-[5] were isolated by preparative recycling GPC. Interestingly, the MALDI-TOF mass analysis and the preparative GPC suggested that little or no acyclic products (acyclic 2-mer to 9-mer) were formed in this reaction.

Scheme 1 Synthesis of chiral 2-[3], 2-[4], and 2-[5].

Fig. 2a shows the X-ray crystallographic structure of cyclic 3-mer (S,S,S)-2-[3],¹⁵ showing a D₃ symmetry. The distance between the spirocarbon units is 8.6 Å. The distortion around the spirocarbon is minimal (89.5°), but the internal benzene ring A is slightly distorted (up to 3.5° for θ₁). The dihedral angle between the spirobifluorene units is 43.0°. The packing structure indicates that CH–π interactions connect the molecules in a side by side arrangement (Fig. S2†). One-dimensional voids filled by solvent are formed by the stacking of the molecules. The crystal structure of the 4-mer (S,S,S,S)-2-[4] is shown in Fig. 2b.¹⁶ The observed structure did not show a D₄ symmetric square but, instead, a D₂ symmetric rectangle. The distances between the spirocarbons are 8.7 and 9.0 Å. The rectangle shape is derived from the large difference in the torsion between the spirobifluorenes (50.1° and 4.2°). The rectangle shape appears to be induced by guest solvents. However, the ¹H NMR spectrum in CDCl₃ at room temperature shows only 7 peaks, indicating that the four spirobifluorene units are equivalent in solution (see ESI†). The packing structure also indicates that CH–π interactions connect the molecules side by side (Fig. S3†). One-dimensional voids filled by solvent are formed by the stacking of the molecules, similar to the 3-mer. The crystal structure of the 5-mer (S,S,S,S,S)-2-[5] has no symmetry, where a distorted structure was observed (Fig. 2c).¹⁷ Concerning the distances between spirocarbons, a significantly short distance (8.3 Å) was observed in one of the five (the other four showed around 8.8–8.9 Å). Considerably small angles (86.6° and 86.7°) between the planes around spirocarbon were also observed in two of the five (the angle for the unstrained ideal one is 90°). A large dihedral angle (84.2°) between the fluorene units, which is almost orthogonal, was observed in one of the five (the other four showed in a range of 32–43°). In addition, each fluorene plane is more or less tilted slightly. These features imply the inherent strain in the crystal structure of (S,S,S,S,S)-2-[5]. The packing structure is complicated, and the columnar stacking like 2-[3] and 2-[4] was not observed (Fig. S4 and S5†).

Fig. 2 (a) ORTEP drawing of (S,S,S)-2-[3], (b) (S,S,S,S)-2-[4] and (c) (S,S,S,S,S)-2-[5] with thermal ellipsoids set at the 40, 30, and 30% probability level, respectively. Hydrogen atoms are omitted for the sake of clarity. Solvent molecules are removed in the refinement process. Angles shown in pink are the angles between the planes around spirocarbon. Angles shown in green are the dihedral angles between the spirobifluorene units.

The total strain energies for 2-[3], 2-[4], and 2-[5] were estimated by the homodesmotic reactions shown in Scheme 2a using DFT-calculations, where one molecule of 2-[n] and n molecules of 4 give n molecules of linear [3]spirobifluorenyl 5. The optimization for 2-[3], 2-[4], and 2-[5] was performed with the D₃, D₄, and D₅ symmetry, respectively, being maintained (Scheme 2b). The total strain energies for the 3-mer and 4-mer are very small [2.3 (0.77) and 2.1 (0.54) kcal mol⁻¹, respectively, where the value in parentheses indicates the value per spirobifluorene unit]. In contrast, the 5-mer 2-[5] has a relatively large strain [12.2 (2.4) kcal mol⁻¹], because each fluorene plane is slightly tilted (Fig. S6†).

Scheme 2 (a) Homodesmotic reactions to calculate strain energy and (b) optimized structures for 2-[3], 2-[4], and 2-[5] [B3LYP/6-31G(d,p)].

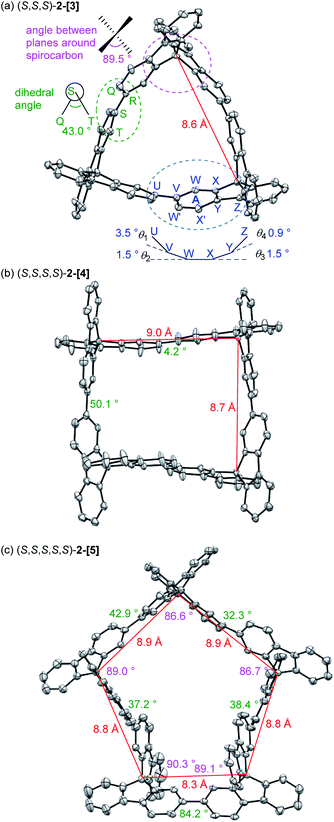
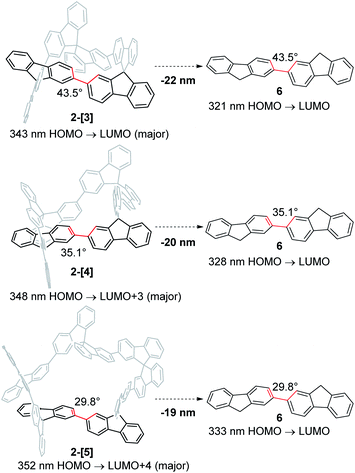
Absorption spectra of 2-[3], 2-[4], and 2-[5] showed that the λ_max in the longer wavelength region is 325, 333, and 329 nm, respectively (Fig. 3a). This order for λ_max is different from the order (2-[3] < 2-[4] < 2-[5]) estimated by TD-DFT calculations shown in Scheme 3. The estimated order reflects the dihedral angle between fluorenes. The red-shift of the cyclic tetramer 2-[4] in the experimental absorption spectrum can be attributed to planarization of the torsion between spirobifluorenes, as shown in the X-ray crystal structure. On the other hand, the dihedral angles for 2-[5] under the experimental conditions are likely to be larger than those estimated by the calculation (29.8°), considering that all of the dihedral angles in the X-ray crystal structure for 2-[5] exceed over 30°. This might account for the small red-shift of 2-[5] as compared to that of 2-[4]. In addition, the solvent molecules included in the cavity of the macrocycles affect the dihedral angles in the experiment in solution. The inversion of the order between the experimental and calculated values for 2-[4] and 2-[5] can happen based on these factors. Absorption spectra are also affected by the through-space interaction between chromophores. To investigate the effects on absorption spectra, the estimated absorption from TD-DFT calculation was compared with bifluorenyl 6 as a reference compound, where the dihedral angles are the same as those of the parent 2-[n] (Scheme 3). As a result, an approximately red-shift of 20 nm was indicated for the interaction in 2-[3], 2-[4], and 2-[5].

Fig. 3 (a) Absorption and (b) emission spectra of (R,R,R)-2-[3] (1.1 × 10⁻⁵ M), (R,R,R,R)-2-[4] (0.92 × 10⁻⁵ M), and (R,R,R,R,R)-2-[5] (1.0 × 10⁻⁵ M) in CH₂Cl₂ using a 1.0 × 10 m⁻² cuvette. (c) CD and (d) CPL spectra of both enantiomers of 2-[3], 2-[4], and 2-[5] (298 K, 1.0 × 10⁻⁵ M in CH₂Cl₂).

Scheme 3 Effect of spiroconjugation, as estimated based on TD-DFT calculations [TD-B3LYP-D3/6-31G(d,p)//B3LYP-D3/6-31G(d,p)].

Spirobifluorene oligomers are known to be strong emitters.¹⁸ Moreover, chiral macrocycles such as 2-[n] would be expected to show emission as well as chiroptical properties. The emission spectroscopy data showed that the 4-mer and 5-mer were red-shifted as compared to that for the 3-mer (Fig. 3b). The quantum yields ϕ_PL of 2-[3], 2-[4], and 2-[5] in CH₂Cl₂ solution were high (95%, 93%, and 94%, respectively, Table 1). In the case of the cyclic 3-mer, the quantum yield was also high in the solid state (65%).

Table 1 Quantum yields ϕ_PL of 2-[3], 2-[4], and 2-[5]

	Quantum yield ϕPL/%
	2-[3]	2-[4]	2-[5]
Solution (CH2Cl2)	95	93	94
Solid	65	16	23

---

The chiroptical properties of 2-[n] were investigated based on circular dichroism (CD) and circular polarized luminescence (CPL) spectroscopy (Fig. 3c and d). Mirror image spectra were obtained in both spectra. A Cotton effect was observed at 338, 345, and 348 nm for the 3-mer, 5-mer, and 4-mer, respectively, in the longer wavelength region of the CD spectra. The dissymmetry factors |g_abs| for 2-[3], 2-[4], and 2-[5] were 5.2 × 10⁻³ at 340 nm, 5.0 × 10⁻³ at 350 nm, and 4.8 × 10⁻³ at 349 nm, respectively. The CPL signals appeared at around 365, 380, and 373 nm, respectively (Fig. 3d). The dissymmetry factors |g_lum| were 1.9 × 10⁻³ at 348 nm, 2.4 × 10⁻³ at 368 nm, and 1.9 × 10⁻³ at 363 nm for the 3-mer, 4-mer, and 5-mer, respectively. The values for the 3-mer and 5-mer are comparable to that for the linear [3]spirobifluorenylene 1 and most of the other chiral small organic molecules listed in a recent review.¹⁹ A large |g_lum| factor with a high ϕ_PL yield is desirable for practical photonics applications. Thus, the carbon nanorings with >90% ϕ_PL yields can be considered to be a potential candidate.

Electrochemical properties of 2-[3], 2-[4], and 2-[5] were investigated by cyclic voltammetry. However, all of the voltammograms were irreversible and unclear. The voltammograms of differential pulse voltammetry showed a broad peak around 0.9–1.0 eV (Fig. S7†).

Spiroconjugation involves through-space interactions of the p-orbitals around the spirocarbon.²⁰ In the case of the spirobifluorene, for example, the through-space interactions of the p-orbitals of the HOMO for a fluorene unit induce the splitting of the HOMO in the spirobifluorene, whereas, the LUMO is degenerate because of the symmetry of the orbitals (Fig. 4a).²¹ In contrast, the macrocycle 2-[n] involves a different type of spiroconjugation because the p-orbitals in the multiple bifluorenyl units are able to interact with each other through space, depending on the number of spirocarbons to result in orbital splitting, where an even-odd effect was observed. Thus, DFT calculations of the cyclic 3-mer 2-[3], which has three spirocarbons connecting three bifluorenyl units, indicate the characteristic splitting of the HOMO and LUMO into three, as shown in Fig. 4b and S8a.† In the case of the splitting of the HOMO, a destabilized MO and two stabilized doubly degenerate MOs are generated. The signs of orbitals around all of the spirocarbons are mismatched with each other in the HOMO of 2-[3], resulting in destabilization. The symmetry of the HOMO in a bifluorenyl unit forbids making the orbital signs around all of the spirocarbons in 2-[3] match because the number of bifluorenyl units is odd (Fig. 4b). In contrast, the splitting of the LUMO of the bifluorenyl unit results in a stabilized MO and two destabilized doubly degenerate MOs. Considering the symmetry of the LUMO in the bifluorenyl unit, the LUMO of 2-[3] would be expected to be triply degenerate, which is similar to the doubly degenerate LUMO of spirobifluorene itself (Fig. 4a). However, the LUMO was split in 2-[3], probably because of the structural change (broken symmetry) of the spirobifluorene skeleton. Spiroconjugation of 3-mer 2-[3] was compared to that of acyclic 3-mer 5 (Fig. S10†). Spiroconjugation in the acyclic one 5 was observed in the only central spirobifluorene moiety. Concerning the splitting way, splitting of the HOMO and almost the degenerate LUMO was observed based on the interaction of the two chromophores, which is different from that for 2-[3]. The energy gap induced by splitting for the HOMO in 2-[3] is 0.11 eV, which is larger than that for the LUMO (0.05 eV) (Table 2). The splitting for the HOMO in 2-[3] is also larger than that for the HOMO in 5 (0.08 eV, Table S2†) but smaller than that for spirobifluorene (0.30 eV).²¹ The size of the orbitals around the spirocarbon in 2-[3] is relatively small, compared to that of spirobifluorene itself, which accounts for the relatively small spiroconjugation. In the case of the 4-mer 2-[4], the HOMO and LUMO split 1 : 2 : 1 as shown in Fig. 5b, S8b, S11,† and Table 2. The signs of orbitals around all of the spirocarbons are mismatched with respect to each other in the HOMO, and matched with respect to each other in the HOMO−3 (Fig. 4c and S8b† for schematic drawing). Since the number of bifluorenyl units is even, the orbital signs around all of the spirocarbons are allowed to be matched in 2-[4]. This is in contrast to the case of 2-[3]. These results clearly suggest the effect of even and odd numbers of chromophore units in matching the signs of the orbitals. The splitting of the LUMO in 2-[4] is quite small (0.01 eV), and the LUMO to LUMO+3 are almost degenerate (Table 2). In the case of the 5-mer 2-[5], the HOMO and LUMO of the bifluorenyl unit are split 1 : 2 : 2 as shown in Fig. 5c, S9, S12,† and Table 2. The signs of the orbitals around all of the spirocarbons are mismatched with respect to each other in the HOMO, resulting in destabilization. As the number of bifluorenyl units is odd, it is not possible to make the orbital signs around all of the spirocarbons match in the splitting for the HOMO of the bifluorenyl unit in 2-[5]. Similar to the 3-mer and 4-mer, splitting of the LUMO (0.02 and 0.03 eV) is small compared to that of the HOMO (0.04 and 0.09 eV) (Table 2).

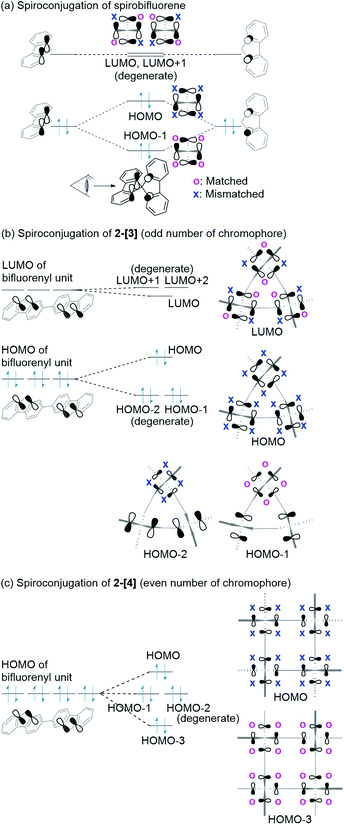Fig. 4 Spiroconjugation of (a) spirobifluorene, (b) 2-[3], and (c) 2-[4]. Here, only the p-orbitals around spirocarbon are shown here.

Table 2 Orbital energy for 2-[3], 2-[4], and 2-[5] [B3LYP-D3/6-31G(d,p)]^a

E/eV
2-[3]	2-[4]	2-[5]
a H: HOMO, L: LUMO.
	−1.25 (L+3)	−1.26 (L+4)
−1.19 (L+1, L+2) [degenerate]	−1.26 (L+1, L+2) [degenerate]	−1.28 (L+2, L+3) [degenerate]
−1.24 (L)	−1.27 (L)	−1.31 (L, L+1) [degenerate]
−5.32 (H)	−5.27 (H)	−5.25 (H)
−5.43 (H−1, H−2) [degenerate]	−5.34 (H−1, H−2) [degenerate]	−5.29 (H−1, H−2) [degenerate]
	−5.43 (H−3)	−5.38 (H−3, H−4) [degenerate]

---

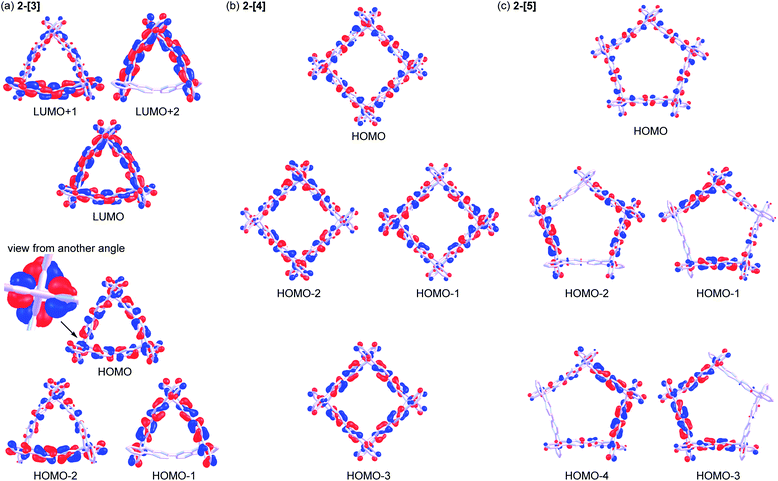Fig. 5 Molecular orbitals for (a) 2-[3], (b) 2-[4], and (c) 2-[5] [B3LYP-D3/6-31G(d,p)] (contour value is 0.025).

Conclusions

In conclusion, chiral cyclic [n]spirobifluorenylenes 2-[3], 2-[4], and 2-[5] consisting of helically arranged quaterphenyl rods, illustrating geometric partial units of a woven textile, were designed and synthesized as a new family of carbon nanorings. The X-ray crystallographic analyses of cyclic 2-[3], 2-[4], and 2-[5] clearly showed the structures representing a part of weave patterns. The carbon nanorings 2-[3], 2-[4], and 2-[5] exhibited strong emissions with high quantum yields in excess of 90%. Chiroptical spectroscopy showed that the g-values for CD and CPL were in the order of 10⁻³. The characteristic spiroconjugation in 2-[n] was induced by multiple (≧3) chromophores (bifluorenyl units). The even-odd effect of the number of units in matching of the signs of the orbitals was indicated by DFT calculations. In the case of an odd number, the symmetry of the HOMO in the bifluorenyl unit forbids making the orbital signs around all of the spirocarbons match, in contrast to the case of an even number. Different from spirobifluorene itself, the LUMO splits although this LUMO splitting is small as compared to that of the HOMO. The carbon nanorings are expected to serve as electroluminescent materials, chiral hosts for molecular recognition, and a three-dimensional π-conjugated system based on spiroconjugation for use in charge carrier transport materials. Research directed toward applications as well as further studies of the synthesis of π-conjugated systems with a woven-like motif is now underway.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by JSPS KAKENHI (20H02724). We wish to thank Professor Toshiyuki Moriuchi and Dr Rika Tanaka in Graduate School of Science, Osaka City University for the X-ray crystallographic analysis. We also wish to thank Professors Youhei Takeda and Satoshi Minakata in Graduate School of Engineering, Osaka University for the quantum yield measurements. We sincerely appreciate Mr Kunihiko Kamon and Mr Hiromi Ohi in Analytical Instrumentation Facility in Graduate School of Engineering, Osaka University for the accurate measurements of small weight.

Notes and references

1. (a) S. Höger, J. Polym. Sci., Part A: Polym. Chem., 1999, 37, 2685; (b) C. Grave and A. D. Schlüter, Eur. J. Org. Chem., 2002, 3075; (c) W. Zhang and J. S. Moore, Angew. Chem., Int. Ed., 2006, 45, 4416; (d) T. Kawase and H. Kurata, Chem. Rev., 2006, 106, 5250; (e) K. Tahara and Y. Tobe, Chem. Rev., 2006, 106, 5274; (f) E. L. Spitler, C. A. Johnson II and M. M. Haley, Chem. Rev., 2006, 106, 5344; (g) R. Gleiter, B. Esser and S. C. Kornmayer, Acc. Chem. Res., 2009, 42, 1108; (h) D. Eisenberg, R. Shenhar and M. Rabinovitz, Chem. Soc. Rev., 2010, 39, 2879; (i) M. Iyoda, J. Yamakawa and M. J. Rahman, Angew. Chem., Int. Ed., 2011, 50, 10522; (j) S. Toyota, H. Ikeda and T. Iwanaga, ChemPlusChem, 2017, 82, 957; (k) K. Yazaki, L. Catti and M. Yoshizawa, Chem. Commun., 2018, 54, 3195; (l) M. A. Majewski and M. Stępień, Angew. Chem., Int. Ed., 2019, 58, 86; (m) Y. Segawa, D. R. Levine and K. Itami, Acc. Chem. Res., 2019, 52, 2760; (n) K. Miki and K. Ohe, Chem.–Eur. J., 2020, 26, 2529.
2. (a) S. Höger, Chem.–Eur. J., 2004, 10, 1320; (b) E. J. Leonhardt and R. Jasti, Nat. Rev. Chem., 2019, 3, 672; (c) M. Ball, B. Zhang, Y. Zhong, B. Fowler, S. Xiao, F. Ng, M. Steigerwald and C. Nuckolls, Acc. Chem. Res., 2019, 52, 1068.
3. (a) H. Omachi, Y. Segawa and K. Itami, Acc. Chem. Res., 2012, 45, 1378; (b) S. Yamago, E. Kayahara and T. Iwamoto, Chem. Rec., 2014, 14, 84; (c) S. E. Lewis, Chem. Soc. Rev., 2015, 44, 2221; (d) E. R. Darzi and R. Jasti, Chem. Soc. Rev., 2015, 44, 6401; (e) Y. Segawa, A. Yagi, K. Matsui and K. Itami, Angew. Chem., Int. Ed., 2016, 55, 5136; (f) D. Wu, W. Cheng, X. Ban and J. Xia, Asian J. Org. Chem., 2018, 7, 2161.
4. (a) Y. Liu, A. Narita, J. Teyssandier, M. Wagner, S. De Feyter, X. Feng and K. Müllen, J. Am. Chem. Soc., 2016, 138, 15539; (b) A. Idelson, C. Sterzenbach, S.-S. Jester, C. Tschierske, U. Baumeister and S. Höger, J. Am. Chem. Soc., 2017, 139, 4429.
5. (a) K. Matsui, Y. Segawa, T. Namikawa, K. Kamada and K. Itami, Chem. Sci., 2013, 4, 84; (b) K. Matsui, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2014, 136, 16452; (c) E. Kayahara, T. Iwamoto, H. Takaya, T. Suzuki, M. Fujitsuka, T. Majima, N. Yasuda, N. Matsuyama, S. Seki and S. Yamago, Nat. Commun., 2013, 4, 2694; (d) S. Cui, G. Zhuang, D. Lu, Q. Huang, H. Jia, Y. Wang, S. Yang and P. Du, Angew. Chem., Int. Ed., 2018, 57, 9330; (e) N. Hayase, J. Nogami, Y. Shibata and K. Tanaka, Angew. Chem., Int. Ed., 2019, 58, 9439.
6. H. Sato, J. A. Bender, S. T. Roberts and M. J. Krische, J. Am. Chem. Soc., 2018, 140, 2455.
7. (a) K. Senthilkumar, M. Kondratowicz, T. Lis, P. J. Chmielewski, J. Cybińska, J. L. Zafra, J. Casado, T. Vives, J. Crassous, L. Favereau and M. Stępień, J. Am. Chem. Soc., 2019, 141, 7421; (b) T. A. Schaub, E. A. Prantl, J. Kohn, M. Bursch, C. R. Marshall, E. J. Leonhardt, T. C. Lovell, L. N. Zakharov, C. K. Brozek, S. R. Waldvogel, S. Grimme and R. Jasti, J. Am. Chem. Soc., 2020, 142, 8763.
8. S. Nishigaki, Y. Shibata, A. Nakajima, H. Okajima, Y. Masumoto, T. Osawa, A. Muranaka, H. Sugiyama, A. Horikawa, H. Uekusa, H. Koshino, M. Uchiyama, A. Sakamoto and K. Tanaka, J. Am. Chem. Soc., 2019, 141, 14955.
9. Y. Segawa, M. Kuwayama, Y. Hijikata, M. Fushimi, T. Nishihara, J. Pirillo, J. Shirasaki, N. Kubota and K. Itami, Science, 2019, 365, 272.
10. J. Oniki, T. Moriuchi, K. Kamochi, M. Tobisu and T. Amaya, J. Am. Chem. Soc., 2019, 141, 18238.
11. Supramolecular chemistry related to the weave motif: (a) Y. Liu, Y. Ma, Y. Zhao, X. Sun, F. Gándara, H. Furukawa, Z. Liu, H. Zhu, C. Zhu, K. Suenaga, P. Oleynikov, A. S. Alshammari, X. Zhang, O. Terasaki and O. M. Yaghi, Science, 2016, 351, 365; (b) U. Lewandowska, W. Zajaczkowski, S. Corra, J. Tanabe, R. Borrmann, E. M. Benetti, S. Stappert, K. Watanabe, N. A. K. Ochs, R. Schaeublin, C. Li, E. Yashima, W. Pisula, K. Müllen and H. Wennemers, Nat. Chem., 2017, 9, 1068; (c) A. M. Champsaur, C. Mézière, M. Allain, D. W. Paley, M. L. Steigerwald, C. Nuckolls and P. Batail, J. Am. Chem. Soc., 2017, 139, 11718.
12. Some π-conjugated molecules with related structures: (a) T. Fukino, N. Fujita and T. Aida, Org. Lett., 2010, 12, 3074; (b) Y. Morisaki, R. Hifumi, L. Lin, K. Inoshita and Y. Chujo, Polym. Chem., 2012, 3, 2727; (c) G. R. Schaller, F. Topić, K. Rissanen, Y. Okamoto, J. Shen and R. Herges, Nat. Chem., 2014, 6, 608; (d) K. Takaishi, T. Yabe, M. Uchiyama and A. Yokoyama, Tetrahedron, 2014, 70, 730; (e) F. Sannicolò, P. R. Mussini, T. Benincori, R. Cirilli, S. Abbate, S. Arnaboldi, S. Casolo, E. Castiglioni, G. Longhi, R. Martinazzo, M. Panigati, M. Pappini, E. Q. Procopio and S. Rizzo, Chem.–Eur. J., 2014, 20, 15298; (f) S. Castro-Fernández, R. Yang, A. P. García, I. L. Garzón, H. Xu, A. G. Petrovic and J. L. Alonso-Gómez, Chem.–Eur. J., 2017, 23, 11747; (g) Y. Nojima, M. Hasegawa, N. Hara, Y. Imai and Y. Mazaki, Chem. Commun., 2019, 55, 2749; (h) R. Katoono, K. Sakamoto and T. Suzuki, Chem. Commun., 2019, 55, 5503.
13. Homoconjugation in the multichromophoric compounds: M. R. Talipov, T. S. Navale and R. Rathore, Angew. Chem., Int. Ed., 2015, 54, 14468.
14. (a) T. P. I. Saragi, T. Spehr, A. Siebert, T. Fuhrmann-Lieker and J. Salbeck, Chem. Rev., 2007, 107, 1011; (b) Q. Yan, Y. Guo, A. Ichimura, H. Tsuji and E. Nakamura, J. Am. Chem. Soc., 2016, 138, 10897; (c) G. Gao, N. Liang, H. Geng, W. Jiang, H. Fu, J. Feng, J. Hou, X. Feng and Z. Wang, J. Am. Chem. Soc., 2017, 139, 15914; (d) H. Hamada, Y. Itabashi, R. Shang and E. Nakamura, J. Am. Chem. Soc., 2020, 142, 2059.
15. CCDC-1991410. See also the attached cif file and ESI† for details.
16. CCDC-1991411. See also the attached cif file and ESI† for details.
17. CCDC-1999349. See also the attached cif file and ESI† for details.
18. Selected examples: (a) K.-T. Wong, Y.-Y. Chien, R.-T. Chen, C.-F. Wang, Y.-T. Lin, H.-H. Chiang, P.-Y. Hsieh, C.-C. Wu, C. H. Chou, Y. O. Su, G.-H. Lee and S.-M. Peng, J. Am. Chem. Soc., 2002, 124, 11576; (b) T.-C. Chao, Y.-T. Lin, C.-Y. Yang, T. S. Hung, H.-C. Chou, C.-C. Wu and K.-T. Wong, Adv. Mater., 2005, 17, 992; (c) L. J. Sicard, H.-C. Li, Q. Wang, X.-Y. Liu, O. Jeannin, J. Rault-Berthelot, L.-S. Liao, Z.-Q. Jiang and C. Poriel, Angew. Chem., Int. Ed., 2019, 58, 3848.
19. N. Chen and B. Yan, Molecules, 2018, 23, 3376.
20. (a) H. Dürr and R. Gleiter, Angew. Chem., Int. Ed. Engl., 1978, 17, 559; (b) R. Gleiter and G. Haberhauer, Aromaticity and Other Conjugation Effects, Wiley-VCH, Wiinheim, 2012, p. 166.
21. (a) A. Schweig, U. Weidner, D. Hellwinkel and W. Krapp, Angew. Chem., Int. Ed., 1973, 12, 310; (b) B. H. Boo, Y. S. Choi, T.-S. Kim, S. K. Kang, Y. H. Kang and S. Y. Lee, J. Mol. Struct., 1996, 377, 129.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1991410, 1991411 and 1999349. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc02452j

---