Open Access Article
Open Access ArticleAu3-to-Ag3 coordinate-covalent bonding and other supramolecular interactions with covalent bonding strength†
Zhou
Lu‡
 a,
Bhaskar
Chilukuri‡
a,
Bhaskar
Chilukuri‡
 ab,
Chi
Yang‡
*ac,
Abdel-Monem M.
Rawashdeh
ab,
Chi
Yang‡
*ac,
Abdel-Monem M.
Rawashdeh
 ad,
Ravi K.
Arvapally
a,
Sammer M.
Tekarli
ae,
Xiaoping
Wang
ad,
Ravi K.
Arvapally
a,
Sammer M.
Tekarli
ae,
Xiaoping
Wang
 f,
Christian T.
Cardenas
a,
Thomas R.
Cundari
f,
Christian T.
Cardenas
a,
Thomas R.
Cundari
 *a and
Mohammad A.
Omary
*a and
Mohammad A.
Omary
 *ad
*ad
aDepartment of Chemistry, University of North Texas, 1155 Union Circle #305070, Denton, Texas 76203, USA. E-mail: t@unt.edu; omary@unt.edu
bDepartment of Chemistry, Illinois State University, Normal, Illinois 61790, USA
cCenter for Materials Research, Norfolk State University, Norfolk, Virginia 23504, USA. E-mail: chi.yang@unt.edu
dDepartment of Chemistry, Yarmouk University, Irbid 21163, Jordan
eNew College, University of North Texas, 2811 Internet Blvd Suite 100, Frisco, Texas 75034, USA
fNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831-6475, USA
First published on 11th September 2020
Abstract
An efficient strategy for designing charge-transfer complexes using coinage metal cyclic trinuclear complexes (CTCs) is described herein. Due to opposite quadrupolar electrostatic contributions from metal ions and ligand substituents, [Au(μ-Pz-(i-C3H7)2)]3·[Ag(μ-Tz-(n-C3F7)2)]3 (Pz = pyrazolate, Tz = triazolate) has been obtained and its structure verified by single crystal X-ray diffraction – representing the 1st crystallographically-verified  stacked adduct of monovalent coinage metal CTCs. Abundant supramolecular interactions with aggregate covalent bonding strength arise from a combination of M–M′ (Au → Ag), metal–π, π–π interactions and hydrogen bonding in this charge-transfer complex, according to density functional theory analyses, yielding a computed binding energy of 66 kcal mol−1 between the two trimer moieties – a large value for intermolecular interactions between adjacent d10 centres (nearly doubling the value for a recently-claimed Au(I) → Cu(I) polar-covalent bond: Proc. Natl. Acad. Sci. U.S.A., 2017, 114, E5042) – which becomes 87 kcal mol−1 with benzene stacking. Surprisingly, DFT analysis suggests that: (a) some other literature precedents should have attained a stacked
stacked adduct of monovalent coinage metal CTCs. Abundant supramolecular interactions with aggregate covalent bonding strength arise from a combination of M–M′ (Au → Ag), metal–π, π–π interactions and hydrogen bonding in this charge-transfer complex, according to density functional theory analyses, yielding a computed binding energy of 66 kcal mol−1 between the two trimer moieties – a large value for intermolecular interactions between adjacent d10 centres (nearly doubling the value for a recently-claimed Au(I) → Cu(I) polar-covalent bond: Proc. Natl. Acad. Sci. U.S.A., 2017, 114, E5042) – which becomes 87 kcal mol−1 with benzene stacking. Surprisingly, DFT analysis suggests that: (a) some other literature precedents should have attained a stacked  product akin to the one herein, with similar or even higher binding energy; and (b) a high overall intertrimer bonding energy by inferior electrostatic assistance, underscoring genuine orbital overlap between M and M′ frontier molecular orbitals in such polar-covalent M–M′ bonds in this family of molecules. The Au → Ag bonding is reminiscent of classical Werner-type coordinate-covalent bonds such as H3N: → Ag in [Ag(NH3)2]+, as demonstrated herein quantitatively. Solid-state and molecular modeling illustrate electron flow from the π-basic gold trimer to the π-acidic silver trimer with augmented contributions from ligand-to-ligand’ (LL′CT) and metal-to-ligand (MLCT) charge transfer.
product akin to the one herein, with similar or even higher binding energy; and (b) a high overall intertrimer bonding energy by inferior electrostatic assistance, underscoring genuine orbital overlap between M and M′ frontier molecular orbitals in such polar-covalent M–M′ bonds in this family of molecules. The Au → Ag bonding is reminiscent of classical Werner-type coordinate-covalent bonds such as H3N: → Ag in [Ag(NH3)2]+, as demonstrated herein quantitatively. Solid-state and molecular modeling illustrate electron flow from the π-basic gold trimer to the π-acidic silver trimer with augmented contributions from ligand-to-ligand’ (LL′CT) and metal-to-ligand (MLCT) charge transfer.
Introduction
Noncovalent interactions are essential in many aspects of supramolecular chemistry, materials science, and biological systems.1,2 These interactions, including but not limited to hydrogen bondings, π–π stackings, electrostatic attractions, and metal–metal interactions, can be tuned by changing functional groups, steric hindrance, electronic configurations, and so on.3–6 Between binary stacked complexes, donor–acceptor type ground-state charge transfer exists due to uneven electron density distribution and will be enhanced by noncovalent interactions.7–10Among stacked complexes, metal–metal (typically metallophilic) interactions cannot be neglected to describe the attraction between homo- and hetero-atomic closed-shell metal ions with shorter distances than the sum of their van der Waals radii in metal complexes.11–13 When it comes to d10 block metals, like CuI, AgI, AuI, and HgII, their electronic configurations still allow attractive forces to occur between metals that typically arise from van der Waals forces.14–17 Theoretically, the strength of aurophilic bonding, generally considered among the strongest closed-shell metallophilic interactions, is considered to be commensurate with hydrogen bonding (∼10 kcal mol−1) due to strong relativistic effects upon the gold orbitals. Moreover, for closed-shell heterometallic complexes, besides metallophilic interactions, covalent bonds were described in an AuI4CuI2-imidazolate/pyrazolate complex with an estimated 35–43 kcal mol−1 binding energy.18
Our group has studied cyclic trinuclear complexes of d10 coinage metal ions – cyclo-M3(μ-L)3 (M = coinage metal, L = anionic ligand) – bearing 9-membered rings (Scheme 1 depicts two examples).19–26 These d10 complexes possess (near-)planar geometries and a variety of properties that can be both fine- and coarse-tuned via rational manipulation of metals (M), ligands (L) and ligand substituents (R), e.g., π vs. Brønsted vs. Lewis acid-base chemistry, host/guest chemistry, supramolecular assemblies, M–M-bonded excimers, ordered monolayers, metalloaromaticity and metallophilic interactions.19–27 These cyclo-M3(μ-L)3 complexes exhibit photoluminescence, thermochromic, acid-base, and donor–acceptor properties.9,27–29 The phenomenal properties of these coinage metal CTCs arise from the interplay of d–d, d–π, π–π interactions that govern their supramolecular assembly via metal–metal, metal–ligand and ligand–ligand moieties in the solid state and concentrated fluid or glassy solutions.
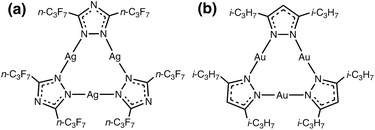 | ||
| Scheme 1 Molecular structure of the: (a) π-acidic acceptor [Ag(μ-Tz-(n-C3F7)2)]3 and (b) π-basic donor [Au(μ-Pz-(i-C3H7)2)]3. | ||
Our research seeks to develop structure (molecular and solid-state)-property (optoelectronic) relationships for CTCs of type cyclo-M3(μ-L-R)3 by varying different M coinage metals (i.e., CuI/AgI/AuI), bridging ligands L (e.g., azolates), and R substituents (e.g., alkyl or perfluoroalkyl) by closely synergizing molecular and solid-state simulations with synthetic and spectroscopic experiments. Molecular electrostatic potential (MEP) and positive charge attraction (PCA) calculations indicate that cyclo-M3(μ-L–R)3 trimers with Ag, triazolate (Tz) ligands and electron withdrawing –CF3 substituents {viz. [Ag(μ-Tz-(CF3)2)]3} give the most π-acidic or n-type semiconducting character to the trimer molecule.30 In contrast, Au, imidazolate (Im) ligand and electron donating –CH3 substituents, [Au(μ-Im-(N–CH3))]3, yield the most π-basic or p-type semiconducting trimer. Given one extreme for the acceptor, whereby we use the M/L/R combination that gives the most favourable acceptor behaviour, we show herein that one may modify M/R for the donor to produce an Ag3/Au3 binary stacked π-acid/base adduct (Scheme 1).
Due to their planar geometry, naked metal sites in the vertical direction and opposite properties of acid–base chemistry, stacked metal–organic trimers were expected to exhibit good potential as semiconductors or optoelectronic devices, as organic devices usually suffer inferior stability, unreliable processing and poor synthetic yield with multiple reaction steps to synthesize perfluorinated acceptors such as perfluoropentacene.31 However, previous attempts to obtain stacked trimers were of limited success. In the early 2000s, Fackler et al. reported the reactions of gold trimers ([Au(μ-Im-(N–Bz))]3 or [Au(μ-(p-Tol)N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OEt))]3, Bz = benzyl, Tol = tolyl) with silver trimer ([Ag(μ-Pz-(3,5-Ph)2)]3, Pz = pyrazolate) in different stoichiometric ratios yielded mixed-metal gold–silver complexes rather than acid-base adducts due to the fact that the electron-donating substituents reduce the π-acidity of the accepting silver trimer.32 Recently, Galassi et al. revealed the formation of stacked complex between [Au(μ-Im-(N–Bz))]3 and [Cu(μ-Pz-(CF3)2)]3 but no crystals of this putative π-acid/base intermediate were obtained.18 All the R variations in the [Au(μ-Im-(N–R))]3 electron-rich CTC from Bz to Me or Et led to heterobimetallic Au2Cu crystallographic products (or pre-dominantly Cu2Au crude products upon altering the stoichiometry) with one combination attaining a claimed hexanuclear cluster with two intertrimer CuI–AuI polar-covalent bonds between adjacent Au2Cu CTCs, which are much shorter (2.875 Å) than the aurophilic interactions between adjacent dimer-of-trimer units (3.488 Å).18 Experimental/computational solution-state studies by Esser and coworkers indicated binding energies between [Au(μ-Py)]3 (Py = pyridinate) and both organic and inorganic acceptors, the latter including [M(μ-Pz-(CF3)2)]3, in the 10–40 kcal mol−1 range – dominated by London dispersion forces.7,8 Results of these investigations manifested the significance of both metals and ligand substituents, using gold and electron-donating groups to build π-donors while silver and electron-withdrawing groups benefiting the strength of inorganic π-acceptors – factors also relevant herein.
C(OEt))]3, Bz = benzyl, Tol = tolyl) with silver trimer ([Ag(μ-Pz-(3,5-Ph)2)]3, Pz = pyrazolate) in different stoichiometric ratios yielded mixed-metal gold–silver complexes rather than acid-base adducts due to the fact that the electron-donating substituents reduce the π-acidity of the accepting silver trimer.32 Recently, Galassi et al. revealed the formation of stacked complex between [Au(μ-Im-(N–Bz))]3 and [Cu(μ-Pz-(CF3)2)]3 but no crystals of this putative π-acid/base intermediate were obtained.18 All the R variations in the [Au(μ-Im-(N–R))]3 electron-rich CTC from Bz to Me or Et led to heterobimetallic Au2Cu crystallographic products (or pre-dominantly Cu2Au crude products upon altering the stoichiometry) with one combination attaining a claimed hexanuclear cluster with two intertrimer CuI–AuI polar-covalent bonds between adjacent Au2Cu CTCs, which are much shorter (2.875 Å) than the aurophilic interactions between adjacent dimer-of-trimer units (3.488 Å).18 Experimental/computational solution-state studies by Esser and coworkers indicated binding energies between [Au(μ-Py)]3 (Py = pyridinate) and both organic and inorganic acceptors, the latter including [M(μ-Pz-(CF3)2)]3, in the 10–40 kcal mol−1 range – dominated by London dispersion forces.7,8 Results of these investigations manifested the significance of both metals and ligand substituents, using gold and electron-donating groups to build π-donors while silver and electron-withdrawing groups benefiting the strength of inorganic π-acceptors – factors also relevant herein.
Expanding upon these findings, herein we report the synthesis, crystal structure, and modelling (molecular and supramolecular solid-state) of the first crystallographically characterized stacked π-base/π-acid Au/Ag cyclotrimer complex, [Au(μ-Pz-(i-C3H7)2)]3·[Ag(μ-Tz-(n-C3F7)2)]3 (1). Besides the choice of CTC metal atoms, selected ligands and substituents – i.e., pyrazolate with i-C3H7 for the Au3 cyclotrimer and triazolate with n-C3F7 for Ag3 – have proven an efficient strategy to enhance the level of electron donation and acceptance, respectively, for each building component to attain this hitherto elusive Au3/Ag3 stacked crystallographic geometry. Remarkably strong supramolecular interactions have been computed, which are in combination of metallophilicity and other dispersion forces, close to covalent boning strength.
Results and discussion
Crystallographic structural characterization
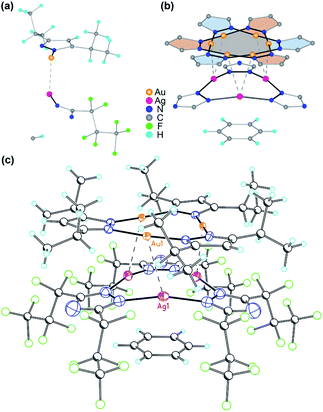
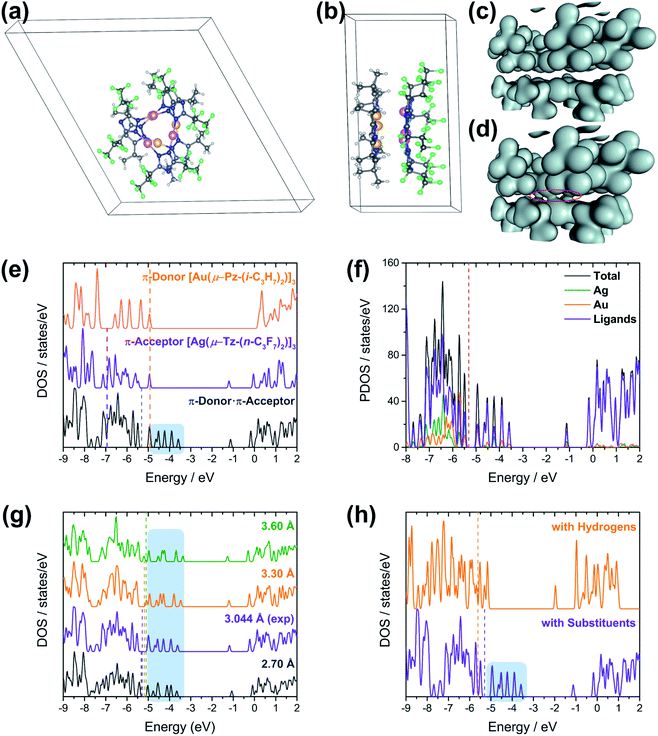
A stacked material [Au(μ-Pz-(i-C3H7)2)]3·[Ag(μ-Tz-(n-C3F7)2)]3 (1) was synthesized and structurally characterized by X-ray crystallography (see Experimental section in ESI† for details), Fig. 1 and 2. The asymmetric unit is depicted in Fig. 1a and the donor (gold) and acceptor (silver) trimers form vertical stacks along the c-axis of the unit cell. Also, the gold trimer exhibits doubly disorder along the C3 axis (Fig. 1b). The closest Au–Ag distance in the synthesized stacked material is 3.0462(18) Å. Experimental bond distances for monovalent ligand-unsupported Au–Ag bonds range from 2.6 to 3.1 Å, among which the shortest distances of 2.6607(15) Å and 2.6772(3) Å were reported.33,34The crystal structure of 1 merits comment. There are three structural figures of merit we adopt from the discussion in ref. 18 as pertains to the presence or absence of M–M′ polar-covalent bonding. First, the crystallographic M–M′ distance showing three instances of short AgI–AuI distances at 3.0462(18) Å. These are to be contrasted with only two (not three) instances of albeit significantly shorter CuI–AuI distances at 2.8750(8) Å in ref. 18. If one accounts for the much larger covalent radius of AgIvs. CuI – i.e., 1.33 Å vs. 1.13 Å or 20 pm larger according to Schmidbaur and coworkers35 or 1.34 Å vs. 1.11 Å or 23 pm larger according to Omary, Dias, and coworkers19 – then one can argue that the bonding herein is stronger given the AgI–AuI distance in 1 is only 17 pm (0.1696 Å) longer than the CuI–AuI distance in compound 4a [Au4(μ-Im-(N–Et))4Cu2(μ-Pz-(CF3)2)2] (see molecular structure of 4a in Scheme S1, ESI†) in ref. 18. The coordination sphere symmetry (approximately D3h for each CTC) and size match – given the i-Pr groups on the gold CTC and n-C3F7 groups on the silver CTC are approximately similar in steric hindrance – likely contributes to the prismatic arrangement herein versus a chair arrangement in ref. 18's 4a, which may partially account for a much stronger interaction in 1 not only based on the 3–6 pm shorter adjusted distances (when accounting for covalent radii) but also a greater number of metal–metal close interactions (three vs. two). The Au3–Ag3 centroids are only 2.916 Å apart so they are, indeed, much closer than the Au(1)–Ag(1) separations.
The second crystallographic figure of merit we adopt from ref. 18 is the affinity of the lighter atom to the heavier atom based on deviation from coordination linearity. Herein, we note that each of the three Ag(1) atoms exhibits rather significant deviation from linearity by bending toward the corresponding Au(1) atoms, affording 165.1° N(1)–Ag(1)–N(1) outside angles. In addition, it is noteworthy that, for complex 2a {[Ag(μ-Tz-(n-C3F7)2)]3·H2OEP} (OEP = 2,3,7,8,12,13,17,18-octaethyl-21H,23H-porphine) from ref. 36 (see molecular structure of 2a in Scheme S1†), the N–Ag–N angle is bent to 145.8° owing to weak coordination between Ag and N atoms from the adjacent porphyrin.36 Meanwhile, the Au(1) atoms remain relatively linear as the N(3)–Au(1)–N(4) angles are 176.0° but are attractive toward Ag(1) atoms nonetheless as the deviation from linearity is such that Au(1) approaches Ag(1) as well. The ∼15° deviation from linear coordination of Ag atoms in 1 is indeed greater than that of Cu atoms in 4a in ref. 18 (167.3° thus 12.7° deviation from linearity) but the Au atoms' attractive deviation is greater in the latter (173.2° so 6.8° deviation vs. 4.0° herein). This trend could also be explained as electron-withdrawing substituents (n-C3F7 here) weaken the Ag–N coordination bonds and make them more labile relative to Au–N bonds where gold is ligated by electron-donating groups.
The third crystallographic figure of merit we adopt from ref. 18 is the affinity of the lighter atom to the heavier atom based on the out-of-plane deviation of metal atoms. Fig. 2 visually illustrates a stark out-of-plane deviation of all three Ag(1) atoms from the plane of the six N(1) atoms to approach the gold atoms in the other CTC. The centroid defined by the three Ag(1) atoms is 27.3 pm away from the centroid of the six N(1) atoms to approach the gold CTC; the analogous planar deviation in 4a in ref. 18 is 20.4 pm for copper atoms. Thus, all three crystallographic figures of merit point to stronger Ag(I)–Au(I) polar-covalent bonding (Au → Ag) in 1 herein vs. the Cu(I)–Au(I) polar-covalent bonding (Au → Cu) claimed for 4a in ref. 18.
Supramolecular interactions
To gain insight into formation and interaction types that govern the stabilization of the stacked complex, supramolecular interactions analyses were performed based on the optimized structure at the level of B97D3 functional to better describe metallophilicity dominated by static correlation (see Computational methodology in ESI† for details).16,37,38 The optimized intermolecular Au–Ag distances range from 3.084 Å to 3.086 Å, marginally longer than values from the single crystal structure determination; this is not unexpected given our recent work on strong metallophillic, polar-covalent, and/or chemisorption interactions whereby DFT methods that account for dispersion interactions have been used.18,36,39–41 In all these precedents, dispersion-corrected DFT methods predicted slightly longer separations than experiment but reproduced the crystallographic geometry accurately and performed much better than conventional DFT functionals such as B3LYP.Before proceeding to the decomposition analysis, we summarize in Scheme 2 and Table 1 the total stabilization energies. Briefly, the reactions of two different cyclotrimers may yield three types of complexes, including (i) binary stacked 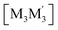 or (ii, iii) [M2M′]2 and
or (ii, iii) [M2M′]2 and 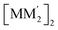 heterometallic dimer-of-cyclotrimer complexes (Scheme 2). A more extensive table that also includes unstacked monomer-of-cyclotrimers and accounts for other thermodynamic parameters (i.e., ΔH, TΔS and ΔG) is provided in the ESI (Table S5†). The findings shed some light upon whether the tendency to form the stacked homometallic arrangement
heterometallic dimer-of-cyclotrimer complexes (Scheme 2). A more extensive table that also includes unstacked monomer-of-cyclotrimers and accounts for other thermodynamic parameters (i.e., ΔH, TΔS and ΔG) is provided in the ESI (Table S5†). The findings shed some light upon whether the tendency to form the stacked homometallic arrangement 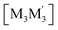 is thermodynamically favoured for the composition herein or whether it is also favoured for some among the other compositions in the literature whereby they could have possibly obtained a kinetic instead of thermodynamic product that had led to [M2M′]2 and/or
is thermodynamically favoured for the composition herein or whether it is also favoured for some among the other compositions in the literature whereby they could have possibly obtained a kinetic instead of thermodynamic product that had led to [M2M′]2 and/or 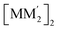 heterometallic dimer-of-cyclotrimer complexes instead. Starting with 1, the Tables 1 and S5† data suggest that there is a significant thermodynamic barrier of ∼8–12 kcal mol−1 that favours the Au3Ag3 homometallic product over either heterobimetallic dimer-of-cyclotrimer (entry 1, type (i) vs. (ii & iii) in Table 1). Thus, this result is consistent with experiment. Surprisingly, in contrast, the heterobimetallic complex 4a in ref. 18 (entry 2, type ii) is, indeed, slightly unfavoured and was, therefore, likely a kinetic product whereas an Au3Cu3 homometallic product (entry 2, type i) should have been the thermodynamic product instead, albeit by a mere 1.7 kcal mol−1. For other literature systems, on the other hand, the opposite situation was attained such that the thermodynamic and experimental crystallographic products were both the same, favouring the [AuAg2]2 and [Au2Ag]2 heterobimetallic dimer-of-cyclotrimer species (entry 3, type iii; entry 4, type ii & iii).32,42 The surprise, however, is that the binding energies for these two other systems (entries 3, 4) calculated herein have surpassed those of both 1 here and 4a in ref. 18 (entries 1, 2), attaining ∼80 kcal mol−1 stabilization energies that represent significant extra stabilization above the systems herein. This result also suggests that electrostatic assistance alone cannot be solely responsible for the M–M′ polar-covalent bonding herein or elsewhere in the pertinent literature precedents because if they were then either 1 ([Au3Ag3]) here or complex 4a ([Au2Cu]) in ref. 18, both of which had a fluorinated Ag(I) triazolate or Cu(I) pyrazolate moiety interacting with an alkylated Au(I) pyrazolate/imidazolate moiety, would have possessed the greater binding energy. Thus, inherently genuine M–M′ polar-covalent bonding must be principally responsible for the total stabilization – among other supramolecular (electrostatic or otherwise) interactions, as will be analysed next herein.
heterometallic dimer-of-cyclotrimer complexes instead. Starting with 1, the Tables 1 and S5† data suggest that there is a significant thermodynamic barrier of ∼8–12 kcal mol−1 that favours the Au3Ag3 homometallic product over either heterobimetallic dimer-of-cyclotrimer (entry 1, type (i) vs. (ii & iii) in Table 1). Thus, this result is consistent with experiment. Surprisingly, in contrast, the heterobimetallic complex 4a in ref. 18 (entry 2, type ii) is, indeed, slightly unfavoured and was, therefore, likely a kinetic product whereas an Au3Cu3 homometallic product (entry 2, type i) should have been the thermodynamic product instead, albeit by a mere 1.7 kcal mol−1. For other literature systems, on the other hand, the opposite situation was attained such that the thermodynamic and experimental crystallographic products were both the same, favouring the [AuAg2]2 and [Au2Ag]2 heterobimetallic dimer-of-cyclotrimer species (entry 3, type iii; entry 4, type ii & iii).32,42 The surprise, however, is that the binding energies for these two other systems (entries 3, 4) calculated herein have surpassed those of both 1 here and 4a in ref. 18 (entries 1, 2), attaining ∼80 kcal mol−1 stabilization energies that represent significant extra stabilization above the systems herein. This result also suggests that electrostatic assistance alone cannot be solely responsible for the M–M′ polar-covalent bonding herein or elsewhere in the pertinent literature precedents because if they were then either 1 ([Au3Ag3]) here or complex 4a ([Au2Cu]) in ref. 18, both of which had a fluorinated Ag(I) triazolate or Cu(I) pyrazolate moiety interacting with an alkylated Au(I) pyrazolate/imidazolate moiety, would have possessed the greater binding energy. Thus, inherently genuine M–M′ polar-covalent bonding must be principally responsible for the total stabilization – among other supramolecular (electrostatic or otherwise) interactions, as will be analysed next herein.
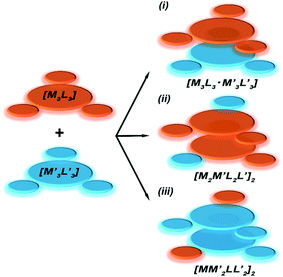 | ||
Scheme 2 Illustration of complexation of a [M3L3] (gold trimer, donor) and a 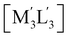 (copper or silver trimer, acceptor). (copper or silver trimer, acceptor). | ||
| Entry | Complex | Type | ΔE |
|---|---|---|---|
| 1 | [M3L3] = [Au(μ-Pz-(i-C3H7)2)]3; 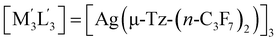 this work this work |
(i) | −62.6 |
| (ii) | −54.6 | ||
| (iii) | −48.4 | ||
| 2 | [M3L3] = [Au(μ-Im-(N–Et))]3; 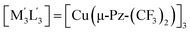 .18 .18 |
(i) | −51.4 |
| (ii) | −49.7 | ||
| (iii) | −45.0 | ||
| 3 | [M3L3] = [Au(μ-Im-(N–Bz))]3; 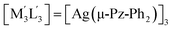 .32 .32 |
(i) | −71.5 |
| (ii) | −67.2 | ||
| (iii) | −81.1 | ||
| 4 | [M3L3] = [Au(μ-(p-Tol)N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OEt))]3; C(OEt))]3; 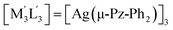 .32,42 .32,42 |
(i) | −78.4 |
| (ii) | −79.2 | ||
| (iii) | −86.9 |
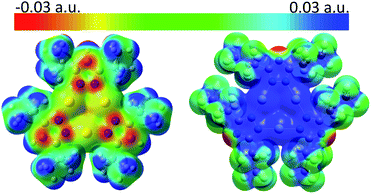
Molecular electrostatic potential (MEP) analysis is an effective method to obtain qualitative analysis of intermolecular interactions or electronic repulsion. Tekarli et al. reported and predicted the π-basicity to follow the trend of [M(μ-Im)]3 > [M(μ-Py)]3 > [M(μ-Cb)]3 > [M(μ-Pz)]3 > [M(μ-Tz)]3 (Cb = carbeniate) for a given monovalent coinage metal ion and Au > Cu > Ag for a given ligand.30 Also, π-acid/π-base properties can be significantly modified by substituted groups on the bridging ligands: electron-donating groups (–i-C3H7 groups of [Au(μ-Pz)]3 here or –CH3 groups in ref. 30) make the nine-membered ring more electron-rich while electron-withdrawing groups (–n-C3F7 groups of [Ag(μ-Tz)]3 here or –CF3 groups in ref. 30) have the opposite effect. As shown in Fig. 3, MEP maps of contacting sides between two trimers clearly show the electrostatic potential to be of opposite signs, helping the two fragments to bind tightly. Quadrupole–quadrupole interactions reinforce the dominant electrostatic attractions, as the value of quadrupole moment tensor in zz direction (Qzz) of the silver-triazolate trimer is 26.4 a.u. and those of gold-pyrazolate trimer and benzene are −18.3 and −5.8 a.u., respectively.36 As a consequence, strong π–π and/or Lewis/π acid-base interactions assist the formation of the stacked structure with the co-crystallized benzene molecule.
Reduced density gradient (RDG) plots reflect the spatial distribution of the various contributing supramolecular interactions and steric repulsions in regions of small electron density [ρ(r)].43 To identify the specific non-covalent interactions in regions where both electron density [ρ(r)] and density gradient [∇ρ(r)] are both small, to analyse the sign of λ2-the second eigenvalue of the electron-density Hessian matrix-would be essential and helpful to discern different types. The more negative the values of the products of sign(λ2) × electron density [ρ(r)], the stronger the interaction or bonding character between molecules and atoms (see Computational methodology in ESI† for details). Between Au and Ag atoms, Fig. S14a and c,† green-blue regions (sign(λ2)ρ ≈ −0.024 a.u.) may be assigned as strong metal–metal interactions arising from strong metallophilicity and/or polar covalency.18,22,41 Such a situation corresponds to opposite π-acid/π-base properties of the two metal atoms and nine-membered rings, which agrees with the green-blue spike (sign(λ2)ρ ≈ −0.017 a.u.) in Fig. S14c.† Large areas of green (sign(λ2)ρ ≈ −0.004 to −0.01 a.u.) are found in Fig. S14b† in the middle region between the benzene ring on the one hand and the silver trimer on the other, corresponding to the sharp green spike in Fig. S14c† and strong Lewis acid/π-base and π-acid/π-base interactions. Moreover, as depicted in both Fig. S14a and b,† green areas spread out in space, resulting from abundant hydrogen-fluorine hydrogen bonding-type interactions (H atoms from i-C3H7 groups and benzene; F atoms from n-C3F7 groups), corresponding to wide green spikes in Fig. S14c.†
Further quantitative analyses of these complementary supramolecular interactions were conducted using energy decomposition analysis-natural orbital of chemical valence (EDA-NOCV) methods. Two models, with and without the co-crystallized benzene molecule, were taken into full consideration whereby the former is considered a perturbation interaction between the benzene ring and the [Ag(μ-Tz)]3 molecule, whereas the latter focuses on the Au3Pz3/Ag3Tz3 interaction, Table 2. The interaction energies of stacked complexes are calculated to be −66 and −87 kcal mol−1, indicating significant stabilization during the stacking process. Note that only the value of −66 kcal mol−1 directly reflects the stabilization energy for Au3Pz3 to Ag3Tz3 while the value of −87 kcal mol−1 contains the attraction energy between benzene and Ag3Tz3 as well. Both electrostatic interactions and London dispersion forces make dominant contributions to binding (>40%), as evidenced in MEP maps and the value of Qzz from strong π-acid/π-base attraction, abundant van der Waals interactions including Lewis acid/π-base interactions. However, the contributing percentage of orbital interaction is ∼16% for both models with and without benzene using the energy decomposition scheme and corresponds to the contribution of induction forces (ca. 10%) from symmetry-adapted perturbation theory (SAPT) from PSI4 (see Table S4 in ESI† for detail). However, more rigorous ab initio methods are warranted and one cannot completely neglect the metal contribution from the dative bonding-type interactions responsible for the Gray–Ballhausen ligand-field theory that imparts covalent stabilization upon M ← L bonding (extrapolation of which to the system herein would imply Ag3 ← Au3 polar-covalent bonding).44,45 To explain this situation further, maps of EDA-NOCV deformation densities were generated (Fig. S15†), which clearly show electron flow from electron-rich areas ([Au(μ-Pz)]3 and benzene, red regions) to electron-deficient areas ([Ag(μ-Tz)]3, blue regions) during the stacking process and quite small formation energies of ∼3 kcal mol−1. Notwithstanding the small magnitude of each constituent force, the overall dimer-of-trimer stabilization magnitude of ∼65 kcal mol−1 herein is even stronger than those in literature precedents of largely undisputed intermolecular covalent bonds, such as those in d1–d1 or d9–d9 ground-state single bonds, 3Πg or 3Σu+ excited-state single bonds in the Hg2 excimer, or singlet (or triplet) π-stacked pyrene2 sandwiched excimers – all of which attain De values in the ≤50 kcal mol−1 range.41,46–51 The stabilization herein is likewise ∼2× higher than that in the claimed polar-covalent bonding reported recently in a heterobimetallic Au2CuIm2Pz complex (De = ∼35–40 kcal mol−1).18
| Au3·Ag3 | Au3·Ag3·benzene | |||
|---|---|---|---|---|
| ΔEint | −66.0 | −86.6 | ||
| ΔEelstat | −68.6 | 43% | −88.4 | 42% |
| ΔEPauli | 93.8 | 124.6 | ||
| ΔEOrbInt | −27.1 | 17% | −34.4 | 16% |
| ΔEDisp | −64.0 | 40% | −88.3 | 42% |
| ΔEOrbInt/ΔEelstat | 40% | 39% | ||
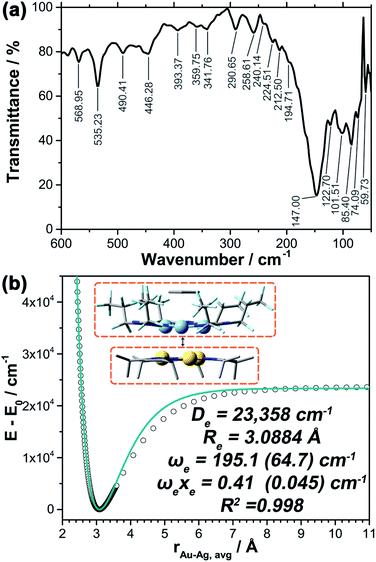
Vibrational frequencies
Fig. 4a shows the experimental far-IR spectrum of the neat solid powder of 1 at room temperature. The distinct bands are at ca. 535, 490, and 446 cm−1, which are generally assigned to νM–L (νAu–N; νAg–N) and δL–M–L/M–L–L (δN–Au–N; δN–Ag–N; δAu–N–N; δAg–N–N; etc.) vibrations, respectively, and could also be simulated and animated in the DFT calculations. Most bands of lower frequencies than 200 cm−1 are potentially reckoned as inter-trimer vAu–Ag vibrations within the twisted trigonal prism.To better understand these spectroscopic results and bond-like interactions in this system, Morse potential energy surface (PES) scan was performed using the fully-optimized structure and separating the Au3 and Ag3–benzene fragments (Fig. 4b). A deep well (De = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 cm−1 or 66.8 kcal mol−1) could be observed for three pairs of Au–Ag bonding characteristics, corresponding to the EDA results of ∼66 kcal mol−1 (vide supra); the equilibrium intermolecular Au–Ag distance (Re) is calculated as 3.0884 Å, which is also in good agreement of 3.0462(18) Å for crystal structure and ca. 3.085 Å for optimization. Analysis of the M06 functional was also conducted to test the sensitivity of interaction energies and vibrational parameters within the framework of DFT methods (Fig. S16†); De and Re are fitted at 20
358 cm−1 or 66.8 kcal mol−1) could be observed for three pairs of Au–Ag bonding characteristics, corresponding to the EDA results of ∼66 kcal mol−1 (vide supra); the equilibrium intermolecular Au–Ag distance (Re) is calculated as 3.0884 Å, which is also in good agreement of 3.0462(18) Å for crystal structure and ca. 3.085 Å for optimization. Analysis of the M06 functional was also conducted to test the sensitivity of interaction energies and vibrational parameters within the framework of DFT methods (Fig. S16†); De and Re are fitted at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 689 cm−1 (59.2 kcal mol−1) and 3.1052 Å, respectively. Further analysis of the PES scan reveals a stretching frequency of 195 cm−1 for the vertical motions, presumed as intertrimer νAu–Ag stretching modes and confirmed by the far-IR spectrum. Considering that only reduced mass of Au and Ag atoms are used to derive the Morse potential results, it is reasonable to propose that the lower-wavenumber vibrations around 60 cm−1 are a face-to-face stretching mode of two cyclotrimers, which also corresponds to the calculated peak at 65 cm−1 using the reduced masses of the two entire CTC molecules. Furthermore, beside of DFT methods, the aforementioned vibrational considerations in the far-IR region and bond-like interactions are also insensitive to correlating approaches.
689 cm−1 (59.2 kcal mol−1) and 3.1052 Å, respectively. Further analysis of the PES scan reveals a stretching frequency of 195 cm−1 for the vertical motions, presumed as intertrimer νAu–Ag stretching modes and confirmed by the far-IR spectrum. Considering that only reduced mass of Au and Ag atoms are used to derive the Morse potential results, it is reasonable to propose that the lower-wavenumber vibrations around 60 cm−1 are a face-to-face stretching mode of two cyclotrimers, which also corresponds to the calculated peak at 65 cm−1 using the reduced masses of the two entire CTC molecules. Furthermore, beside of DFT methods, the aforementioned vibrational considerations in the far-IR region and bond-like interactions are also insensitive to correlating approaches.
Solid-state modelling and charge transfer
To gain a better understanding of absorption ability of cyclotrimers and binary stacked Au3/Ag3, UV-vis absorption spectra in both solution and solid state were conducted (Fig. 5 and S10†). Dilute-solution state UV-vis absorption spectra reveal the high-energy absorption peaks (∼280 nm) of [Au(μ-Pz)]3 and [Ag(μ-Tz)]3, whereas 1 exhibits a low-energy shoulder band around 325 nm of low intensity. In the solid state, the main absorption peaks of [Au(μ-Pz)]3 and [Ag(μ-Tz)]3 are still around 280 nm with a whole transparent visible region. On the contrary, the ∼325 nm shoulder band of 1 turns dominant with an additional should band around 550 nm, hinting the charge transfer (CT) characteristics of this binary stacked complex.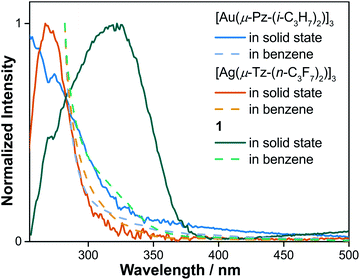 | ||
| Fig. 5 UV-vis absorption spectra of [Au(μ-Pz-(i-C3H7)2)]3, [Ag(μ-Tz-(n-C3F7)2)]3 and 1 in benzene solution and solid states, respectively. | ||
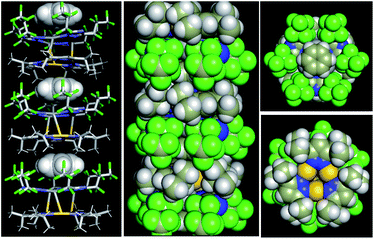
In the view of CT interactions, we modified the experimental unit cell (Fig. 6a) due to disorder present in the X-ray structure for solid-state calculations. The lattice parameters are not changed, but are reduced to a single (non-disordered) molecular stack inside the unit cell (Fig. 6a and b). This assumption is not expected to fundamentally change the present results since the Au3 trimer disorders along the C3 rotation axis and the charge-transfer between Au3 and Ag3 trimer would not be significantly and electronically influenced (Fig. S20†). Note that the difference between an individual aggregate of Au3/Ag3 molecules vs. the a periodic unit cell of Au3/Ag3 (Fig. 6a and b) is that in the latter case, the trimers stack infinitely with intermolecular interactions along the stack (c-direction of unit cell), while no such interaction is present in individual aggregates. This stacking appears to be the source of charge transfer in Au3/Ag3 complexes (vide infra). Furthermore, this assumption is supported by similar stacking and semi-conduction patterns observed for cyclo-trimer [Au(μ-Cb)]3 complexes.26,52
Charge densities obtained from the solid-state calculations are mapped in Fig. 6c and d. What is interesting is that there is no evidence of direct interaction between the Ag and Au trimers near a typical covalent bonding density isovalue (0.04 a.u. in Fig. 6c). However, overlap of the electron density envelopes of the individual molecular components within the stack can be seen closer to an isovalue more appropriate for mapping van der Waals radii (0.02 a.u. in Fig. 6d). The charge density analysis thus suggests that the interaction between the trimers arises from non-covalent forces. This evidence further supports a proposal that interaction among the trimers within a stack has a significant CT component.
The [Au(μ-Pz-(i-C3H7)2)]3 (D) unit cell was built from that of [Au(μ-Pz-(i-C3H7)2)]3·[Ag(μ-Tz-(n-C3F7)2)]3 (D·A) by removing the Ag3 (A) stack from the D·A unit cell, D = donor, A = acceptor. Similarly, crystalline A was built by removing D from the D·A unit cell. The density of states (DOS) obtained from plane-wave DFT calculations are depicted in Fig. 6e, which summarizes three different calculations, one each on the D, A, and D·A stacks, respectively.
Comparing the DOS of D, A, and D·A (Fig. 6e), two main points of interest can be noted. First, the Fermi level (Ef) of D·A is shifted with respect to Ef for D and A. The Fermi energy (−4.9 eV) for isolated D is higher than the Fermi energy (−6.9 eV) for isolated A. Interestingly, the Fermi energy (−5.3 eV) of D·A lies in between the D and A Fermi energies. These Ef dispositions are consistent with the flow of electrons from D → A (i.e., Au trimer to Ag trimer within a stack). A second point of interest is the presence of CT states (shaded region on DOS of D·A system in Fig. 6e).53,54 The CT states can be viewed as mid-gap states of the D·A system. These states are not seen in either the DOS of isolated D or isolated A (Fig. 6e), but exclusively in D·A. The presence of CT states for D·A supports the inference of intra-stack CT of electrons from D → A that was deduced from the calculated Fermi energies. Experimentally, diffuse reflectance spectrophotometry of neat powder [Au(μ-Pz-(i-C3H7)2)]3 (D), [Ag(μ-Tz-(n-C3F7)2)]3 (A), and 1 (D·A) were conducted and analysed based on a Kubelka–Munk method (Fig. S12†). The optical band gaps of D, A, and D·A were derived as 3.42, 3.90, and 3.13 eV, respectively, reminding of 1 (D·A) as a wide-bandgap semiconductor. These results are consistent with the calculated trend of band gaps with slight underestimation that are sensitive to the selection of DFT functionals.
To further understand the nature of charge transfer behaviour in the D·A stack, the total DOS has been decomposed to respective contributions from the metals Ag, Au and ligands, which is depicted in Fig. 6f. A closer inspection of the population projections of metal (Ag and Au individually) and ligand (via subtraction of Ag and Au projections from the total) contributions to the total DOS indicate that near the Fermi level, and in particular near the CT states, that while there are contributions from both the ligands and the metals there is considerably more contribution from the ligands. These results suggest that the type of CT between these trimers is primarily of the ligand-to-ligand charge transfer (LL′CT) type augmented by some metal-to-ligand charge transfer (MLCT) character. This result is also confirmed by UV-vis absorption spectra (Fig. S10†) that CT interaction occurs in the electronic ground state, where the broad peak around 325 nm can be attributed as donor–acceptor charge transfer (DACT) as well.55
The effect of donor–acceptor interaction with respect to distance between the stacks is tested within the solid-state framework, Fig. 6g. This test is important because one expects the strength of interaction between trimer units to change with the intra-stack distance between them. Moreover, the inter-trimer distance may be experimentally tuned via the choice of ligand substituents. The distances between the D and A stacks are analysed in the range of 2.7 to 3.6 Å. These distances correspond to the experimental range of monovalent ligand-unsupported Ag–Au bond lengths from the Cambridge Structural Database, where the shortest distance of 2.6607(15) Å and 2.6772(3) Å were included.56 Interestingly, no notable differences are observed in the DOS of the D·A system as a function of D/A separation. The CT states (shaded region in Fig. 6g) are present in the DOS of the D·A system within the experimentally relevant Ag–Au range. Further, the changes in total energy and Fermi energy at different separations within the computed range have been noted (Table S6†). The Fermi energy of D·A increases with increase in distance between the trimers. The minimum total energy is found at 3.2 Å in contrast to the experimental distance of 3.046 Å. However, the plane-wave DFT simulations indicate a very soft potential surface in the D·A systems, which is consistent with the wide range of experimental separations that may be observed in solid-state structures of coinage metal trimer materials. One may envisage that the degree of charge transfer in the D·A system will be less sensitive to changes in D/A separation than would be the case if the bonding were dominated by ionic/covalent interactions, further supporting the hypothesis as to the CT mechanism of intra-stack semi-conduction for these materials.
To gain insight into CT interactions between A and D, we modified the trimers by replacing their substituents with hydrogen atoms. The n-C3F7 on the triazolate ligands of the Ag trimer and the i-C3H7 on the pyrazolate ligands of the Au trimer were replaced with hydrogen atoms, thus reducing the acceptor (n-type) ability of the former and donor (p-type) ability of the latter. All unit cell and calculation parameters are otherwise identical to the previous simulations. Calculations are then performed for the hydrogen-decorated DH, AH, and DH·AH systems. The DOS of DH·AH and D·A are depicted in Fig. 6h. The most exciting finding from the DOS comparison of these systems is the absence of CT peaks (shaded region) for DH·AH. Also, the Fermi energy of DH·AH (−5.6 eV) lies below Ef for both DH (−5.4 eV) and AH (−5.2 eV) materials (not shown). This disposition is inconsistent with a flow of electrons (charge transfer) from DH → AH. The absence of a mid-gap state and the Fermi energies in DH·AH clearly indicate that substituents on the ligands of Ag and Au trimers play a key role in charge transfer and hence semi-conductive properties of these materials.
Molecular modelling of charge transfer
Given the difficulties in quantifying atomic populations within the plane-wave DFT approximation, charge transfer was done with Gaussian-based DFT techniques. This approach has been used with success in previous reports of related 2D CT materials.10,57 The calculated atomic charges derived from Bader charge analyses, Table 3, indicate that there is ca. four times that charge transfer for the substituted dimer-of-trimers (DOT, 0.568 e−) in comparison with non-substituted DOT ([Au(μ-Pz)]3·Ag(μ-Tz)]3, 0.130 e−). Meanwhile, as depicted in Fig. S21,† the charge density difference (CDD) maps also imply the flowing directions of electrons are from the relatively π-basic Au3 trimer to π-acidic Ag3 trimers in ground states.| Dimer-of-trimers (DOT) model | Charge transfer |
|---|---|
| 1 | 0.568 |
| [Au(μ-Pz)]3·[Ag(μ-Tz)]3 | 0.130 |
| [Au(μ-Im)]3·[Ag(μ-Tz)]3 | 0.190 |
| [Au(μ-Pz(Me)2)]3·[Ag(μ-Tz(CF3)2)]3 | 0.442 |
| [Au(μ-Pz(Me)2)]3·[Ag(μ-Pz(CF3)2)]3 | 0.358 |
| [Au(μ-Im(Me)2]3·[Ag(μ-Tz(CF3)2)]3 | 0.456 |
| [Au(μ-Cb(Me)2)]3·[Ag(μ-Tz(CF3)2)]3 | 0.448 |
Furthermore, the CT for [Au(μ-Im)]3·[Ag(μ-Tz)]3 is 0.190 e−, which is close to that for [Au(μ-Pz)]3·[Ag(μ-Tz)]3 but half the CT for [Au(μ-Im-(Me)2)]3·[Ag(μ-Tz(CF3)2)]3 (0.456 e−), suggesting [M(μ-Im)]3 is more π-basic than [M(μ-Pz)]3 and electron donating/withdrawing substituents contribute significantly to π-electron properties. Comparing the CT values for [Au(μ-Cb(Me)2)]3·[Ag(μ-Tz(CF3)2)]3 (0.448 e−), [Au(μ-Pz(Me)2)]3·[Ag(μ-Tz(CF3)2)]3 (0.442 e−), and [Au(μ-Pz(Me)2)]3·[Ag(μ-Pz(CF3)2)]3 (0.358 e−), the same tendency of reported and predicted π-basicity could also be concluded as [M(μ-Cb)]3 > [M(μ-Pz)]3 > [M(μ-Tz)]3. Taken together, the significant CT differences further corroborate the plane-wave DOS results, which suggests that the CT between fragment D and A is significant and remarkably sensitive to the ligands and their substituents.
Conclusions
In conclusion, experimental and computational studies of the first crystallographically-verified binary stack, [Au(μ-Pz-(i-C3H7)2)]3·[Ag(μ-Tz-(n-C3F7)2)]3 (1), among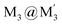 stacked adducts of cyclotrimeric monovalent coinage metals are disclosed in this paper. By comparing binding energies and other thermodynamic parameters of possible combinations of CTCs whose syntheses were attempted but failed in the literature, a predictive model for obtaining stacked complexes is also developed herein in order to assess their thermodynamic stabilities vis-à-vis heterobimetallic analogues. By supramolecular interaction analysis, the nature and strength of the interactions reveal the significant role coordinate-covalent-bonding plays in the formation of these stacked complexes as well as strong London dispersion forces among the ligands. This work manifests the importance of exploiting combinations of M/L/R to tune the π-acid/base properties, electron-accepting/-donating abilities and metallophilicity or polar-covalent bonding for cyclic trinuclear complexes (CTCs). Solid-state and molecular simulations support a dominant semi-conduction mechanism from the donor (D) Au trimer to the acceptor (A) Ag trimer involving charge transfer. The CT proposal is further supported by density of state (DOS) analysis of D, A, and D·A systems via solid-state periodic DFT computations. All calculations suggest that the type of ligands and substituents on the ligands are key ingredients in tuning the amount and strength of CT in these materials through their impact on the bonding properties of the coinage metal components in the stacks. Finally, these results shed light on the possible tuning of these and related chemical systems for molecular electronic applications based on CTCs and charge-transfer complexes, such as n- and p-type semiconductors and p/n junctions, via fine and coarse tuning of the inter-trimer bonding through judicious choice of different M/L/R combinations.
stacked adducts of cyclotrimeric monovalent coinage metals are disclosed in this paper. By comparing binding energies and other thermodynamic parameters of possible combinations of CTCs whose syntheses were attempted but failed in the literature, a predictive model for obtaining stacked complexes is also developed herein in order to assess their thermodynamic stabilities vis-à-vis heterobimetallic analogues. By supramolecular interaction analysis, the nature and strength of the interactions reveal the significant role coordinate-covalent-bonding plays in the formation of these stacked complexes as well as strong London dispersion forces among the ligands. This work manifests the importance of exploiting combinations of M/L/R to tune the π-acid/base properties, electron-accepting/-donating abilities and metallophilicity or polar-covalent bonding for cyclic trinuclear complexes (CTCs). Solid-state and molecular simulations support a dominant semi-conduction mechanism from the donor (D) Au trimer to the acceptor (A) Ag trimer involving charge transfer. The CT proposal is further supported by density of state (DOS) analysis of D, A, and D·A systems via solid-state periodic DFT computations. All calculations suggest that the type of ligands and substituents on the ligands are key ingredients in tuning the amount and strength of CT in these materials through their impact on the bonding properties of the coinage metal components in the stacks. Finally, these results shed light on the possible tuning of these and related chemical systems for molecular electronic applications based on CTCs and charge-transfer complexes, such as n- and p-type semiconductors and p/n junctions, via fine and coarse tuning of the inter-trimer bonding through judicious choice of different M/L/R combinations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Welch Foundation (B-1542) and the U.S. National Science Foundation (CHE-1413641). The authors also acknowledge the support by the National Science Foundation through grant of CHE-1531468 (for computing equipment).Notes and references
- J.-M. Lehn, Supramolecular Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 1995 Search PubMed.
- J. W. Steed and J. L. Atwood, Supramolecular Chemistry, John Wiley & Sons, Ltd, 2009 Search PubMed.
- A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775–2825 Search PubMed.
- D. L. Caulder and K. N. Raymond, Acc. Chem. Res., 1999, 32, 975–982 Search PubMed.
- Q. Wan, J. Xia, W. Lu, J. Yang and C.-M. Che, J. Am. Chem. Soc., 2019, 141, 11572–11582 Search PubMed.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 Search PubMed.
- R. Hahn, F. Bohle, W. Fang, A. Walther, S. Grimme and B. Esser, J. Am. Chem. Soc., 2018, 140, 17932–17944 Search PubMed.
- R. Hahn, F. Bohle, S. Kotte, T. J. Keller, S.-S. Jester, A. Hansen, S. Grimme and B. Esser, Chem. Sci., 2018, 9, 3477–3483 Search PubMed.
- J. Zheng, H. Yang, M. Xie and D. Li, Chem. Commun., 2019, 55, 7134–7146 Search PubMed.
- A. H. Woomer, D. L. Druffel, J. D. Sundberg, J. T. Pawlik and S. C. Warren, J. Am. Chem. Soc., 2019, 141, 10300–10308 Search PubMed.
- J. C. Vickery, M. M. Olmstead, E. Y. Fung and A. L. Balch, Angew. Chem., Int. Ed., 1997, 36, 1179–1181 Search PubMed.
- E. Y. Fung, M. M. Olmstead, J. C. Vickery and A. L. Balch, Coord. Chem. Rev., 1998, 171, 151–159 Search PubMed.
- M. M. Olmstead, F. Jiang, S. Attar and A. L. Balch, J. Am. Chem. Soc., 2001, 123, 3260–3267 Search PubMed.
- H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2008, 37, 1931–1951 Search PubMed.
- H. Schmidbaur and A. Schier, Angew. Chem., Int. Ed., 2015, 54, 746–784 Search PubMed.
- A. C. Tsipis, Coord. Chem. Rev., 2017, 345, 229–262 Search PubMed.
- Y.-C. Tsai, N. V. S. Harisomayajula and S. Makovetskyi, Chem.–Eur. J., 2019, 25, 8936–8954 Search PubMed.
- R. Galassi, M. M. Ghimire, B. M. Otten, S. Ricci, R. N. McDougald Jr, R. M. Almotawa, D. Alhmoud, J. F. Ivy, A.-M. M. Rawashdeh, V. N. Nesterov, E. W. Reinheimer, L. M. Daniels, A. Burini and M. A. Omary, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E5042–E5051 Search PubMed.
- M. A. Omary, M. A. Rawashdeh-Omary, M. W. A. Gonser, O. Elbjeirami, T. Grimes, T. R. Cundari, H. V. K. Diyabalanage, C. S. P. Gamage and H. V. R. Dias, Inorg. Chem., 2005, 44, 8200–8210 Search PubMed.
- M. A. Omary, M. A. Rawashdeh-Omary, H. V. K. Diyabalanage and H. V. R. Dias, Inorg. Chem., 2003, 42, 8612–8614 Search PubMed.
- H. V. R. Dias, H. V. K. Diyabalanage, M. A. Rawashdeh-Omary, M. A. Franzman and M. A. Omary, J. Am. Chem. Soc., 2003, 125, 12072–12073 Search PubMed.
- M. M. Ghimire, V. N. Nesterov and M. A. Omary, Inorg. Chem., 2017, 56, 12086–12089 Search PubMed.
- M. A. Rawashdeh-Omary, M. D. Rashdan, S. Dharanipathi, O. Elbjeirami, P. Ramesh and H. V. R. Dias, Chem. Commun., 2011, 47, 1160–1162 Search PubMed.
- T. Grimes, M. A. Omary, H. V. R. Dias and T. R. Cundari, J. Phys. Chem. A, 2006, 110, 5823–5830 Search PubMed.
- I. I. Vorontsov, A. Y. Kovalevsky, Y.-S. Chen, T. Graber, M. Gembicky, I. V. Novozhilova, M. A. Omary and P. Coppens, Phys. Rev. Lett., 2005, 94, 193003 Search PubMed.
- R. N. McDougald Jr, B. Chilukuri, H. Jia, M. R. Perez, H. Rabaâ, X. Wang, V. N. Nesterov, T. R. Cundari, B. E. Gnade and M. A. Omary, Inorg. Chem., 2014, 53, 7485–7499 Search PubMed.
- J. Zheng, Z. Lu, K. Wu, G.-H. Ning and D. Li, Chem. Rev., 2020, 120, 9675–9742 Search PubMed.
- A. Burini, R. Bravi, J. P. Fackler Jr, R. Galassi, T. A. Grant, M. A. Omary, B. R. Pietroni and R. J. Staples, Inorg. Chem., 2000, 39, 3158–3165 Search PubMed.
- A. A. Mohamed, M. A. Rawashdeh-Omary, M. A. Omary and J. P. Fackler Jr, Dalton Trans., 2005, 41, 2597–2602 Search PubMed.
- S. M. Tekarli, T. R. Cundari and M. A. Omary, J. Am. Chem. Soc., 2008, 130, 1669–1675 Search PubMed.
- Y. Sakamoto, T. Suzuki, M. Kobayashi, Y. Gao, Y. Fukai, Y. Inoue, F. Sato and S. Tokito, J. Am. Chem. Soc., 2004, 126, 8138–8140 Search PubMed.
- A. A. Mohamed, R. Galassi, F. Papa, A. Burini and J. P. Fackler Jr, Inorg. Chem., 2006, 45, 7770–7776 Search PubMed.
- A. Laguna, T. Lasanta, J. M. López-de-Luzuriaga, M. Monge, P. Naumov and M. E. Olmos, J. Am. Chem. Soc., 2010, 132, 456–457 Search PubMed.
- R. Donamaría, M. C. Gimeno, V. Lippolis, J. M. López-de-Luzuriaga, M. Monge and M. E. Olmos, Inorg. Chem., 2016, 55, 11299–11310 Search PubMed.
- A. Bayler, A. Schier, G. A. Bowmaker and H. Schmidbaur, J. Am. Chem. Soc., 1996, 118, 7006–7007 Search PubMed.
- C. Yang, R. K. Arvapally, S. M. Tekarli, G. A. Salazar, O. Elbjeirami, X. Wang and M. A. Omary, Angew. Chem., Int. Ed., 2015, 54, 4842–4846 Search PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 Search PubMed.
- P. Ai, M. Mauro, C. Gourlaouen, S. Carrara, L. De Cola, Y. Tobon, U. Giovanella, C. Botta, A. A. Danopoulos and P. Braunstein, Inorg. Chem., 2016, 55, 8527–8542 Search PubMed.
- R. Galassi, S. Ricci, A. Burini, A. Macchioni, L. Rocchigiani, F. Marmottini, S. M. Tekarli, V. N. Nesterov and M. A. Omary, Inorg. Chem., 2013, 52, 14124–14137 Search PubMed.
- H. Rabaâ, M. A. Omary, S. Taubert and D. Sundholm, Inorg. Chem., 2018, 57, 718–730 Search PubMed.
- B. M. Otten, K. M. Melançon and M. A. Omary, Comments Inorg. Chem., 2018, 38, 1–35 Search PubMed.
- A. A. Mohamed, A. Burini and J. P. Fackler Jr, J. Am. Chem. Soc., 2005, 127, 5012–5013 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 Search PubMed.
- P. S. Bagus and F. Illas, Phys. Rev. B, 2011, 42, 10852–10857 Search PubMed.
- P. S. Bagus and K. Hermann, Appl. Surf. Sci., 2002, 22–23, 444–451 Search PubMed.
- V. J. Catalano, B. L. Bennett, S. Muratidis and B. C. Noll, J. Am. Chem. Soc., 2001, 123, 173–174 Search PubMed.
- T. D. Lohrey, L. Maron, R. G. Bergman and J. Arnold, J. Am. Chem. Soc., 2019, 141, 800–804 Search PubMed.
- F. Jalilehvand, M. Maliarik, M. Sandström, J. Mink, I. Persson, P. Persson, I. Tóth and J. Glaser, Inorg. Chem., 2001, 40, 3889–3899 Search PubMed.
- P. Jerabek, B. von der Esch, H. Schmidbaur and P. Schwerdtfeger, Inorg. Chem., 2017, 56, 14624–14631 Search PubMed.
- F. G. Baddour, A. S. Hyre, J. L. Guillet, D. Pascual, J. M. Lopez-de-Luzuriaga, T. M. Alam, J. W. Bacon and L. H. Doerrer, Inorg. Chem., 2016, 56, 452–469 Search PubMed.
- M. Baya, Ú. Belío, I. Fernández, S. Fuertes and A. Martín, Angew. Chem., Int. Ed., 2016, 55, 6978–6982 Search PubMed.
- L. Zhu, V. Coropceanu, Y. Yi, B. Chilukuri, T. R. Cundari and J.-L. Brédas, J. Phys. Chem. Lett., 2013, 4, 2186–2189 Search PubMed.
- L. Giordano and G. Pacchioni, Phys. Chem. Chem. Phys., 2006, 8, 3335–3341 Search PubMed.
- C. Di Valentin, G. Pacchioni and A. Selloni, Phys. Rev. Lett., 2006, 97, 166803 Search PubMed.
- C. Browning, J. M. Hudson, E. W. Reinheimer, F.-L. Kuo, R. N. McDougald Jr, H. Rabaâ, H. Pan, J. Bacsa, X. Wang, K. R. Dunbar, N. D. Shepherd and M. A. Omary, J. Am. Chem. Soc., 2014, 136, 16185–16200 Search PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, B72, 171–179 Search PubMed.
- T. R. Cundari, B. Chilukuri, J. M. Hudson, C. Minot, M. A. Omary and H. Rabaâ, Organometallics, 2010, 29, 795–800 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of experimental procedures, crystallographic data, computational methodology and calculations, supporting figures S1–S20 and tables S1–S6, crystallography data for 1. CCDC 1899711. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc02520h |
| ‡ Z. L., B. C., C. Y. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |