Open Access Article
Open Access ArticleHard X-ray magnetochiral dichroism in a paramagnetic molecular 4f complex†
Dmitri
Mitcov
 a,
Mikhail
Platunov‡
a,
Mikhail
Platunov‡
 b,
Christian D.
Buch
b,
Christian D.
Buch
 a,
Anders
Reinholdt§
a,
Anders
Reinholdt§
 a,
Anders R.
Døssing
a,
Anders R.
Døssing
 a,
Fabrice
Wilhelm
b,
Andrei
Rogalev
*b and
Stergios
Piligkos
a,
Fabrice
Wilhelm
b,
Andrei
Rogalev
*b and
Stergios
Piligkos
 *a
*a
aDepartment of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100, Copenhagen, Denmark. E-mail: piligkos@chem.ku.dk
bESRF – The European Synchrotron, CS 40220, 38043 Grenoble Cedex 9, France. E-mail: rogalev@esrf.fr
First published on 30th July 2020
Abstract
Magnetochiral dichroism (MΧD) originates in the coupling of local electric fields and magnetic moments in systems where a simultaneous break of space parity and time-reversal symmetries occurs. This magnetoelectric coupling, displayed by chiral magnetic materials, can be exploited to manipulate the magnetic moment of molecular materials at the single molecule level. We demonstrate herein the first experimental observation of X-ray magnetochiral dichroism in enantiopure chiral trigonal single crystals of a chiral mononuclear paramagnetic lanthanide coordination complex, namely, holmium oxydiacetate, at the Ho L3-edge. The observed magnetochiral effect is opposite for the two enantiomers and is rationalised on the basis of a multipolar expansion of the matter–radiation interaction. These results demonstrate that 4f–5d hybridization in chiral lanthanoid coordination complexes is at the origin of magnetochiral dichroism, an effect that could be exploited for addressing of their magnetic moment at the single molecule level.
Introduction
Future information technology devices will incorporate molecular magnetic materials.1 This allows for device miniaturisation with respect to the use of nanoscale materials but also offers the possibility to exploit the quantum properties that matter exhibits at the molecular scale.2 To this purpose the capability to address and to individually manipulate molecular magnetic moments is a prerequisite.3–5 This is possible for chiral magnetic materials displaying the magnetoelectric effect,6–9 where the absence of inversion symmetry leads to efficient coupling of local electric fields to the molecular magnetic moment.10–12 This magnetoelectric coupling leads to magnetochiral dichroism (MΧD),13–26 a remarkable optical property that differentiates the optical response of chiral systems subjected to magnetic fields for counter-propagating light beams. This second order non-reciprocal (directional) dichroism was experimentally discovered less than 25 years ago, first with visible light15 and soon after with X-rays.17 Magnetochiral phenomena are not limited to photons but also occur for particles such as electrons,27 and even for quasiparticles like magnons28 or phonons.29MΧD can be harnessed by electromagnetic radiation from microwaves30 to hard X-rays,17,18,20 irrespective of its polarization and for a large variety of systems exhibiting simultaneous breaking of parity and time reversal symmetries. In diamagnetic or paramagnetic materials, time reversal can be broken by application of an external magnetic field resulting in occurrence of a field induced magnetic moment. The experimental manifestation of MΧD is the differential absorption of light with respect to the relative orientation of the wave vector of the incident light, k, and the applied external magnetic field, B, the effect being of opposite sign for enantiomers. In chiral magnetic materials, the observation of magnetochiral dichroism and birefringence is concomitant with natural circular dichroism (NCD) and birefringence and magneto-circular dichroism (MCD) and birefringence, associated with odd parity and a spontaneous or induced magnetization, respectively.14,31–33 Thus, the experimental difficulty lies in eliminating the effects of all other anisotropies which are typically larger than MΧD and therefore mask its weak response.
Results and discussion
An elegant molecular theory for MΧD has been proposed14 but it requires knowledge of all transition moments involved for a quantitative comparison with experimental results. To this end, the interaction Hamiltonian between the incident electromagnetic radiation and the molecular system can be expressed in terms of electromagnetic multipoles EJ and MJ, J being the multipolarity, as:Ĥint = Ê1 + ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) 1 + Ê2 + 1 + Ê2 + ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) 2 + Ê3 + … 2 + Ê3 + … | (1) |
The absorption cross-section, σ, is proportional to the square of the transition moment, 〈i|Ĥint|f〉, with |i〉 and |f〉 the initial and final states, respectively. We may write quantitatively:
| σ ∝ σ0 + σ1 + σ2 | (2) |
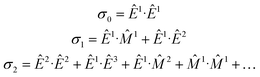 | (3) |
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) 1) and electric dipole–electric quadrupole (Ê1·Ê2) contributions in σ1 are at the origin of natural optical activity (natural circular birefringence and circular dichroism). These interference terms can be non-zero only in systems having no inversion symmetry since they mix multipoles of opposite parity. Whenever the molecule is odd both with respect to space parity (chirality) and time-reversal symmetry (magnetic order or external magnetic field), the Ê1·
1) and electric dipole–electric quadrupole (Ê1·Ê2) contributions in σ1 are at the origin of natural optical activity (natural circular birefringence and circular dichroism). These interference terms can be non-zero only in systems having no inversion symmetry since they mix multipoles of opposite parity. Whenever the molecule is odd both with respect to space parity (chirality) and time-reversal symmetry (magnetic order or external magnetic field), the Ê1·![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) 1 and Ê1·Ê2 terms are at the origin of non-reciprocal optical activity effects, such as magnetochiral dichroism and birefringence. Pure electric dipole transitions (σ0), as well as those quadratic in k (σ2) mix same parity multipole moments and hence cannot contribute to optical activity effects.
1 and Ê1·Ê2 terms are at the origin of non-reciprocal optical activity effects, such as magnetochiral dichroism and birefringence. Pure electric dipole transitions (σ0), as well as those quadratic in k (σ2) mix same parity multipole moments and hence cannot contribute to optical activity effects.
In the context of X-ray spectroscopy, magnetic dipole transitions (![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) 1) are very weak34 and can be neglected. On the contrary, ample experimental evidence demonstrates significant electric quadrupole contributions to hard X-ray absorption spectra.35 Thus, optical activity effects in the hard X-ray range arise from interference of electric dipole and electric quadrupole transitions as it has been experimentally demonstrated36–38 and theoretically confirmed.39 These interference contributions average to zero in randomly oriented samples (polycrystalline powders or liquids) and can only be detected on orientation ordered systems, e.g. single crystals. Furthermore, X-ray MΧD (XMΧD) was shown to be due to orbital toroidal currents in absorbing atoms,20,40 which are relevant to many phenomena, ranging from multiferroicity to superconductivity.
1) are very weak34 and can be neglected. On the contrary, ample experimental evidence demonstrates significant electric quadrupole contributions to hard X-ray absorption spectra.35 Thus, optical activity effects in the hard X-ray range arise from interference of electric dipole and electric quadrupole transitions as it has been experimentally demonstrated36–38 and theoretically confirmed.39 These interference contributions average to zero in randomly oriented samples (polycrystalline powders or liquids) and can only be detected on orientation ordered systems, e.g. single crystals. Furthermore, X-ray MΧD (XMΧD) was shown to be due to orbital toroidal currents in absorbing atoms,20,40 which are relevant to many phenomena, ranging from multiferroicity to superconductivity.
MΧD is, in general, a very weak effect with only very few examples reported to date. A prediction of MΧD was made by Groenewege31 in 1962 and was first observed in 1997 by Rikken and Raupach, in the visible luminescence spectra of a chiral Eu(III) complex.15 MΧD has since only been observed for a Ni(II) complex,16 two-dimensional chiral Cr(III)–Mn(II) ferrimagnets,21,22 for a diamagnetic molecular Zn(II) aggregate,23 for some diamagnetic organic compounds,24–26 in the photolysis of Cr(III) oxalates41,42 and in Bragg scattering.43 There are even fewer reports on observation of XMΧD. XMΧD was first observed in the Cr2O3 antiferromagnet17 and subsequently in the GaFeO3 ferrimagnet18 and more recently in Mn(II) and Co(II) molecule-based helices.20 The first attempt to observe XMΧD for molecular lanthanoid (Ln) complexes was performed on the 3d–4f coordination complex TbNi6.19 However, the validity of these results is not firmly established as the reported experimental XMΧD is too large for a paramagnetic system measured at room temperature and at relatively low magnetic field (1 T). We present herein the first example of unambiguous experimental observation of XMΧD for a mononuclear Ln complex, namely, Na5[Ho(ODA)3](BF4)2·6(H2O), (1), with ODA2− = oxydiacetate. Such mononuclear Ln-based complexes have been proposed as single-ion magnets44–48 displaying magnetic hysteresis at liquid nitrogen temperatures,49,50 electron-based qubits,51–54 coupled qubit–qudits55,56 and single molecule transistors.3–5,57–60
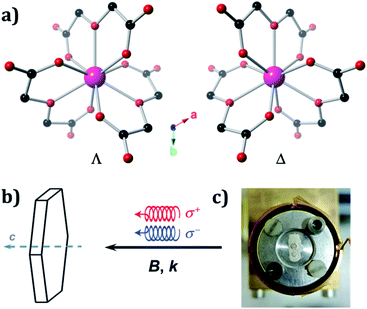
The crystal structures of Ln oxydiacetates have been previously described in detail.61 In 1, Ho(III) coordinates to three virtually planar tridentate ODAs to form the two enantiomers (Λ and Δ) of the nine-coordinate complex anion, [Ho(ODA)3]3− (Fig. 1A). The coordination geometry around Ho(III) is distorted face-centred trigonal prismatic (D3). 1 undergoes spontaneous resolution upon crystallisation. The crystal structures for 1Λ and 1Δ were refined in the trigonal R32 Sohncke space group with Flack parameters62,63 of 0.008(4) and 0.015(4), respectively (Table S1†).
In search of XMΧD of 1 we performed experiments at the L3 absorption edge of Ho exploiting the ESRF beamline ID12 dedicated to polarization dependent X-ray spectroscopy. At this edge, absorption of an incident X-ray photon promotes a 2p3/2 core electron into empty 5d or 6s valence states via the allowed electric dipole transitions (Δl = ±1) or to 6p or 4f states (Δl = 0,+2) via electric quadrupole transitions. Such quadrupolar 2p–4f transitions are easily distinguishable either in X-ray MCD (XMCD) or in resonant inelastic X-ray scattering spectra at the L3-edge64,65 of rare-earths, whereas their contribution at the L2-edge is more difficult to disentangle.66
We used left (L) or right (R) circularly polarised X-rays whose wave vector, k, was parallel (+) or antiparallel (−) to the external magnetic field, B. To identify two enantiomeric single crystals of 1 each displaying an optimal response, X-ray NCD (XNCD) spectra were recorded at room temperature on several crystals already characterised by X-ray crystallography, as crystals of macroscopically similar appearance do not yield the same XNCD intensity (Fig. S1†). This is because the penetration depth of X-rays at the L3-edge of rare-earths is typically of the order 10 microns, making the obtained response sensitive to the structural quality of this near-surface layer. The identified crystals were then inserted into an experimental station equipped with a 17 T superconducting magnet and a constant flow helium cryostat, where they were mounted on a cold finger oriented with the crystallographic, trigonal, c axis parallel to k and B (Fig. 1b and c).
For each enantiomerically pure crystal we acquired four distinct absorption spectra corresponding to different experimental configurations for the relative orientation of k and B and the polarization of X-rays, namely, L+, L−, R+, R−. From these, one can obtain the polarization averaged X-ray absorption spectrum (XAS) and the three dichroic contributions (XNCD, XMCD and XMΧD), allowed by the crystal symmetry, as:
| XAS = [(L+) + (R+) + (L−) + (R−)]/4 | (4) |
| XNCD = [{(L+) − (R+)} + {(L−) − (R−)}]/2 | (5) |
| XMCD = [{(L+) − (R+)} − {(L−) − (R−)}]/2 | (6) |
| XMΧD = [{(L+) + (R+)} − {(L−) + (R−)}]/2 | (7) |
The underlying physics of these three dichroisms is very different and the corresponding effective operators are very distinct: of purely electric charge nature for XNCD, of purely magnetic nature for XMCD, whereas magnetoelectric for XMΧD.40,67 The normalised XAS, XNCD, XMCD and XMΧD spectra of 1Λ and 1Δ are shown in Fig. 2. Note that the XAS and XMCD spectra should be strictly identical for two enantiomeric crystals, whereas the XNCD and XMΧD spectra should be of opposite sign. This is precisely what we observed experimentally. The XAS spectrum is dominated by the electric dipole allowed (Ê1·Ê1) transitions to localized 5d orbitals, giving rise to a very strong resonance at 8078 eV, the so-called “white-line”. Dipole allowed transitions to extended 6s states are much weaker and cannot be easily disentangled from the XAS spectrum. Electric quadrupole transitions (Ê2·Ê2) to strongly localized unoccupied 4f orbitals are also very weak and are barely noticeable in the XAS spectrum as a pre-edge feature at 8069 eV.68 The quadrupole contribution to the spectrum appears at about 9 eV below the “white-line” because of much stronger Coulomb interaction of the 4f electrons with the 2p3/2 hole.69
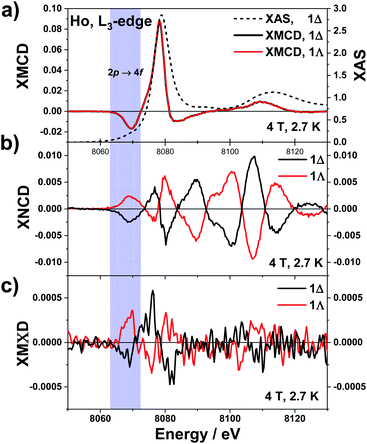 | ||
| Fig. 2 Normalised X-ray dichroic traces recorded on 1Λ and 1Δ at the Ho L3-edge, at 2.7 K with an applied magnetic field of 4 T. (a) XAS (right scale) and XMCD (left scale). (b) XNCD and (c) XMΧD. | ||
The low temperature XNCD spectra are practically noise-free and have the same spectral shape and intensity as those measured at room temperature. This indicates that there is no symmetry change of the crystals in the studied temperature range. The intensity of the normalized XNCD is approaching 1%, which is significantly larger than previously reported values for XNCD at the L-edge of chiral Ln complexes.37,70 XNCD measures the mixing of electronic states with opposite parity in the ground state, which is at the origin of the non-linear optical properties of chiral systems. In the case of an L3 absorption edge, the selection rules for the Ê1·Ê2 interference term39 allow only transitions to the intra-atomic (d, p) and (d, f) hybridized states. The relatively weak XNCD intensities at photon energies corresponding to transitions to the 4f states (ca. 8069 eV) can reasonably be explained by their very strong localization and quasi-atomic character. As a result, they are only weakly hybridised with the 5d states and very little affected by the local chiral surroundings. The largest XNCD signal is observed at about 30 eV above the “white-line” and is extended over a very broad energy range of at least 70 eV. This indicates that extended intra-atomic states (6d, 6p, …) are strongly hybridized and strongly affected by the chiral ligand arrangement.
Contributions from quadrupole transitions are expected to be more pronounced in the XMCD spectra of Ho at the L3 edge because the 4f states have intrinsically magnetic character. For crystals that exhibit XNCD, the true artefact-free XMCD can be obtained only as a combination of four spectra measured independently, as given by eqn (6). The XMCD signal is obtained as the difference of two XNCD spectra measured with opposite directions of applied magnetic field. However, the microscopic origin of these two circular dichroisms is fundamentally different; only pure dipole transitions or absorption terms quadratic in k (see eqn (3)) contribute to XMCD. The XMCD intensity is about an order of magnitude larger than the XNCD one and contrary to XNCD the spectra are identical for both enantiomers. They consist of two main features: a large positive peak close to the XAS “white-line”, arising from dipole transitions to unoccupied 5d states and a well-defined negative peak about 8 eV lower in energy which is due to quadrupole transitions to unoccupied 4f states. This spectral shape is typical for Ho(III) ions66 and the assignment of the spectral features is in line with results of X-ray resonant magnetic scattering of Ho metal.71
The magnetic field dependence of the XMCD of 1 at 2.7 K (Fig. S2†) displays a rapid increase between 0 and 4 T, above which a more slow linear increase is observed, up to 17 T. Given that the XMΧD response is expected to be proportional to the sample's magnetisation,20 measurements were performed at applied magnetic fields of ±4 T to optimise between the field sweep waiting time for successive measurements and the sample's magnetization (about 80% of the maximum reachable value). This turns out to be very important because the measured XMΧD is at least two orders of magnitude weaker than the XMCD. XMΧD spectra were extracted from the same four experimental spectra according to eqn (7) where absorption of unpolarised X-rays was simulated by the sum of L and R spectra.
The same electric dipole-quadrupole interference terms (Ê1·Ê2) as for XNCD, but combined with the orbital toroidal current in the hybridised ground states, are responsible for XMΧD. Noisy but clearly observable XMΧD spectra of opposite sign for 1Λ and 1Δ were detected at the pre-edge (8069 eV) and the main (8078 eV) absorptions but not in the extended region. This indicates that the nonmagnetic empty extended states like 6p, or 6d do not contribute to XMΧD signal. On the contrary, the hybridised 4f–5d orbitals that contain a significant amount of orbital angular momentum give a sizeable contribution and carry a toroidal orbital moment. However, the fact that the XMΧD response depends on the same electric dipole-quadrupole interference terms (Ê1·Ê2) as for XNCD and on the orbital toroidal current of the hybridised states carrying the magnetic moment, responsible for XMCD, does not mean that the XMΧD response is simply the product of XMCD and XNCD. Even though the amplitude of the XMΧD response is in a first place indicating so, the sign of the XMΧD does not confirm this interpretation. It is true that the XMΧD spectral shape looks somewhat similar to the XNCD one and that the main features of the former have the same sign as these of the latter. However, these are not the same spectra. Furthermore, they are neither the product of the XNCD and XMCD responses. The XMCD signal changes sign around 8.072 keV. At the same energy the XNCD response also changes sign. Thus if the XMΧD response was defined by the product of the XMCD and XNCD responses, its sign should be conserved. However, it is experimentally observed that this is not the case since a clear sign change of the XMΧD response is observed around 8.072 keV. Furthermore, the XMΧD signal vanishes above 8.085 keV whereas the XNCD features are the most intense in this energy interval.
These findings confirm that X-ray spectroscopy is an excellent technique for the investigation of local chiral and magnetic properties in Ln-based coordination complexes, provided that the studied single crystals are of high enough enantiopurity to display strong XNCD, which is crucial for the observation of XNCD and XMΧD.
Conclusions
We present herein the first detection of XMΧD for a mononuclear, thus purely Ln-based, coordination complex. The parity and time reversal symmetry of the observed dichroic responses of 1Λ and 1Δ unambiguously confirm that all detected dichroic responses are genuine. However, the detected XMΧD at the L3-edge of Ho, although measurable, is still of small magnitude, contrary to what was expected for rare-earth systems.70 Thus, the magnitude of the detected XMΧD effect remains small even when the corresponding XNCD is large for 4f systems with intrinsically large orbital magnetisation. This observation can be ascribed to the very strong localization and quasi-atomic character of the 4f states that are very little affected by the local chiral surroundings. Furthermore the small magnitude of the detected XMΧD response indicates that these 4f states are only weakly hybridised with the largely more spatially extended 5d states, very susceptible to the local chiral surroundings. Thus, the high intrinsic magnetic moment of 4f states combined with a large admixture of these with extended 5d states emerges like a design criterion for the generation of large magnetochiral responses in lanthanoid based chiral coordination complexes. The underlying strong magnetoelectric coupling evidenced by such large magnetochiral responses can be exploited directly or indirectly for the electric field addressing of magnetic moments. The direct exploitation of magnetochiral dichroism for the electric field addressing of magnetic moments passes via the ‘inverse’ magnetochiral effect, which consists in inducing magnetic polarisation by absorption of unpolarised light.20 This theoretically predicted72 effect has never been experimentally demonstrated.20 Indirectly, magnetochiral dichroism can be used to establish a sizable magnetoelectric coupling which is the fundamental ingredient for the coherent manipulation of magnetic moments by static or pulsed electric fields in pulse electron paramagnetic resonance experiments.11,12,73,74 These results are important for the perspective of manipulating the magnetic moment of molecular magnetic materials, at the single-molecule level, via external stimuli such as unpolarised light or applied electric fields. Such a capability is a prerequisite for the integration of molecular magnetic materials into molecular quantum spintronics devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
SP thanks the VILLUM FONDEN for research grant 13376. SP and DM thank the Danish Ministry of Higher Education and Science for travel support through the Instrument Center DANSCATT. AR thanks the Carlsberg Foundation (grant CF18-0613) and the Independent Research Fund Denmark (grant 9036-00015B) for funding. MP thanks the Russian Science Foundation (grant 19-72-00002) for funding.Notes and references
- A. R. Rocha, V. M. Garcia-Suarez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Nat. Mater., 2005, 4, 335–339 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klyatskaya, J. P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502–506 CrossRef CAS PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360 CrossRef CAS PubMed.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138 CrossRef CAS.
- S.-W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6, 13–20 CrossRef CAS PubMed.
- D. I. Khomskii, J. Phys.: Condens. Matter, 2010, 22, 164209 CrossRef CAS PubMed.
- N. A. Spaldin and M. Fiebig, Science, 2005, 309, 391–392 CrossRef CAS PubMed.
- W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759–765 CrossRef CAS PubMed.
- M. Trif, F. Troiani, D. Stepanenko and D. Loss, Phys. Rev. Lett., 2008, 101, 217201 CrossRef PubMed.
- M. Fittipaldi, A. Cini, G. Annino, A. Vindigni, A. Caneschi and R. Sessoli, Nat. Mater., 2019, 18, 329–334 CrossRef CAS PubMed.
- J. Liu, J. Mrozek, W. K. Myers, G. A. Timco, R. E. P. Winpenny, B. Kintzel, W. Plass and A. Ardavan, Phys. Rev. Lett., 2019, 122, 037202 CrossRef CAS PubMed.
- N. B. Baranova and B. Y. Zeldovich, Mol. Phys., 1979, 38, 1085–1098 CrossRef CAS.
- L. D. Barron and J. Vrbancich, Mol. Phys., 1984, 51, 715–730 CrossRef CAS.
- G. Rikken and E. Raupach, Nature, 1997, 390, 493–494 CrossRef CAS.
- G. Rikken and E. Raupach, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 5081–5084 CrossRef CAS.
- J. Goulon, A. Rogalev, F. Wilhelm, C. Goulon-Ginet, P. Carra, D. Cabaret and C. Brouder, Phys. Rev. Lett., 2002, 88, 237401 CrossRef CAS PubMed.
- M. Kubota, T. Arima, Y. Kaneko, J. P. He, X. Z. Yu and Y. Tokura, Phys. Rev. Lett., 2004, 92, 137401 CrossRef CAS PubMed.
- M. Ceolin, S. Goberna-Ferron and J. Ramon Galan-Mascaros, Adv. Mater., 2012, 24, 3120–3123 CrossRef CAS PubMed.
- R. Sessoli, M. E. Boulon, A. Caneschi, M. Mannini, L. Poggini, F. Wilhelm and A. Rogalev, Nat. Phys., 2015, 11, 69–74 Search PubMed.
- C. Train, R. Gheorghe, V. Krstic, L.-M. Chamoreau, N. S. Ovanesyan, G. L. J. A. Rikken, M. Gruselle and M. Verdaguer, Nat. Mater., 2008, 7, 729–734 CrossRef CAS.
- M. Atzori, I. Breslavetz, K. Paillot, K. Inoue, G. L. J. A. Rikken and C. Train, J. Am. Chem. Soc., 2019, 141, 20022–20025 CrossRef CAS.
- Y. Kitagawa, T. Miyatake and K. Ishii, Chem. Commun., 2012, 48, 5091–5093 RSC.
- P. Kleindienst and G. H. Wagniere, Chem. Phys. Lett., 1998, 288, 89–97 CrossRef CAS.
- Y. Kitagawa, H. Segawa and K. Ishii, Angew. Chem., Int. Ed., 2011, 50, 9133–9136 CrossRef CAS PubMed.
- M. Vallet, R. Ghosh, A. Le Floch, T. Ruchon, F. Bretenaker and J. Y. Thepot, Phys. Rev. Lett., 2001, 87, 183003 CrossRef.
- T. Yokouchi, N. Kanazawa, A. Kikkawa, D. Morikawa, K. Shibata, T. Arima, Y. Taguchi, F. Kagawa and Y. Tokura, Nat. Commun., 2017, 8, 866 CrossRef CAS PubMed.
- Y. Takahashi, R. Shimano, Y. Kaneko, H. Murakawa and Y. Tokura, Nat. Phys., 2012, 8, 121–125 Search PubMed.
- T. Nomura, X. X. Zhang, S. Zherlitsyn, J. Wosnitza, Y. Tokura, N. Nagaosa and S. Seki, Phys. Rev. Lett., 2019, 122, 145901 CrossRef CAS PubMed.
- Y. Okamura, F. Kagawa, S. Seki, M. Kubota, M. Kawasaki and Y. Tokura, Phys. Rev. Lett., 2015, 114, 197202 CrossRef CAS PubMed.
- M. P. Groenewege, Mol. Phys., 1962, 5, 541–563 CrossRef CAS.
- N. B. Baranova, Y. V. Bogdanov and B. Y. Zeldovich, Opt. Commun., 1977, 22, 243–247 CrossRef CAS.
- G. Wagniere and A. Meier, Chem. Phys. Lett., 1982, 93, 78–81 CrossRef CAS.
- J. W. Cooper, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 1841–1851 CrossRef CAS PubMed.
- C. Brouder, A. Juhin, A. Bordage and M.-A. Arrio, J. Phys.: Condens. Matter, 2008, 20, 455205 CrossRef.
- J. Goulon, C. Goulon-Ginet, A. Rogalev, V. Gotte, C. Malgrange, C. Brouder and C. R. Natoli, J. Chem. Phys., 1998, 108, 6394–6403 CrossRef CAS.
- L. Alagna, T. Prosperi, S. Turchini, J. Goulon, A. Rogalev, C. Goulon-Ginet, C. R. Natoli, R. D. Peacock and B. Stewart, Phys. Rev. Lett., 1998, 80, 4799–4802 CrossRef CAS.
- B. Stewart, R. D. Peacock, L. Alagna, T. Prosperi, S. Turchini, J. Goulon, A. Rogalev and C. Goulon-Ginet, J. Am. Chem. Soc., 1999, 121, 10233–10234 CrossRef CAS.
- C. R. Natoli, C. Brouder, P. Sainctavit, J. Goulon, C. Goulon-Ginet and A. Rogalev, Eur. Phys. J. B, 1998, 4, 1–11 CrossRef CAS.
- P. Carra, A. Jerez and I. Marri, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 045111 CrossRef.
- G. Rikken and E. Raupach, Nature, 2000, 405, 932–935 CrossRef CAS PubMed.
- E. Raupach, G. L. J. A. Rikken, C. Train and B. Malezieux, Chem. Phys., 2000, 261, 373–380 CrossRef CAS.
- C. Koerdt, G. Duchs and G. Rikken, Phys. Rev. Lett., 2003, 91, 073902 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Phys. Chem. B, 2004, 108, 11265–11271 CrossRef CAS.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931–2935 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651 CrossRef CAS PubMed.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- J. J. Baldovi, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Arino and H. Prima-Garcia, Chem. Commun., 2013, 49, 8922–8924 RSC.
- A. Gaita-Arino, H. Prima-Garcia, S. Cardona-Serra, L. Escalera-Moreno, L. E. Rosaleny and J. J. Baldovi, Inorg. Chem. Front., 2016, 3, 568–577 RSC.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Arino, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS PubMed.
- E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC.
- R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818 CrossRef CAS PubMed.
- M. Ganzhorn, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Nat. Nanotechnol., 2013, 8, 165–169 CrossRef CAS PubMed.
- M. Ganzhorn, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Nat. Commun., 2016, 7, 11443 CrossRef CAS PubMed.
- C. Godfrin, A. Ferhat, R. Ballou, W. Wernsdorfer, F. Balestro, C. Godfrin, A. Ferhat, R. Ballou, W. Wernsdorfer, F. Balestro, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef CAS PubMed.
- C. Godfrin, S. Thiele, A. Ferhat, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, ACS Nano, 2017, 11, 3984–3989 CrossRef CAS PubMed.
- C. Kremer, J. Torres and S. Domínguez, J. Mol. Struct., 2008, 879, 130–149 CrossRef CAS.
- H. D. Flack, Acta Crystallogr., Sect. A: Found. Crystallogr., 1983, 39, 876–881 CrossRef.
- H. D. Flack, Helv. Chim. Acta, 2003, 86, 905–921 CrossRef CAS.
- L. Badía-Romano, J. Rubín, F. Bartolomé, J. Bartolomé, J. Luzón, D. Prodius, C. Turta, V. Mereacre, F. Wilhelm and A. Rogalev, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 064411 CrossRef.
- C. Dallera, M. Krisch, A. Rogalev, J. Goulon and F. Sette, Phys. B, 2002, 312–313, 850–852 CrossRef.
- M. Platunov, N. Kazak, V. Dudnikov, V. Temerov, I. Gudim, Y. Knyazev, S. Gavrilkin, V. Dyadkin, I. Dovgaliuk, D. Chernyshov, A. Hen, F. Wilhelm, A. Rogalev and S. Ovchinnikov, J. Magn. Magn. Mater., 2019, 479, 312–316 CrossRef CAS.
- J. Goulon, A. Rogalev, F. Wilhelm, C. Goulon-Ginet, P. Carra, I. Marri and C. Brouder, J. Exp. Theor. Phys., 2003, 97, 402–431 CrossRef CAS.
- F. Bartolomé, J. M. Tonnerre, L. Sève, D. Raoux, J. Chaboy, L. M. García, M. Krisch and C. C. Kao, Phys. Rev. Lett., 1997, 79, 3775–3778 CrossRef.
- X. Wang, T. C. Leung, B. N. Harmon and P. Carra, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 9087–9090 CrossRef CAS PubMed.
- I. Mihalcea, M. Perfetti, F. Pineider, L. Tesi, V. Mereacre, F. Wilhelm, A. Rogalev, C. E. Anson, A. K. Powell and R. Sessoli, Inorg. Chem., 2016, 55, 10068–10074 CrossRef CAS PubMed.
- L. Bouchenoire, A. Mirone, S. D. Brown, P. Strange, T. Wood, P. Thompson, D. Fort and J. Fernández-Rodríguez, New J. Phys., 2009, 11, 123011 CrossRef.
- G. Wagniere, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 2437–2440 CrossRef CAS PubMed.
- J. Robert, N. Parizel, P. Turek and A. K. Boudalis, J. Am. Chem. Soc., 2019, 141, 19765–19775 CrossRef CAS PubMed.
- A. K. Boudalis, J. Robert and P. Turek, Chem.–Eur. J., 2018, 24, 14896–14900 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on the synthesis and crystallographic characterization of 1. CCDC 1899691 for 1Δ and 1899692 for 1Λ. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc02709j |
| ‡ Current address: Kirensky Institute of Physics, Federal Research Center KSC SB RAS, Akademgorodok 50, Bld. 38, 660036 Krasnoyarsk, Russia. |
| § Current address: Department of Chemistry, University of Pennsylvania, 231 South 34th Street, Philadelphia, PA 19014-6323. |
| This journal is © The Royal Society of Chemistry 2020 |