Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Semiquinone radical-bridged M2 (M = Fe, Co, Ni) complexes with strong magnetic exchange giving rise to slow magnetic relaxation†
Khetpakorn
Chakarawet
 a,
T. David
Harris
a,
T. David
Harris
 a and
Jeffrey R.
Long
a and
Jeffrey R.
Long
 *abc
*abc
aDepartment of Chemistry, University of California Berkeley, Berkeley, California 94720, USA. E-mail: jrlong@berkeley.edu
bDepartment of Chemical and Biomolecular Engineering, University of California Berkeley, Berkeley, California 94720, USA
cMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
First published on 21st July 2020
Abstract
The use of radical bridging ligands to facilitate strong magnetic exchange between paramagnetic metal centers represents a key step toward the realization of single-molecule magnets with high operating temperatures. Moreover, bridging ligands that allow the incorporation of high-anisotropy metal ions are particularly advantageous. Toward these ends, we report the synthesis and detailed characterization of the dinuclear hydroquinone-bridged complexes [(Me6tren)2MII2(C6H4O22−)]2+ (Me6tren = tris(2-dimethylaminoethyl)amine; M = Fe, Co, Ni) and their one-electron-oxidized, semiquinone-bridged analogues [(Me6tren)2MII2(C6H4O2−˙)]3+. Single-crystal X-ray diffraction shows that the Me6tren ligand restrains the metal centers in a trigonal bipyramidal geometry, and coordination of the bridging hydro- or semiquinone ligand results in a parallel alignment of the three-fold axes. We quantify the p-benzosemiquinone–transition metal magnetic exchange coupling for the first time and find that the nickel(II) complex exhibits a substantial J < −600 cm−1, resulting in a well-isolated S = 3/2 ground state even as high as 300 K. The iron and cobalt complexes feature metal–semiquinone exchange constants of J = −144(1) and −252(2) cm−1, respectively, which are substantially larger in magnitude than those reported for related bis(bidentate) semiquinoid complexes. Finally, the semiquinone-bridged cobalt and nickel complexes exhibit field-induced slow magnetic relaxation, with relaxation barriers of Ueff = 22 and 46 cm−1, respectively. Remarkably, the Orbach relaxation observed for the Ni complex is in stark contrast to the fast processes that dominate relaxation in related mononuclear NiII complexes, thus demonstrating that strong magnetic coupling can engender slow magnetic relaxation.
Introduction
Semiquinone is a ubiquitous free radical in living systems, acting as a radical scavenger1 and as a facilitator of electron-transfer processes in photosynthesis2 and aerobic respiration.3 In these systems, the p-quinone molecule serves as an electron reservoir, shuttling between the three consecutive oxidation states of quinone, semiquinone, and hydroquinone (Scheme 1, top). Although the free semiquinone radical cannot be isolated due to its short lifetime, it can be stabilized by coordination to one or more metal centers. Nevertheless, despite the abundance of quinone in living systems, to our knowledge, there are only six studies reporting crystal structures of p-semiquinone stabilized by transition metal or lanthanide centers.4–9 Of these examples, only one features the p-semiquinone radical anion (p-C6H4O2˙−), as isolated in a structure consisting of two π-stacked radicals coordinated to two MnII(cyclam) units.8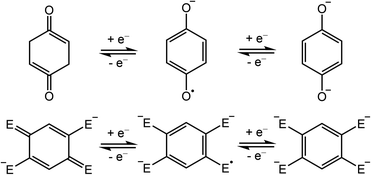 | ||
| Scheme 1 Redox series of bis(monodentate) p-quinone (top) and its bis(bidentate) derivatives (bottom; E = O, NR, S). | ||
In addition to their importance in biological processes, organic radicals have generally garnered much attention as ligands in the design of single-molecule magnets.10 In particular, radicals can engage in strong, direct magnetic exchange coupling with metal-based spins, giving rise to energetically well-isolated spin ground states that are necessary to realize slow magnetic relaxation at high temperatures. Semiquinone-based radicals are particularly well-suited toward this end, owing to their negative charge, which enables stronger interactions with metal ions relative to neutral radicals, and their chemical versatility. For instance, 2,5-disubstituted semiquinone derivatives, which can act as bis(bidentate) bridging ligands (Scheme 1, bottom),11,12 have been employed to synthesize radical-bridged dinuclear complexes exhibiting strong magnetic exchange coupling13–16 and in some cases single-molecule magnet behavior.17–20 In contrast, magnetic coupling involving the bis(monodentate) benzosemiquinone molecule (Scheme 1, top) has not been reported.
The use of bis(monodentate) semiquinone as a bridging ligand for magnetic molecules offers several key potential advantages over the more common bis(bidentate) analogues.11 First, the presence of only one donor atom per metal ion reduces the overall number of atoms over which the unpaired electron is delocalized, thereby concentrating spin density and promoting stronger exchange. Second, having donor atoms on only two C atoms of the quinone ring leaves the additional four C atoms available for chemical modification. Finally, the occupation of only one metal coordination site by the bridging ligand allows access to metal ions in different coordination geometries. Of particular interest in this regard are trigonal bipyramidal complexes of Ni2+, which have been shown to exhibit exceptionally large axial zero-field splitting (D) owing to the presence of nearly degenerate dx2−y2 and dxy orbitals.21,22 For instance, the compound [(Me6tren)NiCl](ClO4) (Me6tren = tris(2-dimethylaminoethyl)amine) has been shown by high-field, high-frequency electron paramagnetic resonance spectroscopy to exhibit −180 ≤ D ≤ −120 cm−1.22 Despite the potential of [(Me6tren)Ni]2+ as a building unit for single-molecule magnets, to date no multinuclear molecule featuring this unit has been reported. Moreover, the only example of any complex incorporating multiple trigonal bipyramidal Ni2+ centers is a dinuclear imidazole-bridged [Ni(μ-Im)NiL](ClO4) complex, which features weak antiferromagnetic coupling between Ni2+ centers.23 This conspicuous dearth of compounds likely stems from synthetic difficulties associated with the tendency of Ni2+ to adopt octahedral coordination.
Herein, we report the synthesis and characterization of the semiquinone-bridged complexes [(Me6tren)2MII2(C6H4O2)]3+ (M = Fe, Co, Ni), obtained via one-electron oxidation of their hydroquinone-bridged precursors. These complexes are the first to feature paramagnetic, trigonal bipyramidal metal centers bridged through a radical ligand and the first examples of any structurally characterized dinuclear complexes bridged through a single semiquinone. Strong, direct magnetic exchange mediated by the semiquinone radical results in well-isolated paramagnetic ground states for all complexes, up to 300 K in the case of Ni. Finally, significant magnetic anisotropy engendered by the trigonal bipyramidal ligand field of the metal centers leads to slow magnetic relaxation under small applied fields, with moderate relaxation barriers for the Co and Ni complexes.
Results and discussion
Synthesis and structures
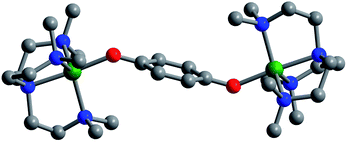
The semiquinone-bridged complexes were synthesized in three steps starting from the mononuclear precursors [(Me6tren)MX]X (X = Cl− or Br−). Initial salt metathesis with K[B(C6F5)4] in acetonitrile afforded [(Me6tren)MX][B(C6F5)4] in quantitative yield, and subsequent reaction with Na2(p-C6H4O2) in tetrahydrofuran (THF) gave the hydroquinone-bridged complexes [(Me6tren)2M2(C6H4O22−)][B(C6F5)4]2 (M = Fe (1), Co (2), Ni (3), Scheme 2) in moderate to high yield. Note that the salt metathesis reaction is necessary to generate a THF-soluble precursor, as it was found that coordinating bis(monodentate) semiquinone is displaced by strong donor solvents such as acetonitrile.Layering Et2O onto THF solutions of 1–3 at room temperature afforded large block-shaped crystals of yellow 1·2THF·Et2O, green 2·2THF·Et2O, and dark brown 3·2THF·Et2O, respectively, which were suitable for single-crystal X-ray diffraction analysis. All three compounds crystallize in the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . Each structure features two metal centers, both in a distorted trigonal bipyramidal geometry with an axial site ligated by an O atom from a bridging dianionic hydroquinone (Fig. S1–S3†). The two metal centers are related through a center of crystallographic inversion symmetry, with M–O–C angles of 124.91(15)°, 131.33(12)°, and 132.08(8)° for Fe, Co, and Ni, respectively (Table 1). Note that 3·2THF·Et2O is only the second example of a multinuclear trigonal bipyramidal NiII complex,23 and it is the first example of any molecule incorporating multiple [(Me6tren)Ni]2+ units.
. Each structure features two metal centers, both in a distorted trigonal bipyramidal geometry with an axial site ligated by an O atom from a bridging dianionic hydroquinone (Fig. S1–S3†). The two metal centers are related through a center of crystallographic inversion symmetry, with M–O–C angles of 124.91(15)°, 131.33(12)°, and 132.08(8)° for Fe, Co, and Ni, respectively (Table 1). Note that 3·2THF·Et2O is only the second example of a multinuclear trigonal bipyramidal NiII complex,23 and it is the first example of any molecule incorporating multiple [(Me6tren)Ni]2+ units.
| Hydroquinone-bridged complexes | Semiquinone-bridged complexesa | |||||
|---|---|---|---|---|---|---|
| 1·2THF·Et2O (M = Fe) | 2·2THF·Et2O (M = Co) | 3·2THF·Et2O (M = Ni) | 4·Et2O (M = Fe) | 5·Et2O (M = Co) | 6·Et2O (M = Ni) | |
| a Values are reported from the non-disordered half-molecules in each structure. | ||||||
| C–O | 1.319(3) | 1.343(2) | 1.3405(14) | 1.291(4) | 1.288(7) | 1.296(7) |
| M–O | 1.9019(17) | 1.8839(14) | 1.8879(9) | 1.936(3) | 1.922(5) | 1.928(4) |
| M–Naxial | 2.2653(19) | 2.2207(15) | 2.1207(10) | 2.202(3) | 2.176(5) | 2.070(5) |
| Mean M–Neq | 2.2097 | 2.1583 | 2.1524 | 2.179 | 2.142 | 2.125 |
| M–O–C | 124.91(15) | 131.33(12) | 132.08(8) | 135.1(2) | 138.1(4) | 136.6(4) |
| τ | 0.814 | 0.837 | 0.720 | 0.788 | 0.820 | 0.672 |
In the equatorial plane of each metal center, the average M–Neq bond length decreases by ∼0.05 Å upon moving from Fe to Co to Ni, from 2.2097 to 2.1583 to 2.1524 Å, respectively, in accord with a progressive decrease in metal ionic radius. In contrast, the M–O bond distance decreases by only ∼0.02 Å upon going from Fe to Co to Ni (1.9019(17), 1.8839(14), and 1.8879(9) Å, respectively), which may suggest the greater trans influence of the hydroquinone for Fe, and to a lesser extent for Co and Ni. The effect is also reflected in the significant decrease (>0.14 Å) of the M–Naxial distance, from 2.2653(19) to 2.2207(15) to 2.1207(10) Å upon moving from Fe to Co to Ni, respectively (Table 1).
Chemical oxidation of 1–3 with one equivalent of [FeCp2][B(C6F5)4] afforded the one-electron-oxidized compounds [(Me6tren)2M2(C6H4O2−˙)][B(C6F5)4]3 (M = Fe (4), Co (5), Ni (6)) in high yield. Surprisingly, these complexes are remarkably air-stable in the solid-state. As monitored by powder X-ray diffraction analysis, 4 shows only slight decomposition after six months, while 5 and 6 maintain crystallinity for an indefinite period of time (Fig. S4–S6†). This kinetic stability may be a result of steric protection of the bridging ligand by the [B(C6F5)4]− counteranions as THF solutions of 4–6 readily decomposed in air.
Layering Et2O onto 1,2-difluorobenzene solutions of 4, 5, and 6 and storage at −25 °C afforded plate-shaped crystals of dark green 4·Et2O, dark brown 5·Et2O, and red 6·Et2O, which were suitable for single-crystal X-ray diffraction analysis. The three compounds crystallize in the space group P21/c and are isostructural (Fig. 1 and S7–S9†). In each structure, the asymmetric unit contains two distinct half-molecules of the cationic complex, three [B(C6F5)4]− counterions, and a molecule of Et2O. The bond distances and angles associated with the two half-molecules differ considerably in each structure, owing to disorder over two positions for one of the half-molecules. For the purpose of structural comparisons in this report, we refer to the half-molecule without disorder.
The metal centers in 4, 5, and 6 retain their trigonal bipyramidal geometry with M–O–C angles of 135.1(2)° (Fe), 138.1(4)° (Co), and 136.6(4)° (Ni), which are slightly greater than those of the unoxidized analogues. Importantly, in contrast to [(cyclam)2Mn2(C6H4O2−˙)2](ClO4)2,8 the two M–O axes of the oxidized complexes here adopt a trans orientation, which results in a parallel alignment of the M–O vectors. As such, we expect a corresponding parallel alignment of the local magnetic anisotropy axes in 4–6, as dictated by a crystallographic inversion symmetry of the molecules. Finally, a similar trend in M–Neqvs. M–O is observed in the oxidized complexes as in the unoxidized congeners described above (Table 1).
A close comparison of bond distances in both series of compounds reveals important information related to the oxidation state of the bridging ligand (Table 1). Upon oxidation, the C–O distances decrease from 1.319(3), 1.343(2), and 1.3405(14) Å, for Fe, Co, and Ni, respectively, to 1.291(4), 1.288(7), and 1.296(7) Å. These changes are consistent with oxidation of the bridging ligand from hydroquinone to semiquinone, which involves a net increase in the C–O bond order. The semiquinone C–O distances in 4, 5, and 6 are also consistent with those observed in the structure of [(cyclam)2Mn2(C6H4O2−˙)2]2+.8 The average C–C bond distances appear unchanged within error upon oxidation (Tables S3 and S4†), but these values are complicated by the presence of crystallographic inversion symmetry. Consistent with the weaker donating ability of the monoanionic semiquinone versus the dianionic hydroquinone, the M–O bond distance increases upon oxidation, from 1.9019(17), 1.8839(14), and 1.8879(9) Å, for Fe, Co, and Ni, respectively, to 1.936(3), 1.922(5), and 1.928(4) Å. Additionally, the average M–Neq distances change only slightly upon oxidation, from 2.2097, 2.1583, and 2.1524 Å, for Fe, Co, and Ni, respectively, to 2.179, 2.142, and 2.125 Å, further supporting a ligand- rather than metal-based oxidation.
Across the two series of compounds, the Co congeners feature geometries closest to a perfect trigonal bipyramid, as reflected in their τ index values of 0.837 (2) and 0.820 (5), where τ = 1 for a perfect trigonal bipyramid and τ = 0 for a perfect square pyramid.24 This approximate three-fold symmetry for CoII is consistent with a fully symmetric (dxz,dyz)4(dx2−y2,dxy)2(dz2)1 electronic configuration. In contrast, the FeII and NiII complexes bear an odd number of electrons in the (dxz,dyz) or (dx2−y2,dxy) sets and therefore experience a Jahn–Teller distortion away from three-fold symmetry, as reflected in their lower τ indices (Table 1).
Spectroscopy
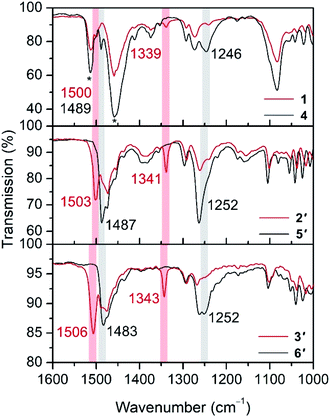
The oxidation of hydroquinone in 1–3 to semiquinone in 4–6 is concomitant with a blue shift in the C–O stretching frequency, for instance from 1489 to 1500 cm−1 upon oxidation of 1 to 4 (Fig. 2). In the case of the Co and Ni congeners, the C–O stretching frequencies were found to overlap with the vibrational modes of [B(C6F5)4]−. We therefore carried out anion exchange reactions for 2, 3, 5, and 6 to access the corresponding PF6− salts, denoted as 2′, 3′, 5′, and 6′, respectively (see the ESI†). The C–O stretches of 1503 and 1506 cm−1 in 5′ and 6′, respectively, are also blue-shifted relative to those for their unoxidized precursors (1487 and 1483 cm−1 for 2′ and 3′, respectively). The C–O vibrational frequencies for all complexes are consistent with values reported previously for hydroquinone and semiquinone coordinated to MnII.4,8 In addition, we carried out density functional theory (DFT) calculations on compounds 3 and 6, which closely reproduce the experimental spectra and support the assignment of the C–O stretching frequencies (Fig. S11†). These calculations also indicate that a second blue-shifted absorption band observed at ∼1340 cm−1 for 4, 5′, and 6′ corresponds to a C–H rocking mode of semiquinone.The 57Fe Mössbauer spectrum collected for 1 at 5 K features a symmetric Lorentzian doublet with an isomer shift of 1.0320(6) mm s−1 and a quadrupole splitting of 3.198(1) mm s−1, consistent with a high-spin, five-coordinate FeII center (Fig. S14†). Upon oxidation, the spectrum for 4 at 20 K is best fit to two similar symmetric Lorentzian doublets, corresponding to the two distinct molecules in the structure, with isomer shifts of 0.996(2) and 1.008(4) mm s−1 and quadrupole splittings of 3.528(8) and 3.23(1) mm s−1 (Fig. S14†). The minimal decrease in isomer shift observed upon oxidation of 1 to 4 is consistent with a ligand-based oxidation, from hydroquinone to semiquinone, and retention of high-spin FeII centers.
The UV-visible spectra for 1, 2, and 3 feature absorption bands at 314 nm (ε = 7 × 103 M−1 cm−1), 298 nm (ε = 3 × 103 M−1 cm−1), and 355 nm (ε = 5 × 103 M−1 cm−1), respectively (Fig. S17–S20†). These bands are assigned to the hydroquinone π–π* transition, which is red-shifted from the free hydroquinone absorption at 288 nm (ε = 2.3 × 103 M−1 cm−1)25 as a result of coordination to the transition metal centers. Several new absorptions were observed in the UV-vis-NIR spectra of 4–6 at longer wavelengths, consistent with transition metal-coordinated semiquinone radical (Fig. S17–S20†),8,26,27 and these transitions shift to longer wavelengths upon moving from Ni to Fe (Fig. S20†). Notably, in the case of 4, these transitions are red-shifted to the NIR region as far as 950 nm.
Static magnetic properties
To probe magnetic coupling in the hydroquinone-bridged compounds 1–3, dc magnetic susceptibility data were collected under an applied field of 1 T, and corresponding plots of χMT vs. T are shown in the top portion of Fig. 3. At 300 K, χMT = 7.40, 5.18, and 3.36 cm3 K mol−1 for 1 (M = Fe), 2 (M = Co), and 3 (M = Ni), respectively, values which are consistent with pairs of magnetically non-interacting S = 2 (g = 2.22), 3/2 (g = 2.35), and 1 (g = 2.59) centers. For each complex, the magnitude of χMT decreases with temperature to minimum values of 0.29 (1), 0.22 (2), and 0.10 cm3 K mol−1 (3) at 2 K, respectively, which behavior is indicative of weak antiferromagnetic superexchange between the metal centers mediated through the diamagnetic hydroquinone ligand. To quantify the strength of this coupling, the susceptibility data and magnetization data were simultaneously fit according to the Hamiltonian in eqn (1):| Ĥ = μBH(gŜ1 + gŜ2) − 2J(Ŝ1·Ŝ2) + (Ŝ1·Dion·Ŝ1 + Ŝ2·Dion·Ŝ2) | (1) |
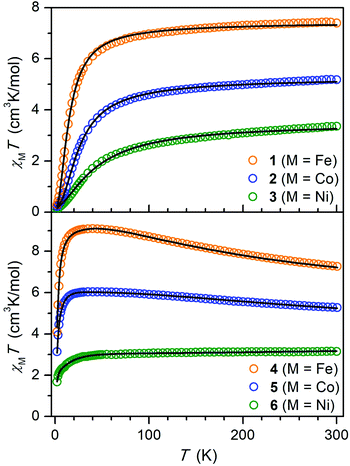 | ||
| Fig. 3 Plots of the molar magnetic susceptibility times temperature (χMT) versus T for 1–3 (top) and 4–6 (bottom) under an applied field of 1 T. Solid lines indicate fits to the data using eqn (1) for 1–3, eqn (2) for 4 and 5, and a giant spin approximation with S = 3/2 for 6, as described in the text. | ||
| Compound | M | g | J (cm−1) | D ion (cm−1) |
|---|---|---|---|---|
| a Obtained by fitting or simulating dc susceptibility data for 1–5 and 6, respectively, as described in the text. b Isotropic g value as calculated from averaging the anisotropic g tensor (Table S7). c The axial component of the Dion tensor. | ||||
| 1 | Fe | 2.23 | −0.847(2) | −10.48(5) |
| 2 | Co | 2.42 | −2.595(5) | −24.4(1) |
| 3 | Ni | 2.72 | −5.94(1) | −96.6(6) |
| 4 | Fe | 2.13 | −144(1) | 7.78(5) |
| 5 | Co | 2.28 | −252(2) | 10.9(1) |
| 6 | Ni | <−600 | ||
The semiquinone-bridged complexes of compounds 4 (M = Fe), 5 (M = Co), and 6 (M = Ni) exhibit starkly different magnetic behavior. In the case of 4 and 5, the χMT curves increase steadily with decreasing temperature to reach maximum values of 9.11 and 6.04 cm3 K mol−1 at 45 K, respectively, before undergoing subsequent downturns. In the case of 6, χMT decreases only slightly in a linear fashion with temperature from 3.15 cm3 K mol−1 at 300 K to 3.00 cm3 K mol−1 at 50 K, characteristic of temperature-independent paramagnetism, before dropping more precipitously below 50 K to a value of 1.68 cm3 K mol−1 at 2 K. For each complex, this behavior is indicative of strong antiferromagnetic coupling between the semiquinone radical and the two metal centers as well as the presence of significant zero-field splitting. To quantify the magnetic coupling, the susceptibility and magnetization data for 4 and 5 were fit using the Hamiltonian given by eqn (2):
| Ĥ = μBH(gŜ1 + gŜ2 + gSQŜSQ) − 2J(Ŝ1·ŜSQ + Ŝ2·ŜSQ) + (Ŝ1·Dion·Ŝ1 + Ŝ2·Dion·Ŝ2) | (2) |
The χMT vs. T data for 6 could not be satisfactorily fit to eqn (2). Nevertheless, simulation of the data revealed the presence of very strong antiferromagnetic coupling with an estimated upper bound of J < −600 cm−1. In line with this result, broken-symmetry DFT calculations carried out using the solid-state structure of 6 predicted an exchange constant of J = −542 cm−1 (see the ESI for details†). Given this large magnitude of J, the S = 3/2 ground state in 6 should be well-isolated from excited states even at 300 K, and indeed the magnetic susceptibility data could be fit using a giant spin approximation with S = 3/2 (Fig. 3, bottom). A simultaneous fit of the susceptibility and low-temperature magnetization data (Fig. S26†) for S = 3/2 yielded the following parameters: g∥ = 2.781(2), g⊥ = 2.357(3), Dmol = −21.4(2) cm−1, Emol = 4.6(2) cm−1, and χTIP = 6.6(2) × 10−4 cm3 mol−1 (Table 3). Note that 6 represents the first multinuclear Ni complex with a thermally isolated magnetically coupled ground state at 300 K.
| Compound | S | g ∥ | g ⊥ | D mol (cm−1) | |Emol| (cm−1) | U calc (cm−1) | U eff (cm−1) | τ 0 (ns) |
|---|---|---|---|---|---|---|---|---|
| 4 | 7/2 | 1.976(7) | 2.2002(9) | 3.95(3) | 0.579(4) | 12.1 | — | — |
| 5 | 5/2 | 1.962(4) | 2.576(1) | 6.18(3) | 1.55(2) | 18.4 | 22.0(1) | 2.6(1) |
| 6 | 3/2 | 2.781(2) | 2.357(3) | −21.4(2) | 4.6(2) | 45.6 | 45.9(4) | 0.40(4) |
The magnetic data obtained for 4–6 are the first reported for any p-semiquinone-bridged transition metal complex, and they demonstrate that the semiquinone radical can facilitate extremely strong magnetic coupling via direct exchange through the ligand-based unpaired electron. Indeed, the magnitudes of J found here are much larger than those mediated via most radical ligands,‡ such as tetrazine (+96 cm−1 with Ni2+),28 nindigo (−138 cm−1 with Co2+),29 and phenazine (+149 cm−1 with Ni2+).30 Further, the coupling observed for 4 and 5 is considerably stronger than that previously reported for bis(bidentate) 2,5-dihydroxy-1,4-benzoquinone derivatives with Fe (J = −57 to −65 cm−1)20 and Co (J = −52 cm−1).15 Likely, this prominent difference results predominantly from the delocalization of the unpaired electron over only two O atoms in semiquinone versus four in the bis(bidentate) analogues. In addition, it is possible that the presence of fewer electronegative O atoms increases the energy of the singly occupied molecular orbital of the semiquinone, thus resulting in a better energy match with the metal orbitals. In fact, the coupling constant for 4 is comparable to that determined for the o-semiquinone radical in the mononuclear [PhTttBu]Fe(phenSQ) complex (JFe–L = −127 cm−1).31 Nevertheless, stronger exchange has been observed for semiquinonoid ligands with N-donors (J < −900 cm−1 with Fe2+ and −440 cm−1 with Co2+),17,19 as expected for a more diffuse, higher-energy SOMO of N compared to O.16,32 As such, incorporation of bridging ligands based on p-phenylenediamine radical may provide a route to complexes with even stronger coupling.
Below 20 K, the magnetization data for 4, 5, and 6 were fit using a giant spin Hamiltonian with values of S = 7/2, 5/2, and 3/2, respectively (Fig. S24–S26†), and the corresponding zero-field splitting parameters are listed in Table 3. With these zero-field splitting parameters, the program PHI33 was used to calculate ground to first excited state splittings (Ucalc) of 12.1, 18.4, and 45.6 cm−1 for 4, 5, and 6, respectively (Table 3).
Dynamic magnetic properties
The static magnetization data for the semiquinone-bridged compounds 4–6 indicate magnetic ground states with significant anisotropy and moderate excited state splittings, suitable for the observation of single-molecule magnet behavior. We thus set out to probe the spin dynamics of each compound via ac magnetic susceptibility measurements. Under a 1000 Oe field, the FeII-containing compound 4 exhibits tails in the out-of-phase molar magnetic susceptibility at the low and high frequency limits of the magnetometer (Fig. S27†). The slow process rapidly diminishes to zero with increasing temperature, which suggests it may be dipolar in origin,34 and the fast process moves out of the magnetometer range with increasing temperature.
at the low and high frequency limits of the magnetometer (Fig. S27†). The slow process rapidly diminishes to zero with increasing temperature, which suggests it may be dipolar in origin,34 and the fast process moves out of the magnetometer range with increasing temperature.
The CoII-containing compound 5 shows slow magnetic relaxation under zero applied field that is further slowed under dc fields (Fig. S29†). Under an optimal field of 2000 Oe, 5 exhibits two peaks in the out-of-phase susceptibility from 1.8–3.0 K, one below 1 Hz that can be ascribed to dipolar interactions34 and a thermally activated process at higher frequencies (Fig. S31†). Similarly, under a 1000 Oe field, the NiII-containing compound 6 exhibits a single peak in  from 1.8 to 5.3 K (Fig. 4), and the data feature slight asymmetry that might arise due to the disordered second molecule in the structure (see the ESI†). The ac magnetic susceptibility data for 5 and 6 were fit using a generalized Debye model35 with two relaxation processes (see the ESI for details†). In the case of 6, the relaxation is dominated by a single major component (Table S9 and Fig. S36†), which is the focus of further discussion below.
from 1.8 to 5.3 K (Fig. 4), and the data feature slight asymmetry that might arise due to the disordered second molecule in the structure (see the ESI†). The ac magnetic susceptibility data for 5 and 6 were fit using a generalized Debye model35 with two relaxation processes (see the ESI for details†). In the case of 6, the relaxation is dominated by a single major component (Table S9 and Fig. S36†), which is the focus of further discussion below.
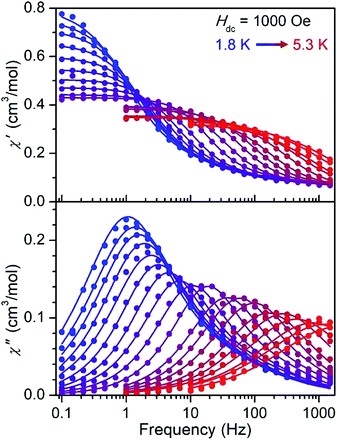 | ||
| Fig. 4 Molar in-phase (top) and out-of-phase (bottom) magnetic susceptibility versus frequency data for compound 6 measured under a 1000 Oe field from 1.8 to 5.3 K. Data are represented by colored symbols and solid lines represent fits to the data using a generalized Debye model33 with two relaxation processes. | ||
Temperature-dependent relaxation times were extracted for 5 and 6 and are plotted versus T in Fig. 5. The Arrhenius plot for each compound exhibits a linear region at high temperatures, which is indicative of spin relaxation through an Orbach process. The temperature-dependent relaxation data were fit to eqn (3):
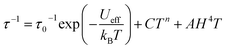 | (3) |
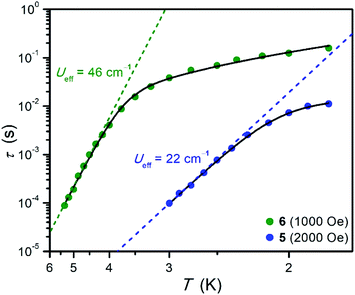 | ||
| Fig. 5 Arrhenius plots of relaxation time for 5 and 6. Data were collected under an optimized dc field of 2000 Oe for 5 and 1000 Oe for 6. Black lines represent fits to the data according to eqn (3), and dashed lines represent the contribution from Orbach relaxation. The error in τ is smaller than the height of the corresponding symbols. | ||
The Orbach relaxation observed for 6 is in remarkable contrast to that observed for mononuclear NiII complexes in similar coordination environments. For example, the trigonal bipyramidal complex in [Ni(MDABCO)2Cl3]ClO4 exhibits very fast relaxation dominated by a Raman process,21 and the compound Li(THF)[Ni((Me3SiNCH2CH2)3N)] does not show slow magnetic relaxation at all.38 Moreover, previous EPR characterization of the compounds [(Me6tren)NiCl]ClO4 and [(Me6tren)NiBr]Br revealed the presence of extremely large values of D, yet no evidence of slow magnetic relaxation was reported.22 Note that the only previously reported example of a complex with multiple trigonal bipyramidal nickel ions is an imidazole-bridged Ni2 complex, which features a non-magnetic ground state.23 Based on these precedents, we postulate that the strong magnetic exchange through the semiquinone bridge in 6 serves to limit fast relaxation via Raman and direct processes and thus enables observation of Orbach relaxation. Our results support a growing number of studies that demonstrate the utility of judiciously selected multinuclear single-molecule magnets featuring radical-bridged, high-anisotropy metal ions for suppressing through-barrier relaxation processes.17–20
Conclusions
The foregoing results show that semiquinone can be employed as a bridging ligand between metal ions to give exceptionally strong metal–radical magnetic coupling and single-molecule magnet behavior in [(Me6tren)2M2(C6H4O2−˙)]3+ (M = Fe, Co, Ni). Magnetic susceptibility data obtained for these complexes reveal the presence of strong metal–semiquinone coupling, with exchange constants of J = −144(1) and −252(2) cm−1 for Fe and Co, respectively, and J < −600 cm−1 for Ni. Importantly, the values of J for Fe and Co are substantially larger in magnitude than those reported for related bis(bidentate) semiquinoid complexes, demonstrating that decreasing the number of donor atoms can increase magnetic coupling strength. Additionally, the enhanced magnetic exchange achieved with semiquinone results in the first multinuclear Ni complex with a thermally isolated ground state. The presence of field-induced molecular slow magnetic relaxation for the Co and Ni semiquinone-bridged complexes further serves to illustrate the efficacy of coupling anisotropic metal centers to engender single-molecule magnet behavior. Current efforts are underway to incorporate semiquinone bridges into molecules with heavier metal ions and into extended networks.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by NSF Grant CHE-1800252. Single-crystal X-ray diffraction data were collected at beamline 12.2.1 at the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. We thank Prof. Christopher J. Chang for the use of the Mössbauer spectrometer and Profs. Gary J. Long and Fernande Grandjean for helpful discussions. Computational work was performed at the UC Berkeley Molecular Graphics and Computation Facility, which is supported by NIH Grant S10OD023532. K. C. thanks the Government of Thailand for support through the Development and Promotion of Science and Technology (DPST) scholarship. We thank Dr Katie R. Meihaus for helpful discussions and editorial assistance.Notes and references
- E. Cadenas, P. Hochstein and L. Ernster, in Advances in Enzymology - and Related Areas of Molecular Biology, ed. F. F. Nord, John Wiley & Sons, Inc., 2006, vol. 65, pp. 97–146 Search PubMed.
- Photosystem II: the light-drive water: plastoquinone oxidoreductase, ed. T. J. Wydrzynski and K. Satoh, Springer, 2006 Search PubMed.
- L. Ernster and G. Dallner, Biochim. Biophys. Acta, Mol. Basis Dis., 1995, 1271, 195–204 CrossRef.
- E. J. Brandon, R. D. Rogers, B. M. Burkhart and J. S. Miller, Chem.–Eur. J., 1998, 4, 1938–1943 CrossRef CAS.
- M. Oh, J. A. Reingold, G. B. Carpenter and D. A. Sweigart, J. Organomet. Chem., 2003, 687, 78–84 CrossRef CAS.
- J. Moussa, C. Guyard-Duhayon, P. Herson, H. Amouri, M. N. Rager and A. Jutand, Organometallics, 2004, 23, 6231–6238 CrossRef CAS.
- Â. Domingos, I. Lopes, J. C. Waerenborgh, N. Marques, G. Y. Lin, X. W. Zhang, J. Takats, R. McDonald, A. C. Hillier, A. Sella, M. R. J. Elsegood and V. W. Day, Inorg. Chem., 2007, 46, 9415–9424 CrossRef PubMed.
- H. Nakamori, T. Matsumoto, T. Yatabe, K. S. Yoon, H. Nakai and S. Ogo, Chem. Commun., 2014, 50, 13059–13061 RSC.
- T. Han, J. B. Petersen, Z.-H. Li, Y.-Q. Zhai, A. Kostopoulos, F. Ortu, E. J. L. McInnes, R. E. P. Winpenny and Y.-Z. Zheng, Inorg. Chem., 2020, 59, 7371–7375 CrossRef CAS PubMed.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176 CrossRef CAS.
- S. Kitagawa, Coord. Chem. Rev., 2002, 224, 11–34 CrossRef CAS.
- B. I. Kharisov, M. A. Méndez-Rojas, A. D. Garnovskii, E. P. Ivakhnenko and U. Ortiz-Méndez, J. Coord. Chem., 2002, 55, 745–770 CrossRef CAS.
- A. Dei, D. Gatteschi, L. Pardi and U. Russo, Inorg. Chem., 1991, 30, 2589–2594 CrossRef CAS.
- K. S. Min, A. L. Rheingold, A. DiPasquale and J. S. Miller, Inorg. Chem., 2006, 45, 6135–6137 CrossRef CAS PubMed.
- K. S. Min, A. G. DiPasquale, J. A. Golen, A. L. Rheingold and J. S. Miller, J. Am. Chem. Soc., 2007, 129, 2360–2368 CrossRef CAS PubMed.
- C. Hua, J. A. DeGayner and T. D. Harris, Inorg. Chem., 2019, 58, 7044–7053 CrossRef CAS PubMed.
- I.-R. Jeon, J. G. Park, D. J. Xiao and T. D. Harris, J. Am. Chem. Soc., 2013, 135, 16845–16848 CrossRef CAS PubMed.
- J. A. DeGayner, I. R. Jeon and T. D. Harris, Chem. Sci., 2015, 6, 6639–6648 RSC.
- U. Albold, H. Bamberger, P. P. Hallmen, J. van Slageren and B. Sarkar, Angew. Chem., Int. Ed., 2019, 58, 9802–9806 CrossRef CAS PubMed.
- A. E. Thorarinsdottir, R. Bjornsson and T. D. Harris, Inorg. Chem., 2020, 59, 4634–4649 CrossRef CAS PubMed.
- K. E. R. Marriott, L. Bhaskaran, C. Wilson, M. Medarde, S. T. Ochsenbein, S. Hill and M. Murrie, Chem. Sci., 2015, 6, 6823–6828 RSC.
- R. Ruamps, R. Maurice, L. Batchelor, M. Boggio-Pasqua, R. Guillot, A. L. Barra, J. Liu, E.-E. Bendeif, S. Pillet, S. Hill, T. Mallah and N. Guihéry, J. Am. Chem. Soc., 2013, 135, 3017–3026 CrossRef CAS PubMed.
- F. El-Khatib, B. Cahier, M. López-Jordà, R. Guillot, E. Rivière, H. Hafez, Z. Saad, J.-J. Girerd, N. Guihéry and T. Mallah, Inorg. Chem., 2017, 56, 10655–10663 CrossRef CAS PubMed.
- A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 7, 1349–1356 RSC.
- J. H. Baxendale and H. R. Hardy, Trans. Faraday Soc., 1953, 49, 1140 RSC.
- S. L. Scott, A. Bakac and J. H. Espenson, J. Am. Chem. Soc., 1992, 114, 4605–4610 CrossRef CAS.
- A. E. Baum, S. V. Lindeman and A. T. Fiedler, Chem. Commun., 2013, 49, 6531–6533 RSC.
- S. Fortier, J. J. Le Roy, C. H. Chen, V. Vieru, M. Murugesu, L. F. Chibotaru, D. J. Mindiola and K. G. Caulton, J. Am. Chem. Soc., 2013, 135, 14670–14678 CrossRef CAS PubMed.
- T. J. Woods, H. D. Stout, B. S. Dolinar, K. R. Vignesh, M. F. Ballesteros-Rivas, C. Achim and K. R. Dunbar, Inorg. Chem., 2017, 56, 12094–12097 CrossRef CAS PubMed.
- X. Ma, E. A. Suturina, M. Rouzières, M. Platunov, F. Wilhelm, A. Rogalev, R. Clérac and P. Dechambenoit, J. Am. Chem. Soc., 2019, 141, 7721–7725 CrossRef CAS PubMed.
- P. Wang, M. M. Killian, M. R. Saber, T. Qiu, G. P. A. Yap, C. V. Poposcu, J. Rosenthal, K. R. Kunbar, T. C. Brunold and C. G. Riordan, Inorg. Chem., 2017, 56, 10481–10495 CrossRef CAS PubMed.
- D. Schweinfurth, M. M. Khusniyarov, D. Bubrin, S. Hohloch, C.-Y. Su and B. Sarkar, Inorg. Chem., 2013, 52, 10332–10339 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- R. Boča, C. Rajnák, J. Titiš and D. Valigura, Inorg. Chem., 2017, 56, 1478–1482 CrossRef PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford Univ. Press, 2006 Search PubMed.
- A. Singh and K. N. Shrivastava, Phys. Status Solidi, 1979, 95, 273–277 CrossRef CAS.
- K. N. Shrivastava, Phys. Status Solidi, 1983, 117, 437–458 CrossRef CAS.
- D. Pinkowicz, F. J. Birk, M. Magott, K. Schulte and K. R. Dunbar, Chem.–Eur. J., 2017, 23, 3548–3552 CrossRef CAS PubMed.
- X. Ma, E. A. Suturina, S. De, P. Négrier, M. Rouzières, R. Clérac and P. Dechambenoit, Angew. Chem., Int. Ed., 2018, 57, 7841–7845 CrossRef CAS PubMed.
- J. O. Moilanen, N. F. Chilton, B. M. Day, T. Pugh and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 5521–5525 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details, crystallographic, additional spectroscopic and magnetic data, and computational details. CCDC 1958690, 1958691, 1958692, 1958693, 1958694 and 1958695. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc03078c |
| ‡ A few exceptions include [(Co(tpy))2(tphz)]3+ which exhibits a well-isolated S = 5/2 ground state39 and [K(18-c-6)][(Co(N(SiMe3)2)2)3-(HAN)] (JCo-rad = −290 cm−1).40 |
| This journal is © The Royal Society of Chemistry 2020 |