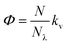DOI:
10.1039/D0SC03152F
(Edge Article)
Chem. Sci., 2020,
11, 8457-8468
Thermodynamics and kinetics of protonated merocyanine photoacids in water†
Received
5th June 2020
, Accepted 27th July 2020
First published on 31st July 2020
Abstract
Metastable-state photoacids (mPAHs) are chemical species whose photo-activated state is long-lived enough to allow for proton diffusion. Liao's photoacid (1) represents the archetype of mPAHs, and is being widely used on account of its unique capability to change the acidity of aqueous solutions reversibly. The behavior of 1 in water, however, still remains poorly understood. Herein, we provide in-depth insights on the thermodynamics and kinetics of 1 in water through a series of comparative 1H NMR and UV-Vis studies and relative modelling. Under dark conditions, we quantified a three-component equilibrium system where the dissociation (Ka) of the open protonated form (MCH) is followed by isomerization (Kc) of the open deprotonated form (MC) to the closed spiropyran form (SP) – i.e., in the absence of light, the ground state acidity can be expressed as KGSa = Ka(1 + Kc). On the other hand, under powerful and continuous light irradiation we were able to assess, for the first time experimentally, the dissociation constant (KMSa) of the protonated metastable state (cis-MCH). In addition, we found that thermal ring-opening of SP is always rate-determining regardless of pH, whereas hydrolysis is reminiscent of what is found for Schiff bases. The proposed methodology is general, and it was applied to two other compounds bearing a shorter (ethyl, 2) and a longer (butyl, 3) alkyl-1-sulfonate bridge. We found that the pKa remains constant, whereas both pKc and pKMSa linearly increase with the length of the alkyl bridge. Importantly, all results are consistent with a four-component model cycle, which describes perfectly the full dynamics of proton release/uptake of 1–3 in water. The superior hydrolytic stability and water solubility of compound 3, together with its relatively high pKGSa (low Kc), allowed us to achieve fully reversible jumps of 2.5 pH units over 18 consecutive cycles (6 hours).
Introduction
The installment of proton gradients across cell membranes is one of the key ingredients nature has developed for sustaining life in all its forms.1 Parallelly to the discovery of bacteriorhodopsin2 – a light-driven proton pump capable of generating proton gradients as high as 3.5 pH units3 – chemists from the 70s begun to engage with the idea of coupling the excited state of organic molecules with proton transfer reactions4 for mimicking similar performance artificially. The possibility of changing persistently and reversibly the acidity of aqueous solutions, however, was established only quite recently with the advent of metastable-state photoacids5 (mPAHs), by which an artificial light-driven pH jump of ca. 2 units was achieved for the first time. Liao's photoacid6 – hereafter referred to compound 1 – represents the archetype of mPAHs. Under dark conditions 1 behaves as weak acid whereas, following visible light absorption, it undergoes photoisomerization leading to the corresponding SP form and the release of a proton (Scheme 1). As compared to spiropyrans7 (SPs), the reason behind this negative photochromism resides for the most part to the lack of electron-withdrawing (EWG) substituents (e.g., p-NO2) on the phenol side, which in turn decrease the stability of the open deprotonated form (MC) in favor of MCH.8 The acidity difference existing between the ground state (pKGSa) and the metastable state (pKMSa), along with a moderately long lifetime of proton photo-dissociation,9 makes 1 and related compounds – referred to here as protonated merocyanines (MCHs) – suitable for controlling remotely any chemical system relying on acidic inputs. MCHs have been used as light-responsive regulators of molecular machines,10 gelation11 and self-assembly12 processes, photochromic systems,13 microbial fuel cell14 and chloroplasts15 activity, anti-bacterial treatments16 and ion-sensors.17 MCHs have also been employed in the remote control of acid-catalyzed reactions such as the hydrolysis of acetals,18 and the polymerization of cyclic lactones,19 whereas diverse polymer scaffolds20 are recently emerging for tuning the switching properties of MCHs in general. Notwithstanding the tremendous impact that 1 has had and is having across multiple research fields, evaluation of its thermodynamics and kinetics in water so far remained inconclusive. The lack of experimental protocols for defining accurately both pKGSa and pKMSa has led to diverse re-interpretations over the past years, and the mechanisms of both hydrolysis and relaxation are still subject of debate. Herein, we rationalize the behaviors of 1 in water through cross-validation of 1H NMR, UV-Vis and pH measurements, and relative modelling. The developed methodology is general and can be easily applied to other MCHs.
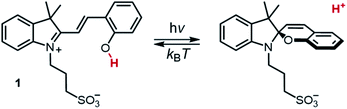 |
| | Scheme 1 Photochemistry of Liao's photoacid. | |
Results and discussion
The ground state
Compound 1 was synthesized by condensation of the corresponding Fisher's base with salicylaldehyde, and fully characterized by high-resolution mass spectrometry (HR-MS), 1H and 13C NMR spectroscopy, as well as X-ray analysis (see ESI† for more details). Our investigations started from a simple observation: aqueous solutions of compound 1, under dark conditions and at known concentration, exhibited pH values diverging substantially from those expected considering previously reported5,6,21 pKa estimates. Initially, we ascribed this outcome to possible differences in (i) temperature and (ii) ionic strength of the sample, as well as (iii) equilibration time before data collection, which are all common parameters to which direct pH readings are sensitive to. Motivated by these results, we decided to employ 1H NMR spectroscopy for quantifying the dissociation behavior of 1 in the ground state. Contrary to common UV-Vis spectroscopic studies, where the absorption of multiple species can overlap, 1H NMR spectroscopy offers the possibility to have a rather wide and more resolved response window, possibly allowing for direct structural characterization and the monitoring of multiple phenomena without mutual interferences. Samples for 1H NMR analysis were prepared by adding an aqueous solution of 1 to potassium phosphate buffers solutions ranging from pH 3 to 10, and subsequently analyzed after an equilibration time of 15 minutes in the dark and at a constant temperature of 25 °C. The 1H NMR spectra obtained for 1 are reported in Fig. 1. At first glance, it appears evident how all the resonances found at low pH progressively shift and weaken in favor of a third species. The doublet centered at around 8.7 ppm – displaying a coupling constant typical of vicinal, trans-alkenyl hydrogens (3Jtrans,a = 16.3 Hz) – confirms that the predominant species at low pH is the open protonated form MCH (represented in black), whereas the chemical shift perturbations associated to it and all the other signals reflect a change of the equilibrium position towards the open deprotonated form MC (represented in blue). Concomitantly, however, the new doublet emerging at around 5.9 ppm – displaying a coupling constant typical of vicinal, cis-alkenyl hydrogens (3Jcis,b* = 10.3 Hz) – indicates a progressive displacement towards a configurational isomer: the closed spiropyran form SP (highlighted in red). The fact that the resonances associated to the methylene protons of the propyl-1-sulfonate bridge, as well as those of the methyl groups, undergo splitting into diastereotopic patterns confirms the installment of a chiral center – i.e., the spiro carbon (labelled to as *). Taken together, these observations suggest that pKGSa should not account merely on a single dissociation event, but rather on a three-component equilibrium (Fig. 1a), as proposed first by Coudret23 and Liao thereafter.20b
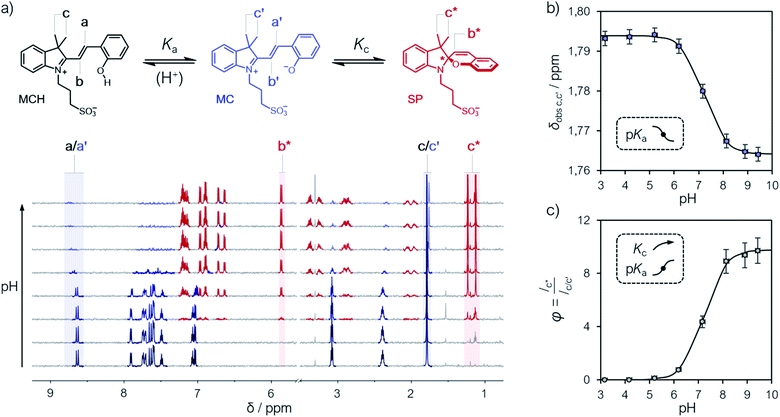 |
| | Fig. 1 (a) Schematic representation of the three-component equilibrium system describing the ground state (top) and 1H NMR spectra at increasing pH values with relative assignments (bottom): the shift from MCH to MC is highlighted with a black-to-blue gradient, whereas the development of SP with a red color. On the right are the profiles of the chemical shifts of c,c′ (b) and the integral ratio between c* and c,c′ (c) reported as a function of the pH; solid lines represent the best fits to eqn (1) and (2), respectively. Experimental conditions: [1] = 0.1 mM, [phosphate buffers] = 20 mM (3 < pH < 10) in H2O/D2O 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, T = 25 °C. With this composition (<50% D2O v/v) the uncertainty of sample's pH due the presence of D2O is ±0.1 pH unit.22 4, T = 25 °C. With this composition (<50% D2O v/v) the uncertainty of sample's pH due the presence of D2O is ±0.1 pH unit.22 | |
The chemical shift perturbations observed for all the resonances associated to the MCH/MC couple reflect a decreasing extent of protonation from low to high pH values and can be considered as the weighted average of the two open forms in equilibrium. This is typical for events happening faster than the NMR timescale and gives the possibility to determine unambiguously the acidity constant of the phenoxyl group – hereafter referred to as Ka. The Ka of 1 was estimated from the chemical shift profiles of suitable well-resolved resonances (e.g., the one associated to the methyl groups c/c′, Fig. 1b) as a function of the pH by non-linear least-squares curve fitting to eqn (1):
| | 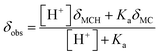 | (1) |
where
δobs is the observed chemical shift, while
δMCH and
δMC are the chemical shifts associated to MCH and MC, respectively. The model fits with very good confidence (
R2 > 0.99) the experimental data and gave a p
Ka value of 7.2 ± 0.1. This value is lower than the one predicted numerically by Coudret (7.75 (
ref. 23)), yet very close to that of
o-nitrophenol
24 in water, and gives a hint of the EWG effect of the indolium moiety on the acidity of the phenoxyl group. Analysis of the integral perturbation in favor of SP offers the possibility to assess simultaneously
Ka and the equilibrium constant of the MC ⇌ SP isomerization – hereafter referred to as
Kc. Indeed, both
Ka and
Kc can be estimated from the profile of suitable integrals ratio (
e.g., that between the integrals of c* and c/c′,
Fig. 1c) as a function of the pH by non-linear least-squares curve fitting to
eqn (2):
| | 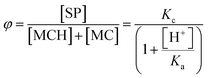 | (2) |
where
φ represents the ratio between the concentration of the closed form and the total concentration of the open forms. This simple model equation suits the three-component equilibrium system depicted in
Fig. 1a and fits with good confidence the experimental data yielding a similar p
Ka (7.2 ± 0.1) and a p
Kc value of −0.99 ± 0.04 (
Fig. 1c).
Having quantified, for the first time experimentally, the equilibria taking part in solution and considering that the proton concentration at equilibrium should satisfy the charge balance – i.e., [H+] = [SP] + [MC] – it follows that KGSa can be expressed as follow:
It should be noticed at this point, the contribution of Kc to the overall extent of proton dissociation in the ground state: for Kc ≪ 1 ([MC] ≫ [SP]) KGSa reduces to Ka, whereas for Kc ≫ 1 ([MC] ≪ [SP]) KGSa can be approximated to KaKc (see ESI† for more details). In the case of 1, none of these two cases apply and by using eqn (3) we obtain a pKGSa value of 6.2 ± 0.1. This value is significantly lower than any of those so far estimated for 1 through simple pH readings in the dark (7.8,6 7.5,21 <7.4 (ref. 5)) and numerical analysis (ca. 7 (ref. 23)), yet fairly in line with some reports on polymers functionalized with SPs lacking the p-NO2 group (6–7 (ref. 25)).
To complement the NMR data, we decided to study the equilibration of MC towards SP by UV-Vis spectroscopy. In general, samples for UV-Vis analysis were prepared starting from stock solutions in dry MeOH, as we found these solutions (ca. 5 mM) underwent negligible10b degradation over two months when stored at 4 °C. The concentration of each stock was determined from a series of three independent potentiometric titrations, using the corresponding second derivative curve for calculating the endpoint (see Fig. S6†). In a typical experiment, aliquots of an aqueous solution of photoacid – 10% MeOH v/v, freshly prepared by dilution of one of the stocks above – were added to potassium phosphate buffers solutions at the desired pH and subsequently analyzed. In order to investigate the MC ⇌ SP isomerization, we decided to operate at pH 9.5 (pH ≫ pKa), where the presence of MCH is negligible and the equilibrium reduces to MC and SP only.
Kinetic analyses were carried out monitoring the decay of the absorption band of the corresponding MC form at temperatures varying from 10 to 30 °C (Fig. 2a). In all cases, data fit well to a first-order decay kinetics as the following:
| | | At = Aeq + (A0 – Aeq)e−kobs,eqt | (4) |
where
At,
A0 and
Aeq are the absorbances (in this case of MC) at any time
t,
t = 0 and at equilibrium, respectively, while
kobs,eq is the apparent first order rate constant of isomerization – see the inset of
Fig. 2a for a glance at the optical readout over time. At any temperature,
Kc was calculated as:
| | 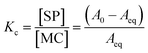 | (5) |
and subsequently used for decomposing the corresponding
kobs,eq into the forward (MC-to-SP,
k2) and backward (SP-to-MC,
k−2) rate constants of isomerization as follows:
| | 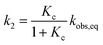 | (6) |
| | 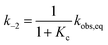 | (7) |
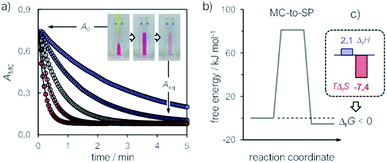 |
| | Fig. 2 (a) Kinetic profiles for the equilibration of MC at different temperatures; solid lines represent the best fits to eqn (4), whereas the inset offers a glimpse of the optical readout over time. Experimental conditions: [1] = 21.5 ± 0.6 μM, [phosphate buffers] = 20 mM, pH 9.5, T ranging from 10 °C (blue) to 30 °C (red) (increment = 5 °C). (b) Energy diagram for the MC ⇌ SP isomerization of 1 obtained from van't Hoff and Eyring plots and (c) corresponding thermodynamic parameters (in kJ mol−1). | |
Consequently, energy diagrams for the MC ⇌ SP isomerization of 1 (Fig. 2b) were obtained by means of van't Hoff analyses and Eyring plots (see Fig. S7†) – all thermodynamic and kinetic parameters obtained in this way are listed in Table S1.† First, we noticed that the MC-to-SP isomerization is endothermic, with a standard enthalpy (ΔrH) of 2.1 ± 0.7 kJ mol−1. In the case of SPs, it has been shown previously26 that the ground state energy of MC becomes lower than that of SP on account of hydrogen bonding interaction with water molecules – i.e., the isomerization of SPs in water is enthalpically-driven, with an equilibrium distribution shifted towards MC. Contrary to SPs, however, here we found that the isomerization of 1 is entropically dominated (Fig. 2c), resulting in a standard free energy of isomerization (ΔrG) of −5.3 ± 1.4 kJ mol−1 at 25 °C – i.e., in an equilibrium distribution shifted in favor of SP. The resulting equilibrium constant is in agreement with the one obtained by 1H NMR. The values found for the enthalpy (ΔH‡) and the entropy (ΔS‡) of activation are 92 ± 1 kJ mol−1 and 37 ± 2 J K−1 mol−1, and both are in line with the activation parameters reported so far26 for SPs in polar protic solvents.
The interpretation of the ground state thermodynamics of 1 emerging from 1H NMR analyses was subsequently validated by UV-Vis titrations. Samples were prepared as described above with potassium phosphate buffer solutions ranging from pH 3 to 10, and subsequently analyzed in the same way as the NMR titrations – one should note at this point the importance of equilibration time in the dark prior to data acquisition (Fig. 2a). The UV-Vis spectra of compound 1 at increasing pH values (Fig. 3a) were recorded after an equilibration time of 15 minutes at 25 °C. The band centered at 424 nm, which progressively decreases as the pH increase, is assigned to the π–π* transition of MCH, whereas the two new bands emerging at 535 and 297 nm are assigned to MC and the π–π* transition of the chromene moiety of SP, respectively.8
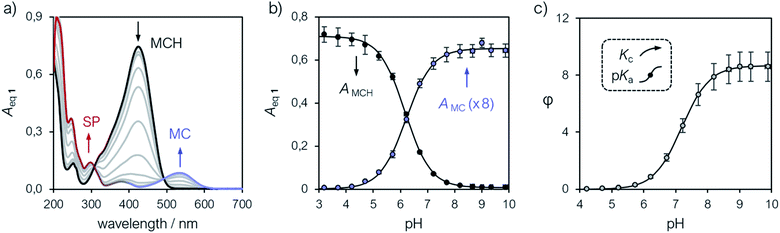 |
| | Fig. 3 (a) UV-Vis spectra of 1 at increasing pH values (increment = 0.5 pH units). Profiles of the absorbances of MCH (424 nm) and MC (535 nm) (b) and of φ (c) obtained as a function of the pH. Solid lines represent the best fits to model eqn (8) and (2), respectively. Experimental conditions: [1] = 22.8 ± 1.5 μM, [phosphate buffers] = 20 mM (3 < pH < 10), T = 25 °C. | |
Compared to SPs, the large hypsochromic shift observed for the band associated to MC (<550 nm) suggests that the phenolate resonance form of MC dominates over the quinoidal one, which indeed is typically favored in non-polar media.27 The pKGSa was calculated from the profiles of the absorbance of either MCH and MC (Fig. 3b) as a function of the pH by non-linear least-squares curve fitting to Boltzmann equation:
| | 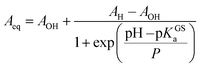 | (8) |
where
AH and
AOH are absorbances detected respectively at low and high pH, respectively, whereas
P represent a fitting factor.
28 The p
KGSa thus obtained (6.20 ± 0.03) is nicely in agreement with that determined above with
eqn (3) and, importantly, with the one (6.23) obtained similarly in a recent study by Zhang and co-workers.
29 Alternatively, knowing the molar absorptivities of all the species taking part in the equilibrium, UV-Vis data can be processed so as to obtain
φ. The molar extinction coefficients of the MCH form were obtained by quantitative calibrations at pH 3 (pH ≪ p
KGSa) in the dark, whereas that of the SP form through calibrations at neutral pH (pH ≫ p
KMSa) under continuous LED-light irradiation (425 nm, 100 mW). Due to the transient nature of the MC form, molar absorptivities were computed knowing the equilibrium composition at pH 9.5 (
vide supra) and the optical readout of the corresponding SP form (see Fig. S9–S11
†). Thus, the speciation diagram of
1 was obtained, for the first time experimentally, from the same UV-Vis titration (
Fig. 3a) knowing the optical readout of SP, MCH and MC at all the corresponding
λmax (see Fig. S13
†). The absorption data allowed us for calculating the parameter
φ as a function of the pH, by which both
Ka and
Kc were determined from fitting to
eqn (2) (
Fig. 3c). We were pleased to see that, despite a larger uncertainty due to error propagation, all the equilibrium constants were fully consistent with those obtained by
1H NMR (see Table S2
†). Overall, the evidences gained so far highlight the importance of the MC ⇌ SP isomerization in determining p
KGSa, unravelling a new design rationale for possibly decreasing the ground state acidity and amplifying the operational pH window of MCHs.
The metastable state
Having assessed the thermodynamics of the ground state by comparative 1H NMR and UV-Vis analyses in the dark, we then moved on investigating the metastable state (Fig. 4a). So far, probing the metastable acid–base equilibrium of 1 in water was claimed to be challenging due to its low solubility and fast reverse reaction, and the corresponding pKMSa was proposed to lay within 1.7–3.2 based on indirect measurements in MeOH.5 Numerical analyses by Coudret and coworkers, however, predicted the pKMSa value of 1 to be 4.3.23 Motivated by this straying results, we opted for UV-Vis titrations under powerful and continuous LED-light irradiation for probing the photostationary state of 1 (Fig. 4a). Samples were prepared as described above, but using aliquots of standard HCl for fixing the pH below 4; the LED-light beam (425 nm, 100 mW) was delivered directly from the top of sample cuvettes by a 3 meter-long optical fiber (Fig. 4b). The UV-Vis spectra obtained exploiting the “room light immunity” feature of our spectrometer are reported in Fig. 4c. The two overlapping bands centered at 330 and 385 nm, which progressively decrease as the pH increase, are assigned respectively to the π–π* transition of the indolium and the chromene parts of the protonated metastable form of 1 (green trace). As compared to the π–π* transition of MCH (424 nm) in the dark, the observed blue shift and splitting can be ascribed to the decreased electronic delocalization of a twisted conformation – i.e., cis-MCH. In the case of SP, electronic delocalization is broken by the spiro carbon, and the same two transitions become distinct8 and narrow at 244 and 297 nm, respectively (red trace). The clear isosbestic point found at 300 nm confirms that the two forms constitute a photostationary state. The pKMSa of 1 was determined from the profiles of the absorbance of either cis-MCH and SP (Fig. 4d) as a function of the pH by non-linear least-squares curve fitting to eqn (8). The pKMSa thus obtained (2.47 ± 0.04) fall exactly between 1.7 and 3.2 (ref. 5) as proposed by Liao. At this point, in an analogy with excited-state photoacids,30 we propose to define the photoacidity of MCHs (referred to here as Π) as the difference between the acidity constants of the ground state and the metastable state:
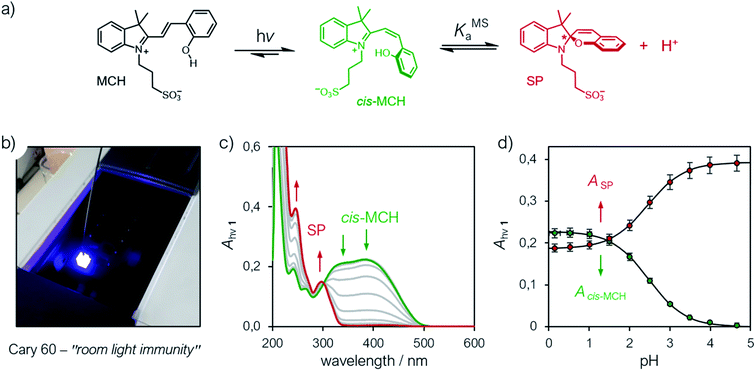 |
| | Fig. 4 (a) Schematic representation of the metastable acid/base equilibrium of MCHs. (b) Representative picture of the setup employed for acquiring UV-Vis spectra under continuous LED-light irradiation. (c) UV-Vis spectra of at increasing pH values (increment = 0.5 pH units) and (d) profiles of the absorbances of cis-MCH (385 nm) and SP (244 nm) obtained as a function of the pH. Solid lines represent the best fits to the eqn (8). Experimental conditions: [1] = 22.8 ± 1.5 μM, [HCl] = 1 to 10−4 M, [phosphate buffers] = 20 mM (pH > 4), T = 25 °C; spectra were acquired under continuous illumination (425 nm, 100 mW). | |
This definition allows for rapid comparison of different MCHs and can be used to easily quantify their capability of changing the acidity of a solution after light irradiation (see below). The photoacidity of 1 was found to be Π = 3.7 ± 0.1.
The hydrolytic stability
A delicate aspect to consider when using MCHs in water is their propensity to hydrolyze irreversibly (Fig. 5a). In the case of SPs, it has been shown previously31 that hydrolysis is initiated by addition of water to the ene-iminium moiety of their MC form, followed by a retro-aldol condensation reaction yielding the products. Water is the major nucleophile involved in the reaction below pH 9, but the MCH form is considered to be not susceptible to hydrolysis.32 On the other hand, compound 1 displays an half-life of 16 hours at pH 5.4 – i.e., at a pH where MCH dominates over MC.21 Also, it has been proposed that electron-donating groups conjugated to ene-iminium moiety may enhance the hydrolytic stability of MCHs in aqueous environments, and that hydrolysis of 1 would be catalyzed by OH−.21 The mechanism by which 1 undergoes hydrolysis, however, remains unclear, and we believed studying it in detail would be of interest in terms of practical applications. Thus, we decided to study the hydrolysis of 1 over the entire pH window ranging from 3 to 9. Kinetic analyses were carried out at 40 °C, monitoring the decay of the absorption band of the MC(H) form. The kinetic profiles were linearized, and apparent first-order rate constants of hydrolysis (kobs,hydr) obtained as the slope of the corresponding linear fit (Fig. 5b). We found that the rate of hydrolysis gradually increases till around pH 6, after that it starts to decrease for becoming progressively independent of pH (Fig. 5c). This bell-shaped profile is reminiscent of those observed for Schiff bases33 and, similarly, we think it could be due to a change in the rate-determining step from decomposition of tetrahedral intermediate X (II) to nucleophilic addition of water (I) at higher pH values (Fig. 5a). Inspired by the seminal work of Jencks and coworkers34 on the hydrolysis of substituted benzylidene-1,1-dimethylethylamines, and applying steady-state conditions in respect to the intermediate species X, we formulate the rate expression for the hydrolysis reaction as follows:| | 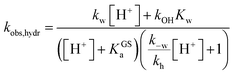 | (10) |
where kw is the rate constant for the attack of water and k−w that for the corresponding reverse reaction, kOH is the rate constant for the nucleophilic attack of hydroxide ion and kh that for the decomposition of X, whereas Kw is the autoprotolysis constant of water (see ESI† for more details). Each kinetic contribution was first estimated independently: (i) kw from the maximum observed rate constant (for which kw[H+] ≫ kOHKw and k−w[H+] ≈ kh) or alternatively from that at neutral pH (where kw[H+] ≫ kOHKw, [H+] < KGSa and k−w[H+]/kh < 1), (ii) kOH from the observed rate constant at pH 9 (where kw[H+] ≪ kOHKw, [H+] ≪ KGSa and k−w[H+]/kh ≪ 1), whereas (iii) k−w/kh from the observed rate constant at pH 3 (where kw[H+] ≫ kOHKw, [H+] ≫ KGSa and k−w[H+]/kh ≫ 1). Thus, non-linear least-squares curve fitting to eqn (10) was performed using these esteems as initial values. The model suits with good confidence (R2 > 0.99) the experimental data (Fig. 5c) and supports the change in rate-determining step proposed above. The same experiment was repeated at 25 °C from pH 3 to 8 (Fig. 5d). In this case, data fitting to eqn (10) (solid black line) followed by refinement with numerical analysis (dotted red line) allowed us to estimate all the forward rate constants involved in the hydrolytic pathway as kw = (2.8 ± 0.4) × 10−3 min−1, kOH = (9.5 ± 0.4) × 103 M−1 min−1 and kh = (2.0 ± 0.2) × 10−2 min−1 (see Fig. S17 and Table S3† for more details), which all in all show that the hydrolysis of 1 is significantly slower than the corresponding MC-to-SP equilibration (e.g., min−1vs. s−1).
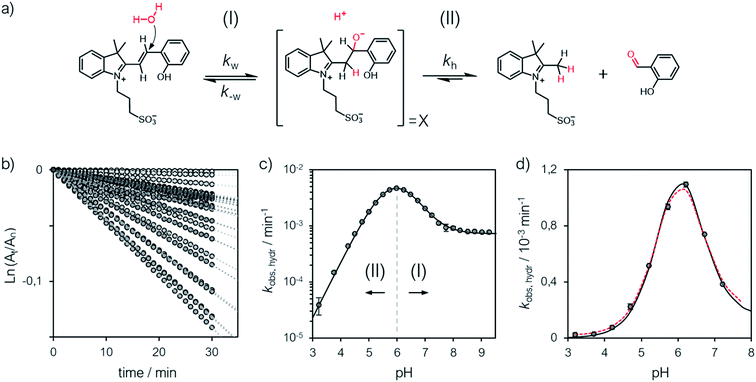 |
| | Fig. 5 (a) Proposed mechanism for the hydrolysis of 1 below pH 9. (b) Linearized absorption data as function of time and profiles of kobs,hydr as a function of the pH obtained at 40 °C (c) and 25 °C (d). Solid black lines represent the best fits to the eqn (10), whereas the dotted red line represent the best fit after refinement with numerical analysis (see ESI† for more details). | |
The metastability
The relative long lifetime of proton-photodissociation is the key feature distinguishing MCHs from other types of photoacids. As for compound 1, Liao and co-workers6 have shown that the relaxation of SP towards MCH obeys first order kinetics, displaying a half-life of 76 s in water. Later on, however, the same group showed that the behavior of 1 strongly depends upon solvent effects: the relaxation kinetics was found to be particularly fast in water as compared to that in ethanol, which in turn was found to be faster than that in dimethylsulfoxide (DMSO).9 This observation set the foundation for the now commonly accepted hypothesis of having protonation involved in the rate determining step, by which second-order rate constants were calculated. The observed marked decrease in rate constant (from 73 to 0.034 M−1 s−1) was ascribed to the hydrogen bond donor acidity of the solvent, which in fact gradually decrease from water to DMSO.9 Recent studies29 in methanol appears to be consistent with this interpretation (see Fig. S18†). Despite the properties of the solvent certainly play a role in determining kinetics in general,27 solvent effects alone do not necessarily indicate a rate determining step of bimolecular nature. Therefore, in order to investigate whether the proton takes part in the rate determining step, we decided to examine the relaxation kinetics of 1 over the entire pH window ranging from 0 to 10 (Fig. 6).
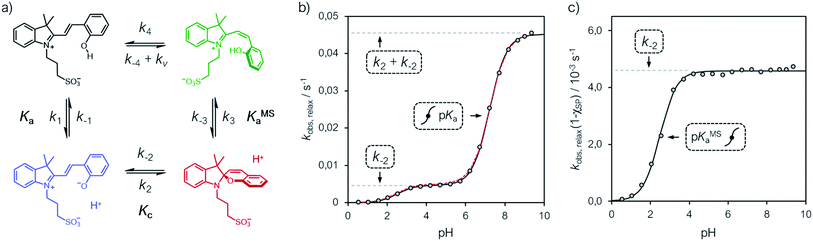 |
| | Fig. 6 (a) Proposed four-component kinetic cycle for the operation of 1 in water and corresponding profiles of kobs,relax (b) and kobs,relax(1 − χSP) (c) obtained as a function of the pH. Solid black lines represent the best fits to the eqn (11), whereas dotted red lines correspond to the best numerical fit to the full model depicted in (a). Experimental conditions [1] = 25 ± 2 μM, [HCl] = 1 to 10−3 M, [phosphate buffers] = 20 mM (pH > 3), T = 25 °C; kinetic data were collected in the dark after photoirradiation (425 nm, 100 mW). | |
In addition, considering all evidences emerging in the above sections, we propose the four-component cycle depicted in Fig. 6a as kinetic model, where k1/k−1 = Ka, k2/k−2 = Kc, k−3/k3 = KMSa, while k−4 and k4 are the kinetic constants associated to the trans-to-cis isomerization of MCH and to the corresponding reverse reaction, respectively, in the dark – i.e., with kv = 0. Kinetic analyses were carried out at 25 °C, monitoring the recovery of the absorption band of the corresponding MC(H) form. Apparent pseudo first-order rate constants of relaxation (kobs,relax) were obtained using eqn (4) (see Fig. S19†), the corresponding profile as a function the pH are reported in Fig. 6b.
We found that the kobs,relax of 1 progressively increase with pH following a double-sigmoidal behavior, displaying two inflection points close to the corresponding pKMSa and pKa. Despite excluding a concerted bimolecular reaction between SP and H+ yielding MCH,8,35 the kinetic model appears to be fully consistent, with numerical fitting curves approaching nicely the experimental profile with good confidence (Fig. 6b, dotted red line). A general way to estimate relaxation rates is to study the non-zero eigenvalues of the rate matrix. In this case, it can be shown that the apparent rate constant of relaxation corresponds the opposite of the largest non-zero eigenvalue (see ESI† for more details). At extremely acidic pH values (pH < pKMSa), the observed rate constants are all very low, suggesting that the cis-MCH form is thermally stable. This is in line with previous reports on the acidochromism of SPs, though the observed low rates were ascribed to existence of an SP form protonated at the indole nitrogen atom5,32,36 acting as “unreactive sink”37 – i.e., SPH. Recent computational studies by Browne and co-workers have shown that, even considering the existence of SPH, proton transfer coupled with C–O cleavage is barrierless and results in the formation of cis-MCH.38 Thus, given the apparent thermal stability of cis-MCH, one may assume SP the only species undergoing relaxation, so as to use the pre-equilibrium approximation39 for deriving the rate expression of relaxation as follows:
| |  | (11) |
Fitting was initialized with the corresponding thermodynamic and kinetic constants obtained above, using the errors associated to each equilibrium constant as constraints and leaving k−2 free to vary. The value obtained for k−2 is in accordance with that found independently at 25 °C from equilibration studies (Table S1†). The model function suits with very good confidence (R2 > 0.99) the experimental profiles (Fig. 6b, solid black line) and strongly suggests a situation where thermal ring opening of SP (k−2) remains rate-determining throughout the entire pH window,32 with cis-to-trans isomerization of cis-MCH (slow) competing significantly only at low pH values. This emerges in a clear manner by looking at the profiles of kobs,relax scaled for the effective concentration of species undergoing isomerization (Fig. 6c), which increase for becoming independent of pH after pKMSa, with a plateau corresponding to k−2. This interpretation explain why the relaxation of 1, in a pH window well above pKMSa, could be fitted well to a first order rate equation6 also in the absence of buffers holding [H+] constant.
Comparative evaluation
Previously, structural modifications of either the chromene13a,19b,40 and/or the indolium29,41 moieties of 1 have been introduced for tuning its photochemistry in both aqueous and organic environments. Little attention, however, has been devoted towards modifying the propyl-1-sulfonate group connected to the iminium nitrogen atom, which is considered to be important for preserving the thermodynamics of MCHs – i.e., stabilizing the open forms MCH and MC.6 Here, we decided to explore the role of the sulfonate group with a series of MCHs bearing an increasingly long alkyl-1-sulfonate bridge (see Scheme S1† with n = 1, 2, 3). Thus, two compounds featuring respectively an ethyl- (2, n = 1) and a butyl-1-sulfonate group42 (3, n = 3) were synthesized similarly to Liao's photoacid (1, n = 2), and fully characterized by HR-MS, 1H and 13C NMR spectroscopy, as well as X-ray analysis (see ESI† for more details). The methodologies presented above are general and both compound 2 and 3 were analyzed in the same way, all results are summarized in Table 1 to aid comparative evaluation as function of n. First, comparison of 1–3 revealed that pKa remains constant within the experimental error, whereas pKc linearly increase with increasing n. This effect correlates with the distance of the sulfonate group from the positive charge localized on the indolium nitrogen: passing two to four carbon atoms, the EWG effect of the sulfonate group attenuate, making the iminium site less and less polarized and prone to react intramolecularly. This was further confirmed by comparative van't Hoff analysis (Fig. S7†), which showed that the ΔrG of MC-to-SP isomerization linearly decrease as function of n (Fig. S8†). With regard to the activation parameters for the MC-to-SP reaction, we found that the ΔH‡ slightly increase with increasing n (Table S1†). We tentatively ascribed this to higher degrees of freedom of the butyl bridge in compound 3, which in turn might take part in increasing the through-space electrostatic repulsions27 between the sulfonate group and the phenolate group, and so the barrier for conversion of trans-MC to cis-MC. On the other hand, the values found for ΔS‡ are all consistent with those reported so far26 for SPs in polar protic solvents, indicating comparable solvent–solute dipolar orientational correlations.43
Table 1 Thermodynamic and kinetic parameters of compounds 1–3 obtained at 25 °C
|
n
|
pKaa |
pKcb |
pKGSac |
pKMSad |
Π
|
S
(mM) |
k
w
(10−3 min−1) |
k
OH
(103 M−1 min−1) |
k
h
(10−2 min−1) |
k
−2 (10−2 s−1) |
Φ
|
|
Average values obtained from both 1H NMR and UV-Vis data with eqn (1) and (2).
Average values obtained from both 1H NMR and UV-Vis data with either eqn (2) and van't Hoff analysis.
Average values obtained from both 1H NMR and UV-Vis data with eqn (2), (3) and (8).
Values obtained from UV-Vis data with eqn (8).
Average values resulting from eqn (9).
Solubilities in aqueous KCl (20 mM).
Average values resulting from before and after numerical refinement.
Values obtained from equilibration kinetics (eqn (4)).
Values obtained from relaxation kinetics (eqn (11)).
Values obtained from multiple pH jumps experiments with eqn (12). All data refer to experiments performed (at least) in duplicate (see Table S2 for more details).
|
| 1 |
7.23 ± 0.06 |
−1.48 ± 0.02 |
5.74 ± 0.08 |
2.14 ± 0.04 |
3.6 ± 0.1 |
0.56 ± 0.05 |
4.2 ± 0.1 |
13 ± 2 |
5.0 ± 0.5 |
0.31h, 0.31i |
0.73 ± 0.09 |
| 2 |
7.20 ± 0.03 |
−0.96 ± 0.03 |
6.19 ± 0.06 |
2.47 ± 0.04 |
3.7 ± 0.1 |
0.19 ± 0.03 |
2.8 ± 0.4 |
9.5 ± 0.4 |
2.0 ± 0.2 |
0.45h, 0.46i |
0.37 ± 0.04 |
| 3 |
7.25 ± 0.05 |
−0.59 ± 0.02 |
6.56 ± 0.07 |
3.07 ± 0.04 |
3.5 ± 0.1 |
2.66 ± 0.28 |
1.7 ± 0.3 |
4.5 ± 0.4 |
0.26 ± 0.03 |
0.59h, 0.60i |
0.22 ± 0.03 |
The solubility (S) of each compound refers to aqueous potassium chloride solutions (see below). S values were determined by both UV-Vis and NMR analysis at 25 °C (see Fig. S20†) and are reported in Table 1 as the average of multiple experiments. We found that S dramatically increase in the order: 1 < 2 < 3. The superior water solubility of compound 3 allowed us to carry out successfully photo-NMR44 investigations by in situ illumination, which, for pH < pKMSa, corroborated the nearly quantitative conversion of MCH into an achiral species displaying a cis-non-coplanar conformation (cis-MCH) (see ESI† for a more detailed discussion). Interestingly, UV-Vis studies revealed that all pKMSa values fall within the range 1.7–3.2 as proposed by Liao5 and, as observed for pKc, progressively increase as a function of n. These results further confirm the interplay between the EWG effect of the sulfonate group and the length of the alkyl bridge in determining the thermodynamics. Hence, subsequent comparison of 1–3 through eqn (9) showed that Π remains fairly constant within the experimental error (3.6 ± 0.2), but gradually shift towards more neutral regions with increasing n (ca. +1 pH unit).
Comparative kinetic analyses of 1–3 were carried out at 25 °C. In the case of hydrolysis we decide to investigate the pH range from pH 3 to 8 (see Fig. S17†). Importantly, all fitting were satisfactory, confirming the mechanism of hydrolysis evoked above is valid for all compounds. Notably, we found that kw, kOH and kh linearly decrease with increasing n, highlighting the role of the proximity of the sulfonate group in dictating the reactivity: the hydrolytic stability of MCHs in water gradually increases with n. With regard to thermal relaxation, experiments were repeated for 2 and 3 covering the full pH window as in the case of 1. Also in this case, we found all fitting were satisfactory (see Fig. S19†): thermal ring-opening of SP is always rate-determining regardless of pH, with k−2 linearly increasing as a function of n. Taken together, these results show that the four-component cycle depicted in Fig. 6a has general applicability.
Reversible proton release in water
We finally focused on studying the proton release/uptake of 1–3 in water by means of direct pH measurements. Saturated solutions of 1–3 were prepared by sonication (10 min), adding an excess amount of crystalline material into aqueous potassium chloride (30 mL, 20 mM). We chose this for reproducing the same ionic strength in the experiments above and for optimal response of the glass electrode. In a typical experiment, the solution was microfiltered and transferred in our in-house designed photochemical vessel (Fig. 7a, see Scheme S2† for more details) and the pH measurements started after 5 minutes of equilibration at 25 °C and under gentle nitrogen bubbling (Fig. 7b–d, black lines). We found that pH readings in the dark were all consistent with the pH value predicted by the weak acid approximation and the corresponding pKGSa – i.e., [H+] = (KGSa × S)1/2. Subsequently, light irradiation induced pH drops down to a stationary value close to −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S, indicating nearly quantitative proton photo-dissociation;6 in the case of 3 (Fig. 7d) the final pH settled to a value very close to its pKMSa – i.e., the maximum possible level of proton release for 3. Inspection of the obtained pH profiles revealed that the pH recovery after light irradiation follows first-order kinetics, with kobs,relax consistent with the corresponding k−2 (see Fig. S21†). As for 3, the explored pH window is such that kobs,relax ≈ k−2/2 (see eqn (11)), in line with the fact the final pH obtained under irradiation (ca. 3.1) equals its pKMSa (3.07 ± 0.04). These observations show that proton release is fully reversible and, again, that the mechanism proposed above for 1 is general. Thus, we decided to investigate whether the four-component kinetic cycle depicted in Fig. 6a is also compatible with the observed full dynamics of proton release/uptake. Simultaneous data fit were performed considering the three distinct data sets of three independent experiments, namely: (i) pH jump, (ii) kobs,hydrvs. pH and (ii) kobs,relaxvs. pH. Combined data fit were initialized with the thermodynamic and kinetic parameters listed in Table 1, and the resulting outcome subjected to Monte Carlo cross validation (see Fig. S23–S25 and Tables S4–S6†). We were very pleased to see that computed dynamics are fully consistent with the experimental profiles (Fig. 7b–d, red lines). In addition, this numerical procedure allowed us to estimate kν, which represents the rate constant of MCH's photo-isomerization and can be used to directly estimate the quantum yield (Φ) as follows:
S, indicating nearly quantitative proton photo-dissociation;6 in the case of 3 (Fig. 7d) the final pH settled to a value very close to its pKMSa – i.e., the maximum possible level of proton release for 3. Inspection of the obtained pH profiles revealed that the pH recovery after light irradiation follows first-order kinetics, with kobs,relax consistent with the corresponding k−2 (see Fig. S21†). As for 3, the explored pH window is such that kobs,relax ≈ k−2/2 (see eqn (11)), in line with the fact the final pH obtained under irradiation (ca. 3.1) equals its pKMSa (3.07 ± 0.04). These observations show that proton release is fully reversible and, again, that the mechanism proposed above for 1 is general. Thus, we decided to investigate whether the four-component kinetic cycle depicted in Fig. 6a is also compatible with the observed full dynamics of proton release/uptake. Simultaneous data fit were performed considering the three distinct data sets of three independent experiments, namely: (i) pH jump, (ii) kobs,hydrvs. pH and (ii) kobs,relaxvs. pH. Combined data fit were initialized with the thermodynamic and kinetic parameters listed in Table 1, and the resulting outcome subjected to Monte Carlo cross validation (see Fig. S23–S25 and Tables S4–S6†). We were very pleased to see that computed dynamics are fully consistent with the experimental profiles (Fig. 7b–d, red lines). In addition, this numerical procedure allowed us to estimate kν, which represents the rate constant of MCH's photo-isomerization and can be used to directly estimate the quantum yield (Φ) as follows:| | 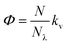 | (12) |
where N is the number of molecules undergoing isomerization, and Nλ is the photon flux – i.e., the number of photons per unit time (see ESI† for more details). Interestingly, we found that Φ gradually decrease with increasing n (Fig. 7e). We ascribed this to the electrophilicity of the spiro carbon, which decrease as a function of n (see above). Independent variable-power pH jump studies revealed linear relationships between kν and Nλ, meaning that Φ does not depend upon the power of the LED light source within the range 50–350 mW (see Fig. S26†) – quantum yields of 1–3 are thus reported in Table 1 as the trimmed mean resulting from multiple pH jump profiles and relative fitting (see Tables S7–S9†). It is worth noting that the quantum yield we obtained in this way for 1 (0.37 ± 0.04) is in good agreement with that (0.38 ± 0.03) previously reported23 for the same compound in water.
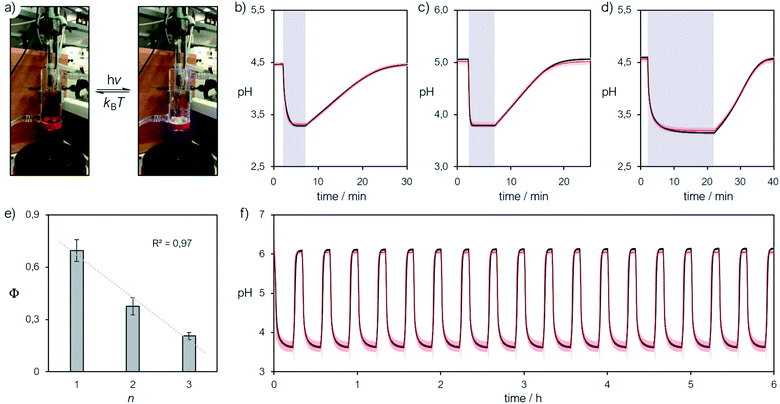 |
| | Fig. 7 (a) Representative picture of the photochemical apparatus during pH measurements; all preparations and experiments were carried out at 25 °C, under dark conditions. Representative pH jump profiles obtained irradiating (425 nm, 340 mW) satd solutions of 2 (n = 1) (b), 1 (n = 2) (c) and 3 (n = 3) (d) in aqueous KCl (20 mM), and (e) corresponding trend of the quantum yield as a function of n. (f) Repetitive pH jumps obtained partially neutralizing a satd solution of compound 3 (2.6 mM) with NaHCO3 (0.25 equivalents). Solid black lines represent the profiles obtained experimentally, whereas solid red lines represent the corresponding curve fitting. | |
In general, the amplitude of the pH jump – and so the potential application of a given MCH – is regulated not only by the complete set of thermodynamic and kinetic constants we have unraveled here but also simply by S. At this point, given the superior hydrolytic stability and water solubility of the new compound 3, along with its relatively high pKGSa, we decided to explore the possibility of amplifying its pH jump by partially neutralizing the solution with a base. Even if this would sacrifice part of the protons available initially, the system will still exhibit pH drops because of the remaining MCH in solution. On this regard, we repeated the same experiment above, but with in situ addition of sodium bicarbonate (0.25 equivalents), the corresponding pH profile is reported in Fig. 7f (see also Fig. S27†). We were very pleased to see that (i) the pH jump passed from ca. 1.5 to 2.5 pH units, (ii) it can be repeated for at least 6 hours without significant loss and, most importantly, (iii) the full dynamics can be simulated nicely adopting the thermodynamic and kinetic parameters obtained above. This result shows that the cyclic model implemented here is robust and can be used to fully predict the behavior of MCHs in water. To the best of our knowledge, the reversible proton release/uptake obtained buffering 3 with NaHCO3 is the deepest and most reproducible light-induced pH jump ever achieved.
Conclusions
In conclusion, we have rationalized the behavior of MCHs in water through a series of 1H NMR and UV-Vis studies and relative modelling. We have provided straightforward methodologies for assessing the acidity constant of both the ground state and the metastable state. In particular, we were able to quantify experimentally the equilibrium of MCHs under dark conditions, and so the effects of the MC ⇌ SP isomerization on proton dissociation – i.e., KGSa = Ka(1 + Kc). In addition, we have shown that the protonated metastable state is an achiral species with a cis-non-coplanar conformation (cis-MCH). We have analyzed the mechanism of both hydrolysis and relaxation kinetics as a function of the pH and found that (i) MCHs hydrolyze similarly to Schiff bases and (ii) re-protonation is not involved in the rate determining step of relaxation. Direct pH measurements are fully consistent with the obtained thermodynamic constants, and the four-component cycle proposed here as model suits very well the observed reversible proton release/uptake dynamics of MCHs in water. We believe these finding lay a solid foundation for further expanding the implementation of MCHs in aqueous-based systems.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Swiss National Science Foundation (SNSF “Ambizione” PZ00P2_180008). We thank Dr Suzanne M. Jansze for providing the X-ray structure of 1.
Notes and references
- N. Lane, BioEssays, 2017, 39, 1600217 CrossRef PubMed.
- D. Oesterhelt and W. Stoeckenius, Proc. Natl. Acad. Sci. U. S. A., 1973, 70, 2853–2857 CrossRef CAS PubMed.
- T. Kouyama, A. N. Kouyama and A. Ikegami, Biophys. J., 1987, 51, 839–841 CrossRef CAS PubMed.
-
(a)
J. F. Ireland and P. A. H. Wyatt, in Adv. Phys. Org. Chem., ed. V. Gold, Academic Press, 1976, vol. 12, pp. 131–221 Search PubMed;
(b) H. Shizuka, Acc. Chem. Res., 1985, 18, 141–147 CrossRef CAS;
(c) L. G. Arnaut and S. J. Formosinho, J. Photochem. Photobiol., A, 1993, 75, 1–20 CrossRef CAS;
(d) S. J. Formosinho and L. G. Arnaut, J. Photochem. Photobiol., A, 1993, 75, 21–48 CrossRef CAS;
(e) P. Wan and D. Shukla, Chem. Rev., 1993, 93, 571–584 CrossRef CAS;
(f) L. M. Tolbert and K. M. Solntsev, Acc. Chem. Res., 2002, 35, 19–27 CrossRef CAS PubMed;
(g) R. M. Nunes, M. Pineiro and L. G. Arnaut, J. Am. Chem. Soc., 2009, 131, 9456–9462 CrossRef CAS PubMed;
(h) R. Simkovitch, S. Shomer, R. Gepshtein and D. Huppert, J. Phys. Chem. B, 2015, 119, 2253–2262 CrossRef CAS PubMed.
- Y. Liao, Acc. Chem. Res., 2017, 50, 1956–1964 CrossRef CAS PubMed.
- Z. Shi, P. Peng, D. Strohecker and Y. Liao, J. Am. Chem. Soc., 2011, 133, 14699–14703 CrossRef CAS PubMed.
- S. Aiken, R. J. L. Edgar, C. D. Gabbutt, B. M. Heron and P. A. Hobson, Dyes Pigm., 2018, 149, 92–121 CrossRef CAS.
- R. Klajn, Chem. Soc. Rev., 2014, 43, 148–184 RSC.
- V. K. Johns, Z. Z. Wang, X. X. Li and Y. Liao, J. Phys. Chem. A, 2013, 117, 13101–13104 CrossRef CAS PubMed.
-
(a) S. Silvi, A. Arduini, A. Pochini, A. Secchi, M. Tomasulo, F. M. Raymo, M. Baroncini and A. Credi, J. Am. Chem. Soc., 2007, 129, 13378–13379 CrossRef CAS PubMed;
(b) L. A. Tatum, J. T. Foy and I. Aprahamian, J. Am. Chem. Soc., 2014, 136, 17438–17441 CrossRef CAS PubMed;
(c) L. P. Yang, F. Jia, J. S. Cui, S. B. Lu and W. Jiang, Org. Lett., 2017, 19, 2945–2948 CrossRef CAS PubMed;
(d) Q. Shi, Z. Meng, J. F. Xiang and C. F. Chen, Chem. Commun., 2018, 54, 3536–3539 RSC.
-
(a) C. Maity, W. E. Hendriksen, J. H. van Esch and R. Eelkema, Angew. Chem., Int. Ed., 2015, 54, 998–1001 CrossRef CAS PubMed;
(b) X. Li, J. Fei, Y. Xu, D. Li, T. Yuan, G. Li, C. Wang and J. Li, Angew. Chem., Int. Ed., 2018, 57, 1903–1907 CrossRef CAS PubMed;
(c) H. Zhang, H. Zeng, A. Priimagi and O. Ikkala, Nat. Commun., 2019, 10, 3267 CrossRef PubMed.
-
(a) P. K. Kundu, D. Samanta, R. Leizrowice, B. Margulis, H. Zhao, M. Borner, T. Udayabhaskararao, D. Manna and R. Klajn, Nat. Chem., 2015, 7, 646–652 CrossRef CAS PubMed;
(b) D. Samanta and R. Klajn, Adv. Opt. Mater., 2016, 4, 1373–1377 CrossRef CAS;
(c) Z. Wang and Y. Liao, Nanoscale, 2016, 8, 14070–14073 RSC;
(d) Q. Shi and C. F. Chen, Org. Lett., 2017, 19, 3175–3178 CrossRef CAS PubMed;
(e) J. Guo, H. Y. Zhang, Y. Zhou and Y. Liu, Chem. Commun., 2017, 53, 6089–6092 RSC;
(f) S. M. Jansze, G. Cecot and K. Severin, Chem. Sci., 2018, 9, 4253–4257 RSC;
(g) D. Go, D. Rommel, Y. Liao, T. Haraszti, J. Sprakel and A. J. C. Kuehne, Soft Matter, 2018, 14, 910–915 RSC;
(h) H. Zhang, J. Muhammad, K. Liu, R. H. A. Ras and O. Ikkala, Nanoscale, 2019, 11, 14118–14122 RSC.
-
(a) S. Kusumoto, T. Nakagawa and Y. Yokoyama, Adv. Opt. Mater., 2016, 4, 1350–1353 CrossRef CAS;
(b) S. Mahvidi, S. Takeuchi, S. Kusumoto, H. Sato, T. Nakagawa and Y. Yokoyama, Org. Lett., 2016, 18, 5042–5045 CrossRef CAS PubMed;
(c) T. Zhang, L. Sheng, J. N. Liu, L. Ju, J. H. Li, Z. Du, W. R. Zhang, M. J. Li and S. X. A. Zhang, Adv. Funct. Mater., 2018, 28, 1705532 CrossRef;
(d) J. Gurke, S. Budzak, B. M. Schmidt, D. Jacquemin and S. Hecht, Angew. Chem., Int. Ed., 2018, 57, 4797–4801 CrossRef CAS PubMed;
(e) L. L. Liu, X. Su, Q. Yu, H. W. Guo, K. Wang, B. H. Yu, M. J. Li, B. Zou, Y. F. Liu and S. X. A. Zhang, J. Phys. Chem. C, 2019, 123, 25366–25372 CrossRef CAS.
- H. Bao, F. F. Li, L. C. Lei, B. Yang and Z. J. Li, RSC Adv., 2014, 4, 27277–27280 RSC.
-
(a) Y. Xu, J. Fei, G. Li, T. Yuan, Y. Li, C. Wang, X. Li and J. Li, Angew. Chem., Int. Ed., 2017, 56, 12903–12907 CrossRef CAS PubMed;
(b) Y. Jia and J. Li, Acc. Chem. Res., 2019, 52, 1623–1631 CrossRef CAS PubMed.
-
(a) Y. Luo, C. Wang, P. Peng, M. Hossain, T. Jiang, W. Fu, Y. Liao and M. Su, J. Mater. Chem. B, 2013, 1, 997–1001 RSC;
(b) J. Xi, J. Zhang, X. Qian, L. An and L. Fan, RSC Adv., 2020, 10, 909–913 RSC.
-
(a) P. K. Patel, V. K. Johns, D. M. Mills, J. E. Boone, P. Calvo-Marzal and K. Y. Chumbimuni-Torres, Electroanalysis, 2015, 27, 677–683 CrossRef CAS;
(b) P. K. Patel and K. Y. Chumbimuni-Torres, Analyst, 2016, 141, 85–89 RSC.
- Z. Wang, V. K. Johns and Y. Liao, Chem.–Eur. J., 2014, 20, 14637–14640 CrossRef CAS PubMed.
-
(a) C. Fu, J. Xu and C. Boyer, Chem. Commun., 2016, 52, 7126–7129 RSC;
(b) M. S. Zayas, N. D. Dolinski, J. L. Self, A. Abdilla, C. J. Hawker, C. M. Bates and J. R. de Alaniz, ChemPhotoChem, 2019, 3, 467–472 CrossRef CAS.
-
(a) V. K. Johns, P. K. Patel, S. Hassett, P. Calvo-Marzal, Y. Qin and K. Y. Chumbimuni-Torres, Anal. Chem., 2014, 86, 6184–6187 CrossRef CAS PubMed;
(b) T. Khalil, A. Alharbi, C. Baum and Y. Liao, Macromol. Rapid Commun., 2018, 39, e1800319 CrossRef PubMed;
(c) M. J. Feeney and S. W. Thomas, Macromolecules, 2018, 51, 8027–8037 CrossRef CAS;
(d) A. Elgattar, N. Abeyrathna and Y. Liao, J. Phys. Chem. B, 2019, 123, 648–654 CrossRef CAS PubMed;
(e) L. Yang, L. Caire da Silva, H. Therien-Aubin, M. B. Bannwarth and K. Landfester, Macromol. Rapid Commun., 2019, 40, e1800713 CrossRef PubMed;
(f) C. Li, A. Iscen, L. C. Palmer, G. C. Schatz and S. I. Stupp, J. Am. Chem. Soc., 2020, 142, 8447–8453 CrossRef CAS PubMed.
- N. Abeyrathna and Y. Liao, J. Phys. Org. Chem., 2017, 30, e3664 CrossRef.
- K. A. Rubinson, Anal. Methods, 2017, 9, 2744–2750 RSC.
- J. Vallet, J. C. Micheau and C. Coudret, Dyes Pigm., 2016, 125, 179–184 CrossRef CAS.
- M. D. Liptak, K. C. Gross, P. G. Seybold, S. Feldgus and G. C. Shields, J. Am. Chem. Soc., 2002, 124, 6421–6427 CrossRef CAS PubMed.
- K. Sumaru, M. Kameda, T. Kanamori and T. Shinbo, Macromolecules, 2004, 37, 4949–4955 CrossRef CAS.
- Y. Shiraishi, M. Itoh and T. Hirai, Phys. Chem. Chem. Phys., 2010, 12, 13737–13745 RSC.
- J. T. C. Wojtyk, A. Wasey, P. M. Kazmaier, S. Hoz and E. Buncel, J. Phys. Chem. A, 2000, 104, 9046–9055 CrossRef CAS.
-
(a) Z. Miskolczy and L. Biczok, J. Phys. Chem. B, 2011, 115, 12577–12583 CrossRef CAS PubMed;
(b) Z. Miskolczy and L. Biczok, Photochem. Photobiol., 2012, 88, 1461–1466 CrossRef CAS PubMed.
- J. Liu, W. Tang, L. Sheng, Z. Du, T. Zhang, X. Su and S. X. Zhang, Chem.–Asian J., 2019, 14, 438–445 CrossRef CAS PubMed.
- H. Kagel, M. Frohme and J. Glökler, J. Cell. Biotechnol., 2018, 4, 23–30 Search PubMed.
- T. Stafforst and D. Hilvert, Chem. Commun., 2009, 287–288 RSC.
- M. Hammarson, J. R. Nilsson, S. Li, T. Beke-Somfai and J. Andreasson, J. Phys. Chem. B, 2013, 117, 13561–13571 CrossRef CAS PubMed.
-
(a) E. H. Cordes and W. P. Jencks, J. Am. Chem. Soc., 1962, 84, 832–837 CrossRef CAS;
(b) R. L. Reeves, J. Am. Chem. Soc., 1962, 84, 3332–3337 CrossRef CAS.
- E. H. Cordes and W. P. Jencks, J. Am. Chem. Soc., 1963, 85, 2843–2848 CrossRef CAS.
-
(a) F. M. Raymo and S. Giordani, J. Am. Chem. Soc., 2001, 123, 4651–4652 CrossRef CAS PubMed;
(b) F. M. Raymo and S. Giordani, J. Am. Chem. Soc., 2002, 124, 2004–2007 CrossRef CAS PubMed;
(c) F. M. Raymo and S. Giordani, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4941–4944 CrossRef CAS PubMed.
- N. Abeyrathna and Y. Liao, J. Photochem. Photobiol., A, 2017, 332, 196–199 CrossRef CAS.
- J. T. C. Wojtyk, A. Wasey, N. N. Xiao, P. M. Kazmaier, S. Hoz, C. Yu, R. P. Lemieux and E. Buncel, J. Phys. Chem. A, 2007, 111, 2511–2516 CrossRef CAS PubMed.
- L. Kortekaas, J. Chen, D. Jacquemin and W. R. Browne, J. Phys. Chem. B, 2018, 122, 6423–6430 CrossRef CAS PubMed.
- M. Rae and M. N. Berberan-Santos, J. Chem. Educ., 2004, 81, 436–440 CrossRef CAS.
-
(a) M. Dong, Y. W. Wang and Y. Peng, Supramol. Chem., 2013, 25, 116–120 CrossRef CAS;
(b) O. S. Shafaat, J. R. Winkler, H. B. Gray and D. A. Dougherty, ChemBioChem, 2016, 17, 1323–1327 CrossRef CAS PubMed;
(c) D. Moldenhauer and F. Grohn, Chem.–Eur. J., 2017, 23, 3966–3978 CrossRef CAS PubMed.
-
(a) V. K. Johns, P. Peng, J. DeJesus, Z. Wang and Y. Liao, Chem.–Eur. J., 2014, 20, 689–692 CrossRef CAS PubMed;
(b) N. Abeyrathna and Y. Liao, J. Am. Chem. Soc., 2015, 137, 11282–11284 CrossRef CAS PubMed;
(c) C. Yang, T. Khalil and Y. Liao, RSC Adv., 2016, 6, 85420–85426 RSC;
(d) P. K. Patel, J. E. Arias, R. S. Gongora, F. E. Hernandez, A. Moncomble, S. Aloise and K. Y. Chumbimuni-Torres, Phys. Chem. Chem. Phys., 2018, 20, 26804–26808 RSC;
(e) O. Alghazwat, A. Elgattar, T. Khalil, Z. Z. Wang and Y. Liao, Dyes Pigm., 2019, 171, 107719 CrossRef CAS.
-
(a) P. Joseph, K. Kundu and P. K. Kundu, ChemistrySelect, 2018, 3, 11065–11070 CrossRef;
(b) M. Schnurbus, M. Kabat, E. Jarek, M. Krzan, P. Warszynski and B. Braunschweig, Langmuir, 2020, 36, 6871–6879 CrossRef CAS PubMed.
- D. E. Wetzler, P. F. Aramendia, M. L. Japas and R. Fernandez-Prini, Phys. Chem. Chem. Phys., 1999, 1, 4955–4959 RSC.
- P. Nitschke, N. Lokesh and R. M. Gschwind, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114, 86–134 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic procedures and experimental details. CCDC 2005262, 2005264 and 1910833. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc03152f |
| ‡ These authors contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Daniel Maria
Busiello‡
a,
Daniel Maria
Busiello‡
 b,
Stefano
Zamuner‡
b,
Euro
Solari
a,
Rosario
Scopelliti
b,
Stefano
Zamuner‡
b,
Euro
Solari
a,
Rosario
Scopelliti
 a,
Farzaneh
Fadaei-Tirani
a,
Farzaneh
Fadaei-Tirani
 a,
Kay
Severin
a,
Kay
Severin
 a and
Cristian
Pezzato
a and
Cristian
Pezzato
 *a
*a

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, T = 25 °C. With this composition (<50% D2O v/v) the uncertainty of sample's pH due the presence of D2O is ±0.1 pH unit.22
4, T = 25 °C. With this composition (<50% D2O v/v) the uncertainty of sample's pH due the presence of D2O is ±0.1 pH unit.22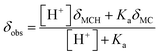
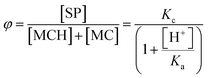
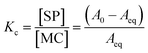
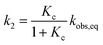
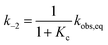


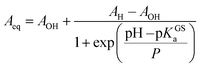

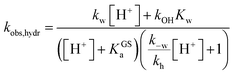



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S, indicating nearly quantitative proton photo-dissociation;6 in the case of 3 (Fig. 7d) the final pH settled to a value very close to its pKMSa – i.e., the maximum possible level of proton release for 3. Inspection of the obtained pH profiles revealed that the pH recovery after light irradiation follows first-order kinetics, with kobs,relax consistent with the corresponding k−2 (see Fig. S21†). As for 3, the explored pH window is such that kobs,relax ≈ k−2/2 (see eqn (11)), in line with the fact the final pH obtained under irradiation (ca. 3.1) equals its pKMSa (3.07 ± 0.04). These observations show that proton release is fully reversible and, again, that the mechanism proposed above for 1 is general. Thus, we decided to investigate whether the four-component kinetic cycle depicted in Fig. 6a is also compatible with the observed full dynamics of proton release/uptake. Simultaneous data fit were performed considering the three distinct data sets of three independent experiments, namely: (i) pH jump, (ii) kobs,hydrvs. pH and (ii) kobs,relaxvs. pH. Combined data fit were initialized with the thermodynamic and kinetic parameters listed in Table 1, and the resulting outcome subjected to Monte Carlo cross validation (see Fig. S23–S25 and Tables S4–S6†). We were very pleased to see that computed dynamics are fully consistent with the experimental profiles (Fig. 7b–d, red lines). In addition, this numerical procedure allowed us to estimate kν, which represents the rate constant of MCH's photo-isomerization and can be used to directly estimate the quantum yield (Φ) as follows:
S, indicating nearly quantitative proton photo-dissociation;6 in the case of 3 (Fig. 7d) the final pH settled to a value very close to its pKMSa – i.e., the maximum possible level of proton release for 3. Inspection of the obtained pH profiles revealed that the pH recovery after light irradiation follows first-order kinetics, with kobs,relax consistent with the corresponding k−2 (see Fig. S21†). As for 3, the explored pH window is such that kobs,relax ≈ k−2/2 (see eqn (11)), in line with the fact the final pH obtained under irradiation (ca. 3.1) equals its pKMSa (3.07 ± 0.04). These observations show that proton release is fully reversible and, again, that the mechanism proposed above for 1 is general. Thus, we decided to investigate whether the four-component kinetic cycle depicted in Fig. 6a is also compatible with the observed full dynamics of proton release/uptake. Simultaneous data fit were performed considering the three distinct data sets of three independent experiments, namely: (i) pH jump, (ii) kobs,hydrvs. pH and (ii) kobs,relaxvs. pH. Combined data fit were initialized with the thermodynamic and kinetic parameters listed in Table 1, and the resulting outcome subjected to Monte Carlo cross validation (see Fig. S23–S25 and Tables S4–S6†). We were very pleased to see that computed dynamics are fully consistent with the experimental profiles (Fig. 7b–d, red lines). In addition, this numerical procedure allowed us to estimate kν, which represents the rate constant of MCH's photo-isomerization and can be used to directly estimate the quantum yield (Φ) as follows: