Nucleation mechanisms and speciation of metal oxide clusters

Abstract

The self-assembly mechanisms of polyoxometalates (POMs) are still a matter of discussion owing to the difficult task of identifying all the chemical species and reactions involved. We present a new computational methodology that identifies the reaction mechanism for the formation of metal-oxide clusters and provides a speciation model from first-principles and in an automated manner. As a first example, we apply our method to the formation of octamolybdate. In our model, we include variables such as pH, temperature and ionic force because they have a determining effect on driving the reaction to a specific product. Making use of graphs, we set up and solved 2.8 × 10⁵ multi-species chemical equilibrium (MSCE) non-linear equations and found which set of reactions fitted best with the experimental data available. The agreement between computed and experimental speciation diagrams is excellent. Furthermore, we discovered a strong linear dependence between DFT and empirical formation constants, which opens the door for a systematic rescaling.

---

Introduction

The intimate mechanisms by which metal oxide clusters form are far from being well understood. This lack of knowledge is particularly relevant for the aqueous chemistry of group V and group VI cations, including V⁵⁺, Nb⁵⁺, Ta⁵⁺, Mo⁶⁺ and W⁶⁺, which are characterized by the growth of discrete anionic polynuclear clusters mostly known as polyoxometalates (POMs).¹ Although the first-ever characterized structure was synthesized by Berzelius almost two centuries ago,² POMs have not ceased to attract attention. As a matter of fact, they display a broad variety of present applications in catalysis,^3–11 nuclear reprocessing,^12,13 electro-chemistry¹⁴ and potential uses in information technologies,^15,16 medicine,^17–19 and energy.^20–22

The synthesis of POMs usually takes place by reacting the corresponding oxo-anion monomer, for instance [MoO₄]²⁻, with additional acids, bases or other salts, in aqueous solution where a plethora of hydrolysis, aggregation and condensation reactions triggers the formation of discrete clusters.²³ The experimental procedure might look straightforward yet the final result vastly depends on detailed control of a number of parameters: pH, temperature, concentrations, presence of addenda metals and/or counter-cations, crystallization conditions, just to mention a few.²⁴ The high sensitivity of the synthetic methods is related to the multiple complex equilibria between transient species that occur rapidly in solution, and that magically favors the prevalence of some building-blocks over others. However, neither the nucleation reaction pathways nor the nature of the building blocks can be controlled at will, and only in few cases the discovery of new POMs relays on rational automated approaches.²⁵

Mass-spectrometry has extensively proved to be an useful technique for identifying species in solution, and has been applied for detecting reaction intermediates, and also their fragmented products, in a short variety of cases: silicates,^26,27 vanadates,^28,29 tungstates^30,31 and molybdates.^32,33 Recently, kinetic investigations have proposed autocatalysis in the formation processes of giant molybdenum oxide clusters.³⁴ Complementarily, computational methods have also emerged as a crucial tool for studying species involved in elementary steps in the formation mechanisms of POMs.^35–40 However we notice that human-derived complex reaction mechanisms, even relying on first-principles methods, present their own shortcomings. In the first place, the analysis of multiple reaction pathways is cumbersome, slow, and mostly restricted to known, a priori expected chemical transformations. In the second place, even ab initio molecular dynamics simulations contain some bias because of the choice of conditions that drive simulations forward to a pre-determined end. In the case of metadynamics simulations, the choice of the collective variables may thus introduce a significant bias.

More importantly, since POMs nucleation processes are specially characterized for having multiple simultaneous coupled equilibria, a classical systematic exploration of such complex reactive systems, if feasible, would hardly provide new clues. A alternative new approach is needed to go one step further in the understanding of this reactivity. There is the need for a tool capable of predicting which species would form under any given experimental conditions, and answer questions as: which species would be the most abundant at a given pH? Or/and, which reaction mechanisms are operative to form a given product?

Here we present the first steps in this direction, beginning with the determination of a suitable speciation model for POMs in solution computationally and in an automated manner, that at the same time provides key information that permits identifying the underlying nucleation mechanisms. We define the speciation model as the set of species and the corresponding chemical equilibrium equations (multi-species chemical equilibrium, MSCE) which determine the concentration of each species as a function of pH. Indeed, pH is one of the most determining factors in controlling the growth processes of POMs. MSCE equations allow taking into account not only the pH but also other important factors (temperature, pressure, concentration, ionic force). The derived MSCE systems of equations are most frequently nonlinear thus they are solved numerically.^41,42 The analysis of the species and their relationships gathered from the speciation model are what define the nucleation mechanism. We have applied this new methodology to the growth process of octamolybdate [Mo₈O₂₆]⁴⁻.

Cruywagen et al.^43,44 determined experimentally the formation constants of several medium-sized polyoxomolybdates involved in the formation of octamolybdate [Mo₈O₂₆]⁴⁻. Further work has been done in that direction, including measurements that combine potentiometric⁴⁵ and spectroscopic^46,47 techniques. These sets of experimentally measured formation constants constitute the simplest speciation model, which includes very few species: monomer, heptamolybdate and octamolybdate only. Hence, we have estimated the accuracy of the new developed protocol based on these experimental data available.

The new strategy to tackle this problem starts by rationally guessing and processing molecular structures potentially involved in the nucleation process. As a matter of fact, Broadbelt et al. pioneered viewing molecular structures as molecular graphs, in which atoms and bonds are represented by nodes and edges, respectively.⁴⁸ Therefore, chemical reactions can be understood as morphological transformations between similar graphs, i.e., isomorphisms. Nonetheless, some heuristics need to be imposed (e.g., atom valences, reaction types, stoichiometric and/or charge balance) to cope with the huge amount of possible isomorphic relationships, so to construct a chemically meaningful reaction network. The availability of open-source libraries facilitates coding graphs,⁴⁹ as we can find several successful applications of chemical reactivity automated discovery applied to, for instance, Claisen condensation,⁵⁰ hydroformylation,^51,52 γ-ketohydroperoxide decomposition,⁵³ formose reaction⁵⁴ and isomerisation of allylic amines.⁵⁵ In the present work, we have developed graph-based algorithms that identify all possible chemical reactions within a set of molecular species, which are described as molecular graphs. Furthermore, the same code builds the corresponding reaction network, which in our formalism is a graph of graphs.

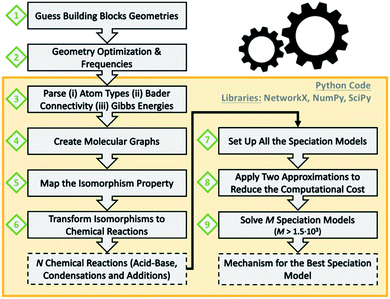
Scheme 1 summarizes the main steps that we followed as a data workflow: (1) prepare a collection of polyoxomolybdates Cartesian files (2) perform geometry optimizations and analytical frequencies; computational details in the ESI† (3) extract atom types, chemical connectivity and free energies from the output files (4) convert chemical molecules to molecular graphs (5) check which graphs are isomorphic (6) transform isomorphisms to chemical reactions; a collection of 72 acid–base, condensation and addition reactions is obtained (7) set up all the possible combinations of multi-species chemical equilibrium models (8) apply two approximations to decrease the computational cost seven orders of magnitude (9) solve 1620 speciation models for a broad range of pH; the best model provides the associated nucleation mechanism.

Scheme 1 Workflow of the current protocol for predicting metal oxide nucleation mechanisms. Orange box delimitates the tasks (bold boxes) performed with the developed python code. Output information is marked in dashed boxes.

Results and discussion

Dataset and molecular graphs

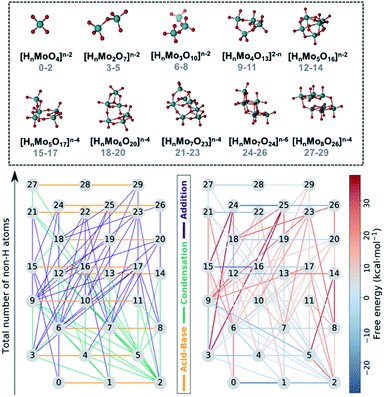
Fig. 1 collects the polyoxomolybdates species considered throughout this work which contain structures from one to eight metal centers at three possible protonation states ([H_mMo_nO_3n+1]^m−2, n = 1, 2, 3, 4, 5; [H_mMo_nO_3n+2]^m−4, n = 5, 6, 7, 8 and [H_mMo_nO_3n+3]^m−6, n = 7). The compounds with the general formula [H_mMo_nO_3n+1]^m−2 have been studied extensively because of their importance in the formation mechanism of the Lindqvist anion.⁴⁰ However, a laminar growth depicted with the formula [H_mMo_nO_3n+2]^m−4 is required for synthesizing the octamolybdate [H_mMo₈O₂₆]^m−4. Cruywagen et al. provided the formation constants of the [H_mMo₇O₂₄]^6−m and [H_mMo₈O₂₆]^4−m.^43,44 Hence, we have estimated the accuracy of the new developed protocol based on experimental data available. The geometries of all the species have been fully optimized using the DFT-based methods as described in the Computational details section. A dataset collection of the computational results is available in the ioChem-BD repository⁵⁶ and can be accessed via: DOI: 10.19061/iochem-bd-1-178.

Fig. 1 Top: Dataset of 30 polyoxomolybdates including the stoichiometries: [H_nMo_mO_3m+1]ⁿ⁻², [H_nMo_mO_3m+2]ⁿ⁻⁴ and [H_nMo_mO_3m+3]ⁿ⁻⁶, m = 1–8, n = 0, 1, 2. Indexes of each species from 0 to 29. Bottom: Reaction maps include the 72 chemical transformations considered in this work. Nodes (chemical species) sorted vertically according to their molecular complexity. Bottom left: Edges (reactions) colored by its type (orange: acid–base, green: condensation, violet: addition). Bottom right: Edges colored according their free reaction energies.

In first place, each chemical compound is converted to a molecular graph (G). To do so, atoms are transformed into nodes and chemical bonds are converted to edges. While the assignation of the nodes is straightforward, it is not exactly the case for the edges. Indeed, weak chemical bonds are hardly ever depicted in the connectivity of the molecule. While for alkaline-side polyoxometalates that might not be problem, polyoxomolybdates aggregate at low pH, which means that the species are protonated and hydrogen bonds have an important role in stabilizing negatively-charged species. In order to add these bonds to the connectivity of each molecule, we relied on the topological analysis of the electronic density developed by Bader in his Theory of Atoms in Molecules (AIM).⁵⁷ This methodology detected all covalent bonds and also hydrogen bonds interactions (see Fig. S1†), thus the connectivity matrix of each species is built automatically. Hence, all the identified bond critical points are converted to edges thus obtaining accurate molecular graphs.

Sampling chemical reactions

In the next step, we aim at obtaining all the possible chemical reactions by only providing the molecular graphs of our initial dataset as inputs. It is worth noting that converting a molecule to a graph involves an unequivocal simplification. Molecules are three-dimensional objects, whereas graphs do not retain any spatial information. Nonetheless, such transformation is done for the sake of profiting from the mathematical properties that graph theory offers. In this case, we are interested in relating molecules which could be potentially involved in a same chemical transformation. Therefore, the isomorphism property is an appropriate tool for such task. An isomorphism states that two graphs (G_i and G_j) will be isomorphic if either G_i contains the same set of nodes and edges than G_j or vice versa, i.e. two molecules might be related by a chemical reaction if they resemble somehow in their relative chemical connectivity.

Knowing all the existing isomorphisms is a prerequisite to determine all the possible chemical reactions unambiguously. However, a final adjustment must be made to convert an isomorphism to a chemical transformation. Isomorphic relationships do not fulfil the stoichiometric balance of any chemical transformation. Therefore, the difference of atoms between each pair of isomorphs provides the stoichiometry of the missing reactant.

In this way, we can convert each isomorphism to a chemical reaction by only adding the compound that is missing. For example, if the difference of atoms between two isomorphs is only one hydrogen atom, then the corresponding reaction would be an acid–base transformation. Analogously, if the difference is one molybdenum atom and three oxygen atoms, or one molybdenum atom and four oxygen atoms, then they would correspond to a condensation or an addition reaction, respectively.

All the chemical reactions that arise from the isomorphisms refinement are listed in the ESI† (including their respective computed free reaction energies) and presented as a reaction network in Fig. 1. The 30 compounds are distributed along the vertical axis according to their number of non-hydrogen atoms or molecular complexity. Consequently, molecules at the same height only differ by the state of protonation. There is a total of 72 chemical reactions which are classified in three main groups: acid–base, condensations, and additions. Horizontal connections refer to the 20 protonation reactions which play a key role in describing the acid–base properties, and which are in general thermodynamically favorable. On the other hand, vertical edges correspond to condensation and addition reactions that are responsible for the growth of the clusters. However, Fig. 1 does not provide a clear picture of which reactions are the most relevant for synthesizing the [H_mMo₈O₂₆]^4−m. Even using raw free reaction energies would not clarify the picture. Actually, POMs' chemistry is known to be very sensitive to other variables such as pH, concentration effects and ionic force. We have used speciation models to account for the aforementioned parameters when determining which is the preferred reaction pathway, instead. This approach has provided us with a more accurate idea of the nucleation mechanism.

Speciation models

Any speciation model consists of a system of n equations, where there are n − 1 equations describing chemical reactions plus one equation related to the overall mass balance. Since there are 30 compounds in our dataset, speciation models consist in systems of 30 equations. Furthermore, 21 out of the 30 equations are invariant, since one refers to the mass balance equation and the other 20 to acid–base reactions, as showed in Fig. 1. This leaves us with nine variable equations, which could be either condensation or addition reactions (see ESI† for more details). However, there are more than nine reactions in the isomorphic matrix. Therefore, we face an overdetermined system, where we have more equations than unknown variables. Since we do not know a priori which is the best combination of equations, we set and solve all the possibilities. Furthermore, in order to determine the accuracy of each model, we have relied on non-linear least squares to supply an estimated solution. Performing regression analysis of both results provide us with an indicator for choosing the best models (R²).

Unfortunately, the amount of combinations resulting from the binomial coefficient involves the resolution of an unfeasible amount of ∼10¹⁰ systems of non-linear equations (Fig. S2†). To overcome this technical problem, two major approximations have been made to reduce the computational cost. Firstly, disregarding all those condensation/addition reactions that do not present a monomer [H_mMoO₄]^m−2 as one of the reactants. Although such assumption involves a strong simplification, we do so based on the widely accepted idea that the monomer is found in relatively high concentrations in the reaction media.^43,45,58 Secondly, we have assumed that, there must be a representation of all species types for each combination as far as the number of metal atoms is concerned. In other words, the nine considered reactions have to contain dimers, trimers, tetramers, …. This condition ensured that we do not bias the results towards any specific compound. Such heuristics reduce the number of speciation models to 1.6 × 10³ (1620 actually), which is an affordable amount given the formidable challenge of solving systems of nonlinear equations for a wide range of concentrations.

Furthermore, some hyperparameters such as: temperature, pressure, ionic force, molybdenum and water concentration, acid–base hydron pair, pH grid and convergence threshold must be fixed as well. The temperature is set to 298 K at normal conditions. The total concentration of molybdenum and water are fixed to 0.005 M and 1 M respectively. Owing to the poor description that the H₃O⁺/H₂O pair offers, we employ the Zundel cation H₅O₂⁺ instead. Each speciation model is solved for an adequate range of pH using a small step of 0.2 pH units. The solution is accepted if Powell's optimizer⁵⁹ ends successfully and the average Root Mean Squared Error (RMSE) for all the pH range is smaller than 5 × 10⁻³ M (<10% error). In addition, the Davies equation is considered to account for the deviation from ideality of relatively high concentrated solutions.⁶⁰ Moreover, given the fact that the experimental data reported by Cruywagen et al. is expressed as the decimal logarithm of the formation constants (pK^Exp_f), we express our results in the same units. Thus, once the concentrations of all the species are known, the formation constants can be obtained straightforwardly (see ESI†).

Following the aforementioned parameters, we have solved the 1.6 × 10³ speciation models (over 2.8 × 10⁵ systems of non-linear equations) relying on a Python code developed in house. Given the huge amount of results, all of them are clustered and summarized in a box plot (Fig. 2). There is a notable variance in the pK^DFT_f values, especially for the largest compounds, yet the median values seem to increase in a systematic manner. Note that the seemingly linear trends from which the box plots are distributed is due to their general formula. Compounds with indexes from 0 to 14 correspond to [H_nMo_mO_3m+1]ⁿ⁻², from 15 to 23 including 27, 28 and 29 correspond to [H_nMo_mO_3m+2]ⁿ⁻⁴ and 24, 25 and 26 are defined by [H_nMo_mO_3m+3]ⁿ⁻⁶. The rather high absolute values for the formation constants foreshadow a mismatch respect to the experiments.

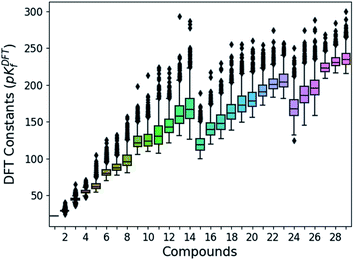Fig. 2 Box plots of the DFT formation constants (pK^DFT_f) for each compound (comprised between 1 to 29). Data obtained from the resolution of the 1620 speciation models.

In order to test the accuracy of the formation constants, we have plotted the speciation diagrams of the three best models according to their R². The results are presented in Fig. 3a–c where the vertical axis refers to the relative abundance and the horizontal axis to the pH scale. Three models (number 45, 450, and 453) are the most accurate out of the 1.6 × 10³ models, given their high correlation coefficients (0.9992, 0.9993 and 0.9993, respectively). Note that the associated formation constants are expressed as pK^DFT_f, since they are obtained by solving systems of non-linear equations using raw DFT reaction free energies. The three models predict the elevated concentration of [MoO₄]²⁻ at high pH which contrasts with the wide number of species at lower pH in the experimental speciation diagram in Fig. 3f. However, at more acidic pH, the discrepancy between Fig. 3a, b and c is more accentuated. In fact, there is a wide number of chemical species but most importantly, [Mo₂O₇]²⁻ and H₂Mo₄O₁₃ appears at significant concentrations. This fact is rather unusual since smaller clusters are very reactive intermediates which rapidly react to form more complex species. However, the most disconcerting feature is the pH scale of the DFT models, which is clearly overestimated when we compare it to the experimental results reported by Cruywagen (Fig. 3f). In addition, the speciation is not properly reproduced since [H₂Mo₇O₂₄]⁴⁻, [Mo₈O₂₆]⁴⁻, [HMo₈O₂₆]³⁻ do not appear in the DFT speciation diagrams. Therefore, we suspect that the main source of error arises from the very poor description of the pK_a acid/base constants. Indeed, it is well-documented that determining acidic dissociation constants using DFT calculations is rather troublesome. For example, an error of 1.36 kcal mol⁻¹ in the deprotonation Gibbs energy in implicit solvent causes an error of 1 pK_a unit.^61,62 In the next section we introduce a rescaling of the DFT energies so as to overcome this challenge and reduce the current gap between computational and experimental results.

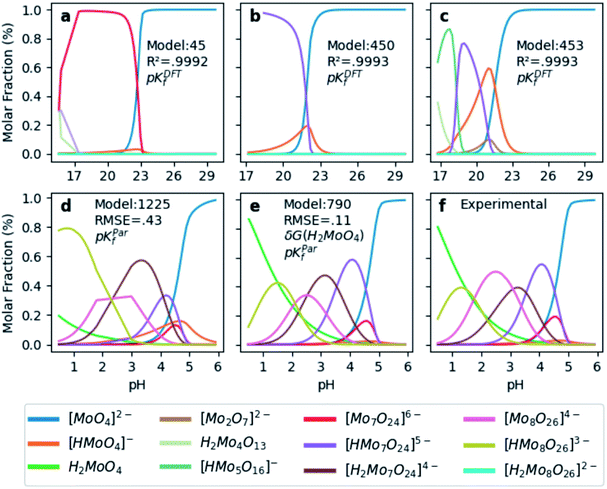Fig. 3 Speciation diagrams according to (a) pK^DFT_f model 45, (b) pK^DFT_f model 450, (c) pK^DFT_f model 453, (d) pK^Par_f model 1225, (e) pK^Par_f model 790 (f) pK^Exp_f (extracted from ref. 43). R² correspond to the correlation between Powell's and least squares solutions. Root Mean Squared Error (RMSE) between pK^Par_f and pK^Exp_f. δG(H₂MoO₄) stands for the ad hoc correction (−9.0 kcal mol⁻¹) applied to the free energy of the molybdic acid. Color legend at the bottom indicates the chemical compounds.

Rescaling of the DFT formation constants

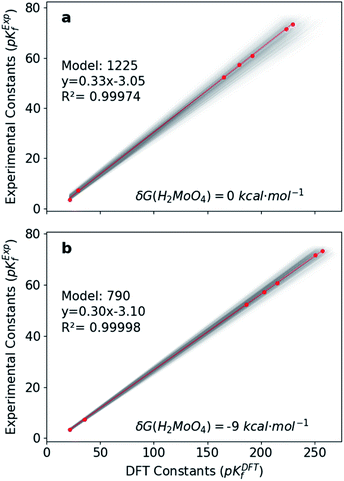
Hitherto, the present DFT energies fail to provide an appropriate description for the speciation diagram, as showed in Fig. 3a–c. Therefore, we believe that the origin of the unsatisfactory results was found in the poor description of the acid–base reactions. Considering that the aforementioned reactions are invariant for all the speciation models, a systematic error can be expected. Therefore, we have focused our attention on rescaling the raw pK^DFT_f values collected in Fig. 2.

Cruywagen determined the formation constants of [MoO₄]²⁻, [HMoO₄]⁻, H₂MoO₄, [Mo₇O₂₄]⁶⁻, [HMo₇O₂₄]⁵⁻, [Mo₇O₂₄]⁴⁻, [Mo₈O₂₆]⁴⁻ and [HMo₈O₂₆]³⁻ by potentiometry.⁴³ Thus, for these compounds already included in our dataset, we have compared their respective sets of pK^Exp_f and pK^DFT_f for each speciation model. We have found that there is a clear linear relationship between both sets as Fig. 4a demonstrates. Linear regressions of all 1.6 × 10³ MSCE models are plotted in a grey color scale according to their linear correlation coefficients. Thus, the lighter ones correspond to poorer linear fits and vice versa. The best linear regression is marked in red and corresponds to model 1225 (R² = 0.99974). Applying its linear equation y = 0.33x − 3.05, the set of pK^DFT_f is rescaled thus obtaining a new set of parametrized formation constants (labeled as pK^Par_f). In addition, we have verified that the linear trend, between pK^DFT_f and pK^Exp_f, is not only found for PBE but for other DFT functionals, as Fig. S4† shows. Next, we have plotted the corresponding speciation diagram using the pK^Par_f for the best fit (model 1225), in order to verify if any enhancement was achieved. Fig. 3d shows the new results as well as the RMSE between the set of pK^Par_f and the pK^Exp_f (0.48 pK_f units). The first enhancement concerns the pH scale since it is no longer overestimated as it is for the pK^DFT_f. Note that the scale has decreased ∼15 pH units, which is a large shift given that the units are logarithmic.

Fig. 4 Linear regressions between pK^Exp_fvs. pK^DFT_f for the 1620 models. Lines colored in grey scale according to the R² of the linear fit; best fit in red. (a) Without δG(H₂MoO₄) correction (b) with δG(H₂MoO₄) = −9 kcal mol⁻¹. Best model ID, linear equation and its R² value.

Furthermore, the general trends showed in Fig. 3f are fairly well-reproduced in Fig. 3d. However, the molar fraction of some species is noticeably different. For example, the concentration of [HMo₈O₂₆]³⁻ is much larger in model 1225 than in experiments. Fig. 3f proves that we have found a good enough speciation model for qualitative results, yet additional refinements must be performed in order to go a step further.

Although the speciation model in Fig. 3d already presents good agreement with the empirical data, we aim at achieving a quantitative prediction of the formation constants. Nonetheless, it is worth considering that reproducing pK_f has the added challenge of dealing with a maximization of the errors given the logarithmic nature of these units. The constraints which are imposed by the mass balance equation in the speciation models are an additional complication. Thus, a poor description on a single concentration causes further deviations, given that all the concentrations are interrelated by the mass balance equation.

In light of this, we analyzed Fig. 3d in detail to discern any possible source of errors. One striking difference between Fig. 3d and f is the high concentration of [HMoO₄]⁻, which has been reported to never reach a greater relative concentration of ∼30%.⁴³ Additionally, the concentration of H₂MoO₄ is lower than the experimental values, which might suggest a bad description of the following acid–base equilibrium: [HMoO₄]⁻ + H₅O₂⁺ → H₂MoO₄ + 2H₂O. This hypothesis is reinforced by the existing controversy involving the solution structure of molybdic acid.^63–65 In general terms, at low pH there is an expansion in the coordination sphere of the acid due to the coordination of two water molecules. Vilà-Nadal et al. reported that the six-coordinated molybdic acid MoO₂(OH)₂(H₂O)₂ was 6 kcal mol⁻¹ more stable than the four coordinated species MoO₂(OH)₂.³⁷ Thus, we have wondered how much the energy of single species could change the overall outcome of the speciation model. Consequently, we have adjusted the free energy of molybdic acid, expressed as δG(H₂MoO₄), for a range of values (comprised between 0 and −20 kcal mol⁻¹) to observe its effect on the calculation of the formation constants. According to Fig. S7,† pK^DFT_f are even in better agreement with experiments when an ad hoc correction of −9 kcal mol⁻¹ (δG) is applied (more details in the ESI†). Therefore, we have employed this correction to the free energy of molybdic acid and re-calculated all the 1.6 × 10³ speciation models. Following the same protocol, we have compared the pK^DFT_f to pK^Exp_f in order to find out the best linear fit to correct the overestimated pK^DFT_f values. Fig. 4b collects the new 1.6 × 10³ linear fits. The best linear regression corresponds now to model 790 (R² = 0.99998) and is highlighted in red. Note that Fig. 4b models present even a better linearity than the ones collected in Fig. 4a, as the correlation coefficient and the variance show. Therefore, from a mathematical point of view, we can state that the ad hoc correction has systematically improved the description of all the 1.6 × 10³ models.

Next, we have applied the linear scaling to generate the new set of pK^Par_f. These new formation constants values are used to plot the speciation diagram depicted in Fig. 3e. The agreement with experiments has significantly enhanced, as the lower RMSE of 0.11 pK_f units suggests. In fact, the concentration of [HMoO₄]⁻ is nearly negligible whereas the concentration of H₂MoO₄ has increased due to δG(H₂MoO₄) ad hoc correction. Furthermore, the description of [HMo₈O₂₆]³⁻ has also improved as a consequence of the mass-balance equation which interrelates all the species. Therefore, our DFT-derived speciation model can accurately predict the speciation diagram of octamolybdate.

Nucleation mechanism

Starting from the pK^DFT_f, we had a first picture of the relative abundances of all species in solution. However, the unsatisfactory estimation of the pK^Exp_f drove us to a linear parametrization based on the strong linearity between the pK^DFT_f and the experimental data.

Good results were obtained yet quantitatively unacceptable as the molybdic acid was poorly modeled. That is why an ad hoc correction on its free energy was applied and excellent results were obtained. With this knowledge in hand, we seek to transfer it to the initial reaction map (Fig. 1) in order to unveil the most relevant chemical paths.

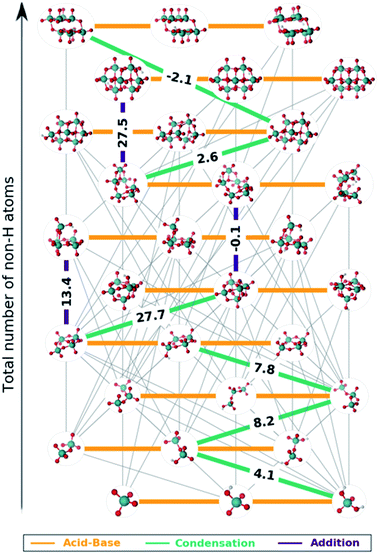
The set of reactions that define the best speciation model are summarized in the ESI† and depicted as a reaction map in Fig. 5. The 29 chemical equations present in speciation model 790 are colored according to their reaction type: orange, green and indigo stand for acid–base, condensation and addition reactions respectively. Moreover, the left out reactions are marked in grey with a lower weight. On the one hand, all the acid–base equilibria are highlighted, since these reactions are present in every speciation model. Therefore, each molybdenum cluster can be found in any protonation state (horizontal axis) depending on the pH at which the reaction takes place. On the other hand, reactions involving the growth of the clusters are unique for each speciation model. Hence, we propose that the nine selected reactions marked in Fig. 5 are the main chemical transformations for reaching octamolybdate, thus the nucleation mechanism.

Fig. 5 Formation mechanism of octamolybdate according to speciation model 790. Connections in grey, orange, green and violet correspond to disregarded reactions, acid–base, condensation and addition reactions, respectively. Free energies of condensation and addition reactions are depicted in the edges in kcal mol⁻¹.

Most of the reactions that are present in the formation of octamolybdate are found to be slightly endergonic. This is so because molybdic acid is involved as a reactant in several reactions and its free energy has been stabilized by the ad hoc correction. Bearing this in mind, the nucleation mechanism starts with the condensation between H₂MoO₄ and [HMoO₄]⁻ to yield [HMo₂O₇]⁻ with a ΔG_reac of 4.08 kcal mol⁻¹. Next, [HMo₂O₇]⁻ reacts with another molybdic acid molecule to generate [Mo₃O₁₀]²⁻ with an endergonic reaction free energy (ΔG_reac of 8.1 kcal mol⁻¹). The nucleation reaction proceeds through a third condensation reaction between [Mo₃O₁₀]²⁻ and H₂MoO₄ yielding [Mo₄O₁₃]²⁻ (ΔG_reac 7.8 kcal mol⁻¹). Hitherto, the growth up to four metal atoms followed an slightly uphill path. The tetramolybdate can either condensate with H₂MoO₄ to trigger the formation of the [Mo₅O₁₆]²⁻ (ΔG_reac +27.7 kcal mol⁻¹) or to aggregate with [HMoO₄]⁻ to form [HMo₅O₁₇]³⁻ (ΔG_reac 13.4 kcal mol⁻¹). Both processes are strongly endergonic, but free reaction energies do not account for concentration effects or pH, that is why speciation models give a more accurate picture of the chemical processes. In addition, [HMo₅O₁₇]³⁻ and [Mo₅O₁₆]²⁻ can be regarded as unstable intermediates which would rapidly be converted to larger clusters. Actually, [Mo₅O₁₆]²⁻ reacts with [HMoO₄]⁻ to yield [Mo₆O₂₀]⁴⁻ through an addition reaction with a ΔG_reac close to equilibrium (−0.1 kcal mol⁻¹). A water condensation takes place between [Mo₆O₂₀]⁴⁻ and H₂MoO₄ to give the heptamer [Mo₇O₂₃]⁴⁻ as a product with a resulting ΔG_reac of 2.6 kcal mol⁻¹. The formation of [H_nMo₇O₂₄]ⁿ⁻⁶ is endergonic (ΔG_reac of 27.5 kcal mol⁻¹) which agrees with preceding studies.⁵⁸ [Mo₇O₂₄]⁶⁻, [HMo₇O₂₄]⁵⁻ and [H₂Mo₇O₂₄]⁴⁻ are present in the experimental speciation diagrams (Fig. 4f) thus emphasizing the importance of accounting for concentration effects and pH. Finally, the octamolybdate [Mo₈O₂₆]⁴⁻ is exothermically formed (−2.1 kcal mol⁻¹) as a result of the condensation reaction between [Mo₇O₂₃]⁴⁻ and H₂MoO₄.

Conclusions

We have developed a new methodology that allows unveiling the nucleation mechanism of metal-oxo clusters in an automated manner. We guessed a set of chemical species, and by making use of ab initio generated molecular graphs, the chemical reactions that connect the species (including acid–base, condensations and additions) were identified. To do so, we took advantage of morphological properties of graphs. In order to provide a realistic picture of the nucleation mechanism, we have considered not only the free reaction energy but also the pH, ionic force, temperature and concentration effects. We have formulated multi-species chemical equilibrium equations which involves solving over 2.8 × 10⁵ non-linear systems equations. Furthermore, we have applied a linear rescaling with experimental data and an ad hoc correction to the energy of a single species. The final outcome is a speciation model that reproduces fairly well the experimental data available for octamolybdate β-[Mo₈O₂₆]⁴⁻. Finally, the chemical reactions included in the speciation model define the significant steps in the growth process, thus the nucleation mechanism.

Although automated, note that our protocol is not fully ab initio since it required corrections using experimental data. The excellent linear fit between experimental and DFT calculated formation constants also holds for the several DFT methods we have tested (see Fig. S4†). We conclude that: (i) there is a systematic error in the calculated pK_a values, which is easy to solve and to transfer to other systems/methods; (ii) those corrections would require validation when applied to other systems. Nonetheless, methods for calculating the pK_a of organic molecules require some fitting as well.

Overall, our POMSimulator offers a systematic and automatic way for predicting the nucleation mechanism of medium size polyoxometalates. Speciation diagrams strongly depend on the ionic force. This dependence can be readily investigated without additional experiments, as Fig. S5† shows. Actually, at high ionic force values, our simulator predicts heptamolybdate as the most abundant species at pH = 4. This is the kind of questions that our simulator can answer. We hope that these and future results will stimulate further experiments.

Further work for extending this protocol to larger clusters and verifying its applicability to other kinds of compounds and chemical transformations is in progress. The biggest challenge that we face is to include additional cations and/or anions in our model. This amplifies the problem. In POMs chemistry, those additives are incorporated in the POM structure, so we expect that our method will shade light into the formation mechanisms of such complex structures.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the ICIQ Foundation, CERCA Program and AGAUR (grant 2017SGR00290) of the Generalitat de Catalunya, and the Spanish Ministerio de Ciencia, Innovacion y Universidades through project CTQ2017-88777-R for financial support.

Notes and references

1. M. Pope and A. Müller, Polyoxometalate Chemistry From Topology via Self-Assembly to Applications, 2001.
2. J. J. Berzelius, Ann. Phys., 1826, 82, 369–392.
3. S. S. Wang and G. Y. Yang, Chem. Rev., 2015, 115, 4893–4962.
4. H. M. Qasim, W. W. Ayass, P. Donfack, A. S. Mougharbel, S. Bhattacharya, T. Nisar, T. Balster, A. Solé-Daura, I. Römer, J. Goura, A. Materny, V. Wagner, J. M. Poblet, B. S. Bassil and U. Kortz, Inorg. Chem., 2019, 58, 11300–11307.
5. I. Julian, J. L. Hueso, N. Lara, A. Solé-Daurá, J. M. Poblet, S. G. Mitchell, R. Mallada and J. Santamaría, Catal. Sci. Technol., 2019, 9, 5927–5942.
6. T. J. Wilke and M. A. Barteau, J. Catal., 2020, 382, 286–294.
7. M. Bugnola, K. Shen, E. Haviv and R. Neumann, ACS Catal., 2020, 10, 4227–4237.
8. M. Bonchio, Z. Syrgiannis, M. Burian, N. Marino, E. Pizzolato, K. Dirian, F. Rigodanza, G. A. Volpato, G. La Ganga, N. Demitri, S. Berardi, H. Amenitsch, D. M. Guldi, S. Caramori, C. A. Bignozzi, A. Sartorel and M. Prato, Nat. Chem., 2019, 11, 146–153.
9. P. Gobbo, L. Tian, B. V. V. S. Pavan Kumar, S. Turvey, M. Cattelan, A. J. Patil, M. Carraro, M. Bonchio and S. Mann, Nat. Commun., 2020, 11, 41.
10. R. Liu, K. Cao, A. H. Clark, P. Lu, M. Anjass, J. Biskupek, U. Kaiser, G. Zhang and C. Streb, Chem. Sci., 2020, 11, 1043–1051.
11. M. Blasco-Ahicart, J. Soriano-Lopez, J. J. Carbo, J. M. Poblet and J. R. Galan-Mascaros, Nat. Chem., 2018, 10, 24–30.
12. M. Nyman and P. C. Burns, Chem. Soc. Rev., 2012, 41, 7354–7367.
13. T. L. Spano, A. Simonetti, L. Corcoran, P. A. Smith, S. R. Lewis and P. C. Burns, J. Nucl. Mater., 2019, 518, 149–161.
14. J. C. Kemmegne-Mbouguen, S. Floquet, D. Zang, A. Bonnefont, L. Ruhlmann, C. Simonnet-Jégat, X. López, M. Haouas and E. Cadot, New J. Chem., 2019, 43, 1146–1155.
15. M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351.
16. N. I. Gumerova, A. Roller, G. Giester, J. Krzystek, J. Cano and A. Rompel, J. Am. Chem. Soc., 2020, 142, 3336–3339.
17. A. Bijelic, M. Aureliano and A. Rompel, Chem. Commun., 2018, 54, 1153–1169.
18. T. J. Paul, T. N. Parac-Vogt, D. Quiñonero and R. Prabhakar, J. Phys. Chem. B, 2018, 122, 7219–7232.
19. A. Bijelic, M. Aureliano and A. Rompel, Angew. Chem., Int. Ed., 2019, 58, 2980–2999.
20. H. Wang, S. Hamanaka, Y. Nishimoto, S. Irle, T. Yokoyama, H. Yoshikawa and K. Awaga, J. Am. Chem. Soc., 2012, 134, 4918–4924.
21. J. J. Chen, J. C. Ye, X. G. Zhang, M. D. Symes, S. C. Fan, D. L. Long, M. Sen Zheng, D. Y. Wu, L. Cronin and Q. F. Dong, Adv. Energy Mater., 2018, 8, 1–6.
22. H. Y. Wu, H. Hu, C. Qin, P. Huang, X. L. Wang and Z. M. Su, Chem. Commun., 2020, 56, 2403–2406.
23. D. L. Long, R. Tsunashima and L. Cronin, Angew. Chem., Int. Ed., 2010, 49, 1736–1758.
24. C. P. Pradeep, D. L. Long and L. Cronin, Dalton Trans., 2010, 39, 9443–9457.
25. V. Duros, J. Grizou, W. Xuan, Z. Hosni, D. L. Long, H. N. Miras and L. Cronin, Angew. Chem., Int. Ed., 2017, 56, 10815–10820.
26. P. Bussian, F. Sobott, B. Brutschy, W. Schrader and F. Schüth, Angew. Chem., Int. Ed., 2000, 39, 3901–3905.
27. S. A. Pelster, W. Schrader and F. Schüth, J. Am. Chem. Soc., 2006, 128, 4310–4317.
28. D. K. Walanda, R. C. Burns, G. A. Lawrance and E. I. Von Nagy-Felsobuki, Inorg. Chem. Commun., 1999, 2, 487–489.
29. M. Wendt, U. Warzok, C. Näther, J. Van Leusen, P. Kögerler, C. A. Schalley and W. Bensch, Chem. Sci., 2016, 7, 2684–2694.
30. H. N. Miras, E. F. Wilson and L. Cronin, Chem. Commun., 2009, 1297.
31. R. S. Winter, J. M. Cameron and L. Cronin, J. Am. Chem. Soc., 2014, 136, 12753–12761.
32. E. F. Wilson, H. N. Miras, M. H. Rosnes and L. Cronin, Angew. Chem., Int. Ed., 2011, 50, 3720–3724.
33. I. Nakamura, H. N. Miras, A. Fujiwara, M. Fujibayashi, Y. F. Song, L. Cronin and R. Tsunashima, J. Am. Chem. Soc., 2015, 137, 6524–6530.
34. H. N. Miras, C. Mathis, W. Xuan, D.-L. Long, R. Pow and L. Cronin, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 10699–10705.
35. L. Vilà-Nadal, A. Rodríguez-Fortea and J. M. Poblet, Eur. J. Inorg. Chem., 2009, 5125–5133.
36. L. Vilà-Nadal, A. Rodríguez-Fortea, L. K. Yan, E. F. Wilson, L. Cronin and J. M. Poblet, Angew. Chem., Int. Ed., 2009, 48, 5452–5456.
37. L. Vilà-Nadal, E. F. Wilson, H. N. Miras, A. Rodríguez-Fortea, L. Cronin and J. M. Poblet, Inorg. Chem., 2011, 50, 7811–7819.
38. L. Vilà-Nadal, S. G. Mitchell, A. Rodríguez-Fortea, H. N. Miras, L. Cronin and J. M. Poblet, Phys. Chem. Chem. Phys., 2011, 13, 20136–20145.
39. J. M. Cameron, L. Vilà-Nadal, R. S. Winter, F. Iijima, J. C. Murillo, A. Rodríguez-Fortea, H. Oshio, J. M. Poblet and L. Cronin, J. Am. Chem. Soc., 2016, 138, 8765–8773.
40. Z. L. Lang, W. Guan, L. K. Yan, S. Z. Wen, Z. M. Su and L. Z. Hao, Dalton Trans., 2012, 41, 11361–11368.
41. P. B. A. Blomberg and P. S. Koukkari, Comput. Chem. Eng., 2011, 35, 1238–1250.
42. J. M. Paz-García, B. Johannesson, L. M. Ottosen, A. B. Ribeiro and J. M. Rodríguez-Maroto, Comput. Chem. Eng., 2013, 58, 135–143.
43. J. J. Cruywagen, Adv. Inorg. Chem., 1999, 49, 127–182.
44. J. J. Cruywagen, A. G. Draaijer, J. B. B. Heyns and E. A. Rohwer, Inorg. Chim. Acta, 2002, 331, 322–329.
45. J. Torres, L. Gonzatto, G. Peinado, C. Kremer and E. Kremer, J. Solution Chem., 2014, 43, 1687–1700.
46. A. Davantès and G. Lefèvre, J. Phys. Chem. A, 2013, 117, 12922–12929.
47. F. Crea, C. De Stefano, A. Irto, D. Milea, A. Pettignano and S. Sammartano, J. Mol. Liq., 2017, 229, 15–26.
48. L. J. Broadbelt, S. M. Stark and M. T. Klein, Ind. Eng. Chem. Res., 1994, 33, 790–799.
49. A. A. Hagberg, D. A. Schult and P. J. Swart, Proc. 7th Python Sci. Conf., 2008, pp. 11–15.
50. Y. Kim, J. W. Kim, Z. Kim and W. Y. Kim, Chem. Sci., 2018, 9, 825–835.
51. S. Habershon, J. Chem. Theory Comput., 2016, 12, 1786–1798.
52. J. A. Varela, S. A. Vázquez and E. Martínez-Núñez, Chem. Sci., 2017, 8, 3843–3851.
53. C. A. Grambow, A. Jamal, Y. P. Li, W. H. Green, J. Zádor and Y. V. Suleimanov, J. Am. Chem. Soc., 2018, 140, 1035–1048.
54. A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1–20.
55. T. Yoshimura, S. Maeda, T. Taketsugu, M. Sawamura, K. Morokuma and S. Mori, Chem. Sci., 2017, 8, 4475–4488.
56. M. Álvarez-Moreno, C. De Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, J. Chem. Inf. Model., 2015, 55, 95–103.
57. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
58. F. Steffler, G. F. de Lima and H. A. Duarte, Chem. Phys. Lett., 2017, 669, 104–109.
59. M. J. D. Powell, Comput. J., 1964, 7, 155.
60. C. W. Davies, Ion Association, Butterworths, London, 1962.
61. K. S. Alongi and G. C. Shields, Annu. Rep. Comput. Chem., 2010, 6, 113–138.
62. P. G. Seybold and G. C. Shields, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 290–297.
63. O. F. Oyerinde, C. L. Weeks, A. D. Anbar and T. G. Spiro, Inorg. Chim. Acta, 2008, 361, 1000–1007.
64. X. Liu, J. Cheng, M. Sprik and X. Lu, J. Phys. Chem. Lett., 2013, 4, 2926–2930.
65. N. Zhang, E. Königsberger, S. Duan, K. Lin, H. Yi, D. Zeng, Z. Zhao and G. Hefter, J. Phys. Chem. B, 2019, 123, 3304–3311.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details, full list of chemical reactions, speciation models and formation constants definitions, plus additional data. See DOI: 10.1039/d0sc03530k

---