Crystallographic characterization of the metal–organic framework Fe₂(bdp)₃ upon reductive cation insertion

Abstract

Precisely locating extra-framework cations in anionic metal–organic framework compounds remains a long-standing, yet crucial, challenge for elucidating structure–performance relationships in functional materials. Single-crystal X-ray diffraction is one of the most powerful approaches for this task, but single crystals of frameworks often degrade when subjected to post-synthetic metalation or reduction. Here, we demonstrate the growth of sizable single crystals of the robust metal–organic framework Fe₂(bdp)₃ (bdp²⁻ = benzene-1,4-dipyrazolate) and employ single-crystal-to-single-crystal chemical reductions to access the solvated framework materials A₂Fe₂(bdp)₃·yTHF (A = Li⁺, Na⁺, K⁺). X-ray diffraction analysis of the sodium and potassium congeners reveals that the cations are located near the center of the triangular framework channels and are stabilized by weak cation–π interactions with the framework ligands. Freeze-drying with benzene enables isolation of activated single crystals of Na_0.5Fe₂(bdp)₃ and Li₂Fe₂(bdp)₃ and the first structural characterization of activated metal–organic frameworks wherein extra-framework alkali metal cations are also structurally located. Comparison of the solvated and activated sodium-containing structures reveals that the cation positions differ in the two materials, likely due to cation migration that occurs upon solvent removal to maximize stabilizing cation–π interactions. Hydrogen adsorption data indicate that these cation–framework interactions are sufficient to diminish the effective cationic charge, leading to little or no enhancement in gas uptake relative to Fe₂(bdp)₃. In contrast, Mg_0.85Fe₂(bdp)₃ exhibits enhanced H₂ affinity and capacity over the non-reduced parent material. This observation shows that increasing the charge density of the pore-residing cation serves to compensate for charge dampening effects resulting from cation–framework interactions and thereby promotes stronger cation–H₂ interactions.

---

Introduction

Porous anionic framework materials feature a host lattice with an overall anionic charge that is charge-balanced by interstitial cations. These materials have been investigated for a number of potential applications, including electrochemical energy storage,^1–5 water remediation,^6,7 and gas storage and separations.^8–10 Importantly, interactions between cations and the framework lattice dictate the functional performance of a given material. For example, strong cation–framework interactions can reduce mobility in single-ion conductors¹¹ or diminish the effective positive charge of cationic binding sites in gas storage media.¹² Accordingly, the unambiguous identification of cation positions and characterization of cation–framework interactions is crucial for developing structure–function relationships that will guide the design of improved anionic framework materials for practical applications.

Due to their large pores and vast synthetic tunability, metal–organic frameworks represent a promising template for the synthesis of anionic materials with structurally defined, weakly coordinated cations.^13–15 Thus far, crystallographic location of these charge-balancing cations has been limited to various bulky alkylammonium ions^16–20 and cobaltocenium,²¹ with only a few examples of monoatomic cations being structurally characterized.^22–25 Interestingly, certain framework materials containing small, charge-dense monoatomic cations have been found to exhibit enhanced gas uptake and binding relative to their parent materials,^20,22–27 but these interactions are much weaker than those characterized in zeolites containing the same cations.^{9,10,24,28–31} Therefore, more precise information regarding the local structure of extra-framework cations is needed to fully understand the adsorption properties of anionic metal–organic frameworks.

Structural characterization of activated anionic frameworks is particularly crucial, as migration of extra-framework cations following solvent removal can drastically change the chemical environment and thus the adsorption properties of the material. However, to the best of our knowledge, there are no reports of activated metal–organic framework structures containing alkali metal cations in the pores, motivating the study of robust frameworks that can withstand harsh metalation and activation conditions while maintaining single crystallinity. The principal challenge here lies in identifying or designing frameworks that can undergo chemical reduction without loss of crystallinity. Toward this end, we identified the robust metal–organic framework Fe₂(bdp)₃ ³² (bdp²⁻ = 1,4-benzenedipyrazolate) as a suitable platform. The structure of this material was previously determined from powder X-ray diffraction data³² and features triangular channels with vertices comprising chains of octahedral iron centers coordinated by pyrazolate linkers. In addition to its enhanced chemical and thermal stability relative to metal–carboxylate frameworks,^33,34 powder X-ray diffraction has shown that this material undergoes topotactic insertion of potassium ions upon chemical reduction.³⁵ While the electronic properties of the reduced framework were previously characterized, structural changes and the position of the cations within the pore have not been studied.

Herein, we report the first synthesis and detailed crystallographic characterization of single crystals of Fe₂(bdp)₃ and reduced, alkali metal cation-containing analogues of the type A_xFe₂(bdp)₃ (A = Li⁺, Na⁺, K⁺). Data obtained for solvated and activated single crystals of the reduced material suggest that cation migration occurs upon solvent removal to maximize stabilizing electrostatic interactions with charge-dense regions of the framework, resulting in partial reduction of the cation charge densities, as suggested by hydrogen adsorption data. We also prepare the novel magnesium-inserted framework Mg_0.85Fe₂(bdp)₃, which exhibits a higher affinity for H₂, indicating that increased cation charge density can promote stronger cation–adsorbate interactions, despite shielding exerted by the pore walls.

Results and discussion

Growth of single crystals and X-ray diffraction analysis of solvated Fe₂(bdp)₃ and A₂Fe₂(bdp)₃

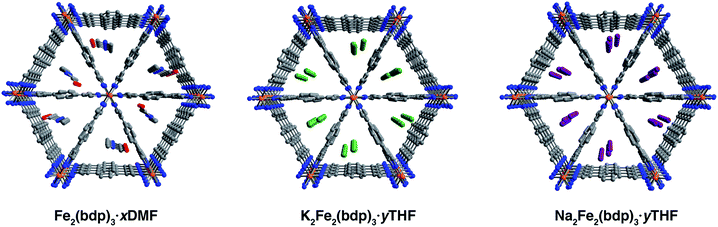
Single crystals of Fe₂(bdp)₃ were prepared by adapting the previously reported method for the microcrystalline powder³² through the addition of an acidic modulator to increase crystallite size. The reaction of Fe(acac)₃ with H₂(bdp) and acetylacetone in N,N-dimethylformamide (DMF) yielded dark yellow, acicular crystals with typical lengths ranging from 28 to 84 μm (Fig. S1‡). In some batches, crystals were also isolated with lengths up to 500 μm, although they diffracted with poor resolution. Single-crystal X-ray diffraction analysis revealed that DMF-solvated Fe₂(bdp)₃ crystallizes in the orthorhombic space group Fddd and features triangular pores occupied by DMF molecules disordered over two positions (Fig. 1, left and S10‡). The asymmetric unit contains one iron center and two crystallographically distinct bdp²⁻ linkers. The single-crystal unit cell parameters agree well with those obtained from refinement of powder X-ray diffraction data³² (Table S2‡), with minor differences attributed to the different data collection temperatures (100 and 298 K, respectively). In subsequent single-crystal reduction reactions, tetrahydrofuran (THF)-solvated materials were employed (see ESI‡), owing to the reactivity of DMF with the reducing naphthalenide salts.

Fig. 1 Single-crystal X-ray structures of DMF-solvated Fe₂(bdp)₃ (left), THF-solvated K₂Fe₂(bdp)₃ (middle), and THF-solvated Na₂Fe₂(bdp)₃ (right). In the structure of Fe₂(bdp)₃·xDMF, the DMF molecules were found to be disordered over two locations due to a two-fold axis along c, but only one set of molecules is shown here for clarity. In the structures of A₂Fe₂(bdp)₃·yTHF, the cations are disordered over three unique positions as shown. Two of the cation locations are duplicated by symmetry and are not shown for clarity. Orange, green, purple, red, blue, and gray spheres represent Fe, K, Na, O, N, and C atoms, respectively; H atoms are omitted for clarity.

Single-crystal-to-single-crystal chemical reductions were carried out using lithium, sodium, or potassium naphthalenide to access the fully reduced framework materials A₂Fe₂(bdp)₃ (A = Li⁺, Na⁺, K⁺, see the ESI‡ for full details). Similar to the reported procedure for the reduction of microcrystalline Fe₂(bdp)₃,³⁵ solutions of Na(C₁₀H₈) or K(C₁₀H₈) in THF were slowly added to crystals of Fe₂(bdp)₃ suspended in THF. In both cases, naphthalenide was added in excess of one equiv. per iron center to account for incomplete solvent exchange and formula unit uncertainty. Storage of these suspensions for one to two months yielded single crystals of A₂Fe₂(bdp)₃·yTHF. In the case of lithium naphthalenide, direct reduction with excess reagent did not afford reduced single crystals suitable for diffraction. Instead, Li₂Fe₂(bdp)₃·yTHF was prepared by suspending crystals of Fe₂(bdp)₃ on a fritted filter within a vial (see Fig. S2‡) containing a slurry of microcrystalline Fe₂(bdp)₃ stirring with lithium naphthalenide in THF. This approach enabled isolation of single crystals of Li₂Fe₂(bdp)₃·yTHF over the course of two to four weeks.

The compounds A₂Fe₂(bdp)₃·yTHF crystallize in the space group Fddd with a framework structure consistent with that of the neutral parent material (Fig. 1). Notably, such topotactic transformations in porous metal–organic materials are rare, particularly when they involve the use of strong chemical reductants.^36,37 While it was not possible to unequivocally locate and refine THF molecules in the difference Fourier maps, their presence is supported by thermogravimetric analysis data (see Fig. S22‡). The solvent present in the pores is highly disordered, leading to very diffuse electron density, which does not contribute significantly to the occupancies of the cations (see the ESI‡ for a discussion regarding occupancies). Changes in the unit cell dimensions upon reduction are minimal (Table S1‡), likely due to partial delocalization of the added electrons, and are consistent with powder diffraction data obtained for the reduced materials in microcrystalline powder form (Table S2‡). A slight increase in the unit cell volume occurs for all reduced frameworks, which can be ascribed in part to the larger radius of iron(II) relative to iron(III). Surprisingly, the Fe–N distances are similar between the neutral and reduced single-crystal frameworks, ranging from 1.940(4) to 1.949(3) Å. Given that the ionic radius of low-spin iron(III) should be substantially smaller than that of high-spin iron(II),^38–40 this result is attributed to the mixed valency and electronic delocalization in these materials, as has been discussed previously.³⁵

It was possible to locate the Na⁺ and K⁺ cations definitively in the difference Fourier maps of the corresponding reduced structures as the strongest, non-framework electron density peaks. Both structures were found to have some or all cation electron density located at a special position, with any remaining electron density at secondary general positions (see Table S3‡). The secondary sites all reside near a two-fold axis along c (perpendicular to the channel direction along a) and are therefore replicated by symmetry. In the single-crystal structure of K₂Fe₂(bdp)₃·yTHF, the potassium cation is disordered over three positions and is located near the center of the triangular pores (Fig. 1, middle). The chemical occupancy of the potassium cation positions was refined to be 102(2)%. Similar to in K₂Fe₂(bdp)₃·yTHF, the sodium cation within Na₂Fe₂(bdp)₃·yTHF was found to be disordered over three positions (Fig. 1, right), with a significant percentage of the disorder represented by a single ellipsoid near the center of the framework channel. The chemical occupancy of Na⁺ was refined to be 103(3)%. Preliminary refinement of Li₂Fe₂(bdp)₃·yTHF revealed that the Li⁺ cations are positioned closer to the corners of the triangular pores, likely due to their smaller size and ability to fit in tighter, more stabilizing spaces within the framework relative to Na⁺ and K⁺. However, the low electron count of Li⁺ made it impossible to unambiguously differentiate the cation positions from any diffuse solvent electron density. Indeed, crystallographic location of Li⁺ sites in metal–organic frameworks is challenging, and has thus far been limited to structures wherein the lithium cations are either anchored to the framework by chelating carboxylate groups²⁵ or are in close proximity to oxygen atoms of metal nodes and guest H₂O molecules in the pores.²² Nevertheless, we were able to determine the structure of activated Li₂Fe₂(bdp)₃, as discussed in the next section.

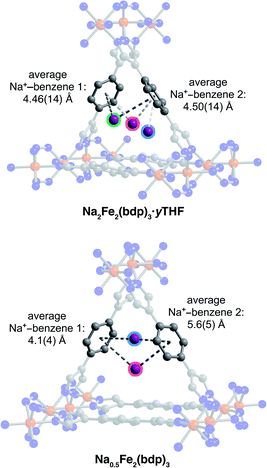
Close inspection of the structures of solvated K₂Fe₂(bdp)₃ and Na₂Fe₂(bdp)₃ reveals a number of potential stabilizing interactions between the ions and the framework scaffold, including van der Waals interactions with the pore edges and weak cation–π interactions with the benzene rings—and to a lesser extent with the pyrazolates—of the bdp²⁻ linkers. Cation–π interactions are prevalent in nature, particularly in protein structures, and have also been observed and exploited in synthetic molecular and supramolecular systems.^41–44 Typically, the affinity of a cation for an aromatic ring increases with the cation charge density, and a greater affinity is associated with shorter interaction distances.⁴⁵ We estimated the strength of all possible cation–π interactions by measuring the distances between each disordered cation position and the centroids of the benzene and pyrazolate rings. A weighted average of these cation–centroid distances was then calculated based on the crystallographic occupancies of the disordered cations to generate representative cation–π distances for K₂Fe₂(bdp)₃·yTHF and Na₂Fe₂(bdp)₃·yTHF (Table 1). Contrary to what would be expected based on charge density differences between Na⁺ and K⁺, one of the potassium–benzene distances measured for K₂Fe₂(bdp)₃·yTHF is shorter than the corresponding sodium–benzene distance in Na₂Fe₂(bdp)₃·yTHF. The cation–benzene distances in both structures are significantly longer than those observed in the gas phase for alkali metal cation–benzene interactions.⁴⁶ This difference is likely a result of solvation effects in the framework structures; intermediating solvent molecules could occlude the cations from the linker aromatic regions and potential solvent coordination to the cations would also diminish their effective charge. Both of these effects would reduce the strength and specificity of any cation–π interactions. Indeed, calculations have suggested that the introduction of water molecules results in lengthening of cation–π distances.^47,48

Table 1 Weighted average of A–centroid distances (Å) in solvated A₂Fe₂(bdp)₃ (A = Na⁺, K⁺) and activated A_xFe₂(bdp)₃ (A = Li⁺, Na⁺; x = 2 and 0.5, respectively). The benzene rings are numbered as illustrated in Fig. 2; the pyrazolates bonded to these benzene rings follow the same numbering scheme. See Fig. S11 for an alternative depiction

	Benzene 1	Benzene 2	Pyrazolate 1	Pyrazolate 2
a The individual occupancies of disordered Na^+ in this structure are low, 11.3% and 13.3%, and their relatively large associated errors of 1.5% and 0.9% contribute to the large overall error associated with the distances for this structure. See Table S4 for the individual cation–centroid distances, occupancies, and errors for each disordered position. b The values listed for this structure correspond to the actual distances, not weighted averages, as only one lithium site was found.
K2Fe2(bdp)3 (solvated)	4.13(11)	4.68(12)	5.23(14)	6.12(16)
Na2Fe2(bdp)3 (solvated)	4.46(14)	4.50(14)	5.16(17)	6.2(2)
Na0.5Fe2(bdp)3 (activated)^a	4.1(4)	5.6(5)	4.7(4)	6.4(6)
Li2Fe2(bdp)3 (activated)^b	3.86(2)	5.26(3)	5.60(1)	6.65(2)

---

Activation and single-crystal X-ray diffraction analysis of A_xFe₂(bdp)₃

Single crystals selected for activation and crystallographic characterization were obtained from the same batch of crystals used to determine the structures of A₂Fe₂(bdp)₃·yTHF. Initial attempts at activation under reduced pressure at room temperature resulted in crystal degradation; therefore, crystals were instead activated by freeze-drying with benzene to preserve their crystallinity (see ESI‡ for details).⁴⁹ Single-crystal X-ray diffraction characterization of the corresponding crystals enabled determination of the structures of activated Na_0.5Fe₂(bdp)₃ (Fig. 2, lower) and Li₂Fe₂(bdp)₃ (Fig. 3). To the best of our knowledge, these are the first single-crystal structures of activated metal–organic framework materials in which extra-framework alkali metal cations have been located within the pores. Attempts to characterize the activated, potassium-inserted materials structurally are ongoing.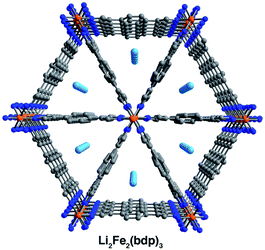

Fig. 2 Single-crystal X-ray structures of Na₂Fe₂(bdp)₃·yTHF (top) and activated Na_0.5Fe₂(bdp)₃ (bottom), highlighting the interactions between the inserted cations and the benzene rings of the ligands. The disordered sites of Na⁺ are highlighted in red, blue, and green. Orange, purple, blue, and gray spheres represent Fe, Na, N, and C atoms, respectively; H atoms and symmetry-generated Na⁺ are omitted for clarity.

Fig. 3 Single-crystal X-ray structures of activated Li₂Fe₂(bdp)₃. Orange, light blue, blue, and gray spheres represent Fe, Li, N, and C atoms, respectively; H atoms are omitted for clarity.

Analogous to the solvated reduced frameworks, the activated compounds retain the space group Fddd. All cation-based electron density was found only at special positions for both structures. In the sodium structure, the cation was found to be disordered over two positions with similar occupancies. The total sodium occupancy was determined to be 25(2)%, thus yielding the formula Na_0.5Fe₂(bdp)₃ (Fig. 2, lower; Table S3‡). The lower chemical occupancy of the sodium cations in the activated crystal structure relative to the solvated structure is at first surprising. As discussed above, the presence of electron density from unrefined THF is not expected to contribute significantly to the sodium occupancy of the solvated structure. However, the crystal used to obtain the activated structure was ∼20% longer than the solvated crystal. Given the relative redox potentials of naphthalenide and Fe₂(bdp)₃, the reduction reaction is likely diffusion-limited, and this size difference may have resulted in some variation in the extent of reduction for the two crystals (see the ESI‡ for a discussion of potential sources of occupancy variance).^35,50 Interestingly, the cations in the solvated sodium structure are located near the center of the pores, but in the activated material they are located much closer to the corners of the pore. This results in shorter cation–π distances with one crystallographically independent pyrazolate and one crystallographically independent benzene ring. Specifically, the average cation position in the activated structure is 0.36 Å closer to the nearest benzene ring and 0.46 Å closer to the closest pyrazolate (see Fig. 2 and Table 1). In the Li₂Fe₂(bdp)₃ structure, the lithium cation was located as the most intense electron density peak and the occupancy was fixed to 100% (Fig. 3). The distance between the lithium cation and the closest benzene ring is 3.86(2) Å, which represents the shortest cation–π interaction distance determined in the reduced materials (see Table 1). This interaction, as well as the shortened cation–π interaction seen in Na_0.5Fe₂(bdp)₃ are clearly visible from the Hirshfeld surface analysis⁵¹ as bright red spots (Fig. S23 and S24‡). In the absence of solvation effects, Li⁺ is the smallest and most charge-dense of the alkali metal cations, and would thus be expected to engage in the strongest interactions with π systems.

Similar to the solvated structures, the weighted averages of the cation–benzene distances in the activated structures (Table 1) are longer than those calculated for M(benzene)⁺ in the gas phase (1.96 to 2.88 Å),⁴⁶ which can be attributed to a more complex distribution of charge density within the extended material. In the gas-phase, it has been shown that the strongest and shortest cation–benzene π interactions exist when the cation interacts directly with the center of the aromatic ring.⁵² However, such a position in the framework materials discussed here would generate a large charge separation between the alkali metal cations and the pyrazolate chains. The proximity of the cations in the activated structures to the pore corners and their distance from the linker benzene rings is indicative of competition between cation–π interactions and the cation⋯pyrazolate coulombic attraction, which would weaken the cation–π interactions and could lead to longer cation–benzene distances than in the gas phase, as observed here.⁵² Such a scenario has been previously characterized in other porous materials,^53,54 wherein the carboxylate oxygen atoms and aromatic portions of linkers compete for cation binding, resulting in cation–π distances similar to those reported here (4.871 to 5.618 Å). Finally, we note that the cation positions in Li₂Fe₂(bdp)₃ and Na_0.5Fe₂(bdp)₃ suggest that their charge density may be partially quenched by interactions with the linkers, as well as by their proximity to the iron–pyrazolate chains. Together, the structural data for the two activated frameworks suggest that the cations undergo a positional shift upon desolvation to maximize stabilizing interactions with the framework. This observation is also supported by in situ single-crystal X-ray diffraction data obtained for the O₂-dosed framework Na_1.2Fe₂(bdp)₃, wherein the positions of the sodium cations are very similar to those reported here for the Na_0.5Fe₂(bdp)₃ structure.⁵⁵

Hydrogen adsorption

With insight into the local structural and chemical environment of the alkali cations in activated A_xFe₂(bdp)₃, we sought to study how these surroundings affect the Lewis acidity of the cations using H₂ as a probe molecule.^56,57 Microcrystalline powders of Li_xFe₂(bdp)₃ (x = 1.18, 1.90), Na_xFe₂(bdp)₃ (x = 1.14, 2.06), and K_xFe₂(bdp)₃ (x = 0.68, 1.33) were prepared via stoichiometric reduction of Fe₂(bdp)₃ with lithium, sodium, or potassium naphthalenide. Two different cation loadings were probed to assess the effect of cation density on H₂ uptake. Powder X-ray diffraction analysis of THF-solvated Li_xFe₂(bdp)₃ and Na_xFe₂(bdp)₃ confirmed that the reductions occur through a topotactic insertion mechanism (see Fig. S13 and S14‡) as shown for K_xFe₂(bdp)₃ ³⁵ and characterization of desolvated Na_xFe₂(bdp)₃ indicated that the materials retain their crystallinity after activation at 180 °C under dynamic vacuum (Fig. S17‡). From charge density considerations alone, it is expected that Li_xFe₂(bdp)₃ would exhibit the greatest affinity for H₂. However, based on the single-crystal structures, the local cation environment is also likely to contribute heavily to the adsorption performance of these materials.

Low-pressure H₂ adsorption data were collected for all activated framework samples at 77 K (see Fig. 4 and S25–S29‡). Data are reported in units of moles of H₂ per mole of the metal–organic framework to account for the different formula unit masses and facilitate comparisons between different cations and different levels of reduction. At 1 bar, Li_1.18Fe₂(bdp)₃ exhibits greater H₂ uptake than Na_1.14Fe₂(bdp)₃ and K_0.68Fe₂(bdp)₃, as well as marginally improved uptake over Fe₂(bdp)₃ at pressures above 100 mbar (Fig. 4). A similar trend is seen for the higher levels of reduction (Fig. S29‡), although the H₂ uptake is diminished overall across all samples, which can be ascribed to the loss of free pore volume with increasing cation loading (see also Fig. S12‡).^26,27,30 Close examination of the low-pressure region for all isotherms (Fig. S28 and S29b‡) revealed that there is no significant enhancement in H₂ uptake for the reduced materials relative to Fe₂(bdp)₃, as would be expected for a strong interaction between H₂ and a polarizing metal site.⁵⁸ It is likely that the cation–π interactions in the activated materials are strong enough to suppress much of the effective positive charge of the cations, thus diminishing their ability to polarize and bind H₂. The slightly increased capacity overall exhibited by Li_1.18Fe₂(bdp)₃ is attributed to the introduction of an electric field that arises as a result of the charged framework and cation,⁵⁹ as well as the creation of smaller cavities within the pores relative to Fe₂(bdp)₃.^60,61

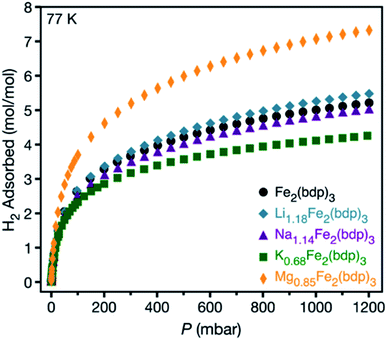Fig. 4 Hydrogen adsorption isotherms for microcrystalline powder samples of neutral and reduced variants of Fe₂(bdp)₃ collected at 77 K.

Based on the above results, achieving strong binding of H₂ through the use of extra-framework cations likely necessitates the use of multivalent ions with greater Lewis acidity, which may remain polarizing even in the presence of cation–π interactions. A number of zeolites are known to accommodate M²⁺ cations within their pores,^10,62,63 although examples of weakly-coordinated divalent guest cations within anionic metal–organic framework hosts are rare.^24,64 Additionally, the reductive insertion of high-valent species can be particularly challenging due to their poor ion diffusivity. Nevertheless, it proved possible to synthesize the magnesium-inserted material Mg_0.85Fe₂(bdp)₃ using magnesium anthracene as a reductant (see the ESI‡ for details).⁶⁵ Powder X-ray diffraction characterization revealed the product to be highly crystalline, with a structure analogous to that of the parent framework (Fig. S18‡), and Mössbauer spectroscopy data confirmed the reductive insertion of Mg²⁺ ions (Fig. S35‡). Significantly, this result is the first example of reductive magnesium insertion in any metal–organic framework and the first use of magnesium anthracene as a magnesium source for a reductive insertion process. Although utilization of a reductant featuring a divalent cation lowers the maximum possible cation density in the resulting anionic framework, the increased charge density per cation compensates for this effect.

Hydrogen adsorption data collected for Mg_0.85Fe₂(bdp)₃ at 77 K revealed a significant enhancement in the total H₂ uptake relative to that determined for Li_1.18Fe₂(bdp)₃. At low pressures, the H₂ uptake in Mg_0.85Fe₂(bdp)₃ is also noticeably steeper than in Fe₂(bdp)₃ (Fig. S30 and S31‡), which is indicative of stronger H₂ binding in the magnesium inserted structure. Adsorption data collected at 77 and 87 K for both frameworks (Fig. S32 and S33‡) were fit using a tri-site Langmuir–Freundlich model (Table S6‡), and the resulting parameters were used with the Clausius–Clapeyron relation to extract isosteric heats (Q_st) of H₂ adsorption of −8.7 and −7.2 kJ mol⁻¹ for Mg_0.85Fe₂(bdp)₃ and Fe₂(bdp)₃, respectively (Fig. S34‡). While the magnitude of the Q_st value for Mg_0.85Fe₂(bdp)₃ is greater than for Fe₂(bdp)₃, this increase is small compared to what would be expected for Mg²⁺ cations with largely unquenched charge density. For example, the measured isosteric heat of adsorption for H₂ at the lattice-confined open Mg²⁺ sites in Mg₂(dobdc)⁶⁶ (dobdc⁴⁻ = 2,5-dioxido-1,4-benzenedicarboxylate) is −10.1 kJ mol⁻¹.⁵⁸ Thus, as determined for the alkali metal cation structures, the Mg²⁺ charge density in Mg_0.85Fe₂(bdp)₃ is likely quenched in part by cation–π interactions involving the framework lattice. Preliminary attempts at single-crystal reductions of Fe₂(bdp)₃ with magnesium anthracene led to a loss of crystallinity and efforts to identify the position of Mg²⁺ by Rietveld refinement of the PXRD data were unsuccessful, but the magnesium cations in Mg_0.85Fe₂(bdp)₃ are presumably situated in a similar local environment as the alkali metal cations. Given the smaller size and higher charge of Mg²⁺ compared to the alkali metal cations, cation–π interactions are expected to be even stronger in Mg_0.85Fe₂(bdp)₃ and may facilitate migration of Mg²⁺ closer to the anionic iron–pyrazolate chains at the corners of the pore, which would decrease their accessibility to gas molecules. However, if this is the case, the H₂ adsorption data suggest that the stronger Lewis acidity of Mg²⁺ may be able to better offset the cation–framework interactions and enhance H₂ uptake and binding.

Conclusions

The foregoing results show that single crystals of the metal–organic framework Fe₂(bdp)₃ can undergo single-crystal-to-single-crystal reduction to yield the solvated framework materials A₂Fe₂(bdp)₃·yTHF (A = Li⁺, Na⁺, K⁺). Remarkably, the solvated crystals diffract well enough that the location of the extra-framework cations can be precisely resolved in the cases of Na⁺ and K⁺. Single-crystal-to-single-crystal activation of the lithium- and sodium-containing frameworks also enabled structural characterization of the desolvated framework materials Li₂Fe₂(bdp)₃ and Na_0.5Fe₂(bdp)₃. To the best of our knowledge, these structures represent the first reported single-crystal structures of activated metal–organic frameworks wherein the extra-framework cations have been structurally located. Comparison of the solvated and activated sodium-containing structures suggests that solvent removal results in a change in the location of the cations to maximize cation–host interactions. Hydrogen adsorption data collected for microcrystalline powder samples of the reduced frameworks revealed that the adsorption capacities are generally lower than that of Fe₂(bdp)₃ and less than expected for materials featuring cations with relatively unquenched charge densities, likely a result of cation–framework interactions. It was further possible to isolate the material Mg_0.85Fe₂(bdp)₃via the first example of reductive insertion using magnesium anthracene. This material features more charge-dense Mg²⁺ cations and notably exhibits significantly enhanced H₂ uptake and binding relative to Fe₂(bdp)₃.

Ultimately, it is apparent that the local environment of extra-framework cations, and particularly non-covalent cation–framework interactions, are essential considerations when evaluating the potential of cation-doped porous materials to adsorb and store gases. Neutron diffraction studies could provide additional insight into the structures of these materials and may allow for the direct observation of the H₂ binding sites. Such information, in combination with the results reported here, could help to inform the development of new materials containing extra-framework cations for gas storage wherein strong cation–host interactions are minimized. Specifically, cation ligating sites in anionic frameworks must be carefully designed so as to maximize exposure if alkali metal cations are to be used to enhance guest binding.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Hydrogen Materials – Advance Research Consortium (HyMARC), established as part of the Energy Materials Network under the U. S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Hydrogen and Fuel Cell Technologies Office, under Contract DE-AC02-05CH11231. Single-crystal X-ray diffraction data were collected at Beamline 11.3.1 and 12.2.1 at the Advanced Light Source at Lawrence Berkeley National Laboratory, which is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under contract no. DE-AC02-05CH11231. Synchrotron powder X-ray diffraction data were collected at Beamline 17-BM-B at the Advanced Photon Source (APS), a U.S. Department of Energy Office of Science User Facility operated by Argonne National Laboratory under contract no. DE-AC02-06CH11357. We thank Dr Julia Oktawiec and Henry Jiang for assistance with synchrotron powder X-ray diffraction experiments; Khetpakorn Chakarawet for assistance with Mössbauer spectroscopy experiments; Dr Simon Teat, Dr Laura McCormick, Dr T. David Harris, and Ever Velasquez for helpful discussions, and Dr Katie Meihaus for editorial assistance.

Notes and references

1. N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama and K. Kawamoto, Nat. Mater., 2011, 10(9), 682.
2. A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144(4), 1188.
3. G. C. Rawsky, T. Fujinami and D. Shriver, Chem. Mater., 1994, 6(12), 2208.
4. J. F. Van Humbeck, M. L. Aubrey, A. Alsbaiee, R. Ameloot, G. W. Coates, W. R. Dichtel and J. R. Long, Chem. Sci., 2015, 6(10), 5499.
5. K. Zaghib, A. Mauger and C. M. Julien, in Rechargeable Batteries, Springer, 2015, pp. 25–65.
6. M. Delkash, B. E. Bakhshayesh and H. Kazemian, Microporous Mesoporous Mater., 2015, 214, 224.
7. J. Sun, L. Liu, X. Zhao, S. Yang, S. Komarneni and D. Yang, RSC Adv., 2015, 5(92), 75354.
8. M. W. Ackley, S. U. Rege and H. Saxena, Microporous Mesoporous Mater., 2003, 61(1–3), 25.
9. S. Cavenati, C. A. Grande and A. E. Rodrigues, J. Chem. Eng., 2004, 49(4), 1095.
10. H. Langmi, D. Book, A. Walton, S. Johnson, M. Al-Mamouri, J. Speight, P. Edwards, I. Harris and P. Anderson, J. Alloys Compd., 2005, 404–406, 637.
11. M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, J. Power Sources, 2010, 195(24), 7904.
12. G. Sethia, R. S. Somani and H. C. Bajaj, RSC Adv., 2015, 5(17), 12773.
13. M. Eddaoudi, D. F. Sava, J. F. Eubank, K. Adil and V. Guillerm, Chem. Soc. Rev., 2015, 44(1), 228.
14. H. He, L. Hashemi, M.-L. Hu and A. Morsali, Coord. Chem. Rev., 2018, 376, 319.
15. Y. Sun, F. Wang and J. Zhang, Inorg. Chem., 2019, 58(7), 4076.
16. B. F. Abrahams, T. A. Hudson, L. J. McCormick and R. Robson, Cryst. Growth Des., 2011, 11(7), 2717.
17. Q. Fang, G. Zhu, M. Xue, Z. Wang, J. Sun and S. Qiu, Cryst. Growth Des., 2007, 8(1), 319.
18. C. J. Kingsbury, B. F. Abrahams, D. M. D'Alessandro, T. A. Hudson, R. Murase, R. Robson and K. F. White, Cryst. Growth Des., 2017, 17(4), 1465.
19. L. Liu, J. A. DeGayner, L. Sun, D. Z. Zee and T. D. Harris, Chem. Sci., 2019, 10(17), 4652.
20. H. J. Park and M. P. Suh, Chem. Sci., 2013, 4(2), 685.
21. M. Meilikhov, K. Yusenko, A. Torrisi, B. Jee, C. Mellot-Draznieks, A. Pöppl and R. A. Fischer, Angew. Chem., Int. Ed., 2010, 49(35), 6212.
22. Y. Han, K. Liu, M. A. Sinnwell, L. Liu, H. Huang and P. K. Thallapally, Inorg. Chem., 2019, 58(14), 8922.
23. B. Liu, R. Zhang, C.-Y. Pan and H.-L. Jiang, Inorg. Chem., 2017, 56(8), 4263.
24. F. Nouar, J. Eckert, J. F. Eubank, P. Forster and M. Eddaoudi, J. Am. Chem. Soc., 2009, 131(8), 2864.
25. S. Yang, X. Lin, A. J. Blake, G. S. Walker, P. Hubberstey, N. R. Champness and M. Schröder, Nat. Chem., 2009, 1(6), 487.
26. C. F. Leong, T. B. Faust, P. Turner, P. M. Usov, C. J. Kepert, R. Babarao, A. W. Thornton and D. M. D'Alessandro, Dalton Trans., 2013, 42(27), 9831.
27. K. L. Mulfort and J. T. Hupp, Inorg. Chem., 2008, 47(18), 7936.
28. K. L. Mulfort, O. K. Farha, C. L. Stern, A. A. Sarjeant and J. T. Hupp, J. Am. Chem. Soc., 2009, 131(11), 3866.
29. K. L. Mulfort and J. T. Hupp, J. Am. Chem. Soc., 2007, 129(31), 9604.
30. K. L. Mulfort, T. M. Wilson, M. R. Wasielewski and J. T. Hupp, Langmuir, 2008, 25(1), 503.
31. H. Langmi, A. Walton, M. Al-Mamouri, S. Johnson, D. Book, J. Speight, P. Edwards, I. Gameson, P. Anderson and I. Harris, J. Alloys Compd., 2003, 356, 710.
32. Z. R. Herm, B. M. Wiers, J. A. Mason, J. M. van Baten, M. R. Hudson, P. Zajdel, C. M. Brown, N. Masciocchi, R. Krishna and J. R. Long, Science, 2013, 340(6135), 960.
33. R. D. Hancock and A. E. Martell, Chem. Rev., 1989, 89(8), 1875.
34. W. Lu, Z. Wei, Z.-Y. Gu, T.-F. Liu, J. Park, J. Park, J. Tian, M. Zhang, Q. Zhang and T. Gentle III, Chem. Soc. Rev., 2014, 43(16), 5561.
35. M. L. Aubrey, B. M. Wiers, S. C. Andrews, T. Sakurai, S. E. Reyes-Lillo, S. M. Hamed, C.-J. Yu, L. E. Darago, J. A. Mason, J.-O. Baeg, F. Grandjean, G. J. Long, S. Seki, J. B. Neaton, P. Yang and J. R. Long, Nat. Mater., 2018, 17(7), 625.
36. J. A. DeGayner, I.-R. Jeon, L. Sun, M. Dincă and T. D. Harris, J. Am. Chem. Soc., 2017, 139(11), 4175.
37. W. Kaveevivitchai, X. Wang, L. Liu and A. J. Jacobson, Inorg. Chem., 2015, 54(4), 1822.
38. S. Calogero, G. G. Lobbia, P. Cecchi, G. Valle and J. Friedl, Polyhedron, 1994, 13(1), 87.
39. Y. Nishida, K. Kino and S. Kida, J. Chem. Soc., Dalton Trans., 1987, 5, 1157.
40. D. L. Reger, J. R. Gardinier, J. D. Elgin, M. D. Smith, D. Hautot, G. J. Long and F. Grandjean, Inorg. Chem., 2006, 45(22), 8862.
41. C. J. Brown, F. D. Toste, R. G. Bergman and K. N. Raymond, Chem. Rev., 2015, 115(9), 3012.
42. A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2012, 113(3), 2100.
43. A. McCurdy, L. Jimenez, D. A. Stauffer and D. A. Dougherty, J. Am. Chem. Soc., 1992, 114(26), 10314.
44. J. S. Mugridge, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2012, 134(4), 2057.
45. J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97(5), 1303.
46. R. A. Kumpf and D. A. Dougherty, Science, 1993, 261(5129), 1708.
47. A. S. Reddy, H. Zipse and G. N. Sastry, J. Phys. Chem. B, 2007, 111(39), 11546.
48. Y. Xu, J. Shen, W. Zhu, X. Luo, K. Chen and H. Jiang, J. Phys. Chem. B, 2005, 109(12), 5945.
49. L. Ma, A. Jin, Z. Xie and W. Lin, Angew. Chem., Int. Ed., 2009, 48(52), 9905.
50. N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96(2), 877.
51. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11(1), 19.
52. M. S. Marshall, R. P. Steele, K. S. Thanthiriwatte and C. D. Sherrill, J. Phys. Chem. A, 2009, 113(48), 13628.
53. Q.-B. Bo, Z.-W. Zhang, J.-L. Miao, D.-Q. Wang and G.-X. Sun, CrystEngComm, 2011, 13(6), 1765.
54. S.-Q. Xia, S.-M. Hu, J.-J. Zhang, X.-T. Wu, J.-C. Dai, Z.-Y. Fu and W.-X. Du, Inorg. Chem. Commun., 2004, 7(2), 271.
55. A. Jaffe, M. E. Ziebel, D. M. Halat, N. Biggins, R. A. Murphy, J. A. Reimer and J. R. Long, J. Am. Chem. Soc., 2020 DOI:10.1021/jacs.0c06570.
56. M. Dinca, A. Dailly, Y. Liu, C. M. Brown, D. A. Neumann and J. R. Long, J. Am. Chem. Soc., 2006, 128(51), 16876.
57. M. T. Kapelewski, S. J. Geier, M. R. Hudson, D. Stück, J. A. Mason, J. N. Nelson, D. J. Xiao, Z. Hulvey, E. Gilmour and S. A. FitzGerald, J. Am. Chem. Soc., 2014, 136(34), 12119.
58. W. Zhou, H. Wu and T. Yildirim, J. Am. Chem. Soc., 2008, 130(46), 15268.
59. J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38(5), 1477.
60. M. I. Gonzalez, E. D. Bloch, J. A. Mason, S. J. Teat and J. R. Long, Inorg. Chem., 2015, 54(6), 2995.
61. B. Schmitz, U. Müller, N. Trukhan, M. Schubert, G. Férey and M. Hirscher, ChemPhysChem, 2008, 9(15), 2181.
62. G. T. Palomino, M. L. Carayol and C. O. Areán, J. Mater. Chem., 2006, 16(28), 2884.
63. G. T. Palomino, M. L. Carayol and C. O. Areán, Catal. Today, 2008, 138(3–4), 249.
64. W.-G. Lu, L. Jiang, X.-L. Feng and T.-B. Lu, Inorg. Chem., 2009, 48(15), 6997.
65. B. Bogdanović, K. Schlichte and U. Westeppe, Chem. Ber., 1988, 121(1), 27.
66. K. Sumida, C. M. Brown, Z. R. Herm, S. Chavan, S. Bordiga and J. R. Long, Chem. Commun., 2011, 47(4), 1157.

---

Footnotes

† In memory of Professor Michael Woolfson FRS, FRAS, FInstP; a brilliant theoretical physicist, crystallographer, astrophysicist and grandfather.

‡ Electronic supplementary information (ESI) available: Full experimental details, supplementary figures and tables, crystallographic information, thermogravimetric analyses, gas sorption data and fits and Mössbauer spectroscopy. CCDC 2010318–2010322. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc03383a

---