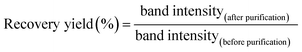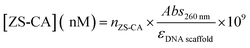Open Access Article
Open Access ArticleEnhanced enzymatic activity exerted by a packed assembly of a single type of enzyme†
Huyen
Dinh
 ,
Eiji
Nakata
,
Eiji
Nakata
 ,
Kaori
Mutsuda-Zapater
,
Masayuki
Saimura
,
Masahiro
Kinoshita
,
Kaori
Mutsuda-Zapater
,
Masayuki
Saimura
,
Masahiro
Kinoshita
 and
Takashi
Morii
and
Takashi
Morii
 *
*
Institute of Advanced Energy, Kyoto University, Uji, Kyoto 611-0011, Japan. E-mail: t-morii@iae.kyoto-u.ac.jp
First published on 27th July 2020
Abstract
In contrast to the dilute conditions employed for in vitro biochemical studies, enzymes are spatially organized at high density in cellular micro-compartments. In spite of being crucial for cellular functions, enzymatic reactions in such highly packed states have not been fully addressed. Here, we applied a protein adaptor to assemble a single type of monomeric enzyme on a DNA scaffold in the packed or dispersed states for carbonic anhydrase. The enzymatic reactions proceeded faster in the packed than in the dispersed state. Acceleration of the reaction in the packed assembly was more prominent for substrates with higher hydrophobicity. In addition, carbonic anhydrase is more tolerant of inhibitors in the packed assembly. Such an acceleration of the reaction in the packed state over the dispersed state was also observed for xylose reductase. We propose that the entropic force of water increases local substrate or cofactor concentration within the domain confined between enzyme surfaces, thus accelerating the reaction. Our system provides a reasonable model of enzymes in a packed state; this would help in engineering artificial metabolic systems.
Introduction
Enzymes are often spatially organized within the cell, either in close proximity on the cell membrane or confined inside a micro-compartment. Such environments are believed to play key roles in enabling the extraordinary efficiency and specificity of sequential metabolic enzymatic reactions.1–3 A typical example is the hetero oligomeric assembly of enzymes. Enzymes for sequential reactions are aligned in close proximity to prevent the loss of intermediate by random diffusion, thereby accelerating its transfer between enzyme subunits.4,5 Compartmentalization also regulates the spatial organization of enzymes. Collaborating enzymes are often packed in bacterial micro-compartments (BMCs) to encapsulate the toxic intermediates or to overcome the intrinsic catalytic inefficiency.6–8 Inside a proteinous shell, the enzyme concentration is in the millimolar range as was recently reported that enzyme aggregates inside a BMC carboxysome, form a dynamic liquid-like matrix internally.9 Autotrophic bacteria concentrate the central enzyme of the Calvin–Bensen–Bassham cycle, ribulose-1,5-bisphosphate carboxylase/oxygenase (RubisCO), responsible for the final step of CO2 fixation, in carboxysomes.10 Around 2000 copies of RubisCO and 80 copies of carbonic anhydrase are encapsulated inside a proteinous shell with diameter of 100–200 nm.11,12 The proteinous shell acts not only as a barrier for ligand diffusion but serves also as a container to confine the enzymes at high density.While the factors controlling the efficiency of sequential reactions by two or three types of enzymes have been actively addressed,13,14 the significance of such highly packed conditions for the reaction of a single type of enzyme remains to be determined. Reaction efficiency in a highly packed assembly could differ from that in a test tube, in which enzymes distribute freely in dilute conditions. To address this issue, protein assembly on a DNA scaffold offers an ideal system to study enzymatic reactions in spatially defined arrangements. DNA nanostructures have been applied as scaffolds for arranging functional molecules and nanomaterials.15–18 In particular, DNA origami-based scaffolds enable the assembly of several different enzymes to address the effect of inter-enzyme distances on sequential reactions.19–24
Here we apply a protein adaptor25 to assemble a single type of monomeric enzyme, carbonic anhydrase, on a DNA scaffold in a packed state with less than a few nanometers inter-enzyme distance or dispersed state and show that the esterase reaction proceeds faster in the packed than in the dispersed state. In the packed assembly, the reaction is accelerated more prominently for substrates with higher hydrophobicity and is more tolerant of inhibitors. When another enzyme xylose reductase was assembled in the packed state, a similar acceleration of the reaction in the packed state over the dispersed state was also observed. We propose that the entropic force of water increases local substrate concentration within the domain confined between enzyme surfaces, thus accelerating the reaction. Our finding offers a new insight on the efficiency of reaction by single type of enzyme in the packed state. The water-entropy effect increases as the enzyme structure becomes less flexible in the packed assembly. Therefore, a greater effect is expected within the spatially more constrained cellular compartments. Our system provides a reasonable model of enzymes in packed state; this would help in engineering artificial metabolic systems.
Results
Constructing the packed state of enzyme on DNA scaffold
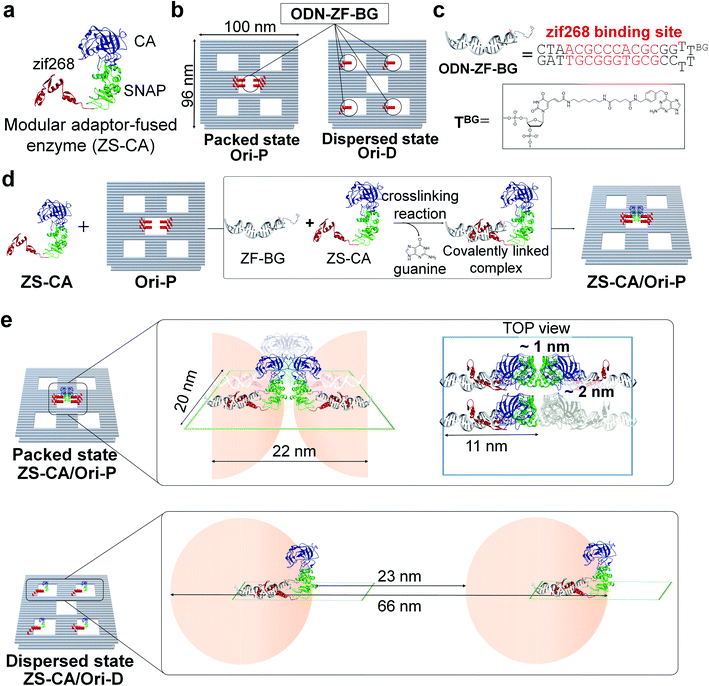
A defined number of molecules of a single type of enzyme were located either in close proximity or far apart on a DNA scaffold (Fig. 1). Monomeric human carbonic anhydrase II (CA) was chosen as the target enzyme because its structure and enzymatic features have been extensively studied.26,27 CA was genetically fused to a modular adaptor (ZS) consisting of a sequence-specific DNA-binding zinc finger protein (zif268) and a self-ligating SNAP-tag.28–30 The resulting adaptor-conjugated enzyme, ZS-CA (Fig. 1 and S1†), showed almost the same enzymatic activity to the parent CA (Fig. S2†) and bound stably at the intended sites in high yields on the DNA scaffold through covalent linkage (Fig. S3†).30A rectangular DNA scaffold with five cavities30–33 was prepared by the DNA origami method.15 Four binding sites for ZS-CA (ODN-ZF-BG) containing the specific binding sequence and benzyl guanine (BG), the SNAP-tag substrate, were placed in the central cavity (Fig. 1b–d and S4†) to keep four ZS-CAs in the packed state (Ori-P). A scaffold mimicking the dispersed state of ZS-CA (Ori-D) contained four binding sites placed solely in the four outer cavities, allowing the four ZS-CAs to remain separated. Considering the flexibility of the connection between ODN-ZF-BG and the DNA scaffold, the distance from the connection to CA was calculated to be 11 nm. When four ZS-CAs were assembled in Ori-P, the inter-enzyme distance between CA regions was <1 nm (Fig. 1e and S5†). This corresponds to the average distance of free ZS-CA in a 18–38 mM solution (see Materials and methods). When four ZS-CA molecules were located in Ori-D, each CA region was completely separated by at least 23 nm (Fig. 1e). These enzyme assemblies on Ori-P and Ori-D allowed us to directly compare the reaction of CA in the packed and dispersed states without increasing its concentration.
Enzymatic activity of ZS-CA in the packed and dispersed states
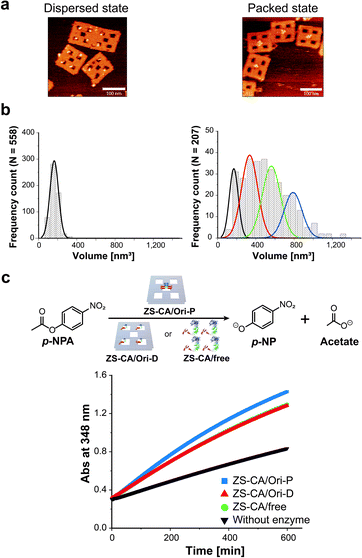
To adjust the concentrations of CA in the packed and the dispersed states, actual numbers of ZS-CA molecules loaded on each scaffold were estimated from AFM images (Fig. 2a, b and S6–S8†).34 In a typical experiment, the number of ZS-CA molecules bound to one Ori-D and Ori-P scaffold were deduced to be 3.1 and 2.6, respectively. The esterase activity of CA was assessed spectrophotometrically at 348 nm using p-nitrophenyl acetate (p-NPA) as a substrate (Fig. 2c), a widely applied ester to assess the activity of CA,27,35,36 with the same concentrations of assembled ZS-CA on Ori-P and Ori-D. The concentrations of assembled ZS-CA on Ori-P and Ori-D were estimated from the concentration of DNA scaffold and the number of ZS-CA molecules bound to each scaffold deduced as described above (Fig. S8†). Time-course profiles for the formation of hydrolysed product, p-nitrophenolate (p-NP), by 4 nM ZS-CA assembled on Ori-P, Ori-D, and in bulk solution are shown in Fig. 2c. The reaction profile of ZS-CA on Ori-D was similar to that in bulk solution, indicating little or no effect of the DNA scaffold on ZS-CA activity. In contrast, the reaction of ZS-CA assembled on Ori-P was faster than that on Ori-D at substrate concentrations ranging from 0.1 to 1 mM (Fig. S9†).Characteristics of the enzymatic activity of ZS-CA in the packed state
An interface composed of two or more ZS-CA molecules is the distinct feature of the packed assembly on Ori-P. Unlike on Ori-P, free ZS-CA in solution or ZS-CA on Ori-D did not approach the inter-enzyme distance of 1 nm at nanomolar concentrations (see Materials and methods). We investigated whether specific interactions between the CA domains in certain orientation(s) in the packed state could enhance the esterase reaction. Accordingly, we devised three types of ZS-CA assemblies that allowed two CA regions to reside face-to-face, side-by-side, or diagonally at an inter-enzyme distance of 1 nm (Fig. 3). We expected that the cooperativity would be induced in certain orientation(s) of ZS-CA within the three assemblies by specific interaction between two CA regions, thus resulting in enhanced efficiency of esterase reactions. However, the reaction of p-NPA was enhanced in all three arrangements to the same extent as observed for the Ori-P assembly. Therefore, the proximal alignment of two ZS-CA molecules, regardless of orientation, was sufficient to increase the esterase reaction of ZS-CA.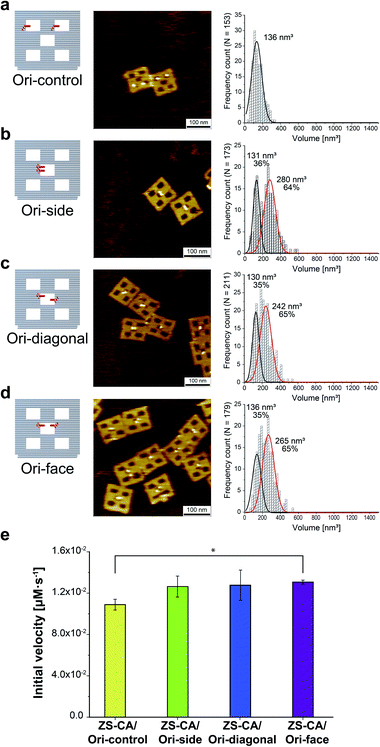 | ||
| Fig. 3 (a–d) Illustration of DNA scaffolds (left) with AFM images (middle) and volume analysis (right) of ZS-CA on DNA scaffolds containing two binding sites per scaffold: in separated cavities (Ori-control, in a); in a center cavity with different orientations: side-by-side (Ori-side, in b), diagonally (Ori-diagonal, in c), or face-to-face (Ori-face, in d). The percentage of ZS-CA-loaded DNA cavities on Ori-control were determined from AFM images as 82% (n = 146). Thus, the numbers of ZS-CA molecules bound to Ori-control were calculated as 1.6 with an average volume of 136 nm3. The volume of ZS-CA on Ori-side, diagonal, face with the respective volumes for one (black line), two (red line) molecules were estimated by fitting.30 The percentages of ZS-CA-loaded DNA cavities on DNA scaffold were determined from AFM images as 99%, 98%, 98%, respectively. In average, numbers of ZS-CA bound to Ori-side, Ori-diagonal and Ori-face were calculated as 1.6 in three cases. (e) Initial velocities of the esterase reaction by each of the four ZS-CA assemblies. Reactions were carried out with 6 nM of DNA origami assembled with ZS-CA in a buffer (pH 7.6) containing 50 mM HEPES, 12.5 mM MgCl2, 1% acetonitrile, 1 μM ZnCl2 and 0.001% Tween 20 with 1 mM p-NPA. Error bars represent the mean ± SD of three independent experiments (*p < 0.005). | ||
It is well known that the presence of polyethylene glycol (PEG) stabilizes enzyme structure through the so-called macromolecular crowding effect.37,38 Based on the findings so far, we assumed that enzyme activity improved with increasing structural stability and the structure of ZS-CA was more stable in Ori-P than in Ori-D. Consequently, addition of PEG could stabilize ZS-CA and enhance its reaction on Ori-D or free ZS-CA to the level seen on Ori-P. Thus, addition of PEG could amplify the differences between these two states in terms of stability and activity. Reactions of ZS-CA (4 nM) in bulk solution, on Ori-P, or Ori-D were carried out in the presence of PEG 6K (Fig. S10†). In all cases, the initial velocity of ZS-CA gradually decreased as PEG 6K concentration rose above 300 mg ml−1; moreover, the difference in activity decreased as PEG concentration increased. Addition of other macromolecular crowding reagents, such as dextran (6K and 60K), PEG 8K, and ethylene glycol also slowed down the reaction of ZS-CA in all cases (Fig. S11†).
From these results, we conclude that acceleration of the ZS-CA esterase reaction in the packed state was not caused by the enhanced stability of proteins as reported for the effect of macromolecular crowding reagents. In addition, the activity of ZS-CA in free solution, on Ori-P or Ori-D, remained unchanged at 25 °C for 12 h (Fig. S12†), indicating that variations in the extent to which ZS-CA in each state retained its activity did not account for the enhanced activity in the packed state.
Effect of sufficiently high concentration of Na2SO4
Steiner and Lindskog39 reported activation of the CA-catalysed hydrolysis of p-NPA in the presence of high concentrations of sodium sulphate (Na2SO4) in the early 70's, and suggested that the effect of ionic strength on the chemical potential of the substrate caused an increase in apparent affinity of the substrate for the active site. In the presence of 0.5 M Na2SO4, the initial velocity of the esterase reaction of ZS-CA was increased by 2.0 times in all cases, i.e., free solution, on Ori-D, and on Ori-P (Fig. 4a). Our interpretation on the effect of Na2SO4 effect is different from that of Steiner and Lindskog as argued in “Effect of salt addition” of the Discussion.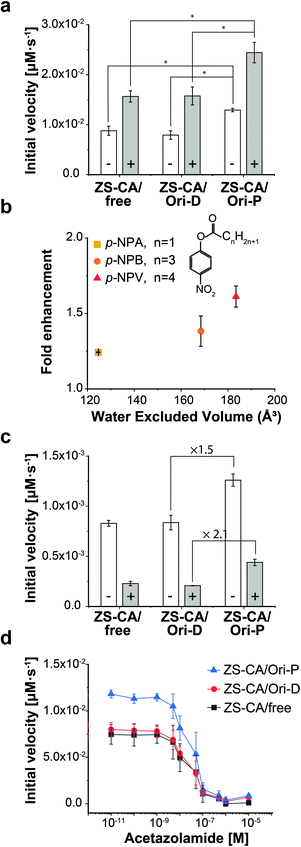 | ||
| Fig. 4 Kinetic properties of the enzymes in dispersed and packed assemblies. (a) The reaction rate of ZS-CA (5.5 nM) assembled on the DNA scaffold with 1 mM p-NPA in the absence (open bars) and presence (grey bars) of 0.5 M Na2SO4 (*p < 0.005). (b) The enhancement factors (initial velocity of CA on Ori-P over that of CA on Ori-D) for the esterase reaction of ZS-CA plotted against the water excluded volume (EV) of p-NPA (128 Å3), p-NPB (165 Å3), and p-NPV (183 Å3).39,40 Reaction included 23 nM ZS-CA and 0.1 mM substrate. (c) Inhibition exerted by 1 M NaBr (grey bars) on the reaction rate of 5.5 nM ZS-CA with 0.1 mM p-NPA. (d) Initial reaction velocity of 5.5 nM ZS-CA assembled on the DNA scaffold (in 1 mM p-NPA) with an increasing concentration of acetazolamide (from 10 pM to 10 μM). Error bars represent the mean ± SD of three independent experiments. | ||
Factors enhancing the enzymatic activity of ZS-CA in the packed state
The esterase reaction of ZS-CA in the packed state was further investigated with p-nitrophenyl butyrate (p-NPB) and p-nitrophenyl valerate (p-NPV), which bear larger, nonpolar acyl groups than p-NPA (Fig. 4b and S13†). With p-NPA as the substrate, the reaction was accelerated 1.3 times on Ori-P over Ori-D, but 1.5 and 1.6 times with p-NPB and p-NPV, respectively, showing the statistical significance of mean differences among experimental groups. As argued in the Discussion, a substrate generates a volume which is inaccessible to the centre of water molecules, which is referred to as the “excluded volume” (EV).40,41 In general, a solute becomes more hydrophobic as its EV increases and its polarity or affinity for water decreases. These EV and affinity effects are entropic and energetic in origin, respectively. For substrates whose energetic affinity for water is not significantly high like p-NPA, p-NPB, and p-NPV, the entropic effect dominates with the result that the hydrophobicity can be discussed in terms of the EV. The esterase reaction of ZS-CA in the packed state was accelerated for substrates with the larger EV as shown in Fig. 4b where factors enhancing the initial velocity of ZS-CA on Ori-D over that on Ori-P for a given substrate (fold enhancement) were plotted against the EV of each substrate.Effects of inhibitors for ZS-CA in the packed and dispersed states
The esterase activity in the packed state was further enhanced for the larger, more hydrophobic substrates that resulted modulation in the substrate specificity of the parent enzyme. The result suggested that the sensitivity of the enzyme to inhibitory molecules or ions could be different depending on the assembly state of enzyme. Therefore, the effect of known CA inhibitors, such as weakly hydrated, large halide anions (i.e., Br− and I−) and sulfonamides,42,43 were investigated in the packed state (Fig. 4c and S14†). In the presence of 1 M NaBr, the initial velocities of p-NPA hydrolysis reactions by ZS-CA on Ori-D and Ori-P were reduced in all cases. Interestingly, the initial velocity of ZS-CA on Ori-P was 2.1 times higher than that on Ori-D or in free solution in the presence of 1 M NaBr. Considering the 1.5 times enhancement for the reaction of ZS-CA on Ori-P in the absence of bromide ion, ZS-CA on Ori-P tolerated better the inhibitory effect of bromide than ZS-CA on Ori-D or in free solution. Inhibition of the esterase reactions by increasing concentrations of acetazolamide also revealed the lower sensitivity of ZS-CA on Ori-P to the inhibitor at up to 100 nM (Fig. 4d). Taken together, the sensitivity of the esterase reaction to inhibitory molecules or ions varies depending on the assembled state of ZS-CA.Enzymatic activity of xylose reductase in the packed and dispersed states
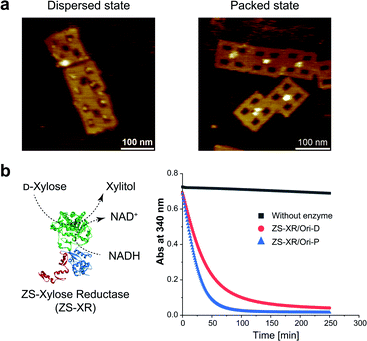
It is interesting to examine another enzymatic reaction in the packed and dispersed states. For this end, reactions in the packed and dispersed states of xylose reductase (XR), an enzyme from xylose metabolic pathway, were investigated. XR converts xylose into xylitol by consuming the cofactor NADH.44 XR was fused to the ZS modular adaptor (ZS-XR)21 to assemble in the packed and dispersed states on DNA scaffold (Fig. 5a). ZS-XR showed high binding yields to Ori-D and Ori-P as determined from AFM images (the percentages of protein-loaded cavities were 82% and 99%, respectively). Volume analysis in each assembly indicated that the average numbers of ZS-XR on DNA scaffold were 2.7 molecules on one Ori-P and 3.2 molecules on Ori-D (Fig. S15†). The reaction of XR was assessed by measuring the oxidation of NADH spectrophotometrically at 340 nm. At the same concentration of enzyme (14 nM) on DNA scaffold, ZS-XR showed higher initial reaction rate in the packed state than in the dispersed state (Fig. 5b). Acceleration in the reaction rate of ZS-XR in packed state was also observed when the concentrations of both D-xylose and NADH were decreased to 5 mM D-xylose and 25 μM NADH (Fig. S16†).Discussion
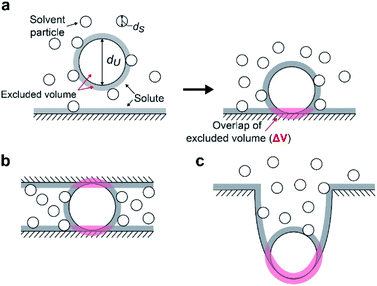
We suggest that the experimental results presented above can be interpreted by applying the entropic excluded-volume (EV) (water-entropy) effect45,46 originating from the translational displacement of water molecules in the entire system. Substrates are enriched within such a domain by the water-entropy effect illustrated in Fig. 6.47 A substrate or an enzyme generates a volume referred to as “excluded volume (EV)”, which is inaccessible to the center of water molecules (Fig. 6a, left panel). When the substrate comes in contact with the enzyme surface, the two EVs overlap (Fig. 6a, right panel). Consequently, the total volume available for the translational displacement of water molecules in the system increases by the overlapping volume, leading to a gain of configurational entropy of water. This entropic force causes enrichment of the substrate near the enzyme. When two enzymes are sufficiently close to each other (Fig. 6b), the substrate can contact both enzyme surfaces and a further increase in the overlapping volume follows. Hence, the local concentration of substrate becomes higher within the confined domain in the packed state than near the single enzyme in the dispersed state or free in solution, leading to a higher initial reaction velocity by the nearest enzyme. The water-entropy effect described above is enhanced upon addition of a salt whose ions are strongly hydrated, such as sulfate ions (SO42−), through modification of the bulk water structure.In what follows, we explain this effect and describe our physical interpretation of the experimental results.
Basic concept based on entropic excluded-volume effect
We consider a simple model system where hard-sphere solutes with diameter dU and a planar hard wall are immersed in small hard spheres with diameter dS forming the solvent. In this hard-body model system where no soft (attractive or repulsive) interaction potentials are present, all of the accessible system configurations share the same energy, and the system behavior is purely entropic in its origin. We discuss the gain of solvent entropy occurring when a solute comes in contact with the wall. As depicted in Fig. 6a, the presence of a solute and a wall generates excluded volumes (EVs) which are inaccessible to the centers of solvent particles. Upon contact, the two EVs overlap (the overlapping volume ΔV (ΔV > 0) is colored pink), and the total EV decreases by ΔV and the total volume available for the translational displacement of solvent particles in the system, V, increases by ΔV (ΔV/V ≪ 1). Applying the expression for the ideal-gas entropy to the solvent entropy, we can formulate the gain of translational, configurational entropy of the solvent upon contact, ΔS°, as ΔS° = kBNSΔV/V (kB and NS denote the Boltzmann constant and the total number of solvent particles in the system, respectively).48 Expressing ΔV by dU and dS, we obtain| ΔS° = kBNS(ΔV/V) = {3(dU/dS) + 1}ηSkB, ηS = πdS3ρS/6, ρS = NS/V | (1) |
| χ = exp{−ΔG°/(kBT)}, ΔG° < 0. | (2) |
The entropic force was referred to as the “depletion force” in a series of pioneering works.49–52 The forces considered were those induced between colloidal particles49–51 or a colloidal particle and a glass surface52 suspended in solution of macromolecules. In these works, however, water was treated as inert background. We remark that this treatment is valid only under a special solution condition in a colloidal system and usually inapplicable to a biological system.47
When a solute comes in contact with two walls as shown in Fig. 6b, ΔV and |ΔG°| become twice larger than those in the contact shown in Fig. 6a, respectively. We note that ΔV is largely dependent on the surface curvature of the wall. When a solute comes in contact with a portion of a wall possessing concave surface, for example, ΔV can be even larger than that in Fig. 6b as illustrated in Fig. 6c.
Application to enzyme–substrate–water system
In our system, the solvent, spherical solute, and wall in cartoons of Fig. 6 correspond to water, a substrate, and an enzyme, respectively. Water exists as dense liquid at ambient temperature and pressure due to hydrogen bonds despite its exceptionally small molecular size. For water, ηS is high though dS is quite small, (refer to the section “Quantitative Analysis on Experimental Results Using Theoretical Model” below), leading to the largest EV effect among the ordinary liquids in nature. It has been shown that the water-entropy gain is a principal driving force of a variety of biological self-assembly processes.45–47,53First, we consider Ori-D where only a single enzyme is present. Applying eqn (1) and (2) to the case where the solvent is water (dS = 0.28 nm and ηS = 0.383) and the substrate is p-NPA (dU ∼ 0.8 nm), we obtain ΔS° ∼ 3.7 kB, ΔG° ∼ −2.2 kcal mol−1, and χ ∼ 40 (refer to the section “Quantitative Analysis on Experimental Results Using Theoretical Model” below). An entropic force, which originates from the translational displacement of water molecules, acts on a substrate. This force drives the substrate to come in contact with the enzyme surface and enriches the substrates near it.
Difference between Ori-D and Ori-P
We then consider Ori-P where two out of four enzymes are put close together. Here, ΔV1 and ΔV2 denote the increases in the total volume available for water molecules occurring when a substrate comes in contact with a single enzyme surface and with two enzyme surfaces, respectively. Hereafter, the subscripts “1” and “2” denote Ori-D and Ori-P, respectively. If Fig. 6 is applicable, ΔV2 = 2ΔV1. In the real system, however, the substrate and the enzyme possess polyatomic structures and the enzyme structure fluctuates to a large extent. Moreover, only small portions of the enzyme surfaces are close to each other. As a consequence, on an average, ΔV2 is considerably smaller than 2ΔV1. Nevertheless, ΔV2 is larger than ΔV1 as far as the surface separation between two enzymes is sufficiently small (i.e., as small as the EV of the substrate) and we can write ΔV2 = ξΔV1 (ξ > 1) and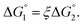 Applying eqn (2) to Ori-D and Ori-P yields
Applying eqn (2) to Ori-D and Ori-P yields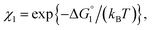 | (3a) |
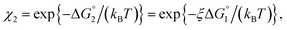 | (3b) |
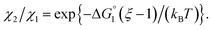 | (3c) |
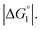 In the ideal case of Fig. 6, ξ = 2 with the result of quite a large value of χ2/χ1. However, this is not realized in our system as mentioned above. Nevertheless, since
In the ideal case of Fig. 6, ξ = 2 with the result of quite a large value of χ2/χ1. However, this is not realized in our system as mentioned above. Nevertheless, since 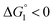 and ξ > 1, χ2/χ1 is larger than unity. For a substrate concentration in the bulk aqueous solution given, it can be considered that the initial reaction velocity of esterase reaction increases in proportion to the degree of substrate enrichment near the enzyme surface. Thus, χ2/χ1 > 1 leads to the acceleration of esterase reaction rate in Ori-P and the enhanced activity of ZS-CA as observed in our experiments. As argued in later sections, the increase of EV of the substrate or the addition of Na2SO4 increases
and ξ > 1, χ2/χ1 is larger than unity. For a substrate concentration in the bulk aqueous solution given, it can be considered that the initial reaction velocity of esterase reaction increases in proportion to the degree of substrate enrichment near the enzyme surface. Thus, χ2/χ1 > 1 leads to the acceleration of esterase reaction rate in Ori-P and the enhanced activity of ZS-CA as observed in our experiments. As argued in later sections, the increase of EV of the substrate or the addition of Na2SO4 increases 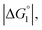 leading to larger χ2/χ1 forξ > 1 (ξ can be considered almost unchanged for an enzyme species given. Refer to the section “Quantitative Analysis on Experimental Results Using Theoretical Model” below.)
leading to larger χ2/χ1 forξ > 1 (ξ can be considered almost unchanged for an enzyme species given. Refer to the section “Quantitative Analysis on Experimental Results Using Theoretical Model” below.)
We note that the substrate-active site binding corresponds to the event illustrated in Fig. 6c. Upon occurrence of the substrate enrichment near an enzyme surface or within the domain confined between two enzyme surfaces, a substrate, which can move along the enzyme surface, can reach the active site of the enzyme.54 In Ori-P, the active site need not be within the domain confined between two enzyme surfaces. The essentially no differences among Ori-side, Ori-diagonal, and Ori-face in terms of the enhanced enzyme activity (Fig. 3e), which were observed in our experiments, is attributable to the large fluctuation of the enzyme structure.
Effect of substrate species
Though the entropic EV (water-entropy) effect is highlighted in the above arguments, in the real system not only this entropic factor but also the energetic one comes into play. Therefore,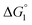 in eqn (3) is influenced by the energetic factor as well. The equation,
in eqn (3) is influenced by the energetic factor as well. The equation, 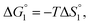 does not hold but eqn (2) and (3) still hold. Entropically, a substrate is always attracted to an enzyme surface, promoting the substrate enrichment near the surface.55 On the other hand, a substrate with high energetic affinity for water (i.e., with high polarity) prefers to be hydrated in the bulk aqueous solution, opposing the substrate enrichment.56 The opposite is true for a substrate with low affinity for water, cooperating with the entropic enrichment. In general, solutes are more enriched near the surface as the solute hydrophobicity becomes higher. With an increase in the solute EV or a decrease in the energetic affinity for water, the solute becomes more hydrophobic. The entropic factor usually dominates, but this is not true for a highly hydrophilic solute:
does not hold but eqn (2) and (3) still hold. Entropically, a substrate is always attracted to an enzyme surface, promoting the substrate enrichment near the surface.55 On the other hand, a substrate with high energetic affinity for water (i.e., with high polarity) prefers to be hydrated in the bulk aqueous solution, opposing the substrate enrichment.56 The opposite is true for a substrate with low affinity for water, cooperating with the entropic enrichment. In general, solutes are more enriched near the surface as the solute hydrophobicity becomes higher. With an increase in the solute EV or a decrease in the energetic affinity for water, the solute becomes more hydrophobic. The entropic factor usually dominates, but this is not true for a highly hydrophilic solute: 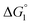 can take a small, positive value for the latter.
can take a small, positive value for the latter.
The three substrates, p-NPA, p-NPB, and p-NPV, are rather hydrophobic. Hence, the water-entropy effect dominates and becomes larger as the EV increases (dU in eqn (1) corresponds to the substrate size, but for polyatomic substrates, the EV is physically more reasonable than the size in discussing the substrate hydrophobicity and the water-entropy effect). The EV follows the order, p-NPA < p-NPB < p-NPV (Fig. 4b). The enrichment of substrates described above becomes stronger in the same order. 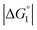 (
(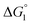 is negative and considerably large for the three substrates) and χ2/χ1 in eqn (3) follow the order, p-NPA < p-NPB < p-NPV, which is in accord with our experimental observations.
is negative and considerably large for the three substrates) and χ2/χ1 in eqn (3) follow the order, p-NPA < p-NPB < p-NPV, which is in accord with our experimental observations.
The results obtained by reactions of ZS-XR assembled on Ori-D and Ori-P can be interpreted as follows (refer to “Summary of Interpretation of Experimental Results” for more details). ZS-XR showed higher initial reaction rate in the packed state than in the dispersed state (Fig. 5b). In water, the solubility of NADH is lower than that of D-xylose by a factor of ∼1/50,57,58 manifesting the rather hydrophobic nature of NADH. This suggests that the acceleration of reaction in Ori-P over Ori-D is attributable to the enrichment of NADH within the domain confined between enzyme surfaces.
Behaviour of reaction products
We comment on the behavior of products of the esterase reaction for p-NPA, p-NP and acetate. p-NP is less hydrophobic than p-NPA and acetate is hydrophilic. Hence,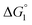 for p-NP should be negative but smaller than that for p-NPA, and
for p-NP should be negative but smaller than that for p-NPA, and 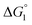 for acetate can be very small (and possibly positive). Therefore, the enrichment of p-NP near the enzyme surface is less promoted than that of p-NPA, and that of acetate is not promoted.
for acetate can be very small (and possibly positive). Therefore, the enrichment of p-NP near the enzyme surface is less promoted than that of p-NPA, and that of acetate is not promoted.
In general, whether solutes come in contact with the surface or dissociate from the surface is dependent on not only 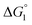 but also the solute concentration (or number density) in the bulk aqueous solution. χ1 in eqn (3a) is the solute concentration at the surface (ρSurface) divided by that in the bulk aqueous solution (ρBulk). Negative
but also the solute concentration (or number density) in the bulk aqueous solution. χ1 in eqn (3a) is the solute concentration at the surface (ρSurface) divided by that in the bulk aqueous solution (ρBulk). Negative 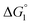 implies that ρBulk is lower than ρSurface (e.g., ρSurface/ρBulk ∼ 40 for χ1 ∼ 40). We note that ρBulk of p-NP or acetate in the bulk aqueous solution is very low in our experiments. Therefore, upon production of p-NP and acetate by the reaction, they favorably dissociate from the enzyme surface. Thus, even the dissociation of hydrophobic reaction products is not hindered by the water-entropy effect as long as their concentrations in the bulk aqueous solution are sufficiently low.
implies that ρBulk is lower than ρSurface (e.g., ρSurface/ρBulk ∼ 40 for χ1 ∼ 40). We note that ρBulk of p-NP or acetate in the bulk aqueous solution is very low in our experiments. Therefore, upon production of p-NP and acetate by the reaction, they favorably dissociate from the enzyme surface. Thus, even the dissociation of hydrophobic reaction products is not hindered by the water-entropy effect as long as their concentrations in the bulk aqueous solution are sufficiently low.
Effect of salt addition
Strongly hydrated ions with high charges and/or small sizes prefer to be present in the bulk water. They are not likely to come in contact with an oppositely charged portion of a solute immersed in water, because it is difficult to dehydrate the ions. For the activation of the CA-catalyzed hydrolysis of p-NPA in the presence of high concentrations of Na2SO4, it was suggested that the effect of ionic strength on the chemical potential of the substrate caused an increase in apparent affinity of the substrate for the active site.39 The addition of Na2SO4 produces strongly hydrated ions SO42− and causes a volume reduction at a constant pressure and higher ηS, leading to an enhanced water-entropy effect.59,60 Therefore, the addition of Na2SO4 results in stronger enrichment of substrates for any portion of the enzyme surface and larger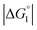 followed by higher values of χ1 and χ2 (also by higher χ2/χ1 for ξ > 1). That is, the esterase reaction rate is accelerated upon Na2SO4 addition not only in Ori-D but also in Ori-P, especially in the latter. These are also in accord with our experimental observations that the esterase reaction rate becomes about 2.0 times higher in Ori-D and Ori-P when Na2SO4 is added in a concentration of 0.5 M. The effect of Na2SO4 addition can be explained even in a quantitative sense as described in the section “Quantitative Analysis on Experimental Results Using Theoretical Model”.
followed by higher values of χ1 and χ2 (also by higher χ2/χ1 for ξ > 1). That is, the esterase reaction rate is accelerated upon Na2SO4 addition not only in Ori-D but also in Ori-P, especially in the latter. These are also in accord with our experimental observations that the esterase reaction rate becomes about 2.0 times higher in Ori-D and Ori-P when Na2SO4 is added in a concentration of 0.5 M. The effect of Na2SO4 addition can be explained even in a quantitative sense as described in the section “Quantitative Analysis on Experimental Results Using Theoretical Model”.
On the other hand, only weakly hydrated ions with low charges and/or large sizes can be dehydrated without difficulty and tend to come in contact with an oppositely charged portion of a solute immersed in water. Br−, for example, preferentially contacts Zn2+ in the active site of CA (this is not the case for SO42−), thus acting as an inhibitor for CA. This is why the addition of NaBr decelerates the reaction rate as observed in our experiments.
Quantitative analysis on experimental results using theoretical model
Our basic strategy of the quantitative analysis, which is performed for ZS-CA and p-NPA, is as follows:(1) Using the parameter values pertinent to our system (dS = 0.28 nm, dU ∼ 0.8 nm, ηS = 0.383, and T = 298 K), we calculate 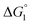 (ΔG° in eqn (2)).
(ΔG° in eqn (2)).
(2) Using the experimental result, χ2/χ1 ∼ 1.3, we estimate ξ in eqn (3c).
(3) Upon addition of Na2SO4 (0.5 M/L), ηS increases to 0.419.61 From the resultant increase in 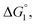 we calculate
we calculate 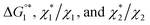 where the superscript “*” denotes the value after the salt addition
where the superscript “*” denotes the value after the salt addition 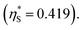 It is assumed that ξ remains unchanged upon the salt addition. The calculated values are compared to our experimentally measured values.
It is assumed that ξ remains unchanged upon the salt addition. The calculated values are compared to our experimentally measured values.
We obtain 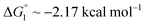 in (1) and ξ ∼ 1.08 in (2) (unfortunately, ξ is much smaller than the ideal value 2). According to eqn (1), |ΔG°| increases in proportion to ηS. However, our more rigorous theory based on statistical mechanics55 suggests that |ΔG°| is more strongly dependent on ηS: when ηS increases further from the value pertinent to water, 0.383, |ΔG°| becomes larger in approximate proportion to ηS2. Using this more rigorous dependence of |ΔG°| on ηS, we obtain
in (1) and ξ ∼ 1.08 in (2) (unfortunately, ξ is much smaller than the ideal value 2). According to eqn (1), |ΔG°| increases in proportion to ηS. However, our more rigorous theory based on statistical mechanics55 suggests that |ΔG°| is more strongly dependent on ηS: when ηS increases further from the value pertinent to water, 0.383, |ΔG°| becomes larger in approximate proportion to ηS2. Using this more rigorous dependence of |ΔG°| on ηS, we obtain 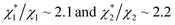 as the theoretical predictions. On the other hand, our experimentally measured values are
as the theoretical predictions. On the other hand, our experimentally measured values are 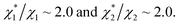 We can conclude that the effects of addition of Na2SO4 can well be explained by our theory even in a quantitative sense.
We can conclude that the effects of addition of Na2SO4 can well be explained by our theory even in a quantitative sense.
Comments on dynamic aspect of system behaviour
We emphasize that all the water molecules in the system, i.e., not only the water molecules near the enzyme surface but also those in the bulk aqueous solution contribute to the water-entropy effect. The contribution from the latter is much larger.45 It is experimentally and theoretically known that the water dynamics is extremely fast and the relaxation (e.g., the structure formation of water near a protein surface) occurs on a picosecond time scale at room temperature.62 Water molecules are supplied in pico seconds upon their consumption by the reaction at the enzyme surface. Hence, neither the participation of water in the reaction nor the consumption of water influences the water-entropy effect.The substrate dynamics should be somewhat slower than the water dynamics. The thermodynamic quantities, S° and G° are introduced to analyze the layer formed near the enzyme surface within which substrates are enriched (the above discussion is focused on the enrichment at the surface). A question then arises: How long will it take for the layer to be formed? Rather hydrophobic substrates are attracted to the enzyme surface through the force which becomes progressively stronger as the distance from the surface x decreases.58 That is, the substrates are driven to move toward the surface by acceleration which increases with decreasing x. Even when the effect of the force is not taken into account, the time required for the substrates to reach the surface can be estimated to be only 10−8 s as explained in what follows. The thickness of the layer l within which substrates are enriched is only several times of the substrate size. When the substrate is p-NPA with a size of ∼0.8 nm, for example, l ∼ 4 nm. The diffusion length (∼the average distance by which substrates can move in t s) L is related to the diffusion coefficient of substrates D as L2 = 2Dt. Substituting L = l = 4 nm and D = 10−5 cm2 s−1 (this is the value for benzene63) in this equation yields t ∼ 10−8 s. In reality, the substrates are strongly attracted to the enzyme surface as mentioned above. It follows that the substrates reach the surface in 10−8 s or much faster (i.e., almost instantaneously). Upon the consumption of substrates near the surface by the chemical reaction, the supply of substrates is also completed almost instantaneously. We can conclude the following: when a physical or chemical process occurring on a many orders of magnitude longer time scale such as the enzymatic reaction is considered, it is rationalized to assume that the equilibrium concentration profile of substrates is always formed near the surface.
Summary of interpretation of experimental results
Strongly hydrated ions (SO42− and Mg2+), somewhat strongly hydrated ions (Na+ and Cl−), and highly hydrophilic solutes such as HEPES are enriched neither near the enzyme surface nor within the domain confined between enzyme surfaces. Unless the substrate is highly hydrophilic, the local concentration of substrates becomes higher within the confined domain in Ori-P than near the single enzyme in Ori-D or free in solution, leading to a higher initial reaction velocity. The water-entropy effect is enhanced upon addition of a salt whose ions are strongly hydrated, such as sulfate ions (SO42−), through modification of the bulk water structure. In the presence of 0.5 M Na2SO4, the initial reaction velocity was increased in all cases, i.e., free solution, on Ori-D, and on Ori-P as discussed in the section “Quantitative Analysis on Experimental Results Using Theoretical Model”. Due to the water-entropy effect, the apparent affinity of the substrate increases for any portion of the enzyme surface, accelerating the esterase reaction in the presence of strongly hydrated SO42−.ΔV1, ΔV2 = ξΔV1 (ξ > 0), 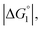 and χ2/χ1 increase as the EV of substrate becomes larger. With p-NPA as the substrate, the reaction was accelerated only 1.3 times on Ori-P over Ori-D, but 1.5 and 1.6 times with p-NPB and p-NPV, respectively. The substrate enrichment is strengthened for a more hydrophobic substrate, leading to larger χ2/χ1. This notion is corroborated in Fig. 4b where the fold enhancement of initial velocity of ZS-CA on Ori-D over that on Ori-P (acceleration factors corresponding to χ2/χ1) for the three substrates are plotted against the EV (Fig. 4b).
and χ2/χ1 increase as the EV of substrate becomes larger. With p-NPA as the substrate, the reaction was accelerated only 1.3 times on Ori-P over Ori-D, but 1.5 and 1.6 times with p-NPB and p-NPV, respectively. The substrate enrichment is strengthened for a more hydrophobic substrate, leading to larger χ2/χ1. This notion is corroborated in Fig. 4b where the fold enhancement of initial velocity of ZS-CA on Ori-D over that on Ori-P (acceleration factors corresponding to χ2/χ1) for the three substrates are plotted against the EV (Fig. 4b).
The sensitivity of the enzyme to inhibitory molecules or ions such as weakly hydrated, large halide anions (i.e., Br− and I−) and sulfonamides should be different depending on its assembly state. In the presence of 1 M NaBr, the initial velocities of p-NPA hydrolysis reactions by ZS-CA on Ori-D and Ori-P were reduced in all cases. Interestingly, the initial velocity of ZS-CA on Ori-P was 2.1 times higher than that on Ori-D or in free solution in the presence of 1 M NaBr (Fig. 4c). Considering the 1.5 times enhancement for the reaction of ZS-CA on Ori-P in the absence of bromide ion, ZS-CA on Ori-P tolerated better the inhibitory effect of bromide than ZS-CA on Ori-D or in free solution. Inhibition of the esterase reactions by increasing concentrations of acetazolamide also indicated the lower sensitivity of ZS-CA on Ori-P to the inhibitor at up to 100 nM (Fig. 4d). Acetazolamide is a competitive inhibitor to carbonic anhydrase activity43 and has lower hydrophobicity than the substrate p-NPA. By following our theory of the water-entropy effect, even in the presence of acetazolamide, enrichment of the more hydrophobic substrate p-NPA is favored over acetazolamide on the surface of packed state of enzyme. Taken together, the sensitivity of the esterase reaction to inhibitory molecules or ions varies depending on the assembled state of ZS-CA, which can reasonably be explained by the substrate enrichment near the enzyme surface driven by the entropic force.
The results obtained by reactions of ZS-XR assembled on Ori-D and Ori-P can be explained as follows. ZS-XR showed higher initial reaction rate in the packed state than in the dispersed state (Fig. 5b). Due to the rather hydrophobic nature of NADH over D-xylose, it can be suggested that the enrichment of NADH is responsible for the observed acceleration. Based on the hypothesis of substrate enrichment for the enzymes on Ori-P, the activity enhancement for the packed state of enzyme should be more prominent at low substrate concentrations. In fact, the activity enhancement is more prominent at low cofactor concentrations for XR as revealed by the reactions of ZS-XR/Ori-P and ZS-XR/Ori-D (Fig. S16†). Kinetic analyses by the Michaelis–Menten model (Fig. S17†) formally provided kinetic parameters for ZS-XR in the packed and the dispersed states. The Km varied little between the packed and the dispersed states for both D-xylose and NADH, while the turn-over number (kcat) was higher in the packed state than in the dispersed state. However, we speculate that the general Michaelis–Menten kinetic equation is not applicable for evaluation of the kinetic data for packed state of enzyme. The increase in local substrate concentration could only increase the enzymatic activity when the substrate concentration is unsaturated. Such a reaction condition is not assumed for the general Michaelis–Menten kinetic analyses. Therefore, it would be irrelevant to have a preconceived idea for the Michaelis–Menten constants on this reaction system. Further analyses on various types of enzymatic reactions in the packed state would address this issue.
We emphasize that all the water molecules in the system, i.e., not only the water molecules near the enzyme surface but also those in the bulk aqueous solution contribute to the water-entropy effect. The contribution from the latter is much larger.45 Moreover, the water dynamics is extremely fast, and water molecules are supplied in pico seconds upon their consumption by the reaction at the enzyme surface. Hence, neither the participation of water in the reaction nor the consumption of water influences the water-entropy effect. As for the reaction products, they rapidly dissociate from the enzyme surface as explained above, and they are not likely to influence the water-entropy effect.
Conclusion
In this study, the packed state of a single type of enzyme contributes to acceleration in the esterase reaction of CA or in the NADH dependent production of xylitol from xylose over those in the dispersed state. Moreover, in the packed state, the reaction proceeds faster for substrates with larger EVs and is more tolerant of inhibitors. We interpreted these results as follows: the reaction for the packed state of enzyme is accelerated by increasing the local concentration of substrate or cofactor within the domain confined between enzyme surfaces. The acceleration of an enzymatic reaction in the packed state over the dispersed one is ubiquitous as long as a component, either a substrate or a cofactor, participating in the reaction is rather hydrophobic and the distance between two enzyme surfaces in the packed state is comparable with the size of this component. Due to the entropic force, this component is enriched near an enzyme surface and even more enriched within the domain confined between enzyme surfaces, which is responsible for the acceleration. The entropic force originates from the translational displacement of water molecules in the entire system. Our finding offers a new insight on the efficiency of enzymatic reactions in the packed state. The water-entropy effect increases as the enzyme structure becomes less flexible in the packed assembly. Therefore, a greater effect is expected within the spatially constrained cellular compartments consisting of multiple types of enzymes, such as the possible internal packed assembly of proteins recently reported for the formation of liquid-like matrix of enzyme condensates inside the carboxysome.9 The controlled packed assembly of enzymes could be used to determine which ones are impacted by the packed state, particularly with respect to acceleration of reactions and interactions with particular substrates. In addition, our designed system enables us to investigate the reaction of not only the same type of enzyme but also that of different types of enzymes, and the ligand binding of receptors in reasonably packed states.Materials and methods
Materials
The single-stranded M13mp18, restriction enzymes (NdeI and NotI) and BG-GLA-NHS (S9151S) were purchased from New England Biolabs. Purified oligonucleotide as the staple strands for DNA origami, oligonucleotide primers for gene construction and all other oligonucleotides were purchased from Sigma-Aldrich (St. Louis, MO), Thermo Fisher Scientific Inc. (Waltham, MA, USA), Japan Bio Services Co., LTD (Saitama, Japan) and Gene Design Inc. (Osaka, Japan). Human Kidney QUICK-Clone™ cDNA was purchased from TaKaRa Bio Inc. (Shiga, Japan). E. coli BL21 (DE3) competent cells were purchased from Invitrogen (Carlsbad, CA). Mini Elute Gel Extraction Kit was purchased from QIAGEN (Tokyo, Japan). HiTrap SP HP column (5 ml), HisTrap HP column (5 ml) and Sephacryl S-400 were purchased from GE Healthcare Japan Inc. (Tokyo, Japan). PrimeSTAR HS DNA polymerase, T4 DNA ligase, and E. coli DH5α competent cells were purchased from TaKaRa Bio Inc. (Shiga, Japan). Ultrafree-MC-DV were purchased from Merck Millipore (Darmstadt, Germany). p-Nitrophenyl acetate (p-NPA), p-nitrophenyl butyrate (p-NPB) and p-nitrophenyl valerate (p-NPV) were purchased from Sigma Aldrich and used without further purification. Connolly solvent excluded volumes calculated by using Chem3D (ver.19, CambridgeSoft) were used as excluded volume (EV). Tetramethylammonium bromide, sodium bromide, and acetazolamide were purchased from Sigma Aldrich.Construction of a vector for ZS-CA
Human carbonic anhydrase II gene from Human Kidney QUICK-Clone™ cDNA and a modular adaptor ZS gene in pET-30a-ZF-SNAP vector30 were amplified by PCR using the primer pairs provided in Table S1.† The PCR products were run on a 1% agarose gel in a buffer (pH 8.3) containing 40 mM Tris–HCl, 20 mM acetic acid and 1 mM EDTA and were purified by Mini Elute Gel Extraction Kit. The PCR products and pET-30a were digested with NdeI and NotI and were purified separately in the same manner. These products were incubated with T4 DNA ligase then transformed into E. coli DH5α competent cells for amplification. The purity and sequence of vector encoding ZS-CA (termed as pET-30a-ZS-CA) were confirmed and transformed into E. coli BL21(DE3) competent cells. As a control, the gene of human carbonic anhydrase II with histidine tag at the N-terminus was also introduced into pET-30a vector digested with NdeI and NotI in the similar manner. Purified vector pET-30a-hCAII was transformed into E. coli BL21(DE3) for protein expression.Overexpression and purification of ZS-CA
The transformed cells were grown at 37 °C until OD600 reached 0.5, and protein expression was induced with 1 mM IPTG for 24 h at 25 °C. The soluble fraction of the cell lysate containing ZS-CA was loaded to a HisTrap HP column in a buffer (pH 7.5) containing 100 mM Tris–HCl, 200 mM NaCl, 5 mM β-mercaptoethanol, 100 μM ZnCl2 and 20 mM imidazole, and eluted using gradient imidazole elution (concentrations from 20 to 500 mM). The main fractions containing ZS-CA were collected and loaded to a HiTrap SP HP column in a buffer (pH 7.2) containing 50 mM HEPES, 5 mM β-mercaptoethanol, and 100 μM ZnCl2; these were then eluted by NaCl gradient. The purified ZS-CA was dialyzed by using a buffer (pH 7.2) containing 50 mM HEPES, 200 mM NaCl, 5 mM β-mercaptoethanol, 100 μM ZnCl2, and 50% glycerol and stored at −20 °C. The purity of ZS-CA was checked by SDS-polyacrylamide gel electrophoresis (PAGE). The major band in SDS-PAGE (Fig. S1†) corresponded to the calculated molecular weight of ZS-CA (62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934 Dalton) with purity over 95% (calculated from ImageJ). Amino acid sequence of ZS-CA was shown in Fig. S1b.† Similarly, the parent carbonic anhydrase with histidine tag at the N-terminus (hCAII) in the vector pET-30a-hCAII was expressed and purified. Esterase activities of ZS-CA and hCAII were compared (Fig. S2†). The binding ability of ZS-CA to the specific binding DNA sequence and kinetic parameters were confirmed (Fig. S3†).
934 Dalton) with purity over 95% (calculated from ImageJ). Amino acid sequence of ZS-CA was shown in Fig. S1b.† Similarly, the parent carbonic anhydrase with histidine tag at the N-terminus (hCAII) in the vector pET-30a-hCAII was expressed and purified. Esterase activities of ZS-CA and hCAII were compared (Fig. S2†). The binding ability of ZS-CA to the specific binding DNA sequence and kinetic parameters were confirmed (Fig. S3†).
Enzyme kinetics of ZS-CA
Assays for esterase activity of ZS-CA and substrates p-nitrophenyl acetate (p-NPA), p-nitrophenyl butyrate (p-NPB), p-nitrophenyl valerate (p-NPV) were carried out in 100 μL volume of 96-well non-binding plate (corning), using a variety of enzyme and substrate concentrations. An acetonitrile solution of each substrate (100 mM) was freshly prepared for each experiment. Due to the low solubility of p-NPA in the buffer, the maximum concentration of p-NPA in reaction was set to 1 mM. Final concentration of acetonitrile in the reaction mixture was kept to 1% in all experiments unless otherwise noted. Reactions were monitored at 384 nm (isosbestic point of p-nitrophenol and p-nitrophenolate) with the extinction coefficients of 5.0 × 103 M−1 cm−1 or at a maximum of absorbance at 400 nm (at pH 7.6) with the extinction coefficients of 1.28 × 104 M−1 cm−1.34 The rate of spontaneous hydrolysis without enzyme was subtracted from the enzymatic initial rate. A buffer (pH 7.6) containing 50 mM HEPES was chosen for the high reaction rate and the low spontaneous hydrolysis rate. The reaction mixture was composed of a buffer (pH 7.6) containing 50 mM HEPES, 12.5 mM MgCl2, 1% acetonitrile, 1 μM ZnCl2 and 0.001% Tween 20 with 1 mM p-NPA and 4 nM ZS-CA in assembly with DNA scaffold or in free solution (Fig. 2c) or 6 nM of DNA origami (with ZS-CA assembly) (Fig. 3e). ZS-CA (5.5 nM) and 1 mM p-NPA (Fig. 4a and d) or 0.1 mM p-NPA (Fig. 4c) were used in the reactions. In Fig. 4b, due to the even lower solubility of substrates p-NPB and p-NPV, all substrates (p-NPA, p-NPB and p-NPV) were prepared in 100% acetone and the reactions were carried out with 23 nM of ZS-CA and 0.1 mM substrates with 5% acetone instead of 1% acetonitrile.Preparation of the DNA scaffold
A solution (50 μL) containing M13mp18 single-stranded DNA (20 nM) and mixture of staple DNA strands (100 nM) of each staple strands, all of the staple strand sequences were shown in the previous report31 in a buffer (pH 8.0) containing 40 mM Tris–HCl, 20 mM acetic acid, 12.5 mM MgCl2 was heated at 95 °C for 1 min, incubated at 53 °C for 30 min, and then cooled down to 4 °C by using a thermal cycler (C1000 Thermal Cycler, BioRad). The sample was purified to remove excess staple strands by gel filtration (500 μL in volume of Sephacryl S-400) in Ultrafree-MC-DV column. The concentration of DNA scaffold was quantified by absorbance at 260 nm (the molar absorbance coefficient of DNA scaffold: εDNA scaffold = 1.27 × 108 M−1 cm−1).Preparation of DNA scaffold assembled with ZS-CA
A typical binding reaction of the purified DNA scaffold and ZS-CA was conducted with 16 nM DNA scaffold (64 nM binding site) and 200 nM ZS-CA in a buffer (pH 8.0) containing 40 mM Tris–HCl, 20 mM acetic acid, 12.5 mM MgCl2, 1 μM ZnCl2, 0.001% Tween 20, 5 mM β-mercaptoethanol and 125 nM of staple strands mixture for DNA scaffold (without the staple strands containing ZS-CA binding site). After 30 min incubation on ice, the mixtures were filtered through 500 μL bed volume of Sephacryl S400 to remove all the non-bound ZS-CA and to exchange with a buffer (pH 7.6) containing 50 mM HEPES, 12.5 mM MgCl2 for enzymatic assay.Atomic force measurement (AFM) imaging and statistical analysis
The purified sample solution was deposited on a freshly cleaved mica (1.5 mm in diameter) surface, adsorbed for 5 min at ambient temperature, and then washed three times with a buffer (pH 8.0) containing 40 mM Tris–HCl, 20 mM acetic acid, 12.5 mM MgCl2. The sample was scanned in solution with tapping mode using a fast-scanning AFM system (Nano Live Vision, RIBM Co. Ltd, Tsukuba, Japan) with a silicon nitride cantilever (Olympus BL-AC10DS-A2). At least three independent preparations of each sample were analysed by AFM, and several images were acquired from different regions of the mica surface. The total number of DNA scaffold corresponds to the number of expected rectangular shape possessing five cavities observed by AFM. The specific and non-specific binding of ZS-CA were counted only for the perfectly folded DNA scaffold.30The yield of specific ZS-CA loaded DNA cavities (Pspecific) was calculated as the percentage of the number of cavity containing ZS-CA molecules at the expected positions (Nexpected posi), e.g., centre cavity in the case of Ori-P, over the total number of ‘specific’ cavities (bearing binding sites) from only well-formed DNA scaffolds (1 × Ntotal for Ori-P with Ntotal is the number of well-formed DNA scaffolds):
| Pspecific = (Nexpected posi/Ntotal) × 100 |
The yield of ZS-CA-loaded DNA cavities at the unexpected positions (Pnonspecific) was calculated as the percentage of cavity containing ZS-CA molecules resided non-specifically (Nunexpected posi), e.g., other cavities beside the centre cavity in the case of Ori-P, over the total number of ‘non-specific’ cavities (without any binding sites) of well-formed DNA scaffold (4 × Ntotal for Ori-P):
| Pnon-specific = (Nunexpected posi/4Ntotal) × 100 |
Volume analysis of AFM images
AFM images of ZS-CA bound on DNA scaffold were analysed by using SPIP™ software (ver. 6.2.8, Image Metrology). First, the image was flattened then the z-volume value (defined as the volume of all pixels inside the shape's contour with a Z value) of particles correspond to ZS-CA on DNA scaffold was collected. The volume data were displayed as a histogram plot and each fraction was analysed by means of non-linear curve fit on a software (Origin Pro, ver. 9.1).30Calculating the inter-enzyme distance of ZS-CA in solution
The average distance separating molecules in solution was calculated as a function of molar concentration.64 In a 1 M enzyme solution, there are 6 × 1023 molecules per litre (0.6 molecules per nm3) or inverting, the volume per molecule is V = 1.66 nm3 per molecule at 1 M. Therefore, for a concentration C, the volume per molecule is V = 1.66/C. By taking the cube root of the volume per molecule, the average distance (d) is obtained from the equation:| d = V1/3 = 1.18/C1/3 |
Estimating the concentration of DNA scaffold and DNA scaffold–protein complexes
To determine the molar absorbance coefficient of DNA scaffold, the recover yield of DNA scaffold after gel filtration was deduced by quantitation of DNA in the agarose gel electrophoresis band (Fig. S6†) by following this equation:The recovery yield of the first purification of DNA scaffold only was estimated to be 83% from the ratio of band intensities (lane 3/lane 2). The recovery yield of the second purification after the binding reaction of DNA scaffold and ZS-CA was estimated to be 33% from the ratio of band intensities (lane 5/lane 4). From the starting concentration of DNA scaffold (20 nM), the concentration of DNA scaffold after each purification process was calculated. In a typical case as shown in Fig. S6, ESI,† the concentration of DNA scaffold after the first purification was 17 nM and after second purification was 4 nM. The concentration of DNA scaffold was quantified by using a NanoDrop spectrophotometer (Thermo Fisher) at 260 nm. The molar absorbance coefficient of DNA scaffold after the first purification (lane 3) was ε = 1.25 × 108 M−1 cm−1; after the second purification (lane 5): ε = 1.31 × 108 M−1 cm−1. The molar absorbance coefficient of ZS-CA was negligible to the value of DNA scaffold. The average of three experiments provided the molar absorbance coefficient of DNA scaffold (ε = 1.27 × 108 M−1 cm−1). The determined molar extinction coefficient is consistent with that of a fully double-stranded M13mp18 molecules (the calculated molar absorbance coefficient is 1.17 × 108 M−1 cm−1 from website: http://www.molbiotools.com/dnacalculator.html).
The concentration of ZS-CA assembled on DNA scaffold was estimated as follow:
Enzyme Assay of ZS-XR
Catalytic activity of ZS-XR on DNA scaffold was analyzed by measuring the changes of absorbance at 340 nm (25 °C) derived from the oxidation of NADH with an Infinite 200 PRO microplate reader (TECAN Austria GmbH). The reaction was started with an addition of ZS-XR/Ori-D or ZS-XR/Ori-P to a mixture of 200 mM D-xylose, 300 μM NADH in a buffer (pH 6.8) containing 50 mM HEPES, 12.5 mM MgCl2, 100 mM NaCl, 1 μM ZnCl2, and 0.001% Tween 20.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers 17H01213 (T. M.) and 19H04653 (E. N.), and by JST CREST Grant Number JPMJCR18H5 (T. M.), Japan.References
- C. A. Kerfeld, S. Heinhorst and G. C. Cannon, Annu. Rev. Microbiol., 2010, 64, 391–408 CrossRef CAS PubMed
.
- K. Jørgensen, A. V. Rasmussen, M. Morant, A. H. Nielsen, N. Bjarnholt, M. Zagrobelny, S. Bak and B. L. Møller, Curr. Opin. Plant Biol., 2005, 8, 280–291 CrossRef PubMed
.
- A. H. Chen and P. A. Silver, Trends Cell Biol, 2012, 22, 662–670 CrossRef CAS PubMed
.
- J. B. Thoden, H. M. Holden, G. Wesenberg, F. M. Raushel and I. Rayment, Biochemistry, 1997, 36, 6305–6316 CrossRef CAS PubMed
.
- D. R. Knighton, C. C. Kan, E. Howland, C. A. Janson, Z. Hostomska, K. M. Welsh and D. A. Matthews, Nat. Struct. Biol., 1994, 1, 186–194 CrossRef CAS PubMed
.
- T. Gabaldón and A. A. Pittis, Biochimie, 2015, 119, 262–268 CrossRef PubMed
.
- C. A. Kerfeld and O. Erbilgin, Trends Microbiol., 2015, 23, 22–34 CrossRef CAS PubMed
.
- T. O. Yeates, C. A. Kerfeld, S. Heinhorst, G. C. Cannon and J. M. Shively, Nat. Rev. Microbiol., 2008, 6, 681–691 CrossRef CAS PubMed
.
- H. Wang, X. Yan, H. Aigner, A. Bracher, N. D. Nguyen, W. Y. Hee, B. M. Long, G. D. Price, F. U. Hartl and M. Hayer-Hartl, Nature, 2019, 566, 131–135 CrossRef CAS PubMed
.
- J. M. Shively, F. Ball, D. H. Brown and R. E. Saunders, Science, 1973, 182, 584–586 CrossRef CAS PubMed
.
- C. V. Iancu, H. J. Ding, D. M. Morris, D. P. Dias, A. D. Gonzales, A. Martino and G. J. Jensen, J. Mol. Biol., 2007, 372, 764–773 CrossRef CAS PubMed
.
- M. F. Schmid, A. M. Paredes, H. A. Khant, F. Soyer, H. C. Aldrich, W. Chiu and J. M. Shively, J. Mol. Biol., 2006, 364, 526–535 CrossRef CAS PubMed
.
- A. Kuzmak, S. Carmali, E. von Lieres, A. J. Russell and S. Kondrat, Sci. Rep., 2019, 9, 1–7 CrossRef CAS PubMed
.
- L. J. Sweetlove and A. R. Fernie, Nat. Commun., 2018, 9, 2136 CrossRef PubMed
.
- P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed
.
- S. M. Douglas, H. Dietz, T. Liedl, B. Högberg, F. Graf and W. M. Shih, Nature, 2009, 459, 414–418 CrossRef CAS PubMed
.
- F. Zhang, J. Nangreave, Y. Liu and H. Yan, J. Am. Chem. Soc., 2014, 136, 11198–11211 CrossRef CAS PubMed
.
- F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS PubMed
.
- J. Fu, M. Liu, Y. Liu, N. W. Woodbury and H. Yan, J. Am. Chem. Soc., 2012, 134, 5516–5519 CrossRef CAS PubMed
.
- Z. Zhao, J. Fu, S. Dhakal, A. Johnson-Buck, M. Liu, T. Zhang, N. W. Woodbury, Y. Liu, N. G. Walter and H. Yan, Nat. Commun., 2016, 7, 10619 CrossRef CAS PubMed
.
- T. A. Ngo, E. Nakata, M. Saimura and T. Morii, J. Am. Chem. Soc., 2016, 138, 3012–3021 CrossRef CAS PubMed
.
- G. Ke, M. Liu, S. Jiang, X. Qi, Y. R. Yang, S. Wootten, F. Zhang, Z. Zhu, Y. Liu, C. J. Yang and H. Yan, Angew. Chem., Int. Ed., 2016, 55, 7483–7486 CrossRef CAS PubMed
.
- T. M. Nguyen, E. Nakata, M. Saimura, H. Dinh and T. Morii, J. Am. Chem. Soc., 2017, 139, 8487–8496 CrossRef CAS PubMed
.
- A. Rajendran, E. Nakata, S. Nakano and T. Morii, ChemBioChem, 2017, 18, 696–716 CrossRef CAS PubMed
.
- T. A. Ngo, H. Dinh, T. M. Nguyen, F. F. Liew, E. Nakata and T. Morii, Chem. Commun., 2019, 55, 12428–12446 RSC
.
- B. Sjöblom, M. Polentarutti, K. Djinovic-Carugo, B. Sjoblom, M. Polentarutti and K. Djinovic-Carugo, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10609–10613 CrossRef PubMed
.
- V. M. Krishnamurthy, G. K. Kaufman, A. R. Urbach, I. Gitlin, K. L. Gudiksen, D. B. Weibel and G. M. Whitesides, Chem. Rev., 2008, 108, 946–1051 CrossRef CAS PubMed
.
- N. P. Pavletich and C. O. Pabo, Science, 1991, 252, 809–817 CrossRef CAS PubMed
.
- A. Keppler, S. Gendreizig, T. Gronemeyer, H. Pick, H. Vogel and K. Johnsson, Nat. Biotechnol., 2003, 21, 86–89 CrossRef CAS PubMed
.
- E. Nakata, H. Dinh, T. A. Ngo, M. Saimura and T. Morii, Chem. Commun., 2015, 51, 1016–1019 RSC
.
- E. Nakata, F. F. Liew, C. Uwatoko, S. Kiyonaka, Y. Mori, Y. Katsuda, M. Endo, H. Sugiyama and T. Morii, Angew. Chem., Int. Ed., 2012, 51, 2421–2424 CrossRef CAS PubMed
.
- T. A. Ngo, E. Nakata, M. Saimura, T. Kodaki and T. Morii, Methods, 2014, 67, 142–150 CrossRef CAS PubMed
.
- H. Dinh, E. Nakata, P. Lin, M. Saimura, H. Ashida and T. Morii, Bioorganic Med. Chem., 2019, 27, 115120 CrossRef PubMed
.
- S. W. Schneider, J. Lärmer, R. M. Henderson and H. Oberleithner, Pflugers Arch, 1998, 435, 362–367 CrossRef CAS PubMed
.
- Y. Pocker and J. Stone, J. Biochemistry, 1967, 6, 668–678 CrossRef CAS PubMed
.
- J. a Verpoorte, S. Mehta and J. T. Edsall, J. Biol. Chem., 1967, 242, 4221–4229 Search PubMed
.
- R. J. Ellis, Trends Biochem. Sci., 2001, 26, 597–604 CrossRef CAS PubMed
.
- A. P. Minton, J. Biol. Chem., 2001, 276, 10577–10580 CrossRef CAS PubMed
.
- H. Steiner and S. Lindskog, FEBS Lett., 1972, 24, 85–88 CrossRef CAS
.
- M. L. Connolly, J. Am. Chem. Soc., 1985, 107, 1118–1124 CrossRef CAS
.
- M. L. Connolly, J. Mol. Graphics, 1993, 11, 139–141 CrossRef CAS PubMed
.
- G. De Simone and C. T. Supuran, J. Inorg. Biochem., 2012, 111, 117–129 CrossRef CAS PubMed
.
-
G. Holló, in Glaucoma, Elsevier, 2nd edn, 2014, vol. 1, pp. 559–565 Search PubMed
.
- S. Watanabe, A. A. Saleh, S. P. Pack, N. Annaluru, T. Kodaki and K. Makino, Microbiology, 2007, 153, 3044–3054 CrossRef CAS PubMed
.
- Y. Harano and M. Kinoshita, Biophys. J., 2005, 89, 2701–2710 CrossRef CAS PubMed
.
- M. Kinoshita, Biophys. Rev., 2013, 5, 283–293 CrossRef CAS PubMed
.
- M. Kinoshita, Chem. Eng. Sci., 2006, 61, 2150–2160 CrossRef CAS
.
- M. Kinoshita and T. Hayashi, J. Mol. Liq., 2017, 247, 403–410 CrossRef CAS
.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256 CrossRef CAS
.
- S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183–192 CrossRef CAS
.
- B. Götzelmann, R. Evans and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6785–6800 CrossRef
.
- C. Bechinger, D. Rudhardt, P. Leiderer, R. Roth and S. Dietrich, Phys. Rev. Lett., 1999, 83, 3960–3963 CrossRef CAS
.
- F. Kamo, R. Ishizuka and N. Matubayasi, Protein Sci., 2016, 25, 56–66 CrossRef CAS PubMed
.
- M. Kinoshita, J. Chem. Phys., 2002, 116, 3493–3501 CrossRef CAS
.
- T. Yoshidome, Y. Harano and M. Kinoshita, Phys. Rev. E - Stat. Nonlinear Soft Matter Phys., 2009, 79, 011912 CrossRef PubMed
.
- M. Kinoshita, Condens. Matter Phys., 2007, 10, 387–396 CrossRef
.
- β-Nicotinamide adenine dinucleotide, reduced disodium salt hydrate; MSDS no. 43423; Sigma-Aldrich: CH-9471 Buchs/Schweiz, 27th Aug 2007.
- X. Gong, C. Wang, L. Zhang and H. Qu, J. Chem. Eng. Data, 2012, 57, 3264–3269 CrossRef CAS
.
- M. Kinoshita, S. Y. Iba and M. Harada, J. Chem. Phys., 1996, 105, 2487–2499 CrossRef CAS
.
- S. Murakami, T. Hayashi and M. Kinoshita, J. Chem. Phys., 2017, 146, 055102 CrossRef PubMed
.
- D. Zezin, T. Driesner and C. Sanchez-Valle, J. Chem. Eng. Data, 2015, 60, 1181–1192 CrossRef CAS
.
- M. Maroncelli, J. Mol. Liq., 1993, 57, 1–37 CrossRef CAS
.
- D. R. Falcone, D. C. Douglass and D. W. McCall, J. Phys. Chem., 1967, 71, 2754–2755 CrossRef CAS
.
- H. P. Erickson, Biol. Proced. Online, 2009, 11, 32–51 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Primer sequences for ZS-CA (Table S1), ZS-CA characterizations (Fig. S1–S3), illustrations of DNA scaffolds (Fig. S4), distance of ZS-CA in the packed state (Fig. S5), purification of DNA scaffolds (Fig. S6), ZS-CA volume analyses (Fig. S7 and S8), initial velocities of ZS-CA assembled on DNA scaffolds (Fig. S9), ZS-CA activity with PEG 6K (Fig. S10), ZS-CA activity with macromolecular crowding reagents (Fig. S11), thermal stability of ZS-CA on DNA scaffolds (Fig. S12), ZS-CA with p-NPA, p-NPB and p-NPV (Fig. S13), effect of bromide ion on the ZS-CA (Fig. S14), analyses of ZS-XR volumes on DNA scaffolds (Fig. S15), kinetic analyses of ZS-XR on DNA scaffolds (Fig. S16 and S17). See DOI: 10.1039/d0sc03498c |
| This journal is © The Royal Society of Chemistry 2020 |