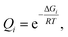Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the solubilization of Ca acetylide with a new computational model for ionic pairs†
Mikhail V.
Polynski
 *ab,
Mariia D.
Sapova
*ab,
Mariia D.
Sapova
 a and
Valentine P.
Ananikov
a and
Valentine P.
Ananikov
 *ab
*ab
aSaint Petersburg State University, Universitetsky Prospect 26, Saint Petersburg 198504, Russia. E-mail: polynskimikhail@gmail.com; val@ioc.ac.ru
bZelinsky Institute of Organic Chemistry, Russian Academy of Sciences, Leninsky Prospect 47, Moscow 119991, Russia
First published on 8th October 2020
Abstract
The unique reactivity of the acetylenic unit in DMSO gives rise to ubiquitous synthetic methods. We theoretically consider CaC2 solubility and protolysis in DMSO and formulate a strategy for CaC2 activation in solution-phase chemical transformations. For this, we use a new strategy for the modeling of ionic compounds in strongly coordinating solvents combining Born–Oppenheimer molecular dynamics with the DFTB3-D3(BJ) Hamiltonian and static DFT computations at the PBE0-D3(BJ)/pob-TZVP-gCP level. We modeled the thermodynamics of CaC2 protolysis under ambient conditions, taking into account its known heterogeneity and considering three polymorphs of CaC2. We give a theoretical basis for the existence of the elusive intermediate HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH and show that CaC2 insolubility in DMSO is of thermodynamic nature. We confirm the unique role of water and specific properties of DMSO in CaC2 activation and explain how the activation is realized. The proposed strategy for the utilization of CaC2 in sustainable organic synthesis is outlined.
C–Ca–OH and show that CaC2 insolubility in DMSO is of thermodynamic nature. We confirm the unique role of water and specific properties of DMSO in CaC2 activation and explain how the activation is realized. The proposed strategy for the utilization of CaC2 in sustainable organic synthesis is outlined.
Introduction
The construction of the carbon framework is one of the main goals of organic synthesis, and can be achieved using simple building blocks such as HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH or, better, HC
CH or, better, HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C− and even C
C− and even C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C2−. To obtain the latter two, one needs to use an acetylide source. Many metal acetylides are known, including acetylides of practically all classes of metals,1–10 and bi-metallic acetylides.11–13
C2−. To obtain the latter two, one needs to use an acetylide source. Many metal acetylides are known, including acetylides of practically all classes of metals,1–10 and bi-metallic acetylides.11–13
Among metal acetylides, widely produced CaC2 now appears to be the most versatile choice for the synthesis of organic substances, including those that are biologically active,14–24 as well as monomers.25–27 Moreover, CaC2 is envisioned to become the feedstock for the sustainable, carbon-neutral chemical industry.16,21,28 It is also considered valuable or promising in the synthesis of nanostructured materials,29,30 agriculture,31–34 and metallurgy (alloy making, see Section 2.3.8 in ref. 28). However, CaC2 is insoluble in organic solvents, which hampers its reactivity in the liquid phase.19,21,23,35,36
Preformed acetylides and acetylide intermediates play a key role in organic synthesis. Copper-catalyzed azide–alkyne cycloaddition (CuAAC)37,38 is a widely used reaction, in which the main intermediate is the unstable Cu acetylide having a Cu–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R moiety. The use of a preformed acetylide makes the reaction significantly more facile.39 Other organometallic acetylides such as those of Au,40 Bi,39 and Pt41 also undergo dipolar cycloaddition to azides; the corresponding AAC reaction products are potent precursors to a wide range of substituted heterocyclic compounds.39
C–R moiety. The use of a preformed acetylide makes the reaction significantly more facile.39 Other organometallic acetylides such as those of Au,40 Bi,39 and Pt41 also undergo dipolar cycloaddition to azides; the corresponding AAC reaction products are potent precursors to a wide range of substituted heterocyclic compounds.39
Activation of HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH or RC
CH or RC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH via acetylide formation is necessary in CuAAC42–45 and other46 reactions. It was proposed that “any s-acetylide that can effectively recruit a p-bound copper atom will undergo annulation with a compatible dipolar partner.”43 Ca acetylides undergo dipolar cycloadditions as well.14,47–49
CH via acetylide formation is necessary in CuAAC42–45 and other46 reactions. It was proposed that “any s-acetylide that can effectively recruit a p-bound copper atom will undergo annulation with a compatible dipolar partner.”43 Ca acetylides undergo dipolar cycloadditions as well.14,47–49
Acetylide species, like HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH, are often assumed to be intermediates in solution-phase organic reactions with CaC2 that is insoluble by itself;19,23,50 however, it is hard to detect these species in the liquid phase. Detection of soluble alkaline acetylides was reported under extremely basic conditions.35,51 Ca acetylide was experimentally detected with Fourier transform infrared spectroscopy in solid CaC2 in a KBr matrix when subjected to trace amounts of H2O.52 Acetylene chemistry in dimethyl sulfoxide (DMSO) under basic and super-basic conditions is a valuable and indispensable tool of modern organic chemistry.46,53–56 Greater potential of practically valuable synthesis with CaC2 can be realized through understanding the unique performance of DMSO solutions.
C–Ca–OH, are often assumed to be intermediates in solution-phase organic reactions with CaC2 that is insoluble by itself;19,23,50 however, it is hard to detect these species in the liquid phase. Detection of soluble alkaline acetylides was reported under extremely basic conditions.35,51 Ca acetylide was experimentally detected with Fourier transform infrared spectroscopy in solid CaC2 in a KBr matrix when subjected to trace amounts of H2O.52 Acetylene chemistry in dimethyl sulfoxide (DMSO) under basic and super-basic conditions is a valuable and indispensable tool of modern organic chemistry.46,53–56 Greater potential of practically valuable synthesis with CaC2 can be realized through understanding the unique performance of DMSO solutions.
Quantum chemical modeling of Ca acetylides in DMSO, reported below, required innovative consideration of ionic pairs in solution that have strong solute–solvent interactions. To obtain consistent models, we combined conformational sampling by molecular dynamics (MD) with the density-functional tight-binding (DFTB) Hamiltonian followed by DFT post-treatment of the conformations and free energy computations. Conformational sampling with fast semi-empirical methods has seen tremendous development recently.57–60 Combining them with DFT post-treatment allows, e.g., estimation of realistic IR spectra in solution61 and reliable exhaustive conformational sampling of organic macrocycles.62
Given the importance of CaC2 as a sustainable carbon source for organic synthesis and Ca acetylides as potent intermediates, we performed this computational study. Obtaining active acetylide intermediates is key to new solution-phase organic reactions with solid CaC2. As the main result, we propose a strategy for the development of new sustainable solution-phase transformations based on the utilization of CaC2.
Results and discussion
Thermodynamic model
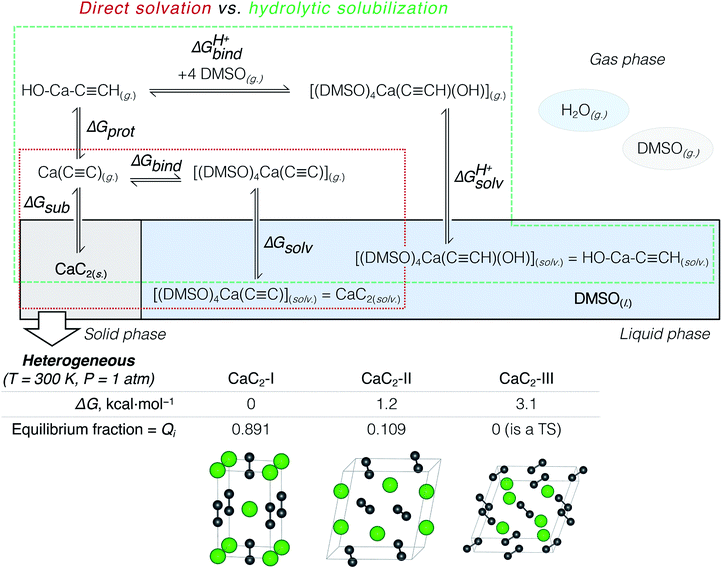
The suggested strategy for modeling the dissolution of ionic solids, possibly including partial solvolysis and (or) solvent coordination, combines DFTB molecular dynamics and static DFT computations. Fig. 1 depicts a schematic description of the methodology. All parameters are listed in the Computational details section below and in the ESI.† By using the suggested methodology, it is possible to obtain dissolution free energies (following all three stages in Fig. 1), as well as to model chemical transformations of ionic pairs in polar coordinating solutions (performing computations in the last two stages).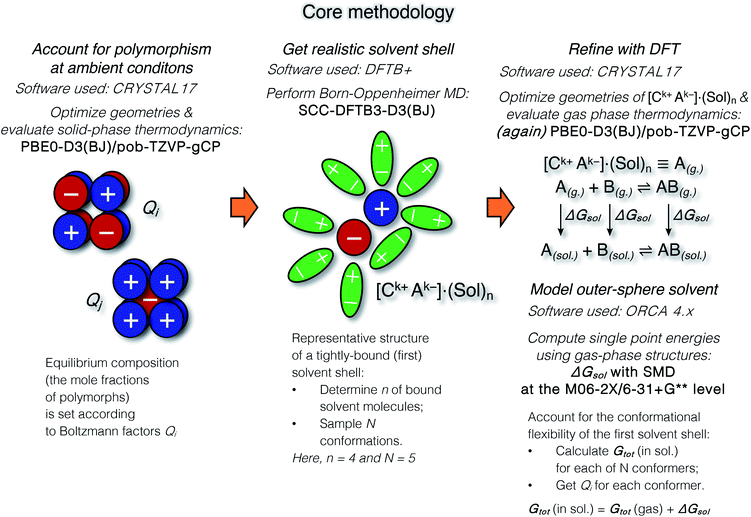 | ||
| Fig. 1 The core methodology and software used to perform the calculations outlined in Fig. 2. | ||
According to previous studies, Ca acetylide can undergo organic transformations in DMSO19,20,23,48,50 and dimethylformamide63 solutions upon the addition of water. That is why the consideration of partial hydrolysis is essential. We compare direct CaC2 solvation and solubilization involving partial hydrolysis by considering the elementary steps depicted in Fig. 2: the consideration starts from solid CaC2 and proceeds in the clockwise direction to solvated species. Note that the states of the intermediates (solid, gas, solvated) are explicitly defined in Fig. 2. We use an analog of the Born–Haber cycle, and model the solvation and hydrolysis as the sequence of hypothetical sublimation (ΔGsub), reactions in the gas phase (ΔGbind, ΔGprot, ΔGprotbind), and the subsequent solvation (ΔGsolv, ΔGprotsolv).
We calculated Boltzmann weights for the stable CaC2 polymorphs, isomers and conformers:
Solid Ca carbide and its sublimation
CaC2 is reported to be a mixture of three polymorphs CaC2-I, CaC2-II, and CaC2-III under ambient conditions.64–66 Because of the inconsistencies in previous studies,64,65 we present a more detailed discussion of our findings on the relative stability of CaC2 polymorphs in Section S2.†We compared the stability (relative ΔG) of these three phases at 200, 300, and 400 K and found that the well-known tetragonal CaC2-I form is the most stable. The equilibrium distribution of stable CaC2 phases under standard conditions was estimated by computing Boltzmann weights according to the calculated ΔG values (see Fig. 2 and the ESI† for details).
According to the harmonic vibrational mode analysis at the PBE0-D3(BJ)/pob-TZVP-gCP level (see Section S2† for details), CaC2-III has an imaginary frequency at Γ point, so we excluded it from the set of allowed thermodynamic states for the sake of model consistency. Excluding CaC2-III from the calculation of ΔGsub in Fig. 2 resulted in a negligible correction of less than 0.1 kcal mol−1 due to its relatively high free energy. In contrast, we did not observe any imaginary modes at the chosen level in the cases of CaC2-I and CaC2-II. The relative and absolute stability of CaC2 polymorphs remains unclear under theoretical considerations with computational methods (see the discussion of the relevant literature in Section S2.1†).
It was hypothesized that anharmonic effects may affect the stability of CaC2 phases.65 We believe that further investigation of potential energy surfaces of CaC2 polymorphs may be worthwhile, ideally, with Born–Oppenheimer MD (BOMD), to elucidate possible anharmonicity of atomic vibrations. As long as the proposed methodology (Fig. 1) is modular, any refinements of ΔG values can easily be incorporated.
The first elementary reaction to consider is the sublimation of CaC2 (ΔGsub). Computed at the PBE0-D3(BJ)/pob-TZVP level, the free energy of sublimation only slightly varied for the stable polymorphs: from 184.5 (CaC2-II) to 185.8 kcal mol−1 (CaC2-I). After Boltzmann averaging over stable CaC2 polymorphs we obtained 185.6 kcal mol−1 for the two-phase acetylide.
Ionic pairs in realistic solvent
DMSO solvates cations very efficiently, even more strongly than water.67,68 Exergonicity of cation solvation in DMSO can be attributed to the formation of strong cation–oxygen bonds in the coordination shell. Using implicit solvent models and neglecting direct Ca–O-bonding when modeling the solvation of CaC2 and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH ionic pairs in DMSO leads to inconsistent results, as demonstrated in Section S3.†
C–Ca–OH ionic pairs in DMSO leads to inconsistent results, as demonstrated in Section S3.†
We used Born–Oppenheimer molecular dynamics with the dispersion-corrected DFTB3-D3(BJ) Hamiltonian to determine the solvation shell of ionic pairs HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH and [Ca2+][C22−] in DMSO. First, we performed 10 ps-long isobaric-isothermal MD runs with the Berendsen thermostat and barostat to equilibrate the systems. Plots depicting the relaxation of the thermodynamic parameters V, P, and T, as well as of the sum U + PV + TSelec, are given in Section S5.†
C–Ca–OH and [Ca2+][C22−] in DMSO. First, we performed 10 ps-long isobaric-isothermal MD runs with the Berendsen thermostat and barostat to equilibrate the systems. Plots depicting the relaxation of the thermodynamic parameters V, P, and T, as well as of the sum U + PV + TSelec, are given in Section S5.†
Time evolution of the radial distribution functions (RDFs) demonstrates the equilibration of Ca2+ coordination number (CN, see Fig. 3 and Section S5†). Four DMSO molecules rapidly coordinate Ca2+ in the system with [Ca2+][C22−]. In the system with HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH, in contrast, the fourth DMSO molecule bonded to Ca2+ only in the last picosecond of the equilibration run (Fig. 3d).
C–Ca–OH, in contrast, the fourth DMSO molecule bonded to Ca2+ only in the last picosecond of the equilibration run (Fig. 3d).
Next, we subjected the HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH system to another 10 ps NPT run, now using the Nosé–Hoover chain thermostat and Berendsen barostat, to sample the configuration space (Fig. 3e). The model of CaC2 in DMSO was subjected to simulated annealing (NVT ensemble, Nosé–Hoover chain thermostat) by gradually heating the system to 600 K for 3 ps, preserving the temperature for 5 ps, gradually cooling the system for 3 ps, and then keeping the temperature at 300 K for another 5 ps.
C–Ca–OH system to another 10 ps NPT run, now using the Nosé–Hoover chain thermostat and Berendsen barostat, to sample the configuration space (Fig. 3e). The model of CaC2 in DMSO was subjected to simulated annealing (NVT ensemble, Nosé–Hoover chain thermostat) by gradually heating the system to 600 K for 3 ps, preserving the temperature for 5 ps, gradually cooling the system for 3 ps, and then keeping the temperature at 300 K for another 5 ps.
In the sampling run, we observed no additional binding of DMSO molecules in both systems (Fig. 3e); analogously, no additional DMSO molecules were bound as a result of the annealing (Fig. 3b). The resulting CNs are obtained from the integrals of the RDFs (Fig. 3c and f). Evidently, Ca2+ is six-coordinated in the HCC–Ca–OH system, which agrees with the experimentally observed CN of six for this cation in DMSO solutions.69 One may consider C22− as a κ2- or, equally, η2-ligand. In dynamics at 300 K, however, C22− mostly resides in the singly coordinated mode, which is why the second peak is present on the corresponding RDF at ∼340 pm (Fig. 3c and Section S6†). Since such behavior of C22− was unexpected, we performed simulated annealing of [Ca2+][C22−] in DMSO instead of an NPT run to check if the solvent shell would equilibrate to the same CN after the annealing and no more DMSO molecules would bind to Ca2+. We suppose that C22− strongly electrostatically repels O-centers in DMSO, so only 4 DMSO molecules could bind to Ca2+ under the selected computational protocol.
We performed Boltzmann averaging over the ensembles of solvated [Ca2+][C22−] and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH to obtain a conformationally sampled structure of Ca2+ solvation shell. For each system, we took 5 snapshots at distant trajectory points and cut Ca2+ with its first solvation shell representing a new model system for step 3 in Fig. 1, right (see Section S1.6† for details). Also, for both systems, we manually constructed conformations of the solvation shell by symmetrically placing 4 DMSO molecules in the equatorial plane of [(DMSO)4Ca(C
C–Ca–OH to obtain a conformationally sampled structure of Ca2+ solvation shell. For each system, we took 5 snapshots at distant trajectory points and cut Ca2+ with its first solvation shell representing a new model system for step 3 in Fig. 1, right (see Section S1.6† for details). Also, for both systems, we manually constructed conformations of the solvation shell by symmetrically placing 4 DMSO molecules in the equatorial plane of [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)] and in the base of the tetragonal pyramidal [(DMSO)4Ca(C
CH)(OH)] and in the base of the tetragonal pyramidal [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)]. The latter artificial conformations were included as a stress test of the presented methodology. As shown below, these artificial conformations are negligible contributors to the pool of conformers. Geometries of all snapshot conformations obtained in this way were optimized at the PBE0-D3(BJ)/pob-TZVP-gCP level.
C)]. The latter artificial conformations were included as a stress test of the presented methodology. As shown below, these artificial conformations are negligible contributors to the pool of conformers. Geometries of all snapshot conformations obtained in this way were optimized at the PBE0-D3(BJ)/pob-TZVP-gCP level.
Using the gas-phase optimized geometries, we calculated ΔGsolv for every conformer structure within the SMD approach (Solvation Model based on Density). We listed relative ΔG of the conformers and the corresponding Qi values in the ESI .xlsx table.† The most populated states (those with the highest Qi) in DMSO and vacuum mostly do not coincide; in all cases except iso1 of [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH) (OH)] (shown in Fig. 4), the highest Qi-conformers in DMSO are minor in a vacuum. Such a discrepancy can be expected because polar DMSO stabilizes polar conformations of the solute.
CH) (OH)] (shown in Fig. 4), the highest Qi-conformers in DMSO are minor in a vacuum. Such a discrepancy can be expected because polar DMSO stabilizes polar conformations of the solute.
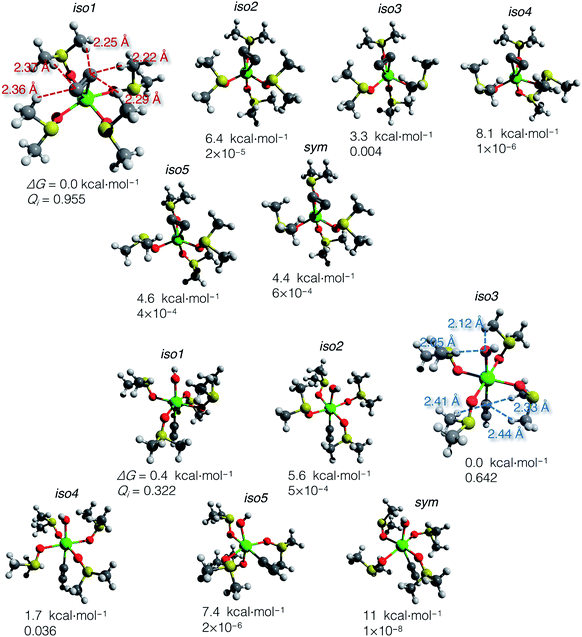 | ||
Fig. 4 Optimized structures of conformers: [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)] (top) and [(DMSO)4Ca(C C)] (top) and [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)] (bottom). Relative Gibbs energies and Boltzmann weights at 300 K are given below the structures. The most abundant conformers iso1 and iso3 are depicted with marked close noncovalent C(sp)–H and O–H contacts. Note that the sum of the van der Waals radii for the C(sp)–H and O–H contacts is 2.88 and 2.62 Å, according to Bondi.70 CH)(OH)] (bottom). Relative Gibbs energies and Boltzmann weights at 300 K are given below the structures. The most abundant conformers iso1 and iso3 are depicted with marked close noncovalent C(sp)–H and O–H contacts. Note that the sum of the van der Waals radii for the C(sp)–H and O–H contacts is 2.88 and 2.62 Å, according to Bondi.70 | ||
The computed ΔG of the conformers in DMSO, the corresponding Boltzmann weights, and the optimized structures are given in Fig. 4. The relative free energies of conformers vary within 8.1 kcal mol−1 for [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)], and 11 kcal mol−1 for [(DMSO)4Ca(C
C)], and 11 kcal mol−1 for [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)].
CH)(OH)].
The DMSO molecules of the solvation shells can form hydrogen bonds with C22−, HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C−, and OH− ligands, thereby giving this considerable spread in relative ΔG in solution with the selected model systems and at the chosen level of theory. Close C–H and O–H contacts, as well as the reference sum of the van der Waals radii, are given in Fig. 4.
C−, and OH− ligands, thereby giving this considerable spread in relative ΔG in solution with the selected model systems and at the chosen level of theory. Close C–H and O–H contacts, as well as the reference sum of the van der Waals radii, are given in Fig. 4.
In contrast to the case of [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)] that is predominantly represented by iso1, the model conformer space of [(DMSO)4Ca(C
C)] that is predominantly represented by iso1, the model conformer space of [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)] has two significant structures iso1 and iso3, and the somewhat minor iso4. All this emphasizes the importance of conformational sampling for cluster-continuum modeling of species in solutions.
CH)(OH)] has two significant structures iso1 and iso3, and the somewhat minor iso4. All this emphasizes the importance of conformational sampling for cluster-continuum modeling of species in solutions.
Boltzmann averaging over the conformers negligibly shifts the Gibbs energy of the ensemble of [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)] by 0.02 kcal mol−1, relative to the lowest energy conformer iso1. Similarly, the ensemble-averaged Gibbs energy of [(DMSO)4Ca(C
C)] by 0.02 kcal mol−1, relative to the lowest energy conformer iso1. Similarly, the ensemble-averaged Gibbs energy of [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)] is 0.19 kcal mol−1 higher than that of iso3. Even though the averaging correction at 300 K is minor, we still suggest using the presented two-step conformational sampling (BOMD plus static DFT). Therefore, in the absence of the sampling, if one considers only a minor conformer with low Qi, ΔG of elementary reaction steps can be inaccurate by several kcal mol−1.
CH)(OH)] is 0.19 kcal mol−1 higher than that of iso3. Even though the averaging correction at 300 K is minor, we still suggest using the presented two-step conformational sampling (BOMD plus static DFT). Therefore, in the absence of the sampling, if one considers only a minor conformer with low Qi, ΔG of elementary reaction steps can be inaccurate by several kcal mol−1.
Now we can estimate ΔG of the following reactions using the averaged free energies of the solvated species:
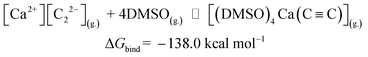 | (1) |
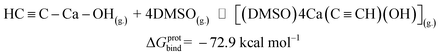 | (2) |
The reactions in eqn (1) and (2) are among the model steps in Fig. 2. We attribute the extremely exergonic effect of reactions (1) and (2) to the formation of strong Ca–O bonds, and—equally importantly—to the formation of many hydrogen bonds in the solvation shell. Even anionic centers of HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C− and C
C− and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C2− ligands are hydrogen bond acceptors, as can be seen from the abundance of close contacts in the structures in Fig. 4.
C2− ligands are hydrogen bond acceptors, as can be seen from the abundance of close contacts in the structures in Fig. 4.
The last step in Fig. 2 is to compute solvation energies of [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)] and [(DMSO)4Ca(C
C)] and [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)] (see eqn (3) and (4) below). The process of the immersion of electro-neutral species [(DMSO)4Ca(C
CH)(OH)] (see eqn (3) and (4) below). The process of the immersion of electro-neutral species [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)] and [(DMSO)4Ca(C
C)] and [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)] into DMSO is moderately exergonic, in contrast to the gas-phase formation of the coordination shell, as in eqn (1) and (2).
CH)(OH)] into DMSO is moderately exergonic, in contrast to the gas-phase formation of the coordination shell, as in eqn (1) and (2).
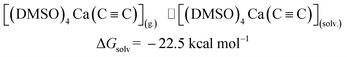 | (3) |
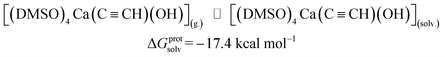 | (4) |
In this work, we selected M06-2X/6-31+G** as the underlying method for SMD computations of ΔGsolv since 6-31+G**71 was included in the original SMD parameterization,72 and since this CSM is often used in conjunction73–75 with the M06-2X functional.76 In Section S4,† we demonstrate that predictions of ΔGsolv with SMD at the M06-2X/6-31+G** level deviate by only 0.7 kcal mol−1 from those obtained at the M05-2X/6-31+G** level that was used in the original parameterization of SMD.72
A closely related two-step model process is the hydration of Ca2+ (Table 1). The details of the performed modeling of Ca2+ solvation in water are described in the ESI table.† As in the previous case with DMSO, most of the solvation exergonicity stems from the formation of the coordination sphere. The experimental value for the hydration of Ca2+ in water varies from −359.7 (ref. 77) to −386.2 (ref. 78) kcal mol−1 (the divergence is equal to 26.5 kcal mol−1), so the comparison with the experiment is possible, but cannot be performed reliably. Depending on the experimental reference, our computational estimation of ΔGsolv deviates from −1.3 to −27.8 kcal mol−1. The continuum models, used directly, i.e., without the explicit inclusion of a solvation shell, yield minimal deviations of +66.0, +64.7, and +75.9 kcal mol−1 for the COnductor-like Screening MOdel (COSMO), conductor-like polarizable continuum model (C-PCM), and SMD, respectively. Cluster-continuum computations, with our two-step calculation of ΔGsolv in H2O being one of this class, are a well-established approach to the modeling of ionic species in solution.79–82
| Transformation | ΔGrxn, kcal mol−1 |
|---|---|
| a The binding of H2O to Ca2+ was modeled at the RIJK-PBE0-D3(BJ)/def2-TZVP-gCP level; the hydration was modeled using SMD (M06-2X/6-31+G**). | |
| Ca(g.)2+ + 7H2O(g.) ⇌ [Ca(H2O)7](g.)2+ | −205.6 |
| [Ca(H2O)7](g.)2+ ⇌ [Ca(H2O)7](aq.)2+ | −181.9 |
| Ca(g.)2+ + 7H2O(g.) ⇌ [Ca(H2O)7](aq.)2+ | −387.5 |
| Experimental reference | −386.2 (ref. 78) to −359.7 (ref. 77) |
| Classical (non-quantum) electrostatic models | −377.3,83 −403.2 (ref. 78) |
Understanding CaC2 solubilization: direct solvation vs. hydrolytic solubilization
Table 2 summarizes the cumulative thermodynamic effect of the CaC2 dissolution in pure DMSO (+25.1 kcal mol−1) and its favorable hydrolysis in the DMSO/water solvent system (−9.1 kcal mol−1). The former is markedly endergonic, in accordance with the experimental observations of CaC2 inactivity in pure DMSO.19,21,23,35,36 Therefore, CaC2 dissolution in DMSO is thermodynamically forbidden. The solubilization can be achieved via the steady protonation of CaC2 at the solid–liquid interface, and the concomitantly formed HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C− can participate in subsequent transformations.
C− can participate in subsequent transformations.
| Transformation | ΔGrxn, kcal mol−1 |
|---|---|
| a Gas-phase thermochemistry was modeled at the PBE0-D3(BJ)/pob-TZVP-gCP level; bulk solvent effects were modeled using SMD (M06-2X/6-31+G**). | |
| Direct solvation | |
| CaC2(s.) ⇌ [Ca2+][C22−](g.) | ΔGsub = 185.6 |
[Ca2+][C22−](g.) + DMSO(g.) ⇌ [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)](g.) C)](g.) |
ΔGbind = −138.0 |
[(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)](g.) ⇌ [(DMSO)4Ca(C C)](g.) ⇌ [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)](solv.) C)](solv.) |
ΔGsolv = −22.5 |
CaC2(s.) ⇌ CaC2(solv.) (same as [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)](solv.)) C)](solv.)) |
ΔGsub + ΔGbind + ΔGsolv = 25.1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Protolysis-assisted solubilization | |
[Ca2+][C22−](g.) ⇌ HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH(g.) C–Ca–OH(g.) |
ΔGprot = −104.5 |
HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH(g.) + 4 DMSO(g.) ⇌ [(DMSO)4Ca(C C–Ca–OH(g.) + 4 DMSO(g.) ⇌ [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)](g.) CH)(OH)](g.) |
ΔGprotbind = −72.9 |
[(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH) (OH)](g.) ⇌ [(DMSO)4Ca(C CH) (OH)](g.) ⇌ [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)](solv.) CH)(OH)](solv.) |
ΔGprotsolv = −17.4 |
CaC2(s.) ⇌ HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ca–OH(solv.) (same as [(DMSO)4Ca(C C–Ca–OH(solv.) (same as [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH) (OH)](solv.)) CH) (OH)](solv.)) |
ΔGsub + ΔGprot + ΔGbindH+ + ΔGsolvH+ = −9.1 |
H2O can easily protonate C22−, as it is a much stronger acid. At the same time, H2O is less acidic than HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH in DMSO/water solutions, as seen from Table 3. We used a coarse quantum chemical approach to calculate free energies of H2O, DMSO, HC
CH in DMSO/water solutions, as seen from Table 3. We used a coarse quantum chemical approach to calculate free energies of H2O, DMSO, HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, and PhC≡CH deprotonation in DMSO (see also the ESI .xlsx table†). The reference pKa values show that H2O is ∼102 times less acidic than HC
CH, and PhC≡CH deprotonation in DMSO (see also the ESI .xlsx table†). The reference pKa values show that H2O is ∼102 times less acidic than HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH, and ∼1010 times less acidic according to our calculations. The deprotonation of HC
CH, and ∼1010 times less acidic according to our calculations. The deprotonation of HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C− yielding C22− should be as unfavorable as DMSO autoprotolysis.
C− yielding C22− should be as unfavorable as DMSO autoprotolysis.
| Transformation | ΔGrxn, kcal mol−1 | Calculated pKa | Reference pKa | Deviationa |
|---|---|---|---|---|
| a Between calculated and reference values. b The Gibbs free energy of a proton in DMSO is taken as the sum of G in the gas phase at 298.15 K and 1 atm (ref. 87) and ΔGsolv of H+ in DMSO.88 | ||||
HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH(solv.) ⇌ HC CH(solv.) ⇌ HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C(solv.)− + H(solv.)+b C(solv.)− + H(solv.)+b |
34.2 | 25.1 | 29.784 | −4.6 |
HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C(solv.)− ⇌ −C C(solv.)− ⇌ −C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C(solv.)− + H(solv.)+ C(solv.)− + H(solv.)+ |
50.6 | 37.1 | — | |
| PhC≡CH(solv.) ⇌ PhC≡C(solv.)− + H(solv.)+ | 34.6 | 25.4 | 28.785 | −3.6 |
| H2O(solv.) ⇌ HO(solv.)− + H(solv.)+ | 48.8 | 35.8 | 31.486 | 4.4 |
| CH3S(O)CH3(solv.) ⇌ CH3S(O)CH2(solv.)− + H(solv.)+ | 50.5 | 37.0 | 35.186 | 1.9 |
Acidities (pKa) of DMSO and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C− (second stage) are nearly equal, according to the PBE0/ma-def2-TZVP + SMD calculation. Therefore, we may suppose DMSO as a possible protolytic agent for C22− in solution. Indeed, C22− anions can undergo rapid protonation by DMSO (see the ESI .xlsx table†), meaning that the formation of free acetylide dianions in such a solution system is hardly possible. The solvent is not aprotic enough, even if we find a way to effectively solvate C22− with anion-sequestering host molecules, e.g., cavitands.
C− (second stage) are nearly equal, according to the PBE0/ma-def2-TZVP + SMD calculation. Therefore, we may suppose DMSO as a possible protolytic agent for C22− in solution. Indeed, C22− anions can undergo rapid protonation by DMSO (see the ESI .xlsx table†), meaning that the formation of free acetylide dianions in such a solution system is hardly possible. The solvent is not aprotic enough, even if we find a way to effectively solvate C22− with anion-sequestering host molecules, e.g., cavitands.
Modeled at the PBE0/ma-def2-TZVP level; bulk solvent effects were accounted for by applying SMD (M06-2X/6-31+G**) (see Section S1.3† for details).
We also estimated the favorability of HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C− protonation by the DMSO molecules of the Ca2+ solvation shell (as in Scheme 1). The free energies of activation of the two evaluated pathways are 20.7 and 21.5 kcal mol−1. Moreover, the process is endergonic by 17.7–20.3 kcal mol−1. Thus, the protonation of the acetylide in [(DMSO)4Ca(C
C− protonation by the DMSO molecules of the Ca2+ solvation shell (as in Scheme 1). The free energies of activation of the two evaluated pathways are 20.7 and 21.5 kcal mol−1. Moreover, the process is endergonic by 17.7–20.3 kcal mol−1. Thus, the protonation of the acetylide in [(DMSO)4Ca(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH)(OH)] is somewhat kinetically unfavorable, also being clearly unfavorable thermodynamically.
CH)(OH)] is somewhat kinetically unfavorable, also being clearly unfavorable thermodynamically.
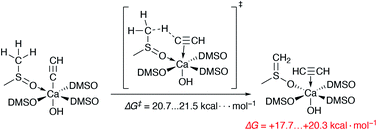 | ||
Scheme 1 The unfavorable process of the HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C− protonation by a DMSO molecule from the first solvation shell. All DMSO molecules are coordinated via O atoms. C− protonation by a DMSO molecule from the first solvation shell. All DMSO molecules are coordinated via O atoms. | ||
Other protic molecules such as inorganic acids HX, HClO4, and CF3SO3H (X = Cl, Br, I) are an inappropriate choice for the protolytic activation of CaC2. These acids are reported to be strong in DMSO.89 That is why their DMSO solutions can protonate not only C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C2− but also HC
C2− but also HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C−, thereby decomposing the reactive acetylide intermediate. Moderate acidity is crucial in our case.
C−, thereby decomposing the reactive acetylide intermediate. Moderate acidity is crucial in our case.
Summary, conclusions, and outlook
A protolytic agent plays a crucial role in the activation of a carbide in solution reactions. Water is a unique agent since it is less acidic than HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH in DMSO. The formation of anionic monoacetylide intermediates is the way to activate CaC2 in liquid-phase organic transformations. The dynamics of CaC2(s.) protolysis, proceeding at the solid–liquid interface, may thus be of paramount importance for further understanding of CaC2 activation. Research on the dynamics of this interface process is currently underway in our group.
CH in DMSO. The formation of anionic monoacetylide intermediates is the way to activate CaC2 in liquid-phase organic transformations. The dynamics of CaC2(s.) protolysis, proceeding at the solid–liquid interface, may thus be of paramount importance for further understanding of CaC2 activation. Research on the dynamics of this interface process is currently underway in our group.
We tested a new modeling strategy for solvated ionic pairs formed in the process of dissolution or protolysis of ionic crystals. It allowed us to obtain ensemble-averaged ΔG of reactions in solutions with species for which no CSM parameterization is available. We plan to further use and test this computational methodology, as well as encourage its use in other groups.
The methodology is modular, as it consists of three distinct steps depicted in Fig. 1. Therefore, evaluating alternative tight-binding parameterizations (e.g., eXtended Tight-Binding methods and GFNn-xTB)90,91 and CSMs (such as COSMO-RS)92 is advised to determine an optimal level of theory. Accounting for anharmonic effects in calculations of free energies can be another option for incremental improvement of the methodology. Such effects can be incorporated in the solid state step (Fig. 1, left),93,94 as well as in the MD95,96 and molecular DFT steps97,98 (Fig. 1, middle and right, respectively), although in the latter two cases this may be technically non-trivial. It was shown in recent studies of solid state and surface systems that anharmonic effects may be crucial.99,100 However, we should also mention a critique of existing approximations for computation of anharmonic free energies.101
Strongly coordinating solvents such as DMSO form a well-defined solvation shell that should be sampled with BOMD. A very economical choice is to use a tight-binding Hamiltonian such as DFTB3 with empirical corrections for non-covalent interactions. In our case, running even relatively short equilibration trajectories of 10 ps yielded ensemble-sampled structures of solvation shells. Free energy computations with MD methods require rather elaborate techniques.102,103 That is why Boltzmann averaging over an MD-obtained set of solvation shell conformers can be a convenient option. The proposed combination of semi-empirical BOMD and static DFT computations of ΔG values is cost-efficient since the most demanding step—the sampling of conformer space with MD—is feasible even on a personal workstation. We performed most of the MD simulations on an entry-level graphics processing unit (GPU) and a gaming central processor (CPU, see the ESI† for details).
As a fundamental result, we propose a strategy for CaC2 activation in organic media that can boost further development of green and sustainable synthetic methodologies based on the use of calcium carbide. DMSO, as well as dimethylformamide which is widely used in reactions with CaC2, is not a particularly “green” solvent. Less toxic polar aprotic solvents that allow water pKa higher than acetylene pKa would be a better choice for future organic synthesis; no less important is the propensity to effectively solvate Ca2+ by forming strong Ca-solvent bonds, such as, e.g., Ca–O. There are few such solvents. Here we assessed H2O as a suitable green protolytic agent for a solid acetylide. However, we hypothesize that any molecule less protic then HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH in a given solvent can play its role, thereby allowing new synthetic transformations. Computational methods, as described in this work, can help in the evaluation of known green solvents for sustainable organic synthesis with CaC2 or in the search for new ones, as well as in the discovery of new protolytic agents for the activation of CaC2.
CH in a given solvent can play its role, thereby allowing new synthetic transformations. Computational methods, as described in this work, can help in the evaluation of known green solvents for sustainable organic synthesis with CaC2 or in the search for new ones, as well as in the discovery of new protolytic agents for the activation of CaC2.
Computational details
Solvation free energies of species in Fig. 2 were estimated using ORCA 4.1.2.104 The solvation model based on density (SMD) was selected for this purpose.72 All implicit solvent computations were performed on gas-phase geometries, as in the original studies.72,105,106 ΔGsolv is the difference between the single point (total) energies of gas-phase geometries with SMD applied, and without. We chose the diffuse basis set (BS) 6-31+G**,71,107,108 since we modeled anionic species in pKa estimations, and, at the same time, this basis set was included in the SMD parameterization. For Ca, we accepted the default ORCA104 choice and used diffuse exponents from 6-311+G**, which was adopted from the EMSL basis set exchange.109–111 In the original work, SMD was parameterized for use at the M05-2X/6-31+G** level of theory;112 the corresponding functional is, however, unavailable in ORCA. Therefore, we selected its successor, M06-2X,76 that is successfully employed in computations with SMD73–75 (see also Sections S1.2 and S4†).The CRYSTAL17 (ref. 113) program was used for evaluation of gas-phase energies and thermodynamic corrections for reactions in Fig. 2. The pob-TZVP basis set was used.114 The PBE0 functional was selected. Empirical corrections for dispersion interactions (D3, including the Becke–Johnson dumping function) and geometrical counterpoise corrections (gCP)115,116 were included (see Section S1.1† for details).
The self-consistent charge density-functional tight-binding method DFTB3 (ref. 117 and 118) was used for Born–Oppenheimer molecular dynamics of model DMSO solutions. The computations were performed in the DFTB+ program (ver. 19.1).119 The Third-Order Parametrization for Organic and Biological Systems (3OB) of SCC-DFTB was used.120–122 All parameters selected in SCC-DFTB3 computations are given in Section S1.6,† together with a description of how model systems with explicit DMSO solvent were constructed.
We modeled C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C2− and –C
C2− and –C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH protonation by DMSO using the B97-3c method123 for gas-phase calculations and SMD for the evaluation of solvation free energies (as described above). These computations were performed with ORCA 4.1.2 (see Section S1.5† for details).
CH protonation by DMSO using the B97-3c method123 for gas-phase calculations and SMD for the evaluation of solvation free energies (as described above). These computations were performed with ORCA 4.1.2 (see Section S1.5† for details).
Travis (update Jan 01, 2019)124 was used to plot radial distribution functions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the Computing Center of the Saint Petersburg State University for providing computational resources. M. V. P. and M. D. S. are grateful to Profs. Robert A. Evarestov and Vitaly V. Porsev for useful discussions on solid-state and cluster modeling. Dr Maria S. Ledovskaya, Dr Vladimir V. Voronin, and Dr Konstantin S. Rodygin are acknowledged for helpful discussions; Alexandra Erofeeva is acknowledged for facilitating research.References
- B. Hajek, P. Karen and V. Brozek, Rev. Inorg. Chem., 1986, 8, 117–160 CAS.
- U. Ruschewitz and W. Kockelmann, Z. Anorg. Allg. Chem., 1999, 625, 1041–1046 CrossRef CAS.
- J. Nylén, S. Konar, P. Lazor, D. Benson and U. Häussermann, J. Chem. Phys., 2012, 137, 224507 CrossRef.
- M. Atoji, J. Chem. Phys., 1974, 60, 3324–3327 CrossRef CAS.
- Y.-L. Lu and H. Zhao, Mod. Phys. Lett. B, 2014, 28, 1450190 CrossRef CAS.
- M. A. Bredig, J. Am. Chem. Soc., 1943, 65, 1482–1483 CrossRef CAS.
- J. E. Hein and V. V. Fokin, Chem. Soc. Rev., 2010, 39, 1302–1315 RSC.
- K. Judai, J. Nishijo and N. Nishi, Adv. Mater., 2006, 18, 2842–2846 CrossRef CAS.
- R. Poettgen and W. Jeitschko, Inorg. Chem., 1991, 30, 427–431 CrossRef CAS.
- T. Sakai, G. Y. Adachi, T. Yoshida and J. Shiokawa, J. Chem. Phys., 1981, 75, 3027–3032 CrossRef CAS.
- U. Ruschewitz, Z. Anorg. Allg. Chem., 2006, 632, 705–719 CrossRef CAS.
- W. Kockelmann and U. Ruschewitz, Angew. Chem., Int. Ed., 1999, 38, 3492–3495 CrossRef CAS.
- U. Cremer and U. Ruschewitz, Z. Anorg. Allg. Chem., 2004, 630, 161–166 CrossRef CAS.
- Y. Yu, Y. Chen, W. Huang, W. Wu and H. Jiang, J. Org. Chem., 2017, 82, 9479–9486 CrossRef CAS.
- W. E. Van Beek, K. Gadde and K. A. Tehrani, Chem.–Eur. J., 2018, 24, 16645–16651 CrossRef CAS.
- K. S. Rodygin, K. A. Lotsman and V. P. Ananikov, ChemSusChem, 2020, 13, 3679–3685 CrossRef CAS.
- S. P. Teong, D. Yu, Y. N. Sum and Y. Zhang, Green Chem., 2016, 18, 3499–3502 RSC.
- Y. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Acc. Chem. Res., 2016, 49, 750–762 CrossRef CAS.
- D. Yu, Y. N. Sum, A. C. C. Ean, M. P. Chin and Y. Zhang, Angew. Chem., Int. Ed., 2013, 52, 5125–5128 CrossRef CAS.
- E. Rattanangkool, T. Vilaivan, M. Sukwattanasinitt and S. Wacharasindhu, Eur. J. Org. Chem., 2016, 2016, 4347–4353 CrossRef CAS.
- Z. Lin, D. Yu, Y. N. Sum and Y. Zhang, ChemSusChem, 2012, 5, 625–628 CrossRef CAS.
- I. Jesin and G. C. Nandi, Eur. J. Org. Chem., 2019, 2019, 2704–2720 CrossRef CAS.
- Y. N. Sum, D. Yu and Y. Zhang, Green Chem., 2013, 15, 2718–2721 RSC.
- R. Fu and Z. Li, Org. Lett., 2018, 20, 2342–2345 CrossRef CAS.
- K. S. Rodygin and V. P. Ananikov, Green Chem., 2016, 18, 482–486 RSC.
- G. Werner, K. S. Rodygin, A. A. Kostin, E. G. Gordeev, A. S. Kashin and V. P. Ananikov, Green Chem., 2017, 19, 3032–3041 RSC.
- M. S. Ledovskaya, V. V. Voronin, K. S. Rodygin, A. V. Posvyatenko, K. S. Egorova and V. P. Ananikov, Synthesis, 2019, 51, 3001–3013 CrossRef CAS.
- K. S. Rodygin, Y. A. Vikenteva and V. P. Ananikov, ChemSusChem, 2019, 12, 1483–1516 CrossRef CAS.
- R. He, Z. Wang and X. Jin, Carbon, 2017, 116, 246–254 CrossRef CAS.
- Y. Jia, X. Chen, G. Zhang, L. Wang, C. Hu and X. Sun, J. Mater. Chem. A, 2018, 6, 23638–23643 RSC.
- M. Yaseen, M. Arshad and A. Khalid, Handb. Environ. Chem. Vol. 5 Water Pollut., 2006, vol. 50, pp. 405–411 Search PubMed.
- M. S. Aulakh, K. Singh and J. Doran, Biol. Fertil. Soils, 2001, 33, 258–263 CrossRef CAS.
- J. R. Freney, C. J. Smith and A. R. Mosier, Fert. Res., 1992, 32, 1–11 CrossRef CAS.
- M. Shakar, M. Yaseen, R. Mahmood and I. Ahmad, N. Z. J. Crop Hortic. Sci., 2017, 45, 251–262 CrossRef CAS.
- M. Hamberger, S. Liebig, U. Friedrich, N. Korber and U. Ruschewitz, Angew. Chem., Int. Ed., 2012, 51, 13006–13010 CrossRef CAS.
- N. Kaewchangwat, R. Sukato, V. Vchirawongkwin, T. Vilaivan, M. Sukwattanasinitt and S. Wacharasindhu, Green Chem., 2015, 17, 460–465 RSC.
- M. Meldal and C. W. Tomøe, Chem. Rev., 2008, 108, 2952–3015 CrossRef CAS.
- E. Haldón, M. C. Nicasio and P. J. Pérez, Org. Biomol. Chem., 2015, 13, 9528–9550 RSC.
- B. T. Worrell, S. P. Ellery and V. V. Fokin, Angew. Chem., Int. Ed., 2013, 52, 13037–13041 CrossRef CAS.
- A. R. Powers, I. Ghiviriga, K. A. Abboud and A. S. Veige, Dalton Trans., 2015, 44, 14747–14752 RSC.
- C. C. Beto, Y. Yang, C. J. Zeman, I. Ghiviriga, K. S. Schanze and A. S. Veige, Organometallics, 2018, 37, 4545–4550 CrossRef CAS.
- R. Chung, A. Vo, V. V. Fokin and J. E. Hein, ACS Catal., 2018, 8, 7889–7897 CrossRef CAS.
- B. T. Worrell, J. A. Malik and V. V. Fokin, Science, 2013, 340, 457–460 CrossRef CAS.
- D. Cantillo, M. Ávalos, R. Babiano, P. Cintas, J. L. Jiménez and J. C. Palacios, Org. Biomol. Chem., 2011, 9, 2952–2958 RSC.
- H. Chen, C. Soubra-Ghaoui, Z. Zhu, S. Li, T. A. Albright and C. Cai, J. Catal., 2018, 361, 407–413 CrossRef CAS.
- E. Y. Schmidt, I. A. Bidusenko, N. I. Protsuk, Y. V. Demyanov, I. A. Ushakov and B. A. Trofimov, Eur. J. Org. Chem., 2019, 2019, 5875–5881 CrossRef CAS.
- Y. Jiang, C. Kuang and Q. Yang, Synlett, 2009, 2009, 3163–3166 CrossRef.
- Y. Yu, W. Huang, Y. Chen, B. Gao, W. Wu and H. Jiang, Green Chem., 2016, 18, 6445–6449 RSC.
- M. S. Ledovskaya, K. S. Rodygin and V. P. Ananikov, Org. Chem. Front., 2018, 5, 226–231 RSC.
- A. Hosseini, D. Seidel, A. Miska and P. R. Schreiner, Org. Lett., 2015, 17, 2808–2811 CrossRef CAS.
- Y. Tanaka, M. Arakawa, Y. Yamaguchi, C. Hori, M. Ueno, T. Tanaka, T. Imahori and Y. Kondo, Chem.–Asian J., 2006, 1, 581–585 CrossRef CAS.
- M. M. Trubyanov, G. M. Mochalov, S. S. Suvorov, E. S. Puzanov, A. N. Petukhov, I. V. Vorotyntsev and V. M. Vorotyntsev, J. Chromatogr. A, 2018, 1560, 71–77 CrossRef CAS.
- Y. L. Frolov, I. V. Guchik, V. A. Shagun and A. V. Vashchenko, J. Struct. Chem., 2005, 46, 979–984 CrossRef CAS.
- B. A. Trofimov and E. Y. Schmidt, Russ. Chem. Rev., 2014, 83, 600–619 CrossRef.
- N. M. Vitkovskaya, V. B. Orel, V. B. Kobychev, A. S. Bobkov, E. Y. Larionova and B. A. Trofimov, J. Phys. Org. Chem., 2017, 30, e3669 CrossRef.
- N. M. Vitkovskaya, V. B. Orel, V. B. Kobychev, A. S. Bobkov, D. Z. Absalyamov and B. A. Trofimov, Int. J. Quantum Chem., 2020, 120, e26158 CrossRef CAS.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- D. I. Sharapa, A. Genaev, L. Cavallo and Y. Minenkov, ChemPhysChem, 2019, 20, 92–102 CAS.
- J. Cuny, K. Korchagina, C. Menakbi and T. Mineva, J. Mol. Model., 2017, 23, 1–8 CrossRef CAS.
- S. A. Katsyuba, E. E. Zvereva and S. Grimme, J. Phys. Chem. A, 2019, 123, 3802–3808 CrossRef CAS.
- O. Gutten, D. Bím, J. Řezáč and L. Rulíšek, J. Chem. Inf. Model., 2018, 58, 48–60 CrossRef CAS.
- Q. Yang, Y. Jiang and C. Kuang, Helv. Chim. Acta, 2012, 95, 448–454 CrossRef CAS.
- A. Kulkarni, K. Doll, J. C. Schön and M. Jansen, J. Phys. Chem. B, 2010, 114, 15573–15581 CrossRef CAS.
- S. Konar, J. Nylén, G. Svensson, D. Bernin, M. Edén, U. Ruschewitz and U. Häussermann, J. Solid State Chem., 2016, 239, 204–213 CrossRef CAS.
- M. Knapp and U. Ruschewitz, Chem.–Eur. J., 2001, 7, 874–880 CrossRef CAS.
- E. Buncel and H. Wilson, Adv. Phys. Org. Chem., 1977, 14, 133–202 CrossRef CAS.
- C. Kalidas, G. Hefter and Y. Marcus, Chem. Rev., 2000, 100, 819–852 CrossRef CAS.
- H. Ohtaki, Monatsh. Chem., 2001, 132, 1237–1268 CrossRef CAS.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- A. C. Chamberlin, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2008, 112, 8651–8655 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543 CrossRef CAS.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Comput.-Aided Mol. Des., 2010, 24, 317–333 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999 RSC.
- A. Kumar, J. Phys. Soc. Jpn., 1992, 61, 4247–4250 CrossRef CAS.
- J. R. Pliego and J. M. Riveros, J. Phys. Chem. A, 2001, 105, 7241–7247 CrossRef CAS.
- Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77 CrossRef.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard III, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS.
- J. R. Pliego and J. M. Riveros, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1440 CAS.
- P. Koehl, H. Orland and M. Delarue, J. Phys. Chem. B, 2009, 113, 5694–5697 CrossRef CAS.
- V. B. Kobychev, V. B. Orel, N. M. Vitkovskaya and B. A. Trofimov, Dokl. Chem., 2014, 457, 126–128 CrossRef CAS.
- F. G. Bordwell, G. E. Drucker, N. H. Andersen and A. D. Denniston, J. Am. Chem. Soc., 1986, 108, 7310–7313 CrossRef CAS.
- W. N. Olmstead, Z. Margolin and F. G. Bordwell, J. Org. Chem., 1980, 45, 3295–3299 CrossRef CAS.
- J. J. Fifen, Z. Dhaouadi and M. Nsangou, J. Phys. Chem. A, 2014, 118, 11090–11097 CrossRef CAS.
- W. R. Fawcett, Langmuir, 2008, 24, 9868–9875 CrossRef CAS.
- A. Trummal, L. Lipping, I. Kaljurand, I. A. Koppel and I. Leito, J. Phys. Chem. A, 2016, 120, 3663–3669 CrossRef CAS.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- A. Erba, J. Maul, M. Ferrabone, P. Carbonnière, M. Rérat and R. Dovesi, J. Chem. Theory Comput., 2019, 15, 3755–3765 CrossRef CAS.
- A. Erba, J. Maul, M. Ferrabone, R. Dovesi, M. Rérat and P. Carbonnière, J. Chem. Theory Comput., 2019, 15, 3766–3777 CrossRef CAS.
- S. Wang, ACS Omega, 2019, 4, 9271–9283 CrossRef CAS.
- F. Schmalz, W. A. Kopp, L. C. Kröger and K. Leonhard, ACS Omega, 2020, 5, 2242–2253 CrossRef.
- Y. P. Li, A. T. Bell and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 2861–2870 CrossRef CAS.
- M. W. D. Hanson-Heine, J. Phys. Chem. A, 2019, 123, 9800–9808 CrossRef CAS.
- A. Lamaire, J. Wieme, S. M. J. Rogge, M. Waroquier and V. Van Speybroeck, J. Chem. Phys., 2019, 150, 094503 CrossRef.
- V. Kapil, J. Wieme, S. Vandenbrande, A. Lamaire, V. Van Speybroeck and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 3237–3249 CrossRef CAS.
- V. Kapil, E. Engel, M. Rossi and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 5845–5857 CrossRef CAS.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CAS.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS.
- W. J. Hehre, K. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459 CrossRef CAS.
- H. Kruse and S. Grimme, J. Chem. Phys., 2012, 136, 154101 CrossRef.
- J. G. Brandenburg, M. Alessio, B. Civalleri, M. F. Peintinger, T. Bredow and S. Grimme, J. Phys. Chem. A, 2013, 117, 9282–9292 CrossRef CAS.
- Y. Yang, H. Yu, D. York, Q. Cui and M. Elstner, J. Phys. Chem. A, 2007, 111, 10861–10873 CrossRef CAS.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948 CrossRef CAS.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS.
- M. Gaus, A. Goez and M. Elstner, J. Chem. Theory Comput., 2013, 9, 338–354 CrossRef CAS.
- M. Gaus, X. Lu, M. Elstner and Q. Cui, J. Chem. Theory Comput., 2014, 10, 1518–1537 CrossRef CAS.
- M. Kubillus, T. Kubař, M. Gaus, J. Řezáč and M. Elstner, J. Chem. Theory Comput., 2015, 11, 332–342 CrossRef CAS.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04752j |
| This journal is © The Royal Society of Chemistry 2020 |