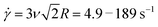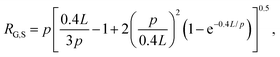Unexpected entanglement dynamics in semidilute blends of supercoiled and ring DNA

Abstract

Blends of polymers of different topologies, such as ring and supercoiled, naturally occur in biology and often exhibit emergent viscoelastic properties coveted in industry. However, due to their complexity, along with the difficulty of producing polymers of different topologies, the dynamics of topological polymer blends remains poorly understood. We address this void by using both passive and active microrheology to characterize the linear and nonlinear rheological properties of blends of relaxed circular and supercoiled DNA. We characterize the dynamics as we vary the concentration from below the overlap concentration c* to above (0.5c* to 2c*). Surprisingly, despite working at the dilute–semidilute crossover, entanglement dynamics, such as elastic plateaus and multiple relaxation modes, emerge. Finally, blends exhibit an unexpected sustained elastic response to nonlinear strains not previously observed even in well-entangled linear polymer solutions.

---

Introduction

DNA is a ubiquitous biopolymer that naturally exists in multiple topologies such as linear, relaxed circular (ring), and supercoiled.^1–3 Due to the unique ability to produce precise lengths and topologies on demand, DNA has been studied extensively over the past few decades as a model system to shed light on controversial polymer physics principles.^4–17 These studies – along with theoretical investigations and synthetic polymer experiments – have enabled a robust understanding of the dynamics of solutions of linear polymers in all three concentration regimes: dilute (c < c*), semidilute (c ∼ c*) and entangled (c ≫ c*), where c* is the concentration at which polymer coils begin to overlap, defined as (3/4π)M/N_AR_G³ where R_G is radius of gyration, N_A is Avogadro's number and M is molecular weight.^16,18–20 However, much less understood are the dynamics of solutions of polymers of different topologies, such as ring and supercoiled constructs, as well as polymer blends.^{2,16,19,21–25} Moreover, the limited studies on these systems have shown that polymeric blends can display unique and surprising viscoelastic properties that are not only intriguing from a physics point of view but also beneficial for the design of new multifunctional materials.^{16,19,26–28} For example, blends of ring and linear polymers have been shown to display increased viscosity, suppressed relaxation, and hindered diffusion compared to monodisperse systems of linear chains or rings.^27,29–33 These results suggest that interactions between topologically distinct polymers are key to emergent mechanics, and could be harnessed to produce tunable materials with a wide parameter space of function. However, the emergent properties reported thus far have only been observed at concentrations above the entanglement concentration c_e which is several times larger than c*.^{12,13,16,26,27}

Here, we combine passive and active microrheology to determine the linear and nonlinear rheological properties of blended solutions of ring and supercoiled DNA (Fig. 1). We show that these blends exhibit surprising signatures of classical polymer entanglements at concentrations much lower than similar monodisperse systems of linear or ring polymers. These emergent properties demonstrate that topological blends can be exploited to create robust and stiff materials with much lower concentrations than monodisperse systems. We hope our surprising results spark theoretical investigations to elucidate the interactions between topologically-distinct polymers that give rise to the emergent phenomena.

Fig. 1 Experimental approach to probe the rheological properties of blends of ring and supercoiled DNA in the dilute–semidilute crossover regime. (a) Cartoon of blends of supercoiled (red) and ring (blue) DNA at four different concentrations that straddle the overlap concentration c*. Dashed circle around each polymer coil represents its area of influence. (b–d) Passive microrheology. (b) Cartoon of 1 μm microspheres diffusing through a DNA blend. Relative sizes of DNA and beads are approximately to scale. Particle-tracking algorithms determine the frame-to-frame displacements of beads. (c) Mean-squared displacements 〈Δr²(t)〉 are determined from the trajectories of ∼2000 beads for each blend. (d) 〈Δr²(t)〉 is used to determine the frequency-dependent elastic and viscous moduli, G′(ω) and G′′(ω). Scaling bars indicate power-law exponents predicted for the terminal regime. (e and f) Active microrheology. (e) An optically trapped 4.5 μm bead is displaced 30 μm through each blend at speeds v = 5–200 μm s⁻¹, corresponding to strain rates where R is the bead radius. Relative sizes of DNA and beads are approximately to scale. (f) Stage position (green) and force exerted on the trapped bead (violet) before (5 s), during (0.15–6 s), and following (9–15 s) the bead displacement (delineated by dashed lines) are recorded at 20 kHz. Data shown is for v = 20 μm s⁻¹.

To frame our results, we provide a brief summary of current understanding of polymer solution dynamics.^{3,6,16–18,34,35} In the dilute regime (c ≪ c*) the Zimm model, which accounts for hydrodynamic effects, describes dynamics.³⁶ Polymers in this regime are predicted to relax over the Zimm time τ_z = η_sR_G³/k_BT where η_s is solvent viscosity.³⁴ The storage and loss moduli, G′(ω) and G′′(ω), are predicted to scale with frequency as G′(ω) ∼ ω² and G′′(ω) ∼ ω at low frequencies with G′′ > G′. The complex viscosity η* is independent of frequency in this regime. At higher polymer concentrations, this terminal regime scaling still holds but only for timescales above the longest relaxation time 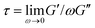.³⁷ As c approaches c* polymers begin to overlap and the Rouse model describes dynamics for lengthscales larger than the correlation blob size ξ_B = R_G(c/c*)^−3/4.^38,39 In this semidilute regime (c ∼ c*) solutions exhibit terminal regime scaling at low frequencies but transition to the scaling G′ ∼ G′′ ∼ ω^1/2 at higher frequencies. The complex viscosity also scales with frequency as η* ∼ ω^−1/2.^6,7,40,41 The primary mode of stress relaxation is elastic retraction which occurs over the Rouse time τ_R = 6R_G²/3π²D where D is the dilute limit diffusion coefficient.^6,8,34,42,43 Once c reaches c_e polymers become entangled and the reptation model describes dynamics.^18,34,35 The longest predicted relaxation time in this regime is the disengagement time τ_D = (18R_G²/a²)τ_R where a is the entanglement tube radius. For τ_R < t < τ_D, G′ > G′′ with G′ exhibiting a frequency-independent plateau G₀ while G′′ transitions from ω¹ to ω^−1/4 scaling.⁴¹ The crossover frequency ω_c at which G′ > G′′ provides a measure of τ_D. The plateau modulus G₀ is predicted to exhibit power-law concentration dependence with scaling exponent of ∼2.3.^37,44 Entangled solutions also exhibit stronger frequency dependence of the complex viscosity than semidilute unentangled solutions with η* ∼ ω^{−(∼0.7–1)}.^{8,22,41,45,46}

In the nonlinear regime, in which the stress is no longer independent of strain, the steady-state viscosity for semidilute and entangled polymers have been shown to exhibit shear-thinning at high strain rates with scaling exponents similar to those measured for complex viscosity η*(ω).^13,22,39,47 This equivalence, known as the Cox–Merz rule, appears to be valid for many polymer systems including linear DNA.^{10,22,41,47–49} The bulk stress response of entangled linear polymers has also been shown to exhibit stress-overshoots before reaching a steady-state value, which has been attributed to chain stretching.^8,50,51 However, microrheological measurements of entangled linear DNA have not found evidence of stress-overshoots.¹⁰

Previous studies on semidilute unentangled and entangled linear DNA have reported dynamics that largely obey the theoretical framework described above.^{10,13,39,41,47} For example, in the semidilute regime shear-thinning has been reported with exponents of ∼0.3–0.5,^40,47 whereas in the entangled regime exponents of ∼0.7–1 have been reported.^8,10 The critical entanglement concentration c_e for DNA has also been shown to be ∼6c* in good solvent conditions (∼3c* in theta solvent conditions).^5,12,13

The dynamics of ring polymers is far more controversial due to their lack of free ends required for classical reptation theory.¹⁶ In the semidilute regime, ring polymer solutions have been reported to have zero shear viscosities ∼2x lower than their linear counterparts with diffusion coefficients that obey Rouse scaling.^12,16 In the nominally entangled regime, rings show no G′ plateau and instead exhibit scaling G′ ∼ G′′ ∼ ω^0.4–0.5 similar to semidilute linear chains.^16,49,52 However, when linear polymer ‘contaminants’ are present, a plateau modulus is again observed as well as viscosities up to ∼2.5x larger than for linear polymers.¹⁶ Further, τ_D for rings has been predicted and observed to be shorter than that for linear chains with τ_D,R/τ_D,L = (a_R/a_L)²(L/2p)^−1/2 where p is persistence length.^42,53,54 Finally, while some studies report terminal regime scaling for entangled rings, others show no signs of reaching the terminal regime scaling (i.e. G′(ω) ∼ ω², G′′(ω) ∼ ω) at low frequencies, which authors suggest arise from slow relaxation modes in entangled rings that are not present in entangled linear chains.^49,52 However, it is expected that at low enough frequencies, below the rate of the slow relaxation modes, that entangled rings will fully relax stress and exhibit terminal regime scaling.

The nonlinear response of rings is less understood than the linear regime dynamics, with very few studies reported to date. One previous study examining entangled polystyrene reported that rings exhibited weaker shear thinning over a broad frequency range and minimal stress overshoots compared to their linear counterparts.²² Authors argued that this difference arose from the more compact structure of rings and their lack of free ends that hinder their ability to deform and stretch in response to strain as easily as linear chains. Importantly, this same study showed that the Cox–Merz rule was valid for ring polymers. The extensional rheology of entangled rings has also been measured.⁵⁵ In this study, the extensional stress as a function of strain for rings was shown to exhibit much more delayed relaxation to steady-state compared to linear chains, increasing approximately linearly with strain for a broad range of strain values.⁵⁵ Rings also exhibited much more pronounced strain-stiffening, in which the slope of the stress curve increased during the strain, compared to linear chains. These distinct features were suggested to arise from the unraveling of the more compact structures that rings assume compared to linear chains. Notably, even less is understood regarding supercoiled polymers or blends of rings and supercoils, with no rheology data or predictions to our knowledge.

Below we present the microrheological properties of topological DNA blends in which we fix the ratio of rings to supercoiled molecules (R : S ≈ 3 : 1) and vary solution concentration from ∼2x below to ∼2x above c*. We show that blends display a crossover at ∼c* to a regime with dynamics that can be described by predictions for entangled polymers, including: elastic plateaus, tube disengagement, and sustained elasticity. Further, our results suggest that interactions between the topologically distinct polymers give rise to entanglement-like dynamics which are distinct in the linear versus nonlinear regimes.

Materials and methods

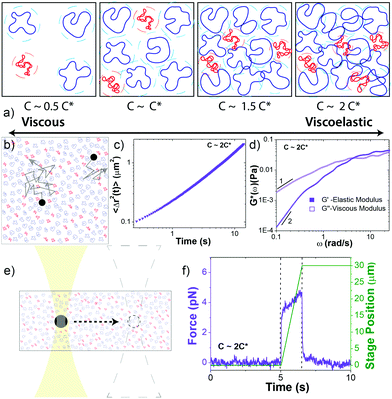
Complete experimental details, summarized below, are provided in ESI.†

Circular 50 kbp DNA was prepared using protocols detailed elsewhere.^4,56 The purified solution had a concentration of 0.56 mg mL⁻¹ and consisted of ∼69% relaxed circular (R), ∼26% supercoiled (S), and ∼5% linear (L) DNA, as quantified via single-molecule ‘counting’ experiments (ESI,† Fig. S1). The topological difference between relaxed circular (ring) and supercoiled DNA is the lack of torsional stress in rings. Both are circular and have no free ends. The two strands of double-stranded supercoiled constructs are twisted such that the torsional stress causes the molecule to assume a tightly coiled conformation. For relaxed circular DNA, one of the double-strands is nicked such that the DNA can unwind and assume a relaxed open circular conformation with no twists or coils. In comparison, for linear DNA the two strands are cut in one position, providing the molecule with free ends. In solution, ring DNA assumes a random coil configuration, similar to linear DNA, with a radius of gyration ∼1.58 times smaller than a linear chain equivalent.⁴ Supercoiled molecules assume a more compact ribbon-like conformation (Fig. S1, ESI†). In dilute solution the diffusion coefficient for supercoiled molecules is ∼1.3 times faster than for ring DNA and ∼1.7 times faster than for linear DNA.⁴

Throughout the text we treat the blend as comprised of rings and supercoiled DNA, largely ignoring the small fraction of linear molecules present. We realize this is an approximation, and, as described in the Introduction, previous studies on synthetic ring polymers have shown that a small fraction of linear chains can impact the rheological properties of ring polymers due to threading events.¹⁶ However, based on our previous steady-state diffusion studies for ring-linear DNA blends,⁵⁷ we do not expect this small fraction of linear chains to play a significant role in our results. In this study we showed that for a comparable DNA length and concentration (45 kbp, 0.5 mg mL⁻¹), the introduction of 5% linear chains into a ring DNA solution only reduced the diffusion of ring DNA by ∼3%. This is compared to a 21% drop measured at ∼25% linear chains. Because the supercoiled contaminants make up >25% of the blend, we assume that it is the presence of supercoiled constructs rather than linear chains that play the dominant role in the mechanics we report. Nonetheless, we cannot unequivocally rule out the possibility that the linear DNA ‘contaminants’ impact our results, and our future work will examine this impact directly by carrying out experiments on blends of ring and linear DNA with varying fractions of linear chains.

We performed measurements at blend concentrations of 0.14, 0.27, 0.41 and 0.51 mg mL⁻¹, chosen to span from ∼2x below to ∼2x above c* (Fig. 1a). To determine an effective c* for blends we started with the expression c* = (3/4π)M/N_AR_G³ that is conventionally used in the literature.³⁷ This expression is derived by equating the solution volume (m/c*, where m is total mass) to the total volume the molecules comprise, i.e. the total number of molecules (N = mN_A/M) multiplied by the volume per molecule (V_m = 4πR_G³/3). We use this approach but consider that each component contributes separately to the total volume the molecules fill in solution: N_SV_m,S + N_RV_m,R + N_LV_m,L = (4π/3)N(0.69R_G,R³ + 0.26R_G,S³ + 0.05R_G,L³). The resulting expression is then: c* = (3/4π)M/N_A(0.69R_G,R³ + 0.26R_G,S³ + 0.05R_G,L³).

The radius of gyration for rings has been shown to be smaller than their linear counterparts with a ratio R_G,L/R_G,R = 1.58 measured for DNA.⁴ The radius of gyration for supercoiled DNA (R_G,S) has likewise been shown to be smaller than linear chains and can be calculated via the worm-like-chain expression for linear polymers assuming a contour length of L_S = 0.4L, where L is the contour length of the polymer:

where p is the persistence length (∼50 nm for DNA).³

Using these expressions and relations, along with reported values of R_G for similarly sized ring and linear DNA, we compute R_G,S ≅ 0.33 μm, R_G,R ≅ 0.37 μm, and R_G,L ≅ 0.56 μm. From these values we calculate c* ≅ 0.25 mg mL⁻¹. As such, our chosen concentrations equate to ∼0.5c*, c*, 1.5c* and 2c*.

To estimate the correlation blob size ξ_B for our system we compute a weighted average of the blob sizes for each topology using the expression ξ_B = R_G(c/c*)^−3/4.^5,38 The effective correlation blob size is then ξ_B ≅ (0.69R_G,R + 0.26R_G,S + 0.05R_G,L)(c/c*)^−3/4 which equates to values of ∼0.57 μm (0.14 mg mL⁻¹), 0.35 μm (0.27 mg mL⁻¹), 0.26 μm (0.41 mg mL⁻¹), and 0.22 μm (0.51 mg mL⁻¹). The mesh size ξ is related to the correlation blob size via ξ = 6^1/2ξ_B.³⁸

Microrheology measurements are described in Fig. 1 and ESI.† The microspheres used in both linear and nonlinear measurements are coated with BSA to enable a no-stick boundary condition between the spheres and the blend.⁵⁸ Further, to ensure that we are probing the bulk rheology rather than the non-continuum local rheology, we chose bead diameters (d = 1 μm and 4.5 μm) that were larger than R_G and ξ_B. This criterion has been theoretically and empirically shown to be sufficient to probe the continuum mechanics of unentangled polymer solutions.^41,59–61 Nonetheless, it is well known that particle-tracking microrheology typically underestimates the magnitudes of G′ and G′′ compared to bulk rheology; however, their dependences on frequency and sample concentration are transferable between the two techniques.^62–65 As such, to facilitate comparison to bulk rheology we focus our discussion on the scalings and trends in the data rather than the absolute magnitudes. In future work we plan to perform macrorheology measurements on this system for direct comparison to our microrheology measurements and bulk rheology results on other polymer systems. However, our current purification methods produce DNA quantities that are too small for accurate experiments with standard bulk rheometers.

Results and discussion

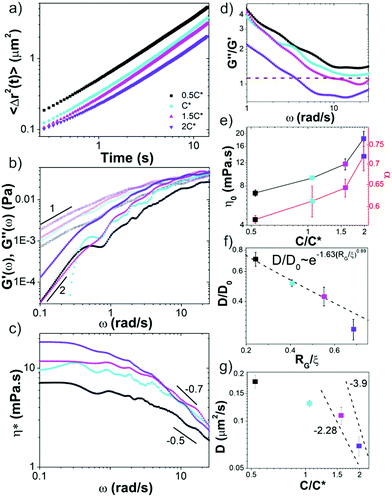
We first analyze trajectories of diffusing microspheres embedded in the blends to determine the dependence of the linear viscoelastic moduli on concentration. At low frequencies all blends exhibit terminal regime scaling with G′ ∼ ω², G′′ ∼ ω¹ and G′′ > G′ (Fig. 2b). While this is expected for linear polymers at these modest concentrations, it contradicts recent findings for ring polymers that show no terminal regime scaling at low frequencies.⁵² For c > c*, a crossover to G′ > G′′ is observed at frequencies of ω_c = 17 rad s⁻¹ and ω_c = 4.25 rad s⁻¹ for 1.5c* and 2c*, corresponding to disengagement times τ_D ≈ 0.4 s and τ_D ≈ 1.5 s (Fig. 2d). Surprisingly, these times are close to τ_D for comparable linear DNA systems with reported values of ∼0.7 s and ∼1.24 s.¹⁰ In contrast, predicted values for rings are an order of magnitude smaller (∼0.05 s, ∼0.07 s). Similarly, zero-shear viscosities for 1.5c* and 2c*, determined from the low-frequency plateau in η*(ω) (Fig. 2c), are markedly similar to reported values for comparable linear DNA systems (45 kbp, 0.5 mg mL⁻¹),¹⁰ while η₀ for rings is predicted to be ≥2x smaller.¹⁶

Fig. 2 Passive microrheology reveals sharp crossover in linear viscoelastic properties of ring-supercoiled blends at the overlap concentration. (a) Mean-squared displacements 〈Δr²(t)〉 of microspheres diffusing through blends of c = 0.5c* − 2c* as listed in legend. (b) Frequency-dependent elastic modulus G′(ω) (closed symbols) and viscous modulus G′′(ω) (open symbols) determined from data shown in (a). Scaling bars indicate power-law exponents predicted for the terminal regime (G′ ∼ ω², G′′ ∼ ω¹). (c) Complex viscosity η*(ω), showing varying degrees of shear thinning (η* ∼ ω^−α) with representative scaling exponents α shown. (d) Loss tangent (G′′/G′) versus ω with dashed line indicating G′ = G′′. The disengagement time for each blend is determined by where the data crosses the dashed line (i.e. ω_c). Note only blends with c > c* exhibit this crossover. (e) Zero shear viscosity η₀ and shear thinning exponent α versus c/c*. (f) Diffusion coefficients D, determined via linear fits to 〈Δr²(t)〉 (shown in (a)) and normalized by the value in buffer conditions D₀, plotted versus R_G/ξ. The dashed line corresponds to the previously reported relation D/D₀ ∼ exp(−1.63(R_G/ξ)^0.89) for particles diffusing in unentangled semidilute linear polymer solutions. (g) D versus c/c* with dashed lines corresponding to D ∼ (c/c*)^−x, where x = 2.28 and 3.9 are the previously reported values for intermediate and large particles respectively, diffusing in entangled linear polymer solutions.

Further, a shift in scaling of η₀ with concentration is also observed for c > c* (Fig. 2c and e). The agreement between η₀ values for c > c* and those from entangled linear DNA suggest that the crossover is to an entanglement-dominated regime. Finally, at high frequencies all solutions exhibit η*(ω) ∼ ω^–α scaling with exponents that increase with concentration (Fig. 2c and e) and exhibit a similar shift for c > c*. Given the small frequency range over which power-law scaling is apparent, along with the noise in the data at high frequencies, we cannot extract exact scaling exponents from the data. However, for the sake of comparison with predictions and previous results, we fit the high-frequency regions of the viscosity curves to power-laws to determine approximate scaling exponents. Exponents for blends with c < c* are in line with the predicted Rouse scaling (0.5) and those reported for linear DNA up to 6c* (≈c_e).^5,7,40 Conversely, for c > c*, scaling exponents match those reported for well-entangled linear DNA (∼0.7–1).^8,41 Our previous studies on entangled linear DNA^10,41 demonstrated the validity of the Cox–Merz rule, which equates the steady-shear viscosity at a given shear rate to the complex viscosity at the same frequency, for these systems. Previous studies on marginally entangled synthetic ring polymers have also demonstrated its validity.²² As such we can compare our η*(ω) ∼ ω^–α scaling to previously reported shear-thinning exponents. Previous studies on semidilute unentangled DNA solutions reported scaling exponents of ∼0.3–0.5 for concentrations up to 0.5 mg mL^−1 47 whereas concentrated linear DNA solutions have been reported to have exponents of ∼0.7–1.⁸ These findings further support our interpretation that our blends exhibit dynamics reminiscent of entangled linear chains for c > c* and semidilute linear chains for c < c*.

We note that while the 1.5c* and 2c* blends appear to reach frequency independent plateaus G₀ at the highest frequencies measured, similar to entangled linear polymers, the scaling with concentration appears to be weaker than the predicted value of ∼2.3.^37,40 However, the frequency range over which the plateaus are apparent, particularly for 1.5c*, is quite small, so determining a scaling law from the data is not possible.

These results suggest that unexpected entanglement-like interactions occur in ring-supercoiled blends with much less coil overlap than their pure linear or ring counterparts. To corroborate this interpretation, we determine the diffusion coefficients D of the particles from the mean-squared displacements (Fig. 2a), and compare to predicted and empirical scalings for semidilute unentangled and entangled linear polymer solutions (Fig. 2f and g).^37,61,66,67 For particle diameters d comparable to the system mesh size ξ, and larger than or equal to R_G (d ≈ ξ, d ≥ R_G), as in our experiments, previous studies on PEG solutions have reported the relationship D/D₀ ∼ exp(−β(R_G/ξ)^δ), with β ≅ 1.63 and δ ≅ 0.89 for unentangled semidilute solutions.⁶¹ This relation implies that the radius of gyration rather than the mesh size is the critical determinant for whether the particles are measuring the solvent viscosity or the bulk viscosity of the polymer solution, the latter of which is the Stokes–Einstein relation. For d > R_G the diffusion coefficient scales according to this expression and the Stoke–Einstein relation is recovered. As shown in Fig. 2f, our data for c ≤ c* aligns with this scaling.

For the entangled regime this same study reports D ∼ (c/c*)^−x with x = −2.28 for d < 2a and x = −3.9, similar to predicted values for large particles,^37,66 for d > 2a. The scaling theory with which these empirical scalings agree, which couples the bead diffusion to the relaxation of the polymers, predicts that intermediate size particles measure an effective viscosity that is equivalent to that of a polymeric fluid in which the polymer size is on the order of the particle size, whereas large particles measure the bulk viscosity dictated by the relaxation of the entire polymer mesh. For linear DNA solutions with similar length and concentration as our highest concentration blend (45 kbp, 0.5 mg mL⁻¹), a ≈ 0.5 μm, so d ≈ 2a in our experiments. As such, if blends were behaving similar to entangled linear polymers for c > c*, as our rheology data suggests, then we should expect scaling in between these two values. The data shown in Fig. 2g is indeed consistent with this picture.

To shed further light on these intriguing mechanical properties we turn to the nonlinear rheological response. To characterize the nonlinear viscoelastic response of the blends we optically drive a microsphere 30 μm through the blends at strain rates of [small gamma, Greek, dot above] = 4.7–189 s⁻¹. As shown in Fig. 3a and Fig. S3 (ESI†), all blends exhibit an initial elastic response in which the force increases linearly with strain followed by softening to a more viscous (i.e. strain-independent) regime. These general features are similar to those previously reported for entangled linear DNA and actin.^10,68 However, the notable difference is the retained elasticity over the entire strain (Fig. 3a and Fig. S3, ESI†). The previously reported systems all soften to a purely viscous response at large strains. This retained elasticity, which implies strong entanglements, is particularly surprising considering the modest concentrations. Interestingly, this sustained elasticity is similar to that reported for the extensional stress response of entangled rings compared to linear polymers, as described in the Introduction.⁵⁵ While microrheological strains are typically assumed to be more analogous to shearing rather than extensional bulk rheology, because we are pulling a microsphere through the blends, there may be components of extensional rheology at work as well, as DNA strands can get momentarily hooked on the bead before slipping off. Further, as shown in ESI,† Fig. S6, our blends exhibit similar strain-stiffening features as ref. 55, with stress curves exhibiting an increase in slope at large strains. This agreement suggests that blends are behaving more closely to entangled ring solutions in the nonlinear regime, as opposed to the linear polymer features exhibited in the linear regime. The authors of ref. 55 postulate that the sustained elasticity and strain-stiffening in rings is a result of the ring chains unraveling from their compact structures in the direction of the strain. Such unraveling could force rings to separate from supercoiled constructs as they unravel in the direction of the strain, and cause rings to self-entangle. We explore this hypothesis further below.

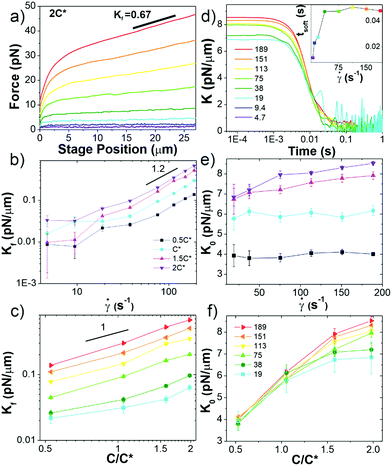Fig. 3 Ring-supercoiled DNA blends straddling c* universally exhibit nonlinear stress response features indicative of strong entanglements. (a) Measured force in response to strain rates of [small gamma, Greek, dot above] = 4.7–189 s⁻¹ as listed in (d). Data shown is for 2c* (see Fig. S3 for other concentrations, ESI†). (b and c) Final differential modulus K_f, determined from the slopes of force curves in the final response phase shown in (a) and Fig. S1 (ESI†), versus (b) [small gamma, Greek, dot above] (see legend) and (c) c (see legend in (f)). (d) Differential modulus, K = dF/dx, as a function of time for 2c* and [small gamma, Greek, dot above] listed in legend (other concentrations shown in Fig. S1, ESI†). Inset: Average softening time t_soft, determined as the time at which K ≈ K_f, versus [small gamma, Greek, dot above] for 2c*. (e) K₀vs. [small gamma, Greek, dot above], only showing [small gamma, Greek, dot above]-dependence for c > c*. (f) Data from (e) plotted as a function of c, showing a crossover from [small gamma, Greek, dot above]-independence to [small gamma, Greek, dot above]-dependent increase of K₀ at ∼c*. All data in (b, c, e and f) have error bars but in some instances they are smaller than symbol sizes.

Finally, we point out that our force curves show no stress overshoots that macrorheology studies on entangled linear polymers find.^10,22 Such overshoots have been attributed to chain stretching, and, as described in the Introduction, previous nonlinear rheology measurements on entangled rings found much less prominent overshoots compared to their linear counterparts, which was attributed to rings not being able to deform in the direction of the strain as easily.²² Our previous nonlinear microrheology studies on entangled linear polymers also showed no overshoot, which we postulated was due to the different scales of the two techniques.¹⁰ Namely, stress overshoots require many chains to be stretched affinely with the strain, as could happen in bulk rheology measurements but less so in microrheology. Further, as described above, stretching of rings may manifest differently than linear chains, exhibiting a much slower relaxation to steady-state and more pronounced stiffening at long times rather than stress overshoots.

In order to further characterize the unexpected elasticity that our blends exhibit, we calculate an effective differential modulus K = dF/dx, which quantifies the stiffness of the system (Fig. 3b–f and Fig. S3, ESI†). As shown in Fig. 3b and c, the K value in the final response phase K_f, which we define as the average value in the plateau region that all K curves exhibit, is nonzero and increases with [small gamma, Greek, dot above] and c (Fig. S4, ESI†). The dependence of K_f on [small gamma, Greek, dot above] demonstrates that measurements are indeed probing the nonlinear regime.¹⁰ However, for [small gamma, Greek, dot above] < 40 s⁻¹ the dependence on [small gamma, Greek, dot above] appears to be weaker than for higher rates which follow a power-law of ∼1.2. This data suggests that lower rates may not be accessing the nonlinear regime, but may rather be in a crossover regime between linear and nonlinear response dynamics.

The initial stiffness K₀ displays a crossover at c* for all rates (Fig. 3d–f). Namely, K₀ is largely independent of [small gamma, Greek, dot above] for c < c* (Fig. 3f), suggestive of a linear response; while for c ≥ c* K₀ increases with [small gamma, Greek, dot above], similar to the nonlinear response observed for entangled linear DNA.¹⁰ The absence of a crossover in K_f for fast rates then suggests that these large strains are sufficient to alter the interactions between polymers such that they exhibit strong entanglement-like interactions even at c < c*. Nonlinear forcing has been shown to induce similar strain-induced network alterations in entangled linear polymers, due to entanglement tube dilation and contraction as well as convective constraint release.^{8,42,46,69–77}

To shed further light on the transition from the initial to final phase of the nonlinear response we determine the time t_stiff at which blends deviate from the initial elastic phase (when K drops to K₀/2), which is a measure of the fastest relaxation time of the system. We find t_stiff = 0.007 ± 0.002 s, independent of [small gamma, Greek, dot above] and c, which agrees with the Zimm time for supercoiled constructs (τ_Z,S ≈ 0.008 s). While Zimm relaxation is expected for c < c*, it is rather surprising that it persists for c > c*, and that there is no evidence of Zimm relaxation for rings.

We also quantify the time at which blends enter the final regime t_soft, which we define as the time at which K first reaches K_f (Fig. S4, ESI†). For all concentrations, t_soft increases with [small gamma, Greek, dot above] for [small gamma, Greek, dot above] < 40 s⁻¹, but for higher rates reaches a [small gamma, Greek, dot above]-independent value of t_soft ≈ 0.047 ± 0.004 s, quite close to the predicted Rouse time for pure ring solutions (τ_R,R ≈ 0.044 s). The crossover seen at [small gamma, Greek, dot above] ≈ 40 s⁻¹, similar to that observed for K_f, corroborates that lower rates are not well within the nonlinear regime.

To verify that we are probing the nonlinear response and test if the slower rates are closer to linear regime expectations we compare our force curves with the expected force growth within the linear viscoelasticity (LVE) framework.³⁷ We compute LVE stress curves σ_LVE(t) by calculating the relaxation modulus G(t) from the viscoelastic moduli presented in Fig. 2 (Fig. S5, ESI†) and carrying out the integral 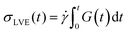.³⁷ As shown in Fig. S6 (ESI†), the nonlinear stress curves are distinctly different from the expected LVE growth, particularly for [small gamma, Greek, dot above] ≥ 40 s⁻¹. Noteworthy distinctions are the strain-stiffening that arises in the nonlinear curves (Fig. S6, ESI,† described above), as well as the initial non-zero stress. Further, the concentration dependence of K₀ is similar to that of the initial G(t) value but the magnitudes differ substantially (Fig. S5, ESI†). Within the LVE framework, nonlinearities are predicted to arise when the shear rate exceeds the terminal relaxation frequency, 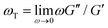. As shown in Fig. S7 (ESI†), ω_T ≤ 0.6 s⁻¹ and our lowest strain rate in nonlinear measurements is 4.7 s⁻¹, so we are indeed beyond the LVE regime. However, the differences between σ_LVE(t) and the nonlinear stress curves are much less dramatic for [small gamma, Greek, dot above] < 40 s⁻¹ suggesting that blends may in fact be in a crossover regime from linear to nonlinear dynamics for these strain rates.

The loss of substantial elasticity over τ_R,R indicates that Rouse-like relaxation of rings and Zimm relaxation of supercoiled molecules are the dominate modes of stress relaxation. However, because blends maintain some elasticity throughout the strain, a slower mode, such as the disengagement time τ_D, must also be present. We offer one possible mechanism, which we alluded to above and explore further below, that could give rise to the emergent physics. Namely, because of the different relaxation timescales and conformations of rings and supercoils, nonlinear strains could force their separation, such that in the vicinity of the strain there are regions of freely diffusing supercoiled constructs that have unthreaded or untangled from rings (undergoing Zimm relaxation), and regions of pure rings that remain entangled or at least strongly overlapping (undergoing Rouse relaxation and disengagement).

Following strain, the probe is halted and the force is measured as the system relaxes (Fig. 1f, 4a and Fig. S8, ESI†). As with previous studies on entangled linear and ring DNA,^42,54 a sum of up to three exponentials (F(t) = C₁e^−t/τ₁ + C₂e^−t/τ₂ + C₃e^−t/τ₃) fits our data well (Fig. S8 and S9, ESI†).

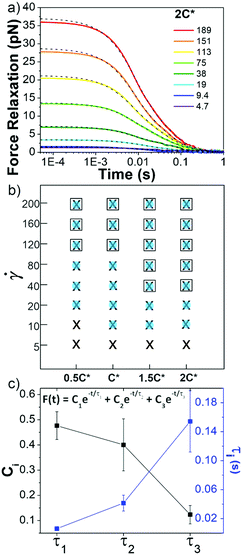Fig. 4 Ring-supercoiled DNA blends exhibit multi-mode relaxation following nonlinear strain. (a) Force relaxation as function of time following strain for [small gamma, Greek, dot above] values (s⁻¹) listed in legend. Each curve is fit to a sum of 1–3 exponential decays (green dashed lines, equation shown in (c)). Data shown is for 2c* (other concentrations in Fig. S5, ESI†). (b) Time constants from exponential decay fits for varying blend concentrations (x-axis) and [small gamma, Greek, dot above] (y-axis). Filled blue circles, black crosses, and open squares represent the fast (τ₁), intermediate (τ₂) and slow (τ₃) time constants, respectively. (c) Relative coefficients C_i (black) and time constants τ_i (blue), averaged over all c and [small gamma, Greek, dot above], for each decay mode.

In all fits the different time constants are separated by close to an order of magnitude with values ∼O(10⁻³) s, O(10⁻²) s, and O(10⁻¹) s. As such, we group time constants into slow, intermediate and fast modes based on this criterion (Fig. 4b), with 99% confidence intervals of τ₁ = 0.006 ± 0.003 s, τ₂ = 0.04 ± 0.01 s, and τ₃ = 0.15 ± 0.04 s and corresponding relative coefficients of C₁ = 0.48 ± 0.05, C₂ = 0.40 ± 0.10 and C₃ = 0.12 ± 0.04 (Fig. 4c). For [small gamma, Greek, dot above] < 40 s⁻¹, single or double exponentials with time constants of τ₁ (single) or τ₁ and τ₂ (double) are sufficient to describe the data, suggesting that the slowest relaxation mode is distinct to the nonlinear regime. We also note there may be higher order relaxation modes that we are unable to resolve but that contribute to the force relaxation. However, fitting our data to more than three exponentials did not result in substantially improved fits and the added decay times were not well-separated from the existing ones. As such, while there may be additional relaxation modes that the polymers undergo, we approximate that there are only up to three primary modes that dictate the relaxation.

τ ₁ is nearly identical to t_stiff measured during strain, corroborating that Zimm relaxation of supercoils is the fastest nonlinear relaxation mode. To understand the relaxation mechanisms associated with the two slower modes we compare our measured values to the predicted and measured values of τ_R and τ_D for linear and ring polymer systems. We find that τ₂ and τ₃ are comparable to τ_R and τ_D for ring DNA (τ_R,R ≈ 0.04 s, τ_D,R ≈ 0.1 s), but significantly shorter than those for linear DNA (τ_R,L ≈ 0.13 s, τ_D,L ≈ 1.24 s).^10,41,53,54 By comparing the contributions from each mode, we see that the system relaxes mainly through apparent Zimm relaxation of supercoils with C₁ ≈ 48% and Rouse-like relaxation with C₂ ≈ 40% (Fig. 4b and c). This result is in line with our t_soft analysis that shows that blends dissipate most of their elastic stress on the order of τ_R,R despite the existence of a slower relaxation mode and sustained elastic response to strain.

It is worth discussing the differences between our nonlinear and linear microrheology data. As described above, we attribute the agreement of linear microrheology results with those of entangled linear polymers to interactions between the two topologies that cause substantial entanglements – similar to entangled linear polymer systems – even in semidilute conditions. However, the agreement of t_soft and τ₂ with τ_R,R rather than τ_R,L, and likewise τ₃ with τ_D,R rather than τ_D,L, suggest that nonlinear forcing is sufficient to alter the interactions between topologically distinct polymers such that they lose blend characteristics and behave closer to pure entangled ring polymer solutions. The difference in the relaxation times for linear and nonlinear regimes is further evidenced by the order of magnitude difference between τ₃ and the longest relaxation time predicted within the LVE framework, 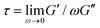(see ESI,† Fig. S7).³⁷ At the same time, while the existence of multiple relaxation modes is in line with our linear regime results that show that for c > c* blends behave as if entangled, in the nonlinear regime these modes persist for all concentrations. These results support our suggested mechanism of nonlinear straining separating supercoils from rings and forming separate regions of densely entangled rings and minimally overlapping supercoils (Fig. 5). We note that this local inhomogeneity is a strain-induced transient effect that arises from the fact that the strain rate is much faster than the system relaxation timescales. Similar behavior has been seen for entangled linear DNA in which nonlinear micro-strains compress polymers in front of the moving bead, thereby increasing the local entanglement density while leaving dilute regions in its wake.⁷⁸ This effect may also explain the emergent sustained elasticity.

Fig. 5 Nonlinear microrheological straining causes re-distribution of rings and supercoiled DNA in ring-supercoiled blends. (top) Cartoon of a steady-state blend of supercoiled (red) and ring (blue) DNA at 2c*. Approximate polymer sizes are increased ∼2x for better visibility. Large grey sphere represents the optically trapped 4.5 μm microsphere. (bottom) Cartoon depicting the hypothesized effect of nonlinear straining on a supercoiled-ring DNA blend. Nonlinear straining separates rings from supercoils such that separate regions of densely entangled rings and dilute supercoiled DNA are formed in front of and in the wake of the moving microsphere, respectively.

Conclusions

In conclusion, we present linear and nonlinear rheological properties of blends of relaxed circular and supercoiled DNA at concentrations that straddle the overlap concentration. Surprisingly, despite being in the dilute–semidilute crossover regime, we observe dynamics indicative of entanglements, which we suggest arise from synergistic interactions between the two topologies. Linear microrheology reveals a crossover at c* from semidilute dynamics to those that align with entangled linear polymers. At the same time, nonlinear microrheology uncovers unique sustained elasticity and multiple relaxation modes not expected at these modest concentrations. Interestingly, while blends exhibit linear viscoelasticity comparable to those of entangled linear polymers, nonlinear response characteristics align more closely with predictions for entangled rings. We interpret these differences as arising from strain-induced network rearrangements that alter the entanglement density and disrupt the interactions between topologically-distinct polymers (Fig. 5). Given the unexpected dynamics that these ring-supercoiled DNA blends exhibit, as compared to previous studies of ring-linear polymer blends,^16,49,79 the unique topology of the supercoiled constructs likely plays an important role in our results.

Nonetheless, the paucity of rheological data on supercoiled polymers and blends thereof demands future work to fully understand this system and validate our interpretations. In fact, we hope that the new phenomena we report spur theoretical investigations into similar topological blends to shed light onto the physical interactions between topologically distinct polymers that give rise to the emergent dynamics they exhibit. Several key questions remain. For example, how does the topology of the supercoiled DNA influence the dynamics? How does the ratio of rings to supercoiled DNA impact the results? Our future work will focus on answering these important questions by performing experiments with analogous blends of ring and linear (rather than supercoiled) DNA, and with ring-supercoiled DNA blends with varying fractions of rings and supercoiled constructs.

In summary, our results reveal that blended solutions of ring and supercoiled polymers exhibit unexpected viscoelastic properties at surprisingly low concentrations. As a result, this study is not only of fundamental importance to polymer physics research but also has commercial applications. Namely, topological blends can potentially be exploited as a route for designing low-mass high-strength viscoelastic materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support from Air Force Office of Scientific Research (AFOSR-FA9550-17-1-0249) and National Science Foundation (NSF-CBET-1603925).

References

1. J. E. Deweese, M. A. Osheroff and N. Osheroff, Biochem. Mol. Biol. Educ., 2008, 37, 2–10.
2. M. T. J. van Loenhout, M. V. de Grunt and C. Dekker, Science, 2012, 338, 94.
3. D. R. Latulippe and A. L. Zydney, Biotechnol. Bioeng., 2010, 107, 134–142.
4. R. M. Robertson, S. Laib and D. E. Smith, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7310.
5. K.-W. Hsiao, C. Sasmal, J. R. Prakash and C. M. Schroeder, J. Rheol., 2016, 61, 151–167.
6. B. A. Krajina, C. Tropini, A. Zhu, P. DiGiacomo, J. L. Sonnenburg, S. C. Heilshorn and A. J. Spakowitz, ACS Cent. Sci., 2017, 3, 1294–1303.
7. J. S. Hur, E. S. G. Shaqfeh, H. P. Babcock, D. E. Smith and S. Chu, J. Rheol., 2001, 45, 421–450.
8. R. E. Teixeira, A. K. Dambal, D. H. Richter, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2007, 40, 2461–2476.
9. T. G. Mason, A. A. Dhople and D. Wirtz, Macromolecules, 1998, 31, 3600–3603.
10. C. D. Chapman and R. M. Robertson-Anderson, Phys. Rev. Lett., 2014, 113, 098303.
11. R. Bandyopadhyay and A. K. Sood, Pramana, 2002, 58, 685–694.
12. R. M. Robertson and D. E. Smith, Macromolecules, 2007, 40, 3373–3377.
13. S. Pan, D. A. Nguyen, T. Sridhar, P. Sunthar and J. R. Prakash, J. Rheol., 2014, 58, 339–368.
14. X. Zhu, B. Kundukad and J. R. C. v. d. Maarel, J. Chem. Phys., 2008, 129, 185103.
15. D. Vlassopoulos, Rheol. Acta, 2016, 55, 613–632.
16. D. Vlassopoulos, R. Pasquino and F. Snijkers, Topological Polymer Chemistry, World Scientific, 2013, pp. 291–316.
17. K. Regan, S. Ricketts and M. R. Robertson-Anderson, Polymers, 2016, 8, 336–358.
18. R. Evaristo, Polymer viscoelasticity: stress and strain in practice, Marcel Dekker, New York, 2000.
19. T. McLeish, Phys. Today, 2008, 61, 40–45.
20. T. C. B. McLeish, Adv. Phys., 2002, 51, 1379–1527.
21. T. McLeish, Science, 2002, 297, 2005.
22. Z.-C. Yan, S. Costanzo, Y. Jeong, T. Chang and D. Vlassopoulos, Macromolecules, 2016, 49, 1444–1453.
23. D. G. Tsalikis, V. G. Mavrantzas and D. Vlassopoulos, ACS Macro Lett., 2016, 5, 755–760.
24. T. Ge, J. T. Kalathi, J. D. Halverson, G. S. Grest and M. Rubinstein, Macromolecules, 2017, 50, 1749–1754.
25. J. Smrek, K. Kremer and A. Rosa, ACS Macro Lett., 2019, 8, 155–160.
26. R. Fitzpatrick, D. Michieletto, K. R. Peddireddy, C. Hauer, C. Kyrillos, B. J. Gurmessa and R. M. Robertson-Anderson, Phys. Rev. Lett., 2018, 121, 257801.
27. Y. Zhou, K.-W. Hsiao, K. E. Regan, D. Kong, G. B. McKenna, R. M. Robertson-Anderson and C. M. Schroeder, Nat. Commun., 2019, 10, 1753.
28. J. D. Halverson, W. B. Lee, G. S. Grest, A. Y. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204904.
29. Y.-B. Yang, Z.-Y. Sun, C.-L. Fu, L.-J. An and Z.-G. Wang, J. Chem. Phys., 2010, 133, 064901.
30. S. Habuchi, N. Satoh, T. Yamamoto, Y. Tezuka and M. Vacha, Angew. Chem., Int. Ed., 2010, 49, 1418–1421.
31. R. M. Robertson and D. E. Smith, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4824.
32. P. J. Mills, J. W. Mayer, E. J. Kramer, G. Hadziioannou, P. Lutz, C. Strazielle, P. Rempp and A. J. Kovacs, Macromolecules, 1987, 20, 513–518.
33. D. G. Tsalikis and V. G. Mavrantzas, ACS Macro Lett., 2014, 3, 763–766.
34. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, New York, 1986.
35. P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, 1979.
36. B. H. Zimm, J. Chem. Phys., 1956, 24, 269–278.
37. R. A. Pethrick, Polym. Int., 2004, 53, 1394–1395.
38. M. Tanoguchi and Y. Murayama, AIP Adv., 2018, 8, 105218.
39. J. R. Prakash, Curr. Opin. Colloid Interface Sci., 2019, 43, 63–79.
40. R. H. Colby, D. C. Boris, W. E. Krause and S. Dou, Rheol. Acta, 2007, 46, 569–575.
41. C. D. Chapman, K. Lee, D. Henze, D. E. Smith and R. M. Robertson-Anderson, Macromolecules, 2014, 47, 1181–1186.
42. R. M. Robertson and D. E. Smith, Phys. Rev. Lett., 2007, 99, 126001.
43. S. T. Milner and T. C. B. McLeish, Phys. Rev. Lett., 1998, 81, 725–728.
44. Y. Heo and R. G. Larson, Macromolecules, 2008, 41, 8903–8915.
45. C. Tsenoglou, Macromolecules, 2001, 34, 2148–2155.
46. P. S. Desai and R. G. Larson, J. Rheol., 2014, 58, 255–279.
47. S. Pan, D. A. Nguyen, B. Dünweg, P. Sunthar, T. Sridhar and J. Ravi Prakash, J. Rheol., 2018, 62, 845–867.
48. X. Xu, J. Chen and L. An, J. Chem. Phys., 2014, 140, 174902.
49. Y. Doi, K. Matsubara, Y. Ohta, T. Nakano, D. Kawaguchi, Y. Takahashi, A. Takano and Y. Matsushita, Macromolecules, 2015, 48, 3140–3147.
50. K. S. Schweizer and S.-J. Xie, ACS Macro Lett., 2018, 7, 218–222.
51. J. A. Cribb, P. A. Vasquez, P. Moore, S. Norris, S. Shah, M. G. Forest and R. Superfine, J. Rheol., 2013, 57, 1247.
52. M. Kapnistos, M. Lang, D. Vlassopoulos, W. Pyckhout-Hintzen, D. Richter, D. Cho, T. Chang and M. Rubinstein, Nat. Mater., 2008, 7, 997.
53. B. V. S. Iyer, A. K. Lele and V. A. Juvekar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021805.
54. R. M. Robertson and D. E. Smith, Macromolecules, 2007, 40, 8737–8741.
55. Q. Huang, J. Ahn, D. Parisi, T. Chang, O. Hassager, S. Panyukov, M. Rubinstein and D. Vlassopoulos, Phys. Rev. Lett., 2019, 122, 208001.
56. S. Laib, R. M. Robertson and D. E. Smith, Macromolecules, 2006, 39, 4115–4119.
57. C. D. Chapman, S. Shanbhag, D. E. Smith and R. M. Robertson-Anderson, Soft Matter, 2012, 8, 9177–9182.
58. T. T. Falzone and R. M. Robertson-Anderson, ACS Macro Lett., 2015, 4, 1194–1199.
59. B. R. Dasgupta, S.-Y. Tee, J. C. Crocker, B. J. Frisken and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 051505.
60. J. H. van Zanten, S. Amin and A. A. Abdala, Macromolecules, 2004, 37, 3874–3880.
61. I. Kohli and A. Mukhopadhyay, Macromolecules, 2012, 45, 6143–6149.
62. F. G. Schmidt, B. Hinner and E. Sackmann, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5646–5653.
63. M. L. Gardel, M. T. Valentine, J. C. Crocker, A. R. Bausch and D. A. Weitz, Phys. Rev. Lett., 2003, 91, 158302.
64. C. Oelschlaeger, M. Schopferer, F. Scheffold and N. Willenbacher, Langmuir, 2009, 25, 716–723.
65. J. C. Crocker and B. D. Hoffman, Methods Cell Biol., 2007, 83, 141–178.
66. L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2011, 44, 7853–7863.
67. N. Ziębacz, S. A. Wieczorek, T. Kalwarczyk, M. Fiałkowski and R. Hołyst, Soft Matter, 2011, 7, 7181–7186.
68. T. T. Falzone, S. Blair and R. M. Robertson-Anderson, Soft Matter, 2015, 11, 4418–4423.
69. S.-Q. Wang, Y. Wang, S. Cheng, X. Li, X. Zhu and H. Sun, Macromolecules, 2013, 46, 3147–3159.
70. S.-Q. Wang, S. Ravindranath, Y. Wang and P. Boukany, J. Chem. Phys., 2007, 127, 064903.
71. D. M. Sussman and K. S. Schweizer, Macromolecules, 2012, 45, 3270–3284.
72. D. M. Sussman and K. S. Schweizer, Macromolecules, 2013, 46, 5684–5693.
73. R. S. Graham, A. E. Likhtman, T. C. B. McLeish and S. T. Milner, J. Rheol., 2003, 47, 1171–1200.
74. G. Marrucci, J. Non-Newtonian Fluid Mech., 1996, 62, 279–289.
75. C. Baig, V. G. Mavrantzas and M. Kröger, Macromolecules, 2010, 43, 6886–6902.
76. A. Dambal, A. Kushwaha and E. S. G. Shaqfeh, Macromolecules, 2009, 42, 7168–7183.
77. B. Gurmessa, R. Fitzpatrick, T. T. Falzone and R. M. Robertson-Anderson, Macromolecules, 2016, 49, 3948–3955.
78. M. Khan, K. Regan and R. M. Robertson-Anderson, Phys. Rev. Lett., 2019, 123, 038001.
79. J. D. Halverson, G. S. Grest, A. Y. Grosberg and K. Kremer, Phys. Rev. Lett., 2012, 108, 038301.

---

Footnote

† Electronic supplementary information (ESI) available: Expanded experimental section; Fig. S1. Single-molecule ‘counting’ experiments to visualize DNA molecules in the blend; Fig. S2. Position and velocity of nanopositioning stage during active microrheology measurement; Fig. S3. Nonlinear force response of blends of ring and supercoiled DNA; Fig. S4. Final phase of differential modulus in response to nonlinear strains; Fig. S5. Linear relaxation modulus G(t) and initial values of G(t) and the nonlinear differential modulus K; Fig. S6. Expected LVE stress growth compared to the nonlinear stress growth measured in nonlinear microrheology experiments; Fig. S7. Terminal linear relaxation frequency and time determined from passive microrheology experiments; Fig. S8. Relaxation of force induced in ring-supercoiled DNA blends following nonlinear strains. Fig. S9. Initial force relaxation following nonlinear strain. See DOI: 10.1039/c9sm01767d

---