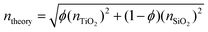Silica–titania hybrids for structurally robust inverse opals with controllable refractive index
Katherine R.
Phillips
 a,
Tanya
Shirman
a,
Tanya
Shirman
 bc,
Michael
Aizenberg
bc,
Michael
Aizenberg
 c,
Grant T.
England
b,
Nicolas
Vogel
c,
Grant T.
England
b,
Nicolas
Vogel
 bd and
Joanna
Aizenberg
bd and
Joanna
Aizenberg
 *abc
*abc
aDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138, USA. E-mail: jaiz@seas.harvard.edu
bJohn A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
cWyss Institute for Biologically Inspired Engineering, Harvard University, Cambridge, MA 02138, USA
dInstitute of Particle Technology and Cluster of Excellence Engineering of Advanced Materials, Friedrich-Alexander-University Erlangen-Nürnberg, 91058 Erlangen, Germany
First published on 21st November 2019
Abstract
Templated from sacrificial colloidal assemblies, inverse opals are comprised of an interconnected periodic network of pores, forming a photonic crystal. They are used in a variety of applications, most of which, especially those in optics and photocatalysis, require a high degree of control over the long-range order, composition and refractive index. It has been shown that hybrid materials combining different components can yield materials with properties that are superior to the individual components. Here, we describe the assembly of hybrid titania/silica inverse opals using sol–gel chemistry, resulting in a mixed oxide with well-dispersed titanium and silicon. Titania has a high refractive index (2.4–2.9), but cracks typically form in the inverse opal structure; conversely, silica can produce highly ordered crack-free inverse opals, but it has a lower refractive index (∼1.4). By adjusting the ratio of titania and silica, the refractive index can be tailored while minimizing the crack density and maintaining structural order, allowing for control over the optical properties of this hybrid nanoporous material.
Introduction
Inverse opals are prepared via templating of a sacrificial colloidal crystal matrix and consist of three-dimensionally ordered, interconnected pores. Their periodicity creates structural color when it is on the same length scale as the wavelength of visible light. Hence, there has been widespread interest in using them in optical and photonic applications,1–7 including as colorants8–10 and sensors.11,12 However, these applications rely on a high degree of regularity and homogeneity. Cracks, in particular, are detrimental to inverse opals’ optical properties because they cause scattering, which reduces the intensity of the color by imposing a whitish appearance.In addition to the ordered structure, the composition of an inverse opal influences its optical properties, and can further improve its mechanical, catalytic and electronic properties.5 For optics, the refractive index (RI) of the material, the RI contrast between the inverse opal matrix and the medium in the pores, and the periodicity of the structure all play important roles in determining the spectral location and intensity of the Bragg resonance. Silica is often used because highly ordered structures can be made;13,14 however, the relatively low RI of amorphous silica (∼1.4) limits its use in any environment other than air, due to color loss upon infiltration of a higher-index media in the pores.11 Titania has a higher RI, which varies from 2.4 for the anatase phase to greater than 2.9 for rutile. This higher RI allows TiO2 inverse opals to retain their color in liquids, making them useful for applications such as liquid-phase photocatalysts,15 sensors,16 or paint formulations,8,9 where the color must remain even when infiltrated.
Due to intense interest in their use, titania inverse opals have been investigated extensively, but to date have only been made with complicated processes, such as using post-assembly exchange,13 backfilling (with nanoparticles,17,18 sol–gel precursors,19–22 or both23), and atomic layer deposition,24 that still produce substantial cracks or nonuniformities in the structure. Longer-range order was attained using co-assembly of the colloidal template with titania nanoparticles,25,26 but the size of the nanoparticles remains a parameter constraining the size of the pores and imparting additional difficulties in controlling the order beyond the micron-scale.
A co-assembly approach13 allows large (cm)-scale crack-free silica inverse opals to be grown using the sol–gel precursor tetraethyl orthosilicate (TEOS) as an additive during the assembly of sacrificial polymeric colloids, which are removed from the assembled structure by dissolution or calcination. The sol–gel chemistry of transition metal oxides and their precursors, such as titania, is generally challenging for the use in the coassembly process, due to their high reactivity towards residual water and large crystallization-induced volume change during calcination, leading to cracking, phase separation and inhomogeneities.26,27 Ligands, such as those present in the water-stable precursor titanium(IV) bis(ammonium lactato)dihydroxide (TiBALDH), can be used to control the hydrolysis of the metal precursor; however, extensive shrinkage followed by cracking upon crystallization of the titania still occurs.13,28,29
Here, we describe the use of TiBALDH and TEOS together in the co-assembly process to achieve mixed silica–titania inverse opals with different compositions and periodicities, in order to combine the structural integrity of silica structures and the high RI of titania.30 Mixing silica and titania has been used before to tune catalytic23 and optical25 effects of inverse opals using backfilling techniques. Herein, we provide a detailed report on how the co-assembly process that avoids backfilling-associated film cracking and overlayer formation13,31 is used to achieve fine control over both the crack density and the RI of inverse opals across the composition range from pure silica to pure titania. The RI is controlled from n = 1.38 to n = 2.5, with mm-scale crack-free regions for samples containing >30% silica. The ability to adjust the RI of the matrix material, while maintaining its structural integrity, significantly expands the possible optical, photocatalytic and photonic applications for inverse opals.
Experimental
Materials
Styrene, acrylic acid, tetraethyl orthosilicate (TEOS), and 0.1 M HCl were obtained from Sigma Aldrich and used as received. Ethanol was obtained from Koptec, ammonium persulfate from OmniPur, titanium(IV) bis(ammonium-lactato)dihydroxide (TiBALDH) from ChemCruz, and deionized water was used from a Milli-Q system. Silicon wafers from Wafer World were used as substrates after cleaning with acid piranha (Caution: Acid piranha is a strong oxidizing agent and should be handled with care using appropriate personal protection), a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of sulfuric acid (Sigma) and hydrogen peroxide (30% in water, BDH Chemicals), and rinsing with copious amounts of water.
1 mixture of sulfuric acid (Sigma) and hydrogen peroxide (30% in water, BDH Chemicals), and rinsing with copious amounts of water.
Assembly of inverse opals
Inverse opals were made using a modified evaporation-induced co-assembly procedure from the literature.13,28 Briefly, polystyrene colloids were synthesized in a range of sizes using a surfactant-free emulsion polymerization with acrylic acid as the co-monomer;32 they were then diluted to 0.1% solid content and combined with different ratios of the silica and titania precursors. The silica precursor solution consisted of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by volume of TEOS, 0.1 M HCl, and ethanol, stirred for 1 h at room temperature. The titania precursor solution consisted of a mixture of TiBALDH and 0.1 M HCl (1
2 by volume of TEOS, 0.1 M HCl, and ethanol, stirred for 1 h at room temperature. The titania precursor solution consisted of a mixture of TiBALDH and 0.1 M HCl (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 by volume), stirred for 1 h. For several values of x between 0 and 1, 7.5 × (x) μL (silica) and 12 × (1 − x) μL (titania) precursor solution was added per mL of assembly solution, resulting in the ratios described in the text. A silicon wafer substrate was cleaned and suspended vertically in the assembly solution, which was left in a Memmert UF110 oven at 65 °C for 2 days to allow evaporation of the solvent. After assembly, samples underwent calcination in a Thermo box furnace at 500 °C with a 2 °C min−1 ramp rate in ambient atmosphere to ensure removal of the polymeric colloidal template.13
5 by volume), stirred for 1 h. For several values of x between 0 and 1, 7.5 × (x) μL (silica) and 12 × (1 − x) μL (titania) precursor solution was added per mL of assembly solution, resulting in the ratios described in the text. A silicon wafer substrate was cleaned and suspended vertically in the assembly solution, which was left in a Memmert UF110 oven at 65 °C for 2 days to allow evaporation of the solvent. After assembly, samples underwent calcination in a Thermo box furnace at 500 °C with a 2 °C min−1 ramp rate in ambient atmosphere to ensure removal of the polymeric colloidal template.13
Sample characterization
Scanning electron microscopy was performed on a Zeiss Ultra Plus field emission scanning electron microscope (SEM) using 1.5 keV acceleration voltage. A JEOL 2100 transmission electron microscope (TEM) was used for high-resolution TEM imaging, and a JEOL 2010 scanning transmission electron microscope equipped with an EDAX detector was used for energy dispersive X-ray spectroscopy (EDS) mapping. X-ray photoelectron spectroscopy (XPS) was performed on a Thermo Scientific K-Alpha instrument. Optical spectra were obtained at normal incidence using a 600 μm Ocean Optics optical fiber connected to an Ocean Optics USB2000+ spectrometer through a 20× air or immersion objective on a custom Leica DMRX microscope. A >96% reflective mirror was used as a reference under identical conditions. Raman spectroscopy was performed on a R200-L SENTERRA Raman Microscope.Shrinkage and crack density calculations
Cross-sectional SEM images were used to measure the pore height and width and average film thickness for all samples. From these values an estimate of the shrinkage could be obtained by assuming that all of the shrinkage comes from the change in film thickness. In order to quantify the cracks, we measured the length of cracks per unit area by manually measuring visible cracks (interacting with ≥3 pores) using ImageJ. The “crack density” was obtained by dividing this crack length by the image area.Theoretical optical fitting
In order to determine the RI, we simulated optical spectra using a transfer matrix method; then, these spectra were matched to experimental optical spectra of silica/titania hybrid inverse opals, using geometric quantities measured from cross-sectional and top-view SEM images to generate the inverse opal lattice for the calculations. The RI of the matrix material was determined by fitting the simulations to the experimental inverse opal optical spectra.Results and discussion
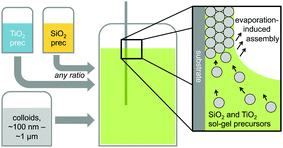
Hybrid silica–titania samples were made by pre-hydrolyzing silica and titania precursors in individually optimized hydrolysis solutions. They were then combined in the assembly solution with polymeric colloids, as shown in Scheme 1.Evaporation of the solvent induces the colloids to assemble on the substrate, with a mixed silica/titania phase filling the interstitial area. Mixing the separately pre-hydrolyzed solutions allowed us to maintain different hydrolysis conditions required for the two precursors, while providing the ability to control the final ratio of titania and silica in the mixed inverse opal. After co-assembling the colloidal crystal and matrix material, followed by removal of the sacrificial colloidal template, the mixed oxide inverse opals were obtained. Fig. 1a–e compares top-view and side-view SEM images of samples assembled from different ratios of titania to silica, all made using 310 nm colloids as template. Pure silica inverse opals are crack-free (Fig. 1e), particularly compared to the pure titania films (Fig. 1a); adding silica to titania improves the order (Fig. 1b–d), particularly starting with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (Fig. 1c). Furthermore, when using a sol–gel precursor instead of nanoparticles, the precursor does not restrain the size of colloids that can be used as the template.26 Samples made from colloids ranging in diameter from 140 nm to 650 nm were successfully prepared with a 1
1 ratio (Fig. 1c). Furthermore, when using a sol–gel precursor instead of nanoparticles, the precursor does not restrain the size of colloids that can be used as the template.26 Samples made from colloids ranging in diameter from 140 nm to 650 nm were successfully prepared with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of titania to silica precursor solutions (Fig. 1f–j). These colloid sizes cover the range typically used to make inverse opals. As SEM images in Fig. 1f–j illustrate, using this approach, good quality inverse opal samples were made for 140, 230, 310, 460, and 650 nm colloids.
1 ratio of titania to silica precursor solutions (Fig. 1f–j). These colloid sizes cover the range typically used to make inverse opals. As SEM images in Fig. 1f–j illustrate, using this approach, good quality inverse opal samples were made for 140, 230, 310, 460, and 650 nm colloids.
TEM imaging has shown that the titania was dispersed throughout the silica matrix in nanodomains of ∼5 nm (Fig. 2), likely as a result of the separate hydrolysis solutions that were used. The lattice fringes with a spacing of 3.51 Å and 2.38 Å can be assigned to (101) and (004) lattice planes of anatase TiO2, respectively33 (Fig. 2a). Polycrystalline growth can also be identified from the random orientation of different lattice planes. A selected area electron diffraction pattern from a pure TiO2 inverse opal shows a series of Debye–Scherrer diffraction rings (Fig. 2a, inset) that indicate the formation of polycrystalline anatase titania. The additional calculated d-spacing values of 1.89, 1.70, and 1.48 Å represent the anatase lattice planes with Miller indices (105), (204) and (200), respectively. Such a polycrystalline structure agrees with the standard data (JCPDS 75-1537) for the anatase phase titanium dioxide. With an increase in SiO2 concentration, the crystalline TiO2 domains become less visible (Fig. 2c and d).
Raman spectra of the pure titania sample provide further support that titania is present as the anatase phase. Only Raman peaks due to anatase and none due to rutile were observed (Fig. 3), as expected for a rather low calcination temperature of 500 °C chosen to remove the colloidal template. Inverse opals made of silica–titania hybrids, however, did not produce Raman peaks of measurable intensity, despite titania crystallites being clearly seen in TEM images of samples up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 titania to silica precursor ratio (Fig. 2d). We attribute this lack of signal to the fact that the titania crystallites present in hybrid silica–titania inverse opals are below the minimum domain size that Raman spectroscopy can identify (∼10 nm).34
3 titania to silica precursor ratio (Fig. 2d). We attribute this lack of signal to the fact that the titania crystallites present in hybrid silica–titania inverse opals are below the minimum domain size that Raman spectroscopy can identify (∼10 nm).34
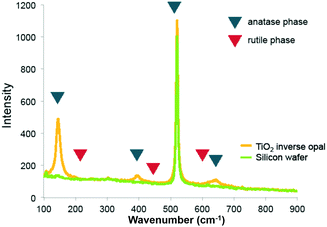 | ||
| Fig. 3 Raman spectrum of titania inverse opal. The 390 cm−1 and 636 cm−1 peaks indicate that titania is present in the anatase phase. | ||
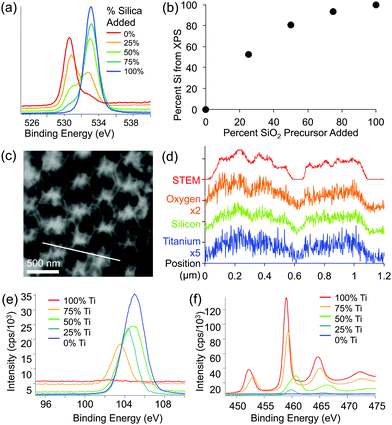
XPS and EDS were used to obtain both qualitative and quantitative information about the elemental composition and distribution of elements within the mixed oxide inverse opal structures. XPS results show a higher Si/Ti ratio in the inverse opal than the ratio used in the precursor mixture, indicating that silica is incorporated slightly more effectively than titania (Fig. 4a and b). Qualitatively, increasing the silica content in the assembly solution increases the O–Si peak at ∼535 eV and lowers the relative height of the O–Ti peak at ∼530 eV (Fig. 4a). Additionally, the peaks in the titanium 2p and silicon 2p XPS regions further confirm these changes (Fig. 4e and f). Ti/Si ratio in the inverse opal, obtained by integrating the O–Si and O–Ti peaks plotted against the ratio of precursors added to the assembly solution, shows that the silica is incorporated about twice as efficiently as the titania (at least in the ∼10 nm deep region probed by XPS) (Fig. 4b). The silicon and titanium curves in the EDS mapping of the samples follow the same pattern, indicating that titanium and silicon are evenly distributed throughout the mixed oxide structures (Fig. 4c and d).
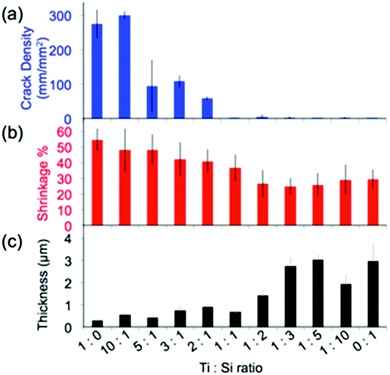
Structural homogeneity and integrity are critical for inverse opals to act as photonic crystals or substrates for photocatalysis. We quantify this homogeneity via the analysis of the lengths of the cracks present in the hybrid inverse opals. It has been shown that co-assembly of inverse silica opals generally avoids the formation of cracks that occurs during the drying stage of evaporative deposition for direct opals;13 however, matrix material shrinkage (which is dependent on the chemical identity of the sol–gel precursor, the composition of the resulting matrix material, the calcination temperature of the structure, etc.) can cause cracking, when thicker colloidal crystals form. Thus, we quantified the opal's thickness and shrinkage, in addition to the crack length, as shown in Fig. 5 and 6, and listed in Table 1. We see a rapid decrease in crack formation with addition of silica precursor to the sol–gel mixture. From a mixture of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 titania to silica precursors, the inverse opals are virtually crack-free over extended areas. “Crack density,” shown in Fig. 5a, corresponds to the sum of the crack lengths for a given area (we note that the crack length does not take into account how wide the cracks are, and thus it underestimates the crack area for samples with wide cracks). Since densification of the matrix plays a major role in crack formation, we used cross-sectional SEM images (Fig. 1a–e) to quantify the amount of shrinkage that each sample undergoes, by first measuring the cross-sectional height and width of the pores, which are listed in Table 1, and then applying these values to calculate the volume shrinkage assuming no contraction in the x–y plane (Fig. 5b) using a method described previously.35
1 titania to silica precursors, the inverse opals are virtually crack-free over extended areas. “Crack density,” shown in Fig. 5a, corresponds to the sum of the crack lengths for a given area (we note that the crack length does not take into account how wide the cracks are, and thus it underestimates the crack area for samples with wide cracks). Since densification of the matrix plays a major role in crack formation, we used cross-sectional SEM images (Fig. 1a–e) to quantify the amount of shrinkage that each sample undergoes, by first measuring the cross-sectional height and width of the pores, which are listed in Table 1, and then applying these values to calculate the volume shrinkage assuming no contraction in the x–y plane (Fig. 5b) using a method described previously.35
 | ||
Fig. 6 SEM images of different titania![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) silica ratios showing reduction in a cracks density from left to right with an increase in SiO2 content. silica ratios showing reduction in a cracks density from left to right with an increase in SiO2 content. | ||
Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si Si |
SEM (Fig. 2) | Crack density (mm−1) | Pore height (mm−1) | Pore width (mm−1) | Shrink% | Thickness (μm) |
|---|---|---|---|---|---|---|
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
A | 275 ± 42 | 146 ± 15 | 321 ± 15 | 54.5 ± 7.1 | 0.31 ± 0.08 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
— | 301 ± 11 | 156 ± 19 | 299 ± 34 | 49 ± 14 | 0.56 ± 0.15 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
— | 95 ± 76 | 166 ± 22 | 320 ± 20 | 48.1 ± 9.8 | 0.44 ± 0.08 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
B | 108 ± 18 | 176 ± 13 | 305 ± 28 | 42 ± 11 | 0.76 ± 0.19 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
— | 58.9 ± 6.1 | 188 ± 16 | 318 ± 16 | 40.9 ± 7.4 | 0.92 ± 0.12 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
C | 0.9 ± 1.1 | 206 ± 19 | 325 ± 19 | 36.6 ± 8.5 | 0.69 ± 0.09 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | 5.4 ± 7.2 | 229 ± 16 | 312 ± 21 | 26.6 ± 8.6 | 1.43 ± 0.26 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
D | 3.3 ± 4.1 | 244 ± 12 | 324 ± 13 | 24.7 ± 5.5 | 2.76 ± 0.39 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | 0.4 ± 0.2 | 229 ± 19 | 309 ± 14 | 25.9 ± 7.7 | 3.03 ± 0.25 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
— | 1.9 ± 2.8 | 2.9 ± 21 | 337 ± 24 | 29.1 ± 9.7 | 1.94 ± 0.42 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
E | 0.3 ± 0.3 | 225 ± 11 | 319 ± 16 | 29.5 ± 6.3 | 2.97 ± 0.85 |
Based on this analysis, the titania samples shrink almost twice as much as the silica samples (55% vs. ∼30%) for a calcination temperature of 500 °C. While a higher calcination temperature would likely lead to partial conversion of anatase to rutile, which would further increase the RI of the opal, it may also increase the cracking and induce significant deformation of the inverse opal structure.35 Note that the assumption of no contraction in the x–y plane is only valid when there are few cracks; cracks will lead to x–y shrinkage that is not calculated. Thus, this method underestimates the reduction in volume when cracks are present (i.e. for the titania samples). The shrinkage is a large component of the increased crack density, but we expect that it is not the only component influencing the cracking, and that a difference in brittleness may also have a contribution. It has been shown that the thickness of the silica inverse opal made by the coassembly approach can also be important, as cracking increases with the increase of the number of colloidal layers.13 However, the silica inverse opals in the current study were thicker than the titania ones on average (Fig. 5c), implying that the thickness is not the main factor influencing cracking. Therefore, since the samples with more titania were generally thinner, the crack density must underestimate the effect of shrinkage due to the competing thickness trend.
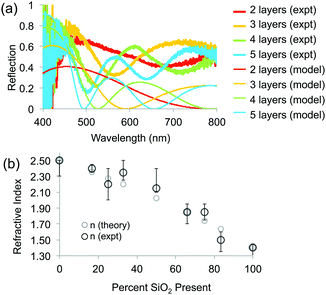
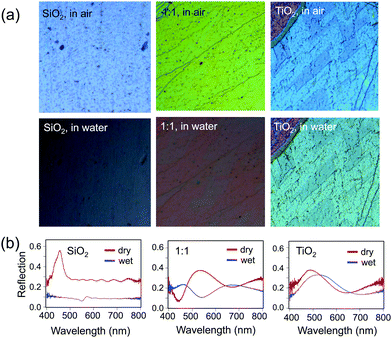
To determine the RI of the resulting structures, we investigated the optical spectra of inverse opals made from a range of titania/silica ratios taken at normal incidence in reflection mode through a microscope objective lens (Fig. 7 and 8). For thin inverse opals, the structural color depends on the number of layers,11 so spectra were acquired for several adjacent layers. These spectra were then used to calculate the RI of the sample, taking into account the geometries of the samples measured from cross-sectional SEM images. Optical reflection spectra of silica/titania hybrid inverse opals were fitted to theoretical curves in order to determine the refractive index of the matrix material (Fig. 7a). For each sample, spectra were taken using a microscope-coupled spectrometer to selectively measure optical spectra at precise locations on the substrate at various layer thicknesses of the inverse opal structure (Fig. 8b, thick lines). Theoretical spectra were generated using transfer matrix calculations using the measured pore heights (Table 1) for the periodicity, and adjusting the refractive index to fit the experimental spectra. An exemplary sample is shown in Fig. 7a, with the experimental spectra (thick lines) corresponding to the theoretical spectra (thin lines) of the same color. Different layer thicknesses have different reflection spectra, so several adjacent layers were used in order to get multiple spectra for a given precursor ratio, represented by different colors in Fig. 7a. The experimental spectra (thick lines) have a higher baseline than the theoretical spectra (thin lines), presumably due to additional scattering that was not incorporated into the simulations. The RI value calculated from experimental spectra for each sample is shown in Fig. 7b as dark circles (labeled “expt”), as a function of the percent silica (as obtained from XPS). Error bars represent the standard deviation in the RI calculated for the different experimental spectra for each sample. The RI of 2.5, derived from optical spectra, matches well with the expected value of 2.4 for anatase titania.
The elemental compositions from the XPS analysis were used to predict a theoretical RI, based on the following equation from effective medium theory:
Finally, the effect of the increased RI of the hybrid opals on their optical properties upon infiltration of the pores with a liquid was probed (Fig. 8). The contrast between the RI of the matrix material and that of infiltrated medium determines the presence or absence of the color and the color intensity.11 Indeed, an infiltrated silica structure loses its color, when filled with water (n = 1.33), leaving only the reflection of the substrate below (Fig. 8a, bottom), whereas the titania sample stays brightly colored, only slightly decreasing in intensity due to the lowered refractive index contrast, with a red shift in the color (Fig. 8a, bottom) due to the higher average RI of the material. As expected, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of silica and titania has both a larger red shift in color and larger loss of intensity as compared to pure titania, but color remains. The optical reflection spectra at normal incidence further support this observation (Fig. 8b).
1 mixture of silica and titania has both a larger red shift in color and larger loss of intensity as compared to pure titania, but color remains. The optical reflection spectra at normal incidence further support this observation (Fig. 8b).
Conclusions
In summary, we report the assembly of crack-free, hybrid inverse opals with high RI by controlling the composition of the inorganic matrix. Combining silica and titania precursors, hybrid inverse opal structures can be grown with a uniform composition featuring domain sizes below 5 nm. The resulting structures combine the structural integrity of silica and the high RI of titania. XPS and EDS results confirm that both silicon and titanium are present, and the RI corresponds well with what is expected for the different compositions. The RI can thus be controlled across the silica–titania range (1.38–2.5) while maintaining structural integrity over macroscopic dimensions with long-range ordered pores and minimal crack appearance, allowing photonic properties to be observed even when immersed in liquids. This technique opens doors to new high-quality hybrid inverse opal materials with the structural integrity, crack-free assembly, and long-range order inherited from the silica sol–gel chemistry, but amplified by additional functional properties emerging from a second component, such as titania.36,37 One can further envision subjecting the samples to selective removal of silica, to introduce mesoporosity into highly ordered inverse opals made from arbitrary materials.We anticipate that these structures hold high potential for a multitude of applications, e.g., in chemical, electrochemical, biochemical, and photocatalysis,31,38–44 in sensors,45–47 and various advanced optical applications.6,35,48–51
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation (NSF) Designing Materials to Revolutionize and Engineer our Future program under award #DMR 1533985. K. R. P. acknowledges support from a DOD graduate fellowship. N. V. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG) under grant number VO1824/9-1. This work was performed in part at the Harvard University Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Coordinated Infrastructure Network (NNCI), which is supported by the National Science Foundation under NSF ECCS award no. 1541959.Notes and references
- A. Stein, F. Li and N. R. Denny, Chem. Mater., 2008, 20, 649–666 CrossRef CAS.
- J. F. Galisteo-López, M. Ibisate, R. Sapienza, L. S. Froufe-Pérez, Á. Blanco and C. López, Adv. Mater., 2011, 23, 30–69 CrossRef.
- A. Stein, B. E. Wilson and S. G. Rudisill, Chem. Soc. Rev., 2013, 42, 2763–2803 RSC.
- G. von Freymann, V. Kitaev, B. V. Lotsch and G. A. Ozin, Chem. Soc. Rev., 2013, 42, 2528–2554 RSC.
- K. R. Phillips, G. T. England, S. Sunny, E. Shirman, T. Shirman, N. Vogel and J. Aizenberg, Chem. Soc. Rev., 2016, 281–322 RSC.
- P. Belleville, F. Benoit, K. Vallé, B. Bertussi, L. Kocon, E. Dieudonné, N. Mallejac and C. Sanchez, J. Sol-Gel Sci. Technol., 2019, 90, 155–161 CrossRef CAS.
- C. I. Aguirre, E. Reguera and A. Stein, Adv. Funct. Mater., 2010, 20, 2565–2578 CrossRef CAS.
- C. I. Aguirre, E. Reguera and A. Stein, ACS Appl. Mater. Interfaces, 2010, 2, 3257–3262 CrossRef CAS.
- N. Koay, I. B. Burgess, T. M. Kay, B. A. Nerger, M. Miles-Rossouw, T. Shirman, T. L. Vu, G. England, K. R. Phillips, S. Utech, N. Vogel, M. Kolle and J. Aizenberg, Opt. Express, 2014, 22, 27750–27768 CrossRef.
- D. P. Josephson, M. Miller and A. Stein, Z. Anorg. Allg. Chem., 2014, 640, 655–662 CrossRef CAS.
- I. B. Burgess, L. Mishchenko, B. D. Hatton, M. Kolle, M. Lončar and J. Aizenberg, J. Am. Chem. Soc., 2011, 133, 12430–12432 CrossRef CAS.
- C. Fenzl, T. Hirsch and O. S. Wolfbeis, Angew. Chem., Int. Ed., 2014, 53, 3318–3335 CrossRef CAS.
- B. Hatton, L. Mishchenko, S. Davis, K. H. Sandhage and J. Aizenberg, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 10354–10359 CrossRef CAS.
- K. Rhee do, B. Jung, Y. H. Kim, S. J. Yeo, S. J. Choi, A. Rauf, S. Han, G. R. Yi, D. Lee and P. J. Yoo, ACS Appl. Mater. Interfaces, 2014, 6, 9950–9954 CrossRef.
- L. N. Quan, Y. H. Jang, K. A. Stoerzinger, K. J. May, Y. J. Jang, S. T. Kochuveedu, Y. Shao-Horn and D. H. Kim, Phys. Chem. Chem. Phys., 2014, 16, 9023–9030 RSC.
- S. Amrehn, X. Wu, C. Schumacher and T. Wagner, Phys. Status Solidi A, 2015, 212, 1266–1272 CrossRef CAS.
- J.-H. Shin, J.-H. Kang, W.-M. Jin, J. H. Park, Y.-S. Cho and J. H. Moon, Langmuir, 2011, 27, 856–860 CrossRef CAS PubMed.
- C.-Y. Cho and J. H. Moon, Langmuir, 2012, 28, 9372–9377 CrossRef CAS PubMed.
- P. D. Qian Zhou and B. Cheng, J. Cryst. Growth, 2006, 292, 320–323 CrossRef.
- J. W. Galusha, C.-K. Tsung, G. D. Stucky and M. H. Bartl, Chem. Mater., 2008, 20, 4925–4930 CrossRef CAS.
- F. Sordello, V. Maurino and C. Minero, J. Mater. Chem., 2011, 21, 19144–19152 RSC.
- D. Qi, L. Lu, L. Wang and J. Zhang, J. Am. Chem. Soc., 2014, 136, 9886–9889 CrossRef CAS.
- J. Liu, M. Li, J. Wang, Y. Song, L. Jiang, T. Murakami and A. Fujishima, Environ. Sci. Technol., 2009, 43, 9425–9431 CrossRef CAS.
- Z. Liang, G. Zheng, W. Li, Z. W. Seh, H. Yao, K. Yan, D. Kong and Y. Cui, ACS Nano, 2014, 8, 5249–5256 CrossRef CAS.
- Z.-Z. Gu, S. Kubo, W. Qian, Y. Einaga, D. A. Tryk, A. Fujishima and O. Sato, Langmuir, 2001, 17, 6751–6753 CrossRef CAS.
- K. R. Phillips, T. Shirman, E. Shirman, A. V. Shneidman, T. M. Kay and J. Aizenberg, Adv. Mater., 2018, 30, 1706329 CrossRef PubMed.
- W. Li, Z. Wu, J. Wang, A. A. Elzatahry and D. Zhao, Chem. Mater., 2014, 26, 287–298 CrossRef CAS.
- Z. Cai, Z. Xiong, X. Lu and J. Teng, J. Mater. Chem. A, 2014, 2, 545–553 RSC.
- D. Scheid, D. Stock, T. Winter, T. Gutmann, C. Dietz and M. Gallei, J. Mater. Chem. C, 2016, 4, 2187–2196 RSC.
- P. Gorbovyi, A. P. Diaz-Gomez, M. Traore, L. Museur, L. Rozes, F. Ribot, C. Sanchez, A. I. Kuznetsov, B. N. Chichkov and A. Kanaev, Mater. Res. Bull., 2019, 114, 130–137 CrossRef CAS.
- E. Shirman, T. Shirman, A. V. Shneidman, A. Grinthal, K. R. Phillips, H. Whelan, E. Bulger, M. Abramovitch, J. Patil, R. Nevarez and J. Aizenberg, Adv. Funct. Mater., 2018, 28, 1704559 CrossRef.
- J. W. Goodwin, J. Hearn, C. C. Ho and R. H. Ottewill, Colloid Polym. Sci., 1974, 252, 464–471 CrossRef CAS.
- S. K. Das, M. K. Bhunia and A. Bhaumik, Dalton Trans., 2010, 39, 4382–4390 RSC.
- J. C. Parker and R. W. Siegel, J. Mater. Res., 2011, 5, 1246–1252 CrossRef.
- K. R. Phillips, N. Vogel, Y. Hu, M. Kolle, C. C. Perry and J. Aizenberg, Chem. Mater., 2014, 26, 1622–1628 CrossRef CAS.
- M. Faustini, L. Nicole, E. Ruiz-Hitzky and C. Sanchez, Adv. Funct. Mater., 2018, 28, 1704158 CrossRef.
- S. Suresh, W. Zhou, B. Spraul, R. M. Laine, J. Ballato and D. W. Smith, Jr., J. Nanosci. Nanotechnol., 2004, 4, 250–253 CrossRef CAS.
- E. Yi, W. Wang, S. Mohanty, J. Kieffer, R. Tamaki and R. M. Laine, J. Power Sources, 2014, 269, 577–588 CrossRef CAS.
- A. M. Sultan, Z. C. Westcott, Z. E. Hughes, J. P. Palafox-Hernandez, T. Giesa, V. Puddu, M. J. Buehler, C. C. Perry and T. R. Walsh, ACS Appl. Mater. Interfaces, 2016, 8, 18620–18630 CrossRef CAS.
- V. Smeets, C. Boissière, C. Sanchez, E. M. Gaigneaux, E. Peeters, B. F. Sels, M. Dusselier and D. P. Debecker, Chem. Mater., 2019, 31, 1610–1619 CrossRef CAS.
- R. Fiorenza, M. Bellardita, S. Scirè and L. Palmisano, Catal. Today, 2019, 321–322, 113–119 CrossRef CAS.
- T. Shirman, J. Lattimer, M. Luneau, E. Shirman, C. Reece, M. Aizenberg, R. J. Madix, J. Aizenberg and C. M. Friend, Chem. – Eur. J., 2018, 24, 1833–1837 CrossRef CAS PubMed.
- G. I. N. Waterhouse, W. T. Chen, A. Chan and D. Sun-Waterhouse, ACS Omega, 2018, 3, 9658–9674 CrossRef CAS.
- G. Collins, E. Armstrong, D. McNulty, S. O'Hanlon, H. Geaney and C. O'Dwyer, Sci. Technol. Adv. Mater., 2016, 17, 563–582 CrossRef CAS PubMed.
- I. B. Burgess, N. Koay, K. P. Raymond, M. Kolle, M. Loncar and J. Aizenberg, ACS Nano, 2012, 6, 1427–1437 CrossRef CAS.
- M. J. Limo, A. Sola-Rabada, E. Boix, V. Thota, Z. C. Westcott, V. Puddu and C. C. Perry, Chem. Rev., 2018, 118, 11118–11193 CrossRef CAS.
- M. Kuang, J. Wang and L. Jiang, Chem. Soc. Rev., 2016, 45, 6833–6854 RSC.
- Y. Heo, H. Kang, J. S. Lee, Y. K. Oh and S. H. Kim, Small, 2016, 12, 3819–3826 CrossRef CAS.
- D. Zhang, S. Chen, M. Jiang and L. Ye, Appl. Opt., 2014, 53, 7624–7628 CrossRef.
- A. Lonergan, D. McNulty and C. O'Dwyer, J. Appl. Phys., 2018, 124, 095106 CrossRef.
- K. T. Hufziger, A. B. Zrimsek and S. A. Asher, ACS Appl. Nano Mater., 2018, 1, 7016–7024 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |