Theoretical perspective for luminescent mechanism of thermally activated delayed fluorescence emitter with excited-state intramolecular proton transfer†
Received
27th September 2019
, Accepted 12th November 2019
First published on 15th November 2019
Abstract
Excited-state intramolecular proton transfer (ESIPT) and thermally activated delayed fluorescence (TADF) are interesting photochemical and photophysical properties for light-emitting materials. Recently, a novel design strategy for TADF molecules was realized in the TQB molecule by ESIPT [ACS Cent. Sci., 2017, 3(7), 769–777]; however, the TADF and ESIPT mechanisms for this molecule are not very clear. In this work, the TADF and ESIPT mechanisms for TQB in both solution and the solid phase were studied based on the calculation of potential energy curves, energy levels and decay rates of the excited states. It was found that proton transfer in S1 for TQB is quite easy in both DMF and the solid phase. In contrast, the proton transfer in T1 and T2 in DMF is slightly difficult, while the barrier in T1 for TQB in the solid phase is comparable with room temperature energy. The T2TQB-TA → S1TQB-TB upconversion path plays a crucial role in the TADF of TQB in solvent, while T2TQB-TB → S1TQB-TB has a dominant contribution to the TADF in the solid phase. Based on the investigation of TQB, we designed two molecules, TQB* with a single hydrogen bond and TQB** with two hydrogen bonds. Our calculation results indicate that the TQB** molecules can realize dual emission by ESIPT and are a potential light-emitting material for white light. No ESIPT can be realized in TQB*, while large energy gaps are found between the higher excited states and lowest excited states. Our investigation provides new perspectives for the ESIPT and TADF mechanisms, which can help in understanding the light-emitting properties of TQB and provide some insights on the design of new functional luminescent molecules.
1 Introduction
Recently, thermally activated delayed fluorescence (TADF) materials have attracted wide attention since 100% exciton usage efficiency can be obtained in organic light-emitting diodes with TADF emitters.1 Although great progress has been achieved for TADF emitters, most of them are composed of donors (D) and acceptors (A) to achieve a smaller energy gap (ΔEST) between the first singlet excited state (S1) and the lowest triplet excited state (T1) by separating the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO).2,3 However, some limitations of TADF molecules have also been observed. Although a separated HOMO–LUMO is favorable for obtaining a small ΔEST, it results in reduced radiative rates. To overcome these shortcomings, molecules designed based on the opposite resonant effect,4 dual emitting core,5 combined charge-transfer pathways6 and intramolecular proton transfer (ESIPT) process7 have been reported. The ESIPT process is a classic photoisomerization process, which is a very fast four-level cyclic proton-transfer reaction between an enol (E) and keto (K) (E → E* → K* → K → E).8,9 Due to the abnormally large Stokes shift between the emission from K* and the absorption from E, self-absorption can be avoided.10 Actually, the first ESIPT molecule combined with the TADF phenomenon was first reported by Park et al. in 2007.11 Nevertheless, this phenomenon is constrained to in solution only. In organic light-emitting diodes (OLEDs), the ESIPT process may be inhibited due to the environment confinement. The triquinolonobenzene (TQB) molecule reported by Mamada et al. is the first rigid TADF–ESIPT molecule without D or A groups, which can overcome the environmental limitation and realize TADF and ESIPT in OLEDs. Their work presented a new design strategy for TADF emitters. Nevertheless, the mechanisms of TADF and ESIPT are still very clear, although some theoretical works have focused on them. Cao et al. performed quantum chemistry and ab initio molecular dynamics calculations and found that the proton transfer from the triplet state of normal TQB to the singlet excited state of ESIPT TQB (3TQB-TA → 1TQB-TB) plays a crucial rule in triplet exciton harvesting.12 Zhao et al. studied the influence of solution polarity on the ESIPT process and found that the ESIPT can be facilitated by polar solvents.13 Why does the conversion from 3TQB-TA to 1TQB-TB play a crucial role in the triplet exciton harvesting of TQB? Are there any other pathways? What about the mechanism in the solid phase? Are the ESIPT process and RISC process similar to that in solvent? Herein, the TADF and ESIPT mechanisms were systematically studied in both solution and solid phase using the polarized continuum model (PCM) and the combined quantum mechanics and molecular mechanics (QM/MM) method. The excited-state decay rates were also calculated based on the thermal vibration correlation function (TVCF) method. In addition, two new molecules were designed based on TQB by breaking its symmetry and also studied for potential application as functional molecules.14 Our theoretical results will not only be helpful for understanding the photophysical phenomenon of TADF–ESIPT molecules but also help in the design of new molecules.
2 Computational details and theoretical methods
In our research, the density functional theory (DFT) was used to optimize the molecular structure in the ground state (S0), while the geometry of the excited states was optimized with the time-dependent density functional theory (TD-DFT). All the above calculations were calculated at the B3LYP/6-31g(d) level. The PCM method was used in the calculation to simulate the solution environment and N,N-dimethylformamide (DMF) solvent was adopted. The reason why we chose to study the light-emitting properties of TQB in DMF is to compare the experimental results where measurements were performed in DMF, tetrahydrofuran (THF) and toluene. Since Cao et al. performed a theoretical simulation on the light-emitting mechanism of TQB in toluene,12 we assumed it is better to study another solvent effect. Considering that DMF (with a permittivity constant of 37.2) is a much stronger polar solvent than toluene (with a permittivity constant of 2.4), the differences for TQB in toluene and in DMF may be more significant. In addition, ESIPT is sensitive to polar environments. If the polarity of the solution is too high, the ESIPT process will be difficult. However, TADF was found for TQB in DMF, which predicts that ESIPT should happen in DMF. Our calculation confirmed the results and it further proved that TQB is a good candidate for TADF emitters by the ESIPT process. For QM/MM calculation, a two-layer ONIOM model was adopted.15–18 The central molecule was set as the high layer, and the QM method was used. The molecules around the central molecule were set as the low layer and calculated using the MM method with the efficient universal force field (UFF). The MM part was frozen during the geometry optimizations for the all states in the QM/MM calculation. The potential energy curves along the proton transfer path for S0, S1 and T1 in DMF and the solid phase were also studied. All the abovementioned calculations were achieved in the Gaussian 16 package.19
Based on the abovementioned calculations, we calculated the decay rates of the excited states. The radiative rate of S1 was obtained using the Einstein spontaneous emission formula:
| | 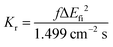 | (1) |
where
f is the oscillator strength and Δ
Efi is the vertical emission energy with the unit wavenumber (cm
−1).
According to Fermi's golden rule (FGR) and the first-order perturbation theory, the nonradiative decay rate can be written as follows:
| | 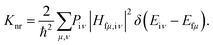 | (2) |
where
Piμ is the Boltzmann distribution function of the initial state and
Hfμ,iν is the interaction between two different Born–Oppenheimer states, which it contains two contributions as follows:
| | 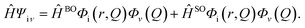 | (3) |
where
ĤBO denotes the nonadiabatic coupling and
ĤSO is the spin–orbit coupling. When a Fourier transform is applied for the delta function, the intersystem crossing rate constant between two electronic states with different spin multiplicity can be written as:
| | 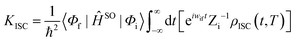 | (4) |
where
ρIC(
t,
T) is the thermal-vibration correlation function and
Zi is the partition function. Both the methodology and application of this formalism can be found in Peng and Shuai's reports.
20–22 The calculations mentioned above can be realized in the MOMAP (Molecular Materials Property Prediction Package promoted by the Institute of Chemistry Chinese Academy of Sciences and Department of Chemistry, Tsinghua University).
23–25
3 Results and discussions
3.1 Geometrical structures
From the chemical structure of TQB, we can deduce that there should be three hydrogen bonds in TQB, and thus three proton transfer states may exist. The molecule without proton transfer is labeled as TQB-TA (shown in Fig. 1(a)). The molecule with one proton transferred is named TQB-TB (shown in Fig. 1(b)). The molecules with two and three protons transferred are called TQB-TC and TQB-TD (shown in Fig. 1(c) and (d)), respectively. To confirm the hydrogen bonds in TQB, the independent gradient model (IGM) method was used to investigate the inter-molecule weak interactions (shown in Fig. S1, ESI†).26 Detailed information about this method can be seen in the Supplementary file. From Fig. S1 (ESI†), we can find obvious hydrogen bond interactions (HBI) at three parts for all the tautomers in both DMF and the solid phase. This means that proton transfer may occur at these three parts.27 We tried to optimize the structure of all the tautomers to obtain the stable geometry. Unfortunately, the stable geometries of TQB-TB in S0 were not obtained in both DMF and the solid state, which is consistent with experimental result. Besides, the stable geometries of all the tautomers in the excited state were also optimized and only TQB-TD in S1 was not obtained. The results are consistent with the experimental result that TQB-TD is not detected experimentally. It should be noted that the optimization for TQB-TA in the solid state was performed based on the crystal structure of TQB obtained experimentally. For the optimization of TQB-TB, TQB-TC and TQB-TD in the solid phase, the crystal structure of TQB was also adopted with the central molecule TQB-TA changed to the molecule with a proton transferred. The QM/MM model is shown in Fig. 1(e). Since S1 is responsible for light emitting and proton transfer, some important geometric parameters for TQB-TA, TQB-TB and TQB-TC in S1 are listed in Table S1 (ESI†) for comparison (definitions of the parameters are shown in Fig. S2, ESI†). It can be found that the bond lengths and angles of the hydrogen bonds obviously change after the proton is transferred. There are no significant differences for the geometric structures except the dihedral angles in the solvent and solid phase. In the solid phase, the planarity of the hydrogen bond and also the symmetry of the molecule are destroyed.
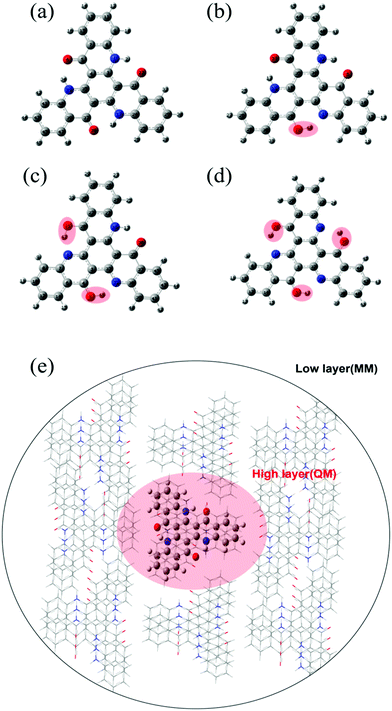 |
| | Fig. 1 Chemical structure of TQB-TA (a), TQB-TB (b), TQB-TC (c) and TQB-TD (d). The positions with proton transfer are marked in red. (e) ONIOM model: the centered TQB is treated as the high layer and surrounding molecules are regarded as the low layer. | |
To explore the light-emitting properties, the emission wavelengths of the three tautomers were calculated in both DMF and the solid phase, as shown in Table 1. It was found that the emission wavelengths for TQB-TA in DMF (375 nm) and the solid phase (374 nm) have a large discrepancy with the experimental values (542 nm). Nevertheless, the emission wavelengths for TQB-TB (513 nm) and TQB-TC (485 nm) in DMF are close to the experimental values. In addition, the values in the solid phase (568 nm and 576 nm) are also close to the experimental values (520 nm). It was deduced that the emission of TQB should come from TQB-TB or TQB-TC. Besides, we found that the oscillator strength for TQB-TA is zero, which indicates that TQB-TA is not responsible for light emitting. It also indicates that it should be easy for a proton to transfer from TQB-TA to TQB-TB. Are both TQB-TB and TQB-TC responsible for the emission? Is it actually easy for a proton to transfer from TQB-TA to TQB-TB? Is it also easy for a proton to transfer from TQB-TB to TQB-TC?
Table 1 Emission wavelengths and oscillator strength calculated for all the tautomers in DMF and the solid phase
|
|
DMF |
Solid |
|
λ (nm) |
f
|
λ (nm) |
f
|
| Exp. is experimental emission wavelength. |
| TQB-TA |
375 |
0.0000 |
374 |
0.0004 |
| TQB-TB |
513 |
0.2539 |
568 |
0.0909 |
| TQB-TC |
485 |
0.3694 |
576 |
0.0958 |
| Exp. |
542 |
|
520 |
|
3.2 Emission mechanism in DMF
To further explore the emission process, the potential energy curve (PEC) along the nitrogen–hydrogen distance for TQB in DMF is shown in Fig. 2. Since the molecular geometry of TQB-TA is symmetric, the three hydrogen bonds should be equivalent in DMF. Both the first and second proton transfer were chosen randomly. From the potential energy curve of S0, it can be found that the energy of TQB-TA is the lowest. The energy barrier from TQB-TA to TQB-TB is as large as 0.41 eV, which means that it is difficult for a proton to transfer in the ground state for TQB. From the potential energy curve of S1, it can be found that TQB-TB is the most stable. The energy barrier from TQB-TA to TQB-TB is only 0.03 eV, which means it is easy for a proton to transfer from TQB-TQ to TQB-TB in the first excited state. The energy barriers from TQB-TB to TQB-TC and back to TQB-TA are as large as 0.48 eV and 0.41 eV, which indicates that it is difficult for double proton transfer and backward single proton transfer, respectively. The molecules tend to stay at TQB-TB in S1, and thus the emission in DMF should come from TQB-TB not TQB-TC.
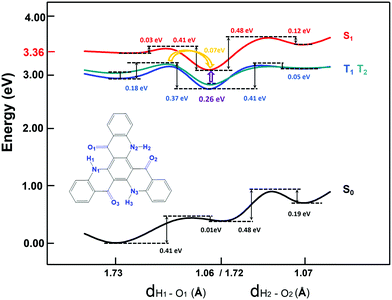 |
| | Fig. 2 Potential energy curves of TQB with ESIPT in DMF. | |
Besides, there TADF was also found for TQB. Thus, the TADF mechanism was also investigated. As is known, TADF is realized by upconversion from the triplet state to the first singlet excited state. Since TQB-TB is responsible for emission, upconversion may also occur in TQB-TB. The energy levels of several low-lying excited states for TQB-TB and other tautomers in DMF are illustrated in Fig. 3. It can be found that there is one triplet excited state below S1 in energy for TQB-TB, and the energy gap between them is 0.26 eV. Although T2 is higher than S1 in energy, their energy gap is as small as 0.06 eV. Both T1 and T2 may participate in the reverse intersystem crossing (RISC) process, while the RISC efficiency should not be very high due to the relatively large energy gap between S1 and T1 as well as the low distribution of the molecule in T2. To confirm our conclusions, the spin–orbit coupling (SOC) constants between S1 and T1 (T2) in DMF were calculated using the Dalton 2013 package (see Table 2).28 It was found that the SOC constants for TQB-TA and TQB-TB are all quite small. The SOC values between S1 and T2 for TQB-TA are zero or close to zero. The SOC constants between S1 and T1 for TQB-TB are slightly larger than that between S1 and T1. The ISC and RISC rates in DMF were also calculated, as shown in Table 3. For TQB-TB, the ISC and RISC rates between S1 and T2 are 4.1 × 104 s−1 and 1.5 × 105 s−1, which shows contribution to the exciton decay. The ISC and RISC rates between S1 and T1 are only 2.6 × 102 s−1 and zero, respectively, which may have little influence in the process of delayed fluorescence. Based on the analysis above, we think that one of the TADF conversion process in DMF is as follows: S1TQB-TA → S1TQB-TB → T2TQB-TB → S1TQB-TB.
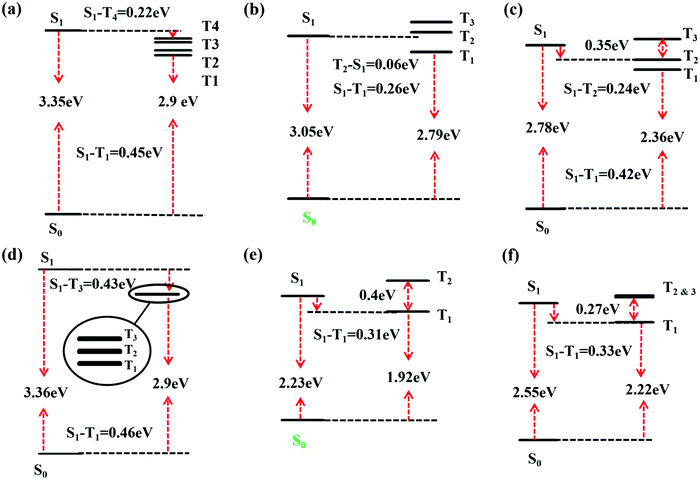 |
| | Fig. 3 Excitation energies based on the optimized geometry of every state for TQB-TA (a), TQB-TB (b), and TQB-TC (c) in DMF and TQB-TA (d), TQB-TB (e), and TQB-TC (f) in the solid phase. | |
Table 2 Spin–orbit coupling (SOC) constants between S1 and triplet states
|
H
so (cm−1) |
TQB-TA |
TQB-TB |
| DMF |
Solid |
DMF |
Solid |
| S1–Tn (n = 1 and 2) based on the optimized single excited state structures and T1–Sn (n = 1 and 2) based on the optimized triplet excited states structures. |
| S1–T1 |
0.018 |
0.539 |
0.004 |
0.175 |
| S1–T2 |
0.000 |
0.226 |
0.015 |
0.199 |
| T1–S1 |
0.018 |
0.749 |
0.004 |
0.186 |
| T2–S1 |
0.002 |
0.219 |
0.018 |
0.229 |
Table 3 Correlation rate calculated for molecular TQB-TA, TQB-TB and TQB-TC in both DMF and the solid phase. Kr is the rate of radiative decay rate, Knr is the nonradiative decay rate, KRISC is the reverse intersystem crossing rate, and KISC is the intersystem crossing rate (unit: s−1)
|
|
TQB-TA |
TQB-TB |
| DMF |
Solid |
DMF |
Solid |
|
K
r (S1 → S0) |
0 |
1.6 × 109 |
1.7 × 108 |
1.9 × 107 |
|
K
ISC (S1 → T1) |
0 |
3.8 × 106 |
2.6 × 102 |
8.3 × 105 |
|
K
ISC (S1 → T2) |
0 |
1.3 |
4.1 × 104 |
4.9 × 106 |
|
K
RISC (T1 → S1) |
0 |
2.1 |
0 |
6.18 |
|
K
RISC (T2 → S1) |
0 |
1.1 × 106 |
1.5 × 105 |
7.9 × 106 |
Recently, Cao et al. proposed that the proton transfer along 3TQB-TA → 1TQB-TB plays crucial role in exciton harvesting. We also noticed that there are four triplet excited states lower in energy than S1 for TQB-TA. The energy gap between S1 and T1 is as large as 0.45 eV, and the gap between S1 and T4 is 0.22 eV. Thus, it can be deduced that it is quite difficult to realize upconversion in TQB-TA. Since T2 in TQB-TA is lower than S1 and higher than S1 in TQB-TB, we deduce that there should be crossing between S1-PEC and T2-PEC. The potential energy curves of T1 and T2 were also studied (shown in Fig. 2). It was found that both T1 and T2 are stable in TQB-TB. However, we found that the energy barrier for T1 and T2 from TQB-TA to TQB-TB is 0.18 eV and 0.11 eV, respectively. This means that proton transfer is slightly difficult in the triplet excited states only relying on the thermal energy at room temperature. Nevertheless, we noticed that T2 of TQB-TA is close in energy to S1 in TQB-TB. It is quite possible for a proton to transfer from T2 to S1. This is also consistent with the conclusion by Cao et al.12 Of course, it should be noted that most of the triplet states should be in T1 of TQB-TA. If the conversion from T2TQB-TA → S1TQB-TB is responsible for the exciton harvesting, the coupling between T1TQB-TA and T2TQB-TA should also be important. From the potential energy curve, we can find that the energy of T1 is really close to T2, which could ensure coupling between them. This is also the reason why T1TQB-TA is generated for photo excitation. Since the molecules are all first excited to the singlet states of TQB-TA for photoexcitation, the generation of T1TQB-TA seems impossible by the ISC process since the ISC rate between T1TQB-TA and S1TQB-TA was calculated to be zero. However, the crossing between the surfaces of S1 and T2 as well as the coupling between T1 and T2 will favor its generation. Considering the difficulty in simulating the electroluminescent properties of molecules in the solid phase, the studies in solvent can also be seen as references for the electroluminescent properties in the solid phase.29 For electroluminescence, more triplet excited states will be generated and the T1TQB-TA → T2TQB-TA → S1TQB-TB process may play a more significant role. In the following section, we study the light-emitting properties of TQB in the solid phase, which can be used to analyze both its photo-luminescence and electro-luminescence properties.
3.3 Emission mechanism in the solid phase
Based on the results above, we found that it is easy for a proton to transfer from S1 of TQB-TA to TQB-TB in DMF. TQB-TB is responsible for light emitting. There are two TADF generation paths: (1) S1TQB-TA → S1TQB-TB → T2TQB-TB → S1TQB-TB and (2) T1TQB-TA → T2TQB-TA → S1TQB-TB. What is the situation for TQB in the solid phase? Here, we also performed a relaxed scan of the potential energy curve of the molecule in the S0, S1 and T1 states (shown in Fig. 4). We found that the hydrogen bonds for TQB-TA in the solid phase are not equivalent due to the different environments in the solid phase. For convenience, three paths are labeled, as shown in Fig. 5, and the single proton transfer process in the three paths was studied. It can be found that it is similar to the situation in DMF. The geometry of TQB-TA is more stable than that of TQB-TB in S0, while TQB-TB is lower in energy than TQB-TA in S1. The energy barriers from S1TQB-TA to S1TQB-TB are 0.004 eV, 0.012 eV and 0.003 eV for Path 1, Path 2 and Path 3, respectively. This means that all three paths are quite easy to be traversed although there is a slight difference among them. In comparison with the results in DMF, the proton transfer in S1 becomes almost barrier free in the solid phase. In addition, the energy barriers from T1TQB-TA to T1TQB-TB or from T2TQB-TA to T2TQB-TB in Path 1 are 0.02 eV and 0.05 eV, respectively, which is much smaller than that in Path 2 and Path 3. This means that proton transfer may also occur in triplet states along Path 1 in the solid phase, which is different from that in DMF. In the solid phase, both singlet and triplet excitons of TQB-TA can decay by proton transfer to TQB-TB.
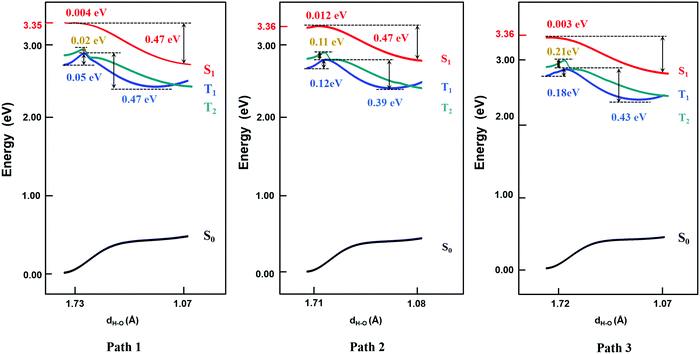 |
| | Fig. 4 Potential energy curves of TQB with single proton transfer in the solid phase. | |
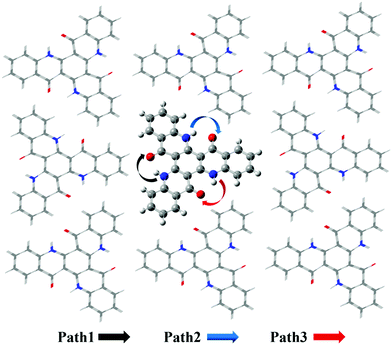 |
| | Fig. 5 Three proton transfer paths in the solid phase. | |
Based on the above analysis, we deduce that TADF in the solid phase should also be realized in TQB-TB. To confirm this deduction, the energy levels of several low-lying excited states are illustrated in Fig. 3. It can be found that the energy gap between S1 and T1 in TQB-TB in the solid phase is 0.31 eV, while the gap between S1 and T2 is only 0.09 eV. This is similar to the situation in DMF, although the energy gaps are slightly larger. The energy gaps between S1 and T1 in TQB-TA and TQB-TC in the solid phase are still quite large. In addition, we calculated the SOC constants between S1 and T1 or T2 (shown in Table 2). It was found that the SOC constants for both TQB-TA and TQB-TB in the solid phase are much larger than that in DMF. The ISC and RISC rates in the solid phase were also calculated, as shown in Table 3. It is obvious that the ISC and RISC rates in the solid phase are also much larger than that in DMF. The ISC rates from S1 to T1 and T2 in TQB-TB are 8.3 × 105 s−1 and 4.9 × 106 s−1, which means that both channels are responsible for the ISC process. However, the RISC rate from T1 to S1 is very small, which means that the RISC process for TQB-TB should be from T2 to S1. The TADF process in the solid phase is confirmed to be T2TQB-TA → T2TQB-TB → S1TQB-TB and T1TQB-TA → T1TQB-TB → T2TQB-TB → S1TQB-TB. Of course, we cannot exclude the path T2TQB-TA → S1TQB-TB. From Fig. 3, it can be found that the energy of T2 in TQB-TA is lower than that of S1, while it is higher than S1 in TQB-TB. From Fig. 4, it can also be found that the energy of T2 in TQB-TA is higher than that of S1 in TQB-TB, and thus energy crossing may also occur in the solid phase.
3.4 Oscillator strength and transition property of excited states
Based on the results above, we found that the oscillator strength for TQB-TA in DMF is zero, while it is much larger for TQB-TB (see Table 1). This means that the oscillator strength can be enlarged after proton transfer. The oscillator strength is highly related to the transition dipole moment (TDM) as follows:| | 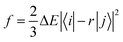 | (5) |
where f is the oscillator strength and ΔE is the energy gap between two states, |i〉 and |j〉. r is the displacement coordinate vector. Since the energy gap between S1 and S0 for TQB-TB is always smaller than that for TQB-TA, the enlarged oscillator strength should be induced by an increase in TDM. The visualization of TDM of the tautomers both in DMF and the solid phase is shown in Fig. 6. The TDM of TQB-TA is quite small, thus the oscillator strength of TQB-TA is close to zero both in DMF and the solid phase. The TDMs of TQB-TB and TQB-TC are clearly larger than that of TQB-TA. To determine why the TDM for TQB-TA is quite small, the molecule was divided into three parts according to symmetry. The TDM for every fragment in TQB-TA points to the center or departs from the center, and thus they counteract with each other. After proton transfer, the TDM of each fragment is different. The two fragments with proton transfer involved contribute to the TDM with a similar direction, and thus induce significant TDM for TQB-TB. In TQB-TC, the fragment with both sides including proton transfer shows little contribution to TDM, and the fragments with single side proton transfer contribute significantly to the TDM. This indicates that the TDM is correlated to the symmetry of the molecule.
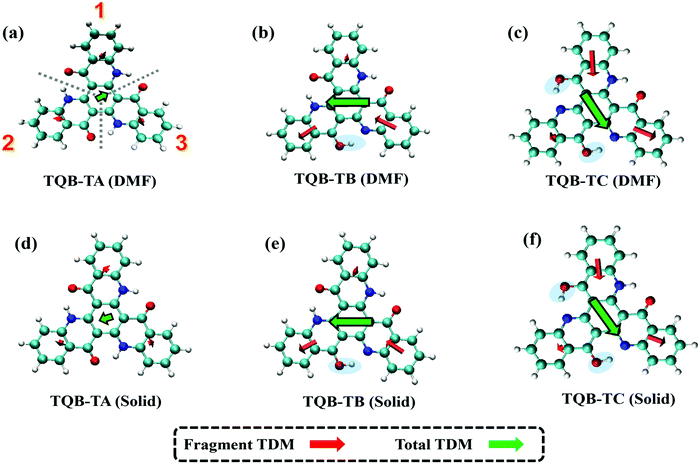 |
| | Fig. 6 Transition dipole moments (TDM) of TQB-TA, TQB-TB and TQB-TC in DMF (a–c) and the solid phase (d–f). For the analysis, the molecules were divided into three parts, as labeled in (a). | |
In addition, the transition properties of the excited states were analyzed. Since more than one molecular orbital contributes to the excitation of S1, the electron–hole distribution of the excited states for the three tautomers in DMF and the solid phase was analyzed (as shown in Fig. 7 and Fig. S3, S4, ESI†). From Fig. 7, it can be seen that the electrons and holes are distributed almost averagely in TQB-TA in both DMF and the solid phase. There is significant separation for electrons and holes in TQB-TB and TQB-TC. Electrons are mainly distributed on fragment 2 and holes are distributed on fragment 3 for TQB-TB, which mean that there is significant charge transfer from fragment 3 to fragment 2 during excitation. For TQB-TC, electrons and holes are located on fragments 1 and 3, respectively. The electron–hole distribution is also confirmed from the heat map shown in the figure, which was obtained using the Multiwfn package program.30 Based on the electron–hole distribution, it can be concluded that the S1 state of TQB-TA is a typical locally excited (LE) state, and the S1 states for both TQB-TB and TQB-TC are charge-transfer states. Since S1TQB-TB is generated from S1TQB-TA by proton transfer, it can be concluded that the proton transfer also induces electron transfer in the excited states. This also indicates that the direction of the proton transfer also influences the direction of the electron transfer. From S1TQB-TA to S1TQB-TB, a proton is transferred from fragment 3 to fragment 2, and thus electrons are transferred from fragment 3 to fragment 2. From S1TQB-TB to S1TQB-TC, one proton is transferred from fragment 3 to fragment 2, and the other proton is transferred from fragment 2 to fragment 1. It can be seen that the proton is transferred from fragment 3 to fragment 1 and no proton is gained or lost in fragment 2. Thus, we think that electrons are transferred from fragment 3 to fragment 1. It seems that proton transfer is also accompanied by electron transfer.
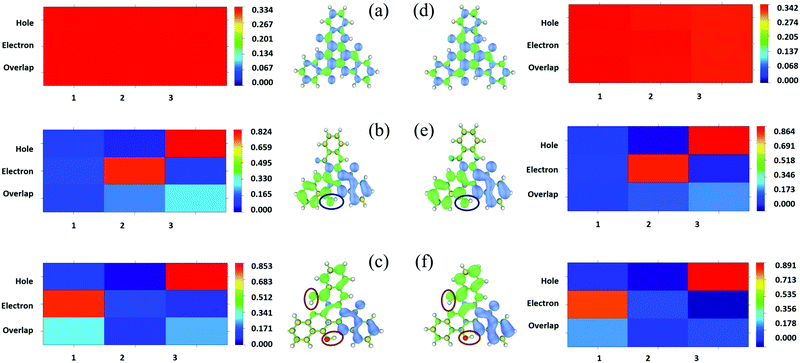 |
| | Fig. 7 Isosurface of the distribution for holes and electrons and heat map of TQB-TA (a), TQB-TB (b) and TQB-TC (c) in DMF and TQB-TA (d), TQB-TB (e) and TQB-TC (f) in the solid phase in the S1 state. | |
From Fig. S3 (ESI†), it can be found that TQB-TA is still an LE state in both DMF and the solid phase, although the LE is only localized on fragment 2 in the solid phase. Both TQB-TB and TQB-TC are still CT states in T1, while there is also some LE component in the transition. For T2, it can be seen that TQB-TA is still an LE state in both DMF and the solid phase, while the transition is only located on one fragment or two fragments (see Fig. S4, ESI†). For TQB-TB and TQB-TC, although CT is significant, more LE component is involved. The transition properties have a close relationship with the photophysical properties. Recent reports showed that vibration coupling between 3CT and 3LE states can provide new paths for upconversion.31–33 The enhancement of the LE components in T2 of TQB-TB may favor the coupling between T1 and T2 and the upconversion process. In addition, the different natures of the singlet and triplet states can favor the ISC process by enhanced spin–orbit coupling.34 The increase in LE component in T1 and T2 can also favor the ISC and RISC processes in TQB-TB. This is also consistent with our calculated SOC values, as shown in Table 2. In general, the LE transition is favorable for radiation since the oscillator strength is proportional to the overlap of excited states 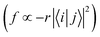 . Nevertheless, the oscillator strength of TQB-TA is close to zero, although the S1 state of TQB-TA is a typical LE state. This should be induced by the strong symmetry of the molecule. Since TQB-TA is symmetric, the displacement vector r is nearly zero during excitation. Thus, the oscillator strength of TQB-TA is nearly zero.
. Nevertheless, the oscillator strength of TQB-TA is close to zero, although the S1 state of TQB-TA is a typical LE state. This should be induced by the strong symmetry of the molecule. Since TQB-TA is symmetric, the displacement vector r is nearly zero during excitation. Thus, the oscillator strength of TQB-TA is nearly zero.
3.5 Modification of TQB
Based on the results above, we found that only the single proton transfer is related to the light-emitting process. The second and third proton transfer are impossible to occur. In addition, we also found that the symmetric structure of TQB makes it non-radiative in S1. Thus, we deduce that the molecule in the normal state can radiate if the symmetry is broken. Based on the above consideration, two molecules with only one hydrogen bond (TQB*) or two hydrogen bonds (TQB**) were designed (as shown in Fig. 8). It was found that the symmetry of the molecules is broken. The excited states and ESIPT states of the two molecules were investigated in toluene. Our calculation indicates that there is no ESIPT state for TQB*, while only single proton transfer can occur for TQB** (defined as TQB**-TB). Consequently, only the proton transfer process of TQB** was studied. The relaxed scanned potential energy curve of TQB** is shown in Fig. 8(d). It can be found that TQB**-TA (the normal state) is more stable than TQB**-TB in S0. The energy values for TQB**-TA in S1 or T1 are quite close to that of TQB**-TB. The energy barriers from TQB**-TA to TQB**-TB in both S1 and T1 (0.17 eV) are relatively higher than room temperature, which means that higher energy is needed for proton transfer. The energy barriers from TQB**-TB back to TQB**-TA are much lower in both S1 and T1. This means that the forward and backward proton transfer processes can be controlled by external conditions. In addition, we also found that the energy of T2 is close to that of S1 during the proton transfer process, which may induce interaction between T2 and S1. The energy levels of several low-lying excited states for TQB**-TA and TQB**-TB are illustrated in Fig. S5 (ESI†). It can be found that the energy gaps between S1 and T1 for TQB**-TA and TQB**-TB are 0.58 eV and 0.47 eV, respectively. The energy of T2 is close to that of S1. In TQB**-TA, T2 is 0.03 eV lower than S1, while it is 0.07 eV higher than S1 in TQB**-TB. The light-emitting properties were also studied for both TQB**-TA and TQB**-TB (as shown in Table 4). The emission wavelengths for TQB**-TA and TQB**-TB are 479 nm and 708 nm, respectively. It should be noted that the emission wavelengths (479 and 708 nm) here are the vertical emission wavelengths, which are different from the energy differences (2.74 and 2.6 eV) between S1 and S0, respectively, in the optimized geometries, as shown Fig. S5 (ESI†). The oscillator strengths of TQB* and TQB** are 0.18 and 0.17, respectively, which are much larger than that of TQB-TA. The TDM of the two molecules are shown in Fig. S6 (ESI†). Significant TDM can be found, which indicates that the molecule can radiate when the symmetry is broken. Based on the calculation results, we deduce that the TQB** molecule can have dual emission and may be used as a light-emitting material for white light.35,36 In addition, TADF may also be found since a large energy gap between T2 and T1 was found for both TQB**-TA and TQB**-TB, which means that the decay from T2 to T1 should be slow and favor the conversion from T2 to S1 due to their close energy levels. For TQB*, the energy levels of several low-lying excited states are also shown in Fig. S5 (ESI†). We found that the energy gap between S1 and T1 is 0.38 eV, which is not favorable for upconversion. However, we found that the energy gap between T2 and T1 is as large as 0.99 eV, which means that the decay from T2 to T1 may be cut off. This is quite similar to the situation in the molecule with hybridized local and charge transfer (HLCT) excited states, as proposed by Ma’ group.37–39 In addition, the vertical excitation energy levels are shown in Fig. S7 (ESI†). It can be found that there is no excited state close in energy to T2, and thus it is difficult for ‘hot exciton’ emission to occur. However, we also noticed that the energy gap between S2 and S1 is also much larger, which is a typical anti-Kasha's rule emission. Thus, we deduce that the TQB* molecule may be used as a light-emitting molecule with anti-Kasha's rule emission.
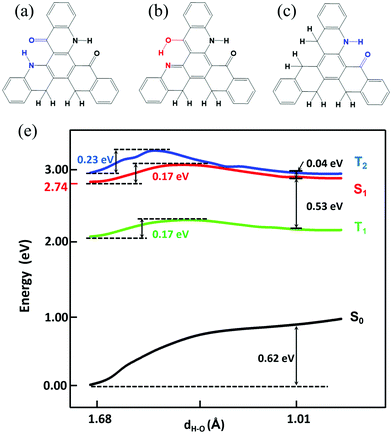 |
| | Fig. 8 Chemical structure of TQB**-TA (a), TQB**-TB (b), and TQB*-TA (c). (d) Potential energy curve of TQB** in toluene. | |
Table 4 Emission wavelengths and oscillator strength calculated for TQB** and TQB* in toluene
|
|
TQB**TA |
TQB**-TB |
TQB*-TA |
| Wavelength (nm) |
479 |
708 |
594 |
|
f
|
0.4702 |
0.1711 |
0.1839 |
|
K
r (s−1) |
1.53 × 108 |
5.02 × 107 |
4.48 × 107 |
4 Conclusions
In summary, the ESIPT and TADF mechanisms for TQB in both DMF and the solid state were studied based on the calculation of excited-state potential curves, energy levels and decay rates of the excited states. It was found that proton transfer in S1 for TQB is quite easy in both DMF and the solid phase. In contrast, the proton transfer in T1 or T2 in DMF is slightly difficult, while the barrier in T1 for TQB in the solid phase is comparable with room temperature energy. Thus, we concluded that proton transfer in the solid phase can be realized in both singlet and triplet excited states. For TQB, two TADF mechanisms were proposed: (1) T2TQB-TB → S1TQB-TB and (2) T2TQB-TA → S1TQB-TB. In DMF, the second mechanism should play a dominant role, while the first mechanism plays a significant role in the solid phase. In addition, the radiative property was found to be correlated with the symmetry and the proton transfer is accompanied by electron transfer. Finally, two molecules, TQB* with a single hydrogen bond and TQB** with two hydrogen bonds, were designed based on TQB. Based on our calculation results, we found that TQB** can realize dual emission and be used in white light OLEDs. The energy gap between T2 and T1 as well as S2 and S1 for TQB* is more than 1 eV, which may show anti-Kasha's rule emission. Our calculation results can not only help in understanding the light-emitting mechanism in the ESIPT-TADF molecule in both solution and the solid state, but also favor the design of functional luminescent molecules.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11974216 and 11874242) and Shandong Provincial Natural Science Foundation, China (ZR2019MA056). Thanks to the supporting of Taishan Scholar Project of Shandong Province. Thanks to the supporting of the Project funded by China Postdoctoral Science Foundation (Grant No. 2018M642689).
References
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Highly efficient organic light-emitting diodes from delayed fluorescence, Nature, 2012, 492(7428), 234–238 CrossRef CAS.
- J. Fan, Y. Zhang, K. Zhang, J. Liu, G. Jiang, L. Lin and C.-K. Wang, Effects of intramolecular and intermolecular interactions on excited state properties of two isomeric Cu complexes with AIE and TADF mechanisms in solid phase: A QM/MM study, Org. Electron., 2019, 71, 113–122 CrossRef CAS.
- J. Liu, Y. Zhang, K. Zhang, J. Fan, C.-K. Wang and L. Lin, Bicolor switching mechanism of multifunctional light-emitting molecular material in solid phase, Org. Electron., 2019, 71, 212–219 CrossRef CAS.
- T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Ultrapure Blue Thermally Activated Delayed Fluorescence Molecules: Efficient HOMO–LUMO Separation by the Multiple Resonance Effect, Adv. Mater., 2016, 28, 2777–2781 CrossRef CAS.
- H.-J. Park, S. H. Han and J. Y. Lee, A Directly Coupled Dual Emitting Core Based Molecular Design of Thermally Activated Delayed Fluorescent Emitters, J. Mater. Chem. C, 2017, 5(46), 12143–12150 RSC.
- X.-L. Chen, J.-H. Jia, R. Yu, J.-Z. Liao, M.-X. Yang and C.-Z. Lu, Combining Charge-Transfer Pathways to Achieve Unique Thermally Activated Delayed Fluorescence Emitters for High-Performance Solution-Processed, Non-doped Blue OLEDs, Angew. Chem., Int. Ed., 2017, 56(47), 15006–15009 CrossRef CAS.
- M. Mamada, K. Inada, T. Komino, W. J. Potscavage Jr., H. Nakanotani and C. Adachi, Highly Efficient Thermally Activated Delayed Fluorescence from an Excited-State Intramolecular Proton Transfer System, ACS Cent. Sci., 2017, 3(7), 769–777 CrossRef CAS.
- J. Zhao, S. Ji, Y. Chen, H. Guo and P. Yang, Excited state intramolecular proton transfer (ESIPT): from principal photophysics to the development of new chromophores and applications in fluorescent molecular probes and luminescent materials, Phys. Chem. Chem. Phys., 2012, 14, 8803–8817 RSC.
- P. Zhou and K. Han, Unraveling the Detailed Mechanism of Excited-State Proton Transfer, Acc. Chem. Res., 2018, 51, 1681–1690 CrossRef CAS.
- J. E. Kwon and S. Y. Park, Advanced Organic Optoelectronic Materials: Harnessing Excited-State Intramolecular Proton Transfer (ESIPT) Process, Adv. Mater., 2011, 23, 3615–3642 CrossRef CAS.
- S. Park, O. H. Kwon, Y. S. Lee, D. J. Jang and S. Y. Park, Imidazole-Based Excited-State Intramolecular Proton-Transfer (ESIPT) Materials:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Observation of Thermally Activated Delayed Fluorescence (TDF), J. Phys. Chem. A, 2007, 111(39), 9649–9653 CrossRef CAS.
Observation of Thermally Activated Delayed Fluorescence (TDF), J. Phys. Chem. A, 2007, 111(39), 9649–9653 CrossRef CAS.
- J. Cao, J. Eng and T. J. Penfold, Excited State Intramolecular Proton Transfer Dynamics for Triplet Harvesting in Organic Molecules, J. Phys. Chem. A, 2019, 123(13), 2640–2649 CrossRef.
- J. Zhao, H. Dong, H. Yang and Y. Zheng, Solvent-Polarity-Dependent Excited-State Behavior and Thermally Active Delayed Fluorescence for Triquinolonobenzene, ACS Appl. Bio. Mater., 2019, 2, 2060–2068 CrossRef CAS.
- K. Wu, T. Zhang, Z. Wang, L. Wang, L. Zhan, S. Gong, C. Zhong, Z. H. Lu, S. Zhang and C. Yang, De Novo Design of Excited-State Intramolecular Proton Transfer Emitters via a Thermally Activated Delayed Fluorescence Channel, J. Am. Chem. Soc., 2018, 140, 8877–8886 CrossRef CAS.
- L. W. Chung, W. M. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H. B. Li, L. Ding and K. Morokuma, The ONIOM Method and Its Applications, Chem. Rev., 2015, 115(12), 5678–5796 CrossRef CAS.
- J. Fan, L. Cai, L. Lin and C. K. Wang, Dynamics of Excited States for Fluorescent Emitters with Hybridized Local and Charge-Transfer Excited State in Solid Phase: A QM/MM Study, J. Phys. Chem. A, 2016, 120, 9422–9430 CrossRef CAS.
- J. Fan, L. Lin and C. K. Wang, Excited state properties of non-doped thermally activated delayed fluorescence emitters with aggregation-induced emission: a QM/MM study, J. Mater. Chem. C, 2017, 5, 8390–8399 RSC.
- L. Lin, J. Fan and C. K. Wang, Theoretical perspective for internal quantum efficiency of thermally activated delayed fluorescence emitter in solid phase: A QM/MM Study, Org. Electron., 2017, 51, 349–356 CrossRef CAS.
-
M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; G. Scalmani; V. Barone; G. A. Petersson; H. Nakatsuji; X. Li; M. Caricato; A. V. Marenich; J. Bloino; B. G. Janesko; R. Gomperts; B. Mennucci; H. P. Hratchian; J. V. Ortiz; A. F. Izmaylov; J. L. Sonnenberg; D. Williams-Young; F. Ding; F. Lipparini; F. Egidi; J. Goings; B. Peng; A. Petrone; T. Henderson; D. Ranasinghe; V. G. Zakrzewski; J. Gao; N. Rega; G. Zheng; W. Liang; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; T. Vreven; K. Throssell; J. A. Montgomery Jr.; J. E. Peralta; F. Ogliaro; M. J. Bearpark; J. J. Heyd; E. N. Brothers; K. N. Kudin; V. N. Staroverov; T. A. Keith; R. Kobayashi; J. Normand; K. Raghavachari; A. P. Rendell; J. C. Burant; S. S. Iyengar; J. Tomasi; M. Cossi; J. M. Millam; M. Klene; C. Adamo; R. Cammi; J. W. Ochterski; R. L. Martin; K. Morokuma; O. Farkas; J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Z. Shuai and Q. Peng, Excited states structure and processes: Understanding organic light-emitting diodes at the molecular level, Phys. Rep., 2014, 537, 123–156 CrossRef CAS.
- Q. Peng, Y. Yi and Z. Shuai, Excited state radiationless decay process with Duschinsky rotation effect: Formalism and implementation, J. Chem. Phys., 2007, 126, 114302, DOI:10.1063/1.2710274.
- Y. Niu, Q. Peng and Z. Shuai, Promoting-mode free formalism for excited state radiationless decay process with Duschinsky rotation effect, Sci. China, Ser. B: Chem., 2008, 51, 1153–1158 CrossRef CAS.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, Theory of Excited State Decays and Optical Spectra: Application to Polyatomic Molecules, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef CAS.
- Q. Peng, Q. Shi, Y. Niu, Y. Yi, S. Sun, W. Li and Z. Shuai, Understanding the efficiency drooping of the deep blue organometallic phosphors: a computational study of radiative and non-radiative decay rates for triplets, J. Mater. Chem. C, 2016, 4, 6829–6838 RSC.
- H. Ma, W. Shi, J. Ren, W. Li, Q. Peng and Z. Shuai, Electrostatic Interaction-Induced Room-Temperature Phosphorescence in Pure
Organic Molecules from QM/MM Calculations, J. Phys. Chem. Lett., 2016, 7, 2893–2898 CrossRef CAS PubMed.
- C. Lefebvre, G. Rubez, H. Khartabil, J. C. Boisson, C. G. Julia and E. Henon, Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density, Phys. Chem. Chem. Phys., 2017, 19, 17928–17936 RSC.
- G.-J. Zhao, J.-Y. Liu, L.-C. Zhou and K.-L. Han, Site-Selective Photoinduced Electron Transfer from Alcoholic Solvents to the Chromophore Facilitated by Hydrogen Bonding:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A New Fluorescence Quenching Mechanism, J. Phys. Chem. B, 2007, 111, 8940–8945 CrossRef CAS.
A New Fluorescence Quenching Mechanism, J. Phys. Chem. B, 2007, 111, 8940–8945 CrossRef CAS.
- Dalton, A Molecular Electronic Structure Program, http://daltonprogram.org.
- H. Sun, Z. Hu, C. Zhong, X. Chen, Z. Sun and J.-L. Bredas, Impact of Dielectric Constant on the Singlet-Triplet Gap in Thermally Activated Delayed Fluorescence Materials, J. Phys. Chem. Lett., 2017, 8(11), 2393–2398 CrossRef CAS.
- T. Lu and F. W. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS.
- X. K. Chen, S. F. Zhang, J. X. Fan and A. M. Ren, Nature of Highly Efficient Thermally Activated Delayed Fluorescence in Organic Light-Emitting Diode Emitters: Nonadiabatic Effect between Excited States, J. Phys. Chem. C, 2015, 119, 9728–9733 CrossRef CAS.
- J. Gibson, A. P. Monkman and T. J. Penfold, The Importance of Vibronic Coupling for Efficient Reverse Intersystem Crossing in Thermally Activated Delayed Fluorescence Molecules, Chem. Phys. Chem., 2016, 17, 2956–2961 CrossRef CAS.
- C. M. Marian, Mechanism of the Triplet-to-Singlet Upconversion in the Assistant Dopant ACRXTN, J. Phys. Chem. C, 2016, 120, 3715–3721 CrossRef CAS.
- P. K. Samanta, D. Kim, V. Coropceanu and J. L. Brédas, Up-Conversion Intersystem Crossing Rates in Organic Emitters for Thermally Activated Delayed Fluorescence: Impact of the Nature of Singlet vs Triplet Excited States, J. Am. Chem. Soc., 2017, 139, 4042–4051 CrossRef CAS PubMed.
- B. Li, L. Zhou, H. Cheng, Q. Huang, J. Lan, L. Zhou and J. You, Dual-emissive 2-(2’-hydroxyphenyl) oxazoles for high performance organic electroluminescent devices: discovery of a new equilibrium of excited state intramolecular proton transfer with a reverse intersystem crossing process, Chem. Sci., 2018, 9, 1213–1220 RSC.
- L. Duarte, J. Germino, J. Berbigier, C. Barboza, M. Faleiros, D. Simoni, M. Galante, M. Holanda, F. Rodembusch and T. Atvars, White-light generation from all-solution-processed OLEDs using a benzothiazole-salophen derivativereactive to the ESIPT process, Phys. Chem. Chem. Phys., 2019, 21, 1172–1182 RSC.
- L. Yao, B. Yang and Y. Ma, Progress in next-generation organic electroluminescent materials: material design beyond exciton statistics, Sci. China: Chem., 2014, 57, 335–345 CrossRef CAS.
- X. Tang, Q. Bai, Q. Peng, Y. Gao, J. Li, Y. Liu, L. Yao, P. Lu, B. Yang and Y. Ma, Efficient Deep Blue Electroluminescence with an External Quantum Efficiency of 6.8% and CIEy < 0.08 based on a Phenanthroimidazole-Sulfone Hybrid Donor-Acceptor Molecule, Chem. Mater., 2015, 27, 7050–7057 CrossRef CAS.
- D. Hu, L. Yao, B. Yang and Y. Ma, Reverse intersystem crossing from upper triplet levels to excited singlet: a ‘hot excition’ path for organic light-emitting diodes, Philos. Trans. R. Soc., A, 2015, 373, 20140318 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The independent gradient model (IGM) method, the visualization of hydrogen bonds, the geometric parameters for S1, the electron–hole distribution of all tautomers in T1 and T2, and excitation energy and transition dipole moment of the designed molecules. See DOI: 10.1039/c9tc05299b |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  ,
Yuzhi
Song
,
Chuan-Kui
Wang
* and
Lili
Lin
,
Yuzhi
Song
,
Chuan-Kui
Wang
* and
Lili
Lin
 *
*
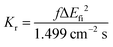
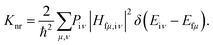
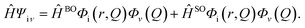
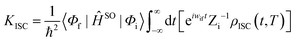

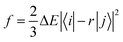

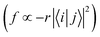 . Nevertheless, the oscillator strength of TQB-TA is close to zero, although the S1 state of TQB-TA is a typical LE state. This should be induced by the strong symmetry of the molecule. Since TQB-TA is symmetric, the displacement vector r is nearly zero during excitation. Thus, the oscillator strength of TQB-TA is nearly zero.
. Nevertheless, the oscillator strength of TQB-TA is close to zero, although the S1 state of TQB-TA is a typical LE state. This should be induced by the strong symmetry of the molecule. Since TQB-TA is symmetric, the displacement vector r is nearly zero during excitation. Thus, the oscillator strength of TQB-TA is nearly zero.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Observation of Thermally Activated Delayed Fluorescence (TDF), J. Phys. Chem. A, 2007, 111(39), 9649–9653 CrossRef CAS.
Observation of Thermally Activated Delayed Fluorescence (TDF), J. Phys. Chem. A, 2007, 111(39), 9649–9653 CrossRef CAS.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A New Fluorescence Quenching Mechanism, J. Phys. Chem. B, 2007, 111, 8940–8945 CrossRef CAS.
A New Fluorescence Quenching Mechanism, J. Phys. Chem. B, 2007, 111, 8940–8945 CrossRef CAS.




