Analysis of an all-solid state nanobattery using molecular dynamics simulations under an external electric field†
Victor
Ponce
 ab,
Diego E.
Galvez-Aranda
ac and
Jorge M.
Seminario
ab,
Diego E.
Galvez-Aranda
ac and
Jorge M.
Seminario
 *abc
*abc
aDepartment of Chemical Engineering, Texas A&M University, College Station, TX 77843, USA. E-mail: seminario@tamu.edu; Tel: +1 979 845-3301
bDepartment of Materials Science and Engineering, Texas A&M University, College Station, TX 77843, USA
cDepartment of Electrical and Computer Engineering, Texas A&M University, College Station, TX 77843, USA
First published on 16th November 2020
Abstract
Present Li-ion battery (LIB) technology requires strong improvements in performance, energy capacity, charging-time, and cost to expand their application to e-mobility and grid storage. Li-metal is one of the most promising materials to replace commercial anodes such as graphite because of its 10 times higher specific capacity. However, Li-metal has high reactivity with commercial liquid electrolytes; thus, new solid materials are proposed to replace liquid electrolytes when Li-metal anodes are used. We present a theoretical analysis of the charging process in a full nanobattery, containing a LiCoO2 cathode, a Li7P2S8I solid-state electrolyte (SSE), a Li-metal anode as well as Al and Cu collectors for the cathode and anode, respectively. In addition, we added a Li3P/Li2S film as a solid electrolyte interphase (SEI) layer between the Li-anode and SSE. Thus, we focus this study on the SEI and SSE. We simulated the charging of the nanobattery with an external voltage by applying an electric field. We estimated temperature profiles within the nanobattery and analyzed Li-ion transport through the SSE and SEI. We observed a slight temperature rise at the SEI due to reactions forming PS3− and P2S74− fragments at the interfaces; however, this temperature profile changes due to the charging current under the presence of the external electric field ε = 0.75 V Å−1. Without the external field, the calculated open-circuit voltage (OCV) was 3.86 V for the battery, which is within the range of values of commercial cobalt-based LIBs. This voltage implies a spontaneous fall of available Li-ions from the anode to the cathode (during discharge). The charge of this nanobattery requires overcoming the OCV plus an additional voltage that determines the charging current. Thus, we applied an external potential able to neutralize the OCV, plus an additional 1.6 V to induce the transport of Li+ from the cathode up to the anode. Several interesting details about Li+ transport paths through the SSE and SEI are discussed.
Introduction
Research on solid-state electrolytes (SSEs) started more than 200 years ago with Faraday's work using Ag2S and PbF2.1 Nowadays, decarbonization is growing to eliminate the effects of carbon fuels in global warming in favor of renewable energies such as solar and wind energies, for which energy storage will play an important role.2 Li-ion batteries are ubiquitous in portable devices; however, their proliferation in e-mobility and grid storage, require strong improvements in performance, energy capacity, charging-time, and cost that cannot be satisfied with the present Li-ion batteries (LIB). Thus, recently, SSEs have been proposed as safe materials against typical problems of Li-metal anodes such as dendrite growing3,4 and low energy-densities.5 In addition, SSEs have much less irreversible capacity losses than liquid electrolytes when using an NMC cathode; the capacity retention is 90.6% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles;6 and SSEs optimize packaging and stacking as well as increase energy density better than commercial liquid electrolytes such as organic and acid-based electrolytes.7 On the other hand, atomistic computational chemistry techniques such as quantum and classical molecular dynamics are tools that become complementary to experimental techniques, helping us to understand how the chemistry works, characterizing new compounds and materials, and processing large amounts of data from the simulations to integrate chemical theory and modeling with experimental observations. Recently, we introduced the concept of a nanobattery,8,9 which, complemented with earlier work, has become our testbed for the testing of proposed materials for several parts of a battery.10–16
000 cycles;6 and SSEs optimize packaging and stacking as well as increase energy density better than commercial liquid electrolytes such as organic and acid-based electrolytes.7 On the other hand, atomistic computational chemistry techniques such as quantum and classical molecular dynamics are tools that become complementary to experimental techniques, helping us to understand how the chemistry works, characterizing new compounds and materials, and processing large amounts of data from the simulations to integrate chemical theory and modeling with experimental observations. Recently, we introduced the concept of a nanobattery,8,9 which, complemented with earlier work, has become our testbed for the testing of proposed materials for several parts of a battery.10–16
In the present work, we aim to understand the atomistic behavior involving reactions, temperature profiles, drift paths, and external electric field effects simulating the charging through molecular dynamics simulations on a full nanobattery with a Li-metal anode, solid-state electrolyte Li7P2S8I, and LiCoO2 cathode, in addition to the usual current collectors of aluminum and copper for the cathode and anode, respectively. Since lithium-metal always presents an undefined native film covering its surface such as Li2O accompanied by LiOH and Li2CO3,17–25 it is good practice to pretreat the native film-free Li metal surface with suitable added films. In this case we have chosen a double layer Li3P/Li2S, which is consistent and compatible with the solid electrolyte Li7P2S8I, since both Li3P and Li2S are products of decomposition of sulfide electrolytes on the Li-metal anode surface.26 In addition, Li2S improves the ionic conductivity and suppresses the Li dendrite growth of Li-metal anodes27 and Li3P suppresses formation of dendrites and enhances the Li diffusion at the interphase SEI-anode.28 Li3P and Li2S were also reported as SEI in experiments using Li7P2S8I in a graphite battery.29 We observe a Li+ hopping diffusion mechanism similar to the one in Li7P2S8I reported by Kang et al.30 and to one in Li10GeP2S12.31 Finally, our results are also in agreement with a report that found that Li+ ionic conductivity in sulfide-based SSE depends on the distribution of PS4 tetrahedrons, which form the Li+ diffusion channel.32
Nanobattery description and methodology
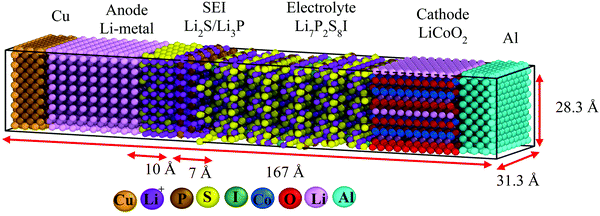
We perform classical molecular dynamics (MD)33 simulations using the large-scale atomic/molecular massively parallel simulation (LAMMPS) program.34 The initial geometry of the simulated full cell (Fig. 1) contains from right to left, Al current collector, LiCoO2 cathode, Li7P2S8I solid state electrolyte, Li3P/Li2S added SEI films, Li-metal anode, and Cu current collector. Although the dimensions of our atomistic-based nanobattery model are roughly three orders of magnitude smaller than those of commercial batteries,35 nevertheless most of the interesting chemistry is local; thus having a few shells of nearest neighbor atoms represented around them plus the use of periodic boundary conditions may strongly alleviate this issue and provide interesting insights.Visualization of trajectories and post-processing analyses are performed with the programs, visualization molecular dynamics (VMD)36 and the open visualization tool (OVITO).37 Periodic boundary conditions (PBC) were applied in the three directions; however, in the longitudinal direction, we set the current collector (Al and Cu) parameters such that they eliminate the interaction of the anode–cathode due to the PBC. Force fields parameters are shown in Table 1. We used a reactive force field for S, P, Li+ and Li-metal in the SEI and anode developed by Islam et al.38 A Morse potential is used for the pair interactions P–S and P–I in the SSE: E(r) = D0(e−2α(r−r0) − 2e−α(r−r0)); D0 = dissociation energy, r0 = equilibrium distance, and α = width parameter, 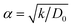 , k = force constant. P–S parameters D0, r0 and k are 1.58 eV, 2.1 Å and 12.2 eV Å−2, respectively.
, k = force constant. P–S parameters D0, r0 and k are 1.58 eV, 2.1 Å and 12.2 eV Å−2, respectively.
P–I parameters for D0, r0 and k are 1.82 eV, 2.5 Å and 9.3 eV Å−1, respectively. P–S and P–I interactions were calculated from the B3PW9139–41/cc-pVTZ(P,S)42–44/LANL2DZ(I)45–48 level of theory using the program Gaussian-16.49 First, we fully optimized PS3I and PS4, which started with tetrahedral geometries;50 then, we stretched the P–I and one P–S bonds, respectively, performing partial optimizations at every point of the potential surface. The threshold for the force was set to 2.5 × 10−7 kcal mol−1 Å−1. For the interactions at the cathode, we use a force field developed in the past for a full Li-ion nanobattery.8 The cathode is modeled with harmonic bond and angle potentials Eb = kb(r − r0)2 and Ea = ka(θ − θ0)2, respectively, where kb = 40 kcal mol−1 Å−2, ka = 139.4 kcal mol(radian)−2, r0 = 1.92 Å, and θ0 = 90°. The current collectors are modeled as inert hypothetical materials with a non-reactive Lennard-Jones potential, ε = 2.5 kcal mol−1 and σ = 2.3 Å for Cu, and ε = 1.0 kcal mol−1 and σ = 2.5 Å for Al. These current collectors also avoid the shifting of atoms due to the periodicity along the longitudinal direction. Cu and Al are set with a weak attractive component using a Lennard-Jones potential with ε = 0.01 kcal mol−1 and σ = 2.4 Å. Specific effects of the current collectors are not being studied this time. All Coulombic charges used in the simulations were the formal charges of 1, 5, −3, −2, and −1 for Li(Li7P2S8I), P(Li7P2S8I), P(Li3P), S(Li7P2S8I/Li2S), and I(Li7P2S8I), respectively. All other atom charges were set to zero.
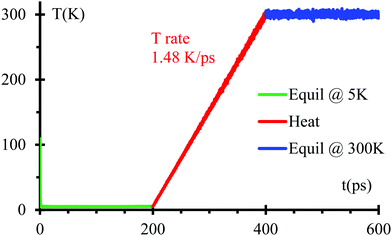
We optimize the initial geometry shown in Fig. 1 using the Polak–Ribiere algorithm51 with a force convergence criterion on each atom of 10−8 kcal mol−1 Å−1 to fix any unusual bond created initially by setting all components. Then, we run MD equilibration steps at 5 K for 200 ps with a time step 0.1 fs under the NPT ensemble52 to eliminate any remaining hot spots in the initial geometry. This is followed by a temperature increase from 5 to 300 K for 200 ps, i.e., with a heating rate of 1.48 K ps−1 under the NPT ensemble. Finally, another equilibration under NPT ensemble for 200 ps (Fig. 2). We use the Nose–Hoover thermostat53 with a damping parameter of 50 fs. This procedure should be sufficient to obtain an equilibrated system as corroborated in Fig. 2.
In order to set an external pressure and temperature to our system, the NPT ensemble with the Nose–Hover thermostat54 described by Melchionna et al.55 is used as implemented in the program LAMMPS.34 Thus, to set the system at temperature Text (e.g., 300 K) and pressure Pext, (e.g., 1 atm) the system (box) should be under a bath of temperature Text and an external pressure Pext performed by a piston with a pseudo mass W; therefore, the equations of motion 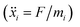 are modified to
are modified to
| νi(t) = sṙi(t) |
| s = e−νTΔt/2 |
where, mi = mass of the atom i; vi = velocity of the atom i at time t; kb = Boltzmann constant; N = total number of atoms in the system.
On the other hand, the instantaneous P(t),
Then, the volume is obtained from
Finally, the instantaneous kinetic energy is given by
Results and discussion
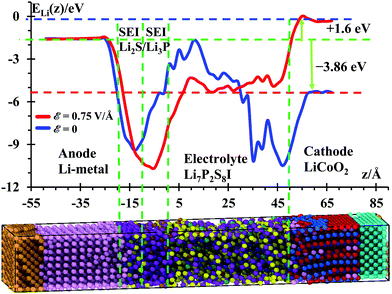
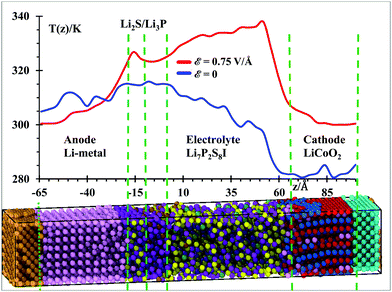
Temperature profiles of the nanobattery were calculated along the longitudinal axis from all atoms, except from those at the current collectors (Al, Cu), during the 50 ps after equilibration at 300 K and during the next first 10 ps during the application of the external electric field (Fig. 3) in longitudinal intervals of 4 Å, which was a good trade-off between resolution and fluctuations. We located a small temperature rise reaching ∼315 K in the SEI when no field was applied; this is, most likely, because the reactions take place around the solid-state electrolyte. However, when the electric field was applied, we observe a larger temperature in the electrolyte (near the cathode). This is due to oxidizing reactions taking place at the electrolyte cathode interface and to less extent to the relatively higher Li-ion-resistance of the electrolyte with respect to the cathode. Kinetic energy from Li-ions is transferred as vibrational energy to the atoms in the electrolyte. After this mismatch of impedances (from cathode to electrolyte), the temperature decreases approaching the SEI, where again a small increase in temperature is observed as it took place without an electric field, during the setting of the battery. The anode is warmer than the cathode and most of the electrolyte because of its metallic character. During the charging cycle, the anode and cathode maintain roughly the same temperature, but the temperature is higher in the electrolyte due to its higher cationic resistance. Although the ionic conductivity of the SSE is 6.3 × 10−4 S cm−1,56 against the 3.4 × 10−5 S cm−1 of the cathode,57 still the resistance can be comparable due to the larger length of the electrolyte. On the other hand, having better electronic conductivity, both electrodes are better heat dissipators, able to maintain lower temperatures. Also, the SEI is a barrier to the thermal phonons from the metallic anode. Therefore, temperature increases in the SEI and SSE due to their larger ionic resistance with respect of the anode and cathode.Under the above conditions, what we obtain is the end of a transient-state of the battery at a global stable temperature of 300 K (Fig. 2); this state is characterized by a steady-state temperature with small fluctuations and a time-independent gradient in the different regions of the battery, typical of an open system as energy is inserted or subtracted to control the temperature or to drive the charging of the battery. Thus, the gradient of temperature is simply due to the different thermal behavior of the components of the battery in response to the external temperature bath or the external power source. Thus, the temperature profile shown in Fig. 3 indicates that the anode and SEI are warmer than the electrolyte and cathode in the unbiased battery. Also shown is the temperature profile when the battery is biased to be charged. In this latter case, in addition to the thermostat, we have the external voltage source adding energy continuously to drive the Li-ions to the anode. Therefore, there is no thermal equilibrium as we are dealing with a nonequilibrium system. After a transient-state, the average temperature as a function of time reaches a constant value but it is not the same spatially. There are no changes of temperature locally as each point in space reaches a constant value, but the temperature as a function of the coordinates is different at each point, simply because of their different response to the thermal and electrical inputs. During the transient state, the local temperatures increase until reaching a constant value. The number of products also reaches a constant value during the period from 400 to 600 ps (Fig. 4) at 300 K, thus the unbiased battery reached its steady-state. Without external bias but with the heat controller, the metallic region of the battery shows higher temperatures than the ceramic oxide or ionic material of the cathode. The temperature slightly increases at the SEI interphase, which behaves like a barrier to thermal phonons from the metallic anode. The temperature reduces in going from the SEI to the cathode because the cathode is an ionic material, the most stable in the battery or the one with the lowest energy but also with a higher heat capacity than the metallic anode; on the other hand, it is easier for the anode than the cathode to dissipate thermal energy because of the higher heat conductivity of the former. When an external power source is applied to the battery (to charge the battery), the temperature increases in the cathode as Li from the cathode is oxidized and leaves the oxide. The temperature further increases in the electrolyte due to the resistance of the electrolyte, which is much longer than the length of cathode traveled by the Li-ion. The temperature decreases again in the anode due to the small resistance of the short path traveled by the Li-ions. The product formations remain constant when the steady state at 300 K is reached; and the product formations increase when the electric field is applied, which becomes a perturbation to the steady state. Before charging the battery, the cathode is less energetic with Li-ions than the anode is, thus Li+ prefers to stay in the cathode; during the battery charging, the cathode becomes more energetic with Li-ions than the anode due to the external bias, thus the Li+ prefers to migrate to the anode. And, as we will see in the next section (Fig. 5), our MD simulations suggest a battery open circuit voltage that is fully compatible with all commercial and experimental Li-ion batteries.
Although an SSE should be a good ion conductor and poor electron conductor, the cathode should also be a good ion conductor as well as electron conductor. Thus, the cathode as a good ion conductor is not different to the electrolyte except when the ion is reduced or neutralized in the cathode, the moment at which the reduced Li (or Li-neutral, or Li and its closest neighborhood) is strongly bonded until it is oxidized again with an external field during the charge of the battery. The low ionic conductivity of the electrolyte is a limiting factor, among several perhaps equally or more important factors such as structural stability and the formation of a benign solid electrolyte interphase. However, the SEI is usually of lower ionic conductivity than electrodes and electrolytes and is the place where most reactions take place when applying the external bias.
Perhaps the presence of temperature gradients before the application of the external electric field might bring some issues regarding the equipartition theorem. Since the thermostat only controls the kinetic energy of the whole system, our reported gradients are not the result of an equilibration, but they corresponded to the end of a transient state at the interfaces perhaps at odds with the equipartition theorem. However, a thermal equilibrium connected to the equipartition theorem is not applicable in some situations; therefore, a mathematical formalism was developed to adapt the equipartition theorem with quantum mechanics, see for instance, Dence.58 Although most of the issues with the equipartition theorem are because of the quantum nature of atomistic systems, classical MD calculations use powerful force fields with some theoretical and empirical information from their quantum character such as the effects of electrons and other quantum effects implicitly fitted in the force fields. Therefore, we expect to get realistic results from our simulations that go beyond the equipartition theorem, especially for solids forming interfaces and interphases, which by their solid nature avoid most of the diffusional equilibrium because most atoms from one type of solid do not travel to another different one. Although the Nose–Hover algorithm has no preference for the energy exchange, still this is an input energy and the response of the different materials to such inputs can be totally different according to the nature of each material (such as their heat capacity and conductivity). Formally speaking, the classical equipartition theorem can be used only if all vibrational modes are fully activated. However, this applies exactly only as the temperature goes to infinity.59,60 For finite temperatures, we can still come close if the thermal energy is high enough versus the energy required to excite the vibrational modes, i.e., kBT ≫ ℏω. Although for most elements, room temperature is high enough to come close to full excitation; however, there are solids such as diamond, silicon, and germanium where room temperature is not enough to validate the equipartition theorem.61–63
Speciation at the SEI
A number of fragments (n) of PS3− and P2S74− (Fig. 4) are formed at lithium-metal/SEI and SEI/SSE interfaces due to the dissociation of PS43− and PS3I2− anions in the absence of an external electric field. PS43− begins to dissociate at 300 K in small amounts n = ∼3, equivalent to only 1.6% of the total PS43−. PS3I2− dissociates into 20 species almost instantly at 5 K, forming PS3− and I−. PS43− reacts with PS3−, forming P2S74− (Fig. 4) under the presence of the external electric field, ε = 0.75 V Å−1. All these species are recreating a new SEI. The n(t) functions are just counters of the number of species being formed or destroyed. Every 100 fs, we count the number of species in the whole simulation box. The species are determined by checking all bonds against threshold bond lengths. Thus, Fig. 4 shows the evolution of the number of products when the interface is formed followed by those products when the battery is set to charge under an external power source. The speciation numbers, n(t), provide important information regarding the initial composition of a solid electrolyte interface, before the application of an external field and right after. A good design of a battery should have a prediction of what the SEI is going to be or if the SEI has the correct characteristics or not. Another direct implication of this plot is the reactive behavior of the Li-metal surface on the solid electrolyte Li7P2S8I, and the native SEI artificially added, Li2S/Li3P, all of which decompose into components PS43− and P2S34− under the presence of thetal surface. Such a reaction can be followed with the good resolution of molecular dynamics methods, providing further decomposition species.These speciation numbers explain experimental evidence and they are related to the transport of Li-ions. For example, they explain the formation of PS3− and P2S74−, which takes place before and after charging. The speciation numbers also predict that the formation of products remains constant before the electric field is applied and once it is applied, the product formations increase; there is experimental evidence for this.64 The use of Li2S in the artificial SEI for the nanobattery is supported by the formation of Li2S at long times and the stabilization of the PS3 and PS4 anions in the SSE phase and interphase, changing the electronic and ionic properties of the SEI.64 Using Li2S as the SEI improves the ionic conductivity and suppresses the Li dendrite growth of the Li metal anode.27
External electric field effect on the battery potentials
Average lithium potential energies (Fig. 5) are calculated in longitudinal slabs of 0.5 Å width along the z-axis. For the curve before applying the external electric field (blue), we calculated the potential energy profile from the potential energy of each atom, we integrated the potential energy of each atom in the longitudinal direction (longitudinal slabs of 0.5 Å each) then we obtained the average of the potential profiles during the last 50 ps of the equilibration at 300 K over 500 frames, each frame was taken every 100 fs. A similar approach was followed for the case with an electric field applied to the nanobattery, except that the geometries are obtained from the MD with ε = 0.75 V Å−1 applied and the average of the potential profiles were obtained during the first 10 ps of the application of ε = 0.75 V Å−1 at 300 K over 100 frames, each frame was taken every 100 fs. In order to simulate the charge of the battery under an external pressure and temperature, we continue using the NPT ensemble under the external electric field as relaxation of the volume during the charging is important to determine the stability of the interphase.Even though canonical ensembles might present problems in calculating dynamical properties at equilibrium and nonequilibrium conditions because of thermostat interference and other approximations, canonical ensembles can still reach equivalent results to those from microcanonical ensembles.65,66 For example, an NVE simulation is equivalent to an NPT at the equilibrated P and T from the NVE ensemble. One could also think that a NVE simulation is all that one needs to simulate any thermodynamic point;67 however, practical simulated systems are usually too small for this to happen, and even in the case where they are big enough, it can be complicated to find out which energy value E is the correct one to simulate the desired thermodynamic point.68,69 This issue becomes more important for unknown materials produced at the interfaces for which we do not know their density or their morphology and therefore their volume, thus, the NPT ensemble is justified for production runs because it allows us to obtain a suitable volume and energy rather than guessing them.66,70,71 In another study, Verners et al.72 performed MD simulations using the canonical NVT ensemble for the production runs to calculate ion diffusivity.
To calculate the voltage in the nanobattery, it requires one to calculate the chemical potentials, which include the effects of entropy, not explicitly included, and pressure, implicitly included in the calculations. The no inclusion of entropy is justified in this type of solids as entropy contribution to the chemical potentials is nominal based on a large amount of reports in the literature that do not use it for solids. None of the materials used in this work classify as high entropy alloys or such like, where a consideration of entropy would be needed. Certainly, there are several other factors, perhaps with stronger effects than entropy that we understand are not included and that could have a larger contribution. For instance, the static effects of the electrons are included only as classical effects fitted into the force fields, but the dynamical component and parts of other quantum mechanical effects are not.
The energy difference ΔE = Ecathode − Eanode = −3.86 eV without any external electric field (blue curve in Fig. 5) yields the open-circuit voltage (OCV = 3.86 V) of this nanobattery, which is consistent with most of the voltages of commercial Li-ion batteries ranging from 3 to 4.1 V. During discharge, the battery should spontaneously yield a discharging external current of electrons from the anode to the cathode as soon as a load (resistance) is connected to the two electrodes; simultaneously and internally, Li-ions travel from anode to cathode (same directions as electrons). To charge this battery (red curve in Fig. 5), we need to apply an external field to at least counteract the OCV plus an additional potential to regulate the amount of current. Based on our previous work, we estimated that an external electric field of ε = 0.75 V Å−1 would be enough to charge nanobatteries in an “acceptable” computational time. It is also important to mention that our computational setup before the application of the external field corresponds to open-circuit conditions, i.e., while the external bias or external device is not externally connected to the nanobattery electrodes. Therefore, no electrons (externally) and no ions (internally) can transfer between electrodes. Also Li-ions cannot penetrate the cathode in an open-circuit condition; they can only penetrate the cathode when the circuit is closed externally with a passive device (e.g., a resistor), i.e., during the discharge of the battery.
In these conditions, the electric field yielded a potential energy of the cathode larger by 1.6 eV than the anode potential. This yields a charging voltage of 5.46 V. The additional 1.6 V is actually too high, in practical terms, to charge a real battery because other unwanted reactions could be activated at this large charging potential, such as poor plating or dendrites growth in the anode or the cathode becoming an oxidizing agent, losing its stability releasing oxygen and producing CO2.73 Certainly, at this point of high pressure, the cell eventually might vent with flame. Thus, in the simulations, a high charging voltage is used with the sole purpose of accelerating the calculations and inducing a faster cationic transport from cathode to anode. There is a potential drop at the cathode/SSE and SSE/SEI interfaces, and an uphill energetic profile is detected to move the ion through the SEI. Therefore, a technological value is found for Li7P2S8I as SSE as it can be expected to yield a dendrite-free anode, as well as a profound computational importance as we are able to predict the working voltage of the battery from the atomistic nature of its components.
Li+ drifts through the two films of SEI, Li3P and Li2S, by a hopping mechanism, where Li+ drifts by into a vacancy, similar to the Li+ diffusion in Li7P2S8I30 and Li10GeP2S1231 solid state electrolytes. In this process, Li+ hops one inter-atomic distance and remains until a vacancy appears adjacent to the Li+ location, then Li+ hops into the vacancy; the vacancy moves away and the process repeats, also partially resembling a knock-off mechanism, especially in the films, as vacancies are also created by the action of the electric field, yielding atomic reorganizations (Fig. 6). Li+ drifts nearby S in the SSE and Li2S, compensating coulombic forces, and correspondingly, nearby P in Li3P, forming ionic bonds at ∼2.4 Å.
Conclusions
We have developed a very useful model of a nano-version of a solid-state battery with a lithium-metal anode. This specific model included a double layer film acting as an artificial solid electrolyte interface, allowing us to study the behavior of interfaces on the anode-electrolyte side. We determine the thermal, speciation, and electrical features of the nanobattery before and after the application of an external field, simulating the charging cycle of a battery. The results were very encouraging as we were able to determine the open-circuit voltage of the nanobattery of 3.86 V, which is in very good agreement with commercial Li-ion based batteries. We also were able to determine the corresponding charging voltage generated by the applied external electrical field. As far as we understand, this type of calculation has not been done before using atomistic approaches. It was determined that the external field of ε = 0.75 V Å−1 yielded an external applied voltage of 5.46 V. It was also determined that before the external field was applied, a small temperature rise was located at the SEI (∼315 K) due to the reactions taking place there; besides, PS3− and P2S74− species are formed at the lithium-metal/SEI and SEI/SSE interfaces from the PS3− and PS3I2− anions under the presence of the external electric field. Li+ drift through the two films of the SEI, Li3P and Li2S by a hopping mechanism; the Li+ transport paths through the SSE and Li3P film is through the vacancies and making ionic bonds of ∼2.4 Å with P or S and supported by vacancies driven by the action of the electric field towards the surface of the films.Basically, what this work tells us is about the possible use of protective films as layers of artificial SEI to cover and protect Li-metal anodes. This allows us to eliminate dendrites and also to have a more stable anode surface as well as acceptable Li-ion diffusion. Another important application is the maps of temperatures as we are able to determine the hot spots, perhaps dangerous, in the battery. Another is the speciation taking place at the interfaces. These are of strong importance for the experimentalists and battery builders. Definitely, our findings provide information to experimentalists to use new materials with calculated improved properties and the best way to exploit these results is to establish collaborations with experimental groups involved in the use of SSE using Li-metal anodes. A theoretical-guided approach to the design of new materials for batteries would be the best way to exploit these techniques.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Assistant Secretary for Energy Efficiency and Renewable Energy, Vehicle Technologies Office of the U.S. Department of Energy under Contract No. DE-EE0007766 under the Advanced Battery Materials Research (BMR) Program and Battery 500 Consortium Award Number DE-EE0008210. Supercomputer resources from Texas A&M University High Performance Computer Center and Texas Advanced Computing Center (TACC) are gratefully acknowledged.References
-
J. Thomas, Solid State Electrochemistry, Cambridge University Press, Cambridge, 8th edn, 1996, p. 344 Search PubMed
.
- M. Arbabzadeh, R. Sioshansi, J. X. Johnson and G. A. Keoleian, The Role of Energy Storage in Deep Decarbonization of Electricity Production, Nat. Commun., 2019, 10, 3413 CrossRef PubMed
.
- H. Liu, X.-B. Cheng, J.-Q. Huang, H. Yuan, Y. Lu, C. Yan, G.-L. Zhu, R. Xu, C.-Z. Zhao, L.-P. Hou, C. He, S. Kaskel and Q. Zhang, Controlling Dendrite Growth in Solid-State Electrolytes, ACS Energy Lett., 2020, 5, 833–843 CrossRef CAS
.
- F. Belviso, V. E. P. Claerbout, A. Comas-Vives, N. S. Dalal, F.-R. Fan, A. Filippetti, V. Fiorentini, L. Foppa, C. Franchini, B. Geisler, L. M. Ghiringhelli, A. Groß, S. Hu, J. Íñiguez, S. K. Kauwe, J. L. Musfeldt, P. Nicolini, R. Pentcheva, T. Polcar, W. Ren, F. Ricci, F. Ricci, H. S. Sen, J. M. Skelton, T. D. Sparks, A. Stroppa, A. Urru, M. Vandichel, P. Vavassori, H. Wu, K. Yang, H. J. Zhao, D. Puggioni, R. Cortese and A. Cammarata, Viewpoint: Atomic-Scale Design Protocols toward Energy, Electronic, Catalysis, and Sensing Applications, Inorg. Chem., 2019, 58, 14939–14980 CrossRef CAS
.
- Y. Jin, K. Liu, J. Lang, X. Jiang, Z. Zheng, Q. Su, Z. Huang, Y. Long, C.-A. Wang, H. Wu and Y. Cui, High-Energy-Density Solid-Electrolyte-Based Liquid Li–S and Li–Se Batteries, Joule, 2020, 4, 262–274 CrossRef CAS
.
- J. Li, C. Ma, M. Chi, C. Liang and N. J. Dudney, Solid Electrolyte: The Key for High-Voltage Lithium Batteries, Adv. Energy Mater., 2015, 5, 1401408 CrossRef
.
- Y.-S. Hu, Batteries: Getting Solid, Nat. Energy, 2016, 1, 16042 CrossRef CAS
.
- V. Ponce, D. E. Galvez-Aranda and J. M. Seminario, Analysis of a Li-Ion Nanobattery with Graphite Anode Using Molecular Dynamics Simulations, J. Phys. Chem. C, 2017, 121, 12959–12971 CrossRef CAS
.
- D. E. Galvez-Aranda, V. Ponce and J. M. Seminario, Molecular Dynamics Simulations of the First Charge of a Li–Ion–Si-Anode Nanobattery, J. Mol. Model., 2017, 23, 120 CrossRef PubMed
.
- N. Kumar and J. M. Seminario, Lithium-Ion Model Behavior in an Ethylene Carbonate Electrolyte Using Molecular Dynamics, J. Phys. Chem. C, 2016, 120, 16322–16332 CrossRef CAS
.
- L. Benitez and J. M. Seminario, Electron Transport and Electrolyte Reduction in the Solid-Electrolyte Interphase of Rechargeable Lithium Ion Batteries with Silicon Anodes, J. Phys. Chem. C, 2016, 120, 17978–17988 CrossRef CAS
.
- L. A. Selis and J. M. Seminario, Dendrite Formation in Silicon Anodes of Lithium-Ion Batteries, RSC Adv., 2018, 8, 5255–5267 RSC
.
- L. A. Selis and J. M. Seminario, Dendrite Formation in Li-Metal Anodes: An Atomistic Molecular Dynamics Study, RSC Adv., 2019, 9, 27835–27848 RSC
.
- S. Jha, V. Ponce and J. M. Seminario, Investigating the Effects of Vacancies on Self-Diffusion in Silicon Clusters Using Classical Molecular Dynamics, J. Mol. Model., 2018, 24, 290 CrossRef PubMed
.
- D. E. Galvez-Aranda and J. M. Seminario, Simulations of a LiF Solid Electrolyte Interphase Cracking on Silicon Anodes Using Molecular Dynamics, J. Electrochem. Soc., 2018, 165, A717–A730 CrossRef CAS
.
- D. E. Galvez-Aranda and J. M. Seminario, Ab Initio Study of the Interface of the Solid-State Electrolyte Li9N2Cl3 with a Li–Metal Electrode, J.
Electrochem. Soc., 2019, 166, A2048–A2057 CrossRef CAS
.
- I. Ismail, A. Noda, A. Nishimoto and M. Watanabe, XPS Study of Lithium Surface after Contact with Lithium-Salt Doped Polymer Electrolytes, Electrochim. Acta, 2001, 46, 1595–1603 CrossRef CAS
.
- K. Kanamura, Chemical Reaction of Lithium Surface During Immersion in LiClO4 or LiPF6/DEC Electrolyte, J. Electrochem. Soc., 1997, 144, 1900 CrossRef CAS
.
- K. Kanamura, X-Ray Photoelectron Spectroscopic Analysis and Scanning Electron Microscopic Observation of the Lithium Surface Immersed in Nonaqueous Solvents, J. Electrochem. Soc., 1994, 141, 2379 CrossRef CAS
.
- K. Kanamura, H. Tamura and Z.-I. Takehara, XPS Analysis of a Lithium Surface Immersed in Propylene Carbonate Solution Containing Various Salts, J. Electroanal. Chem., 1992, 333, 127–142 CrossRef CAS
.
- K. Kanamura, H. Tamura, S. Shiraishi and Z.-I. Takehara, XPS Analysis for the Lithium Surface Immersed in Γ-Butyrolactone Containing Various Salts, Electrochim. Acta, 1995, 40, 913–921 CrossRef CAS
.
- K. Kanamura, XPS Analysis of Lithium Surfaces Following Immersion in Various Solvents Containing LiBF4, J. Electrochem. Soc., 1995, 142, 340 CrossRef CAS
.
- S.-T. Hong, J.-S. Kim, S.-J. Lim and W. Y. Yoon, Surface Characterization of Emulsified Lithium Powder Electrode, Electrochim. Acta, 2004, 50, 535–539 CrossRef CAS
.
- S. Shiraishi, K. Kanamura and Z. Takehara, Effect of Surface Modification Using Various Acids on Electrodeposition of Lithium, J. Appl. Electrochem., 1995, 25, 584–591 CrossRef CAS
.
- E. P. Kamphaus, S. Angarita-Gomez, X. Qin, M. Shao, M. Engelhard, K. T. Mueller, V. Murugesan and P. B. Balbuena, Role of Inorganic Surface Layer on Solid Electrolyte Interphase Evolution at Li-Metal Anodes, ACS Appl. Mater. Interfaces, 2019, 11, 31467–31476 CrossRef CAS PubMed
.
- L. E. Camacho-Forero and P. B. Balbuena, Exploring Interfacial Stability of Solid-State Electrolytes at the Lithium-Metal Anode Surface, J. Power Sources, 2018, 396, 782–790 CrossRef CAS
.
- F. Liu, L. Wang, Z. Zhang, P. Shi, Y. Feng, Y. Yao, S. Ye, H. Wang, X. Wu and Y. Yu, A Mixed Lithium-Ion Conductive Li2S/Li2Se Protection Layer for Stable Lithium Metal Anode, Adv. Funct. Mater., 2020, 30, 2001607 CrossRef CAS
.
- L. Lin, F. Liang, K. Zhang, H. Mao, J. Yang and Y. Qian, Lithium Phosphide/Lithium Chloride Coating on Lithium for Advanced Lithium Metal Anode, J. Mater. Chem. A, 2018, 6, 15859–15867 RSC
.
- T. Yamamoto, N. H. H. Phuc, H. Muto and A. Matsuda, Preparation of Li7P2S8I Solid Electrolyte and Its Application in All-Solid-State Lithium-Ion Batteries with Graphite Anode, Electron. Mater. Lett., 2019, 15, 409–414 CrossRef CAS
.
- J. Kang and B. Han, First-Principles Characterization of the Unknown Crystal Structure and Ionic Conductivity of Li7P2S8I as a Solid Electrolyte for High-Voltage Li Ion Batteries, J. Phys. Chem. Lett., 2016, 7, 2671–2675 CrossRef CAS PubMed
.
- Y. Mo, S. P. Ong and G. Ceder, First Principles Study of the Li10GeP2S12 Lithium Super Ionic Conductor Material, Chem. Mater., 2012, 24, 15–17 CrossRef CAS
.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, High-Power All-Solid-State Batteries Using Sulfide Superionic Conductors, Nat. Energy, 2016, 1, 16030 CrossRef CAS
.
- W. F. Van Gunsteren, H. J. C. Berendsen and A. Leap-Frog, Algorithm for Stochastic Dynamics, Mol. Simul., 1988, 1, 173–185 CrossRef
.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- R. Spotnetz, Lithium-Ion Batteries. The Basics, American Institute of Chemical Enginneering CEP, 2013, 39–43 Search PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
.
- S. Alexander, Visualization and Analysis of Atomistic Simulation Data with OVITO – the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef
.
- M. M. Islam and A. C. T. van Duin, Reductive Decomposition Reactions of Ethylene Carbonate by Explicit Electron Transfer from Lithium: An Ereaxff Molecular Dynamics Study, J. Phys. Chem. C, 2016, 120, 27128–27134 CrossRef CAS
.
- A. D. Becke, Density Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- J. P. Perdew, K. Burke and Y. Wang, Generalized Gradient Approximation for the Exchange-Correlation Hole of a Many-Electron System, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS PubMed
.
- J. P. Perdew, J. Chevary, S. Vosko, K. A. Jackson, M. R. Pederson, D. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed
.
- T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS
.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS
.
- K. A. Peterson, D. E. Woon and T. H. Dunning, Benchmark Calculations with Correlated Molecular Wave Functions. IV. The Classical Barrier Height of the H + H2 → H2 + H Reaction, J. Chem. Phys., 1994, 100, 7410–7415 CrossRef CAS
.
-
T. H. Dunning and P. J. Hay, Modern Theoretical Chemistry, Plenum Press, New York, 3rd edn, 1977 Search PubMed
.
- P. J. Hay and W. R. Wadt, Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS
.
- W. R. Wadt and P. J. Hay, Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for Main Group Elements Na to Bi, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS
.
- P. J. Hay and W. R. Wadt, Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for K to Au Including the Outermost Core Orbitals, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- M. Sumita, Y. Tanaka and T. Ohno, Possible Polymerization of PS4 at a Li3PS4/FePO4 Interface with Reduction of the FePO4 Phase, J. Phys. Chem. C, 2017, 121, 9698–9704 CrossRef CAS
.
- K. M. Khoda, Y. Liu and C. Storey, Generalized Polak-Ribière Algorithm, J. Optim. Theory Appl., 1992, 75, 345–354 CrossRef
.
- V. V. Nauchitel, Energy-Distribution Function for the NVT Canonical Ensemble, Mol. Phys., 1981, 42, 1259–1265 CrossRef CAS
.
- G. Kalibaeva, M. Ferrario and G. Ciccotti, Constant Pressure-Constant Temperature Molecular Dynamics: A Correct Constrained NPT Ensemble Using the Molecular Virial, Mol. Phys., 2003, 101, 765–778 CrossRef CAS
.
- S. Nosé, A Molecular Dynamics Method for Simulations in the Canonical Ensemble, Mol. Phys., 1984, 52, 255–268 CrossRef
.
- S. Melchionna, G. Ciccotti and B. Lee Holian, Hoover NPT Dynamics for Systems Varying in Shape and Size, Mol. Phys., 1993, 78, 533–544 CrossRef CAS
.
- E. Rangasamy, Z. Liu, M. Gobet, K. Pilar, G. Sahu, W. Zhou, H. Wu, S. Greenbaum and C. Liang, An Iodide-Based Li7P2S8I Superionic Conductor, J. Am. Chem. Soc., 2015, 137, 1384–1387 CrossRef CAS PubMed
.
- J. Xie, N. Imanishi, T. Matsumura, A. Hirano, Y. Takeda and O. Yamamoto, Orientation Dependence of Li–Ion Diffusion Kinetics in LiCoO2 Thin Films Prepared by RF Magnetron Sputtering, Solid State Ionics, 2008, 179, 362–370 CrossRef CAS
.
- J. B. Dence, Heat Capacity and the Equipartition Theorem, J. Chem. Educ., 1972, 49, 798 CrossRef CAS
.
- V. Khodel, J. Clark, V. R. Shaginyan and M. Zverev, Second Wind of the Dulong-Petit Law at a Quantum Critical Point, JETP Lett., 2010, 92, 532–536 CrossRef CAS
.
-
C. Pickover, Archimedes to Hawking: Laws of Science and the Great Minds Behind Them, Oxford University Press, 2008 Search PubMed
.
- D. G. Hicks, T. R. Boehly, J. H. Eggert, J. E. Miller, P. M. Celliers and G. W. Collins, Dissociation of Liquid Silica at High Pressures and Temperatures, Phys. Rev. Lett., 2006, 97, 025502 CrossRef CAS PubMed
.
- A. Naumovets, Y. Poluektov and V. Khodusov, Nonlinear Effects in the Phonon System of Diamond Crystal, East Eur. J. Phys., 2003, 2, 124–135 Search PubMed
.
- S. S. Rekhviashvili and K. L. Kunizhev, Investigation of the Influence of Lattice Anharmonicity on the Heat Capacities of Diamond, Silicon, and Germanium, High Temp., 2017, 55, 312–314 CrossRef CAS
.
- T. Rödl, R. Weihrich, J. Wack, J. Senker and A. Pfitzner, Rational Syntheses and Structural Characterization of Sulfur-Rich Phosphorus Polysulfides: α-P2S7 and β-P2S7, Angew. Chem., Int. Ed., 2011, 50, 10996–11000 CrossRef PubMed
.
- S. Toxvaerd, Dynamics of Homogeneous Nucleation, J. Chem. Phys., 2015, 143, 154705 CrossRef PubMed
.
- M. Chalaris and J. Samios, Systematic Molecular Dynamics Studies of Liquid N,N-Dimethylformamide Using Optimized Rigid Force Fields: Investigation of the Thermodynamic, Structural, Transport and Dynamic Properties, J. Chem. Phys., 2000, 112, 8581–8594 CrossRef CAS
.
- K. D. Hammonds and D. M. Heyes, Shadow Hamiltonian in Classical NVE Molecular Dynamics Simulations: A Path to Long Time Stability, J. Chem. Phys., 2020, 152, 024114 CrossRef CAS PubMed
.
- R. S. Ellis, H. Touchette and B. Turkington, Thermodynamic Versus Statistical Nonequivalence of Ensembles for the Mean-Field Blume–Emery–Griffiths Model, Physica A, 2004, 335, 518–538 CrossRef
.
- H. Touchette, R. S. Ellis and B. Turkington, An Introduction to the Thermodynamic and Macrostate Levels of Nonequivalent Ensembles, Physica A, 2004, 340, 138–146 CrossRef
.
- Y. Xu and H. Jiang, Self-Assembly of Supported Lipid Multi-Bilayers Investigated by Time-Resolved X-Ray Diffraction, Biochim. Biophys. Acta, Biomembr., 2020, 1862, 183437 CrossRef CAS PubMed
.
- R. Ombrato, L. Console, B. Righino, C. Indiveri, A. Arduini and M. C. De Rosa, Structure-Based Virtual Screening to Identify Novel Carnitine Acetyltransferase Activators, J. Mol. Graphics Modell., 2020, 100, 107692 CrossRef CAS PubMed
.
- O. Verners, A. C. T. V. Duin, M. Wagemaker and A. Simone, Molecular Dynamics Modeling of Structural Battery Components, in 20th International Conference on Composite Materials, Copenhagen, 19–24th July, 2015.
- T. Ohsaki, T. Kishi, T. Kuboki, N. Takami, N. Shimura, Y. Sato, M. Sekino and A. Satoh, Overcharge Reaction of Lithium-Ion Batteries, J. Power Sources, 2005, 146, 97–100 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp02851g |
| This journal is © the Owner Societies 2021 |

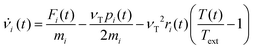
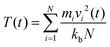
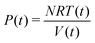
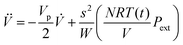
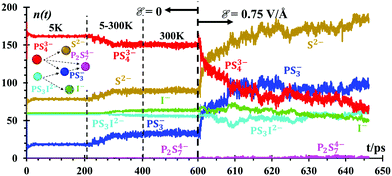
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = 0.75 V Å−1 is applied at 600 ps. The inset shows the most likely reaction/degradation network about the SSE during the simulations. Speciation analyses were limited to the SEI and SSE,
= 0.75 V Å−1 is applied at 600 ps. The inset shows the most likely reaction/degradation network about the SSE during the simulations. Speciation analyses were limited to the SEI and SSE,