Cyclic peptides: backbone rigidification and capability of mimicking motifs at protein–protein interfaces†
He
Huang‡
 ,
Jovan
Damjanovic‡
,
Jovan
Damjanovic‡
 ,
Jiayuan
Miao
,
Jiayuan
Miao
 and
Yu-Shan
Lin
and
Yu-Shan
Lin
 *
*
Department of Chemistry, Tufts University, Medford, Massachusetts 02155, USA. E-mail: yu-shan.lin@tufts.edu
First published on 17th December 2020
Abstract
Cyclization is commonly employed in efforts to improve the target binding affinity of peptide-based probes and therapeutics. Many structural motifs have been identified at protein–protein interfaces and provide promising targets for inhibitor design using cyclic peptides. Cyclized peptides are generally assumed to be rigidified relative to their linear counterparts. This rigidification potentially pre-organizes the molecules to interact properly with their targets. However, the actual impact of cyclization on, for example, peptide configurational entropy, is currently poorly understood in terms of both its magnitude and molecular-level origins. Moreover, even with thousands of desired structural motifs at hand, it is currently not possible to a priori identify the ones that are most promising to mimic using cyclic peptides nor to select the ideal linker length. Instead, labor-intensive chemical synthesis and experimental characterization of various cyclic peptide designs are required, in hopes of finding one with improved target affinity. Herein, using molecular dynamics simulations of polyglycines, we elucidated how head-to-tail cyclization impacts peptide backbone dihedral entropy and developed a simple strategy to rapidly screen for structures that can be reliably mimicked by preorganized cyclic peptides. As expected, cyclization generally led to a reduction in backbone dihedral entropy; notably, however, this effect was minimal when the length of polyglycines was >9 residues. We also found that the reduction in backbone dihedral entropy upon cyclization of small polyglycine peptides does not result from more restricted distributions of the dihedrals; rather, it was the correlations between specific dihedrals that caused the decrease in configurational entropy in the cyclic peptides. Using our comprehensive cyclo-Gn structural ensembles, we obtained a holistic picture of what conformations are accessible to cyclic peptides. Using “hot loops” recently identified at protein–protein interfaces as an example, we provide clear guidelines for choosing the “easiest” hot loops for cyclic peptides to mimic and for identifying appropriate cyclic peptide lengths. In conclusion, our results provide an understanding of the thermodynamics and structures of this interesting class of molecules. This information should prove particularly useful for designing cyclic peptide inhibitors of protein–protein interactions.
Introduction
Peptides have many unique properties that make them promising candidates for the development of chemical probes and therapeutics.1–3 For example, they can be used to inhibit protein–protein interactions, which are involved in many biological processes and diseases.5–7 However, peptides come with many liabilities, including structural flexibility that often leads to relatively poor affinity, selectivity, and bioavailability. In an effort to address these deficiencies, peptide cyclization is now a common strategy to rigidify these molecules and thereby improve their binding affinity, selectivity, and bioavailability.3,8–10 Notably, more than seven thousand “hot loops” were recently identified at interfaces of protein–protein interactions.11,12 These hot loops have been proposed to be viable starting points for using cyclic peptides to inhibit protein–protein interactions.Although the potential applications of peptide cyclization are well-demonstrated, it remains very difficult to predict conformational outcomes of cyclization and the magnitude of the associated decrease in peptide configurational entropy. NMR measurements show that head-to-tail cyclization indeed leads to rigidification of the peptide backbones, resulting in, for example, smaller amide temperature coefficients and an increase in the order parameter.13 However, thermodynamic measurements of binding show that addition of a conformational restraint does not always confer favorable changes in binding entropy.14,15 It is possible, for instance, that the favorable change in peptide entropy is compensated by an unfavorable change in solvation entropy; however, it is challenging to separate these two contributions using thermodynamic measurements. Therefore, the change of peptide entropy upon cyclization remains poorly understood, both in terms of its magnitude, the molecular-level sources of the change, and its dependence on peptide size. Moreover, cyclization is not always beneficial and it can have deleterious effects on binding affinities.10,15–18 Because it remains difficult to rationally design linkers that can properly rigidify the peptides of interest into desired conformations, synthesis of many variants is required, in hopes of finding one with appropriate conformational properties. In sum, the impact of cyclization on peptide properties is neither well-understood nor straightforward. Guidelines on appropriate linker choices and what conformations can be reliably mimicked by cyclic peptides would be highly beneficial.
Molecular dynamics (MD) simulations are a powerful tool to study molecules with atomic-level detail. They have been used to characterize the thermodynamic properties and structural ensembles of linear and cyclic peptides. For instance, using MD simulations of linear polyglycines as model systems, Drake et al. found that the dihedral configurational entropy of such peptides increases linearly with their chain lengths.4 MD simulations have also been applied to estimating the conformational entropy for a series of cyclic RGD peptides with a variety of modifications.19 MD simulations can further characterize the conformational ensembles of cyclic peptides, enabling understanding of their activities and designing well-structured cyclic peptides.20–23
However, while previous simulations have provided useful information and insights, they generally focused on either linear peptides or cyclic peptides. In this report, we perform a systematic comparative study of both linear and cyclic peptides to compare and contrast the differences in their configurational entropy (Fig. 1A). Furthermore, as mentioned previously, thousands of hot loops at protein–protein interfaces have been identified as ideal starting points for cyclic peptide inhibitor design. Closely mimicking the structure of a protein–protein interface has been used to great effect in macrocycle inhibitor design, and presents a strong starting point for structure-based inhibitor development.12,24,25 Nonetheless, it remains difficult to a priori know even whether a given hot loop can indeed be mimicked by a cyclic peptide in the first place, let alone what the appropriate cyclic peptide size should be. Here, we use the structural ensembles of cyclic polyglycines to provide a quick way to determine which sizes of cyclic peptides (if any) may be the most promising at mimicking the hot loop of interest. The premise is that cyclic polyglycines are the most flexible cyclic peptides and the most likely to sample various conformations adoptable by cyclic peptides. By comparing a hot loop conformation to a cyclo-Gn structural ensemble, we can then determine whether the specific hot loop conformation is mimicable by cyclic peptides of size n (Fig. 1B). Our results provide clear guidelines on the “easiest” hot loops for cyclic peptides to mimic and suggest candidate cyclic peptide sizes to test.
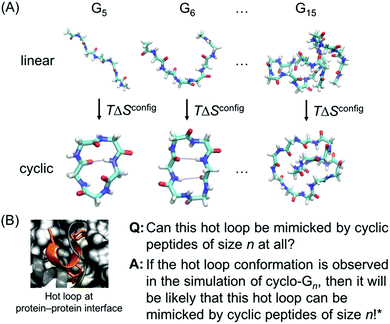 | ||
| Fig. 1 (A) Linear and cyclic polyglycines with length ranging from 5 to 15 residues are used to study the size-dependent effects of cyclization on the thermodynamic and structural properties of peptides. (B) If a desired hot loop conformation is observed in a cyclo-Gn structural ensemble, it is assumed that a cyclic peptide of size n should be viable for mimicking the specific hot loop. The next step can be simulating cyclic peptides of size n with the specific hot loop sequence incorporated. The hot loop shown is 52DLIYY56 from chain A in PDB ID = 2JB0; the sidechains of the hotspot residues (D52, Y55, and Y56) are highlighted. *However, this does not conclude that if the desired structure is not observed in a cyclo-Gn structural ensemble, it will not be mimicked by a cyclic peptide of size n. | ||
Methods
A. Linear and cyclic peptides of G5 to G15
Linear and head-to-tail cyclized polyglycine peptides with length varying from 5 to 15 residues, denoted as linear- and cyclo-Gn, with 5 ≤ n ≤ 15, were built and simulated (Fig. 1A). The linear peptides were capped with an acetyl group on the N-terminus and with an N-methyl amide group on the C-terminus. The capping prevented creation of charged termini, which could have led to strong Coulombic interaction. It also ensured that linear and cyclic peptides of the same length had the same number of backbone ϕ/ψ dihedrals. For each peptide system, two sets of simulations and analyses, starting from two different initial structures, were performed in parallel to verify the convergence of the simulation results. Details on how the initial structures were generated can be found in the ESI.†B. Molecular dynamics simulations
To characterize their thermodynamic and structural properties, all the cyclic and linear peptides were simulated using molecular dynamics (MD) simulations. All the simulations were performed using the GROMACS 4.6.7 suite26 with the RSFF2 force field and TIP3P water model.27,28 The RSFF2 force field was parameterized using a coil library and was previously shown to be able to fold well-behaved peptides29 and recapitulate the crystal structures of cyclic peptides reasonably well.30 Two sets of simulations starting from two different initial structures were performed for each peptide system (herein called S1 and S2, simulations 1 and 2). Each initial structure was solvated, equilibrated, and a 1.0 μs production run was then performed at 300 K and 1 bar with trajectories output every 1.0 ps for subsequent analysis. Details on the simulation setup can be found in the ESI.†C. Bias-exchange metadynamics simulations
Besides using the two independent simulations S1 and S2 starting from different initial structures to verify the convergence of the simulation results, bias-exchange metadynamics (BE-META) simulations were carried out for selected systems of linear-Gn (n = 5, 10, 15) and cyclo-Gn (n = 5–10, 15) to further validate the convergence of the thermodynamic analysis results. BE-META simulations were performed for 250 ns using the PLUMED 2 plugin for the GROMACS 4.6.7 suite.31 Each replica was biased along (ϕi, ψi) or (ψi, ϕi+1), which were previously shown to represent the essential transitional motions of cyclic peptides and greatly enhance their conformational sampling.32 Additionally, five neutral replicas with no bias were added to generate unbiased trajectories for structural analysis. Exchanges between replicas were attempted every 5 ps; Gaussian hills with a height of 0.1 kJ mol−1 and a width of 0.314 rad in each dimension were added every 4 ps. The simulation trajectories were saved every 1 ps for subsequent analysis.D. Estimation of backbone configurational entropy
For a system with N degrees of freedom, its configurational entropy Sconfig is: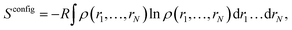 | (1) |
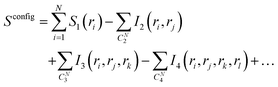 | (2) |
In eqn (2), S1(ri) is the marginal entropy of degree of freedom ri; I2(ri,rj) is the pairwise joint mutual information measuring the correlation between two degrees of freedom ri and rj, which is calculated as the difference between the simple summation of S1(ri) and S1(rj) and the actual joint entropy, S2(ri,rj):
| I2(ri,rj) = S1(ri) + S1(rj) − S2(ri,rj). | (3) |
Similarly, I3 is calculated as
| I3(ri,rj,rk) = S1(ri) + S1(rj) + S1(rk) − S2(ri,rj) − S2(rj,rk) − S2(ri,rk) + S3(ri,rj,rk), | (4) |
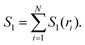 | (5) |
The second order MIE approximation (SMIE2) incorporates the pairwise mutual information terms:
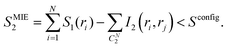 | (6) |
In this paper, we focused on the backbone ϕ and ψ angles and computed both the S1 and SMIE2, using the latter to provide a lower bound of the backbone configurational entropy. It was assumed that only the backbone ϕ and ψ dihedral angles contribute to the difference of configurational entropy between linear and cyclic peptides, and contributions from the other degrees of freedom, including the bonds, angles, and nearly rigid ω angles could be neglected in the entropy estimations.4
To obtain an upper bound of the configurational entropy, the maximum information spanning tree (MIST) algorithm was used:34
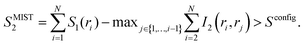 | (7) |
Instead of subtracting all the possible I2 terms as in eqn (6), in eqn (7) only the N − 1 pairwise terms that facilitate the maximal mutual information sum are considered. Therefore, in contrast to SMIE2, which provides a lower bound, SMIST2 provides an upper bound of the configurational entropy.34
For each simulation, ϕ(C′–N–Cα–C) and ψ(N–Cα–C–N′′) backbone dihedrals were calculated and used as input for an in-house Python adaptation of the PARENT program to calculate S1, SMIE2, and SMIST2.35 120 bins were used for each dimension to construct the probability density functions. Our modified PyPARENT code follows previous standards, which apply a bias correction for systematic errors in entropy calculations due to finite sampling.35–37 The calculated entropies showed very little dependence on the number of bins used (Fig. S1, ESI†).
E. Structural comparison to hot loops
Approximately seven thousand “hot loops” have been identified at various protein–protein interactions.11,12 These hot loops are loop-like structures predicted to have high binding affinity to their partner proteins by Rosetta-based alanine scanning.38,39 From among all loops at protein–protein interfaces, three criteria were used to identify the “hot loops”: the average ΔΔGres of the loop ≥0.6 Rosetta Energy Units, the number of hot spots in the loop ≥3, and the loop representing ≥50% of the total predicted interface energy. Out of the 7225 hot loops identified, 210 satisfied all three criteria and were considered the best starting points for peptide therapeutic design of protein–protein interaction inhibitors.12 Here we estimated the likelihood that cyclic peptides of different sizes could be used to mimic each of these 210 hot loops. Three of the 210 hot loops seemed to have additional residues that were not included in the original hot loop library and thus were not used in the analysis here. Furthermore, fourteen hot loops had cis peptide bonds and were also excluded from the analysis. For the 193 all-trans hot loops, the dihedral angles ψ1, ϕ2, ψ2,…,ϕm were computed (where m was the size of the hot loop). These dihedrals were compared to the cyclo-Gn conformations sampled in the MD simulations with cyclic degeneracy taken into consideration.Results and discussion
Changes in configurational entropy upon cyclization
Peptide entropy generally decreases when a peptide binds to a target, constituting a thermodynamic cost that can dramatically reduce binding affinity. It is generally presumed that covalent cyclization of the peptide helps sidestep this cost by rigidifying the peptide's structure even in the unbound state, remedying the loss of peptide entropy upon binding and improving the peptide's binding affinity. To determine how much decrease in configurational entropy can be obtained by peptide cyclization, as well as to understand the length dependence and molecular origins of such a decrease, we performed simulations of both linear and cyclic polyglycines, estimated their configurational entropy, and investigated the sources of the entropy difference between linear and cyclic peptides.As it is difficult to obtain probability density functions (PDFs) in ≥3 dimensions with sufficient statistics to calculate the configurational entropy (eqn (1) and (2)), we used SMIE2 (eqn (6); all N × (N − 1)/2 pairwise mutual information terms included) to provide a lower bound of the configurational entropy and SMIST2 (eqn (7); only N − 1 pairwise mutual information terms included) to provide an upper bound of the configurational entropy for each peptide. Consequently, we obtain a range of TΔSconfig between cyclo-Gn and linear-Gn: the lower bound of TΔSconfig was [TSMIE2 of cyclo-Gn − TSMIST2 of linear-Gn], while the upper bound of TΔSconfig was [TSMIST2 of cyclo-Gn − TSMIE2 of linear-Gn] (Fig. 2A, the range between the bounds of TΔSconfig was shaded in gray).
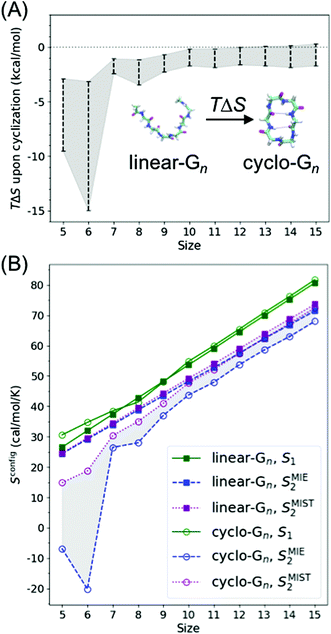 | ||
| Fig. 2 (A) Change in backbone dihedral configurational entropy upon cyclization of polyglycines as a function of peptide size at 300 K. (B) Backbone dihedral configurational entropy for linear-Gn (square line symbols) and cyclo-Gn (circle line symbols) calculated using the first-order approximation (S1, green solid lines), the second-order MIE approximation (SMIE2, blue dashed line), and the second-order MIST approximation (SMIST2, purple dotted line). SMIE2 and SMIST2 serve as the lower and upper bounds for Sconfig, respectively; areas between SMIE2 and SMIST2 are thus shaded to indicate where the true Sconfig would lie. Error bars are calculated from two simulations starting from two different initial structures and are plotted here; however, the error bars are smaller than the symbol sizes and thus not visible. Comparison of the results from the MD simulations (shown here) to the results from the BE-META simulations can be found in Fig. S2 (ESI†), showing that the two sets of simulations provided similar results. Note that Sconfig for linear-Gn scaled linearly with chain length. Fitting the three curves (S1, SMIE2, and SMIST2) using a linear regression model yielded an R2 coefficient ≥0.99 in all three cases. The slopes for TS1, TSMIE2, and TSMIST2 were 1.625, 1.413, and 1.471 kcal mol−1 per residue (at 300 K), respectively (Table S1, ESI†). These values were comparable with the 1.16–1.67 kcal mol−1 per residue previously reported in the work of Drake et al.4 | ||
Similar to the previous study of linear peptides,4 our calculation and analysis of configurational entropy focused on the backbone ϕ and ψ dihedrals. Because linear-Gn and cyclo-Gn have different numbers of atoms, thus different numbers of degrees of freedom, it is not straightforward to compare their configurational entropy with all degrees of freedom included (they do have the same number of ϕ and ψ dihedrals though). To circumvent this issue and test the effects of including other degrees of freedom, we used the PARENT software35 to calculate the configurational entropy using all internal degrees of freedom; however, the atoms in the N- and C-terminal caps of linear-Gn were excluded in the entropy calculation to obtain the same number of atoms as in cyclo-Gn. Fig. S3 (ESI†) shows that the resulting TΔS plot was qualitatively similar to that when only backbone dihedrals were included in the entropy calculation (Fig. 2A). By comparing different types of S1 and MI terms in the PARENT output, we also found that the dihedral S1 and the pair MI terms involving dihedrals contribute most significantly to the TΔS between linear- and cyclo-Gn. For simplicity and straightforward comparison, the following analysis and discussion of configurational entropy focused on and referred to configurational entropy of backbone dihedrals.
Fig. 2A shows cyclization indeed led to a loss in configurational entropy, although this effect was far more pronounced with shorter chain lengths. Particularly noteworthy, cyclization of peptides longer than 9 residues had minimal effects on configurational entropy. Below, we analyze the configurational entropy results in more detail to understand the origin of the differences between linear and cyclic peptides.
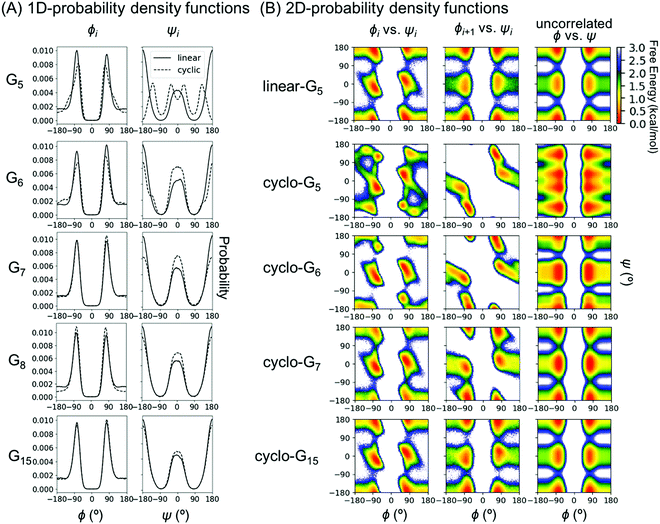
To understand this phenomenon, we compared the 1D probability density functions (PDFs) along ϕ and ψ dihedrals for linear and cyclic G5, G6, G7, G8, and G15 (Fig. 3A). The 1D-PDFs were very similar for all the linear peptides of various sizes, and for the larger cyclic peptides such as cyclo-G15. For example, their ψ PDFs all displayed a major peak at ±180° and a minor peak at 0°. However, the 1D-PDFs for cyclo-G5, cyclo-G6, and cyclo-G7 deviated significantly from those of the linear peptides, in particular their ψ PDFs (Fig. 3A). The ±180° and 0° peaks were more equally populated in cyclo-G6 and cyclo-G7, and cyclo-G5 showed four peaks in its ψ PDFs, resulting in a larger S1. This observation suggests that, owing to restraints imposed by the formation of a head-to-tail cyclized backbone, not all residues in, for example, a cyclic pentapeptide are able to adopt the dihedral angles preferred under a relaxed environment; rather, their ψ angles need to follow specific patterns to satisfy the ring closure condition.
As S1 only considers 1D-PDFs, it overestimates the configurational entropy because it does not take into account the correlations between different dihedrals. The inclusion of mutual information terms in the entropy calculations, as in the computation of SMIE2 and SMIST2, should theoretically result in a reduction in the configurational entropy estimation. We observed that both SMIE2 and SMIST2 were indeed smaller than S1 for all the systems (Fig. 2B; blue and purple lines vs. green). However, the decrease from S1 to SMIE2 and SMIST2 was much more prominent in cyclic peptides, especially for small cyclic peptides. These results confirm that the reduction in configurational entropy upon cyclization (Fig. 2A) stems from higher mutual information in the cyclized peptides.
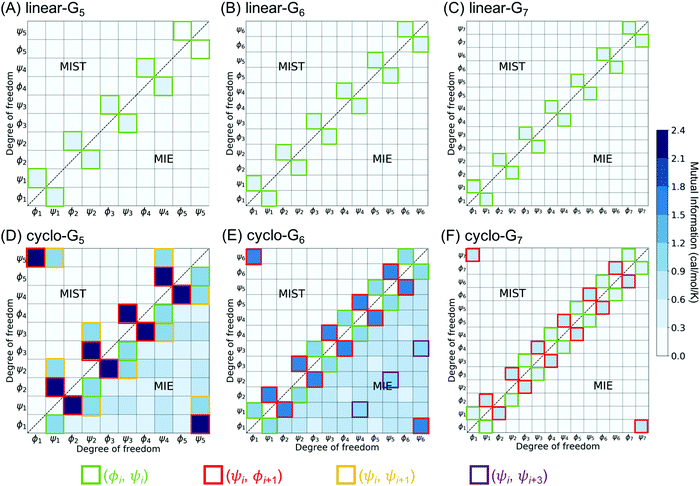
To investigate which pairwise mutual information terms contributed most significantly to the reduction in SMIE2 and SMIST2 when the peptides were cyclized, Fig. 4 reports each pairwise mutual information term for linear- and cyclo-G5–7 (see Fig. S4, ESI,† for mutual information for linear- and cyclo-G8–15). In the linear-Gn peptides, the largest pairwise mutual information occurred between ϕ and ψ within the same residues (highlighted in green boxes in Fig. 4A–C). In other words, the correlations between intra-residual ϕi and ψi were the most significant in linear peptides. The top row of Fig. 3B shows the Ramachandran plot, i.e., 2D-PDF of (ϕi, ψi), 2D-PDF of (ϕi+1, ψi), and a simple product of 1D-PDF of ϕ and 1D-PDF of ψ for linear-G5. We observed that, while the 2D-PDF of (ϕi+1, ψi) resembled the uncorrelated (ϕ, ψ) plot, the 2D-PDF of (ϕi, ψi) showed considerable deviation, implying more significant mutual information between ϕi and ψi in linear-G5. All these (ϕi, ψi) mutual information terms were used in the MIST calculations, which was consistent with the observation that SMIE2 and SMIST2 were very close in value for linear-Gn (Fig. 2B, blue and purple lines with solid square symbols).
In fact, the pairwise mutual information terms in cyclo-G5, cyclo-G6, and cyclo-G7 each displayed unique patterns. Cyclo-G5 had large mutual information between (ψi, ϕi+1), and also between (ϕi, ψi) and (ψi, ψi+1) (highlighted in red, green, and orange boxes, respectively, in Fig. 4D). Cyclo-G6 displayed the most significant mutual information between (ψi, ϕi+1), (ϕi, ψi) and (ψi, ψi+3) (highlighted in red, green, and purple boxes, respectively, in Fig. 4E). The largest mutual information terms in cyclo-G7 were between (ψi, ϕi+1) and (ϕi, ψi) (highlighted in red and green boxes, respectively, in Fig. 4F). As the size of the cyclic peptides increased, the mutual information patterns in cyclo-Gn gradually approached those in their linear counterparts, particularly for n ≥ 10, where the mutual information contributions of (ψi, ϕi+1) were reduced to being insignificant (<0.2 cal mol−1 K−1, equivalent to 0.06 kcal mol−1 at 300 K) (Fig. S4, ESI†).
We noticed in Fig. 2B that SMIE2 was much lower for cyclo-G6 than for cyclo-G5. This phenomenon is likely caused by cyclo-G6 typically adopting rather stable conformations of two β turns opposing each other with two intramolecular hydrogen bonds formed in the middle (Fig. 1A). Although the mutual information between (ψi, ϕi+1) (highlighted in red boxes) and between (ψi, ψi+1) (highlighted in yellow boxes) was larger in cyclo-G5 (2.38 and 0.97 cal mol−1 K−1) than in cyclo-G6 (1.71 and 0.76 cal mol−1 K−1), all the other mutual information terms were larger in cyclo-G6 than in cyclo-G5. In particular, the (ψi, ψi+3) terms (highlighted in purple boxes) were prominent in cyclo-G6 (1.05 cal mol−1 K−1), resulting from the β turn + β turn conformations the cyclic peptide preferred.
To test how the results on the effect of cyclization of polyglycine can be extrapolated to other polypeptides, we performed BE-META simulations of linear and cyclic An and calculated TΔSconfig between linear and cyclic polyalanines. The results (Fig. S5, ESI†) were qualitatively similar to those of linear and cyclic Gn (Fig. 2A), showing a significant decrease in entropy for small peptides, especially sizes 5 and 6. We note that linear polyalanines displayed some helical propensity.27 For mimicking hot loops at protein–protein interfaces, the peptide sequences of interest likely do not form (extended) helices but rather random coils, making (the cyclization of) Gn a better model for cyclization of hot loop sequences.
Overall, our results suggest that the reduction in Sconfig upon cyclization can be as large as 2–3 kcal mol−1 in small peptides (of lengths 5 and 6 with the most conservative estimation, Fig. 2A and Fig. S5, ESI†), although the actual number will depend on the specific sequence of interest. Such a reduction can, in principle, improve KD by a factor of 50. However, this observation does not mean that cyclization with the shortest possible linker should always be preferred, nor that cyclization of large peptides would have no impact on binding affinity. For example, rigidifying a short peptide into a conformation that is not compatible with the desired structure would be fruitless, even though the cyclization indeed reduces the peptide entropy (see the next section for results and discussion on the capability of cyclic peptides of various sizes to mimic different hot loops). For peptides of larger sizes, although a linear peptide and a cyclic peptide may have similar peptide configurational entropy, they are still likely to adopt different structures. For binding affinity, attention should also be paid to how much of the whole peptide structural ensemble is capable of mimicking the target conformation of the segment of interest. Furthermore, even if cyclization properly pre-organizes the segment of interest and leads to a favorable change in Sconfig of the unbound peptide, the impact on binding affinity may be compensated by an unfavorable change in TΔSsolvation, in ΔH, or even in Sconfig of the complex.
Ability of cyclic peptides to mimic hot loops
Further, we compared the cyclo-Gn conformational ensembles to NMR structures of cyclic peptides reported by Hosseinzadeh et al.40 Four out of nine cyclic peptides had matching conformations, and eight out of nine were found to have conformations with dihedral deviations of no more than 40°. The motifs less likely to be sampled in cyclo-Gn simulations again turned out to be structures in longer (n > 8) cyclic peptides and driven by the presence of proline residues. While the Ramachandran region typical of proline is a subset of that of glycine, the resulting conformational constraints are likely to favor otherwise rarely sampled conformations. Detailed results are shown in Table S3 (ESI†).
Based on these results, it is clear that, while there are structures that can be mimicked by (typically proline-containing) cyclic peptides but not sampled by cyclo-Gn, cyclic polyglycines do indeed present a robust way to check whether a conformation is accessible to a head-to-tail cyclized peptide. In other words, a negative result at this stage does not entirely rule out a cyclic peptide design target, as a structure inaccessible to a polyglycine backbone could still be accomplished via additional conformational restraints, e.g. using proline residues or residues capable of forming stabilizing side chain–backbone hydrogen bonds. However, we have shown above that cyclo-Gn are capable of sampling conformations assumed by a highly-varied set of sequences – therefore, there is nonetheless plenty of utility in identifying the more “obvious” candidates using this approach. A positive result here suggests that optimizing a cyclic peptide sequence of a given length to mimic the desired target is a worthwhile task.
 | ||
| Fig. 5 MD simulations of cyclo-Gn were used to gauge the conformational space accessible to cyclic peptides of different sizes and evaluate whether the cyclic peptide conformational space overlaps with the structures of hot loops observed at protein–protein interfaces. The three hot loops shown on the left of this figure are 52DLIYY56 from chain A in PDB ID = 2JB0 (top), 556PSSPYSA562 from chain B in PDB ID = 1BXK (middle), and 93YNHNGWEC100 from chain C in PDB ID = 1JU5 (bottom); the sidechains of the hotspot residues are highlighted. | ||
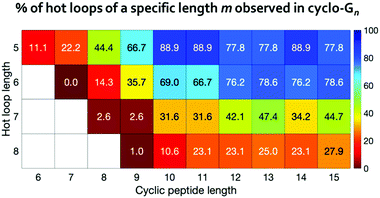
For 120 out of the 193 all-trans hot loops, we found at least one mimicking conformation in the cyclo-G5 to cyclo-G15 simulations. These 193 hot loops span from five- to eight-residues-long and there are 9, 42, 38, and 104 hot loops of lengths five, six, seven, and eight, respectively. We further separated these hot loops based on their lengths, and calculated the percentage of each length category whose conformations were observed in the simulations of cyclo-Gn of equal or greater length (Fig. 6). For instance, for 8 of the 9 five-residue-long hot loops, we found in the simulations of cyclo-G10 at least one conformation with a deviation <25° to every hot loop dihedral, resulting in the percentage of 88.9%, as shown in Fig. 6. These results suggest that even among hot loops of the same length, there are differences as to the cyclic peptide size needed to mimic a given loop. Table S4 (ESI†) provides detailed information on the 193 hot loops and the minimal cyclic peptide size where a conformation similar to each hot loop was observed.
To provide more detailed information on each hot loop, we also calculated how many conformations out of the two million frames in each cyclo-Gn structural ensemble were indeed similar to each of the hot loops. The fractions (in ppm) for the 9 five-residue-long hot loops are reported in Fig. 7. Conformations of some hot loops (for example, LDLGV, RDLIG, and DLIYY) were readily sampled by cyclo-Gn, suggesting that they are more compatible with the cyclic peptide structural ensembles; on the other hand, conformations of some hot loops (such as PHRLL and GQWNK) were barely or never observed in our cyclo-Gn data sets. Results similar to Fig. 7, but for all of the 193 hot loops, can be found in Fig. S6 (ESI†), which can be particularly helpful for choosing hot loops that are likely the easiest to mimic using cyclic peptides.
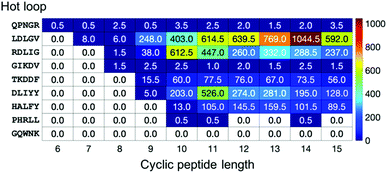 | ||
| Fig. 7 Fraction (in ppm) of each cyclo-Gn simulation whose conformations had a deviation <25° to every dihedral of the 9 five-residue-long hot loops. | ||
Overall, our analysis suggests that cyclic peptides could be used to effectively mimic some but not all of the hot loops previously identified at protein–protein interfaces. The conformations of certain hot loops appear to be less compatible with the conformations adopted by cyclic peptides. In those cases, using cyclization to rigidify the hot loops would likely be counterproductive, as it may actually prevent the peptide from adopting the conformation of interest. The phenomenon that the resulting cyclic peptide conformations may be incompatible with the desired structure could explain at least in part why cyclization can have deleterious effects on binding affinity.10,15–18
For hot loops that are mimicable by cyclic peptides, our results provide helpful information for prioritizing which cyclic peptide sizes to test. For example, using cyclic decapeptides may be promising for mimicking the RDLIG hot loop shown in Fig. 7. However, a balance also needs to be struck with how much entropy reduction one can obtain from cyclization, which favors smaller cyclic peptide sizes, as discussed in the previous section. For instance, although cyclo-G14 has the highest fraction of conformations that are similar to the LDLGV hot loop (Fig. 7), one should still consider even cyclic nonapeptides, as the fraction value for cyclo-G9 is still notable and the corresponding macrocycle is much smaller in size. Furthermore, because the purpose of the analysis here is to provide a general guideline for cyclic peptide designs by using cyclo-Gn to map out the maximum accessible conformational space, none of these results are tailored or optimized for any specific hot loop sequence. Additional simulations of, for example, cyclo-(LDLGVG4), cyclo-(LDLGVG5),…, and cyclo-(LDLGVG9) will be helpful in further narrowing down the candidate cyclic peptide sizes to use for mimicking the LDLGV hot loop. In this example, because the desired conformation for the LDLGV region is the same, a higher fraction in an all-glycine system could suggest a better ability of cyclic peptides with that size at mimicking the hot loop conformation and a better starting position for sequence optimization. It is plausible that, owing to the different constraints induced by different sizes of cyclization, the different potential interactions they introduce, and the different difficulty at optimizing the linker sequences to stabilize the target cyclic peptide structures, the optimal linker length may ultimately change. In that case, this screening method should be thought of as identifying the hot loop targets most compatible with conformations accessible to head-to-tail cyclic peptide and the most likely optimal linker lengths, all of which can be simulated to obtain a more complete picture.
Additionally, the information obtained by this approach can be used for other structure-based design strategies. For instance, structures sampled by cyclo-Gn can be utilized as a starting point for docking simulations with side chains mutated to the sequence of interest, to determine whether those conformations, along with corresponding side chain orientations, would lead to favorable binding to the target surface.
Lastly, NMR studies show that most cyclic peptides adopt multiple conformations in solution, existing as structural ensembles.41–51 Currently, robust experimental methods for structurally characterizing each conformation in an ensemble do not exist.52 Such information, however, can be obtained from MD simulations, making them indispensable in demystifying the impact of cyclization on peptide structure and binding affinity.
Conclusions
Using MD simulations of model polyglycine peptides we examined the differences in configurational entropy between linear and cyclic peptides. We found that the decrease in configurational entropy observed in cyclic polyglycines resulted from stronger correlation between dihedral angles. For small cyclic polyglycines, the pairwise dihedral correlation displayed specific patterns. Our results also show that cyclization can be a promising strategy to reduce peptide configurational entropy, especially for peptides shorter than 10 residues. However, attention must be paid to whether the conformations of the resulting cyclic peptides are compatible with the desired structure. Using cyclo-Gn structural ensembles, we identified hot loops whose conformations should be mimicable by cyclic peptides. This analysis provides quick guidelines on potential cyclic peptide sizes for mimicking various hot loops. The approach of using cyclo-Gn as a surrogate of the accessible conformational space can be applied to gauge whether cyclic peptides of any given size n are capable of mimicking target structures besides the hot loops tested here. More focused simulations of cyclic peptides incorporating the specific (hot loop) sequences of interest could then be further performed to help determine whether a particular cyclic peptide length or design should be pursued.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the support of the Knez Family Faculty Investment Fund and the National Institute of General Medical Sciences of the National Institutes of Health under award number R01GM124160 (PI: Y.-S. L.) We thank support from the Tufts Technology Services and computer resources from Tufts Research Cluster. Initial structures of the simulations were built using UCSF Chimera, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, with support from NIH P41-GM103311. We thank Prof. Joshua Kritzer and Stephanie Kearing for their helpful discussions and comments on the manuscript.References
- M. R. Naylor, A. T. Bockus, M. J. Blanco and R. S. Lokey, Curr. Opin. Chem. Biol., 2017, 38, 141 CrossRef CAS PubMed
.
- D. S. Nielsen, N. E. Shepherd, W. Xu, A. J. Lucke, M. J. Stoermer and D. P. Fairlie, Chem. Rev., 2017, 117, 8094 CrossRef CAS PubMed
.
- X. Jing and K. Jin, Med. Res. Rev., 2020, 40, 753 CrossRef CAS PubMed
.
- J. A. Drake and B. M. Pettitt, Biophys. J., 2018, 114, 2799 CrossRef CAS PubMed
.
- S. Rubin and N. Qvit, Crit. Rev. Eukaryotic Gene Expression, 2016, 26, 199 CrossRef PubMed
.
- A. Zorzi, K. Deyle and C. Heinis, Curr. Opin. Chem. Biol., 2017, 38, 24 CrossRef CAS PubMed
.
- Z. Qian, P. G. Dougherty and D. Pei, Curr. Opin. Chem. Biol., 2017, 38, 80 CrossRef CAS PubMed
.
-
O. Demmer, A. O. Frank and H. Kessler, in Peptide and Protein Design for Biopharmaceutical Applications, ed. K. J. Jensen, John Wiley & Sons, Ltd, Chichester, UK, 2009, pp. 133–176 Search PubMed
.
- C. J. White and A. K. Yudin, Nat. Chem., 2011, 3, 509 CrossRef CAS PubMed
.
-
B. Claro, M. Bastos and R. Garcia-Fandino, Pept. Appl. Biomed., Biotechnol. Bioeng., 2018, p. 87 Search PubMed
.
- J. Gavenonis, B. A. Sheneman, T. R. Siegert, M. R. Eshelman and J. A. Kritzer, Nat. Chem. Biol., 2014, 10, 716 CrossRef CAS PubMed
.
- T. R. Siegert, M. J. Bird, K. M. Makwana and J. A. Kritzer, J. Am. Chem. Soc., 2016, 138, 12876 CrossRef CAS PubMed
.
- C. K. Wang, J. E. Swedberg, S. E. Northfield and D. J. Craik, J. Phys. Chem. B, 2015, 119, 15821 CrossRef CAS PubMed
.
- D. G. Udugamasooriya and M. R. Spaller, Biopolymers, 2008, 89, 653 CrossRef CAS PubMed
.
- J. E. Delorbe, J. H. Clements, B. B. Whiddon and S. F. Martin, ACS Med. Chem. Lett., 2010, 1, 448 CrossRef CAS PubMed
.
- K. Burgess, D. Lim and S. A. Mousa, J. Med. Chem., 1996, 39, 4520 CrossRef CAS PubMed
.
- W. R. Baumbach, M. H. P. Tikva, A. Carrick, B. Bingham, D. Carmignac, I. C. A. F. Robinson, R. Houghten, C. M. Eppler, L. A. Price and J. R. Zysk, Mol. Pharmacol., 1998, 54, 864 CrossRef CAS PubMed
.
- A. Roxin and G. Zheng, Future Med. Chem., 2012, 4, 1601 CrossRef CAS PubMed
.
- A. E. Wakefield, W. M. Wuest and V. A. Voelz, J. Chem. Inf. Model., 2015, 55, 806 CrossRef CAS PubMed
.
- D. P. Slough, S. M. McHugh, A. E. Cummings, P. Dai, B. L. Pentelute, J. A. Kritzer and Y. S. Lin, J. Phys. Chem. B, 2018, 122, 3908 CrossRef CAS PubMed
.
- C. Paissoni, M. Ghitti, L. Belvisi, A. Spitaleri and G. Musco, Chem. – Eur. J., 2015, 21, 14165 CrossRef CAS PubMed
.
- A. S. Kamenik, U. Lessel, J. E. Fuchs, T. Fox and K. R. Liedl, J. Chem. Inf. Model., 2018, 58, 982 CrossRef CAS PubMed
.
- A. E. Cummings, J. Miao, D. P. Slough, S. M. McHugh, J. A. Kritzer and Y. S. Lin, Biophys. J., 2019, 116, 433 CrossRef CAS PubMed
.
- B. Laudet, C. Barette, V. Dulery, O. Renaudet, P. Dumy, A. Metz, R. Prudent, A. Deshiere, O. Dideberg, O. Filhol and C. Cochet, Biochem. J., 2007, 408, 363 CrossRef CAS PubMed
.
- N. London, B. Raveh, D. Movshovitz-Attias and O. Schueler-Furman, Proteins, 2010, 78, 3140 CrossRef CAS PubMed
.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435 CrossRef CAS PubMed
.
- C. Y. Zhou, F. Jiang and Y. D. Wu, J. Phys. Chem. B, 2015, 119, 1035 CrossRef CAS PubMed
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS
.
- C.-Y. Zhou, F. Jiang and Y.-D. Wu, J. Chem. Theory Comput., 2015, 11, 5473 CrossRef CAS PubMed
.
- H. Geng, F. Jiang and Y. D. Wu, J. Phys. Chem. Lett., 2016, 7, 1805 CrossRef CAS PubMed
.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604 CrossRef CAS
.
- S. M. McHugh, J. R. Rogers, H. Yu and Y.-S. Lin, J. Chem. Theory Comput., 2016, 12, 2480 CrossRef CAS PubMed
.
- B. J. Killian, J. Y. Kravitz and M. K. Gilson, J. Chem. Phys., 2007, 127, 024107 CrossRef PubMed
.
- B. M. King and B. Tidor, Bioinformatics, 2009, 25, 1165 CrossRef CAS PubMed
.
- M. Fleck, A. A. Polyansky and B. Zagrovic, J. Chem. Theory Comput., 2016, 12, 2055 CrossRef CAS PubMed
.
- J. Numata and E.-W. Knapp, J. Chem. Theory Comput., 2012, 8, 1235 CrossRef CAS PubMed
.
- H. Herzel, O. Schmitt and W. Ebeling, Chaos, Solitons Fractals, 1994, 4, 97 CrossRef
.
- T. Kortemme and D. Baker, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 14116 CrossRef CAS PubMed
.
- T. Kortemme, D. E. Kim and D. Baker, Sci. STKE, 2004, 219, pl2 Search PubMed
.
- P. Hosseinzadeh, G. Bhardwaj, V. K. Mulligan, M. D. Shortridge, T. W. Craven, F. Pardo-Avila, S. A. Rettie, D. E. Kim, D.-A. Silva, Y. M. Ibrahim, I. K. Webb, J. R. Cort, J. N. Adkins, G. Varani and D. Baker, Science, 2017, 358, 1461 CrossRef CAS PubMed
.
- K. D. Kopple, A. Go, R. J. Logan, Jr. and J. Savrda, J. Am. Chem. Soc., 1972, 94, 973 CrossRef CAS PubMed
.
- A. E. Tonelli and A. I. Brewster, J. Am. Chem. Soc., 1972, 94, 2851 CrossRef CAS PubMed
.
- K. D. Kopple, A. Go and T. J. Schamper, J. Am. Chem. Soc., 1978, 100, 4289 CrossRef CAS
.
- E. R. Blout, Biopolymers, 1981, 20, 1901 CrossRef CAS
.
- C.-H. Yang, J. N. Brown and K. D. Kopple, J. Am. Chem. Soc., 1981, 103, 1715 CrossRef CAS
.
- K. I. Varughese, G. Kartha and K. D. Kopple, J. Am. Chem. Soc., 1981, 103, 3310 CrossRef CAS
.
- K. D. Kopple, Y.-S. Wang, A. G. Cheng and K. K. Bhandary, J. Am. Chem. Soc., 1988, 110, 4168 CrossRef CAS
.
- S. J. Stradley, J. Rizo, M. D. Bruch, A. N. Stroup and L. M. Gierasch, Biopolymers, 1990, 29, 263 CrossRef CAS PubMed
.
- K. D. Kopple, J. W. Bean, K. K. Bhandary, J. Briand, C. A. D'Ambrosio and C. E. Peishoff, Biopolymers, 1993, 33, 1093 CrossRef CAS PubMed
.
- D. G. Alberg and S. L. Schreiber, Science, 1993, 262, 248 CrossRef CAS PubMed
.
-
G. R. Marshall, D. D. Beusen and G. V. Nikiforovich, in Peptides: Synthesis, Structures, and Applications, ed. B. Gutte, 1995, p. 193 Search PubMed
.
- D. H. Brookes and T. Head-Gordon, J. Am. Chem. Soc., 2016, 138, 4530 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on system setup and MD simulations; dependence of the calculated backbone dihedral entropy on the number of bins used (Fig. S1); tabulated results of backbone dihedral entropy calculation for linear- and cyclo-G5–15 (Table S1); comparison of backbone dihedral entropy estimation from MD and BE-META simulations (Fig. S2); change in configurational entropy upon cyclization of polyglycines calculated by the PARENT software (Fig. S3); results of mutual information calculation for linear- and cyclo-G8–15 (Fig. S4); change in backbone dihedral entropy upon cyclization of polyalanines (Fig. S5); comparison of the cyclo-Gn structural ensembles and the structures of a number of experimentally characterized cyclic peptides (Tables S2 and S3); hot loop sequences and the minimal size of cyclic peptides needed to mimic each hot loop (Table S4); fraction of the cyclo-Gn structural ensembles mimicking each hot loop (Table S5). See DOI: 10.1039/d0cp04633g |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2021 |