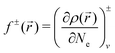Relation between structural patterns and magnetism in small iron oxide clusters: reentrance of the magnetic moment at high oxidation ratios†‡
R. H.
Aguilera-del-Toro
 a,
F.
Aguilera-Granja
a,
F.
Aguilera-Granja
 b,
M. B.
Torres
b,
M. B.
Torres
 *c and
A.
Vega
*c and
A.
Vega
 a
a
aDepartamento de Física Teórica, Atómica y Óptica, Universidad de Valladolid, E-47011 Valladolid, Spain
bInstituto de Física, Universidad Autónoma de San Luis Potosí, Mexico
cDepartamento de Matemáticas y Computación, Universidad de Burgos, Spain. E-mail: begonia@ubu.es
First published on 19th November 2020
Abstract
Due to quantum confinement effects, the understanding of iron oxide nanoparticles is a challenge that opens the possibility of designing nanomaterials with new capacities. In this work, we report a theoretical density functional theory study of the structural, electronic, and magnetic properties of neutral and charged iron oxide clusters FenOm0/± (n = 1–6), with m values until oxygen saturation is achieved. We determine the putative ground state configuration and low-energy structural and spin isomers. Based on the total energy differences between the obtained global minimum structure of the parent clusters and their possible fragments, we explore the fragmentation channels for cationic oxides, comparing with experiments. Our results provide fundamental insight on how the structural pattern develops upon oxidation and its connection with the magnetic couplings and net total moment. Upon addition of oxygen, electronic charge transfer from iron to oxygen is found which weakens the iron–iron bond and consequently the direct exchange coupling in Fe. The binding energy increases as the oxygen ratio increases, rising faster at low oxidation rates. When molecular oxygen adsorption starts to take place, the binding energy increases more slowly. The oxygen environment is a crucial factor related to the stabilities and to the magnetic character of iron oxides. We identified certain iron oxide clusters of special relevance in the context of magnetism due to their high stability, expected abundance and parallel magnetic couplings that cause large total magnetic moments even at high oxidation ratios.
1 Introduction
Iron oxides are very common and abundant in natural conditions. They are also formed as corrosion products and can be easily synthesized. The unavoidable oxidation in certain environmental conditions facilitates their production. Besides, they are relatively easy to prepare with low cost. Designing nanoparticles that retain a net magnetic moment in realistic conditions is challenging. In addition, iron oxide nanoparticles are of great interest from both the fundamental and technological points of view.1 Since the properties of a material can be drastically modified at the nanoscale due to quantum confinement effects, with non-monotonous dependencies on the cluster size, composition, and number of electrons, understanding the physics and chemistry of iron oxide nanoparticles is nowadays a great challenge, but at the same time opens the possibility of finding and designing systems with new capabilities. The intrinsic magnetic properties and biocompatibility of iron oxide clusters make them one of the most suitable candidates for nanomedicine. Those smaller than 30 nm are superparamagnetic at room temperature and can be used for drug delivery,2,3 for cancer therapy through magnetic hyperthermia,4 as contrast agents for Magnetic Resonance Imaging (MRI),5 and in the emerging technique of Magnetic Particle Imaging (MPI).6 Recent work7 suggests that prostate tumours with high nerve densities are more likely to grow and spread than those with low nerve densities. Such high-risk cases can be identified using a combination of MRI, magnetic particle imaging (MPI) and functionalized iron-oxide nanoparticles. In experiments with mice, researchers also used the same nanoparticles to deliver a drug that blocks nerve function, with successful results. You et al.7 developed a contrast agent that targets nervous tissue specifically. The team started with iron oxide nanoparticles, which have already found use in both MRI and MPI, and joined them to the nerve-binding peptide NP41. It is, therefore, not surprising that iron oxide clusters or nanoparticles have been the subject of numerous experimental and theoretical studies during the last few years, a representative number of which are summarized in the following part of the introduction (we apologize if our search was not complete).Iron oxides FeOm− and Fe2Om− (m = 1–4 and m = 1–5, respectively) have been studied by anion photoelectron spectroscopy8 at 3.49 and 4.66 eV photon energies. The vibrationally resolved photoelectron spectra and low-lying excited states were obtained. The photoelectron spectra were better resolved for those clusters with a big ratio of oxygen atoms. The results indicated that the electron affinity of the neutral ones increases with the number of oxygen atoms, suggesting a sequential oxidation behavior. Photoelectron spectra of small anionic iron clusters FenOm− (n = 1–4, m = 1–6) have been obtained by Wang et al.9 They concluded that the oxidation can be viewed as sequential oxygen atom adsorption at the surfaces of the Fe3 and Fe4 clusters, leading to a nearly linear increase of the electron affinity with the number of oxygen atoms.
A guided ion beam was used for the study of the reaction of cationic Fen+ clusters (n = 2–18) with CO210 and O211 in order to determine the bond energies of those iron clusters with oxide and dioxide; with the former, the bond energies are between 3.0 and 6.5 eV, whilst for the second one the bond energies are between 3.6 and 5.15 eV. Cationic iron oxide clusters, FenOm+, were also produced12 by chemical ionization of Fe(CO)5/O2 mixtures. They exhibit remarkable fragmentation trends that can be attributed to the formal oxidation states of iron. For clusters with n/m ≥ 1, the loss of atomic oxygen and FeO units is preferred. For FenOm+ with 1 > n/m > 2/3, in addition to the loss of O and FeO, loss of neutral FeO2 was also observed. Finally, for rich oxygen clusters (n/m = 2/3), loss of molecular oxygen predominates. Photodissociation of cationic FenOm+ (n = 1–15) clusters was studied by Molek et al.13 Clusters were produced by laser vaporization in a pulsed nozzle (355 nm) cluster source and detected with Time-Of-Flight (TOF) mass spectrometry. The results indicated that dissociation occurs mainly in two ways; the first one is the loss of molecular oxygen, and the second is a fission process. For n ≤ 5, the oxygen elimination process takes place until m = n. Then, no more oxygen loss was observed; instead a fission process takes place losing smaller clusters. Iron oxide clusters FenOm+ (n = 1–3, m = 1–6) have been synthesized in a laser vaporization source and dissociated via CID by Li14et al. Examining the dissociation behavior in a wide range of energies, these authors showed that the clusters can be dissociated by evaporation of the Fe and O atoms, as well as the fission of the neutral O2, FeO, FeO2, Fe2O2 and Fe2O3 fragments. In general, they found that the predominant dissociation pathways correlate with the oxidation state of iron in the cluster.
Regarding theoretical studies, and small molecules, the Fe2 dimer was investigated with more accurate wave function methods. However, there is no consensus as regards the ground state magnetic configuration. Tomonari et al.15 and Noro et al.16 used a multireference (MR) configuration interaction (CI) method with certain dynamical correlations. Hubner et al.17 used IC-MRCI starting from a CASSCD wave function. C. W. Bauschlicher et al.18 used also CI-MRCI and they pointed out that the septet state should be the true ground state in order to fit the experiment. Moreover, Bauschlicher et al.19 used the complete-active space SCF/internally contracted averaged coupled pair functional approach (CASSCF/ICACPF) to study the diatomic molecule FeO, among other small molecules, obtaining a quintet state and an interatomic distance of 1.61 Å, in good experimental agreement. In previous work, Bauschlicher et al.20 performed, for small molecules, an exhaustive study of dipole moments and other properties, also with high level theoretical approaches. The CAS11 FeO interatomic distance was slightly larger than that calculated at the MRCI11 level. The dipole moments were calculated, as well as the electron affinities of Fe, with DFT and CCSD(T), those calculated with CCSD(T) being more accurate.
Shiroishi et al.21,22 performed Density Functional Theory (DFT) calculations of FenOm (n = 1–3) and FenOm− with (n = 3, 4) using first principles molecular dynamics within the Generalized Gradient Approximation (GGA) for the exchange correlation (xc) energy with the PW91 functional. For all studied clusters, bridge positions were preferred. The magnetic couplings change from parallel to antiparallel in m = n, except for Fe4Om−, in which the change takes place at m = 3. Vertical detachment energies were calculated and compared with experimental results.9 The structural and magnetic properties of (Fe2O3)n (n = 1–5) clusters were investigated by Erlebach et al.23 All DFT calculations were performed using the TURBOMOLE program package along with the B3LYP xc-functional. The Multipole Accelerated Resolution of the Identity (MARI-J) method for the Coulomb term employing a triple-zeta valence plus polarization (TZVP) basis set for all atoms was used. The results found good agreement with experimental collision cross sections. A theoretical study of (FeO)n0/± clusters (n = 1–8) was performed by Ju et al.24 using the GAUSSIAN 09 package in the GGA approximation with the PW91 functional and 6-311+G* basis set. The results showed that (FeO)4− and (FeO)4+ clusters have the largest HOMO–LUMO gap values, an indication of their high stability.
Reilly et al.25,26 carried out a combined experimental and theoretical study of the structures and reactivity of FenOm+ and FenOm− (n = 1–2 and m = 3–5, 6), respectively, with CO. Clusters were produced by laser vaporization and were characterized by employing a guided ion beam mass spectrometer. Moreover, energy-resolved Collision-Induced Dissociation (CID) experiments were conducted in order to study the fragmentation patterns of those clusters. Theoretical calculations were performed within the DFT-GGA via PBE functional, as implemented in the code deMon2k, using the DZVP basis set for C and O, the Wachters-F basis set for Fe, the GEN-A2 auxiliary function set for C and O, and the GEN-A2* function set for Fe. Dissociation energies and vertical detachment energies were calculated, with which our results will be compared. Another combined experimental and theoretical study was carried out recently for cationic FenOm+ (n = 2–6) clusters by Koyama et al.27 They performed a theoretical (n = 4, m = 1–8) and experimental (n = 2–6) study of the dissociation energy for O2 release. Clusters were formed by laser ablation in a source and selected using mass spectrometry in combination with the post-heating method. A clear relation between the temperature and the intensity ratios of Fe2Om+ was found: as the temperature increases, the abundance of the oxygen-rich clusters decreases. Moreover, as the relative abundance of the Fe2O6+ clusters decreases, the abundance of Fe2O4+ clusters increases, until approximately 550 K; after that, the relative abundance of these clusters decreases, whilst the abundance of Fe2O2+ ones increases to the same extent that Fe2O6+ decreases. Consequently, it was deduced that oxygen is released molecularly in the following form: Fe2O6+ → Fe2O4+ + O2 → Fe2O2+ + 2(O2). To complete the experimental work, theoretical calculations were performed using the GAUSSIAN 09 program with the B3LYP functional and 6-311+G* basis set.
In a more general context, Wang et al.28 investigated the structural and magnetic properties of late transition metal oxide clusters TMnOm (TM = Fe, Co, Ni, n = 1–2, m = 1–6) by using also DFT with the PBE functional combined with a double numerical basis set including d-polarization functions (DND) for O atoms and DFT-based relativistic semicore pseudopotential (DSPP) for TM atoms, implemented in the DMOL package. Fen adopts three-dimensional structures while Con and Nin clusters form planar geometries. The binding energies per atom increase with the increase of O atoms for both n = 1–2, reaching a peak at m = n. Datta et al.29 carried out DFT-VASP calculations of M4O4 and M4S4 clusters (M = Mn, Fe, Co, Ni, Cu) using the pseudopotential plane wave method with the GGA to the XC energy functional as formulated by PBE. The wave functions were expanded with a plane wave basis set. For Fe4O4 oxide, a ring-like structure was obtained with antiparallel couplings, and a total magnetic moment of 0 μB. The high spin state with 8 μB was found with an energy difference of 75 meV. The cube structure is much less stable that the ring-like one. Recently, Wang et al.30 presented a first principles study of the spin properties of triplet TM3O3 (TM = Fe, Co, Ni) clusters and their laser-induced ultrafast spin dynamics. The clusters were optimized at the Hartree–Fock (HF) level with the Lanl2DZ basis set using the Gaussian 16 package. These results provided additional information relevant in the context of ultrafast optical control of magnetism in transition-metal oxide systems.
In the work reported here, we systematically studied FenOm0/± oxide clusters with n = 1–6 and m values until oxygen saturation is reached. We carried out DFT calculations within the generalized gradient approximation (GGA) for exchange and correlation. We focused on the structural and electronic properties, with a special emphasis on magnetism, and charge effects. For cations, the fragmentation channels were calculated and compared with previous experimental results of Molek et al.13 and Li et al.14 We found some nanoparticles that retain a net magnetic moment despite having a high oxidation ratio. The paper is organized as follows. In Section 2, we describe the theoretical and computational approaches and compare some results about Fe20/± and Fe2Om0/± (m = 1–2) with previous ones available in the literature, which allow us to benchmark our theoretical approach and to have a good starting point. In Section 3, we show the results, which are discussed in different subsections: Section 3.1 is devoted to ground state structures and their nearest structural isomers depending on size n, on oxidation ratio m, and on the charge state. Structural properties and absolute and relative stabilities are also discussed. In Section 3.2, fragmentation channels are studied for the cationic clusters by comparing the minimum energy needed for the separation in different possible fragments. In Section 3.3 we discuss the electronic properties as well as the magnetism of FenOm0/±. Finally, the conclusions are summarized in Section 4.
2 Theoretical approach and computational details
We performed fully self-consistent DFT calculations using the SIESTA code.31 For the exchange and correlation (xc) potential we used the Perdew–Burke–Ernzerhof form of the generalized gradient approximation (GGA).32 We employed norm-conserving scalar relativistic pseudopotentials33 in their fully nonlocal form,34 generated from the atomic valence configuration 3d74s1 for Fe (with core radii 2.00 a.u. for s, p and d orbitals), and 2s22p4 for O (with core radii 1.14 a.u. for s, p and d orbitals). Non-linear partial core corrections,35 which are known to be important for transition metal pseudopotentials, were included for Fe at core radius 0.7 Å. Valence states were described using double-ζ basis sets for O and Fe with maximum cutoff radii 4.93 Å (2p) and 8.10 Å (3d, 4s), respectively. A 4p polarization orbital was also considered for Fe, with cutoff radius 8.10 Å.The energy cutoff used to define the real-space grid for numerical calculations involving the electron density was 250 Ry. The Fermi distribution function that enters in the calculation of the density matrix was smoothed with an electronic temperature of 15 meV. We used an energy criterion of 10−4 eV for converging the electronic part.
In the calculations, the individual clusters were placed in a cubic supercell of 20 × 20 × 20 Å3, a size large enough to neglect the interaction between the cluster and its replicas in neighboring cells. Only the Γ point (k = 0) was considered when integrating over the Brillouin zone, as usual for finite systems. The equilibrium geometries resulted from an unconstrained conjugate-gradient structural relaxation using the DFT forces. The initial geometries were built by considering different arrangements of the Fe and O atoms without privileging those formed from given Fe subclusters. Thus, an exhaustive sampling of possible geometries was tested, including those in which the possibly strong Fe–O bonding prevents the nucleation of compact Fe subclusters. In addition, we tested other geometries that were built using local Fukui functions to locate O atoms in the more nucleophilic sites of the host. Fukui functions allow one to determine the most reactive sites according to purely electronic arguments. The Fukui functions36–38f+ and f− are defined as
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the spatial charge density, and Ne the number of electrons, and the subscript indicates that the right/left derivatives have to be calculated at constant external potential, i.e. by keeping the atomic coordinates fixed. The scalar fields f± measure the local variations in electronic charge induced by the addition or removal of electrons, and so they can be used as useful local indices of electronic reactivity. f+ refers to the electron density response upon addition of electrons, and so it is an indicator of locally electrophilic regions which are more susceptible to nucleophilic attack; similarly, f− locates the most nucleophilic regions within the system, susceptible to electrophilic attack. Larger positive values of f± correspond to more reactive sites. Coupling the Fukui function with Bader analysis, we can define atom-resolved condensed Fukui functions fi± for each atom i, by calculating the variation in electronic charge inside each of the Bader atomic basins. Following the standard practice, we have approximated the derivatives by simple finite differences:
) is the spatial charge density, and Ne the number of electrons, and the subscript indicates that the right/left derivatives have to be calculated at constant external potential, i.e. by keeping the atomic coordinates fixed. The scalar fields f± measure the local variations in electronic charge induced by the addition or removal of electrons, and so they can be used as useful local indices of electronic reactivity. f+ refers to the electron density response upon addition of electrons, and so it is an indicator of locally electrophilic regions which are more susceptible to nucleophilic attack; similarly, f− locates the most nucleophilic regions within the system, susceptible to electrophilic attack. Larger positive values of f± correspond to more reactive sites. Coupling the Fukui function with Bader analysis, we can define atom-resolved condensed Fukui functions fi± for each atom i, by calculating the variation in electronic charge inside each of the Bader atomic basins. Following the standard practice, we have approximated the derivatives by simple finite differences:fNe+(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = ρNe+1( ) = ρNe+1(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − ρNe( ) − ρNe(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ) |
fNe−(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = ρNe( ) = ρNe(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − ρNe−1( ) − ρNe−1(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ) |
The global minimum and low-energy isomers found for the neutral oxides are used as inputs for their charged counterparts. The ground state geometry of charged clusters is not always the obtained global minimum structure of the neutral ones, as it will be seen in the next section. Charged systems can be dealt with through the addition of a Madelung correction. Although the finite difference expressions provide the exact value for the derivative according to DFT,38 in practical calculations the expressions are not exact due to the self-interaction error of approximate exchange–correlation functionals. Nevertheless, the standard usage of those finite difference approximations is justified by the fact that approximate xc-functionals are much more accurate for integer numbers than for fractional numbers of electrons.
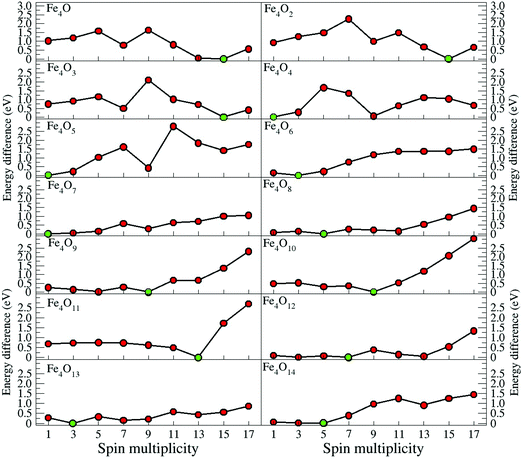
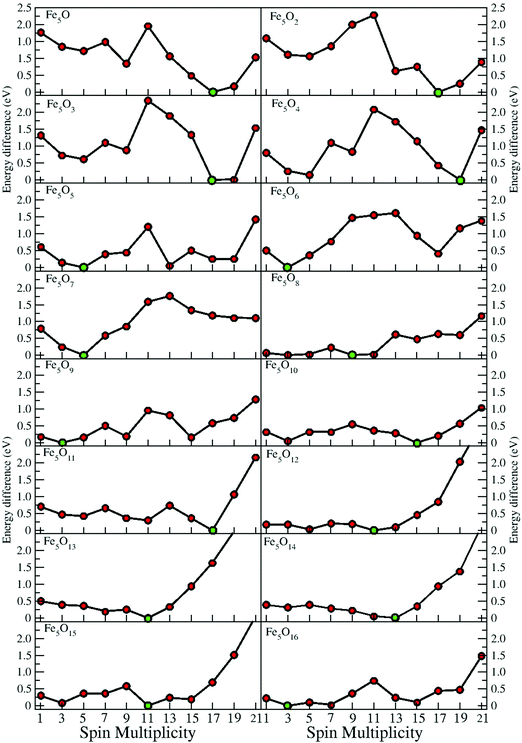
The structures were relaxed without any symmetry constraints until the interatomic forces were smaller than 0.003 eV Å−1. All possible spin multiplicities and different initial parallel or antiparallel arrangements for each different structural geometry with different oxygen environments have been considered in order to be sure of the putative global minimum. In the search for spin isomers, the criterion for the maximum interatomic forces was further reduced to 0.001 eV Å−1.
In order to understand the magnetic couplings of the iron oxides it is necessary to consider first the magnetic coupling of Fe20/±, FeO0/± dimers, and even of FeOm0/±, since they are the basic units of the FenOm0/± clusters, as it will be seen below, and compare our theoretical approach with other DFT results available in the literature (see Tables 1 and 2). The Fe2 dimer has been theoretically investigated with more accurate wave function methods, and experimental data is also available. There is, however, no consensus as regards the ground state magnetic configuration. Tomonari et al.15 and Noro et al.16 obtained a ground state with a total spin moment of 6 μB (septet state) using a multireference (MR) configuration interaction (CI) method with certain dynamical correlations. Hubner et al.17 obtained a total spin moment of 6 μB (nonet state) using IC-MRCI starting from a CASSCD wave function, but their interatomic distance (2.19 Å) overestimates the experimental data [1.87 ± 0.13 Å] measured by Montano et al.,39 or [2.02 ± 0.02 Å] measured by Purdum et al.40 C. W. Bauschlicher et al.,18 using also a CI-MRCI method, confirmed the experimental results,17 but they pointed out that in order to fit the experiment, the septet state should be the true ground state, a fact that was later confirmed by Casula et al.41 through quantum Monte Carlo calculations. Therefore, no consensus exists in regard to the spin state of the ground state, but it seems that the septet state fits better the experimental interatomic distance. We have calculated the Fe2 dimer with our DFT setup with the PBE functional in order to compare with the aforementioned calculations. We have obtained the septet state as the ground state with an interatomic distance of 2.04 Å (in rather good agreement with the experimental data) and binding energy (1.56 eV) of the same order as values predicted with the more accurate methods. The nonet state is a metastable state with an interatomic distance of 2.23 Å, which overestimates the experimental value, as is the case with more accurate methods. Therefore, our tests for the Fe2 dimer are of good quality as compared with more accurate wave function methods and with the experimental data. For Fe2+ and Fe2− dimers, the magnetic moment is 7 μB and the interatomic distances are 2.18 Å and 2.11 Å, respectively, in agreement with Reilly et al.25 In general, when antiparallel magnetic couplings appear in Fe systems, it means that Fe atoms have somehow lost their identity (either they separate from each other, or they lose electronic charge and electronically approach Mn). Moreover, the preferred magnetic Fe–O coupling is also parallel. Bauschlicher and Maitre19 used the complete-active space SCF/internally contracted averaged coupled pair functional approach (CASSCF/ICACPF) to study the diatomic molecule FeO, among other small molecules, obtaining a quintet state (corresponding to a spin moment of 4 μB) and an interatomic distance of 1.61 Å, quite similar to the experimental one. In previous work, Bauschlicher et al.20 performed an exhaustive study of dipole moments and other relevant quantities of small molecules, also with high level theoretical approaches. The CAS11 FeO interatomic distance was 1.69 Å, slightly larger than that calculated at the MRCI11 level (1.63 Å). Our DFT-PBE results are in good agreement; we obtain the same spin state as Bauschlicher and Maitre and an interatomic distance of 1.67 Å. The calculated transferred electronic charge from iron to oxygen is 0.46 e and the local magnetic moments of iron and oxygen are, respectively, 3.4 and 0.6 μB, giving a total moment of 4 μB. Wang et al.28 also found a quintet state for FeO oxide with a bond length of 1.61 Å. Our results also agree with available data from other authors regarding interatomic distances and total magnetic moments.21,26 For FeO+ (FeO−) a total magnetic moment of 5 μB (3 μB) is found, in agreement with previous results.25,26
| Cation | Neutral | Anion | ||||
|---|---|---|---|---|---|---|
| μ | d | μ | d | μ | d | |
| a 1.87 ± 0.13 Å (experimental value39), 2.02 ± 0.02 Å (experimental value40). b 1.61 Å (CASSSCF/ICACPF value19), 1.69 Å (CAS11 value40), 1.63 Å (MRCI11 value40). | ||||||
| Fe2 | 725 | 2.18 | 615,16,18,41 | 2.04a | 725 | 2.11 |
| FeO | 524,25 | 1.71 | 419,21,24,26,28 | 1.67b | 324,26 | 1.69 |
| FeO2 | 125 | 1.65 | 226,28 | 1.62 | 326 | 1.71 |
FeO2 is a triplet isosceles triangle as in previous results,26,28 with a magnetic moment of 2 μB, in good agreement with earlier infrared absorption measurements combined with theory.42 For the FeO2+ cation, the total moment is probably more ambiguous. The theoretical research of Schroder et al.12 predicted a high spin trimer with a total moment of 5 μB, and FeO distances of 1.63 Å, and a spin isomer with 3 μB, at only 0.04 eV in energy. The doublet isomer was found at 3 eV higher in energy. However, Reilly et al.25 found a doublet ground state. Our low spin result for FeO2+ is in agreement with Reilly et al.25 Notice that Schroder et al.12 found that FeO2+ with an oxygen molecule bonded was at 0.22 eV in energy, explaining the low energy process of loss of molecular O2 from FeO2. For FeO2− our results agree with previous ones,26 giving a magnetic moment of 3 μB. Moreover, our results about the dissociation energies of FeOm0/+ (m = 1–2) and O2, shown in Table 2, are also in good agreement with previous results. Previous results available in the literature show the antiparallel arrangement of FeOm0/± (m = 3, 4) upon addition of more oxygen. The neutral FeO3 cluster has a low spin state with 0 μB and, consequently, the total magnetic moment decreases by 2 μB upon addition of each O atom for neutral FeOm (m = 1–3) clusters.26 This happens because the Fe atom transfers two electrons to O. FeOm+ (m = 3–4) have both low spin states with 1 μB.25 FeOm− anions keep a magnetic moment of 3 μB up to m = 3, and the value does not change to 1 μB until the Fe atom is coordinated with four oxygens.26
Therefore, for Fe20/±, the parallel couplings are maintained regardless of the charge state. However, when the magnetic iron atom is oxidized, the results about the magnetic character change and depend on the charge. For FeO0/±, the magnetic moment decreases by 1 μB from the cationic to the anionic state. When the oxidation ratio increases, for FeO20/±, the magnetic moment increases by 1 μB from the cation to the anion. Moreover, although FeO3 does not present magnetism, FeO3− still preserves a magnetic moment of 3 μB like FeO2− and FeO−. Consequently, for low oxidation ratios of the Fe atom, the magnetic results depend strongly on the charge. Extrapolating our and previous results about Fe20/± and FeOm0/± (m = 1–4) to bigger iron oxide clusters such as those investigated in the present work, some trends are expected as the oxidation ratio increases: firstly, a decrease in the total magnetic moment upon oxygen addition and, secondly, a significant effect of charge on the magnetism. Once good agreement is obtained with previous studies of the basic units of the iron oxides, we are confident in the results that we present and discuss in the next section for FenOm0/± with n = 2–6.
3 Results and discussion
In this section, firstly, we discuss the main structural features and stability of the optimized iron oxides FenOm0/± (n = 2–6) with different oxidation ratios; secondly, we present the fragmentation paths that we will compare with experimental results. These structural features and fragmentation paths are connected with the electronic and magnetic properties that will be discussed in the third subsection.The relative strength of the iron–iron and iron-oxygen bonds is an important factor related to the stability and structure of iron oxide nanoparticles. Electronic charge transfer occurs from the iron to the oxygen atoms, which weakens the iron–iron bonding. Moreover, with respect to iron clusters that have larger spin-polarization per atom than the iron bulk, a decrease of the tendency to parallel magnetic couplings is expected for the iron oxide clusters. Due to these interrelated factors and to the non-scalability of the magnetic properties with size in nanoparticles, it is necessary to perform calculations for each size and composition to obtain reliable structural, electronic and magnetic properties as well as to understand the experimental fragmentation paths.
3.1 Geometrical configurations and electronic properties
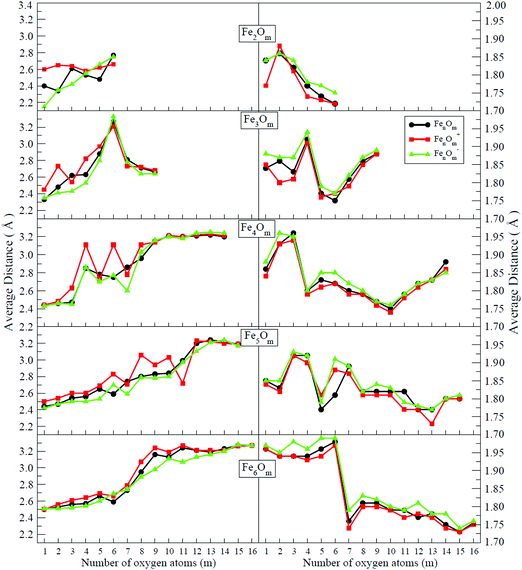
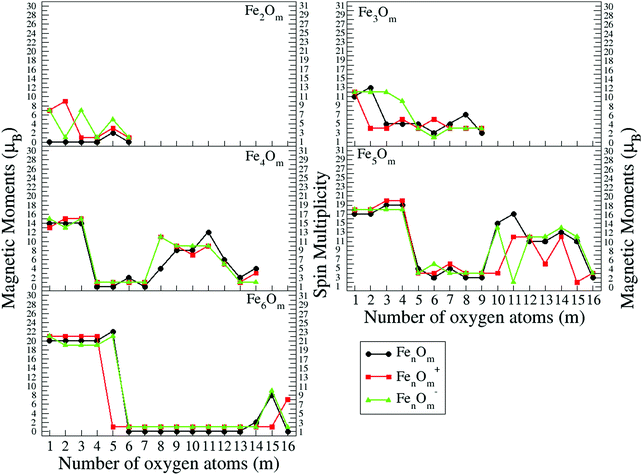
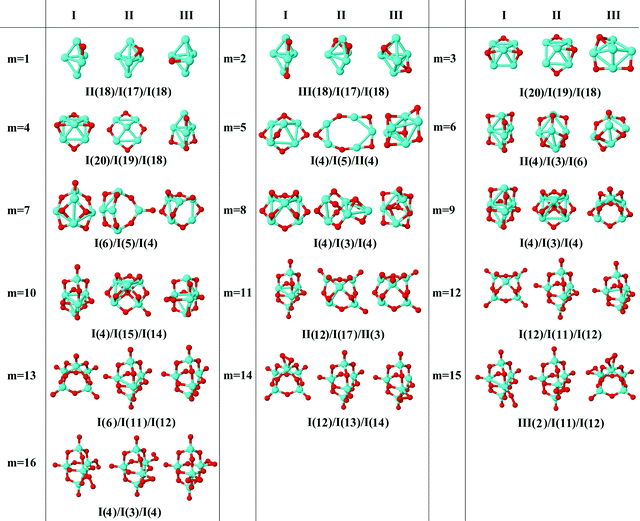
In the following, iron oxide clusters FenOm0/± with n = 2–6 will be denoted by (n, m)0/±. The global minimum structures and several low-lying energy configurations are depicted in Fig. 1–5 with the n.m-Label signature, Label being a roman number, to distinguish the different geometrical isomers with n iron and m oxygen atoms. The signature n.m-I always corresponds to the global minimum of the neutral oxide. The ground state structure of the cationic and anionic oxides, when it is not the same, corresponds to one of the two lowest-energy isomers of the neutral. Below the structures of each (n, m) composition, the ground state geometry for the cation, neutral and anion oxides is indicated, respectively, by its corresponding label. The numbers in parentheses correspond to the spin multiplicity, M, for each state of charge, which will be related to the structural arrangements. The energy differences between the different geometric isomers are shown in Tables I–V of the ESI.‡ Moreover, ionization potentials and electron affinities are also gathered. Fig. 6 shows the interatomic distance of the different bonds (Fe–Fe and Fe–O) as a function of the oxidation ratio, m, for each n value, for the ground state of both neutral and charged oxides, using different colours.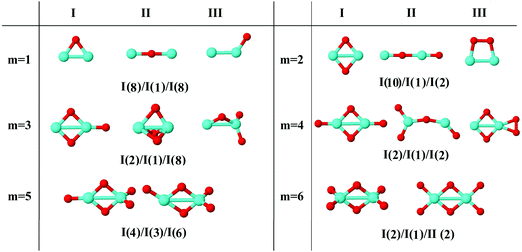 | ||
| Fig. 1 Putative ground state and first two low-energy isomers of Fe2Om neutral clusters with m = 1–6. The notation is 2.m-Label, with Label in roman letters in decreasing order of stability for each (2,m). The ground state of charged oxides, when it is not the same, corresponds to one of the two lowest-energy isomers. Below the structures of each (2,m) composition, the ground state geometry for the cation, neutral and anion oxides is indicated, respectively, by its corresponding label. The numbers in parentheses correspond to the spin multiplicity for each state of charge. We note that for the cation with m = 2 the Fe dimer is larger than those for the neutral and anion, and for anions with m = 1, 3 the Fe dimer is shorter (see Fig. 6). The energy differences between the different geometrical isomers, for each one of the charge states, are given in Table I of the ESI.‡ | ||
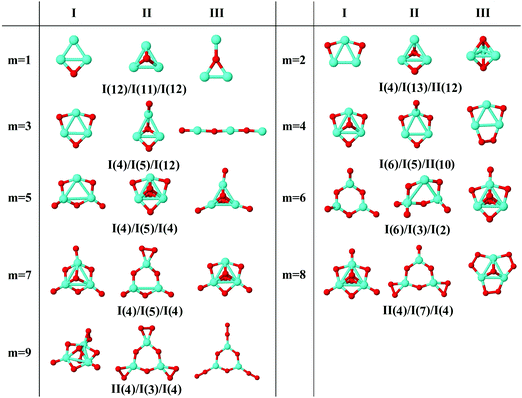 | ||
| Fig. 2 Putative ground state and first two low-energy isomers of Fe3Om neutral clusters with m = 1–9. The notation is 3.m-Label, with Label in roman letters in decreasing order of stability for each (3,m). The ground state of charged oxides, when it is not the same, corresponds to one of the two lowest-energy isomers. Below the structures of each (3,m) composition, the ground state geometry for the cation, neutral and anion oxides is indicated, respectively, by its corresponding label. The numbers in parentheses correspond to the spin multiplicity for each state of charge. We note that for the cation with m = 2 the Fe subcluster is more open than those for the neutral and anion (see Fig. 6). The energy differences between the different geometrical isomers, for each one of the charge states, are given in Table II of the ESI.‡ | ||
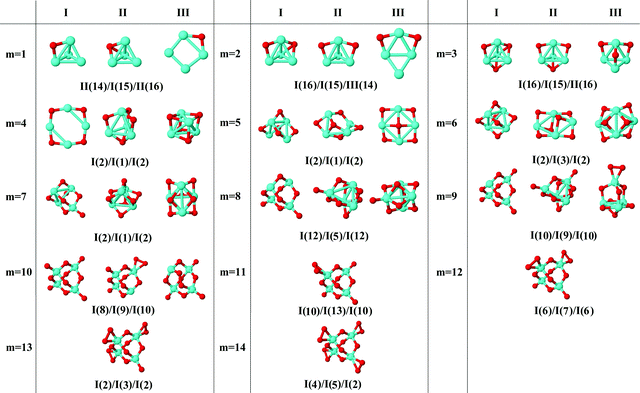 | ||
| Fig. 3 Putative ground state and first two low-energy isomers of Fe4Om neutral clusters with m = 1–14. The notation is 4.m-Label, with Label in roman letters in decreasing order of stability for each (4,m). The ground state of charged oxides, when it is not the same, corresponds to one of the two lowest-energy isomers. Below the structures of each (4,m) composition, the ground state geometry for the cation, neutral and anion oxides is indicated, respectively, by its corresponding label. The numbers in parentheses correspond to the spin multiplicity for each state of charge. We note that for the cation with m = 4, 6 the Fe subcluster is more open (nearly broken) than those of the neutral and anion (see Fig. 6). The energy differences between the different geometrical isomers, for each one of the charge states, are given in Table III of the ESI.‡ | ||
 | ||
| Fig. 4 Putative ground state and first two low-energy isomers of Fe5Om neutral clusters with m = 1–15. The notation is 5.m-Label, with Label in roman letters in decreasing order of stability for each (5,m). The ground state of charged oxides, when it is not the same, corresponds to one of the two lowest-energy isomers. Below the structures of each (5,m) composition, the ground state geometry for the cation, neutral and anion oxides is indicated, respectively, by its corresponding label. The numbers in parentheses correspond to the spin multiplicity for each state of charge. We note that for the cation with m = 6, 8, and 10 the Fe subcluster is more open than those for the neutral and anion (see Fig. 6). The energy differences between the different geometrical isomers, for each one of the charge states, are given in Table IV of the ESI.‡ | ||
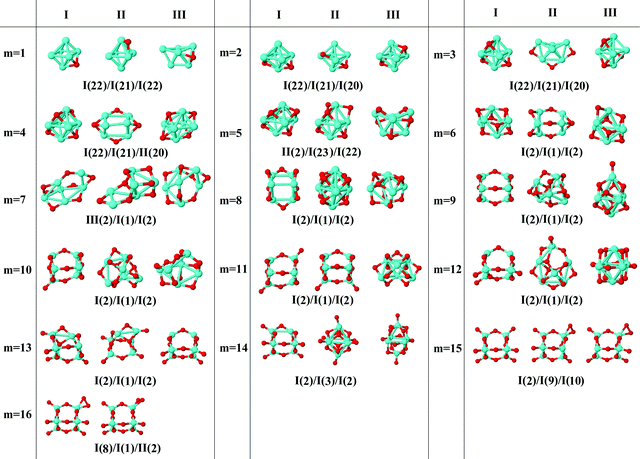 | ||
| Fig. 5 Putative ground state and first two low-energy isomers of Fe6Om neutral clusters with m = 1–16. The notation is 6.m-Label, with Label in roman letters in decreasing order of stability for each (6,m). The ground state of charged oxides, when it is not the same, corresponds to one of the two lowest-energy isomers. Below the structures of each (6,m) composition, the ground state geometry for the cation, neutral and anion oxides is indicated, respectively, by its corresponding label. The numbers in parentheses correspond to the spin multiplicity for each state of charge. The energy differences between the different geometrical isomers, for each one of the charge states, are given in Table V of the ESI.‡ | ||
There are some magnitudes related to the structural features and stability. Thus, the binding energy for neutral iron oxides FenO0m is defined as
| Eb(n, m)0 = [n × E(Fe) + m × E(O) − E(n, m)0] | (1) |
| Eb(n,m)± = [E(Fe)± + (n − 1) × E(Fe) + m × E(O) − E(n, m)±] | (2) |
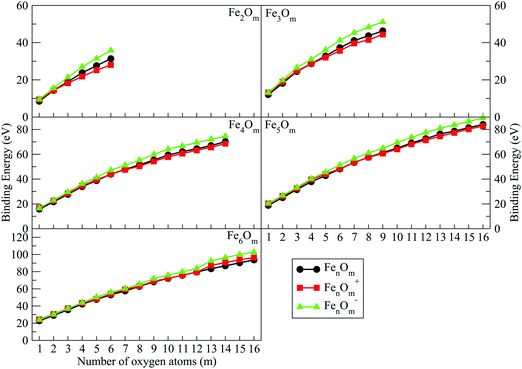 | ||
| Fig. 7 Binding energies of FenOm0/± oxides (n = 2–6) as a function of the number of oxygen atoms, m. Red, black and green curves correspond to cationic, neutral and anionic oxides, respectively. | ||
The second total energy difference in neutral and charged iron oxides FenOm0/± is defined as
| Δ2(n, m) = E(n, m − 1)0/± + E(n, m + 1)0/± − 2 × E(n, m)0/± | (3) |
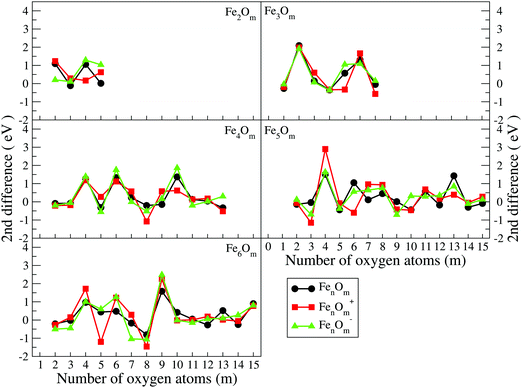 | ||
| Fig. 8 Second energy differences of FenOm0/± (n = 2–6) as a function of the number of oxygen atoms, m. Red, black and green curves correspond to cationic, neutral and anionic oxides, respectively. | ||
Before going into the structural details for each n series, we summarize general trends that are common to most of the iron oxide clusters investigated here.
(a) In the initial stages of oxidation, a compact Fen subcluster is formed, and the preferred positions of the oxygen atoms are the bridge or hollow sites. The preference of iron–oxygen bonds can be understood from the larger iron–oxygen binding energies (5.49 eV) than iron–iron ones (3.12 eV). The absolute maximum of the Fe–O distance takes places at a m value close to the n one. Meanwhile, the Fe–Fe distance increases.
(b) For n = 2, 3, 4 and m = n, ring-like structures are obtained. This trend was already discussed in our previous work for Ni oxide clusters.49
(c) In most cases for which all bridge positions are occupied by oxygen atoms, the Fe–O distance reaches relative minima. Moreover, the iron subcluster is more open but it exists, except for some cations in which the positive charge tends to further increase the distance between Fe atoms.
(d) When all bridge (hollow) sites are saturated, oxygen atoms tend to occupy top iron positions, and when there are no more top positions available, oxygen starts to be adsorbed molecularly. This happens at high values of m due to the strong Fe–O bonds.
(e) Because of the charge transfer from iron to oxygen atoms, an uniform distribution of the oxygen atoms is observed. The growth mechanism tends to maximize the number of oxygen–iron bonds. Fig. 9 and 10 show the local electronic charges on the atoms of the respective structures for the ground states of Fe4Om (m = 1–14) and Fe6Om (m = 1–16). The excess (or deficiency) of the electronic charge for O (Fe) is given for each atom.
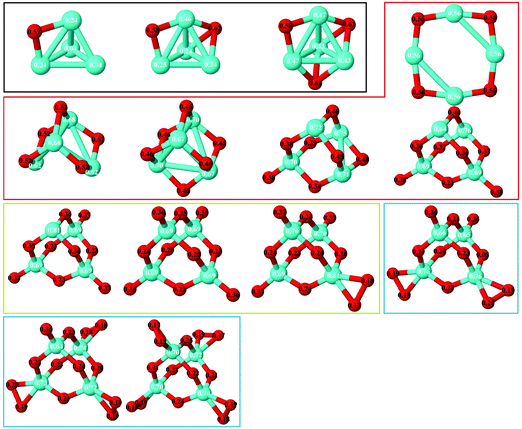 | ||
| Fig. 9 Ground states of Fe4Om (m = 1–14) oxides. The excess (or deficiency) of the electronic charge for O (Fe) is given for each atom with black (white) numbers. | ||
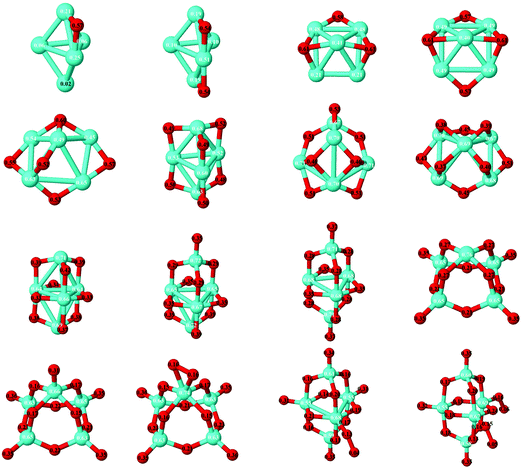 | ||
| Fig. 10 Ground states of Fe5Om (m = 1–16) oxides. The excess (or deficiency) of the electronic charge for O (Fe) is given for each atom with black (white) numbers. | ||
(f) When all bridge and top sites are occupied by oxygen atoms, the Fe–O (Fe–Fe) distances present the absolute minimum (maximum) value. This occurs at (3,6), an iron broken triangle with six oxygen atoms at three bridge and three top positions, at (4,10), an iron tetrahedral-like broken structure with ten oxygen atoms at six bridge and four top positions, at (5,13), an iron broken square pyramid-like configuration with thirteen oxygen atoms at eight bridge and five top positions, and at (6,15), an iron triangular prism-like broken structure with fifteen oxygen atoms at nine bridge and six top positions. For these oxide clusters, Fe–O bonds are more important as manifested in the decrease of the Fe–O distance. Moreover, the Fe–Fe distances show maximum values due to weak Fe–Fe bonds and, consequently, a compact iron subcluster is not identified in the oxide structures.
(g) For high oxidation states in which molecular oxygen adsorption occurs, the Fe–O distance increases and the Fe–Fe distance remains large.
(h) The binding energy quickly increases upon addition of oxygen atoms, until all bridge positions are occupied by oxygen atoms. Then, it increases more slowly until an m value for which all bridge and top positions are occupied, and for which the binding energy still takes a high value, with small (large) Fe–O (Fe–Fe) distances. It can be said that the covalent bonding between Fe atoms contributes less than the partially ionic Fe–O bonding to the stability of these (n,m) iron oxides. The binding energy increases much more slowly when oxygen starts to bind molecularly, a trend related to the large Fe–Fe and Fe–O distances.
(i) The charge has an important influence on the binding energy. In the initial oxidation states, anionic oxides have higher energy values, while neutral oxides have lower values. However, from the m value for which all bridge positions have been occupied, the binding energy of cations becomes lower than that of the neutral ones. It is remarkable that the high binding energy for anions is quite a lot higher than that for neutral and cationic oxides. This will have important consequences.
(j) The positive peaks in the second energy difference are reached when the oxides are very stable. Consequently, maxima are reached when oxygen atoms occupy all bridge positions, (3,3), (4,4), (4,6), (5,8), (5,9), and (6,9), or most of them, (5,4), (6,4), and (6,6), and when all bridge and top positions are occupied, (3,6), (3,7), (4,10), (5,13), and (6,15).
(k) The magnetic character (and in particular the magnetic coupling) is strongly connected to the geometrical structure and the oxygen environment. Consequently, and related to the above trends, we have identified highly stable Fe oxide clusters with a high oxidation ratio that have a large total magnetic moment due to high spin polarization and parallel couplings, something unexpected in transition metal oxide nanoparticles.
Once the main general trends have been established, let us describe in more detail the structural and electronic properties for each n series. As previously stated, the non-scalability at the nanoscale makes it appealing to explore each size and composition in detail and to analyze exceptions to the general trends.
The (2,m)0/± oxide structures, with m = 1–6, are shown in Fig. 1. All of them have an iron dimer. The oxygen environment is the same for all charges at each oxidation ratio m, except for Fe2O6−. There is a clear tendency to maximize the number of iron–oxygen bonds. For m = 1, a triangle with two iron atoms and one bonded oxygen atom on the bridge position is found as the ground state geometry, 2.1-I. The second oxygen bonds also on the bridge position and a rhombus is found in agreement with earlier calculations.25,26,28 The 2.2-I structure is a reference building block in the n = 2 series, and for m = 2–5 the charge does not influence the oxygen environment around the iron dimer. Consequently, for m = 3, the 2.3-I structure has the previous 2.2.I geometry, with the third oxygen atom at the top of an iron atom. For m = 4, the 2.4-I structure is obtained by adding two oxygen atoms on the 2.2-I geometry, each of them at a top position of each iron atom. For m = 5, the lowest energy structure, 2.5-I, is found by capping an oxygen atom at the top position of the previous 2.4-I geometry. Finally, for m = 6, the structure consists of the 2.2-I rhombus with four terminal oxygen atoms. Notice that the two O–O axes are perpendicular to the Fe2 axis, resulting in the 2.6-I structure, except for the anion with the 2.6-II structure, in which the four oxygen atoms are on the same plane.
The Fe–O distance increases at low oxidation values and presents the absolute maximum when all oxygen atoms occupy bridge positions at m = 2 (see Fig. 6). However, when the oxygen atoms bind on top positions, the Fe–O distance decreases significantly as all bridge and top positions are occupied by oxygen atoms at m = 4. At this oxidation ratio, FeO units and their bond become more important, and the Fe–O distances are nearly constant up to m = 6. The charge only has an influence on the Fe–O distance at m = 1 as manifested in the linear structure (2.1-II) of the cation. However, the Fe–Fe distance is very sensitive to the charge (see Fig. 6). In the case of neutral and anionic oxides, the minimum distance occurs at m = 2, when the robust rhombus 2.2-I is found. For the neutral case, when one more oxygen is added, the Fe–Fe distance increases, being quite similar for m = 3–5. The most open neutral dimer is obtained when it is saturated with oxygen, at m = 6. For anionic oxides, the main differences in Fe–Fe distances with the neutral case occur at m = 3, as a consequence of the antiparallel couplings of this oxide, as will be seen in the following section. The parallel coupling between the local magnetic moments of the Fe atoms exists when the distance between them is of the order of the unoxidized iron dimer. In the case of cationic oxide clusters, the Fe–Fe distances are almost constant and large along all the m range, as a consequence of the ionic repulsion between the Fe atoms due to their positive charge.
The binding energy, shown in Fig. 7, increases quickly at low oxidation ratios, m ≤ 4 (m ≤ 3), for the neutral and anionic (cationic) oxides, as a consequence of the highest strength of the iron–oxygen bonding as compared to the iron–iron one. As the oxygen content increases, the iron–iron weakens, the FeO units being more predominant, until the binding energy increases more slowly. Important differences with the charge are found. The anionic oxides show the highest binding energies in all the m range. Moreover, although the cationic oxides show higher binding energy than the neutral ones for m = 1, they are the least stable from m = 3, and this behaviour remains for all the FenOm+ series. Fig. 8 shows the second energy difference. We see a first maximum at m = 2 for all charge states. Additionally, for the neutral and anionic oxides a second peak is found at m = 4, corresponding to the high relative stability for Fe2O4. Instead, the cationic oxide is less stable than the neighbours since the binding energy decreases at m = 4 as mentioned above.
In the initial stages of oxidation, the preferred positions of the oxygen atoms are the bridge sites (the only exception is Fe3O2−, already mentioned). At m = 3, all bridge positions become saturated (3.3-I), independently of the charge.30 The fourth oxygen atom locates on the iron face (for the cationic and neutral oxides, 3.4-I) or it binds on the top position (3.4-II structure, for the anionic case; this structure is also the second isomer in the neutral case with an energy difference of 0.04 eV with respect to the 3.4-I ground state). At this oxidation ratio, m = 4, the Fe–O distance presents its absolute maximum value (see Fig. 6). The next two oxygen atoms bind on top positions, and the same structures (3.5-I and 3.6-I) are preserved for all neutral and charged oxides. The Fe–O distances decrease from m = 4 to m = 6, at which oxygen atoms occupy all possible bridge and top sites (3.6-I), and the Fe–Fe distances, which had increased almost monotonously up to this m = 6 oxidation ratio (except for the cation with m = 2, with a more open Fe triangular cluster), present their maximum value (Fig. 6). Moreover, the Fe–O units become more relevant and a reconstruction is observed from an initial iron subcluster (3.5-I) to a structure built of FeO subunits (3.6-I). The energy difference between this 3.6-I reconstructed structure and the 3.5-I one, adding an oxygen on top, is 0.23 eV per atom, which gives an idea of why the reconstruction is observed. The seventh and eighth oxygen atoms locate on the iron face for all charge states (3-7-I) and isomers with one oxygen molecule are found. The fact that the Fe subcluster is planar favors the adsorption of more atomic oxygen, keeping the Fe–Fe distances not as large as those of m = 6, as can be seen in Fig. 6. At m = 9, and for all states of charge, oxygen binds molecularly. In this region, m = 7–9, the Fe–O distances increase.
The general structural trends are consistent with the binding energy plotted in Fig. 7. In general, iron oxides show higher absolute stability than nickel oxides,49 which may be important for practical purposes. It is noteworthy that the cationic oxides, which have a higher binding energy than the neutral ones in the initial states of oxidation ratios, exhibit the lowest binding energy from m = 4, as compared to the other charge states. However, the anionic oxides from m = 3 keep the highest binding energy, that is, they can be highly oxidized while remaining very stable. Consequently, the charge of oxides is an important factor. Fig. 8 shows the second energy difference, with a first maximum at m = 3, independently of the charge, and a second maximum at m = 6 (anions) and m = 7 (neutral and cations).
The general trend of the preference of oxygen atoms for bridge (4.1-I, 4.2-II, and 4.2-III) or hollow sites (4.1-II, 4.2-I, 4.3-I, and 4.3-II), followed by top sites, is fulfilled. When m = 4, all bridge positions are saturated independently of the charge, and the Fe–O (Fe–Fe) distances reach the first minimum (maximum) value (see Fig. 6), in accordance with the formation of two Fe2O units bound by two oxygen atoms, giving a planar ring-like atomic arrangement (4.4-I). The next oxygen atoms, from five to six, bind to tetrahedral bridge positions (4.5-I and 4-6-I), and when m = 6 all possible bridge positions of a tetrahedral structure are occupied, the Fe–O distance reaching a maximum, whereas the Fe–Fe distance still reflects the existence of an open tetrahedral iron subcluster. The cation in an exception since it is much more open, practically broken. Then, oxygen atoms, from seven to ten, occupy the four possible top positions; in this region (7 ≤ m ≤ 10) the Fe–O distances decrease and reach the absolute minimum value at m = 10, with all bridge and top positions occupied. From m = 9, the Fe–Fe distances are noticeably large and a compact iron subcluster does not form. The main interaction is through Fe–O bonds, resulting in structures that resemble that of zincblende. No molecular absorption has been observed in the ground states until m = 11. From 11 ≤ m ≤ 14, due to the molecular adsorption (4.m-I), the Fe–O distances increase and Fe–Fe distances remain large.
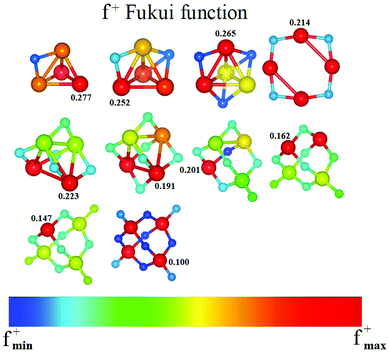
Another way in which we built the input structures was through the Fukui functions, as mentioned in the previous section. For example, we calculated the Fukui function for the ground state of m = 1, and, where the Fukui function was a maximum, we placed the next oxygen atom to obtain an input structure for m = 2, and so on. We repeated this process for all other clusters. In general, this way of building the clusters is very effective. In Fig. 11, we give the Fukui function for the neutral Fe4Om series. We note that it is possible to build the ground state structure Fe4Om+1 from the Fukui function of the previous oxide, except for Fe4O3 and Fe4O4, which depart from the rule.
As expected, and as a general trend, O being more electronegative than Fe in this case, charge transfer from Fe to O takes place, and, Fe having an open 3d shell, most of the spin-polarization is contributed by Fe. Fig. 9 shows the excess (or deficiency) of the electronic charge for O (Fe) for the neutral Fe4Om oxides. With regard to the Fe atoms, (i) for m = 1–4 and as the oxidation increases, they gradually lose electronic charge until 0.56 e for m = 4, where the charge loss of each Fe atom equals the charge excess of each O atom, resulting in a planar structure; (ii) for m = 4–6, the Fe atoms lose more electronic charge until about 0.70 e for m = 6, resulting in a 3D structure with all oxygens occupying bridge positions; and (iii) for m = 6–14, the loss of electronic charge remains practically constant, about 0.70 e, for each Fe atom; in other words, each Fe atom loses the same charge regardless of having on the top position oxygen atoms or molecules. With regard to the O atoms, (iv) for m = 1–4, each O atom has an excess of electronic charge of about 0.56 e; (v) for m = 4–10, the charge excess on each of the O atoms decreases, taking values of 0.46 e for m = 6, where all bridge positions are occupied by oxygen, and approximately 0.22 e for m = 10, where all bridge and top positions are occupied by oxygen; and (vi) for m = 10–14, the charge excess of each bridge O atom in the bridge remains practically constant, regardless of whether there are atoms or molecules of oxygen at the top positions. Moreover, the top O atoms have a charge excess of about 0.36 e, and this value is practically the same for the molecules bonded to the Fe atoms.
Just like for n = 3, the cationic oxides with n = 4 show the lowest binding energy, from m = 6, compared to those of the other charge states. However, the anionic oxides from m = 6 to n = 10 keep a very high binding energy, much higher than that of the neutral oxides and cations with any oxidation ratio. When molecular adsorption takes place, the binding energy decreases, being higher for the anionic oxides. The most stable clusters against the addition or subtraction of one oxygen atom are found at m = 4, 6, 10, for which maximum values in the second energy difference are obtained regardless of the charge state (see Fig. 8). These clusters have all bridge (4.4-I and 4.6-I) and bridge and top positions (4.10-I) occupied.
The general trend of oxygen atoms to occupy, firstly, from m = 1–9, the bridge (5.1-I, 5.2-I, 5.2-II, 5.5-I, 5.5-II, 5.6-I, 5.8-I, and 5.9-I) or hollow positions (5.1-II, 5.2-III, 5.3-I, 5.4-II, and 5.6-II) is fulfilled except for m = 7, where an oxygen atom is bonded on the top position, 5.7-I.
In some cases, the prevalence of the hexahedron-like or square pyramid-like structures is related to the number of bridges in each one of the geometries. The maximum number of bridge positions for the hexahedron-like structure is nine, three of them in the equatorial plane and six other bridges outside it. Oxygen atoms prefer to bind, firstly, on this other kind of bridge of the hexahedron-like structure, as can be seen in the initial states of oxidation, 5.1-I and 5.2-I, and for 5.6-I, with these six bridges occupied. The nine bridges are occupied at m = 9, resulting in the 5.9-I structure. For the rest of the intermediate oxidation ratios, bridge (5.3-I, 5.4-I, 5.5-I, 5.7-I and 5.8-I) or/and hollow (5.3-I and 5.4-I) positions of the square pyramid-like structure are occupied. The eight bridges of this other structure are occupied at m = 8, resulting in the 5.8-I structure. In the case of this square pyramid-like structure, oxygen atoms prefer to bind first to the bridges situated on the pyramid basis, as can been seen at 5.3-I, 5.4-I, 5.5-I and 5.7-I. Regarding the Fe–O distances, in the initial stages of oxidation, they are shorter for the bridge bonds (m = 1, 2) and hexahedron-like structure, increasing for the hollow cases (m = 3, 4) and square pyramid-like one. A more open iron subcluster is maintained until m = 8 and m = 9, where all bridge positions of the square pyramid-like and of the hexahedron like structures are occupied, respectively. The cationic oxides with oxygen atoms in all bridge positions are much more open at m = 8–10, similarly to the cations with n = 4 and m = 4, 6. From m = 10 to m = 13, oxygen atoms bind on top positions of the hexahedron-like (m = 10, 11) or of the square pyramid-like (m = 12, 13) structures. From m = 12, there is not an iron subcluster, as can be seen from the maximum of the Fe–Fe distance, the FeO units becoming much more preponderant. The 5.13-I geometry has all bridge and top positions of the square pyramid-like structure occupied by oxygen atoms, which is reflected in the minimum (maximum) value of the Fe–O (Fe–Fe) distances, such as happened for previous (3,6) and (4,10) iron oxides. The first oxygen molecule is found at an m = 14 oxidation ratio, the Fe–O distances begin to increase, and the Fe–Fe distances remain large.
As expected, charge transfer from Fe to O takes place. Fig. 10 shows the excess (or deficiency) of the electronic charge for O (Fe) for the neutral Fe5Om oxides. With regard to the Fe atoms, (i) for m = 1 to m = 8 and 9 and as the oxidation increases, they gradually lose electronic charge until 0.7 e, resulting in 3D structures with all oxygens occupying bridge positions; (ii) for m = 9–14, the loss of electronic charge remains practically constant, about 0.6–0.7 e, for each Fe atom, regardless of having on the top position atoms or O molecules; and (iii) for m = 15–16, with oxygen molecules bonded by only an O atom, the loss is slightly smaller. With regard to the O atoms, (iv) for m = 1–3, each O atom has an excess of electronic charge of about 0.5 e, and, for m = 4–5, with all bridge positions occupied by oxygen, the value is a little less (0.4 e); (v) for m = 5–16, the charge excess on each of the O atoms decreases, taking a value of 0.17 e for m = 12; and (vi) for m = 10–16, the top O atoms have a charge excess of about 0.36 e, and this value is practically the same for the oxygen molecules with the two atoms bonded to the Fe atoms, being smaller for those bonded by only an oxygen atom.
The most stable oxides are found at m = 4, 8, and 13, where maximum values in the second energy difference are observed regardless of the state of charge (see Fig. 8). Also, the neutral case shows a maximum at m = 6, with a square pyramid-like structure also found at m = 5 and 7 neighbouring stoichiometries. These most stable clusters are obtained when all bridge (5.8-I) or most of them (5.4-I and 5.6-I) and bridge and top positions (5.13-I) are occupied.
Hollow positions of the oxygen are observed from m = 1 to m = 6 for the octahedral structure (6.m-I, m = 1–6). When the seventh oxygen atom binds, an important structural change takes place, and a tetrahedron with an additional dimer is obtained by the seven oxygen atoms occupying the bridge positions (6.7-I). From m = 8, a triangular prism is obtained, and when the ninth oxygen atom binds, each one of the nine oxygen atoms occupies each of the nine possible bridge sites (6.9-I). Again, the structure preferred by the iron oxides is the one that gets oxygen atoms occupying all bridge sites. From m = 10 to m = 15, top positions are the most favorable ones, resulting in a prism triangular symmetry with all the bridge and top sites occupied by fifteen oxygen atoms, for both neutral and charged oxides (6.15-I). Molecular adsorption begins at m = 16, where the 6.16-I structure is found for all charge states. The average Fe–O interatomic distances for the octahedral family are larger than for the triangular prism (see Fig. 6). In this case, the distances decrease as the oxygen ratio increases, reaching a relative minimum at m = 15, with all bridge and top sites occupied (6.15-I), increasing later when the first oxygen molecule is obtained (6.15-II). Additionally, the Fe–Fe average distance increases with the number of oxygen atoms up to a maximum at m = 9; after that, no Fe–Fe bonds are observed, with FeO units prevailing. It is worth noticing that for oxygen-rich clusters, the oxygen atoms that surround the Fe atoms show local tetrahedral symmetry, recalling a diamond-like structure or zincblende.
As in the previous cases, the binding energy is higher for anions at any oxidation ratio, particularly in the highest ones. Consequently, the anionic oxides better hold the oxidation. The second energy differences (Fig. 8) show peaks at m = 4, 6, and 9, this last one being the biggest, corresponding to the first structure where all the Fe–Fe bonds are broken and all bridge positions are occupied by oxygen atoms. Moreover, at m = 15 (the last value with the second energy difference calculated, and for which oxygen occupies all bridge and top positions) a higher value is obtained as compared with the previous one at m = 14.
In general and summarizing subsection A, a detailed computational study has been done taking into account different spin isomers, with different parallel and antiparallel arrangements. For n = 1, the results are in agreement with previous calculations, showing a decrease of the magnetic moment of the iron atom upon addition of oxygen. The ground state structures are planar for n = 2–3 and especially at low oxidation ratios, whereas the ground state structures for n = 4–6 are three dimensional (3D). Due to the strong iron–oxygen bonding, a uniform oxygen distribution is found. Firstly, oxygen atoms preferably occupy bridge or hollow sites, and when all sites are saturated, they tend to bond on top positions. Further oxidation takes place through molecular adsorption. As the oxygen content increases, the iron–iron bond weakens, which is reflected in the increasing Fe–Fe bond length. From a certain size, there is no longer an iron subcluster surrounded by oxygen and FeO units become more preponderant.
3.2 Fragmentation channels of cationic clusters
The reaction of iron cluster cations Fen+ (n = 2–18) with O2 was studied by Griffin et al.10 and the kinetic energy dependence of these reactions over a wide range, using guided ion beam mass spectrometry, was examined. Analyzing the kinetic energy dependence of these processes, quantitative data regarding the thermodynamics of the oxidation reactions were obtained. Consequently, the oxygen bond energies, FenO+, defined as D(Fen–O+) = E(Fen+) + E(O) − E(FenO+), were gathered. A key to this analysis was the availability of quantitative thermo-chemistry regarding the stability of the bare iron clusters previously measured. The energy dependence of cross sections in the threshold region was modeled,10 where one of the parameters is the threshold for the corresponding reaction, E0. Two reactions were used to form FenO+. In the first reaction, Fen+ + O2 → FenO+ + O, the bond energies were derived by using the equation D(Fen–O+) = D(O2) − E0. The resulting bond energy values are listed in the first column of Table 3. An alternative method of deriving bond energies notes that they are related to the difference between the thresholds for reactions Fen+ + O2 → Fen−1+ + Fe + O2 and Fen+ + O2 → Fen−1O+ + Fe + O. Specifically, the bond energies are calculated as D(Fen−1–O+) = D(O2) + E0(1) − E0(2). The threshold for the first reaction, E0(1), is equivalent to the bond energies of the bare iron cluster ions, D(Fen−1–Fe+), and has been measured previously. The threshold for the second reaction, E0(2), was obtained using the analysis of cross sections in the threshold region as outlined above. The second column of Table 3 lists the bond dissociation energies D(Fen–O+) obtained from these thresholds using the two previous equations.| n | Fen+ + O2 → | Fen+ + O2 → | Fen+ + CO2 → | This work |
|---|---|---|---|---|
| FenO+ + O* | Fen−1O+ + Fe + O* | Fen−1O+ + Fe + CO** | ||
| 2 | 5.15 ± 0.12 | — | 5.1 ± 0.2 | 5.04 |
| 3 | 4.70 ± 0.13 | — | 4.5 ± 0.2 | 5.52 |
| 4 | 4.00 ± 0.15 | — | 5.9 ± 0.3 | 5.96 |
| 5 | 4.60 ± 0.15 | 5.10 ± 0.29 | 5.7 ± 0.3 | 5.78 |
| 6 | 4.00 ± 0.15 | 5.60 ± 0.31 | 5.5 ± 0.3 | 5.69 |
Moreover, the kinetic energy dependence of the reactions of Fen+ (n = 2–18) with CO2 was studied by Griffin et al.11 in a guided ion-beam mass spectrometer. The bond energies for FenO+, D(Fen–O+), were measured by determining the difference between the thresholds for reactions Fen+ + CO2 → Fen−1+ + Fe + CO2 and Fen+ + CO2 → Fen−1O+ + Fe + CO. Specifically, the bond energies are calculated as D(Fen−1+–O) = D(O–CO) + E0(3) − E0(4), where E0(3) is equivalent to the bond energies of the bare iron cluster ions, D(Fen−1+–Fe), measured previously. The threshold for the second reaction, E0(4), was obtained using the analysis of cross sections in the threshold region as outlined above. The resulting D(Fen–O+) bond energies are gathered in the third column of Table 3. Our calculated D(Fen–O+) bond energies are shown in the last column and great agreement with experimental results10,11 is obtained.
In the context of investigating the stability of small iron oxide clusters and their dependence on the stoichiometry, Molek et al.13 showed that photofragmentation studies of cations can be used to determine relative cluster stabilities. It is more difficult to dissociate stable clusters and, therefore, they are often obtained upon the dissociation of larger clusters. In the following, FenOm+ oxides with n = 2–6 are denoted by (n,m)+. In this section, we discuss the results of the fragmentation patterns of (n,m)+ oxides, for which experimental results are available. For this purpose, we calculated the fragmentation energies defined as follows:
| Ef(n,m) = E(n,m)+ − E(x,y)+ − E(n − x,m − y) | (4) |
| O2 | O | Fe | FeO | FeO2 | Fe+ | Fe2+ | FeO+ | Fe2O2+ | |
|---|---|---|---|---|---|---|---|---|---|
| Fe2O+ | — | 4.91 | 4.86 | 3.91 | — | 3.91 | 4.91 | 4.86 | — |
| Fe2O2+ | 4.92 | 5.08 | 7.49 | 4.28 | 4.50 | 4.50 | 4.92 | 4.28 | — |
| Fe2O3+ | 3.70 | 3.86 | 7.90 | 5.86 | 4.12 | 3.70 | — | 4.12 | 3.86 |
| Fe2O4+ | 2.36 | 3.58 | 9.11 | 5.99 | 5.41 | — | — | — | 2.36 |
| Fe2O5+ | 1.91 | 3.41 | — | 7.03 | 5.37 | — | — | — | — |
| Fe2O6+ | 1.62 | — | — | — | 6.29 | — | — | — | — |
| Fe3O+ | — | 5.52 | 3.77 | 3.36 | — | 4.68 | 3.36 | 5.51 | 3.36 |
| Fe3O2+ | 6.16 | 5.71 | 4.57 | 3.99 | 4.75 | 4.59 | 4.75 | 5.86 | 4.57 |
| Fe3O3+ | 6.53 | 5.90 | 6.60 | 4.97 | 5.56 | 5.78 | 6.42 | 5.95 | 4.97 |
| Fe3O4+ | 4.73 | 3.91 | 6.90 | 5.02 | 4.56 | 4.87 | 6.98 | 5.15 | 4.56 |
| Fe3O5+ | 1.43 | 2.60 | 6.13 | 4.05 | 3.30 | 3.70 | — | 2.93 | 2.80 |
| Fe3O6+ | 2.02 | 4.50 | 7.34 | 5.14 | 4.22 | 4.44 | — | 3.66 | 3.95 |
| Fe4O+ | — | 5.96 | 3.82 | 3.85 | — | 4.91 | 4.19 | — | — |
| Fe4O2+ | 6.53 | 5.65 | 3.76 | 3.98 | 5.18 | 4.50 | 4.04 | 6.02 | 5.20 |
| Fe4O3+ | 6.44 | 5.86 | 3.72 | 4.13 | 5.52 | 4.03 | 5.32 | 5.82 | 5.70 |
| Fe4O4+ | 6.83 | 6.04 | 5.86 | 4.27 | 6.85 | 5.83 | 6.54 | 5.53 | 5.94 |
| Fe4O5+ | 5.83 | 4.86 | 8.12 | 5.23 | 5.11 | 7.50 | 7.63 | 6.16 | 6.10 |
| Fe4O6+ | 4.37 | 4.59 | 8.21 | 7.21 | 5.49 | 7.14 | 8.46 | 7.55 | 5.86 |
| Fe5O+ | — | 5.79 | 3.43 | 3.90 | — | 4.63 | 4.15 | — | — |
| Fe5O2+ | 6.72 | 6.01 | 3.79 | 3.95 | 5.58 | 4.80 | 4.10 | 6.10 | — |
| Fe5O3+ | 6.97 | 6.05 | 3.97 | 4.34 | 5.67 | 4.77 | 3.81 | 6.30 | 6.07 |
| Fe5O4+ | 8.18 | 7.21 | 5.14 | 5.69 | 7.22 | 5.81 | 6.79 | 7.44 | 7.22 |
| Fe5O5+ | 6.45 | 4.31 | 4.54 | 3.96 | 5.68 | 5.23 | 7.91 | 5.59 | 5.21 |
| Fe5O6+ | 3.63 | 4.39 | 4.40 | 3.49 | 4.03 | 4.40 | 7.35 | 5.08 | — |
| Fe5O7+ | 4.31 | 5.00 | 5.93 | 4.90 | 4.47 | 5.52 | 9.21 | 4.86 | 7.17 |
| Fe5O8+ | 3.96 | 4.04 | 7.70 | 4.48 | 4.22 | 5.91 | 10.07 | 5.02 | 6.26 |
| Fe6O+ | — | 5.63 | 4.03 | 4.32 | — | 5.63 | 4.47 | — | — |
| Fe6O2+ | 6.81 | 6.25 | 4.27 | 4.79 | 6.25 | 5.62 | 4.88 | 7.34 | — |
| Fe6O3+ | 7.68 | 6.51 | 4.74 | 5.29 | 6.97 | 5.74 | 5.32 | 7.59 | 7.10 |
| Fe6O4+ | 7.79 | 6.36 | 3.89 | 5.60 | 7.33 | 5.66 | 5.51 | 7.55 | 7.62 |
| Fe6O5+ | 6.70 | 5.42 | 4.99 | 3.82 | 6.70 | 6.25 | 6.03 | 6.54 | 6.97 |
| Fe6O6+ | 5.40 | 5.06 | 5.66 | 5.05 | 4.55 | 5.85 | 5.88 | 6.77 | 5.86 |
| Fe6O7+ | 5.15 | 5.17 | 5.82 | 5.33 | 5.40 | 5.80 | 7.16 | 6.47 | 6.12 |
| Fe6O8+ | 3.86 | 4.33 | 5.56 | 4.71 | 4.78 | 5.42 | 7.28 | 5.04 | 4.69 |
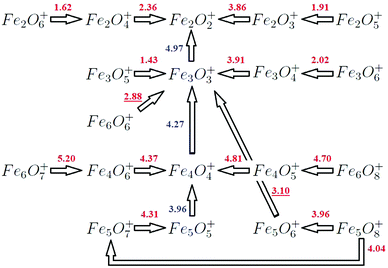
Our aim is to corroborate our previous DFT results about the structural properties and stabilities of iron oxides by comparing them with experimental results, which only exist for the cations with n ≤ 2,14 and with n = 2–6 and m ≥ n.13 Multiphoton absorption was necessary to fragment those iron oxide clusters, which is consistent with the strong metal–oxygen bond shown in the previous section. Our calculations reproduce the main features of the mass spectra. The general trends can be summarized as follows: for oxygen-poor clusters (m < n), the most favorable fragmentation channel is the loss of one FeO unit (Fe atom) for the smallest (largest) sizes studied, n = 2–3 (n = 4–6). Table 5 reports some dissociation energies, reaching good agreement with previous results. Oxides with n = m do not eliminate oxygen, but lose a neutral FeO unit, keeping n = m and producing very stable species. An exception is the (6,6)+ oxide whose most favorable channel is its fragmentation into the neutral (3,3) and the cation (3,3)+, both with n = m and both very stable, in good agreement with experiments. The decomposition of larger oxides with m > n produces a variety of product cations, but those with n = m are always the most prominent and these same species are produced repeatedly from different parent ions, except (5,5)+, which appears neither in the experimental spectra of the oxygen-rich oxides with n = 5, nor in the spectra of n = 6. This fact is understandable, since this cluster does not present the highest stability in the n = 5 series according to our calculations. For n = 6, and m > n, the fragmentation does not produce oxygen, but the structures fragment experimentally producing the subclusters that are preformed, which supports our results. Fig. 12 shows the theoretical fragmentation channels predicted in our calculations, for m ≥ n, in good agreement with experiments from Molek.13
For the (2,1)+ oxide, with a triangular structure 2.1-I, the two preferred fragmentation channels produce the (1,1) unit or an Fe atom (and Fe+ or (1,1)+, respectively) with energies of 3.91 eV and 4.86 eV. These results are in good agreement with Li14 and experimental results (Table 4). We find that for n = 3 and m = 1–2, the most favorable fragmentation channel corresponds to the loss of a (1,1) unit, results consistent with the 3.1-I and 3.2-I structures found (Fig. 2). The loss of a neutral Fe atom is the next favorable channel at 0.41 eV and 0.58 eV, respectively. This channel, in which the oxides lose a neutral Fe atom, becomes the preferred one for all n = 4–6 oxygen-poor iron oxides (m = 1–3) with m < n. The fragmentations are compatible with the tetrahedral, pyramidal, hexahedral and octahedral structures found (Fig. 3–5). The only exception is (5,3)+, whose fragmentation, by the loss of Fe2+ (Table VI, ESI‡), instead of an Fe atom, produces the very stable neutral (3,3) iron oxide. Moreover, from (4,3)+ and (5,4)+, the iron fragmentations result in very stable (3,3)+ and (4,4)+ oxides, respectively. The second preferential channel for n = 4–6 iron oxides with m < n is the loss of a (1,1) unit.
For n = 2 and m > 2, the preferred channels are the loss of an oxygen atom (m = 3) or molecular oxygen (m = 4–6), in agreement with Li14 and Molek,13 and this fact corroborates the structures and stabilities that we have obtained (2.n-I, see Fig. 1). For m = 3, the 2.3-I calculated structure of (2,3)+ has a terminal oxygen atom added to the 2.2-II rhombic structure of (2,2)+, and the calculated energy of 3.86 eV to evaporate an oxygen atom is in good agreement with Li et al.14 (3.82 eV). Competing with this dissociation, the formation of (1,1)+ as well as (1,2), which involves the same bond breaking as the fragmentation of (2,2)+ into Fe+ and (1,2), has a similar energy of 4.12 eV versus 4.28 eV. The calculated energy of 4.12 eV is also in agreement with Li et al.14 (3.96 eV). The thermodynamically favored process is the loss of O2, which is presumably more favorable for (2,3)+ (3.70 eV) than for (2,2)+ (4.92 eV), probably due to the existence of an oxygen top atom that is closer to the bridging oxygens than they are to each other in (2,2)+. However, Li noted14 that the loss of O2 still requires a more constrained pathway, being entropically disfavored. For m = 4, the calculated ground state structure of (2,4)+ starts with the rhombic structure of (2,2)+ and has two extra oxygen atoms (2.4-I); the loss of molecular oxygen is the preferred channel (2.36 eV) to fragment into very stable (2,2)+. In this case, no geometrical rearrangement is necessary. For m = 5–6, the calculated ground state structures (2.5-I and 2.5-II) add additional terminal oxygens to the 2.4-I geometry. The fact that the energy required to lose O2 from both is small, 1.91 and 1.62 eV, respectively, is consistent with the 2.5-I and 2.6-I structures found. Moreover, the (2,2)+ fragment could also result from the (2,6)+ cationic parent after the elimination of two oxygen molecules.
It is worth noting that small n = 2 iron oxides are oxygen-rich from most m values (m > 2), and a recurrent trend is found: the loss of oxygen, also reported by Castleman et al.26 in the collision dissociation of oxygen-rich iron. This behavior supports the sequential fragmentation shown in Fig. 12, resulting in the cationic Fe2O2+ iron oxide as a fragment from more oxide species as a consequence of the high stability of this oxide (see Fig. 8), which is also in keeping with results from Molek13 and Li.14
On the other hand, (3,3)+ is also obtained in the fragmentation of (3,m)+ (m > 3), exhibiting a high peak at m = 3 in the mass spectra of n = 3 iron oxides with m > 3, as a consequence of the high stability of the (3,3)+ oxide. Experiments13 show that (3,3)+ was even produced from larger iron oxide clusters, and that it was found as the most stable cationic iron oxide in the n = 3 series. This result is in good agreement with ours (Fig. 8). Likewise, the (3,4)+ cluster shows a 3.4-I structure formed by adding a terminal oxygen to one of the iron atoms of (3,3)+ (see Fig. 2). Now, cleavage of the terminal FeO bond, losing an oxygen atom (3.91 eV), leads to the primary (3,3)+ product observed,13 preserving the ring structure. In addition, (2,2)+ (Fe+) cations coming from the sequential fragmentation of the (3,3)+ oxide could also result from parallel fragmentation from the (3,4)+ parent ion, with an energy difference of 0.65 (0.96) eV. Moreover, (3,5)+ and (3,6)+ fragment into (3,3)+ (1.43 eV) and (3,4)+ (2.02 eV), respectively, via the loss of molecular oxygen, in agreement with the experimental mass spectra.13 Reilly25,26 also reported the loss of molecular oxygen in the collisional dissociation of iron oxides rich in oxygen. These results are also coherent with our predicted structures, 3.5-I and 3.6-I (Fig. 2).
The resulting sequential fragmentation of (3,m)+ oxides, explained above, can explain the experimental spectra, as shown in Fig. 12.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, fragments via an initial loss of an FeO unit (3.96 eV) reaching the (4,4)+ oxide, which is very stable (Fig. 3). This fact is consistent with the ground state structures of both systems, 5.5-I and 4.4-I (Fig. 3 and 4). Subsequently, the steps above explained for this fragment follow and two FeO units are consecutively detached, resulting in (4,4)+, (3,3)+, and (2,2)+, as reported in the experimental mass spectra. The (5/7)+ oxygen-rich cluster, in the same way as previous cases for n = 2–4, loses an oxygen molecule (4.31 eV), producing the (5,5)+ fragment. Following its fragmentation process, our results explain the experimental mass spectrum of (5,7)+, resulting in the cationic (5,5)+, (4,4)+, (3,3)+, and (2,2)+.
1 stoichiometry, fragments via an initial loss of an FeO unit (3.96 eV) reaching the (4,4)+ oxide, which is very stable (Fig. 3). This fact is consistent with the ground state structures of both systems, 5.5-I and 4.4-I (Fig. 3 and 4). Subsequently, the steps above explained for this fragment follow and two FeO units are consecutively detached, resulting in (4,4)+, (3,3)+, and (2,2)+, as reported in the experimental mass spectra. The (5/7)+ oxygen-rich cluster, in the same way as previous cases for n = 2–4, loses an oxygen molecule (4.31 eV), producing the (5,5)+ fragment. Following its fragmentation process, our results explain the experimental mass spectrum of (5,7)+, resulting in the cationic (5,5)+, (4,4)+, (3,3)+, and (2,2)+.
In the case of (5,8)+, some changes happen (Fig. 12). As we will see below, for n = 6 (and other sizes not studied here) it is not possible to explain some experimental spectra from a single sequential process. The first step is the loss of molecular oxygen resulting in the (5,6)+ fragment, whose mass spectrum is not shown in the experimental work. One option could be, a priori, the loss of an O atom reaching the (5,5)+ oxide (4.39 eV). However, the detachment of the neutral (2,3) fragment to give (3,3)+ only needs 3.10 eV from our calculations. Moreover, (5,5)+ does not result in a very stable cluster from our calculations, because it does not have all bridge or all bridge and top positions occupied by oxygen atoms. Therefore we propose that the next step for the resulting cationic (5,6)+ fragment is to reach the very stable cationic (3,3)+ oxide by losing the neutral (2,3) fragment. Then the (3,3)+ oxide would follow the steps explained above. Moreover, in the (5,8)+ spectrum, there are some additional small peaks and a peak associated with (4,4)+ that is not as high as the one associated with (3,3)+. We propose a parallel fragmentation from the (5,8)+ parent (Fig. 12), losing an oxygen atom (with an energy of 4.04 eV, just 0.08 eV higher than that of the first fragmentation to (5,6)+) and resulting in the (5,7)+ oxide, which fragments to (5,5)+ and consecutively to the very stable (4,4)+ oxide, which shows13 a higher peak than the previous less stable (5,7)+ and (5,5)+ fragments (whose signal is only slightly noticeable). Afterwards, the (4,4)+ fragment follows its fragmentation process as explained above, which would also explain the larger height of the experimental peak associated with the (3,3)+ fragment. These results are consistent with the fact that the (5,5)+ oxide is not as stable (Fig. 8 and experimental (5/8)+ spectrum13), and that not all clusters with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry are those with very high stability as we have seen in our previous section.
1 stoichiometry are those with very high stability as we have seen in our previous section.
The fragmentation of (6,7)+ and (6,8)+ essentially jumps over the possible n = 5 fragments. (6,7)+ produces instead (4,6)+ and (2,1) (5.20 eV) (Table VI of the ESI‡), which is consistent with structure 6.7-II obtained with the preformed 4.6-I and 2.1-I subclusters. After, (4,6)+ fragments into (4,4)+. We found both oxides as the most stable ones for the n = 4 series (Fig. 8), with all bridge positions occupied by oxygen. Then, (4,4)+ follows the fragmentation process explained above reproducing the experimental mass spectrum. The (6,8)+ oxide produces the (4,5)+ one after the release of the (2,3) fragment (4.70 eV). This type of fragmentation was also found for (5,8)+, and the 2/3 stoichiometry is the same as that of the common bulk phase as was also indicated in the experiments.13 Although we find more favorable energetic channels related to the loss of oxygen for the (6,7)+ and (6,8)+ oxides, they would imply an important geometric arrangement, whereas both oxides have the resulting experimental fragments as preformed subclusters.
In general and summarizing subsection B, the fragmentation process is consistent with a sequential mechanism (Fig. 12), with a few exceptions such as the (5,8)+ spectrum and the small peaks that are experimentally found in the (6,6)+ spectrum. Moreover, although the n = 7 series is not studied here, experiments also found some fragmentation channels that can only be explained by a parallel fragmentation mechanism. We also found channels close to the most favorable one, which could explain the large height of some peaks. On the other hand, the above results about fragmentation energies are in keeping with the trends discussed in the previous section about structural arrangements and stabilities from the calculations of second energy differences: (i) For low oxidation ratios (n < m) where there is an Fe subcluster with some oxygen atoms, Fe or FeO can be released. (ii) The (2,2)+, (3,3)+, and (4,4)+ oxides are very stable, with all bridge positions occupied, and are most often obtained from larger clusters. They fragment by releasing an FeO unit and moving on to the previous one. (iii) The most favorable channel for the (6,6)+ oxide, which does not have all bridge positions occupied, is the one leading to two neutral and charged (3,3) clusters. (iv) The oxygen-rich clusters with n = 2–5 and m > n, with an open iron subcluster, release an oxygen atom or O2 until they find a very stable oxide, usually with m = n (or (4,6)+, which also has all bridge positions occupied and exhibits high stability from our calculations). (v) Oxygen-rich clusters with n = 6 fragment into two pre-formed subclusters in their geometric arrangement.
3.3 Magnetic properties
We discuss here the magnetic properties of iron oxide clusters with a particular focus on their net magnetic moment as a function of the oxidation ratio. Fig. 13 shows the total magnetic moment of FenOm0/± (m = 1–6) and spin multiplicities as a function of the oxygen ratio m, for each n value. Moreover, in Fig. 1–5, and for each (n,m) value, the spin multiplicities are given in parenthesis for each charge state, to better identify possible relations with the structural arrangements. For all n values, there are, in principle, two different initial magnetic phases depending on the oxygen concentration (see Fig. 13). The first one (low oxygen concentration) is a high magnetic moment phase. The second one (high oxygen concentration) is a low magnetic moment phase. But, as we will see, a further unexpected phase with magnetic reentrance may arise at an even higher oxidation ratio.In relation to the behavior of larger Fe oxides, the strong influence of charge on the magnetic character is remarkable. On the other hand, when an oxygen atom is added on the top position in the Fe dimer (2.1-III geometry) it results in parallel couplings (see the ESI,‡ Table I). This behavior, which can also be seen for the 2.3-III geometry (ESI,‡ Table I), for both neutral and charged cases, will have a significant impact on oxides with high oxidation ratios that have not yet reached saturation, as we will see. Moreover, the antiparallel couplings for n = 2 at low oxidation ratios will also be found for n = 3 anions, and for the rest of the iron oxide sizes (n = 4–6) for all charge states. The reentrance of magnetism for n = 2, at m = 5, after the antiferromagnetic phase at m = 4, will also be a finding for larger clusters, where a high-spin region will be found for several oxidation values after the low-spin phase.
For n = 3, the negative charge supports the parallel couplings upon addition of oxygen atoms, from m = 1 to m = 4. This effect, related to the negative charge, was already described above for FeOm− (m = 1–3). However, for neutral and cationic oxides, the parallel couplings also remain until low oxidation ratios, m = 2 and m = 1, respectively. Although for n = 3 two high-spin and low-spin phases can be observed, a very slight emergence of magnetic character for Fe3O6+ and Fe3O8 is found.
For n = 4–6, in addition to both high and low magnetic moment phases, two further phases appear, resulting in four magnetic phases in total (see Fig. 13). For n = 4 and 5, both the neutral and charged oxides, and for n = 6, both the neutral and anionic oxides, have high spin from m = 1 to m = n − 1. The first ferromagnetic region extends up to m = 4 in the case of n = 6 and cationic oxides, probably due to the different oxygen environment. There is a second low-spin region, for all charge states. The third one consists of a reentrance of the magnetic moment at about m = n + 5, since the charge also influences the magnetism for n = 4–6, especially at oxidation ratios that are in the limit between different magnetic regions. In the fourth phase, antiparallel couplings are observed again.
In general, upon addition of oxygen on iron clusters, they change from genuine parallel couplings with some oxygen atoms around them, to clusters formed by Fe2O units with bridging oxygen atoms and antiparallel couplings, towards clusters of FeO units with parallel couplings in which there are no long bonds between iron atoms, to finally reach oxygen saturation with the formation of oxygen molecules, with both the Fe–O and Fe–Fe distances increasing, and consequently losing stability.
The magnetic phases are closely related to the structural geometry, to the number of atomic oxygens bound at hollow, bridge and top positions (oxygen environment), and to the number of oxygen molecules formed. There is also a relationship of all these structural and magnetic properties with the stability of the oxides, as will be seen below. Fig. 15 shows, for the n = 4 neutral case and for each oxidation ratio m = 1–14, the total and local magnetic moments in each one of the Fe and O atoms of the corresponding geometrical structure. The four magnetic phases described above, m = 1–3, m = 4–8, m = 9–11, and m = 12–14, are indicated with black, red, green and blue colors, respectively, and highlighted in the n = 4 graph of Fig. 13, included also as an inset in Fig. 15. In the first high-spin phase, few oxygen atoms bind on bridge sites of the iron cluster. In the second low-spin phase, almost all (m = 5) or all (m = 4, 6) bridge sites of the cluster are occupied. After that, there are some oxygen atoms (one for m = 7 and two for m = 8) that bind on top positions. In the third high-spin phase, almost all (m = 9) or all (m = 10) top positions are already occupied by oxygen atoms and the first oxygen molecule appears (m = 11). In the fourth phase, two, three and four molecules are bonded (m = 12, 13, 14), until the structure is completely oxygen-saturated at m = 14.
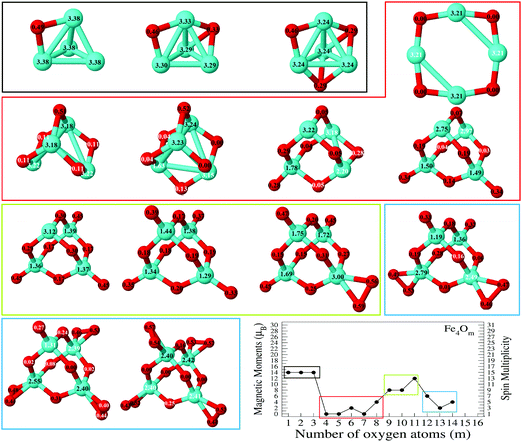 | ||
| Fig. 15 Ground states of neutral Fe4Om (m = 1–14) oxides. The local magnetic moments of Fe and O atoms are indicated. The numbers in black (white) indicate spin up (down) polarization. The n = 4 graph of Fig. 13 is included as an inset. | ||
Besides the different total magnetic moment of each of the four magnetic phases, Fe atoms present different local moments in each one of them. In the first phase, the magnetic couplings are parallel and the high total magnetic moment of the oxide clusters, 14 μB, is due to high spin polarization in the iron atoms. The local magnetic moments, 3.4 (Fe) and 0.5 (O), are similar to those of the FeO dimer (3.4 μB in Fe and 0.6 μB in O). It can be seen from Fig. 14 that the ground state clearly has a high magnetic moment. The compact iron subclusters are preserved (see Fig. 6) and the Fe–Fe couplings are parallel, like in the bare Fe clusters. The oxygen atoms bind on some bridge or hollow positions. In the second phase, the low magnetic moment is due to high spin-polarization (about 3.2 μB, or 1.5–1.7 μB for iron atoms with top oxygen atoms) but with antiparallel couplings. Oxygen atoms that bind on bridge iron atoms with parallel coupling are, practically, magnetically frustrated. In this magnetic phase, most of the bridge positions (m = 5) or all (m = 4, 6) of the iron subcluster are occupied. The m = 4 oxide shows antiparallel coupling between the four iron atoms, with all oxygen atoms magnetically frustrated. We highlight the n = 5–6 low-spin oxides, where the iron subclusters are still preserved although more open (Fig. 6). Their ground states have clearly a low-spin character, as can be seen from Fig. 14. They can be seen as sub-divided into two Fe2O parts with parallel couplings, one part with spin up and the other one with spin down, and, consequently, with an antiparallel coupling between them; the oxygen atoms that are between these two sub-parts have zero, m = 5, or almost zero magnetic moment, m = 6 (a spin isomer with zero magnetic moment is at 0.04 eV, see Fig. 14). Both iron oxides with all bridge positions occupied by oxygen (m = 4, 6) present maxima in the second differences in energy, which reflects their high relative stability, and the m = 6 oxide has also the maximum value of the second energy difference. Then, for m = 7, an oxygen atom binds on top positions and for m = 8 the total magnetic moment increases (4 μB) and the energy difference between the low and high magnetic moment spin isomers becomes smaller (see Fig. 14). In the third phase, a reentrance of the magnetic moment is found, which is an unexpected trend in transition-metal oxides. The high magnetic moment comes from parallel couplings, but iron atoms have low local magnetic moment (low spin polarization region). The local moments of iron are lower than those of previous phases as a consequence of its high oxygen coordination (similarly to FeOm studied in the second section), and decrease from 3.1 μB to 1.3 μB, the value reached by those iron atoms with oxygen bound at top positions. Also, the local magnetic moments of oxygen atoms become lower when there are oxygen atoms bound at top positions. A minimum value of the FeO distance occurs at m = 10, and the local moments of oxygen (0.3–0.4 μB) are closer to that in the FeO unit (0.6 μB). FeO units become more preponderant. In addition, a compact iron subcluster can not be identified (see Fig. 6). At this third high-spin phase, iron oxides are more similar to clusters of FeO units with parallel couplings bonded by oxygen atoms than to iron clusters with adsorbed oxygen atoms like in the first high-spin phase. We highlight the Fe4O10 oxide, which, having a high oxidation ratio, shows parallel couplings and a total magnetic moment of 8 μB. Fe4O10 presents a maximum in the second total energy difference. This iron oxide has all possible bridge and top positions occupied. Finally, in the fourth low-spin phase, two ferromagnetic oxide subclusters can be again identified, with magnetic moments in opposite directions, and the oxygen atoms, located between those sub-clusters, are magnetically frustrated. There is not an iron subcluster. Oxygen binds molecularly, so that Fe coordinates with O2, which weakens the Fe–O bonds (because the oxygen bond of O2 is strong). FeO units become less preponderant and the Fe–O distance increases, reaching similar values to those of the first phase. We highlight Fe4O14, with all bridge and top positions occupied and four oxygen molecules, with a clearly low-spin ground state with antiparallel couplings (Fig. 14). Low-lying spin isomers with 0 μB and 2 μB, at 0.06 eV and 0.02 eV, respectively, are found.
Based on the above results, we identify three particularly interesting Fe oxide clusters due to their high global and relative stability that exhibit different magnetic characters. The first two are the planar (4,4) oxide, with Fe2O units antiferromagnetically coupled by magnetically frustrated oxygens (indirect exchange), and (4,6), a tetrahedral iron motif also formed by two Fe2O units antiparallel coupled by four oxygens, practically magnetically frustrated. The spin isomer (0.04 eV from the ground state) has the four oxygen atoms magnetically frustrated and the two units with identical up and down magnetic polarization. Both the (4,4) and (4,6) oxides have all bridge positions occupied by oxygen atoms. Additionally, the third is the high-spin (4,10) oxide (8 μB), which has a high oxidation ratio and all bridge and top positions occupied, where FeO units are more important and the Fe subcluster is broken.
Fig. 16 shows the total density of states (DOS), and the partial contribution of iron atoms (cyan line) and oxygen atoms (red lines), for neutral Fe4Om oxides and for each oxidation ratio (m = 1–14). Vertical lines indicate the Fermi level. The magnetic behavior of the Fe4Om oxides discussed above is reflected in the DOS. The four magnetic phases are well differentiated. For m = 1–3, the parallel couplings are remarkable. The contribution of oxygen is higher at m = 3, although most of the contribution in this first high-spin phase comes from the iron subcluster. For m = 4, an antiferromagnetic state can be observed with identical up and down contributions of both iron and oxygen. At this oxidation ratio, a remarkable change in the density of states happens, resulting in a similar density of states for n = 5–8, with clear antiparallel couplings. The density of states changes dramatically for m = 9–10, with oxygen atoms bound on top positions of the iron atoms, with parallel couplings, but where, unlike the first phase, the contribution of oxygen to the total density is much higher. For m = 11, the oxidation ratio where oxygen starts to bind molecularly, the density of states changes, as a consequence of the antiparallel couplings of the last phase, and, for m = 13–14, the existence of highly coordinated and oxygen-saturated iron atoms is reflected.
Therefore, for n = 5, we highlight four clusters due to their high stability, with different magnetic behaviour: the high-spin (5,4) oxide (first magnetic phase, μ = 18 μB), the low-spin (5,6) hexahedral-like structure with six bridging oxygens and (5,8) pyramid-like structure with all bridge positions occupied by oxygen (second magnetic phase μ = 2 μB), and the high-spin (5,13) pyramid-like structure with oxygen atoms occupying all bridge and top positions (third magnetic phase, μ = 10 μB).
As for the other sizes, the reentrance of the magnetic moment also takes place for n = 6 and m = 15 with all bridge and top positions, of an already open triangular prism, occupied by oxygen atoms (for the cationic oxide the ferromagnetic isomer is at 0.03 eV with 7 μB). Then, when the first oxygen molecule binds to an iron atom, only the cationic oxide keeps a high total moment, while the neutral and the anion become again low-spin oxides.
In general and summarizing subsection C, we have found related effects between the geometrical structures, oxygen environment and magnetism. We have found a reentrance of the magnetic moment at high oxidation ratios and we have identified certain oxides (4,10)0/±, (5,13)0/− and (6,15)0/− with parallel couplings and a considerably large total magnetic moment, as well as high relative stability.
4 Conclusions
The connection between the structural patterns and magnetic properties of FenOm0/± (n = 1–6) oxide clusters has been investigated by means of DFT-GGA calculations that allowed us to compare the fragmentation channels of cationic oxides with experimental results so as to confirm plausible geometrical arrangements. The ground state structures have been obtained by testing a large number of initial geometries and different oxygen environments and optimizing them by means of conjugate gradients. Those initial geometries were constructed (i) as planar and three dimensional arrangements of FeO units; (ii) as small pure iron clusters covered with consecutive oxygen atoms and molecular oxygen absorption for the highest oxidation ratios; and (iii) with the help of Fukui functions to locate the most nucleophilic regions to be covered by oxygen. A rich map of structural and spin isomers is found, for each of the states of charge, once a detailed computational study has been done taking into account different spin isomers with parallel and antiparallel arrangements for each of the geometric isomers with different oxygen environments. For n = 1, the results are in agreement with previous calculations, showing a decrease of the magnetic moment of the iron atom upon addition of oxygen, with an important effect of the added or subtracted charge. For n = 2–3 the ground state structures are planar and, especially at low oxidation ratios, the charge has also an important influence. For n = 4–6 the ground state structures are three dimensional (3D) with tetrahedral (n = 4), pyramidal and hexahedral (n = 5), decahedral, octahedral (n = 6) and zincblende-like geometries as the cluster size increases.Due to the strong iron–oxygen bonding, there is a clear tendency to maximize the number of iron–oxygen bonds and, as consequence of the electron transfer from iron to oxygen atoms, a uniform oxygen distribution is found. Oxygen atoms preferably occupy bridge or hollow sites, and when all sites are saturated, they tend to bond on top positions. Further oxidation takes place through molecular adsorption. As the oxygen content increases, the iron–iron bond weakens, due to the charge transfer from iron to oxygen, which is reflected in the increasing Fe–Fe bond length. Consequently, from a certain size there is no longer an iron subcluster surrounded by oxygen, and FeO units become more preponderant. This fact is reflected in minimum values of FeO distances when all bridge and top positions are occupied. The binding energy increases faster at low oxidation ratios. Once molecular adsorption takes place, the FeO distances increase, the Fe–Fe distances being at the same time very high, and thus the binding energy increases slowly. For cationic oxides, the fragmentation channels of these clusters are obtained and compared with experimental measurements of photofragmentation, reproducing the main features of experiments and providing support to our calculated structural geometries and energetic stabilities.
Interrelated effects between the geometrical structures, oxygen environment, magnetism and stability of iron oxides, with an important effect of the charge, especially on the stability, result in the finding of very stable low-spin (with more open iron subclusters), and very stable high-spin iron oxide nanoparticles (with a broken iron subcluster), both with high oxidation states. The total magnetic moment of iron oxides reflects the couplings between local magnetic moments of different sites. Iron atoms preserve their high local magnetic moment as long as the oxidation ratio is low. When the oxygen content increases, and all or almost all bridge sites are occupied, the iron couplings become antiparallel. The oxidation ratio at which oxygen atoms start to bind on top positions results in a small energy difference between the high-spin and low-spin isomers. Moreover, the local magnetic moment of iron atoms with oxygen bound on top strongly decreases. When almost all or all top positions are occupied by oxygen, the local moments of iron atoms are about 1.4 μB, but the couplings become again parallel and, surprisingly, oxide clusters with high oxidation ratios and with high magnetic moments are found. Finally, at very high oxidation ratios, oxygen molecules cause the iron oxides to become antiferromagnetic, and the binding energy to decrease. The effect of the charge excess or deficiency on the magnetic properties becomes more important at those oxidation ratios between high and low spin phases where spin isomers (with parallel and antiparallel couplings) could coexist.
The positive peaks in the second energy difference show the most stable oxides. When all bridge positions or most of them are occupied, the maxima correspond to clear oxide clusters with parallel coupling, whereas when all bridge and top positions are occupied, the maxima correspond to clear magnetic ones. This means that, despite the high degree of oxidation, certain oxide clusters which are very stable retain a high magnetic moment. We have found a reentrance of the magnetic moment never reported before for iron oxide clusters, to our knowledge. We have identified certain oxides (4,10)0/±, (5,13)0/− and (6,15)0/− with parallel couplings and a considerably large total magnetic moment, as well as high relative stability, an interesting result in the context of magnetic grain design. These magnetic properties and the bio-compatibility of iron oxide nanoparticles with high binding energy might be interesting also in nanomedicine. The large moment of these high-spin oxides is due to the promotion of parallel magnetic couplings, despite their significant oxidation ratio, an unavoidable fact in environmental conditions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Spanish Ministry of Economy and Competitiveness (Grant PGC2018-093745-B-I00), Junta de Castilla y León (Project No. VA124G18). R.H.A-T acknowledges the fellowships (E-47-2019-0197368) from the University of Valladolid.References
- Y. Bao, T. Wen, A. C. S. Samia, A. Khandhar and M. Krishnan, Magnetic nanoparticles: material engineering and emerging applications in lithography and biomedicine, J. Mater. Sci., 2016, 51, 513–553 CrossRef CAS PubMed.
- J. Xie, J. Huang, X. Li, S. Sun and X. Chen, Iron oxide nanoparticle platform for biomedical applications, Curr. Med. Chem., 2009, 16(10), 1278–1294 CrossRef CAS PubMed.
- M. Namdeo, S. Saxena, R. Tankhiwale, M. Bajpai, Y. M. Mohan and S. K. Bajpai, Magnetic nanoparticles for drug delivery applications, J. Nanosci. Nanotechnol., 2008, 8(7), 3247–3271 CrossRef CAS.
- F. Gazeau, M. Levy and C. Wilhelm, Optimizing magnetic nanoparticle design for nanothermotherapy, Nanomedicine, 2008, 3(6), 831–844 CrossRef CAS.
- P. Reimer and T. Balzer, Ferucarbotran (Resovist): a new clinically approved RES-specific contrast agent for contrast-enhanced MRI of the liver: properties, clinical development, and applications, Eur. Radiol., 2003, 13(6), 1266–1276 CrossRef PubMed.
- K. M. Krishnan, Biomedical nanomagnetics: a spin through possibilities in imaging, diagnostics, and therapy, IEEE Trans. Magn., 2010, 46(7), 2523–2558 CAS.
- H. You, W. Shang, X. Min, J. Weinreb, Q. Li and M. Leapman, et al., Sight and switch off: Nerve density visualization for interventions targeting nerves in prostate cancer, Sci. Adv., 2020, 6(6), eaax6040 CrossRef CAS PubMed.
- H. Wu, S. R. Desai and L.-S. Wang, Observation and Photoelectron Spectroscopic Study of Novel Mono- and Diiron Oxide Molecules: FeOy− (y = 14) and Fe2Oy− (y = 15), J. Am. Chem. Soc., 1996, 118(22), 5296–5301 CrossRef CAS.
- L.-S. Wang, H. Wu and S. R. Desai, Sequential Oxygen Atom Chemisorption on Surfaces of Small Iron Clusters, Phys. Rev. Lett., 1996, 76(25), 4853–4856 CrossRef CAS PubMed.
- J. B. Griffin and P. B. Armentrout, Guided ion-beam studies of the reactions of Fen+ (n = 1–18) with CO2: Iron cluster oxide bond energies, J. Chem. Phys., 1997, 107(14), 5345–5355 CrossRef CAS.
- J. B. Griffin and P. B. Armentrout, Guided ion beam studies of the reactions of Fen+ (n = 2–18) with O2: Iron cluster oxide and dioxide bond energies, J. Chem. Phys., 1997, 106(11), 4448–4462 CrossRef CAS.
- D. Schroder, P. Jackson and H. Schwarz, Dissociation Patterns of Small FemOn+ (m = 1–4, n≤6) Cluster Cations Formed Upon Chemical Ionization of Fe(CO)5O2 Mixtures, Eur. J. Inorg. Chem., 2000, 1171–1175 CrossRef CAS.
- K. S. Molek, C. Anfuso-Cleaty and M. A. Duncan, Photodissociation of Iron Oxide Cluster Cations, J. Phys. Chem. A, 2008, 112(39), 9238–9247 CrossRef CAS PubMed 2000, 117-1175.
- M. Li, S. R. Liu and P. B. Armentrout, Collision-induced dissociation studies of FemOn+: Bond energies in small iron oxide cluster cations, FemOn+ (m = 1–3, n = 1–6), J. Chem. Phys., 2009, 131(14), 144310 CrossRef.
- M. Tomonari and H. Takewaki, The ground, excited, and negatively ionized states of Fe2, J. Chem. Phys., 1988, 88(3), 1828–1836 CrossRef CAS.
- T. Noro, C. Ballard, M. H. Palmer and H. Tatewaki, The ground state of the Fe2 molecule, J. Chem. Phys., 1994, 100(1), 452 CrossRef CAS.
- O. Hubner and J. Sauer, Confirmation of and ground states of 9Σg− and 8Σu− ground states of Fe2 and Fe2 by CASSCF/MRCI, Chem. Phys. Lett., 2002, 358(5–6), 442–448 CrossRef CAS.
- C. W. Bauschlicher and A. Ricca, Can all of the Fe2 experimental results be explained, Mol. Phys., 2002, 101(1), 93–98 Search PubMed.
- C. W. Bauschlicher, Maitre. Theoretical study of the first transition row oxides and sulfides, Theor. Chim. Acta, 1995, 90(3), 189–203 CrossRef CAS.
- C. W. Bauschlicher, S. R. Langhoff and A. Komornicki, The calculation of the dipole moments of NiH, TiO, and FeO, Theor. Chim. Acta, 1990, 77(4), 263–279 CrossRef CAS.
- H. Shiroishi, T. Oda, I. Hamada and N. Fujima, Structure and magnetism on iron oxide clusters FenOm (n = 1–5): Calculation from first principles, Eur. Phys. J. D, 2003, 24(1), 85–88 CrossRef CAS.
- H. Shiroishi, T. Oda, I. Hamada and N. Fujima, Structure and magnetism of anion iron oxide clusters, FenOm− (n = 3,4), Polyhedron, 2005, 24(16–17), 2472–2476 CrossRef CAS.
- A. Erlebach, C. Hühn, R. Jana and M. Sierka, Structure and magnetic properties of (Fe2O3)n clusters (n = 1–5), Phys. Chem. Chem. Phys., 2014, 16(48), 26421–26426 RSC.
- M. Ju, J. Lv, X.-Y. Kuang, L.-P. Ding, C. Lu, J.-J. Wang, Y.-Y. Jin and G. Maroulis, Systematic theoretical investigation of geometries, stabilities and magnetic properties of iron oxide clusters (FeO)n (n = 1–8, = 0,±1): insights and perspectives, RSC Adv., 2015, 5(9), 6560–6570 RSC.
- N. M. Reilly, J. U. Reveles, G. E. Johnson, J. M. del Campo, S. N. Khanna, A. M. Ko1ster and A. W. Castleman Jr., Experimental and Theoretical Study of the Structure and Reactivity of FemOn+ (m = 1,2; n = 15) with CO, J. Phys. Chem. C, 2007, 111(51), 19086–19097 CrossRef CAS.
- N. M. Reilly, J. U. Reveles, G. E. Johnson, S. N. Khanna and A. W. Castleman Jr., Experimental and Theoretical Study of the Structure and Reactivity of Fe1–2O≤6− Clusters with CO, J. Phys. Chem. A, 2007, 111(20), 4158–4166 CrossRef CAS PubMed.
- K. Koyama, S. Kudoh, K. Miyajima and F. Mafune, Dissociation energy for O2 release from gas-phase iron oxide clusters measured by temperature-programmed desorption experiments, Chem. Phys. Lett., 2015, 625, 104–109 CrossRef CAS.
- Y. Wang, Q. Chen and J. Wang, Ab Initio Study of Structure and Magnetism of Late Transition Metal Oxide TMnOm Clusters (TM = Fe, Co, Ni, n = 1,2, m = 1–6), J. Nanosci. Nanotechnol., 2012, 12(8), 6488–6493 CrossRef CAS.
- S. Datta and B. Rahaman, First principles study of electronic structure for cubane-like and ring-shaped structures of M4O4, M4S4 clusters (M = Mn, Fe, Co, Ni, Cu), AIP Adv., 2015, 5(11), 117231 CrossRef.
- P. Wang, M. Qiu, X. Lu, W. Jin, C. Li, G. Lefkidis and W. Hubner, First-principles study of spin properties and laser-induced ultrafast spin dynamics in transition-metal oxide clusters TM3O30/+ (TM = Fe,Co, and Ni), Phys. Rev. B, 2020, 101(10), 104414 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garc a, J. Junquera, P. Ordejón and D. J. Sánchez-Portal, The SIESTA method for ab initio order-N materials simulation, J. Phys.: Condens. Matter, 2002, 14(11), 2475–2779 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS.
- N. Troullier and J. L. Martins, Efficient pseudopotentials for plane-wave calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(3), 1993–2006 CrossRef CAS.
- L. Kleinman and D. M. Bylander, Efficacious Form for Model Pseudopotentials, Phys. Rev. Lett., 1982, 48(20), 1425–1428 CrossRef CAS.
- S. G. Louie, S. Froyen and M. L. Cohen, Nonlinear ionic pseudopotentials in spin-density-functional calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26(4), 1738–1742 CrossRef CAS.
- P. Fuentealba, P. Pérez and R. Contreras, On the condensed Fukui function, J. Chem. Phys., 2000, 113(7), 2544–2551 CrossRef CAS.
- W. Yang and R. G. Parr, Hardness. Hardness, softness, and the fukui function in the electronic theory of metals and catalysis, Proc. Natl. Acad. Sci. U. S. A., 1985, 82(20), 6723–6726 CrossRef CAS PubMed.
- P. Geerlings, F. De Proft and W. Langenaeker, Conceptual Density Functional Theory, Chem. Rev., 2003, 103(5), 1793–1874 CrossRef CAS PubMed.
- P. A. Montano and G. K. Shenoy, EXAFS study of iron monomers and dimers isolated in solid argon, Solid State Commun., 1980, 35(1), 53–56 CrossRef CAS.
- K. Purdum, et al., Extended-x-ray-absorption-fine-structure study of small Fe molecules isolated in solid neon, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25(7), 4412–4417 CrossRef.
- M. Casula, M. Marchi, S. Azadi and S. Sorella, A consistent description of the iron dimer spectrum with a correlated single-determinant wave function, Chem. Phys. Lett., 2009, 477(4–6), 255–258 CrossRef CAS.
- G. L. Gutsev, S. N. Khanna, B. K. Rao and P. Jena, Electronic Structure and Properties of FeOn and FeOn− Clusters, J. Phys. Chem. A, 1999, 103(29), 5812–5822 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure: IV, Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979 Search PubMed.
- S. G. Lias, J. E. Bartmess, J. F. Leibman, J. L. Levin, R. D. Levin and W. G. Mallard, Gas-phase ion and neutral thermochemistry, J. Phys. Chem. Ref. Data, 1988, 17(Suppl. No), 1 Search PubMed.
- S. Smoes and J. Drowart, Determination of the Dissociation Energies of Gaseous Iron Monoxide and Manganese Monoxide by the Mass Spectrometric Knudsen Cell Method, in Modern High Temperature Science, ed. J. L. Margrave, Humana Press, 1984, ch. 17. Available from: 10.1007/978-1-4612-5180-42 Search PubMed.
- A. J. Merer, Spectroscopy of the Diatomic 3d Transition Metal Oxides, Annu. Rev. Phys. Chem., 1989, 40, 407–438 CrossRef CAS.
- E. R. Fisher, J. L. Elkind, D. E. Clemmer, R. Georgiadis, S. K. Loh, N. Aristov, L. S. Sunderlin and P. B. Armentrout, Reactions of fourthperiod metal ions (Ca+Zn+) with O2: Metal-oxide ion bond energies, J. Chem. Phys., 1990, 93(4), 2676 CrossRef CAS.
- S. K. Loh, L. Lian and P. B. Armentrout, Oxidation reactions at variably sized transition metal centers: Fen+ and Nbn+ + O2 (n = 1–3), J. Chem. Phys., 1989, 91(10), 6148 CrossRef CAS.
- R. H. Aguilera-del-Toro, F. Aguilera-Granja, L. C. Balbás and A. Vega, Structure, fragmentation patterns, and magnetic properties of small nickel oxide clusters, Phys. Chem. Chem. Phys., 2017, 19(4), 3366–3383 RSC.
Footnotes |
| † PACS 75.75 + a; 36.40Cg; 75.30.Pd; 75.50.-y. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp03795h |
| This journal is © the Owner Societies 2021 |