Quantum electronic control on chemical activation of methane by collision with spin–orbit state selected vanadium cation
Cheuk-Yiu
Ng
 *a,
Yuntao
Xu
*a,
Yuntao
Xu
 a,
Yih-Chung
Chang
a,
Yih-Chung
Chang
 a,
Anna
Wannenmacher
a,
Matthew
Parziale
a and
P. B.
Armentrout
b
a,
Anna
Wannenmacher
a,
Matthew
Parziale
a and
P. B.
Armentrout
b
aDepartment of Chemistry, University of California, Davis, CA 95616, USA. E-mail: cyng@ucdavis.edu
bDepartment of Chemistry, University of Utah, Salt Lake City, UT 84112, USA
First published on 18th December 2020
Abstract
By coupling a newly developed quantum-electronic-state-selected supersonically cooled vanadium cation (V+) beam source with a double quadrupole-double octopole (DQDO) ion–molecule reaction apparatus, we have investigated detailed absolute integral cross sections (σ's) for the reactions, V+[a5DJ (J = 0, 2), a5FJ (J = 1, 2), and a3FJ (J = 2, 3)] + CH4, covering the center-of-mass collision energy range of Ecm = 0.1–10.0 eV. Three product channels, VH+ + CH3, VCH2+ + H2, and VCH3+ + H, are unambiguously identified based on Ecm-threshold measurements. No J-dependences for the σ curves (σ versus Ecm plots) of individual electronic states are discernible, which may indicate that the spin–orbit coupling is weak and has little effect on chemical reactivity. For all three product channels, the maximum σ values for the triplet a3FJ state [σ(a3FJ)] are found to be more than ten times larger than those for the quintet σ(a5DJ) and σ(a5FJ) states, showing that a reaction mechanism favoring the conservation of total electron spin. Without performing a detailed theoretical study, we have tentatively interpreted that a weak quintet-to-triplet spin crossing is operative for the activation reaction. The σ(a5D0, a5F1, and a3F2) measurements for the VH+, VCH2+, and VCH3+ product ion channels along with accounting of the kinetic energy distribution due to the thermal broadening effect for CH4 have allowed the determination of the 0 K bond dissociation energies: D0(V+–H) = 2.02 (0.05) eV, D0(V+–CH2) = 3.40 (0.07) eV, and D0(V+–CH3) = 2.07 (0.09) eV. Detailed branching ratios of product ion channels for the titled reaction have also been reported. Excellent simulations of the σ curves obtained previously for V+ generated by surface ionization at 1800–2200 K can be achieved by the linear combination of the σ(a5DJ, a5FJ, and a3FJ) curves weighted by the corresponding Boltzmann populations of the electronic states. In addition to serving as a strong validation of the thermal equilibrium assumption for the populations of the V+ electronic states in the hot filament ionization source, the agreement between these results also confirmed that the V+(a5DJ, a5FJ, and a3FJ) states prepared in this experiment are in single spin–orbit states with 100% purity.
I. Introduction
Methane (CH4) is the simplest and most widespread alkane on earth. As the main component of natural gas that has been used as a combustion fuel, CH4 is also one of the main non-CO2 green-house gases, which is reported to be about 30 times more potent than CO2 in the measure of global warming potential.1 In addition, CH4 is found on other planets and satellites in the solar system,2,3 such as Mars and Titan; and CH4 clathrates are one of the important carbon-containing ices in comets, interstellar space, and outer solar systems.4,5As one of the four main C1 molecules on earth,6 CH4 has been proposed as a useful chemical feedstock to produce more-valued chemical species and intermediates, including methylene radical (CH2) and methanol molecule (CH3OH). Nevertheless, the activation and oxygenation of the C–H bond of CH4 have been categorized as one of the “Holy Grails” in chemistry,7 Due to its notorious thermodynamic stability and chemical inertness, the understanding of detailed mechanisms for chemical activation and functionalization of CH4 remains far from completion.8,9 Currently, large scale applications of CH4 in industry have mainly been concerned with the conversion of CH4 to H2, which can then be used for the synthesis of straight-chain hydrocarbons via the Fischer–Tropsch process,10,11 However, this method is highly energy intensive and thus expensive, making the development of new pathways for CH4 activation with lower costs extremely desirable.
For decades, transition metal (TM) cations have been shown to exhibit very promising unique effects on activation of hydrocarbons including CH4.12–15 As early as in 1979, TM cations were reported to efficiently cleave alkanes by breaking the C–C and C–H bonds.16 Since then, a great wealth of both experimental and theoretical works on CH4 activation have been published; and some summaries of these studies can be found in ref. 13, 15 and 17 The research of CH4 activation has attracted good attention because it is a prototypical system for alkane activation as well as being abundant on earth.18
In 1987, the Armentrout group reported a heroic experiment concerning chemical reactivity dependences upon translational and electronic energy for the V+ + CH4 reaction using a guided ion beam (GIB) tandem mass spectrometer.19 The effects of electronic energy were probed by varying the ion source conditions, such as the temperature (T) of the hot surface ionization (SI) filament and the electron ionization energy of the electron ionizer. However, due to the lack of energy resolution and the state-specific detection method, quantitative absolute integral cross section (σ) measurements for individual V+ spin–orbit electronic states were not achieved, although approximate state-specific σ determinations were made. Nevertheless, based on observations of the GIB experiment, it was suggested that the mechanism for the activation of CH4 by V+ preferentially proceeds through a triplet spin V+ inserted [H–V+–CH3] intermediate, favoring the conservation of total electron spin.
In 1997, the Brucat group reported a photodissociation study of V+CH4 ion–molecule complexes formed in a laser-driven-plasma supersonic beam source.20 The majority of complexes thus formed was believed to have the structure of the charge-induced dipole ion–molecule complex [V+–CH4]. However, the authors could not preclude the existence of a minor amount with the structure of the V+ inserted [H–V+–CH3] intermediate.
A density functional (DFT) theoretical study was later performed for the V+ + CH4 reaction system by Sicilia and Russo in 2002, which has provided some valuable insights into the activation mechanism,21 and agreed with the qualitative potential energy surface originally suggested by Aristov and Armentrout.19 The DFT calculation suggested that three reaction intermediates may be formed along the reaction coordinates: the first one is the ion-induced-dipole complex [V+–CH4], which may evolve to the inserted intermediate [H–V+–CH3]. This second intermediate, in which the C–H bond of CH4 has been activated, was expected to lead to the formation of VH+ and VCH3+. The last intermediate may be the [H2–V+–CH2] structure formed via rearrangement of the other two intermediates, leading to the formation of the VCH2+ + H2 product channel. The mechanism, invoking the conservation of total electron spins, is also revealed in the DFT theoretical study.
In 2009, the Bohme group reported a systematic kinetic study on the reactions between CH4 and 59 atomic metal cations, which included the V+ ion at room temperature prepared by using a plasma selected ion flow tube tandem mass spectrometer.17 In these reactions, internal excitations of the reactant TM cations were supposed to be quenched down to the ground state by collisions with the carrier gas, such as helium. However, the authors admitted that the exact electronic states and the relative populations of the reactant TM ions after the collisions are uncertain. This may due to different relaxation mechanisms involved for different long-lived electronically excited TM ions.22–24 To the best of our knowledge, no σ measurements with reactant V+ ions prepared in single electronic states, especially in excited V+ states, have been reported previously for the V+ + CH4 reaction. The successful search of quantum electronic state controls of chemical reactivity of V+ ion in its excited electronic states is expected to promote new reaction pathways of catalytic relevance.
Recently, we have developed a two-color visible-ultraviolet (VIS-UV) laser pulsed field ionization-photoion (PFI-PI) detection method, which can be used to prepare V+ ions in 13 different spin–orbit coupled electronic states, a5DJ (J = 0–4), a5FJ (J = 1–5), and a3FJ (J = 2–4), with high laboratory kinetic energy (Elab) resolution or narrow ΔElab spread for V+ ion. This development has made possible systematic chemical reactivity measurements of quantum state-selected V+ ions with simple atmospheric gases.25 Combining the VIS-UV laser PFI-PI ion source with the double quadrupole-double octopole (DQDO) ion–molecule reaction apparatus, we have previously investigated detailed chemical reactivity of V+ ion by activating CO2, D2 and O2 as a function of electronic state and kinetic energy of V+ ion.24,26,27 The main observation of these latter experiments is that the triplet electronic states (a3F2–4) are much more reactive in activating CO2 and D2 than the other two quintet electronic states, in agreement with the more qualitative determinations of the Armentrout group on the same systems.23,28 No J dependences are observed for the σ values of individual V+[a5DJ (J = 0, 2), a5FJ (J = 1, 2), and a3FJ (J = 2, 3)] electronic states to CO2 and D2 activation reaction, while the J-state effect for the V+(a3F2,3) + O2 reactions are unambiguously identified,29 where J is the total angular momentum quantum number of the spin–orbit state of V+ ion. Furthermore, the σ curves (σ versus Ecm plots) observed show that both electronic and Ecm energies of the reaction can effectively couple with the reaction coordinates, allowing the Ecm-threshold measurements to yield reliable thermochemical properties, such as 0 K bond dissociation energies (D0's) and heats of formation (ΔfH0's) for TM containing molecular species, many of which are still unavailable in the literature. To examine whether the dominant reaction mechanism observed in the V+ + D2(CO2) reaction systems is also valid for the V+ + CH4 reaction is a major motivation of the present quantum electronic state selected study.
Here, we present the σ values for the V+ + CH4 reaction when V+ ions are prepared into single spin–orbit electronic states, covering the Ecm range from 0.1 to 10.0 eV. Detailed dependences of the spin–orbit electronic states and the Ecm on σ values and product branching ratios (BR's) have also been investigated in the present study for the first time. Since the two-color VIS-UV laser PFI-PI method is readily applicable to other TM cation species, this work can also be considered as a demonstration experiment, illustrating that chemical reactivity of TM ions toward hydrocarbons can be readily examined experimentally with TM ions prepared in single, pure electronic states, one spin–orbit state at a time. Thus, the results of this study would serve as a guiding experiment for future state-selected ion–molecule reaction studies involving other TM cations.
II. Experimental considerations
Since the detailed arrangement of the two-color VIS-UV laser PFI-PI ion source and procedures used for σ measurements employing the DQDO ion–molecule reaction apparatus have been reported previously,24,25,30,31 only a brief description is given below.(a) Two-color VIS-UV laser PFI-PI ion source
The VIS-UV laser PFI-PI detection scheme has been recently developed in our group to prepare gaseous V+ ions in one of the thirteen quantum spin–orbit electronic states: a5DJ (J = 0–4), a5FJ (J = 1–5), and a3FJ (J = 2–4) in the form of a pulsed supersonic beam, achieving Ecm values down to thermal energies. The precursor neutral V atom sample, in the form of a pulsed (30 Hz) supersonically cooled atomic beam, is generated by a Smalley-type pulsed laser ablation TM beam source. The laser system used for photo-exciting the neutral V atoms consists of two independently tunable dye lasers pumped by one pulsed Nd:YAG laser operated at 30 Hz. The first dye laser is pumped by the third harmonics of the Nd:YAG laser to generate the VIS output (ω1). The second dye laser is pumped by the second or third harmonics of the same Nd:YAG laser to provide the UV output (ω2) after passing through a frequency doubling crystal. The VIS ω1 and UV ω2 laser beams are then merged into the photoexcitation (PEX) region by using a dichroic mirror. The VIS and UV laser beams perpendicularly intersect the neutral V atom sample in the form of a supersonically cooled V/He seeded beam. The VIS ω1 is fixed to excite the neutral V atoms from the ground state to a selected neutral intermediate state, and the UV ω2 is tunable such that the total photoexcitation frequency of (ω1 + ω2) covers the photoexcitation transition frequencies needed for photoionization from the ground state to the spin–orbit electronic states of interest. High-n (n > 60) Rydberg states of V [V*(n)] converging to the ionic states of interest are ionized by PFI to produce PFI-PIs in one of the V+ [a5DJ (J = 0–4), a5FJ (J = 1–5), and a3FJ (J = 2–4)] spin–orbit J-states.Because prompt ions without pure state selection can also be produced along with PFI-PI formation, the most important issue is to reject prompt ions from the PFI-PI beam, and this is achieved as described in detail elsewhere.24–26,30,31 Readers are referred to the two-color laser PFI-PI spectra for V+[a5DJ (J = 0–4)], V+[a5FJ (J = 1–5)], and V+[a3FJ (J = 2–4)] shown in Fig. 8(a), (b), and (c) of ref. 25, respectively. The fully J-resolved PFI-PI spectra observed indicate that the preparation of V+ ion in single quantum spin–orbit electronic states is well achieved.
(b) DQDO ion–molecule reaction apparatus and σ measurements
The DQDO ion–molecule reaction apparatus consists of, in sequential order, a supersonically cooled V atom source produced by pulsed laser ablation of a rotating and translating V-rod, a reactant quadrupole mass filter (QMF), a reaction gas cell situated between two radio frequency (rf)-octopole ion guides, a product QMF, and a Daly-type ion detector.32 The second harmonic output of an Nd:YAG laser operated at 2 mJ and 30 Hz is employed as the ablation laser. The V gaseous plumes formed by ablation are merged into a He gas flow, forming a V/He seeded beam. Cooling of the V atom sample occurs as the V/He seeded gas undergoes supersonic expansion. Charged species, which are also formed by laser ablation, are deflected away from the V/He beam path by a pair of ion repeller plates biased at a sufficiently high DC electric field. In this experiment, the reactant QMF is only used as an ion lens. The dual set of rf-octopoles can be used to extract slow product ions formed inside the gas cell and maintain high ion transmission through the gas cell by applying a small dc field between the two rf-octopoles. The gas cell is connected with an electromagnetic valve for gas filing; and the gas cell pressure is monitored by an MKS Baratron. In this study, the pressure of CH4 in the gas cell is maintained at (1.0 or 2.0) × 10−4 torr, which is low enough to satisfy the thin target conditions.33,34 The product QMF and the modified Daly-type detector form the detection system for reactant and product ions.The σ measurement involves the determination of intensities of the reactant and products ions. Based on the thin target ion-neutral scattering scheme, the σ value can be deduced as [(kT)/(Pl)][ln((I + i)/I)], where k, T, P, l, I, and i represent the Boltzmann constant, the temperature and the pressure of the neutral reactant in the reactant gas cell, the effective length of the gas cell, the intensity of the unreacted reactant V+ ions, and the intensity of the product ions, respectively. Under the thin target conditions, product ions formed by secondary reactions are negligible. All σ curves shown in this work are the averaged results of at least three independent measurements. The run-to-run uncertainties are found in the range of 5–10% and the absolute uncertainties of σ's determined in this work are estimated to be ≤30%.
The Ecm is converted from the laboratory kinetic energy (Elab) by using the formula Ecm = Elab [M/(m+ + M)], where m+ and M represent the masses of V+ ion and CH4 molecule, respectively. As pointed out previously, the thermal motion of neutral CH4 molecules inside the gas cell can give rise to the kinetic energy distribution, which is referred to here as the “thermal broadening” effect. This distribution can significantly affect the Ecm spread or ΔEcm resolution.35 Thus, for energetic measurements, such as bond dissociation energies (D0's) deduced in the studies of the V+ + D2 (CO2, CH4) reactions, we have taken into account the kinetic energy distribution as described below.
III. Results and discussions
(a) Mass spectra
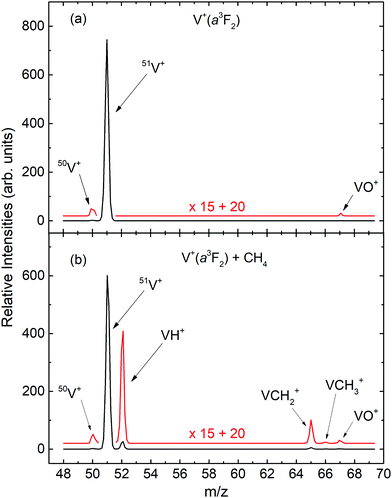
The mass spectra for the quantum spin–orbit electronic state-selected V+(a3F2) ion source and the V+(a3F2) + CH4 reaction are shown as the black curves in Fig. 1(a) and (b), respectively. For both mass spectra, Ecm was set at 2.0 eV. To better view the weak mass peaks with low intensities, the original mass spectra in black are magnified by a factor of 15. The magnified mass spectra thus obtained are shown in red. As shown in Fig. 1(a), the three ion peaks observed at the mass to charge ratios of m/z = 50, 51, and 67 can readily be assigned as 50V+, 51V+, and VO+, respectively. We note that the intensity ratio of the mass peaks for 50V+ and 51V+ are found to be consistent with the known natural abundances of the V+ isotopes.36 Since this mass spectrum for the V+(a3F2) ion source was recorded without CH4 in the reaction gas cell, all the ion peaks, except the one for 51V+, can be considered as background ions.Different from the spectrum of Fig. 1(a), the mass spectrum in Fig. 1(b) exhibits six ion peaks at m/z = 50, 51, 52, 65, 66, and 67, which are marked in Fig. 1(b) as 50V+, 51V+, VH+, VCH2+, VCH3+, and VO+, respectively. We find that the intensity of the m/z = 67 (assigned as VO+) peak of Fig. 1(b) is very similar to that of Fig. 1(a), consistent with its formation from reactions of V+ with trace amounts of O2 or H2O, where the reactions occur with near unit efficiency.29 Since the m/z values for VO+ and VCH4+ are identical, this observation can be taken as evidence that negligible VCH4+ ion–molecule complexes are formed by multiple collision events in the reaction gas cell. The mass spectrum of Fig. 1(b) also shows no evidence for the formation of VCH+ ion. Similar observations were also obtained from the mass spectra recorded with V+ ion prepared in different electronic states at different Ecm values. Therefore, we can conclude that VH+, VCH2+, and VCH3+ ions are identified as the major primary product ions in the present experiment. However, this observation cannot exclude the formation of VCH+ ion. Based on σ measurements presented below, if VCH+ is formed, we estimate its σ value to be about ≤0.001 Å2.
The reaction product channels or states associated with the formation of product ions are listed in reactions (1)–(3), along with the corresponding apparent threshold energies of reaction (ET) observed here at the reactant sample temperature T, which is mostly determined by the thermal energy of neutral methane in this case but also includes the minor ion kinetic energy distribution.
| V+(a5D0) + CH4(X1A1) → VH+(X4Δ) + CH3(X2A2′′) ET = 1.9 ± 0.1 eV | (1) |
| V+(a5D0) + CH4(X1A1) → VCH2+(X3A1) + H2(X1Σg+) ET = 1.2 ± 0.1 eV | (2) |
| V+(a5D0) + CH4(X1A1) → VCH3+(X4B1) + H(2S1/2) ET = 1.8 ± 0.1 eV | (3) |
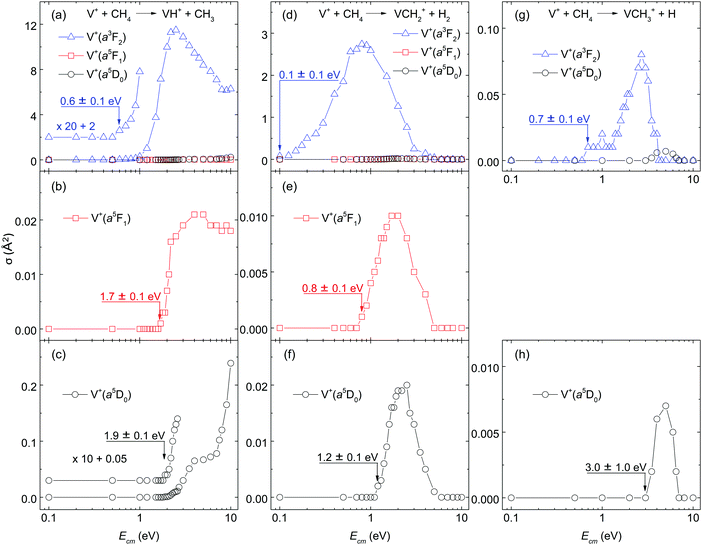
Because of the very low σ(a5D0: VCH3+) and σ(a5F1: VCH3+) values, the Ecm-thresholds for these σ curves cannot be determined with high precision. However, a more precise Ecm-threshold for σ(a5D0: VCH3+) can be determined by adding the electronic energy of 1.1 eV for σ(a3F2: VCH3+) to the measured Ecm-threshold of 0.7 ± 0.1 eV for σ(a3F2: VCH3+), yielding a Ecm-threshold value of 1.8 ± 0.1 eV for the σ(a5D0: VCH3+). This value thus obtained is in marginal agreement with the directly measured Ecm-threshold of 3.0 ± 1.0 eV for the σ(a5D0: VCH3+), after taking into account of the experimental uncertainties. We note that the large Ecm step size (1 eV) used for recording the latter spectrum makes it undesirable for use of precise energetic deductions.
On the basis of the σ(a5F1: VCH2+) measurements of Fig. 2(e), the detection sensitivity of the instrument for σ measurements used is estimated to be 0.001 Å2 for σ(VCH+). Although this experiment cannot exclude VCH+ as a primary product ion, if it is formed, σ(VCH+) is expected to be ≤0.001 Å2. As mentioned above, the pressure of CH4 in the gas cell used in this work was controlled to sufficiently low values in order to minimize multiple-collision events.
(b) Quantum electronic state effects
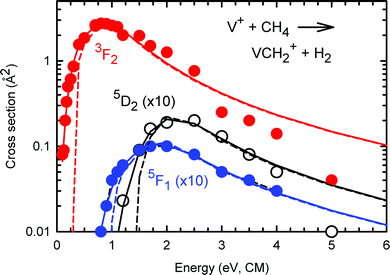
The σ(VH+), σ(VCH2+) and σ(VCH3+) curves are depicted in Fig. 2(a)–(c), Fig. 2(d)–(f), and Fig. 2(g)–(h), respectively. The σ's for the V+(a5D0, a5F1, and a3F2) states are depicted with black circles, red squares, and blue triangles in Fig. 2(a)–(h). For σ(VH+), Fig. 2(a) shows the direct contrast when V+ is prepared in the a5D0, a5F1, and a3F2 spin–orbit states, and Fig. 2(b) and (c) provide a magnified view for σ(a5F1: VH+) and σ(a5D0: VH+), respectively. Similar comparisons for σ(VCH2+) are made in Fig. 2(d) and (f), as well as for σ(VCH3+) in Fig. 2(g) and (h). Since σ(a5F1: VCH3+) was below the detection limit of ≈0.001 Å2 in the Ecm range of interest, no σ(a5F1: VCH3+) curve was recorded.One of the major observations for quantum electronic state effects on chemical reactivity of the V+(a3F2, a5F1, and a5D0) + CH4 reaction system [as shown in Fig. 2(a)–(h)] is that the triplet reactant ion, V+(a3F2), is much more reactive than the quintet reactant ions, V+(a5D0) and V+(a5F1). Specifically, as depicted in Fig. 2(a), σ(a3F2: VH+) is dominantly higher than σ(a5D0: VH+) by 1000, 120, and 25 times at Ecm = 2.0, 5.0, and 10.0 eV, respectively. Similarly, in Fig. 2(d), σ(a3F2: VCH2+) is higher than σ(a5D0: VCH2+) by 65 and 12 times at Ecm = 2.0, and 5.0 eV, respectively; and in Fig. 2(g), the peak value of σ(a3F2: VCH3+) is about 10 times higher than that of σ(a5D0: VCH3+).
Chemical reactivity enhancement observed for the V+(a3F2) + CH4 reaction can be rationalized by the conservation rule of total electron spins.19,21,24,26 The surmised reaction mechanisms are depicted in the schematic energy level diagram of Fig. 3. On the left side of Fig. 3, we show the three reactant states, V+(a3F2) + CH4(X1A1) in red, and V+(a5F1) + CH4(X1A1) and V+(a5D0) + CH4(X1A1) states in black. The three product states, VH+(X4Δ) + CH3(X2A2′′), VCH3+(X4B1) + H(2S1/2), and VCH2+(X3A1) + H2(X1Σg+), identified in this experiment are shown on the right side of Fig. 3 according to their energy order. At higher energies, we also include in Fig. 3 the possible dissociative product channels, V+(a5D0) + CH3(X2A2′′) + H(2S1/2) and VCH2+(X3A1) + H(2S1/2) + H(2S1/2). The lack of precise energetics has limited the inclusion of other possible product states in the energy level diagram. With the exception of the VCH2+(X3A1) + H2(X1Σg+) product state, which can only correlate adiabatically to triplet reactant states, the other product states of Fig. 3 are shown in blue, indicating that they can correlate to both triplet and quintet reactant states.
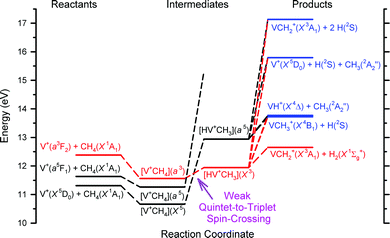 | ||
| Fig. 3 Schematic energy level diagram of the surmised reaction mechanism for the V+ + CH4 reaction system, where the zero energy is set by the energy of the V+(a5D0) ground state. The colors of each component are based upon the total coupled electron spins or multiplicity: red for the triplet, black for the quintet, and purple for both the triplet and quintet. On the left side are the three reactant states, in the middle are the proposed reaction intermediates, and on the right side are the selected product channels. The main reaction mechanism of the V+ + CH4 reaction is interpreted here to favor the conservation of the total electron spins with a “weak quintet-to-triplet spin crossing”, which is marked nominally by the purpled dashed arrow near the middle bottom of the figure. We note that the a5FJ state does not correlate with the [V+CH4](X5) ground state, but rather with another excited state of this species still having quintet spin. This is shown in the potential energy surface in ref. 19. The purple arrow points to the crossing between the triplet and quintet dashed lines. | ||
As suggested by the previous experimental results19 and DFT calculations,21 two kinds of reaction intermediates, [V+CH4] and [HVCH3+], are involved, and each intermediate can be formed in the triplet as well as quintet states. These intermediates are shown in the middle of the energy level diagram of Fig. 3 according to the DFT predictions and are highlighted in colors based on their multiplicities: red for triplet states and black for quintet states. Since the bond dissociation energy of V+–H is much weaker than that of H–CH3, the formation of the [V+CH4] intermediate is not expected to lead to the cleavage of the C–H bond of CH4. Thus, as depicted in Fig. 3, the ion–molecule complex [V+CH4] may proceed to rearrange forming the inserted [HVCH3+] structure.
The key reaction intermediate proposed by the previous DFT calculation21 has an inserted triplet [HV+CH3](X3) structure19,21 at an energy lower than that of the V+(a3F2) + CH4(X1A1) reactant state. Therefore, the V+(a3F2) + CH4(X1A1) reactant state can form the inserted [HV+CH3](X3) intermediate via the [V+CH4](a3) ion–molecule complex without flipping electron spins because both of them are in reaction surfaces with the same multiplicity. Meanwhile, reactant states, V+(a5D0) + CH4(X1A1) and V+(a5F1) + CH4(X1A1), may form a quintet inserted intermediate [HV+CH3](a5) by conserving the total electron spins. Based on the previous experimental and theoretical work,19,21 the [HV+CH3](X3) and [HV+CH3](a5) intermediates are estimated to be 0.6 and 1.6 eV, respectively, higher than the V+(a5D0) + CH4(X1A1) ground reactant state. Meanwhile, V+(a3F2) is known to be about 1.1 eV higher than V+(a5D0). Thus, V+(a3F2) + CH4(X1A1) is both exothermic (by 0.5 eV) and spin-allowed when forming the [HV+CH3](X3) intermediate. In contrast, both reactant states, V+(a5D0) + CH4(X1A1) and V+(a5F1) + CH4(X1A1), are endothermic and spin-forbidden when forming the [HV+CH3](X3) intermediate, which may lead to very low reactivity of V+(a5D0) and V+(a5F1) compared with V+(a3F2) towards the activation of CH4 leading to VCH2+ + H2. The “weak quintet-to-triplet spin crossing” region is marked nominally by the purple dashed arrow in the schematic energy level diagram of Fig. 3. The observation of the product state, VCH2+(X3A1) + H2(X1Σg+), of reaction (2) is a strong manifestation of the “weak electron spin crossing” mechanism. If the reaction of V+ + CH4 strictly follows a “no spin-crossing” reaction mechanism, the triplet product state, VCH2+(X3A1) + H2(X1Σg+), could not have been formed from the quintet reactant states, V+(a5D0) + CH4(X1A1) and V+(a5F1) + CH4(X1A1). We are grateful to a reviewer who has pointed out that the observed product distribution could be explained by a statistical analysis of the lifetime of the V+(CH4) collision complex and the barriers involved for the relevant reaction steps. Because this theoretical analysis is beyond the scope of the present work, we hope that the results of this experiment will interest in such future theoretical studies. We note that at sufficiently high Ecm values, the collision complex dissociation model is likely to be invalid.
The observed Ecm-thresholds of 0.1 ± 0.1 eV for σ(a3F2: VCH2+), 0.8 ± 0.1 eV for σ(a5F1: VCH2+), and 1.2 ± 0.1 eV for σ(a5D0: VCH2+) as shown in Fig. 2(d)–(f) are consistent with the electronic energies of 0.3 eV for V+(a5F1) and 1.1 eV for V+(a3F2) measured with respect to that for V+(a5D0).38 The operation of a “weak quintet-to-triplet spin crossing” allows a very minor fraction of the quintet reactant states, V+(a5D0) + CH4(X1A1) and V+(a5F1) + CH4(X1A1), to “switch” to form the triplet [HV+CH3](X3) intermediate. Thus, the operation of this “weak quintet-to-triplet spin crossing” mechanism is consistent with the fact that both the σ(a5D0: VCH2+) and σ(a5F1: VCH2+) values are very small compared with the σ(a3F2: VCH2+).
As shown in Fig. 2(a)–(f), the ground state V+(a5D0) ion is mildly more reactive with CH4 than the first excited state V+(a5F1) ion, even though the latter has a 0.3 eV higher energy level. Similar reactivity behaviors have been observed in other reaction systems, such as the V+ + CO2 and V+ + D2 reactions.24,26 As discussed previously, the high-spin coupled 4s electron of the V+(a5F1) ion is believed to adversely affect the bonding and chemical reactivity.12,23 The 4s electron is speculated to generate larger repulsive interactions between the V+ ion and CH4 molecule than the 4d electrons when the two moieties approach each other; and the larger repulsive interaction leads to lower reaction probabilities. Notably, even though the V+(a5F1) with CH4 reaction is less efficient than the other states, the Ecm-thresholds for endothermic reactions observed in the present study are consistent among all states. As shown in Fig. 2(b), (c), (e), and (f), the threshold positions for the reactant state of V+(a5F1) + CH4(X1A1) is between 0.2 and 0.4 eV lower than that of V+(a5D0) + CH4(X1A1), which is in accord with the relative energies of the two V+ electronic states. This observation indicates that both the electronic energy of V+ and the kinetic energy Ecm of the V+ + CH4 reaction can couple with the reaction coordinates to facilitate product ion formation. Furthermore, this observation also supports the conclusion that the reactant V+ ions prepared in this experiment are in pure, single electronic states.
(c) Kinetic energy effects
Besides the quantum electronic state effects, the kinetic energy effects for the reaction system of V+ + CH4 can also be observed in Fig. 2(a)–(h). As shown in these figures, all the reaction product channels or states observed for this reaction system are endothermic, which is in agreement with the thermochemistry analysis as the electronic energies of V+ are changed. For the σ(VH+) shown in Fig. 2(a)–(c), in order to display the threshold regions more clearly, the σ(a3F2: VH+) and σ(a5D0: VH+) curves are amplified by a factor of 20 and 10, respectively. As shown in Fig. 2(a)–(c), the σ(a3F2: VH+), σ(a5F1: VH+), and σ(a5D0: VH+) curves exhibit distinct behaviors, indicating that the electronic states of V+ ions play an important role in the formation of this reaction channel. Specifically, σ(a3F2: VH+) has a threshold near Ecm = 0.6 eV and then increases almost exponentially above the threshold. At Ecm = 2.5 eV, σ(a3F2: VH+) reaches the peak value of ≈11.5 Å2. This σ value is quite high for an endothermic reaction, Above 2.5 eV, σ(a3F2: VH+) decreases almost exponentially until Ecm = 8.0 eV. At Ecm = 8.0–10.0 eV, the decreasing trend versus Ecm ends and even starts to increase mildly. Different from σ(a3F2: VH+), σ(a5F1: VH+) has a threshold at Ecm = 1.7 eV and then reaches a peak value of ≈0.02 Å2 near Ecm = 3.0 eV. Above 3.0 eV, σ(a5F1: VH+) is almost flat. The σ(a5D0: VH+) shows similar profiles as that of σ(a5F1: VH+) when Ecm ≤ 3.0 eV except the threshold position is 1.9 eV. However, σ(a5D0: VH+) keeps increasing as Ecm further increases above 3.0 eV. As shown in Fig. 3, when Ecm is high enough to form the quintet [HV+CH3](a5) intermediate, it can lead to the formation of VH+ and VCH3+ without “weak quintet-to-triplet spin crossing”. Thus, σ(VH+) and σ(VCH3+) are expected to be observed at high Ecm values. The trends of σ(a3F2: VH+), σ(a5F1: VH+), and σ(a5D0: VH+) curves shown in Fig. 2(a)–(c), suggest that these curves may consist of a higher and a lower Ecm overlapping components. As the electronic energy is decreased, the lower Ecm component is found to diminish, resulting in the domination of the higher Ecm component of σ(a5D0: VH+) curve as depicted in Fig. 2(c), To understand the dynamics features observed for the σ(VH+) as a function of Ecm and electronic state of V+, rigorous theoretical dynamics calculations based on accurate reaction potential energy surfaces are required.One different feature for σ(VH+) in Fig. 2(a)–(c) compared to σ(VCH2+) in Fig. 2(d)–(f), and σ(VCH3+) in Fig. 2(h) and (g) is that σ(VH+) remains high at Ecm (≥4.0 eV) values. This observation could be the result of different reaction dynamics involved in the formation of different reaction product channels. At sufficiently high Ecm values (≥4.482 eV), the collision-induced dissociation (CID) product channels, such as reaction (4), are expected to occur.
| V+(a5D0) + CH4(X1A1) → V+(a5D0) + CH3(X2A2′′) + H(2S1/2) E0 = 4.482 ± 0.001 eV | (4) |
The formation of the CID product channel in reaction (4) can also be considered as generated from the further dissociation of the excited VH+ and/or VCH3+ ions initially produced in the collision of V+(a5D0) + CH4(X1A1).
The Ecm dependences of σ(VCH2+) are shown in Fig. 2(d)–(f). Similar to the σ(VH+), all three σ(VCH2+) reaction channels are found to be endothermic. The Ecm-thresholds are observed at Ecm = 0.1 ± 0.1, 0.8 ± 0.1, and 1.2 ± 0.1 eV for σ(a3F2: VCH2+), σ(a5F1: VCH2+), and σ(a5D0: VCH2+), respectively. The differences of these Ecm-thresholds observed are consistent with the electronic energies of the corresponding V+ ions. The σ(a3F2: VCH2+), σ(a5F1: VCH2+), and σ(a5D0: VCH2+) curves are found to have similar profiles exhibiting a single peak. The σ(a3F2: VCH2+) starts to rise at its Ecm-threshold of 0.1 ± 0.1 eV, and reaches the peak value of 2.7 Å2 at Ecm ≈ 0.8 eV. Above 0.8 eV, σ(a3F2: VCH2+) decreases rapidly down to zero at Ecm ≈ 5.0 eV. Similarly, σ(a5F1: VCH2+) [σ(a5D0: VCH2+)] reaches the peak value of 0.01 Å2 at Ecm ≈ 2.0 eV [0.02 Å2 at Ecm ≈ 2.5 eV], and decreases quickly down to zero at Ecm ≈ 5.0 eV. The decrease down to zero at high Ecm values could be attributed to the dissociation of excited VCH2+ ions, as well as the CID of CH4, as shown in reaction (4), but these processes occur at higher energies. Rather, as previously described,19 it can be seen that the peaks in the VCH2+ cross sections match the onsets of VH+ + CH3 formation. As the latter channel can be formed by simple bond cleavage from an H–V+–CH3 intermediate, whereas dehydrogenation is entropically more difficult, competition between these channels explains the decline in the VCH2+ + H2 cross sections. Another reaction involving the formation of VCH2+ at high Ecm values is shown in reaction (5). However, because of the high endothermicity of 5.7 eV, the occurrence of this reaction channel is expected to have very low probability.
| V+(a5D0) + CH4(X1A1) → VCH2+(X3A1) + H(2S1/2) + H(2S1/2) E0 = 5.7 ± 0.1 eV | (5) |
The σ(VCH3+) reaction channels are also endothermic, as shown in Fig. 2(g) and (h). Due to the very low reactivity for this reaction channel, only σ(a3F2: VCH3+) and σ(a5D0: VCH3+) have been detected. Attempts were made to measure σ(a5F1: VCH3+) in the Ecm range 0.1 to 10.0 eV, but it was observed that the product VCH3+ ion signal was below the detection limit when the reactant V+ ions were prepared in the a5F1 state. In addition, for the same reason, the σ(a5D0: VCH3+) curve was only measured with very crude Ecm step size of 1.0 eV; and the peak value is observed as ≈0.007 Å2 at Ecm = 5.0 eV. As the highest cross section among the three, σ(a3F2: VCH3+) has an Ecm-threshold of Ecm = 0.7 ± 0.1 eV and reaches a peak value of 0.08 Å2 near Ecm = 2.7 eV. A flat profile for σ(a3F2: VCH3+) is observed at Ecm = 0.7 to 1.3 eV. Above 1.3 eV, σ(a3F2: VCH3+) starts to increase exponentially, which may indicate the formation of a new reaction channel involving VCH3+ populated in an excited state. After reaching the peak value, σ(a3F2: VCH3+) decreases rapidly to zero near Ecm = 4.0 eV. Similar to σ(VCH2+), the decay of σ(VCH3+) can be related to the further dissociation of primary excited VCH3+ product ions.
(d) Spin–orbit J-state effects
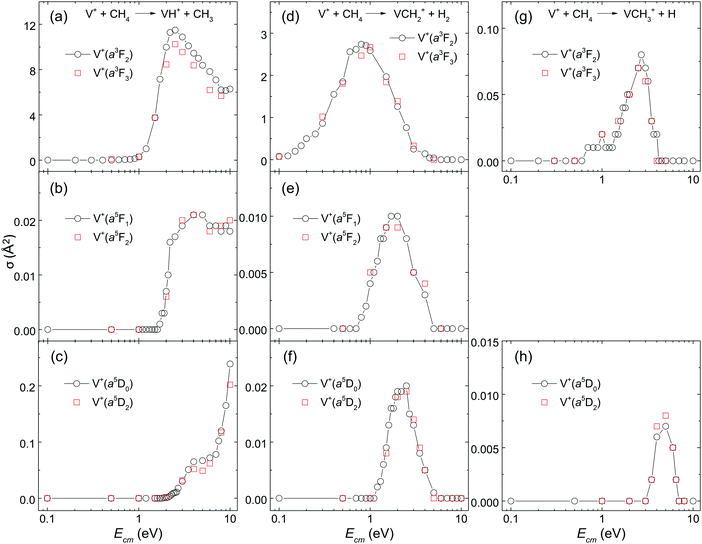
To our best knowledge, no experimental σ measurements for this reaction system with V+ ion prepared in single J states have previously been reported. The main reason for this challenge can be attributed to the lack of general experimental schemes for the preparation of TM cations in the selected J states. From the point of view of fundamental research, unravelling the J-state effects in chemical reactions involving TM cations is closely related to understanding the roles played by different kinds of angular momenta: spin (S), orbital angular momentum (L), and the total angular momentum (J) arising from the spin–orbit coupling.In this work, by preparing reactant V+ ions in single J states, the J-state effects have been examined for the V+ + CH4 reaction. The comparisons of σ(a3FJ: VH+, J = 2 versus 3), σ(a5FJ: VH+, J = 1 versus 2), σ(a5DJ: VH+, J = 0 versus 2), σ(a3FJ: VCH2+, J = 2 versus 3), σ(a5FJ: VCH2+, J = 1 versus 2), σ(a5DJ: VCH2+, J = 0 versus 2), σ(a3FJ: VCH3+, J = 2 versus 3), and σ(a5DJ: VCH3+, J = 0 versus 2) are shown in Fig. 4(a)–(h), respectively. There it can be seen that the two corresponding J states exhibit essentially identical σ curves as shown in the figures. These results clearly show that no discernible J-state effects are observed for this V+ + CH4 reaction system. This conclusion is in agreement with that observed in the recent study of other reaction systems, i.e., V+ + CO2, and V+ + D2,24,26 indicating that the spin–orbit coupling of V+ is weak in the chemical reaction system of V+ + CH4.
This observation of Fig. 4(a)–(h) is also consistent with the “weak quintet-to-triplet spin crossing” mechanism. The spin–orbit coupling is known to facilitate the mixing among electronic states of TM cations with different multiplicities.39,40 Thus, if the spin–orbit coupling is strong enough to mix reaction surfaces with different multiplicities, similar chemical reactivity would be observed for TM cations in electronic states with different multiplicities. However, distinct chemical reactivity is observed in this work when the V+ ion is prepared in single electronic states with different spins. Therefore, this observation is in accordance with weak spin–orbit interaction, suggesting that electron spin S, not J, of the reactant V+ ion is the constraining factor in determining the chemical reactivity of the V+ + CH4 reaction.
It is interesting to note that spin–orbit coupling might have been expected to conserve the total electronic angular momentum J. If this were the case, then the 5D0 level should not couple efficiently with a3F1,2,3, whereas the a5D1,2 levels could. The observation that a5D0 and a5D2 have essentially identical reactivities suggests that molecular angular momentum allows coupling of surfaces of different J.
(e) Branching ratios
The branching ratios (BR's) of the product channels, VH+ + CH3, VCH2+ + H2, and VCH3+ + H, of the reaction system V+(a5D0, a5F1, or a3F2) + CH4(X1A1) in the Ecm range from 0.1 to 10.0 eV are summarized in Table 1 by comparing the relative product VH+, VCH2+, and VCH3+ ion intensities. This comparison reveals that as the Ecm is increased, BR(VH+) increases monotonically from 0% to 100%, while BR(VCH2+) shows the opposite trend. Furthermore, the BR(VCH3+) values are found to have very small values, which are less than 10%.| E cm (eV) | V+(a5D0) + CH4 | V+(a5F1) + CH4 | V+(a3F2) + CH4 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| VH+ | VCH2+ | VCH3+ | VH+ | VCH2+ | VCH3+ | VH+ | VCH2+ | VCH3+ | |
| a The BRs are listed as zero if they are less than 0.01 and as “—” when all three product channels (or states) have zero σ values. | |||||||||
| 0.1 | — | — | — | — | — | — | 0.00 | 1.00 | 0.00 |
| 0.5 | — | — | — | — | — | — | 0.00 | 1.00 | 0.00 |
| 1.0 | — | — | — | 0.00 | 1.00 | 0.00 | 0.10 | 0.89 | 0.01 |
| 1.5 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.65 | 0.34 | 0.01 |
| 2.0 | 0.05 | 0.95 | 0.00 | 0.41 | 0.59 | 0.00 | 0.88 | 0.11 | 0.01 |
| 2.5 | 0.33 | 0.67 | 0.00 | 0.68 | 0.32 | 0.00 | 0.93 | 0.06 | 0.01 |
| 3.0 | 0.70 | 0.30 | 0.00 | 0.79 | 0.21 | 0.00 | 0.97 | 0.02 | 0.01 |
| 4.0 | 0.85 | 0.07 | 0.08 | 0.87 | 0.13 | 0.00 | 0.98 | 0.01 | 0.01 |
| 5.0 | 0.90 | 0.01 | 0.09 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 |
| 6.0 | 0.94 | 0.00 | 0.06 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 |
| 7.0 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 |
| 8.0 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 |
| 9.0 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 |
| 10.0 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 |
(f) Simulation of literature σ(SI) curves by using state-selected σ(a5DJ, a5FJ, and a3FJ) curves
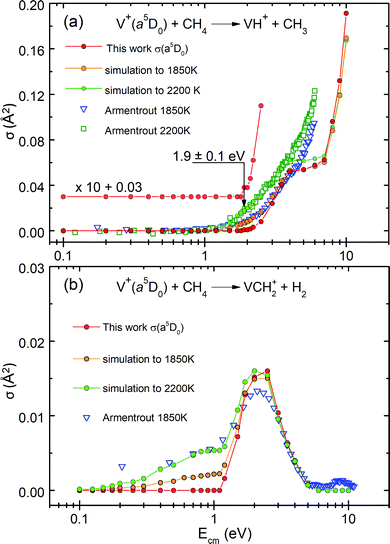
The previous GIB mass spectrometric experiment was conducted about 33 years ago by the Armentrout group using a hot filament SI ion source at T = 1850–2200 K. The populations of the V+(a5DJ, a5FJ, and a3FJ) states thus generated were assumed to be governed by the Boltzmann distribution.19 In order to shed light into this assumption, we have performed a simulation of the experimental σ(SI-1850 K) and σ(SI-2200 K) curves. Here, we use the state-selected σ(a5DJ, a5FJ, and a3FJ) curves obtained in the present study. This simulation also aims to illustrate that hot-band excitations arising from impurity states in σ(SI) measurements can easily prevent the observation of the Ecm-thresholds or the ET values.As shown below, by taking the linear combination of state-selected σ(a5DJ, a5FJ, and a3FJ) curves determined in the present PFI-PI measurements, along with weighted Boltzmann populations of these electronic states,19 we show in Fig. 5(a) and (b) that excellent simulations of the respective experimental σ(SI-1850 K: VH+) and σ(SI-2200 K: VCH2+) curves can be achieved. Fig. 5(a) compares the σ(a5D0: VH+) curve with the experimental and simulated σ(SI-1850 K: VH+) and σ(SI-2200 K: VH+) curves. The V+ ions produced by thermal SI at 1850–2200 K cannot be in single quantum states. They are expected to populate mostly in the ground a5DJ cationic state, along with minor populations in the excited a5FJ and a3FJ states, which are governed by the Boltzmann distribution. By setting the SI source at 1850 K (2200 K), previous studies assumed that the relative populations of the V+(a5DJ), V+(a5FJ), and V+(a3FJ) states were 0.854, 0.145, and 0.00083 (0.800, 0.191, and 0.0023), respectively.
Since we have obtained detailed quantum state-selected cross section measurements: σ(a5D0: VH+), σ(a5F1: VH+), σ(a3F2: VH+), σ(a5D0: VCH2+), σ(a5F1: VCH2+), and σ(a3F2: VCH2+) curves, we should be able to obtain the simulated σ(SI-1850 K) and σ(SI-2200 K) curves by using these state-selected σ curves and their assumed Boltzmann thermal populations.
In Fig. 5(a), the red solid circle curve represents the σ(a5D0: VH+) curve obtained from this work, which has been rescaled by a factor of 0.80 in order to emphasize the similarity in the energy dependence. The blue open triangles and green open squares mark the experimental σ(SI-1850 K: VH+) and σ(SI-2200 K: VH+) curves, respectively. The orange solid circle curve shows the simulated curve obtained according to the thermal Boltzmann populations at 1850 K calculated as: σ(SI-1850 K: VH+) = [0.854 × σ(a5D0: VH+) + 0.145 × σ(a5F1: VH+) + 0.00083 × σ(a3F2: VH+)] × 0.8. The green solid circle curve shows the simulated σ(SI-2200 K: VH+) curve, calculated based on the weighted Boltzmann populations as: [0.800 × σ(a5D0: VH+) + 0.191 × σ(a5F1: VH+) + 0.0023 × σ(a3F2: VH+)] × 0.8. These simulations thus calculated reveal that V+(a3FJ) ions make a significant contribution of broadening of the σ curve involved and to the hot-band tailing structure observed around and below the reaction onset, even though the population of the a3FJ state is only 0.00083 and 0.0023 at 1850 and 2200 K, respectively. This is because the hot-band contribution of the σ(a3FJ: VH+) curve is hugely amplified by the much higher reactivity of the triplet a3FJ state compared to that of the quintet states. Thus, hot-band excitations, as in this case, can prevent observation of the true reaction onset.
By comparing the σ(SI-1850 K: VH+) and σ(SI-2200 K: VH+) curves with the σ(a5D0: VH+) curve obtained in this study, we can conclude that the hot-band excitation of the σ(a5D0: VH+) curve is much reduced; showing that the true 0 K ET onset, i.e., E0, is located at a higher Ecm still. As shown in Fig. 5(a), the σ(SI) curves observed at 1850 and 2200 K are in excellent agreement with the simulated σ(SI) curves at Ecm ≤ 4 eV, where the simulation of the σ(SI) curves can be obtained by the linear combination of the σ(a5D0: VH+), σ(a5F1: VH+), and σ(a3F2: VH+) curves. The fact that the experimental σ(SI-1850 K: VH+) and σ(SI-2200 K: VH+) curves can be well simulated based on the weighted Boltzmann populations is a strong support of the thermal equilibrium assumption. However, the comparison of Fig. 5(a) reveals deviation between the experimental σ(SI) and the simulated curves at Ecm ≥ 4 eV; and the nature of this deviation is not known.
By using similar procedures, we have also obtained excellent simulations for the σ(SI-1850 K: VCH2+) and σ(SI-2200 K: VCH2+) curves as depicted in Fig. 5(b). Here, the red solid circle curve is the σ(a5D0: VCH2+) curve obtained from this work, whereas the blue open triangle curve is the experimental σ(SI-1850 K: VCH2+) curve obtained previously by the Armentrout group. The orange solid circle and green solid circle curves are the simulated curves obtained as the linear combination of the σ(a5D0: VCH2+), σ(a5F1: VCH2+), and σ(a3F2: VCH2+) curves with weighted populations in accordance with the Boltzmann thermal populations observed at T = 1850–2200 K. The simulations of Fig. 5(b) indicate that the hot-tail appearing in the low Ecm region is overwhelmingly contributed by the excited triplet V+(a3FJ) electronic state in the σ(SI-1850–2200 K: VCH2+) measurements.
In addition to validating the thermal equilibrium assumption for the populations of the V+ electronic states generated by thermal excitations, the excellent simulation observed can also be taken as strong confirmation that the σ(a5D0), σ(a5F1), and σ(a3F2) curves produced in the present PFI-PI study are in single quantum electronic states with 100% purity.
(g) Comparison of present spin–orbit state-selected cross sections with previous results
The fact that the present state-specific results can be used to reproduce the previous data obtained using a surface ionization source also suggests that the assumptions made in this previous work regarding the distribution of electronic states was reasonable. This hypothesis can be further checked by comparing the approximate state-specific cross sections provided by Aristov and Armentrout19 with the robust determinations obtained here. Fig. 6 compares the present results for σ(a5D0: VH+) and σ(a3F2: VH+) with those from ref. 19 (taken from Fig. 2 and scaled by the inverse populations: 1/0.854 for the quintet states and 1/0.00083 for the triplets). Clearly, both the shapes and the magnitudes agree well, further validating the accuracy of the present results. A similar comparison of the σ(a5D0: VCH2+) and σ(a3F2: VCH2+)s with those from ref. 19 (taken from Fig. 8 directly) find similar agreement in shapes and magnitudes for the quintet states, but the previous data for triplet states is about two times larger in magnitude than the present results, a discrepancy that can be attributed to the extrapolation needed in the previous work. Notably, no reasonable information regarding the a5F state was obtained in the previous work, which the present study clearly shows is primarily because it is so much less reactive.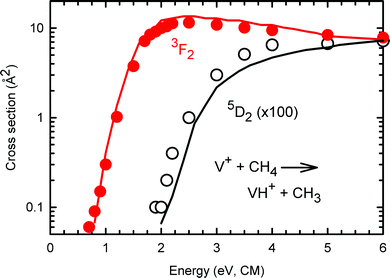 | ||
| Fig. 6 State-selected σ(a5D2: VH+) curve in black circles and σ(a3F2: VH+) curve in solid red circles for the reaction channels of V+ + CH4. The solid lines show the extrapolated state-specific results from ref. 19 for triplet (red) and quintet (black) states. Both data sets for the quintet states have been multiplied by a factor of 100. | ||
(h) Bond dissociation energies of V+–H, V+–CH2, and V+–CH3
The D0 values of V–H+, V–CH2+, and V–CH3+ can be derived from Ecm-threshold energies or threshold energies of reaction (ET's) determined in the present experiment. Similar to the derived procedures used in the study of the reaction systems of V+ + D2 (CO2),24,26 we can show that the D0 values are related to ET at T = 0 (or E0) of reactions (1)–(3), given as E0(1), E0(2), and E0(3), in eqn (6)–(8), respectively.| D0(V+–H) = D0(H–CH3) – E0(1) | (6) |
| D0(V+–CH2) = D0(H–CH3) + D0(H–CH2) − 2ΔfH0(H) − E0(2) | (7) |
| D0(V+–CH3) = D0(H–CH3) − E0(3) | (8) |
As shown in Fig. 2(a)–(c), the Ecm-thresholds or ET values observed for σ(a3F2: VH+), σ(a5F1: VH+), and σ(a5D0: VH+) are 0.6 ± 0.1, 1.7 ± 0.1, and 1.9 ± 0.1 eV, which give the values of bond dissociation energy of VH+ (D0(V+–H)) as 2.8 ± 0.1, 2.5 ± 0.1, and 2.6 ± 0.1 eV, respectively. Thus, the averaged value of D0(V+–H) can be determined as 2.6 ± 0.2 eV, which is in good agreement with the D0(V+–D) value of 2.5 ± 0.2 eV that has been deduced recently in the study of another reaction system of V+ + D2.26 Similarly, the D0(V+–CH2) can be derived as 3.6 ± 0.1, 3.7 ± 0.1, and 3.6 ± 0.1 eV, corresponding to the ET's of 0.1 ± 0.1, 0.8 ± 0.1, and 1.2 ± 0.1 eV for σ(a3F2: VCH2+), σ(a5F1: VCH2+), and σ(a5D0: VCH2+) in Fig. 2(d)–(f), respectively. Thus, the averaged D0(V+–CH2) is 3.6 ± 0.2 eV. For σ(VCH3+) shown in Fig. 2(g) and (h), due to the very low reactivity, only the ET for σ(a3F2: VCH3+) has been determined with sufficiently high quality for reliable bond energy determination. Based on the latter ET value of 0.7 ± 0.1 eV for σ(a3F2: VCH3+), the D0(V+–CH3) is deduced as 2.7 ± 0.2 eV.
We emphasize that the direct D0 determination as shown in eqn (6)–(8) requires the E0 instead of the ET measurement. The most important thermal energy correction for the conversion of ET to E0 measurement is expected to be the thermal energy of reactant CH4 molecule, in this case. Since the thermal energy for CH4 has not been properly accounted and corrected for in the above thermochemical analyses and derivation, all the D0 values deduced above associated with the reaction systems of V+ + D2 (CO2, CH4) are upper bound values, which are found to be higher than the accepted corresponding literature values by ≈0.3–0.5 eV. That is, following the data analysis as given above, we have: D0(V+–H) ≤ 2.6 ± 0.2 eV, D0(V+–CH2) ≤ 3.6 ± 0.2 eV, and D0(V+–CH3) ≤ 2.7 ± 0.2 eV.
As pointed out earlier, the shifting of the Ecm-threshold positions of σ(VH+), σ(VCH2+), and σ(VCH3+) observed, due to the change of the quantum electronic states of the reactant V+ ions, indicates that the quantum electronic energy can couple with the reaction coordinates in promoting accessible chemical reaction channels, similar to the Ecm.
(i) Modelling of kinetic energy distribution due to thermal broadening
Previous studies have shown that, in order to obtain reliable 0 K bond dissociation energies for simple TM-ligated molecules, such as D0(V+–H), D0(V+–CH2), and D0(V+–CH3), it is necessary to account for the proper correction of thermal energies involved, particularly on the thermal energy associated with the neutral reactant CH4 molecule in this case. On the basis of the theoretical analysis of Chantry35 and Lifshitz et al.,43 the Armentrout group has developed a simulation program for the determination of the threshold energy of reaction E0 and the kinetic energy distribution by fitting the experimental σ curves based on the semi-empirical modified line-of-centers (MLOC) model as shown in eqn (9).44,45| σ0(Ecm) = ∑gi(Ecm + Eel + Ei − E0)n/Ecm | (9) |
Threshold energies of reaction can be converted to thermochemical parameters and properties using eqn (6)–(8). This assumes that the thresholds correspond to the asymptotic product energies, such that there are no reverse activation barriers. This result is expected in the present system for all reactions. As reported above, relevant literature thermochemistry includes the active thermochemical table (aTcT) values of D0(CH2–H2) = 4.743 eV and D0(CH3–H) = 4.482 eV.41,42
To extract meaningful thermochemistry from the kinetic energy dependent cross sections, they were modeled using eqn (9), which explicitly includes all sources of energy after convolution with the kinetic energy distributions of both reactants. Because the density of data points is relatively low, it is not possible to allow all parameters in this equation to vary freely, hence the modeling results from Aristov and Armentrout17 were used as a guide for selecting the value of n coupled with whether the cross section was adequately reproduced. In all cases, the simple line-of-centers (LOC) model where n = 1 reproduces the data well. The optimized parameters used are listed in Table 2. For the formation of VCH2+ + H2, the thresholds for the a5F1 and a3F2 excited levels are smaller than that for the a5D0 ground level by 0.46 ± 0.09 and 1.11 ± 0.09 eV, in reasonable agreement with the excitation energies of 0.32 and 1.07 eV.38 Likewise, for the VH+ + CH3 channel, the thresholds shift by 0.24 ± 0.12 and 1.06 ± 0.12 eV, respectively. In both cases, the thresholds obtained provide weighted average bond dissociation energies of D0(V+–CH2) = 3.40 ± 0.14 eV and D0(V+–H) = 2.02 ± 0.09 eV (where the uncertainties are two standard deviations of the mean). The former value can be compared to that obtained by Aristov and Armentrout of 3.30 ± 0.06 eV (from reactions of V+ with C2H2p)48 and by Aristov and Armentrout of 3.47 ± 0.13 eV (from reaction of V+ with CH4),19 both at 298 K. The latter result was later adjusted to a 0 K value of 3.37 ± 0.06 eV by Armentrout and Kickel.49 Likewise, the value for D0(V+–H) obtained here agrees nicely with that obtained by Elkind and Armentrout, 2.05 ± 0.06 eV (reaction of V+ + H2 and D2),23 and with that obtained by combining these earlier results with state-selected experiments on the reaction V+ + D2 similar to the present study, 2.07 ± 0.09 eV.27
| Product | State | σ 0 | N | E 0 (eV) | D 0(V+–X) |
|---|---|---|---|---|---|
| a Uncertainties (one standard deviation) in parentheses. | |||||
| VCH2+ | V+(a5D0) | 0.075 (0.005) | 1.0 (0.1) | 1.41 (0.08) | 3.33 (0.08) |
| V+(a5F1) | 0.025 (0.004) | 1.0 (0.1) | 0.95 (0.06) | 3.47 (0.06) | |
| V+(a3F2) | 3.9 (0.2) | 1.0 (0.1) | 0.30 (0.06) | 3.37 (0.06) | |
| VH+ | V+(a5D0) | 0.14 (0.03) | 0.9 (0.2) | 2.42 (0.10) | 2.06 (0.10) |
| V+(a5F1) | 0.22 (0.02) | 1.0 (0.1) | 2.18 (0.06) | 1.98 (0.06) | |
| V+(a3F2) | 28.5 (0.5) | 1.0 (0.1) | 1.36 (0.06) | 2.05 (0.06) | |
| VCH3+ | V+(a3F2) | 0.15 (0.1) | 1.0 (0.1) | 1.34 (0.09) | 2.07 (0.09) |
In contrast to the results for VCH2+ and VH+ products, only the thresholds obtained using the LOC model for VCH3+ + H reaction from the a3F2 state yields a reliable threshold that corresponds to D0(V+-CH3) = 2.07 ± 0.09 eV. This value agrees with that previously obtained by Aristov and Armentrout48 after being adjusted to 0 K by Armentrout and Kickel, 2.00 ± 0.07 eV.49 Furthermore, it is similar to the value obtained here for D0(V+–H). As discussed by Armentrout and Kickel,49 this similarity, which holds for all first-row transition metal cations, is expected because both molecules involve single covalent bonds to V+.
(j) E T-threshold energy of reaction approach for bond energy measurements
As pointed out above, the effect of the thermal motion of neutral gaseous molecules in the reaction cell contributes significant uncertainty of collision energy. Chantry35 has shown that the kinetic energy distribution at Ecm has the full-width-at-half-maximum of| W1/2 = √[11.1 × γkT × Ecm]. | (10) |
| W1/2 = √[0.217 × E0] = √[0.217 × (ET + ΔE)] = 2ΔE | (11) |
| 4ΔE2 − 0.217 ΔE − (0.217ET) = 0 | (12) |
| Product | State | Simulation approach | E T-threshold approach | ||
|---|---|---|---|---|---|
| E 0 (eV) | D 0(V+–X) (eV) | E 0 (eV) | D 0(V+–X) (eV) | ||
| a Uncertainties (one standard deviation) in parentheses. b Weighted averages of D0(V+–X), X = H and CH2. c Ref. 23. d Ref. 49. e Ref. 27. | |||||
| VH+ | V+(a5D0) | 2.42 (0.10) | 2.06 (0.10) | 2.25 (0.17) | 2.23 (0.17) |
| V+(a5F1) | 2.18 (0.06) | 1.98 (0.06) | 2.03 (0.17) | 2.13 (0.17) | |
| V+(a3F2) | 1.36 (0.06) | 2.05 (0.06) | 0.81 (0.10) | 2.60 (0.10) | |
| 2.02 (0.05)b | 2.43 (0.26)b | ||||
| 2.05 (0.06)cd | |||||
| 2.07 (0.09)e | |||||
| VCH2+ | V+(a5D0) | 1.41 (0.08) | 3.33 (0.08) | 1.48 (0.14) | 3.26 (0.14) |
| V+(a5F1) | 0.95 (0.06) | 3.47 (0.06) | 1.01 (0.12) | 3.41 (0.14) | |
| V+(a3F2) | 0.30 (0.06) | 3.37 (0.06) | 0.21 (0.10) | 3.47 (0.10) | |
| 3.40 (0.07)b | 3.40 (0.11)b | ||||
| 3.37 (0.06)d | |||||
| VCH3+ | V+(a3F2) | 1.34 (0.09) | 2.07 (0.09) | 0.92 (0.10) | 2.48 (0.10) |
| 2.00 (0.07)d | |||||
IV. Conclusions
In this work, the σ(VH+), σ(VCH2+), and σ(VCH3+) of the reaction system V+(a5D0, a5F1, and a3F2) + CH4(X1A1) have been measured in the Ecm range from 0.1 to 10.0 eV, by coupling a novel two-color VIS-UV laser PFI-PI V+ ion source with a DQDO ion–molecule reaction apparatus. Both quantum spin–orbit electronic state and Ecm effects on chemical reactivity for this reaction system have been examined in detail. The triplet V+(a3FJ) ion is found to exhibit much higher chemical reactivity than that of the two quintet ions, V+(a5DJ) and V+(a5FJ), confirming the more qualitative conclusions of previous studies.19 Without a detailed theoretical examination of the reaction dynamics of the titled reaction system, this observation is tentatively interpreted by a weak quintet-to-triplet spin crossing mechanism, favoring dominantly the conservation of total electron spin. The preference for the conservation of total electron spin may promote the formation of an inserted intermediate, [HV+CH3], which can thus enhance the reactivity of the triplet V+(a3FJ) ion. Although the electronic energy of V+(a5FJ) ion is 0.3 eV higher than that of the V+(a5DJ) ion, the reactivity of the V+(a5FJ) ion is found to be lower than that of the V+(a5DJ) ion, indicating that chemical reactivity of V+ ions is governed by quantum state effects rather than energy effects.The Ecm-thresholds of σ(VH+), σ(VCH2+), and σ(VCH3+) for V+ prepared in the a5D0, a5F1, or a3F2 states have been determined except that for σ(a5FJ: VCH3+). From the ET-threshold energies of reaction measurements, the upper limits for D0(V+–H), D0(V+–CH2), and D0(V+–CH3) values have been deduced. By properly accounting for the thermal kinetic energy distribution primarily resulting from the thermal broadening effects of the neutral reactant CH4 molecule, we have obtained reliable D0 values for these V+-ligated molecular ions. The differences of Ecm-thresholds observed are consistent with the electronic state energy levels of reactant V+ ions, indicating that quantum electronic energies of V+ ions similar to Ecm, can couple effectively with the reaction coordinates of the V+ + CH4 reaction system. No J effect has been observed, which may mean that the spin–orbit coupling of V+(a5D0, a5F1, or a3F2) of V+ ion is weak and J is not a constraining factor to this reaction system. The weak spin–orbit coupling is expected to lower the mixing of electronic states with different multiplicities (or spins), which is in accordance with the distinct differences of observed chemical reactivity for V+ ions prepared in electronics states with different spins. Detailed BR's have also been obtained as a function of Ecm and electronic states of V+ ion, together with quantum state-selected σ's, can serve as experimental benchmarks for state-of-the-art theoretical calculations of model reaction systems. The much higher reactivity and product selectivity of the V+(a3FJ) + CH4 reaction leading to H2 formation observed in this work may provide valuable insight into designing more effective catalytic pathways for CH4 activation. This and the recent V+ state-selected ion–molecule reaction experiments have shown that the ET-threshold energy and σ curve measurements represent a fruitful experimental and theoretical research area for the study of chemical bonding between TM cations and ligands.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Science Foundation, Grant CHE-1763319 (CYN) and CHE-1664618 (PBA). CYN is also grateful to Dr Huie Tarng Liou for his generous donation of research support for the Ng Laboratory.References
- S. A. Montzka, E. J. Dlugokencky and J. H. Butler, Nature, 2011, 476, 43–50 CrossRef CAS PubMed.
- C. R. Webster, P. R. Mahaffy, S. K. Atreya, G. J. Flesch, M. A. Mischna, P. Y. Meslin, K. A. Farley, P. G. Conrad, L. E. Christensen, A. A. Pavlov, J. Martín-Torres, M. P. Zorzano, T. H. McConnochie, T. Owen, J. L. Eigenbrode, D. P. Glavin, A. Steele, C. A. Malespin, P. D. Archer, Jr., B. Sutter, P. Coll, C. Freissinet, C. P. McKay, J. E. Moores, S. P. Schwenzer, J. C. Bridges, R. Navarro-Gonzalez, R. Gellert and M. T. Lemmon, Science, 2015, 347, 415–417 CrossRef CAS PubMed.
- S. K. Atreya, E. Y. Adams, H. B. Niemann, J. E. Demick-Montelara, T. C. Owen, M. Fulchignoni, F. Ferri and E. H. Wilson, Planet. Space Sci., 2006, 54, 1177–1187 CrossRef CAS.
- C. J. Bennett, C. S. Jamieson, Y. Osamura and R. I. Kaiser, Astrophys. J., 2006, 653, 792–811 CrossRef CAS.
- O. Mousis, E. Chassefiere, N. G. Holm, A. Bouquet, J. H. Waite, W. D. Geppert, S. Picaud, Y. Aikawa, M. Ali-Dib, J.-L. Charlou and P. Rousselot, Astrobiology, 2015, 15, 308–326 CrossRef CAS PubMed.
- C. Mesters, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 223–238 CrossRef PubMed.
- A. Bard, G. M. Whitesides, R. N. Zare and F. W. McLafferty, Acc. Chem. Res., 1995, 28, 91 CrossRef CAS.
- H. Schwarz, Angew. Chem., Int. Ed., 2011, 50, 10096–10115 CrossRef CAS PubMed.
- L. Barelli, G. Bidini, F. Gallorini and S. Servili, Energy, 2008, 33, 554–570 CrossRef CAS.
- M. E. Dry, Catal. Today, 2002, 71, 227–241 CrossRef CAS.
- H. Jahangiri, J. Bennett, P. Mahjoubi, K. Wilson and S. Gu, Catal. Sci. Technol., 2014, 4, 2210–2229 RSC.
- J. C. Weisshaar, Acc. Chem. Res., 1993, 26, 213–219 CrossRef CAS.
- J. Roithová and D. Schröder, Chem. Rev., 2010, 110, 1170–1211 CrossRef PubMed.
- P. B. Armentrout and J. L. Beauchamp, J. Am. Chem. Soc., 1981, 103, 784–791 CrossRef CAS.
- P. B. Armentrout and J. L. Beauchamp, Acc. Chem. Res., 1989, 22, 315–321 CrossRef CAS.
- J. Allison, R. B. Freas and D. P. Ridge, J. Am. Chem. Soc., 1979, 101, 1332–1333 CrossRef CAS.
- A. Shayesteh, V. V. Lavrov, G. K. Koyanagi and D. K. Bohme, J. Phys. Chem. A, 2009, 113, 5602–5611 CrossRef CAS PubMed.
- D. Schröder and H. Schwarz, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18114–18119 CrossRef PubMed.
- N. Aristov and P. B. Armentrout, J. Phys. Chem., 1987, 91, 6178–6188 CrossRef CAS.
- T. Hayes, D. Bellert, T. Buthelezi and P. J. Brucat, Chem. Phys. Lett., 1997, 264, 220–224 CrossRef CAS.
- E. Sicilia and N. Russo, J. Am. Chem. Soc., 2002, 124, 1471–1480 CrossRef CAS PubMed.
- E. U. Condon and G. H. Shortley, The Theory of Atomic Spectra, Cambridge University Press, 1951 Search PubMed.
- J. L. Elkind and P. B. Armentrout, J. Phys. Chem., 1985, 89, 5626–5636 CrossRef CAS.
- Y. C. Chang, Y. Xu and C.-Y. Ng, Phys. Chem. Chem. Phys., 2019, 21, 6868–6877 RSC.
- Y. C. Chang, B. Xiong, Y. Xu and C.-Y. Ng, J. Phys. Chem. A, 2019, 123, 2310–2319 CrossRef CAS PubMed.
- Y. Xu, Y.-C. Chang and C.-Y. Ng, J. Phys. Chem. A, 2019, 123, 5937–5944 CrossRef CAS PubMed.
- P. B. Armentrout, Y.-C. Chang and C.-Y. Ng, J. Phys. Chem. A, 2020, 124(26), 5306–5313 CrossRef CAS PubMed.
- M. R. Sievers and P. B. Armentrout, J. Chem. Phys., 1995, 102, 754–762 CrossRef CAS.
- Y. C. Chang, Y. Xu, B. Xiong and C.-Y. Ng, Mol. Phys., 2020, 1–11 Search PubMed.
- Y. C. Chang, H. Xu, Y. Xu, Z. Lu, Y.-H. Chiu, D. J. Levandier and C. Y. Ng, J. Chem. Phys., 2011, 134, 201105 CrossRef PubMed.
- Y. C. Chang, Y. Xu, Z. Lu, H. Xu and C. Y. Ng, J. Chem. Phys., 2012, 137, 104202 CrossRef PubMed.
- N. R. Daly, Rev. Sci. Instrum., 1960, 31, 264–267 CrossRef CAS.
- Y. Xu, B. Xiong, Y. C. Chang and C.-Y. Ng, Astrophys. J., 2018, 861, 17 CrossRef.
- Y. Xu, B. Xiong, Y. C. Chang and C.-Y. Ng, J. Phys. Chem. A, 2018, 122, 6491–6499 CrossRef CAS PubMed.
- P. J. Chantry, J. Chem. Phys., 1971, 55, 2746–2759 CrossRef CAS.
- G. Friedlander, J. W. Kennedy and E. S. Macias, Nuclear and radiochemistry, John Wiley & Sons, 1981 Search PubMed.
- J. E. Sansonetti and W. C. Martin, J. Phys. Chem. Ref. Data, 2005, 34, 1559–2259 CrossRef CAS.
- A. Kramida, Y. Ralchenko, J. Reader and N. A. Team, National Institute of Standards and Technology, Gaithersburg, MD, 2012.
- H. Schwarz, Int. J. Mass Spectrom., 2004, 237, 75–105 CrossRef CAS.
- J. N. Harvey, Phys. Chem. Chem. Phys., 2007, 9, 331–343 RSC.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef CAS.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.122g of the Thermochemical Network, available at ATcT.anl.gov, accessed 4/29/20.
- C. Lifshitz, R. L. C. Wu, T. O. Tiernan and D. T. Terwilliger, J. Chem. Phys., 1978, 68, 247–260 CrossRef CAS.
- R. H. Schultz, K. C. Crellin and P. Armentrout, J. Am. Chem. Soc., 1991, 113, 8590–8601 CrossRef CAS.
- N. Dalleska, K. Honma, L. Sunderlin and P. Armentrout, J. Am. Chem. Soc., 1994, 116, 3519–3528 CrossRef CAS.
- K. M. Ervin and P. B. Armentrout, J. Chem. Phys., 1985, 83, 166–189 CrossRef CAS.
- M. E. Weber, J. L. Elkind and P. B. Armentrout, J. Chem. Phys., 1986, 84, 1521–1529 CrossRef CAS.
- N. Aristov and P. B. Armentrout, J. Am. Chem. Soc., 1986, 108, 1806–1819 CrossRef CAS.
- P. B. Armentrout and B. L. Kickel, in Organometallic Ion Chemistry, ed. B. S. Freiser, Kluwer, Dordrecht, 1996, pp. 1–45 Search PubMed.
| This journal is © the Owner Societies 2021 |