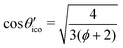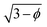First-principles calculation of 11B solid-state NMR parameters of boron-rich compounds I: the rhombohedral boron modifications and B12X2 (X = P, As, O)†
Martin
Ludwig
a and
Harald
Hillebrecht
 *ab
*ab
aInstitut für Anorganische und Analytische Chemie, Albert-Ludwigs-Universität, Albertstr. 21, 79104 Freiburg, Germany. E-mail: harald.hillebrecht@ac.uni-freiburg.de
bFreiburger Materialforschungszentrum FMF, Stefan-Meier-Str. 21, 79104 Freiburg, Germany
First published on 10th November 2020
Abstract
In the present study, solid-state nuclear magnetic resonance (NMR) spectra under magic angle spinning conditions of the rhombohedral structures α-B and B12P2 are reported together with the corresponding parameter sets from first principles calculations on α-B B12X2 (X = P, As, O). With the combination of density functional theory (DFT) and the gauge-including projector-augmented wave (GIPAW) approach as the theoretical tools at hand the computed 11B parameters lead to unambiguous explanation of the measurements. Thereby, we overcome common obstacles of processing recorded NMR spectra of solid-state compounds with several crystallographic positions, in particular non-trivial signal assignments and parameter determination due to peak overlap or even unexpected intensity/area ratios. In fact, we find very good agreement between the theoretical results and measured spectra without applying fitting procedures. Using the Perdew–Burke–Ernzerhof (PBE) functional, the results of the common construction types for pseudopotentials and referencing methods for the chemical shift determination are compared. Suggestions and conclusions from experimental 11B NMR studies on parameters according to the icosahedral positions are critically discussed, for instance the early suspected correlation to chemical shifts is not confirmed. Regarding the electric field gradient (EFG) a detailed explanation for obtaining small deviations amongst all investigated structures of the icosahedral polar sites compared to the equatorial sites is given. Our results show an important link between the exohedral bonding situation of compounds with icosahedral structure elements and the main axis of the EFG and therefore, also measurable quadrupole coupling constants if certain geometrical conditions are fulfilled. Finally, this work also contributes to establishing the number of unique sites measured by solid-state NMR methods within the modification of β-B.
1 Introduction
With the analysis of the electronic structure of a regular icosahedron of B atoms by Longuet-Higgins and Roberts,1 research and discussion, and thus also challenges posed by the element B, still remain vivid nowadays for both experimentalists and theoreticians.2 The formation of multi-center bonds, for which B is prominent, extends to the icosahedral arrangement from the molecular world3–6via its rhombohedral modifications α-B (α-rB12)7–11 and β-B (β-rB105)12,13 to numerous solid phase compounds with rhombohedral structures.14–28As an analytical tool nuclear magnetic resonance (NMR) spectroscopy is capable of providing multiple insights into structure–property relations of a compound through parameters that characterize the tensors of chemical shift, quadrupolar coupling and spin–spin interaction.29–31 In contrast to molecules in solutions, the orientation-dependent, that is the anisotropic, effects play a crucial role in the signal shape of solid-state NMR (SSNMR) spectra and can cumber their processing. One way to minimize a large number of these perturbations is to rotate the solid phase sample sufficiently fast by the so-called magic angle relative to the external magnetic field. Still, issues may remain in spectral processing, especially for measurements of different crystallographic positions. For quadrupolar nuclei with spin I larger than one-half, such as 10B and 11B, anisotropic second-order interactions cannot be removed under magic angle spinning (MAS) conditions resulting in non-trivial signal assignments and parameter determination.29,30 This is especially true for systems with multiple symmetry sites. Due to the presence of quadrupolar coupling, peak overlap may arise in the procedure of spectral simulation parameter sets that are ambiguous and hinder a full exploration of meaningful results.31,32
To overcome this issue experimentalists propose certain assumptions in order to reduce the parameters and, hence, the problem complexity to reproduce a measured spectrum via fit algorithms. These educated guesses to the geometrical or electronic situation for the compound under investigation are sometimes not justified and become even more precarious considering that measured intensity/area ratios may show noticeable deviation from the expected position multiplicities.33
Regarding the structural element of B12 icosahedra, besides molecular crystals of boranes,34,35 in boron-rich compounds, mainly rhombohedral phases such as the modification β-rB10536,37 and boron carbide (B4C)32,36,38–43 have been investigated by SSNMR spectroscopy. As has been shown from recent analysis of β-rB105 spectra,37 the anisotropy of the chemical shift and the dipolar homo- and heteronuclear coupling can be excluded as dominant mechanisms of signal broadening. Thus, the main interactions influencing recorded signals can be suspected to be the isotropic chemical shift in combination with the quadrupolar coupling interaction.
In this context, it is surprising that there are hitherto no published MAS NMR spectra as well as corresponding parameters of the commonly known α-rB12. Although this modification contains the characteristic structure element of many boron-rich compounds, that is interconnected B12 icosahedra, to the best of the authors' knowledge only one static NMR measurement has been reported,41 but without quantified statements on characteristic NMR parameters. Note that the mentioned solid phases of β-rB105 and B4C are known for various defect variants and partial occupations.12–16,44,45 Therefore, and together with the aforementioned obstacles of spectra processing it is just reasonable to first study and understand compounds that are well-ordered or at least simpler in their structural building units, such as the rhombohedral phases B12X2 (X = P, As, O), in order to go beyond accumulation of information by conceptual studies. Nonetheless, these missing investigations seem to be caused by the fact that the synthesis and quantification of samples with high phase purity remain a major experimental challenge.
By the aid of the gauge-including projector-augmented wave (GIPAW) method46 which allows for an ab initio calculation of the NMR parameters of systems under periodic boundary conditions the above mentioned issues in the obligatory fit process to simulate recorded solid-state spectra can be made feasible.30,47 With its high accuracy, the range of a parameter set for nuclei at certain atomic positions is significantly reduced as it is shown in the example of the spectral assignments for different 17O sites in the zeolite Ferrierite.48 Regarding 11B NMR, the ionic compounds of simple alkaline (earth) borohydrides49 and borates50 are particularly noteworthy. The latter study shows on the basis of calculations that certain assumptions about the shielding tensor for simulating recorded spectra are made without justification and, consequently, the parameters obtained from fitting algorithms are proved to be incorrect.
In their pioneering work Mauri et al.51 have applied GIPAW to determine the most common type of defect in B4C, that is B11C icosahedra with C–B–C chains. This, however, was achieved by investigating isotropic chemical shifts of 13C for several structural arrangements relating them to experimental observations. Considering the mentioned obstacles for quadrupolar nuclear species it becomes clear that a detailed exploration of possible parameters for the B sites in B4C is cumbersome and even less promising. Accordingly, no concrete chemical shifts of 11B are reported and it is noted with respect to the plotted model spectra that a distinct isotropic shift of B in the C–B–C unit is found in the range of 67 ppm, whereas a signal is observed at 37 ppm in experiments.32,40
While Mauri et al. suggested further experimental measurements because of discrepancy to the calculation, we believe that this deviation in value is an effect caused by strong quadrupolar coupling. Because the larger the quadrupolar interaction becomes the more one has to consider a high-/upfield shift of the center of gravity for the central transition (−1/2 ↔ 1/2).52 This effect implies that the bare observation from the MAS NMR spectrum for an assignment of a peak may lead to the impression of a species being more shielded than the actual isotropic chemical shift, calculated for example by theory, would suggest.53 Although this effect decreases with increasing external magnetic field, the second-order quadrupole interaction is inversely proportional to the applied field, it also plays an important role in recent NMR studies on the reorientation dynamics of molecular glass former trimethoxyboroxine.54 Thus, the consideration of both the chemical shift as well as the quadrupole coupling is essential for an elaborated description of 10B and 11B MAS NMR spectra of boron-rich compounds.29
In fact, with their early study in 1959 Silver and Bray38 already suggested from the experimental quadrupole coupling of 5.58 ± 0.02 the existence of a linear C–B–C unit in B4C. Later on, Schwarz et al.55 confirmed this assignment by first-principles computations of the electric field gradient (EFG). Also, the much smaller values of the icosahedral B atoms predicted by these calculations are found to be consistent with measurements. In general, quantum chemical calculations are mandatory for a sophisticated understanding of connections between the bonding situation and parameters arising from the EFG as had been shown for molecules34,56,57 but also for periodic systems,58,59 in particular various borides.60,61
However, except for the work of Mauri et al.51 on 13C shifts in B4C, and of Schwarz et al.55 on the EFG of α-rB12 and B4C no theoretical investigation of the SSNMR parameters exists to date of boron-rich compounds with icosahedral structure element, and none reporting on explicit information regarding the chemical 11B shift tensor. One of the main challenges seems to be the prediction on isotropic chemical shifts by GIPAW for B in homonuclear bonds, as the example of molecular crystals with diboron units connecting cyclic systems may suggest.62 There, the calculated values consistently diverge by at least 14 ppm compared to experiment, whereas a treatment of the magnetic shielding based on molecular models reduces the error by half. By contrast, our investigation63 showed that chemical 11B shifts of icosahedral molecules with multi-center bonds can be determined by GIPAW. Depending on the type of referencing approach the errors of 1 ppm to 2 ppm correspond very well to those of conventional molecular methods that use localized basis sets. The mimic of inner shell electrons by pseudopotentials (PPs) does not play a significant role due to the error compensation in the calculation of relative shift values. On the other hand, the quadrupole interaction is described by the EFG which depends strongly on the electron density in the vicinity of the nucleus.47,48 In this case, a careful check on the description of the inner shell electrons might be mandatory when the approximation of pseudoization is considered.
The objective of this study is to investigate whether DFT calculations with GIPAW are capable of providing SSNMR parameters that can explain our measured MAS NMR spectra of α-rB12 and B12P2 which are reported for the first time to the best of our knowledge. The used sample of high purity α-rB12 was kindly provided by Prof. Dr Ismail Duman,64 while B12P2 was synthesized in our laboratories according to ref. 17. Both compounds have been characterized by X-ray diffraction (XRD) analysis. The calculated parameter sets of the closely related thermodynamically stable rhombohedral phases B12As2 and B12O2 are additionally presented. On this, we compare the two common construction approaches of PPs and find good agreement for chemical shift tensors but differences for the quadrupole parameters. The results are compared to those of other theoretical and experimental work on borides. In detail, the connections of the nuclear quadrupole coupling constants of the sites in α-rB12 to closely related β-rB105 and (B12H12)2− in ionic boronates are discussed. This may contribute to the question which crystallographic positions are responsible for measured quadrupole frequencies in β-rB105.36,37 Furthermore, the parameters are discussed in terms of information extracted from the calculated electron density by Bader's analysis.65 Other than assumed by static measurements on α-rB12, β-rB105 and B4C,41 the results do not indicate a trend in the chemical shifts with respect to the B position, that is the linkage to an atom outside the B12 icosahedron. Instead, we obtain and explain relationships between the quadrupole coupling and the bonding situation. The calculations and considerations on structural constraints are in contradiction to the often made assumption of a symmetrically distributed electron density around the intericosahedral bond, which may have an effect on the determined quadrupolar coupling constants and the corresponding frequencies in spectral processing procedures.
2 Methods
2.1 Definitions and theoretical background
The eigenvalues of the calculated absolute shielding tensor σxx, σyy, and σzz are given in parts per million (ppm) and define its isotropic value σiso = (σxx + σyy + σzz)/3. For reporting our results we follow the recommendation of ref. 66 and choose |σzz − σiso| ≥ |σxx − σiso| ≥ |σyy − σiso|. The absolute magnetic shielding is related to the chemical shift by δ = (σref − σsample)/(1 − σref) which can be approximated in the case of light nuclei to δ ≈ σref − σsample (|σref| ≪ 1). Accordingly, there are two main methods in the literature30 for the conversion of calculated isotropic shieldings to chemical shifts that one may generalize to| δcalciso = m·σcalciso + σrefiso, | (1) |
| δcsa = m·(σzz − σiso), | (2) |
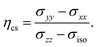 | (3) |
A nucleus with spin I > 1/2 possesses a quadrupole moment Q which couples with the gradient of the electric field in its vicinity. The EFG is a groundstate property and its 3 × 3 tensor components can be directly computed from the charge density ρ(r)48
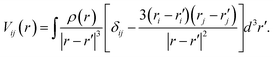 | (4) |
The EFG's eigenvalues are conventionally designated Vxx, Vyy, and Vzz and chosen as |Vzz| ≥ |Vyy| ≥ |Vxx|. Due to Laplace's equation the sum of these components vanishes and only two parameters are required for a complete description, namely the quadrupole coupling constant Cq (in magnitudes of Hz)
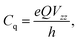 | (5) |
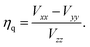 | (6) |
SSNMR experiments only give the absolute value of the quadrupole coupling constant |Cq| and it is also convenient to refer to the quadrupolar frequency νq
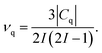 | (7) |
For the two isotopes 10B (I = 3) and 11B (I = 3/2) we consider the quadrupole moments Q(10B) = 8.459 × 10−30 m2 and Q(11B) = 4.059 × 10−30 m2 reported by Pyykkö.69
2.2 Computational details
All presented results of the ab initio electron structure calculations are obtained with the periodic code Quantum ESPRESSO (QE)70,71 using DFT on the level of the Perdew–Burke–Ernzerhof (PBE) exchange correlation functional.72 Description of the core-valence interactions is based on applying suitable PPs with an energy cutoff of 80 Ry (≈1088 eV) for all calculations. Self-consistency was reached within an energy error of less than 0.3 μeV. We sample the Brillouin zone by a Monkhorst–Pack mesh73 of 6 × 6 × 6 for the rhombohedral unit cells. Convergence is assumed due to negligible changes in the absolute values of the presented quantities. Conversion of the crystallographic information files for the plane-wave input of QE was done by the program CIF2CELL.74Based on the experimental determined crystal structures (see Table 1) geometry is optimized under the constraint of constant lattice parameters.75 We want to note that boron suboxide is known to occur as non-stoichiometric B12O2−x (x ≈ 0.5). However, in the present study we assume all positions to be fully occupied and thus, refer to the compound as B12O2. The applied PPs are generated under the Goedecker–Hartwigsen–Hutter contraction considering scalar relativistics76 which had been proven to result in reliable geometries for boron compounds with multi-center bonds.63 We assume convergence when all components of all forces are smaller than 2.5 meV Å−1. Structure parameters before and after relaxation can be found in Table S1 of the ESI.†
| α-rB127 | B12P217 | B12As214 | B12O218 | |
|---|---|---|---|---|
| a Primitive cell. b Hexagonal. c No experimental deviations reported. d Rhombohedral. | ||||
| Compositiona | B12 | B12P2 | B12As2 | B12O2 |
| Crystal system | Rhombohedral | |||
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 166) m (no. 166) |
|||
| Lattice parametersb | ||||
| a (Å) | 4.9179c | 5.9752(10) | 6.1490(15) | 5.3862(3) |
| c (Å) | 12.5805 | 11.8230(20) | 11.9140(10) | 12.3190(10) |
| Volume (Å) | 263.5 | 365.6 | 390.1 | 309.5 |
| Lattice parametersd | ||||
| a (Å) | 5.0643 | 5.2376(7) | 5.3268(8) | 5.1510(3) |
| α (°) | 58.10 | 69.56(1) | 70.50(1) | 63.05(1) |
| Volume (Å) | 87.8 | 121.9 | 130.0 | 103.2 |
Investigation on the charge distributions of the optimized structures is performed by Bader's quantum theory of atoms in molecules (QTAIM).65 Besides the charges the bond critical points (BCPs) are determined for detailed analysis. For this the electron density was recalculated with projector augmented-wave (PAW) PPs in the Kresse–Joubert contraction77 including nonlinear core correction scalar-relativistics. The real space grid was chosen to be three times denser in all lattice directions than the default settings of the QE program package. Using the post processing tool the all-electron charge density is reconstructed and analyzed by CRITIC278,79 using the Yu-Trinkle integration80 to obtain the presented Bader charges.
For the calculation of the presented MAS NMR parameters we used the GIPAW method46 in combination with Troullier–Martins normconserving (NC) PPs,81 for which we proofed reliability and accuracy of chemical 11B shifts within 2.5 ppm or less for compounds with multi-center bonds.63 According to Cuny et al.47 one should be aware that nonphysical shape of the pseudowave functions give meaningless results especially for eqn (4) where the charge density distribution close to the nucleus is crucial. Therefore, the presented parameters are additionally evaluated with the aforementioned PAW PPs. The calculated shielding values are determined under consideration of the term σ(G = 0) = −(8π/3)χ with the macroscopic magnetic susceptibility χ,82,83 assuming spherical shape of the sample.
For simulating the MAS NMR spectra from the calculated parameters we use the DMfit program package.84 In detail, we applied the model “Quad 1st” with intensities and line widths under consideration of measurements and under guidance by eye. Central transitions of the recorded spectra are fitted using the “Gaus/Lor” model (see the ESI,† for further information). The ellipsoids associated with the EFG tensor components are visualized by the webbrowser application MagresView.85 With this software we also determined the corresponding Euler angles (Table S4 of the ESI†). All crystal structures in this work are drawn using the VESTA package.86
2.3 NMR spectroscopy
The reported SSNMR experiments were performed using 2.5 mm rotors on a Bruker Avance 500 MHz solid-state NMR spectrometer (11.7 T) operating at a Lamor frequency νl = 160.48 MHz for 11B. Radio frequency pulses were applied at a transverse B1 field of 125 kHz corresponding to a π/2 pulse width of 2 ms. All spectra were recorded under MAS conditions at 30 kHz with bearing gas at ambient temperature, leading to sample temperatures of approximately 323 K due to frictional heating. 11B spectra were recorded using a rotor-synchronized Hahn-Echo experiment. The background signal originating from the BN-stator was recorded in a separate experiment and subtracted. The spectra were referenced according to IUPAC recommendations for the unified chemical shift scale using the residual protons in D2O as secondary standard and the substitution method without reshimming the magnet (Ξ(11B) = 32.083974%).663 Results and discussion
3.1 Structural aspects, bonding situation and QTAIM analysis
α-rB12 and B12X2 (X = P, As, O) crystallize in the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with an icosahedral arrangement of the B atoms shown in Fig. 1. The B12 building units form cubic closest packing with only slight deviations in the ABC-stacking sequence of layers. Geometrically, the arrangement of the icosahedra can be viewed as being placed on the eight vertices of a rhombohedron with one of the threefold axis along the [111]-direction. This leads to a reduction from point group symmetry Ih to D3d. Within the rhombohedral unit cell one may, therefore, distinguish between polar B(1) positions on the rhombohedral sites forming equilateral triangles and equatorial B(2) positions of the staggered belt around the B12 icosahedron. Selected distances of the intra- and intericosahedral atomic positions after geometry optimization are given in Table 2.
m with an icosahedral arrangement of the B atoms shown in Fig. 1. The B12 building units form cubic closest packing with only slight deviations in the ABC-stacking sequence of layers. Geometrically, the arrangement of the icosahedra can be viewed as being placed on the eight vertices of a rhombohedron with one of the threefold axis along the [111]-direction. This leads to a reduction from point group symmetry Ih to D3d. Within the rhombohedral unit cell one may, therefore, distinguish between polar B(1) positions on the rhombohedral sites forming equilateral triangles and equatorial B(2) positions of the staggered belt around the B12 icosahedron. Selected distances of the intra- and intericosahedral atomic positions after geometry optimization are given in Table 2.
| α-rB12a | B12P2 | B12As2 | B12O2 | |
|---|---|---|---|---|
| a With X as exohedral RCP from QTAIM analysis. b Both atoms located in the mirror plane σd. | ||||
| Intraicosahedral | ||||
| B(1)–B(1) | 1.749 | 1.875 | 1.904 | 1.781 |
| B(1)–B(2) | 1.805 | 1.768 | 1.780 | 1.779 |
| B(1)–B(2)b | 1.797 | 1.804 | 1.813 | 1.812 |
| B(2)–B(2) | 1.780 | 1.745 | 1.730 | 1.749 |
| Average | 1.787 | 1.792 | 1.801 | 1.780 |
| Intericosahedral | ||||
| B(1)–B(1) | 1.676 | 1.734 | 1.774 | 1.697 |
| B(2)–B(2) | 2.020 | |||
| Others | ||||
| B(2)–X | 1.167 | 1.910 | 2.005 | 1.503 |
| X–X | 2.243 | 2.406 | 2.979 | |
The structural arrangement is well-known for its versatile bonding situation1 in molecular systems3–6 as well as in solid-state compounds:8,9,20–25 In the radial direction 2-electron-2-center (2e2c) bonds are formed while on the polyhedral surface multi-center connectivity occurs like in 2-electron-3-center (2e3c) bonds. For the investigated rhombohedral compounds the six B(1) vertices of one icosahedron connect to two neighboring layers via six 2e2c bonds extended along the rhombohedral diagonal to the polar vertices of six other icosahedra. Being formed outside the B12 unit we refer to them as exohedral bonds, whereas the term endohedral indicates the electronic situation inside a polyhedron. In α-rB12 the equatorial B(2) atoms of one B12 unit give rise to six 2e3c exohedral bonds interconnecting the icosahedra within the same layer. In contrast, in B12X2 (X = P, As, O) the B(2) sites extend with exohedral 2e2c bonds to an interstitial X2 unit placed in the octahedral voids of the cubic closed packing. X is tetrahedrally coordinated by three B(2) and one X atom. In the case of B12O2 the two O atoms do not form bonds with each other, as will be discussed in further detail below. The resulting effect of interstitial intercalation on the crystal structure is an extension of the hexagonal a axis and a reduction in the c direction as shown in Table 1. Inter- and intraicosahedral B(1)–B(1) distances increase while intraicosahedral B(2)–B(2) distances decrease. Compared to α-rB12 the intraicosahedral B(1)–B(2) distances located in the mirror plane σd remain rather constant while the others are shortened. All intraicosahedral distances are in the range of 1.745 Å to 1.904 Å showing for each compound minor deviations from the average value87 and indicating small distortions of the B12 unit from a regular icosahedron.
The electronic structure of the investigated compounds had been studied and discussed in detail in several works. Our results are in good agreement with those reported in ref. 8–10 and 20–25. Table 3 summarizes the QTAIM analysis of the calculated electron density in a way that gives an overview of the bonding situation important for understanding the later analysis of the EFGs. The charges are consistent with the results of ref. 25 determined by the (linear)-augmented-plane-wave (LAPW) method. Small deviations are mainly caused by geometry relaxation. In α-rB12 there is a small amount of charge transfer from the polar B(1) to the equatorial B(2) site in agreement with the former reports.10 The participation of the more electronegative interstitial atoms causes the B12 units in B12X2 to be positively charged. This is in contrast to the expectations based on Wade's rules3 suggesting B122−X22+ but is closer to the real charge distribution. A considerably high amount of charge on the X2 unit can be compensated with only small charge changes of icosahedral B atoms. Compared to α-rB12 we find main impact of the interstitial atoms on B(2) while charges associated with B(1) atoms show only minor changes.
| Compound | Site | QTAIM charge | Properties of BCP | |||
|---|---|---|---|---|---|---|
| Ref. 25 | q PAW | ρ(rBCP) | ∇2ρ(rBCP) | d X–BCP | ||
| a LAPW (PW91-LDA) without geometry optimization. b Intraicosahedral BCP to B(2): ρ(rBCP) = 0.799 e Å−3, ∇2ρ(rBCP) = −2.739 e Å−5. c Intraicosahedral BCP to B(2): ρ(rBCP) = 0.857 e Å−3, ∇2ρ(rBCP) = −4.263 e Å−5. | ||||||
| α-rB12 | B(1) | 0.06 | 0.09 | 1.067 | −10.120 | 0.838 |
| B(2) | −0.06 | −0.09 | 0.531b | −1.276 | 1.067 | |
| B12P2 | B(1) | 0.13 | 0.13 | 0.974 | −7.749 | 0.867 |
| B(2) | 0.06 | 0.04 | 0.932 | −7.490 | 0.691 | |
| P | −0.52 | −0.55 | 0.774 | −3.778 | 1.122 | |
| B12As2 | B(1) | 0.13 | 0.15 | 0.914 | −6.660 | 0.887 |
| B(2) | −0.04 | −0.10 | 0.822c | −5.279 | 0.794 | |
| As | −0.27 | −0.15 | 0.625 | −1.973 | 1.203 | |
| B12O2 | B(1) | 0.12 | 0.12 | 1.017 | −7.798 | 0.848 |
| B(2) | 0.41 | 0.41 | 0.985 | 12.018 | 0.487 | |
| O | −1.58 | −1.58 | 0.053 | 0.285 | 1.490 | |
Let us start the discussion of the bonding situation with the connectivity in the structural building elements B12 and X2. In all compounds BCPs are located near the edges and ring critical points (RCPs) in the center of the triangular faces of the B polyhedra corresponding to endohedral multi-center bonds in accordance to ref. 10 and 25. For all interstitial X2 units we obtain BCPs with vanishing ellipticity. The increase of the unit cell volume for B12X2 is a consequence of the enlargement of the interstitial voids which is strongly correlated with the bonding situation of X2 and the size of X.27 Applying QTAIM analysis we consider a bond formation by a BCP with non-vanishing electron density. Therefore, in B12P2 and B12As2 the interstitial atoms are bonded to each other. In contrast, the BCP of the O2 unit in B12O2 has negligible electron density with a slight positive Laplacian. In their calculations Li and Ching23 also found a vanishing charge density distribution along the O–O path and Lee et al.20 reported a small but non-negligible stress on the O2 dumbbell corresponding to Coulomb repulsion by overlapping charges. Together with conceptual arguments of Slack and Morgan27 and the large atomic distance of 2.979 Å in Table 2 our results confirm that the O atoms are not bound to each other.
For all intericosahedral B(1)–B(1) bonds the BCPs are located at the center of the bonding paths (see also Table 2 and dX–BCP in Table 3) and show vanishing ellipticities. These bonds can be considered as classic covalent indicated by the negative Laplacian being straight and cylindric. Turning to the exohedral B(2)–X connection we find that the electron density on the BCP increases with a decrease of atom distance from which we conclude bond strengthening. As the electronegativity of the interstitial atom rises the BCP shifts towards the B(2) site. In B12O2 the positive Laplacian for the B(2)–O bond illustrates an ionic interaction in correspondence to the results from calculations with local basis sets.23 The B(2) atoms in α-rB12 form exohedral bonds to two neighboring B12 polyhedra with multi-center characteristics.8–10 We find a longer bonding path than the atomic intericosahedral distance of 2.020 Å, a bending angle B(2)–BCP–B′(2) of 142.6° and an ellipticity of 3.6 indicating a considerably high bond asphericity. The three BCPs of these exohedral bonds form an equilateral triangle with a RCP in its center. With results from analysis by the electron localizability indicator25 and other reports9,10 we may interpret this RCP as the center of this intericosahedral bond formation. Its distance from the B(2) site is listed together with B(2)–X bond lengths in Table 2.
In general the results from QTAIM analysis show for the polar B(1) sites that the bonding distance corresponds to the electron density on the BCP and, thus, to the bond strength. In fact, the values of ρ(rBCP) shown in Table 3 are the highest of all BCPs found for a respective site. Exceptions are the BCPs associated with bonds of the B(2) atoms of α-rB12 and B12As2 where maximum values of ρ(rBCP) occur for the endohedral bonds to another B(2) atom. Therefore, one should differentiate for the equatorial B(2) sites: The strongest bond formation is exohedral to the interstitial atoms in B12O2 and B12P2, whereas it is endohedral to B(2) atoms in α-rB12 and B12As2. On the basis of this result the term “inverted molecular solid” introduced by Emin19 should be used with caution as it does not generally hold true as in the case of B12As2.
3.2 Calculated NMR parameters and measured MAS NMR spectra
The calculated 11B NMR parameters are given in Table 4 where the results of PPs under NC and PAW construction are compared. For conversion of the magnetic shieldings to chemical shifts we show the results of referencing via linear regression as well as by applying the conservative approach selecting (B12H12)2− as a reference substance. The differences in values for the PPs of NC type increase the more deshielded the 11B site is. Note that the chemical shift asymmetry ηcs is not influenced by the choice of reference method. We found that the macroscopic correction with the magnetic susceptibility assuming spherical system82 is essential for the here reported values of δiso and also influences ηcs.‡ Shift parameters determined by NC and PAW with the conservative referencing method deviate from each other in a similar way to that reported by studies on more shielded 11B species in borohydrides.49 An exception is the asymmetry ηcs of B(1) and the anisotropy δcsa of B(2) in B12As2 which is related to the construction of the PPs. For NC, the values of linear regression differ from the conservative ones the more deshielded the B site is, in particular caused by the applied parameters of our preceding work.63 In total, all δiso agree in the range of 2 ppm regardless of the referencing method or PP type used which is comparable to the accuracy of computations for experimental values of structurally related molecules.| Compound | Site | NC | PAW | Exp | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Linear regressiona | Conservative | η cs | |Cq| | η q | Conservative | η cs | |Cq| | η q | δ cg | ||||||
| δ iso | δ regcsa | δ iso | δ regcsa | δ iso | δ csa | δ ctf | |||||||||
| a Referencing according to ref. 63, δregcsa/δrefcsa = 0.866 is assumed (see methods for details). b δ cg = δiso + δq with δq = −Cq2(1 + ηq2/3)/(40νl).52,54 c For details of the central transition fit see the ESI. | |||||||||||||||
| α-rB12 | B(1) | 2.6 | −7.7 | 5.5 | −8.9 | 0.01 | 1706 | 0.20 | 4.5 | −8.6 | 0.07 | 1651 | 0.20 | 3.6 | 5.6 |
| B(2) | 5.0 | 15.4 | 8.2 | 17.7 | 0.59 | 887 | 0.38 | 7.4 | 17.5 | 0.54 | 838 | 0.38 | 7.2 | −11.9 | |
| B12P2 | B(1) | −2.2 | −6.0 | −0.1 | −6.9 | 0.49 | 1611 | 0.20 | −0.8 | −7.0 | 0.53 | 1483 | 0.28 | −1.5 | −8.1 |
| B(2) | −9.3 | 17.0 | −8.3 | 19.6 | 0.38 | 85 | 0.57 | −8.9 | 19.0 | 0.37 | 251 | 0.47 | −8.9 | ||
| B12As2 | B(1) | −0.9 | 4.5 | 1.3 | 5.2 | 0.77 | 1466 | 0.26 | 1.5 | 5.0 | 0.57 | 1384 | 0.29 | 0.9 | |
| B(2) | −6.5 | −10.6 | −5.0 | −12.3 | 0.95 | 328 | 0.77 | −5.1 | 14.3 | 0.92 | 203 | 0.30 | −5.1 | ||
| B12O2 | B(1) | −14.9 | −10.9 | −14.8 | −12.6 | 0.11 | 1405 | 0.13 | −13.7 | −13.0 | 0.12 | 1416 | 0.10 | −14.3 | |
| B(2) | −0.3 | 12.0 | 2.1 | 13.9 | 0.84 | 1260 | 0.17 | 3.4 | 14.4 | 0.78 | 1430 | 0.10 | 2.8 | ||
The calculated δiso values are in the same range as that found for experimental MAS NMR spectra of B4C32 within 10 ppm to −15 ppm but indicate overall more deshielded 11B species than icosahedral closo-borane molecules.68 In all cases the interstitial X2 unit in B12X2 leads to more shielded B sites compared to α-rB12. However, this increase in shielding correlates neither with the position nor with the charge situation: Relative to polar B(1) sites, the B(2) site in α-rB12 and B12O2 shows smaller shielding, whereas the opposite is true for the remaining compounds. The nature of the exohedral bonds is, therefore, not clearly related to the differences in chemical shifts as proposed from experimental study.41 As for their molecular counterparts there is no simple relation between charge and chemical shift which may be a consequence of the distinct covalent bonding character in these icosahedral compounds.63
Usually NMR is not sign sensitive for the coupling constant Cq31 and so only absolute values are reported in Table 4. Comparing NC and PAW we observe noteworthy deviations for the B(2) site in B12P2 and B12As2 between the parameters |Cq| and ηq describing the quadrupolar interaction. This becomes more evident with the investigation of the principal axes of the EFG tensor in the following section as we obtain a change in the sign of Vzz. Furthermore, the orientations of the EFG main axes change relative to those of the barely changing chemical shift tensors which leads to different Euler angles (see Table S4 in the ESI†). These discrepancies do not change with a finer k-grid sampling or an increase of the plane wave cutoff. Being a “core” property the EFG is highly sensitive to the electronic wave functions and density in the vicinity of the nucleus under investigation (see eqn (4)) and so nonphysical forms of the pseudowave functions for inner shell contributions may lead to meaningless results.47 Since the PAW method works with the full reconstruction of the all-electron wave functions, potentials and density77 we rely on those values for further discussion.
For all compounds the |Cq| values of B(1) are in the range of about 1450 kHz while we find high fluctuations for B(2). Besides small structural deviations clearly the influence of the interstitial unit causes this effect for which the polar positions seem to be rather unaffected. The magnitude of the calculated quadrupole coupling constants of 11B in Table 4 agrees well with observations reported for other compounds containing icosahedral boron sites such as 450 ± 250 and 1300 ± 100 kHz,38 361, 380 and 513 kHz41 or 840 kHz42 for B4C and 1240 kHz42 for rhombohedral silicon boride α-SiB3−x.88 It is interesting that for α-rB12 the |Cq| values correspond to B(1) for measurements in carborane B10C2H12 of 1430 ± 20 kHz34 and on the other hand for B(2) to constants measured in closo-dodecaborates M2[B12H12] (M = K, Rb, Cs, NH4, N(CH3)4) in the range of 650 kHz to 700 kHz.35 This will become more clear in the next section where the orientation and magnitude of the principal axes of the EFG tensor are analyzed in more detail.
The B(1) sites connecting the B12 icosahedra show higher coupling constants than for other structural arrangements such as octahedra in YB6 with an experimental value of 1200 kHz60 or B12 cuboctahedra in TB12 (T = Y, Zr, Lu) with about 1100 kHz.61 The presented |Cq| of B(2) is in the range of those obtained in YT′B4 (T′ = Mo, W, Re)33 consisting of two dimensional boron networks. Turning to the asymmetry ηq in Table 4 the polar site is in general lower than or equal to that for the equatorial one indicating a more symmetric distribution of the electron density around the largest principal axis Vzz of the EFG tensor. In contrast, values of ηq ≈ 0.95 for the aforementioned dodecaboride TB12 imply a highly asymmetric electronic distribution.61
Compared to GIPAW calculations and measured parameters of borate crystals and glasses in ref. 50 and references therein the here investigated boron-rich compounds are in general more shielded with chemical shift anisotropies δcsa of the same magnitude of 10 ppm. The quadrupolar coupling constants |Cq| of the polar B(1) sites are smaller than for trigonal BO3 units while those for the equatorial B(2) sites in B12P2 and B12As2 are comparable to tetrahedral BO4 formation.
Fig. 2 and 3 show our measured MAS NMR spectra of α-rB12 and B12P2 together with contributions from the two different B sites. For the simulations we used the theoretical PAW parameters and adjusted the remaining magnitudes as described in the methods section. To the knowledge of the authors, only static samples of α-rB12 were measured41 which are unsuitable for comparisons of our calculations or recorded spectra. It is difficult to extract reasonable parameters from the measured 11B spectra alone which is also known from reports32,41,42 on B4C. Even with the expectation to obtain contributions of the B(1) and B(2) site it seems less appropriate to apply conventional fitting procedures due to the abundance of possible value combinations for parameter assignment. This is even more severe considering ref. 33 which reports that the intensity ratios of side band patterns show a noticeable deviation from expected signal area ratios in the 11B MAS NMR spectrum of YWB4 (at 14.1 T under 20 kHz spinning), and the same is true in the region of the central transition. Nonetheless, we report shifts δctf in Table 4 obtained from a central transition fit of the recorded spectra (see the ESI† for details). Comparisons to the theoretical expected shift for the center of gravity δcg show good agreement and indicate that individual site contributions of α-rB12 and B12P2 are not resolved separately. The shoulder at −11.9 ppm in the spectrum of α-rB12 will be addressed in more detail below.
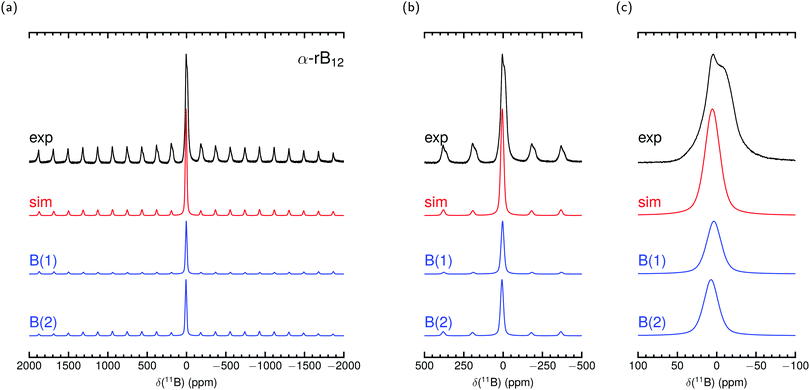 | ||
| Fig. 2 Experimental 11B MAS NMR spectrum of α-rB12 measured at 11.7 T with 30 kHz spinning frequency and simulation with parameters from PAW calculation in Table 4 together with site contributions. δcg is used in the simulation to set the shift position. Intensities and line widths adjusted by eye for the best fit of central transition shown in (c) (see Table S3 in the ESI† for further details). | ||
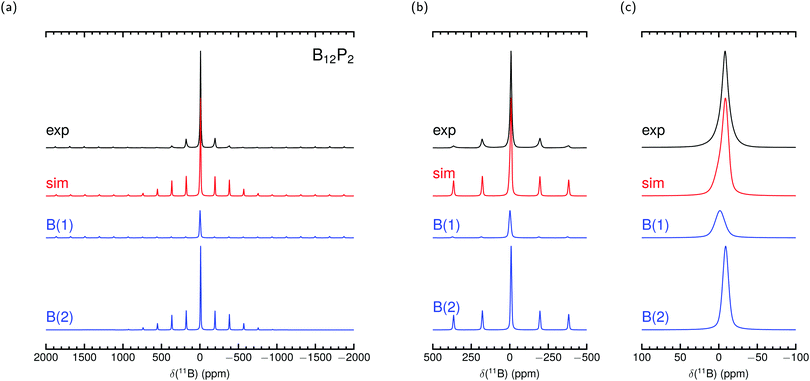 | ||
| Fig. 3 Experimental 11B MAS NMR spectrum of B12P2 measured at 11.7 T with 30 kHz spinning frequency and simulation with parameters from PAW calculation in Table 4 together with site contributions. δcg is used in the simulation to set the shift position. Intensities and line widths adjusted by eye for the best fit of central transition shown in (c) (see Table S3 in the ESI† for further details). | ||
The parameters arising from the EFG tensor may have a dominant influence not only on the signal shape but also, more importantly, on the center of gravity for observed signals/peaks being shifted high-/upfield.52,53 This effect turns out to play a significant role in the experimental observed 11B shift for the atom in the C–B–C chain in B4C. This can be convincingly demonstrated by inserting values of the experimental setup of Simeone et al.32 (νl = 96.216 MHz, 300 MHz spectrometer) into the equation given in the footnote of Table 4. Together with the measured Cexpq = 5580 kHz ± 20 kHz38 or theoretical Ctheoq = 5722 kHz55 one receives δexpq = −27.0 ± 0.2 or δtheoq = −28.4 ppm.89 Mauri et al.51 mentioned theoretical δiso of 67.3 ppm and 66.1 ppm for the chain center depending on the considered structure model with the remark on discrepancies to the measurement of Simeone et al. with a small signal at 37 ppm. But for δcg the resulting range can be estimated from 40.5 ppm to 37.7 ppm. Therefore, the calculated δiso is neither unreasonable nor are the measurements deficient, it is just that the shift of the center of gravity on the central transition was not considered for the computed values. For the here investigated cases of α-rB12 and B12X2 (X = P, As, O) the Cq leads to δq ≤ 1 ppm. However, we choose them to set the shift positions in the simulation and contributions in Fig. 2 and 3. Note that δcg (given in ppm) is related to the NMR experiment because it depends apart from the Larmor frequency νl also on the used carrier frequency.
By using the parameter sets from PAW calculations in Table 4 a reasonable assignment of contributions from the polar and equatorial sites in the spectra of α-rB12 and B12P2 is possible because they can explain the observed central transition and side band patterns. The theoretical results suggest that the difference of the chemical shifts for the B(1) and B(2) sites in α-rB12 and B12P2 is smaller than their line broadening and, hence, can be expected to be not resolved in the experimental MAS NMR spectra of Fig. 2 and 3. Therefore, the strong shoulder obtained for α-rB12 cannot be explained by our calculated values and might not be related to the theoretical assumption of an infinite expanded periodic structure. Indeed, powder XRD measurements and scanning electron microscopy (SEM) reveal a particle size of ≈30 nm. So, a significant share of the B12 icosahedra is located on the surface of the particle with a different electronic surrounding (≈10% assuming a diameter of 5 Å for a B12 icosahedron). Furthermore, there may occur a reconstruction of the (111) surface of α-rB12 with single bridging interstitial B atoms.11 Our suggestion is also supported by studies37 on the structurally closely related β-rB105 showing that the two apparent peaks of the static sample41 get removed under MAS measurement to result in only one peak around 14.2 ppm. In this regard it is important to note that the results in Table 4 are based on modeling well-ordered crystal structures. This might not be always the case and even hard to afford for experimental samples as for compound B12O2 where we assumed all sites to be completely occupied throughout this work although it occurs as non-stoichiometric B12O2−x.27
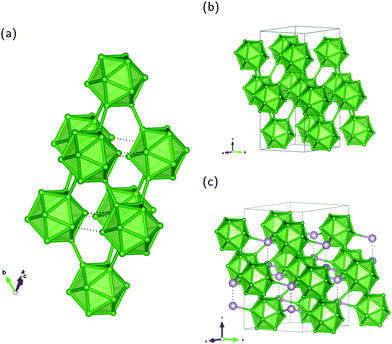
Our results also provide insight into the problem of establishing the number of unique sites detected by NMR experiments of the other B modification β-rB105.36,37 The idealized crystal structure shown in Fig. 4a may be described2 by placing B84 polyhedra in Fig. 4b on the corners of the rhombohedral unit cell. As illustrated, each of the 12 atoms of the central icosahedron bonds to a pentagonal cap resulting in the arrangement of a “super-icosahedron”. The pentagonal caps in polar positions are linked to polar caps of other B84 units while the equatorial ones are attached to B10–B–B10 (B21) chains visualized with condensed icosahedra in Fig. 4c. Each pentagonal cap within B84 is connected to another one and forms the half of an icosahedron. Therefore, all 84 atoms are sixfold coordinated intericosahedral positions comparable to the polar B(1) site in α-rB12. In the following we refer to the numbering of ref. 12 for the distinguishable sites in β-rB105. Three different B84 units are connected via the B10 unit which is formed by the four B sites B11, B12, B13 and B14 (see Fig. 4c). These atoms have no exohedral 2e2c bond following the icosahedral fivefold main axis. B13 is partially occupied and coordinates twice to itself and to the solitary B15 site. The central B14 links with 3 × 3 = 9 bonds to B11, B12 and (with partial 0.75) to B13. B12 has two bonds to B13 (partial), 2 × 2 = 4 bonds to outer B sites (B3 and B4) of two different B84 units and one bond each to the inner atoms of the B11 and B14 sites. B11 is connected twice to itself, with one bond each to the inner B12 and B14 sites as well as overall 2 × 2 = 4 bonds to outer B sites (B4 and B10) of two different B84 units. The bonding situation of these inner atoms, that is within the B10 unit, thus shows a certain similarity to the equatorial B(2) atoms in α-rB12, since they do not have exohedral 2e2c bonds, but are exclusively involved in multi-center bonds. In the idealized structure shown in Fig. 4a the local symmetry of the B14 site is C3v while the B15 site is located in a trigonal-antiprismatic (distorted octahedral) D3d arrangement.
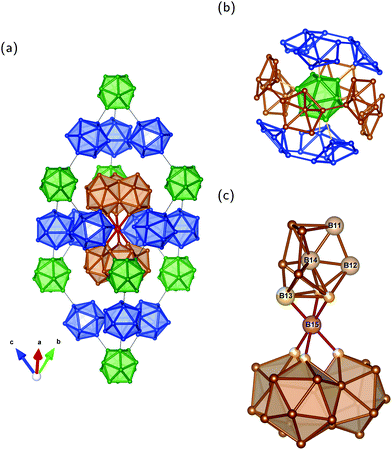 | ||
| Fig. 4 Unit cell of idealized β-rB105 and structure elements: (a) rhombohedral setting; (b) B84 unit; and (c) B21 configuration with condensed icosahedra formed by two B10 units (upper part) coordinating the central B atom (B15 site) trigonal-antiprismatic. The shown numbering of B sites and partial occupation refer to ref. 12. Note that partially occupied positions (B13 site) of the B10 unit are shown as full spheres in (a). Colors are meant to support the understanding of the crystal structure in terms of Samson polyhedra (see also ref. 2). | ||
Turning to the NMR experiments, Turner et al.37 excluded a dominant influence of chemical shift anisotropy as well as homo- and heteronuclear dipolar broadening mechanisms on the spectral shape in β-rB105 which is in accordance to our theoretical findings for α-rB12 in Table 4. In fact, second-order quadrupolar interactions with varying magnitudes are identified as main contribution in the 10B wide-line spectrum of static polycrystalline β-rB105 samples which is in accordance with older investigations on 11B.36 The corresponding frequencies νq are obtained by comparison of simulated spectra with the recordings under the assumption of ηq = 0 and are associated with three distinguishable groups. Note that for β-rB105 an assignment to the corresponding sites is difficult by experimental observation alone for there are at least 17 distinguishable atom positions reported in recent studies.12,13 Therefore, the most recent investigation37 reported νq for the sake of comparison while in the former one36 used presumptions based on intensity ratios. The converted values of frequencies determined via |Cq| from PAW for α-rB12 (see Table 4) are listed together with the observed groups for β-rB105 in Table 5; we tabulate the data for both isotopes for benefit of discussion. The data sets of both experimental studies agree well with each other for group I and are in the same range of value as the polar B(1) site in α-rB12. Thus, our first-principles calculations confirm the suggestion of Hynes and Alexander36 to assign the largest νq to the sixfold coordinated B nuclei of the intericosahedric linkage forming the B84 unit depicted in Fig. 4b.90
Notwithstanding this, the following three observations lead us to a suggestion for signal assignment for the measured groups that differs from the one given by Hynes and Alexander:36 The experimental frequencies obtained for group II clearly differ from each other (i). In addition, only ref. 37 reports on the evidence of group III with the remark that the choice of ηq indirectly influences νq obtained by the spectra simulation process, whereas in ref. 36 the occurrence of νq ≈ 0 kHz is simply expected from symmetry considerations for the B sites B14 and B15 (ii). On the other hand, the agreement of values for the equatorial B(2) position in α-rB12 with those of Turner et al.37 is striking, although no fivefold coordinated atomic positions are obtained in the idealized structure of β-rB105 (iii).
According to Hynes and Alexander36 the atoms of the B11, B12 and B13 sites are assigned to the frequency group characterized with 130 ± 30 kHz (for 11B). Because a higher coordination number leads in general to a decrease of |Cq| and, hence, to νq as it is exemplarily shown for 23Na in several idealized environments in ref. 57 and 58. On the other hand, it is postulated that the central atoms of the B10 and B21 units on the B14 and B15 sites should lead to νq = 0 kHz. But in fact, investigating the geometrical arrangements of both centers in the idealized structure (B13 site fully occupied) shows that the conditions for which the EFG contributions add up to zero are not satisfied considering C3v or D3d symmetry, respectively.§ So it is much more likely that the corresponding νq is very small but not vanishing. This is also consistent with the recent observation37 that within the spectra simulations the signal features associated with a certain asymmetry parameter ηq can also be obtained by small variations in the quadrupolar frequency but with a slightly different ηq and, thereby, a supposed νq = 0 kHz is the consequence of assuming ηq = 0. As shown in tab:nmr and in the discussion of the next section this assumption is, however, not supported by theoretical calculations in general for B atoms in icosahedral arrangements. For these reasons, we argue that the associated group III of ref. 37 actually corresponds to groups II and III given in ref. 36. With the previous discussion on the B11, B12, B13 and B14 sites of the B10 unit forming multi-center bonds we conclude that these should be assigned to group II with 84 kHz measured in ref. 37. The contribution of group III might be related by the B15 site but a definite conclusion by comparison with α-rB12 only is not possible.
In addition, the interstitial B atoms on the partially occupied positions must also be taken into account in order to fully understand the experimental NMR spectrum. A relatively homogeneous electron density distribution can be assumed due to the delocalization of the electrons over all boron polyhedra, but the EFGs of B atoms close to the defect can be expected to differ significantly. Since the NMR is a local probe, ordered models have to be set up taking symmetry reduction into account. Our preliminary calculations on β-rB105 clearly indicate the trends for the fully occupied sites discussed here. A sophisticated way to model fractional site occupancy is provided by the SOD (site-occupancy disorder) program92 considering not only the energetic but also entropic contribution of a certain atomic configuration. Such inclusion of reasonable order variants is required for deeper exploration of the quadrupolar interactions in β-rB105.
3.3 Analysis of the EFG
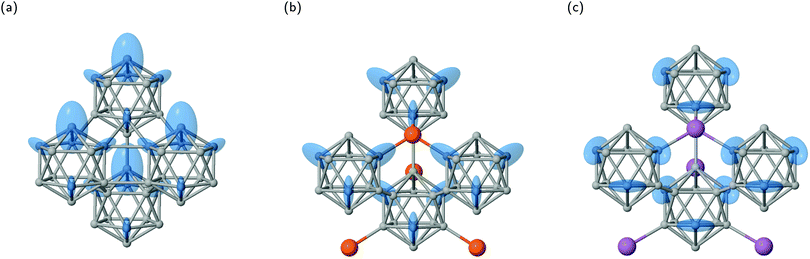
As the EFG is related to the charge distribution in the vicinity of the probe nucleus it follows from symmetry considerations that if the nuclear site is located on the rotational axis in an environment of Cnv symmetry the principal axis Vzz coincides with this axis. This is reported for example for B atoms in C2v site symmetry of dodecaborides with cuboctahedral B12 units where the exohedral bond is formed along the rotation axis.61 For the here investigated structures the B12 symmetry of Ih reduces to D3d and consequently the local environment of the nucleus changes from C5v to Cs. In this case, the remaining restriction for the orientation of two EFG principal axes is to lie within the plane σd causing the third axis to be exclusively perpendicular to σd. Based on this analysis, it becomes clear why values of ηq in Table 4 are not zero, that is the reduction of symmetry from Ih to D3d forces that the small orthogonal axes Vxx and Vyy cannot occur with the same magnitude. An a priori designation of ηq = 0 for icosahedral positions commonly made in experimental studies37,38,42,43 is, therefore, not justified from symmetry restriction. In fact, this misconception can even lead to deviations from the actual |Cq| (and νq) values by applied simulation procedures to recorded spectra.36,41It is illustrative to visualize the principal axes of the EFG tensor in their magnitude and orientation as ellipsoids as shown for α-rB12, B12P2 and B12As2 in Fig. 5. The large EFG axis Vzz coincides with the longest ellipsoid axis and the value of ηq influences the shape. The more symmetric or asymmetric the electron density is distributed around Vzz the more prolate (ηq = 0) or oblate (ηq = 1) the ellipsoid appears.
At first sight one would expect the highest gradients of the electric field running radial from the icosahedral center due to the dominance of the 2e2c exohedral bond formation1,19 as well as by the observation that the B12 polyhedron contains almost no electronic charge.25 And, thus, it might seem plausible that a pseudo fivefold axis of an icosahedral atom arrangement leads to the large principal axis pointing along the exohedral bond as in Fig. 5a and b. However, this is not true in general, as shown for carboranes,34 and can be even misleading as in the case of the equatorial B(2) site in B12As2 (see Fig. 5c).
More detailed information on the orientation of the EFG tensor's principal axes is provided by Table 6 with angles between Vzz and the radial axis of the B12 unit pointing along its center of mass ΘVzz, as well as between Vzz and the exohedral bond denoted by ΦVzz. Additionally, we refer to the averaged apex angles θav and 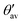 (see Fig. 6a for their definition) as a measure of deformation for the B12 polyhedra compared to the regular icosahedron after structure optimization. Their root-mean-square deviations can be found together with the kink angles of the exohedral bonds in Table S5 of the ESI.† The compound (B12H12)2− is added for comparison as a closely related structure of Ih symmetry using the geometry reported in ref. 63. Overall, we observe small angles between the Vzz axis and the bonding partner ΘVzz except for the B(2) site of B12As2 where also the apex angles are expanded the most compared to (B12H12)2−. In fact, the angle to the radial axis ΦVzz is smaller than ΘVzz for most cases. As one expects for (B12H12)2− the exohedral bond coincides with the large principal axis of the EFG. Note also how the B12 unit in α-rB12 shows the smallest deviations from the Ih symmetry with the Vzz axis pointing almost in the radial direction for both the 2e2c and 2e3c bond formations.
(see Fig. 6a for their definition) as a measure of deformation for the B12 polyhedra compared to the regular icosahedron after structure optimization. Their root-mean-square deviations can be found together with the kink angles of the exohedral bonds in Table S5 of the ESI.† The compound (B12H12)2− is added for comparison as a closely related structure of Ih symmetry using the geometry reported in ref. 63. Overall, we observe small angles between the Vzz axis and the bonding partner ΘVzz except for the B(2) site of B12As2 where also the apex angles are expanded the most compared to (B12H12)2−. In fact, the angle to the radial axis ΦVzz is smaller than ΘVzz for most cases. As one expects for (B12H12)2− the exohedral bond coincides with the large principal axis of the EFG. Note also how the B12 unit in α-rB12 shows the smallest deviations from the Ih symmetry with the Vzz axis pointing almost in the radial direction for both the 2e2c and 2e3c bond formations.
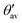 (see Fig. 6a for definition). Δ
(see Fig. 6a for definition). Δ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) denotes the absolute mean deviation from the magic angle θmag (≈54.74°) defined as |(θav +
denotes the absolute mean deviation from the magic angle θmag (≈54.74°) defined as |(θav + 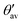 )/2 − θmag|. All values according to optimized structures
)/2 − θmag|. All values according to optimized structures
| Compound | Site | EFG related | Geometry related | |||
|---|---|---|---|---|---|---|
| Θ V zz | Φ V zz | θ av | Δ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) |
|||
| a Related to the center of the intericosahedral 2e3c bond. b Perpendicular to σd, see Fig. 5c. c All θ′ > θmag. | ||||||
| α-rB12 | B(1) | 7.66 | 0.47 | 58.43 | 52.77 | 0.86 |
| B(2) | 9.73a | 0.98 a | 58.14 | 52.46 | 0.56 | |
| B12P2 | B(1) | 5.44 | 4.44 | 56.34 | 50.56 | 1.29 |
| B(2) | 5.21 | 1.45 | 60.22 | 54.75 | 2.75 | |
| B12As2 | B(1) | 5.84 | 5.90 | 55.67 | 49.87 | 1.97 |
| B(2) | 90.00b | 60.89 | 55.52c | 3.47 | ||
| B12O2 | B(1) | 5.40 | 7.22 | 57.31 | 51.58 | 0.29 |
| B(2) | 5.55 | 3.52 | 59.26 | 53.69 | 1.74 | |
| (B12H12)2− | 0.02 | 0.02 | 58.28 | 52.62 | 0.71 | |
For simplicity and a better qualitative understanding of the meaning of the EFG components, we may analyze the Vzz values along the icosahedral diagonal by considering the point charge model (PCM). This method had been applied to understand and construct quite unexpected geometrical arrangements for molecules93 and solid phases91,94 where the EFG vanishes besides cubic symmetry. For instance, a charge distribution symmetric to the rotational axis of a cone with an opening angle twice the magic angle θmag, satisfying (3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θmag − 1) = 0, leads to an overall null tensor at the apex point of the cone. In fact, considering an in-depth treatment of second-order quadrupole effects, multiple magic angles can be derived not only from terms containing the Legendre polynomial of second-order P2(cos
θmag − 1) = 0, leads to an overall null tensor at the apex point of the cone. In fact, considering an in-depth treatment of second-order quadrupole effects, multiple magic angles can be derived not only from terms containing the Legendre polynomial of second-order P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ) but also from such fourth-order P4(cos
ϑ) but also from such fourth-order P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ).95 Here we only refer to the former one with θmag ≈ 54.74°.
ϑ).95 Here we only refer to the former one with θmag ≈ 54.74°.
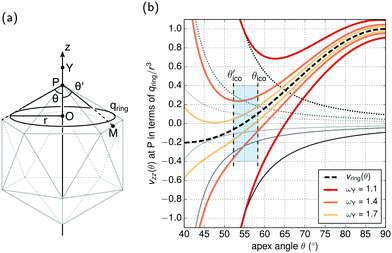
Let us consider Fig. 6a with the B atom under investigation at point P and where the z-axis coincides with the fivefold rotation axis as do the direction of the exohedral bond due to a geometrical arrangement of Ih symmetry. Since the EFG components scale with the inverse cubic distance (eqn (4)) we may assume that its contributions at point P are only given by the charged ring with radius r representing the endohedral bonds and a charge placed at point Y along the exohedral bond. There are many combinations of parameters to consider but we may write the resultant value of Vzz solely in terms of the apex angle θ and the ring charge to cubic radius ratio qring/r3. The corresponding curvature and its contributions are shown in Fig. 6b for the charge ratio |qY/qring| = 0.1. Reasonable distances between P and Y are indicated by the dimensionless constant ωY = OY/a with a as the edge length of the icosahedron. As shown in the Appendix, ωY increases with the distance PY. The two characteristic apex angles of the regular icosahedron 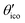 (≈52.62°) and θico (≈58.28°) are also illustrated in Fig. 6b for further discussion. It is important to mention that Vzz becomes negative in the marked region for charges on the ring and Y with the same sign. If we assume that the contribution of qring rises from electrons on the icosahedral surface this accordingly implies negative charge on Y causing a negative value of Vzz which is consistent with the more sophisticated explanation in ref. 57. As it is evident from Fig. 6b the ring contribution vring is zero for θmag and, hence, the contribution of the charge at Y is significant, this holds also true for angles θ in the interval
(≈52.62°) and θico (≈58.28°) are also illustrated in Fig. 6b for further discussion. It is important to mention that Vzz becomes negative in the marked region for charges on the ring and Y with the same sign. If we assume that the contribution of qring rises from electrons on the icosahedral surface this accordingly implies negative charge on Y causing a negative value of Vzz which is consistent with the more sophisticated explanation in ref. 57. As it is evident from Fig. 6b the ring contribution vring is zero for θmag and, hence, the contribution of the charge at Y is significant, this holds also true for angles θ in the interval 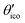 ≤ θ ≤ θico. The former theoretical and experimental investigations5,6,25,26 showed that the electron density is only significant on the icosahedron surface as well as on the exohedral bonds and vanishes rapidly elsewhere. Correspondingly, relaxing the assumption of point charges to a continuous charge density evenly spread on the surface leads to an endohedral contribution that nearly vanishes. And for this reason, EFG components Vzz pointing along the radial direction mainly reflect the charge distribution along the exohedral bonds. It is crucial to clarify that this is not true for vertex positions of other boron polyhedra as for example for octahedra in hexaborides55,96 because the geometry of the regular icosahedron is such that
≤ θ ≤ θico. The former theoretical and experimental investigations5,6,25,26 showed that the electron density is only significant on the icosahedron surface as well as on the exohedral bonds and vanishes rapidly elsewhere. Correspondingly, relaxing the assumption of point charges to a continuous charge density evenly spread on the surface leads to an endohedral contribution that nearly vanishes. And for this reason, EFG components Vzz pointing along the radial direction mainly reflect the charge distribution along the exohedral bonds. It is crucial to clarify that this is not true for vertex positions of other boron polyhedra as for example for octahedra in hexaborides55,96 because the geometry of the regular icosahedron is such that 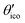 and θico are close to θmag with (
and θico are close to θmag with (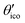 + θico)/2 ≈ θmag. This assists the understanding why |Cq| values in Table 4 for the B(1) atoms are approximately constant in the range of 1450 kHz and can be expected to barely change in other structurally related compounds. Furthermore, we may conceptualize with this geometric interpretation that for the B(2) site in B12As2 the Vzz axis is perpendicular to the B(2)–As bond as we observe such an increase in angles θ and θ′ in Table 6, that the influence of the endohedral bonds has a more significant impact on the EFG components compared to all other positions of the investigated compounds. In order to further illustrate this we additionally list in Table 6 the absolute mean deviation from the magic angle as Δ
+ θico)/2 ≈ θmag. This assists the understanding why |Cq| values in Table 4 for the B(1) atoms are approximately constant in the range of 1450 kHz and can be expected to barely change in other structurally related compounds. Furthermore, we may conceptualize with this geometric interpretation that for the B(2) site in B12As2 the Vzz axis is perpendicular to the B(2)–As bond as we observe such an increase in angles θ and θ′ in Table 6, that the influence of the endohedral bonds has a more significant impact on the EFG components compared to all other positions of the investigated compounds. In order to further illustrate this we additionally list in Table 6 the absolute mean deviation from the magic angle as Δ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) = |(θav + θav′)/2 − θmag|. Especially for B12As2 and the B(2) site in B12P2 the highest deviations occur indicating for geometrical reasons a growing influence of the endohedral bonding situation on the orientation of the Vzz axis.
= |(θav + θav′)/2 − θmag|. Especially for B12As2 and the B(2) site in B12P2 the highest deviations occur indicating for geometrical reasons a growing influence of the endohedral bonding situation on the orientation of the Vzz axis.
Table 7 shows the full set of EFG components related to the parameters given in Table 4 for both types of used PPs together with those calculated for the (B12H12)2− molecule. The magnitude of values is in the range of other computational investigations.60,61 For other borides and for α-rB12 our results agree well with calculated Vzz values by Schwarz et al.55 for B(1) and B(2) with −15.4 × 1020 and 8.8 × 1020 V m2, respectively.
| Compound | Site | NC | PAW | ||||
|---|---|---|---|---|---|---|---|
| V xx | V yy | V zz | V xx | V yy | V zz | ||
| a V zz axis perpendicular to σd, see Fig. 5c. b V zz axis along the B(2)–X direction. c V xx = Vyy. | |||||||
| α-rB12 | B(1) | 6.9 | 10.4 | −17.4 | 6.7 | 10.1 | −16.8 |
| B(2) | −2.8 | −6.2 | 9.0 | −2.7 | −5.9 | 8.5 | |
| B12P2 | B(1) | 6.5 | 9.9 | −16.4 | 5.5 | 9.6 | −15.1 |
| B(2) | −0.2 | −0.7 | 0.9a | 0.7 | 1.9 | −2.6b | |
| B12As2 | B(1) | 5.5 | 9.4 | −14.9 | 5.0 | 9.1 | −14.1 |
| B(2) | −0.4 | −3.0 | 3.3b | 0.7 | 1.3 | −2.1a | |
| B12O2 | B(1) | 6.2 | 8.1 | −14.3 | 6.5 | 8.0 | −14.5 |
| B(2) | −5.3 | −7.5 | 12.8 | −6.6 | −8.0 | 14.6 | |
| (B12H12)2− | 4.3c | −8.5 | 4.1c | −8.1 | |||
For now, we exclusively refer to the PAW values given in Table 7. The results of both PPs are discussed and compared below. From eqn (4) it follows that 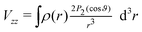 within the principal axis system of the EFG tensor. One may decompose Vzz into a lattice Vlatzz and spherical part Vllzz related to non-vanishing terms of angular momenta.59 Defining an anisotropy count Δnpz = (npx + npy)/2 − npz with partial charges npi in the corresponding p orbitals in a muffin tin sphere, it was shown for borides that the contribution
within the principal axis system of the EFG tensor. One may decompose Vzz into a lattice Vlatzz and spherical part Vllzz related to non-vanishing terms of angular momenta.59 Defining an anisotropy count Δnpz = (npx + npy)/2 − npz with partial charges npi in the corresponding p orbitals in a muffin tin sphere, it was shown for borides that the contribution 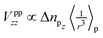 is much larger than Vlatzz, Vsdzz and Vpfzz.60,61 In the orbital picture one may, thus, neglect in good approximation the contributions by s orbitals and terms of mixtures with higher angular momenta as also discussed in the early work of Townes and Dailey56 for molecular systems. In fact, compared to hexaborides the factor
is much larger than Vlatzz, Vsdzz and Vpfzz.60,61 In the orbital picture one may, thus, neglect in good approximation the contributions by s orbitals and terms of mixtures with higher angular momenta as also discussed in the early work of Townes and Dailey56 for molecular systems. In fact, compared to hexaborides the factor 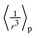 shows an increase by more than 50% for the icosahedral sites in α-rB12 and B4C.55 This is a consequence of the observation that 80% of the EFG components stem from contributions within a sphere of 0.69 Å around the B nuclei. Note that this is in the distance range dX–BCP of the B sites to the exohedral BCP in Table 3. Therefore, the rather large positive value of Vzz for the B(2) site of α-rB12 can be explained by the depopulation of the pz orbital donating electron density to the intericosahedral 2e3c bond. The density on the BCP ρ(rBCP) is the smallest value compared to all other BCPs and indicates the weakest bond in this compound which is in accordance with Lee et al.8 In B12O2 the O atom clearly dominates the bonding situation of the B(2) site as the interstitial bond is the shortest occurring amongst all compounds investigated here (see Table 2). The value ρ(rBCP) is the highest of all exohedral B(2) bonds which is in total agreement with the orientation of the large principal axis. Consequently, the positive Vzz value reflects the large shift of the BCP towards the B(2) atom with dB(2)–BCP = 0.487 Å and the strong ionic bond character confirmed by the positive Laplacian ∇2ρ(rBCP) = 12.018 e Å−5. Regarding B12P2 and B12As2 there are intraicosahedral distances smaller than the interstitial bond lengths. Further analysis of ρ(rBCP) shows that the largest value of the equatorial B(2) is given by the exohedral bond in B12P2, whereas we obtain the maximal ρ(rBCP) for the endohedral B(2)–B(2) bond in B12As2 (see also Table 3). In the case of B12P2 we interpret the negative value of Vzz caused by depopulation of the pz orbital by bond polarisation of the more electronegative P atom. In contrast to B12O2, this bond is covalent, in particular there is much less depopulation, which leads to a more moderate decrease of electron density compared to endohedral B(1)–B(2) or B(2)–B(2) bonds. Consequently, the charge anisotropy Δnpz tends to zero and causes small negative Vzz. In B12As2 we obtain the exohedral B(2)–As bond to be weaker than the B(2)–P interaction. This is in accordance with increasing bond distance and the decrease of electronegativity difference from P to As as compared to B. Additionally, the intraicosahedral B(2)–B(2) distance in B12As2 is shortened compared to the one in B12P2 culminating to domination of this endohedral bond formation. This is in contrast to all other sites investigated in this work and leads to the large principal axis Vzz being perpendicular to σd as shown in Fig. 5c.
shows an increase by more than 50% for the icosahedral sites in α-rB12 and B4C.55 This is a consequence of the observation that 80% of the EFG components stem from contributions within a sphere of 0.69 Å around the B nuclei. Note that this is in the distance range dX–BCP of the B sites to the exohedral BCP in Table 3. Therefore, the rather large positive value of Vzz for the B(2) site of α-rB12 can be explained by the depopulation of the pz orbital donating electron density to the intericosahedral 2e3c bond. The density on the BCP ρ(rBCP) is the smallest value compared to all other BCPs and indicates the weakest bond in this compound which is in accordance with Lee et al.8 In B12O2 the O atom clearly dominates the bonding situation of the B(2) site as the interstitial bond is the shortest occurring amongst all compounds investigated here (see Table 2). The value ρ(rBCP) is the highest of all exohedral B(2) bonds which is in total agreement with the orientation of the large principal axis. Consequently, the positive Vzz value reflects the large shift of the BCP towards the B(2) atom with dB(2)–BCP = 0.487 Å and the strong ionic bond character confirmed by the positive Laplacian ∇2ρ(rBCP) = 12.018 e Å−5. Regarding B12P2 and B12As2 there are intraicosahedral distances smaller than the interstitial bond lengths. Further analysis of ρ(rBCP) shows that the largest value of the equatorial B(2) is given by the exohedral bond in B12P2, whereas we obtain the maximal ρ(rBCP) for the endohedral B(2)–B(2) bond in B12As2 (see also Table 3). In the case of B12P2 we interpret the negative value of Vzz caused by depopulation of the pz orbital by bond polarisation of the more electronegative P atom. In contrast to B12O2, this bond is covalent, in particular there is much less depopulation, which leads to a more moderate decrease of electron density compared to endohedral B(1)–B(2) or B(2)–B(2) bonds. Consequently, the charge anisotropy Δnpz tends to zero and causes small negative Vzz. In B12As2 we obtain the exohedral B(2)–As bond to be weaker than the B(2)–P interaction. This is in accordance with increasing bond distance and the decrease of electronegativity difference from P to As as compared to B. Additionally, the intraicosahedral B(2)–B(2) distance in B12As2 is shortened compared to the one in B12P2 culminating to domination of this endohedral bond formation. This is in contrast to all other sites investigated in this work and leads to the large principal axis Vzz being perpendicular to σd as shown in Fig. 5c.
The two Vzz for the B(2) site in α-rB12 and the B atoms in (B12H12)2− show different signs but lead to similar |Cq| values. From the former analysis it is clear that the resulting similarity in the quadrupolar constant |Cq| is coincidental because it arises from two completely different electronic situations: In α-rB12 the lack of electron population along the Vzz axis leads to a positive value, whereas the negative sign for (B12H12)2− corresponds to the covalent exohedral B–H formation. Compared to the homonuclear B(1)–B(1) bonds the more positive value of −8.1 × 1020 V m2 can be explained by the bond polarisation caused from the more electronegative H atom depopulating the pz orbital in the vicinity of the B nucleus.
Turning to the applied PP types, NC and PAW yield similar components except for the equatorial B(2) sites in B12P2 and B12As2 where we obtain different orientations for the large principal axis Vzz. This can be explained by the inadequate description of the electron density close to the nucleus under investigation by PPs relying on the NC construction. The represented charge density distribution in the vicinity of the B(2) sites differ and accordingly the EFG components become sensitive to the theoretical description by the selected PP. For these sites we also obtain the largest Δ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) in Table 6 meaning that the correct modelling of the endohedral bonding situation becomes more crucial the more distorted the B12 unit is.
in Table 6 meaning that the correct modelling of the endohedral bonding situation becomes more crucial the more distorted the B12 unit is.
Furthermore, this shows that the orientation of the principal axes can have major influence on ηq. Regarding B12As2, the different oriented Vzz axis for NC and PAW also changes the orientation and magnitude of the two small principal axes Vxx and Vyy. This in turn modifies the ratio of (Vxx − Vyy)/Vzz causing ηq in Table 4 to result in significant different values for B(2) of 0.77 and 0.29. Concomitantly, we want to hint on the sensitivity of ηq with regard to the component value Vzz. The smaller the calculated Vzz values are the more significant the relative deviations in Vxx and Vyy become. For example, in B12P2 and B12O2 the absolute values of |Vyy − Vxx| for the B(2) site are comparable but result in very different ηq in Table 4. In summary, the reliability of theoretical values is critical for small |Cq| and explains rather large deviations between NC and PAW in ηq for the B(2) sites in Table 4. Therefore, we recommend a careful check of calculated “core” properties by the PAW construction when the approximation with pseudoization of inner shell electrons is applied, even for the 1s2 configuration.
With this we conclude that the main principal axis of the EFG tensor indicates under particular symmetry restrictions the strongest or weakest bond formation in the investigated compounds. Besides the electronegativity difference to exohedral bonding partners, geometric aspects of the B12 unit, in particular its distortion, are also mandatory for an in-depth understanding of the Vzz values for the various B sites in boron-rich borides with icosahedral structure elements. Both the electronic and the geometric structures do not influence the quadrupolar interaction independently but need to be considered in conjunction with each other.
4 Conclusions
In this paper we calculated the quadrupolar interaction and, for the first time, chemical shift parameters of the rhombohedral phases α-rB12 and B12X2 (X = P, As, O) where B12 icosahedra are the main structure element. The GIPAW approach is capable of providing parameter sets which show a good bridging between XRD and NMR models for our recorded MAS spectra of α-rB12 and B12P2. The shift parameters are in good agreement for both established construction schemes of PPs with exceptions for δcsa and ηcs in B12As2. Despite the pseudoization of the inner shell electrons by NC conditions, the PAW construction allows an all electron treatment. This becomes more significant when quadrupolar parameters are considered which are directly related to the EFG tensor. Consequently, the measured MAS NMR spectra and especially their side band patterns should be addressed with results from PAW. For the systems at hand, the calculated coupling constants are in general too small to obtain second-order quadrupolar splittings as had been proposed by other studies.38,41 Furthermore, the determined |Cq| values of α-rB12 enabled us to draw a connection to observed quadupolar frequencies νq of β-rB105, which can be divided into three distinct groups. We suggest an assignment based on the results of our calculations and discuss the indirect influence of the assumption ηq = 0 for values of |Cq| or νq yielded by the usual fitting procedure of measured spectra. The reduction of symmetry from Ih to D3d of the B12 units excludes this commonly a priori applied postulation for ηq in general which might be only justified for ionic cases or at least strong bond polarisations where Vxx − Vyy values are of smaller magnitude than Vzz as for instance in B12O2. We want to point out that a guessed value of ηq also implies an expectation of orientation for the Vzz axis and the symmetry of its environment. Accordingly, the distribution of the electron density in the vicinity of the nucleus and possibly also the predominant bond formation is assumed. However, this is not always clear without quantum chemical calculations or XRD measurements and can lead to inaccurate results for |Cq| or νq obtained by simulations of experimental spectra. Further investigations on the here studied compounds by more sophisticated NMR techniques such as multimagnetic field or multiquantum MAS measurements will help for more detailed insight into experimental values. In this context one should not forget that XRD produces average structural models over long atomic distances whereas both DFT calculations and NMR measurements are based on the local environment of atoms.The analysis of the polyhedral arrangement of the B atoms by distances and apex angles indicates small distortions in the order of α-rB12, B12O2, B12P2 and B12As2 from a regular icosahedron. Applying QTAIM analysis we observe charges and bond formation that are in general agreement with other investigations on the electronic structures. However, these charges indicate no simple relation to the calculated isotropic chemical shifts which might be a consequence of the covalent character of the studied compounds as this is also obtained for the more shielded 11B species in icosahedral closo-dodecaheteroboranes.63 Thus, our results do not confirm the presumption stated by Lee et al.41 that measured differences in chemical shifts of the B atoms relate to the bonds they form outside the icosahedron. Interpreting the charge density on a BCP ρ(rBCP) to be correlated with bond strength, the polar B(1) sites exclusively form strongest bonds exohedral to other B12 units. This holds also true for the equatorial B(2) sites of B12P2 and B12O2 connected to the interstitial unit X2, whereas we find for α-rB12 but more surprisingly for B12As2 highest ρ(rBCP) for endohedral B(2)–B(2) bonds.
Investigating the principal axes of the EFG tensor we obtain a good approximation that Vzz is oriented along the exohedral bond except for B(2) of B12As2 where it is perpendicular to the mirror plane σd. A general inspection of the apex angles 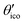 and θico of the regular icosahedron in combination with the PCM reveals that the most significant contribution for Vzz can be expected from the electronic situation within the nuclear vicinity along the exohedral bond. Therefore, the sign and magnitude of Vzz is nearly constant for the B(1) sites (|Cq| ≈ 1450 kHz) and strongly correlated with the electron density on the exohedral bonding path of the B(2) sites. This effect is closely related to the special icosahedral geometry for which (
and θico of the regular icosahedron in combination with the PCM reveals that the most significant contribution for Vzz can be expected from the electronic situation within the nuclear vicinity along the exohedral bond. Therefore, the sign and magnitude of Vzz is nearly constant for the B(1) sites (|Cq| ≈ 1450 kHz) and strongly correlated with the electron density on the exohedral bonding path of the B(2) sites. This effect is closely related to the special icosahedral geometry for which (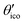 + θico)/2 ≈ θmag is well fulfilled and consequently the influence by endohedral bonding partners is of minor significance. Note that other regular polyhedra such as the cube or octahedron do not meet this spatial condition. Accordingly, we find for the B(2) sites in B12P2 and B12As2 not only strong distortions for the apex angles but also that the description of Vzz in orientation and magnitude depends critically on the type of PP. With PAW, the Vzz axis of B(2) in B12P2 lines up with the exohedral B(2)–P bond whereas in B12As2 it points along the direction of the endohedral B(2)–B(2) bond. Thus, the orientation of the large principal axis of the EFG tensor indicates under particular symmetry restrictions the strongest or, in the case of the B(2) site of α-rB12, the weakest bond formation for the here investigated compounds.
+ θico)/2 ≈ θmag is well fulfilled and consequently the influence by endohedral bonding partners is of minor significance. Note that other regular polyhedra such as the cube or octahedron do not meet this spatial condition. Accordingly, we find for the B(2) sites in B12P2 and B12As2 not only strong distortions for the apex angles but also that the description of Vzz in orientation and magnitude depends critically on the type of PP. With PAW, the Vzz axis of B(2) in B12P2 lines up with the exohedral B(2)–P bond whereas in B12As2 it points along the direction of the endohedral B(2)–B(2) bond. Thus, the orientation of the large principal axis of the EFG tensor indicates under particular symmetry restrictions the strongest or, in the case of the B(2) site of α-rB12, the weakest bond formation for the here investigated compounds.
Altogether GIPAW may be utilized not only to study structural changes with theoretical modeling and compare to NMR experiments, but to address the obstacles for 11B measurements on solid-state compounds, in particular peak overlap and possibly uncorrelated site to actual peak intensity/area ratio. Thus, calculated parameters may clarify and elucidate which site is measured and to which certain extent they contribute to signals in a variety of complex spectra. With this at hand, one is able to expand to even more complicated systems and investigate certain structural or electronic influences and open the possibility to understand more complex NMR spectra and conceptualize results on theoretical foundation.
Conflicts of interest
There are no conflicts to declare.Appendix: qualitative understanding by the point charge model
For the qualitative understanding of the EFG we consider Fig. 6 showing Vzz along the fivefold rotation axis of the icosahedron assuming the PCM. For a derivation let us assume the electric field![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) on a given point
on a given point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) caused by a set of point charges qi located at
caused by a set of point charges qi located at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i in atomic units (Eh/(ea0)) as
i in atomic units (Eh/(ea0)) as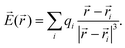 | (8) |
Since the EFG scales with the inverse cube of distance we only consider for the electric field in point P (five evenly spaced) charges on a ring summing up to qring and the charge qY on point Y. Choosing the center of the ring as the origin O the contributions for the EFG component Vzz = Vring(z) + VY(z) in P along the z-axis can be obtained by differentiation of eqn (8) yielding93
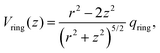 | (9) |
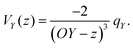 | (10) |
In general there is a very wide combination of possible parameters to analyze the behaviour of the EFG. However, we may reduce this complexity by expressing Vzz in terms of qring/r3 as vzz(θ) = vring(θ) + vY(θ) leading to sole dependence on the apex angle θ
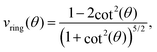 | (11) |
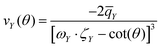 | (12) |
![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) Y = qY/qring as well as the geometrical characteristic ratios ζY and ωY. Note that this expression is related to atomic units, in particular it holds 4πε0 = 1.
Y = qY/qring as well as the geometrical characteristic ratios ζY and ωY. Note that this expression is related to atomic units, in particular it holds 4πε0 = 1.
Table 8 shows geometrical quantities of a regular icosahedron with edge length a. Due to the fivefold rotation axis the golden ratio ϕ plays an important role in icosahedral geometry. Assuming that the electronic charge is located on the midpoint of all bonds a reasonable estimation is given by 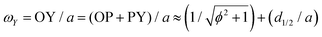 with d1/2 as half of the exohedral bonding distance. Accordingly, the depicted values of ωY in Fig. 6 correspond to the cases of B(2) in Table 2 for α-rB12 and B12As2. For reasons of appearance
with d1/2 as half of the exohedral bonding distance. Accordingly, the depicted values of ωY in Fig. 6 correspond to the cases of B(2) in Table 2 for α-rB12 and B12As2. For reasons of appearance ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) Y = 0.1 is selected.
Y = 0.1 is selected.
Acknowledgements
The authors thank Prof. Dr Ismail Duman for a high purity sample of α-rB12, and Dr Anke Schaub for the MAS NMR measurements.References
- H. Longuet-Higgins and M. D. V. Roberts, Proc. R. Soc. London, Ser. A, 1955, 230, 110–119 CAS.
- B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668 CrossRef CAS PubMed.
- K. Wade, J. Chem. Soc. D, 1971, 792–793 RSC.
- P. Melichar, D. Hnyk and J. Fanfrlík, Chem. Phys. Phys. Chem., 2018, 20, 4666–4675 RSC.
- D. Förster, PhD thesis, Freie Universität Berlin, 2008.
- S. Mebs, R. Kalinowski, S. Grabowsky, D. Förster, R. Kickbusch, E. Justus, W. Morgenroth, C. Paulmann, P. Luger, D. Gabel and D. Lentz, Inorg. Chem., 2011, 50, 90–103 CrossRef CAS PubMed.
- G. Will and B. Kiefer, Z. Anorg. Allg. Chem., 2001, 627, 2100–2104 CrossRef CAS.
- S. Lee, D. M. Bylander and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 1316–1320 CrossRef CAS PubMed.
- D. Li, Y.-N. Xu and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 5895–5905 CrossRef CAS PubMed.
- U. Häussermann and A. S. Mikhaylushkin, Inorg. Chem., 2010, 49, 11270–11275 CrossRef.
- X. F. Zhou, A. R. Oganov, X. Shao, Q. Zhu and H. T. Wang, Phys. Rev. Lett., 2014, 113, 1–5 Search PubMed.
- G. A. Slack, C. I. Hejna, M. F. Garbauskas and J. S. Kasper, J. Solid State Chem., 1988, 76, 52–63 CrossRef CAS.
- A. T. Lech, C. L. Turner, R. Mohammadi, S. H. Tolbert and R. B. Kaner, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3223–3228 CrossRef CAS PubMed.
- B. Morosin, T. L. Aselage and R. S. Feigelson, MRS Proc., 1987, 97, 145–150 CrossRef CAS.
- B. Morosin, G. Kwei, A. Lawson, T. Aselage and D. Emin, J. Alloys Compd., 1995, 226, 121–125 CrossRef CAS.
- G. H. Kwei and B. Morosin, J. Phys. Chem., 1996, 100, 8031–8039 CrossRef CAS.
- N. Vojteer, PhD thesis, Albert-Ludwigs-Universität Freiburg im Breisgau, 2008.
- H. Bolmgren, T. Lundström and S. Okada, AIP Conf. Proc., 1991, pp. 197–200 Search PubMed.
- D. Emin, Phys. Today, 1987, 40, 55–62 CrossRef CAS.
- S. Lee, S. W. Kim, D. M. Bylander and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 3550–3554 CrossRef CAS PubMed.
- I. Morrison, D. M. Bylander and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 1533–1537 CrossRef CAS.
- D. Li and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 17073–17083 CrossRef CAS.
- D. Li and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1451–1454 CrossRef CAS.
- F. Gao, X. Qin, L. Wang, Y. He, G. Sun, L. Hou and W. Wang, J. Phys. Chem. B, 2005, 109, 14892–14895 CrossRef CAS PubMed.
- V. Sagawe, PhD thesis, Albert-Ludwigs-Universität Freiburg im Breisgau, 2013.
- D. Emin, D. G. Evans and S. S. McCready, Phys. Status Solidi B, 1998, 205, 311–313 CrossRef CAS.
- G. A. Slack and K. E. Morgan, J. Phys. Chem. Solids, 2014, 75, 1054–1074 CrossRef CAS.
- D. Eklöf, A. Fischer, A. Ektarawong, A. Jaworski, A. J. Pell, J. Grins, S. I. Simak, B. Alling, Y. Wu, M. Widom, W. Scherer and U. Häussermann, ACS Omega, 2019, 4, 18741–18759 CrossRef PubMed.
- T. Bräuniger and M. Jansen, Z. Anorg. Allg. Chem., 2013, 639, 857–879 CrossRef.
- S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204 RSC.
- Y. T. Angel Wong and D. L. Bryce, Recent Advances in 11B Solid-State Nuclear Magnetic Resonance Spectroscopy of Crystalline Solids, Elsevier Ltd., 1st edn, 2018, vol. 93, pp. 213–279 Search PubMed.
- D. Simeone, C. Mallet, P. Dubuisson, G. Baldinozzi, C. Gervais and J. Maquet, J. Nucl. Mater., 2000, 277, 1–10 CrossRef CAS.
- C. Benndorf, M. de Oliveira, C. Doerenkamp, F. Haarmann, T. Fickenscher, J. Kösters, H. Eckert and R. Pöttgen, Dalton Trans., 2019, 48, 1118–1128 RSC.
- A. Lötz and J. Voitländer, J. Chem. Phys., 1991, 95, 3208–3212 CrossRef.
- I. Tiritiris, T. Schleid and K. Müller, Appl. Magn. Reson., 2007, 32, 459–481 CrossRef CAS.
- T. V. Hynes and M. N. Alexander, J. Chem. Phys., 1971, 54, 5296–5310 CrossRef CAS.
- C. L. Turner, R. E. Taylor and R. B. Kaner, J. Phys. Chem. C, 2015, 119, 13807–13813 CrossRef CAS.
- A. H. Silver and P. J. Bray, J. Chem. Phys., 1959, 31, 247–253 CrossRef CAS.
- R. J. Kirkpatrick, T. Aselage, B. L. Phillips and B. Montez, AIP Conf. Proc., 1991, pp. 261–270 Search PubMed.
- T. Harazono, Y. Hiroyama and T. Watanabe, Bull. Chem. Soc. Jpn., 1996, 69, 2419–2423 CrossRef CAS.
- D. Lee, P. J. Bray and T. L. Aselage, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 11, 4435–4450 CrossRef CAS.
- K. Kanehashi and K. Saito, J. Mol. Struct., 2002, 602–603, 105–113 CrossRef CAS.
- K. Kanehashi, K. Saito and H. Sugisawa, Chem. Lett., 2000, 588–589 CrossRef CAS.
- J. Hoard, D. Sullenger, C. Kennard and R. Hughes, J. Solid State Chem., 1970, 1, 268–277 CrossRef CAS.
- B. Callmer, Acta Crystallogr., Sect. B: Struct. Sci., 1977, 33, 1951–1954 CrossRef.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- J. Cuny, R. Gautier and J.-F. Halet, Handbook Solid State Chemistry, Wiley, 2017, pp. 607–646 Search PubMed.
- M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541–548 CrossRef CAS PubMed.
- F. Franco, M. Baricco, M. R. Chierotti, R. Gobetto and C. Nervi, J. Phys. Chem. C, 2013, 117, 9991–9998 CrossRef CAS.
- S. Sen, Mol. Simul., 2008, 34, 1115–1120 CrossRef CAS.
- F. Mauri, N. Vast and C. J. Pickard, Phys. Rev. Lett., 2001, 87, 85506 CrossRef CAS.
- A. Samoson, Chem. Phys. Lett., 1985, 119, 29–32 CrossRef CAS.
- D. Freude, J. Haase, J. Klinowski, T. A. Carpenter and G. Ronikier, Chem. Phys. Lett., 1985, 119, 365–367 CrossRef CAS.
- L. Hoffmann, J. Beerwerth, D. Greim, J. Senker, C. Sternemann, W. Hiller and R. Böhmer, J. Chem. Phys., 2020, 152, 034503 CrossRef CAS PubMed.
- K. Schwarz, H. Ripplinger and P. Blaha, Z. Naturforsch., A: Phys. Sci., 1996, 51, 527–533 CrossRef CAS.
- C. H. Townes and B. P. Dailey, J. Chem. Phys., 1949, 17, 782–796 CrossRef CAS.
- J. Autschbach, S. Zheng and R. W. Schurko, Concepts Magn. Reson., Part A, 2010, 36A, 84–126 CrossRef CAS.
- A. P. Kentgens, Geoderma, 1997, 80, 271–306 CrossRef CAS.
- P. Blaha, K. Schwarz and P. H. Dederichs, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 2792–2796 CrossRef CAS PubMed.
- B. Jäger, S. Paluch, W. Wolf, P. Herzig, O. J. Zoga&poll, N. Shitsevalova and Y. Paderno, J. Alloys Compd., 2004, 383, 232–238 CrossRef.
- B. Jäger, S. Paluch, O. J. Zoga&poll, W. Wolf, P. Herzig, V. B. Filippov, N. Shitsevalova and Y. Paderno, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 18, 2525–2535 Search PubMed.
- F. A. Perras and D. L. Bryce, J. Chem. Phys., 2013, 138, 174202 CrossRef PubMed.
- M. Ludwig, D. Himmel and H. Hillebrecht, J. Phys. Chem. A, 2020, 124, 2173–2185 CrossRef CAS PubMed.
- From Technical University Instanbul, Turkey.
- R. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1994 Search PubMed.
- R. K. Harris, E. D. Becker, S. M. Cabral De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59–84 CAS.
- M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330 CrossRef CAS PubMed.
- S. Heřmánek, Inorg. Chim. Acta, 1999, 289, 20–44 CrossRef.
- P. Pyykkö, Mol. Phys., 2018, 116, 1328–1338 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 21, 395502 Search PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 29, 465901 CrossRef CAS PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- T. Björkman, Comput. Phys. Commun., 2011, 182, 1183–1186 CrossRef.
- All atomic positions are perturbed assuming P1 symmetry.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. Otero-de-la Roza, M. A. Blanco, A. M. Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157–166 CrossRef CAS.
- A. Otero-de-la Roza, E. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018 CrossRef CAS.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 64111 CrossRef PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- F. Mauri, B. G. Pfrommer and S. G. Louie, Phys. Rev. Lett., 1996, 77, 5300–5303 CrossRef CAS PubMed.
- F. Mauri and S. G. Louie, Phys. Rev. Lett., 1996, 76, 4246–4249 CrossRef CAS PubMed.
- D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J.-O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Magn. Reson. Chem., 2002, 40, 70–76 CrossRef CAS.
- S. Sturniolo, T. F. Green, R. M. Hanson, M. Zilka, K. Refson, P. Hodgkinson, S. P. Brown and J. R. Yates, Solid State Nucl. Magn. Reson., 2016, 78, 64–70 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- Almost all deviations are less than 0.08.
- As recent studies ref. 28 discuss the compound denoted with SiB4 in ref. 42 refers to the α-SiB3−x phase .
- Symmetry forces that ηq = 0.
- The corresponding sites of ref. 12 are enumerated from B1 to B10.
- O. Knop, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 147–149 CrossRef.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 19, 256201 CrossRef.
- J. W. Akitt and W. S. McDonald, J. Magn. Reson., 1984, 58, 401–412 CAS.
- O. Knop, E. M. Palmer and R. W. Robinson, Acta Crystallogr., Sect. A: Found. Crystallogr., 1975, 31, 19–31 CrossRef.
- K. J. D. MacKenzie and M. E. Smith, Multinuclear Solid-State NMR of Inorganic Materials, Elsevier, 2002, pp. 23–108 Search PubMed.
- R. E. J. Sears, J. Chem. Phys., 1982, 76, 5651–5652 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04061d |
| ‡ Without consideration of χ the shifts δiso are deshielded by about 10 ppm to 15 ppm, whereas only minor changes occur for δcsa; for details see Table S2 in the ESI.† |
| § For this, we refer to expressions (3) and (4) of ref. 91. |
| This journal is © the Owner Societies 2021 |