Branched versus linear lactide chains for cellulose nanoparticle modification: an atomistic molecular dynamics study

Abstract

We studied the structure of brushes consisting of branched oligolactide (OLA) chains grafted onto the surface of cellulose nanoparticles (CNPs) in polylactide (PLA) and compared the outcomes to the case of grafting linear OLA chains using atomistic molecular dynamics simulations. The systems were considered in a melt state. The branched model OLA chains comprised one branching point and three branches, while the linear OLA chains examined had a molecular weight similar to the branched chains. It was shown that free branches of the branched OLA chains tend to fold back toward the CNPs due to dipole–dipole interactions within the grafted layer, in contrast to the well-established behavior of the grafted uncharged branched chains. This result, however, is in qualitative agreement with the conformational behavior known for linear OLA chains. At the same time, no significant difference in the effectiveness of covering the filler surface with grafted branched or linear OLA chains was found. In terms of the expelling ability of the grafted chains and the interaction between PLA and CNP or OLA, the linear chains were broadly similar (sparse grafting) or better (intermediate or dense grafting) compared to the branched ones. Thus, the grafted lactide chains with a linear architecture, rather than their branched counterpart, may be preferable for the covalent modification of cellulose nanoparticles.

---

1 Introduction

Eco-friendly polylactide (PLA)-based composites filled with cellulose nanoparticles (CNPs) are of profound interest today for both experimental and theoretical research.^1–4 Their composition is indeed intriguing. They include PLA, a commercial, biodegradable and biocompatible polymer binder as their key component.⁵ The second, but equally important component, is CNPs used as a “green” nanofiller, due to their wide availability, low cost and excellent performance.^6–9 Therefore, these composites have become attractive for practical implementation in different fields, particularly, in agriculture, food packaging and medicine.^1,2,10

Although CNPs are used for the application-oriented control of nanocomposites’ properties, they often tend to aggregate in the PLA due to a weak adhesion between the hydrophilic nanofiller and the hydrophobic binder.^11,12 This in turn may lead to a decrease in the CNPs’ surface area available for interaction with the PLA, and thus to the impossibility of attaining the required improvement in the properties of the nanocomposite.^13–17 This aggregation can be overcome by using CNPs with a chemically modified surface.^7,12 Various synthetic techniques for the modification have been successfully developed, with one of the most used being a covalent grafting of linear lactide chains onto a nanofiller surface (a brush-like coating).^{1,7,12,13,15,17–25}

However, recently the grafting of branched chains has gained increased research interest due to advancements in chemical synthesis.^26–31 For example, multi-walled carbon nanotubes covalently modified by the grafting of four-arm PLA stars have been used as a filler to obtain PLA-based composites with improved morphological, rheological, and mechanical properties.³² Nevertheless, the synthesis and study of grafted chains with a branched architecture remain problematic from the experimental standpoint.^29,31 This fact has inspired numerous theoretical studies focused on a detailed description of the structure of these special polymer systems.^33–51

In particular, mean field theory,^{33,35,40,43,46,48,49} analytical^{36–39,46,47,49,50} and numerical^{33,35–42,46,47,50} self-consistent field calculations, and PRISM theory,⁵¹ as well as Langevin^{34,43,44,46,48,51} and Brownian⁴⁵ dynamics computer simulations have been used to investigate polymer brushes consisting of grafted branched chains immersed in a solvent or polymer melt. The typical systems studied were described using coarse-grained models.^33–51 They consisted of an impenetrable surface decorated by the grafted chains. Either a freely joined or a bead-spring chain represented each grafted chain. Correspondingly, the structural unit of the models was a statistical segment or a bead. Note that such a generic coarse-grained description significantly reduces the number of degrees of freedom under consideration and, consequently, the computational cost of calculations in comparison with atomistic models. This is one of the main reasons why the coarse-grained models of polymer brushes consisting of branched chains have been employed so far. These models allowed for a systematic determination of the structure of the grafted branched chains in a wide range of grafting densities and chain lengths, especially for chains with a varying complexity of architecture.^33–51 These theoretical efforts have formed a fundamental understanding of the molecular features inherent to polymer brushes consisting of grafted branched chains, which could prove important to the development of PLA-based composites.

For example, evaluation of the influence of the grafting density σ on the structure of brushes consisting of uncharged chains with one branching point of the functionality three (three-arm stars) showed that the grafted chains are weakly extended under sparse grafting.^40,41 An increase in σ may result in stretching of the grafted chains due to excluded volume interactions between them. However, reaching the extension limit for the root branch (the branch through which the chain is grafted onto the surface) at a certain σ value may result in the separation of the grafted chains into two populations with weakly and strongly stretched branches.^{34,35,40,41,45} In the latter case, the free branches of strongly stretched chains forming the brush periphery can be considered as a familiar linear brush.^33,37,46,48 The transition to a two population brush structure was obtained by Polotsky et al.⁴⁰ using self-consistent field calculations and was confirmed by Merlitz et al.³⁴ and Gergidis et al.⁴⁵ using Langevin and Brownian dynamics simulations, respectively.

It is worth noting that an important characteristic emerges in the brushes consisting of regularly branched chains, namely a number of repeating units L in the “longest path” connecting the grafting point in the root branch with any of the free chain ends. Obviously, in the case of grafted linear chains, L is equal to the degree of polymerization n of the entire macromolecule, L = n, whereas for grafted branched chains L < n. The degree of polymerization n defines the “load”, which is the mass of the grafted polymer per unit surface area, while the “longest path” determines the maximum possible brush thickness H (obviously, H ≤ L). Therefore, branched chains can form a denser grafted layer with a smaller thickness than linear chains with the same molecular weight.^35,38,40 On the one hand, it can be assumed that a similar coverage of the grafting surface may be obtained using branched chains at a lower σ value than that in the case of linear chains, i.e. grafted branched chains have a higher effectiveness in terms of covering the filler surface. On the other hand, the lesser thickness of the grafted layer consisting of branched chains indicates that they expel the surrounding free chains at smaller distances than linear chains, i.e. grafted branched chains have a lower expelling ability. Meanwhile, Kazakov et al.⁵⁰ demonstrated that the penetration depth between grafted chains and free chains of a polymer binder is lower in the case of branched chains than for linear ones. This penetration depth determines the wetting of grafted chains by the free chains and, in turn, the dispersion of the filler in the system.^52,53 A decrease in the penetration depth, which is the case for branched chains as compared to linear chains, can result in a decrease of the filler's dispersibility.^51–57 However, it was reported that the use of branched grafted chains may stabilize colloidal suspensions better than the use of linear ones.^27,49

While these studies^{1,7,12,27,32,35,38,40,50–57} represent significant contributions in the fields of polymer composites and polymer brushes, it is unclear which chain architecture (linear or branched) of lactide chains should be preferably used to modify the CNPs’ surface, this choice being especially difficult due to the doubtful applicability of the previous data^33–51 on the structure of grafted branched chains to the branched lactide chains grafted to the CNPs’ surface. In particular, previously used theoretical models did not consider grafting of branched chains with dipolar repeating units. It is known from atomistic molecular dynamic (MD) simulations and self-consistent field calculations that dipole–dipole interactions may result in the tendency of the grafted dipolar linear chains to backfold toward the filler surface.^58–62 The segregation of grafted linear lactide chains into populations of backfolded and stretched chains can be observed even under dense grafting.^58,60 Densely grafted linear lactide chains composed of at least 30 repeating units (∼10 Kuhn segments) may form an ordered structure with a fraction of grafted chain fragments adopting a helical conformation similar to that of a PLA α-crystal.⁶¹ Thus, dipolar interactions significantly affect the structure of grafted linear lactide chains. However, the question as to what role these interactions play in the grafted lactide chains with branched architecture remains open.

Hence, special attention must be paid to a detailed analysis of the structure of these grafted chains in comparison with the previous results for coarse-grained model brushes consisting of uncharged branched chains. This analysis is one of the main objectives of the present study. To this end, we examine branched lactide chains grafted to the CNPs’ surface immersed in PLA using atomistic MD simulations. Another objective of the study is to compare the structure of the grafted linear (previously studied^58–63) and branched lactide chains, and to evaluate whether the chains with a linear architecture are inferior to the branched ones in terms of their use for CNP surface modification required in practically valuable PLA-based composites.

The reminder of this paper is organized as follows. In Section 2, we describe the models and simulations protocol employed to study PLA-based composites filled with CNPs modified by grafted branched or linear lactide chains. Section 3 contains the main results, which are divided into two logical parts: (i) a detailed analysis of the structure of brushes consisting of grafted lactide chains with a branched architecture; (ii) a comparison of the structure of grafted branched and linear lactide chains, as well as the interaction energy between the surrounding polymer binder and the filler or grafted chains considered. Finally, we outline the conclusions in Section 4.

2 Model and simulation method

Polylactide-based composites filled with cellulose nanoparticles, surface-modified by the grafting of branched or linear lactide chains, were studied using MD simulations, see Fig. 1a. The setup of the atomistic model systems was similar to that in our previous studies.^58–63 Each CNP comprised 36 cellulose chains with the degree of polymerization n = 6, see Fig. 1b. These chains were put into three layers of 12 chains each to form the cellulose Iβ crystal.^64,65 The filler was periodic in the X–Y plane, and its dimensions were 6.47 × 6.18 × 1.84 nm. Thus, the model filler may imitate a flat nanocrystalline cellulose surface in a PLA-based nanocomposite. Both the top and bottom surface layers of the CNPs were chemically modified, with the primary hydroxyl groups being substituted by OLA chains in order to uniformly cover the filler surface. The number of grafted chains was 18, 36, or 72 on each CNP's surface layer, giving grafting density values σ of 0.44, 0.88, or 1.76 nm⁻², respectively. These grafting densities are among those reported from the experiments.^66–68 For the CNPs’ surface modification, branched or linear oligolactide (OLA) chains were used, see Fig. 1c and d. As is common in synthesis, glycerol branching points were examined within the branched OLA chains.^69,70 In turn, the degree of polymerization n of each branch was 13. Hence, the grafted branched chains were composed of one branching point and 39 repeating units (three-arm star-like chains). This choice for the grafted chain composition enabled us to compare the branched OLA chains to the linear OLA chains with n = 40, which were studied in previous simulations.⁶¹ In other words, the molecular weights of the branched and linear OLA chains were almost the same. Surface-modified CNPs were surrounded by 20 free PLA chains with the degree of polymerization n = 150, see Fig. 1d.

Fig. 1 (a) A snapshot of the typical configuration of the PLA-based nanocomposite filled with CNP surface-modified by the grafting of branched OLA chains (grafting density σ = 0.88 nm⁻²) after 1 μs-long simulations. Hydrogens, oxygens, and carbons are colored in white, red, and cyan, respectively. Arrows indicate PLA, OLA, and CNP in the nanocomposite. Chemical structure of repeating units of (b) cellulose, (c) branched and (d) linear lactide chains selected for this study. Blue ovals show the primary hydroxyl groups, green circles denote the carbons used for grafting to the CNP surface.

The simulation procedure consisted of several stages.^58–63 During the first stage, surface-modified CNPs were surrounded by pre-equilibrated PLA chains. In turn, compression of the systems obtained was carried out for 5 ns at a pressure of 50 bar along the Z-axis perpendicular to the filler surface. Compressed systems were then simulated for 1 μs at a pressure of 1 bar. Based on the analysis of the autocorrelation functions for the grafted chains sizes, the first 0.2 μs of the simulations were determined as the equilibration period.⁵⁸ Meanwhile, the remaining 0.8 μs-long simulations were used as the production run for the structural analysis. The simulation temperature T_sim was equal to 600 K, which is above the PLA melting temperature T_m ≈ 450 K,⁷¹ in order to represent the composites in a melt state and to decrease equilibration times. It is noteworthy that the difference between the PLA processing temperature T_proc ≈ 465 K⁷¹ and the glass transition temperature T_g ≈ 330 K⁷¹ is essentially close to that between the simulation temperature T_sim = 600 K and the glass transition temperature T_g,sim ≈ 415 K obtained for PLA in our previous simulations⁷² using a similar model. It should also be noted that the atomistic model and simulation trajectories for the system in the case of linear OLA chains at σ = 1.76 nm⁻² were taken from ref. 61, while all the other systems described above were developed and simulated in the present study.

The MD simulations were carried out using the Gromacs 5.1.4 package.^73,74 The General Amber Force Field (GAFF) was utilized to parametrize bonded and non-bonded interactions within the composites.⁷⁵ This force field has already been applied to study the structure of various polymer systems,^{61,62,72,76–78} especially PLA-based blends⁷² and composites.^61,62 Atomic partial charges for PLA chains, pristine cellulose chains, and cellulose chains modified by the grafting of linear OLA chains were taken from ref. 62 and 72. To simulate the grafted branched OLA chains in the present study, we additionally evaluated the partial charges for the branching points, see the ESI.† Following the recommendations to the GAFF force field parametrization, the partial charges were calculated by the HF/6-31G*(RESP) method using the Gaussian 09 software.^75,79

Equations of motion were integrated with a timestep of 1 fs.^74,80 The simulations were performed in a rectangular simulation cell with three-dimensional periodic boundary conditions.⁷⁴ To maintain the CNPs’ stability, a position restraints algorithm was applied to the backbone atoms of the cellulose chains.^63,74 Constant temperature and pressure were maintained using the Berendsen thermostat and barostat with time relaxation constants of τ_T = 0.1 ps and τ_P = 1 ps, respectively.^72,81 Electrostatic interactions were handled by the particle-mesh Ewald (PME) method.⁸² Non-bonded interactions were truncated at 1 nm.^72,83,84 The structure of the composites under study was analyzed using the MDAnalysis Python library.⁸⁵

3 Results

3.1 Structure of the grafted layer of branched OLA chains

Let us start by analyzing the influence of grafting density σ on the density profile ρ(z) and the order parameter P₂(z) of the grafted layer of branched chains with respect to the CNP surface, see Fig. 2. Note that all atoms were considered when computing these characteristics. The order parameter is calculated using the second Legendre polynomial P₂(z) = 0.5 (3〈cos²θ(z)〉 − 1), where θ(z) denotes the angle between the vector along the repeating unit of the grafted chain and the normal to the CNP surface at the distance z from the CNP surface, 〈…〉 is the averaging over all the vectors at the distance z and over the entire production run.⁸⁶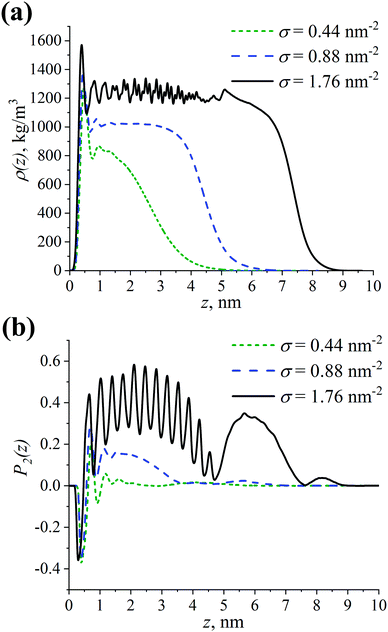

Fig. 2 (a) Density profile ρ(z) and (b) order parameter P₂(z) of the grafted branched OLA chains with respect to the CNP surface (z = 0 nm) at different grafting densities σ.

As can be seen in Fig. 2, the ρ(z) and P₂(z) dependences have peaks near z = 0 nm, regardless of the σ value. These peaks could correspond to the presence of a short-range ordering of grafted chains near the CNP surface.⁸⁷ Since the P₂(z) values are close to −0.4, the first repeating unit of the OLA chains grafted to the CNP is likely to almost lie down on the surface, see Fig. 2b. At σ = 0.44 nm⁻², the first peak is followed by a gradual decay of the density profile to zero. This type of shape for ρ(z) indicates that the grafted chains interact weakly with each other. Their degree of extension from the CNP surface is also weak as confirmed by P₂(z) ≈ 0. An increase in σ from 0.44 nm⁻² to 0.88 nm⁻² leads to both the broadening of the grafted chains’ density profile to greater z values, and to the emergence of the plateau region in ρ(z) at z ≈ 0.7–3 nm, see Fig. 2a. A similar behavior is observed for the P₂(z) dependence in this case, with a plateau value equal to approximately 0.2, see Fig. 2b. This is possibly due to the fact that the interactions between the grafted chains, as well as the chains’ extension from the surface become strong.^86,88 At the maximum considered grafting density σ of 1.76 nm⁻², the shape of the ρ(z) dependence is almost step-like, which is an indicator of a very strong extension of the grafted chains from the surface, see Fig. 2a. The small peak at z ≈ 5 nm may be due to the location of the branching points of the grafted chains mainly in this region.³⁴ Moreover, one can note the presence of oscillations in ρ(z) at z ≈ 1–4 nm. The order parameter also oscillates within this range of distances, see Fig. 2b. Note that the oscillations occur around P₂(z) ≈ 0.4, and that there is an additional high peak in P₂(z) at z ≈ 5–7 nm. Thus, the grafted chains strongly interact between each other, leading to their very strong extension from the surface.

It is worthwhile to examine more closely the oscillations found in ρ(z) and P₂(z) at σ = 1.76 nm⁻². As pointed out in the Introduction, the structural ordering of the grafted layer characterized by the formation of helical fragments of densely grafted chains can be seen in the case of linear lactide chains. In our previous study,⁶¹ it was shown that this ordering manifests itself via oscillations in the ρ(z) and P₂(z) dependencies. However, the amplitude and frequency of the oscillations in Fig. 2 are different from those observed previously. Therefore, the structure of the grafted branched and linear lactide chains may be different. In order to verify this assumption, we additionally compared the P₂(z) dependence for the linear chains computed in our previous study⁶¹ with the P₂(z) dependencies calculated separately for the root and free branches of the branched chains, see Fig. S1 (ESI†). On the one hand, the order parameter for different branch types shows that the oscillations for the branched chains are caused mainly by the structure of the root branches. It can also be noted that the additional high peak in P₂(z) at z ≈ 5–7 nm stems from the free branches. On the other hand, the P₂(z) values oscillate at a much higher level for the root branches than for the linear chains. Such a difference in P₂(z) reflects the fact that the degree of alignment normal to the CNP surface is significantly greater for the root branches than for the helical fragments of the linear chains. Therefore, a possible reason for the oscillations observed for the branched chains is a very strong extension of their root branches due to the high grafting density.

Overall, the extension of the grafted chains from the CNP surface increases with increasing grafting density. Moreover, in terms of the grafted chains extension, the grafting densities considered can be conventionally divided into three qualitatively different cases: sparse, intermediate, and dense grafting at σ = 0.44, 0.88, and 1.76 nm⁻², respectively.

3.2 Extension of root branches of grafted branched OLA chains

To further analyze the structure of the grafted layer of the branched OLA chains, the distribution of the branching points’ positions of the grafted chains p_b(z) with respect to the CNP surface is studied at different grafting densities σ.

Fig. 3 shows the presence of a peak near z = 0 nm at σ = 0.44 nm⁻², possibly due to an increased residence time of the branching points within the dense region near the CNP surface, see Fig. 2a. The peak area is fairly small, so this peak is essentially irrelevant. In general, the p_b(z) distribution is unimodal, i.e. it has one peak, at all grafting densities examined. The position of the peak shifts toward greater values as the grafting density σ increases. Given that the contour length L of the root branch is approximately equal to 5.3 nm, the root branch extension varies from weak at σ = 0.44 nm⁻² to very high at σ = 1.76 nm⁻². In the latter case, the degree of extension of the root branch corresponds to an almost fully extended branch. Note that this result supports our assumption on the possible origin of oscillations in the corresponding ρ(z) and P₂(z) dependencies in Fig. 2. Thus, an increase in grafting density leads to an increase in the extension of the root branches from the CNP surface.

Fig. 3 Distribution of the branching point positions p_b(z) of the grafted branched OLA chains with respect to the CNP surface (z = 0 nm) at different grafting densities σ. The gray vertical dashed line indicates the contour length L of the root branch of the grafted chains.

The shape of the p_b(z) distribution in Fig. 3, however, contradicts the data from ref. 33, 38, 40 and 41 obtained for brushes consisting of the uncharged branched chains. Specifically, in the present simulations, the shape deviates from the plateau-like under sparse grafting, whereas under dense grafting a unimodality instead of a bimodality of the p_b(z) distribution is observed. Therefore, conformations of dipolar grafted OLA chains with a branched architecture can differ from those for uncharged grafted chains. Let us now turn to conformational characteristics of grafted branched OLA chains in the next section.

3.3 Conformations of grafted branched OLA chains

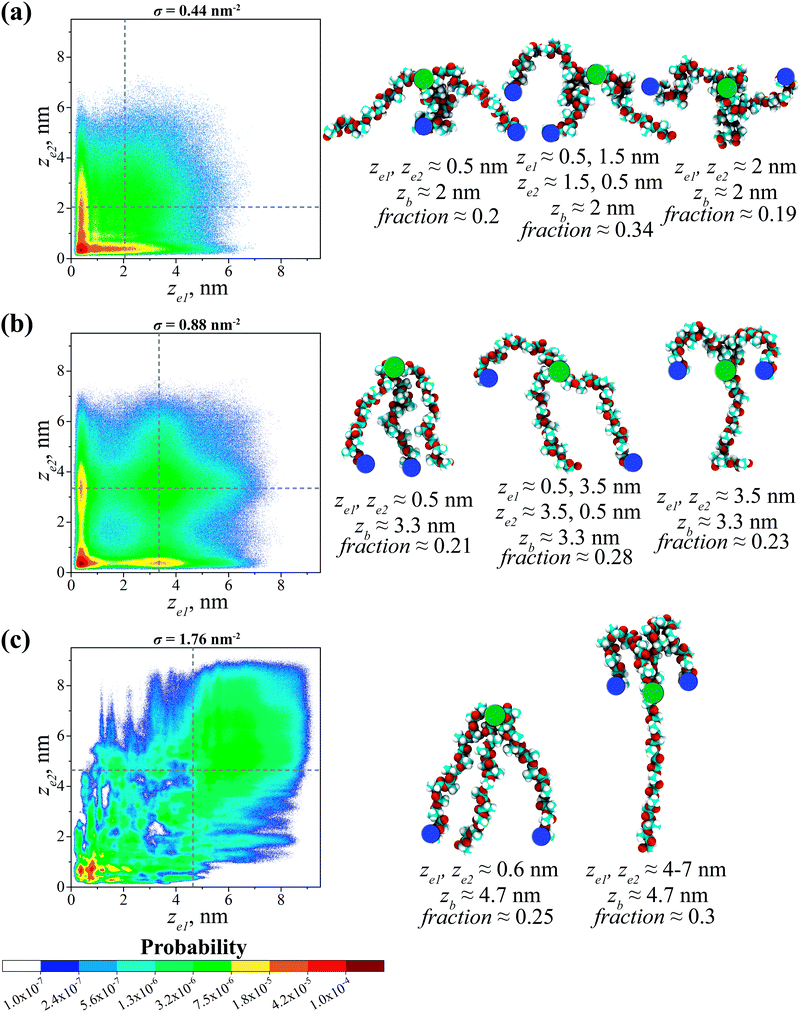
The conformations of grafted branched OLA chains are studied using bivariate joint probability distribution P(z_e1, z_e2), where z_e1 and z_e2 are the z coordinates of the two free ends of a grafted branched chain with respect to the CNP surface. The color of a point in the P(z_e1, z_e2) distribution indicates the probability of finding the conformation of a graft with parameters (z_e1, z_e2), with a “warmer” color denoting a higher probability. To facilitate the analysis, the dotted lines showing the most probable positions for the branching points of grafted chains are plotted in each P(z_e1, z_e2) distribution for a given σ value. These positions are determined as the position of the peak in the corresponding p_b(z) distribution examined above, see Fig. 3. In addition, the total probability of the conformational states within the certain regions of each P(z_e1, z_e2) distribution is calculated to obtain fractions of the observed conformations. The borders of the corresponding regions are described in Table S1 (ESI†), while the states outside these regions can be considered as transitional. The P(z_e1, z_e2) distributions computed at different grafting densities σ are presented in Fig. 4.

Fig. 4 Bivariate joint probability distributions P(z_e1, z_e2), where z_e1 and z_e2 are the z coordinates of the two free ends of a grafted branched OLA chain with respect to the CNP surface (z_e1, z_e2 = 0 nm) at the grafting densities σ of (a) 0.44 nm⁻², (b) 0.88 nm⁻², and (c) 1.76 nm⁻². The dashed gray lines in the P(z_e1, z_e2) distributions show the most probable positions for branching points of the grafted chains. On the right side, the snapshots of preferable conformations of the grafted branched OLA chains are shown, where the free ends and branching points are indicated by blue and green circles, respectively.

Fig. 4a shows that the P(z_e1, z_e2) distribution has a maximum at z_e1 = z_e2 ≈ 0.5 nm where σ = 0.44 nm⁻². As will be shown below, the presence of the maximum in this region is typical for all the grafting densities under study. Such a maximum corresponds to a preferable conformation, in which both free ends of a grafted chain are located near the CNP surface. The representative snapshot of this chain is shown in Fig. 4a. Note that the root branch of this chain is weakly extended according to the distribution of the branching points’ positions in Fig. 3. The fraction f_b of grafted chains adopting this conformation is approximately 0.2. Additionally, the maxima at z_e1 ≈ 0.5 nm and z_e2 ≈ 1.5 nm or z_e1 ≈ 1.5 nm and z_e2 ≈ 0.5 nm can be distinguished in the P(z_e1, z_e2) distribution. They indicate the presence of chains (f_b ≈ 0.34) with a weak extension of the root branch, while their two free ends are simultaneously located near the CNP surface and the branching point, respectively. Moreover, the region of an increased probability of finding the free ends can be noted at z_e1, z_e2 ≈ 2 nm, possibly due to the formation of conformations (f_b ≈ 0.19) with both free ends located near the branching points. Thus, the three preferable conformations of the grafted chains occur within the grafted layer, see Fig. 4a.

At σ = 0.88 nm⁻², one can find the maxima in the P(z_e1, z_e2) distribution in the following regions: (1) z_e1 and z_e2 ≈ 0.5 nm; (2) z_e1 ≈ 0.5 nm and z_e2 ≈ 3.5 nm or z_e1 ≈ 3.5 nm and z_e2 ≈ 0.5 nm; (3) z_e1 and z_e2 ≈ 3.5 nm, see Fig. 4b. These maxima point to the presence of three qualitatively different preferable conformations of the grafted chains. The root branches of such chains are moderately extended from the CNP surface, see Fig. 3. Both free ends of the grafted chains in the first preferable conformation (f_b ≈ 0.21) backfold toward the CNP surface and locate near it. The second preferable conformation (f_b ≈ 0.28) is characterized by the simultaneous location of two free ends near the CNP surface and the branching point, respectively. In the third preferable conformation (f_b ≈ 0.23), both free ends are located near the branching points. The snapshots of the grafted chains adopting the three preferable conformations can be seen in Fig. 4b.

Upon a further increase in the grafting density to σ = 1.76 nm⁻², two preferable conformations of the grafted chains can be distinguished, see Fig. 4c. In both cases, the chains have very strongly extended root branches, see Fig. 3. Meanwhile, the chains with both free ends located near the surface constitute the first preferable conformation as follows from the presence of a maximum in P(z_e1, z_e2) at z_e1 and z_e2 ≈ 0.6 nm. Note that the fraction f_b of chains in this conformation is approximately 0.25, despite dense grafting. The chains in the second preferable conformation (f_b ≈ 0.3) have free ends that both backfold toward the branching points, see the P(z_e1, z_e2) distribution at z_e1 and z_e2 ≈ 4–7 nm. One may also note the regions of an increased probability scattered in the P(z_e1, z_e2) distribution, but the contribution of each of them is small. Two preferable conformations found at σ = 1.76 nm⁻² are presented in Fig. 4c.

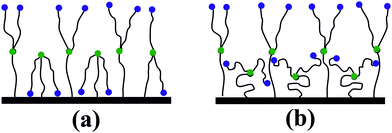
To explain the conformations observed, let us turn to a simpler case, namely, to the brushes consisting of uncharged branched chains, which have been intensively studied in the literature. As was already noted in the Introduction, one of the most remarkable features of these brushes is the formation of “layered” structures due to the segregation of the grafted chains into two groups, or populations, differing in the degree of their branches’ extension.^{33,34,37,41,45} The reason for this effect is the necessity to solve the problem of branches “packing” within the grafted layer, taking into account the branched architecture of the grafted chains and the finite extensibility of branches. Two different solutions to this “packing problem” can be proposed: (a) all the branches, including the root ones, are strongly stretched, while there is a fraction of free branches that are folded back to the surface, see Fig. 5a; (b) root spacers of chains are stretched differently, and there is a fraction of weakly stretched grafted chains filling the inner part of the brush (the inner sublayer), as well as grafted chains with very strongly stretched root branches and strongly stretched free branches forming the brush periphery (the outer sublayer), see Fig. 5b. In both cases, the brush can be viewed as two sublayers, where the peripheral sublayer is nothing but a “standard” polymer brush consisting of linear chains.

Fig. 5 Schematic illustration of two possibilities of solving the “packing problem” in the brushes consisting of densely grafted uncharged branched chains. The free ends and branching points are indicated by blue and green circles, respectively. See the explanation in the text.

As was shown in ref. 33, 34, 37, 41 and 45, for brushes consisting of uncharged branched chains, the choice between the solutions (a) and (b) is made in favor of (b) because of the significant entropy loss due to the stretching of all branches in each grafted chain in the solution (a).

The presence of electrostatic interactions between dipoles in the systems under the present study possibly changes this balance – the dipole–dipole interaction energy minimized with the aid of branches backfolding may exceed the corresponding entropy losses, and therefore the inner layer may acquire the structure as shown in Fig. 5a. In other words, the solution (a) becomes more favorable. The outer layer, as already indicated, is a brush of linear chains, and therefore behaves appropriately – the free branches in this layer form hairpins.

This corresponds perfectly to the observations in Fig. 4b and c at σ = 0.88 nm² and 1.76 nm⁻². Interestingly, in the case of intermediate grafting (σ = 0.88 nm⁻²), the system contains both variants of grafted chain conformations, where either one or two free branches backfold to the surface, whereas under dense grafting (σ = 1.76 nm⁻²) only conformations with two backfolded free branches remain.

Under sparse grafting (σ = 0.44 nm⁻²), the problem of branches “packing” within the grafted layer is not critical, and therefore we do not observe conformations with a strongly stretched root branch here; the primary task is to minimize the energy of the dipoles’ interaction. This is implemented through the conformations shown in Fig. 4a, the mutual orientations of the branches in these conformations are, in principle, similar to those observed at σ = 0.88 nm⁻², which follows from both the positions of the maxima on the joint probability distributions, and the typical snapshots of the preferable conformations.

Overall, the free ends of the grafted branched OLA chains tend to backfold to the CNP surface at all the grafting densities studied. This result stems from the fact that such a backfolding decreases the number of unfavorable dipole–dipole interactions between parallel oriented dipoles within the grafted layer.^58,60 In turn, the conformational behavior of the grafted branched lactide chains under study qualitatively agrees with that in the case of grafted linear lactide chains.^58,60 Moreover, the backfolding of free branches of the grafted branched chains may contribute to an additional extension of the root branches. This is a possible explanation as to why the distribution of the branching points’ positions of the branched OLA chains in the frames of the model systems accounting for dipolar interactions differs from that obtained previously^40,41 for uncharged grafted branched chains. Thus, it is confirmed that the conformational characteristics of the grafted branched OLA chains and the uncharged grafted branched chains studied previously^40,41 differ significantly.

3.4 Branched vs. linear chains: density profile

The analysis carried out in the previous sections allows us to describe the structure of the grafted layer of branched OLA chains in great detail. To understand whether linear OLA chains are inferior to branched ones in terms of their effectiveness of covering the filler surface, a comparative study of their structure is performed.

Let us consider the density profiles ρ(z) of the grafted linear and branched OLA chains. Fig. 6 shows that an increase in the grafting density σ results in an increase of both the extension of the grafted chains from the CNP surface and the thickness of the grafted layers under study. In addition, it is shown that the higher grafting density, the greater expelling of the free PLA chains from the filler surface, see Fig. S2 (ESI†). Meanwhile, the ρ(z) dependencies for the linear and branched chains are very close to each other at σ = 0.44 nm⁻², see Fig. 6a. As the σ value increases, the difference between the density profiles for the two chain types also slightly increases. In particular, the density in the plateau region for the branched chains becomes slightly higher than that for the linear chains. Nevertheless, in the cases of σ = 0.88 and 1.76 nm⁻², this difference does not exceed approximately 5% and 10%, respectively, see Fig. 6b and c. In other words, the values of the local densities of the grafted layers consisting of the linear or branched chains do not differ significantly. Thus, the effectiveness of covering the filler surface for the grafted linear and branched chains is broadly similar.

Fig. 6 Density profile ρ(z) of the grafted branched and linear OLA chains with respect to the CNP surface (z = 0 nm) at grafting densities σ of (a) 0.44 nm⁻², (b) 0.88 nm⁻², and (c) 1.76 nm⁻².

Despite the slight difference in the local density values, Fig. 6 also shows that the density profile decreases to zero value slower in the case of the linear grafted chains compared to the branched chains. This could indicate the presence of a slight difference in the thickness of the grafted layers consisting of the grafted chains studied, as well as in the penetration depth between grafted and free chains in the systems. We focus on these characteristics in the next section.

3.5 Branched vs. linear chains: the thickness of the grafted layer and the penetration depth between grafted and free chains

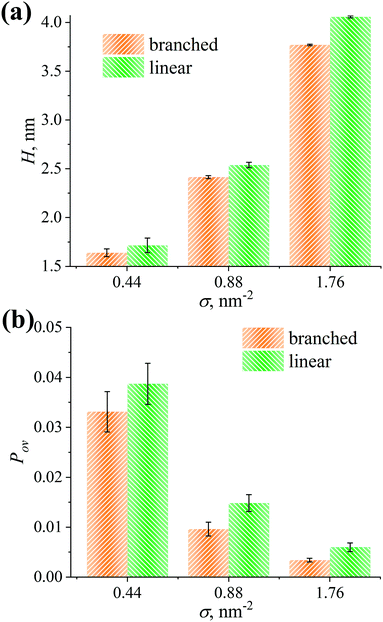
We compute the thickness H of the grafted layers considered as the first moment of the density profiles ρ(z):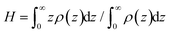 , see Fig. 7a.⁸⁹ As can be seen from Fig. 7a, the H values increase as the grafting density σ increases. Moreover, the thicknesses for the linear and branched chains turn out to be equal within the margin of error at σ = 0.44 nm⁻². However, in the case of the other grafting densities under investigation, the H value of the grafted layer consisting of the linear chains is higher compared to the branched chains.

Fig. 7 (a) Thickness H of the grafted layer and (b) overlap parameter P_ov between the grafted OLA and free PLA chains for the grafted branched and linear OLA chains at different grafting densities σ.

To quantify the penetration depth between the grafted OLA and free PLA chains, the overlap parameter P_ov is evaluated from the density profiles ρ(z) and ρ_PLA(z) of the corresponding chains via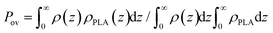.⁹⁰Fig. 7b shows the P_ov values calculated for the branched and linear chains at various grafting densities. It can be seen that the overlap parameter P_ov decreases with increasing grafting density σ. Its values for both types of the grafted chains are similar within the margin of error at σ = 0.44 nm⁻². Meanwhile, the overlap parameter P_ov in the case of the linear chains is greater than that in the case of the branched ones at σ = 0.88 and 1.76 nm⁻².

It is worth mentioning that a lower thickness for the grafted layer and a lesser penetration depth between the grafted and free chains were expected from ref. 40 and 50 for the branched OLA chains compared to linear chains. However, these characteristics are found, in contrast, to be equal for the grafted branched and linear OLA chains at σ = 0.44 nm⁻². Analysis of H and P_ov confirms the expected behavior only in the cases of σ = 0.88 and 1.76 nm⁻². These results of the current simulations are additionally supported by the corresponding density profiles in Fig. 6.

3.6 Branched vs. linear chains: PLA-CNP and PLA-OLA interactions

The difference in density profiles, thicknesses, and penetration depths for the cases of branched and linear grafted chains is found to be almost absent at σ = 0.44 nm⁻² and slight at σ = 0.88 and 1.76 nm⁻². However, these structural characteristics are among the main ones influencing interactions between the free PLA chains and the CNP or the grafted OLA chains in the composites studied. In turn, these interactions may affect both the compatibility between the filler and polymer binder and the distribution of the filler in the system.^51–57 It is therefore important to analyze if the obtained slight differences between branched and linear grafted chains manifest themselves in the PLA-CNP and PLA-OLA interactions. In order to compare these interactions for the cases of grafted branched and linear chains, we evaluate the total interaction potential energies E^PLA-CNP and E^PLA-OLA between the PLA-CNP and PLA-OLA pairs of components, respectively. They are computed as the sum of the Lennard-Jones and Coulomb potential energies using the force field parameters and the atomic coordinates. The data obtained at different grafting densities σ are presented in Fig. 8.

Fig. 8 Interaction energy (a) E^PLA-CNP between the free PLA chains and the CNP chains and (b) E^PLA-OLA between the free PLA and grafted OLA chains for the grafted branched and linear OLA chains at different grafting densities σ.

Fig. 8a shows that the interaction energies E^PLA-CNP for both branched and linear chains are indistinguishable within the margin of error at σ = 0.44 nm⁻², possibly due to a negligible difference in the density profiles and the thicknesses of grafted layers consisting of these chains, see Fig. 6a and 7a. Note that the E^PLA-CNP values are slightly negative. This indicates an attraction between the PLA and CNP chains in the system, which can be caused by a slight adsorption of the binder on the filler surface under sparse grafting, see Fig. S2 (ESI†). However, an increase in grafting density to σ = 0.88 or 1.76 nm⁻² leads to a repulsion between PLA and CNP, see Fig. 8a. This repulsion can stem from electrostatic interactions since the free PLA chains are expelled far from the filler surface (Fig. S2, ESI†), and therefore the impact of short-ranged van der Waals interactions is most likely negligible. Moreover, this repulsion for the linear chains is slightly higher than that for the branched chains. Such a result may be related to the higher thickness of the grafted layer consisting of the linear chains as compared to the case of branched chains, see Fig. 7a.

As can be seen from Fig. 8b, the E^PLA-OLA values are negative and reveal the presence of an attraction between the free PLA and grafted OLA chains, regardless of the grafted chain type and the grafting density under study. For the branched and linear chains at σ = 0.44 nm⁻², these values are also indistinguishable from each other. At σ = 0.88 and 1.76 nm⁻², the attraction of PLA becomes greater for the linear chains than for the branched ones, in line with a higher penetration depth between the PLA and linear OLA chains, see Fig. 7b.

Taken together, the expelling ability of the grafted chains and the interaction between the free and grafted chains are broadly similar for both linear and branched OLA chains at σ = 0.44 nm⁻². In the case of the other grafting densities σ considered, one can conclude that the grafted linear OLA chains expel the free PLA chains from the filler surface and interact with the free PLA chains better than the grafted branched chains.

4 Summary

We have used atomistic molecular dynamics simulations to perform a comparative investigation of brushes consisting of branched or linear OLA chains grafted on the CNPs’ surface in PLA-based nanocomposites. The branched and linear dipolar chains were of the same molecular weight, the former consisting of one branching point and three branches. The CNPs’ surface coverage was varied from sparse chains grafting at a grafting density σ = 0.44 nm⁻² to dense chains grafting at σ = 1.76 nm⁻².

Detailed structural analysis of the grafted branched OLA chains revealed that backfolding of a part of the free branches takes place toward the CNPs’ surface, contrary to the standard picture of conformational behavior of uncharged branched chains. On the one hand, this backfolding led to a separation of the grafted branched OLA chains into several populations differing in the chain conformation. On the other hand, an additional extension of the root branches from the filler surface was found, possibly due to the presence of backfolded free branches inside the grafted layer. Thus, our results confirmed a significant difference in conformational characteristics between the grafted branched OLA chains and the uncharged grafted branched chains studied previously. This difference stems from the dipolar nature of the grafted OLA chains, which leads to the backfolding as a result of dipole–dipole interactions between the OLA repeating units.

Critical comparison of the branched and linear OLA chains structure allowed us to establish that local density values for both types of grafted chains are fairly similar. In other words, the effectiveness of covering the filler surface of these grafted chains did not differ significantly. To detect subtle differences between the grafted chains, the thickness of the grafted layers and the penetration depth between the grafted and free chains were evaluated. Although these characteristics were broadly independent of the grafted chain type under sparse grafting, they were greater for the linear OLA chains than for the branched ones under intermediate or dense grafting. In line with these data, under sparse grafting no significant difference was detected in the interaction energy between the free chains and the filler or grafted chains for the OLA chains examined. At the same time, the linear OLA chains provided a slightly greater repulsion between the free PLA and CNP chains, as well as a greater attraction between the free PLA and grafted OLA chains under intermediate or dense grafting. This indicates that the grafted linear OLA chains both expel the free chains from the filler surface and interact with the free chains slightly better than the branched chains.

In conclusion, the choice of the grafted chains’ architecture may have a prominent influence on the aggregation behavior of CNPs in PLA-based nanocomposites. In terms of a potential application for CNP modification, grafted linear lactide chains may be preferable to branched chains.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank A. V. Yakimansky and S. G. Falkovich for fruitful discussions on the chemical structure of branched lactide chains. Simulations were performed using cluster at the Institute of Macromolecular Compounds of the Russian Academy of Sciences, equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University, resources of the federal collective usage center Complex for Simulation and Data Processing for Mega-science Facilities at NRC “Kurchatov Institute” (ministry subvention under agreement RFMEFI62117X0016, http://ckp.nrcki.ru/), resources of Peter the Great Saint Petersburg Polytechnic University (www.spbstu.ru), and supercomputers at Joint Supercomputer Center of the Russian Academy of Sciences (JSCC RAS). Financial support was provided by the Russian Science Foundation (State Agreement No. 16-13-10485).

References

1. A. Khosravi, A. Fereidoon, M. M. Khorasani, G. Naderi, M. R. Ganjali, P. Zarrintaj, M. R. Saeb and T. J. Gutiérrez, Food Packag. Shelf Life, 2020, 23, 100429.
2. H. Kargarzadeh, J. Huang, N. Lin, I. Ahmad, M. Mariano, A. Dufresne, S. Thomas and A. Gałęski, Prog. Polym. Sci., 2018, 87, 197–227.
3. M. Murariu and P. Dubois, Adv. Drug Delivery Rev., 2016, 107, 17–46.
4. D. Puglia, E. Fortunati and J. Kenny, Multifunctional Polymeric Nanocomposites Based on Cellulosic Reinforcements, Elsevier, 2016.
5. S. Farah and D. G. Anderson, Adv. Drug Delivery Rev., 2016, 107, 367–392.
6. R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994.
7. B. Thomas, M. C. Raj, K. B. Athira, M. H. Rubiyah, J. Joy, A. Moores, G. L. Drisko and C. Sanchez, Chem. Rev., 2018, 118, 11575–11625.
8. C. Miao and W. Y. Hamad, Cellulose, 2013, 20, 2221–2262.
9. F. V. Ferreira, A. Dufresne, I. F. Pinheiro, D. H. S. Souza, R. F. Gouveia, L. H. I. Mei and L. M. F. Lona, Eur. Polym. J., 2018, 108, 274–285.
10. M. Ramos, A. Valdés and M. C. Garrigós, Multifunctional Polymeric Nanocomposites Based on Cellulosic Reinforcements, Elsevier, 2016, pp. 177–204.
11. R. Scaffaro, L. Botta, F. Lopresti, A. Maio and F. Sutera, Cellulose, 2017, 24, 447–478.
12. E. Lizundia, E. Meaurio and J. L. Vilas, Multifunctional Polymeric Nanocomposites Based on Cellulosic Reinforcements, Elsevier, 2016, pp. 61–113.
13. A.-L. Goffin, J.-M. Raquez, E. Duquesne, G. Siqueira, Y. Habibi, A. Dufresne and P. Dubois, Biomacromolecules, 2011, 12, 2456–2465.
14. M. P. Arrieta, E. Fortunati, F. Dominici, E. Rayón, J. López and J. M. Kenny, Carbohydr. Polym., 2014, 107, 16–24.
15. B. Braun, J. R. Dorgan and L. O. Hollingsworth, Biomacromolecules, 2012, 13, 2013–2019.
16. A. P. Mathew, K. Oksman and M. Sain, J. Appl. Polym. Sci., 2005, 97, 2014–2025.
17. A. Mujica-Garcia, S. Hooshmand, M. Skrifvars, J. M. Kenny, K. Oksman and L. Peponi, RSC Adv., 2016, 6, 9221–9231.
18. L. Xiao, Y. Mai, F. He, L. Yu, L. Zhang, H. Tang and G. Yang, J. Mater. Chem., 2012, 22, 15732–15739.
19. Y. Yoo and J. P. Youngblood, ACS Sustainable Chem. Eng., 2016, 4, 3927–3938.
20. H. Wu, S. Nagarajan, J. Shu, T. Zhang, L. Zhou, Y. Duan and J. Zhang, Carbohydr. Polym., 2018, 197, 204–214.
21. E. Lizundia, E. Fortunati, F. Dominici, J. L. Vilas, L. M. León, I. Armentano, L. Torre and J. M. Kenny, Carbohydr. Polym., 2016, 142, 105–113.
22. A. Gupta and V. Katiyar, ACS Sustainable Chem. Eng., 2017, 5, 6835–6844.
23. P. Dhar, D. Tarafder, A. Kumar and V. Katiyar, Polymer, 2016, 87, 268–282.
24. S. Gårdebjer, A. Bergstrand, A. Idström, C. Börstell, S. Naana, L. Nordstierna and A. Larsson, Compos. Sci. Technol., 2015, 107, 1–9.
25. E. L. de Paula, F. Roig, A. Mas, J. P. Habas, V. Mano, F. V. Pereira and J. J. Robin, Eur. Polym. J., 2016, 84, 173–187.
26. T. Gillich, E. M. Benetti, E. Rakhmatullina, R. Konradi, W. Li, A. Zhang, A. D. Schlüter and M. Textor, J. Am. Chem. Soc., 2011, 133, 10940–10950.
27. T. Gillich, C. Acikgöz, L. Isa, A. D. Schlüter, N. D. Spencer and M. Textor, ACS Nano, 2013, 7, 316–329.
28. P. Y. J. Yeh, R. K. Kainthan, Y. Zou, M. Chiao and J. N. Kizhakkedathu, Langmuir, 2008, 24, 4907–4916.
29. C. Schüll and H. Frey, Polymer, 2013, 54, 5443–5455.
30. L. R. Cajero-Zul, F. A. López-Dellamary, S. Gómez-Salazar, M. Vázquez-Lepe, R. Vera-Graziano, M. R. Torres-Vitela, M. A. Olea-Rodríguez and S. M. Nuño-Donlucas, J. Biomater. Sci., Polym. Ed., 2019, 30, 163–189.
31. M. Bochenek, N. Oleszko-Torbus, W. Wałach, D. Lipowska-Kur, A. Dworak and A. Utrata-Wesołek, Polym. Rev., 2020, 60, 717–767.
32. Z. Jing, X. Shi and G. Zhang, Polym. Compos., 2015, 37, 2744–2755.
33. A. A. Polotsky, A. K. Misorin, E. B. Zhulina and T. M. Birshtein, Macromol. Symp., 2015, 348, 33–43.
34. H. Merlitz, C.-X. Wu and J.-U. Sommer, Macromolecules, 2011, 44, 7043–7049.
35. F. A. M. Leermakers, E. B. Zhulina and O. V. Borisov, Curr. Opin. Colloid Interface Sci., 2016, 27, 50–56.
36. E. B. Zhulina, F. A. M. Leermakers and O. V. Borisov, Polymer, 2018, 144, 142–149.
37. E. B. Zhulina, V. M. Amoskov, A. A. Polotsky and T. M. Birshtein, Polymer, 2014, 55, 5160–5167.
38. E. B. Zhulina, F. A. M. Leermakers and O. V. Borisov, Polymer, 2017, 120, 223–235.
39. I. O. Lebedeva, E. B. Zhulina, F. A. M. Leermakers and O. V. Borisov, Langmuir, 2017, 33, 1315–1325.
40. A. A. Polotsky, T. Gillich, O. V. Borisov, F. A. M. Leermakers, M. Textor and T. M. Birshtein, Macromolecules, 2010, 43, 9555–9566.
41. A. A. Polotsky, F. A. M. Leermakers, E. B. Zhulina and T. M. Birshtein, Macromolecules, 2012, 45, 7260–7273.
42. A. A. Polotsky, A. D. Kazakov and T. M. Birshtein, Polymer, 2017, 130, 242–249.
43. W. Cui, C. F. Su, H. Merlitz, C.-X. Wu and J.-U. Sommer, Macromolecules, 2014, 47, 3645–3653.
44. C. F. Su, H. Merlitz, C.-X. Wu and J.-U. Sommer, J. Chem. Phys., 2016, 145, 234905.
45. L. N. Gergidis, A. Kalogirou and C. Vlahos, Langmuir, 2012, 28, 17176–17185.
46. C. W. Li, H. Merlitz, C.-X. Wu and J.-U. Sommer, Polymer, 2016, 98, 437–447.
47. E. B. Zhulina, F. A. M. Leermakers and O. V. Borisov, Langmuir, 2015, 31, 6514–6522.
48. H. Merlitz, C. W. Li, C.-X. Wu and J.-U. Sommer, Polymer, 2016, 103, 57–63.
49. O. V. Borisov, E. B. Zhulina, A. A. Polotsky, F. A. M. Leermakers and T. M. Birshtein, Macromolecules, 2014, 47, 6932–6945.
50. A. D. Kazakov, A. A. Polotsky, E. B. Zhulina, T. M. Birshtein, F. A. M. Leermakers and O. V. Borisov, Macromolecules, 2020, 53, 387–397.
51. K. J. Modica, T. B. Martin and A. Jayaraman, Macromolecules, 2017, 50, 4854–4866.
52. C. Gay, Macromolecules, 1997, 2, 5939–5943.
53. V. Ganesan and A. Jayaraman, Soft Matter, 2014, 10, 13–38.
54. T. B. Martin, K. I. S. Mongcopa, R. Ashkar, P. Butler, R. Krishnamoorti and A. Jayaraman, J. Am. Chem. Soc., 2015, 137, 10624–10631.
55. T. B. Martin and A. Jayaraman, Mater. Res. Express, 2016, 3, 034001.
56. P. F. Green, Soft Matter, 2011, 7, 7914.
57. W. R. Lenart and M. J. A. Hore, Nano-Struct. Nano-Objects, 2018, 16, 428–440.
58. A. D. Glova, S. V. Larin, S. G. Falkovich, V. M. Nazarychev, D. A. Tolmachev, N. V. Lukasheva and S. V. Lyulin, Soft Matter, 2017, 13, 6627–6638.
59. A. D. Glova, S. G. Falkovich, S. V. Larin, D. A. Mezhenskaia, N. V. Lukasheva, V. M. Nazarychev, D. A. Tolmachev, A. A. Mercurieva, J. M. Kenny and S. V. Lyulin, Polym. Int., 2016, 65, 892–898.
60. T. M. Birshtein, A. A. Polotsky, A. D. Glova, V. M. Amoskov, A. A. Mercurieva, V. M. Nazarychev and S. V. Lyulin, Polymer, 2018, 147, 213–224.
61. A. D. Glova, S. D. Melnikova, A. A. Mercurieva, S. V. Larin and S. V. Lyulin, Polymers, 2019, 11, 2056.
62. A. D. Glova, S. V. Larin, V. M. Nazarychev, M. Karttunen and S. V. Lyulin, Macromolecules, 2020, 53, 29–38.
63. S. G. Falkovich, S. V. Larin, N. V. Lukasheva, V. M. Nazarychev, D. A. Tolmachev, A. D. Glova, D. A. Mezhenskaia, J. M. Kenny and S. V. Lyulin, Multifunctional Polymeric Nanocomposites Based on Cellulosic Reinforcements, Elsevier, 2016, pp. 313–341.
64. Y. Nishiyama, P. Langan and H. Chanzy, J. Am. Chem. Soc., 2002, 124, 9074–9082.
65. D. A. Tolmachev and N. V. Lukasheva, Langmuir, 2012, 28, 13473–13484.
66. H. Wu, S. Nagarajan, J. Shu, T. Zhang, L. Zhou, Y. Duan and J. Zhang, Carbohydr. Polym., 2018, 197, 204–214.
67. S. Gårdebjer, A. Bergstrand, A. Idström, C. Börstell, S. Naana, L. Nordstierna and A. Larsson, Compos. Sci. Technol., 2015, 107, 1–9.
68. Y. Yoo and J. P. Youngblood, ACS Sustainable Chem. Eng., 2016, 4, 3927–3938.
69. A. Michalski, M. Brzezinski, G. Lapienis and T. Biela, Prog. Polym. Sci., 2019, 89, 159–212.
70. S. Corneillie and M. Smet, Polym. Chem., 2015, 6, 850–867.
71. D. Garlotta, J. Polym. Environ., 2001, 9, 63–84.
72. A. D. Glova, S. G. Falkovich, D. I. Dmitrienko, A. V. Lyulin, S. V. Larin, V. M. Nazarychev, M. Karttunen and S. V. Lyulin, Macromolecules, 2018, 51, 552–563.
73. D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
74. M. J. Abraham, D. van der Spoel, E. Lindahl and B. Hess and the GROMACS development team, GROMACS User Manual Version 5.1.4, 2016.
75. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
76. P.-H. Lin and R. Khare, Macromolecules, 2009, 42, 4319–4327.
77. F. Khabaz, S. Mani and R. Khare, Macromolecules, 2016, 49, 7551–7562.
78. K. S. Khare, F. Khabaz and R. Khare, ACS Appl. Mater. Interfaces, 2014, 6, 6098–6110.
79. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009.
80. V. M. Nazarychev, A. V. Lyulin, S. V. Larin, I. V. Gofman, J. M. Kenny and S. V. Lyulin, Macromolecules, 2016, 49, 6700–6710.
81. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
82. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089.
83. S. V. Lyulin, S. V. Larin, A. A. Gurtovenko, V. M. Nazarychev, S. G. Falkovich, V. E. Yudin, V. M. Svetlichnyi, I. V. Gofman and A. V. Lyulin, Soft Matter, 2014, 10, 1224–1232.
84. G. A. Cisneros, M. Karttunen, P. Ren and C. Sagui, Chem. Rev., 2014, 114, 779–814.
85. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327.
86. G. Rossi, I. G. Elliott, T. Ala-Nissila and R. Faller, Macromolecules, 2012, 45, 563–571.
87. D. Deb, A. Winkler, M. H. Yamani, M. Oettel, P. Virnau and K. Binder, J. Chem. Phys., 2011, 134, 214706.
88. D. I. Dimitrov, A. Milchev and K. Binder, J. Chem. Phys., 2007, 127, 084905.
89. M. Murat and G. S. Grest, Macromolecules, 1989, 22, 4054–4059.
90. Z. Benková and M. N. D. S. Cordeiro, Langmuir, 2015, 31, 10254–10264.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04556j

---