Transformation of a graphene nanoribbon into a hybrid 1D nanoobject with alternating double chains and polycyclic regions†
Alexander S.
Sinitsa
 a,
Irina V.
Lebedeva
a,
Irina V.
Lebedeva
 b,
Yulia G.
Polynskaya
b,
Yulia G.
Polynskaya
 c,
Dimas G.
de Oteyza
c,
Dimas G.
de Oteyza
 def,
Sergey V.
Ratkevich
def,
Sergey V.
Ratkevich
 g,
Andrey A.
Knizhnik
c,
Andrey M.
Popov
g,
Andrey A.
Knizhnik
c,
Andrey M.
Popov
 *h,
Nikolai A.
Poklonski
*h,
Nikolai A.
Poklonski
 g and
Yurii E.
Lozovik
hi
g and
Yurii E.
Lozovik
hi
aNational Research Centre “Kurchatov Institute”, Kurchatov Square 1, Moscow 123182, Russia
bCIC nanoGUNE BRTA, Avenida de Tolosa 76, San Sebastian 20018, Spain
cKintech Lab Ltd., 3rd Khoroshevskaya Street 12, Moscow 123298, Russia
dDonostia International Physics Center, San Sebastián, Spain
eCentro de Física de Materiales (CFM-MPC), CSIC-UPV/EHU, San Sebastián, Spain
fIkerbasque, Basque Foundation for Science, Bilbao, Spain
gPhysics Department, Belarusian State University, Nezavisimosti Ave. 4, Minsk, 220030, Belarus
hInstitute for Spectroscopy of Russian Academy of Sciences, Fizicheskaya Street 5, Troitsk, Moscow 108840, Russia. E-mail: popov-isan@mail.ru
iNational Research University Higher School of Economics, 109028 Moscow, Russia
First published on 23rd November 2020
Abstract
Molecular dynamics simulations show that a graphene nanoribbon with alternating regions which are one and three hexagons wide can transform into a hybrid 1D nanoobject with alternating double chains and polycyclic regions under electron irradiation in HRTEM. A scheme of synthesis of such a nanoribbon using Ullmann coupling and dehydrogenation reactions is proposed. The reactive REBO-1990EVC potential is adapted for simulations of carbon–hydrogen systems and is used in combination with the CompuTEM algorithm for modeling of electron irradiation effects. The atomistic mechanism of formation of the new hybrid 1D nanoobject is found to be the following. Firstly hydrogen is removed by electron impacts. Then spontaneous breaking of bonds between carbon atoms leads to the decomposition of narrow regions of the graphene nanoribbon into double chains. Simultaneously, thermally activated growth of polycyclic regions occurs. Density functional theory calculations give barriers along the growth path of polycyclic regions consistent with this mechanism. The electronic properties of the new 1D nanoobject are shown to be strongly affected by the edge magnetism and make this nanostructure promising for nanoelectronic and spintronic applications. The synthesis of the 1D nanoobject proposed here can be considered as an example of the general three-stage strategy of production of nanoobjects and macromolecules: (1) precursors are synthesized using a traditional chemical method, (2) precursors are placed in HRTEM with the electron energy that is sufficient only to remove hydrogen atoms, and (3) as a result of hydrogen removal, the precursors become unstable or metastable and transform into new nanoobjects or macromolecules.
1. Introduction
The progress in high-resolution transmission electron microscopy (HRTEM) has made it possible to study transformations of nanostructures induced by electron irradiation in situ. In particular, notable observations for carbon nanostructures include the reconstruction of zigzag graphene edges terminated by hexagons into alternating pentagons and heptagons,1,2 the evolution of atomic-scale vacancies in the graphene layer into holes3,4 and the cutting of carbon nanotubes by osmium5 and nickel6 clusters under the simultaneous action of electron irradiation. Structural transformations of carbon nanostructures induced by electron irradiation in HRTEM give rise to the formation of nanoobjects initially absent in the sample. Examples of such nanoobject formation are the transformation of a graphene flake into a fullerene,7 the formation of a double-walled carbon nanotube from a peapod carbon nanotube,8 the transformation of a bilayer graphene nanoribbon (GNR) into a flat carbon nanotube,9 or the transformation of GNRs1,9–12 and carbon nanotubes13,14 into single, double and triple atomic carbon chains. Moreover, transformation under electron irradiation can lead to the synthesis of nanoobjects which have not been obtained using other methods. For instance, the formation of an endohedral metallofullerene from a nickel cluster surrounded by amorphous carbon has been observed in HRTEM,15 whereas endohedral metallofullerenes with transition metal cores have not been produced yet using traditional methods of fullerene synthesis.Although HRTEM is a useful tool for the formation of new nanoobjects, their synthesis is limited by the availability of appropriate initial nanostructures that may be transformed under electron irradiation into these nanoobjects. For example, the formation of long atomic carbon chains of several hundred atoms in length upon heating of zigzag graphene nanoribbons (GNR) with a regular structure of two hexagon rows has been predicted by recent molecular dynamics (MD) simulations,16 while the typical length of chains obtained in HRTEM from GNRs with an irregular structure is only tens of atoms.1,9–12 Thus, GNRs can be used as a starting point for the formation of new 1D nanoobjects under electron irradiation. Early studies on GNR production typically relied on top-down production methods (lithography, unzipping of carbon nanotubes, etc.) that unfortunately lack atomic precision. However, in 2010 the seminal work of Cai et al. demonstrated that atomically precise GNRs can be synthesized using a bottom-up approach.17 The appropriate precursor molecules were dosed onto a surface and heated to activate their chemical transformation. Their chemical design was such that the activated reactions followed well-defined paths, ultimately resulting in GNRs whose structure was precisely determined by the utilized reactant. Such findings triggered enormous research efforts along these lines that have led to great advances, as is the successful synthesis of atomically precise GNRs with different widths, edge orientations, edge structures, heteroatoms, or with periodically added side groups.18,19 Most of those achievements are based on adequately modified designs of the reactant molecules, and further variations may still provide many other GNRs with new structures to be investigated in the future. By way of example, the use of appropriately functionalized polyacene derivatives may result, after Ullmann coupling and dehydrogenation reactions,20 in a new type of GNR with alternating regions of different widths of one and three hexagon rows, as described below. Hydrogen can be easily removed by electron irradiation as seen in HRTEM images. In turn, the one-hexagon wide zigzag GNR segment is relatively unstable and decomposes into two chains10 once it loses its hydrogen terminations. We thus suggest that electron irradiation of the proposed GNR can lead to formation of a hybrid 1D nanoobject with alternating chains and polycyclic graphene-like regions.
To demonstrate the possibility of obtaining the new 1D carbon nanoobjects, we have performed MD simulations of the transformation process under the action of electron irradiation using the CompuTEM algorithm.21,22 This algorithm takes into account the annealing of the system between changes induced by irradiation in the local structure and allows rescaling of the structure evolution time to the experimental conditions in HRTEM taking into account electron scattering cross-sections. Previously, MD simulations using the CompuTEM algorithm have been applied to study transformation of graphene flake into fullerene,21,22 formation of metal heterofullerenes23 and endohedral metallofullerenes15 and cutting of carbon nanotubes by the nickel cluster6 under electron irradiation. The excellent agreement of the principal features of structural transformations and structure evolution times with the experimental HRTEM observations have been revealed.6,15
Recently, we reparametrized the popular Brenner potential24 for carbon–hydrogen systems to describe energies of pristine graphene edges, vacancy migration in graphene and formation of atomic carbon chains.16,25 In the present article we test the potential for graphene edges functionalized by hydrogen and modify the relevant parameters to improve its performance. This potential, specifically suited for modelling of transformations of carbon nanostructures, is used in our MD simulations.
To distinguish the roles of spontaneous and irradiation-induced breaking and formation of bonds between carbon atoms, electron beams with different kinetic energies of electrons are considered here in the MD simulations. The atomistic mechanism of formation of 1D nanoobjects and fractions of polycyclic graphene-like regions with different structures derived from the wide regions of the GNR under electron irradiation are determined. The MD simulations are supplemented with DFT calculations of barriers for the formation of new bonds between carbon atoms to confirm the atomistic mechanism of formation of the 1D nanoobjects revealed. The electronic and magnetic properties of the 1D nanoobject with the most abundant polycyclic regions are also studied via the DFT calculations.
The article is organized in the following way. Section 2 is devoted to the re-parametrization of the REBO potential used and details of MD simulations and DFT calculations. The results of MD simulations of the formation of hybrid 1D nanoobjects as well as DFT calculations of their structure, electronic properties and the energetics along the growth path are presented in Section 3. The discussions and conclusions are given in Section 4.
2. Methods
2.1. Modification of interatomic potential
The original Brenner potential24 (REBO-1990) was designed to describe the bulk of carbon crystals and small hydrocarbons. In the present article, however, we perform simulations for GNRs, which are different from both of these cases. It is important for us to describe precisely not only the graphene bulk but also its edges. Irradiation of GNRs implies the formation of local structure defects such as vacancies as well as atomic chains at the edges. To adequately model pristine graphene edges, vacancy migration in graphene and the formation of atomic carbon chains, we have previously reparametrized the Brenner potential16,25 (REBO-1990EVC). Here we test this potential for graphene edges functionalized by hydrogen and improve some of the corresponding parameters (REBO-1990EVC_CH).In REBO-1990, the binding energy is written in the form
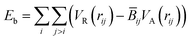 | (1) |
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ij is the bond-order term describing how the bond energy depends on the coordination.
ij is the bond-order term describing how the bond energy depends on the coordination.
The bond-order term is computed as
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ij = (Bij + Bji)/2 + F(Ntij,Ntji,Nconjij)/2 ij = (Bij + Bji)/2 + F(Ntij,Ntji,Nconjij)/2 | (2) |
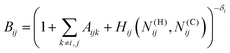 | (3) |
The total number of neighbours is computed as
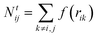 | (4) |
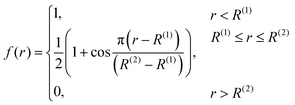 | (5) |
The numbers N(H)ij and N(C)ij are defined in the way similar to Ntij (see eqn (4)) but the summation is performed only over hydrogen or carbon neighbours of atom i except atom j, respectively.
The number Nconjij is expressed as
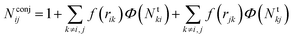 | (6) |
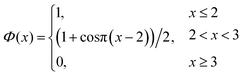 | (7) |
The fitting set for the pairwise terms and bond orders of REBO-1990 included the experimental and first-principles results on cohesive energies and lattice constants of diverse carbon crystals: diamond, graphite, simple cubic and face-centered cubic structures. The function F(n1,n2,n3) for integers n1, n2 and n3 was obtained from atomization energies of small hydrocarbons and tight-binding data on the formation energies of vacancies in graphite and diamond. For non-integer numbers n1, n2 and n3 the values of the function F are found via interpolation. Also the function F complies with the conditions F(n1,n2,n3) = F(n2,n1,n3) and F(n1,n2,n3 > 2) = F(n2,n1,2). Two sets of the parameters were presented in the original Brenner paper but we use only the second set (Table III of ref. 24), which provides better force constants.
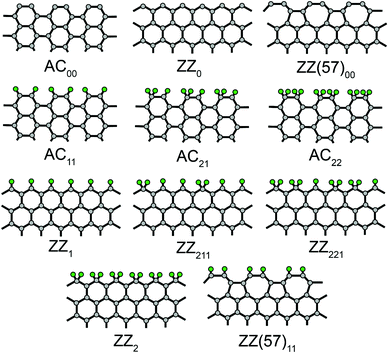
In our previous version REBO-1990EVC of the potential,16,25 the following parameters were changed: (1) F(1,1,2) to fit the formation energy of carbon chains; (2) F(1,2,2) to fit the energies of pristine ZZ0 (zigzag), ZZ(57)00 (reconstructed zigzag with alternating pentagons and heptagons26) and (armchair) edges; and (3) F(2,3,2) to fit the energy of the symmetric saddle point for vacancy migration. Here we check the performance of this potential for various edges functionalized by hydrogen: AC11, AC21, AC22, ZZ(57)11, ZZ1, ZZ211, ZZ221 and ZZ2 (Fig. 1, the subscript denotes the number of hydrogen atoms bonded to each edge carbon atom within the elementary period of the GNR27). We propose some improvements within the new version REBO-1990EVC_CH. The parameters of the different versions of the potential are listed in Table 1.
| Parameter | REBO-1990 | REBO-1990EVC | REBO-1990EVC_CH |
|---|---|---|---|
| F(1,1,2) | 0.108 | 0.02514818 | 0.02514818 |
| F(1,2,2) | −0.0243 | −0.038 | −0.038 |
| F(2,3,2) | −0.0363 | −0.088 | −0.088 |
| F(3,3,2) | 0 | 0 | −0.156 |
| H CH(1,2) | −0.4449 | −0.4449 | −0.615 |
To compute the edge energies, we consider 20-AGNR and 36-ZGNR (armchair GNR with 20 rows and zigzag GNR with 36 rows, respectively, see ref. 28 for GNR notations). We start from the structures with the bond length equal to the optimal one for the infinite graphene layer. The simulation box with periodic boundary conditions includes 18 and 10 unit cells along the nanoribbon axis for AGNR and ZGNR, respectively. To obtain the ribbon with the ZZ(57)00 edges, the hexagons at the 36-ZGNR edges are converted into alternating pentagons and heptagons. To construct hydrogen-functionalized nanoribbons, hydrogen atoms are added at a distance of 1 Å from the edge carbon atoms. The structures of the GNRs are geometrically optimized using the method of conjugated gradients keeping the size of the simulation box fixed until the energy change in consecutive iterations becomes less than 10−10 eV per atom. The edge energies per unit edge length are calculated as Eed = (EGNR − NCεgr − NHεH)/(2LGNR), where EGNR is the ribbon energy per unit cell, NC and NH are the numbers of carbon and hydrogen atoms in the ribbon per unit cell, respectively, εgr is the binding energy of bulk graphene per atom, εH is the binding energy of hydrogen molecule per atom and LGNR is the length of the GNR unit cell. For all the considered versions of the potential, εgr = −7.376 eV and εH = −2.375 eV. To test the performance of different versions of the potential for small hydrocarbons, we have also performed geometrical optimization for the molecules considered in the original Brenner paper24 with the stopping criterion given above.
The energies of pristine and functionalized graphene edges computed for different versions of the Brenner potential (Table 1) are presented in Table 2. For reference, the available DFT data26–32 are also given. A more detailed comparison with the results of DFT calculations for pristine edges can be found in ref. 16.
| Edge | REBO-1990 | REBO-1990EVC | REBO-1990EVC_CH | DFT |
|---|---|---|---|---|
| a Ref. 27 (PBE). b Ref. 29 (LDA). c Ref. 26 (PBE). d Ref. 30 (PW91). e Ref. 31 (LDA). f Ref. 32 (LDA). | ||||
| Pristine | ||||
| AC00 | 0.999 | 1.032 | 1.032 | 1.0078a, 1.202b, 0.98c |
| ZZ0 | 1.032 | 1.198 | 1.198 | 1.1452a, 1.391b, 1.31c, 1.21d |
| ZZ(57)00 | 0.937 | 0.966 | 0.966 | 0.9650a, 1.147b, 0.96c, 0.97d |
| H-terminated | ||||
| AC11 | 0.078 | 0.078 | 0.078 | 0.0321a, 0.012b, 0.01c, 0.019f |
| AC21 | 0.231 | 0.487 | 0.096 | 0.2092a |
| AC22 | 0.153 | 0.405 | −0.070 | −0.0710a, −0.186e, −0.174f |
| ZZ1 | 0.067 | 0.067 | 0.067 | 0.0809a, 0.090b, 0.06c, 0.11d, 0.105e, 0.100f |
| ZZ211 | 0.154 | 0.301 | 0.077 | 0.0119a, 0.03d, −0.016e, −0.011f |
| ZZ221 | 0.237 | 0.530 | 0.079 | 0.1007a |
| ZZ2 | 0.321 | 0.759 | 0.080 | 0.2224a |
| ZZ(57)11 | 0.293 | 0.293 | 0.293 | 0.3337a, 0.352b, 0.34c, 0.36d |
Original REBO-1990 describes very well (within 0.1 eV Å−1 from the most common DFT results) the energies of the ZZ(57)00, AC00, ZZ(57)11, AC11, AC21 and ZZ1 edges (Table 2). However, the energy of the ZZ0 is underestimated by 0.2–0.3 eV Å−1. As follows from the DFT calculations,26,27,29,32 the ZZ1 edge should be less stable than the AC11 edge by 0.05–0.08 eV Å−1, while according to REBO-1990, the ZZ1 edge is very slightly but more stable than the AC11 edge (just by 0.01 eV Å−1). The DFT calculations27 also predict that the energy of the zigzag edge should depend non-monotonically on the fraction of edge carbon atoms bonded to two hydrogen atoms. The smallest edge energy corresponds to ZZ211, which is more stable than ZZ1 and ZZ221 by about 0.1 eV Å−1 and ZZ2 by 0.2 eV Å−1. Differently, REBO-1990 predicts a monotonic growth of energy from ZZ1 to ZZ2 with an energy increase by about 0.08 eV Å−1 upon increasing the fraction of edge carbon atoms bonded to two hydrogen atoms by one third. REBO-1990 also overestimates by more than 0.2 eV Å−1 the energy of the AC22 edge. This edge should be more favourable than the AC11 edge27,32 but this is not the case for REBO-1990.
In REBO-1990EVC, the energy of the pristine ZZ0 edge is improved (Table 2). However, the energies of the edges in which each edge carbon atom is bonded to one hydrogen atom are the same as in REBO-1990 and the energies of the edges where there are carbon atoms bonded to two hydrogen atoms are worse. The energy of the edges where each edge carbon atom is bonded to one hydrogen atom, ZZ1, AC11 and ZZ(57)11, can be modified through the parameters HCH(0,2) and F(2,2,2). Nevertheless, the energy of the bonds inside graphene layers also depends on F(2,2,2), which is set strictly to zero, and changing this parameter would destroy the description of bulk graphene properties.24 Modifying only HCH(0,2), we do not achieve correction of the relative stability of the ZZ1 and AC11 edges, while their absolute energies get even worse. Therefore, there is no point in changing this parameter either and we leave the description of the ZZ1, AC11 and ZZ(57) edges to be the same as in the original version of the potential.
The energies of the zigzag edges where there are carbon atoms bonded to two hydrogen atoms, ZZ211, ZZ221 and ZZ2, depend on the parameters HCH(1,2) and F(2,3,2). The latter was fitted in REBO-1990EVC to describe the structure of the symmetric transition state and the corresponding barrier for vacancy migration16 and it is undesirable to change it again. It is not possible to describe accurately the non-monotonic dependence of the edge energy on the fraction of edge carbon atoms bonded to two hydrogen atoms changing only one parameter HCH(1,2). However, modifying this parameter in REBO-1990EVC_CH (Table 1), we at least achieve that the energies of the ZZ211, ZZ221 and ZZ2 edges become close to the energy of the ZZ1 edge and deviate by no more than 0.15 eV Å−1 from the results of the DFT calculations27 (Table 2). The energies of the armchair edges where there are carbon atoms bonded to two hydrogen atoms, AC21 and AC22, depend additionally on F(3,3,2). We tune this parameter (Table 1) to fit the energy of the AC22 edge and to provide the correct order of the armchair edges functionalized by hydrogen in energy (Table 2).
Modification of several parameters in REBO-1990EVC and REBO-1990EVC_CH as compared to REBO-1990 degrades the description of the energies of some small hydrocarbons (Table 3). But such species are not important for our simulations. Both pristine and hydrogen-terminated edges relevant for our simulations are sufficiently well described in REBO-1990EVC_CH (Table 2). Furthermore, it properly describes vacancy migration and chain formation, the same as the previous version REBO-1990EVC.16,25 Therefore, in the following we use REBO-1990EVC_CH in our studies.
| Hydrocarbon | REBO-1990 | REBO-1990EVC | REBO-1990EVC_CH | Experiment |
|---|---|---|---|---|
| Alkanes | ||||
| Methane | 17.6 | 17.6 | 17.6 | 17.6 |
| Ethane | 29.7 | 29.7 | 29.7 | 29.7 |
| Propane | 42.0 | 42.0 | 43.7 | 42.0 |
| n-Butane | 54.3 | 54.3 | 57.7 | 54.3 |
| n-Pentane | 66.5 | 66.5 | 71.6 | 66.6 |
| Cyclopropane | 35.0 | 35.0 | 41.0 | 35.8 |
| Cyclobutane | 47.8 | 47.8 | 52.5 | 48.2 |
| Cyclohexane | 73.6 | 73.6 | 83.8 | 73.6 |
| Alkenes | ||||
| Ethylene | 23.6 | 23.6 | 23.6 | 23.6 |
| Propene | 36.2 | 35.7 | 35.7 | 36.0 |
| 1-Butene | 48.5 | 48.0 | 48.3 | 48.5 |
| Alkynes | ||||
| Acetylene | 17.1 | 17.1 | 17.1 | 17.1 |
| Propyne | 29.4 | 29.4 | 29.4 | 29.7 |
| Aromatics | ||||
| Benzene | 57.5 | 57.5 | 57.5 | 57.5 |
| Toulene | 69.6 | 69.1 | 69.1 | 70.1 |
| Naphtalene | 91.4 | 91.4 | 91.4 | 91.2 |
2.2. Details of molecular dynamics simulations
The minimal transferred energies Tmin used for hydrogen and carbon atoms are 1 and 5 eV, respectively. The distributions of successful electron impacts producing structural changes over the energies transferred to carbon and hydrogen atoms show that nearly all the successful impacts occur at the transferred energies considerably greater than the chosen values of Tmin (see Fig. S1 in ESI†). Thus, almost all successful electron impacts are taken into account with such a choice of Tmin. Neglecting the impacts with the energies below the minimal transferred ones (which virtually do not lead to any structural changes), the total cross-sections σH and σC of electron scattering for hydrogen and carbon atoms, respectively, can be calculated as functions of the kinetic energy Ee of electrons in HRTEM. The differential scattering cross-section is computed according to the McKinley and Feshbach formula:35
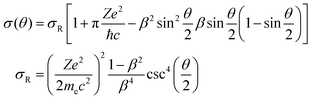 | (8) |
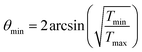 | (9) |
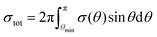 | (10) |
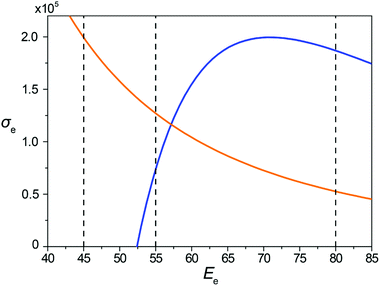
The dependences of the total cross-sections σH and σC for hydrogen and carbon atoms, respectively, on the electron energy Ee obtained using eqn (9) for the minimal transferred energies of 1 and 5 eV for hydrogen and carbon atoms, respectively, are shown in Fig. 2.
The total structure evolution time under the experimental conditions in HRTEM can be expressed as a sum of the time periods between subsequent irradiation-induced events. The time period tev between the events is defined as the inverse of the product of the overall cross-section σ corresponding to all atoms of the system and the electron current density j as tev = 1/jσ, where σ = NHσH + NCσC, NH and NC are the numbers of hydrogen and carbon atoms, respectively, in the system. This allows the direct comparison of the simulated and experimentally observed processes under electron irradiation (all impacts, including those unsuccessful, which do not lead to bond rearrangements, are included in this expression). For all the electron energies considered in the present article, the same value of the electron current density j = 4.1 × 106 e− (nm2 s)−1 is used. This electron current density lies within the range used for observation of formation of endohedral metallofullerenes from nickel clusters surrounding by amorphous carbon15 and cutting of carbon nanotubes by nickel cluster6 under electron irradiation in HRTEM. Below we show that such a choice of the electron current density should make the visual observation of the structural transformation of the GNR into the hybrid 1D nanoobject possible.
The kinetic energies of electrons considered in our MD simulations are chosen on the basis of Fig. 2. The values 45, 55 and 80 keV correspond to different ratios of the total cross-sections for carbon and hydrogen atoms (computed using the minimal transferred energies listed above that allow to take into account virtually all successful impacts). Comparison of structure evolution under electron irradiation with these electron energies allows distinguishing the roles of spontaneous and irradiation-induced breaking and the formation of bonds between carbon atoms during the formation of 1D nanoobjects. For the electron energy of 80 keV, the total cross-section for carbon atoms is considerably greater than that for hydrogen atoms. Thus, a significant number of irradiation-induced events caused by electron impacts on carbon atoms should occur before hydrogen removal by electron impacts. For the electron energy of 55 keV, the total cross-section for hydrogen atoms is about twice greater than the one for carbon atoms. Therefore, the role of irradiation-induced events caused by electron impacts on carbon atoms in this case is considerably lower than for the electron energy of 80 keV. For the electron energy of 45 keV, electron impacts on carbon atoms are excluded as the total cross-section for them equals zero. This means that only spontaneous and thermally induced breaking and formation of bonds between carbon atoms can occur under 45 keV electron irradiation after hydrogen removal.
2.3. Details of DFT calculations
To calculate the energy characteristics of 1D nanoobjects obtained in our MD simulations we have performed spin-polarized DFT calculations using the VASP code40 with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.41 The interaction of valence electrons with the atomic cores is described by the projector augmented-wave method.42 The maximal kinetic energy of the plane-wave basis set is 400 eV. The second-order Methfessel–Paxton smearing43 with a width of 0.1 eV is applied. The size of the simulation cell with periodic boundary conditions is L × 20 × 20 Å, where L is the elementary period of the 1D nanoobject. For the chosen simulation cell, the distance between periodic images of the system in neighbouring simulation cells exceeds 20 Å which is large enough to exclude possible interactions between them. The integration over the Brillouin zone is carried out using the Monkhorst–Pack method44 with the 6 × 1 × 1 k-point grid. The structures are geometrically optimized until the residual force acting on each atom becomes less than 0.03 eV Å−1. Barriers for transitions between different polycyclic regions are calculated using the nudged elastic band method (NEB).45Spin-polarized calculations of electronic properties have been performed using Quantum Espresso.46–48 The PBE functional is used. The first-order Methfessel–Paxton smearing43 with a width of 0.07 eV is applied. The maximal kinetic energy of the plane-wave basis set is 816 eV. The kinetic energy cutoff for charge density and potential is 4500 eV. The stopping criterion for self-consistent cycles is 10−5 eV. The simulation cell of the same size as in the calculations of the barriers is considered. The 6 × 1 × 1 k-point grid is used for the ground state and the 60 × 1 × 1 k-point grid for band structure calculations. The positions of ions within the simulation cell are optimized until the maximum residual force becomes less than 0.05 eV Å−1 and the change in the total energy in successive iterations is less than 3 meV.
3. Results
3.1. Scheme of graphene nanoribbon synthesis
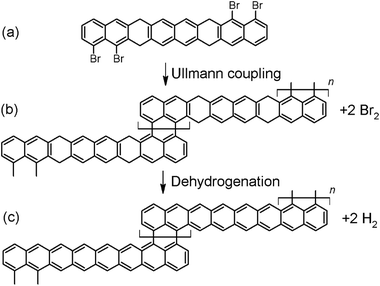
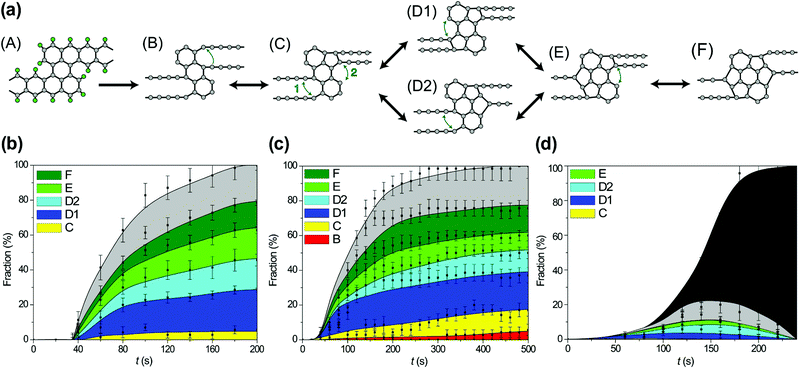
Let us consider a possible reaction scheme for the synthesis of a new type of GNRs with alternating regions of different widths displaying one and three hexagon rows, respectively. Among the most common reactions used in “on-surface synthesis”,20 the bottom-up approach whereby a great variety of atomically precise GNRs have been readily synthesized,18,19 we find Ullmann-coupling and dehydrogenation reactions. Herein we propose a new reactant that could use those two reactions to afford GNRs with periodically alternating sections of one and three hexagonal carbon rings across their width. The reactant consists of an appropriately functionalized octacene derivative (Fig. 3a). Polyacenes featuring six or more rings display a partial open-shell character, which compromises their stability and makes their synthesis extremely challenging.49 However, if some of the C atoms are functionalized in such a way that the conjugation is broken, the molecules gain back their stability and closed-shell character.49–51 One of the approaches successfully used to break the conjugation is the double hydrogenation of the outer C atoms in a ring,49,51,52 as proposed in Fig. 3a on the third ring from either side. On the other hand, the halogen atoms on the two terminal rings on either side of the molecule allow for the polycondensation via Ullmann coupling,20 which would result in the polymer shown in Fig. 3b. Further annealing of the polymer would eventually trigger the dehydrogenation of the sp3 carbon atoms51,52 and the ultimate formation of the unsubstituted and fully conjugated GNR strycture displayed in Fig. 3c.3.2. MD simulations of hybrid 1D nanoobject formation
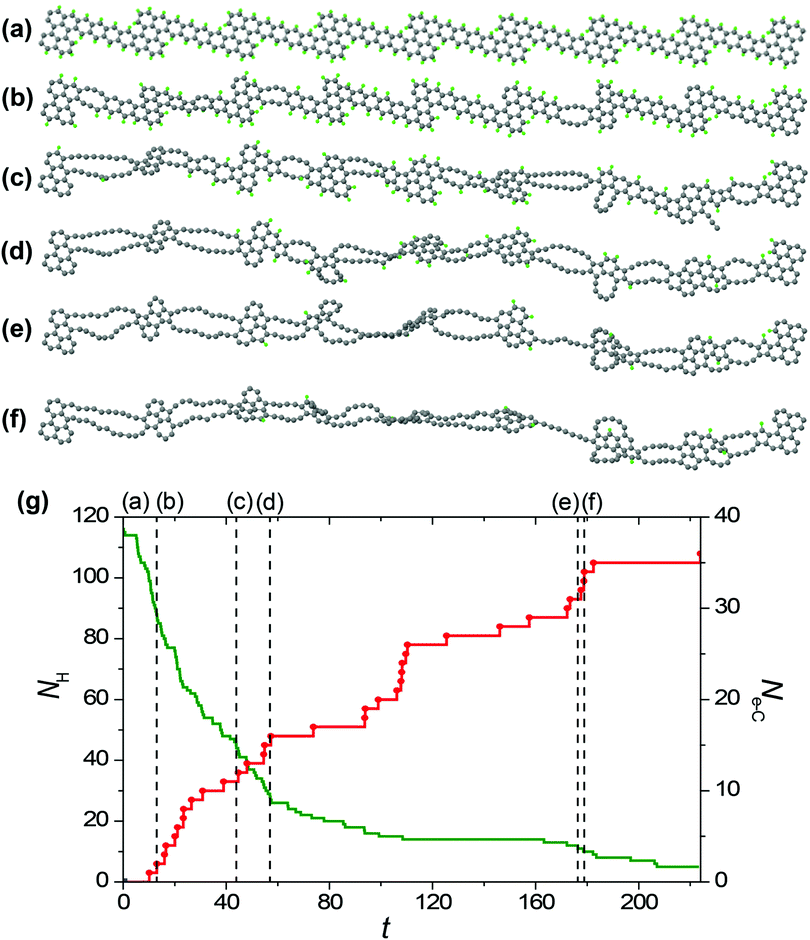
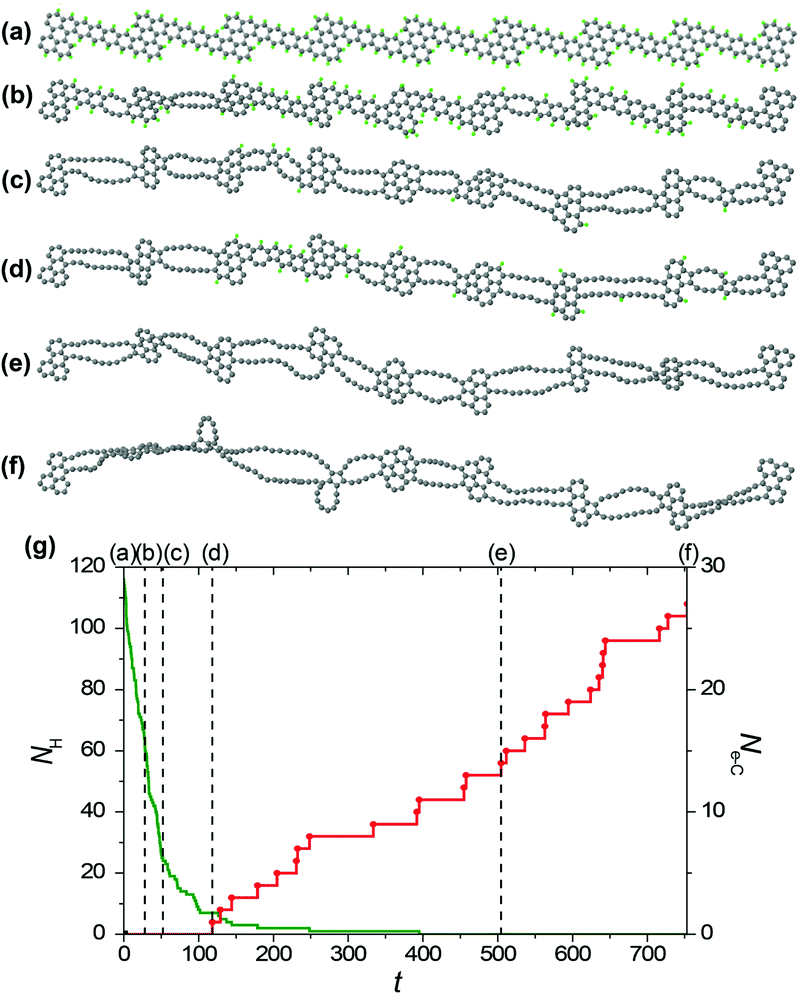
To study the formation of hybrid 1D nanoobjects with alternating double chains and polycyclic graphene-like regions under electron irradiation of the GNRs in HRTEM we have performed reactive MD simulations using the REBO-1990EVC_CH potential and CompuTEM algorithm described above. In total, we have performed 10 MD simulation runs for each of the considered electron kinetic energies (80, 55 and 45 keV) starting from the chosen initial GNR based on the structure described in the previous chapter and consisting of 7 elementary periods. One elementary period includes one narrow and one wide region of the proposed GNR, see the upper structure shown in Fig. 4a. The length of the elementary period is 16.3 Å and the total length of the GNR is 125.6 Å. Twelve atoms at each end of the GNR were kept fixed during the simulations. All simulation runs for the electron energy of 80 keV were performed until the rupture of the forming 1D nanoobject. All simulation runs for the electron energy of 55 keV were carried out for 500 s, which is 10 times longer than the minimum time of hydrogen removal from a single elementary period of the GNR. Indeed, all hydrogen atoms were removed by electron impacts due to the formation of 1D nanoobject within this time. All simulation runs for electron energy 45 keV were performed until the removal of all hydrogen atoms from the forming 1D nanoobject since electron impacts on carbon atoms do not lead to any structural changes at this electron energy.The visual analysis of structure evolution reveals the formation of alternating double atomic carbon chains and polycyclic regions from narrow and wide regions of the initial GNR, respectively, after removal of hydrogen atoms by electron impacts for all the considered kinetic energies of electrons of 45, 55 and 80 keV. The typical examples of the structural evolution of the GNR with edges terminated by hydrogen atoms under 80 and 55 keV electron irradiation in the HRTEM images observed in the MD simulations are shown in Fig. 4a and 5a, respectively. Transformation of the GNR structure under electron irradiation for the electron energy of 45 keV occurs in a similar manner. According to the DFT calculations,10 1-ZGNR is unstable and should decompose into double atomic carbon chains.This explains why double atomic carbon chains are formed after hydrogen removal for all the considered kinetic energies of electrons. However, the structure of polycyclic regions formed under irradiation by electrons with energies 45 and 55 keV considerably differs from their structure formed under 80 keV electron irradiation. In particular, the polycyclic regions formed under 45 and 55 keV electron irradiation contain on average more polygons and the diversity of such regions is reduced in comparison with polycyclic regions formed under 80 keV electron irradiation. Fig. 4b and 5b show that number of successful electron impacts on carbon atoms, i.e. those producing structural changes, before removal of all hydrogen atoms is considerably greater for the case of electron irradiation with the largest considered energy of 80 keV. Note that for the electron kinetic energies of 55 and 80 keV, the ratio of the number of removed hydrogen atoms to the number of successful electron impacts on carbon atoms correlates excellently with the calculated ratio of electron scattering cross-sections for hydrogen and carbon atoms shown in Fig. 2. The successful electron impacts on carbon atoms are completely absent under 45 keV electron irradiation. It is clear that successful electron impacts on carbon atoms prevent formation of the polycyclic regions which contain from 5 to 7 polygons. Moreover, successful electron impacts on carbon atoms eventually lead to rupture of the forming 1D nanoobject. In the case of the GNR transformation under 80 keV electron irradiation, the average rupture time is 164 ± 12 s. About 80% of the 1D nanoobject parts corresponding to the former elementary periods of the initial GNR still contain at least one hydrogen atom at the rupture moment.
Let us consider the atomistic mechanism of formation of 1D nanoobjects and statistics for different structures of polycyclic regions obtained on the basis of simulation runs for transformation of the GNR structure under 45 and 55 keV electron irradiation. The average time of total hydrogen removal from one elementary period of the GNR is 119 ± 8 and 72 ± 3 s for the kinetic energies of electrons of 55 and 45 keV, respectively. The ratio of these times equals 1.65, which is in excellent agreement with the ratio of calculated electron scattering cross-sections for hydrogen at the corresponding electron kinetic energies (which is 1.56, see Fig. 2). It should be mentioned, however, that the time of total hydrogen removal differs considerably for elementary periods of the GNR and, for example, ranges from 24 to 439 s for the kinetic energy of electrons of 55 keV. Formation of double atomic carbon chains and polycyclic regions takes place after hydrogen removal from the narrow and wide regions of the initial GNR, respectively. Note that formation of double chains can occur before the total hydrogen removal from the wide regions of the GNR.
After hydrogen removal from the wide regions of the GNR, formation of new bonds between carbon atoms leading to an increase in the number of polygons in the polycyclic regions of the forming 1D nanoobject from 3 hexagons (in the initial structure of the wide region of the GNR) to the limit of 7 polygons is observed. Subsequent stages of polycyclic region growth and notations assigned to the polycyclic regions of different structures along the growth path are shown in Fig. 6a. All 4 new polygons formed as a result of bond formation after hydrogen removal are pentagons. Not only bond formation but also breaking of these bonds both due to electron impacts and thermal activation have been observed for all the reactions shown in Fig. 6a. To determine abundant polycyclic regions, the fractions of these regions have been calculated taking into account only the number and relative positions of the polygons in accordance with Fig. 6a (that is, the calculated fractions include several structures with different numbers of atoms in the polygons, which are formed occasionally due to electron impacts on carbon atoms under 55 and 80 keV electron irradiation). Fig. 6b shows these calculated fractions of different polycyclic graphene-like regions as functions of time during 1D nanoobject formation for all the considered kinetic energies of electrons of 45, 55 and 80 keV. Evidently, the low fraction of the polycyclic regions corresponding to the revealed growth path under 80 keV electron irradiation is related to the considerable number of electron impacts on carbon atoms leading to structural changes which spoil the structure of the polycyclic regions (see Fig. 6c). In spite of the presence of some electron impacts on carbon atoms under 55 keV electron irradiation, the calculated fractions of 1D nanoobjects with polycyclic regions D1, D2, E and F are the same for the kinetic energies of electrons of 45 and 55 keV at the same moments of time within statistical errors. The 1D nanoobject with the polycyclic regions D1 which consists of 5 polygons is found to be the most abundant for these electron energies with the fraction 25–30% at the moment of about 200 s, when hydrogen is almost removed. The total amount of four abundant polycyclic regions shown in Fig. 6a, D1 and D2 (5 polygons), E (6 polygons) and F (7 polygons), is up to 80% of all polycyclic regions formed under 45 keV electron irradiation. The analysis of transitions observed between the 1D nanoobjects with the polycyclic regions corresponding to the growth path shows that the greater fraction of the 1D nanoobjects with the polycyclic regions C formed under 55 keV electron irradiation in comparison with this fraction under 45 keV electron irradiation is explained by the transitions from the 1D nanoobjects with the polycyclic regions D1 induced by electron impacts on carbon atoms.
3.3. DFT study of hybrid 1D nanoobjects
The detailed DFT study of structure and electronic properties of the hybrid 1D nanoobjects with different polycyclic regions revealed here in the MD simulations will be performed elsewhere. Here we restrict ourselves to the consideration of energetics of the polycyclic regions observed and barriers for the reactions of bond formation along the growth path presented in Fig. 6a. Additionally, electronic properties of the 1D nanoobject with polycyclic regions of the most abundant structure D1 are studied.| Polycyclic region | L 0, Å | E 0, eV |
|---|---|---|
| B | 26.32 ± 0.05 | 0 |
| D1 | 26.32 ± 0.05 | −2.74 |
| F | 24.32 ± 0.05 | −4.53 |
To confirm the atomistic mechanism of 1D-nanoobject formation observed in the MD simulations, the energetics of each step of the polycyclic region growth path shown in Fig. 6a has been studied using the NEB method via both DFT and empirical potential-based calculations. Because of the restrictions of the NEB method, the same length of the simulation cell 26.32 Å along the 1D-nanoobject axis has been used in all calculations. This length of the simulation cell corresponds to the calculated optimal elementary periods of the 1D nanoobjects with the polycyclic regions B and D1. The calculations with the fixed length of the simulation cell can correspond to the experimental conditions in which the initial GNR is suspended with the ends fixed (see, for example, ref. 54 on the GNR-based transistor). The calculated energies E1 of the 1D nanoobjects with the polycyclic regions corresponding to the growth path and related barriers for reactions of bond formation are given in Tables 5 and 6, respectively. Fig. 7 shows a schematic representation of energetics along the 1D nanoobject growth path that follows from the DFT calculations.
| Polycyclic region | E 1, eV | |
|---|---|---|
| DFT (PAW PBE) | Potential REBO-1990EVC_CH | |
| B | 0 | 0 |
| C | Unstable | Unstable |
| D1 | −2.74 | −3.75 |
| D2 | −2.29 | −3.70 |
| E | −3.13 | −5.41 |
| F | −3.58 | −7.84 |
| Reaction | E a, eV | |
|---|---|---|
| DFT (PAW PBE) | REBO-1990EVC_CH | |
| B → D1 | 0 | 0.22 |
| B → D2 | 0.35 | 0.21 |
| D1 → E | 0.44 | 0.12 |
| D2 → E | 1.92 | 2.03 |
| E → F | 0.55 | 0.14 |
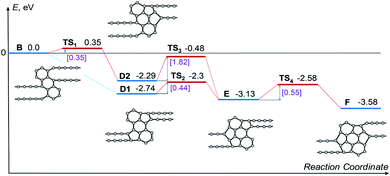 | ||
| Fig. 7 Schematic representation of energetics along the revealed growth path presented in Fig. 6a following from the DFT calculations. All the calculated energies, including the energies of transition states TS, are given relative to the energy of the 1D nanoobject with the polycyclic regions of type B, which is set to zero. The values of the barriers of transitions between the nanoobjects with polycyclic regions of different types are indicated in square brackets. | ||
According to the DFT calculations, formation of new bonds between carbon atoms during the polycyclic region growth leads to the decrease of the 1D nanoobject energy by about 0.5–1 eV per one new bond. Note that the energy of the 1D nanoobject with the polycyclic regions F and the elementary period 26.32 Å is 0.95 eV greater than the energy of this nanoobject with the optimal elementary period 24.32 Å. Both DFT calculations and those using the empirical potential show that the flat 1D nanoobject with the polycyclic regions C is unstable. This explains the small fraction of the 1D nanoobjects with the polycyclic regions C observed in our MD simulations of the GNR transformation under 45 keV electron irradiation, where successful electron impacts on carbon atoms leading to structural changes are absent. The observation of the 1D nanoobject with the polycyclic regions C in our MD simulations can be possibly attributed to the metastability of this nanoobject if it is twisted or bent at nonzero temperature (see Fig. 5f and Video in ESI†). All the barriers for new bond formation along the 1D-nanoobject growth path obtained by the DFT calculations are within 0.55 eV. These small values of the barriers and the considerable decrease of the 1D-nanoobject energy along the growth path excellently confirm the atomistic mechanism of the 1D nanoobject formation revealed by the MD simulations using the classical empirical potential.
Although the calculations based on the empirical potential overestimate the energy decrease along the 1D-nanoobject growth path, the differences between the values of the barriers obtained by the DFT calculations and using the potential are within 0.4 eV. It is a good accuracy for reaction barrier estimates using a reactive empirical potential. Thus, the REBO-1990EVC_CH potential developed here is adequate for atomistic simulations of GNR transformations.
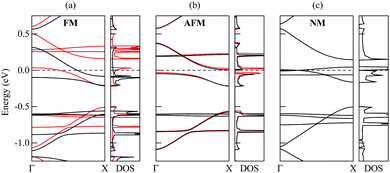
According to our calculations, the ground state of the 1D nanoobject corresponds to the FM state. However, the energy difference between the AFM and FM states is only 0.9 meV per elementary period of the 1D nanoobject. The NM state is much more unstable, with the relative energy with respect to the FM state of 37 meV per elementary period. The 1D nanoobject in the AFM state has an indirect band gap (Fig. 8b) with the maximum of the valence band at the Γ point (0,0,0) and minimum of the conductance band at the X point (π/L0,0,0). This band gap is very small, only 0.06 eV. The direct band gaps along the Γ–X path lie in the range from 0.17 eV to 0.25 eV.
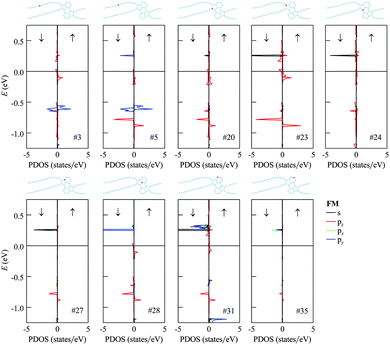
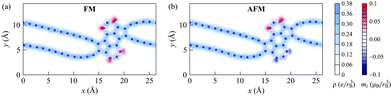
The analysis of partial densities of states for atoms of the 1D nanoobject reveals that the bands close to the Fermi level originate mostly from pz orbitals (Fig. 9 for the FM state and Fig. S3 of ESI† for the AFM state; the z axis is directed perpendicular to the ribbon plane). The shapes of the partial densities of states for neighboring atoms alternate both in the chains and in the polycyclic regions. It is confirmed that the flat bands at 0.2–0.3 eV relative to the Fermi level in the FM and AFM states are mostly formed by the s, px and py orbitals of two-coordinated carbon atoms at the edges of the polycyclic regions, more exactly from the first and third ones in the three-atom chains at the edges (see the results for atom #31 in Fig. 9 and Fig. S3 of the ESI†; the x axis is directed along the ribbon axis and the y axis is perpendicular to the x and z axes). There is also a significant contribution from the three-coordinated atom that is the second-order neighbor of these atoms within the same hexagonal ring (atom #28). The flat bands at about −0.6 eV relative to the Fermi level in the FM and AFM states are formed mostly by px and py orbitals of atoms in the chains (e.g., atoms #3 and #5). The lower-lying flat bands at about −0.8 eV come from pz orbitals of atoms both in the chains and within the polycyclic regions.
The effect of edge magnetization on the band structure is well studied for zigzag GNRs.30,55–58 The presence of the magnetic order at the edges of zigzag GNRs was demonstrated experimentally at room temperature for ribbons up to 7 nm in width.58 According to the DFT calculations,55 the energy difference between the FM and AFM states for the widest of such ribbons can be as small as 0.4 meV per unit cell. This suggests that it might be possible to observe the magnetic effects in the 1D nanoobjects studied here. Note that for zigzag GNRs,30,55–57 the AFM state is preferred over the FM one, differently from the 1D nanoobjects. Band gaps of several hundreds of meV have been reported for narrow zigzag GNRs with pristine edges in the AFM state.30,55,56 They are much greater than the indirect band gap found for the 1D nanoobjects but are comparable to the direct band gaps.
Our calculations show that the bond lengths in the chains of the 1D nanoobject composed of 16 atoms each alternate because of the Peierls distortion11,59–64 (Fig. S2 of ESI†). Correspondingly, there is a variation in the bond order along the chains, which can be appreciated from the distribution of the electron density (Fig. 10). Thus, the chains in the 1D nanoobject are polyyne-like. The bond length alternations computed according to papers59,60 are found to be 6.0 pm and 5.8 pm for the two chains within the elementary period of the nanoobject (eqn (S1) of ESI†). Such a bond length alternation gives rise to a band gap in isolated carbon chains.11,59–64 The 1D nanoobject studied here, however, is metallic in the FM state, while the band gap in the AFM state is extremely small. Therefore, the chains connecting the polycyclic region within the 1D nanoobject display a metallic behavior. A significant metal-like conductivity has been reported previously for polyyne-like chains connecting metal electrodes, where a charge transfer from the metal to the chains takes place.65,66 A charge transfer should also occur in the 1D nanoobject between the chains and polycyclic regions. Note that the structure of the polycyclic regions is destabilized by the presence of the dangling bonds at the edges. Stabilization of the edges of the polycyclic regions through passivation with hydrogen should affect the charge transfer and might change the character of the 1D nanoobject to semiconducting.
The spatial distributions of the charge and magnetization densities over the 1D nanoobject in the FM and AFM states are shown in Fig. 10. It is seen that the magnetization density is mostly localized at the edge atoms of the polycyclic regions. The signs of the magnetic moments alternate for neighboring atoms within the polycylic regions, the same as for zigzag GNRs.55 The magnetic moments of the atoms in the chains are very small, in agreement with previous findings for polyyne-like carbon chains with an even number of atoms.59–61 (Note that the situation is different in odd chains, where the bond alternation cannot be fulfilled everywhere: uncompensated delocalized charge and, correspondingly, a nonzero magnetic moment arise there from the switching of the bond type from single/triple at the chain ends to double/double in the middle of the chain.60) The total magnetization of the 1D nanoobject in the FM state is found to be 2.8μB, where μB is the Bohr magneton.
Spin transport through atomic carbon chains connecting GNR electrodes has been recently studied in connection with the potential of such systems for spintronic devices.60,67,68 We observe that for the ground-state FM ordering, the band structures of the 1D nanoobject are rather different for spin up and spin down (Fig. 8a). It is seen from these band structures that it might be possible to shift the Fermi level by about 0.1 eV, e.g., by doping or application of a gate potential, to the energy where the density of states for one of the spin channels is zero and for the other it is not. In this case, the 1D nanoobject can be metallic for one of the spin orientations and semiconducting for the other, which makes this structure interesting for spintronic applications.
4. Conclusions
The present article is devoted to the reactive MD study of formation of the new hybrid type of 1D nanoobject consisting of alternating double atomic carbon chains and graphene-like polycyclic regions from initial GNRs of alternating width. The scheme of synthesis of the GNR with alternating regions that are single and three hexagons wide using Ullmann coupling and dehydrogenation reactions is proposed. It is worth keeping in mind that the proposed GNR structure could be easily varied by modifying the starting reactant. Although we have herein proposed the use of an octacene derivative, longer or shorter polyacene derivatives could be used to increase or decrease the length of the narrow single hexagon wide region. Indeed, following similar on-surface synthesis concepts as proposed here, unsubstituted polyacenes with as many as twelve rings have been successfully synthesized,71 which could equally well be used as the repeating unit in GNR formation. Assuming a similar behaviour upon irradiation with high energy electrons, the length of the single atoms chains linking the polycyclic regions could thus be controllably varied.We have improved the reactive Brenner potential24 for carbon–hydrogen systems. In our previous studies,16,25 we have reparameterized this potential to accurately describe the energies of pristine graphene edges, vacancy migration in graphene and the formation of atomic carbon chains. Here, we have also extended the potential to the case of graphene edges functionalized by hydrogen, which is important for adequate modeling of the system studied.
The MD simulations performed using this advanced potential reveal the formation of double chains and polycyclic regions from the narrow and wide regions of the proposed initial GNR, respectively, under electron irradiation in HRTEM for all the considered electron energies of 45, 55 and 80 keV. Thus, the 1D nanoobject with alternating double chains and polycyclic regions is formed from the initial GNR. The atomistic mechanism of the 1D nanoobject formation is found to be the following. Firstly hydrogen is removed by electron impacts. After that breaking and formation of bonds between carbon atoms occur for narrow and wide regions of the GNR, respectively. Namely, the narrow regions of the initial GNR spontaneously decompose into the double chains (the zigzag GNR with only one hexagon row in width is unstable10). Simultaneously the wide regions of the initial GNR grow from initial 3 hexagons to polycyclic regions composed of 5 to 7 polygons with 5 different polycyclic regions found for the path of this growth. It is of interest that all the newly formed polygons are pentagons.
The fractions of polycyclic regions corresponding to the growth path of the 1D nanoobject formed are calculated. The maximal yield of abundant polycyclic regions is achieved at the lowest electron energies of 45 and 55 keV. That is, the total yield of 4 abundant polycyclic regions is about 80%, while the yield of the most abundant polycyclic region which consists of 5 polygons reaches up to 30%. This is a rather high yield in comparison with the typical yield in synthesis of various nanoobjects. For example, a yield of 13% has been achieved for the synthesis of carbon rings from cyclocarbon oxide C24O6.72 Reactions induced by electron impacts on carbon atoms are absent under 45 keV electron irradiation. This means that formation of new bonds between carbon atoms of polycyclic regions occurs spontaneously or due to thermal activation. On the contrary, the total yield of abundant polycyclic regions is very low (less than 10%) under high 80 keV electron irradiation since electron impacts on carbon atoms lead to etching of polycyclic regions and eventually to rupture of the forming 1D nanoobject. Note that the formation of graphene-like polycyclic regions efficiently occurs without electron impacts on carbon atoms in contrast with reconstruction of zigzag graphene edges2 or narrow GNRs1 under electron irradiation. Thus, to produce 1D nanoobjects, the electron energy should correspond to the range where hydrogen atoms are efficiently removed by electron impacts but electron impacts on carbon atoms are almost absent and the choice of the electron energy in HRTEM cannot be used to increase the yield of abundant polycyclic regions.
To confirm the atomistic mechanism of formation of the 1D nanoobject revealed by the MD simulations, energy differences and activation barriers for the transitions with new bond formation along the growth path of polycyclic regions have been obtained using the DFT calculations. All the barriers for the transitions along the polycyclic region growth path observed in the MD simulations are within 0.55 eV. It is found that some bonds are formed without a barrier. This confirms that formation of the 1D nanoobject with the polycyclic regions can easily take place after hydrogen removal by electron impacts. Note that the differences in the values of the barriers obtained by the DFT calculations and using the advanced reactive potential are within 0.4 eV.
The DFT calculations performed show that the formation of each new bond along the polycyclic region growth path leads to a decrease of the 1D nanoobject energy. That is the lowest energy corresponds to the 1D nanoobject with the polycyclic region consisting of 7 polygons. Therefore, the yield of the 1D nanoobject with this polycyclic region can be increased by control of the temperature regime during or after electron irradiation in HRTEM. Since strain affects the energy difference between different polycyclic regions and activation barriers for transitions between them, it can be also used to increase the yield of given polycyclic regions. Note that application of strain12 or heating11 simultaneously with the electron irradiation influences the yield of atomic carbon chains formed from GNRs.
The DFT calculations of the 1D nanoobject with the polycyclic regions of the most abundant structure composed of 5 polygons show that the non-magnetic state is unstable against magnetic ordering of spins at two edges of the polycyclic regions similar to the phenomenon observed in zigzag GNRs.30,55–58 In the ground state, the 1D nanoobject is found to be ferromagnetic with parallel spins at the edges of the polycyclic regions. However, the aniferromagnetic state with antiparallel spins at the edges of the polycyclic regions is only slightly higher in energy. The chains of the 1D nanoobject composed of an even number of atoms display virtually no magnetism. The calculations of the band structures suggest that in the ferromagnetic state, the 1D nanoobject should behave as a metal, while in the antiferromagnetic state, a small band gap is opened. The band structures computed for spins up and down in the ferromagnetic case are rather different. There are energy windows where the density of states is non-zero for only one spin channel. This opens possibilities for the use of the 1D nanoobject in spintronic applications.
We believe that the synthesis of hybrid 1D nanoobjects proposed in the present paper can be considered as an example of the following general three-stage strategy of synthesis of new nanoobjects or macromolecules. Firstly precursors of organic nanoobjects or macromolecules are synthesized by the traditional chemical methods. Then these precursors are placed in HRTEM with the electron energy that is sufficient to remove hydrogen atoms but is not sufficient to cause breaking or forming of bonds between atoms heavier than hydrogen. As a result of hydrogen removal, the precursors become unstable or metastable and transform spontaneously or due to thermal activation into new nanoobjects or macromolecules which cannot be produced by the traditional chemical methods. Previously the analogous process of formation of crosslinking bonds between polymer molecules after hydrogen removal by electron impacts has been observed only for 3D samples of polymers.73,74 Here we propose such a way of synthesis for production of isolated nanoobjects and macromolecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. S. S., A. M. P. and A. A. K. acknowledge the Russian Foundation of Basic Research (Grants 18-02-00985 and 20-52-00035). S. V. R. and N. A. P. acknowledge the Belarusian Republican Foundation for Fundamental Research (Grant No. F20R-301) and Belarusian National Research Program “Convergence-2020”. This work has been carried out using the computing resources of the federal collective usage center Complex for Simulation and Data Processing for Mega-science Facilities at NRC “Kurchatov Institute”, http://ckp.nrcki.ru/ and was supported by the Research Center “Kurchatov Institute (order No. 1569 of July 16, 2019). D. G. O. has received funding from the Spanish Agencia Estatal de Investigación (Grant No. PID2019-107338RB-C63).References
- A. Chuvilin, J. C. Meyer, G. Algara-Siller and U. Kaiser, From Graphene Constrictions to Single Carbon Chains, New J. Phys., 2009, 11, 083019 CrossRef.
- K. Kim, S. Coh, C. Kisielowski, M. F. Crommie, S. G. Louie, M. L. Cohen and A. Zettl, Atomically Perfect Torn Graphene Edges and Their Reversible Reconstruction, Nat. Commun., 2013, 4, 2723 CrossRef PubMed.
- C. J. Russo and J. A. Golovchenko, Atom-By-Atom Nucleation and Growth of Graphene Nanopores, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 5953–5957 CrossRef CAS PubMed.
- J. H. Warner, M. H. Rümmeli, L. Ge, T. Gemming, B. Montanari, N. M. Harrison, B. Büchner and G. A. D. Briggs, Structural Transformations in Graphene Studied with High Spatial and Temporal Resolution, Nat. Nanotechnol., 2009, 4, 500–504 CrossRef CAS PubMed.
- T. Zoberbier, T. W. Chamberlain, J. Biskupek, N. Kuganathan, S. Eyhusen, E. Bichoutskaia, U. Kaiser and A. N. Khlobystov, Interactions and Reactions of Transition Metal Clusters with the Interior of Single-Walled Carbon Nanotubes Imaged at the Atomic Scale, J. Am. Chem. Soc., 2012, 134, 3073–3079 CrossRef CAS PubMed.
- I. V. Lebedeva, T. W. Chamberlain, A. M. Popov, A. A. Knizhnik, T. Zoberbier, J. Biskupek, U. Kaiser and A. N. Khlobystov, The Atomistic Mechanism of Carbon Nanotube Cutting Catalyzed by Nickel under an Electron Beam, Nanoscale, 2014, 6, 14877–14890 RSC.
- A. Chuvilin, U. Kaiser, E. Bichoutskaia, N. A. Besley and A. N. Khlobystov, Direct Transformation of Graphene to Fullerene, Nat. Chem., 2010, 2, 450–453 CrossRef CAS PubMed.
- J. Sloan, R. E. Dunin-Borkowski, J. L. Hutchison, K. S. Coleman, V. C. Williams, J. B. Claridge, A. P. E. York, C. G. Xu, S. R. Bailey, G. Brown, S. Friedrichs and M. L. H. Green, The Size Distribution, Imaging and Obstructing Properties of C60 and Higher Fullerenes Formed Within Arc-Grown Single Walled Carbon Nanotubes, Chem. Phys. Lett., 2000, 316, 191–198 CrossRef CAS.
- B. Song, G. F. Schneider, Q. Xu, G. Pandraud, C. Dekker and H. Zandbergen, Atomic-Scale Electron-Beam Sculpting of Near-Defect-Free Graphene Nanostructures, Nano Lett., 2011, 11, 2247–2250 CrossRef CAS PubMed.
- C. Jin, H. Lan, L. Peng, K. Suenaga and I. Iijima, Deriving Carbon Atomic Chains from Graphene, Phys. Rev. Lett., 2009, 102, 205501 CrossRef PubMed.
- O. Cretu, A. R. Botello-Mendez, I. Janowska, C. Pham-Huu, J.-C. Charlier and F. Banhart, Electrical Transport Measured in Atomic Carbon Chains, Nano Lett., 2013, 13, 3487–3493 CrossRef CAS PubMed.
- Y. C. Cheng, H. T. Wang, Z. Y. Zhu, Y. H. Zhu, Y. Han, X. X. Zhang and U. Schwingenschlögl, Strain-Activated Edge Reconstruction of Graphene Nanoribbons, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 073406 CrossRef.
- H. E. Troiani, M. Miki-Yoshida, G. A. Camacho-Bragado, M. A. L. Marques, A. Rubio, J. A. Ascencio and M. Jose-Yacaman, Direct Observation of the Mechanical Properties of Single-Walled Carbon Nanotubes and Their Junctions at the Atomic Level, Nano Lett., 2003, 3, 751–755 CrossRef CAS.
- G. Casillas, A. Mayoral, M. Liu, A. Ponce, V. I. Artyukhov, B. I. Yakobson and M. Jose-Yacaman, New Insights into the Properties and Interactions of Carbon Chains as Revealed by HRTEM and DFT Analysis, Carbon, 2014, 66, 436–441 CrossRef CAS.
- A. S. Sinitsa, T. W. Chamberlain, T. Zoberbier, I. V. Lebedeva, A. M. Popov, A. A. Knizhnik, R. L. McSweeney, J. Biskupek, U. Kaiser and A. N. Khlobystov, Formation of Nickel Clusters Wrapped in Carbon Cages: Toward New Endohedral Metallofullerene Synthesis, Nano Lett., 2017, 17, 1082–1089 CrossRef CAS PubMed.
- A. S. Sinitsa, I. V. Lebedeva, A. M. Popov and A. A. Knizhnik, Long Triple Carbon Chains Formation by Heat Treatment of Graphene Nanoribbon: Molecular Dynamics Study with Revised Brenner Potential, Carbon, 2018, 140, 543–556 CrossRef CAS.
- J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen and R. Fasel, Atomically Precise Bottom-Up Fabrication of Graphene Nanoribbons, Nature, 2010, 466, 470–473 CrossRef CAS PubMed.
- M. Corso, E. Carbonell-Sanromà and D. G. de Oteyza, in On-Surface Synthesis II, Advances in Atom and Single Molecule Machines, ed. D. G. de Oteyza and C. Rogero, Springer, Thun, 2018, pp. 113–152 Search PubMed.
- X. Zhou and G. Yu, Modified Engineering of Graphene Nanoribbons Prepared via On-Surface Synthesis, Adv. Mater., 2019, 32, 1905957 CrossRef.
- S. Clair and D. G. de Oteyza, Controlling a Chemical Coupling Reaction on a Surface: Tools and Strategies for On-Surface Synthesis, Chem. Rev., 2019, 119, 4717–4776 CrossRef CAS PubMed.
- S. T. Skowron, I. V. Lebedeva, A. M. Popov and E. Bichoutskaia, Approaches to Modelling Irradiation-Induced Processes in Transmission Electron Microscopy, Nanoscale, 2013, 5, 6677–6692 RSC.
- A. Santana, A. Zobelli, J. Kotakoski, A. Chuvilin and E. Bichoutskaia, Inclusion of Radiation Damage Dynamics in High-Resolution Transmission Electron Microscopy Image Simulations: The Example of Graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 094110 CrossRef.
- A. S. Sinitsa, I. V. Lebedeva, A. A. Knizhnik, A. M. Popov, S. T. Skowron and E. Bichoutskaia, Formation of Nickel-Carbon Heterofullerenes under Electron Irradiation, Dalton Trans., 2014, 43, 7499–7513 RSC.
- D. W. Brenner, Empirical Potential for Hydrocarbons for Use in Simulating the Chemical Vapor Deposition of Diamond Films, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9458–9471 CrossRef CAS.
- A. S. Sinitsa, I. V. Lebedeva, A. M. Popov and A. A. Knizhnik, Corrigendum to “Long Triple Carbon Chains Formation by Heat Treatment of Graphene Nanoribbon: Molecular Dynamics Study with Revised Brenner Potential (Potential), Carbon, 2018, 140, 543–556 ( Carbon , 2019 , 146 , 841 ) CrossRef CAS.
- P. Koskinen, S. Malola and H. Häkkinen, Self-Passivating Edge Reconstructions of Graphene, Phys. Rev. Lett., 2008, 101, 115502 CrossRef PubMed.
- T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and F. Mauri, Structure, Stability, Edge States, and Aromaticity of Graphene Ribbons, Phys. Rev. Lett., 2008, 101, 096402 CrossRef PubMed.
- Y. Hancock, A. Uppstu, K. Saloriutta, A. Harju and M. J. Puska, Generalized Tight-Binding Transport Model for Graphene Nanoribbon-Based Systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245402 CrossRef.
- C. K. Gan and D. J. Srolovitz, First-Principles Study of Graphene Edge Properties and Flake Shapes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125445 CrossRef.
- J. Kunstmann, C. Özdoğan, A. Quandt and H. Fehske, Stability of Edge States and Edge Magnetism in Graphene Nanoribbons, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045414 CrossRef.
- P. Wagner, V. V. Ivanovskaya, M. Melle-Franco, B. Humbert, J.-J. Adjizian, P. R. Briddon and C. P. Ewels, Stable Hydrogenated Graphene Edge Types: Normal and Reconstructed Klein Edges, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 094106 CrossRef.
- P. Wagner, C. P. Ewels, J.-J. Adjizian, L. Magaud, P. Pochet, S. Roche, A. Lopez-Bezanilla, V. V. Ivanovskaya, A. Yaya, M. Rayson, P. Briddon and B. Humbert, Band Gap Engineering via Edge-Functionalization of Graphene Nanoribbons, J. Phys. Chem. C, 2013, 117, 26790–26796 CrossRef CAS.
- N. F. Mott, On the Interpretation of the Relativity Wave Equation for Two Electrons, Proc. R. Soc. London, Ser. A, 1929, 124, 422–425 CAS.
- N. F. Mott, The Polarisation of Electrons by Double Scattering, Proc. R. Soc. London, Ser. A, 1932, 135, 429–458 CAS.
- W. A. McKinley and H. Feshbach, The Coulomb Scattering of Relativistic Electrons by Nuclei, Phys. Rev., 1948, 74, 1759–1763 CrossRef CAS.
- A. A. Knizhnik, MD-kMC code, Kintech Lab Ltd., Moscow, 2006–2018 Search PubMed.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, A Computer Simulation Method for the Calculation of Equilibrium Constants for the Formation of Physical Clusters of Molecules: Application to Small Water Clusters, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular Dynamics with Coupling to an External Bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- D. C. Franzblau, Computation of Ring Statistics for Network Models of Solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 4925–4930 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- M. Methfessel and A. T. Paxton, High-Precision Sampling for Brillouin-Zone Integration in Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- G. Henkelman and H. Jonsson, Improved Tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr., A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, Advanced Capabilities For Materials Modelling With Quantum ESPRESSO, J. Phys.: Condens. Matter., 2017, 29, 465901 CrossRef CAS.
- Quantum ESPRESSO code; http://www.quantum-espresso.org, 2020.
- R. Dorel and A. M. Echavarren, Strategies for the Synthesis of Higher Acenes, Eur, J. Org. Chem., 2017, 14–24 CrossRef CAS PubMed.
- J. Krüger, F. Eisenhut, J. M. Alonso, T. Lehmann, E. Guitián, D. Pérez, D. Skidin, F. Gamaleja, D. A. Ryndyk, C. Joachim, D. Peña, F. Moresco and G. Cuniberti, Imaging the Electronic Structure of On-Surface Generated Hexacene, Chem. Commun., 2017, 53, 1583–1586 RSC.
- R. Zuzak, R. Dorel, M. Krawiec, B. Such, M. Kolmer, M. Szymonski, A. M. Echavarren and S. Godlewski, Nonacene Generated by On-Surface Dehydrogenation, ACS Nano, 2017, 11, 9321–9329 CrossRef CAS PubMed.
- L. Colazzo, M. S. G. Mohammed, R. Dorel, P. Nita, C. G. Fernández, P. Abufager, N. Lorente, A. M. Echavarren and D. G. de Oteyza, On-Surface Synthesis of Heptacene on Ag(001) from Brominated and Non-Brominated Tetrahydroheptacene Precursors, Chem. Commun., 2018, 54, 10260–10263 RSC.
- R. G. Lawton and W. E. Barth, Synthesis of Corannulene, J. Am. Chem. Soc., 1971, 93, 1730–1745 CrossRef CAS.
- P. B. Bennett, Z. Pedramrazi, A. Madani, Y. C. Chen, D. G. de Oteyza, C. Chen, F. R. Fischer, F. Crommie and J. Bokor, Bottom-Up Graphene Nanoribbon Field-Effect Transistors, Appl. Phys. Lett., 2013, 103, 253114 CrossRef.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Energy Gaps in Graphene Nanoribbons, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed.
- G. Lee and K. Cho, Electronic Structures of Zigzag Graphene Nanoribbons with Edge Hydrogenation and Oxidation, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165440 CrossRef.
- Y. C. Cheng, Z. Y. Zhu and U. Schwingenschlögl, Mechanical Failure of Zigzag Graphene Nanoribbons under Tensile Strain Induced by Edge Reconstruction, J. Mater. Chem., 2012, 22, 24676–24680 RSC.
- G. Z. Magda, X. Jin, I. Hagymási, P. Vancsó, Z. Osváth, P. Nemes-Incze, C. Hwang, L. P. Biró and L. Tapasztó, Room-Temperature Magnetic Order on Zigzag Edges of Narrow Graphene Nanoribbons, Nature, 2014, 514, 608–611 CrossRef CAS.
- L. Ravagnan, N. Manini, E. Cinquanta, G. Onida, D. Sangalli, C. Motta, M. Devetta, A. Bordoni, P. Piseri and P. Milani, Effect of Axial Torsion on sp Carbon Atomic Wires, Phys. Rev. Lett., 2009, 102, 245502 CrossRef.
- Z. Zanolli, G. Onida and J.-C. Charlier, Quantum Spin Transport in Carbon Chains, ACS Nano, 2010, 4, 5174–5180 CrossRef CAS.
- M. Liu, V. I. Artyukhov, H. Lee, F. Xu and B. I. Yakobson, Carbyne from First Principles: Chain of C Atoms, a Nanorod or a Nanorope, ACS Nano, 2013, 7, 10075–10082 CrossRef CAS PubMed.
- V. I. Artyukhov, M. Liu and B. I. Yakobson, Mechanically Induced Metal–Insulator Transition in Carbyne, Nano Lett., 2014, 14, 4224–4229 CrossRef CAS.
- A. La Torre, A. Botello-Mendez, W. Baaziz, J.-C. Charlier and F. Banhart, Strain-Induced Metal–Semiconductor Transition Observed in Atomic Carbon Chains, Nat. Commun., 2015, 6, 6636 CrossRef CAS PubMed.
- F. Börrnert, C. Börrnert, S. Gorantla, X. Liu, A. Bachmatiuk, J.-O. Joswig, F. R. Wagner, F. Schäffel, J. H. Warner, R. Schönfelder, B. Rellinghaus, T. Gemming, J. Thomas, M. Knupfer, B. Büchner and M. H. Rümmeli, Single-Wall-Carbon-Nanotube/Single-Carbon-Chain Molecular Junctions, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085439 CrossRef.
- Ž. Crljen and G. Baranović, Unusual Conductance of Polyyne-Based Molecular Wires, Phys. Rev. Lett., 2007, 98, 116801 CrossRef PubMed.
- N. D. Lang and P. Avouris, Oscillatory Conductance of Carbon-Atom Wires, Phys. Rev. Lett., 1998, 81, 3515–3518 CrossRef CAS.
- M. G. Zeng, L. Shen, Y. Q. Cai, Z. D. Sha and Y. P. Feng, Perfect Spin-Filter and Spin-Valve in Carbon Atomic Chains, Appl. Phys. Lett., 2010, 96, 042104 CrossRef.
- Y. Zhou, Y. Li, J. Li, J. Dong and H. Li, Electronic Transport Properties of Carbon and Boron Nitride Chain Heterojunctions, Mater. Chem. C, 2017, 5, 1165–1178 RSC.
- N. A. Poklonski; A. T. Vlassov; S. A. Vyrko; E. F. Kislyakov; S. V. Ratkevich and A. I. Siahlo, in Physics, Chemistry and Applications of Nanostructures, ed. V. E. Borisenko, S. V. Gaponenko, V. S. Gurin and C. H. Kam, World Scientific, Singapore, 2013, pp. 36–39 Search PubMed.
- N. A. Poklonski, S. A. Vyrko, A. I. Siahlo, O. N. Poklonskaya, S. V. Ratkevich, N. N. Hieu and A. A. Kocherzhenko, Synergy of Physical Properties of Low-Dimensional Carbon-Based Systems for Nanoscale Device Design, Mater. Res. Express, 2019, 6, 042002 CrossRef.
- F. Eisenhut, T. Kühne, F. García, S. Fernández, E. Guitián, D. Pérez, G. Trinquier, G. Cuniberti, C. Joachim, D. Peña and F. Moresco, Dodecacene Generated On Surface: Reopening of the Energy Gap, ACS Nano, 2020, 14, 1011–1017 CrossRef CAS PubMed.
- K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, An Sp-Hybridized Molecular Carbon Allotrope, Cyclo[18]Carbon, Science, 2019, 365, 1299–1301 CrossRef CAS PubMed.
- S. Dadbin, M. Frounchi, M. H. Saeid and F. Gangi, Molecular Structure and Physical Properties of E-Beam Crosslinked Low-Density Polyethylene for Wire and Cable Insulation Applications, J. Appl. Polym. Sci., 2002, 86, 1959–1969 CrossRef CAS.
- D. D. Manas, M. Ovsik, A. Mizera, M. Manas, L. Hylova, M. Bednarik and M. Stanek, The Effect of Irradiation on Mechanical and Thermal Properties of Selected Types of Polymers, Polymers, 2018, 10, 158 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Figures illustrating distributions of successful electron impacts over the energies transferred to hydrogen and carbon atoms for the chosen minimal transferred energies, figures illustrating DFT studies of the 1D nanoobject with D1 polycyclic regions: bond length alternation in carbon chains and partial densities of states in the antiferromagnetic state, video files showing examples of the structure evolution observed in molecular dynamics simulations of the 1D nanoobject formation from the graphene nanoribbon with alternating width. See DOI: 10.1039/d0cp04090h |
| This journal is © the Owner Societies 2021 |