Electronic structure modelling of the edge-functionalisation of graphene by MnxOy particles†
Richard N. L.
Terrett
 *a,
George
Tsekouras
*a,
George
Tsekouras
 b,
Takuya
Tsuzuki
b,
Takuya
Tsuzuki
 b,
Gerhard F.
Swiegers
b,
Gerhard F.
Swiegers
 c,
Ronald J.
Pace
a and
Robert
Stranger
c,
Ronald J.
Pace
a and
Robert
Stranger
 a
a
aComputational Quantum Chemistry Group, Research School of Chemistry, Australian National University, Canberra, Australian Capital Territory 0200, Australia. E-mail: rterrett@rsc.anu.edu.au
bResearch School of Electrical, Energy and Materials Engineering, Australian National University, Canberra, Australian Capital Territory 0200, Australia
cIntelligent Polymer Research Institute, Australian Institute for Innovative Materials, University of Wollongong, Wollongong, New South Wales 2522, Australia
First published on 11th December 2020
Abstract
The use of graphenic carbon is attractive as a basal or intermediate support for catalytic particles in advanced catalytic electrodes. This popularity is motivated by its excellent electrical properties and ability to form foliated conformal coatings of exceptional surface area and flexibility. Surface- and edge-functionalisation of graphene sheets affords diverse routes to the covalent attachment of candidate catalytic species. Of particular interest to advanced water oxidation is the possibility of covalent attachment of MnxOy species partially recapitulating the chemistry of the Mn4O5Ca active site of Photosystem II (PSII), which achieves the four-electron oxidation of water under physiological conditions. Here, we report aperiodic density functional theory (DFT) investigations of candidate attachment geometries for a variety of manganese oxide particles to graphene sheets. We find that the flexibility of graphene sheets as well as the conformational degrees of freedom of candidate edge functionalisation permits a large variety of realistic attachment geometries that can act as attachment sites for molecular manganese-oxide species or nuclei for the growth of periodic manganese oxides. We find that substantially simplified models of graphene attachment afford an excellent compromise between computational efficiency, tractability, and accuracy, and characterise the accuracy of these models in detail.
1 Introduction
Graphene is an atomic monolayer of graphite comprised of a hexagonal periodic 2D lattice of sp2-hybridised carbon atoms, with an idealised nearest-neighbour C–C distance of 142 pm.1,2 Graphene has a range of superlative physical properties, including an exceptional Young's modulus (≈1.0 TPa) making it one of the strongest materials known,3 very high specific surface area (theoretically up to 2630 m2 g−1),‡ exceptional thermal conductivity,6 and unique optical and electron transport behaviour.2,7–9Graphene and its derivatives are attractive as a basal or intermediate component of high-performance electrodes because of their excellent electrical conductivity and ability to form a highly foliated and flexible conformal coating on other substrates. These properties facilitate the creation of electrodes with very high electrochemically sensible surface areas for use in catalysis,10–12 sensors,13–15 supercapacitors,16–21 and metal ion batteries.14,22,23 The Hummers process and its modifications24,25 effect the chemical exfoliation of graphite to graphene oxide (GO), which may then be partially reduced to obtain reduced graphene oxide (rGO) by chemical,19,26–28 thermal,29 or photolytic reduction.30,31 However, GO produced by the Hummers process is substantially defective with respect to pristine graphene, typically being heavily topologically damaged and refunctionalised with carboxylic acid, epoxide, hydroxide, and ketone moieties at both surfaces and edges.32,33 Reduction to rGO imperfectly recovers some of the desirable properties of unmodified graphene, including improvement in electrical conductivity.30,33,34 However, multiple routes to bulk graphene exist, including bottom-up synthesis to obtain pristine graphene of regular dimensions,35 unzipping of carbon nanotubes (CNTs),36 and mechanical delamination of graphite to obtain pristine monolayers.9
A large number of publications report the association of metal oxide nanoparticles with graphene in various forms, to create materials with potential or actual synergistic electrochemical functionality. This functionality may be in the form of providing a high surface area and conductive support for charge carrier exchange with metal oxide particles, or by the creation of semiconductor heterojunctions.15 Moreover, the activation of graphene to catalytic reactivity by incorporation in metal oxide/graphene van der Waals heterostructures has been elucidated theoretically.37 A representative sample of experimentally prepared oxo-metal/graphene composites are summarised in Table 1. A preponderance of associations between metal oxide nanoparticles and graphene sheets in the literature appear to be of a noncovalent nature, however some covalently attached particles are noted (e.g.ref. 38). Alternatively, precipitation of Mn3O4 particles with presumed high specificity to ionic functionalities is also known.10
| Year | Method | Application | TMO identity | TMO disposition | Graphene disposition | Ref. |
|---|---|---|---|---|---|---|
| 2008 | Photoredox | Solar cell | TiO2 | ‘nanoparticles’ | rGO | 39 |
| 2009 | Redox | Supercapacitor | SnO2 | ‘nanoparticles’ | rGO | 16 |
| 2009 | Self-assembly | Lithium ion battery | SnO2 | ‘nanoparticles’ | rGO | 22 |
| 2010 | Photoredox | rGO dispersion | H3PW12O40 | Keggin cluster | rGO | 28 |
| 2011 | Electrostatic coprecip. | Supercapacitor | MnO2 | ‘nanosheets’ | rGO | 17 |
| 2011 | Electrostatic coprecip. | ORR | Mn3O4 | ‘nanoparticles’ | IL-rGO | 10 |
| 2012 | Carboxylate coord. | LED | ZnO | ‘nanoparticles’ | GO | 38 |
| 2012 | Reductive precipitation | Supercapacitor | MnO2 | ‘nanoparticles’ | ‘aMEGO’ | 40 |
| 2012 | Self-assembly | Pollutant degradation | ZnO | ‘nanoparticles’ | rGO | 11 |
| 2013 | Mechanical milling | Supercapacitor | α-MnO2 | ‘nanorods/particles’ | GO | 18 |
| 2014 | Several | Lithium ion battery | Mn3O4/MnO | ‘nanoparticles’ | GO/rGO | 23 |
| 2015 | Reductive precipitation | HCOOH dehydration | AuPd–MnOx | ‘nanocomposite’ | ZIF-8/rGO | 12 |
| 2016 | Aminosiloxane linkage | Microbicide | ZnO | ‘nanoparticles’ | GO | 41 |
| 2017 | Hydrothermal | Gas sensor | SnO2 | ‘nanorods’ | rGO | 14 |
| 2019 | Electrodeposition | Supercapacitor | MnO2 | ‘nanosheets’ | rGO | 20 |
| 2020 | Reductive precipitation | Supercapacitor | Mn3O4 | ‘nanoclusters’ | rGO | 42 |
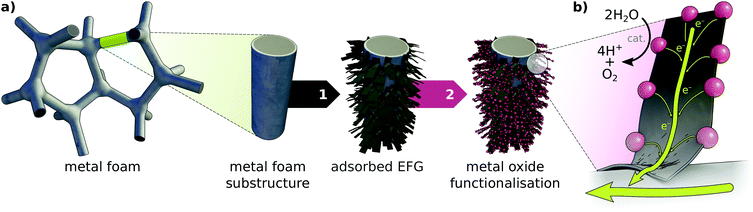
This work seeks to characterise bichelation of a number of notional MnxOy clusters via edge-functionalised graphene (EFG) sheets. These clusters resemble known or potential water oxidation catalysts (WOCs), with similarity to the Mn4O5Ca oxygen evolving complex (OEC) of the Photosystem II (PSII) holoenzyme.43 This complex effects the four-electron photo-driven oxidation of water, the first step of oxygenic photosynthesis in plants and cyanobacteria.44 These clusters may represent molecular catalytic or procatalytic particles of definite nuclearity, or represent points of attachment of arbitrarily large TMO nanoparticles or nanosheets. We conceive of such attachment of TMO particles to graphene sheets as an essential component in the construction of notional hierarchically structured electrodes (HSEs) for water oxidation, which employ EFG as an intermediate electron transport system of exceptional surface area (illustrated in Fig. 1). MnxOy/graphene composites for electrochemical applications have been reported with MnxOy particles in a number of dispositions, including surfacially adsorbed ‘amorphous or poorly crystalline’ MnO2 particles of diameter 2–3 nm,40 adsorbed mesoporous Mn3O4 nanoclusters of diameter 2–20 nm,42 non-uniform aggregates of relatively monodisperse (9.45 ± 1.72 nm) Mn3O4 spheroids on functionalised rGO,10 precipitation of birnessite-like MnO2 nanosheets (of a characteristic scale of hundreds of nanometers) in an electrostatic heterostructure with functionalised rGO,17 and electrostatic precipitation of ‘ultrahigh MnO2[nanosheet] loading’ on a topologically complex rGO aerogel.20 These examples attest to a diversity of MnxOy stoichiometries, particle scales, dispersities, and aspect ratios which are accessible through a range of synthetic techniques.
Amide coupling is an established method of derivatisation of carboxylic acid moieties produced graphene sheets (e.g.ref. 10, 45 and 46). Here we consider the attachment of MnxOy particles to extended polycyclic aromatic hydrocarbons (PAHs) through the intermediation of amide moieties. These PAHs are intended to be representative of substructures of graphene sheets which have been selectively oxidised at their edges to produce carboxylic acid moieties, which are then condensed with 3- and 4-aminobenzoic acid to afford protrusive carboxylate ligands for coordination of oxo-manganese clusters. We hypothesised that the large number of conformational degrees of freedom afforded by typical amide functionalisation at graphene edges—as well as the intrinsic flexibility of graphene itself—would facilitate attachment of MnxOy particles of a wide variety of shapes to a wide range of edge-functionalised graphene models. Manganese oxide clusters attached to graphene sheets may be construed either as molecular species of definite nuclearity, or as the attachment points for precipitation of large-scale periodic structures at nucleation sites provided by edge functionalisation of graphene.
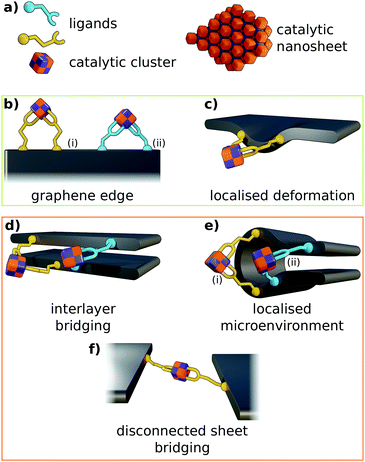
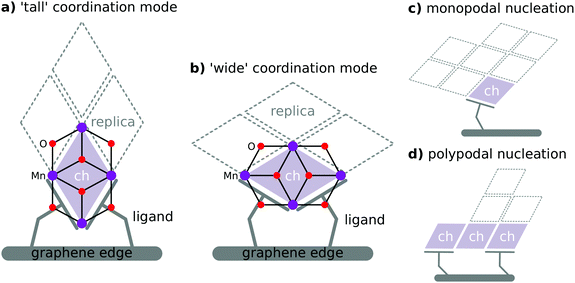
Carboxylate residues are capable of coordinating transition metals as a monodentate, chelating, or bridging ligand. Therefore, carboxylate edge-functionalisation of graphene is anticipated to permit binding of metal oxide clusters in a wide variety of configurations (Fig. 2). The allowable binding configurations are controlled by a number of factors:
• Graphene sheets are liable to possess multiple geometrically distinct micro-environments at their perimeters, and edge-functionalisation of the graphene at these environments will yield salient carboxylate ligands more or less suited to coordinating metal oxide clusters of differing geometry.
• Carboxylate ligand identity informs the coordination geometries that are allowable for a given edge functionalisation pattern. Particularly, the length and flexibility of aliphatic chains present in the ligand is of capital importance.
• Differing metal oxide cluster topologies will facilitate differing modes of coordination by carboxylate ligands.
This work was undertaken to probe the energetic and geometric behaviour of a range of plausible edge functionalisation schemes, as well as to characterise the extent of electronic coupling between the TMO cluster and the EFG. In the case of coordination by a single ligand, attachment of a cluster to EFG is substantially conformationally unconstrained. However, chelation of a TMO cluster by two or more ligands will place constraints on the relative geometry of (a) the EFG sheet, (b) the points of attachment of the ligands, (c) the conformation of those ligands, and (d) the conformation of the TMO cluster. Therefore, we sought to estimate the energetics of binding TMO particles by bichelate attachment to EFG model edges and determine how the degrees of freedom present in the EFG–TMO cluster complexes contribute to these energetics.
Graphene is quite flexible, and experimentally characterised graphene is commonly very crumpled (see e.g.ref. 47). The stability of highly folded graphene implies that arbitrarily separated functional groups may participate in the chelation of a TMO cluster. Indeed, coordinating functional groups chelating a TMO cluster may be located on distinct graphene sheets. The flexibility of graphene over large scales and its interaction with edge functionalisation and coordination complexes cannot be directly assessed by the density functional theory methodology we have adopted, and therefore we measure the energy associated with small scale folding of a graphene edge to indirectly characterise the extent to which this degree of freedom may participate in stabilising TMO cluster chelation.
2 Methodology
2.1 Computational details
Calculations were performed in the ORCA 4 electronic structure suite48 running on 64-bit Linux. Electronic structures were computed by spin-unrestricted density functional theory (DFT), using the Split-RI-J approximation to the Coulomb energy.49 The exchange and correlation interactions were approximated by the combined functional of Becke and Perdew (BP86).50,51 The Grimme3 dispersion correction (D3BJ) was applied to model the noncovalent dispersion interactions within the molecule.52,53Typically, geometry optimisations were performed in a multi-step process proceeding from a MD simulation using the Unified Forcefield (UFF) model,54 followed by DFT optimisation with a heterogeneous basis set55 (def2-SVP on nonmetal atoms, and def2-TZVP on metal atoms) and variable SCF and grid precisions that are adjusted to obtain convergence in the potential energy gradient. Unless otherwise indicated, high-quality geometry convergence was obtained to a BP86/def2-TZVP/D3BJ level of theory on all atoms, with an SCF convergence criterion of ≤1 × 10−9Eh and numerical grid quality settings of at least Grid3 and FinalGrid5. Calculations using heterogeneous basis sets retain these settings but substitute a 6-31G* basis on designated atoms. Final geometries are converged to the default criteria of ORCA (ΔE: ≤5 × 10−6Eh, ∇ERMS: ≤1 × 10−4Eh·a0−1, ∇Emax: ≤3 × 10−4Eh·a0−1, Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) RMS: ≤2 × 10−3a0, Δ
RMS: ≤2 × 10−3a0, Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) max: ≤4 × 10−3a0).
max: ≤4 × 10−3a0).
Gaussian integrals are calculated by the LIBINT library.56 The def2/J auxiliary basis was used for the Split-RI-J approximation.57 Where calculations are solvent corrected, the CPCM continuum approximation with preset parameters for water (ε = 80.4 D (2.682 × 10−28 C m−1), n = 1.33) used, alongside the SMD augmentation of Marenich, Cramer, and Truhlar.58 Intrinsic bond strength index59 analysis (IBSI) was performed using MultiWfn.60
Initial construction of molecular models was undertaken using the SAMSON and Avogadro programs.61,62 Structural visualisation was achieved using the PyMOL molecular graphics suite v2.2.063 and the Blender 3D graphics program.
2.2 Graphene model
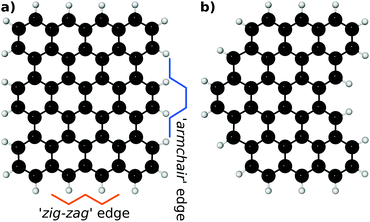
Pristine EFG may provide a large number of micro-environments based on both the edge functionalisation pattern and the structure of the incipient graphene lattice. An idealised, straight-edged graphene sheet can provide two different edge geometries (so-called ‘armchair’ and ‘zig-zag’ edges) with differing periodic lengths and derived functionalisation geometries. Less regular edge structures (which we will term ‘ragged’ offer more possibilities, including two-dimensional prominences and pockets). These terms are illustrated in Fig. 3.To constrain the large number of potential coordination geometries, in the present work we consider bi-functionalisation of a zig-zag edge.
2.3 Criteria for model MnxOy species
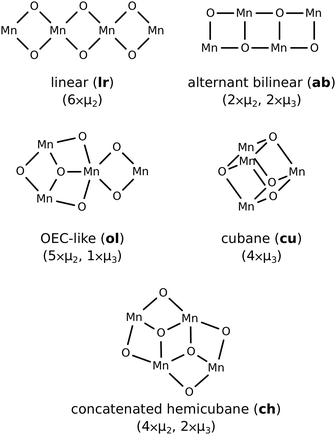
Manganese oxide clusters of even low nuclearity possess a very high combinatoric complexity in their number of potential configurations of the cluster oxomanganese skeleton, bridging ligands, protonation states, oxidation states, and Jahn–Teller activities. Candidate manganese oxide clusters in the present study are constrained by the geometry of salient carboxylate ligands reasonably possessed by an EFG sheet. Four additional constraints are employed to reduce the list of clusters considered for simulation. These are (a) cluster nuclearity ≤4, (b) high symmetry, (c) termination by water and/or hydroxide ligands, and (d) bridging ligands of order ≤3. Five MnxOy clusters with unique connectivity graphs satisfying the aforementioned constraints were shortlisted for investigation, however, in the present study we limit our analysis to three of these, selected for compatibility with bidentate ligation to a zig-zag graphene edge and similarity to both the PSII OEC active site substructures of laminar oxo-manganese minerals with putative water oxidising activity. Two of these structures are different attachment configurations of the concatenated hemicubane structure (ch) and the third is the cubane (cu) structure indicated in in Fig. 4.3 Results
3.1 Intrinsic flexibility of graphene sheet
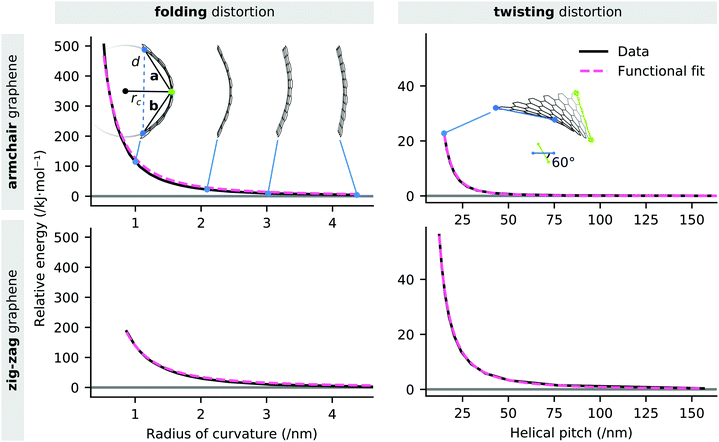
As previously established, graphene is a highly flexible material that is capable of high local curvatures, stabilised by van der Waals self-interaction. This suggests that chelation of TMO clusters or nanoparticles by EFG may involve flexion of the graphene edge, however such effects are computationally expensive to systematically explore at a DFT level of theory. The strain energy associated with folding and twisting a graphene sheet at the chosen level of theory was modelled by deformation of a pair of rectangular graphene nanosheets and distinguished by whether their long edges possess the armchair or zig-zag structure. The edges of each sheet are saturated with hydrogen atoms. The bending of each sheet was effected by varying the distance d between two carbon atoms at opposite short edges of the sheet. Helical torsion was applied to the sheet by varying the dihedral angle of the corners of the sheet between 0 and 60° in 5° increments.The radius of curvature of the sheet is estimated as the radius of the circumcircle defined by the positions of the indicated edge carbon atoms and the centroid of the central aromatic ring of the sheet. The radius rc is related to the vectors connecting the edge atoms to the ring centroid a and b by the formula given in eqn (1). Whilst the graphene sheet model deviates from strict conformation to a cylindrical section, we posit the described curvature measure to be an acceptable first-order approximation. The helical pitch p of a graphene sheet undergoing twisting deformation is the extrapolated sheet length required to achieve a full rotation at the nominal twist angle.
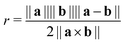 | (1) |
The strain energy induced in the graphene nanosheet by the radius of curvature rc and helical pitch p of the sheet is illustrated in Fig. 5. The strain energy associated with bending deformations (Fig. 5a) is appropriately approximated (R2 = 0.997) by the functional form 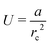 , where a has a best-fit value of approximately 1.26 × 102 kJ nm2 mol−1. We note that modelling the graphene sheet as a deflected beam indicates that the sheet has nonlinear elasticity. The strain energy associated with twisting deformations along the armchair axis (Fig. 5b) is appropriately approximated (R2 = 0.999) by the functional form
, where a has a best-fit value of approximately 1.26 × 102 kJ nm2 mol−1. We note that modelling the graphene sheet as a deflected beam indicates that the sheet has nonlinear elasticity. The strain energy associated with twisting deformations along the armchair axis (Fig. 5b) is appropriately approximated (R2 = 0.999) by the functional form 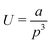 , where a is approximately 7.54 × 104 kJ nm3 mol−1. However, helical deformation of a sheet along the zig-zag direction is approximated (R2 > 0.999) by the functional form
, where a is approximately 7.54 × 104 kJ nm3 mol−1. However, helical deformation of a sheet along the zig-zag direction is approximated (R2 > 0.999) by the functional form 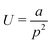 , where a is approximately 8.43 × 103 kJ nm2 mol−1. It should be noted that the relative energy associated with deformations of each graphene sheet is an extensive quantity, and therefore the zig-zag and armchair nanosheets are not directly comparable. Nevertheless, these data demonstrate that the energies associated with out-of-plane deformations of zig-zag and armchair edges are of the same order of magnitude, and that they are adequately characterised by simple functional forms.
, where a is approximately 8.43 × 103 kJ nm2 mol−1. It should be noted that the relative energy associated with deformations of each graphene sheet is an extensive quantity, and therefore the zig-zag and armchair nanosheets are not directly comparable. Nevertheless, these data demonstrate that the energies associated with out-of-plane deformations of zig-zag and armchair edges are of the same order of magnitude, and that they are adequately characterised by simple functional forms.
These data indicate that non-negligible distortions of graphene fragments are accessible at low energies, however the corresponding strain energy rapidly increases below a radius of curvature of less than approximately 2 nm, or a helical pitch of less than 25 nm. At large deflections, a small negative Gaussian curvature (i.e. a ‘saddle’ curvature) is developed in the sheet. This curvature is likely to be due to the limitation that the transit constraint which has been applied only constrains three atoms lying along the centreline of the sheet.
3.2 Concatenated hemicubane models
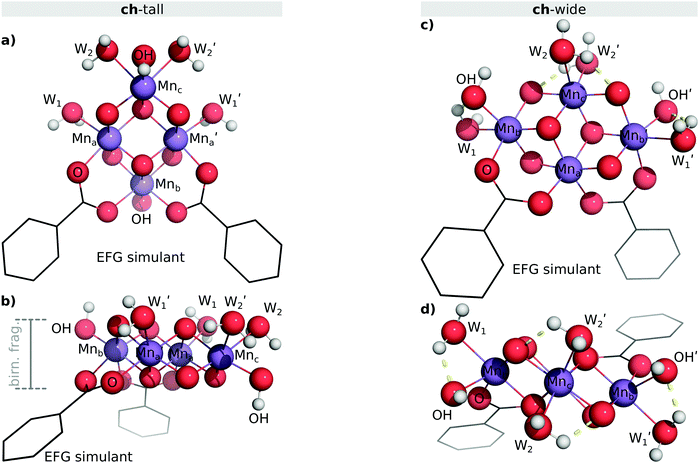
The concatenated hemicubane structure (ch) can be interpreted as a minimal capped fragment of a birnessite (MnO2) sheet (or other laminar metal oxide with a 1T lattice structure). Birnessite has been identified as a water oxidation catalyst.64 Indeed, the ultimate active form of the Mn4O4 cubane catalyst65 of Dismukes, et al.—which alongside the PSII OEC serves as structural inspiration for the cu model—has been proposed as a variety birnessite based on EXAFS evidence.66 The birnessite structure is composed of face-sharing MnO6 octahedra. As such, the surfaces presented on either side of the lamina are entirely composed of μ3-oxo caps, and all interior Mn ions are coordinatively saturated. Therefore, covalent coordination of Mn ions in birnessite can only take place at defect sites (e.g. oxygen vacancies, Rütschi defects) or at the edges of MnO2 laminae. The ch skeleton is an attractive structure for study not only as a potential water oxidation catalyst precursor, but also as a plausible substructure of an EFG-attached birnessite nanoparticle.We explored two potential coordination modes of the minimal ch skeleton to EFG. These modes are denoted ch-tall and ch-wide. These clusters differ in the coordination of the EFG simulant carboxylate ligands. Their attachment to a notional EFG sheet via two colocated carboxylate ligands is illustrated in Fig. 6. ch-tall and ch-wide have equivalent ligand sets and therefore can be usefully considered to be related by an isodesmic transformation. Where ligation of an extended birnessite sheet to EFG is considered, a functionally infinite variety of coordination modes exist. These include bridging of multiple graphene sheets by a single birnessite sheet, coordination involving defective structures, or coordination geometries relying upon long-range warping of graphene and/or birnessite sheets. These possibilities are not amenable to the form of electronic structure analysis undertaken here for reasons of combinatoric complexity and computational expense.
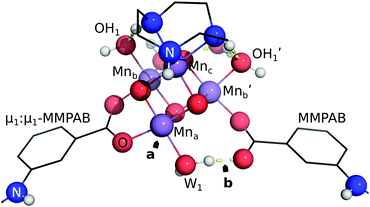
The ch-wide isomer possesses quasi-C2 symmetry. The ch skeletal geometry prevents collinear coordination of κ2:κ2-carboxylato ligands to the same side of the cluster, however it is presumed that the rotational degrees of freedom of the 4-formamidobenzoic acid moieties attached to an EFG sheet, as well as coordinative micro-environments created by ragged graphene edges, will comfortably accommodate the coordination geometry enforced by the oxomanganese cluster.
The ch-wide isomer possesses an implicit MnIV oxidation state configuration on all Mn ions (confirmed via Mulliken spin population analysis) equivalent to ch-tall. All waters exist as aqua ligands (Mn–O: 211 ± 3 pm), and a symmetric hydrogen bonding network exists between the aqua, hydroxo, and two μ2-oxo ligands. The obtained geometry is depicted in Fig. 7b.
The gas phase and solvent corrected geometries of ch-wide are virtually identical, however the hydrogen bonding network previously described is erased. The aqua ligands are deactivated to 204 ± 0 pm and proton reorientations occur which break hydrogen bonding with both the μ2-oxo and hydroxo ligands.
3.3 Cubane (cu) model
The cubane model consists of a Mn4O4 cluster with similar coordination geometry to the ch-tall model, however each Mn ion in this complex is in the +3 oxidation state, and hence each ion expresses a Jahn–Teller axis of elongation. This cluster is illustrated in Fig. 8d and 10. The Mnc ion most distal from the coordinating carboxylate ligands is coordinated by a neutral κ3-triazacyclononane (TACN) ligand, whilst the coordination spheres of all other Mn ions are completed by aqua and hydroxo ligands. In practice, cooperativity between the Jahn–Teller activation of MnO bonds and the ligand hydrogen bonding network leads to deligation of an aqua ligand. Similarly labile behaviour is a common feature of solvated models of Jahn–Teller active MnxOy clusters with aqua and hydroxo ligands.In all three clusters, structural perturbations imposed by solvent correction consisted of minor reorientations of terminal ligands. Therefore, we opted to compute further model calculations in the gas phase. Intrinsic bond strength index (IBSI) analysis (see ESI†) of the ch-wide and ch-tall clusters indicate that Mn-aqua bonds in these complexes are exceptionally weak (competitive with hydrogen bonds), and therefore these reorientations are interpreted as low-energy phenomena.
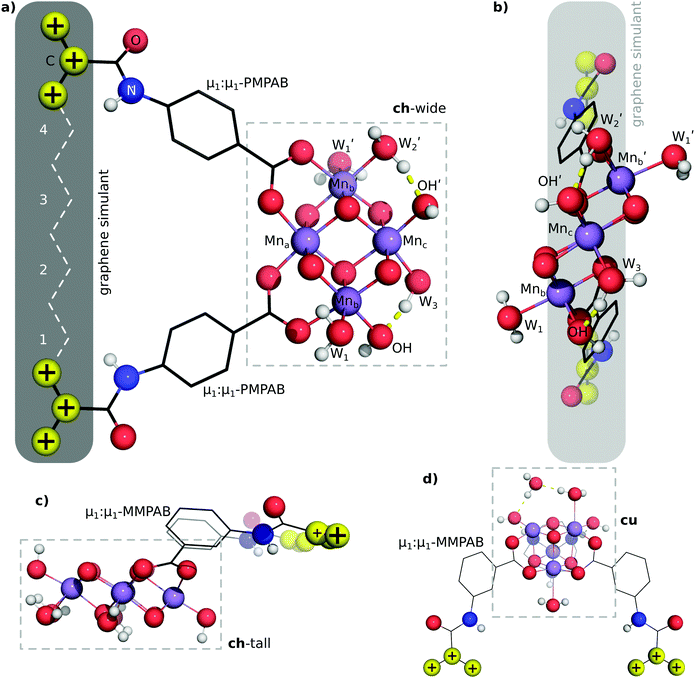
EFG attachment of the ch-tall and cu models is simulated by the use of μ1:μ1-MMPAB ligands. These alternative EFG ligands are required to obtain approximately collinear terminal propenyl moieties compatible with graphene attachment. Whereas the EFG simulant ligands and oxo-manganese cluster of the ch-wide model are essentially coplanar, the ch-tall and cu models lie out of plane with the graphene-consistent ligand constraints.
3.4 Linear transit of attachment geometries
Linear transit was employed to establish the potential energy surface associated with differing attachment points of the cluster to the graphene ‘zig-zag’ edge, distinguished by different numbers of intervening phenyl rings between the attachment points (between 2 and 6 rings). The computational procedure adopted involves increasing and decreasing the distance between pins in 49.2 pm increments (i.e. 246 pm divided by 5). These interpolating geometries are necessary to obtain SCF convergence, and also provide information about plausible energetics for cluster attachment to deformed graphene sheets.The potential energy surfaces associated with linear transit of the ligand constraints for models ch-wide, ch-tall, and cu are depicted in Fig. 9. These transits reveal that the most energetically favourable attachment geometry in each case has an edge functionalisation separation of four phenyl rings, which comports with the initial ‘guess’ geometries which were constructed (depicted in Fig. 9). The potential energy surface of each linear transit (prior to any bond rearrangement) is adequately (R2 = 0.85–0.99) described by a quadratic model which indicates that the elasticity of each cluster is quasi-Hookean over this domain (k ≈ 385–503 kJ nm−2). Data relating to these quadratic fits (as well as corresponding mixed-basis models) are presented in the ESI.†
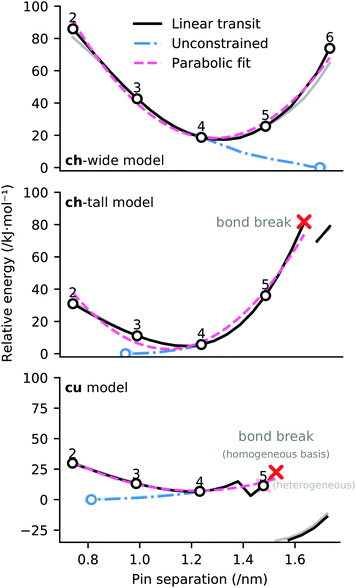 | ||
| Fig. 9 Potential energy surfaces for linear transit of EFG simulant pinning distances (black). Interligand separations consistent with the periodic structure of the graphene ‘zig-zag’ edge are indicated with black circles, annotated by the equivalent number of phenyl rings separating the ligands. Potential energy surface of relaxation of pinning constraints from a separation of 1.232 nm (consistent with a separation of four phenyl rings) is indicated in blue. Equilibrium geometry of unpinned structure is indicated with blue circle. A parabolic fit in three variables (E = v0(x + v1)2 + v2) to the linear transit energies is indicated in pink. n.b. in each case, analogous linear transits using heterogeneous basis sets (consistent with the partitioning scheme indicated in Fig. 13) are underlaid in faded colours, however in the case of the ch-tall and cu models these potential energy surfaces are substantially occluded due to their close similarity to the homogeneous basis results. | ||
These data indicate a modest degree of flexibility in permissible EFG coordination of each cluster. However, ch-tall and cu models reveal somewhat lower compatibility with high pin separations: the energy associated with linear transit of both models become non-monotonic, and this is explained in both models by the breakage of a bond between Mna and a MMPAB ligand. In the case of the cu model, bond breakage and internal rearrangement of a aqua ligand to participate in hydrogen bonding with the deligated oxygen of a nascent monodentate MMPAB ligand is noted (Fig. 10). This configuration surprisingly obtains a lower total interaction energy than either the four-ring separated structure or the unconstrained structure (−20 kJ mol−1 with respect to unconstrained structure) and is suggestive of additional potentially catalytically significant coordination modes for molecular oxo-manganese clusters, however exploration of these modes is beyond the scope of this manuscript.
Partial release of the constraints applied to each model (i.e. the internal constraints of each pin were maintained, however the pins were allowed to move with respect to one another) depicted in Fig. 8 establishes an estimate of the conformational strain of attachment of ΔE ≤ 20 kJ mol−1 (the blue branches of Fig. 9). These data indicate that the ch-wide ligands are placed under compression at a four-ring separation, whilst the other two models are placed under tension.
3.5 Conformational strain of ligand/graphene dihedral angle
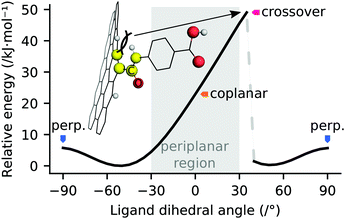
The edge-functionalisation of graphene by amide linkage is liable to result in sterically hindered ligands, due to steric clashes between the amide proton and carboxylate oxygen of the ligand and the salient protons of the graphene sheet. A linear transit of the 4-formamidobenzoic acid ligand dihedral from −90° to 90° with respect to a graphene fragment was undertaken to investigate the energetics of this steric clash, the results of which are depicted in Fig. 11. These data reveal a 23 kJ mol−1 barrier to achieving a coplanar configuration of the ligand amide moiety with the graphene sheet, however substantial deformation of the zig-zag edge occurs due to the steric clash. The ligand dihedral may be rotated in a sterically clashed state by a further 35° before the clash is resolved and the graphene sheet reacquires a quasi-planar configuration, with a 49 kJ mol−1 barrier to complete rotation. The potential energy surface of this transit is markedly asymmetric due to the path-dependence of the geometry in that region. Transit of the dihedral angle from the opposite direction would be expected to yield a mirror image of the obtained potential energy surface, by symmetry. These data indicate that dihedral angles deflected by approximately 50° from coplanarity with the graphene sheet are favoured for EFG achieved by amide linkage, plausibly attributable to a balance of weak resonance stabilisation and the aforementioned steric collision. Outside of the periplanar region, essentially unhindered rotation of the EFG ligand is permitted.3.6 Distortion of oxo-manganese cluster by coordination environment
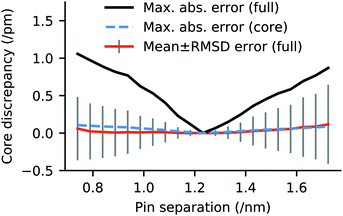
Measurement of the core geometry of the ch-wide model as a function of the linear transit coordinate indicates that the internal structure of the oxo-manganese cluster is remarkably insensitive to the large changes in coordination geometry seen over the course of the linear transit. These data indicate an approximately linear relationship between increase or decrease of the pinning distance of the EFG simulant and the maximum absolute deviation and RMS deviation of all Mn–O bond lengths in the cluster, with respect to the 4 phenyl ring separation equilibrium state. The mean deviation in the core geometry across the linear transit is negligible. Moreover, the distortion of the oxo-manganese core is dominated by elongation and contraction of the metal–carboxylate bonds between the benzoate moieties of the EFG simulant and the Mn ions of the cluster. When this is neglected, the oxo-manganese cluster and its remaining ligands are essentially structurally invariant over the course of the transit. These data are illustrated in Fig. 12. Moreover, the core geometry is also negligibly perturbed by release of the pinning constraints (RMSD discrepancy 0.25 pm, maximum discrepancy 0.52 pm), affirming that structural investigations of the oxo-manganese core may be made without applying graphene-consistent ligand constraints.3.7 Comparison with integrated models
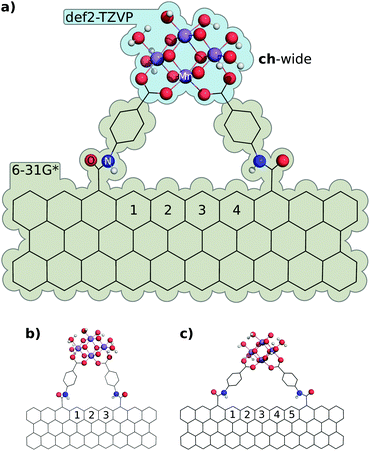
Obtaining electronic structures for integrated graphene/oxo-manganese cluster complexes is very difficult due to the exceptional complexity of SCF convergence in such models. Nevertheless, structures corresponding to coordination of ch-wide to the zig-zag edge of a graphene nanosheet were obtained for 3, 4, and 5 ring interligand separations, and a corresponding ch-tall model was obtained with a 4-ring separation. These structures require a lower-quality (6-31G*) basis set on the graphene nanosheet and non-carboxylate ligand atoms to obtain SCF convergence. An illustrative subset of these structures, as well as the basis set partitioning scheme used, are illustrated in Fig. 13. The results of these calculations reveal a remarkable similarity with structures obtained under the graphene-consistent ligand constraints previously enumerated. In each instance, coordination of the ch-wide cluster to the graphene edge induces a helical deformation in the sheet, however the deviation from planarity is quite small, and therefore the helical pitches associated with these distortions are exceptionally long (157 to 280 nm).We hypothesised that—because the geometry of the cluster represents a balance of forces—the independent conformational energies arising from flexion in the graphene sheet and compression or tension of the cluster would be approximately equal. Our hypothesis is not borne out by conformational analysis of the separated components of the complex: folding and helical deformations of the graphene sheet (estimated by consistent angular/dihedral constraints on separated graphene nanosheets) are of a substantially lower energy than the total conformational energy of the attached cluster. Rather, the energy of relaxation of the ch-wide fragment is −44 kJ mol−1, whilst the energy of relaxation of the graphene nanosheet fragment is −8 kJ mol−1. Of this, the energy attributable to the helical distortion of the graphene nanosheet is approximately 0.1 kJ mol−1. As such, approximately 35 kJ mol−1 arises from interactions between the fragments, plausibly consisting of a combination of steric and π···π interactions between the graphene sheet edge and the PMPAB ligands. Further exploring the decomposition of conformational factors in the energy of attachment of the ch-tall cluster to the graphene nanosheet, we find that the conformational energy of the large-scale sheet deformation seen—whilst more substantial than that of ch-wide—is only 1.2 kJ mol−1. Therefore, we propose the following conformational energy decomposition of cluster chelation:
| Eclustot. = Eclussteric + Ecluspin + Esheet |
| Model | Conformational energy (kJ mol−1) | ||||
|---|---|---|---|---|---|
| Cluster sterics | Cluster pinning | ||||
| Total | Integrated model | Integrated model | GCLC | Error | |
| ch-wide | 43.7 | 19.7 | 24.0 | 19.6 | 4.4 |
| ch-tall | 20.4 | 15.0 | 5.4 | 5.4 | 0.0 |
We find that the GCLC pinning energy is remarkably consistent (ΔE ≤ 4.4 kJ mol−1) with that obtained by decomposition of the integrated model. However, steric interactions are a significant contributor to the total conformational energy, and these are not captured by GCLC models. Nevertheless, comparison of the relative energies and interligand distances of graphene-integrated ch-wide clusters at 3–5 rings of separation (achieved as an isodesmic series) with the corresponding GCLC models obtains an extraordinary level of agreement (ΔE ≤ 1.3 kJ mol−1, Δdist ≤ 9 pm) over this domain (Table 3), which implies that Eclussteric is markedly insensitive to ligand separation, and that neglecting this contribution to the Eclustot. is an appropriate approximation and may also hold for similar ligands and interligand separations. Based on the recovered Eclussteric energy of ch-wide at a 4-ring separation (Table 2), a tentative steric contribution of approximately 20 kJ mol−1 (i.e. 10 kJ mol−1 per PMPAB ligand) may be assigned. Attempts to produce a simple functional model of the steric energy associated with a deformed PMPAB ligand in two dihedral parameters proved unsatisfactory, only recovering approximately half of the expected energy, suggesting that the steric contribution to the energy is the result of many geometric parameters of small individual effect. These efforts are discussed in the ESI.†
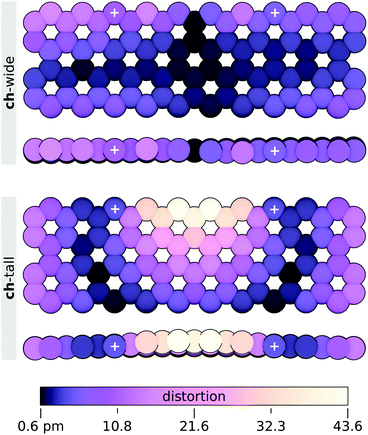
Distortion of the graphene sheets by attachment of the ch-wide and ch-tall clusters was found to be surprisingly mild. Least-squares structural alignment of relaxed and constrained graphene sheets extracted from ch-wide and ch-tall integrated models (4-ring separation) were performed on carbon atoms using the align function in PyMOL with default settings. These alignments reveal a negligible (Δmin = 0.6 pm, Δmax = 16.16 pm, Δmean = 5.3 ± 3.8 pm) helical distortion in the ch-wide isomer and a moderate (Δmin = 0.7 pm, Δmax = 43.6 pm, Δmean = 11.5 ± 9.9 pm) localised fold distortion in the ch-tall isomer. The absolute displacements of the carbon atoms of each sheet are illustrated in Fig. 14, and essentially capture out-of-plane distortions. These distortions are almost certainly overestimated by the finite graphene nanosheet model, because the peripheral carbons of the sheet are likely to have greater conformational freedom than the corresponding carbons in an infinite graphene sheet. Rather, in infinite or much larger graphene sheets, distortions induced by edge attachment of clusters are expected to attenuate over very short distances.
| Ring sep. | Interligand distance (nm) | Relative energy (kJ mol−1) | ||||
|---|---|---|---|---|---|---|
| Integrated model | GCLC | Error | Integrated model | GCLC | Error | |
| 3 | 0.995 | 0.986 | −0.009 | 22.7 | 23.9 | +1.2 |
| 4 | 1.240 | 1.232 | −0.008 | 0.0 | 0.0 | — |
| 5 | 1.479 | 1.478 | −0.001 | 5.6 | 6.9 | +1.3 |
Core geometries of graphene-integrated clusters are essentially unperturbed with respect to GCLC models, to the point of visual indistinguishability (maximum core bond length discrepancy ≤1 pm, maximum core RMSD displacement (all-atom) of 2.4 pm). These data are consistent with earlier core distortion results (Section 3.6) and indicate that the cluster core geometry is insensitive to both the steric influence of the graphene sheet upon the ligands, and hypothetical electronic coupling between the oxo-manganese cluster and the graphene sheet intermediated through the amidobenzoate ligand.
4 Discussion
4.1 Utility of structural models
The structural models presented in this report are notional, as the disposition of graphene edge functionalisation and TMO nanoparticles is a function of a large number of variables. Particularly, it is not known whether catalytically active sites will be in the form of molecular clusters of low nuclearity such as those demonstrated herein, or in the form of nanoscale/microscale periodic structures generated through edge-attached nucleation sites. Analytic techniques such as SEM, HRTEM, and/or EXAFS are likely to shed significant light on the nature of EFG-attached catalytic particles in situ.The clusters demonstrated in this work nevertheless represent useful limiting cases for incipient crystal growth from EFG, and thereby afford information on how such crystals may be attached to-and perturbed by-EFG.
4.2 EFG is anticipated to flexibly bind oxo-manganese clusters
This work has demonstrated a number of coordination geometries consistent with the ligation environment provided by edge functionalisation of a rigid, linear graphene edge are capable of chelating a compact oxo-manganese cluster at two points. It is likely that EFG will provide a massive number of geometrically distinct ligand sets capable of coordinating oxo-manganese clusters on account of the large number of degrees of freedom of the EFG ligands and the underlying graphene sheet they are attached to.4.3 Oxo-manganese clusters are anticipated to be very structurally insensitive to EFG coordination
Linear transit investigation has revealed that the birnessite-like oxo-manganese cluster ch-wide is insensitive to significant shifts in EFG simulant pinning distance (spanning 0.984 nm). This observation suggests that oxo-manganese clusters in general are plausibly much more rigid than the coordinating ligands provided by EFG, and that structural perturbations of oxo-manganese clusters imposed by EFG coordination are sufficiently small that they may be neglected from models. However, at extreme pinning distances fundamental incompatibility of the ligation environment resulted in dismemberment of the ch-tall and ch-wide cluster, with partial deligation of a μ1:μ1-MMPAB ligand to the corresponding monodentate species and internal rearrangement of the oxo-manganese core, indicating that a degree of caution should be taken in establishing a reasonable domain in which ligand effects may be neglected for a novel cluster or ligand set.4.4 Graphene-consistent ligand constraints are anticipated to be a suitable approximation of explicit graphene coordination
We have found that GCLC models preserve important features of their corresponding integrated models, including excellent maintenance of the oxo-manganese core geometry and the relative energetics of interligand separation. We have performed analysis of the conformational deformations imposed by cluster attachment to a graphene sheet and have determined that the majority of this deformation is in the form of steric clashes between the graphene nanosheet edge and ligand amide moiety, and that this steric component of the conformational energy is implied to be an approximately constant factor over the species investigated. Surprisingly, in spite of the flexibility of graphene, bulk deformations of the graphene nanosheet due to cluster attachment are vanishingly small.5 Conclusions
Herein, we have illustrated a number of case studies modelling the connection of low-nuclearity MnxOy clusters to graphene edges. Whereas explicit modelling of such clusters attached to graphene nanosheet fragments is extremely computationally expensive, we have developed a methodology which probes the conformational energetics of oxo-manganese cluster deformation and graphene edge deformation as separable problems, without significant loss of fidelity. This approach greatly simplifies modelling of proposed EFG/oxo-manganese composites.The calculations presented here are of practical relevance to the creation of manganese oxide/graphene composite materials because they indicate that covalent chelation of MnxOy clusters by edge-functionalised graphene is a low-energy proposition, even where the linking moiety is compact and quasi-rigid. These results strongly indicate that edge-functionalised graphene is capable of forming robust associations with MnxOy particles without disruption of the electronic properties of the graphene sheet interior. The degrees of conformational freedom revealed by this work are therefore anticipated to guide the rational design of linking ligands for the covalent coupling of graphene edges to transition metal oxides in a generic sense. On account of the flexibility seen here, an outstanding question is whether linking ligands are strictly necessary to effect coordination of TMO clusters, or whether carboxylate moieties obtained by oxidation of graphene edges are intrinsically capable of TMO coordination.
Calculations modelling small-scale deformations of graphene edges reveal a modest flexibility in out-of-plane bending and helical torsion which we anticipate will reduce the energetic barrier to coordination. As such, the potential energy surfaces we have obtained represent a limiting ‘worst case’ scenario. In spite of this constraint, linear transit of the ch-wide model indicates compatibility with a number of graphene edge consistent coordination geometries.
We note that the ch-wide model core geometry is nearly totally insensitive to applied intramolecular torques consistent with strained chelation geometries. This fact strongly suggests that geometric effects in oxo-manganese clusters arising from polydentate chelation at an EFG edge may be freely neglected in energetically plausible cases. The ch-wide geometry offers a rich array of proximately located H2O and OH− ligands singly ligated to Mn atoms, which suggests potential importance to water splitting function, which is a target for future investigations. However, sufficiently elongated inter-pin separations were found to induce carboxylate–Mn bond scission in the ch-tall and cu cluster models.
Actually existing graphene edges are commonly ragged and therefore possess a large number of geometric micro-environments which may fortuitously support edge functionalisation and chelation of manganese oxide particles. This, combined with possibility of large-scale deformations of graphene sheets and inter-sheet coordination, comprise a nearly unrestricted set of geometries and topologies for cluster attachment and nanoparticle/sheet nucleation at EFG. The investigation of these possibilities is likely to defy electronic structure methods for the foreseeable future. Nevertheless, TMO chelation at closely-spaced edge functionalities represents a high-density scenario for molecular TMO attachment and is presently amenable to DFT methods, permitting some useful bounds to be assigned to the geometric configuration space of such clusters. Contrariwise, monodentate attachment of TMOs to EFG is plausibly only constrained by the steric interactions between the EFG ligand and the graphene edge. We have investigated this for a realistic EFG ligand and found high rotational freedom outside of the periplanar region.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The amidobenzoate graphene edge functionalisation environment underpinning the computational models in this work is based on synthetic work performed by Dr Danijel Boskovic, which we gratefully acknowledge. This work was financially supported by the Australian Renewable Energy Agency (ARENA), contract number 2018/RND004. This activity received funding from ARENA as part of ARENA's Research and Development Program-Renewable Hydrogen for Export. The views expressed herein are not necessarily the views of the Australian Government and the Australian Government does not accept responsibility for any information or advice contained herein. This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI Australia), an NCRIS enabled capability supported by the Australian Government.References
- A. Geim and K. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- A. Castro Neto, F. Guinea, N. Peres, K. Novoselov and A. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- C. Lee, X. Wei, J. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- M. Stoller, S. Park, Y. Zhu, J. An and R. Ruoff, Nano Lett., 2008, 8, 3498–3502 CrossRef CAS PubMed.
- Z. Li, S. Wu, D. Zheng, J. Liu, H. Liu, H. Lu, Q. Huo, J. Guan and Q. Kan, Appl. Organomet. Chem., 2014, 28, 317–323 CrossRef CAS.
- A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. Lau, Nano Lett., 2008, 8, 902–907 CrossRef CAS PubMed.
- X. Du, I. Skachko, A. Barker and E. Andrei, Nat. Nanotechnol., 2008, 3, 491–495 CrossRef CAS PubMed.
- R. Nair, P. Blake, A. Grigorenko, K. Novoselov, T. Booth, T. Stauber, N. Peres and A. Geim, Science, 2008, 320, 1308 CrossRef CAS PubMed.
- A. Geim, Science, 2009, 324, 1530–1534 CrossRef CAS PubMed.
- J.-S. Lee, T. Lee, H.-K. Song, J. Cho and B.-S. Kim, Energy Environ. Sci., 2011, 4, 4148 RSC.
- J. Wang, T. Tsuzuki, B. Tang, X. Hou, L. Sun and X. Wang, ACS Appl. Mater. Interfaces, 2012, 4, 3084–3090 CrossRef CAS PubMed.
- J.-M. Yan, Z.-L. Wang, L. Gu, S.-J. Li, H.-L. Wang, W.-T. Zheng and Q. Jiang, Adv. Energy Mater., 2015, 5, 1500107 CrossRef.
- M. Wang, W. Zhu, L. Ma, J. Ma, D. Zhang, Z. Tong and J. Chen, Biosens. Bioelectron., 2016, 78, 259–266 CrossRef CAS PubMed.
- H. Chen, H. Xu, S. Wang, T. Huang, J. Xi, S. Cai, F. Guo, Z. Xu, W. Gao and C. Gao, Sci. Adv., 2017, 3, 1–8 Search PubMed.
- D. Sun, Y. Luo, M. Debliquy and C. Zhang, Beilstein J. Nanotechnol., 2018, 9, 2832–2844 CrossRef CAS PubMed.
- F. Li, J. Song, H. Yang, S. Gan, Q. Zhang, D. Han, A. Ivaska and L. Niu, Nanotechnology, 2009, 20, 455602 CrossRef PubMed.
- J. Zhang, J. Jiang and X. Zhao, J. Phys. Chem. C, 2011, 115, 6448–6454 CrossRef CAS.
- C. Jafta, F. Nkosi, L. le Roux, M. Mathe, M. Kebede, K. Makgopa, Y. Song, D. Tong, M. Oyama, N. Manyala, S. Chen and K. Ozoemena, Electrochim. Acta, 2013, 110, 228–233 CrossRef CAS.
- P. Jha, S. Singh, V. Kumar, S. Rana, S. Kurungot and N. Ballav, Chem, 2017, 3, 846–860 CAS.
- B. Yao, S. Chandrasekaran, J. Zhang, W. Xiao, F. Qian, C. Zhu, E. Duoss, C. Spadaccini, M. Worsley and Y. Li, Joule, 2019, 3, 459–470 CrossRef CAS.
- Z. Li, S. Gadipelli, H. Li, C. Howard, D. Brett, P. Shearing, Z. Guo, I. Parkin and F. Li, Nat. Energy, 2020, 5, 160–168 CrossRef CAS.
- S.-M. Paek, E. Yoo and I. Honma, Nano Lett., 2009, 9, 72–75 CrossRef CAS PubMed.
- F. Gao, J.-Y. Qu, Z.-B. Zhao, Y.-F. Dong, J. Yang, Q. Dong and J.-S. Qiu, New Carbon Mater., 2014, 29, 316–321 CrossRef.
- W. Hummers and R. Offeman, J. Am. Chem. Soc., 1958, 80, 1339 CrossRef CAS.
- A. Dimiev and J. Tour, ACS Nano, 2014, 8, 3060–3068 CrossRef CAS PubMed.
- S. Stankovich, D. Dikin, R. Piner, K. Kohlhaas, A. Kleinhammes, Y. Jia, Y. Wu, S. Nguyen and R. Ruoff, Carbon, 2007, 45, 1558–1565 CrossRef CAS.
- J. Zhang, H. Yang, G. Shen, P. Cheng, J. Zhang and S. Guo, Chem. Commun., 2010, 46, 1112–1114 RSC.
- H. Li, S. Pang, X. Feng, K. Müllen and C. Bubeck, Chem. Commun., 2010, 46, 6243 RSC.
- X. Mei, X. Meng and F. Wu, Phys. E, 2015, 68, 81–86 CrossRef CAS.
- Y. Matsumoto, M. Koinuma, S. Kim, Y. Watanabe, T. Taniguchi, K. Hatakeyama, H. Tateishi and S. Ida, ACS Appl. Mater. Interfaces, 2010, 2, 3461–3466 CrossRef CAS PubMed.
- R. Gengler, D. Badali, D. Zhang, K. Dimos, K. Spyrou, D. Gournis and R. Miller, Nat. Commun., 2013, 4, 1–5 Search PubMed.
- A. Lerf, H. He, M. Forster and J. Klinowski, J. Phys. Chem. B, 1998, 102, 4477–4482 CrossRef CAS.
- W. Gao, L. Alemany, L. Ci and P. Ajayan, Nat. Chem., 2009, 1, 403–408 CrossRef CAS PubMed.
- C. Gómez-Navarro, R. Weitz, A. Bittner, M. Scolari, A. Mews, M. Burghard and K. Kern, Nano Lett., 2007, 7, 3499–3503 CrossRef PubMed.
- X. Yang, X. Dou, A. Rouhanipour, L. Zhi, H. Räder and K. Müllen, J. Am. Chem. Soc., 2008, 130, 4216–4217 CrossRef CAS PubMed.
- D. Kosynkin, A. Higginbotham, A. Sinitskii, J. Lomeda, A. Dimiev, B. Katherine Price and J. Tour, Nature, 2009, 458, 872–876 CrossRef CAS PubMed.
- R. Gholizadeh, Y.-X. Yu and Y. Wang, Appl. Surf. Sci., 2017, 420, 944–953 CrossRef CAS.
- D. Son, B. Kwon, D. Park, W.-S. Seo, Y. Yi, B. Angadi, C.-L. Lee and W. Choi, Nat. Nanotechnol., 2012, 7, 465–471 CrossRef CAS PubMed.
- G. Williams, B. Seger and P. Kamat, ACS Nano, 2008, 2, 1487–1491 CrossRef CAS PubMed.
- X. Zhao, L. Zhang, S. Murali, M. Stoller, Q. Zhang, Y. Zhu and R. Ruoff, ACS Nano, 2012, 6, 5404–5412 CrossRef CAS PubMed.
- L. Zhong and K.-S. Yun, Int. J. Nanomed., 2015, 79–92 CAS.
- S. Daripa, S. Zaeem, B. Kuila and S. Das, Ionics, 2019, 26, 2623–2631 CrossRef.
- M. Suga, F. Akita, K. Hirata, G. Ueno, H. Murakami, Y. Nakajima, T. Shimizu, K. Yamashita, M. Yamamoto, H. Ago and J.-R. Shen, Nature, 2014, 517, 99–103 CrossRef PubMed.
- J.-R. Shen, Annu. Rev. Plant Biol., 2015, 66, 23–48 CrossRef CAS PubMed.
- H. Bao, Y. Pan, Y. Ping, N. Sahoo, T. Wu, L. Li, J. Li and L. Gan, Small, 2011, 7, 1569–1578 CrossRef CAS PubMed.
- A. Kasprzak, A. Zuchowska and M. Poplawska, Beilstein J. Org. Chem., 2018, 14, 2018–2026 CrossRef CAS PubMed.
- W. E. Rouby, RSC Adv., 2015, 5, 66767–66796 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327 Search PubMed.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed.
- J. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- A. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. Rappe, C. Casewit, K. Colwell, W. Goddard and W. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- E. Valeev, Libint: A library for the evaluation of molecular integrals of many-body operators over Gaussian functions, http://libint.valeyev.net/, 2019, version 2.6.0-beta.2.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- A. Marenich, C. Cramer and D. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- J. Klein, H. Khartabil, J.-C. Boisson, J. Contreras-García, J.-P. Piquemal and E. Hénon, J. Phys. Chem. A, 2020, 124, 1850–1860 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2011, 33, 580–592 CrossRef PubMed.
- SAMSON: Software for Adaptive Modeling and Simulation Of Nanosystems, 2020, https://www.samson-connect.net.
- M. Hanwell, D. Curtis, D. Lonie, T. Vandermeersch, E. Zurek and G. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- Schrödinger, LLC, The PyMOL Molecular Graphics System Version 2.2.0, https://www.pymol.org.
- M. Wiechen, I. Zaharieva, H. Dau and P. Kurz, Chem. Sci., 2012, 3, 2330 RSC.
- G. Dismukes, R. Brimblecombe, G. Felton, R. Pryadun, J. Sheats, L. Spiccia and G. Swiegers, Acc. Chem. Res., 2009, 42, 1935–1943 CrossRef CAS PubMed.
- R. Hocking, R. Malaeb, W. Gates, A. Patti, S. Chang, G. Devlin, D. MacFarlane and L. Spiccia, ChemCatChem, 2014, 6, 2028–2038 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04178e |
| ‡ n.b. that the surface area of preparations of bulk graphene may be considerably lower than this value and highly variable, as established by Brunauer–Emmett–Teller (BET) assays of reduced graphene oxides (rGO).4,5 |
| This journal is © the Owner Societies 2021 |