Non-stoichiometric molybdenum sulfide clusters and their reactions with the hydrogen molecule†
Yan
Chen
ab,
Jia-Jun
Deng
*ab,
Wen-Wen
Yao
ab,
Joseph Israel
Gurti
ab,
Wei
Li
ab,
Wen-Jie
Wang
 ab,
Jian-Xi
Yao
cd and
Xun-Lei
Ding
ab,
Jian-Xi
Yao
cd and
Xun-Lei
Ding
 *ab
*ab
aSchool of Mathematics and Physics, North China Electric Power University, Beinong Road 2, Huilongguan, Beijing 102206, P. R. China. E-mail: dingxl@ncepu.edu.cn; djiaj@ncepu.edu.cn
bInstitute of Clusters and Low Dimensional Nanomaterials, North China Electric Power University, Beinong Road 2, Huilongguan, Beijing 102206, P. R. China
cState Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China
dBeijing Key Laboratory of Energy Safety and Clean Utilization, North China Electric Power University, Beijing 102206, China
First published on 8th December 2020
Abstract
Structures of non-stoichiometric MoxSy clusters (x = 2–4; y = 2–10) were studied by density functional calculations with global optimization. Besides 1T phase like structures, a novel regular grid structure in which Mo atoms are well separated by S atoms was found, which might be used as a building-block to construct a new type of two-dimensional molybdenum sulfide monolayer. The hydrogen molecule prefers to be adsorbed onto Mo atoms rather than S atoms, and Mo atoms with less S coordination have a higher ability to adsorb H2. In addition, the reaction pathways for H2 dissociation were studied on two clusters with the highest H2 adsorption energy (Mo2S4 and Mo3S3). The vacant bridge site of Mo–Mo in S-deficient clusters, which corresponds to the sulfur vacancy in the bulk phase MoS2, is favored by H atom adsorption and plays an important role in the H atom transfer on MoxSy clusters. Our results provide a new aspect to understand the reason why S defect in MoS2 and MoS2 with an Mo-edge could enhance the catalytic performance in the hydrogen evolution reaction.
Introduction
Hydrogen is being pursued as a future source of energy in the current transition process of fossil energy to clean energy.1–3 As a vital approach to producing sustainable hydrogen, the hydrogen evolution reaction (HER, e.g., water decomposition) has attracted more and more attention.4 Advanced catalysts for the electrochemical HER are able to reduce the over-potential and thus improve the efficiency of this important electrochemical process. The most effective catalysts are platinum group metals, which are too expensive for a wide range of applications. It is an inevitable trend to develop active catalysts based on more abundant and cheaper materials.5 In the past few decades, transition metal dichalcogenides (TMDs), represented as MX2 (M = transition metals, X = S, Se, and Te), have become a type of promising candidate compound to replace traditional catalysts based on platinum. Among these TMDs, molybdenum disulfide (MoS2) has been proven to be an attractive HER catalyst with high chemical stability and good electrocatalytic performance.5–8 Compared with bulk MoS2, a two-dimensional MoS2 monolayer has better catalytic performance due to the exposure of a large fraction of active sites.9,10 Several methods could further improve the catalytic activity of MoS2, including choosing the Mo-edge of MoS2 or introducing sulfur vacancy on the basal plane of MoS2 as active sites.11–16 In addition, some studies indicated that MoS2 can also be used as a promising hydrogen storage material,17 or as an excellent support18 and catalyst19–21 in the process of hydrogen storage. MoS2-like nanostructures have also been widely studied for their high catalytic performance in hydrodesulfurization (HDS) of sulfur-containing compounds in fuels, and S–H groups were suggested to play an important role in supplying the hydrogen during HDS.22,23 However, the morphology of MoS2 nanoclusters in the catalyst is very complex, and the clusters on surfaces may have different shapes determined by the conditions under which they are synthesized.22It is difficult to understand the reaction mechanism of catalytic reactions on the surface of molybdenum sulfide materials due to the complexity of real catalysts. However, clusters composed of limited number of atoms are experimentally and computationally tractable systems, so studies on rational cluster models may serve as a bottom-up strategy to understand complex systems and processes.24,25 As for molybdenum sulfide clusters, the stable structures and properties of small stoichiometric (MoS2)n clusters have been investigated.26,27 Our previous work27 reveals that the structure of stoichiometric (MoS2)n clusters can be viewed as fragments of the MoS2 monolayer with the 1T phase, which implies a connection between the clusters and bulk phase materials. Considering that the high reactivity of molybdenum disulfide catalysts is mostly due to the edges or sulfur vacancies, it is of vital importance to research non-stoichiometric molybdenum sulfide clusters which are more suitable for simulating imperfect local structures of the surface or amorphous molybdenum sulfide than the stoichiometric ones. Some stable structures and properties of non-stoichiometric MoxSy clusters have been obtained,28–33 and other studies used these structures as models to study the adsorption or reaction for small molecules, such as H2 and CO2, to synthesize methanol. Different catalytic properties of stoichiometric and non-stoichiometric clusters have been found.34 Baloglou et al.24 studied the structures of Mo3S132− and its protonated forms. They found that the H atoms prefer to make the S–H bond rather than the Mo–H bond in these S-rich clusters and suggested the “sulfur-centered” mechanism of HER catalysis. Recently, Raghavachari and Gupta et al.35 investigated the adsorption and dissociation of the H2 molecule on some anionic MoxSy− clusters (x = 1, y = 3–5; x = 2, y = 2–4; x = 3, y = 3–5). They found that the formation of the Mo–H bond is preferred by not only S-deficient clusters (e.g., Mo2S2−) but also some S-rich clusters (e.g., Mo2S5−), while the H atom is more likely to combine with the S atom and finally form the H2S molecule only for MoS4− and MoS5−, in which the only Mo atom is coordinated with four S atoms and has no coordination space for H or H2. They also investigated the reactions of some anionic MoxSy− with H2O to reveal the mechanisms of the HER with cluster models.36–38
It is clear that different ratios of x to y influence the reaction mechanisms to a large extent, and the charge state of clusters may also have a significant impact on their reactivity. Since in previous work, much attention has been paid to anionic MoxSy− clusters, a systematic study on neutral non-stoichiometric MoxSy clusters is needed to obtain the comprehensive information of the structures of MoxSy and the relationship with the reactivity towards H2. Here, we report the structures of MoxSy (x = 2–4; y = 2–10) clusters obtained by density functional theory (DFT) calculations. Based on that, we further discuss the adsorption and dissociation of H2 on some typical clusters. The formation of the H2 molecule from two H atoms on surfaces and the desorption of H2 from the surface are two important steps in the HER. Our studies on the adsorption and dissociation of H2 on clusters may be viewed as the reverse processes of the two steps, which may provide some useful information for understanding the mechanisms of the HER. The adsorption and dissociation processes studied in this work also have a close relationship with the fields of hydrogen storage and HDS.
Theoretical methods
All our DFT calculations were performed using the Gaussian 16 program suite.39 A Fortran code based on a genetic algorithm and DFT calculations was developed40 to generate sufficient and reasonable initial structures of MoxSy clusters, which has also been successfully applied to some other clusters.41–43 Then different isomers were optimized with the B3LYP hybrid density functional44–46 and the def2-TZVP basis set.47 The B3LYP functional was chosen since it has been adopted in some previous studies on MoxSy clusters and provided reasonable results.31,36,48,49 Dispersion correction50 and diffuse functions51 were involved in all calculations, which may be necessary for the reliable description of the interaction between H2 and the clusters. Systems with Mo atoms may have complicated electronic states, so the singlet, triplet and quintet states were all taken into account in our calculations, as was done in previous work.52,53 Electrostatic potential (ESP) analysis was performed to investigate the favorite adsorption site of MoxSy for the hydrogen molecule. Natural bond orbital (NBO) analysis54 was performed to acquire the electron transfer in the adsorption complexes and orbital interactions through second order perturbation theory. Harmonic vibrational frequency calculations were performed on optimized structures at the same theoretical level to ascertain the nature of the stationary points (no imaginary frequencies for minima and only one imaginary frequency for transition states). All energies reported in this work are total electronic energy with zero-point vibrational energy (ZPE) correction, except that the Gibbs free energy was reported for the dissociation reaction of H2 on clusters. The Gibbs free energy was calculated with the standard temperature (298.15 K) and pressure (1 atm), which was commonly used in previous theoretical studies on the HER.15,35,37,55,56Results and discussion
Structures of MoxSy clusters (x = 2–4; y = 2–10)
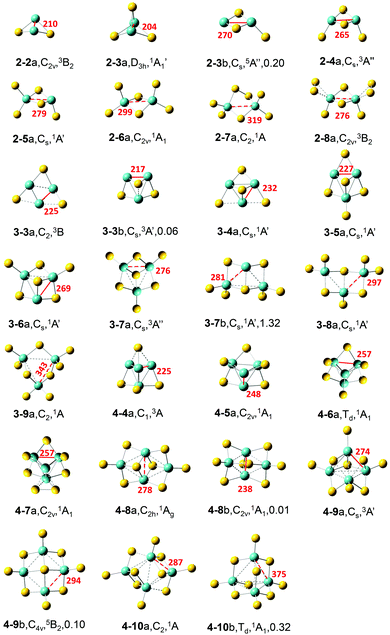
The most stable and some typical low-lying isomers of MoxSy clusters (x = 2–4; y = 2–10) are shown in Fig. 1. Considering the accuracy of calculation methods, the most stable structure under a certain theoretical level may not necessarily be the ground state of the cluster. In addition, the studied clusters are used to simulate the local structures on surfaces, and metastable structures of clusters may also exist on surfaces. Therefore, besides the most stable structure, we also provided several metastable structures of each cluster in this work (Fig. S1–S3 in the ESI†).Most low-lying isomers tend to have singlet electronic states, and triplet is also quite common. Specifically, the most stable structures of the studied MoxSy (denoted as x–ya) are all singlet, except that the triplet is preferred for Mo2S2,4,8, Mo3S3, and Mo4S9. For some clusters, the singlet and triplet have very close energies: the singlet of 3–7a/4–4a is only 0.03/0.06 eV higher in energy than the corresponding triplet, while the singlet of 3–4a/4–8b is more stable than the triplet by only 0.01/0.03 eV, respectively. Therefore, the ground states of these clusters could be either singlet or triplet. Quintet electronic states generally have higher energies than the singlets and triplets for all the obtained structures (as shown in Fig. 1 and Fig. S1–S3, ESI†), except 2–3b and 4–9b. For most clusters, x–ya is lower in energy than the corresponding second most stable structure (denoted as x–yb) by more than about 0.2 eV, so it is quite reliable to assign that x–ya is the ground state structure for each cluster. There are three exceptions, Mo3S3, Mo4S8 and Mo4S9, for which the difference between x–ya and x–yb is less than 0.1 eV. So, for these clusters, the x–yb structures are also reliable candidates for ground state structures.
Below, we focus on the most stable structure of each cluster. When x = 2, an Mo2-2SB (SB is for the bridging S) moiety with a rhombus structure is found in all of the most stable structures except 2–7a. As y increases, the structures 2–3a, 2–4a, 2–5a, and 2–6a can be constructed from 2–2a by adding one SB, two, three, and four ST (terminal S) atoms, respectively. 2–7a can be viewed as 2–6a with one Mo–SB–Mo unit replaced by Mo–S–S–Mo. 2–8a can be formed by 2–4a with two S22− ions. The Mo–Mo bond length (dMo–Mo) for the S-deficient Mo2Sy clusters (y < 2x, here x = 2) is quite short (Table 1, 210 and 204 pm for y = 2 and 3, respectively), and it increases remarkably to 265 pm in stoichiometric Mo2S4, while that for all the S-rich Mo2Sy clusters (y > 4) is larger than 275 pm. Considering the values of the bond lengths in the bulk MoS2 (275 pm for the 1T phase and 316 pm for the 2H phase57), the short dMo–Mo (shorter than 275 pm) values for S-deficient and stoichiometric Mo2Sy clusters indicate that Mo–Mo interactions are strongly favored in these clusters. Short dMo–Mo in these clusters was suggested to have a close relationship with the high activity of amorphous and 1T phase MoS2 in the HER.57 The bonds with dMo–Mo between 275 and 380 pm (ca. 316 pm *1.2) indicate a medium interaction between the two Mo atoms (shown as dashed lines in Fig. 1), and all the calculated S-rich Mo2Sy clusters have medium dMo–Mo.
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ) in the most stable structure of MoxSy clusters (Mo–Mo distances longer than 380 pm are ignored). All values are in picometer
) in the most stable structure of MoxSy clusters (Mo–Mo distances longer than 380 pm are ignored). All values are in picometer
| Mo2Sy | Mo3Sy | Mo4Sy | |
|---|---|---|---|
| y |
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif)
|
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif)
|
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif)
|
| 2 | 210 | ||
| 3 | 204 | 244 | |
| 4 | 265 | 242 | 250 |
| 5 | 279 | 255 | 254 |
| 6 | 299 | 273 | 257 |
| 7 | 319 | 288 | 257 |
| 8 | 276 | 297 | 280 |
| 9 | 347 | 315 | |
| 10 | 308 |
For x = 3, an Mo3 core capped with an SF (SF is for face-capping S) is favored in Mo3S3–7. 3–3b with such an Mo3–SF moiety is higher in energy than 3–3a by only 0.06 eV. 3–4a can be obtained by 3–3a with an additional SF or by 3–3b with an SB. 3–5a, 3–6a, and 3–7a can be constructed by adding one, two, and three ST atoms to 3–4a, respectively. The average distances between the Mo atoms (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ) as well as the shortest distances (d1) gradually elongate as y increases from 3 to 9 (Table 1 and Fig. 1. Values for all the Mo–Mo distances are in Table S1 in the ESI†). S-deficient Mo3Sy clusters have short dMo–Mo, while stoichiometric Mo3S6 has the dMo–Mo near to the experimental value of the bulk MoS2 with the 1T phase. In 3–8a, the Mo3 core is broken with one Mo–Mo distance as large as 409 pm, and in 3–9a, all the three Mo–Mo distances are longer than 340 pm.
) as well as the shortest distances (d1) gradually elongate as y increases from 3 to 9 (Table 1 and Fig. 1. Values for all the Mo–Mo distances are in Table S1 in the ESI†). S-deficient Mo3Sy clusters have short dMo–Mo, while stoichiometric Mo3S6 has the dMo–Mo near to the experimental value of the bulk MoS2 with the 1T phase. In 3–8a, the Mo3 core is broken with one Mo–Mo distance as large as 409 pm, and in 3–9a, all the three Mo–Mo distances are longer than 340 pm.
For x = 4, a three-dimensional tetrahedron Mo4 core is favored for the most stable structures of S-deficient Mo4S4–7. All the S atoms locate on the edges of the Mo4 tetrahedron as SB for y = 4–6, and 4–7a can be viewed as 4–6a with one SB replaced by an S–S moiety. For the Mo4 core, all the Mo–Mo distances are small (less than 259 pm) and the values of ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) gradually elongate from 250 to 257 pm as y increases from 4 to 7. The Mo4 core does not exist in the most stable structures of stoichiometric Mo4S8 and S-rich Mo4S9,10 clusters. In the 1T-phase structure of the stoichiometric 4–8a, four Mo atoms form a rhombus structure with
gradually elongate from 250 to 257 pm as y increases from 4 to 7. The Mo4 core does not exist in the most stable structures of stoichiometric Mo4S8 and S-rich Mo4S9,10 clusters. In the 1T-phase structure of the stoichiometric 4–8a, four Mo atoms form a rhombus structure with ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) being 280 pm. 4–9a has a distorted tetrahedral Mo4 whose Mo–Mo distances are much longer than those in S-deficient Mo4S4–7, and on it there are two SB, three SF, and four ST atoms. In 4–10a four Mo atoms form a rhombus structure, similar to 4–8a but with longer
being 280 pm. 4–9a has a distorted tetrahedral Mo4 whose Mo–Mo distances are much longer than those in S-deficient Mo4S4–7, and on it there are two SB, three SF, and four ST atoms. In 4–10a four Mo atoms form a rhombus structure, similar to 4–8a but with longer ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) , and there are two SF, four SB, and four ST atoms.
, and there are two SF, four SB, and four ST atoms.
In all stable geometric structures shown in Fig. 1 (and also those in Fig. S1–S3, ESI†), the oxidation state of each Mo atom is no more than +6, if we roughly assume that each ST on the Mo atom contributes +2, while each SB contributes +1. This is consistent with that each Mo atom has 6 valence electrons. Mo atoms with the +6 oxidation state first appear in S-rich clusters 2–5a and 3–9a (also 4–10c in Fig. S3, ESI†). As for the coordination of Mo atoms, it is found that each Mo tends to have bonds with at most four S atoms in the studied clusters, with only a few exceptions in which the coordination number of Mo is five (e.g., 2–8a and 4–9a), while for the bulk materials, each Mo atom is coordinated with six SF atoms in both the 1T and 2H phase monolayers.
Gemming et al. studied the structures of MoxSy clusters (x = 1 and 2, y = 1–6; and x = 4, y = 1–12)31 and anionic Mo3Sy− (y = 0–12).33 Our calculations with different basis sets confirm their findings for MoxSy (x = 2, y = 2–6; x = 4, y = 4–10) and provide more low-lying structures for each cluster. Moreover, their structure for Mo4S8 is actually 4–8b in our calculations which is slightly higher in energy than 4–8a by 0.01 eV. They suggested that 4–6a with a high symmetry (Td) is a magic cluser with extraordinarily high stability according to its relatively high average binding energy of S atoms among Mo4Sy− (y = 1–10) clusters. Our calculations further confirm that 4–6a is very stable since the energy difference between 4–6a and 4–6b is as large as 3.34 eV. Additionally, isomer 4–10b also has Td symmetry, and its structure is the same as that of V4O10, which has many interesting properties.58,59
In our previous work,27 the most stable structures and some low-lying structures for (MoS2)n (n = 1–6) have been obtained by using B3LYP and PW91 functionals with def2-TZVP basis sets. A type of structure that can be viewed as fragments of monolayer MoS2 with the 1T phase was found in these stoichiometric (MoS2)n clusters. In this work, after including dispersion correction and adding diffuse functions to the basis sets, similar results are obtained for the clusters studied in both studies (i.e., Mo2S4, Mo3S6, and Mo4S8), which further confirmed the reliability of the theoretical level we used in both studies. In this work, we find that the 1T-type structure found in stoichiometric (MoS2)n clusters also exists in non-stoichiometric clusters, such as 3–7a. Additionally, we find another type of structure, as in 3–7b, 3–8a, and 4–9b, which has a regular bonding mode with square Mo2S2 units, and all the Mo atoms are well separated by S atoms. The distance between the two Mo atoms in the square Mo2S2 unit is longer than 280 pm, even longer than the Mo–Mo distance in the 1T phase MoS2 monolayer. We speculate that this grid structure might be used as a building-block to construct a new type of two-dimensional molybdenum sulfide monolayer, in which four-coordinated S atoms exist as in 4–9b. Preliminary calculations with a two-dimensional periodic slab model, including zone centered (Γ-point) vibrational frequencies and ab initio molecular dynamics calculations, show that this type of grid structure is quite stable under room temperature (detailed calculation results are in the ESI†). Further investigations on this novel structure are required to verify the stability and reveal more unique properties.
Adsorption of the H2 molecule on MoxSy clusters
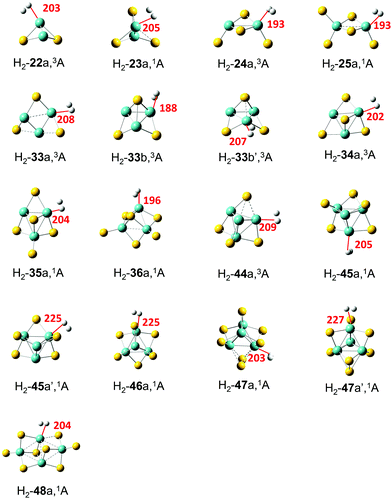
Adsorption of the H2 molecule on the most stable MoxSy clusters was studied with different adsorption sites and possible spin multiplicities. For clusters 3–3, 4–8, and 4–9, two low-lying isomers (a and b) were calculated since they are both considered as candidates for the most stable structures. Seventeen adsorption complexes with relatively large adsorption energy (will be described clearly later) have been obtained (Fig. 2). The symbol H2-xya(b) stands for the adsorption complex of H2 on x–ya(b). For H2-33b, H2-45a, and H2-47a, two different adsorption sites have been found, and the second one is labelled with an apostrophe (′). Spin multiplicities do not change after the adsorption of H2, except that for 3–4a, the singlet is more stable than the triplet by 0.01 eV before adsorption, while the triplet is lower in energy by 0.10 eV for H2-34a. In these clusters, H2 is adsorbed on Mo atoms with the oxidation state not exceeding +4, which is similar to the results of the H2 adsorption on anionic MoxSy− clusters.35 Xu et al.10 revealed that S vacancies in two dimensional MoS2 would contribute to a significant enhancement of the HER performance. It is clear that the S vacancy in the bulk phase MoS2 could cause the oxidation state of Mo being less than +4, leading to easy adsorption of H2, which is consistent with our findings.Several properties are used to evaluate the strength of the interaction between H2 and MoxSy clusters (Table 2). Ead is a direct measure of the strength, which is defined as Ead = E(H2) + E(MoxSy) − E(H2 − MoxSy). Note that in the calculation of Ead for systems like H2-33b, the energy of 3–3b (not the more stable 3–3a) is used for E(MoxSy). All the MoxSy clusters with the ratio of x to y no more than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 can adsorb H2 with an adsorption energy larger than 0.1 eV, while all the S-rich clusters cannot adsorb H2 except Mo2S5. It was suggested that the binding energy of hydrogen to an ideal hydrogen storage material should be intermediate between physisorption and chemisorption, about 0.2–1.0 eV.60 For the listed clusters in Fig. 2, Ead ranges from 0.12 to 0.49 eV (H2-24a has the highest Ead), indicating that molybdenum sulfide may be acceptable hydrogen storage materials for some special occasions.
2 can adsorb H2 with an adsorption energy larger than 0.1 eV, while all the S-rich clusters cannot adsorb H2 except Mo2S5. It was suggested that the binding energy of hydrogen to an ideal hydrogen storage material should be intermediate between physisorption and chemisorption, about 0.2–1.0 eV.60 For the listed clusters in Fig. 2, Ead ranges from 0.12 to 0.49 eV (H2-24a has the highest Ead), indicating that molybdenum sulfide may be acceptable hydrogen storage materials for some special occasions.
| Clusters | E ad | ΔG | Q | d H–Mo | d H–H | v s(Mo–H2) | v a(Mo–H2) | v(H–H) |
|---|---|---|---|---|---|---|---|---|
| H2 | 74 | 4418 | ||||||
| H2-22a | 0.25 | 0.61 | 0.14 | 203 | 79 | 716 | 1242 | 3628 |
| H2-23a | 0.12 | 3.15 | 0.18 | 205 | 78 | 668 | 1214 | 3761 |
| H2-24a | 0.49 | −4.54 | 0.27 | 193 | 81 | 867 | 1440 | 3336 |
| H2-25a | 0.40 | −2.47 | 0.25 | 193 | 81 | 839 | 1441 | 3372 |
| H2-33a | 0.16 | 2.09 | 0.17 | 208 | 78 | 611 | 1107 | 3823 |
| H2-33b | 0.47 | −4.22 | 0.22 | 188 | 85 | 892 | 1571 | 2800 |
| H2-33b′ | 0.28 | −0.51 | 0.19 | 207 | 78 | 667 | 1077 | 3770 |
| H2-34a | 0.33 | −1.81 | 0.35 | 202 | 78 | 733 | 1213 | 3747 |
| H2-35a | 0.21 | 1.93 | 0.27 | 204 | 78 | 699 | 1235 | 3816 |
| H2-36a | 0.31 | −0.75 | 0.24 | 196 | 80 | 1011 | 1400 | 3443 |
| H2-44a | 0.28 | 0.15 | 0.19 | 209 | 77 | 636 | 1082 | 3883 |
| H2-45a | 0.30 | −0.77 | 0.25 | 205 | 78 | 676 | 1150 | 3805 |
| H2-45a′ | 0.13 | 2.92 | 0.24 | 225 | 77 | 3121 | 994 | 4152 |
| H2-46a | 0.13 | 1.40 | 0.23 | 225 | 76 | 2933 | 972 | 4136 |
| H2-47a | 0.34 | −1.45 | 0.32 | 203 | 78 | 722 | 1192 | 3862 |
| H2-47a′ | 0.12 | 3.19 | 0.22 | 227 | 76 | 2866 | 969 | 4128 |
| H2-48a | 0.16 | 3.57 | 0.28 | 204 | 78 | 687 | 1224 | 3858 |
Kubas61 found that when H2 is bound to a transition metal atom, electrons will transfer from the hydrogen molecule to the unfilled d-orbital of the transition metal atom with back-donation of electrons from the transition metal to the antibonding orbitals of H2. In Table 2, the electron transfer from H2 to the cluster (Q) is listed. For all clusters, Q is positive and ranges from 0.14 |e| for H2-22a to 0.35 |e| for H2-34a. However, the amount of Q does not have a clear relationship with Ead (Fig. S4 in the ESI†). Further NBO analysis on interactions between the filled donor and empty acceptor NBOs of the adsorption complexes estimates the energetic importance of these interactions through second order perturbation theory. The results (Table S2 in the ESI†) indicate that the dominant interaction is the H–H bond as the donor NBO and the Mo–Mo or Mo–S anti-bond as the acceptor with a high second-order perturbation energy (ΔE2, also be termed as the donor–acceptor orbital interaction stabilization energy) while the back-donation with the lone-pair Mo NBO as the donor and the H–H anti-bond as the acceptor usually has low values of ΔE2 in most adsorption systems.
From the geometric point of view, when H2 is adsorbed on an Mo atom in MoxSy clusters, the distance between H2 and Mo can be another indicator of the strength of adsorption. The H2 molecule is always side-on adsorbed on one Mo atom, and the short one of the distances between Mo and the two H atoms is denoted as dH–Mo (Fig. 2 and Table 2). It is clear that dH–Mo is closely related to Ead (Fig. S5 in the ESI†): three adsorption complexes with the shortest dH–Mo (≤193 pm for H2-24a, 25a, and 33b) have the highest Ead (≥0.40 eV), while three complexes with the longest dH–Mo (≥225 pm for H2-45a′, 46a, and 47a′) all have very small Ead (≤0.13 eV). Another geometric parameter is the bond length of H–H (dH–H). Considering the charge transfer mechanism of H2 adsorption, it is expected that stronger adsorption will lead to longer dH–H. Our results (Fig. S6 in the ESI,† or Table 2) generally agree with this expectation. Compared with the dH–H of the free H2 molecule (74 pm), the dH–H is lengthened significantly (≥81 pm) in three complexes with the highest Ead (H2-24a, 25a, 33b), indicating that H2 in these complexes is activated to some extent.
Vibrational frequencies of adsorption complexes are useful information to identify the structures of different adsorption sites when compared with Fourier transform infrared (FTIR) or Raman experiments. Three vibrational modes have been found associated with H2 for each adsorption complex, namely, the symmetric vibration between Mo and H2 (vs(Mo–H2)), in which two H atoms move in the same direction to Mo, the asymmetric one (va(Mo–H2)), in which two H atoms move in the opposite direction to Mo, and the stretch vibration of the H–H bond (v(H–H)). High values of vs(Mo–H2) and va(Mo–H2) generally indicate higher interaction strength between H2 and the clusters (Fig. S7 and S8 in the ESI,† or Table 2). Three complexes with the longest dH–Mo (H2-45a′, 46a, 47a′) are exceptions – they have extremely high values of vs(Mo–H2), even larger than 2850 cm−1, while their interactions with the clusters are very small (e.g., with very small Ead). Upon adsorption, the H–H bond will be weakened, leading to a decrease of v(H–H) values in the adsorption complexes, and larger Ead may cause smaller v(H–H) in general (Fig. S9 in the ESI,† or Table 2). Specifically, H2-33b has the smallest value (2800 cm−1) of v(H–H), which is much smaller than the free H2 (4418 cm−1). H2-33b has the smallest value for v(H–H) and the largest value for d(H–H), indicating the greatest extent of H2 activation on it; H2-33b also has the shortest dH–Mo and the largest va(Mo–H2), which corresponds to the strong interaction between H2 and clusters. Note that the total energy of H2-33b is lower than that of H2-33a, although 3–3a is more stable than 3–3b, which further implies that H2-33b is very stable and the adsorption capacity of 3–3b is particularly strong.
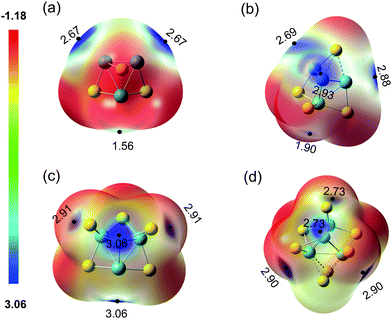
The electric field produced by metal cations can polarize the H2 molecule and enhance the binding of H2 on metal atoms.62 For the clusters studied in this work, different adsorption sites may have a distinct ability to polarize H2, leading to the variation of the adsorption strength. To investigate the polarization ability of MoxSy clusters, the molecule surface electrostatic potentials (ESPs) of typical clusters (3–3b, 4–4a, 4–5a, and 4–7a) are calculated and shown in Fig. 3. The local maximum values of the ESP (Vmax)63,64 are also listed. There are two types of Mo atoms in 3–3b: the one with one SB and one SF has Vmax = 2.67 V nearby (denoted as Mo_I), and the one with two SB and one SF has Vmax = 1.56 V (Mo_II). H2 adsorption on Mo_I corresponds to H2-33b, while H2 on Mo_II corresponds to H2-33b′. All the properties discussed above (Table 2) indicate that the adsorption of H2 in H2-33b is much stronger than that in H2-33b′ (e.g., Ead is 0.47 and 0.28 eV, respectively). In addition, for each cluster shown in Fig. 3, the larger Ead is always accompanied by the higher Vmax for different adsorption sites. Mo atoms with less coordination (lower oxidation state) tend to have higher Vmax. Therefore, they have a higher ability to adsorb the H2 molecule.
Dissociation of H2 on Mo2S4 and Mo3S3
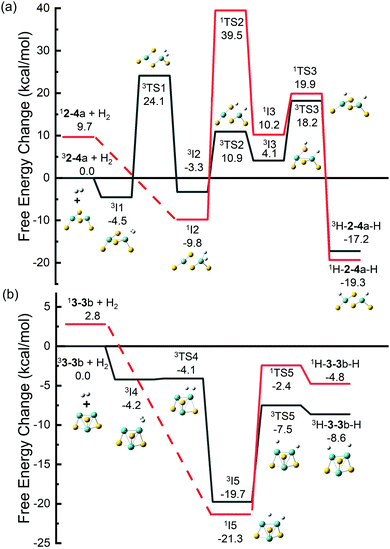
Dissociation of H2 was studied on the selected MoxSy clusters. For comparing the results with those obtained by other research groups6,35 more conveniently, we used Gibbs free energy in this section. The adsorption of H2 on clusters would cause a decrease in the entropy and an increase of the Gibbs free energy of the system, and the increased value was estimated to be about 0.26 eV under room temperature.65 So systems with small values of Ead (Table 2) may be unstable under thermal conditions. The free energy change (ΔG) for the adsorption process is listed in Table 2. H2-24a (stoichiometric) and H2-33b (non-stoichiometric) have the most negative values of ΔG. Therefore, they were selected as two typical adsorption systems for investigation of the dissociation of H2 on MoxSy clusters. Both singlet and triplet states were calculated along the reaction paths since spin-crossover was found to occur commonly during these reactions,66,67 although the ground states of 2–4a and 3–3b are both triplet. The sum of the free energies of infinite separated H2 and triplet 2–4a or 3–3b was set to zero, respectively.Fig. 4(a) shows the reaction path of 2–4a with H2. It starts from the triplet 2–4a (lower in energy than 12–4a by 9.7 kcal mol−1) and forms 3I1 with −4.5 kcal mol−1 after adsorption. Then the H–H bond in 3I1 (dH–H = 81 pm) breaks, forming 3I2 (−3.3 kcal mol−1, and dH–H = 177 pm) with a high energy barrier of 24.1 kcal mol−1, or 1I2 (−9.8 kcal mol−1) through a spin-crossover. 1I2 is energetically more favorable than 3I2, and it can also be obtained directly from the adsorption of H2 on singlet 2–4a without any energy barriers. From 1I2, one H atom may transfer to a neighboring S atom to form 1I3 or 3I3. The barrier is very high (39.5 kcal mol−1) along the path with the singlet state. The path from 1I2 to 3I3 with a spin-crossover is more favorable, but it still has an overall barrier (10.9 kcal mol−1), and 3I3 has a positive relative energy. The H atom on S in 3I3 tends to transfer to the other Mo atom to form 1H-2–4a-H or 3H-2–4a-H. Although these products are lower in energy than 1I2, they actually cannot be formed in reactions of H2 with 2–4a considering the high energy barriers from 1I2 to them. Recently, Gupta et al. studied the dissociation of H2 on anionic Mo2S4−,35 and our results on neutral Mo2S4 have many similarities to theirs. Both neutral and anionic systems start with high spin multiplicity (triplet and quartet for neutral and anionic clusters, respectively) which is lower in energy, while low spin multiplicity is preferred for the dissociative adsorption of H2 on one Mo atom (e.g., 1I2 in this work). The low spin state isomers with two H atoms adsorbed separately on different Mo atoms are found to be the most stable intermediates for both charge states. The only difference is that for a neutral system, there exists a stable adsorption isomer (3I1) in which H2 is not dissociated, which may be a favorable factor for H2 adsorption in the initial stage.
Different situations are found for H2 on 3–3b, whose ground state is also a triplet (Fig. 4(b)). H2 can be adsorbed on one Mo atom to form 3I4, but 3I4 is not stable and it can transform to a much more stable isomer (3I5) with a negligible barrier (3TS4, 0.1 kcal mol−1 with respect to 3I4). The singlet 1I5, which could be obtained directly from 3–3b or from 3I4 through a spin-crossover, is even more stable than 3I5, but the energy difference is only 1.6 kcal mol−1. 1I5 and 3I5 are the most stable intermediates for H2 on 3–3b, in which H2 is dissociated with one H on an Mo atom and the other one on the bridge site of Mo–Mo. The bridging bonded H atom can move to the other Mo atom to form H-3–3b-H (two H atoms adsorbed on different Mo atoms). The relative energies of all isomers and transition states are less than zero, indicating that the transformation of H2 on 3–3b is much easier than that on 2–4a.
For 3–3b, the vacant bridge site of Mo–Mo is a favorite site for H atom adsorption (see 1I5 and 3I5 with very low relative energy), and the H atom can be transferred between the two Mo atoms through this bridge site easily (a bridge for H atom transfer). On the other hand, the bridge sites in 2–4a have been occupied by S atoms, leading to the difficulty in the H atom transfer on 2–4a. The vacant Mo–Mo bridge site corresponds to the S vacancy in the bulk phase MoS2, and the dissociation reaction could be viewed as the reverse process of the HER. Therefore, our findings that 3–3b with a vacant Mo–Mo bridge site has lower barriers for both H2 dissociation and the HER are consistent with previous studies on the bulk phase MoS2 in which promising electrocatalysts for the HER can be obtained by increasing the number of S vacancies in MoS2.68,69 Our results also indicate that H atoms prefer to be bound to Mo atoms rather than S atoms, which may be another aspect to understand the previous study that monolayer MoS2 with the Mo edge is more likely to adsorb H atoms and realize the HER.11,12
Conclusions
The geometric and electronic properties of non-stoichiometric neutral MoxSy clusters (x = 2–4; y = 2–10) for the most stable structures and low-lying isomers, together with the adsorption and dissociation of the H2 molecule on selected clusters, were systematically studied by DFT calculations. In the S-deficient clusters, Mo atoms are more likely to come together and form an Mox core. Structures like the bulk 1T phase could be seen not only in stoichiometric clusters but also in non-stoichiometric MoxSy clusters. Another type of structure with square Mo2S2 units was found, which might be a new primary unit for two-dimensional molybdenum sulfides. The hydrogen molecule prefers to be adsorbed onto Mo atoms rather than S atoms, and Mo atoms with less coordination of S tend to have a higher local ESP and higher ability to adsorb H2. Among the studied clusters, 2–4a and 3–3b have the highest H2 adsorption energy, on which the H2 molecule is significantly activated. As a reverse reaction of HER, the dissociation of H2 on 2–4a and 3–3b was studied. Hydrogen atoms are found to be adsorbed onto Mo atoms rather than S atoms, especially on the vacant bridge site of Mo–Mo in 3–3b, which could be seen as the S vacancy in the bulk phase MoS2. The bridge site of Mo–Mo facilitates the transfer of H atoms on MoxSy clusters, indicating that S vacancies and Mo-edges in the bulk MoS2 are beneficial for both H2 dissociation and the HER. The H atom adsorbed on the bridge site of Mo–Mo may serve as another way to supply hydrogen in HDS, which may be verified by further investigations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 91545122 and No. 61704054), the Fundamental Research Funds for the Central Universities (JB2015RCY03, JB2019MS052, and JB2017MS056) supported by the fund of North China Electric Power University, and the National Key Research and Development Program of China (2016YFA0202401).Notes and references
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. B. Chorkendorff, J. K. Norskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- S. Chu, Y. Cui and N. Liu, Nat. Mater., 2017, 16, 16 CrossRef PubMed.
- X. L. Wang, Y. J. Tang, W. Huang, C. H. Liu, L. Z. Dong, S. L. Li and Y. Q. Lan, ChemSusChem, 2017, 10, 2402 CrossRef PubMed.
- X. X. Zou and Y. Zhang, Chem. Soc. Rev., 2015, 44, 5148 RSC.
- D. Voiry, J. Yang and M. Chhowalla, Adv. Mater., 2016, 28, 6197 CrossRef PubMed.
- X. L. Wang, C. Z. Xue, N. N. Kong, Z. Wu, J. X. Zhang, X. Wang, R. Zhou, H. P. Lin, Y. Y. Li, D. S. Li and T. Wu, Inorg. Chem., 2019, 58, 12415 CrossRef PubMed.
- J. S. Wang, J. Liu, B. Zhang, X. Ji, K. Xu, C. Chen, L. Miao and J. J. Jiang, Phys. Chem. Chem. Phys., 2017, 19, 10125 RSC.
- J. Kang, S. Tongay, Z. Jian, J. Li and J. Wu, Appl. Phys. Lett., 2013, 102, 012111 CrossRef.
- M.-R. Gao, M. K. Y. Chan and Y. Sun, Nat. Commun., 2015, 6, 7493 CrossRef PubMed.
- Y. Xu, L. Wang, L. Xia, S. Zhang, C. Liu, D. Yan, Y. Zeng, P. Yong, Y. Liu and S. L. Luo, J. Mater. Chem. A, 2016, 4, 16524 RSC.
- T. F. Jaramillo, K. P. Jorgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100 CrossRef PubMed.
- K. K. Ghuman, S. Yadav and C. V. Singh, J. Phys. Chem. C, 2015, 119, 6518 CrossRef.
- A. Y. Lu, X. L. Yang, C. C. Tseng, S. X. Min, S. H. Lin, C. L. Hsu, H. N. Li, H. C. Idriss, J. L. Kuo, K. W. Huang and L. J. Li, Small, 2016, 12, 5530 CrossRef PubMed.
- L. X. Lin, N. H. Miao, Y. Wen, S. W. Zhang, P. Ghosez, Z. M. Sun and D. A. Allwood, ACS Nano, 2016, 10, 8929 CrossRef PubMed.
- H. Li, C. Tsai, A. L. Koh, L. Cai, A. W. Contryman, A. H. Fragapane, J. Zhao, H. S. Han, H. C. Manoharan, F. Abild-Pedersen, J. K. Nørskov and X. Zheng, Nat. Mater., 2015, 15, 364 CrossRef PubMed.
- C. Tsai, H. Li, S. Park, J. Park, H. S. Han, J. K. Norskov, X. L. Zheng and F. Abild-Pedersen, Nat. Commun., 2017, 8, 15113 CrossRef PubMed.
- J. Chen, N. Kuriyama, H. Yuan, H. T. Takeshita and T. Sakai, J. Am. Chem. Soc., 2001, 123, 11813 CrossRef PubMed.
- N. H. Song, Y. S. Wang, H. Y. Gao, W. F. Jiang, J. Zhang, B. Xu, Q. Sun and Y. Jia, Phys. Lett. A, 2015, 379, 815 CrossRef.
- Z. M. Yuan, B. W. Zhang, Y. H. Zhang, S. H. Guo, X. P. Dong and D. L. Zhao, J. Mater. Sci. Technol., 2018, 34, 1851 CrossRef.
- E. J. Setijadi, X. Li, A. F. Masters, T. Maschmeyer and K.-F. Aguey-Zinsou, Int. J. Hydrogen Energy, 2016, 41, 3551 CrossRef.
- Y. H. Jia, S. M. Han, W. Zhang, X. Zhao, P. F. Sun, Y. Q. Liu, H. Shi and J. S. Wang, Int. J. Hydrogen Energy, 2013, 38, 2352 CrossRef.
- J. V. Lauritsen, M. V. Bollinger, E. Laegsgaard, K. W. Jacobsen, J. K. Norskov, B. S. Clausen, H. Topsoe and F. Besenbacher, J. Catal., 2004, 221, 510 CrossRef.
- P. G. Moses, B. Hinnemann, H. Topsoe and J. K. Norskov, J. Catal., 2007, 248, 188 CrossRef.
- A. Baloglou, M. Oncak, M. L. Grutza, C. van der Linde, P. Kurz and M. K. Beyer, J. Phys. Chem. C, 2019, 123, 8177 CrossRef PubMed.
- Q. Y. Liu and S. G. He, Chem. J. Chin. Univ.-Chin., 2014, 35, 665 CrossRef.
- P. Murugan, V. Kumar, Y. Kawazoe and N. Ota, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 063203 CrossRef.
- Y. Y. Wang, J. J. Deng, X. Wang, J. T. Che and X. L. Ding, Phys. Chem. Chem. Phys., 2018, 20, 6365 RSC.
- H. Jiao, Y.-W. Li, B. Delmon and J.-F. Halet, J. Am. Chem. Soc., 2001, 123, 7334 CrossRef PubMed.
- X. Zhang, X. Liu, R. Xu, N. Wu, X. Huang and B. Wang, Chin. J. Struct. Chem., 2018, 37, 497 Search PubMed.
- M. Ziane, F. Amitouche, S. Bouarab and A. Vega, J. Nanopart. Res., 2017, 19, 380 CrossRef.
- S. Gemming, J. Tamuliene, G. Seifert, N. Bertram, Y. D. Kim and G. Gantefor, Appl. Phys. A: Mater. Sci. Process., 2006, 82, 161 CrossRef.
- N. Bertram, Y. D. Kim, G. Gantefor, Q. Sun, P. Jena, J. Tamuliene and G. Seifert, Chem. Phys. Lett., 2004, 396, 341 CrossRef.
- S. Gemming, G. Seifert, M. Götz, T. Fischer and G. Ganteför, Phys. Status Solidi B, 2010, 247, 1069 CrossRef.
- P. Liu, Y. Choi, Y. X. Yang and M. G. White, J. Phys. Chem. A, 2010, 114, 3888 CrossRef PubMed.
- A. K. Gupta, J. E. Topolski, K. A. Nickson, C. C. Jarrold and K. Raghavachari, J. Phys. Chem. A, 2019, 123, 7261 CrossRef PubMed.
- N. J. Mayhall, E. L. Becher, A. Chowdhury and K. Raghavachari, J. Phys. Chem. A, 2011, 115, 2291 CrossRef PubMed.
- J. E. Topolski, A. K. Gupta, K. A. Nickson, K. Raghavachari and C. C. Jarrold, Int. J. Mass Spectrom., 2018, 434, 193 CrossRef.
- A. Saha and K. Raghavachari, J. Chem. Phys., 2013, 139, 12 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. A.03, Gaussian Inc, Wallingford, CT, 2016 Search PubMed.
- X. L. Ding, Z. Y. Li, J. H. Meng, Y. X. Zhao and S. G. He, J. Chem. Phys., 2012, 137, 214311 CrossRef PubMed.
- L. F. Li and L. J. Cheng, J. Chem. Phys., 2013, 138, 094312 CrossRef PubMed.
- X. N. Li, L. N. Wang, L. H. Mou and S. G. He, J. Phys. Chem. A, 2019, 123, 9257 CrossRef PubMed.
- X. L. Ding, D. Wang, R. J. Li, H. L. Liao, Y. Zhang and H. Y. Zhang, Phys. Chem. Chem. Phys., 2016, 18, 9497 RSC.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- B. Liang and L. Andrews, J. Phys. Chem. A, 2002, 106, 6295 CrossRef.
- B. Wang, N. Wu, X. B. Zhang, X. Huang, Y. F. Zhang, W. K. Chen and K. N. Ding, J. Phys. Chem. A, 2013, 117, 5632 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295 Search PubMed.
- N. Bridonneau, J. Long, J. L. Cantin, J. von Bardeleben, S. Pillet, E. E. Bendeif, D. Aravena, E. Ruiz and V. Marvaud, Chem. Commun., 2015, 51, 8229 RSC.
- B. Bishnoi and B. Ghosh, J. Comput. Electron., 2014, 13, 394 CrossRef.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0., Madison, WI, Theoretical Chemistry Institute, University of Wisconsin, 2013 Search PubMed.
- P. Xiao, W. Chen and X. Wang, Adv. Energy Mater., 2015, 5, 1500985 CrossRef.
- J. K. Norskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- L. Wu, A. Longo, N. Y. Dzade, A. Sharma, M. Hendrix, A. A. Bol, N. H. de Leeuw, E. J. M. Hensen and J. P. Hofmann, ChemSusChem, 2019, 12, 4383 CrossRef PubMed.
- N. Kaur, I. Kumari, S. Gupta and N. Goel, J. Phys. Chem. A, 2016, 120, 9588 CrossRef PubMed.
- J. B. Ma, X. N. Wu, X. X. Zhao, X. L. Ding and S. G. He, Phys. Chem. Chem. Phys., 2010, 12, 12223 RSC.
- P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755 CrossRef PubMed.
- G. J. Kubas, Acc. Chem. Res., 1988, 21, 120 CrossRef.
- J. Niu, B. K. Rao and P. Jena, Phys. Rev. Lett., 1992, 68, 2277 CrossRef.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef.
- T. Lu and F. W. Chen, J. Mol. Graphics, 2012, 38, 314 CrossRef.
- X. X. Wang, X. Liu, Q. Zhang and H. S. Chen, Acta Phys. Sin., 2017, 66, 103601 Search PubMed.
- P. B. Armentrout, Science, 1991, 251, 175 CrossRef PubMed.
- D. Schroder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139 CrossRef PubMed.
- D. Kiriya, P. Lobaccaro, H. Y. Y. Nyein, P. Taheri, M. Hettick, H. Shiraki, C. M. Sutter-Fella, P. D. Zhao, W. Gao, R. Maboudian, J. W. Ager and A. Javey, Nano Lett., 2016, 16, 4047 CrossRef PubMed.
- M. C. He, F. P. Kong, G. P. Yin, Z. Lv, X. D. Sun, H. Y. Shi and B. Gao, RSC Adv., 2018, 8, 14369 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: All data for Mo–Mo distances, natural bond orbital analysis for H2…MoxSy clusters, all obtained structures of MoxSy clusters, the relationship between Ead and other adsorption properties, and preliminary calculations on the grid structure. See DOI: 10.1039/d0cp04457a |
| This journal is © the Owner Societies 2021 |