Ab initio molecular dynamics study of sodium NMR chemical shifts in the methylamine solution of [Na+ [2.2.2]cryptand Na−]†
Laura
Abella
 ,
Adam
Philips
,
Adam
Philips
 and
Jochen
Autschbach
and
Jochen
Autschbach
 *
*
Department of Chemistry University at Buffalo State University of New York Buffalo, NY 14260-3000, USA. E-mail: jochena@buffalo.edu
First published on 9th December 2020
Abstract
The sodium anion (Na−) was once thought to behave like a ‘genuine’ anion, with both the [Ne] core and the 3s valence shell interacting very weakly with their environments. In the present work, following a recent study of the surprisingly small quadrupolar line widths of Na−, NMR shielding calculations were carried out for the Na−/Na+ [2.2.2]cryptand system solvated in methylamine, based on ab initio molecular dynamics simulations, followed by detailed analyses of the shielding constants. The results confirm that Na− does not act like a quasi-free ion that interacts only weakly with its surroundings. Rather, the filled 3s shell of Na− interacts strongly with its chemical environment, but only weakly with the ion's own core and the nucleus, and it isolates the core from the chemical environment. As a consequence, the Na− ion appears in NMR experiments like a free ion.
1 Introduction
Alkali metals atoms are strongly reducing, as the loss of the valence electron produces a closed-shell octet. The most famous chemical demonstration of this is the violent reaction of alkali metals with water. Metal-ammonia solutions, in which the alkali valence electrons become solvated, have also attracted significant attention.1–4 These elements have also generated much interest in regards to the formation of the corresponding negative alkalide ions,5 which have a closed-shell ns2 valence electron configuration. Exotic chemical species tend to grab the attention of scientists, and therefore alkalide ions and related systems have been studied repeatedly since their existence was first reported.6–17 Alkali metal solutions can react with cryptands and form salts, crystalline or in solution. For instance, the Na+/Na− salt with the 2.2.2 cryptand, viz. [Na+ [2.2.2]cryptand Na−] has been isolated and characterized in detail by Ceraso et al.18,19 This system is abbreviated as [Na+c222Na−] in the following. The existence of alkalide ions in solutions and solids was established by nuclear magnetic resonance (NMR) spectroscopy,18–22 allowing the simultaneous identification of both types of ion.For [Na+c222Na−], the 23Na NMR spectra have been reported in several studies.8,19,23,24 The Na+ ion is enclosed within the cryptand cage and separated from the solvent, if present, resulting in a chemical shift that is essentially solvent independent. For Na−, the chemical shift is also essentially independent of solvent, and it has been argued that its observed chemical shift is almost the same as the ion would have in gas phase.23 NMR data for other alkali metal anions (K−, Rb−, and Cs−) with the [2.2.2]cryptand displayed a stronger sensitivity to the chemical environment.8,13,19,25 Experimental investigations, with supporting theoretical data, concluded that Na− acts as a ‘genuine’ (spherical) anion, i.e. both the [Ne] core and the 3s valence shell interact very weakly with their surroundings.23,24,26 This conclusion was supported by the extremely narrow observed NMR line widths of Na−. 23Na is quadrupolar, which means that deformations of the ion in solution (or in a low-symmetry site in a crystal) should lead to substantial quadrupolar line broadening. The latter is caused by fast nuclear spin relaxation, driven by the interaction of the nuclear quadrupole with an electric field gradient (EFG). An EFG goes along with a non-spherical ion electron density and a low-symmetry arrangement of (partial) charges surrounding the ion.
The curiously small quadrupolar relaxation rates for Na− in a methylamine solution of [Na+c222Na−] was studied by us recently.27 Given that the 3s2 shell of Na− is diffuse, and extremely easily polarizable, it seemed to us that the assumption of a spherical Na− ion in such a solution cannot be valid. For instance, a visualization from a mixed quantum/classical simulation of Na− ion in tetrahydrofuran in ref. 28 appears to show a strongly deformed 3s shell in the ground state. It is important to distinguish here between ‘spherical on average’ vs. ‘genuinely spherical’. The EFG fluctuations and time-autocorrelations in the former case drive the relaxation rates of all mono-atomic ions with quadrupolar nuclei in isotropic solutions. In the previous study, we showed by ab initio molecular dynamics (aiMD) simulations that the sodium anion gets strongly deformed in the solution, as one might expect. However, its diffuse, filled, 3s shell interacts only weakly with the ion's own core and the nucleus. This causes the EFG to de-correlate rapidly, which results in slow nuclear relaxation and narrow lines. This led us to conclude that Na− appears in NMR experiments like a spherical ion, even though it is actually strongly deformed by the dynamic interactions with the solvent. Some of its electron density may even delocalize into the solvent shell. Dye et al.19 in 1975 speculated—correctly in hindsight—that the large extension of the 3s shell of Na− is responsible for the ion's curious behavior in the NMR experiments.
It remains to connect the experimental observations regarding the 23Na NMR chemical shifts with the ions' dynamic behavior in solution, and to re-examine the assumption that the Na− shift is gas-phase like. To this end, we calculated the nuclear magnetic shielding constants based on the same aiMD trajectories that were generated for the quadrupolar relaxation study27 and, for selected aiMD configurations, we analyzed the NMR shielding tensors in terms of contributions from core and valence shell orbitals. The Na− shielding constants were also correlated to close-distance interactions with the solute, to show that solute–solvent collisions have an important influence on the chemical shift of this ion.
2 Theoretical and computational details
Density functional theory (DFT) based Car–Parrinello aiMD simulations were performed previously27 with Quantum-Espresso (QE) version 6.0,29,30 using the Becke, Lee, Yang and Parr (BLYP) functional,31,32 semi-empirical dispersion corrections,33 and periodic boundary conditions (cubic cells, 12.71 Å). The BLYP functional along with the dispersion corrections were selected because of their good performance in previous studies.34–37 The temperature of 258 K in the simulations was the same as in the NMR experiments. Fifteen independent trajectories were spawned, each with a total production time around 20 ps, which was long enough to capture the dynamics as far as the NMR relaxation is concerned.27 NMR nuclear magnetic shielding tensors were newly calculated for the present work for 140 evenly spaced ‘snapshot’ configurations in each of the 15 trajectories, using the gauge-including projector-augmented wave (GIPAW) module of QE version 6.4.1,29,38 the Perdew–Burke–Ernzerhof (PBE) functional,39 a kinetic energy cutoff of 1361 eV (100 Ry) for the plane-wave basis, and non-relativistic, small-core pseudopotential for Na (with the 2s and 2p shells of Na treated in the valence space, not in the core). Schwartz et al.,17 in mixed quantum/classical simulations of solvated sodide, emphasized the importance of explicit quantum mechanical treatment of the outer electrons. Previous research by Zurek et al. showed that, likely, GIPAW calculations are close to the basis set limit for chemical shifts.40 A previous benchmark41 for molecules showed that the functional chosen for the NMR calculations, PBE, performs almost as well as the hybrid variant PBE0, and noticeably better than commonly used other hybrid functionals. For the periodic boundary calculations, a hybrid functional would be too demanding on computational resources in any case, and therefore PBE is a good compromise for NMR calculations. Due to the high demand of the QE NMR calculations on computational resources, we also used the CASTEP program (version 19.11)42 for extensive convergence tests of the GIPAW shielding running averages,43,44 with comparable technical settings, except that ultra-soft pseudopotentials were generated on the fly (784 eV energy cutoff) using the CASTEP algorithms.Additional nuclear magnetic shielding calculations were carried out with non-periodic boundary conditions, using the Amsterdam Density Functional (ADF) suite,45 the PBE functional, and all-electron Slater type orbital (STO) basis sets. For comparison, calculations were also performed with the PBE041 hybrid functional (25% exact exchange). A triple-ζ polarized basis (TZP) was used for Na+. For Na−, TZP was augmented with diffuse functions (ATZP). For other elements, a double-ζ polarized basis (DZP) was selected. Test calculations with a quadruple-ζ quadruply polarized basis (QZ4P) for the sodium ions were also performed for comparison, showing negligible differences with TZP. The data are provided in the ESI.† Additional calculated data, also shown in the ESI,† demonstrate quite good agreement between the sodium shielding constants obtained with PBE and PBE0, further validating the computational model. Finite [Na+c222Na−] – methylamine clusters of varying size were extracted from the MD trajectories. The conductor-like screening model (COSMO)46 with a dielectric constant for methylamine (9.4) was used to describe bulk solvent effects. The NMR shielding tensors were analyzed47 in terms of contributions from natural bond orbitals (NBOs) or natural localized molecular orbitals (NLMOs) generated with the NBO 6.0 program.48 Six snapshots from the aiMD simulations were selected for these analyses.
For brevity, we refer to the shielding calculations with the QE and ADF program by the acronyms PAW and STO, respectively, to reflect the main technical differences. Several types of sampling errors, and the approximations in the electronic structure calculations, influence the results. One concern is the number of MD configurations, and their time spacing, used to compute the trajectory-averaged shielding constants. Related data are gathered in Tables S1–S3 in the ESI.† A sampling of 140 configurations for each 20 ps production trajectory produces the sodium shielding constants with just under 1 ppm standard error in the 15-trajectory average for Na−. For several of the individual trajectory averages, the standard error in the Na− shielding is between 1 and 2 ppm. As Tables S1 and S2 (ESI†) show, the averaged shielding constants did not change significantly when going from 140 to a much larger number of configurations. Therefore, the value of 140 chosen for the full set of trajectories appears to be a good compromise.
3 Results and discussion
It is worthwhile to discuss, first, the experimental data for the [Na+c222Na−] – methylamine system at 258 K, reported by Dye et al.19 in 1975. Let Δσ = σ(Na−) − σ(Na+). The chemical shift of Na+, with Na− being the reference, is δ = [σ(Na−) − σ(Na+)]/[1 − σ(Na−)]. Given that the absolute shielding of light elements such as sodium is small, hence the unit of ppm, one can set the denominator equal to one, and therefore δ = Δσ. Dye et al. used a difference of 2.6 ppm between the absolute shielding constants for isolated (‘gas phase’) Na− and Na0, from nonrelativistic Hartree–Fock (HF) theoretical data of ref. 49, and listed the value as the relative shielding for Na− with respect to the neutral atom in their data collection. In the same table column, experimental relative shielding constants of −49.8 ppm for Na+ and +1.4 ppm for Na− were provided for the cryptand – methylamine system. This gives δ = Δσ = 51.2 ppm for the experiment. Dye et al. further provided a shielding of −60.5 ± 1 ppm for Na+(aq) in infinite dilution, relative to the neutral Na atom in its 2S1/2 ground state in gas phase. This value was reported by Beckmann et al. in 1974,50 and determined from a combination of molecular beam data for Na0, NMR frequency ratios for Na+(aq) and 2H, and other data such as a theoretical value of the electron g factor of the hydrogen atom. Dye et al. also used a Na+(aq) reference in the NMR experiments. Therefore, most likely, the 60.5 ppm from Beckmann et al. were subtracted from the experimental chemical shifts to arrive at the reported shielding constants relative to gas phase Na0. The thus derived experimental relative shielding of +1.4 ppm for Na− in the solvated cryptand system is indeed almost identical to the calculated 2.6 ppm shielding difference from ref. 49. We will return to the discussion of the shielding constants later.Table 1 provides the 15-trajectory averages of the shielding constants and δ, and data for the trajectory with the smallest and the largest average chemical shift, respectively, obtained from the PAW calculations. Table S3 (ESI†) provides the data for all individual trajectories. The overall average is δ = Δσ = 42 ppm. Although this calculated result underestimates the experimental value somewhat, it can be considered satisfactory. [We note in passing that the GIPAW results that we obtained with CASTEP consistently underestimate the ions' average shielding per trajectory (as well as the free ion shielding constants), but more so for Na+ than for Na−.] The individual trajectory averages for δ range from 29 to 54 ppm. The shifts are between 44 and 54 ppm for the majority of trajectories, i.e., close to the experiment. However, several trajectories produce a very low shift, around 30 ppm, decreasing the total average. A comparison between the chemical shifts and the calculated quadrupolar line widths of Na− and Na+ of ref. 27 shows that the trajectories with a low chemical shift also produce comparatively large line widths for Na− (see Table S3, ESI†), whereas the large chemical shifts correlate with small line widths. This seems to indicate a common underlying mechanism.
| MD | Ion | σ | δ = Δσ |
|---|---|---|---|
| a PAW/GIPAW calculations, 258 K. Average over 15 aiMD trajectories. The data for the trajectory with the smallest and largest chemical shift, respectively, are also given. Chemical shift of Na+ with respect to Na− as reference. Simulations cells contained [Na+c222Na−] and 24 methylamine molecules. Shielding constants were computed for 140 snapshot clusters from the aiMD simulations. All values are given in ppm. The experimental chemical shift is 51.2 ppm.19 | |||
| 8 | Na− | 621.7 (0.6) | 53.6 |
| Na+ | 568.1 (0.4) | ||
| 13 | Na− | 607.8 (1.3) | 29.1 |
| Na+ | 578.7 (0.4) | ||
| Average | Na− | 618.2 (0.9) | 42.2 |
| (15 traj.) | Na+ | 576.1 (0.4) | |
Fig. 1 shows the instantaneous shielding in two of the individual simulations, MD-01 and MD-14, which were chosen as representatives of the simulations with small and large chemical shifts, respectively. For the encapsulated Na+ ion, the shielding oscillates between about 560 and 585 ppm in both simulations. The shielding averages are 578 and 572 ppm for MD-01 and MD-14, respectively, with small standard errors of 0.4 to 0.5. For Na−, the MD simulations display two distinct regimes instead, which are both represented in Fig. 1. For the trajectories with a large chemical shift, the instantaneous Na− shielding remains relatively steady, i.e., without strong fluctuations. This is exemplified by the data from MD-14 in Fig. 1, which lead to an averaged chemical shift of 53.5 ppm, close to the experiment. Conversely, trajectories that give a small shift exhibit very strong fluctuations in the shielding constants over short periods of time, as seen in the MD-01 plot in Fig. 1.
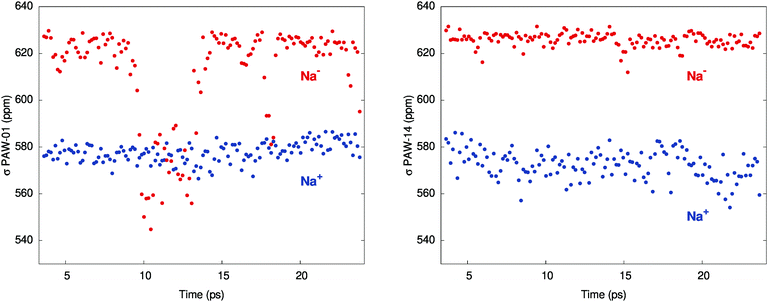 | ||
| Fig. 1 Shielding constants (PAW simulations) for Na− and Na+ along two of the trajectories: MD-01 (left) and MD-14 (right). | ||
The underestimation of the averaged chemical shift δ between Na+ and Na− in the calculations is tentatively attributed to an underestimation of the absolute shielding of Na− in the MD simulations, on average, due to an over-sampling of events that lead to the large drops of the Na− shielding constant exemplified by MD-01 in Fig. 1. In turn, this is related to the necessary approximations in the computations, among which are limitations in the simulation box dimensions, finite simulation times, and the description of the inter-atomic potentials by the chosen functional. Test calculations performed with a hybrid functional PBE0 in the STO calculations indicated that the PBE functional used for the NMR trajectory averages is likely not the main cause of the somewhat too low calculated shift (ESI,† Tables S6, S8 and S14).
Structural and dynamic analyses were performed to rationalize the strong drops of the Na− shielding in some of the trajectories. Fore instance, the strong shielding fluctuations clearly correlate with strong fluctuations of the EFG along the simulation (see Fig. S6, ESI†). This explains, in part, why the trajectories with a small δ produce large quadrupolar line widths, as the latter is proportional to the variance of the EFG tensor components. A very clear picture emerges when the instantaneous shielding is plotted together with the distance between the Na− ion and the nearest nitrogen from the methylamine solvent, as shown in Fig. 2 for MD-01. Low shielding constants reflect short N–Na− distances. Evidently, close contacts with the solvent molecules cause the strong decrease of the Na− shielding, leading to the low chemical shift for the trajectory average. Likewise, these close solvent–solute contacts correlate directly with the strong variations in the EFG tensor components, as shown in Fig. S7 and S8 (ESI†).
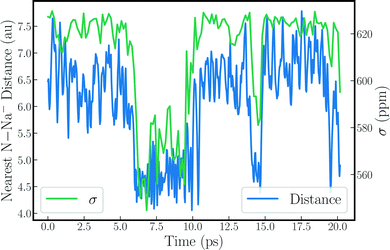 | ||
| Fig. 2 Nearest N–Na− distance plotted alongside 23Na nuclear magnetic shielding for the sodium anion along the MD-01 trajectory. | ||
We note that the 2S1/2 state of the Na atom has an unpaired electron spin in the 3s shell, which may therefore cause a paramagnetic (pNMR) contribution to the NMR shielding,51 in addition to the usual ‘orbital’ shielding. For not too low temperature T, the pNMR contribution is proportional to 1/T for a system in thermal equilibrium. It is unlikely that the pNMR formalism is transferable to the conditions in the molecular beam experiments of Beckmann et al.50 In any case, our understanding of the procedure used by Beckmann et al. is that the reported shielding difference for Na+(aq) versus Na0 is to be understood mostly, although perhaps not exactly, as the difference in the orbital shielding. For a spherical ion or atom, the orbital shielding depends only on the ground state electron density, and this is the shielding obtained in the HF calculations of ref. 49. Therefore, the conclusion drawn by Dye et al., that the shielding of solvated Na− is very similar to that of the free ion, appears to be mostly correct.
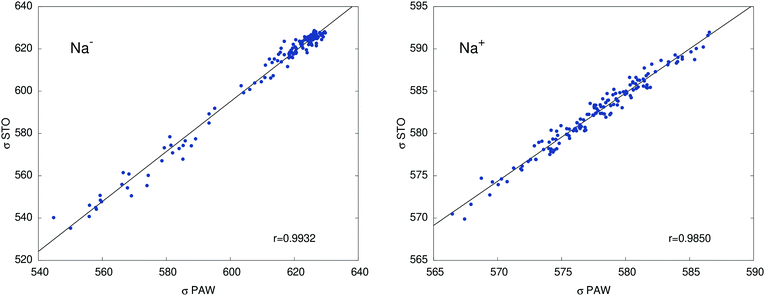
Table 2 collects calculated orbital shielding constants for the isolated ions Na+ and Na− (PBE/STO), and their breakdown into contributions from different atomic shells according to NBO analyses. Additional calculated data in Table S7 (ESI†) shows that free ion calculations with PAW, using large simulation cells that only contain Na+ or Na−, give near-perfect agreement with the STO calculations, with deviations not exceeding 0.4 ppm. Our DFT results are also very similar to the old HF results from ref. 49. The minor differences are due to the slightly different electron densities and the consideration of scalar relativistic effects in the DFT calculations. Comparisons between STO and PAW calculations for one of the cryptand – methylamine trajectories in Fig. 3 show somewhat larger deviations compared to the free ions, which we attribute mainly to the approximation of the system in the STO calculations as finite clusters embedded in a polarizable continuum. However, the agreement between the two sets of data is sufficiently good such that an analysis of the STO results can provide meaningful insight into the NMR shielding constants of the two ions.
| Ions | Na− | Na+ |
|---|---|---|
| a PBE STO calculations. All shielding data in ppm. Shielding tensor contributions from Na 1s, Na 2s, Na 2p, Na 3s, diffuse Na centered NBOs, and contributions from other atoms are listed. The calculated ‘orbital’ shielding for Na0 is 628.6 ppm. b Sum of contributions from diffuse Na-centered NBOs (‘Rydberg’ NBOs). c Sum of contributions from other atoms. d Sum of all NBO contributions with a print threshold above 1% of the total shielding. | ||
| Isotropic shielding tensor analysis | ||
| 1s + 2s | 442.1 | 441.8 |
| 2p | 181.1 | 181.5 |
| 3s | 8.4 | 0.0 |
| 2p + 3s | 189.5 | 181.5 |
| Diffuseb | 0.0 | 0.0 |
| Otherc | 0.0 | 0.0 |
| Σ analysisd | 631.6 | 623.3 |
| Total calcd | 631.7 | 623.3 |
| Chemical shift | 8.4 | |
According to our calculations, the gas phase orbital shielding of Na0 is 52.5 ppm higher than the aiMD averaged shielding of Na+ in the cryptand – methylamine system. According to the experiments by Dye et al., Na+ in the cryptand is 10.5 ppm more shielded than Na+(aq) in infinite dilution. This places the shielding of Na+(aq) 63 ppm below the orbital shielding of Na0, which is in good agreement with the 60.5 ± 1 ppm estimate from Beckmann et al. This lends further support to the assumption that the error in the calculated chemical shift is mainly due to the aiMD average of the Na− shielding being too low, most likely as a result of over-sampling the negative spikes in the instantaneous shielding when close solvent–solute contacts take place. (This does not preclude other systematic errors that affect all calculated shielding constants in the same way.)
For the free Na− ion, the calculated shielding is 632 ppm. The aiMD average for the cryptand system is 618 ppm. Assuming that all of the deviation between the calculated and the experimental chemical shift is indeed due to an underestimation of the Na− shielding, then a corrected aiMD average Na− shielding would be 10 ppm higher, about 628 ppm. This is indeed very close to the gas phase shielding. However, as we already demonstrated in the EFG study, the ion is not genuinely spherical, and as shown in Fig. 1 there can be strong fluctuations of the Na− shielding as a function of time. This is likely true for the real system, too, except less frequently or less severe.
For comparison with the free ion data of Table 2, Table 3 provides an NBO analysis of the isotropic shielding of selected trajectory snapshots of the [Na+c222Na−]–methylamine system. Due to its time-consuming nature, the analysis was limited to six representative configurations chosen as follows: three configurations with a chemical shift around 45 ppm, representing the trajectories that give average shifts close to the experiment, and three of the configurations with very low Na− shielding constants. The latter snapshots were randomly taken from the 10–15 ps production interval of MD-01. The following data extracted from the NBO calculation are additionally provided in the table to help with the interpretation: the population of the sodium 3s NBOs, the composition of the 3s NLMO of Na− in terms of Na-centered contributions from p and d angular momenta and the total weight from its ideally localized ‘parent NBO’, and the total ion electron count from the natural population analysis.
| Snapshot # | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| a PBE STO calculations. All shielding data in ppm. Shielding tensor contributions from Na 1s, Na 2s, Na 2p, Na 3s, diffuse Na centered NBOs, and contributions from other atoms are listed. b Sum of contributions from diffuse Na-centered NBOs (‘Rydberg’ NBOs). c Sum of contributions from other atoms. d Sum of all NBO contributions with a print threshold above 1% of total shielding. e 23Na NMR chemical shift. PAW and STO calculations in ppm. f The populations are 1.999 or greater for each of the 2p orbitals. g Weight of ‘parent NBO’ 3s in the NLMO. The p and d weights are for the Na-centered part of the NLMO. The weight of s is 98% or higher and not printed individually. | ||||||
| Na− isotropic shielding tensor analysis | ||||||
| 1s + 2s | 441.7 | 441.7 | 441.7 | 441.7 | 441.7 | 441.7 |
| 2p | 178.7 | 179.3 | 177.7 | 169.6 | 139.4 | 157.8 |
| 3s | 9.0 | 7.4 | 8.5 | −33.7 | −24.3 | −17.4 |
| 2p + 3s | 187.7 | 186.7 | 186.2 | 135.9 | 115.1 | 140.4 |
| Diffuseb | 0.0 | 0.0 | 0.0 | 5.4 | 16.8 | 0.0 |
| Otherc | 0.0 | 0.0 | 0.0 | −31.5 | −23.0 | −10.5 |
| Σ analysisd | 627.8 | 628.4 | 628.0 | 551.5 | 550.6 | 571.6 |
| Total calcd | 626.2 | 623.8 | 623.6 | 554.3 | 543.9 | 564.2 |
| Na+ isotropic shielding tensor analysis | ||||||
| 1s + 2s | 441.8 | 441.8 | 441.8 | 441.8 | 441.8 | 441.8 |
| 2p | 161.9 | 162.3 | 171.4 | 163.9 | 153.0 | 160.0 |
| 3s | 0.0 | −7.9 | 10.2 | −33.7 | 0.0 | 0.0 |
| 2p + 3s | 161.9 | 154.5 | 181.6 | 163.9 | 153.0 | 160.0 |
| Diffuseb | −8.0 | −6.4 | −10.9 | −9.2 | −7.8 | −5.9 |
| Otherc | 0.0 | 0.0 | −6.6 | 0.0 | −12.9 | −8.7 |
| Σ analysisd | 595.6 | 589.8 | 605.8 | 596.5 | 574.1 | 587.1 |
| Total calcd | 585.7 | 589.0 | 583.3 | 585.1 | 578.2 | 578.9 |
| 23Na NMR shifte | ||||||
| STO | 40.5 | 34.8 | 40.3 | −30.8 | −34.3 | −14.7 |
| PAW | 45.0 | 40.7 | 48.3 | −21.29 | −18.17 | −15.31 |
| NBO populationsf | ||||||
| Na+ 3s | 0.084 | 0.087 | 0.082 | 0.098 | 0.095 | 0.093 |
| Na− 3s | 1.678 | 1.680 | 1.662 | 1.216 | 1.315 | 1.420 |
| Composition of the 3s NLMO of Na− | ||||||
| % 3s NBOg | 84.1 | 84.2 | 83.5 | 66.0 | 68.0 | 71.9 |
| % p | 0.30 | 0.34 | 0.58 | 8.67 | 3.98 | 1.31 |
| % d | 0.01 | 0.01 | 0.02 | 0.05 | 0.01 | 0.01 |
| Total natural populations | ||||||
| Na+ | 10.16 | 10.15 | 10.14 | 10.19 | 10.18 | 10.16 |
| Na− | 11.71 | 11.72 | 11.70 | 11.38 | 11.41 | 11.47 |
The low ‘parent’ NBO weights in the 3s NLMO of Na−, especially in the low-shielding snapshots 4–6, indicate delocalization of the 3s electron density onto the solvent, which we noted already in our previous EFG study.27 The 3s delocalization goes along with a formal electron count for the anion significantly below the formal 12. The delocalization, and the low Na− shielding values, also go along with a significant polarization of the 3s shell, as evidenced in particular by the weights of p angular momenta. The 3s delocalization and polarization show up in visibly deformed and delocalized isosurfaces, as seen in Fig. S4 and S5 (ESI†). On the contrary, the natural population analysis ascribes a minor degree of electron donation from the cryptand to the encapsulated Na+, such that 3s has a population of just under 0.1.
For the free ions, the electron density in the 1s, 2s, and 2p shells is similar enough such that the shielding contributions are nearly identical, 442 ppm for 1s + 2s, and between 181 to 182 ppm for 2p. The 8.4 ppm diamagnetic shielding from 3s then gives essentially all of the shielding difference between the two ions. These numbers for Na− translate almost un-changed to snapshots 1, 2, and 3 of the cryptand – methylamine system. There is a small reduction of the 2p contribution, which arises from the magnetic-field response of 2p due to the lower-than-spherical instantaneous symmetry of the solvated ion. This so-called ‘paramagnetic’ response typically—as it does here—reduces the absolute shielding, whereas it must vanish for a spherical ion. However, the effects on Na− in snapshots 1–3 are minor. This is attributable to the large radius of 3s, which shields the 2p shell from its surrounding. In these configurations, the ion's NMR shielding is indeed free-ion like. In comparison, the 2p shell of Na+ senses the asymmetric environment inside the cryptand much more strongly, and the de-shielding contributions from 2p and ‘diffuse’ Na orbitals cause most of the lowering of the shielding of Na+. There are also ‘Other’ orbital contributions, which are from NBOs that are centered on cryptand (for Na+) or solvent (for Na−) atoms. The appearance of these contributions in the analysis is related to orbital overlap, and partial covalent bonding or antibonding interactions, and seen to contribute to the de-shielding of Na+ when the ion gets close to the cryptand atoms.
The most interesting effects appear for the Na− shielding in the ‘close-contact’ snapshots 4–6 of the cryptand - methylamine system. As for the cation, the 1s and 2s shells of Na− remain un-polarized, and their diamagnetic shielding contributions are the same as for Na+ and for the free ions. However, there is now a sizable paramagnetic shielding from the 2p shell, caused by the strongly asymmetric environment, an accompanying paramagnetic response from the deformed 3s shell due to its 3p admixture, and large negative contributions from solvent-centered NBOs. The latter are a direct consequence of the close solute–solvent contacts.
4 Summary and conclusions
In conclusion, this work provides the theoretical analysis of the NMR shielding constants of 23Na− and 23Na+ for [Na+ [2.2.2]cryptand Na−] solvated in methylamine, based on aiMD simulations. The calculated chemical shift of Na+ with Na− as a reference is comparable with experiments. We already argued in a previous study, focusing on the 23Na quadrupolar line widths, that the notion of Na− being a genuine spherical ion in this system is untenable. However, as underlined by the present study, even though Na− may become strongly perturbed in the cryptand-methylamine system, its NMR shielding for the majority of configurations is free-ion like. As it was speculated by Dye et al.,19 we can confirm that the large radial extension of the 3s shell isolates the 1s22s22p6 core from the chemical environment, at least as far as the NMR shift and quadrupolar line broadening are concerned. At the same time, the shielding contribution from 3s itself is relatively small, such that even strong relative variations in this contribution do not translate into a sizable chemical shift. (The data in Table 3 for snapshots 1–3 suggests that variations in the 3s shielding contribution may well end up canceling.) The sharp 23Na− NMR signals are likewise caused by the spatial and electronic isolation of the ion's core from its valence shell, such that sizable EFGs—which do appear in Na−—rapidly de-correlate and therefore do not cause line broadening. As we have seen, in some instances in the trajectories, the Na− shielding becomes as strongly perturbed by the solvent as that of Na+ in the cryptand or in aqueous solution. However, these instances are not sufficiently common to change the overall picture and, likely, somewhat over-sampled in our study. In combination with the previous study of the line broadening,27 we now have a complete picture of the NMR of Na− in the cryptand – methylamine system: Na− does not behave like a quasi-free ion that interacts only weakly with its surroundings. Rather, the filled 3s shell of Na− interacts strongly with its environment, but only weakly with the ion's own core and the nucleus, as far as the NMR parameters are concerned, because the diffuse 3s shell isolates the core spatially and electronically from the environment. Consequently, the Na− ion appears in NMR experiments like a free ion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Center for Computational Research (CCR) at the University at Buffalo for providing computational resources. This work has been supported by Grant CHE-1855470 from the National Science Foundation. J. A. thanks Dr Herman Cho, Pacific Northwest National Laboratory, for thoughtful comments regarding the Na+(aq) shielding from ref. 50.References
- T. Buttersack, P. E. Mason, R. S. McMullen, H. C. Schewe, T. Martinek, K. Brezina, M. Crhan, A. Gomez, D. Hein, G. Wartner, R. Seidel, H. Ali, S. Thürmer, O. Marsalek, B. Winter, S. E. Bradforth and P. Jungwirth, Science, 2020, 368, 1086–1091 CrossRef CAS.
- M. C. R. Symons, Q. Rev., Chem. Soc., 1959, 13, 99–115 RSC.
- P. P. Edwards, J. Phys. Chem., 1984, 88, 3772–3780 CrossRef CAS.
- E. Zurek, P. P. Edwards and R. Hoffmann, Angew. Chem., Int. Ed., 2009, 48, 8198–8232 CrossRef CAS.
- J. L. Dye, Sci. Am., 1977, 237, 92–107 CrossRef CAS.
- J. L. Dye and M. G. DeBacker, Annu. Rev. Phys. Chem., 1987, 38, 271–299 CrossRef CAS.
- M. J. Wagner and J. L. Dye, Annu. Rev. Mater. Sci., 1993, 23, 223–253 CrossRef CAS.
- J. L. Dye, Angew. Chem., Int. Ed. Engl., 1979, 18, 587–598 CrossRef.
- F. J. Tehan, B. L. Barnett and J. L. Dye, J. Am. Chem. Soc., 1974, 96, 7203–7208 CrossRef CAS.
- M. Sokol, J. Grobelny, Z. Grobelny and A. Stolarzewicz, J. Phys. Chem., 1993, 97, 763–766 CrossRef CAS.
- M. G. DeBacker, E. B. Mkadmi, F. X. Sauvage, J.-P. Lelieur, M. J. Wagner, R. Concepcion, J. Kim, L. E. H. McMills and J. L. Dye, J. Am. Chem. Soc., 1996, 118, 1997–2003 CrossRef CAS.
- P. P. Edwards, A. S. Ellaboudy, D. M. Holton and N. Pyper, Mol. Phys., 1990, 69, 209–227 CrossRef CAS.
- J. Kim, J. L. Eglin, A. S. Ellaboudy, L. E. H. McMills, S. Huang and J. L. Dye, J. Phys. Chem., 1996, 100, 2885–2891 CrossRef CAS.
- E. Zurek, J. Am. Chem. Soc., 2011, 133, 4829–4839 CrossRef CAS.
- E. R. Barthel, I. B. Martini and B. J. Schwartz, J. Chem. Phys., 2000, 112, 9433–9444 CrossRef CAS.
- C. J. Smallwood, W. B. Bosma, R. E. Larsen and B. J. Schwartz, J. Chem. Phys., 2003, 119, 11263–11277 CrossRef CAS.
- W. J. Glover, R. E. Larsen and B. J. Schwartz, J. Chem. Phys., 2008, 129, 164505 CrossRef.
- J. M. Ceraso and J. L. Dye, J. Chem. Phys., 1974, 61, 1585–1587 CrossRef CAS.
- J. L. Dye, C. W. Andrews and J. M. Ceraso, J. Phys. Chem., 1975, 79, 3076–3079 CrossRef CAS.
- J. Dye, A. Ellaboudy and J. Kim, Modern NMR Techniques and Their Application in Chemistry, Marcel Dekker, Inc., New York, 1991 Search PubMed.
- A. Ellaboudy and J. L. Dye, J. Magn. Reson., 1986, 66, 491–502 CAS.
- R. C. Phillips, S. Khazaeli and J. L. Dye, J. Phys. Chem., 1985, 89, 606–612 CrossRef CAS.
- N. C. Pyper and P. P. Edwards, J. Am. Chem. Soc., 1986, 108, 78–81 CrossRef CAS.
- J. Kim and J. L. Dye, J. Phys. Chem., 1990, 94, 5399–5402 CrossRef CAS.
- P. P. Edwards, A. S. Ellaboudy and D. M. Holton, Nature, 1985, 317, 242–244 CrossRef CAS.
- A. S. Ellaboudy, D. M. Holton, N. C. Pyper, P. P. Edwards, B. Wood and W. McFarlane, Nature, 1986, 321, 684–685 CrossRef CAS.
- L. Abella, A. Philips and J. Autschbach, J. Phys. Chem. Lett., 2020, 11, 843–850 CrossRef CAS.
- W. J. Glover, R. E. Larsen and B. J. Schwartz, J. Chem. Phys., 2010, 132, 144102 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Mater, 2009, 21, 395502 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Kúçúkbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- A. Philips, A. Marchenko, L. A. Truflandier and J. Autschbach, J. Chem. Theory Comput., 2017, 13, 4397–4409 CrossRef CAS.
- A. Philips, A. Marchenko, L. C. Ducati and J. Autschbach, J. Chem. Theory Comput., 2019, 15, 509–519 CrossRef CAS.
- S. Badu, L. A. Truflandier and J. Autschbach, J. Chem. Theory Comput., 2013, 9, 4074–4086 CrossRef CAS.
- S. Biswas and B. S. Mallik, Phys. Chem. Chem. Phys., 2017, 19, 9912–9922 RSC.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- E. Zurek, C. J. Pickard, B. Walczak and J. Autschbach, J. Phys. Chem. A, 2006, 110, 11995–12004 CrossRef CAS.
- C. Adamo and V. Barone, Chem. Phys. Lett., 1998, 298, 113–119 CrossRef CAS.
- S. Clark, M. D. Segall, C. Pickard, P. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101–2451013 CrossRef.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401–0244011 CrossRef.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, O. Baseggio, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, A. Förster, C. F. Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. Goez, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert, J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Stener, M. Swart, D. Swerhone, V. Tognetti, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF 2019.3, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com, accessed 07/20.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- M. Srebro and J. Autschbach, Chem. – Eur. J., 2013, 19, 12018–12033 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0.
- G. Malli and S. Fraga, Theor. Chim. Acta, 1967, 7, 75–79 CrossRef CAS.
- A. Beckmann, K. D. Böklen and D. Elke, Z. Phys., 1974, 270, 173–186 CrossRef CAS.
- J. Autschbach, Annual Reports in Computational Chemistry, Elsevier, Amsterdam, 2015, vol. 11, pp. 3–36 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: NMR shielding data for the individual trajectories, comparisons between different types of calculations, additional free ion data, isosurfaces of selected NBOs and NLMOs, additional NBO analysis data, and additional structural and dynamic analyses. See DOI: 10.1039/d0cp06012g |
| This journal is © the Owner Societies 2021 |