Hydroxide promotes ion pairing in the NaNO₂–NaOH–H₂O system

Abstract

Nitrite (NO₂⁻) is a prevalent nitrogen oxyanion in environmental and industrial processes, but its behavior in solution, including ion pair formation, is complex. This solution phase complexity impacts industries such as nuclear waste treatment, where NO₂⁻ significantly affects the solubility of other constituents present in sodium hydroxide (NaOH)-rich nuclear waste. This work provides molecular scale information into sodium nitrite (NaNO₂) and NaOH ion-pairing processes to provide a physical basis for later development of thermodynamic models. Solubility isotherms of NaNO₂ in aqueous mixtures with NaOH and total alkalinity were also measured. Spectroscopic characterization of these solutions utilized high-field nuclear magnetic resonance spectroscopy (NMR) and Raman spectroscopy, with additional solution structure detailed by X-ray total scattering pairwise distribution function analysis (X-ray PDF). Despite the NO₂⁻ deformation Raman band's insensitivity to added NaOH in saturated NaNO₂ solutions, ²³Na and ¹⁵N NMR studies indicated the Na⁺ and NO₂⁻ chemical environments change likely due to ion pairing. The ion pairing correlates with a decrease in diffusion coefficient of solution species as measured by pulsed field gradient ²³Na and ¹H NMR. Two-dimensional correlation analyses of the 2800–4000 cm⁻¹ Raman region and X-ray PDF indicated that saturated NaNO₂ and NaOH mixtures disrupt the hydrogen network of water into a new structure where the length of the O⋯O correlations is contracted relative to the typical H₂O structure. Beyond describing the solubility of NaNO₂ in a multicomponent electrolyte mixture, these results also indicate that nitrite exhibits greater ion pairing in mixtures of concentrated NaNO₂ and NaOH than in comparable solutions with only NaNO₂.

---

1. Introduction

In solutions of extreme alkalinity, a deficiency of water necessitates a contraction of both cation–cation and anion–anion distances, leading to local ion configurations of greater complexity than cation–anion ion pairs and solvent-separated ion pairs due to geometric packing constraints.^1,2 These hydroxide (OH⁻)-bearing solutions are complex relative to other monovalent anions, due to proton transfer mechanisms and other transport pathways, facilitated by the reactive OH⁻ ion.^3–5 The convolution of contracted ion–ion distances, reactive OH⁻ species, and low water activity, make it challenging to unravel the molecular scale interactions that influence the solubility of salts (e.g., sodium nitrite, NaNO₂) at extreme alkalinity.

Without knowledge of these molecular scale interactions, it is not possible to predict ion pairing processes and rheological properties of the solution, which are important in many industries.^6–8 For example, in concentrated alkaline aqueous solutions, the sorption of nitric oxide can be leveraged to treat flue gas and simultaneously generate marketable salts.⁶ Sodium nitrite is also abundant in alkaline radioactive waste, currently stored in huge underground tanks at the U.S. Department of Energy legacy sites, such as the Hanford site, Washington State (USA). Within these radioactive wastes, NO₂⁻ is present in a concentrated mixture of electrolytes, with concentrations of sodium in excess of 10 moles per liter (M).⁷ Nitrite is also present at other radioactive waste sites, such as the Savannah River Site, in South Carolina (USA), where the influence of the NO₂⁻ ion has been investigated in sodium hydroxide (NaOH) recoveries using electrochemical separations.⁸ For both of these examples, disentangling the influence of specific ions, such as OH⁻ and NO₂⁻, on the solubility of ions and the rheology of concentrated electrolytes, is an ongoing effort.

In sodium hydroxide solutions, NO₂⁻ and nitrate (NO₃⁻) were recently found to increase the solubility of gibbsite (Al(OH)₃), which is an aluminum hydroxide mineral found in nuclear waste.^9,10 However, addition of NO₂⁻ to alkaline sodium hydroxide solutions was also reported to decrease the solubility of amorphous zeolites in solutions also containing sodium aluminate and sodium nitrate.¹¹ These contradictory results highlight the need to understand ion-specific effects and their influence on solution properties in mixtures of electrolytes.

Both measurements and theoretical calculations have provided insight into the solvation structure of separate systems of either sodium nitrite or sodium hydroxide and water. NO₂⁻ is classified as a chaotrope, a structure breaker, for its ability to dissolve and form hydrated ions that disrupt water structure to a greater extent relative to other monovalent ions.¹² The NO₂⁻ ion has an N–O bond distance of 1.23 Å with an ∠ONO angle of 116°.¹³ Recent molecular dynamics simulations under infinitely dilute conditions showed that NO₂⁻ has 5 water molecules in the first solvation shell, and is asymmetrically solvated with water preferentially coordinated to the nitrite oxygens.^14,15 However, at greater concentrations of NaNO₂, there is insufficient water to form a complete solvation shell. For example, at NaNO₂ concentrations of 5 moles per kilogram solvent (molal, m), the NO₂⁻ ion was associated with 3.7 water molecules, as measured using neutron diffraction.¹⁶ This is comparable but not identical to structures generated by classical molecular dynamics, which predicted NO₂ to be solvated by 7–8 water, defined with a cutoff radial distance of 4 Å, even at concentrations of approximately 5 m NaNO₂.¹⁷ In simple NaNO₂ solutions without NaOH, the weak ion pairing between Na⁺ and NO₂⁻ is such that the solubility of NaNO₂ can be modeled with parameters which indicate only weak ion pairing.¹⁸ In contrast, OH⁻ is classified as a kosmotropic ion relative to NO₂⁻,¹⁹ and the ion templates the structure of water and forms ion pairs with Na⁺ in aqueous solution.²⁰ The ions in the NaOH solutions access a variety of local ion configurations to form corner-, edge-, and face-sharing polyhedral networks.²¹

Here, the physical rational behind the inclusion or omission of Na–NO₂ ion-pair formation terms in solubility models describing the NaNO₂–NaOH mixtures is explored via spectroscopy and diffraction. Solubility isotherms are presented for NaNO₂ in mixtures containing NaOH and H₂O. The concentration of NO₂⁻ in solution was measured using ion chromatography (IC) and total alkalinity (OH⁻) was measured by titration to a phenolphthalein endpoint. The NO₂⁻ and sodium solvation environment and the translational dynamics of H-bearing species and sodium ions were quantified using multinuclear NMR at 17.6 T (²³Na, ¹⁵N, and ¹H), Raman spectroscopy, and solution-state X-ray total scattering pairwise distribution function analysis (X-ray PDF). The results indicate that there is greater ion pairing in mixtures of concentrated NaNO₂ and NaOH than in comparable solutions with only NaNO₂ by the reduction in ¹H and ²³Na diffusivity, and the contraction of long-range correlations in X-ray total scattering. The new solubility data and molecular scale insight into the chemical environment of NO₂⁻ in concentrated alkaline electrolytes provides a foundational basis from which systems of greater complexity can be studied in order to better understand solubility, ion pairing, and rheology in alkaline solutions pertinent to flue gas treatment and nuclear waste processing.

2. Experimental methods

2.1 Solution preparation and solubility experiments

Solution preparation and solubility experiments with NaNO₂–NaOH solutions were conducted in an Ar-atmosphere (Oxarc) glove box to minimize carbon dioxide uptake in the alkaline solutions. Sodium nitrite (NaNO₂, Fischer, >97%) was dried in an oven at 80 °C to constant mass, with a mass loss of about 0.6 wt%. A 1, 3 and 6 m NaOH stock solution was prepared by dissolving sodium hydroxide (Sigma Aldrich, >98%) in N₂-sparged water (18 MΩ cm) in a 250 mL fluorinated ethylene propylene Erlenmeyer bottle.

To measure solubility from undersaturation, NaNO₂ was added to the solutions in quantities expected to exceed the solubility of NaNO₂ by a factor of 1.3. Details regarding the solubility prediction are available in the ESI† and summarized in Table S1. NaNO₂ was weighed out into 15 ml Teflon tubes for experiments at ambient temperature (28 °C) and into 50 mL Teflon tubes for 40, 60 and 80 °C experiments. Then, 6 mL of the respective NaOH stock solution for experiments at 28 °C and 13 mL of the respective NaOH stock solution for experiments at 40, 60 and 80 °C was added. Systems were typically prepared in triplicate. Given that the conditions in Table 1 vary with temperature, concentrations are reported in units of molality (moles kg⁻¹ solvent) and not molarity (moles L⁻¹). For solubility experiments performed at 28 °C shown in Table 1, the PTFE lined reaction vessels were placed on a rocking platform to provide continuous agitation. For solubility experiments performed at 40, 60 and 80 °C also shown in Table 1, the reaction vessels were placed in an aluminum enclosure on a heating stir plate and mixed at 50–150 rpm via magnetic PTFE lined stir bar. The temperature stability during the experiment was ±1 °C, as measured by National Institute of Standards and Technology (NIST) traceable, calibrated thermometers (Fisher Digital Lollipop Thermometer and Fisher big-digit see-thru Thermometer). The thermometers were calibrated in compliance with ISO/IEC 17025:2005, ANSl/NCSL Z540-1-1994 Part 1, and ISO 9001.

Table 1 System compositions at selected temperatures for NaNO₂ solubility studies

Solution + Solid composition				Solution composition
NaOH (g)	NaNO2 (g)	H2O (g)	Temp (°C)	NaOH (molal, moles kg^−1)	NaNO2 (molal, moles kg^−1)	Density (g cm^−1)
a Solution conditions were approached from both over and undersaturation, with results shown in Table S2 in the ESI. b Single measurement only. c Additional experiments characterized solids at approximately these conditions with Raman spectroscopy, X-ray diffraction, and scanning electron microscopy, with results showing that NaNO2 is the solid phase in Fig. S5–S7 in the ESI.
0.0	107.6	100.0	27.6^c	0	13.1(4)	1.378(4)
4.0	98.7	100.0	27.6	0.9(1)	11.9(1)	1.379(8)
12.0	84.3	100.0	27.6	2.8(1)	10.1(1)	1.372(7)
24.0	61.0	100.0	27.6^c	5.4(2)	7.1(1)	1.391(4)
4.0	116.6	100.0	41.1^a	0.9(1)	13.5(1)	1.375(1)
12.0	98.7	100.0	41.1^a	2.9(1)	11.5(1)	1.357(13)
24.0	78.0	100.0	41.1^a^b	5.6	8.8	1.340
4.0	143.5	100.0	58.2	0.9(1)	15.5(4)	1.394(0)
12.0	125.6	100.0	58.2	2.8(1)	13.2(1)	1.389(2)
24.0	98.7	100.0	56.6	5.7(1)	10.0(4)	1.382(1)
0	176.5	100.0	79.2^c	0	18.9(1)	1.413(4)
4.0	161.5	100.0	79.0	1.0(2)	18.9(3)	1.366(10)
12.0	143.5	100.0	78.4	3.3(1)	17.1(1)	1.348(4)
24.0	125.6	100.0	79.6^c	6.3(1)	14.4(4)	1.350(9)

---

Solutions were sampled after 1 week for systems at 28, 40, and 60 °C and after 2 days for systems at 80 °C. Good agreement between measured and literature²² NaNO₂ solubility in the absence of NaOH for control experiments at 28 and 80 °C, and the near equivalent solution compositions acquired from oversaturation and undersaturation approaches provides compelling evidence that solutions were essentially at equilibrium when compositions were determined. To measure solubility from oversaturation, the NaNO₂ and NaOH solutions prepared at 80 °C were cooled to 40 °C which resulted in near equivalent NaNO₂ concentrations. See Table S2 in the ESI for additional results.†

2.2 Ion chromatography

To determine the concentration of NaNO₂, pipette tips were preheated to the solution temperature, and aliquots of approximately 0.2 mL were collected from the reaction vessels at temperature, and rapidly filtered through pre-heated 0.2 μm polyvinylidene difluoride filters. To confirm that filtering the solutions did not influence the results, NaNO₂ concentrations were determined in: (i) solutions that had been filtered; and (ii) the supernatant from solutions following sedimentation, with the agreement in measured solution concentrations shown in Table S3 and Fig. S4 in the ESI.†

For IC measurements of NO₂⁻ concentrations, samples were diluted with water. Two instruments were used for ion chromatography (IC) analysis: (i) a Dionex Reagent Free Ion Chromatography System 5000 (RFICS-5000) with an AS-AP auto-sampler, and (ii) a Dionex Reagent Free Ion Chromatography System 2000 (RFICS-2000) with an AS-1 auto-sampler. Calibration curves (multi-component anion solutions, SPEX CertiPrep) were collected periodically and solution blanks were included to validate lack of sample carryover. IC was also performed to validate the lack of inorganic contaminants. Specifically, the solution of 13 m NaNO₂ and 5 m NaOH contained trace concentrations of chloride (<250 ppm), bromide (<500 ppm), fluoride (<100 ppm), phosphate (<750 ppm), and sulfate (<750 ppm), which are not considered significant. There are similarly insignificant carbonate impurities, based on Raman spectra of concentrated NaNO₂ and NaOH solutions (Fig. S8, ESI†).

2.3 Total alkalinity

Total alkalinity [OH⁻] was measured using a titrator (Metrohm 888 Titrando) with Tiamo software (v 2.4), by titration with 0.02 N sulfuric acid (H₂SO₄) to a phenolphthalein endpoint (pH of 8.3).

2.4 NMR spectroscopy

Single pulse direct excitation ²³Na and ¹⁵N NMR and pulsed field gradient ²³Na and ¹H NMR were conducted on an Agilent spectrometer at a field strength of 17.6 T, using a broadband probe, operating at 25 °C. The temperature was calibrated with the ¹H chemical shifts of ethylene glycol.²³ The corresponding Larmor frequencies for ²³Na, ¹⁵N, and ¹H are 198.424, 76.039, and 750.130 MHz, respectively. Solutions were loaded into 5 mm PTFE sample liners, coaxially inserted into 5 mm NMR tubes in an Ar-filled glovebox.

The single pulse direct excitation ²³Na NMR spectra were acquired with a π/2 liquid-state pulse, an acquisition time of 600 ms, a delay between transients of 2 s, and 16 transients. Chemical shifts are internally referenced to a physically separated solution of 0.76 M NaCl in H₂O, the resonance of which was assigned to 0 ppm. The ²³Na NMR spectra were processed in Mestrenova (version 14.01-23559, released 2019-06-07, Mestrelab Research S.L.), where the free induction decay was zero-filled once, and the spectra are shown with 2 Hz of exponential line broadening. The single pulse direct excitation ¹⁵N NMR spectra were collected with a π/6 excitation pulse, an acquisition time (at) of 1.678 s, a delay between transients (d1) of 5 s, and 64 transients. Given the spin–lattice recovery coefficient (T₁) of ¹⁵N is such that the expression {at + d1 < 5 T₁} is true, only the chemical shifts of the ¹⁵N resonances are discussed here; the ¹⁵N intensities were not analyzed quantitatively because of saturation effects. NO₂⁻ concentrations were determined by IC, as described above. The ¹⁵N NMR spectra were externally referenced to acetonitrile, which was assigned a chemical shift of 130.2 ppm (relative to 0 ppm defined by 1 M solution of H¹⁵NO₃ in D₂O).²⁴ The ¹⁵N NMR spectra were processed in Mestrenova, where the free induction decay was truncated to 0.6 s and the spectra are shown with 2 Hz of exponential line broadening. Single pulse direct excitation spectra were fit using purely Lorentzian line shapes.

Pulsed field gradient ²³Na and ¹H NMR spectra were also collected to investigate the translational motion of Na⁺ and H₂O/OH⁻ at millisecond timescales. For ²³Na, diffusion coefficients were acquired with the vendor-supplied bipolar gradient pulse pair stimulated echo with convection compensation (Dbppste_cc). For ¹H, diffusion coefficients were acquired with the vendor-supplied DOSY gradient compensated stimulated echo with spin lock and convection compensation sequence (DgcsteSL_cc). The π/2 pulse widths were calibrated for each sample for both nuclei. Acquisition with either pulse sequence used 16 spatially-dependent gradient pulse strength increments, where the spatially-dependent gradient pulse duration and amplitude were optimized for each sample. ²³Na pulsed field gradient (PFG)-NMR experiments were conducted with an acquisition time of 800 ms and a delay between experiments of 2 s, and ¹H PFG-NMR experiments were conducted with an acquisition time of 2.7 s and a delay between experiments ranging between 7 and 12 s, depending on T₁. ²³Na and ¹H PFG-NMR spectra used diffusion delays of 40.5 and 30 ms, respectively, and the diffusion coefficients were calculated using single-component, spline-modeling in vNMRJ (v. 3.2). The gradient calibration value (gcal) used to determine absolute diffusion coefficients was calibrated using the self-diffusion coefficient of H₂O at 25 °C.²⁵

2.5 Raman spectroscopy

Raman spectra were collected on solutions with a Horiba LabRam HR spectrometer on a Nikon Ti-E inverted microscope with a 40× objective using a continuous 632.81 nm laser. Spectra were acquired between 100–4000 cm⁻¹. Select regions were deconvoluted using Lorentzian line shape parameters following background correction with spline functions. Additional processing utilized 2DShige (v1.3, © Shigeaki Morita, Kwansei-Gakuin University, 2004–2005) to extract autocorrelation spectra from the generalized two-dimensional correlation spectra produced from (i) a concentration array of 1, 3, 6 m NaOH in H₂O and (ii) a concentration array of saturated NaNO₂ in NaOH solution (entries described in row 2–4, as listed in Table 1) using the NaOH concentration as the perturbation variable.

2.6 X-ray total scattering

X-ray total scattering was measured to determine the atomic pair distribution function (PDF). Solutions were loaded into 2 mm ID polyimide capillaries at the Advanced Photon Source (APS), beamline 11-ID-B.²⁶ Immediately after, scattered radiation from the incident beam (∼58.6 keV, λ = 0.2114 Å; beam size of 350 × 350 μm²) was measured in transmission mode using an amorphous-Si detector system manufactured by Perkin Elmer™ (2048 × 2048 pixels, 200 × 200 μm² pixel size). The program GSAS-II was used to sum 2D scans and perform integration to 1D profiles using a polarization correction.²⁷ The detector non-orthogonality and the sample-to-detector distance were calibrated using a CeO₂ standard (NIST diffraction standard set 674a) diluted 1 : 25 with glassy carbon. PDFgetX3 was used to process the 1D profiles obtained from GSAS-II and to subtract the background contributions associated with the polyimide capillary and air scattering.²⁸ For PDFgetX3, the compositions were assumed to be that of the as-prepared solutions. The Q_max for the Fourier transformation was set to 24.26 Å⁻¹. The resultant pairwise distribution function, G(r), was output from 0.0 to 16.0 Å with a step size of 0.1 Å. A default value of 0.9 was used for Rpoly, and a background factor of 1.0 was used to subtract the air-filled polyimide capillary. To better understand the X-ray weighted contributions of each i–j type pair (i, j = H, N, Na, and O atoms), the weighting factor (w_ij) was calculated as: 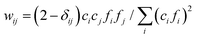, where δ_ij is the Kronecker delta, f_i is the X-ray atomic scattering factor, and c_i is the atomic fraction. The atomic fraction is defined by c_i = N_i/N, where N_i and N are the number of atoms of type i and the total number of atoms in the solution, respectively.

3 Results and discussion

3.1 Solubility measurements for NaNO₂ and NaOH mixtures

There are few studies of the solubility of NaNO₂ in the NaNO₂–Na₂O–H₂O system in the literature. One such study details the solubility of NaNO₂ in NaOH solutions at 20 and 25 °C, but no data above room temperature was collected,²⁹ and other studies of NaNO₂ solubility in NaOH solutions at elevated temperatures were in multicomponent systems containing significant amounts of sodium nitrate (NaNO₃), tetrasodium ethylenediaminetetraacetate, trisodium citrate, sodium phosphate, sodium carbonate, and sodium sulfate.³⁰ Therefore in this work, the solubility of NaNO₂ was determined to close the identified knowledge gap associated with the NaNO₂–Na₂O–H₂O system at temperatures greater than 25 °C. An experiment matrix was prepared with three variables: temperature and the concentrations of NaOH and NaNO₂ (Table 1). The equilibrium concentration of NaNO₂ in solutions containing a range of NaOH concentrations at 27, 40, 60 and 80 °C is shown in Fig. 1 and Table 1.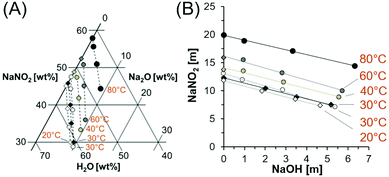

Fig. 1 Compositions of saturated solutions in the NaNO₂–Na₂O–H₂O system. (A) The datapoints from this study in the ternary diagram are marked with circles, with colors corresponding to the temperature of the solution. Datapoints marked with diamonds are comparable literature values in mixed NaNO₂–Na₂O–H₂O systems at 20 and 30 °C and interpolated solubilities for the NaNO₂–H₂O system at 40 and 60 °C.^22,29 The dotted lines are drawn only to guide the eyes. (B) The solubility data is also depicted on cartesian coordinates with units of molality. Temperatures are denoted with one significant figure, see Tables 1 and 2 and literature references²⁹ for more precise temperature values.

As shown in Fig. 1, the solubility of NaNO₂ increases as a function of temperature and is inversely correlated with the NaOH concentration. The data compare well with prior literature trends of NaNO₂ solubility in NaOH solutions at 20 and 25 °C,²⁹ which are also shown in Fig. 1. Reported concentrations correspond to concentrations near equilibrium, as confirmed by the agreement of the solubility of NaNO₂ in water at 27 °C and 80 °C with literature values.²²Fig. 1B shows the linear dependence of NaNO₂ solubility to the concentration of added NaOH. The regressed parameters (Table 2) indicate that the slope has a relatively small temperature dependence. The near equivalent slopes in Fig. 1B, which relate the decrease in solubility of NaNO₂ as a function of NaOH, indicate that the addition of NaOH to a saturated solution of NaNO₂ will maintain the total sodium concentration, while decreasing the amount of NO₂⁻, in solution. This is consistent with the common ion effect, defined here by unity between moles of added Na-bearing salt and precipitation of an equivalent amount of a second Na-bearing salt on a mole basis.¹²

Table 2 Linear regression of NaNO₂ solubility as a function of NaOH

Temperature [°C]	Slope [unitless]	y-Intercept [m]	R ^2 [unitless]
20	−0.958	11.802	0.999
25	−0.930	12.263	0.999
28	−1.093	13.045	0.997
41	−0.924	14.102	0.987
58	−1.068	16.180	0.991
79	−0.856	19.848	0.999

---

Solubility models are available in the literature for NaNO₂–Na₂O–H₂O systems near ambient temperatures,^18,31 and a Pitzer model of this system including these datasets is currently under development. A prior Pitzer model found that no ion pair association was required for sodium hydroxide up to 11 molal NaOH concentration but an ion pair association term was included in solutions of sodium nitrite.¹⁸ Recent work by another group also employed sodium nitrite ion-pair terms in a thermodynamic model of the NaNO₂–H₂O system in order to fit the water activity of aqueous NaNO₂ solutions.³² This group inferred from their results that the ion pairs were poorly hydrated,³² which was proposed previously for large monovalent ions in aqueous solution.³³

Analysis of empirical thermodynamic models is challenging because the stability of ion pairs in thermodynamic models does not necessarily correspond to the ion pair stability evaluated by spectroscopy.³⁴ Often, the stability of ion pairs determined by spectroscopy is dependent on the spectroscopic method.³⁴ This is likely because the different spectroscopic methods probe molecular interactions at different time scales. Therefore, in this work, the molecular nature of Na⁺, NO₂⁻, OH⁻, and H₂O and the chemical environment of the individual ions were investigated across a wide range of timescales and length scales using multinuclear NMR spectroscopy, Raman spectroscopy, and X-ray total scattering.

3.2 NMR spectroscopy

Spectroscopy and diffraction were performed on solutions with a total concentration of ions greater than 24 molal, which corresponds to approximately 2.3 moles of water per mole of ion assuming complete ion dissociation. This is far less than the predicted hydration number of nitrite at dilute conditions, which is around 4–8 water molecules per nitrite ion.^14–17 These solution compositions are listed in Table 3 where the sodium nitrite concentration is determined at 27.6 °C and the solutions are composed of saturated sodium nitrite in 1, 3 and 5 m sodium hydroxide. The purpose of the spectroscopy and solution characterization is to provide a physical rational for the inclusion or omission of Na–NO₂ ion-pair formation terms in solubility models describing the NaNO₂–NaOH mixtures.

Table 3 Solution compositions and NMR line shape parameters

NaNO2 [m]	NaOH [m]	^15N maxima [ppm]	^15N fwhm [Hz]	^23Na maxima [ppm]	^23Na fwhm [Hz]
5	0	497.9	5	−0.5	16
13	0	498.8	5	−1.1	23
12	1	498.8	5	−0.8	23
10	3	499.0	5	−0.3	28
7	5	499.3	5	0.6	38

---

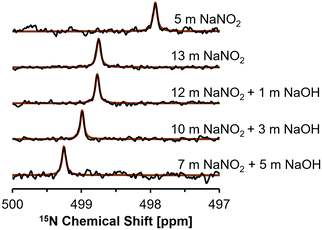
NMR studies were conducted on this subset of solutions to investigate for spectroscopic signatures of ion pairing by changes in the chemical environment of NO₂⁻ and Na⁺ ions. The ¹⁵N NMR nucleus is spin 1/2, and typically yields narrow resonances, but direct interrogation of this nucleus is usually challenging due to poor sensitivity resulting from its low relative abundance of 0.03%.³⁵ One strategy to overcome this is to use ¹⁵N enrichment, which has been used to investigate nitrite in acidic or neutral conditions,^36–38 however studies at high alkalinities are rare. High concentrations of nitrite facilitate natural abundance ¹⁵N studies, and recent studies utilized natural abundance samples to investigate photolysis products in NaOH and NaNO₂ solutions.³⁹ Here, ¹⁵N NMR spectra were acquired to investigate the effects of NaOH concentration on the shielding of ¹⁵NO₂⁻. ¹⁵N NMR spectra acquired at a field strength of 17.6 T are shown in Fig. 2.

Fig. 2 Natural abundance, single pulse, direct excitation ¹⁵N NMR results of the solutions acquired at 17.6 T at 25 °C, where the spectra are normalized to the same maximum intensity and the brown line shows the regressed Lorentzian line shape fit of the data in black.

Single pulse, direct excitation ¹⁵N NMR spectra show that the NMR resonance of NO₂⁻ appears at higher frequencies as the NaNO₂ concentration is increased from an undersaturated solution (5 m NaNO₂) to a 13 m NaNO₂ solution (Fig. 2). In saturated sodium nitrite solutions containing 1, 3, and 5 m NaOH there is a progressive increase in chemical shift from 498.8 ppm to 499.3 ppm, despite the decrease in NO₂⁻ concentration from 12 m to 7 m (Table 3). In general, the sensitivity of the ¹⁵N chemical shift in these samples can be attributed to: (i) changes in the bulk dielectric constant; (ii) hydrogen bonding, which is particularly important for these N-species that bear lone pair electrons; and (iii) ion-pairing processes, which also perturb the lone pair electrons of NO₂⁻ in the chemical environment surrounding the ion.³⁵ When comparing the ¹⁵N concentration-dependent trend of the NaNO₂ solutions with no added NaOH with studies in literature on the related nitrogen oxyanion, nitrate (NO₃⁻), it is apparent that the increase in ¹⁵N chemical shift occurs with increasing salt concentration in both salt systems.⁴⁰ However, when comparing trends it is important to note that the NaNO₃ solutions reported in literature were of lower concentration (<1 m NaNO₃).⁴⁰

Contributions to the chemical shifts arising from intermolecular changes in NO₂⁻ was also considered, but changes in N–O bond distance or ONO angle is unlikely for the following reasons. While describing crystalline NaNO₂, theoretical analysis of ¹⁵N NMR spectra for NaNO₂ demonstrated that the chemical shift is extremely sensitive to the N–O bond distance, and also exhibits sensitivity to the ONO angle.¹³ Specifically, a decrease of N–O bond distance by 2 picometers (from 1.24 to 1.22 Å) with a conserved ONO angle of 115° corresponded to an increase in the ¹⁵N chemical shift by ca. 40 ppm. In comparison, widening the ONO angle by 2° (115 to 117°) with a conserved N–O distance of 1.22 Å decreased the ¹⁵N chemical shift by ca. 20 ppm.¹³ Given the ¹⁵N chemical shift of the solutions is observed to only vary by a few ppm in the saturated solutions, the N–O bond distance and ONO angle are likely conserved in the solutions described here. Given this, the higher frequencies of ¹⁵N resonances in mixtures of NaNO₂ and NaOH is interpreted as an increase in ion–ion interactions in mixtures of NaOH and NaNO₂ beyond those in single-component NaNO₂ solutions at equivalent sodium concentrations.

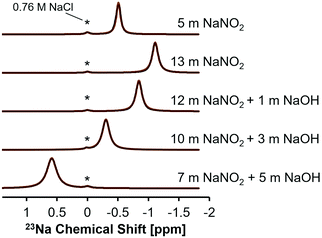
This interpretation of the ¹⁵N NMR data was further rationalized by single pulse direct excitation ²³Na NMR studies (Fig. 3). ²³Na is a 100% abundant, quadrupolar nuclei (spin 3/2) and, in electrolyte solutions, the chemical shift is sensitive both to ionic strength and anion composition.⁴⁰ In the NaNO₂–Na₂O–H₂O system studied here, the ²³Na chemical shift progressively resonates at higher frequencies in NaNO₂ solutions as the NaOH concentration increases, whereas the ²³Na chemical shift moves to lower frequencies as the concentration of NaNO₂ increases in solutions without NaOH.

Fig. 3 Single pulse, direct excitation ²³Na NMR results of the solutions acquired at 17.6 T at 25 °C, where the asterisk marks the resonance of the physically separated chemical shift reference solution of 0.76 M NaCl in H₂O, the brown line shows the sum of the regressed Lorentzian line shapes fits, and the data are shown in black. The spectra are normalized by their maximum intensity.

Increasing the concentration of NaNO₂ from 5 to 13 m corresponds with a decrease in the frequency of the ²³Na resonance from −0.5 to −1.1 ppm. Given that concentrated, water-in-salt electrolytes have too few water molecules to satisfy ion hydration numbers found under dilute conditions, these solutions can be considered as intermediates between dilute electrolytes and molten salts. Thus, analysis of the chemical shift trend can benefit from comparison to the isotropic ²³Na chemical shift of crystalline NaNO₂ and NaOH. The isotropic ²³Na chemical shift in crystalline NaNO₂ is significantly lower, corresponding with −13 ppm at room temperature and −14 ppm at 517 K in molten form, relative to 1 M NaCl in H₂O.^41,42 Conversely, anhydrous sodium hydroxide has an isotropic ²³Na chemical shift of ca. 26 ppm relative to 1 M NaCl in H₂O.⁴³ Increasing solution NaNO₂ concentrations from 5 to 13 m corresponds with the ²³Na chemical shift of those solutions approaching the negative isotropic ²³Na chemical shift of crystalline NaNO₂ (Fig. 3 and Table 3). Similarly, solutions with greater NaOH concentration approach the positive isotropic ²³Na chemical shift of crystalline NaOH. These results indicate that both the ¹⁵N and ²³Na chemical environment is changed by introducing NaOH to saturated NaNO₂ solutions and therefore the introduction of hydroxide ions likely facilitates NO₂ interactions with other solution constituents, such as Na⁺.

Additional pulsed-field gradient (PFG)-NMR experiments were used to investigate the translational motion of H-bearing species (H₂O and OH⁻) and Na⁺, respectively. While translational motion within electrolyte solutions is often studied by conductivity measurements combined with viscosity measurements using falling ball, capillary, or rotational viscometry or with dielectric relaxation to measure rotational motion,^44,45 an alternative description of translational motion across millisecond timescales can be obtained by determining diffusivity coefficients with PFG-NMR spectroscopy.

In the case of PFG-NMR, the displacement of H-bearing species (OH⁻ and H₂O) and Na⁺ ions are probed over millisecond timescales by the application of spatially-dependent, pulsed magnetic field gradients.⁴⁶ The ¹H PFG-NMR coefficients (Fig. 4), confirm that all solutions are more viscous than pure water, in which the various forms of translational mobility of protons in water lead to a diffusivity of ca. 23 EE-10 m² s⁻¹ at 25 °C.²⁵ The mobility of the protonated species in NaNO₂ and NaOH solutions is progressively reduced by addition of NaOH but, the diffusion coefficient of protonated species remains higher than that of Na⁺ across the range of concentrations. The diffusion coefficient of the Na⁺ ions in a mixture of NaNO₂ and NaOH can be compared to literature ²³Na PFG-NMR values of Na⁺ ions in NaOH solution (Fig. 4).⁴⁷

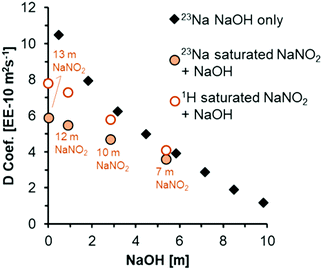Fig. 4 Diffusion coefficients acquired at 25 °C from analysis of ¹H and ²³Na PFG-NMR spectra of the solutions acquired at 17.6 T. To compare to literature values of ²³Na diffusion in concentrated NaOH solutions (dataset labeled ²³Na NaOH only),⁴⁷ the x-axis is plotted as a function of NaOH concentrations. The concentration of NaNO₂ is annotated for ¹H and ²³Na diffusion coefficients acquired from PFG-NMR for solutions composed of a mixture of NaNO₂ and NaOH.

There are only slight differences between the ²³Na diffusion coefficient of 3.9 EE-10 m² s⁻¹ in 5 m NaOH, and 3.6 EE-10 m² s⁻¹ in the mixture of 5 m NaOH with 7 m NaNO₂. Based on the ²³Na diffusion coefficient of ca. 9.8 EE-10 m² s⁻¹ in the simple solution of 5 m NaNO₂ (Table S3, ESI†), the diffusion coefficient of Na⁺ ions in NaNO₂ solutions is larger, almost double that of NaOH solutions at equivalent molalities. Since the diffusion coefficients in the mixture of 5 m NaOH and 7 m NaNO₂ are approximately equivalent to the diffusion coefficient in the absence of added NaNO₂, it is suggested that NaOH concentration influences solution rheology more strongly than NaNO₂ concentration, which is interpreted as being attributable to more extensive ion pairing in mixtures containing OH⁻ ions. Although ion specific effects on rheological properties such as viscosity and diffusivity remain an active area of research, a similar enhanced contribution of OH⁻ ions to the rheological properties relative to other ions in multicomponent electrolytes was also shown by the deviation of measured viscosities relative to those predicted by Young's rule for mixtures of electrolytes, and this is in agreement with the observations presented here.⁴⁸ Given that the chemical environment of NO₂⁻ and Na⁺ as measured by ¹⁵N and ²³Na NMR were found to be sensitive to NaOH addition to saturated NaNO₂ solutions, Raman spectra were acquired to interrogate the optical properties of the H₂O molecules, and also the NO₂⁻ and OH⁻ ions.

3.3 Raman spectroscopy

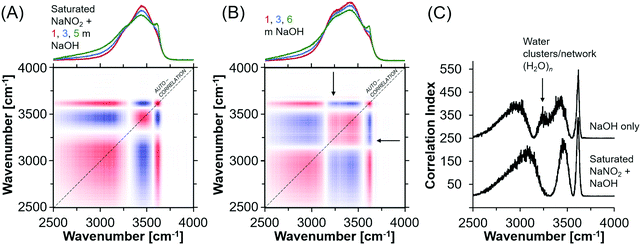
In general, oxyanion mixtures yield well resolved Raman bands sensitive to both the oxyanion composition^49,50 and the chemical environment, as characterized by ion-pairing and solvation.^51,52 Despite this, the Raman spectra exhibited very little change in the vibrational modes of the NO₂⁻ ion, which indicates that ion pairing between Na⁺ and NO₂⁻ is not strong enough to deform the geometry of the NO₂⁻ ion even in the presence of hydroxide ions. Fig. S8 (ESI†) shows the Raman spectra of the NaNO₂ solutions, where the deformation band can be fit by a single Lorentzian function. Also shown in Fig. S8 (ESI†) are the other vibrational modes of NO₂⁻, and the H₂O bending and stretching modes. The insensitivity of the nitrite vibrational bands does not indicate that there are no NO₂⁻ ions in the first coordination shell of Na⁺. This is because splitting of the deformation band does not occur even in solid NaNO₂, where there is direct contact between the Na⁺ and NO₂⁻ ions.³¹ Therefore the deformation bands of nitrite within ion-aggregates, contact and solvent separated ion-pairs, in addition to as solvated ions are likely poorly resolved from each other. For example, a series of Lorentzian bands assigned to solvated ions, solvent-separated ion-pairs, and ion aggregates, or sodium nitrite solutions was used to deconvolute the single quasi-Lorentzian symmetric stretching vibration in concentrated sodium nitrate solutions.⁵³

Given the insensitivity of the NO₂⁻ vibrational modes to ion pairing, further analysis focused on the OH⁻ bending region of the Raman spectra. In particular, the H₂O stretching mode is sensitive to the addition of NaOH and the relatively sharp band appearing ca. 3600 cm⁻¹ and broad band near 3000 cm⁻¹ are attributed to the solvated hydroxides [(OH⁻)·nH₂O].²⁰ Importantly, the OH stretching region is composed of many overlapping bands, leading to non-unique fitting results with Lorentzian deconvolutions. Therefore, synchronous autocorrelation Raman spectra of the OH⁻ stretching region were acquired using the NaOH concentration as the perturbation variable. Analysis of synchronous autocorrelation Raman spectra is particularly useful for improving resolution of overlapping bands in crowded spectra,⁵⁴ and the analysis was supplemented by comparison to additional solutions prepared with comparable NaOH concentrations without NaNO₂. These solutions are 1, 3, and 6 m NaOH in H₂O.

The synchronous correlation Raman spectra and corresponding autocorrelation function (Fig. 5) indicate that while the hydroxide peak near 3600 cm⁻¹ does not vary between the two sets of solutions, there are discernable differences between the correlation index around 3250 cm⁻¹ (filled arrow), which is a feature of the OH stretching region assigned to a network of water.^20,55,56 This difference is apparent but less obvious in the traditional Raman spectra. Specifically, the water network vibrational modes are absent in concentrated NaNO₂ and NaOH solutions. There are also shifts in the band energies at 3500 and 3000 cm⁻¹, both of which are shifted to higher wavenumbers, and those bands are assigned to H₂O with an incomplete tetrahedral network, such as small clusters of H₂O, and to solvated hydroxide ions, respectively.⁵⁷ Given that these differences indicate a perturbed solution structure at the molecular level in concentrated NaNO₂ and NaOH solutions, X-ray total scattering measurements were performed to further describe the chemical environment of the ions and solvating water.

Fig. 5 Synchronous correlation Raman spectra of (A) the subset of NaOH solutions saturated with NaNO₂ and (B) the solutions prepared only with addition of NaOH to water. Red denotes a positive correlation index and blue denotes a negative correlation index. The x-axis projection shows the baseline corrected spectra, where the units of the y-axis are arbitrary units. (C) The synchronous autocorrelation spectra are shown, where the series are vertically offset from each other, and the feature attributed to water clusters and network formation in the absence of saturated NaNO₂ is marked with an arrow.

3.4 X-ray total scattering measurements

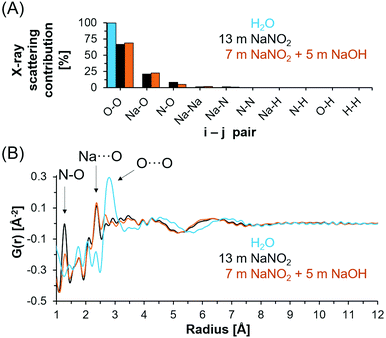
X-ray total scattering and PDF analysis was performed to complement the spectroscopic techniques employed to investigate the chemical environment of NO₂⁻, Na⁺ and H-bearing species in the NaNO₂–Na₂O–H₂O system. X-ray total scattering analysis is inherently insensitive to hydrogen and instead measures N, Na and O correlations. Based on the electron density of each element and the stoichiometry of the solution, the X-ray scattering contributions of each i–j pair can be calculated (Fig. 6A). The relative contribution of i–j pairs indicates that intra and intermolecular O–O bonds dominate the scattering signal for both deionized water and saturated solutions of NaNO₂, both with and without NaOH.

Fig. 6 High energy X-ray scattering contributions and X-ray PDF results. (A) Calculated i–j pairwise X-ray scattering contributions, which includes both intramolecular and intermolecular pairs and (B) X-ray PDF of select solutions following subtraction in reciprocal space of an air-filled Kapton capillary.

In Fig. 6B, the X-ray PDFs of deionized water, 5 m NaOH with 7 m NaNO₂ and 13 m NaNO₂ are shown. In deionized water, the tetrahedral structure of the water network is apparent from the broad O⋯O distances at 4.3 Å along with nearest neighbor O⋯O atom pairs near 2.8 Å.²¹ A reduction in both O⋯O correlations is observed when comparing deionized water with saturated NaNO₂ and saturated NaNO₂ with 5 m NaOH. This reduction in O⋯O correlation length is generally consistent with theoretical analysis of neutron diffraction experimental data of concentrated NaOH solutions.⁵⁸

In addition, the X-ray PDF shows well resolved intramolecular (covalent) N–O bonds in NO₂⁻ at 1.2 Å with additional features attributed to intramolecular ONO correlations observed at ∼2.1 Å. The lack of change in the N–O correlation distance between samples is consistent with the few ppm shifts in ¹⁵N NMR spectra and insensitivity of the vibrational modes of the nitrite ion. Features of the Na⁺ solvation shell occur at approximately 2.3 Å, and include both Na⋯OH₂ and Na⋯OH in hydroxide bearing solutions.^59,60 The radial distance of the sodium solvation shell is consistent with prior ab initio molecular dynamics simulations of concentrated NaOH, in which an ensemble of ion cluster species was related to their individual X-ray PDF features at similar distances of 2.2–2.3 Å.²¹ Further comparison of scattering from solutions of 13 m NaNO₂ and solutions of 7 m NaNO₂ with 5 m NaOH indicates significantly more order in the solution containing OH⁻ ions at distances greater than 3 Å. Specifically, the O⋯O peak observed at 2.8 Å in bulk water is significantly reduced in intensity and the maxima of the first long range oscillation O⋯O is reduced from 4.3 Å to 3.5 Å. This is interpreted as arising from the disruption of water's hydrogen bond network and the consequent collapse of the second neighboring hydration shell due to the ion solvation and association interactions. The correlations at distances greater than 3.5 Å in the concentrated electrolytes is then attributed to predominantly O⋯O correlations in hydrated ion networks, and these correlations occur at shorter distances in solutions containing NaOH and NaNO₂⁻. The long-range order of the saturated solutions is distinct from simulated X-ray PDFs of crystalline NaNO₂, NaOH·H₂O, and NaOH polymorphs as shown in Fig. S10–S11 in the ESI.†

4. Conclusions

This study aimed to improve prediction of ion pairing processes, solution rheology properties, and ultimately the solubilities of NaNO₂ in highly alkaline NaOH-containing aqueous solutions. Despite the ability for solubility to be modeled with only formalism of very weak Na⁺–nitrite ion pairs, the spectroscopy in this work indicates that the addition of NaOH perturbs the chemical environment of water, sodium, and nitrite compared to pure NaNO₂ solutions of comparable amounts of sodium. The change in the chemical environment around water is shown directly by relatively large changes in the OH stretching region. In addition to the changes in the vibrational properties of H₂O, ²³Na and ¹⁵N NMR shows that shielding of ²³Na⁺ and of ¹⁵NO₂⁻ are sensitive to NaOH concentration, with the chemical shift of both species increasing to higher frequencies as a function of NaOH concentration. NaOH concentration also significantly influences the rheological properties of the solution, progressively reducing the diffusion of Na- and H-bearing species. Analysis of X-ray PDF data indicated a reduction in length of O⋯O correlations in saturated nitrite solutions relative to deionized water. The reduction in O⋯O correlation length was greater for lower concentrations (7 m) of NaNO₂ in the presence of NaOH, than for higher concentrations (13 m) of NaNO₂ in H₂O.

While further work in related electrolytes is underway to better link the absence of fundamental vibrations of the water networks in the OH⁻ stretching region to changes in long range O⋯O correlations obtained via analysis of X-ray PDF, the presence of this more ordered structure in concentrated electrolytes with NaOH correlates with less diffusion of H-bearing species and Na⁺ on millisecond timescales, and with the disappearance of the vibrational mode corresponding to H₂O clusters in autocorrelation Raman spectra. The greater change in the chemical environment of H₂O in mixed NaOH–NaNO₂ systems relative to solutions with only NaNO₂ is shown in X-ray PDF from the greater compaction of the long range O⋯O correlations, although this observation is convoluted with the other long range O⋯O correlations beyond that of H₂O, such as those including contributions from oxygen correlations between NO₂⁻ and OH⁻. The results indicate that there is greater ion pairing in mixtures of concentrated NaNO₂ and NaOH than in comparable solutions with only NaNO₂. These studies, pairing solubility and spectroscopy to elucidate molecular-scale speciation of significant ions in multicomponent electrolyte mixtures of relevance to flue gas treatment and radioactive waste processing, generate new knowledge of solution processes that can reduce the technical risks associated with unit operations.

Conflicts of interest

The authors whose names are listed immediately below certify that they have NO affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers’ bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript. Trent R. Graham, Mateusz Dembowski, Hsiu-Wen Wang, Sebastian T. Mergelsberg, Emily T. Nienhuis, Jacob G. Reynolds, Calvin H. Delegard, Yihui Wei, Michelle Snyder, Ian I. Leavy, Steven R. Baum, Matthew S. Fountain, Sue B. Clark, Kevin M. Rosso, and Carolyn I. Pearce.

Acknowledgements

NMR spectroscopy, Raman spectroscopy, scanning electron microscopy, powder X-ray diffraction, and high-energy X-ray PDF were supported by IDREAM (Interfacial Dynamics in Radioactive Environments and Materials), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES). The solubility experiments were conducted in support of the River Protection Project (RPP) Integrated Flowsheet group to identify and close flowsheet model and operations gaps and realize opportunities to reduce the waste treatment mission cost, schedule, and technical risk, funded by Washington River Protection Solutions. NMR, SEM, pXRD, and Raman spectroscopy were performed using facilities at the Environmental Molecular Science Laboratory (EMSL, grid.436923.9), a DOE Office of Science User Facility sponsored by the Office of Biological and Environmental Research at Pacific Northwest National Laboratory (PNNL). PNNL is a multi-program national laboratory operated for DOE by Battelle Memorial Institute operating under Contract No. DE AC05-76RL0-1830. This project used resources of the Advanced Photon Source, a U.S. DOE Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357, where data acquisition was performed at beam line 11-ID-B. Construction of the ternary diagram utilized Triplot (v 1.4).⁶¹

References

1. S. M. Chalanchi, I. Alkorta, J. Elguero and D. Quiñonero, Hydrogen Bond versus Halogen Bond in Cation–Cation Complexes: Effect of the Solvent, ChemPhysChem, 2017, 18, 3462–3468,  DOI:10.1002/cphc.201700819.
2. I. Mata, E. Molins, I. Alkorta and E. Espinosa, The paradox of hydrogen-bonded anion–anion aggregates in oxoanions: A fundamental electrostatic problem explained in terms of electrophilic-nucleophilic interactions, J. Phys. Chem. A, 2015, 199, 183–194,  DOI:10.1021/jp510198g.
3. D. Marx, A. Chandra and M. E. Tuckerman, Aqueous basic solutions: Hydroxide solvation, structural diffusion, and comparison to the hydrated proton, Chem. Rev., 2010, 110, 2174–2216,  DOI:10.1021/cr900233f.
4. M. E. Tuckerman, D. Marx and M. Parrinello, The nature and transport mechanism of hydrated hydroxide ions in aqueous solution, Nature, 2002, 417, 925–929,  DOI:10.1038/nature00797.
5. M. Hellström, M. Ceriotti and J. Behler, Nuclear Quantum Effects in Sodium Hydroxide Solutions from Neural Network Molecular Dynamics Simulations, J. Phys. Chem. B, 2018, 122, 10158–10171,  DOI:10.1021/acs.jpcb.8b06433.
6. N. J. Suchak, K. R. Jethani and J. B. Joshi, Absorption of Nitrogen Oxides in Alkaline Solutions: Selective Manufacture of Sodium Nitrite, Ind. Eng. Chem. Res., 1990, 29, 1492–1502,  DOI:10.1021/ie00103a059.
7. R. A. Peterson, E. C. Buck, J. Chun, R. C. Daniel, D. L. Herting, E. S. Ilton, G. J. Lumetta and S. B. Clark, Review of the Scientific Understanding of Radioactive Waste at the U.S. DOE Hanford Site, Environ. Sci. Technol., 2018, 52, 381–396,  DOI:10.1021/acs.est.7b04077.
8. D. T. Hobbs, Caustic recovery from alkaline nuclear waste by an electrochemical separation process, Sep. Purif. Technol., 1999, 15, 239–253,  DOI:10.1016/S1383-5866(98)00105-1.
9. P. Bénézeth, S. Hilic and D. A. Palmer, The Solubilities of Gibbsite and Bayerite Below 100 °C in Near Neutral to Basic Solutions, J. Solution Chem., 2016, 45, 1288–1302,  DOI:10.1007/s10953-016-0470-1.
10. M. Dembowski, M. M. Snyder, C. H. Delegard, J. G. Reynolds, T. R. Graham, H.-W. Wang, I. I. Leavy, S. R. Baum, O. Qafoku, M. S. Fountain, K. M. Rosso, S. B. Clark and C. I. Pearce, Ion–ion interactions enhance aluminum solubility in alkaline suspensions of nano-gibbsite (α-Al(OH)₃) with sodium nitrite/nitrate, Phys. Chem. Chem. Phys., 2020, 8, 4368–4378,  10.1039/C9CP05856G.
11. J. Addai-Mensah, J. Li, S. Rosencrance and W. Wilmarth, Solubility of amorphous sodium aluminosilicate and zeolite a crystals in caustic and nitrate/nitrite-rich caustic aluminate liquors, J. Chem. Eng. Data, 2004, 49, 1682–1687,  DOI:10.1021/je049889f.
12. J. G. Reynolds, Salt Solubilities in Aqueous Solutions of NaNO₃, NaNO₂, NaCl, and NaOH: A Hofmeister-like Series for Understanding Alkaline Nuclear Waste, ACS Omega, 2018, 3, 15149–15157,  DOI:10.1021/acsomega.8b02052.
13. P. J. Barrie, C. J. Groombridge, J. Mason and E. A. Moore, Nitrogen-15 nuclear magnetic shielding tensors in nitrite and nitrate ion. Experimental and theoretical determinations, Chem. Phys. Lett., 1994, 219, 491–496,  DOI:10.1016/0009-2614(94)00111-1.
14. S. Yadav and A. Chandra, Solvation Shell of the Nitrite Ion in Water: An Ab Initio Molecular Dynamics Study, J. Phys. Chem. B, 2020, 124, 7194–7204,  DOI:10.1021/acs.jpcb.0c02221.
15. S. Vchirawongkwin, C. Kritayakornupong, A. Tongraar and V. Vchirawongkwin, Hydration properties determining the reactivity of nitrite in aqueous solution, Dalton Trans., 2014, 32, 12164–12174,  10.1039/c4dt00273c.
16. Y. Kameda, H. Arakawa, K. Hangai and O. Uemura, The Structure around the Nitrite Ion in Concentrated Aqueous Solutions, Bull. Chem. Soc. Jpn., 1992, 65, 2154–2156,  DOI:10.1246/bcsj.65.2154.
17. R. M. Cordeiro, M. Yusupov, J. Razzokov and A. Bogaerts, Parametrization and Molecular Dynamics Simulations of Nitrogen Oxyanions and Oxyacids for Applications in Atmospheric and Biomolecular Sciences, J. Phys. Chem. B, 2020, 124, 1082–1089,  DOI:10.1021/acs.jpcb.9b08172.
18. J. G. Reynolds, R. Carter and A. R. Felmy, A Pitzer interaction model for the NaNO₃-NaNO₂-NaOH-H₂O system from 0 to 100 °C, Ind. Eng. Chem. Res., 2015, 54, 3062–3070,  DOI:10.1021/acs.iecr.5b00016.
19. A. M. Hyde, S. L. Zultanski, J. H. Waldman, Y. L. Zhong, M. Shevlin and F. Peng, General Principles and Strategies for Salting-Out Informed by the Hofmeister Series, Org. Process Res. Dev., 2017, 21, 1355–1370,  DOI:10.1021/acs.oprd.7b00197.
20. M. Moskovits and K. H. Michaelian, Alkali Hydroxide Ion Pairs. A Raman study, J. Am. Chem. Soc., 1980, 102, 2209–2215,  DOI:10.1021/ja00527a010.
21. D. Semrouni, H. W. Wang, S. B. Clark, C. I. Pearce, K. Page, G. Schenter, D. J. Wesolowski, A. G. Stack and A. E. Clark, Resolving local configurational contributions to X-ray and neutron radial distribution functions within solutions of concentrated electrolytes-a case study of concentrated NaOH, Phys. Chem. Chem. Phys., 2019, 13, 6828–6838,  10.1039/c8cp06802j.
22. E. Washburn, International Critical Tables of Numerical Data, Physics, Chemistry and Technology, New York, New York, 1928.
23. D. S. Raiford, C. L. Fisk and E. D. Becker, Calibration of methanol and ethylene glycol nuclear magnetic resonance thermometers, Anal. Chem., 1979, 51, 2050–2051,  DOI:10.1021/ac50048a040.
24. I. Yavari and J. D. Roberts, Nitrogen-15 Nuclear Magnetic Resonance Spectroscopy. Carbodiimides, J. Org. Chem., 1978, 43, 4689–4693,  DOI:10.1021/jo00419a001.
25. P. T. Callaghan, M. A. Le Gros and D. N. Pinder, The measurement of diffusion using deuterium pulsed field gradient nuclear magnetic resonance, J. Chem. Phys., 1983, 79, 6372–6381,  DOI:10.1063/1.445745.
26. A. Hoeher, S. Mergelsberg, O. J. Borkiewicz, P. M. Dove and F. Marc Michel, A new method for in situ structural investigations of nano-sized amorphous and crystalline materials using mixed-flow reactors, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 758–765,  DOI:10.1107/S2053273319008623.
27. B. H. Toby and R. B. Von Dreele, GSAS-II: The genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549,  DOI:10.1107/S0021889813003531.
28. P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, PDFgetX3: A rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions, J. Appl. Crystallogr., 2013, 46, 560–566,  DOI:10.1107/S0021889813005190.
29. V. F. Plekhotkin and L. P. Bobrovskaya, Russ. J. Inorg. Chem., 1970, 15, 842–844.
30. D. A. Reynolds and D. L. Herting, Solubilities of sodium nitrate, sodium nitrite, and sodium aluminate in simulated nuclear waste, Richland, WA, 1984.
31. R. K. Toghiani, V. A. Phillips, L. T. Smith and J. S. Lindner, Solubility in the Na + SO₄ + NO₃ and Na + SO₄ + NO₂ systems in water and in sodium hydroxide solutions, J. Chem. Eng. Data, 2008, 53, 798–804,  DOI:10.1021/je700666t.
32. A. A. Zavitsas, Ideal thermodynamic behaviors of aqueous electrolyte solutions at very high concentrations, Chem. Phys. Lett., 2020, 759, 137941,  DOI:10.1016/j.cplett.2020.137941.
33. R. M. Diamond, The aqueous solution behavior of large univalent ions. A new type of ion-pairing 1a, J. Phys. Chem., 1963, 67, 2513–2517,  DOI:10.1021/j100806a002.
34. G. Hefter, When spectroscopy fails: The measurement of ion pairing, Pure Appl. Chem., 2006, 78, 1571–1586,  DOI:10.1351/pac200678081571.
35. G. A. Webb and M. Witanowski, Nitrogen NMR and molecular interations, Proc. Indian Acad. Sci., 1985, 94, 241–290.
36. G. K. Surya Prakash, L. Heiliger and G. A. Olah, ¹⁵N NMR Spectroscopic investigation of nitrous and nitric acids in sulfuric acid solutions of varying acidities, Inorg. Chem., 1990, 29, 4965–4968,  DOI:10.1021/ic00349a027.
37. R. L. Van Etten and J. M. Risley, ¹⁸O-Isotope-Induced Shifts in ¹⁵N Nuclear Magnetic Resonance Spectroscopy. 1. Isotope Shift in Nitrite and Its Application to the Study of Oxygen Exchange of Sodium [¹⁵N,¹⁸O₂]Nitrite, J. Am. Chem. Soc., 1981, 103, 5633–5636,  DOI:10.1021/ja00409a002.
38. K. A. Thorn and M. A. Mikita, Nitrite Fixation by Humic Substances Nitrogen-15 Nuclear Magnetic Resonance Evidence for Potential Intermediates in Chemodenitrification, Soil Sci. Soc. Am. J., 2000, 64, 568–582,  DOI:10.2136/sssaj2000.642568x.
39. E. D. Walter, K. C. Schwarz, S. A. Kumar, Y. Chen, M. Sassi, Z. Wang and K. M. Rosso, Evolution of Radicals from the Photolysis of High Ionic Strength Alkaline Nitrite Solutions, J. Phys. Chem. A, 2020, 124, 3019–3025,  DOI:10.1021/acs.jpca.9b11438.
40. W. Makulski, Multinuclear Magnetic Resonance Study of Sodium Salts in Water Solutions, Magnetochemistry, 2019, 5, 1–12,  DOI:10.3390/magnetochemistry5040068.
41. S. V. Baryshnikov, E. V. Stukova, E. V. Charnaya, C. Tien, M. K. Lee, W. Böhlmann and D. Michel, Dielectric and NMR studies of nanoporous matrices loaded with sodium nitrite, Phys. Solid State, 2006, 48, 593–599,  DOI:10.1134/S1063783406030292.
42. A. G. Gorchakov, P. S. Sedykh, E. V. Charnaya, S. V. Baryshnikov, C. Tien and D. Michel, MAS NMR studies of nanoporous matrices filled with sodium nitrite, Phys. Solid State, 2009, 51, 2152–2156,  DOI:10.1134/S1063783409100266.
43. L. Gao, J. Chen, Y. Liu, Y. Yamauchi, Z. Huang and X. Kong, Revealing the chemistry of an anode-passivating electrolyte salt for high rate and stable sodium metal batteries, J. Mater. Chem. A, 2018, 6, 12012–12017,  10.1039/c8ta03436b.
44. R. Buchner, P. Sipos, G. Hefter and P. M. May, Dielectric relaxation of concentrated alkaline aluminate solutions, J. Phys. Chem. A, 2002, 28, 6527–6532,  DOI:10.1021/jp0143589.
45. P. C. Ho, D. A. Palmer and R. H. Wood, Conductivity measurements of dilute aqueous LiOH, NaOH, and KOH solutions to high temperatures and pressures using a flow-through cell, J. Phys. Chem. B, 2000, 104, 12084–12089,  DOI:10.1021/jp000845x.
46. T. R. Graham, K. S. Han, M. Dembowski, A. J. Krzysko, X. Zhang, J. Hu, S. B. Clark, A. E. Clark, G. K. Schenter, C. I. Pearce and K. M. Rosso, ²⁷Al Pulsed Field Gradient, Diffusion-NMR Spectroscopy of Solvation Dynamics and Ion Pairing in Alkaline Aluminate Solutions, J. Phys. Chem. B, 2018, 122, 10907–10912,  DOI:10.1021/acs.jpcb.8b10145.
47. J. Mitchell, Can sodium NMR provide more than a tracer for brine in petrophysics?, J. Pet. Sci. Eng., 2016, 146, 360–368,  DOI:10.1016/j.petrol.2016.05.035.
48. G. Hefter, P. M. May, P. Sipos and A. Stanley, Viscosities of concentrated electrolyte solutions, J. Mol. Liq., 2003, 103–104, 261–273,  DOI:10.1016/S0167-7322(02)00145-9.
49. F. Zapata, F. Ortega-Ojeda, C. García-Ruiz and M. González-Herráez, Selective monitoring of oxyanion mixtures by a flow system with Raman detection, Sensors, 2018, 18, 1–10,  DOI:10.3390/s18072196.
50. G. M. Maggioni, S. Kocevska, M. A. Grover and R. W. Rousseau, Analysis of Multicomponent Ionic Mixtures Using Blind Source Separation: A Processing Case Study, Ind. Eng. Chem. Res., 2019, 58, 22640–22651,  DOI:10.1021/acs.iecr.9b03214.
51. J. B. Gill, Solute-Solute Interactions in Liquid Ammonia Solutions: A Vibrational Spectroscopic View, Pure Appl. Chem., 1981, 53, 1365–1381,  DOI:10.1351/pac198153071365.
52. A. G. Miller and J. A. Macklin, Matrix Effects on the Raman Analytical Lines of Oxyanions, Anal. Chem., 1980, 52, 807–812,  DOI:10.1021/ac50056a009.
53. R. L. Frost and D. W. James, Ion–ion–solvent interactions in solution. Part 3.—Aqueous solutions of sodium nitrate, J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases, 1982, 78, 3223–3234,  10.1039/F19827803223.
54. L. Ma, V. Sikirzhytski, Z. Hong, I. K. Lednev and S. A. Asher, Insight into Resolution Enhancement in Generalized Two-Dimensional Correlation Spectroscopy, Appl. Spectrosc., 2013, 67, 283–290,  DOI:10.1366/11-06541.
55. J. Stefanski, C. Schmidt and S. Jahn, Aqueous sodium hydroxide (NaOH) solutions at high pressure and temperature: insights from in situ Raman spectroscopy and ab initio molecular dynamics simulations, Phys. Chem. Chem. Phys., 2018, 20, 21629–21639,  10.1039/C8CP00376A.
56. J.-B. Brubach, A. Mermet, A. Filabozzi, A. Gerschel and P. Roy, Signatures of the hydrogen bonding in the infrared bands of water, J. Chem. Phys., 2005, 122, 184509,  DOI:10.1063/1.1894929.
57. J. Stefanski, C. Schmidt and S. Jahn, Aqueous sodium hydroxide (NaOH) solutions at high pressure and temperature: insights from in situ Raman spectroscopy and ab initio molecular dynamics simulations, Phys. Chem. Chem. Phys., 2018, 20, 21629–21639,  10.1039/C8CP00376A.
58. A. Botti, F. Bruni, S. Imberti, M. A. Ricci and A. K. Soper, Ions in water: The microscopic structure of concentrated NaOH solutions, J. Chem. Phys., 2004, 120, 10154–10162,  DOI:10.1063/1.1705572.
59. T. Megyes, S. Bálint, T. Grósz, T. Radnai, I. Bakó and P. Sipos, The structure of aqueous sodium hydroxide solutions: A combined solution X-ray diffraction and simulation study, J. Chem. Phys., 2008, 128, 1–12,  DOI:10.1063/1.2821956.
60. T. Radnai, P. M. May, G. T. Hefter and P. Sipos, Structure of Aqueous Sodium Aluminate Solutions: A Solution X-ray Diffraction Study, J. Phys. Chem. A, 1998, 102, 7841–7850,  DOI:10.1021/jp981244x.
61. D. J. Graham and N. G. Midgley, Graphical Representation of Particle Shape Using Triangular Diagrams: An Excel Spreadsheet Method, Earth Surf. Processes Landforms, 2000, 25, 1473–1477 , DOI: 10.1002/1096-9837(200012)25:13<1473::AID-ESP158>3.0.CO;2-C.

---

Footnote

† Electronic supplementary information (ESI) available: Additional results from solubility studies approaching equilibrium concentrations from oversaturation and undersaturation, additional experimental results from studies comparing concentrations acquired with filtering versus sampling of supernatant, additional Raman results of nitrite vibrational bands including discussion of relevant literature, and tabulated ¹H and ²³Na diffusion coefficients. See DOI: 10.1039/d0cp04799f

---