The effects of Feshbach resonance on spectral shifts in photoassociation of Cs atoms
Yuqing
Li
 ab,
Xiaofeng
Wang
a,
Jizhou
Wu
ab,
Xiaofeng
Wang
a,
Jizhou
Wu
 ab,
Guosheng
Feng
a,
Wenliang
Liu
ab,
Vladimir B.
Sovkov
ab,
Guosheng
Feng
a,
Wenliang
Liu
ab,
Vladimir B.
Sovkov
 c,
Jie
Ma
*ab,
Bimalendu
Deb
*d,
Liantuan
Xiao
ab and
Suotang
Jia
ab
c,
Jie
Ma
*ab,
Bimalendu
Deb
*d,
Liantuan
Xiao
ab and
Suotang
Jia
ab
aState Key Laboratory of Quantum Optics and Quantum Optics Devices, Institude of Laser Spectroscopy, College of Physics and Electronics Engineering, Shanxi University, Taiyuan 030006, China. E-mail: mj@sxu.edu.cn
bCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, Shanxi 030006, China
cSt. Petersburg State University, 7/9 Universitetskaya nab., St. Petersburg 199034, Russia
dSchool of Physical Sciences, Indian Association for the Cultivation of Science, Jadavpur, Kolkata 700032, India. E-mail: msbd@iacs.res.in
First published on 28th November 2020
Abstract
We study the effects of magnetic Feshbach resonance on the shifts in photoassociation (PA) spectra of ultracold Cs atoms. A series of atom loss spectra show a linear variation of the frequency shift with the PA laser intensity at different magnetic fields near the d-wave Feshbach resonance of optically trapped Cs atoms. The magnetic field-dependence of the slope of the shift on the PA laser intensity exhibits a dispersive change near the Feshbach resonance. The theoretical formula derived from a model based on Fano resonance fits well with the experimental data. Using a model rectangular potential with tunable well depth and applying the Franck–Condon principle, we obtain numerical results, which are found to be largely in disagreement with the experimental findings.
I. Introduction
Precision atom loss spectra in the photoassociation (PA) of ultracold atoms are important for determining the long-range coefficients of molecular potentials,1,2 producing ultracold molecules3 and altering the scattering length of colliding atoms by optical Feshbach resonance.4 In PA spectra, the frequency of the resonance transition from ground atoms to excited molecules displays a shift with the increasing PA laser intensity, as experimentally demonstrated in the context of formation of molecules from atoms, including ultracold helium molecules 4He2,5 ultracold alkali molecule samples such as 7Li2,6–8 Na29 and Cs2,10,11 and the heteronuclear molecule NaCs.12 The PA spectral shifts have been calculated using the multichannel scattering theory.13,14Magnetically controlled collisions of ultracold atoms in the presence of a PA laser have attracted increasing research interests.15–17 It has been experimentally shown that the frequency shift in the PA spectra of 7Li atoms has a strong dependence on the magnetic field near Feshbach resonance (FR) with an anomalous blueshift for the fields just below the FR.8 The slope of the spectral shift in the PA of Cs atoms exhibits a linear variation when the magnetic field is tuned far away from FR.11 A large number of studies have reported on the direct measurements of the spectral shift.5–7,9,10,12 The precise control over the spectral shift by a magnetic field will provide more accurate information about the ultracold molecular rovibrational levels, opening a new perspective in the applications of PA spectral shifts.18
In this paper, the frequency shifts in PA spectra of optically trapped Cs atoms are measured in the vicinity of a d-wave Feshbach resonance. The variation of the slope of the PA spectral shift shows a dispersive curve with the magnetic field near the FR. This result shows that the FR can be used to control the spectral shift of PA. The experimental data can be well fitted by using the theoretical expression derived from the model of Fano resonance. Besides, the data are also analyzed by using the Franck–Condon principle involving a single channel rectangular potential with the tunable well depth. We find that the model based on Franck–Condon principle can not satisfactorily explain the observed data, while the model with Fano resonance shows quite good agreement with the experimental results.
II. Experimental setup
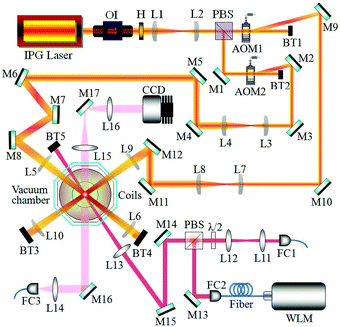
Cold Cs atoms are collected in a vapor-loaded magneto-optical trap (MOT), and then the compressed MOT and optical molasses are successively implemented to increase atomic density and lower atomic temperature. Afterwards, three-dimensional (3D) degenerated Raman sideband cooling (DRSC) is performed to spin polarize the atoms in the desired F = 3, mF = 3 state and to lower the temperature of atoms to ∼1.7 μK. The low temperature obtained by the 3D DRSC prevents endothermic inelastic two-body collisions of Cs atoms in the F = 3, mF = 3 state. As shown in Fig. 1, two horizontally crossing 1064 nm laser beams with the powers of 7 and 7.2 W at an angle of 90° are weakly focused on the trap center with the beam waists of ∼230 and 240 μm to form a crossed dipole trap, respectively. The cooled atomic sample is efficiently loaded into the optical dipole trap by applying the method of magnetic levitation, which is implemented by the application of both the magnetic field gradient of 31.3 G cm−1 and the bias field of 75 G.19 The magnetic field gradient and the bias field are produced by a pair of quadrupole coils in an anti-Helmholtz configuration and a pair of bias coils in a Helmholtz configuration, respectively. We observe that the system approaches thermal equilibrium quite rapidly by the 500 ms plain evaporation at the bias field of 75 G.To study the effect of the FR on the spectral shifts, the PA laser with a beam waist of 150 μm is switched on to illuminate the atomic cloud for 90 ms after tuning the magnetic field to the vicinity of the d-wave FR. The PA laser is provided by a widely tunable Ti:sapphire laser system and the frequency jitter is less than 500 kHz by locking to its self-reference cavity. The absolute frequency of PA laser is measured by a high-precision wavelength meter (HighFinesse WSU), which is repeatedly calibrated against the resonance transition frequency of the repumping laser at the beginning of each experimental cycle. The frequency of the PA laser is tuned near the resonance of the v = 17, J = 0 molecular rovibrational level of the Cs2 0−g pure long-range state below the 6S1/2 + 6P3/2 dissociation limit.20 PA resonances can be detected, because PA causes a reduction in atom number when excited molecules spontaneously decay into the ground molecules and the pairs of hot atoms that escape the trap. Before switching on the PA laser, the atomic density and temperature are 4 × 1011 cm−3 and 3.5 μK, respectively.
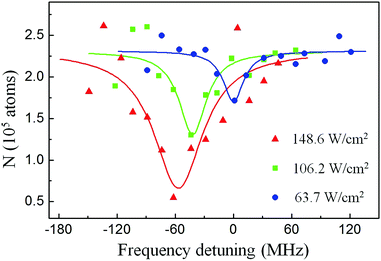
Fig. 2 shows the PA spectra, which are obtained by scanning PA laser frequency near 11681.9300 cm−1 with the PA laser intensities of IPA = 63.7 W cm−2 (blue circles), 106.2 W cm−2 (green squares) and 148.6 W cm−2 (red triangles) at the magnetic field of 47.731(5) G. The atom loss reaches maximum when the frequency of the PA laser is tuned on the resonance transition to the excited molecules from the colliding ground atoms. The location of PA resonance at a particular intensity is determined by fitting the resonance lineshape to a Lorentzian curve. As the PA laser intensity is varied, the resonance position has an IPA-induced shift. Additionally, the data clearly show that the increase of PA laser intensity induces the broadening of the linewidth of the PA resonance spectrum.
III. Experimental results
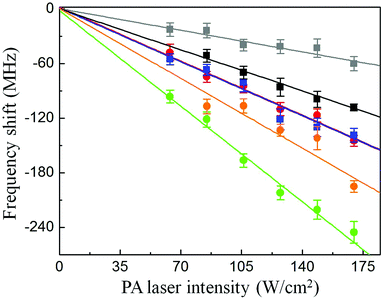
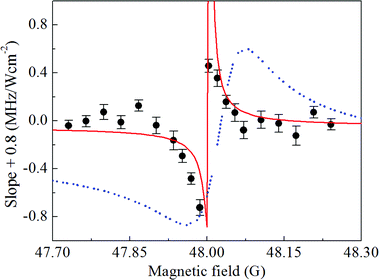
For ultracold Cs atoms in the F = 3, mF = 3 state, there is a narrow d-wave FR, which alters the collisions of ultracold atoms by coupling the scattering atomic state to a bound d-wave molecular state.21–23 The magnetic field is ramped from 75 G to the different final values near the FR within 30 ms. In Fig. 3, the variation of spectral shift with the intensity of PA laser is shown for six different magnetic fields, which are symmetrically chosen on both sides of the FR location. For a good signal-to-noise ratio of PA spectroscopy, we chose the PA laser intensity in the range from 63.7 W cm−2 to 169.9 W cm−2. The observed linear dependence of spectral shift on the laser intensity is consistent with the calculation based on the multichannel scattering theory.6,14 For the magnetic fields away from the FR, the spectral shifts show the variations with a similar slope. However, as the magnetic field increases and passes through the resonance location of the FR, the frequency shift shows a great change with the PA laser intensity. In other words, the FR has a great effect on the PA spectral shift.The slope of spectral shift near the FR is derived by linear fitting of the variation of spectral shift with the PA laser intensity at different magnetic fields around the FR. As shown in Fig. 4, the FR has a significant effect on the slope of the frequency shift in PA spectra of ultracold Cs atoms. Far from the FR, the slope becomes a constant, which equals −0.8 MHz (W cm−2)−1. As the magnetic field approaches the FR location from relatively low field, the amplitude of the slope of spectral shift below the FR becomes large. The amplitude of the slope of spectral shift decreases above the FR. In the experiment, the errors are mainly from the fitting error in determining PA resonant transition frequency, the error in measuring PA laser frequency, the systematic uncertainty induced by the fluctuation of the number of atoms prepared in each experimental cycle and the small uncertainties in controlling the magnetic field near the FR and measuring the intensity of PA laser.
IV. Model simulation
Here we discuss the model, which is used to explain the obtained experimental data. This model is based on an adaptation of Fano's theory24,25 of continuum-bound coupled systems to the ultracold atom-molecule coupled systems. Though the model was presented in earlier works,26 for the sake of completeness, we discuss the salient features of the model and reproduce some of the analytical results. In this model of Fano resonance, we consider that multiple bound states can be coupled to a continuum of states and there are bound–bound couplings as well. All the couplings including magnetic and optical couplings are treated on an equal footing, making the model suitable for nonperturbative calculations, which can result in a nonlinear Fano effect.27Following Fano's theory, one can obtain a continuum-bound dressed state known as Fano state by diagonalizing the Hamiltonian involving one bound state interacting with a continuum of states. The well-known Beutler-Fano asymmetric spectral profile arises when optical dipole transitions occur between this Fano state and another bound state. In the linear Fano effect, the optical dipole coupling is treated perturbatively. As in Fano's theory, the theory of Feshbach resonance provides exact diagonalization of a continuum-bound coupled system. While Feshbach resonance normally refers to a scattering resonance, Fano resonance is a spectral resonance. However, both resonances can be treated with a unified approach of multichannel quantum scattering theory.28
In the present case, we have two bound states coupled to the continuum of atomic scattering states. In the absence of PA laser, the external magnetic field induces Feshbach resonance modeled by a simplified two-channel model in which one is open and the other is a closed channel. A quasi-bound state is supported by the closed channel. The PA laser couples both the quasi-bound state and the open-channel continuum states to an excited molecular bound state. We exactly diagonalize the system. The detailed calculations are given in the following derivation of spectral shift using the Fano model. The solution to the model provides analytical expression for nonperturbative spectral shift ΔE = Sq(B,E)ΓPA where ΓPA is the linewidth of PA spectrum in the absence of magnetic field and is a linear function of the laser intensity IPA and
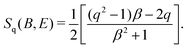 | (1) |
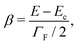 | (2) |
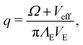 | (3) |
Our theory shows that the slope of the spectral shift is proportional to Sq(B,E) of eqn (1). The proportional constant is denoted by C = ΓPA/IPA. At a fixed temperature which determines the collision energy E, Sq(B,E) mainly depends on the magnetic field. So we fit this theoretical formula of S = CSq(B,E) with the parameters q and C. For the best fitting, we find C = 9.58 ± 0.75 MHz (W cm−2)−1 and q = −0.42 ± 0.02. For the ultracold Cs atoms in the F = 3, mF = 3 state, the parameters of the d-wave FR such as B0, δμ, Γf and Bc are given in ref. 22 and 23. As shown on the red line in Fig. 4, the fitting shows good agreement with experimental results. Since we found −1 < q < 0 from the fitting, we have Ω < |Veff| according to the definition of q as given in eqn (3). Under the present physical conditions, this implies that the continuum-mediated bound–bound coupling Veff dominates over the direct bound–bound coupling Ω as Veff < 0 at low energy. The slope clearly shows the dispersive behavior, which can be described by the profile function Sq(B,E). The variation of magnetic field leads to the variation of β, that is, the energy detuning due to the magnetic tuning of the open and closed channel thresholds. We here remark that our theory is a simplified model calculation.
Compared to the PA near a broad s-wave Feshbach resonance in ref. 8, our case shows the effect of a narrow d-wave Feshbach resonance on the PA. We use a different theoretical model, which is based on Fano resonance to explain our data and our theoretical result shows good agreement with experimental data. In ref. 8, the continuum-bound coupling dominates over the bound–bound coupling with the Fano asymmetry parameter |q| > 1,29 while in our work the bound–bound coupling is significant and comparable with the continuum-bound coupling because in our work q is found to be −1 < q < 1.
Additionally, we verify whether the magnetic field-dependence of the slope of spectral shifts can be analyzed in terms of the Franck–Condon (FC) principle6,14 and also the effect of external magnetic fields on the scattering wavefunction of colliding atom-pairs. According to the FC principle, PA predominately occurs at the Condon radius of RC ≃ 25.203 Å.20 A theoretical model with the depth-adjustable square potential is used to acquire the influence of external magnetic fields on the atomic scattering wavefunction in a short interatomic separation, in which the effective PA occurs.30 As a result, the magnetic field-induced variation of the scattering length of colliding atoms22 predominantly alters the atomic scattering wavefunction in the short interatomic separation (see the calculation based on FC principle). Although the calculation exhibits a tunable slope for the spectral shift near the FR, there is a large disagreement between the blue theoretical curve and the experimental data, as shown in Fig. 4. Previously the FC calculation with a depth-adjustable square potential was used to explain the variation of PA rate with the magnetic field far away from the FR location. However, the comparison of the theoretical calculation based on the FC principle to experimental data indicates that the FC calculation with a depth-adjustable square potential can not capture the physics when two coupled transitions are considered. The reasonable agreement between the Fano theory and the experimental data illustrates the coupling between the continuum-bound and bound–bound transitions.
V. Derivation of spectral shift using Fano model
The derivation of the shift of eqn (3) follows the same method as given in ref. 26. But, for the sake of completeness we here briefly discuss the method of derivation. Near the d-wave FR of Cs atoms, the atomic scattering state |E〉 is coupled to a quasi-bound d-wave molecular state |bc〉 by the second order spin–orbit and spin–spin dipole interactions,21,23 which are collectively modeled by the coupling parameter VE. When the frequency of the PA laser is resonantly tuned to the transition from the state |E〉 to the state |be〉, the same PA laser induces an effective coupling between the states |E〉 and |bc〉. Veff is the continuum-mediated coupling between the bound states. To explain the measured atom loss, an artificial channel |E′′〉art is introduced to mimic the decay of the excited molecular state |be〉14,31 with the decay constant γ.The Hamiltonian H0 is given as
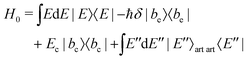 | (4) |
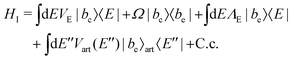 | (5) |
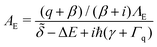 | (6) |
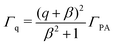 | (7) |
![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) = ħδ − E0shift with E0shift being the PA shift of |be〉 in the absence of a magnetic field. Here ΔE = Sq(B,E)ΓPA are the magnetic field- and energy-dependent spectral shifts where Sq(B,E) is given by eqn (1). The Fano asymmetry parameter q can be obtained as a fitting parameter. In the experiment, we have a certain colliding energy determined by the atomic temperature and so the Sq(B,E) is mainly dependent on the magnetic field.
= ħδ − E0shift with E0shift being the PA shift of |be〉 in the absence of a magnetic field. Here ΔE = Sq(B,E)ΓPA are the magnetic field- and energy-dependent spectral shifts where Sq(B,E) is given by eqn (1). The Fano asymmetry parameter q can be obtained as a fitting parameter. In the experiment, we have a certain colliding energy determined by the atomic temperature and so the Sq(B,E) is mainly dependent on the magnetic field.
VI. Calculation based on the Franck–Condon principle
We also carry out calculations based on the FC principle to see whether this can explain the observed slope of PA spectral shift. Here we use the theoretical expression of the frequency shift as given in ref. 6 and 14. The frequency shift is proportional to the product of the PA laser intensity and the overlap integral between the wavefunctions of the atomic scattering state and the excited molecular state. According to the FC principle, PA mainly occurs at the Condon radius, and the slope of frequency shift is proportional to the FC overlap integral 〈be|E〉. The wavefunction |be〉 is calculated using the potential curve of excited Cs molecules.32 About the atomic wavefunction, we need to achieve the theoretical dependence of atomic wavefunction on the magnetic field near the FR. Multichannel calculations of magnetic FR, using up-to-date and high-precision molecular potential data from Cs2, require at least 24 hyperfine channels to obtain agreement with the observed magnetic FR.21 Instead of the extremely complicated multichannel calculations, we use a single-channel square potential with the tunable potential depth, which was proposed and tested in ref. 22 and 33, to simulate the scattering behavior of Cs atoms near the d-wave FR. Considering the threshold behavior of atomic scattering state under the van der Waals interaction, the size of the square well, which is used to calculate the continuum state |E〉, is taken to be the mean scattering length ā = 95.7a0.22,30 For r > ā, the scattering wavefunction is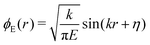 , where
, where 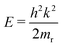 is the collision energy. The scattering phase shift η is given by cot
is the collision energy. The scattering phase shift η is given by cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η = −1/(ak) + r0k/2, where a is the s-wave scattering length and r0 is the effective range. For r ≤ ā, ϕE(r) = A
η = −1/(ak) + r0k/2, where a is the s-wave scattering length and r0 is the effective range. For r ≤ ā, ϕE(r) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(k′r), where the parameters A and k′ can be derived using the scattering boundary condition at r = ā. When the magnetic field is tuned near the FR, the wavefunction ϕE(r) for r > ā varies with η. According to the requirement of the continuous boundary condition, the wavefunction for r ≤ ā changes with the variable k′, which is dependent on the depth of the square potential. As a result, the slope of frequency shift shows a variation near the FR. The theoretical calculation of the slope of frequency shift is shown in Fig. 4. Compared to the theoretical result based on the model of Fano resonance, there is a large disagreement between the theory based on the FC principle and the experiment.
sin(k′r), where the parameters A and k′ can be derived using the scattering boundary condition at r = ā. When the magnetic field is tuned near the FR, the wavefunction ϕE(r) for r > ā varies with η. According to the requirement of the continuous boundary condition, the wavefunction for r ≤ ā changes with the variable k′, which is dependent on the depth of the square potential. As a result, the slope of frequency shift shows a variation near the FR. The theoretical calculation of the slope of frequency shift is shown in Fig. 4. Compared to the theoretical result based on the model of Fano resonance, there is a large disagreement between the theory based on the FC principle and the experiment.
VII. Conclusions
In conclusion, we have investigated the effect of the d-wave magnetic FR on the spectral shift for the PA resonance of optically trapped ultracold Cs atoms. The slope of spectral shift to the PA laser intensity shows a dispersive variation as a function of magnetic field across the FR location. The theoretical formula derived from the model of Fano resonance is fitted on the observed dependence of the slope on the magnetic field near the FR, and the theory shows good agreement with the experiment. A model calculation based on FC principle was also carried out by using a single channel rectangular potential with a tunable well depth, which is introduced to acquire the influence of the magnetic field on the atomic scattering wavefunction in the effective PA range. Compared to the model of Fano resonance, the calculation based on the FC principle seems to be inadequate to account for the experimental data. A particularly interesting aspect of our study is the narrow dispersive behavior of the slope of PA spectral shift, which can be well explained by the model of nonlinear or non-perturbative Fano resonance. The d-wave Feshbach resonance used for our study has a very narrow width. Accordingly, Fano dip, which occurs due to quantum interference-induced dark resonance, has a narrow width.34 Since Fano minimum implies reduction of absorption or enhanced transparency, it might be an interesting study to explore the effects of dispersive slope of PA spectral shift on the propagation of light through Fano-resonant ultracold atomic medium.Author contributions
Y. L., X. W., G. F., and W. L. peformed the experiments. J. W., V. S. and J. M. supervised the experimental work. B. D. contributed theoretical analysis. All authors contributed to the analysis and discussions of the results and the preparation of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The National Key Research and Development Program of China (Grant No. 2017YFA0304203), the National Natural Science Foundation of China (Grant No. 61722507, 61675121, 61705123, and 61901249), PCSIRT (No. IRT17R70), STIP, the Program for the Outstanding Innovative Teams of Higher Learning Institutions of Shanxi (OIT), the Applied Basic Research Project of Shanxi Province, China (Grant No. 201901D211191, and 201901D211188), the collaborative grant by RFBR and NNSF of China (No. 2053-53025), and the Open Research Fund Program of the State Key Laboratory of Low-Dimensional Quantum Physics, are acknowledged.Notes and references
- M. Pichler, H. Chen and W. C. Stwalley, J. Chem. Phys., 2004, 121, 1796 CrossRef CAS PubMed.
- J. Ma, Y. Q. Li, W. L. Liu, P. Chen, G. S. Feng, C. Y. Hu, J. Z. Wu, L. T. Xiao and S. T. Jia, Opt. Express, 2014, 22, 3756 Search PubMed.
- K.-K. Ni, S. Ospelkaus, M. H. G. de Miranda, A. Pe'er, B. Neyenhuis, J. J. Zirbel, S. Kotochigova, P. S. Julienne, D. S. Jin and J. Ye, Science, 2014, 322, 231 CrossRef PubMed.
- M. Theis, G. Thalhammer, K. Winkler, M. Hellwig, G. Ruff, R. Grimm and J. H. Denschlag, Phys. Rev. Lett., 2004, 93, 123001 CrossRef CAS PubMed.
- M. Portier, S. Moal, J. Kim, M. Leduc, C. CohenTannoudji and O. Dulieu, J. Phys. B., 2006, 39, S881 CrossRef CAS.
- J. M. Gerton, B. J. Frew and R. G. Hulet, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 053410 CrossRef.
- I. D. Prodan, M. Pichler, M. Junker, R. G. Hulet and J. L. Bohn, Phys. Rev. Lett., 2003, 91, 080402 CrossRef PubMed.
- M. Junker, D. Dries, C. Welford, J. Hitchcock, Y. P. Chen and R. G. Hulet, Phys. Rev. Lett., 2008, 101, 060406 CrossRef CAS PubMed.
- C. McKenzie, J. H. Denschlag, H. Häffner, A. Browaeys, L. E. E. de Araujo, F. K. Fatemi, K. M. Jones, J. E. Simsarian, D. Cho, A. Simoni, E. Tiesinga, P. S. Julienne, K. Helmerson, P. D. Lett, S. L. Rolston and W. D. Phillips, Phys. Rev. Lett., 2002, 88, 120403 CrossRef CAS PubMed.
- J. Z. Wu, Z. H. Ji, Y. C. Zhang, L. R. Wang, Y. T. Zhao, J. Ma, L. T. Xiao and S. T. Jia, Opt. Lett., 2011, 36, 2038 CrossRef CAS PubMed.
- Y. Q. Li, G. S. Feng, W. L. Liu, J. Z. Wu, J. Ma, L. T. Xiao and S. T. Jia, Opt. Lett., 2015, 40, 2241 CrossRef CAS PubMed.
- W. L. Liu, X. F. Wang, J. Z. Wu, X. L. Su, S. Wang, V. B. Sovkov, J. Ma, L. T. Xiao and S. T. Jia, Phys. Rev. A: At., Mol., Opt. Phys., 2017, 96, 022504 CrossRef.
- P. O. Fedichev, Y. Kagan, G. V. Shlyapnikov and J. T. M. Walraven, Phys. Rev. Lett., 1996, 77, 2913 CrossRef CAS PubMed.
- J. L. Bohn and P. S. Julienne, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 414 CrossRef CAS.
- B. L. Tolra, N. Hoang, B. T'Jampens, N. Vanhaecke, C. Drag, A. Crubellier, D. Comparat and P. Pillet, Europhys. Lett., 2003, 64, 171 CrossRef CAS.
- P. Pellegrini, M. Gacesa and R. Côté, Phys. Rev. Lett., 2008, 101, 053201 CrossRef PubMed.
- S. P. Krzyzewski, T. G. Akin, J. Dizikes, M. A. Morrison and E. R. I. Abraham, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 062714 CrossRef.
- K. M. Jones, E. Tiesinga, P. D. Lett and P. S. Julienne, Rev. Mod. Phys., 2006, 78, 483 CrossRef CAS.
- Y. Q. Li, G. S. Feng, R. D. Xu, X. F. Wang, J. Z. Wu, G. Chen, X. C. Dai, J. Ma, L. T. Xiao and S. T. Jia, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 053604 CrossRef.
- A. Fioretti, D. Comparat, C. Drag, C. Amiot, O. Dulieua, F. Masnou-Seeuws and P. Pillet, Eur. Phys. J. D, 1999, 5, 389 CrossRef CAS.
- C. Chin, V. Vuletić, A. J. Kerman, S. Chu, E. Tiesinga, P. J. Leo and C. J. Williams, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 032701 CrossRef.
- A. D. Lange, K. Pilch, A. Prantner, F. Ferlaino, B. Engeser, H.-C. Nägerl, R. Grimm and C. Chin, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 013622 CrossRef.
- C. Chin, R. Grimm, P. S. Julienne and E. Tiesinga, Rev. Mod. Phys., 2010, 82, 1225 CrossRef CAS.
- U. Fano, Phys. Rev., 1961, 124, 1866 CrossRef CAS.
- A. E. Miroshnichenko, S. Flach and Y. S. Kivshar, Rev. Mod. Phys., 2010, 82, 2257 CrossRef CAS.
- B. Deb, J. Phys. B., 2010, 43, 085208 CrossRef.
- M. Kroner, A. O. Govorov, S. Remi, B. Biedermann, S. Seidl, A. Badolato, P. M. Petroff, W. Zhang, R. Barbour, B. D. Gerardot, R. J. Warburton and K. Karrai, Nature, 2008, 451, 311 CrossRef CAS PubMed.
- J. P. Connerade, Highly excited atoms, Cambridge University Press, 1998 Search PubMed.
- B. Deb and G. S. Agarwal, J. Phys. B., 2009, 42, 215203 CrossRef.
- G. S. Feng, Y. Q. Li, X. F. Wang, J. Z. Wu, V. B. Sovkov, J. Ma, L. T. Xiao and S. T. Jia, Sci. Rep., 2017, 7, 13677 CrossRef PubMed.
- Y. Q. Li, G. S. Feng, J. Z. Wu, J. Ma, B. Deb, A. Pal, L. T. Xiao and S. T. Jia, Phys. Rev. A: At., Mol., Opt. Phys., 2019, 99, 022702 CrossRef CAS.
- N. Bouloufa, A. Crubellier and O. Dulieu, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 052501 CrossRef.
- C. Chin, arXiv:cond-mat., 2005, 0506313.
- S. Moal, M. Portier, J. Kim, J. Dugué, U. D. Rapol, M. Leduc and C. Cohen-Tannoudji, Phys. Rev. Lett., 2006, 96, 023203 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2021 |