Quantification of cation–cation, anion–anion and cation–anion correlations in Li salt/glyme mixtures by combining very-low-frequency impedance spectroscopy with diffusion and electrophoretic NMR†
Received
26th November 2020
, Accepted 2nd December 2020
First published on 17th December 2020
Introduction
The liquid electrolytes used in state-of-the art lithium-ion batteries are based on volatile organic carbonates. Due to their volatility, the electrolytes are flammable, leading to serious safety concerns. Consequently, there is strong interest in using alternative classes of highly concentrated electrolytes with low vapor pressure, such as solvent-in-salt electrolytes and electrolytes based on ionic liquids (ILs).1–10 ILs can be separated into four groups, namely aprotic, protic, inorganic and solvate (or chelate) ILs.11 For battery applications, most studies have focused on aprotic and solvate ILs. In the case of aprotic ILs, lithium salts have to be added in order to generate Li+ ion conductivity. However, the addition of lithium salts often leads to high viscosities and to low Li+ transport numbers.12,13 Furthermore, lithium transference numbers are often low and have even been reported to exhibit a negative sign.14–16 This was found in electrophoretic NMR (eNMR) studies and attributed to a vehicular transport mechanism of lithium in negatively charged lithium–anion complexes.
On the other hand, lower viscosities and higher Li+ transport numbers have been achieved for solvate ionic liquids (SILs), which consist of equimolar mixtures of a lithium salt with glymes. The glyme molecules form strong complexes with the Li+ ions.17,18 Examples are equimolar mixtures of triglyme (G3) or tetraglyme (G4) with lithium bis(trifluoromethanesulfonyl)imide (LiTFSI)19,20 or lithium bis(fluoro-sulfonyl)imide (LiFSI).13,21 These mixtures exhibit ionic conductivities in the range of 10−3 S cm−1 and Li+ transport numbers, derived from the diffusion coefficients of the ions, around 0.5.13,22 Recent eNMR measurements showed virtually identical mobilities of Li+ ions and G4 molecules, pointing to the migration of complex [Li(G4)]+ cations instead of single Li+ ions.23 SILs are thus prototypic highly concentrated electrolytes with properties similar to conventional ionic liquids.17 Thus they also exhibit strong interionic interactions, which lead to strongly correlated movements of the ions.22–25 This implies directional correlations between the movements of distinct cations, between the movements of distinct anions, and also between the movements of cations and anions. Correlations can be positive, if distinct ions move preferentially into the same direction, or negative, if distinct ions move preferentially into opposite directions.26 These ion correlations exert a strong influence on the transport properties of the electrolytes in batteries. One important implication of ion correlations is that diffusion-based Li+ transport numbers measured by pulsed-field gradient NMR (PFG-NMR)13 are distinct from mobility-based Li+ transference numbers measured by electrophoretic NMR (eNMR)14,15 and also distinct from Li+ transference numbers under anion-blocking conditions measured by potentiostatic polarization or very-low-frequency impedance spectroscopy (VLF-IS).24,27 By independently employing either eNMR or VLF-IS, we have recently demonstrated the role of ion correlations. For example, we have shown that the application of SILs in lithium-ion batteries suffers from very low Li+ transference numbers under anion-blocking conditions caused by anticorrelated movements of cations and anions.22,24 The large role of cation–anion anticorrelations is also shown by the decrease of the Haven ratio with increasing Li salt to glyme ratio. Interestingly, when comparing Li salt/G4 mixtures containing either lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) or lithium tetrafluoroborate (LiBF4), anticorrelations between the complex cation and the anion are most dominant at high salt concentrations. This fact clearly points at a dominant role of momentum conservation.23 MD simulations predicted that the addition of glyme to SILs weakens the cation–anion anticorrelations leading to higher Li+ transference numbers under anion-blocking conditions.24 So far, while techniques such as VLF-IS and eNMR have been helpful to qualitatively elucidate the role of ion correlations, either of them separately does not deliver sufficient information for a full description of ion correlations, for example in the framework of Onsager coefficients.
In this framework, the ionic conductivity of a binary electrolyte containing a monovalent salt can be written as:
| | | σion = σself+ + σdistinct++ + σself− + σdistinct−− − 2σ+− | (1) |
The self-parts
σself+ and
σself− are related to the self-diffusion coefficients of cations,
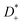
, and anions,
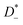
, respectively:
| | 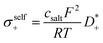 | (2) |
| | 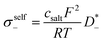 | (3) |
Here,
csalt denotes the salt concentration, while
F,
R and
T are the Faraday constant, the ideal gas constant and the temperature, respectively. The transport coefficients
σdistinct++,
σdistinct−− and
σ+− account for cation–cation, anion–anion, and cation–anion correlations.
26 For a complete description of the ion transport properties of a binary electrolyte, the five transport coefficients on the right-hand side of
eqn (1) and the thermodynamic factor
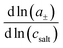
, with
a± denoting the cations’ and anions’ mean activity, are needed. Consequently, six measurable quantities are required in order to derive the five coefficients and the thermodynamic factor. In this way, information about cation–cation, anion–anion and cation–anion correlations and their impact on the transport properties can be obtained. To our knowledge, there is only a single example in the literature with such a complete experimental information.
25 On the other hand, a small number of recent MD studies on ion correlations in concentrated electrolytes has been published.
28–30 Harris showed that under the assumption of strict ion momentum conservation in a solvent-free electrolyte with only a single type of cations and anions, measurements of the ionic conductivity and of the self-diffusion coefficients of the ions are sufficient for elucidating all ion correlations.
31,32 However, this approach cannot be applied to electrolytes with more than two ionic species or to solvent-containing electrolytes, such as solvent-in-salt electrolytes and solvate ionic liquids.
In this paper, we combine, for the first time, very-low-frequency impedance spectroscopy on symmetrical Li|electrolyte|Li cells with pulsed-field gradient NMR and electrophoretic NMR, and we show that this is a powerful combination for the quantification of the ion transport coefficients in eqn (1), fully based on experimental data. We use the ion correlations in SILs and in diluted Li salt/glyme mixtures as a showcase to demonstrate the potential of this methodological combination. Complete experimental information is obtained for LiFSI/glyme mixtures with molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5, and 1
1.5, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in VLF-IS, PFG-NMR and eNMR, while using our previous VLF-IS results for the LiFSI/G4 1
2 in VLF-IS, PFG-NMR and eNMR, while using our previous VLF-IS results for the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture.22 In addition, for comparison, we use previously published eNMR and VLF-IS data of a LiTFSI/G4 1
1 mixture.22 In addition, for comparison, we use previously published eNMR and VLF-IS data of a LiTFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture.23,27 In this way, we analyse both the influence of salt concentration and anion type on the ion correlations. We discuss the impact of different correlations (cation–cation, anion–anion, and cation–anion) on the Li+ transference number under anion-blocking conditions, on the mobility-based Li+ transference number, and on the Haven ratio. In order to rationalize the experimental findings, we derive and discuss linear response theory expressions for a binary electrolyte with dipole fluctuations and center-of-mass fluctuations.
1 mixture.23,27 In this way, we analyse both the influence of salt concentration and anion type on the ion correlations. We discuss the impact of different correlations (cation–cation, anion–anion, and cation–anion) on the Li+ transference number under anion-blocking conditions, on the mobility-based Li+ transference number, and on the Haven ratio. In order to rationalize the experimental findings, we derive and discuss linear response theory expressions for a binary electrolyte with dipole fluctuations and center-of-mass fluctuations.
Experimental section
Electrolyte preparation
The chemical structures of the different electrolytes studied in this work are shown in Fig. 1. They were prepared in an argon inert gas atmosphere with water and oxygen content below 1 ppm. The electrolyte compositions listed in Table 1 were prepared by solving lithium bis(fluorosulfonyl)imide (LiFSI) (Fluorochem. Ltd, battery grade) and lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) (Sigma-Aldrich, 99.95% trace metals basis), respectively, in tetraglyme (G4) (Sigma-Aldrich, >99%) while stirring overnight, until a homogeneous mixture was obtained. Prior to use, the G4 was flushed with dry argon, degassed carefully in vacuum and dried over molecular sieve (3 Å) for at least 24 h.
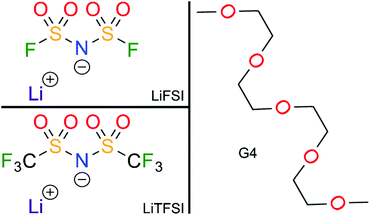 |
| | Fig. 1 Chemical structures of the different electrolyte components studied in this work. | |
Table 1 Composition of the different electrolytes studied in this work
| LiFSI/G4 |
Ratio |
x
G4
|
x
salt
|
c
salt/mol l−1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 |
0.50 |
0.50 |
3.23 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
0.667 |
0.60 |
0.40 |
2.38 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.5 |
0.67 |
0.33 |
1.72 |
| LiTFSI/G4 |
Ratio |
x
G4
|
x
salt
|
c
salt/mol l−1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1 |
0.50 |
0.50 |
2.75 |
Total ionic conductivity
Ionic conductivity measurements were carried out using a closed TSC70 liquid sample cell with a Microcell HC cell stand (rhd instruments). The cell consists of a PEEK crucible, which was filled with 70 μl of the electrolyte, and of two polished platinum electrodes. The impedance measurements were conducted in a frequency range from 100 kHz to 1 Hz with an ac voltage of 10 mVrms by means of an Alpha-A impedance analyzer (Novocontrol Technologies) equipped with a ZG2 interface. The temperature was varied from 10 °C to 80 °C by means of an Eurotherm 2416 temperature controller (accuracy ±0.1 K). The cell constant of the liquid sample cell was determined using a 0.1 mol l−1 KCl standard solution (HANNA instruments). The software RelaxIS (rhd instruments) was used for fitting the impedance spectra with an equivalent circuit consisting of a resistance in series with a constant phase element (CPE). The resistance describes the bulk ion transport in the electrolyte, while the CPE accounts for electrode polarization.
Very-low-frequency impedance spectroscopy
In order to study Li+ ion transport under anion-blocking conditions, very-low-frequency impedance spectroscopic (VLF-IS) measurements on symmetrical Li|electrolyte|Li cells27 were carried out. The distance between the two parallel lithium electrodes with 12 mm diameter was varied between 100 μm and 350 μm. The cells were assembled in a glovebox under inert gas atmosphere and were subsequently closed airtight. Then the cells were connected to an Alpha-A impedance analyzer (Novocontrol Technologies) equipped with a ZG2 interface and a Quatro Cryosystem.
Before carrying out the very-low-frequency impedance measurements, the stability of the Li|electrolyte interface was monitored by continuous impedance measurements at 30 °C in a frequency range from 1 MHz to 0.1 Hz over several hours. After achieving a stable interfacial impedance, the very-low-frequency impedance measurements were carried out at 30 °C in a frequency range from 1 MHz to 100 μHz using an ac voltage of 2 mVrms. The measurements were done at different distances between the Li electrodes. The software RelaxIS (rhd instruments) was used for the fitting of the impedance data.
Diffusion NMR and electrophoretic NMR
All NMR investigations were performed on a 400 MHz AVANCE III HD NMR spectrometer (Bruker) equipped a gradient probe head (Bruker, Diff50), providing a maximum gradient strength of 30 T m−1. Selective radiofrequency inserts for 1H, 7Li and 19F were used with 5 mm sample tubes. A power source designated for eNMR experiments was employed to provide electric field pulses (P&L Scientific, Sweden). An in-house designed eNMR probe33 was equipped with palladium wire electrodes at a distance of 22 mm. For each measurement 19 mm long gas chromatography capillaries (fused silica capillary tubing, Polymicro Technologies, ID = 250 μm, OD = 350 μm), dried at 100 °C under high vacuum overnight, were placed between the electrodes before filling the probe with the liquid sample under argon atmosphere. They serve to prevent convection during the experiment.
Diffusion experiments were conducted at 30 °C using a stimulated echo pulse sequence with magnetic field gradient pulses.34 The observation time Δ was 100 ms, and the applied gradient duration δ was set depending on the observed nucleus (1 ms for 1H and 19F, and 3 ms for 7Li). The gradient pulse strength was increased, until the observed NMR signal was attenuated by at least two orders of magnitude. The self-diffusion coefficients of G4, Li+, and FSI− were determined from 1H, 7Li, and 19F PFG-NMR measurements via the Stejskal–Tanner equation,34,35 with the gyromagnetic ratio γ, the applied magnetic field gradient pulse strength G, the magnetic field gradient pulse duration δ, the observation time Δ, and the self-diffusion coefficient 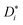 , see eqn (4).
, see eqn (4).
| | 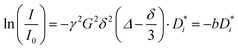 | (4) |
The eNMR experiments were conducted at 30 °C using a double stimulated echo pulse sequence in combination with two electric field pulses of opposite polarity and four magnetic field gradient pulses.
36 The voltage was incremented from 0 to 100 V, and the magnetic field gradient strength set to a constant value depending on the investigated sample and nucleus. The observation time
Δ was 100 ms. The gradient duration
δ was set depending on the observed nucleus (1 ms for
1H and
19F, 3 ms for
7Li). eNMR spectra were recorded at distinct voltages and the phase shifts analyzed
via spectral deconvolution using single or multiple phase-sensitive Lorentz profiles, as described earlier.
14 The electrophoretic mobility was extracted from a linear fit of the resulting phase angles against the voltage. In the following, mobility values are given as the average of the slopes of at least 3 independent experiments per sample and nucleus.
Results and discussion
Total ionic conductivities, Li+ transference numbers under anion-blocking conditions and salt diffusion coefficients
In Fig. 2a, we show an Arrhenius plot of the total ionic conductivity σion of all samples. The ionic conductivity is lowest for the LiTFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture and slightly higher for the LiFSI/G4 1
1 mixture and slightly higher for the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture. With increasing G4 content of the LiFSI/G4 mixtures, the total ionic conductivity increases.
1 mixture. With increasing G4 content of the LiFSI/G4 mixtures, the total ionic conductivity increases.
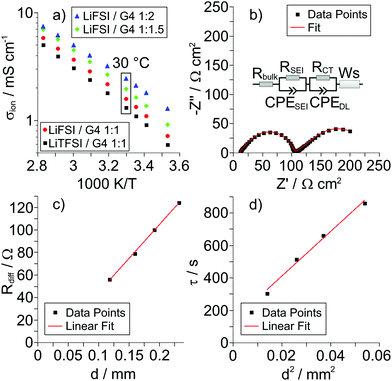 |
| | Fig. 2 (a) Arrhenius plots for the different Li salt/G4 mixtures. (b) Very-low-frequency impedance spectrum and fit for the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 mixture at 30 °C and at an electrode distance d of 0.192 mm. The inset shows the equivalent circuit used for fitting. (c) Diffusion resistance Rdiffvs. electrode distance d and (d) time constant τ vs. squared electrode distance d2 for the LiFSI/G4 1 1.5 mixture at 30 °C and at an electrode distance d of 0.192 mm. The inset shows the equivalent circuit used for fitting. (c) Diffusion resistance Rdiffvs. electrode distance d and (d) time constant τ vs. squared electrode distance d2 for the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 mixture shown in (b). 1.5 mixture shown in (b). | |
In Fig. 2b, very-low-frequency (VLF) impedance spectra of a LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 mixture between two Li electrodes with a distance of 192 μm are shown. The equivalent circuit for fitting is shown in the inset. The circuit consists of a bulk resistance Rbulk caused by the total ionic conductivity of the electrolyte, in series with two R-CPE elements accounting for the Li|electrolyte interface (impedance of solid electrolyte interphase and charge transfer impedance), in series with a Warburg-short (Ws) element describing the formation of salt diffusion layers and the stationary Li+ current under anion-blocking conditions. The Warburg-short impedance is given by:
1.5 mixture between two Li electrodes with a distance of 192 μm are shown. The equivalent circuit for fitting is shown in the inset. The circuit consists of a bulk resistance Rbulk caused by the total ionic conductivity of the electrolyte, in series with two R-CPE elements accounting for the Li|electrolyte interface (impedance of solid electrolyte interphase and charge transfer impedance), in series with a Warburg-short (Ws) element describing the formation of salt diffusion layers and the stationary Li+ current under anion-blocking conditions. The Warburg-short impedance is given by:
| | 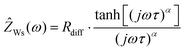 | (5) |
Here,
Rdiff denotes a diffusion resistance,
ω the angular frequency,
j the imaginary unit,
τ a characteristic time for establishing stationary salt diffusion profiles across the electrolyte, and
α is a characteristic exponent.
τ can be written as:
| | 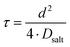 | (6) |
with
Dsalt and
d denoting the salt diffusion coefficient and the distance between the Li electrodes. In
Fig. 2c and d, we plot
Rdiffversus d and
τ versus d2, respectively. The plots verify the expected linear dependence of
Rdiff on
d and the expected quadratic dependence of
τ on
d, respectively. From the slope of the data in
Fig. 2d, the salt diffusion coefficient
Dsalt is obtained.
The Li+ transference number under anion-blocking conditions is given by:22
| | 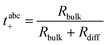 | (7) |
In Table 2, we summarize the results obtained for the total ionic conductivity σion, the Li+ transference number under anion-blocking conditions tabc+ and the salt diffusion coefficient Dsalt of all mixtures. The data for LiTFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were taken from ref. 27 and the data for LiFSI/G4 1
1 were taken from ref. 27 and the data for LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 from ref. 22, respectively.
1 from ref. 22, respectively.
Table 2 Ionic conductivities σion, lithium ion transference numbers under anion-blocking conditions tabc+ and salt diffusion coefficients Dsalt obtained at 30 °C for the different Li salt/G4 mixtures
| LiFSI/G4 |
σ
ion/mS cm−1 |
t
abc+
|
D
salt/cm2 s−1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 122 |
1.58 |
0.015 ± 0.003 |
(5.3 ± 0.5) × 10−8 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
1.95 |
0.082 ± 0.015 |
(1.8 ± 0.5) × 10−7 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2.45 |
0.091 ± 0.015 |
(4.4 ± 3.1) × 10−7 |
| LiTFSI/G4 |
σ
ion/mS cm−1 |
t
abc+
|
D
salt/cm2 s−1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127 127 |
1.31 |
0.025 ± 0.005 |
(7.0 ± 0.9) × 10−8 |
Li+ transport numbers and mobility-based Li+ transference numbers
The self-diffusion coefficients of G4, Li+, and FSI− were determined from 1H, 7Li, and 19F PFG-NMR measurements. The signal attenuation I/I0 for each NMR nucleus of LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 as an exemplary sample is shown in Fig. 3a in dependence of b. In this depiction, the slope is a direct representation of the self-diffusion coefficient
1.5 as an exemplary sample is shown in Fig. 3a in dependence of b. In this depiction, the slope is a direct representation of the self-diffusion coefficient 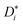 , which is evaluated according to eqn (4). As expected, we observe a monoexponential decay of the investigated NMR signals with increasing b values. This behavior indicates the fast exchange averaging of the diffusion coefficient in case of the existence of different species, such as single ions or complexes containing the observed nucleus during the observation time of 100 ms. In the case of LiFSI/G4 1
, which is evaluated according to eqn (4). As expected, we observe a monoexponential decay of the investigated NMR signals with increasing b values. This behavior indicates the fast exchange averaging of the diffusion coefficient in case of the existence of different species, such as single ions or complexes containing the observed nucleus during the observation time of 100 ms. In the case of LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, 7Li and 1H exhibit the same slope (see Fig. S1 in ESI†), and therefore the same diffusion coefficient. In the past, this behavior was attributed to the formation of a complex [Li(G4)]+ solvate cation, and is the main characteristic of solvate ionic liquids.13,17,37 With decreasing lithium to glyme ratio, G4 diffuses faster than Li+, as indicated by a steeper slope for 1H, see Fig. 3a.
1 mixture, 7Li and 1H exhibit the same slope (see Fig. S1 in ESI†), and therefore the same diffusion coefficient. In the past, this behavior was attributed to the formation of a complex [Li(G4)]+ solvate cation, and is the main characteristic of solvate ionic liquids.13,17,37 With decreasing lithium to glyme ratio, G4 diffuses faster than Li+, as indicated by a steeper slope for 1H, see Fig. 3a.
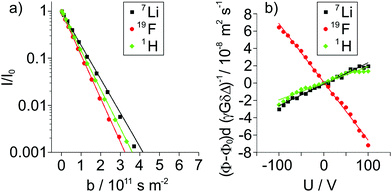 |
| | Fig. 3 (a) Signal attenuation I/I0 observed in 1H, 7Li and 19F PFG-NMR experiments and (b) voltage U dependent reduced phase shift values (ϕ − ϕ0)dγ−1G−1δ−1Δ−1 observed via1H, 7Li and 19F eNMR for the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 mixture. 1.5 mixture. | |
The electrophoretic mobilities μi were determined from the voltage-dependent phase shift ϕ − ϕ0 observed via1H, 7Li and 19F eNMR, as shown in the example in Fig. 3b. According to eqn (8), the signal phase shift is linearly depending on the applied voltage U divided by the electrode distance d, the gyromagnetic ratio γ, the applied magnetic field gradient pulse strength G, its duration δ, the observation time Δ and the mobility μLF.38,39
| | 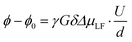 | (8) |
In order to compare eNMR measurements conducted on distinct nuclei using different experimental parameters, reduced phase shift values (
ϕ −
ϕ0)
dγ−1G−1δ−1Δ−1 are depicted in
Fig. 3b for a measurement series for an exemplary LiFSI/G4 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1.5 mixture. In this depiction, the slope represents the mobility
μLF of the observed nucleus in the laboratory reference frame (LF). As expected, the depicted eNMR results exhibit a phase shift linearly depending on the applied voltage. While the scattering of the phase shift is rather low for
1H and
19F, it is somewhat larger for
7Li, due to the lower signal-to-noise ratio of
7Li spectra, resulting from a lower value of
γ compared to
1H and
19F.
The opposite sign of the slopes of the 7Li and 19F phase shifts signifies their migration in opposite directions as a consequence of the opposite sign of charge of Li+ and FSI−. Despite G4 lacking an own nominal charge, the observed 1H phase shift values exhibit the same slope, and therefore mobility, as 7Li for the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture (see Fig. S2 in ESI†). This observation shows the migration of a complex cation [Li(G4)]+ in an electric field in the LiFSI/G4 1
1 mixture (see Fig. S2 in ESI†). This observation shows the migration of a complex cation [Li(G4)]+ in an electric field in the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, similar to the previously studied SIL systems Li(G4)TFSI and Li(G4)BF4,14,23 underlining the ionic liquid-like character of Li(G4)FSI. All resulting mobility values obtained from 1H, 7Li and 19F eNMR measurements on the LiFSI/G4 samples are given in Fig. 4 as open symbols. The overall trend is a reduction of the modulus of mobility with increasing salt concentration related to a viscosity increase. With decreasing lithium salt to glyme ratio, the fast exchange averaging over free glyme molecules exhibiting no nominal charge and glyme molecules bound to lithium leads to an average mobility of G4, which is lower than that of lithium, compare open squares and diamonds in Fig. 4. This hints at the coexistence of free glyme molecules and Li/glyme complexes in the dilute samples, which will be discussed in more detail below.
1 mixture, similar to the previously studied SIL systems Li(G4)TFSI and Li(G4)BF4,14,23 underlining the ionic liquid-like character of Li(G4)FSI. All resulting mobility values obtained from 1H, 7Li and 19F eNMR measurements on the LiFSI/G4 samples are given in Fig. 4 as open symbols. The overall trend is a reduction of the modulus of mobility with increasing salt concentration related to a viscosity increase. With decreasing lithium salt to glyme ratio, the fast exchange averaging over free glyme molecules exhibiting no nominal charge and glyme molecules bound to lithium leads to an average mobility of G4, which is lower than that of lithium, compare open squares and diamonds in Fig. 4. This hints at the coexistence of free glyme molecules and Li/glyme complexes in the dilute samples, which will be discussed in more detail below.
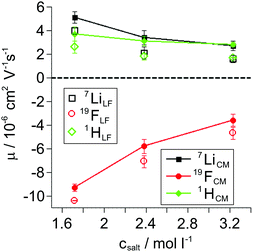 |
| | Fig. 4 Electrophoretic mobilities μ obtained from 1H, 7Li, and 19F eNMR measurements in the laboratory (LF, open symbols) and center-of-mass (CM, filled symbols) reference frames. Salt concentrations correspond to LiFSI/G4 molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1 2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5, and 1 1.5, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (from left to right). 1 (from left to right). | |
Mobilities μLF extracted from eNMR are based on drift velocities determined from the particles’ displacements in space in the laboratory reference frame (LF). During the two electric field pulses with opposite sign, the pulse sequence ensures constructive addition of the phase shifts. On the other hand, in the ideal case, the ion displacements in space during either pulse should exactly compensate, which implies a net zero drift of the center-of-mass of the whole electrolyte. In practice, the ideal compensation is often not given, possible sources of experimental imperfections could be Joule heating, gravitational effects causing differences between upper and lower electrode, or irreversible electrochemical decomposition processes at the electrodes. As a consequence, in eNMR experiments, the net drift of the center-of-mass may deviate from zero. Several methodological papers have dealt with describing and partially improving the effect of experimental imperfections.40–42 While several improvements have been achieved concerning the effects of electroosmotic flow and convection, at the current state there is still a net drift of the center-of-mass observed. Consequently, in order to minimize the influence of the experimental imperfections on our present results, we chose to impose a first order correction by transforming the mobilities to the center-of-mass reference frame (CM) according to eqn (9a) and (9b). The net drift of the center-of-mass is calculated by summing over all molecular species i in the electrolyte with ci as the molar concentration, the molar mass Mi, the respective mobility μLFi obtained from eNMR experiments, and the electrolyte density ρ.
| | 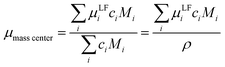 | (9a) |
| | μCMi = μLFi − μmass![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) center center | (9b) |
The mobilities in the center-of-mass reference frame
μCMi are depicted as full symbols in
Fig. 4. They differ slightly from the lab frame values, visualizing the effect of experimental imperfections, while the qualitative behavior of the different species and their concentration dependence remains the same. We note that this transformation also relates to an earlier discussion of reference frames in eNMR experiments on concentrated electrolytes, where the CM frame was suggested as an internal reference frame with the benefit of allowing comparison to simulations or other theoretical approaches which presume momentum conservation.
43 Similar to the diffusion data, upon enhancing salt concentration, the mobilities also reflect the viscosity influence, and in addition the merging of Li and glyme mobilities due to complex cation formation.
The mobilities μCMi and mobility-based lithium ion transference numbers tμ+ in the center-of-mass reference frame (see eqn (10)) as well as self-diffusion coefficients 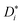 and diffusion-based lithium ion transport numbers tPFG+ (see eqn (11)) for the different electrolyte compositions compared in this work are summarized in Tables 3 and 4.
and diffusion-based lithium ion transport numbers tPFG+ (see eqn (11)) for the different electrolyte compositions compared in this work are summarized in Tables 3 and 4.
| | 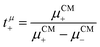 | (10) |
| | 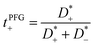 | (11) |
In the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 samples, the respective cation and glyme mobilities agree within error (see
Table 3), consistent with the formation of a complex cation [Li(G4)]
+ as the only cationic species. In the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2 sample, however, cation and glyme mobilities do not agree within error, reflecting an averaging over different glyme-containing species, possibly free glyme and complexes [Li(G4)
n]
+, with different integer values of the coordination number
n. Assuming that the species in this sample would be [Li(G4)
1]
+ complexes and free G4 with zero mobility, the resulting average glyme mobility would be
μG4 = 0.5
μ+. If on the other hand exclusively [Li(G4)
2]
+ complexes existed, the G4 mobility would be
μG4 =
μ+. Experimentally, we find
μG4 = 0.73
μ+. This points to an average coordination number
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
between 1 and 2. We will discuss the complex compositions in more detail at the end of the discussion and provide an estimate of
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
for the dilute samples.
Table 3 Center-of-mass frame based mobilities μCMi and mobility-based Li+ transference numbers tμ+ obtained at 30 °C for the different electrolyte mixtures
| LiFSI/G4 |
μ
CM+/cm2 (V s)−1 |
μ
CM−/cm2 (V s)−1 |
μ
CMG4/cm2 (V s)−1 |
t
μ
+
|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(2.7 ± 0.4) × 10−6 |
(−3.6 ± 0.5) × 10−6 |
(2.8 ± 0.2) × 10−6 |
0.43 ± 0.05 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
(3.4 ± 0.6) × 10−6 |
(−5.8 ± 0.6) × 10−6 |
(3.1 ± 0.4) × 10−6 |
0.37 ± 0.05 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
(5.1 ± 0.5) × 10−6 |
(−9.3 ± 0.3) × 10−6 |
(3.7 ± 0.6) × 10−6 |
0.36 ± 0.02 |
| LiTFSI/G4 |
μ
CM+/cm2 (V s)−1 |
μ
CM−/cm2 (V s)−1 |
μ
CMG4/cm2 (V s)−1 |
t
μ
+
|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123 123 |
(3.3 ± 0.7) × 10−6 |
(−2.4 ± 1.0) × 10−6 |
(3.0 ± 0.7) × 10−6 |
0.58 ± 0.11 |
Table 4 Self-diffusion coefficients 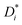 and diffusion-based Li+ transport numbers tPFG+ obtained at 30 °C for the different electrolytes
and diffusion-based Li+ transport numbers tPFG+ obtained at 30 °C for the different electrolytes
Calculation of transport coefficients from the experimental data
In a first step, we split the ionic conductivity into three Onsager coefficients:26,27| | | σion = σ++ + σ−− − 2σ+− | (12) |
In the framework of the Onsager formalism, the Li+ transference number under anion-blocking conditions and the mobility-based Li+ transference number are given by:26,27| | 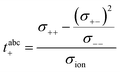 | (13) |
| | 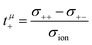 | (14) |
Solving eqn (12)–(14) for the Onsager coefficients results in:| | 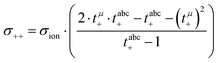 | (15) |
| | 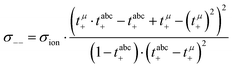 | (16) |
| | 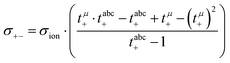 | (17) |
Furthermore, the salt diffusion coefficient can be written as:26| | 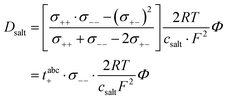 | (18) |
Thus, the thermodynamic factor 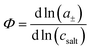 is given by:
is given by:| | 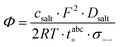 | (19) |
Finally, we split the Onsager coefficients σ++ and σ−− into their self- and distinct-parts:| | | σ++ = σdistinct++ + σself+ | (20) |
| | | σ−− = σdistinct−− + σself− | (21) |
with the self-parts obtained from eqn (2) and (3).
The obtained results are summarized in Tables 5 and 6 and are illustrated in Fig. 5. We start by comparing the diffusion-based Li+ transport numbers and the mobility-based Li+ transference numbers (Fig. 5a). In the case of LiTFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, we find tμ+ > tPFG+, while for LiFSI/G4 1
1, we find tμ+ > tPFG+, while for LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, we observe tμ+ ≲ tPFG+. In Fig. 5b, the strength of the cation–cation and anion–anion correlations is illustrated by plotting the distinct-parts of σ++ and σ−− normalized by their self-part. In the case of LiTFSI/G4 1
1, we observe tμ+ ≲ tPFG+. In Fig. 5b, the strength of the cation–cation and anion–anion correlations is illustrated by plotting the distinct-parts of σ++ and σ−− normalized by their self-part. In the case of LiTFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the cation dynamics is characterized by cation–cation anticorrelations with a ratio of σdistinct++/σself+ = −0.66, see open black square. This number implies that cation–cation anticorrelations reduce the contribution of diffusive cationic displacements to the ionic conductivity by 66%. The anion dynamics shows even stronger anticorrelations with a ratio of σdistinct−−/σself− = −0.80, see open red circle. The stronger anion–anion anticorrelations reduce the anionic contribution to the conductivity and lead to tμ+ > tPFG+. In contrast, in the case of LiFSI/G4 1
1, the cation dynamics is characterized by cation–cation anticorrelations with a ratio of σdistinct++/σself+ = −0.66, see open black square. This number implies that cation–cation anticorrelations reduce the contribution of diffusive cationic displacements to the ionic conductivity by 66%. The anion dynamics shows even stronger anticorrelations with a ratio of σdistinct−−/σself− = −0.80, see open red circle. The stronger anion–anion anticorrelations reduce the anionic contribution to the conductivity and lead to tμ+ > tPFG+. In contrast, in the case of LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the cation–cation anticorrelations are slightly stronger (σdistinct++/σself+ = −0.78) than the anion–anion anticorrelations (σdistinct−−/σself− = −0.68). This leads to tμ+ ≲ tPFG+. It is thus evident that like-ion anticorrelations are responsible for the deviations of transference numbers from transport numbers. In this context, it should be noted that the molar mass of FSI anions (M = 178 g mol−1) is lower than the molar mass of [Li(G4)]+ complex cations (M = 229 g mol−1), while the molar mass of TFSI anions (M = 280 g mol−1) is higher. Consequently, our results suggest that the respective heavier ion type shows stronger anticorrelations.
1, the cation–cation anticorrelations are slightly stronger (σdistinct++/σself+ = −0.78) than the anion–anion anticorrelations (σdistinct−−/σself− = −0.68). This leads to tμ+ ≲ tPFG+. It is thus evident that like-ion anticorrelations are responsible for the deviations of transference numbers from transport numbers. In this context, it should be noted that the molar mass of FSI anions (M = 178 g mol−1) is lower than the molar mass of [Li(G4)]+ complex cations (M = 229 g mol−1), while the molar mass of TFSI anions (M = 280 g mol−1) is higher. Consequently, our results suggest that the respective heavier ion type shows stronger anticorrelations.
Table 5 Onsager conductivity coefficients σ++, σ−− and σ+− obtained at 30 °C for the different electrolyte mixtures
| LiFSI/G4 |
σ
++/mS cm−1 |
σ
−−/mS cm−1 |
σ
+−/mS cm−1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.30 ± 0.07 |
0.52 ± 0.16 |
−0.38 ± 0.01 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
0.34 ± 0.06 |
0.84 ± 0.41 |
−0.39 ± 0.04 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.40 ± 0.04 |
1.14 ± 0.32 |
−0.45 ± 0.03 |
| LiTFSI/G4 |
σ
++/mS cm−1 |
σ
−−/mS cm−1 |
σ
+−/mS cm−1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.44 ± 0.16 |
0.24 ± 0.07 |
−0.31 ± 0.02 |
Table 6 Self and distinct parts of the Onsager conductivity coefficients σself+, σself−, σdistinct++ and σdistinct−−, obtained at 30 °C for the different electrolyte mixtures
| LiFSI/G4 |
σ
self+/mS cm−1 |
σ
self−/mS cm−1 |
σ
distinct++/mS cm−1 |
σ
distinct−−/mS cm−1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.37 ± 0.07 |
1.65 ± 0.08 |
−1.07 ± 0.10 |
−1.13 ± 0.18 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
1.52 ± 0.08 |
1.95 ± 0.10 |
−1.19 ± 0.10 |
−1.11 ± 0.42 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
1.74 ± 0.09 |
2.29 ± 0.11 |
−1.33 ± 0.10 |
−1.15 ± 0.34 |
| LiTFSI/G4 |
σ
self+/mS cm−1 |
σ
self−/mS cm−1 |
σ
distinct++/mS cm−1 |
σ
distinct−−/mS cm−1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.28 ± 0.06 |
1.23 ± 0.06 |
−0.84 ± 0.18 |
−0.99 ± 0.09 |
 |
| | Fig. 5 (a) Lithium ion transference numbers tabc+ and tμ+ as well as transport numbers tPFG+ and (b) ion correlations manifesting in the ratios σdistinct++/σself+, σdistinct−−/σself− and σ+−/σion for the different electrolyte mixtures, see text for further explanation. | |
The same is true for the more dilute (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 and 1
1.5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) LiFSI/G4 mixtures, where tμ+ < tPFG+ is valid for both concentrations. Thus, in all FSI-containing mixtures, due to cation–cation anticorrelations being stronger than anion–anion anticorrelations, the cationic contribution to the conductivity is lower than expected from the diffusion coefficients. While the cation–cation anticorrelation is similar for all investigated LiFSI/G4 mixtures, both anion–anion and cation–anion anticorrelations decrease with decreasing LiFSI/G4 ratio.
2) LiFSI/G4 mixtures, where tμ+ < tPFG+ is valid for both concentrations. Thus, in all FSI-containing mixtures, due to cation–cation anticorrelations being stronger than anion–anion anticorrelations, the cationic contribution to the conductivity is lower than expected from the diffusion coefficients. While the cation–cation anticorrelation is similar for all investigated LiFSI/G4 mixtures, both anion–anion and cation–anion anticorrelations decrease with decreasing LiFSI/G4 ratio.
We note that we have also calculated the thermodynamic factor from eqn (19). The obtained values are given in Fig. S3 (ESI†).
The Li+ transference numbers under anion-blocking conditions tabc+ are much lower than tμ+ and tPFG+, see black squares in Fig. 5a. For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures, the very small numbers obtained previously, i.e. tabc+ = 0.025 for LiTFSI/G427 and tabc+ = 0.015 for LiFSI/G4,22 are caused by cation–anion anticorrelations due to ion momentum conservation. Since the exchange of the G4 molecules between [Li(G4)]+ complexes is slower than the elementary displacement steps of the ions, there is virtually no momentum exchange between G4 molecules and ions, so that ion momentum conservation plays an important role.24,27 Ion momentum conservation implies that under anion-blocking conditions in a battery, the cation momentum becomes very small.
1 mixtures, the very small numbers obtained previously, i.e. tabc+ = 0.025 for LiTFSI/G427 and tabc+ = 0.015 for LiFSI/G4,22 are caused by cation–anion anticorrelations due to ion momentum conservation. Since the exchange of the G4 molecules between [Li(G4)]+ complexes is slower than the elementary displacement steps of the ions, there is virtually no momentum exchange between G4 molecules and ions, so that ion momentum conservation plays an important role.24,27 Ion momentum conservation implies that under anion-blocking conditions in a battery, the cation momentum becomes very small.
With decreasing ratio of LiFSI/G4, the strength of the cation–anion anticorrelations, manifesting in the ratio σ+−/σion, decreases, namely from −0.24 for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture to −0.19 for the 1
1 mixture to −0.19 for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture, see Fig. 5b. According to eqn (13), this leads to a considerably larger Li+ transference number under anion-blocking conditions for the 1
2 mixture, see Fig. 5b. According to eqn (13), this leads to a considerably larger Li+ transference number under anion-blocking conditions for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture (tabc+ = 0.091).
2 mixture (tabc+ = 0.091).
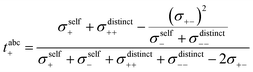
In Fig. 6a, we illustrate the influence of cation–cation, anion–anion, and cation–anion correlations on the two transference numbers tμ+ and tabc+ of the two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures. These illustrations are based on rewriting eqn (13) and (14) as:
1 mixtures. These illustrations are based on rewriting eqn (13) and (14) as:
| |  | (22) |
| |  | (23) |
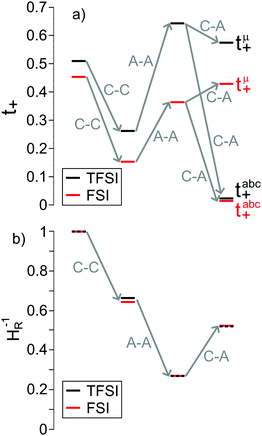 |
| | Fig. 6 Influence of the cation–cation (C–C), anion–anion (A–A) and cation–anion (C–A) correlations on (a) the two transference numbers tabc+ and tμ+ (eqn (22) and (23)) and (b) the inverse Haven ratio HR−1 (eqn (25)) for the two Li salt/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures. 1 mixtures. | |
In the absence of ion correlations (σdistinct++ = 0, σdistinct−− = 0, σ+− = 0), both transference numbers are identical to the transport number tPFG+. In the illustration in Fig. 6a, we start from tPFG+ and then consecutively insert the non-zero values for σdistinct++, σdistinct−− and σ+− into eqn (22) and (23). The plot illustrates the implications of the different strength of the anticorrelations in the two electrolytes for tμ+ and tabc+. While the cation–cation anticorrelations reduce tμ+, the anion–anion anticorrelations have the opposite effect. The influence of the cation–anion anticorrelations on tμ+ depends on the mass ratio of the [Li(G4)]+ cation to the anion. The cation–anion anticorrelations enhance the conductivity contribution of the heavier ion more strongly than the contribution of the lighter ion. Consequently, tμ+ is enhanced in the FSI system, while it is reduced in the TFSI system.
The most important ion correlation for tabc+ is the cation–anion anticorrelation. This anticorrelation decreases tabc+ severely, since the strong cation–anion correlations imply that under anion-blocking conditions, the cation current is strongly hindered. Thus, the large difference between tabc+ and tμ+ for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures is clearly a consequence of the cation–anion anticorrelation.
1 mixtures is clearly a consequence of the cation–anion anticorrelation.
Next we discuss the influence of the ion correlations on the Haven ratio HR, which is defined as:
| |  | (24) |
The calculated values for
HR of the different electrolyte mixtures are summarized in
Table 7.
Table 7 Haven ratios HR for the different electrolyte mixtures
| LiFSI/G4 |
H
R
|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.9 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
1.8 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
1.6 |
| LiTFSI/G4 |
H
R
|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.9 |
The inverse Haven ratio HR−1
| |  | (25) |
is sometimes termed as “ionicity”. In the absence of ion correlations, the inverse Haven ratio would be unity. As illustrated in
Fig. 6b, the cation–cation and anion–anion anticorrelations lower the inverse Haven ratio, while the cation–anion anticorrelations increase the inverse Haven ratio. Overall, the influence of the like-ion anticorrelations (cation–cation and anion–anion) dominates, so that the inverse Haven ratio is <1 and the Haven ratio is >1. This shows clearly that the term “ionicity” for the inverse Haven ratio does not properly describe the physical origin of
HR > 1. The Haven ratio might partly be enhanced by the formation of ion pairs, however, this contribution would manifest in positive cation–anion correlations (movements of the cations and anions bound in pairs into the same direction). Since the latter are negative, our analysis clearly demonstrates the dominating relevance of anticorrelation contributions. These occur between all types of ions and depend strongly on the relative mass of cationic and anionic species. Thus, the molecular picture of ion correlations is far less than anticipated influenced by Coulombic and dispersive interactions and potential pair formation, but rather by momentum exchange between the ions.
Relation to center-of-mass and dipole fluctuations by linear response theory
In order to rationalize our results for the cation–cation, anion–anion, and cation–anion correlations, we start with a general linear response theory expression for the ionic conductivity of an isotropic liquid electrolyte:26| | 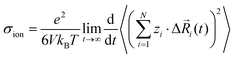 | (26) |
Here, N is the total number of ions in the electrolyte, zi is the charge number of ion i, and V is the sample volume. kB and T denote Boltzmann's constant and the temperature, respectively. The brackets 〈…〉 stand for the ensemble average. The ion displacement vectors Δ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) i(t) refer to the self-diffusive displacements in thermal equilibrium in the absence of an electric field. Δ
i(t) refer to the self-diffusive displacements in thermal equilibrium in the absence of an electric field. Δ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) i(t) consists of three components in x, y, and z direction:
i(t) consists of three components in x, y, and z direction:| | 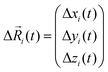 | (27) |
For isotropic materials, we can write:| | 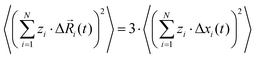 | (28) |
and we can express the ionic conductivity via the ionic displacements in x direction:| | 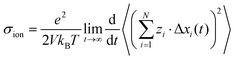 | (29) |
We assume that the ion dynamics is diffusive, i.e.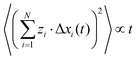 . In this case, we can rewrite eqn (29) as:
. In this case, we can rewrite eqn (29) as:| | 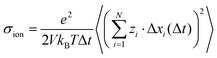 | (30) |
with xi(Δt) denoting the ionic displacements during a time interval Δt.
Now we consider a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte with ionic charge numbers z+ = 1 and z− = −1 and with identical numbers of cations and anions, N+ = N− = N/2. We note that the ions might be single ions or complex ions, such as [Li(G4)]+. From the displacements of the cations, x+i, and of the anions, x−i, during a time interval Δt, the Onsager coefficients σ++, σ−−, and σ+− can be calculated:
1 electrolyte with ionic charge numbers z+ = 1 and z− = −1 and with identical numbers of cations and anions, N+ = N− = N/2. We note that the ions might be single ions or complex ions, such as [Li(G4)]+. From the displacements of the cations, x+i, and of the anions, x−i, during a time interval Δt, the Onsager coefficients σ++, σ−−, and σ+− can be calculated:
| | 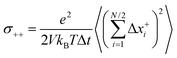 | (31a) |
| | 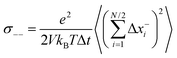 | (31b) |
| | 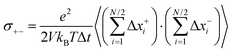 | (31c) |
The Onsager coefficients
σ++ and
σ−− can be split into self- and distinct-parts:
| |  | (32a) |
| | 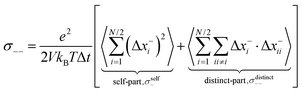 | (32b) |
The ionic displacements during the time interval Δ
t lead to a center-of-mass fluctuation and to a dipole fluctuation, which can be expressed as:
| | 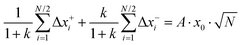 | (33a) |
| | 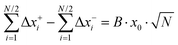 | (33b) |
Here,
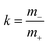
denotes the mass ratio of the ions.
A and
B characterize center-of-mass and dipole fluctuations in the electrolyte, respectively, and exhibit ensemble averages, 〈
A〉 = 0 and 〈
B〉 = 0, and variances 〈
A2〉 and 〈
B2〉. These variances are limited by intermolecular forces, which prevent the formation of large local center-of-mass and large local dipole fluctuations.
x0 is a characteristic length scale, which is explained below, and the
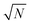
factor accounts for the dependence of fluctuations on the number of particles in a system.
Now we express the ionic displacement as follows:
| | | Δx+i = x0(gi + a+i·A + b+i·B) | (34a) |
| | | Δx−i = x0(gi + a−i·A + b−i·B) | (34b) |
with
gi denoting a displacement distribution function with zero particle mean,
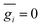
, and variance
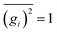
.
Eqn (34a) and (34b) imply that the characteristic length scale
x0 is identical to the root mean square displacement of both types of ions in the absence of center-of-mass and dipole fluctuations. The quantities
a±i and
b±i characterize the individual contributions of cations and anions to the center-of-mass and to the dipole fluctuation, respectively.
Inserting eqn (34a) and (34b) into (33a) and (33b) results in (see ESI† for details):
| | 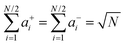 | (35a) |
| | 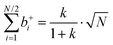 | (35b) |
| | 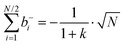 | (35c) |
Now, we insert
eqn (34a), (34b) and (35a)–(35c) into
(31a)–(31c), (32a) and (32b) in order to obtain expressions for the different transport coefficients (see ESI
† for details):
| | 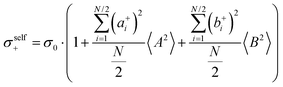 | (36a) |
| | 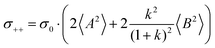 | (36b) |
| | 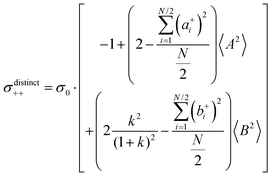 | (36c) |
| | 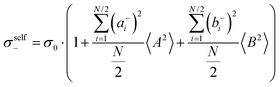 | (36d) |
| | 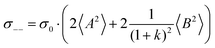 | (36e) |
| | 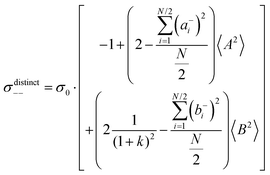 | (36f) |
| | 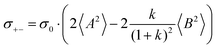 | (36g) |
with
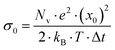
. Here,
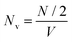
denotes the number density of each type of ion.
The cationic and anionic contributions to the ionic conductivity can then be expressed as (see ESI† for details):
| | 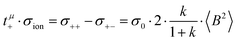 | (37a) |
| | 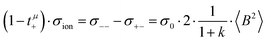 | (37b) |
The cation transport coefficient under anion-blocking conditions,
tabc+·
σion, can be written as:
| | 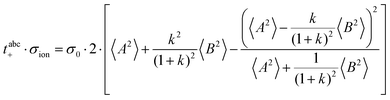 | (38) |
If center-of-mass fluctuations are much weaker than dipole fluctuations, such that
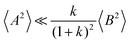
and
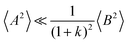
, the cation transport coefficient under anion-blocking conditions can be approximated by (see ESI
† for details):
| | | tabc+·σion ≈ σ0·2·(1 + k)2·〈A2〉 | (39) |
Finally, we calculate the ratio of the distinct-parts of
σ++ and
σ−− to their self-parts in order to interpret the data in
Fig. 5b in terms of fluctuations. If the fluctuation terms in the self-parts and in the distinct-parts are much smaller than unity,
i.e.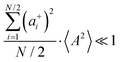
,
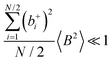
,
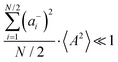
, and
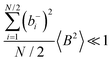
, the ratios can be approximated by (see ESI
† for details):
| | 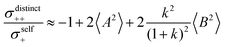 | (40a) |
| | 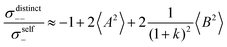 | (40b) |
From eqn (36)–(40), we draw the following conclusions: (i) While the self- and distinct-parts σself+, σdistinct++, σself−, and σdistinct−− depend on the distribution function of the prefactors ai and bi, the Onsager coefficients σ++, σ−−, and σ+− are independent of this distribution function (eqn (36a)–(36g)). (ii) In the case of weak center-of-mass and dipole fluctuations, such that 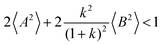 (eqn (40a)) and
(eqn (40a)) and 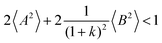 (eqn (40b)), the distinct-parts σdistinct++ and σdistinct−− are negative, i.e. cation–cation and anion–anion anticorrelations prevail. The physical reason is that anticorrelated displacements of the same type of ions create neither a large dipole nor a large center-of-mass shift. This is illustrated schematically in Fig. 7a and b. (iii) According to eqn (36g), the Onsager coefficient σ+− is negative, if the center-of-mass fluctuations are weaker than the dipole fluctuations, such that
(eqn (40b)), the distinct-parts σdistinct++ and σdistinct−− are negative, i.e. cation–cation and anion–anion anticorrelations prevail. The physical reason is that anticorrelated displacements of the same type of ions create neither a large dipole nor a large center-of-mass shift. This is illustrated schematically in Fig. 7a and b. (iii) According to eqn (36g), the Onsager coefficient σ+− is negative, if the center-of-mass fluctuations are weaker than the dipole fluctuations, such that 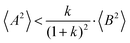 . The reason is that a dipole fluctuation without a center-of-mass fluctuation is only possible, if the center-of-mass of the cations moves into the opposite direction as the center-of-mass of the anions, as illustrated schematically in Fig. 7c. (iv) While the Onsager coefficients σ++, σ−− and σ+− depend on the mass ratio k as well as on the center-of-mass and dipole fluctuations 〈A2〉 and 〈B2〉, the ionic conductivity σion (eqn (36h)) depends exclusively on the dipole fluctuations 〈B2〉. (v) If center-of-mass fluctuations are absent, i.e. 〈A2〉 = 0 in eqn (36b), (36e), and (36g), the Onsager coefficients exhibit the following mass dependence:
. The reason is that a dipole fluctuation without a center-of-mass fluctuation is only possible, if the center-of-mass of the cations moves into the opposite direction as the center-of-mass of the anions, as illustrated schematically in Fig. 7c. (iv) While the Onsager coefficients σ++, σ−− and σ+− depend on the mass ratio k as well as on the center-of-mass and dipole fluctuations 〈A2〉 and 〈B2〉, the ionic conductivity σion (eqn (36h)) depends exclusively on the dipole fluctuations 〈B2〉. (v) If center-of-mass fluctuations are absent, i.e. 〈A2〉 = 0 in eqn (36b), (36e), and (36g), the Onsager coefficients exhibit the following mass dependence: 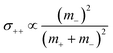 ;
; 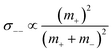 ; and
; and 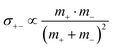 , in agreement with the results obtained by Kashyap et al.44 (vi) The mobility-based cation transference number, according to eqn (37a) and (37b), exhibits the following mass dependence:
, in agreement with the results obtained by Kashyap et al.44 (vi) The mobility-based cation transference number, according to eqn (37a) and (37b), exhibits the following mass dependence: 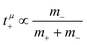 , which does not depend on the center-of-mass fluctuations 〈A2〉. While the relation
, which does not depend on the center-of-mass fluctuations 〈A2〉. While the relation 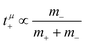 is evident in solvent-free systems,32,45 since it follows from ion momentum conservation, our derivation implies that even in case of diluted systems containing free solvent molecules, tμ+ does not depend on center-of-mass fluctuations. (vii) Following eqn (39), the center-of-mass fluctuations 〈A2〉 govern the cation transport under anion-blocking conditions. In the absence of center-of-mass fluctuations, tabc+·σion = 0. For 〈A2〉 > 0 it follows that tabc+·σion > 0.
is evident in solvent-free systems,32,45 since it follows from ion momentum conservation, our derivation implies that even in case of diluted systems containing free solvent molecules, tμ+ does not depend on center-of-mass fluctuations. (vii) Following eqn (39), the center-of-mass fluctuations 〈A2〉 govern the cation transport under anion-blocking conditions. In the absence of center-of-mass fluctuations, tabc+·σion = 0. For 〈A2〉 > 0 it follows that tabc+·σion > 0.
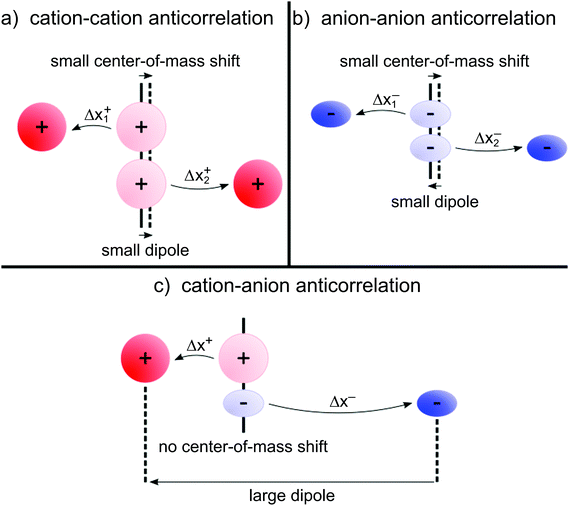 |
| | Fig. 7 (a and b) Illustration of anticorrelated displacements of the same type of ion, yielding negative contributions to σdistinct++ and σdistinct−−, respectively. These anticorrelated displacements create neither a large dipole nor a large center-of-mass shift. (c) Illustration of anticorrelated cation–anion displacements, resulting in a negative contribution to σ+−. These displacements create a large dipole, but not necessarily a center-of-mass shift. Thus, cation–anion anticorrelations prevail in electrolytes, in which dipole fluctuations are much stronger than center-of-mass fluctuations. | |
Now, we use these equations to derive values for the mass ratio k and for fluctuation parameters 〈A2〉 and 〈B2〉, presented in Table 8. The mass ratio k can be directly determined from the mobility-based transference number tμ+, see eqn (36h) and (37a).
| | 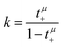 | (41) |
Table 8 Center-of-mass and dipole fluctuations 〈A2〉 and 〈B2〉 as well as ion mass ratio k and average coordination number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) for the different electrolytes
for the different electrolytes
| LiFSI/G4 |
〈A2〉 |
〈B2〉 |
k
|
Average coordination number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.003 ± 0.0015 |
0.57 ± 0.25 |
0.76 ± 0.15 |
1.0 ± 0.3 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 1.5 |
0.021 ± 0.010 |
0.65 ± 0.25 |
0.59 ± 0.11 |
1.3 ± 0.4 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.027 ± 0.008 |
0.71 ± 0.22 |
0.55 ± 0.055 |
1.4 ± 0.2 |
| LiTFSI/G4 |
〈A2〉 |
〈B2〉 |
k
|
Average coordination number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.002 ± 0.001 |
0.54 ± 0.28 |
1.4 ± 0.62 |
0.90 ± 0.25 |
We note that with this experimental determination of the mass ratio k, no assumption about the nature or stoichiometry of the ionic species, in particular of the complex cations, needs to be made. For a known value of k, then a combination of either eqn (40a) or eqn (40b) with equation
| | 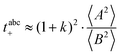 | (42) |
can be used to determine 〈
A2〉 and 〈
B2〉. The choice of
eqn (40a) or
eqn (40b) depends on whether the approximations
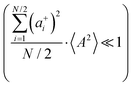
and
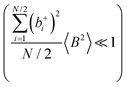
or the approximations
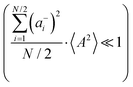
and
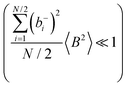
are better fulfilled, which is the case for the ion type with the stronger like-ion anticorrelations, namely the cations in the case of FSI-containing mixtures and the anions in the case of TFSI-containing mixtures.
The obtained values for 〈A2〉, 〈B2〉, and k are given in Table 8. The 〈A2〉 values obtained for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures are very small compared to 〈B2〉 implying that center-of-mass fluctuations of the ions are much weaker than their dipole fluctuations. This implies quite strict ion momentum conservation due to the slow exchange of the G4 molecules between [Li(G4)]+ complexes in comparison to the elementary displacement steps of the ions, as discussed above. With increasing dilution of the Li salt (1
1 mixtures are very small compared to 〈B2〉 implying that center-of-mass fluctuations of the ions are much weaker than their dipole fluctuations. This implies quite strict ion momentum conservation due to the slow exchange of the G4 molecules between [Li(G4)]+ complexes in comparison to the elementary displacement steps of the ions, as discussed above. With increasing dilution of the Li salt (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 and 1
1.5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures), the center-of-mass fluctuations of the ions increase significantly, since excess G4 molecules exist, which are not strongly bound to Li+ ions. These excess G4 molecules are able to exchange momentum with the ions, so that ion momentum conservation is much less strictly fulfilled.
2 mixtures), the center-of-mass fluctuations of the ions increase significantly, since excess G4 molecules exist, which are not strongly bound to Li+ ions. These excess G4 molecules are able to exchange momentum with the ions, so that ion momentum conservation is much less strictly fulfilled.
For all electrolytes, dipole fluctuations 〈B2〉 are significantly larger than center-of-mass fluctuations 〈A2〉, and the dipole fluctuations show only a slight relative increase with increasing dilution, see Table 8. This suggests that the microscopic mechanisms limiting the equilibrium center-of-mass and dipole fluctuations in these electrolytes are distinct and should be considered separately in computer simulations of electrolytes. In particular, the mechanisms limiting center-of-mass fluctuations have not been analysed in detail, but are highly relevant, since Li+ transport under anion-blocking conditions is governed by center-of-mass fluctuations, see eqn (39).
For the interpretation of the obtained k values, we assume that the Li+ ions form complex cations [Li(G4)n]+, where different integer values of n may coexist. With ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) denoting the average number of G4 molecules bound to a single Li+ ion, the mass ratio k is given by:
denoting the average number of G4 molecules bound to a single Li+ ion, the mass ratio k is given by:
| | 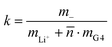 | (43) |
The obtained values for
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
are also given in
Table 8. As expected, for the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 mixtures,
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
is close to unity within the experimental error. However, with increasing dilution,
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
becomes significantly larger than unity, suggesting that, on average, more than one G4 molecule is bound to a Li
+ ion. Evidence for this is also directly seen from the similar mobilities of Li
+ and G4 in the sample with Li salt/G4 of 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2 in
Fig. 4. If only one G4 molecule was bound to a Li
+ ion, a mobility of
μG4 = 1/2
μLi would be expected, since the G4 mobility results as a fast exchange average of the bound and the free glyme molecules. Instead, the experimental value of
μG4 is clearly larger than 1/2
μLi. However, since
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
is lower than the molar mixing ratio G4/Li salt, a significant amount of free G4 molecules exist in the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1.5 and 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2 mixtures, which are not strongly bound to Li
+ ions. This is consistent with the large center-of-mass fluctuations of the ionic species observed in these mixtures.
Conclusions
We have combined, for the first time, very-low-frequency impedance spectroscopy on symmetrical Li|electrolyte|Li cells with diffusion and electrophoretic NMR in order to obtain quantitative information about ion correlations in Li salt/G4 mixtures with molar ratios between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Our results show that cation–cation, anion–anion, and cation–anion movements are anticorrelated. The anticorrelations are particularly strong in the 1
2. Our results show that cation–cation, anion–anion, and cation–anion movements are anticorrelated. The anticorrelations are particularly strong in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture and decrease with decreasing molar ratio of Li salt to G4. Like-ion anticorrelations are generally stronger than cation–anion anticorrelations and are particularly strong for the heavier type of ion. We have analyzed in detail the influence of these ion correlations on two types of Li+ transference numbers, namely the mobility-based Li+ transference numbers and the Li+ transference numbers under anion-blocking conditions, as well as on the Haven ratio. Our results are at variance with concepts explaining transference numbers and Haven ratio by ion pair formation and ionicity exclusively, since these imply positive cation–anion correlations. We conclude that in the present systems, momentum conservation and the resulting ion anticorrelations are far more important than ion pair formation.
1 mixture and decrease with decreasing molar ratio of Li salt to G4. Like-ion anticorrelations are generally stronger than cation–anion anticorrelations and are particularly strong for the heavier type of ion. We have analyzed in detail the influence of these ion correlations on two types of Li+ transference numbers, namely the mobility-based Li+ transference numbers and the Li+ transference numbers under anion-blocking conditions, as well as on the Haven ratio. Our results are at variance with concepts explaining transference numbers and Haven ratio by ion pair formation and ionicity exclusively, since these imply positive cation–anion correlations. We conclude that in the present systems, momentum conservation and the resulting ion anticorrelations are far more important than ion pair formation.
In order to rationalize our findings, we have derived linear response theory expressions for all correlations and for the resulting charge and mass transport coefficients of the electrolytes. These expressions show that the Li+ ion transport under anion-blocking conditions in a battery is governed by equilibrium center-of-mass fluctuations in the electrolytes. Therefore, we suggest that in future computer simulations of battery electrolytes, not only dipole fluctuations should be considered, which govern the overall ionic conductivity, but that particular attention should be paid to the analysis of center-of-mass fluctuations.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Financial support of this work by the Federal State of Hesse is gratefully acknowledged. Furthermore, we thank Albemarle (Rockwood Lithium GmbH) for providing the lithium foil.
Notes and references
- S. Zhang, N. Sun, X. He, X. Lu and X. Zhang, J. Phys. Chem. Ref. Data, 2006, 35, 1475–1517 CrossRef CAS.
- Y. Zhang and E. J. Maginn, J. Phys. Chem. Lett., 2015, 6, 700–705 CrossRef CAS PubMed.
- A. Thum, A. Heuer, K. Shimizu and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2020, 22, 525–535 RSC.
- J. von Zamory, G. A. Giffin, S. Jeremias, F. Castiglione, A. Mele, E. Paillard and S. Passerini, Phys. Chem. Chem. Phys., 2016, 18, 21539–21547 RSC.
- V. Baranauskaite, O. Pestova, M. Vovk, V. Matveev and E. Lähderanta, Phys. Chem. Chem. Phys., 2019, 21, 22895–22901 RSC.
- R. Bouchal, Z. Li, C. Bongu, S. Le Vot, R. Berthelot, B. Rotenberg, F. Favier, S. A. Freunberger, M. Salanne and O. Fontaine, Angew. Chem., Int. Ed., 2020, 59, 15913–15917 CrossRef CAS PubMed.
- F. Chen and M. Forsyth, Phys. Chem. Chem. Phys., 2016, 18, 19336–19344 RSC.
- L. Chen, J. Zhang, Q. Li, J. Vatamanu, X. Ji, T. P. Pollard, C. Cui, S. Hou, J. Chen, C. Yang, L. Ma, M. S. Ding, M. Garaga, S. Greenbaum, H.-S. Lee, O. Borodin, K. Xu and C. Wang, ACS Energy Lett., 2020, 5, 968–974 CrossRef CAS.
- C.-H. Lin, K. Sun, M. Ge, L. M. Housel, A. H. McCarthy, M. N. Vila, C. Zhao, X. Xiao, W.-K. Lee, K. J. Takeuchi, E. S. Takeuchi, A. C. Marschilok and Y.-C. K. Chen-Wiegart, Sci. Adv., 2020, 6, eaay7129 CrossRef CAS PubMed.
- J. M. Wrogemann, S. Künne, A. Heckmann, I. A. Rodríguez-Pérez, V. Siozios, B. Yan, J. Li, M. Winter, K. Beltrop and T. Placke, Adv. Energy Mater., 2020, 10, 1902709 CrossRef CAS.
- C. A. Angell, Y. Ansari and Z. Zhao, Faraday Discuss., 2012, 154, 9–27 RSC.
- A. Lewandowski and A. Świderska-Mocek, J. Power Sources, 2009, 194, 601–609 CrossRef CAS.
- K. Ueno, K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2012, 116, 11323–11331 CrossRef CAS PubMed.
- F. Schmidt, A. Pugliese, C. C. Santini, F. Castiglione and M. Schönhoff, Magn. Reson. Chem., 2020, 58, 271–279 CrossRef CAS PubMed.
- M. Gouverneur, F. Schmidt and M. Schönhoff, Phys. Chem. Chem. Phys., 2018, 20, 7470–7478 RSC.
- M. Brinkkötter, G. A. Giffin, A. Moretti, S. Jeong, S. Passerini and M. Schönhoff, Chem. Commun., 2018, 54, 4278–4281 RSC.
- K. Yoshida, M. Nakamura, Y. Kazue, N. Tachikawa, S. Tsuzuki, S. Seki, K. Dokko and M. Watanabe, J. Am. Chem. Soc., 2011, 133, 13121–13129 CrossRef CAS PubMed.
- T. Tamura, K. Yoshida, T. Hachida, M. Tsuchiya, M. Nakamura, Y. Kazue, N. Tachikawa, K. Dokko and M. Watanabe, Chem. Lett., 2010, 39, 753–755 CrossRef CAS.
- T. M. Pappenfus, W. A. Henderson, B. B. Owens, K. R. Mann and W. H. Smyrl, J. Electrochem. Soc., 2004, 151, A209–A215 CrossRef CAS.
- T. Murphy, S. K. Callear, N. Yepuri, K. Shimizu, M. Watanabe, J. N. Canongia Lopes, T. Darwish, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2016, 18, 17224–17236 RSC.
- S. Seki, K. Takei, H. Miyashiro and M. Watanabe, J. Electrochem. Soc., 2011, 158, A769–A774 CrossRef CAS.
- F. Sälzer, L. Pateras Pescara, F. Franke, C. Müller, J. Winkler, M. Schwalm and B. Roling, Batteries Supercaps, 2020, 3, 117–125 CrossRef.
- F. Schmidt and M. Schönhoff, J. Phys. Chem. B, 2020, 124, 1245–1252 CrossRef CAS PubMed.
- D. Dong, F. Sälzer, B. Roling and D. Bedrov, Phys. Chem. Chem. Phys., 2018, 20, 29174–29183 RSC.
- K. Shigenobu, K. Dokko, M. Watanabe and K. Ueno, Phys. Chem. Chem. Phys., 2020, 22, 15214–15221 RSC.
- N. M. Vargas-Barbosa and B. Roling, ChemElectroChem, 2020, 7, 367–385 CrossRef CAS.
- F. Wohde, M. Balabajew and B. Roling, J. Electrochem. Soc., 2016, 163, A714–A721 CrossRef CAS.
- Z. Li, R. Bouchal, T. Mendez-Morales, A.-L. Rollet, C. Rizzi, S. Le Vot, F. Favier, B. Rotenberg, O. Borodin, O. Fontaine and M. Salanne, J. Phys. Chem. B, 2019, 123, 10514–10521 CrossRef CAS PubMed.
- J. G. McDaniel and C. Y. Son, J. Phys. Chem. B, 2018, 122, 7154–7169 CrossRef CAS PubMed.
- A. Eilmes and P. Kubisiak, J. Phys. Chem. B, 2013, 117, 12583–12592 CrossRef CAS PubMed.
- K. R. Harris, J. Phys. Chem. B, 2016, 120, 12135–12147 CrossRef CAS.
- K. R. Harris, Phys. Chem. Chem. Phys., 2018, 20, 30041–30045 RSC.
- M. Gouverneur, J. Kopp, L. van Wüllen and M. Schönhoff, Phys. Chem. Chem. Phys., 2015, 17, 30680–30686 RSC.
- J. E. Tanner, J. Chem. Phys., 1970, 52, 2523–2526 CrossRef CAS.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS.
- E. Pettersson, I. Furó and P. Stilbs, Concepts Magn. Reson., Part A, 2004, 22A, 61–68 CrossRef CAS.
- K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2011, 115, 18384–18394 CrossRef CAS.
- M. Holz and C. Müller, Ber. Bunsenges. Phys. Chem., 1982, 86, 141–147 CrossRef CAS.
- M. Holz, C. Müller and A. M. Wachter, J. Magn. Reson., 1986, 69, 108–115 CAS.
- F. Hallberg, I. Furó, P. V. Yushmanov and P. Stilbs, J. Magn. Reson., 2008, 192, 69–77 CrossRef CAS.
- Y. Saito, H. Kataok and S. Deki, J. Electrochem. Soc., 2001, 148, E382–E385 CrossRef CAS.
- Y. Fang, P. V. Yushmanov and I. Furó, J. Magn. Reson., 2020, 318, 106796 CrossRef CAS PubMed.
- M. Schönhoff, C. Cramer and F. Schmidt, Phys. Chem. Chem. Phys., 2018, 20, 30046–30052 RSC.
- H. K. Kashyap, H. V. R. Annapureddy, F. O. Raineri and C. J. Margulis, J. Phys. Chem. B, 2011, 115, 13212–13221 CrossRef CAS PubMed.
- B. R. Sundheim, J. Phys. Chem., 1957, 61, 485–486 CrossRef CAS.
Footnote |
† Electronic supplementary information (ESI) available: Plots of PFG-NMR and eNMR data for the different LiFSI/G4 mixtures, plot of the thermodynamic factor for the LiTFSI/G4 and LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures, and derivations of linear response theory expressions. See DOI: 10.1039/d0cp06147f 1 mixtures, and derivations of linear response theory expressions. See DOI: 10.1039/d0cp06147f |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Florian
Ackermann
b,
Fabian
Sälzer
a,
Florian
Ackermann
b,
Fabian
Sälzer
 a,
Monika
Schönhoff
a,
Monika
Schönhoff
 *b and
Bernhard
Roling
*b and
Bernhard
Roling
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. We find that all correlations are negative, with like-ion anticorrelations (cation–cation and anion–anion) being generally stronger than cation–anion anticorrelations. In addition, we observe that like-ion anticorrelations are stronger for the heavier type of ion and that all anticorrelations become weaker with decreasing Li salt to G4 ratio. These findings are in contrast to theories considering exclusively anion–cation correlations in form of ion pairs, as the latter imply positive cation–anion correlations. We analyze in detail the influence of anticorrelations on Li+ transference numbers and on the Haven ratio. In order to rationalize our results, we derive linear response theory expressions for all ion correlations. These expressions show that the Li+ ion transport under anion-blocking conditions in a battery is governed by equilibrium center-of-mass fluctuations in the electrolytes. This suggests that in future electrolyte theories and computer simulations, more attention should be paid to equilibrium center-of-mass fluctuations.
2. We find that all correlations are negative, with like-ion anticorrelations (cation–cation and anion–anion) being generally stronger than cation–anion anticorrelations. In addition, we observe that like-ion anticorrelations are stronger for the heavier type of ion and that all anticorrelations become weaker with decreasing Li salt to G4 ratio. These findings are in contrast to theories considering exclusively anion–cation correlations in form of ion pairs, as the latter imply positive cation–anion correlations. We analyze in detail the influence of anticorrelations on Li+ transference numbers and on the Haven ratio. In order to rationalize our results, we derive linear response theory expressions for all ion correlations. These expressions show that the Li+ ion transport under anion-blocking conditions in a battery is governed by equilibrium center-of-mass fluctuations in the electrolytes. This suggests that in future electrolyte theories and computer simulations, more attention should be paid to equilibrium center-of-mass fluctuations.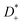 , and anions,
, and anions, 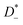 , respectively:
, respectively: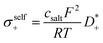
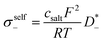
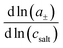 , with a± denoting the cations’ and anions’ mean activity, are needed. Consequently, six measurable quantities are required in order to derive the five coefficients and the thermodynamic factor. In this way, information about cation–cation, anion–anion and cation–anion correlations and their impact on the transport properties can be obtained. To our knowledge, there is only a single example in the literature with such a complete experimental information.25 On the other hand, a small number of recent MD studies on ion correlations in concentrated electrolytes has been published.28–30 Harris showed that under the assumption of strict ion momentum conservation in a solvent-free electrolyte with only a single type of cations and anions, measurements of the ionic conductivity and of the self-diffusion coefficients of the ions are sufficient for elucidating all ion correlations.31,32 However, this approach cannot be applied to electrolytes with more than two ionic species or to solvent-containing electrolytes, such as solvent-in-salt electrolytes and solvate ionic liquids.
, with a± denoting the cations’ and anions’ mean activity, are needed. Consequently, six measurable quantities are required in order to derive the five coefficients and the thermodynamic factor. In this way, information about cation–cation, anion–anion and cation–anion correlations and their impact on the transport properties can be obtained. To our knowledge, there is only a single example in the literature with such a complete experimental information.25 On the other hand, a small number of recent MD studies on ion correlations in concentrated electrolytes has been published.28–30 Harris showed that under the assumption of strict ion momentum conservation in a solvent-free electrolyte with only a single type of cations and anions, measurements of the ionic conductivity and of the self-diffusion coefficients of the ions are sufficient for elucidating all ion correlations.31,32 However, this approach cannot be applied to electrolytes with more than two ionic species or to solvent-containing electrolytes, such as solvent-in-salt electrolytes and solvate ionic liquids.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5, and 1
1.5, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in VLF-IS, PFG-NMR and eNMR, while using our previous VLF-IS results for the LiFSI/G4 1
2 in VLF-IS, PFG-NMR and eNMR, while using our previous VLF-IS results for the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture.22 In addition, for comparison, we use previously published eNMR and VLF-IS data of a LiTFSI/G4 1
1 mixture.22 In addition, for comparison, we use previously published eNMR and VLF-IS data of a LiTFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture.23,27 In this way, we analyse both the influence of salt concentration and anion type on the ion correlations. We discuss the impact of different correlations (cation–cation, anion–anion, and cation–anion) on the Li+ transference number under anion-blocking conditions, on the mobility-based Li+ transference number, and on the Haven ratio. In order to rationalize the experimental findings, we derive and discuss linear response theory expressions for a binary electrolyte with dipole fluctuations and center-of-mass fluctuations.
1 mixture.23,27 In this way, we analyse both the influence of salt concentration and anion type on the ion correlations. We discuss the impact of different correlations (cation–cation, anion–anion, and cation–anion) on the Li+ transference number under anion-blocking conditions, on the mobility-based Li+ transference number, and on the Haven ratio. In order to rationalize the experimental findings, we derive and discuss linear response theory expressions for a binary electrolyte with dipole fluctuations and center-of-mass fluctuations.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1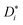 , see eqn (4).
, see eqn (4).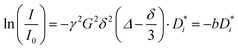
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture and slightly higher for the LiFSI/G4 1
1 mixture and slightly higher for the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture. With increasing G4 content of the LiFSI/G4 mixtures, the total ionic conductivity increases.
1 mixture. With increasing G4 content of the LiFSI/G4 mixtures, the total ionic conductivity increases.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 mixture between two Li electrodes with a distance of 192 μm are shown. The equivalent circuit for fitting is shown in the inset. The circuit consists of a bulk resistance Rbulk caused by the total ionic conductivity of the electrolyte, in series with two R-CPE elements accounting for the Li|electrolyte interface (impedance of solid electrolyte interphase and charge transfer impedance), in series with a Warburg-short (Ws) element describing the formation of salt diffusion layers and the stationary Li+ current under anion-blocking conditions. The Warburg-short impedance is given by:
1.5 mixture between two Li electrodes with a distance of 192 μm are shown. The equivalent circuit for fitting is shown in the inset. The circuit consists of a bulk resistance Rbulk caused by the total ionic conductivity of the electrolyte, in series with two R-CPE elements accounting for the Li|electrolyte interface (impedance of solid electrolyte interphase and charge transfer impedance), in series with a Warburg-short (Ws) element describing the formation of salt diffusion layers and the stationary Li+ current under anion-blocking conditions. The Warburg-short impedance is given by: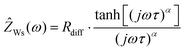
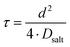
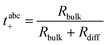
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were taken from ref. 27 and the data for LiFSI/G4 1
1 were taken from ref. 27 and the data for LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 from ref. 22, respectively.
1 from ref. 22, respectively.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122
122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127
127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 as an exemplary sample is shown in Fig. 3a in dependence of b. In this depiction, the slope is a direct representation of the self-diffusion coefficient
1.5 as an exemplary sample is shown in Fig. 3a in dependence of b. In this depiction, the slope is a direct representation of the self-diffusion coefficient 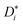 , which is evaluated according to eqn (4). As expected, we observe a monoexponential decay of the investigated NMR signals with increasing b values. This behavior indicates the fast exchange averaging of the diffusion coefficient in case of the existence of different species, such as single ions or complexes containing the observed nucleus during the observation time of 100 ms. In the case of LiFSI/G4 1
, which is evaluated according to eqn (4). As expected, we observe a monoexponential decay of the investigated NMR signals with increasing b values. This behavior indicates the fast exchange averaging of the diffusion coefficient in case of the existence of different species, such as single ions or complexes containing the observed nucleus during the observation time of 100 ms. In the case of LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, 7Li and 1H exhibit the same slope (see Fig. S1 in ESI†), and therefore the same diffusion coefficient. In the past, this behavior was attributed to the formation of a complex [Li(G4)]+ solvate cation, and is the main characteristic of solvate ionic liquids.13,17,37 With decreasing lithium to glyme ratio, G4 diffuses faster than Li+, as indicated by a steeper slope for 1H, see Fig. 3a.
1 mixture, 7Li and 1H exhibit the same slope (see Fig. S1 in ESI†), and therefore the same diffusion coefficient. In the past, this behavior was attributed to the formation of a complex [Li(G4)]+ solvate cation, and is the main characteristic of solvate ionic liquids.13,17,37 With decreasing lithium to glyme ratio, G4 diffuses faster than Li+, as indicated by a steeper slope for 1H, see Fig. 3a.
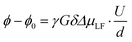
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 mixture. In this depiction, the slope represents the mobility μLF of the observed nucleus in the laboratory reference frame (LF). As expected, the depicted eNMR results exhibit a phase shift linearly depending on the applied voltage. While the scattering of the phase shift is rather low for 1H and 19F, it is somewhat larger for 7Li, due to the lower signal-to-noise ratio of 7Li spectra, resulting from a lower value of γ compared to 1H and 19F.
1.5 mixture. In this depiction, the slope represents the mobility μLF of the observed nucleus in the laboratory reference frame (LF). As expected, the depicted eNMR results exhibit a phase shift linearly depending on the applied voltage. While the scattering of the phase shift is rather low for 1H and 19F, it is somewhat larger for 7Li, due to the lower signal-to-noise ratio of 7Li spectra, resulting from a lower value of γ compared to 1H and 19F.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture (see Fig. S2 in ESI†). This observation shows the migration of a complex cation [Li(G4)]+ in an electric field in the LiFSI/G4 1
1 mixture (see Fig. S2 in ESI†). This observation shows the migration of a complex cation [Li(G4)]+ in an electric field in the LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, similar to the previously studied SIL systems Li(G4)TFSI and Li(G4)BF4,14,23 underlining the ionic liquid-like character of Li(G4)FSI. All resulting mobility values obtained from 1H, 7Li and 19F eNMR measurements on the LiFSI/G4 samples are given in Fig. 4 as open symbols. The overall trend is a reduction of the modulus of mobility with increasing salt concentration related to a viscosity increase. With decreasing lithium salt to glyme ratio, the fast exchange averaging over free glyme molecules exhibiting no nominal charge and glyme molecules bound to lithium leads to an average mobility of G4, which is lower than that of lithium, compare open squares and diamonds in Fig. 4. This hints at the coexistence of free glyme molecules and Li/glyme complexes in the dilute samples, which will be discussed in more detail below.
1 mixture, similar to the previously studied SIL systems Li(G4)TFSI and Li(G4)BF4,14,23 underlining the ionic liquid-like character of Li(G4)FSI. All resulting mobility values obtained from 1H, 7Li and 19F eNMR measurements on the LiFSI/G4 samples are given in Fig. 4 as open symbols. The overall trend is a reduction of the modulus of mobility with increasing salt concentration related to a viscosity increase. With decreasing lithium salt to glyme ratio, the fast exchange averaging over free glyme molecules exhibiting no nominal charge and glyme molecules bound to lithium leads to an average mobility of G4, which is lower than that of lithium, compare open squares and diamonds in Fig. 4. This hints at the coexistence of free glyme molecules and Li/glyme complexes in the dilute samples, which will be discussed in more detail below.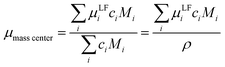
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) center
center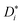 and diffusion-based lithium ion transport numbers tPFG+ (see eqn (11)) for the different electrolyte compositions compared in this work are summarized in Tables 3 and 4.
and diffusion-based lithium ion transport numbers tPFG+ (see eqn (11)) for the different electrolyte compositions compared in this work are summarized in Tables 3 and 4.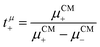
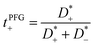
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 samples, the respective cation and glyme mobilities agree within error (see Table 3), consistent with the formation of a complex cation [Li(G4)]+ as the only cationic species. In the 1
1 samples, the respective cation and glyme mobilities agree within error (see Table 3), consistent with the formation of a complex cation [Li(G4)]+ as the only cationic species. In the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 sample, however, cation and glyme mobilities do not agree within error, reflecting an averaging over different glyme-containing species, possibly free glyme and complexes [Li(G4)n]+, with different integer values of the coordination number n. Assuming that the species in this sample would be [Li(G4)1]+ complexes and free G4 with zero mobility, the resulting average glyme mobility would be μG4 = 0.5μ+. If on the other hand exclusively [Li(G4)2]+ complexes existed, the G4 mobility would be μG4 = μ+. Experimentally, we find μG4 = 0.73μ+. This points to an average coordination number
2 sample, however, cation and glyme mobilities do not agree within error, reflecting an averaging over different glyme-containing species, possibly free glyme and complexes [Li(G4)n]+, with different integer values of the coordination number n. Assuming that the species in this sample would be [Li(G4)1]+ complexes and free G4 with zero mobility, the resulting average glyme mobility would be μG4 = 0.5μ+. If on the other hand exclusively [Li(G4)2]+ complexes existed, the G4 mobility would be μG4 = μ+. Experimentally, we find μG4 = 0.73μ+. This points to an average coordination number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) between 1 and 2. We will discuss the complex compositions in more detail at the end of the discussion and provide an estimate of
between 1 and 2. We will discuss the complex compositions in more detail at the end of the discussion and provide an estimate of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) for the dilute samples.
for the dilute samples.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123
123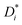 and diffusion-based Li+ transport numbers tPFG+ obtained at 30 °C for the different electrolytes
and diffusion-based Li+ transport numbers tPFG+ obtained at 30 °C for the different electrolytes
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123
123
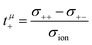

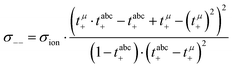

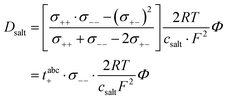
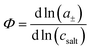 is given by:
is given by: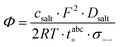
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, we find tμ+ > tPFG+, while for LiFSI/G4 1
1, we find tμ+ > tPFG+, while for LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, we observe tμ+ ≲ tPFG+. In Fig. 5b, the strength of the cation–cation and anion–anion correlations is illustrated by plotting the distinct-parts of σ++ and σ−− normalized by their self-part. In the case of LiTFSI/G4 1
1, we observe tμ+ ≲ tPFG+. In Fig. 5b, the strength of the cation–cation and anion–anion correlations is illustrated by plotting the distinct-parts of σ++ and σ−− normalized by their self-part. In the case of LiTFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the cation dynamics is characterized by cation–cation anticorrelations with a ratio of σdistinct++/σself+ = −0.66, see open black square. This number implies that cation–cation anticorrelations reduce the contribution of diffusive cationic displacements to the ionic conductivity by 66%. The anion dynamics shows even stronger anticorrelations with a ratio of σdistinct−−/σself− = −0.80, see open red circle. The stronger anion–anion anticorrelations reduce the anionic contribution to the conductivity and lead to tμ+ > tPFG+. In contrast, in the case of LiFSI/G4 1
1, the cation dynamics is characterized by cation–cation anticorrelations with a ratio of σdistinct++/σself+ = −0.66, see open black square. This number implies that cation–cation anticorrelations reduce the contribution of diffusive cationic displacements to the ionic conductivity by 66%. The anion dynamics shows even stronger anticorrelations with a ratio of σdistinct−−/σself− = −0.80, see open red circle. The stronger anion–anion anticorrelations reduce the anionic contribution to the conductivity and lead to tμ+ > tPFG+. In contrast, in the case of LiFSI/G4 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the cation–cation anticorrelations are slightly stronger (σdistinct++/σself+ = −0.78) than the anion–anion anticorrelations (σdistinct−−/σself− = −0.68). This leads to tμ+ ≲ tPFG+. It is thus evident that like-ion anticorrelations are responsible for the deviations of transference numbers from transport numbers. In this context, it should be noted that the molar mass of FSI anions (M = 178 g mol−1) is lower than the molar mass of [Li(G4)]+ complex cations (M = 229 g mol−1), while the molar mass of TFSI anions (M = 280 g mol−1) is higher. Consequently, our results suggest that the respective heavier ion type shows stronger anticorrelations.
1, the cation–cation anticorrelations are slightly stronger (σdistinct++/σself+ = −0.78) than the anion–anion anticorrelations (σdistinct−−/σself− = −0.68). This leads to tμ+ ≲ tPFG+. It is thus evident that like-ion anticorrelations are responsible for the deviations of transference numbers from transport numbers. In this context, it should be noted that the molar mass of FSI anions (M = 178 g mol−1) is lower than the molar mass of [Li(G4)]+ complex cations (M = 229 g mol−1), while the molar mass of TFSI anions (M = 280 g mol−1) is higher. Consequently, our results suggest that the respective heavier ion type shows stronger anticorrelations.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 and 1
1.5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) LiFSI/G4 mixtures, where tμ+ < tPFG+ is valid for both concentrations. Thus, in all FSI-containing mixtures, due to cation–cation anticorrelations being stronger than anion–anion anticorrelations, the cationic contribution to the conductivity is lower than expected from the diffusion coefficients. While the cation–cation anticorrelation is similar for all investigated LiFSI/G4 mixtures, both anion–anion and cation–anion anticorrelations decrease with decreasing LiFSI/G4 ratio.
2) LiFSI/G4 mixtures, where tμ+ < tPFG+ is valid for both concentrations. Thus, in all FSI-containing mixtures, due to cation–cation anticorrelations being stronger than anion–anion anticorrelations, the cationic contribution to the conductivity is lower than expected from the diffusion coefficients. While the cation–cation anticorrelation is similar for all investigated LiFSI/G4 mixtures, both anion–anion and cation–anion anticorrelations decrease with decreasing LiFSI/G4 ratio.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures, the very small numbers obtained previously, i.e. tabc+ = 0.025 for LiTFSI/G427 and tabc+ = 0.015 for LiFSI/G4,22 are caused by cation–anion anticorrelations due to ion momentum conservation. Since the exchange of the G4 molecules between [Li(G4)]+ complexes is slower than the elementary displacement steps of the ions, there is virtually no momentum exchange between G4 molecules and ions, so that ion momentum conservation plays an important role.24,27 Ion momentum conservation implies that under anion-blocking conditions in a battery, the cation momentum becomes very small.
1 mixtures, the very small numbers obtained previously, i.e. tabc+ = 0.025 for LiTFSI/G427 and tabc+ = 0.015 for LiFSI/G4,22 are caused by cation–anion anticorrelations due to ion momentum conservation. Since the exchange of the G4 molecules between [Li(G4)]+ complexes is slower than the elementary displacement steps of the ions, there is virtually no momentum exchange between G4 molecules and ions, so that ion momentum conservation plays an important role.24,27 Ion momentum conservation implies that under anion-blocking conditions in a battery, the cation momentum becomes very small.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture to −0.19 for the 1
1 mixture to −0.19 for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture, see Fig. 5b. According to eqn (13), this leads to a considerably larger Li+ transference number under anion-blocking conditions for the 1
2 mixture, see Fig. 5b. According to eqn (13), this leads to a considerably larger Li+ transference number under anion-blocking conditions for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture (tabc+ = 0.091).
2 mixture (tabc+ = 0.091).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures. These illustrations are based on rewriting eqn (13) and (14) as:
1 mixtures. These illustrations are based on rewriting eqn (13) and (14) as:


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures.
1 mixtures.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures is clearly a consequence of the cation–anion anticorrelation.
1 mixtures is clearly a consequence of the cation–anion anticorrelation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1
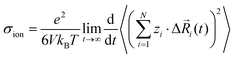
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) i(t) refer to the self-diffusive displacements in thermal equilibrium in the absence of an electric field. Δ
i(t) refer to the self-diffusive displacements in thermal equilibrium in the absence of an electric field. Δ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) i(t) consists of three components in x, y, and z direction:
i(t) consists of three components in x, y, and z direction: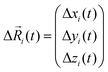
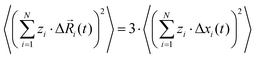
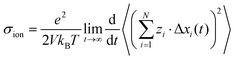
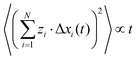 . In this case, we can rewrite eqn (29) as:
. In this case, we can rewrite eqn (29) as: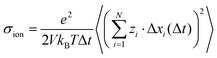
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte with ionic charge numbers z+ = 1 and z− = −1 and with identical numbers of cations and anions, N+ = N− = N/2. We note that the ions might be single ions or complex ions, such as [Li(G4)]+. From the displacements of the cations, x+i, and of the anions, x−i, during a time interval Δt, the Onsager coefficients σ++, σ−−, and σ+− can be calculated:
1 electrolyte with ionic charge numbers z+ = 1 and z− = −1 and with identical numbers of cations and anions, N+ = N− = N/2. We note that the ions might be single ions or complex ions, such as [Li(G4)]+. From the displacements of the cations, x+i, and of the anions, x−i, during a time interval Δt, the Onsager coefficients σ++, σ−−, and σ+− can be calculated: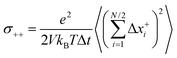
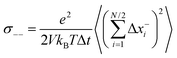
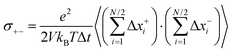

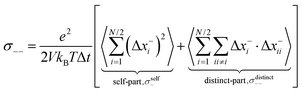
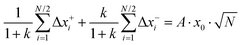
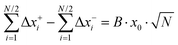
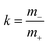 denotes the mass ratio of the ions. A and B characterize center-of-mass and dipole fluctuations in the electrolyte, respectively, and exhibit ensemble averages, 〈A〉 = 0 and 〈B〉 = 0, and variances 〈A2〉 and 〈B2〉. These variances are limited by intermolecular forces, which prevent the formation of large local center-of-mass and large local dipole fluctuations. x0 is a characteristic length scale, which is explained below, and the
denotes the mass ratio of the ions. A and B characterize center-of-mass and dipole fluctuations in the electrolyte, respectively, and exhibit ensemble averages, 〈A〉 = 0 and 〈B〉 = 0, and variances 〈A2〉 and 〈B2〉. These variances are limited by intermolecular forces, which prevent the formation of large local center-of-mass and large local dipole fluctuations. x0 is a characteristic length scale, which is explained below, and the 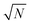 factor accounts for the dependence of fluctuations on the number of particles in a system.
factor accounts for the dependence of fluctuations on the number of particles in a system.
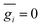 , and variance
, and variance 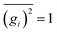 . Eqn (34a) and (34b) imply that the characteristic length scale x0 is identical to the root mean square displacement of both types of ions in the absence of center-of-mass and dipole fluctuations. The quantities a±i and b±i characterize the individual contributions of cations and anions to the center-of-mass and to the dipole fluctuation, respectively.
. Eqn (34a) and (34b) imply that the characteristic length scale x0 is identical to the root mean square displacement of both types of ions in the absence of center-of-mass and dipole fluctuations. The quantities a±i and b±i characterize the individual contributions of cations and anions to the center-of-mass and to the dipole fluctuation, respectively.
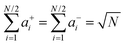
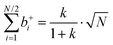
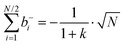
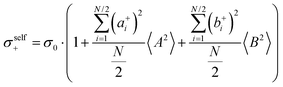
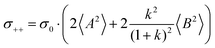
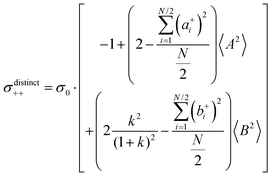
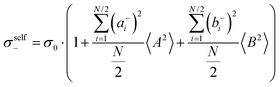
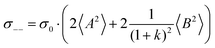
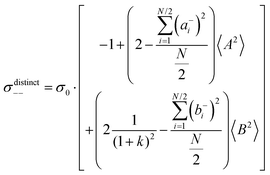
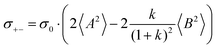
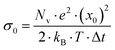 . Here,
. Here, 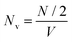 denotes the number density of each type of ion.
denotes the number density of each type of ion.
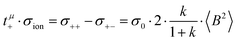
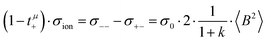
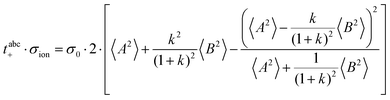
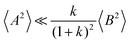 and
and 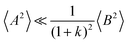 , the cation transport coefficient under anion-blocking conditions can be approximated by (see ESI† for details):
, the cation transport coefficient under anion-blocking conditions can be approximated by (see ESI† for details):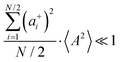 ,
, 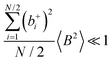 ,
, 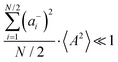 , and
, and 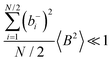 , the ratios can be approximated by (see ESI† for details):
, the ratios can be approximated by (see ESI† for details):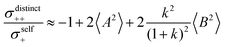
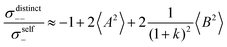
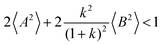 (eqn (40a)) and
(eqn (40a)) and 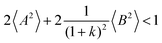 (eqn (40b)), the distinct-parts σdistinct++ and σdistinct−− are negative, i.e. cation–cation and anion–anion anticorrelations prevail. The physical reason is that anticorrelated displacements of the same type of ions create neither a large dipole nor a large center-of-mass shift. This is illustrated schematically in Fig. 7a and b. (iii) According to eqn (36g), the Onsager coefficient σ+− is negative, if the center-of-mass fluctuations are weaker than the dipole fluctuations, such that
(eqn (40b)), the distinct-parts σdistinct++ and σdistinct−− are negative, i.e. cation–cation and anion–anion anticorrelations prevail. The physical reason is that anticorrelated displacements of the same type of ions create neither a large dipole nor a large center-of-mass shift. This is illustrated schematically in Fig. 7a and b. (iii) According to eqn (36g), the Onsager coefficient σ+− is negative, if the center-of-mass fluctuations are weaker than the dipole fluctuations, such that 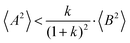 . The reason is that a dipole fluctuation without a center-of-mass fluctuation is only possible, if the center-of-mass of the cations moves into the opposite direction as the center-of-mass of the anions, as illustrated schematically in Fig. 7c. (iv) While the Onsager coefficients σ++, σ−− and σ+− depend on the mass ratio k as well as on the center-of-mass and dipole fluctuations 〈A2〉 and 〈B2〉, the ionic conductivity σion (eqn (36h)) depends exclusively on the dipole fluctuations 〈B2〉. (v) If center-of-mass fluctuations are absent, i.e. 〈A2〉 = 0 in eqn (36b), (36e), and (36g), the Onsager coefficients exhibit the following mass dependence:
. The reason is that a dipole fluctuation without a center-of-mass fluctuation is only possible, if the center-of-mass of the cations moves into the opposite direction as the center-of-mass of the anions, as illustrated schematically in Fig. 7c. (iv) While the Onsager coefficients σ++, σ−− and σ+− depend on the mass ratio k as well as on the center-of-mass and dipole fluctuations 〈A2〉 and 〈B2〉, the ionic conductivity σion (eqn (36h)) depends exclusively on the dipole fluctuations 〈B2〉. (v) If center-of-mass fluctuations are absent, i.e. 〈A2〉 = 0 in eqn (36b), (36e), and (36g), the Onsager coefficients exhibit the following mass dependence: 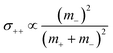 ;
; 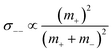 ; and
; and 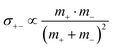 , in agreement with the results obtained by Kashyap et al.44 (vi) The mobility-based cation transference number, according to eqn (37a) and (37b), exhibits the following mass dependence:
, in agreement with the results obtained by Kashyap et al.44 (vi) The mobility-based cation transference number, according to eqn (37a) and (37b), exhibits the following mass dependence: 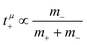 , which does not depend on the center-of-mass fluctuations 〈A2〉. While the relation
, which does not depend on the center-of-mass fluctuations 〈A2〉. While the relation 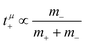 is evident in solvent-free systems,32,45 since it follows from ion momentum conservation, our derivation implies that even in case of diluted systems containing free solvent molecules, tμ+ does not depend on center-of-mass fluctuations. (vii) Following eqn (39), the center-of-mass fluctuations 〈A2〉 govern the cation transport under anion-blocking conditions. In the absence of center-of-mass fluctuations, tabc+·σion = 0. For 〈A2〉 > 0 it follows that tabc+·σion > 0.
is evident in solvent-free systems,32,45 since it follows from ion momentum conservation, our derivation implies that even in case of diluted systems containing free solvent molecules, tμ+ does not depend on center-of-mass fluctuations. (vii) Following eqn (39), the center-of-mass fluctuations 〈A2〉 govern the cation transport under anion-blocking conditions. In the absence of center-of-mass fluctuations, tabc+·σion = 0. For 〈A2〉 > 0 it follows that tabc+·σion > 0.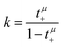
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) for the different electrolytes
for the different electrolytes
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1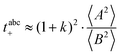
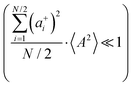 and
and 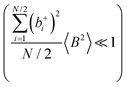 or the approximations
or the approximations 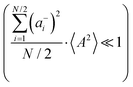 and
and 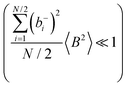 are better fulfilled, which is the case for the ion type with the stronger like-ion anticorrelations, namely the cations in the case of FSI-containing mixtures and the anions in the case of TFSI-containing mixtures.
are better fulfilled, which is the case for the ion type with the stronger like-ion anticorrelations, namely the cations in the case of FSI-containing mixtures and the anions in the case of TFSI-containing mixtures.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures are very small compared to 〈B2〉 implying that center-of-mass fluctuations of the ions are much weaker than their dipole fluctuations. This implies quite strict ion momentum conservation due to the slow exchange of the G4 molecules between [Li(G4)]+ complexes in comparison to the elementary displacement steps of the ions, as discussed above. With increasing dilution of the Li salt (1
1 mixtures are very small compared to 〈B2〉 implying that center-of-mass fluctuations of the ions are much weaker than their dipole fluctuations. This implies quite strict ion momentum conservation due to the slow exchange of the G4 molecules between [Li(G4)]+ complexes in comparison to the elementary displacement steps of the ions, as discussed above. With increasing dilution of the Li salt (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 and 1
1.5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures), the center-of-mass fluctuations of the ions increase significantly, since excess G4 molecules exist, which are not strongly bound to Li+ ions. These excess G4 molecules are able to exchange momentum with the ions, so that ion momentum conservation is much less strictly fulfilled.
2 mixtures), the center-of-mass fluctuations of the ions increase significantly, since excess G4 molecules exist, which are not strongly bound to Li+ ions. These excess G4 molecules are able to exchange momentum with the ions, so that ion momentum conservation is much less strictly fulfilled.![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) denoting the average number of G4 molecules bound to a single Li+ ion, the mass ratio k is given by:
denoting the average number of G4 molecules bound to a single Li+ ion, the mass ratio k is given by: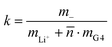
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) are also given in Table 8. As expected, for the 1
are also given in Table 8. As expected, for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures,
1 mixtures, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is close to unity within the experimental error. However, with increasing dilution,
is close to unity within the experimental error. However, with increasing dilution, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) becomes significantly larger than unity, suggesting that, on average, more than one G4 molecule is bound to a Li+ ion. Evidence for this is also directly seen from the similar mobilities of Li+ and G4 in the sample with Li salt/G4 of 1
becomes significantly larger than unity, suggesting that, on average, more than one G4 molecule is bound to a Li+ ion. Evidence for this is also directly seen from the similar mobilities of Li+ and G4 in the sample with Li salt/G4 of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in Fig. 4. If only one G4 molecule was bound to a Li+ ion, a mobility of μG4 = 1/2μLi would be expected, since the G4 mobility results as a fast exchange average of the bound and the free glyme molecules. Instead, the experimental value of μG4 is clearly larger than 1/2μLi. However, since
2 in Fig. 4. If only one G4 molecule was bound to a Li+ ion, a mobility of μG4 = 1/2μLi would be expected, since the G4 mobility results as a fast exchange average of the bound and the free glyme molecules. Instead, the experimental value of μG4 is clearly larger than 1/2μLi. However, since ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is lower than the molar mixing ratio G4/Li salt, a significant amount of free G4 molecules exist in the 1
is lower than the molar mixing ratio G4/Li salt, a significant amount of free G4 molecules exist in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 and 1
1.5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures, which are not strongly bound to Li+ ions. This is consistent with the large center-of-mass fluctuations of the ionic species observed in these mixtures.
2 mixtures, which are not strongly bound to Li+ ions. This is consistent with the large center-of-mass fluctuations of the ionic species observed in these mixtures.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Our results show that cation–cation, anion–anion, and cation–anion movements are anticorrelated. The anticorrelations are particularly strong in the 1
2. Our results show that cation–cation, anion–anion, and cation–anion movements are anticorrelated. The anticorrelations are particularly strong in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture and decrease with decreasing molar ratio of Li salt to G4. Like-ion anticorrelations are generally stronger than cation–anion anticorrelations and are particularly strong for the heavier type of ion. We have analyzed in detail the influence of these ion correlations on two types of Li+ transference numbers, namely the mobility-based Li+ transference numbers and the Li+ transference numbers under anion-blocking conditions, as well as on the Haven ratio. Our results are at variance with concepts explaining transference numbers and Haven ratio by ion pair formation and ionicity exclusively, since these imply positive cation–anion correlations. We conclude that in the present systems, momentum conservation and the resulting ion anticorrelations are far more important than ion pair formation.
1 mixture and decrease with decreasing molar ratio of Li salt to G4. Like-ion anticorrelations are generally stronger than cation–anion anticorrelations and are particularly strong for the heavier type of ion. We have analyzed in detail the influence of these ion correlations on two types of Li+ transference numbers, namely the mobility-based Li+ transference numbers and the Li+ transference numbers under anion-blocking conditions, as well as on the Haven ratio. Our results are at variance with concepts explaining transference numbers and Haven ratio by ion pair formation and ionicity exclusively, since these imply positive cation–anion correlations. We conclude that in the present systems, momentum conservation and the resulting ion anticorrelations are far more important than ion pair formation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures, and derivations of linear response theory expressions. See DOI: 10.1039/d0cp06147f
1 mixtures, and derivations of linear response theory expressions. See DOI: 10.1039/d0cp06147f