Spatial dimensionality and the binding of small clusters†
Received
21st September 2020
, Accepted 10th November 2020
First published on 10th November 2020
Abstract
The effect of spatial dimensionality D on the near-threshold binding of small clusters of identical particles is shown. Estimates of the threshold coupling constants for 2 and N bosons are given for D equal to 1 to 5 and the relation to conditions for the Efimov effect is discussed. Variational trial functions for 4 identical spin-½ fermions in D = 2 are given.
I. Introduction
Helium atoms provide extreme examples of quantum effects in the binding of small atomic clusters. For 4He, the dimer,1,2 the ground-state trimer,3,4 and the Efimov state of the excited trimer5 have been detected in experiments with atomic beams. The corresponding clusters 3He2 and 3He3 of 3He are not self-bound. One direction of research has been to follow the (possible) binding in larger clusters.6–8
On the other hand, one may study the relation of the stability of small clusters relative to such self-bound many-body liquids as liquid 4He (N-bosons) and liquid 3He (N-fermions). This turns out to be strongly dependent on the spatial dimension9–11 (integer) D, as is further discussed here in Section II for N-boson thresholds. Related ideas of corresponding states have been used for families of pair potentials in the inert gases,12 for the effects of quantum mechanics on the gas–liquid critical point,13 and for the evolution of the ground state of a many-body system from gas to liquid to solid as a function of the quantum parameter.9,11 The information for the many-fermion system is more limited. There has been a demonstration of dimerization for 4-fermions near the dimer threshold in two dimensions (D = 2).14 In Section III, an extension of the spin algebra for 4 identical spin-½ fermions15 to D = 2 is given and the relation to estimates based on 2-body thresholds16,17 is discussed.
Throughout this paper, atoms of mass m are assumed to interact via central pair potentials. Quantitative results in Section II are given for threshold coupling constants for the Lennard-Jones (12,6) potential,
| | | ϕ(r) = 4ε[(σ/r)12 − (σ/r)6], | (1) |
with energy minimum
ε and length scale
σ. The coupling constant is defined to be
K = 4
mεσ2/
ħ2 which is related to the de Boer parameter
Λ* by
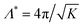
. This potential is often used as a near-realistic model in corresponding states scalings.
11,13 Formulation of phase diagrams or critical point parameters as a function of
K enables extrapolations and interpolations when estimating the effects of the changes in effective potential that occur in transferring from
D = 3 to an adsorbed monolayer.
Efimov states for three atoms arise for 4He3ref. 5 and in observations of trapped atoms.18 There are19,20 very weakly self-bound nominally 2D phases of 3He that have been modeled as many-fermion bound states.21,22 While the present paper treats systems of identical particles, it is important to note theoretical treatments of cluster of unequal masses that demonstrate the Efimov effect23 may occur in other dimensions.24–27
The organization of this paper is as follows: Section II contains the treatment of 2 and N identical spin-0 bosons and Section III reports results for 4 identical spin-½ fermions. Section IV contains conclusions.
II. Two and N bosons
Efimov23 showed that for coupling constants in a very narrow range close to the dimer threshold there is a series of loosely bound excited trimer states. His construction, for three spatial dimensions (D = 3), showed that the threshold coupling constant for the ground state trimer is less than that for the dimer. Lim et al.28 demonstrated the existence of a very weakly bound (ca. 1 mK) excited state of 4He3 and later calculations5 confirmed that the excited state does depend on coupling constant as predicted by Efimov. However, although the Efimov effect of three identical bosons does not occur in two spatial dimensions (D = 2), there does exist a weakly bound trimer excited state near the dimer threshold29,30 and universality conditions apply for finite range potentials.30,31
It is noteworthy that a variational calculation of the N-boson threshold coupling constant coincides with the dimer threshold in D = 29 and D = 1.10 Studies in fractional dimension ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) show27,30 that the Efimov effect occurs only for 2.3 <
show27,30 that the Efimov effect occurs only for 2.3 < ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) < 3.8. Here, variational estimates32 of the 2-boson and N-boson threshold will be given for dimension D = 1, 2, 3, 4, 5. The pair potential is the LJ(12,6) model of eqn (1) and the N-boson variational trial function has the Jastrow form
< 3.8. Here, variational estimates32 of the 2-boson and N-boson threshold will be given for dimension D = 1, 2, 3, 4, 5. The pair potential is the LJ(12,6) model of eqn (1) and the N-boson variational trial function has the Jastrow form
| | 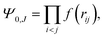 | (2) |
with factors
f of the form
the length scale
b and the power
s are variational parameters. A cluster expansion of the trial energy
Et for
N bosons in the
D-dimensional volume
Ω gives a low density estimate:
| | 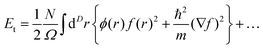 | (4) |
subject to
| | 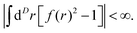 | (5) |
The integral in
eqn (4) also appears in the expectation value for the dimer trial energy but using a trial function
ψ(
r) subject to a different boundary condition than
f(
r). The form used here is
where
η depends on
D and the angular momentum; it is chosen to make the large-
r asymptote of
ψ match to the subdominant solution to the zero energy two-body Schrödinger equation. Upper bounds on the threshold coupling constants for 2 and
N bosons are obtained by locating the coupling constant
K that makes the corresponding
r-integrals equal zero after optimization of
b and
s. With these trial functions, the integrals are done analytically in terms of
Γ-functions.
32 More generally this condition may also be satisfied by integrating a two-body zero-energy Schrödinger equation, but in the cases where that has been done, the results from the variational calculation are within 0.1% of those of the numerical integrations. Results are shown for the 2 (S – wave) and
N-boson thresholds for
D = 1 to 5 in
Table 1. Additionally the thresholds for dimers with 1 and 2 units of angular momentum (“P” and “D”) in 2 and 3 dimensions are given in
Table 2, where it may be seen that the simple correlation factor
eqn (3) gives a fine approximation.
Table 1 Variational estimates of threshold coupling constants K2 and KN for the 2 (L = 0,S-wave) and many-boson ground states with the Lennard-Jones (12,6) pair potential in D dimensions. η is the power law for the dimer trial function
|
D
|
η
|
K
2
|
K
N
|
|
Krotscheck et al.10
Using14η = 1/2 leads to K2 = 17.96, and does not give a bound 3He2, for which K ≃ 16.6.
Miller and Nosanow9 and Cabral33 give for the Schrödinger solution K2 = KN = 14.744.
Schrödinger solutions are K2 = 22.362 and KN = 8.6725.
|
| 1 |
0 |
22.368 |
22.368a |
| 2 |
0 |
14.753bc |
14.753c |
| 3 |
1 |
22.368 |
8.676d |
| 4 |
2 |
31.54 |
4.16 |
| 5 |
3 |
42.23 |
1.218 |
Table 2 Dimer threshold coupling constants for the Lennard-Jones(12,6) pair potential for states with 1 (“P”) and 2 (“D”) units of orbital angular momentum, using the dimer trial functions of eqn (7)
|
D
|
η
P
|
K
P
|
η
D
|
K
D
|
|
Schrödinger solution33 gives 31.516.
Schrödinger solutions35 give 42.2 and 68.2, respectively.
|
| 2 |
1 |
31.54a |
2 |
54.35 |
| 3 |
2 |
42.23b |
3 |
68.23b |
It is remarkable that the 2 and N-boson threshold are identical in D = 1 and 2 and that the difference increases for higher dimension. Although the N-boson values are based on the Jastrow trial function, there is no example showing that this fails to locate the threshold in D = 2. A search for the Efimov effect for 3 identical bosons in D = 2, which would have demonstrated a failure of the Jastrow form in D = 2, was unsuccessful29 and later work27,30 reinforced the conclusion that the effect is absent in D = 2 and also showed it is absent for D = 4. Thus the results for D = 4 and 5 in Table 1 show that another mechanism must be acting to separate the 2 and N boson thresholds there.
III. Binding of four identical fermions
Quantum statistics effects, arising from the requirement of antisymmetric total wave functions, lead to more complex analyses for identical spin-½ fermions.14,15,33,34 For two such particles, the spatial component of the ground state wave function can be the same as for bosons of the same mass, with the antisymmetry arising from the spin component. Already for three and four fermions, the mixing of space and spin components introduces enough complexity that there are few systematic studies available for four fermions.14,34 Bounds on the ground state energy using 2-body comparison problems, the Hall-Post inequalities,16,17 provide some indirect information. Here results for 4-fermions in D = 3 are extended to D = 2 (a Cartesian x–y plane) and a comparison is given to results for Hooke's law oscillators.
Jacobi coordinates for 4 identical particles are
| | 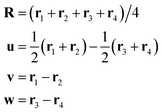 | (7) |
The states of total spin S for 4 spin-½ fermions are one of S = 2 (degeneracy 5), three of S = 1 (each of degeneracy 3) and two of S = 0 (each non-degenerate). The total wave function for S = 2 is a product of space and spin factors, but for S = 1 and S = 0 the total wave function is a sum of factored pieces. The requirements imposed by antisymmetry of the total wave function have been given elsewhere.15 For D = 3, trial wave functions based on the Jastrow product eqn (2) and factors with 0 (S = 2), 1 (S = 1) and 2 or 0 (S = 0) units of orbital angular momentum have been given.15
Analytical results for the 4-body problem using the Hooke's law pair potential,
| | 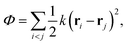 | (8) |
are known in terms of normal modes. The internal Jacobi coordinates
u,
v,
w all have oscillator frequencies
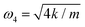
, while the frequency for a dimer of reduced mass
μ is
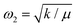
. The (Hall) lower bounds
15,16 in terms of the ground state and first odd parity excited state energies of two-body problems with effective mass
μ,
E0(2,
μ) and
E1(2,
μ) are
| | | E0(4f,S = 2) ≥ 6E1(2,m) = 3ħω4[1 + (D/2)]. | (9) |
| | | E0(4f,S = 1) ≥ 2[E0(2,m) + 2E1(2,m)] = ħω4[2 + (3D/2)]. | (10) |
| | | E0(4f,S = 0) ≥ 3[E0(2,m) + E1(2,m)] = ħω4[(3/2)(D + 1)]. | (11) |
The final equalities in these equations are the values obtained for Hooke's law oscillators in
D-dimensions. The analytic solution for Hooke's law oscillators achieves the lower bounds in
D = 3 for
S = 2 and
S = 1 but not for
S = 0. For the 3-fermion cases, the corresponding lower bounds are achieved
15 for both
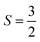
and
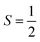
. The lower bound for 4 bosons,
E0(4
b) ≥ 6
E0(2,
m) is also achieved.
16
In extending the results15 to D = 2, two difficulties arise: (1) the spatial component of the S = 2 trial function is a determinant that does not adapt to D = 2. (2) The spatial factors of nonzero angular momentum in D = 3 are given in terms of a real component of the spherical harmonics but that does not arise in D = 2. Resolutions to both difficulties are given here.
To begin a resolution of (1), a totally antisymmetric spatial wave function factor F2 for the S = 2 case is constructed with 4 factors of the internal Jacobi coordinates. It is, for Cartesian components of the Jacobi coordinates α to δ chosen to be x or y of D = 2,
| | 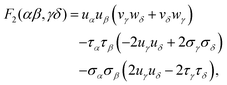 | (12) |
with
σα = (
vα +
wα)/2 and
τα = (
vα −
wα)/2. However this is not an angular momentum eigenstate. The two trial functions
| | | Ψ(0,F) = [F2(xy,xx) − F2(xy,yy)]Ψ0,J | (13) |
| | | Ψ(4,F) = [F2(xx,xy) + F2(yy,xy)]Ψ0.J | (14) |
are totally antisymmetric wavefunctions that are eigenfunctions of
Lz2 (
Lz is the
z-component of total angular moment) with eigenvalues
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2ħ2
z2ħ2, for
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z
z = 0 and 2, respectively.
The resolution of (2) for D = 2 needed for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z ≠ 0, which also applies in adapting trial functions presented for D = 3, is to form the combination
z ≠ 0, which also applies in adapting trial functions presented for D = 3, is to form the combination
| | Ψ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z) = [ z) = [![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) zħ + Lz]Ψ( zħ + Lz]Ψ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2,F), z2,F), | (15) |
which is an antisymmetric trial function with
Lz eigenvalue
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) zħ
zħ.
Ψ(
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2
z2,
F) for
D = 2 is given in
eqn (14). Although this trial function is formally complex, expectation values reduce to real-number calculations,
e.g.,
| | (Ψ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z),HΨ( z),HΨ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z)) = 2 z)) = 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2ħ2(Ψ( z2ħ2(Ψ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2,F),HΨ( z2,F),HΨ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2,F)) z2,F)) | (16) |
for a Hamiltonian
H that commutes with
Lz. Then the wave functions of
eqn (13) and (14) lead to variational estimates
E(4
f,
S = 2)
t = 7
ħω4 for the Hooke's law model and do not achieve the lower bound 6
ħω4 of
eqn (9). To summarize, the lower bound for
S = 2 is achieved for
D ≥ 3 and for
S = 1 is achieved for
D ≥ 2, but the lower bound for
S = 0 is not achieved for either
D = 3 or
D = 2; in fact,
E0(4
f,
S = 0) =
ħω4[(3
D/2) + 2]. The general inequalities are satisfied in these cases though.
There is limited computational experience with such fermion trial functions. Lim and co-workers34 treated the S = 0 case of 3He4 in D = 3 and found no self-binding. They did find that the L = 2 configuration seemed to be closer to binding than the L = 0 configuration and interpreted this difference as arising from wave function nodes that occur as a function of angle rather than as a function of radius. A similar phenomenon happens35 for 3 boson in D = 3. Vranjeŝ and Kilić14 treated the S = 0, L = 0 case in D = 2 and found dimerization (2 S = 0 dimers) for 3He parameters, but not a self-bound configuration of 3He4. That result is consistent with the conclusion of Miller and Nosanow9 that the threshold for many-fermion self-binding is significantly larger than the dimer threshold.
It is not known what if any connection there is between these results and the dimerization observed for trapped atoms.36 The corresponding question in nuclear physics, the stability of the tetra-neutron, remains unsettled.37
IV. Conclusions
The merging of threshold coupling constants for 2 and N bosons in D = 1 and D = 2 correlates with the absence of the Efimov effect there. However the Efimov effect is absent also for D = 4 and D = 5 while the 2 and N boson threshold coupling constants are well-separated there. Whether this contrast is coincidental is not known. It may be clarified with extensions of the construction originally used by Efimov23 to demonstrate the existence of long-range effective interactions.
Hooke's law springs have provided many examples where the Hall-Post lower bounds on the ground state energies of few-body systems are attained. The 4-fermion system in D = 2 and D = 3 provides cases where the lower bound is not attained. More systematic studies using group theoretic constraints for few-fermion systems near threshold appear to be warranted, especially as there is a self-bound state of 3He on graphite that has a very low areal density.19,22
Conflicts of interest
There are no conflicts to declare.
References
- F. Luo, G. C. McBane, G. Kim, C. F. Giese and W. R. Gentry, J. Chem. Phys., 1993, 98, 3564–3567 CrossRef CAS.
- W. Schöllkopf and J. P. Toennies, Science, 1994, 266, 1345–1348 CrossRef.
- L. W. Bruch, W. Schöllkopf and J. P. Toennies, J. Chem. Phys., 2002, 117, 1544–1566 CrossRef CAS.
- J. Voigtsberger, S. Zeller, J. Becht, N. Neumann, F. Sturm, H.-K. Kim, M. Waitz, F. Trinter, M. Kunitski, A. Kalinin, J. Wu, W. Schöllkopf, D. Bressanini, A. Czasch, J. B. Williams, K. Ullmann-Pfleger, L. Ph. H. Schmidt, M. S. Schöffler, R. E. Grisenti, T. Jahnke and R. Dörner, Nat. Commun., 2014, 5, 5765 CrossRef CAS.
- M. Kunitski, S. Zeller, J. Voigtsberger, A. Kalinin, L. Ph. H. Schmidt, M. Schöffler, A. Czasch, W. Schöllkopf, R. E. Grisenti, T. Jahnke, D. Blume and R. Dörner, Science, 2015, 348, 551–555 CrossRef CAS.
- M. Lewerenz, J. Chem. Phys., 1997, 106, 4596–4603 CrossRef CAS; E. Krotscheck and R. Zillich, J. Chem. Phys., 2001, 115, 10161–10174 CrossRef.
- V. R. Pandharipande, S. C. Pieper and R. B. Wiringa, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 4571–4582 CrossRef CAS.
- E. Sola, S. Casulleras and J. Boronat, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 092515 CrossRef.
- M. D. Miller and L. H. Nosanow, J. Low Temp. Phys., 1978, 32, 145–157 CrossRef CAS.
- E. Krotscheck, M. D. Miller and J. Wojdylo, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 13028–13037 CrossRef CAS.
- L. H. Nosanow, L. J. Parish and F. J. Pinski, Phys. Rev. B: Solid State, 1975, 11, 191–204 CrossRef CAS.
- K. T. Tang and J. P. Toennies, J. Chem. Phys., 2003, 118, 4976–4983 CrossRef CAS.
-
J. de Boer and R. B. Bird, in Molecular Theory of Gases and Liquids, ed. J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Wiley, New York, 1965, ch. 10 Search PubMed.
- L. Vranjeŝ and S. K. Kilić, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 042506 CrossRef.
- L. W. Bruch, J. Chem. Phys., 1980, 72, 5511–5515 CrossRef CAS.
- R. L. Hall, J. Phys. A: Gen. Phys., 1968, 1, 468–474 CrossRef.
- J. M. Richard, A. Volcarce and J. Vijande, Ann. Phys., 2020, 412, 168009 CAS.
- R. Grimm, Few-Body Syst., 2019, 60, 23 CrossRef.
- D. Sato, K. Naruse, T. Matsui and H. Fukuyama, Phys. Rev. Lett., 2012, 109, 25306 Search PubMed.
- S. Nakamura, K. Matsui, T. Matsui and H. Fukuyama, Phys. Rev. B, 2016, 94, 180501 CrossRef.
- M. Ruggeri, E. Vitali, D. E. Galli, M. Boninsegni and S. Morono, Phys. Rev. B, 2016, 93, 104102 CrossRef.
- M. C. Gordillo and J. Boronat, Phys. Rev. Lett., 2016, 116, 145301 CrossRef CAS.
- V. Efimov, Phys. Lett. B, 1970, 33, 563–564 CrossRef CAS ; Sov. J. Nucl. Phys., 1971, 12, 589–595 [Yad. Fiz., 1970, 12, 1080–1091].
- S. Moroz, J. P. D'Inaco and D. S. Petrov, Phys. Rev. Lett., 2015, 115, 180406 CrossRef.
- M. T. Yamahsita, Few-Body Syst., 2019, 60, UNSP22 CrossRef.
- Y. Nishida, Phys. Rev. Lett., 2017, 118, 230601 CrossRef.
- D. E. Rosa, T. Frederico, G. Kreim and M. T. Yamashita, Phys. Rev. A, 2018, 97, 050701 CrossRef CAS.
- T. K. Lim, K. Duffy and W. C. Damert, Phys. Rev. Lett., 1977, 38, 341–343 CrossRef CAS.
- L. W. Bruch and J. A. Tjon, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 19, 425–432 CrossRef CAS.
- E. Nielsen, D. V. Fedorov, A. S. Jensen and A. Garrido, Phys. Rep., 2001, 347, 373–459 CrossRef CAS.
- D. Blume, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 095410 CrossRef.
- L. W. Bruch, Phys. Rev. B: Solid State, 1976, 13, 2873–2876 CrossRef CAS ; 1984, 30, 6769(E).
- F. Cabral and L. W. Bruch, J. Chem. Phys., 1979, 70, 4669–4672 CrossRef CAS.
- S. Nakaishi-Maeda, T. K. Lim and Y. Akaishi, J. Chem. Phys., 1982, 77, 5581–5583 CrossRef.
- L. W. Bruch, J. Chem. Phys., 1999, 110, 2410–2413 CrossRef CAS.
- M. Yu. Kagan and A. V. Turlapov, Phys.-Usp., 2019, 62, 215–248 CrossRef CAS.
- M. D. Higgins, C. H. Greene, A. Kievsky and M. Viviani, Phys. Rev. Lett., 2020, 125, 052501 CrossRef CAS; O. Ivanytskyi, M. Angeles Perez Garcia and C. Albertus, Eur. Phys. J. A, 2019, 55, 184 CrossRef; M. Kisamori,
et al.
, Phys. Rev. Lett., 2016, 116, 052501 CrossRef.
Footnote |
| † PACS numbers: 36.40.-c, 31.15.ac. |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here. 
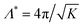 . This potential is often used as a near-realistic model in corresponding states scalings.11,13 Formulation of phase diagrams or critical point parameters as a function of K enables extrapolations and interpolations when estimating the effects of the changes in effective potential that occur in transferring from D = 3 to an adsorbed monolayer.
. This potential is often used as a near-realistic model in corresponding states scalings.11,13 Formulation of phase diagrams or critical point parameters as a function of K enables extrapolations and interpolations when estimating the effects of the changes in effective potential that occur in transferring from D = 3 to an adsorbed monolayer.
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) show27,30 that the Efimov effect occurs only for 2.3 <
show27,30 that the Efimov effect occurs only for 2.3 < ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) < 3.8. Here, variational estimates32 of the 2-boson and N-boson threshold will be given for dimension D = 1, 2, 3, 4, 5. The pair potential is the LJ(12,6) model of eqn (1) and the N-boson variational trial function has the Jastrow form
< 3.8. Here, variational estimates32 of the 2-boson and N-boson threshold will be given for dimension D = 1, 2, 3, 4, 5. The pair potential is the LJ(12,6) model of eqn (1) and the N-boson variational trial function has the Jastrow form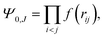
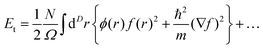
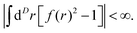
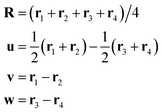
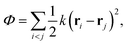
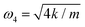 , while the frequency for a dimer of reduced mass μ is
, while the frequency for a dimer of reduced mass μ is 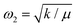 . The (Hall) lower bounds15,16 in terms of the ground state and first odd parity excited state energies of two-body problems with effective mass μ, E0(2,μ) and E1(2,μ) are
. The (Hall) lower bounds15,16 in terms of the ground state and first odd parity excited state energies of two-body problems with effective mass μ, E0(2,μ) and E1(2,μ) are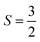 and
and 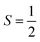 . The lower bound for 4 bosons, E0(4b) ≥ 6E0(2,m) is also achieved.16
. The lower bound for 4 bosons, E0(4b) ≥ 6E0(2,m) is also achieved.16
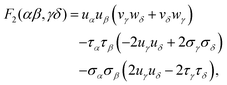
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2ħ2, for
z2ħ2, for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z = 0 and 2, respectively.
z = 0 and 2, respectively.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z ≠ 0, which also applies in adapting trial functions presented for D = 3, is to form the combination
z ≠ 0, which also applies in adapting trial functions presented for D = 3, is to form the combination![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z) = [
z) = [![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) zħ + Lz]Ψ(
zħ + Lz]Ψ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2,F),
z2,F),![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) zħ. Ψ(
zħ. Ψ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2,F) for D = 2 is given in eqn (14). Although this trial function is formally complex, expectation values reduce to real-number calculations, e.g.,
z2,F) for D = 2 is given in eqn (14). Although this trial function is formally complex, expectation values reduce to real-number calculations, e.g.,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z),HΨ(
z),HΨ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z)) = 2
z)) = 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2ħ2(Ψ(
z2ħ2(Ψ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2,F),HΨ(
z2,F),HΨ(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) z2,F))
z2,F))