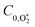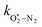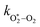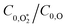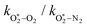Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photoacoustic studies of energy transfer from ozone photoproducts to bath gases following Chappuis band photoexcitation†
Michael I.
Cotterell
 *a,
Kate
Szpek
*a,
Kate
Szpek
 b,
David A.
Tiddeman
b,
Jim M.
Haywood
bc and
Justin M.
Langridge
b
b,
David A.
Tiddeman
b,
Jim M.
Haywood
bc and
Justin M.
Langridge
b
aSchool of Chemistry, University of Bristol, Bristol, BS8 1TS, UK. E-mail: m.cotterell@bristol.ac.uk
bObservation Based Research, Met Office, Exeter, EX1 3PB, UK
cCollege for Engineering, Mathematics and Physical Sciences, University of Exeter, Exeter, EX4 4QF, UK
First published on 8th December 2020
Abstract
Photoacoustic spectroscopy (PAS) is a sensitive technique for the detection of trace gases and aerosols and measurements of their absorption coefficients. The accuracy of such measurements is often governed by the fidelity of the PAS instrument calibration. Gas samples laden with O3 of a known or independently measured absorption coefficient are a convenient and commonplace route to calibration of PAS instruments operating at visible wavelengths (λ), yet the accuracy of such calibrations remains unclear. Importantly, the photoacoustic detection of O3 in the Chappuis band (λ ∼ 400–700 nm) depends strongly on the timescales for energy transfer from the nascent photoproducts O(3P) and O2(X, v > 0) to translational motion of bath gas species. Significant uncertainties remain concerning the dependence of these timescales on both the sample pressure and the bath gas composition. Here, we demonstrate accurate characterisation of microphone response function dependencies on pressure using a speaker transducer to excite resonant acoustic modes of our photoacoustic cells. These corrections enable measurements of photoacoustic response amplitudes (also referred to as PAS sensitivities) and phase shifts with variation in static pressure and bath gas composition, at discrete visible wavelengths spanning the Chappuis band. We develop and fit a photochemical relaxation model to these measurements to retrieve the associated variations in the aforementioned relaxation timescales for O(3P) and O2(X, v > 0). These timescales enable a full assessment of the accuracy of PAS calibrations using O3-laden gas samples, dependent on the sample pressure, bath gas composition and PAS laser modulation frequency.
1 Introduction
Photoacoustic spectroscopy (PAS) has become a central technique for sensitive and accurate measurements of trace gases,1–6 and aerosol light absorption.7–14 A central and motivating feature of our research is the application of PAS to measurements of absorption coefficients (αabs) at visible wavelengths for atmospheric aerosol, and developing PAS instruments that operate from the UK BAe-146 atmospheric research aircraft.15–19 The magnitude of aerosol light absorption, and thus the representation of absorbing aerosols in climate models, is highly uncertain.20,21 PAS is also an invaluable tool in the study of aerosol mixing state, with our spectroscopic measurements enabling changes in particle composition to be inferred and the validity of optical mixing rules (effective medium approximations) to be challenged.10,22 Underpinning measurements of αabs using PAS is the accurate calibration of PAS instruments. This work assesses rigorously the conditions under which PAS instruments operating at visible wavelengths are calibrated accurately using O3-laden gas, a common calibrant of photoacoustic spectrometers.Previous work suggested that O3-laden gas samples could be a poor calibrant of PAS instruments operating at visible wavelengths.8 Meanwhile, our own PAS studies at visible wavelengths have demonstrated that calibrations using O3-laden gas can provide calibrations of high accuracy under specific conditions,10 and that the level of accuracy is sensitive to the bath gas composition.23,24 Importantly, O3 undergoes photolysis at visible wavelengths (Chappuis band) and the bath gas composition governs the timescales on which energy from the nascent photoproducts transfers into translational motion of the bath species that drives the formation of a photoacoustic pressure wave.
One remaining knowledge gap, particularly relevant to PAS measurements from research aircraft at reduced atmospheric pressures, is the dependence of the calibration accuracy on pressure. These measurements are particularly challenging as they require methods to correct for other pressure dependencies in the photoacoustic transduction process, including the response function for the detection microphone. Moreover, direct measurements have not been reported for the photoproduct relaxation timescales that govern the accuracy of calibrations. Here, we report measurements of the variation in photoacoustic calibration coefficient (referred to as the sensitivity) with the bath gas composition (consisting of controlled fractions of O2 and N2) and the sample pressure over the range 300–1000 hPa. To enable these measurements, we validate a pressure correction scheme that accounts for changes in the microphone response function and the resonance characteristics of a photoacoustic resonator that amplifies generated photoacoustic pressure waves. Importantly, we also measure the photoacoustic phase shift with respect to the periodic modulation cycle of the excitation laser source, providing a direct measurement of the relaxation timescale for the nascent O3 photoproducts. We then demonstrate closure between our measured PAS sensitivities and phase shifts with a photochemical model that describes the relaxation of Chappuis band photoproducts in different bath gas mixtures and sample pressures.
In the remainder of this introduction, Section 1.1 describes pertinent aspects to photoacoustic signal generation and detection, Section 1.2 compares approaches to PAS instrument calibration, Section 1.3 describes the impact of Chappuis-band photochemistry on calibrations using O3-laden gas, and Section 1.4 outlines the remaining knowledge gaps that preclude assessments of the fidelity of O3-based calibrations that form the motivation for this work.
1.1 Photoacoustic signal generation and detection
A typical PAS instrument uses laser light to irradiate a light absorbing sample contained within a photoacoustic cell.25 In our detection scheme, the laser intensity I is modulated periodically at an angular frequency ω such that I(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = I0g(
,t) = I0g(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )(1 + eiωt)/2, in which I0 is the intensity amplitude, g(
)(1 + eiωt)/2, in which I0 is the intensity amplitude, g(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the intensity distribution function with position
) is the intensity distribution function with position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , and t is time. The sample irradiated by the laser will absorb light, and energy is deposited in the photoacoustic cell with an energy density H(
, and t is time. The sample irradiated by the laser will absorb light, and energy is deposited in the photoacoustic cell with an energy density H(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) described by:
,t) described by:H(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = αabs( ,t) = αabs(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )I( )I(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) ,t) | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the spatial distribution in the sample absorption coefficient. Following light absorption, the analyte (i.e. an aerosol particle or a gaseous absorber) is photoexcited; for aerosols, this photoexcitation energy rapidly transfers into translational energy on a rapid picosecond timescale that heats the droplet. The generation of a photoacoustic signal requires this highly localised energy to transfer to translational modes of the surrounding bath gas. The increase in bath gas translational energy close to the heated or photoexcited sample causes adiabatic expansion of the bath gas and creates a pressure disturbance. Thus, the transient nature to H(
) is the spatial distribution in the sample absorption coefficient. Following light absorption, the analyte (i.e. an aerosol particle or a gaseous absorber) is photoexcited; for aerosols, this photoexcitation energy rapidly transfers into translational energy on a rapid picosecond timescale that heats the droplet. The generation of a photoacoustic signal requires this highly localised energy to transfer to translational modes of the surrounding bath gas. The increase in bath gas translational energy close to the heated or photoexcited sample causes adiabatic expansion of the bath gas and creates a pressure disturbance. Thus, the transient nature to H(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) through periodic modulation of the laser intensity forms pressure (acoustic) waves in the bath gas. For coherent generation of a photoacoustic signal, we require efficient (fast) energy transfer from the sample into bath gas translational energy. Energy transfer can be slow for large aerosol particles (larger than ∼2 μm in diameter) or those containing volatile components that facilitate energy dissipation through latent heat flux, leading to notable suppression in the generated acoustic pressure waves.26–28 For photoexcitation of gaseous light absorbers, energy transfer to bath gas translational modes occurs through vibration-to-translation (V–T) transitions and is often in competition with processes that do not contribute to acoustic signal generation.6,24,29 Such processes include photodissociation, fluorescence and vibration-to-vibration transitions. We discuss these aspects of quenching timescales and competing energy transfer pathways for photoexcited O3 in more detail below. Following their generation, acoustic pressure waves are coupled into a resonant mode of a photoacoustic cell and are amplified. This cell has an eigenmode pressure distribution that is intrinsic to the cell geometry, with an associated resonance frequency (eigenfrequency) at which the eigenmode is optimally excited.25,30,31 By modulating the laser intensity at the cell eigenfrequency, the generated photoacoustic waves resonantly excite the cell eigenmode. The quality (Q) factor (which describes the acoustic energy stored in the eigenmode relative to that lost through damping processes) is typically in the range 50–90; higher Q denotes larger acoustic amplification factors. A sensitive microphone is placed at an antinode in the eigenmode pressure distribution for detection of the amplified pressure response. For efficient excitation of a single pressure eigenmode pn (with n denoting the mode index) at the corresponding eigenfrequency fn = ωn/(2π), the acoustic pressure at the microphone location is described by:25,30,31
,t) through periodic modulation of the laser intensity forms pressure (acoustic) waves in the bath gas. For coherent generation of a photoacoustic signal, we require efficient (fast) energy transfer from the sample into bath gas translational energy. Energy transfer can be slow for large aerosol particles (larger than ∼2 μm in diameter) or those containing volatile components that facilitate energy dissipation through latent heat flux, leading to notable suppression in the generated acoustic pressure waves.26–28 For photoexcitation of gaseous light absorbers, energy transfer to bath gas translational modes occurs through vibration-to-translation (V–T) transitions and is often in competition with processes that do not contribute to acoustic signal generation.6,24,29 Such processes include photodissociation, fluorescence and vibration-to-vibration transitions. We discuss these aspects of quenching timescales and competing energy transfer pathways for photoexcited O3 in more detail below. Following their generation, acoustic pressure waves are coupled into a resonant mode of a photoacoustic cell and are amplified. This cell has an eigenmode pressure distribution that is intrinsic to the cell geometry, with an associated resonance frequency (eigenfrequency) at which the eigenmode is optimally excited.25,30,31 By modulating the laser intensity at the cell eigenfrequency, the generated photoacoustic waves resonantly excite the cell eigenmode. The quality (Q) factor (which describes the acoustic energy stored in the eigenmode relative to that lost through damping processes) is typically in the range 50–90; higher Q denotes larger acoustic amplification factors. A sensitive microphone is placed at an antinode in the eigenmode pressure distribution for detection of the amplified pressure response. For efficient excitation of a single pressure eigenmode pn (with n denoting the mode index) at the corresponding eigenfrequency fn = ωn/(2π), the acoustic pressure at the microphone location is described by:25,30,31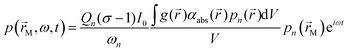 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the eigenmode pressure distribution and pn(
) is the eigenmode pressure distribution and pn(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M) is the eigenmode pressure at the location of the microphone. The voltage output from the microphone is thus a sinusoidal waveform, the amplitude of which is referred to as the photoacoustic signal amplitude S. A further quantity extracted from the microphone waveform is the phase shift in the microphone response with respect to the laser power modulation (θ). This phase is a direct measure of the timescale (τ) of energy transfer to bath gas translational modes:6
M) is the eigenmode pressure at the location of the microphone. The voltage output from the microphone is thus a sinusoidal waveform, the amplitude of which is referred to as the photoacoustic signal amplitude S. A further quantity extracted from the microphone waveform is the phase shift in the microphone response with respect to the laser power modulation (θ). This phase is a direct measure of the timescale (τ) of energy transfer to bath gas translational modes:6| θ = tan−1(ωnτ) | (3) |
1.2 Calibration of photoacoustic spectrometers
Assuming that energy transfer to bath gas translational modes is fast and efficient, the PAS sensitivity (C) is defined by: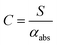 | (4) |
In contrast, PAS calibrations using a gaseous light absorber typically pass the gas sample through both a PAS instrument and a cavity ring-down spectrometer in a serial flow configuration, with cavity ring-down spectroscopy providing an independent and direct (calibration-free) measurement of αabs for gases. Commonly, calibration gases for visible wavelength PAS instruments contain concentrations of either NO2,35–37 or O3.10,38–40 NO2 has a strong and broad absorption band across the visible spectrum.41 However, the high photolysis quantum yield for NO2 at visible wavelengths below 420 nm degrades the calibration accuracy.36,42 When using NO2 to calibrate PAS instruments operating at wavelengths (λ) of 375 and 405 nm, Nakayama et al. observed biases in C of 48% and 36% respectively attributed to NO2 photolysis, while no detectable biases were observed for longer wavelength PAS instruments (λ = 532, 781 nm).36
Ozone also has a broad absorption band (Chappuis band) over the visible wavelength range 400–700 nm.41,43 Chappuis band absorption is up to five orders of magnitude weaker than that for NO2 at short visible wavelengths. Nonetheless, O3-laden gas has been used successfully to calibrate PAS instruments at discrete visible wavelengths spanning the Chappuis band.10,22,32,38–40 Until recently, the impacts of O3 photolysis in the Chappuis band on the accuracy of PAS calibrations had not been explored. However, Fischer and Smith23 and ourselves24 have reported the strong impact of bath gas and wavelength-dependent O3 photolysis on the accuracy of these calibrations and we now discuss these dependencies.
1.3 The impact of O3 photochemistry on calibrations of photoacoustic spectrometers
We have previously reported accurate calibrations of our PAS instruments (λ = 405, 514 and 658 nm) using O3-laden air, with O3 concentrations up to 680 ppmv diluted into a bath gas of air.10,22 Using our O3-calibrated PAS, we compared measured aerosol absorption cross sections with those calculated by a Lorenz–Mie routine for laboratory-generated dry nigrosin aerosols. Importantly, there were no detectable biases in C within the measurement uncertainty of the aerosol cross sections at the three discrete PAS wavelengths.Recognising that researchers often use different bath gas compositions for their O3-laden calibration gases, Fischer and Smith measured the dependence of C on the bath gas composition.23 The authors varied the relative bath gas fractions of O2 and N2 and recorded the associated variations in C for λ = 532, 662, 780 nm. They reported that C increased with the O2 fraction and approached an asymptote in the limit of pure O2 that agreed with calibrations performed using either NO2-laden gas or using aerosol calibrants. Meanwhile, C reduced by a factor of two in the limit of a pure N2 bath gas. Within measurement uncertainty, the asymptote for C was attained for a bath gas O2 mass fraction xO2 ≥ 0.2. This latter observation agrees with our aforementioned finding that accurate calibrations of PAS instruments can be achieved with O3-laden air (xO2 ∼ 0.25). Fischer and Smith accounted for the measured asymptotic behaviour using a kinetic model that treated the relative rates with which photoexcited O3 is quenched by either O2 or N2 bath species. Their model attributed the drop in C at low O2 concentrations to inefficient energy transfer from photoexcited O3 to N2 translational modes and the authors recommended that calibrations used a bath gas of O2.
Fischer and Smith did not assess the bath gas dependence in C for short visible wavelengths, such as for λ = 405 nm that is used in our instruments. Moreover, the quenching model developed by Fisher and Smith attributed the photoacoustic signal generation to direct relaxation of 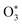 (with the superscript * implying that O3 is in an electronically excited state) and did not account for the known photodissociation of O3 within the Chappuis band. Thus, our more recent publication assessed the bath gas composition dependence to C for our own spectrometers and observed wavelength dependence to this bath gas dependency.24 Our λ = 658 nm measurements demonstrated an asymptote in agreement with Fischer and Smith's observations, while measurements for λ = 405 nm found that C was maximised for xO2 in the range 0.2–0.3 and decreased by 11% as the bath gas composition tended to pure O2. We then developed a photochemical model of the dependence of C on both xO2 and wavelength that considered fully Chappuis band photochemistry, and the best fit of this model reproduced our observed trends in C. We now describe this photochemical model, that is central to this paper.
(with the superscript * implying that O3 is in an electronically excited state) and did not account for the known photodissociation of O3 within the Chappuis band. Thus, our more recent publication assessed the bath gas composition dependence to C for our own spectrometers and observed wavelength dependence to this bath gas dependency.24 Our λ = 658 nm measurements demonstrated an asymptote in agreement with Fischer and Smith's observations, while measurements for λ = 405 nm found that C was maximised for xO2 in the range 0.2–0.3 and decreased by 11% as the bath gas composition tended to pure O2. We then developed a photochemical model of the dependence of C on both xO2 and wavelength that considered fully Chappuis band photochemistry, and the best fit of this model reproduced our observed trends in C. We now describe this photochemical model, that is central to this paper.
Chappuis band photoexcitation leads to prompt photodissociation to form O(3P) and O2(X3Σ−g, v > 0) in which the nascent O2 photofragment is vibrationally excited:43
| O3 + hν(λ = 400–700 nm) → O(3P) + O2(X3Σ−g, v > 0) | (R1) |
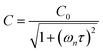 | (5) |
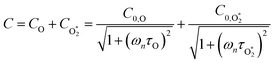 | (6) |
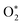 represents ground-state O2 in a vibrationally excited state. Thus, we can model the variation in C with bath gas composition if we can quantify the associated variations of the relaxation timescales τO and
represents ground-state O2 in a vibrationally excited state. Thus, we can model the variation in C with bath gas composition if we can quantify the associated variations of the relaxation timescales τO and 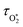 . We can derive expressions for these timescales by considering the subsequent collisional processes of the nascent photoproducts.
. We can derive expressions for these timescales by considering the subsequent collisional processes of the nascent photoproducts.
The nascent O2(X3Σ−g, v > 0) is formed in the ground electronic state but is vibrationally excited, with v = 0 dominating at λ = 620 nm, v = 4–8 dominating at λ = 450–500 nm, and even higher v expected to dominate for λ < 450 nm.45,46 This vibrational energy is transferred to translational modes of bath gas species M = N2, O2 through V–T energy transfer:
| O2(X3Σ−g, v) + M(v′) → O2(X3Σ−g, v − 1) + M(v′) | (R2) |
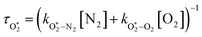 | (7) |
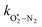 and
and 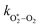 are quenching rate constants in bath gas N2 or O2, respectively, and [N2] and [O2] are the concentrations of the corresponding bath gases.
are quenching rate constants in bath gas N2 or O2, respectively, and [N2] and [O2] are the concentrations of the corresponding bath gases.
The nascent O(3P) rapidly combines with bath gas O2 (collision frequency of ∼1012 s−1) to form ground state O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) viareactions (R3) and (R5):
) viareactions (R3) and (R5):
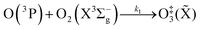 | (R3) |
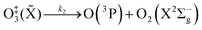 | (R4) |
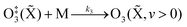 | (R5) |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) that has an internal energy above the energy dissociation threshold correlating to O(3P) + O2(X3Σ−g). Through reactions (R3) and (R5), the resulting O3(
) that has an internal energy above the energy dissociation threshold correlating to O(3P) + O2(X3Σ−g). Through reactions (R3) and (R5), the resulting O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) is in the ground electronic state but is vibrationally excited (v > 0). The collisional stabilisation of O‡3(
, v > 0) is in the ground electronic state but is vibrationally excited (v > 0). The collisional stabilisation of O‡3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) (R5) competes with the re-dissociation of O‡3(
) (R5) competes with the re-dissociation of O‡3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) to O(3P) + O2(X3Σ−g) (R4), with this latter process expected to be fast compared to the stabilisation pathway. The contribution to the PAS signal from O3(
) to O(3P) + O2(X3Σ−g) (R4), with this latter process expected to be fast compared to the stabilisation pathway. The contribution to the PAS signal from O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) will depend on (i) the rate at which stabilised O3(
, v > 0) will depend on (i) the rate at which stabilised O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) is formed, and (ii) the rate of V–T energy transfer from vibrationally excited O3(
, v > 0) is formed, and (ii) the rate of V–T energy transfer from vibrationally excited O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) to translational motion of N2 and O2. Our previous work discussed that, for measurements at equilibrium pressures >950 hPa, the latter process is sufficiently fast that we need only consider the rate at which vibrationally-stabilised O3(
, v > 0) to translational motion of N2 and O2. Our previous work discussed that, for measurements at equilibrium pressures >950 hPa, the latter process is sufficiently fast that we need only consider the rate at which vibrationally-stabilised O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) is formed.24 Applying the steady state approximation to reactions (R3)–(R5), the time dependence in the loss of O(3P), and the formation of O3(
, v > 0) is formed.24 Applying the steady state approximation to reactions (R3)–(R5), the time dependence in the loss of O(3P), and the formation of O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) follows an exponential form with a time constant:
, v > 0) follows an exponential form with a time constant:| τO = (kO–O2–N2[O2][N2] + kO–O2–O2[O2]2)−1 | (8) |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) (k1), the O‡3(
) (k1), the O‡3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) re-dissociation rate (k2), and the quenching rate of O‡3(
) re-dissociation rate (k2), and the quenching rate of O‡3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) by M to form O3(X, v > 0) (k3), for N2 or O2 bath gas species respectively.
) by M to form O3(X, v > 0) (k3), for N2 or O2 bath gas species respectively.
Using this photochemical model (eqn (6)–(8)), we reproduced our measured variations in C with bath gas composition and wavelength.24 We recommended that PAS calibrations are performed in a bath gas of air (xO2 ∼ 0.2–0.3). The reduced sensitivity in the limit of pure N2 corresponded to slow recombination of O(3P) with bath gas O2, with eqn (8) demonstrating the energy quenching timescale τO tends to infinity as [O2] → 0. Meanwhile, the reduced sensitivity as [O2] → 1 was attributed to a lower V–T quenching rate for O2(X, v > 0) by bath gas O2 compared to that by N2.
1.4 Remaining knowledge gaps
The above discussion has shown that quantifying energy transfer timescales for the nascent O(3P) and O2(X3Σ−g, v > 0) photoproducts is crucial to assess the fidelity of visible-wavelength photoacoustic methods for detection of O3. We acknowledge two deficiencies in our earlier assessments of these energy transfer timescales. First, our previous work demonstrated that fitting the above photochemical model to measured variations in C with bath gas composition constrained poorly the relative rates of quenching of the O‡3 complex by either N2 or O2 bath gas. Second, we need to quantify the dependencies of the energy transfer timescales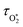 and τO on pressure. During photoacoustic measurements, such as from an atmospheric research aircraft (our application area), the equilibrium sample pressure can vary over the range 300–1000 hPa and we need to quantify the dependence of C on equilibrium (static) pressure. Microphones have a pressure dependent response function,7,47 since the motion of the microphone membrane is progressively damped as static pressure increases. Our experience shows that this response function can change over time and vary between microphones. This response function needs to be corrected for during post-processing of PAS measurements, yet this correction is often neglected.38,40 In recent years, we have sought to correct for this pressure-dependent microphone response using our ozone-based calibration approach to measure C at different static pressure levels within the range 300–1000 hPa.15 This approach assumes that there is no pressure-dependent quenching of the ozone photoproducts and that pressure dependence arises only from changes in the microphone response function. While this approach might seem logical without prior appreciation of the ozone photoproduct quenching timescales, we show in this work that there are fundamental issues associated with this calibration approach and describe a new measurement strategy for determining pressure-dependent microphone response functions.
and τO on pressure. During photoacoustic measurements, such as from an atmospheric research aircraft (our application area), the equilibrium sample pressure can vary over the range 300–1000 hPa and we need to quantify the dependence of C on equilibrium (static) pressure. Microphones have a pressure dependent response function,7,47 since the motion of the microphone membrane is progressively damped as static pressure increases. Our experience shows that this response function can change over time and vary between microphones. This response function needs to be corrected for during post-processing of PAS measurements, yet this correction is often neglected.38,40 In recent years, we have sought to correct for this pressure-dependent microphone response using our ozone-based calibration approach to measure C at different static pressure levels within the range 300–1000 hPa.15 This approach assumes that there is no pressure-dependent quenching of the ozone photoproducts and that pressure dependence arises only from changes in the microphone response function. While this approach might seem logical without prior appreciation of the ozone photoproduct quenching timescales, we show in this work that there are fundamental issues associated with this calibration approach and describe a new measurement strategy for determining pressure-dependent microphone response functions.
This work addresses the two aforementioned knowledge gaps by performing measurements of the variation in C with bath gas composition, wavelength and static pressure. Moreover, for the first time, we report the associated variations in the PAS phase shift θ (eqn (3)). This phase shift provides the much-needed additional constraint on the associated rate constants. The following section describes in detail the photoacoustic transduction processes that depend on static pressure, and describes a measurement approach for characterising pressure dependence in the microphone response function that enables us to study the relaxation timescales of Chappuis band photoproducts at reduced pressures. Section 3 describes the experimental methods used in this work, for both the characterisation of pressure dependent microphone response functions and measurements of C and θ for O3-laden samples. Then, Section 4 reports our measurement results, including a comparison of measured variations in C and θ with predictions from our ozone photochemical model.
2 Pressure-dependent processes in photoacoustic measurements
We now consider how the static pressure P0 affects various stages of the photoacoustic transduction process and approaches to correcting for static pressure effects. Fig. S1-1 in the ESI† summarises this transduction and highlights the pressure dependent processes. We will initially assume that the analyte behaves ideally, i.e. energy transfer from the analyte to bath gas translational modes is always fast and thus ωnτ ≪ 1. This assumption is valid for typical non-volatile aerosols of sub-micrometre diameter at ambient pressure.26,27 Using the model of Chan,48 the characteristic cooling time for black carbon particles with an effective spherical diameter of 1 μm (i.e. the largest particle size measured with our instruments) increases from 4.8 μs for P0 = 1000 hPa to 5.1 μs for P0 = 300 hPa. These timescales are much shorter than the 620–660 μs modulation timescales for our PAS instruments. Furthermore, the aerosol cooling timescales reduce significantly for smaller aerosol diameters D; a 300 nm diameter (a typical median diameter for our measurements) black carbon particle has a cooling timescale of ∼0.4–0.5 μs.Assuming efficient energy transfer to bath gas translational modes, the absorbing sample is homogeneously distributed within the PAS cell, and single eigenmode excitation of the PAS cell at the corresponding resonance frequency, the photoacoustic pressure at the location of the microphone is given by eqn (2). In this expression, both Qn and ωn depend on the density of the bath gas and, therefore, on P0.7,38 There is also a small dependence of the adiabatic coefficient on P0, but the factor σ − 1 varies by less than 0.5% over the pressure range of interest in this work (300–1000 hPa). Meanwhile, the terms I0, g(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), V, and pn(
), V, and pn(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) are independent of P0. By definition, the sample absorption coefficient will decrease with the absorber concentration that inherently scales with pressure, although measurements of the PAS sensitivity C are normalised for the independently measured sample absorption (eqn (4)). Similarly, the impacts of pressure broadening on the spectral linewidths of molecular absorption bands are corrected for in measurements of C. Thus, ignoring variations in αabs, the normalised photoacoustic signal |p(
) are independent of P0. By definition, the sample absorption coefficient will decrease with the absorber concentration that inherently scales with pressure, although measurements of the PAS sensitivity C are normalised for the independently measured sample absorption (eqn (4)). Similarly, the impacts of pressure broadening on the spectral linewidths of molecular absorption bands are corrected for in measurements of C. Thus, ignoring variations in αabs, the normalised photoacoustic signal |p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M)|/(Qn/ωn) is independent of P0. We validated the above transduction model using a finite element method (FEM) model. We have described our FEM model in previous publications30,31 that predicts |p(
M)|/(Qn/ωn) is independent of P0. We validated the above transduction model using a finite element method (FEM) model. We have described our FEM model in previous publications30,31 that predicts |p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M)| for our PAS cells. Fig. S1-2(a) in the ESI† shows the FEM-predicted |p(
M)| for our PAS cells. Fig. S1-2(a) in the ESI† shows the FEM-predicted |p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M,ω)| with variation in the PAS modulation frequency for four different P0 values over the range 400–1000 hPa. The photoacoustic pressure maximum at resonance |p(
M,ω)| with variation in the PAS modulation frequency for four different P0 values over the range 400–1000 hPa. The photoacoustic pressure maximum at resonance |p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M,ωn)| decreases with a reduction in P0, while Fig. S1-2(c) (ESI†) shows that the normalised signal |p(
M,ωn)| decreases with a reduction in P0, while Fig. S1-2(c) (ESI†) shows that the normalised signal |p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M,ωn)|/(Qn/ωn) is indeed independent of P0.
M,ωn)|/(Qn/ωn) is indeed independent of P0.
The amplified photoacoustic wave drives motion of a microphone diaphragm. We used miniature electret microphones in which the diaphragm is composed of a dielectric material with a permanent electric dipole moment. Motion of this diaphragm with respect to a stationary back plate drives a change in capacitance. A small perforation in the diaphragm allows the static pressure to equalise across this membrane. The output microphone voltage Vmic is then proportional to the photoacoustic pressure p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M) at the microphone surface that drives displacement of the microphone diaphragm:
M) at the microphone surface that drives displacement of the microphone diaphragm:
Vmic(t) = kMp(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M) M) | (9) |
Our challenge is to correct the recorded microphone voltage for the pressure dependent processes above and arrive at a quantity that is directly proportional to αabs. It is straightforward to correct Vmic for variations in the PAS cell amplification by dividing Vmic by Qn/ωn; Section 3 describes our measurements of Qn and ωn whenever the bath gas density changes (through variations in P0 or composition) by exciting PAS cell eigenmodes using a speaker transducer. To correct for the P0-dependence of the microphone response function kM we used a measurement approach similar to Arnott et al. to characterise the relative variation in kM with P0.7 Arnott and co-workers measured the microphone response to the pressure field induced by a piezoelectric transducer. The transduction pathway for generating a microphone response from excitation of the PAS cell using a speaker transducer is different to that for photoacoustic transduction, because the speaker transducer directly drives periodic displacement of the bath gas. The acoustic pressure amplitude |pspk| immediately in front of the speaker diaphragm is related to the amplitude of the diaphragm displacement amplitude xspk by:52
| |pspk| = ρvωxspk | (10) |
|p(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) M)| = BρvQnxspk M)| = BρvQnxspk | (11) |
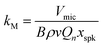 | (12) |
3 Experimental methods
Section 3.1 describes pertinent aspects to our cavity ring-down spectroscopy (CRDS) and PAS measurements. Section 3.2 describes our methods for measuring aerosol absorption with variation in P0 for aerosol standards that provide data sets for characterising pressure-dependent microphone responses. Then, Section 3.3 outlines our methods for measuring C and θ using O3-laden gas samples at controlled pressures, bath gas compositions and for varying photolysis wavelengths.3.1 Photoacoustic and cavity ring-down instruments
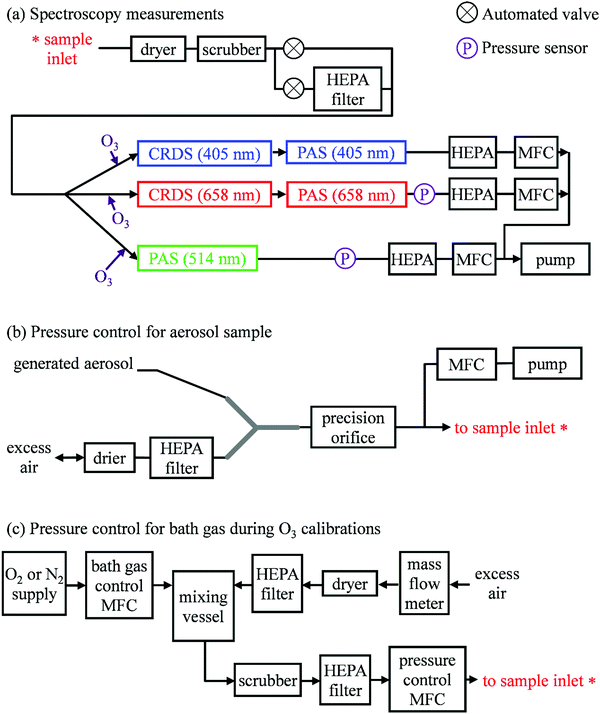
Our previous publication described the construction and flow configuration of our CRDS and PAS instruments, and the associated calibration of our PAS instruments using O3-laden gas samples.24 We only summarise our instruments here and highlight differences to our previous work. One difference is that the PAS instruments used in this work used an optimised two-resonator photoacoustic cell that we described recently and that maximises the sensitivity of photoacoustic detection.31Fig. 1(a) summarises the arrangement and flow configuration for the spectrometers. Our PAS instruments operated at wavelengths λ = 405, 514, 658 nm, while our CRDS instruments used λ = 405, 658 nm only. Sample flow was drawn through three parallel flow lines, with each line corresponding to a different spectroscopy wavelength. When both a CRDS and PAS spectrometer were available at the same wavelength, the CRDS and PAS instrument were arranged in a serial flow configuration such that the sample was drawn first through the CRDS instrument. Mass flow controllers (MFCs) regulated the volumetric sample flow rate drawn through each flow line to a set-point of 1 L min−1. The sample was drawn through a common inlet, before passing through a Nafion dryer and an activated charcoal scrubber to remove trace NOx and O3 gases that absorb light at our spectroscopy wavelengths. Automated valves controlled whether the sample was routed through a HEPA filter prior to passing through the spectrometers. This filtering stage removed aerosol to enable background measurements required for characterising the empty-cavity ring-down time (for the CRDS) and background microphone response (for the PAS). For measurements of C and θ using O3-laden gas samples, an ozonized oxygen flow (i.e. an O3–O2 mixture) was diluted into the conditioned sample flow immediately prior to our spectrometers.A speaker transducer excited PAS cell eigenmodes to enable quantification of Qn and fn, in addition to changes in kM. A speaker was located close to the centre of the lower resonator of our two-resonator cell. This speaker was driven by a voltage waveform that, in the frequency domain, had a top hat distribution over the frequency range 1300–1700 Hz. This acoustic spectral range extended across the eigenmode spectral width. Speaker-excitation of the PAS cell was performed immediately prior to any measurements of light-absorbing aerosol or O3-laden gas, and after any changes in the bath gas density (through changes in either P0 or composition). During the speaker excitation period (of 30 s duration), the microphone waveform was recorded in 1 s intervals, with each waveform processed through a fast Fourier transform that gave the power spectrum for the eigenmode excitation. A Lorentzian function was fitted to this power spectrum to retrieve Qn, fn and the peak signal amplitude (denoted Sspk). A software-controlled feedback used the determined fn to set the laser power modulation frequencies for each PAS instrument.
Several sensors were integrated into the flow system to measure P0. The MFCs regulating the volumetric flow rates for each flow line provided pressure readings. However, these MFCs were located downstream of a HEPA filter (see Fig. 1(a)), and a small pressure drop across this filter reduced the pressure at the MFCs. Instead, separate Precision Pressure Transducers (PPTs, Honeywell PPT-series) were located immediately after the 514 and 658 nm PAS instruments. Fig. S2-1 in the ESI† compares the pressures recorded by our five pressure sensors and demonstrates the reduced pressures recorded by the three MFC sensors compared to those by the two PPT sensors. In principle, the PPT sensors should record the same pressure value and represent the sample pressure in all spectrometers; there were no elements of the flow system that would lead to differences in P0 between spectrometers. The pressure recorded by the PPT sensor located in the 658 nm sample flow line was consistently higher by 3.3 ± 0.5 hPa compared to that in the 514 nm line. We took the mean P0 provided by these two pressure sensors as representing the pressure in all five spectrometers.
3.2 Measurements of aerosol absorption at reduced pressure for aerosol standards
Aerosol coalbedo (the ratio of the absorption to extinction coefficient) is independent of pressure. Moreover, Section 2 showed that sub-micron non-volatile aerosols can be considered to liberate their heat to the surrounding bath gas instantaneously on our PAS modulation timescales and over the P0 range 300–1000 hPa. Thus, measurements of the coalbedo from PAS-measured aerosol absorption coefficients in combination with CRDS-measured extinction coefficients should be invariant with P0 if the microphone response function is independent of static pressure. Providing that the size distribution for the sampled aerosol is not affected by changes in P0, any discrepancy between the measured coalbedo at ambient pressure and that at reduced P0 is attributed to changes in kM.In these measurements, our spectrometers sampled laboratory generated light absorbing aerosol standards at different P0. Our aerosol generation and conditioning methods follow closely the methods we reported in ref. 22, to which we refer the reader for specifications of equipment used. We used two aerosol standards; monodisperse dyed PolyStyrene Latex (PSL) spheres or nigrosin dye aerosols.
In the PSL measurements, an aqueous stock solution containing 250 nm diameter PSL spheres (Thermo Scientific, Custom Black polystyrene microspheres in water, CAT No. SAM-423) was passed to the input of a constant output atomiser. A constant flow of high purity (99.999%) zero air from a gas cylinder with an outlet pressure of 2400 hPa generated aqueous aerosol that passed through two indicating silica gel diffusion driers that dried the aerosol sample to a relative humidity of <5%, as determined by a humidity probe placed immediately after the second drier. Fig. 1(b) shows how we regulated the pressure of the aerosol sample. The dried sample passed to an input of a ‘Y’ flow splitter (Brechtel Manufacturing Inc.), with our CRDS-PAS instruments drawing aerosol sample (via a precision orifice) from one exit port of this splitter, while the other port was connected to a filter and drier (containing indicating silica gel desiccant) to dump excess sample. The aerosol-laden flow to the CRDS-PAS passed through a constricted precision orifice (O’Keefe Controls Co.); we used a range of orifice diameters to control the output sample pressure, with orifice diameters in the range 0.51–0.69 mm. This orifice created a pressure drop, with the static pressure at the orifice output determined by the orifice diameter and the volumetric flow rate through the orifice. The output of this orifice was connected, via a ‘T’ flow splitter (also referred to commonly as a ‘union Tee’), to the common sample inlet of our CRDS-PAS instruments. A further MFC (referred to as the ‘dump MFC’) was connected to the second output from the ‘T’ splitter and was used to draw sample immediately after the constricted orifice to an exhaust pump. By controlling the orifice diameter and the dump MFC flow rate, we could vary P0 of the aerosol-laden sample over the range 300–1000 hPa. The aerosol extinction and absorption coefficients were recorded at 1 Hz sampling frequencies for 5 minutes at each P0. At each pressure level and prior to sampling aerosol-laden air samples, we recorded the CRDS empty cavity ring-down times and the background microphone responses enabled through the automated routing of the sample through a HEPA filter prior to spectroscopic measurements. The particulate filter used during these measurements (Headline Filters, DIF-LK40) had a large filter area that created a minimal sample pressure drop (∼2.5 hPa). Furthermore, we used speaker excitation of the PAS cell to characterise Sspk, Qn and fn at each P0. Again, we refer the reader to our recent publication for details of the post-processing of the raw spectroscopy data, calibration of the PAS instruments using O3-laden air, and assessments of the accuracy of our extinction and absorption measurements.22
The measurements using nigrosin aerosol were similar to those using dyed PSL spheres. The aqueous stock solution supplying the atomiser contained water soluble nigrosin dye (Sigma Aldrich, CAS number 8005-03-6, lot number MKBR1705V) with a solute concentration of 2 g L−1. To prevent complete attenuation of the intra-cavity ring-down laser beam, we controlled the aerosol number concentration by passing the aerosol-laden flow through a differential mobility analyser (DMA) prior to the ‘Y’ flow splitter in Fig. 1(b). The DMA was set to pass aerosol particles with a mobility-selected diameter of 200 nm. The DMA sheath and aerosol sample flows were 1.0 and 0.61 L min−1 respectively, with the sheath flow set deliberately to a low value such that the DMA transfer function was wide enough to pass a high particle number concentration for maximising the signal-to-noise ratio in extinction and absorption measurements, but remained sufficiently narrow to prevent complete attenuation of our intra-cavity ring-down laser beam. A final distinguishing factor between the PSL and nigrosin measurements was that, in the case of nigrosin, the dump MFC was not required and the pressure drop was controlled by varying the diameter of the precision orifice only over the range 0.46–0.89 mm.
3.3 Sensitivity and phase shift measurements for O3-laden gas samples at reduced pressures
We measured C and θ for O3 added to bath gases composed of various O2–N2 mixtures at different static pressures. We describe only the differences to the methods we reported in ref. 24. Specifically, we discuss the control of P0 during measurements (which was not varied in previous work), and measurements of θ (which was not investigated previously).Fig. 1(c) shows how we controlled the bath gas composition and pressure during measurements of O3-laden samples, while Fig. 1(a) indicates the locations at which an ozonized-O2 gas flow was diluted into the pressure-controlled bath gas. We regulated the mass flow of O2 or N2 from a high purity (99.999%) gas cylinder into a 1.1 L aluminium mixing vessel, in which the high purity gas was mixed with ambient air (∼21% O2, 78% N2, 1% argon and trace amounts of other gases) drawn through an in-line dryer (containing indicating silica gel desiccant) and a HEPA filter. A mass flow meter monitored the mass flow rate of ambient air into the mixing volume. By changing the mass flow rate of the high purity gas into the mixing volume, we varied the O2 mass fraction of the bath gas over the range 0.0–1.0. The mixed gas was then drawn through a Purafil-containing gas scrubber to remove trace NOx/O3 species, before passing through a further HEPA filter. The bath gas passed to the common sample inlet (indicated in Fig. 1(a)) via a pressure controller (Alicat PC Series) that regulated the bath gas pressure. We measured C and θ for five values of O2 mass fraction (xO2 = 0.02, 0.05, 0.25, 0.63, 1.00) and five values of static pressure (P0 = 1007.5, 901.9, 702.5, 503.1, 304.1 hPa). The specified values for xO2 account for small contributions to the bath gas compositions from the CRDS mirror purge flows and the O2 contribution from the ozonized oxygen calibration gas. The P0 values chosen were informed by our experience from our research aircraft measurements, during which the ambient pressure approaches 300 hPa at altitudes close to 10 km.
The measurements of C are corrected for the impacts of both P0 and bath gas composition on the amplification characteristics of the PAS cell (Qn and fn), absorber concentration, and small variations in the intra-cavity laser power, in addition to changes in microphone response kM using the new approach described in Section 2 and validated in Section 4.1. Thus, any variations in the measured C presented here with either P0 or bath gas are attributed to changes in the rates for energy transfer from the nascent photofragments following O3 photolysis to bath gas translational modes. The phase shift provides a more direct measurement of relaxation timescales in photoacoustic processes compared to C. We define θ as the difference in phases recorded for the microphone waveform and that for the sinusoidal waveform used to drive the laser power modulation. Section S3 of the ESI† describes how these individual phase shifts are acquired and how θ is processed. Specifically, no correction for microphone response, PAS cell amplification characteristics or small drifts in laser power are needed, although a background instrument phase shift subtraction is required in addition to a correction for small (≤0.5 Hz) mismatches between the laser modulation frequency and that of the PAS cell eigenmode, both of which are straightforward corrections (see Section S3 of the ESI†).
4 Results and discussion
4.1 Validation of approach to measuring relative variations in kM with changes in P0
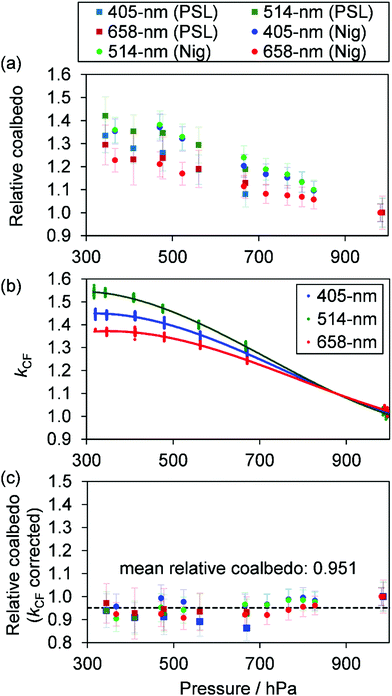
Measurements of coalbedo for benchmark light absorbing aerosols at different P0 enabled us to validate our approach to characterising pressure dependent microphone responses as described in Section 2. To provide a metric for the fractional change in measured aerosol coalbedo with P0, we define the relative coalbedo as the ratio of the coalbedo to that measured at the highest pressure (P0 ∼ 1000 hPa). Initially, the absorption measurements are corrected only for the P0 dependences of Qn, fn and small variations in the laser power. Fig. 2(a) shows the variation in relative coalbedo with P0 for both dyed PSL and nigrosin aerosols. The extinction measured by the 658 nm CRDS instrument was used in calculating the relative coalbedo for all channels as these 658 nm extinction measurements were superior in precision compared to those recorded by the 405 nm CRDS instrument. This approach is sound and the exact value for coalbedo is unimportant; simply, we are using the extinction measurements to normalise the PAS-measured absorption values for the reduction in aerosol number concentration that occurs with a reduction in pressure. We recognise that we could have used a condensation particle counter to measure these changes in number concentration, thus enabling measurements of aerosol absorption cross sections that are pressure-independent quantities. However, the particle counters available in our laboratory operate only at pressures in the range 750–1050 hPa.For both nigrosin and PSL aerosol measurements, the measured coalbedo increases by 30–45% as P0 is reduced from 1000 to 300 hPa. As these coalbedo measurements are already corrected for pressure dependence in Qn and fn, in addition to small variations in laser power, the remaining pressure dependence is attributed to changes in kM. Using the approach described in Section 2, speaker excitation measurements of Qn and Sspk are used to characterise the pressure dependent microphone response function. From eqn (12), we can define a correction factor kCF as the ratio kM to that at P0 = 1000 hPa:
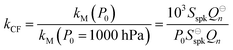 | (13) |
4.2 The impact of P0 and bath gas composition on the energy transfer timescales from Chappuis band photoproducts
Here, we present measurements of C and θ from PAS measurements on O3-laden gas samples and demonstrate that characterising relative variations in kM is critical to quantifying accurately the impacts of slow O3 photoproduct energy transfer rates on the photoacoustic signal. Notably, we show that kCF depends on the ratio of N2 and O2 in the bath gas, even at fixed pressure, and accounting for this dependence revises our previous recommendations for accurate calibrations of PAS instruments at visible wavelengths using O3-laden gas samples.24Our previous publication demonstrated that the quenching timescales for energy transfer from Chappuis band O3 photoproducts to the bath gas can be similar to our photoacoustic laser modulation period for some bath gas compositions, causing a negative bias in measurements of C.24 We measured this negative bias for bath gas mixtures of N2 and O2 for pressures P0 ∼ 1000 hPa only. However, our photochemical model predicts this negative bias to worsen at reduced pressures. Section 1.3 summarised the photochemistry of O3 and the relaxation of the nascent photoproducts following Chappuis band photoexcitation. The timescales of energy transfer from the O2(X3Σ−g, v > 0) and O(3P) photoproducts to the bath gas (described by eqn (7) and (8), respectively) govern the measured C and θ (through eqn (6) and (3)). Importantly, eqn (7) and (8) predict these energy transfer timescales to depend inversely on the gas concentrations [N2] and [O2] that scale directly with P0 through the ideal gas law. Therefore, from the outset, we expect these timescales to significantly increase at lower pressures and cause significant bias in PAS measurements of C and increase the associated phase shift θ.
In addition to the dependence of kCF on P0, the microphone response function also depends on the bath gas composition. This composition dependence was ignored in the last section, which considered measurements on aerosols suspended in air only. Changes in gas composition affect the microphone response function by impacting on various terms in eqn (12), including on the gas density (through changes in the mean molecular weight) and speed of sound. The dependence of ρ on P0 and the mean molecular weight M for an ideal gas is given by:
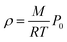 | (14) |
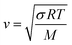 | (15) |
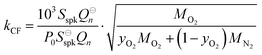 | (16) |
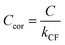 | (17) |
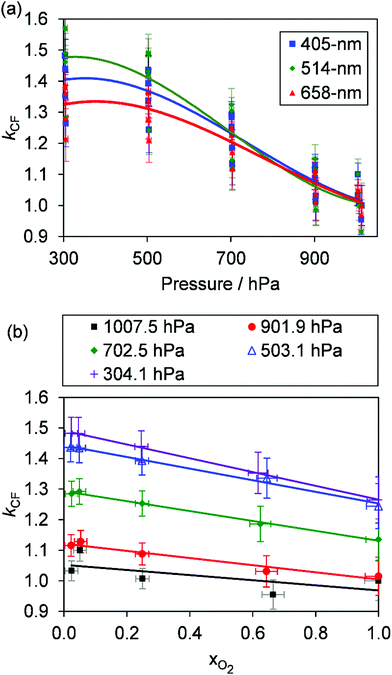 | ||
| Fig. 3 (a) The variation in kCF with P0 for our three PAS spectrometers operating at wavelengths of 405, 514 and 658 nm. These data show larger variation at any given P0 compared to those presented in Fig. 2(b) owing to the dependence of kCF on the bath gas composition. (b) The variation in kCF with xO2 at different P0 for the 405 nm PAS instrument only. Lines are to guide the eye only. | ||
Fig. 4 shows the variation in Ccor with xO2 for different P0. Data are shown for measurements at λ = 405, 658 nm only; measurement of Ccor require PAS measurements of photoacoustic response in addition to CRDS measurements of the O3 absorption coefficient (see eqn (4)), and a CRDS spectrometer was not available at λ = 514 nm. For both the 405 and 658 nm measurements, Ccor is maximised as xO2 → 1. This conclusion is different to our previous work that found strong wavelength dependence to the PAS sensitivity; while our previous λ = 658 nm measurements observed similar trends with a plateau in the PAS sensitivity attained for xO2 > 0.25, measurements at λ = 405 nm demonstrated a maximum at xO2 ∼ 0.25 before the sensitivity dropped as xO2 increased further.24 We emphasise, however, that our previous work studied variations in C and not Ccor, and thus did not explore corrections for bath gas mixing state. Indeed, Fig. S4-1 in the ESI† shows the PAS sensitivity without the correction for kCF and demonstrates similar trends (for the P0 = 1007.5 hPa data) to that in our previous publication. Moreover, the uncorrected C show trends that are inconsistent with our expectation that C should decrease for reduced P0. For example, the C for 405 nm measurements at xO2 = 0.25 increases as P0 decreases from 1007.5 hPa to 503.1 hPa, before a large reduction in C as P0 decreases further to a level of 304.1 hPa. Meanwhile, Ccor in Fig. 4 shows variations with P0 that are consistent with our understanding of the dependence of energy quenching on pressure (although we defer an explanation of our model fits in this figure to the following section).
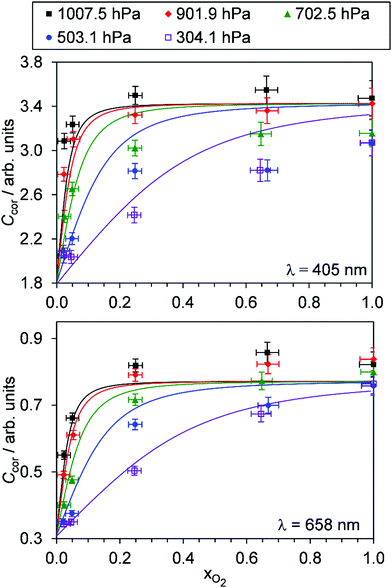 | ||
| Fig. 4 The variation in Ccor with O2 mass fraction. The different data series correspond to different P0 values. Data are shown for spectroscopy wavelengths of 405 and 658 nm only. Error bars represent 1σ standard error in the measured quantities. The solid lines represent the best fit of the O3 photochemical relaxation model described by eqn (6) and (18)–(24) to measurements of both Ccor and θ. | ||
For each of our three PAS spectroscopy wavelengths, Fig. 5 shows the variation in θ with xO2 and P0. Fig. S4-2 of the ESI† compares the measured θ from each spectrometer directly and shows that the phase shift variations with P0 and xO2 are similar for each measurement wavelength; all phase shift measurements are well correlated, with those measured at 514 and 658 nm wavelengths ∼15% larger than those recorded at 405 nm. This similarity across wavelengths implies that the relaxation timescales of O(3P) and O2(X3Σ−g, v > 0) are nearly independent of photolysis wavelength in the Chappuis band. To understand the variations in Ccor and θ with P0 and xO2, we fit our photochemical model to our measurements.
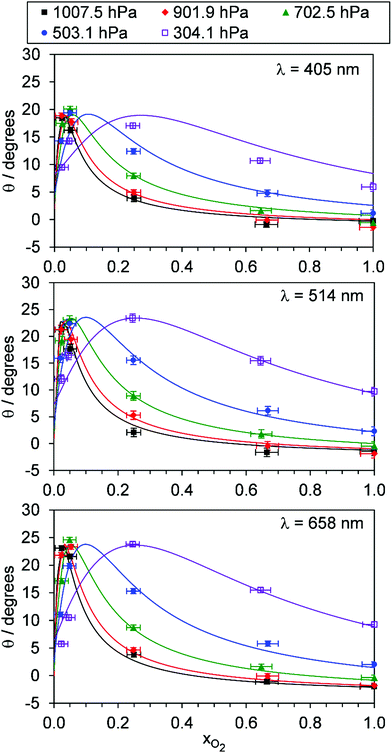 | ||
| Fig. 5 The variation in photoacoustic phase shift with xO2. The different data series correspond to different P0 values. Data are shown for spectroscopy wavelengths of 405, 514 and 658 nm. Error bars represent 1σ standard error in the measured quantities. The solid lines represent the best fit of the O3 photochemical relaxation model described by eqn (6) and (18)–(24) to measurements of both Ccor and θ. | ||
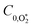 were varied as fit parameters. The timescales
were varied as fit parameters. The timescales 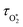 and τO are described by eqn (7) and (8), respectively, in terms of the bath gas concentrations [O2] and [N2]. We can re-define these expressions as functions of P0 and xO2:
and τO are described by eqn (7) and (8), respectively, in terms of the bath gas concentrations [O2] and [N2]. We can re-define these expressions as functions of P0 and xO2: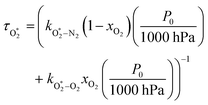 | (18) |
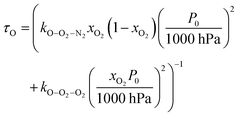 | (19) |
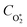 to Ccor:
to Ccor: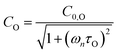 | (20) |
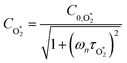 | (21) |
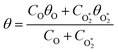 | (22) |
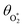 are the phase shifts attributed to O(3P) and O2(X3Σ−g, v > 0) and depend on their associated quenching timescales viaeqn (3):
are the phase shifts attributed to O(3P) and O2(X3Σ−g, v > 0) and depend on their associated quenching timescales viaeqn (3):| θO = tan−1(ωnτO) | (23) |
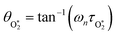 | (24) |
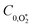 ,
,  ,
,  , kO–O2–N2 and kO–O2–O2. This least-squares minimisation optimised our model simultaneously to measured Ccor and θ for all measurement wavelengths. In this least-squares fit, we constrained
, kO–O2–N2 and kO–O2–O2. This least-squares minimisation optimised our model simultaneously to measured Ccor and θ for all measurement wavelengths. In this least-squares fit, we constrained 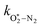 ,
, 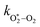 , kO–O2–N2 and kO–O2–O2 to be invariant with photolysis wavelength, justified by our aforementioned observations of only a weak dependence of phase shift on wavelength. Moreover, this latter treatment of rate constants is consistent with that in our previous work.24 Similarly, we followed the same treatment in our previous work by allowing C0,O and
, kO–O2–N2 and kO–O2–O2 to be invariant with photolysis wavelength, justified by our aforementioned observations of only a weak dependence of phase shift on wavelength. Moreover, this latter treatment of rate constants is consistent with that in our previous work.24 Similarly, we followed the same treatment in our previous work by allowing C0,O and 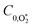 to vary with wavelength. In addition to these parameters, we allowed a small phase shift offset (with magnitudes up to 3.4°) to be added to the modelled phase at each photolysis wavelength to account for inaccuracies in the subtraction of instrument phase shifts. The best fit parameters from this least-squares optimisation are summarised in Table 1 and the modelled Ccor and θ are compared against measurements in Fig. 4 and 5, respectively.
to vary with wavelength. In addition to these parameters, we allowed a small phase shift offset (with magnitudes up to 3.4°) to be added to the modelled phase at each photolysis wavelength to account for inaccuracies in the subtraction of instrument phase shifts. The best fit parameters from this least-squares optimisation are summarised in Table 1 and the modelled Ccor and θ are compared against measurements in Fig. 4 and 5, respectively.
Fig. 4 shows that, overall, the model is in good agreement with the measured trends in Ccor with both P0 and xO2. On average, the mean absolute difference between the modelled and measured Ccor is 7.3% and 5.1% at wavelengths of 405 and 658 nm, respectively. There are numerous sources that could contribute to these small levels of disagreement. First, the error bars on Fig. 4 for the measured Ccor reflect the 1σ precision and do not include uncertainty arising from potential biases in the correction factor kCF. Our measurements in Section 4.1 indicated that kCF is accurate to within 5% for P0 over the range 300–1000 hPa. However, these accuracy assessments apply to a bath gas of air only, and the accuracy in our kCF characterisations for different bath gas compositions has not been assessed. Second, our model fit could be optimised to a local minimum. The high number of fit parameters (13), that were varied in fitting our photochemical model to measurements, increases the likelihood of optimising to a local minimum in the least-squares residual. We mitigated against optimisation to a local minimum by initialising our fit parameters from numerous initial values prior to minimisation, and these best fit parameters converged consistently to the same optimal values. Third, our quenching model contains some deficiency in modelling accurately the quenching of energy from O(3P). Specifically, we highlight that eqn (19) for the timescale τO represents the timescale with which nascent O(3P) is lost through recombination with bath O2(X3Σ−g) and the resulting unstable intermediate O‡3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) stabilised via a further collision with a bath gas species to form vibrationally hot O3(
) stabilised via a further collision with a bath gas species to form vibrationally hot O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) (see reactions (R3)–(R5)). The vibrational energy from this hot O3(
, v > 0) (see reactions (R3)–(R5)). The vibrational energy from this hot O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) product remains to be transferred to the bath gas. Thus, in stating τO to represent the timescale of energy transfer from the O(3P) photoproduct to bath gas translational energy, we inherently assume that V–T energy transfer from O3(
, v > 0) product remains to be transferred to the bath gas. Thus, in stating τO to represent the timescale of energy transfer from the O(3P) photoproduct to bath gas translational energy, we inherently assume that V–T energy transfer from O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) to the bath gas is fast compared to the photoacoustic modulation period.24 Indeed, Ménard-Bourcin et al.53 and Zeninari et al.54 measured similar rates for the single-quantum V–T energy transfer from vibrationally excited O3(
, v > 0) to the bath gas is fast compared to the photoacoustic modulation period.24 Indeed, Ménard-Bourcin et al.53 and Zeninari et al.54 measured similar rates for the single-quantum V–T energy transfer from vibrationally excited O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) to bath O2 or N2 of ∼7.6 × 105 s−1 atm−1, corresponding to a characteristic timescale of 1.4 μs at P0 = 950 hPa. This timescale is fast compared to the 620–660 μs modulation timescales for our PAS instruments. However, O3(
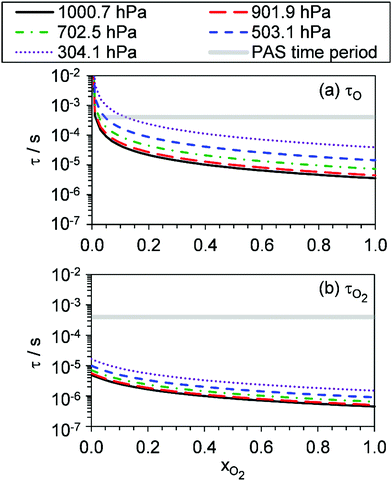
, v > 0) to bath O2 or N2 of ∼7.6 × 105 s−1 atm−1, corresponding to a characteristic timescale of 1.4 μs at P0 = 950 hPa. This timescale is fast compared to the 620–660 μs modulation timescales for our PAS instruments. However, O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) could be formed in vibrational states with populations as high as (7,0,0) at short photolysis energies55 and, at reduced pressures, the timescale for quenching of this state could be up to ∼60 μs for P0 = 300 hPa. Fig. 6 shows our modelled timescales τO and τO2 with variation in xO2 and P0. Clearly, an upper estimate of 60 μs for the V–T energy transfer from O3(
, v > 0) could be formed in vibrational states with populations as high as (7,0,0) at short photolysis energies55 and, at reduced pressures, the timescale for quenching of this state could be up to ∼60 μs for P0 = 300 hPa. Fig. 6 shows our modelled timescales τO and τO2 with variation in xO2 and P0. Clearly, an upper estimate of 60 μs for the V–T energy transfer from O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) is comparable to the modelled timescale for τO. However, the addition of the O3(
, v > 0) is comparable to the modelled timescale for τO. However, the addition of the O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) V–T energy transfer step is not straightforward and the additional fit parameters that arise reduce the fidelity of our best-fit model. Moreover, we expect the mean timescale for V–T relaxation of O3(
, v > 0) V–T energy transfer step is not straightforward and the additional fit parameters that arise reduce the fidelity of our best-fit model. Moreover, we expect the mean timescale for V–T relaxation of O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) to be much less than this 60 μs upper estimate, as an ensemble of (v1, v2, v3) states is produced and the single quantum transition from some states (namely, the v2 state) is particularly fast to the ground state.
, v > 0) to be much less than this 60 μs upper estimate, as an ensemble of (v1, v2, v3) states is produced and the single quantum transition from some states (namely, the v2 state) is particularly fast to the ground state.
Fig. 5 shows good agreement between our modelled and measured phase shifts; the mean discrepancies between these are 1.3°, 1.1° and 1.0° at our 405, 514 and 658 nm spectroscopy wavelengths, respectively. Importantly, the measured values are subject to less uncertainty compared to those for Ccor, as the measurement of θ does not require normalisation for O3 concentrations using independent (e.g. CRDS) techniques or a correction for the microphone response function. We also stress that phase shift is a direct measure of relaxation timescales, and the level of agreement between our measurements and our best-fit photochemical model indicates that the aforementioned model assumption of instantaneous V–T relaxation of O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) is reasonable. The measured θ might be expected to follow a similar trend to that of the best-fit model timescales presented in Fig. 6, with large values at low xO2 and P0, which then decrease with increasing xO2 and P0. This trend in θ is largely observed in the xO2 range ∼0.2–1.0, while θ approaches zero as xO2 → 0. To understand this latter observation, we recall that the θ derived from the microphone waveform corresponds to a photoacoustic amplitude weighting of the phase shifts associated with energy transfer from both nascent photoproducts O(3P) and O2(X3Σ−g, v > 0). Eqn (19) shows that the timescale for energy transfer from O(3P) tends to infinity as xO2 → 0. This long timescale is associated with a large 90° phase for θO (eqn (23)). However, the associated contribution to the photoacoustic signal is very small; Fig. 4 demonstrates a significant drop in Ccor as xO2 → 0. Thus, recalling that the measured θ is a photoacoustic amplitude weighting of the two phase shift contributions from quenching of O(3P) and O2(X3Σ−g, v > 0) (eqn (22)), the observed phase shift is expected to tend to zero as xO2 → 0.
, v > 0) is reasonable. The measured θ might be expected to follow a similar trend to that of the best-fit model timescales presented in Fig. 6, with large values at low xO2 and P0, which then decrease with increasing xO2 and P0. This trend in θ is largely observed in the xO2 range ∼0.2–1.0, while θ approaches zero as xO2 → 0. To understand this latter observation, we recall that the θ derived from the microphone waveform corresponds to a photoacoustic amplitude weighting of the phase shifts associated with energy transfer from both nascent photoproducts O(3P) and O2(X3Σ−g, v > 0). Eqn (19) shows that the timescale for energy transfer from O(3P) tends to infinity as xO2 → 0. This long timescale is associated with a large 90° phase for θO (eqn (23)). However, the associated contribution to the photoacoustic signal is very small; Fig. 4 demonstrates a significant drop in Ccor as xO2 → 0. Thus, recalling that the measured θ is a photoacoustic amplitude weighting of the two phase shift contributions from quenching of O(3P) and O2(X3Σ−g, v > 0) (eqn (22)), the observed phase shift is expected to tend to zero as xO2 → 0.
Our measurements allow us to form recommendations on using O3-laden gas as a calibrant of photoacoustic spectrometers. Many researchers calibrate using O3-laden air.10,15,22,40 Our Ccor measurements demonstrate that such calibrations in air (i.e. xO2 ∼ 0.25) are accurate at P0 in excess of 1000 hPa, and this conclusion is reinforced by our measured θ that are <5° and indicate fast energy transfer, compared to our photoacoustic modulation period, from the Chappuis band photoproducts to N2 and O2 bath species. However, the accuracy of these calibrations is very sensitive to P0, with notable biases in Ccor at P0 < 900 hPa. In contrast, calibrations using O3-laden O2 exhibit no detectable bias for P0 > 900 hPa and negligible phase shift for P0 > 500 hPa, with the sensitivity in Ccor to P0 much lower than that at other bath gas mixing states. For measurements at PAS modulation frequencies <2 kHz, we thus recommend calibrating PAS instruments using O3-laden gas in a bath gas with xO2 ≥ 0.25 and P0 > 900 hPa. The latter pressure threshold can be relaxed at higher xO2. Crucially, these criteria depend strongly on the photoacoustic modulation timescale; some researchers may wish to perform measurements at very high frequencies (>30 kHz) such as that afforded by tuning fork detection. Such researchers will find the timescales presented in Fig. 6 most useful in ascertaining whether such calibrations are accurate given their choice of photoacoustic modulation timescale, xO2, and P0.
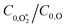 increases with photolysis energy, consistent with an increasing fraction of energy partitioning to O2(X) vibrational modes at shorter wavelengths. This finding is consistent with our previous measurements,24 and with studies reported by others that show that higher O2(X) vibrational states are populated following photodissociation in the Chappuis band at shorter wavelengths.45,46
increases with photolysis energy, consistent with an increasing fraction of energy partitioning to O2(X) vibrational modes at shorter wavelengths. This finding is consistent with our previous measurements,24 and with studies reported by others that show that higher O2(X) vibrational states are populated following photodissociation in the Chappuis band at shorter wavelengths.45,46
The quotient kO–O2–O2/kO–O2–N2 is 1.27. Previously, we demonstrated that kO–O2–O2 and kO–O2–N2 are given by k1k3/k2, in which k1, k2 and k3 are defined in reactions (R3)–(R5).24 The rate coefficients k1 and k2 are independent of bath gas, while k3 depends on the ability of the bath gas to quench energy efficiently from the unstable O‡3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) intermediate. Therefore, the ratio kO–O2–O2/kO–O2–N2 is equivalent to k3,O2/k3,N2. While V–T rates for O‡3(
) intermediate. Therefore, the ratio kO–O2–O2/kO–O2–N2 is equivalent to k3,O2/k3,N2. While V–T rates for O‡3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) have not been studied directly, these rates have been studied for excitations of the (v1,v2,v3) states of the stable O3(
) have not been studied directly, these rates have been studied for excitations of the (v1,v2,v3) states of the stable O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) species.53,54 The direct relaxation from v1 (symmetric stretch) and v3 (asymmetric stretch) are comparatively slow compared to the interconversion v1, v3 → v2 and then subsequent quenching from v2. Thus, vibrationally excited O3 is quenched mostly from the v2 state. The ratio of v2 quenching rates in O2 and N2 bath gases is 1.10 ± 0.17 (Menard-Bourcin et al.)53 or 1.07 ± 0.16 (Zeninari et al.),54 in near agreement with our measured ratio kO–O2–O2/kO–O2–N2 = 1.27. Our new measurements reconcile a discrepancy in our previously published work in which we determined kO–O2–O2/kO–O2–N2 = 11.1. This reconciliation is achieved through the additional constraint on the best-fit rate coefficients provided by phase shift measurements, and through the improved accuracy of our PAS sensitivity measurements; measured C are now corrected for the microphone response function dependence on bath gas density. For the individual rate coefficients, we measure kO–O2–O2 = 2.77 × 105 s−1 and kO–O2–N2 = 2.18 × 105 s−1 at P0 = 1000 hPa, while Ménard-Bourcin et al. predict limiting rates for v2 quenching to be faster at rates of (8.23 ± 0.8) × 105 s−1 in O2 and (7.5 ± 0.9) × 105 s−1 in N2.53 Similarly, Zeninari et al. reported v2 quenching rates of (5.6 ± 0.8) × 105 s−1 in O2 and (5.3 ± 0.4) × 105 s−1 in N2.54 However, there are several factors that contribute to an expected difference between our rates and the limiting v2 quenching rates reported in previous studies. First, the total relaxation rates kO–O2–O2 and kO–O2–N2 are attributed to relaxation through the transition v1, v3 → v2 in addition to that from v2. Second, the total quenching rate will depend on the number of quanta in vibrational energy levels, with the rates reported in previous studies corresponding to single quantum transitions, while our measurements will involve O3 with multiple vibrational quanta distributed over v1, v2, and v3. Third, our measured rates correspond to quenching from vibrational states above the dissociation energy threshold for O3, while the rates reported by the aforementioned literature studies correspond to vibrational states below this threshold.
, v > 0) species.53,54 The direct relaxation from v1 (symmetric stretch) and v3 (asymmetric stretch) are comparatively slow compared to the interconversion v1, v3 → v2 and then subsequent quenching from v2. Thus, vibrationally excited O3 is quenched mostly from the v2 state. The ratio of v2 quenching rates in O2 and N2 bath gases is 1.10 ± 0.17 (Menard-Bourcin et al.)53 or 1.07 ± 0.16 (Zeninari et al.),54 in near agreement with our measured ratio kO–O2–O2/kO–O2–N2 = 1.27. Our new measurements reconcile a discrepancy in our previously published work in which we determined kO–O2–O2/kO–O2–N2 = 11.1. This reconciliation is achieved through the additional constraint on the best-fit rate coefficients provided by phase shift measurements, and through the improved accuracy of our PAS sensitivity measurements; measured C are now corrected for the microphone response function dependence on bath gas density. For the individual rate coefficients, we measure kO–O2–O2 = 2.77 × 105 s−1 and kO–O2–N2 = 2.18 × 105 s−1 at P0 = 1000 hPa, while Ménard-Bourcin et al. predict limiting rates for v2 quenching to be faster at rates of (8.23 ± 0.8) × 105 s−1 in O2 and (7.5 ± 0.9) × 105 s−1 in N2.53 Similarly, Zeninari et al. reported v2 quenching rates of (5.6 ± 0.8) × 105 s−1 in O2 and (5.3 ± 0.4) × 105 s−1 in N2.54 However, there are several factors that contribute to an expected difference between our rates and the limiting v2 quenching rates reported in previous studies. First, the total relaxation rates kO–O2–O2 and kO–O2–N2 are attributed to relaxation through the transition v1, v3 → v2 in addition to that from v2. Second, the total quenching rate will depend on the number of quanta in vibrational energy levels, with the rates reported in previous studies corresponding to single quantum transitions, while our measurements will involve O3 with multiple vibrational quanta distributed over v1, v2, and v3. Third, our measured rates correspond to quenching from vibrational states above the dissociation energy threshold for O3, while the rates reported by the aforementioned literature studies correspond to vibrational states below this threshold.
The quotient 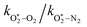 is 11.1. In previous work, we reported
is 11.1. In previous work, we reported 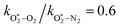 ,24 although we highlighted that the fit of our photochemical model was rather insensitive to changes in this ratio when fitting to PAS sensitivity measurements. However, the phase data that are now included in our model optimisation enable more sensitive retrievals of
,24 although we highlighted that the fit of our photochemical model was rather insensitive to changes in this ratio when fitting to PAS sensitivity measurements. However, the phase data that are now included in our model optimisation enable more sensitive retrievals of 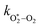 and
and 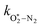 . The best fit model rate constant
. The best fit model rate constant 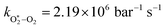 (8.85 × 10−14 cm3 s−1) corresponds to a relaxation timescale of ∼0.5 μs for xO2 → 1 and for P0 = 1000 hPa (see Fig. 6(b)), while the associated measured phase shifts <3° correspond directly to quenching timescales <5 μs. These timescales indicate that O2(X, v > 0) relaxation occurs efficiently relative to our PAS modulation periods as xO2 → 1 and for P0 > 1000 hPa. We can compare our measured rates of O2(X, v > 0) quenching with theoretical V–T rates calculated by Coletti and Billing, who predicted rates <2 × 10−17 cm3 s−1 for vibrational quantum numbers v < 10 at ambient temperature.56 Meanwhile, Huestis performed a reanalysis of a range of V–T energy transfer studies of vibrationally excited O2 and recommended a V–T quenching rate of 2.7 × 10−18 cm3 s−1 for v = 1 at temperatures of 300 K.57 These rates are ∼4 orders of magnitude slower than the rates we determine for
(8.85 × 10−14 cm3 s−1) corresponds to a relaxation timescale of ∼0.5 μs for xO2 → 1 and for P0 = 1000 hPa (see Fig. 6(b)), while the associated measured phase shifts <3° correspond directly to quenching timescales <5 μs. These timescales indicate that O2(X, v > 0) relaxation occurs efficiently relative to our PAS modulation periods as xO2 → 1 and for P0 > 1000 hPa. We can compare our measured rates of O2(X, v > 0) quenching with theoretical V–T rates calculated by Coletti and Billing, who predicted rates <2 × 10−17 cm3 s−1 for vibrational quantum numbers v < 10 at ambient temperature.56 Meanwhile, Huestis performed a reanalysis of a range of V–T energy transfer studies of vibrationally excited O2 and recommended a V–T quenching rate of 2.7 × 10−18 cm3 s−1 for v = 1 at temperatures of 300 K.57 These rates are ∼4 orders of magnitude slower than the rates we determine for 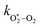 as xO2 → 1 and for P0 > 1000 hPa. Such slow V–T rates would correspond to phase shifts approaching 90° at our PAS modulation frequencies. Although the stated uncertainties in the V–T rates reported by Coletti and Billing (2002) are >25% for v < 10, we fail to reconcile our measurements with predictions from theoretical models. We cannot find any literature measurements to support the V–T rates reported by theoretical studies for v < 8; Park and Slanger58 and Hickson et al.59 only confirmed the predicted total quenching rates (the sum of V–T and vibrational-to-vibrational energy transfer rates) for v > 8. Nonetheless, it is unlikely that we can explain our observed O2(X, v > 0) quenching rate by considering quenching by O2 bath gas alone. To reconcile our measurements with models, it is possible that O2(X, v > 0) is effectively quenched by O3(
as xO2 → 1 and for P0 > 1000 hPa. Such slow V–T rates would correspond to phase shifts approaching 90° at our PAS modulation frequencies. Although the stated uncertainties in the V–T rates reported by Coletti and Billing (2002) are >25% for v < 10, we fail to reconcile our measurements with predictions from theoretical models. We cannot find any literature measurements to support the V–T rates reported by theoretical studies for v < 8; Park and Slanger58 and Hickson et al.59 only confirmed the predicted total quenching rates (the sum of V–T and vibrational-to-vibrational energy transfer rates) for v > 8. Nonetheless, it is unlikely that we can explain our observed O2(X, v > 0) quenching rate by considering quenching by O2 bath gas alone. To reconcile our measurements with models, it is possible that O2(X, v > 0) is effectively quenched by O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) in the bath gas. The reverse energy transfer process (i.e. O3(
) in the bath gas. The reverse energy transfer process (i.e. O3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) , v > 0) quenched by O2(X)) has been studied extensively and the corresponding V–T rate is ∼3 × 10−14 cm3 s−1.53,54 However, the concentrations of O3 measured by our CRDS instruments are <2000 ppm, which will reduce the total rate of O2 quenching by O3. Alternatively, there may be trace impurities in our bath gas, although this is unlikely given the use of high purity N5-grade O2. For the relaxation of O2(X, v > 0) in bath gas N2, we determine
, v > 0) quenched by O2(X)) has been studied extensively and the corresponding V–T rate is ∼3 × 10−14 cm3 s−1.53,54 However, the concentrations of O3 measured by our CRDS instruments are <2000 ppm, which will reduce the total rate of O2 quenching by O3. Alternatively, there may be trace impurities in our bath gas, although this is unlikely given the use of high purity N5-grade O2. For the relaxation of O2(X, v > 0) in bath gas N2, we determine 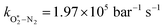 . For this relaxation, Billing reported V–T rate constants for v > 13 only,60 with such high v not expected to be populated at our photolysis energies; Flöthmann et al.45 and Levene et al. show that v = 0 dominates at all wavelengths,46 with a shoulder in this distribution appearing corresponding to population of v = 4–8 at λ = 450–500 nm, and with higher v expected to dominate for λ < 450 nm. Thus, it is again difficult to assess the accuracy of our determined rate constant in the context of previous theoretical investigations.
. For this relaxation, Billing reported V–T rate constants for v > 13 only,60 with such high v not expected to be populated at our photolysis energies; Flöthmann et al.45 and Levene et al. show that v = 0 dominates at all wavelengths,46 with a shoulder in this distribution appearing corresponding to population of v = 4–8 at λ = 450–500 nm, and with higher v expected to dominate for λ < 450 nm. Thus, it is again difficult to assess the accuracy of our determined rate constant in the context of previous theoretical investigations.
5 Conclusions
We have demonstrated the accurate correction of photoacoustic response for changes in microphone response function kM with static pressure P0 from measurements of the relative variations in microphone amplitude and PAS instrument quality factors using a speaker transducer for PAS cell eigenmode excitation. Indeed, our correction strategy is similar to that reported by other researchers.7 This method of correcting for kM has the advantage that regular and fast characterisations of the microphone response function (via speaker-excitation measurements of Qn and Sspk) can be made without the need for controlled generation of a test sample. This microphone response calibration method enabled the first studies of the pressure dependence to photoacoustic sensitivity (Ccor) for O3-laden gas samples in the Chappuis band (λ ∼ 400–700 nm) for various bath gas mass mixtures containing mass fractions of O2 (xO2) in N2. Moreover, we have reported associated measurements of the phase shift θ that allow direct assessments of photoproduct relaxation timescales. There are strong variations in both Ccor and θ with P0 and xO2 that are described well by the best-fit of a photochemical relaxation model we develop that retrieves the associated variations in the timescales for energy transfer (see Fig. 6) from the nascent Chappuis band photoproducts (O(3P) and O2(X, v > 0)) to translational motion of the bath gas species. We have shown that the accuracy of O3-based calibrations of visible-wavelength PAS instruments is optimal as xO2 → 1, in agreement with the conclusions of studies by other researchers.23 The reduced Ccor and extended timescales for photoproduct relation in N2 bath gas are associated with the inefficient recombination of O(3P) with O2 and the slower V–T relation of O2(X, v > 0) in collisions with N2. For measurements at PAS modulation frequencies <2 kHz, we recommend that measurements in the Chappuis band are performed for xO2 ≥ 0.25 and P0 > 900 hPa, although the latter pressure threshold can be relaxed at higher xO2. Crucially, these criteria depend strongly on the photoacoustic modulation timescale and researchers wishing to assess the accuracy of relevant measurements at higher PAS modulation frequencies should find the timescales presented in Fig. 6 useful.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Met Office funded the development of laboratory instruments for this work. Michael I. Cotterell acknowledges the support of the Natural Environment Research Council through an Independent Research Fellowship (NE/S014314/1). Jim M. Haywood and Michael I. Cotterell thank the Natural Environment Research Council for support through the CLARIFY-2017 grant (NE/L013797/1).References
- C. Risser, B. Parvitte, R. Vallon and V. Zeninari, Optimization and complete characterization of a photoacoustic gas detector, Appl. Phys. B: Lasers Opt., 2014, 118, 319–326 CrossRef
.
- R. E. Lindley, A. M. Parkes, K. A. Keen, E. D. McNaghten and A. J. Orr-Ewing, A sensitivity comparison of three photoacoustic cells containing a single microphone, a differential dual microphone or a cantilever pressure sensor, Appl. Phys. B: Lasers Opt., 2007, 86, 707–713 CrossRef CAS
.
- F. G. C. Bijnen, J. Reuss and F. J. M. Harren, Geometrical Optimization of a Longitudinal Resonant Photoacoustic Cell for Sensitive and Fast Trace Gas Detection, Rev. Sci. Instrum., 1996, 67, 2914–2923 CrossRef CAS
.
- C. Brand, A. Winkler, P. Hess, A. Miklós, Z. Bozóki and J. Sneider, Pulsed-laser excitation of acoustic modes in open high-Q photoacoustic resonators for trace gas monitoring: results for C(2)H(4), Appl. Opt., 1995, 34, 3257–3266 CrossRef CAS PubMed
.
- A. A. Kosterev, F. K. Tittel, D. V. Serebryakov, A. L. Malinovsky and I. V. Morozov, Applications of quartz tuning forks in spectroscopic gas sensing, Rev. Sci. Instrum., 2005, 76, 043105 CrossRef
.
- A. A. Kosterev, T. S. Mosely and F. K. Tittel, Impact of humidity on quartz-enhanced photoacoustic spectroscopy based detection of HCN, Appl. Phys. B: Lasers Opt., 2006, 85, 295–300 CrossRef CAS
.
- W. P. Arnott, J. W. Walker, H. Moosmüller, R. A. Elleman, H. H. Jonsson, G. Buzorius, W. C. Conant, R. C. Flagan and J. H. Seinfeld, Photoacoustic insight for aerosol light absorption aloft from meteorological aircraft and comparison with particle soot absorption photometer measurements: DOE Southern Great Plains climate research facility and the coastal stratocumulus imposed perturbation, J. Geophys. Res., 2006, 111, D05S02 CrossRef
.
- N. Bluvshtein, J. M. Flores, Q. He, E. Segre, L. Segev, N. Hong, A. Donohue, J. N. Hilfiker and Y. Rudich, Calibration of a multi-pass photoacoustic spectrometer cell using light-absorbing aerosols, Atmos. Meas. Tech., 2017, 10, 1203–1213 CrossRef
.
- E. C. Browne, X. Zhang, J. P. Franklin, K. J. Ridley, T. W. Kirchstetter, K. R. Wilson, C. D. Cappa and J. H. Kroll, Effect of heterogeneous oxidative aging on light absorption by biomass burning organic aerosol, Aerosol Sci. Technol., 2019, 53, 663–674 CrossRef CAS
.
- N. W. Davies, M. I. Cotterell, C. Fox, K. Szpek, J. M. Haywood and J. M. Langridge, On the accuracy of aerosol photoacoustic spectrometer calibrations using absorption by ozone, Atmos. Meas. Tech., 2018, 11, 2313–2324 CrossRef CAS
.
- M. E. Diveky, S. Roy, J. W. Cremer, G. David and R. Signorell, Assessing relative humidity dependent photoacoustics to retrieve mass accommodation coefficients of single optically trapped aerosol particles, Phys. Chem. Chem. Phys., 2019, 21, 4721–4731 RSC
.
- K. Foster, R. Pokhrel, M. Burkhart and S. Murphy, A novel approach to calibrating a photoacoustic absorption spectrometer using polydisperse absorbing aerosol, Atmos. Meas. Tech., 2019, 12, 3351–3363 CrossRef CAS
.
- D. A. Lack, M. S. Richardson, D. Law, J. M. Langridge, C. D. Cappa, R. J. McLaughlin and D. M. Murphy, Aircraft Instrument for Comprehensive Characterization of Aerosol Optical Properties, Part 2: Black and Brown Carbon Absorption and Absorption Enhancement Measured with Photo Acoustic Spectroscopy, Aerosol Sci. Technol., 2012, 46, 555–568 CrossRef CAS
.
- H. Moosmüller, R. K. Chakrabarty and W. P. Arnott, Aerosol light absorption and its measurement: A review, J. Quant. Spectrosc. Radiat. Transfer, 2009, 110, 844–878 CrossRef
.
- N. W. Davies, C. Fox, K. Szpek, M. I. Cotterell, J. W. Taylor, J. D. Allan, P. I. Williams, J. Trembath, J. M. Haywood and J. M. Langridge, Evaluating biases in filter-based aerosol absorption measurements using photoacoustic spectroscopy, Atmos. Meas. Tech., 2019, 12, 3417–3434 CrossRef CAS
.
- F. Peers, P. Francis, C. Fox, S. J. Abel, K. Szpek, M. I. Cotterell, N. W. Davies, J. M. Langridge, K. G. Meyer, S. E. Platnick and J. M. Haywood, Observation of absorbing aerosols above clouds over the south-east Atlantic Ocean from the geostationary satellite SEVIRI – Part 1: Method description and sensitivity, Atmos. Chem. Phys., 2019, 19, 9595–9611 CrossRef CAS
.
- F. Peers, P. Francis, S. J. Abel, P. A. Barrett, K. N. Bower, M. I. Cotterell, I. Crawford, N. W. Davies, C. Fox, S. Fox, J. M. Langridge, K. G. Meyer, S. E. Platnick, K. Szpek and J. M. Haywood, Observation of absorbing aerosols above clouds over the South-East Atlantic Ocean from the geostationary satellite SEVIRI - Part 2: Comparison with MODIS and aircraft measurements from the CLARIFY-2017 field campaign, Atmos. Chem. Phys. Discuss., 2020, 1–30, DOI:10.5194/acp-2019-1176
.
- J. W. Taylor, H. Wu, K. Szpek, K. Bower, I. Crawford, M. J. Flynn, P. I. Williams, J. Dorsey, J. Langridge, M. I. Cotterell, C. Fox, N. W. Davies, J. M. Haywood and H. Coe, Absorption closure in highly aged biomass burning smoke, Atmos. Chem. Phys., 2020, 20, 11201–11221 CrossRef CAS
.
- H. Wu, J. W. Taylor, K. Szpek, J. M. Langridge, P. I. Williams, M. Flynn, J. D. Allan, S. J. Abel, J. Pitt, M. I. Cotterell, C. Fox, N. W. Davies, J. M. Haywood and H. Coe, Vertical variability of the properties of highly aged biomass burning aerosol transported over the southeast Atlantic during CLARIFY- 2017, Atmos. Chem. Phys., 2020, 20, 12697–12719 CrossRef CAS
.
- P. Stier, J. H. Seinfeld, S. Kinne and O. Boucher, Aerosol absorption and radiative forcing, Atmos. Chem. Phys., 2007, 7, 5237–5261 CrossRef CAS
.
- G. Myhre, B. H. Samset, C. W. Mohr, K. Alterskjær, Y. Balkanski, N. Bellouin, M. Chin, J. Haywood, Ø. Hodnebrog, S. Kinne, G. Lin, M. T. Lund, J. E. Penner, M. Schulz, N. Schutgens, R. B. Skeie, P. Stier, T. Takemura and K. Zhang, Cloudy-sky contributions to the direct aerosol effect, Atmos. Chem. Phys., 2020, 20, 8855–8865 CrossRef CAS
.
- M. I. Cotterell, K. Szpek, J. M. Haywood and J. M. Langridge, Sensitivity and accuracy of refractive index retrievals from measured extinction and absorption cross sections for mobility-selected internally mixed light absorbing aerosols, Aerosol Sci. Technol., 2020, 54(9), 1034–1057 CrossRef CAS
.
- D. Al Fischer and G. D. Smith, Can ozone be used to calibrate aerosol photoacoustic spectrometers?, Atmos. Meas. Tech., 2018, 11, 6419–6427 CrossRef CAS
.
- M. I. Cotterell, A. J. Orr-Ewing, K. Szpek, J. M. Haywood and J. M. Langridge, The impact of bath gas composition on the calibration of photoacoustic spectrometers with ozone at discrete visible wavelengths spanning the Chappuis band, Atmos. Meas. Tech., 2019, 12, 2371–2385 CrossRef CAS
.
- A. Miklós, P. Hess and Z. Bozóki, Application of acoustic resonators in photoacoustic trace gas analysis and metrology, Rev. Sci. Instrum., 2001, 72, 1937–1955 CrossRef
.
- M. E. Diveky, S. Roy, G. David, J. W. Cremer and R. Signorell, Fundamental investigation of photoacoustic signal generation from single aerosol particles at varying relative humidity, Photoacoustics, 2020, 18, 100170 CrossRef PubMed
.
- J. W. Cremer, K. M. Thaler, C. Haisch and R. Signorell, Photoacoustics of single laser-trapped nanodroplets for the direct observation of nanofocusing in aerosol photokinetics, Nat. Commun., 2016, 7, 10941 CrossRef CAS PubMed
.
- D. M. Murphy, The Effect of Water Evaporation on Photoacoustic Signals in Transition and Molecular Flow, Aerosol Sci. Technol., 2009, 43, 356–363 CrossRef CAS
.
- J. Kalkman and H. W. van Kesteren, Relaxation effects and high sensitivity photoacoustic detection of NO2 with a blue laser diode, Appl. Phys. B: Photophys. Laser Chem., 2008, 90, 197–200 CrossRef CAS
.
- M. I. Cotterell, G. P. Ward, A. P. Hibbins, J. M. Haywood, A. Wilson and J. M. Langridge, Optimizing the performance of aerosol photoacoustic cells using a finite element model. Part 1: Method validation and application to single-resonator multipass cells, Aerosol Sci. Technol., 2019, 53, 1107–1127 CrossRef CAS
.
- M. I. Cotterell, G. P. Ward, A. P. Hibbins, A. Wilson, J. M. Haywood and J. M. Langridge, Optimizing the performance of aerosol photoacoustic cells using a finite element model. Part 2: Application to a two-resonator cell, Aerosol Sci. Technol., 2019, 53, 1128–1148 CrossRef CAS
.
- D. A. Lack, E. R. Lovejoy, T. Baynard, A. Pettersson and A. R. Ravishankara, Aerosol Absorption Measurement using Photoacoustic Spectroscopy: Sensitivity, Calibration, and Uncertainty Developments, Aerosol Sci. Technol., 2006, 40, 697–708 CrossRef CAS
.
- K. J. Zarzana, C. D. Cappa and M. A. Tolbert, Sensitivity of Aerosol Refractive Index Retrievals Using Optical Spectroscopy, Aerosol Sci. Technol., 2014, 48, 1133–1144 CrossRef CAS
.
- R. E. H. Miles, S. Rudić, A. J. Orr-Ewing and J. P. Reid, Sources of Error and Uncertainty in the Use of Cavity Ring Down Spectroscopy to Measure Aerosol Optical Properties, Aerosol Sci. Technol., 2011, 45, 1360–1375 CrossRef CAS
.
- W. P. Arnott, H. Moosmüller and J. W. Walker, Nitrogen dioxide and kerosene-flame soot calibration of photoacoustic instruments for measurement of light absorption by aerosols, Rev. Sci. Instrum., 2000, 71, 4545 CrossRef CAS
.
- T. Nakayama, H. Suzuki, S. Kagamitani, Y. Ikeda, A. Uchiyama and Y. Matsumi, Characterization of a Three Wavelength Photoacoustic Soot Spectrometer (PASS-3) and a Photoacoustic Extinctiometer (PAX), J. Meteorol. Soc. Japan Ser. II, 2015, 93, 285–308 CrossRef
.
- D. Fischer and G. D. Smith, A portable, four-wavelength, single-cell photoacoustic spectrometer for ambient aerosol absorption, Aerosol Sci. Technol., 2018, 52, 393–406 CrossRef CAS
.
- D. A. Lack, M. S. Richardson, D. Law, J. M. Langridge, C. D. Cappa, R. J. McLaughlin and D. M. Murphy, Aircraft Instrument for Comprehensive Characterization of Aerosol Optical Properties, Part 2: Black and Brown Carbon Absorption and Absorption Enhancement Measured with Photo Acoustic Spectroscopy, Aerosol Sci. Technol., 2012, 46, 555–568 CrossRef CAS
.
- C. D. Cappa, T. B. Onasch, P. Massoli, D. R. Worsnop, T. S. Bates, E. S. Cross, P. Davidovits, J. Hakala, K. L. Hayden, B. T. Jobson, K. R. Kolesar, D. A. Lack, B. M. Lerner, S.-M. Li, D. Mellon, I. Nuaaman, J. S. Olfert, T. Petaja, P. K. Quinn, C. Song, R. Subramanian, E. J. Williams and R. A. Zaveri, Radiative Absorption Enhancements Due to the Mixing State of Atmospheric Black Carbon, Science, 2012, 337, 1078–1081 CrossRef CAS PubMed
.
- B. Mason, N. L. Wagner, G. Adler, E. Andrews, C. A. Brock, T. D. Gordon, D. A. Lack, A. E. Perring, M. S. Richardson, J. P. Schwarz, M. A. Shook, K. L. Thornhill, L. D. Ziemba and D. M. Murphy, An intercomparison of aerosol absorption measurements conducted during the SEAC 4 RS campaign, Aerosol Sci. Technol., 2018, 52, 1012–1027 CrossRef CAS
.
-
J. B. Burkholder, S. P. Sander, J. P. D. Abbatt, J. R. Barker, R. E. Huie, C. E. Kolb, M. J. Kurylo, V. L. Orkin, D. M. Wilmouth and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation Number 18, JPL Publ, 2015
.
- N. Sharma, I. J. Arnold, H. Moosmüller, W. P. Arnott and C. Mazzoleni, Photoacoustic and nephelometric spectroscopy of aerosol optical properties with a supercontinuum light source, Atmos. Meas. Tech., 2013, 6, 3501–3513 CrossRef
.
- S. Y. Grebenshchikov, Z. W. Qu, H. Zhu and R. Schinke, Phys. Chem. Chem. Phys., 2007, 9, 2044–2064 RSC
.
- R. Kaiser, On the theory of the spectrophone, Can. J. Phys., 1959, 37, 1499–1513 CrossRef CAS
.
- H. Flöthmann, R. Schinke, C. Woywod and W. Domcke, Photodissociation of ozone in the Chappuis band. III. Product state distributions, J. Chem. Phys., 1998, 109, 2680–2684 CrossRef
.
- H. B. Levene, J. Nieh and J. J. Valentini, Ozone visible photodissociation dynamics, J. Chem. Phys., 1987, 87, 2583–2593 CrossRef CAS
.
- W. G. Thomas, M. J. Preslar and J. C. Farmer, Calibration of Condenser Microphones under Increased Atmospheric Pressures, J. Acoust. Soc. Am., 1972, 51, 6–14 CrossRef CAS PubMed
.
- C. H. Chan, Effective absorption for thermal blooming due to aerosols, Appl. Phys. Lett., 1975, 26, 628–630 CrossRef
.
-
Y.-H. Pao, Optoacoustic Spectroscopy and Detection, Academic Press, New York, 1st edn, 1977 Search PubMed
.
-
A. Rosencwaig, Photoacoustics and Photoacoustic Spectroscopy, John Wiley and Sons, Inc., 1980 Search PubMed
.
- C. W. Tan, Z. Wang, J. Miao and X. Chen, A study on the viscous damping effect for diaphragm-based acoustic MEMS applications, J. Micromech. Microeng., 2007, 17, 2253–2263 CrossRef
.
-
P. A. Tipler and G. Mosca, Physics for Scientists and Engineers, W. H. Freeman and Company, New York, 6th edn, 2008 Search PubMed
.
- F. Ménard-Bourcin, J. Ménard and L. Doyennette, Vibrational relaxation of ozone in O3–O2 and O3–N2 gas mixtures from infrared double-resonance measurements, J. Chem. Phys., 1991, 94, 1875–1881 CrossRef
.
- V. Zeninari, B. A. Tikhomirov, Y. N. Ponomarev and D. Courtois, Photoacoustic measurements of the vibrational relaxation of the selectively excited ozone (v3) molecule in pure ozone and its binary mixtures with O2, N2, and noble gases, J. Chem. Phys., 2000, 112, 1835–1843 CrossRef CAS
.
- R. Siebert, P. Fleurat-Lessard, R. Schinke, M. Bittererová and S. C. Farantos, The vibrational energies of ozone up to the dissociation threshold: Dynamics calculations on an accurate potential energy surface, J. Chem. Phys., 2002, 116, 9749–9767 CrossRef CAS
.
- C. Coletti and G. D. Billing, Vibrational energy transfer in molecular oxygen collisions, Chem. Phys. Lett., 2002, 356, 14–22 CrossRef CAS
.
- D. L. Huestis, Vibrational Energy Transfer and Relaxation in O2 and H2O, J. Phys. Chem. A, 2006, 110, 6638–6642 CrossRef CAS PubMed
.
- H. Park and T. G. Slanger, O2 (X, v = 8–22) 300 K quenching rate coefficients for O2 and N2, and O2(x) vibrational distribution from 248 nm O3 photodissociation, J. Chem. Phys., 1994, 100, 287–300 CrossRef CAS
.
- K. M. Hickson, P. Sharkey, I. W. M. Smith, A. C. Symonds, R. P. Tuckett and G. N. Ward, Formation and relaxation of O2(X3Σg-) in high vibrational levels (18 < v < 23) in the photolysis of O3 at 266 nm, J. Chem. Soc., Faraday Trans., 1998, 94, 533–540 RSC
.
- G. D. Billing, VV and VT rates in N2-O2 collisions, Chem. Phys., 1994, 179, 463–467 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05056c |
| This journal is © the Owner Societies 2021 |