Quantum and semiclassical dynamical studies of nonadiabatic processes in solution: achievements and perspectives

Abstract

We concisely review the main methodological approaches to model nonadiabatic dynamics in isotropic solutions and their applications. Three general classes of models are identified as the most used to include solvent effects in the simulations. The first model describes the solvent as a set of harmonic collective modes coupled to the solute degrees of freedom, and the second as a continuum, while the third explicitly includes solvent molecules in the calculations. The issues related to the use of these models in semiclassical and quantum dynamical simulations are discussed, as well as the main limitations and perspectives of each approach.

---

1 Introduction

In the last decade the computational study of the nonadiabatic excited-state dynamics in medium-size molecular systems has seen impressive advances, as witnessed, inter alia, by many authoritative reviews in this field.^1–13 Nonadiabatic processes are intrinsically quantum phenomena that couple electronic and vibrational states.¹⁴ Therefore, in principle, quantum dynamics (QD), i.e. the propagation in time of the vibronic wavefunction or the vibronic density matrix, represents the natural theoretical framework to describe their time evolution. However, the cost of traditional QD methods scales exponentially with the number of degrees of freedom, limiting their application to small systems. Many approaches have been developed in the last decades to break this limit,¹⁵ ranging from full QD methods^3,4 and semiclassical (SC) path-integral methods,¹⁶ to a multitude of hybrid methods that mix quantum and classical dynamics, generally indicated as mixed quantum classical (MQC).^1,17 The interaction of the system undergoing a nonadiabatic transition with an environment, like a solvent, protein, or surface adds an additional level of complexity to the theoretical modeling, leading to the so called open quantum systems (OQS) problem,^18,19 and many approaches have been proposed to extend dynamical methods for isolated species to this new situation.

Despite the fact that all the approaches just mentioned have been applied also to study photoactivated processes in solution, the large majority of the dynamical studies of nonadiabatic processes in the literature concerns systems in the gas phase,^{1–6,20–22} or, alternatively, chromophores embedded in a macromolecular matrix, e.g. a protein or a membrane.^23–34 The number of computational studies of a molecular system in an isotropic solution is instead more limited, despite the fact that most of the photoactivated processes of biological and technological interest occur in solution.

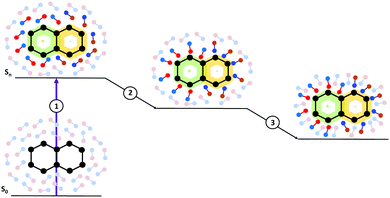
Moreover, from the methodological point of view, inclusion of solvent effects in the dynamical calculations raises many challenging issues. A basic one concerns the treatment of the solvation dynamics. Any change in the population of the different electronic states following light absorption/emission, or during the excited state dynamics, is mirrored by changes in the solute electron density, which induces a solvent response. As schematically depicted in Fig. 1, the adjustment of the solvent is not instantaneous, it involves different processes occurring on different time-scales, from sub-fs to several ps, without considering strongly viscous solvents. For example, electrons of the solvent (the electronic polarization) can be considered to readjust instantaneously to the solute electronic density (process 1 in Fig. 1). The structural rearrangements of the first solvation shell, e.g. shifts of the hydrogen bond distances, individual librations and reorientation of the solvent molecules, are slower and, though they are collected in process 2 in Fig. 1, can have different characteristic times. Finally, some motions (process 3 in Fig. 1) require a collective rearrangement of the outer solvation shells and, therefore, longer times. An additional issue is that the solvent reaction field may act as an additional, time-dependent, source of coupling between the different electronic states, leading to a highly non-linear problem. In particular, when excited state processes are non-Markovian, i.e. they occur on the same time-scale as the solvation dynamics, a reliable computational description becomes very challenging. As we will discuss later, this task is rather difficult in the framework of implicit solvation models, where the solvent is characterized ‘simply’ by some macroscopic features.

Fig. 1 Schematic description of dynamical solvation effects triggered by exciting the solute. (1) Electronic polarization, (2) librational solvent modes of the first solvation shell and (3) global rearrangements of the outer solvation shells.

Dynamical solvation effects are instead more straightforwardly considered within an explicit solvation model, where solvent molecules are included in an atomistic fashion in the calculations. However, in order to reproduce solvent effect, it is necessary (i) to consider a very large number of solvent molecules and (ii) to properly average among all the possible conformations. As a consequence, in order to reduce the computational cost, the large majority of studies resort to a classical description of the solvent molecules, and, thus, to parametrized force fields (FFs) when building the potential energy surfaces (PESs) the dynamics is based on. In principle a different parametrization is necessary for each of the solute electronic states, making an accurate treatment of dynamical solvation effects more cumbersome in explicit solvation models, especially when polarizable FFs are adopted.³⁵

However, despite these difficulties, many interesting dynamical computational studies in solution have appeared in the last few years, and promising methodological developments have been proposed. In this contribution, we shall thus concisely review the papers reporting quantum, semiclassical, and MQC dynamics simulations in isotropic solvents. We shall focus in particular on the main approaches followed to include solvent effects, and take a number of specific examples to evaluate the effect that inclusion of the solvent environment has, in particular when there are gas phase results available for comparison. A key issue we will tackle concerns the coupling between the solvation degrees of freedom and the solute excited state dynamics. This review does not therefore cover all the studies where the environment can be considered almost frozen with respect to the chromophore excited state dynamics, an approximation often adopted, for example, for the photoisomerization or excitation transfer processes occurring within a protein.^23,36 Moreover, this review does not include the papers dealing with the study in the gas phase of molecules surrounded by a small cluster of solvent molecules. Though they can provide useful insights on the dynamics in solution, their methodological framework is the same as that of gas phase calculations. It is clear that many dynamical spectral parameters, e.g. time-resolved dynamic Stokes shift, are ruled by solvation dynamics, and their analysis, by using either continuum^37,38 or explicit solvation models,^39–41 can give crucial insights on the interplay between ultrafast electronic relaxation of solute and solvent molecules. Nonetheless, due to their large number, we shall not discuss the studies aimed essentially to include solvent effects in the calculations of the PES or the related spectral parameters (for example, the vertical absorption or emission energies⁴²), as well as excited-state dynamical studies that do not explicitly address nonadiabatic processes, but focus on solvent relaxation (e.g.ref. 43), or on reactivity on adiabatic surfaces (like proton transfer^44,45).

Key features that characterize the different possible approaches to a dynamical description of the nonadiabatic processes in solution are the solvent models (implicit, as a bath of modes, and explicit), different dynamical approaches, how potentials on which nuclei move are built (derived from quantum electronic theory versus classical FFs), and finally which partition is adopted to define the classical and quantum parts of the system.

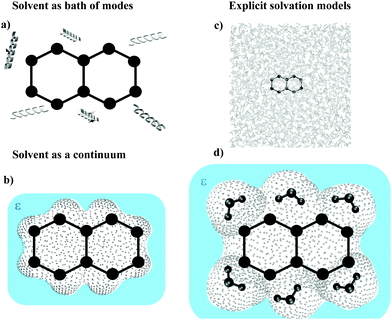
To be as focused as possible on the inclusion of the solvent effect, we organized this perspective on the grounds of different solvent models, as summarized in Fig. 2. We will first review recent progresses, relevant for processes in solution, of the well-known system-bath approaches for open quantum systems (OQS). Afterward we will focus on the recent advances of methods based on a continuum, and then on an explicit atomistic description of the solvent. Finally, in the Discussion section we will critically evaluate the state of the art and highlight the most promising perspectives.

Fig. 2 Schematic classification of the main classes of models used in nonadiabatic simulations: (a) the solvent is described as a bath of modes, (b) the solvent is described as a dielectric continuum, (c) solvent molecules are explicitly considered and (d) a limited number of solvent molecules are included, while bulk effects are treated by a continuum model.

2 Solvent as a bath of modes

One of the most popular approaches in the field of OQS¹⁸ is to simplify the Hamiltonian of the system + environment to describe the environment (the solvent) as a set of effective harmonic degrees of freedom (a bath) coupled bilinearly to the system (the solute). In this limit the effect of the bath on the system is completely described by the so-called spectral density, which provides the spectral distribution of the bath mode frequencies weighted by the system-bath couplings. Such a model has been deeply investigated, representing a playground for the development of many different theoretical methods. The basic, yet potentially relevant, studies in this field are too many to be exhaustively reviewed here. We therefore limit ourselves to cite concisely the methodological papers most influential for the applications we discuss. The interested reader can refer to the papers therein cited. Most of the ‘system-bath’ methods are rooted in the density matrix formalism and on the quantum master equations (QMEs) for the time-evolution of the reduced density relevant for the solute.⁴⁶ Formally exact equations of motion are provided by the Nakajima–Zwanzig equation,^19,47,48 or the Shibata–Takahashi–Hashitsume equation⁴⁹ but they can be solved only by introducing approximations. The most well-known case is probably the Markov limit, i.e. when the system dynamics is much slower than the bath one, leading to the well-known Lindblad,^50,51 or Redfield⁵² equations. Although interesting applications of such theories have been presented to nonadiabatic processes at a conical intersection (CoI),⁵³ in general the time separation regime assumed in the Markov limit is not adequate for subpicosecond nonadiabatic processes in solution. Several approaches have been proposed for non-Markov processes, like modified Redfield theory.^54–56 Most of them are cast in a mixed quantum classical scheme, formalized with the so-called quantum classical Liouville equation (QCLE).⁵⁷ Among them we quote the reduced density matrix hybrid approach,⁵⁸ the forward–backward trajectory solution,^59,60 and the linearized⁶¹ and partially linearized density matrix (PLDM) approaches obtained in the framework of path integrals.^62,63 As an example, PLDM was recently applied to model the excitation energy transfer (EET) between a donor and an acceptor describing the solvent as a Lorentzian-truncated Ohmic spectral density. The dependence of the EET rate on the solvent reorganization energy was investigated obtaining a very good agreement with the exact results obtained by the hierarchical equation of motion (HEOM) approach.⁶⁴

The HEOM formalism^65,66 is a numerically exact method of studying the time evolution of the reduced density matrix for system-bath problems, and it has also been applied to the study of nonadiabatic dynamics in dissipative media. For example, a counterintuitive enhancement of the lifetime of coherence was demonstrated in the S₂/S₁ decay of pyrazine coupled to a bath with a Drude spectral function.⁶⁷ Moreover, the shapes of the two-dimensional electronic spectra of adenine in water were computed with a two or three-state model simulating the effect of water with a Debye spectral density in an overdamped regime.⁶⁸ Finally, within the realm of numerically exact methods for propagating the reduced density matrix, it is worthwhile to also mention the quasi adiabatic propagator path integral (QUAPI) approach.^69–71

Wigner transformation to phase space allows one to develop new methods that share similarities with well-known approaches of statistical mechanics, leading, for example, to the formulation of the multistate Fokker–Planck and the Smoluchovski equations,^72–75 and introducing concepts like friction and diffusion. The Redfield and Smoluchovski theories have been recently combined to study the dynamics of a resonant energy transfer (RET) between two dyes, DCM and Nile red, in chloroform.⁷⁶ The solvent is described by a bath of fast modes (Redfield) plus a slow bath representing the orientational reaction field and described with drift diffusion Smoluchovski dynamics. Fig. 3 shows the initial (D*A) and final (DA*) PES with respect to the slow polar solvation coordinates described by distributions evolving according to the Smoluchovski equation (panel a) and with respect to D and A intramolecular coordinates (panel b). The black traces document the irreversible dynamics. By varying the longitudinal relaxation time it is shown that solvent dynamical disorder can boost the RET efficiency by increasing the possibility that donor and acceptor are found in a favorable orientation for RET.

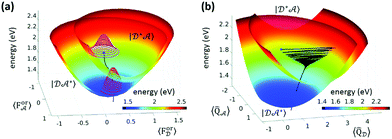Fig. 3 Resonance energy transfer from DCM (the donor, D) and Nile red (the acceptor, A). (a) Initial (D*A) and final (DA*) PES with respect to the slow polar solvation coordinates, and the orientational reaction fields F^or_D and F^or_A. Solvent distribution at time = 0 and 2.7 ps as magenta and red 3D contours, respectively, and the black trace represents the trajectory of the energy of the system in time. (b) The same PES plotted with respect to effective intramolecular coordinates of D and A. The black trace is the average trajectory showing strong initial oscillations along Q_D that are progressively quenched and a coupled slow movement along Q_A toward the minimum of the DA* PES. Adapted from ref. 76 with permission from the Royal Society of Chemistry.

The impressive progress in the development of multiconfigurational time-dependent Hartree (MCTDH),^3,77 and its multilayer extension,^78–81 has also opened the route to a full QD solution of the system-bath problem. The spectral density is translated into a finite number of modes by a discretized sampling of the frequencies, adopting a step Δω so that the Poincaré recurrence time is long with respect to the simulation time.⁸² Hierarchical transformations of the bath modes in a chain of sequentially bilinearly coupled effective oscillators provide further attractive possibilities.^82–86 MCTDH can also be combined with a density matrix formalism, in order to inquire about the effect of temperature, by truncating the hierarchy at a given order and substituting the remaining modes with a dissipative term.⁸²

Spectral densities for a specific electronic state of the system in a given environment can be obtained by post-processing the results of a classical molecular dynamics (MD) simulation. More precisely, the spectral density can be obtained by the Fourier transform of the excitation energy fluctuation correlation (EEFC) function computed along an MD trajectory.⁶³ For this, a sufficient number of snapshots along the MD trajectory need to be extracted, and the excitation energies computed with a suitable level of electronic structure theory, whilst describing the environment effect with some quantum mechanical/molecular mechanical (QM/MM) embedding model. The underlying idea is to describe the effect of the generally non-harmonic dynamics of the solute and the solvent on the nonadiabatic process with a set of effective displaced harmonic oscillators, assuming further that they have the same frequencies in the ground and excited electronic states. Fig. 4 reports such spectral density computed for the charge transfer (CT) between ferrocene and ferrocenium in liquid hexane and how the population of the donor decays according to the quantum-classical path-integral (QCPI) approach (further details in Section 4).

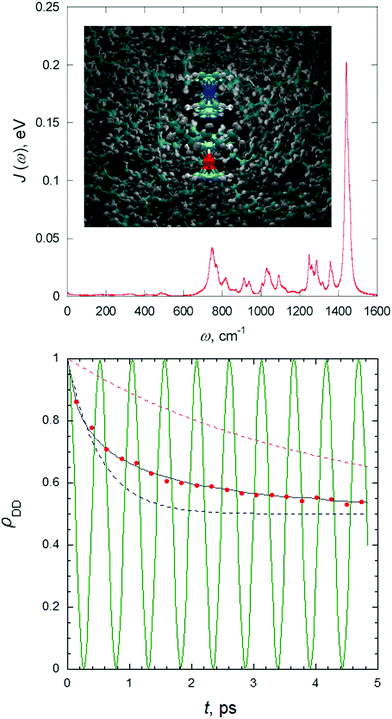Fig. 4 Charge transfer between ferrocene (Fe²⁺ in red) and ferrocenium (Fe³⁺ in blue) in liquid hexane computed with path-integral approaches. In the top panel the spectral density obtained by a classical MD is given. In the bottom panel, such spectral density is adopted to compute the decay of the population of the donor with a system-bath model with the QCPI approach (black line), and compared with Marcus predictions (dashed blue line), and from a rate coefficient extracted from the long-time exponential behavior of the population (dashed violet line). The red dots report the predictions obtained with a path-integral without reducing the solvent to a harmonic bath. For this case, the inset in the top panel reports a snapshot 0.4 ps after the start of the process and a superposition of three quantum-classical paths. Finally, the green line in the bottom panel reports the donor population in the absence of the solvent. Adapted with permission from P. L. Walters and N. Makri, J. Phys. Chem. Lett., 2015, 6, 4959. Copyright (2015) American Chemical Society. The reader can find further details in the original publication.⁹⁰

MD runs are usually driven by approximate classical MM FFs. The inaccuracies of the FFs for the solute can be mitigated either adopting quantum-mechanically derived (QMD) FFs,⁸⁷ or with a two step procedure in which the intramolecular contributions are recalculated by geometry optimizations and excited-state gradient calculations.⁸⁸ These techniques have been mainly adopted to study EET in multichromophoric systems.⁸⁹ For example, realistic spectral densities were employed to simulate the EET in the Fenna–Matthews–Olson (FMO) photosynthetic complex,⁶³ in combination with a PLDM dynamical approach. In that study, however, the main focus was on the role of intramolecular and intermolecular contributions to the spectral density, whereas the role of the solvent was not discussed in detail.

3 Solvent as a continuum

A basic way to include some solvent effect in dynamical calculations is that of considering the solvent when computing the PESs used in the simulation. This procedure is straightforward when solvent effects are taken into account by a continuum model⁹¹ and this has been applied in a number of studies that will be detailed below. Some of them define a collective solvation coordinate, whilst others describe the solvent as a polarizable continuum, as done in most of the single point energy calculations in solution.

Before reviewing these contributions, let us focus on the most delicate issues for the use of many continuum models in dynamical calculations. The first point concerns the use of the mean field approximation, i.e. that an average of the dynamics with different initial solvent configurations is substituted with a single dynamics on an average potential. We shall discuss the possible consequences of this limitation in Section 4.1. Actually, being based on an ‘average’ description of solute/solvent interactions, the most standard implementations of continuum model are ‘static’. On the other hand, it is possible to consider, at least partially, dynamical solvation effects. In the simplest and most commonly adopted approach, two different limits of ‘static’ time-regimes are identified. As depicted in Fig. 1, in the first time regime, the non-equilibrium one, following photoexcitation the fast degrees of freedom (electronic polarization) reach instantaneously to equilibrium with the electron density of the state of interest, whereas the slow degrees of freedom (e.g. the inertial ones) are still in equilibrium with the initial state. The non-equilibrium time regime is ruled by the optical dielectric constant, computed as the square of the refractive index of the solvent. In the equilibrium time regime, which is ruled by the static dielectric constant, all the solvent degrees of freedom are equilibrated with the electron density of the state of interest (therefore it applies when both processes 2 and 3 of Fig. 1 are completed).⁹¹

This approach is conceptually simple, and there are some limiting cases where it is not expected to lead to large errors in the dynamics. For example, on the ultrafast time-scale (less than a few dozen fs) it can be safely assumed that the non-equilibrium time-regime is suitable. On the other hand, full solvent equilibration requires a few ps (depending on the solvent) and, therefore, it is not clear which time-regime should be used in this time-scale.

The importance of dynamical solvent effects can be appreciated already in seminal calculations on the isomerization of a Schiff base, studied as a model of retinal,^92–95 where the excited state involved has CT character. Burghardt and Hynes use a two-electron–two-orbital electronic model, two vibrational coordinates for the solute and a collective coordinate for the solvent, described as a dielectric continuum. A mass and a frequency (governing its inertial behavior in non-equilibrium calculations) are assigned to the solvent, based on the computed solvent reorganization energy and the results of time-dependent fluorescence studies.⁹⁴ Static and dynamical solvation effects have a substantial impact on the position and the feature of the S₁/S₀ CoI and on the dynamics (see panels a and b of Fig. 5), which is simulated by using surface hopping semiclassical calculations.⁹⁴ In the equilibrium case the decay to S₀ is ∼2.5 times faster and, once the CoI is reached, the trajectories stay in its proximity. Whereas in the non-equilibrium time-regime, the systems exhibit significant oscillation on the solvent coordinate, giving an account of the slower decay.⁹⁴ In a subsequent study of the same system in acetonitrile and water, the short-time dynamical friction effects of momentum and energy transfer between the three degrees of freedom considered in the model Hamiltonian and the remaining ones are included via a generalized Langevin equation.⁹⁵ Inclusion of dissipative effects corrects some unphysical prediction of the simpler no-friction inertial model and significantly affects the isomerization yield, as shown in the panel (c) of Fig. 5.⁹⁵

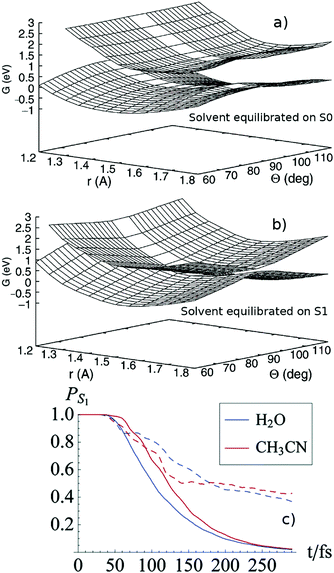Fig. 5 Potential energy surface for the isomerization of a PSB model, computed by equilibrating the solvent to the S₀ (a, top panel) or on the S₁ (b, middle panel) density. See ref. 94. Adapted with permission from R. Spezia, I. Burghardt and J. T. Hynes, Mol. Phys., 2006, 104, 903, see http://www.tandfonline.com. (c) Excited-state population time evolution for the PSB model for water (blue) and acetonitrile (red) with (bold lines) or without (dashed lines) friction. Adapted with permission from J. P. Malhado, R. Spezia and J. T. Hynes, J. Phys. Chem. A, 2011, 115, 3720. Copyright (2011) American Chemical Society.⁹⁵

An effective solvation coordinate was also used to describe the effect of the static disorder of a polar solvent on the nonadiabatic dynamics and time-resolved spectra of photoexcited dipolar and quadrupolar dyes. It was shown that the solvent can be responsible for inhomogeneous broadening but also, in some categories of quadrupolar dyes, for a removal of the symmetry with the activation of complex intramolecular solute motions.⁹⁶

Hammes-Schiffer et al. have also used effective solvation coordinates in combination with a Langevin equation and surface hopping dynamics to model non-equilibrium solvation within electron transfer⁹⁷ and proton-coupled electron transfer^98–100 processes. The results were compared to an explicit solvent model, which revealed two time scales, with the faster corresponding to the librational motion of the solvent in the first solvation shell, and the slower to the bulk solvent dielectric response (steps 2 and 3 in Fig. 1). The implicit solvent model was able to reproduce qualitatively similar results, further illustrating the capability of continuum models with an effective solvent coordinate to reproduce non-equilibrium dynamical effects.^97,98

Continuum solvation approaches commonly used within electronic structure theory programs⁹¹ (which, however, do not consider dynamical solvation effects) have also been used with nonadiabatic dynamics calculations, in the context of ‘on-the-fly’ surface hopping calculations, and for building the PES for use with MCTDH wavepacket propagations. For the former, efficient conductor-like solvation approaches (conductor-like screening model, COSMO,¹⁰¹ and conductor-like polarizable continuum model, CPCM¹⁰²) have been implemented within the NEXMD program,^103–105 which uses the collective electronic oscillator method^106,107 in combination with semiempirical Hamiltonians and surface hopping dynamics to simulate nonadiabatic dynamics of large, conjugated, organic molecules. In particular, CPCM has been used to investigate the effect of solvent polarity on the isomerization of 4-styrylquinoline¹⁰⁸ and the dynamics of derivatives of the push–pull π-conjugated oligomer p-phenylenevinylene.¹⁰⁹

For the MCTDH computations, continuum solvation models have been used in building a linear vibronic coupling (LVC) Hamiltonian including spin–orbit coupling (SOC) to study the excited state dynamics in several Re(I) carbonyl diimine complexes in acetonitrile^110,111 and water.^112,113 In the latter two studies,^112,113 the solvent effect of water on the PES was included with COSMO, whilst in the former two studies,^110,111 the solvent effect of acetonitrile on the PES was included with PCM.⁹¹ Although a comparison to gas phase dynamics was not reported in these studies, the importance of solvent effect had previously been highlighted in absorption spectral calculations, with TD-DFT computations including solvent effect with COSMO better able to reproduce the experimental spectra than a higher level of theory (MS-CASPT2) without solvent effects.¹¹⁴

PCM has also been used to build the PES used in quantum dynamical study of the ultrafast ππ*/nπ* photoactivated dynamics of uracil^115,116 and 5-fluorouracil¹¹⁵ in acetonitrile, and thymine in water.¹¹⁷ The former studies^115,116 consider two-coupled anharmonic diabatic PESs along three vibrational degrees of freedom, namely two collective variables leading from the Franck–Condon (FC) point to the minima of the diabatic states, and the third a non-total symmetric mode inducing the largest coupling between the diabatic states. Diabatic ππ* and nπ* states were defined from the S₁ and S₂ adiabatic states with a property-based diabatization, whilst the time-dependent Schrödinger equation for the wave packet evolution was solved numerically by an orthogonalized-Lanczos method. A more recent study,¹¹⁷ discussed in detail in the next section, used the MCTDH method, with a LVC model.

Though this approach does not describe dynamical solvent effects, i.e. the fact that the solvent response changes in time, it can be useful in the ultrafast regime (<100 fs) and it has proven to be able to describe dramatic changes in the population dynamics with respect to gas phase simulations. In many cases, immediately after the photoexcitation, solvent affects the dynamics essentially by modulating the energy difference between the different excited states involved. As a matter of fact, a first important solvent effect on photoexcited nonadiabatic dynamics is due to the modulation of the average energy gap between the coupled states and can be captured even with a static non-equilibrium description of the solvent. For example, the two lowest energy excited states of thymine and uracil can be described as a bright ππ* (hereafter Sππ*) and a dark nπ* transition (hereafter Snπ*). This Snπ* state, involving the transfer of an electron from a carbonyl lone pair toward a π* orbital delocalized on the ring, is strongly destabilized in polar and, especially, protic solvents.

For uracil in the gas phase the Snπ* is more stable by ∼0.5 eV at the PBE0/6-311+G(2d,2p) level.¹¹⁸ In polar solution, the two states are closer in energy. In acetonitrile Snπ* is more stable by ≤0.2 eV¹¹⁵ whereas in water, at the same level of theory, the relative stability of the two states is reversed, Sππ* being more stable than Snπ* by ∼0.2 eV. The quantum dynamical simulations (see Fig. 6) predict that in acetonitrile and in water a significant percentage (10–25%) of the population of the spectroscopic Sππ* decays to Snπ*, in agreement with the experimental indications in water.¹¹⁹ No gas phase simulation of uracil or thymine, adopting a similar vibronic Hamiltonian to that used in ref. 115, is available, making more difficult directly assessing the role played by the solvent. However in ref. 120 and 121 the Sππ* decay to Snπ* of thymine in gas and water (PCM) was investigated with an LVC model, predicting that the transfer is almost complete in gas-phase and very limited in solution.

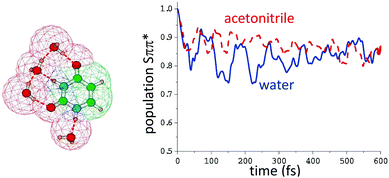Fig. 6 Left: Computational model used in ref. 115 to compute the population transfer between the bright state (Sππ*) and the close-lying nπ* of uracil in water, also including four water molecules of the first solvation shell. Bulk solvent effects were included by PCM, whose cavity is also depicted. Right: Simulated population dynamics of (Sππ*) in water (blue) and acetonitrile (red-dashed). Data taken from ref. 115.

Continuum models are very cost-effective but suffer from evident limitations that are more acute when they are applied to dynamical studies. First, they should treat different electronic states with the same accuracy and, as previously highlighted in the context of single point energy calculations, this is often not the case.¹²² Some limitations are intrinsic to the solvation models. For example, continuum models rely on the definition of a molecular cavity, whose parameters are often optimized to reproduce some ground state property (e.g. the solvation energy) and, in any case, are not expected to be the same for any electronic state.¹²³ For example, according to PCM/TD-PBE0/6-311+G(2d,2p) calculations, at the FC point the energy gap between Snπ* and Sππ* for uracil in acetonitrile is 0.23 eV when using UAHF parameterization for the cavity radii and 0.03 eV for the UA0 radii.¹¹⁵ This difference translates to a much larger Sππ* → Snπ* population transfer in the latter case, (∼35% vs. ∼20%) on a ∼500 fs time scale.¹¹⁵

Other issues are instead related to the electronic method used in building the PES. This is the case, for example, for the methods exploiting the linear response implementation of PCM in excited state calculations, such as PCM-TD-DFT, which is one of the most commonly used in excited state calculations. It has been shown that this implementation is not suitable to describe excited states involving large changes in the electronic density, such as those with significant CT character.^124–127 Clearly, a balanced description of the excited state PES in solution is a prerequisite for any reliable dynamical study.

The other critical issue concerns the treatment of dynamical solvation effects, discussed above. In this respect some interesting methodological developments have been recently proposed, allowing a time-dependent extension of PCM.^128–133 They exploit the Debye dielectric model,¹³⁴ where the solvent is characterized by a complex dielectric function allowing to interpolate between the static and the dynamic dielectric constants. The authors of ref. 130, based on the frequency-dependent dielectric constant of the solvent, derive an equation of motion for the dielectric polarization within the PCM framework, which is numerically integrated simultaneously with the TD Hartree–Fock/density functional theory equations. This method is applied to model processes as the photoactivated CT in nitroaniline.

By using real-time (RT) TD-DFT theory,¹³⁵ the absorption spectrum of azobenzene, including cavity field effects and a more sophisticated treatment of the dielectric function, has been computed in water and in other solvents,¹³³ showing the importance of considering a realistic shape for the solute cavity. (RT)-TD-DFT¹³⁵ can also be used with explicit solvation models, which, as discussed in the next subsections, can overcome the limitations of implicit approaches. Recent studies have combined (RT)-TD-DFT with polarizable FFs for the solvent, pointing out the role played by the mutual solute/solvent electronic polarization in electronic spectra and electronic dynamics.^135–137

The effect on the calculations of energies and properties of the implicit time-separation between solute and solvent electrons, assumed in the most popular self-consistent polarizable continuum implementations, has been recently re-examined.¹³⁸ Moreover, a very-promising new formulation of a solute in PCM in the framework of OQS has been proposed, leading to a time-dependent OQS-PCM Schrödinger equation¹³⁹ that allows the limits of the approximated time-separation between solute and solvent electronic dynamics to be overcome. Coupling this approach with the stochastic Schrödinger equation¹⁹ represents a very promising route to explicitly account for dynamical solvent effects.

Another strategy to address deficiencies in the implicit description of the solvent is the “dynamic continuum approach”,¹⁴⁰ which accounts for the effect of the solvent on the QD propagation by adding a frictional term to the Hamiltonian. Such an additional potential is related to the changes on the cavity surface with respect to the solute coordinates, and it can be especially relevant for bond cleavage processes, where the formation of two fragments drastically increases the surface area. This approach has been applied to study the C–P bond dissociation of diphenylmethylphosphonium cation (Ph₂CH–PPh₃⁺) in acetonitrile on the S₁ state, adopting a reduced 2D PES. It shows that the solvent cage decelerates the dissociation wavepacket, promoting alternative decay pathways.

Furthermore, it is worth mentioning attempts to account for solvent effects on nonadiabatic dynamics with a mesoscopic description of the solvent, in terms of its local density and its momentum density.¹⁴¹ The equations of motion are derived in a QCLE formalism and are able to also accurately describe solvent effects on electronic coherence. At the state of the art, this approach has been applied only to model systems like a nonadiabatic transition of NO in superfluid argon.^142,143

3.1 Solute–solvent cluster models embedded in a continuum

In a study of the photoactivated dynamics of uracil in water,^115,116 a cluster including the solute and four water molecules of the first solvation shell was considered and embedded in PCM (in non-equilibrium regime) to account for bulk solvent effects (see Fig. 6). The quantum dynamics was run on reduced dimensionality diabatic models, defining three collective coordinates that also include some rearrangement of the explicit molecules between the different diabatic minima. In hydrogen-bonding solvents, such a mixed approach is advantageous with respect to pure continuum models, because it can better describe the strongly directional solute–solvent interactions. The importance of a proper treatment of solute–solvent hydrogen bonds can be appreciated studying the Sππ* → Snπ* population transfer of 5-fluorouracil in acetonitrile and water.¹¹⁵ These two states have similar stability when only bulk solvent effects are considered, whereas Sππ* is 0.5 eV more stable when 4 water molecules of the first solvation shell are included in the calculations. Quantum dynamical simulation therefore predicts a substantial (∼30%) Sππ* → Snπ* population transfer in acetonitrile and a negligible one in water within 500 fs. In addition to a more accurate description of the PES, mixed models enable the inclusion of the effect of the solvent molecules on the nonadiabatic couplings and decrease the impact of some of the limitations of the continuum model in describing dynamical solvent effects. On the other hand, due to the absence of the outer solvation shells, the solute/solvent interaction and the mobility of the water molecules tend to be overestimated.⁴⁰

4 Explicit solvation models

As anticipated in the introduction, explicitly considering the molecular nature of the solvent can in principle give a more direct access to dynamical environmental effects, as the characteristic times associated with the molecular motions are considered in the computational model. Since the study of the excited states often requires computationally expensive methods, solvent molecules are usually considered by using classical FFs. This methodological machinery, commonly used for single point energy calculations, is the hybrid QM/MM method as pioneered by Warshel and Levitt.¹⁴⁴

In this method the electronic part of a system is split into two regions: the QM one, which for excited state dynamics commonly comprises the chromophore; and the MM one, which is commonly the protein environment or solvent, although in this present perspective we are only considering examples where the MM region includes the solvent. General information for the QM/MM methods can be found in ref. 27, 35 and 145–150. A key question for QM/MM, in particular with regards to its use in excited state dynamics, is how to compute the interaction between QM and MM subsystems, with approaches classified as either mechanical embedding (ME), electrostatic embedding (EE), or polarizable embedding (PE).¹⁵⁰ The ME approach treats the electrostatic interaction at the MM level, by applying the charge model of the MM region to the QM region. This is computationally the most efficient approach; however typically it is also the least accurate. The EE approach instead incorporates the MM point charges as one-electron terms in the QM Hamiltonian, such that the QM region is polarised by the presence of the MM region. However, this does not take into account the polarisation of the MM region by the QM region, for example the solvent responding to different charge densities of the chromophore in different excited states. Therefore, in principle the PE approach, which does take this into account, should be the most accurate. However, in practice this is very difficult to implement due to competing linear response (LR) and state-specific (SS) effects (an issue also for continuum models).^126,127 The LR scheme can naturally consider multiple electronic states at the same time, whilst the application of the SS approach would in principle require a different calculation for each coupled surface. On the other hand, the LR scheme lacks the contribution to the polarization of solvent induced by the change of electronic density from one state to another, whilst the SS can account for this.³⁵ Because of these issues, at present there has been no application of QM/MM to nonadiabatic excited state dynamics using a PE approach. Recent studies by Cao et al. on thiobases in water^151,152 have used AMEOBA polarizable FF;^153,154 however the response of the water to the density change of the thiobases in different states was switched off, rendering the approach not a complete nonadiabatic PE scheme. Instead, the EE approach, in which only the chromophore is polarised by the solvent, has been the main embedding approach used, due to greater simplicity compared to PE and greater accuracy compared to ME.

We split the remainder of the section into two parts, depending on how the nuclear dynamics of the solute are treated. In the first part, we describe examples of how explicit solvation has been implemented into on-the-fly nonadiabatic dynamics methods that utilise classical trajectories. The QM/MM implementation of explicit solvation is relatively straightforward for these approaches, being performed in the same manner as for single point energy QM/MM computations. Therefore, rather than further discussion of the QM/MM approach itself, we will focus on the main applications, considering the effect the inclusion of solvent has on the dynamics, and methodological issues of the on-the-fly classical trajectory approaches.

In the second part, we consider methods that incorporate nuclear quantum effects into the dynamics of the solute. Due to the delocalised nature of these methods, and the fact that the PES need to be precomputed, more specialised methods of incorporating explicit solvation have been devised, and so we will describe these approaches in more detail. It is worth noting that whilst the methods in the first part have been referred to as mixed quantum classical (MQC) in the literature, due to the use of classical trajectories combined with a quantum treatment of electrons,¹ we will also refer to the approaches in the second part as MQC, with the partition being in terms of the nuclear dynamics, with the solute typically being in the quantum region and solvent in the classical region.

4.1 Methods that move the nuclei classically

The two predominantly used on-the-fly classical trajectory-based approaches are the fewest switches surface hopping (FSSH),¹⁵⁵ and Martínez's ab initio multiple spawning (AIMS).²¹ Despite being based on classical trajectories, AIMS can however take nuclear quantum effects into account, since each trajectory is dressed with a Gaussian wavefunction and brings a time-dependent phase, giving rise to quantum interferences. The number of trajectories used is often too small and the basis set too disperse for these quantum interferences to be included everywhere; however they can be important in ‘spawning’ regions, usually in the vicinity of a CoI.²

The FSSH and AIMS methods evaluate the PES at each step in the dynamics via electronic structure theory computations, and the incorporation of solvent effects with QM/MM can be accomplished in the same manner as for single point energy computations. The rate limiting step is generally the evaluation of the electronic structure, as for excited state calculations an ab initio multi-reference method such as state averaged complete active space self-consistent field (SA-CASSCF), multistate complete active space second order perturbation theory (MS-CASPT2), or multi-reference configuration interaction (MRCI) is required for accurate propagation, in particular around the near degeneracy of a CoI. Therefore, notwithstanding the recent progress in GPU-accelerated electronic structure calculations,^156–158 and machine learning approaches,^159,160 these methods are computationally expensive (particularly MS-CASPT2 and MRCI) and are thus limited to small-to-medium-sized molecules with tens of atoms.

Some of these smaller molecules studied with multi-reference methods include azomethane,¹⁶¹ protonated Schiff bases,^162,163 and formamide¹⁶⁴ in hexane and water; and the chromophore of photoactive yellow protein,^27,165,166 the chromophore of green fluorescent protein,¹⁶⁶ an ethylene bridged azobenzene,¹⁶⁷ hypoxanthine derivatives,^168,169 and thiouracil¹⁷⁰ in water.

Some examples of the effect of including explicit solvent via QM/MM for these molecules are given in the following. First, let us consider the chromophore of photoactive yellow protein, p-coumaric acid (pCA). This has been studied by different dynamical methods (AIMS¹⁶⁶ and surface hopping^25,26,165) and in different environments: gas phase,¹⁶⁶ water^165,166 where an anionic model p-hydroxybenzylidene acetone (pCK-) was used, and embedded in protein.^25,26 Excited state deactivation of the chromophore was identified to occur via a rotation of either the ethylenic double bond (DB) or the phenyl-adjacent single bond (SB), both of which promoted the S₁/S₀ CoI. In the gas phase, the rate of deactivation was slow in AIMS¹⁶⁶ and not observed in 5 ps in surface hopping,¹⁶⁵ due to a large gap between the DB- and SB-rotated structures and the S₁/S₀ CoI. In water, the rate of deactivation was much faster,^165,166 (and comparable for surface hopping and AIMS, see Fig. 7c) due to stabilisation of the SB- and DB-rotated structures in the S₁ state from the solvent. The specific arrangement of the solvent molecules mediates the deactivation, with the SB-rotated structure possessing three hydrogen bonds from solvent to the carbonyl oxygen and a weak hydrogen bond from the solvent to the phenolate oxygen, whilst the DB-rotated structure has at least two strong hydrogen bonds from solvent to the phenolate oxygen, and one or two weak hydrogen bonds from the solvent to the carbonyl oxygen.¹⁶⁵ These hydrogen bonding arrangements in solvent are shown in Fig. 7a and b, and the surface hopping calculations found that deactivation via the SB-rotated structure was favoured,¹⁶⁵ whilst the AIMS calculations found more comparable deactivation via SB- and DB-rotated structures.¹⁶⁶ Similar hydrogen bonding arrangements and SB- and DB-rotated structures have also been found in protein environments.^25,26

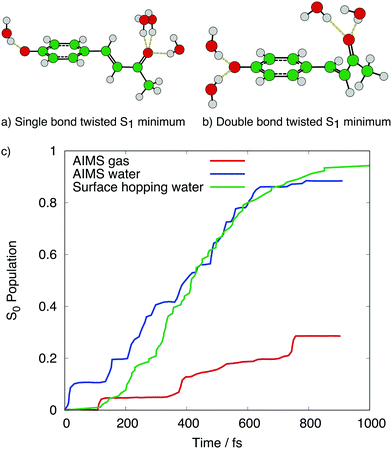Fig. 7 S₁ minimum energy configurations of pCK – in the (a) single bond- and (b) double bond-rotated structures, including the main hydrogen bonding effects from solvent. Structural data from ref. 165. Panel (c) shows the population transfer to S₀ for AIMS in the gas phase and water, and surface hopping in water, when initially excited to S₁. Data from ref. 165 and 166.

QM(GVB-CAS)/MM dynamics on trans-azomethane revealed that the decay lifetimes, associated with the torsion around the central double bond, are mainly influenced by mechanical restrictions from interactions with the solvent, and do not depend on the polarity, with similar decay times in polar and non-polar solvents.¹⁶¹ Furthermore, these simulations also confirmed the absence of dissociation processes in solution, in agreement with experimental results¹⁷¹ and other dynamic studies.¹⁷²

Surface hopping SA-CASSCF(10,8)/MM simulations have been performed on 9H-hypoxanthine and its methylated derivative (9M-hypoxanthine) in the gas phase and water. These studies concluded that whereas the 9M-hypoxanthine S₁ → S₀ decay is marginally affected by water, it is three times slower in the non-methylated species compared to that of the gas phase, pointing to a different hydrogen bond environment in aqueous solution in both molecules.^168,169

In order to reduce the computational cost of the electronic structure to study larger molecules, a popular choice has been to use the floating occupation molecular orbital (FOMO) method,^173–179 in conjunction with semiempirical evaluation of electronic integrals via the neglect of differential diatomic overlap (NDDO).^180,181 In the FOMO method, a single configuration SCF calculation is conducted, in which the molecular orbitals are allowed to have non-integer populations in an energy window around the Fermi level. An orbital energy width parameter is chosen to account for the spread of the orbitals above and below the Fermi level, and the total number of electrons is fixed. Subsequently, these FOMO orbitals are used in a CI calculation, or in a chosen active space for a CAS-CI calculation, without any further orbital optimization. This approach permits a multi-reference character to be introduced, as is necessary for use with on-the-fly dynamics, whilst the use of a single configuration, as opposed to multiple configurations, and semiempirical, rather than ab initio, evaluation of the electronic integrals allows the FOMO-(CAS)CI method to be much less computationally expensive than CASSCF, CASPT2 and MRCI. However, some extra effort may be required in reparamaterizing the semiempirical Hamiltonian, as they are typically optimized for ground state rather than excited state computations.¹⁶⁶ The FOMO method has been used in on-the-fly dynamics calculations with different applications,^{11,166,178,179,182–188} some of them paying special attention to the role of solvent in the photodynamics. For example, simulations of azobenzene in vacuo, n-hexane, methanol and in ethylene glycol revealed that a delay in isomerization was predicted to depend more on the size and mass of the solvent molecules than on the intermolecular interactions, being fastest in vacuo, intermediate in methanol and hexane, and slowest in ethylene glycol.¹⁸² This longer excited state lifetime in more viscous solvents successfully explained the experimental findings concerning trans → cis photoconversion yields, fluorescence lifetimes and depolarization.

Semiempirical Hamiltonians have also been used in combination with MRCI to study the excited state dynamics of the adenine and guanine nucleobases in water.^189–192 The effect of water in their nonradiative decay is system-dependent; with the nonadiabatic dynamics of adenine found to be comparable in water and the gas phase¹⁸⁹ and around 10 times longer in (dA)₁₀ oligomers,¹⁹¹ whereas the preferred S₁ → S₀ decay mechanisms of guanine change and slightly accelerate the internal conversion in water compared to the gas phase. For guanine, a CoI via a ‘boat-like’ or NH₂ out of plane conformation is preferred in the gas phase, whilst a carbonyl oxygen out of plane conformation is preferred in water. It was hypothesized that hydrogen bonding effects in water assisted the out of plane motion of this oxygen atom, leading to the CoI.¹⁹⁰

DFT-based calculations have been exploited to reduce computational expense for other DNA systems. For example, Marwick et al.¹⁹³ studied excited state proton transfer (PT) in guanine–cytosine Watson–Crick pairs both in vacuum and in water, combining Car–Parrinello dynamics with BLYP in the ground state, and surface hopping dynamics with restricted open shell Kohn–Sham theory for the excited state. The first excited state was found to obtain some CT character, larger in water, before PT occurs. However the solvent effect on this reaction was predicted to be small.

A more common DFT-based approach for the excited states is to use TD-DFT,¹⁹⁴ and whilst it is well known that TD-DFT cannot accurately model a CoI between the ground and excited states,¹⁹⁵ they can be approached close enough to permit surface hopping calculations. In a very recent contribution¹⁹⁶ Ibele et al. studied the excited state dynamics of a single strand oligomer (dA)₂₀ by surface hopping QM/MM simulations in a local diabatization approach.¹⁹⁷ Four adenine bases are described by TD-CAM-B3LYP and the remaining part of the system and the solvent at the MM level. Confirming the general picture provided by static calculations,¹⁹⁸ they describe how the delocalized excitons produced by light absorption give rise to monomer-like excited states and excimers in the first ∼100 fs. CT states are formed on a longer timescale, but already after 400 fs, they represent ∼40% of the excited state population.

TD-DFT in combination with surface hopping has also been used for other medium-sized molecules^{151,152,199,200} and more challenging metal complexes in solvent.^201–203 An interesting medium-sized molecular example is that of indole in water, with a comparison between indole in the gas phase, indole with a classical water sphere in a QM/MM scheme, and the QM/MM scheme with indole plus the three closest water molecules in the QM region.¹⁹⁹ After initial excitation to the S₂ state, ultrafast (17 fs) conversion to the S₁ state was observed for isolated indole, which was slowed slightly (77 fs) with the classical water sphere. Extremely slow conversion to S₀ (>30 ps) was seen for isolated indole, and no transition to S₀ was observed for indole with the classical water sphere. The slower conversion in water was attributed to polarization effects due to the solvent, and friction effects of the solvent leading to slower nuclear motion and lower couplings between the states. For the calculation that included three water molecules in the QM region, an in-between time constant for the internal conversion of S₂ to S₁ was observed (46 fs). Moreover, in contrast to the other two calculations, there was ultrafast decay to S₀ (30% population after 300 fs). This was attributed to a CT to solvent state, confirming previous theoretical prediction,²⁰⁴ and experimental observations of solvated electrons.²⁰⁵ This study highlights that, depending on the system, a QM treatment of solvent can be necessary.

For metal complexes such as [Ru(bpy)₃]²⁺ (bpy = 2,2′-bipyridine),²⁰¹ [Re(CO)₃(im)(phen)]⁺ (im = imidazole, and phen = phenanthroline)²⁰² and Os(bpy)₃²⁰³ the focus has been to simulate intersystem crossing rates in solution. These surface hopping QM(TD-DFT)/MM studies, using BP, B3LYP or BP86 functionals and a spin–orbit Hamiltonian, obtained lifetimes in good agreement with experimental results.

Turning to the deficiencies of the surface hopping approach, FSSH suffers from an inaccurate description of electronic coherence, partially ameliorated by the so-called “decoherence corrections”.²⁰⁶ Always adopting the same quantum-classical partition in which the quantum subset includes the electronic states, while the nuclear motion is classical, methods grounded in the formalism of QCLE allows in principle a better description of the electronic coherence. In this framework, Markland and co-workers^207,208 have derived a generalized quantum master equation (GQME) in which the memory kernel is approximated with a Ehrenfest mean field (MF-GQME) approach. Application to a CT of a model donor–acceptor system in explicit water shows that MF-GQME delivers results remarkably more accurate than those of FSSH and direct Ehrenfest dynamics.

An alternative approach is based on the QCPI formalism,²⁰⁹ as briefly mentioned at the end of Section 2. It combines a path-integral representation of the quantum system with a description in terms of classical trajectories of the solvent. The straightforward evaluation of the QCPI time-evolution requires a sum over all possible quantum paths, which increases exponentially with the number of time steps N, due to memory effects. Exploiting the concept of decoherence it is possible to speed up the calculations by orders of magnitude, making possible its application to processes as complex as the outer-sphere CT between ferrocene and ferrocenium in liquid hexane, described at the atomistic level. In this way strongly non-exponential behaviours can be described.⁹⁰ Some results, including a snapshot of solvent configurations obtained with three different quantum-classical paths, are reported in Fig. 4 and compared with those obtained with a system-bath approach.

4.2 Methods aiming to include (some) nuclear quantum effects

At the state of the art, most of the quantum dynamical simulations in explicit environments, like several layers of solvent molecules, are based on MQC partitions,^{117,210–212} where only a reduced number of nuclear degrees of freedom (DoFs) are propagated with QD, while the remaining ones evolve in time according to classical MD. As mentioned previously, here the MQC partition is based on the different treatment of nuclear dynamics, and usually the solute is included in the quantum region and the solvent in the classical one. Two main families of MQC approaches are possible: (i) those that account for the effect of the fluctuations of the solvent before the photoexcitation takes place, but then assume that the solvent is so slow to be frozen during the excited-state dynamics (“static disorder”), and (ii) those which truly account for coupled solute/solvent dynamics during the nonadiabatic process. The development of the first kind of method is much more straightforward. A ground-state MD trajectory provides a set of representative snapshots of the solute + solvent. At each of them coupled PESs for the solute are obtained and a QD is run, which is specific for that particular solvent configuration. This approach thus basically provides a set of static coupled PESs over which solute DoFs propagate. Such PESs can be built by low-order Taylor expansions like the so-called vibronic coupling (VC) models, including linear (LVC) or also quadratic (QVC) couplings, which require energies and their first or first and second derivatives with respect to nuclear coordinates, which can be computed with a QM/MM scheme. In some cases, cheaper strategies have been adopted, which consider the shape of the PES of each snapshot equal to an average obtained for the solute in PCM. A QM/MM scheme (EE embedding) is then used to recompute only the energy gap between the coupled PESs, since, in many cases, it is the determining factor in the ultrafast timescale.^117,213

This approach was recently adopted to evaluate the average potential of diabatic Sππ* and Snπ* states of thymine in water,¹¹⁷ showing a marked dependence of the population transfer yield on the solvent fluctuations. Similar indications were obtained for the singlet/triplet excited state of metal ligand CT states in transition-metal complexes.²¹³ In both applications, the differences between the results averaged over different dynamics and those for a single dynamics on average PES, obtained either with PCM,^117,213 or with energy-gaps averaged over all the snapshots,¹¹⁷ were found to be moderate, indicating in any case a nonlinear dependence of the quantum yield on the energy gap.¹¹⁷ While the above approaches use LVC for all solute DoFs (rigid systems), it has been recently shown that the adoption of proper iterative projectors in curvilinear coordinates allows these kind of approaches to also be extended to the computation of vibronic spectra of flexible molecules in explicit solvents, where both the solute soft-modes and the solvent modes are treated with classical MD.²¹⁴ Therefore, a generalization to nonadiabatic dynamics of flexible systems is at hand.

Other recent works^210,211 incorporate the static disorder of the solvent on the generally anharmonic adiabatic PES computed on a grid of points, although either ignoring nonadiabatic couplings,²¹⁰ or transferring them from gas phase calculations,²¹¹ and neglecting the fluctuations of transition energy. In these examples, only the few (2–3) solute DoFs most relevant to the QD propagation are considered, and the contribution of the solvent at each configuration is added to the reduced dimensionality PES of the isolated solute. The solvent contribution is computed by either the adoption of additive schemes with precomputed interaction energies between the solute and one solvent molecule on a spatial grid,²¹⁰ or by means of scans along the relevant solute coordinates at each solvent configuration, followed by subtraction of the same scans of the isolated solute in the ground state.²¹¹ In ref. 210, the authors analyzed a bond dissociation of diphenylmethylphosphonium cation (Ph₂CH–PPh₃⁺) in acetonitrile already investigated in ref. 140 adopting a continuum solvent model. Concretely, they take a bond length and an out-of-plane angle connected to the bond cleavage process as the solute DoFs included in the reduced dimensionality model. In ref. 211, uracil decay from the S₂ state in solvated RNA was studied, taking the vectors from FC point to the CoI (FC → CoI) and to the minimum of the state (FC → S^min₂) as relevant solute coordinates (with a third additional solute coordinate also investigated but found irrelevant). In this work, the hybrid MQC approach predicted population dynamics between S₂ and S₁, which showed a large variability with respect to the initial solvent configuration, allowing the detection of decays from the S₂ state with longer relaxation times with respect to the isolated nucleobase, which helps to rationalize experimental observations.

In many cases, the average change of stability and the static disorder experienced by the chromophore in solution are the most important effects that the solvent has on its excited state dynamics, and they can be effectively captured by the methods just described. When the solvent response to the electronic excitation takes place in a time scale similar to that of the non-adiabatic process, more sophisticated approaches are needed instead. In these cases, such as ultrafast water dynamics detected around photoexcited proteins,²¹⁵ it is necessary to propagate the coupled nuclear dynamics of both the quantum and classical regions with the MQC partition. This is the second family of methods mentioned at the beginning of this section whose development is still an open question. A possible strategy to describe approximately the coupling between the quantum and classical DoFs is provided by a mean-field/Ehrenfest approach, in which classical DoFs feel the average potential exerted from the quantum density, while the QD includes solvent coordinates as TD parameters.^117,212 In ref. 117 Sππ* → Snπ* decay for thymine in water was investigated, performing QD simulations of the coupled diabatic states described with a LVC model, and adopting ML-MCTDH to propagate a wavepacket along all solute coordinates on the coupled PESs, while water molecules move classically. At each extracted snapshot from ground state MD, a new propagation of quantum and classical DoFs was started. Coupling was introduced with an iterative scheme, according to which at regular time intervals (5 fs), the LVC model and solvent FFs were updated to account, respectively, for the new position of the solvent molecules and the new electrostatic potential exerted by the solute on the solvent due to the ongoing population transfer. In practice, in this specific application,¹¹⁷ for the QD only the Sππ*–Snπ* energy gap of the LVC Hamiltonian was considered time-dependent, whereas for the classical propagation of the solvent the partial charges over thymine were obtained as an average of those evaluated at Sππ* and Snπ* pure states, weighted by the time-dependent populations of each state. Along with solvent coordinates, translation and rotation of the solute were also propagated, representing the solute as a rigid body with the PCM-optimized internal geometry. The general framework allows, in principle, to further update solute coordinates for each MD step with the expected values taken from the QD step. These simulations indicate that the ultrafast dynamics of the solvent has an impact on the population dynamics already on the ∼50 fs time scale, through librational motions leading to a reorganization of the H-bonds.

Fig. 8a presents different scenarios depending on the set of charges selected for thymine in the ground state MD (CM5 or RESP) and the inclusion (QMsol) or not (PCsol) of a first quantum solvation shell in the computation of the solvent effect on the energy gap driving the QD. In the setting more favorable to Sππ* (RESP-QMsol) the tendency to transfer population to Snπ* is scarce. In this case the dynamics of the solvent stabilizes the most populated excited state even further. This disfavors the population transfer in the coupled dynamics QD-MD, with respect to what happens assuming that the solvent is frozen (only static disorder “FluctΔE”). The simulations adopting RESP-PCsol settings provide a similar picture. When, however, the stability of the states is similar (CM5-PCsol), and therefore the tendency to equilibrate their populations is large, solvent dynamics only causes an initial slowing down of the transfer, but the long-time yield is similar. Fig. 8b shows for one case (RESP-PCsol) the striking dependence of the QD on the different initial positions of the solvent.

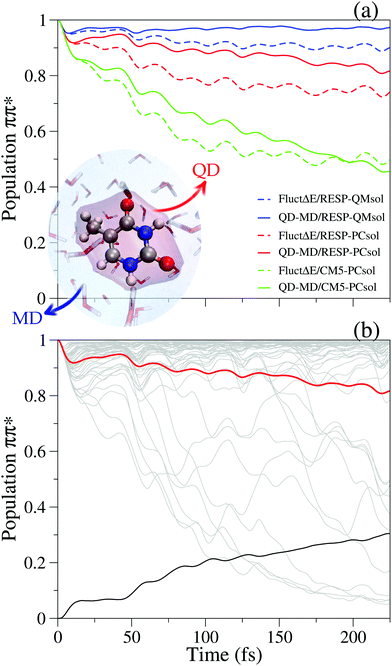Fig. 8 Sππ*/Snπ* coupled dynamics of thymine in water reported in ref. 117 on the grounds of PBE0 calculations. “FluctΔE” simulations only account for static disorder, whilst QD-MD indicates coupled solute/solvent dynamics. Different decays of the initial Sππ* (ππ*) population are shown in panel (a) for different computational settings explained in the text. For RESP-PCsol calculations, panel (b) reports the population dynamics for the individual 50 trajectories (gray), their average (red) and their standard deviation values (black). A scheme of the adopted computational model is reported in the inset. Adapted with permission from (J. Cerezo, Y. Liu, N. Lin, X. Zhao, R. Improta and F. Santoro, J. Chem. Theory Comput., 2018, 14, 820). Copyright (2018) American Chemical Society.

The comparison of QD-MD results for the two solvent models QMsol and PCsol also clearly shows that inclusion of a first solvent shell at QM level remarkably impacts on the nonadiabatic dynamics. In this case this phenomenon occurs because solute/solvent mutual polarization stabilizes Sππ* more than Snπ*. This finding further highlights the importance of mutual solute/solvent polarization when studying excited-states properties and dynamics, in line with the indications arising from the analysis of solvent shifts,^216,217 dynamical Stokes shifts,⁴¹ and electronic spectra and dynamics.¹³⁶

A similar MQC approach is adopted in ref. 212 where the S₂ → S₁ decay of uracil in water is simulated. A reduced dimensionality (2D) representation of the solute is adopted, in keeping with previous investigations of the effect of static disorder,²¹¹ using a similar strategy to account for the effect of the explicit solvent coordinate on this 2D-PES. Moreover, the S₂–S₁ coupling parameters are considered independent of solvent coordinates. The MQC approach is similar to that reported above, with solvent coordinates propagated with MD and solute (reduced-dimensionality) internal coordinates evolving according to QD, both coupled through an Ehrenfest scheme. External (translation and rotation) coordinates of the solute are treated with a similar rigid body approach along the MD step. In this case, however, partial charges over uracil within the MD step are taken from standard FF (AMBER14SB). The reported results, which focus on the S₂ to S₁ population transfer show, however, no significant effect of the solvent on nonadiabatic dynamics, with a decay similar to what is obtained in the gas phase.

Though being able to deliver very interesting results and suggesting physically significant trends, these approximate coupling schemes have intrinsic limitations in the description of the energy flow between the classical and quantum DoFs, and they can clearly define and ensure energy conservation only in the “static disorder” limit. One critical step for energy conservation has been identified in the scheme adopted to update the frozen coordinates of the solute for the MD propagation, finding the use of expectation values from the QD density as an efficient and accurate protocol.²¹² In any case, this issue is affected by other factors, including the method to update the forces acting on the solute coordinates and the population-average charges over the solute for each MD step. Therefore, new developments in this field are highly desirable.

The dynamical effect of the solvent on CT and inter-system crossing (ISC) transitions has also been recently studied, coupling classical MD and the so-called perturbation matrix method.^218,219 In this approach, the solute is referred to as the quantum center (QC), and the states of the QC are perturbed by interaction with the time-dependent electric field produced by the solvent. Transition probabilities between states are obtained via application of a Landau–Zener formula. A kinetic model allows the rate probability averaged on a representative ensemble of MD trajectories to be reconstructed. The method is able to include vibrational as well as electronic states for the QC, and is effective enough to study reactive processes on different time scales: for instance the CT between 1,4-dimethoxynaphthalene and 1,2-dicyanoethylene in THF (computed lifetime 822 ± 20 fs, and experimental one 360 fs) and the ISC of fluorenilydene in acetonitrile (computed lifetime 312 ± 40 ps, and experimental one 440 ps).²²⁰

5 Discussion

In this contribution we have reviewed the main methods to include solvent effect in nonadiabatic dynamical simulations and their applications. Keeping in mind that each classification is always somewhat arbitrary and that, as we have documented, several mixed approaches have been proposed, we have identified three main classes of solvent models. Some methods are more suitable to reproduce bulk solvent effects on dynamics (e.g. shifts in energy of the excited states), whereas other ones can more easily describe localised effects, such as steric hindrance to rotation/isomerisation, and/or hydrogen bonding. Moreover, since it is possible to combine all the solvation models with different dynamical methods (e.g. semiclassical, and quantum), additional methodological issues arise. Finally, some specific problems (not discussed in this contribution) are related to the coupling between the solvation model with the electronic method used to map the PES, since the possible limitations of the latter can be amplified in solution. In any case, each approach appears to have its strengths and its limitations, the latter being the focus of on-going research efforts, with encouraging indications.

Several accurate quantum and semiclassical dynamical approaches are mature for the system-bath models described in Section 2. They can be combined with available tools for obtaining realistic spectral densities through MD runs, although in the literature more applications to cases where the environment is a heterogeneous scaffold like a protein exist. It should be highlighted, however, that at the state-of-the-art these approaches appear better tailored for processes like EET or CT where it is easier to compute separate spectral densities for the donor and acceptor states (the diabatic states of the dynamical treatment). The situation is more complicated in the case of two electronic states of a single molecule forming a CoI, since at each snapshot along the MD trajectory adiabatic states can arise from a different mixing of the diabatic states, making computation of the EEFC troublesome. In this respect, it is conceivable to combine the calculation of EEFC with diabatization techniques to have generalized spectral densities including coupling terms. The advantage of most of the system-bath approaches is that they provide an accurate description of quantum features like electronic and nuclear coherence. At the same time, most of these methods are effective especially if the solute undergoes small nuclear rearrangements, enabling the description of the PES with simple (e.g. quadratic) functions. Once more, these two features make them ideal for studying quantum coherence in EET and CT. On the other hand, in many reactive and non-reactive processes through a CoI, molecules follow complex potential energy surfaces and undergo large distortions. In these cases, the most popular strategy at the state-of-the-art is to describe in a more approximate way the quantum coherence but in a more accurate way the PES. This naturally leads to on-the-fly methods, which do not need pre-determined PESs, and have the benefit to be naturally ready to be coupled with an atomistic description of the solvent, with QM/MM approaches.

The wide family of methods that treat the solvent as a continuum, like an effective coordinate, a time-evolving density, or as a polarizable continuum are well established cost-effective strategies, although remarkable progresses are still on-going. In particular, when electrostatic effects are dominant, PCM or similar methods are very effective for including gross effects by modulating the shape of the PES. On the other hand, they suffer clear limitations in describing dynamical solvation effects, and more generally whenever it is important to address the ‘molecularity’ of the solvent. In this respect the very interesting methodological advances exploiting the frequency-dependent dielectric constant of the solvent^130,133 appear more suitable to study processes/systems where the coupling between the solute and the solvent degrees of freedom is weak. Mixed explicit/implicit schemes that use continuum models only to describe the polarizable effects of far solvation spheres, i.e. the bulk solvent, when molecularity is less important, will probably represent a significant advance in this field. Since QM/MM methods with localised basis sets are more straightforwardly applied without periodic boundary conditions, non-periodic approaches, like the generalized liquid optimized boundary (GLOB) model,^44,221,222 will probably play an important role. Recent attempts to combine GLOB ideas with the use of polarizable FFs look very promising.³⁵

Another possible weakness of continuum models like PCM is related to the use of parameters, which are tuned on the ground electronic state, such as the cavity radii. In principle, these could instead have a different value for any electronic state. This leads to a more general issue, in that in the presence of any ‘empirical’ parameter it is important to understand how to switch from one set to another at a crossing between different electronic states. As a consequence, this can be a critical point also for the methods including explicitly solvent molecules in the dynamics simulation, since they are usually described by empirical FFs. In this respect, the advances in the development and use of polarizable FFs^35,41,223 are surely promising, at least in the case where electrostatic terms are those ruling solute–solvent interactions. However, as mentioned above, to be applied to nonadiabatic dynamics, they require a SS description.

The effect of mutual solute–solvent polarization is expected to have a significant impact on nonadiabatic dynamics especially when close-lying states interact differently with the environment.¹¹⁷ For short time-scales a wise increase of the QM subset to include some solvent molecules is an option, at least in the case of well-defined specific solute–solvent interactions.⁴⁴ On the other hand, the number of discrete QM solvent molecules necessary to simulate bulk properties is a currently open question, even for static properties.^216,224

In terms of the dynamics methods to be combined with explicit solvent approaches, at-the-state of the art the most popular and widely used are those that propagate all nuclear degrees of freedom with classical dynamics. Among them, for its simplicity, surface hopping is the most used method, and it can account for some nuclear quantum effects in the initial conditions (sampling the Wigner distribution) and ameliorate over-coherence problems with decoherence corrections. In any case, new methods designed for an improved treatment of coherence, based on generalized quantum master equations or on path integral approaches,²⁰⁷ also look promising.⁹⁰ The other main classical trajectory-based approach, of which a number of applications that incorporate solvent effect in a QM/MM fashion have been documented, is AIMS. It is able to account for more nuclear quantum effects than surface hopping, due to coupling between trajectories, and is naturally able to overcome the coherence problems associated with surface hopping.²²⁵

Practical methods aimed to combine a further QD description of some nuclear degrees of freedom with a classical, atomistic (and generally anharmonic), description of the solvent are still in their infancy. First attempts either consider the solvent too slow to move on the timescale of the nonadiabatic process (i.e. account only for static disorder) or approximate the coupling of the quantum and classical DoFs with a mean-field Ehrenfest approach. At the state of the art they seem suited either to treat only few coordinates in the quantum set²¹² or to adopt model (harmonic) Hamiltonians, being therefore limited to rigid systems, if all solute coordinates are in the quantum set.¹¹⁷ In the latter case, ideas proposed for steady-state spectroscopy can be exploited to also treat systems with some flexibility.²¹⁴ Developments on both formal aspects and practical implementations in the field of coupled quantum and classical dynamics are urgently needed.

From the point of view of the FFs, it can be foreseen that for accurate applications, besides the introduction of polarizable FFs to account for the mutual solute–solvent polarization already mentioned, general purpose FFs will be replaced by QMD-FFs, optimized both for the solute–solvent interactions, and also for the intramolecular motion of the solute and specific for each of its electronic states.^226–229 QMD-FFs offer the possibility to replace a QM/MM trajectory with a much faster fully MM/MM trajectory, and have been proven to be helpful to investigate solvation problems.⁴³ They should be particularly suited when extended sampling before photoexcitation is required, or when many initial conditions and/or long excited-state propagations are needed. Their adoption can be also beneficial in coupled quantum-classical nuclear propagations (like those described in Section 4.2) when rapid calculations of forces are needed.¹¹⁷ It is clear however that the simplification of the QM/MM to MM/MM (e.g. from the QM density to a set of charges) may be too approximate for realistic applications,¹¹⁷ and therefore further developments are also needed in this field.

Methods based on path-integral molecular dynamics, like the ring-polymer MD (RPMD)^230–234 represent a further promising route to account for some quantum nuclear effects in nonadiabatic processes in solution. Indeed, generalizations of the FSSH method in which the nuclei move according to RPMD have been proposed and applied to the description of CT in molecular dimers.²³⁵ Applications to nonadiabatic dynamics in the condensed phase are still lacking, although RPMD has already been adopted to highlight the importance of nuclear quantum effects on electronic spectra.^236,237 While these methods will surely improve the description of the nuclear density, they however are expected to share similar limitations as more traditional surface hopping schemes for the electronic coherence. Therefore further developments will probably be needed.

The family of on-the-fly QD methods, which adopt a basis set of Gaussian wavefunctions moving in time, represent probably the most promising route to achieve a future gold standard for quantum dynamical simulations in explicit solvents. The idea to decompose the time-dependent wavefunction in terms of localized Gaussians, first proposed by Heller,²³⁸ and then exploited also in AIMS,²¹ has also been introduced in a MCTDH scheme, with the so called G-MCTDH variant,²³⁹ which has the advantage that the equations of motion are derived from a variational principle. When the basis set for all nuclear degrees of freedom is made by Gaussians, the method is ready for on-the-fly or direct dynamics (DD), and is known as DD-variational multiconfigurational Gaussian (DD-vMCG).^240–242 Though, for the time being, applications are still limited to gas-phase problems,²⁴³ or system-bath cases, new developments are underway, for example a new version of G-MCTDH for OQS in a density matrix formalism.²⁴⁴ The multiconfigurational Ehrenfest (MCE) method²² is another Gaussian-based QD approach, which uses Ehrenfest rather than classical or variational trajectories. It is able to treat system-bath problems,²⁴⁵ and has been paired with electronic structure theory for on-the-fly computations.^246,247 However, similar to DD-vMCG, only gas phase applications have been studied at present,^248,249 although in principle it could be combined with QM/MM to incorporate solvent effects, similar to AIMS.

At present, the computational bottleneck for all on-the-fly approaches has been the evaluation of the electronic energies, forces, and nonadiabatic couplings. In this respect, the further development of GPU-accelerated electronic structure,^156–158 and potential use of machine learning^159,160 represent promising avenues to overcome this bottleneck. Within solute–solvent systems, this leads to the possibility of greater averaging over solvent configurations due to faster computational time, treatment of larger solutes, and inclusion of solvent molecules in the QM region. At the state of the art these frontier applications are still to come.

This review cannot be considered exhaustive, since, especially for what concerns the methodological developments, it touches several open questions that are at the basis of many fields of chemical and physical research: (i) how to make a distinction between the ‘core’ and the ‘environment’ in a given process and (ii) how to describe the interactions between these two sub-systems. The number of potentially relevant approaches to these topics is gargantuan and defies a concise description. On the other hand, we hope that we have succeeded in providing a fairly complete review and perspective of a lively and, promising research field.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has received funding from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Skodowska-Curie grant agreement no. 765266 (LightDyNAmics). LMF and JC acknowledge the MICINN Project PID2019-110091GB-I00 for financial support. The authors thank Haritha Asha (IBB-CNR) and Martha Yaghoubi (ICCOM-CNR) for careful reading of the manuscript and suggestions.

Notes and references

1. R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026.
2. B. F. E. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305–3336.
3. Multidimensional Quantum Dynamics: MCTDH Theory and Applications, ed. F. Meyer, H.-D. Gatti and G. A. Worth, Wiley-VCH, Weinheim, 2009.
4. H.-D. Meyer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 351–374.
5. G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158.
6. S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.
7. S. Mai and L. González, Angew. Chem., Int. Ed., 2020, 59, 16832–16846.
8. Quantum Chemistry and Dynamics of Excited States: Methods and Applications, ed. L. González and R. Lindh, John Wiley & Sons, Chichester, U.K., 2020.
9. M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26.
10. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025.
11. M. Persico and G. Granucci, Theor. Chem. Acc., 2014, 133, 1–28.
12. F. Agostini and B. F. E. Curchod, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1417.
13. T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-Alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Chem. Rev., 2020, 120, 2215–2287.
14. L. S. Cederbaum, in Born-Oppenheimer Approximation and Beyond, ed. W. Domcke, R. Yarkony and H. Köppel, World Scientific Publishing Co., Singapore, 2004, pp. 3–40.
15. F. Santoro, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2015.
16. D. J. Tannor, Introduction to Quantum Mechanics: A Time-Dependent Perspective, University Science Books, Sausalito, CA, 2007.
17. I. Burghardt, K. Möller and K. Hughes, Quantum Hydrodynamics and a Moment Approach to Quantum-Classical Theory, 2007, pp. 369–390.
18. U. Weiss, Quantum Dissipative Systems, World Scientific Publishing Co., Singapore, 1993.
19. P. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford University Press, New York, 2002.
20. A. Raab, G. A. Worth, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1999, 110, 936–946.
21. M. Ben-Nun, J. Quenneville and T. J. Martínez, J. Phys. Chem. A, 2000, 104, 5161–5175.
22. D. V. Makhov, C. Symonds, S. Fernandez-Alberti and D. V. Shalashilin, Chem. Phys., 2017, 493, 200–218.
23. F. Segatta, L. Cupellini, M. Garavelli and B. Mennucci, Chem. Rev., 2019, 119, 9361–9380.
24. L. V. Schâfer, G. Groenhof, M. Boggio-Pasqua, M. A. Robb and H. Grubmûller, PLoS Comput. Biol., 2008, 4, 1–14.
25. G. Groenhof, M. Bouxin-Cademartory, B. Hess, S. P. de Visser, H. J. C. Berendsen, M. Olivucci, A. E. Mark and M. A. Robb, J. Am. Chem. Soc., 2004, 126, 4228–4233.
26. G. Groenhof, L. V. Schäfer, M. Boggio-Pasqua, H. Grubmüller and M. A. Robb, J. Am. Chem. Soc., 2008, 130, 3250–3251.
27. M. Boggio-Pasqua, C. F. Burmeister, M. A. Robb and G. Groenhof, Phys. Chem. Chem. Phys., 2012, 14, 7912–7928.
28. X. Li, L. W. Chung, H. Mizuno, A. Miyawaki and K. Morokuma, J. Phys. Chem. Lett., 2010, 1, 3328–3333.
29. S. Hayashi, E. Tajkhorshid and K. Schulten, Biophys. J., 2009, 96, 403–416.
30. B. P. Fingerhut, S. Oesterling, K. Haiser, K. Heil, A. Glas, W. J. Schreier, W. Zinth, T. Carell and R. de Vivie-Riedle, J. Chem. Phys., 2012, 136, 204307.
31. O. Weingart, P. Altoè, M. Stenta, A. Bottoni, G. Orlandi and M. Garavelli, Phys. Chem. Chem. Phys., 2011, 13, 3645–3648.
32. D. Polli, P. Altoè, O. Weingart, K. M. Spillane, C. Manzoni, D. Brida, G. Tomasello, G. Orlandi, P. Kukura, R. A. Mathies, M. Garavelli and G. Cerullo, Nature, 2010, 467, 440–443.
33. A. Warshel, Nature, 1976, 260, 679–683.
34. A. Warshel and Z. T. Chu, J. Phys. Chem. B, 2001, 105, 9857–9871.
35. M. Bondanza, M. Nottoli, L. Cupellini, F. Lipparini and B. Mennucci, Phys. Chem. Chem. Phys., 2020, 22, 14433–14448.
36. C. Curutchet and B. Mennucci, Chem. Rev., 2017, 117, 294–343.
37. R. Improta, V. Barone and F. Santoro, Angew. Chem., Int. Ed., 2007, 46, 405–408.
38. R. Improta, V. Barone and F. Santoro, J. Phys. Chem. B, 2007, 111, 14080–14082.
39. A. Petrone, G. Donati, P. Caruso and N. Rega, J. Am. Chem. Soc., 2014, 136, 14866–14874.
40. A. Petrone, J. Cerezo, F. J. A. Ferrer, G. Donati, R. Improta, N. Rega and F. Santoro, J. Phys. Chem. A, 2015, 119, 5426–5438.
41. E. Heid, S. Schmode, P. Chatterjee, A. D. MacKerell and C. Schröder, Phys. Chem. Chem. Phys., 2019, 21, 17703–17710.
42. J. J. Nogueira and L. González, Annu. Rev. Phys. Chem., 2018, 69, 473–497.
43. G. Prampolini, F. Ingrosso, J. Cerezo, A. Iagatti, P. Foggi and M. Pastore, J. Phys. Chem. Lett., 2019, 10, 2885–2891.
44. U. Raucci, M. G. Chiariello and N. Rega, J. Chem. Theory Comput., 2020, 16, 7033–7043.
45. S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657–4667.
46. K. Blum, Density Matrix Theory and Applications, Plenum Press, New York, 1981.
47. S. Nakajima, Prog. Theor. Phys., 1958, 20, 948–959.
48. R. Zwanzig, J. Chem. Phys., 1960, 33, 1338–1341.
49. F. Shibata, Y. Takahashi and N. Hashitsume, J. Stat. Phys., 1977, 17, 171–187.
50. G. Lindblad, Commun. Math. Phys., 1976, 48, 119–130.
51. D. Manzano, AIP Adv., 2020, 10, 025106.
52. A. G. Redfield, Adv. Magn. Reson., 1965, 1, 1.
53. A. Kühl and W. Domcke, J. Chem. Phys., 2002, 116, 263–274.
54. W. M. Zhang, T. Meier, V. Chernyak and S. Mukamel, J. Chem. Phys., 1998, 108, 7763–7774.
55. M. Yang and G. R. Fleming, Chem. Phys., 2002, 282, 163–180.
56. Y.-H. Hwang-Fu, W. Chen and Y.-C. Cheng, Chem. Phys., 2015, 447, 46–53.
57. R. Kapral and G. Ciccotti, J. Chem. Phys., 1999, 110, 8919–8929.
58. T. C. Berkelbach, D. R. Reichman and T. E. Markland, J. Chem. Phys., 2012, 136, 034113.
59. C.-Y. Hsieh and R. Kapral, J. Chem. Phys., 2013, 138, 134110.
60. R. Kapral, J. Phys.: Condens. Matter, 2015, 27, 073201.
61. S. Bonella and G. Ciccotti, Eur. Phys. J.: Spec. Top., 2015, 2247, 2305–2320.
62. P. Huo and D. F. Coker, J. Chem. Phys., 2012, 137, 22A535.
63. M. K. Lee, P. Huo and D. F. Coker, Annu. Rev. Phys. Chem., 2016, 67, 639–668.
64. A. Ishizaki and G. R. Fleming, J. Chem. Phys., 2009, 130, 234111.
65. Y. Tanimura and R. Kubo, J. Phys. Soc. Jpn., 1989, 58, 101–114.
66. Y. Tanimura, J. Chem. Phys., 2020, 153, 020901.
67. L. Chen, M. F. Gelin, V. Y. Chernyak, W. Domcke and Y. Zhao, Faraday Discuss., 2016, 194, 61–80.
68. A. G. Dijkstra and V. I. Prokhorenko, J. Chem. Phys., 2017, 147, 064102.
69. N. Makri, J. Math. Phys., 1995, 36, 2430–2457.
70. N. Makri, J. Phys. Chem. A, 1998, 102, 4414–4427.
71. M. Thorwart, J. Eckel, J. Reina, P. Nalbach and S. Weiss, Chem. Phys. Lett., 2009, 478, 234–237.
72. Y. Tanimura and S. Mukamel, J. Chem. Phys., 1994, 101, 3049–3061.
73. V. Chernyak and S. Mukamel, J. Chem. Phys., 1996, 105, 4565–4583.
74. Y. Tanimura, J. Phys. Soc. Jpn., 2006, 75, 082001.
75. T. Ikeda and Y. Tanimura, J. Chem. Theory Comput., 2019, 15, 2517–2534.
76. F. Di Maiolo and A. Painelli, Phys. Chem. Chem. Phys., 2020, 22, 1061–1068.
77. M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105.
78. H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299.
79. U. Manthe, J. Chem. Phys., 2008, 128, 164116.
80. U. Manthe, J. Chem. Phys., 2009, 130, 054109.
81. O. Vendrell and H.-D. Meyer, J. Chem. Phys., 2011, 134, 044135.
82. K. H. Hughes, C. D. Christ and I. Burghardt, J. Chem. Phys., 2009, 131, 124108.
83. K. H. Hughes, C. D. Christ and I. Burghardt, J. Chem. Phys., 2009, 131, 024109.
84. I. Burghardt, R. Martinazzo and K. H. Hughes, J. Chem. Phys., 2012, 137, 144107.
85. K. H. Hughes, B. Cahier, R. Martinazzo, H. Tamura and I. Burghardt, Chem. Phys., 2014, 442, 111.
86. H. Liu, L. Zhu, S. Bai and Q. Shi, J. Chem. Phys., 2014, 140, 134106.
87. O. Andreussi, I. G. Prandi, M. Campetella, G. Prampolini and B. Mennucci, J. Chem. Theory Comput., 2017, 13, 4636–4648.
88. M. K. Lee and D. F. Coker, J. Phys. Chem. Lett., 2016, 7, 3171–3178.
89. F. Segatta, L. Cupellini, M. Garavelli and B. Mennucci, Chem. Rev., 2019, 119, 9361–9380.
90. P. L. Walters and N. Makri, J. Phys. Chem. Lett., 2015, 6, 4959–4965.
91. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
92. I. Burghardt, L. S. Cederbaum and J. T. Hynes, Faraday Discuss., 2004, 127, 395–411.
93. I. Burghardt and J. T. Hynes, J. Phys. Chem. A, 2006, 110, 11411–11423.
94. R. Spezia, I. Burghardt and J. T. Hynes, Mol. Phys., 2006, 104, 903.
95. J. P. Malhado, R. Spezia and J. T. Hynes, J. Phys. Chem. A, 2011, 115, 3720–3735.
96. C. Sissa, F. Delchiaro, F. Di Maiolo, F. Terenziani and A. Painelli, J. Chem. Phys., 2014, 141, 164317.
97. C. A. Schwerdtfeger, A. V. Soudackov and S. Hammes-Schiffer, J. Chem. Phys., 2014, 140, 034113.
98. B. Auer, A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. B, 2012, 116, 7695–7708.
99. A. V. Soudackov, A. Hazra and S. Hammes-Schiffer, J. Chem. Phys., 2011, 135, 144115.
100. A. Hazra, A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. B, 2010, 114, 12319–12332.
101. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
102. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
103. J. A. Bjorgaard, V. Kuzmenko, K. A. Velizhanin and S. Tretiak, J. Chem. Phys., 2015, 142, 044103.
104. J. A. Bjorgaard, K. A. Velizhanin and S. Tretiak, J. Chem. Phys., 2015, 143, 054305.
105. W. Malone, B. Nebgen, A. White, Y. Zhang, H. Song, J. A. Bjorgaard, A. E. Sifain, B. Rodriguez-Hernandez, V. M. Freixas, S. Fernandez-Alberti, A. E. Roitberg, T. R. Nelson and S. Tretiak, J. Chem. Theory Comput., 2020, 16, 5771–5783.
106. S. Mukamel, S. Tretiak, T. Wagersreiter and V. Chernyak, Science, 1997, 277, 781–787.
107. S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171–3212.
108. A. E. Sifain, B. J. Gifford, D. W. Gao, L. Lystrom, T. R. Nelson and S. Tretiak, J. Phys. Chem. A, 2018, 122, 9403–9411.
109. A. E. Sifain, J. A. Bjorgaard, T. R. Nelson, B. T. Nebgen, A. J. White, B. J. Gifford, D. W. Gao, O. V. Prezhdo, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, J. Chem. Theory Comput., 2018, 14, 3955–3966.
110. J. Eng, C. Gourlaouen, E. Gindensperger and C. Daniel, Acc. Chem. Res., 2015, 48, 809.
111. Y. Harabuchi, J. Eng, E. Gindensperger, T. Taketsugu, S. Maeda and C. Daniel, J. Chem. Theory Comput., 2016, 12, 2335–2345.
112. M. Fumanal, E. Gindensperger and C. Daniel, J. Chem. Theory Comput., 2017, 13, 1293.
113. M. Fumanal, E. Gindensperger and C. Daniel, Phys. Chem. Chem. Phys., 2018, 20, 1134.
114. R. Heydová, E. Gindensperger, R. Romano, J. Sýkora, A. Vlček, S. Záliš and C. Daniel, J. Phys. Chem. A, 2012, 116, 11319–11329.
115. R. Improta, V. Barone, A. Lami and F. Santoro, J. Phys. Chem. B, 2009, 113, 14491.
116. F. Santoro, R. Improta and V. Barone, Theor. Chem. Acc., 2009, 123, 273–286.
117. J. Cerezo, Y. Liu, N. Lin, X. Zhao, R. Improta and F. Santoro, J. Chem. Theory Comput., 2018, 14, 820–832.
118. R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540.
119. P. M. Hare, C. E. Crespo-Hernández and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 435–440.
120. D. Picconi, A. Lami and F. Santoro, J. Chem. Phys., 2012, 136, 244104.
121. Y. Liu, J. Cerezo, N. Lin, X. Zhao, R. Improta and F. Santoro, Theor. Chem. Acc., 2018, 137, 40.
122. R. Improta, UV-Visible Absorption and Emission Energies in Condensed Phase by PCM-TD-DFT Methods, in Computational Strategies for Spectroscopy: From Small Molecules to Nanosystems, ed. V. Barone, John Wiley & Sons, Chichester, U.K., 2011, pp. 39–76.
123. R. Improta and V. Barone, THEOCHEM, 2009, 914, 87–93.
124. R. Cammi, S. Corni, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 122, 104513.
125. M. Caricato, B. Mennucci, J. Tomasi, F. Ingrosso, R. Cammi, S. Corni and G. Scalmani, J. Chem. Phys., 2006, 124, 124520.
126. R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 54103.
127. R. Improta, G. Scalmani, M. J. Frisch and V. Barone, J. Chem. Phys., 2007, 127, 74504.
128. B. Mennucci, Theor. Chem. Acc., 2006, 116, 31–42.
129. P. Nguyen, F. Ding, S. Fischer, W. Liang and X. Li, J. Phys. Chem. Lett., 2012, 3, 2898.
130. F. Ding, D. B. Lingerfelt, B. Mennucci and X. Li, J. Chem. Phys., 2015, 142, 034120.
131. S. Corni, S. Pipolo and R. Cammi, J. Phys. Chem. A, 2015, 119, 5405–5416.
132. S. Pipolo, S. Corni and R. Cammi, J. Chem. Phys., 2017, 146, 064116.
133. G. Gil, S. Pipolo, A. Delgado, C. A. Rozzi and S. Corni, J. Chem. Theory Comput., 2019, 15, 2306–2319.
134. P. Debye, Verh. Dtsch. Phys. Ges., 1913, 15, 777.
135. X. Li, N. Govind, C. Isborn, A. E. DePrince and K. Lopata, Chem. Rev., 2020, 120, 9951–9993.
136. G. Donati, A. Wildman, S. Caprasecca, D. B. Lingerfelt, F. Lipparini, B. Mennucci and X. Li, J. Phys. Chem. Lett., 2017, 8, 5283–5289.
137. X. Wu, J.-M. Teuler, F. Cailliez, C. Clavaguéra, D. R. Salahub and A. de la Lande, J. Chem. Theory Comput., 2017, 13, 3985–4002.
138. D. K. A. Phan Huu, R. Dhali, C. Pieroni, F. Di Maiolo, C. Sissa, F. Terenziani and A. Painelli, Phys. Rev. Lett., 2020, 124, 107401.
139. C. A. Guido, M. Rosa, R. Cammi and S. Corni, J. Chem. Phys., 2020, 152, 174114.
140. S. Thallmair, M. Kowalewski, J. P. P. Zauleck, M. K. Roos and R. de Vivie-Riedle, J. Phys. Chem. Lett., 2014, 5, 3480–3485.
141. I. Burghardt and B. Bagchi, Chem. Phys., 2006, 329, 343–356.
142. D. Bousquet, K. H. Hughes, D. A. Micha and I. Burghardt, J. Chem. Phys., 2011, 134, 064116.
143. K. H. Hughes, S. N. Baxter, D. Bousquet, P. Ramanathan and I. Burghardt, J. Chem. Phys., 2012, 136, 014102.
144. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
145. H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2007, 117, 185.
146. L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796.
147. Combining Quantum Mechanics and Molecular Mechanics. Some Recent Progresses in QM/MM Methods, ed. J. R. Sabin and E. Brändas, Academic Press, 2010, vol. 59.
148. H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
149. E. Brunk and U. Rothlisberger, Chem. Rev., 2015, 115, 6217–6263.
150. D. Bakowies and W. Thiel, J. Phys. Chem., 1996, 100, 10580–10594.
151. J.-X. Duan, Y. Zhou, Z.-Z. Xie, T.-L. Sun and J. Cao, Phys. Chem. Chem. Phys., 2018, 20, 15445–15454.
152. J. Cao and D.-c. Chen, Phys. Chem. Chem. Phys., 2020, 22, 10924–10933.
153. P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947.
154. J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564.
155. J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071.
156. I. S. Ufimtsev and T. J. Martínez, Comput. Sci. Eng., 2008, 10, 26–34.
157. A. V. Titov, I. S. Ufimtsev, N. Luehr and T. J. Martinez, J. Chem. Theory Comput., 2013, 9, 213–221.
158. J. W. Snyder, B. F. E. Curchod and T. J. Martínez, J. Phys. Chem. Lett., 2016, 7, 2444–2449.
159. J. Westermayr and P. Marquetand, Mach. Learn.: Sci. Technol., 2020, 1, 043001.
160. J. Westermayr and P. Marquetand, Chem. Rev., 2020.
161. M. Ruckenbauer, M. Barbatti, B. Sellner, T. Muller and H. Lischka, J. Phys. Chem. A, 2010, 114, 12585–12590.
162. M. Ruckenbauer, M. Barbatti, T. Müller and H. Lischka, J. Phys. Chem. A, 2010, 114, 6757–6765.
163. M. Ruckenbauer, M. Barbatti, T. Müller and H. Lischka, J. Phys. Chem. A, 2013, 117, 2790.
164. I. Antol, M. Eckert-Maksić, M. Vazdar, M. Ruckenbauer and H. Lischka, Phys. Chem. Chem. Phys., 2012, 14, 13262–13272.
165. M. Boggio-Pasqua, M. A. Robb and G. Groenhof, J. Am. Chem. Soc., 2009, 131, 13580–13581.
166. A. M. Virshup, C. Punwong, T. V. Pogorelov, B. A. Lindquist, C. Ko and T. J. Martínez, J. Phys. Chem. B, 2009, 113, 3280.
167. J. Cao, L.-H. Liu, W.-H. Fang, Z.-Z. Xie and Y. Zhang, J. Chem. Phys., 2013, 138, 134306.
168. X. Guo, Y. Zhao and Z. Cao, Phys. Chem. Chem. Phys., 2014, 16, 15381–15388.
169. X. Guo, H. Yuan, B. An, Q. Zhu and J. Zhang, J. Chem. Phys., 2016, 144, 154306.
170. R. Borrego-Varillas, D. C. Teles-Ferreira, A. Nenov, I. Conti, L. Ganzer, C. Manzoni, M. Garavelli, A. Maria de Paula and G. Cerullo, J. Am. Chem. Soc., 2018, 140, 16087–16093.
171. R. F. Hutton and C. Steel, J. Am. Chem. Soc., 1964, 86, 745–746.
172. P. Cattaneo and M. Persico, J. Am. Chem. Soc., 2001, 123, 7638–7645.
173. P. Cattaneo, M. Persico and A. Tani, Chem. Phys., 1999, 246, 315–322.
174. G. Granucci and A. Toniolo, Chem. Phys. Lett., 2000, 325, 79–85.
175. G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615.
176. A. Toniolo, M. Ben-Nun and T. J. Martínez, J. Phys. Chem. A, 2002, 106, 4679–4689.
177. A. Toniolo, G. Granucci and T. J. Martínez, J. Phys. Chem. A, 2003, 107, 3822–3830.
178. A. Toniolo, S. Olsen, L. Manohar and T. J. Martínez, Faraday Discuss., 2004, 127, 149–163.
179. M. Persico, G. Granucci, S. Inglese, T. Laino and A. Toniolo, THEOCHEM, 2003, 621, 119.
180. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909.
181. J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209–220.
182. T. Cusati, G. Granucci and M. Persico, J. Am. Chem. Soc., 2011, 133, 5109–5123.
183. V. Cantatore, G. Granucci and M. Persico, Comput. Theor. Chem., 2014, 1040, 126.
184. N. O. Carstensen, Phys. Chem. Chem. Phys., 2013, 15, 15017–15026.
185. C. Punwong, J. Owens and T. J. Martínez, J. Phys. Chem. B, 2015, 119, 704–714.
186. W. Thongyod, C. Buranachai, T. Pengpan and C. Punwong, Phys. Chem. Chem. Phys., 2019, 21, 16258–16269.
187. N. Aguilera-Porta, I. Corral, J. Munoz-Muriedas and G. Granucci, Comput. Theor. Chem., 2019, 1152, 20–27.
188. L. Martinez-Fernandez, G. Granucci, M. Pollum, C. E. Crespo-Hernandez, M. Persico and I. Corral, Chem. – Eur. J., 2017, 23, 2619–2627.
189. Z. Lan, Y. Lu, E. Fabiano and W. Thiel, ChemPhysChem, 2011, 12, 1989–1998.
190. B. Heggen, Z. Lan and W. Thiel, Phys. Chem. Chem. Phys., 2012, 14, 8137–8146.
191. Y. Lu, Z. Lan and W. Thiel, J. Comput. Chem., 2012, 33, 1225–1235.
192. J. Petersen, M. Wohlgemuth, B. Sellner, V. Bonačić-Koutecký, H. Lischka and R. Mitrić, Phys. Chem. Chem. Phys., 2012, 14, 4687–4694.
193. P. R. L. Markwick and N. L. Doltsinis, J. Chem. Phys., 2007, 126, 175102.
194. I. Tavernelli, Acc. Chem. Res., 2015, 48, 792–800.
195. B. G. Levine, C. Ko, J. Quenneville and T. J. Martínez, Mol. Phys., 2006, 104, 1039–1051.
196. L. M. Ibele, P. A. Sánchez-Murcia, S. Mai, J. J. Nogueira and L. González, J. Phys. Chem. Lett., 2020, 11, 7483–7488.
197. F. Plasser, G. Granucci, J. Pittner, M. Barbatti, M. Persico and H. Lischka, J. Chem. Phys., 2012, 137, 22A514.
198. R. Improta and V. Barone, Angew. Chem., Int. Ed., 2011, 50, 12016–12019.
199. M. Wohlgemuth, V. Bonačić-Koutecký and R. Mitrić, J. Chem. Phys., 2011, 135, 054105.
200. M. Mališ, J. Novak, G. Zgrablić, F. Parmigiani and N. Došlić, Phys. Chem. Chem. Phys., 2017, 19, 25970–25978.
201. I. Tavernelli, B. F. Curchod and U. Rothlisberger, Chem. Phys., 2011, 391, 101.
202. S. Mai and L. González, Chem. Sci., 2019, 10, 10405–10411.
203. Y.-G. Fang, L.-Y. Peng, X.-Y. Liu, W.-H. Fang and G. Cui, Comput. Theor. Chem., 2019, 1155, 90–100.
204. A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 2000, 329, 130–137.
205. J. Peon, G. C. Hess, J.-M. L. Pecourt, T. Yuzawa and B. Kohler, J. Phys. Chem. A, 1999, 103, 2460–2466.
206. G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114.
207. W. C. Pfalzgraff, A. Kelly and T. E. Markland, J. Phys. Chem. Lett., 2015, 6, 4743–4748.
208. A. Kelly, N. Brackbill and T. E. Markland, J. Chem. Phys., 2015, 142, 094110.
209. T. Banerjee and N. Makri, J. Phys. Chem. B, 2013, 117, 13357–13366.
210. S. Thallmair, J. P. P. Zauleck and R. de Vivie-Riedle, J. Chem. Theory Comput., 2015, 11, 1987–1995.
211. S. Reiter, D. Keefer and R. de Vivie-Riedle, J. Am. Chem. Soc., 2018, 140, 8714–8720.
212. J. P. P. Zauleck, M. T. Peschel, F. Rott, S. Thallmair and R. de Vivie-Riedle, J. Phys. Chem. A, 2018, 122, 2849–2857.
213. M. Pápai, M. Abedi, G. Levi, E. Biasin, M. M. Nielsen and K. B. Møller, J. Phys. Chem. C, 2019, 123, 2056–2065.
214. J. Cerezo, D. Aranda, F. J. Avila Ferrer, G. Prampolini and F. Santoro, J. Chem. Theory Comput., 2020, 16, 1215–1231.
215. C. C. Jumper, P. C. Arpin, D. B. Turner, S. D. McClure, S. Rafiq, J. C. Dean, J. A. Cina, P. A. Kovac, T. Mirkovic and G. D. Scholes, J. Phys. Chem. Lett., 2016, 7, 4722–4731.
216. J. M. Milanese, M. R. Provorse, E. Alameda and C. M. Isborn, J. Chem. Theory Comput., 2017, 13, 2159–2171.
217. A. Segalina, J. Cerezo, G. Prampolini, F. Santoro and M. Pastore, J. Chem. Theory Comput., 2020, 16, 7061–7077.
218. M. Aschi, R. Spezia, A. Di Nola and A. Amadei, Chem. Phys. Lett., 2001, 344, 374–380.
219. A. Amadei, M. D'Alessandro, M. D'Abramo and M. Aschi, J. Chem. Phys., 2009, 130, 084109.
220. A. Amadei and M. Aschi, RSC Adv., 2018, 8, 27900–27918.
221. N. Rega, G. Brancato and V. Barone, Chem. Phys. Lett., 2006, 422, 367–371.
222. G. Brancato, N. Rega and V. Barone, J. Chem. Phys., 2008, 128, 144501.
223. T. Giovannini, A. Puglisi, M. Ambrosetti and C. Cappelli, J. Chem. Theory Comput., 2019, 15, 2233–2245.
224. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2015, 119, 958–967.
225. B. Mignolet and B. F. E. Curchod, J. Phys. Chem. A, 2019, 123, 3582–3591.
226. I. Cacelli and G. Prampolini, J. Chem. Theory Comput., 2007, 3, 1803–1817.
227. L. Greff da Silveira, M. Jacobs, G. Prampolini, P. R. Livotto and I. Cacelli, J. Chem. Theory Comput., 2018, 14, 4884–4900.
228. K. Claridge and A. Troisi, J. Phys. Chem. B, 2019, 123, 428–438.
229. G. Belletti, E. Schulte, E. Colombo, W. Schmickler and P. Quaino, Chem. Phys. Lett., 2019, 735, 136778.
230. I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2004, 121, 3368–3373.
231. I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2005, 122, 084106.
232. I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2005, 123, 034102.
233. S. Habershon, D. E. Manolopoulos, T. E. Markland and T. F. Miller, Annu. Rev. Phys. Chem., 2013, 64, 387–413.
234. J. O. Richardson and M. Thoss, J. Chem. Phys., 2013, 139, 031102.
235. S. Ghosh, S. Giannini, K. Lively and J. Blumberger, Faraday Discuss., 2020, 221, 501–525.
236. Y. K. Law and A. A. Hassanali, J. Chem. Phys., 2018, 148, 102331.
237. T. J. Zuehlsdorff, J. A. Napoli, J. M. Milanese, T. E. Markland and C. M. Isborn, J. Chem. Phys., 2018, 149, 024107.
238. E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555.
239. I. Burghardt, M. Nest and G. A. Worth, J. Chem. Phys., 2003, 119, 5364–5378.
240. G. A. Worth and I. Burghardt, Chem. Phys. Lett., 2003, 368, 502–508.
241. B. Lasorne, M. A. Robb and G. A. Worth, Phys. Chem. Chem. Phys., 2007, 9, 3210–3227.
242. G. Richings, I. Polyak, K. Spinlove, G. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308.
243. G. W. Richings and G. A. Worth, Chem. Phys. Lett., 2017, 683, 606–612.
244. D. Picconi and I. Burghardt, J. Chem. Phys., 2019, 150, 224106.
245. O. Bramley, C. Symonds and D. V. Shalashilin, J. Chem. Phys., 2019, 151, 064103.
246. K. Saita and D. V. Shalashilin, J. Chem. Phys., 2012, 137, 22A506.
247. D. V. Makhov, W. J. Glover, T. J. Martinez and D. V. Shalashilin, J. Chem. Phys., 2014, 141, 054110.
248. D. V. Makhov, K. Saita, T. J. Martinez and D. V. Shalashilin, Phys. Chem. Chem. Phys., 2015, 17, 3316–3325.
249. J. A. Green, D. V. Makhov, N. C. Cole-Filipiak, C. Symonds, V. G. Stavros and D. V. Shalashilin, Phys. Chem. Chem. Phys., 2019, 21, 3832–3841.

---