Lithium ion battery degradation: what you need to know

Abstract

The expansion of lithium-ion batteries from consumer electronics to larger-scale transport and energy storage applications has made understanding the many mechanisms responsible for battery degradation increasingly important. The literature in this complex topic has grown considerably; this perspective aims to distil current knowledge into a succinct form, as a reference and a guide to understanding battery degradation. Unlike other reviews, this work emphasises the coupling between the different mechanisms and the different physical and chemical approaches used to trigger, identify and monitor various mechanisms, as well as the various computational models that attempt to simulate these interactions. Degradation is separated into three levels: the actual mechanisms themselves, the observable consequences at cell level called modes and the operational effects such as capacity or power fade. Five principal and thirteen secondary mechanisms were found that are generally considered to be the cause of degradation during normal operation, which all give rise to five observable modes. A flowchart illustrates the different feedback loops that couple the various forms of degradation, whilst a table is presented to highlight the experimental conditions that are most likely to trigger specific degradation mechanisms. Together, they provide a powerful guide to designing experiments or models for investigating battery degradation.

---

Introduction

Understanding battery degradation is critical for cost-effective decarbonisation of both energy grids¹ and transport.² However, battery degradation is often presented as complicated and difficult to understand. This perspective aims to distil the knowledge gained by the scientific community to date into a succinct form, highlighting the minimum number of papers that need to be read in order to understand lithium ion battery (LIB) degradation. Other recent reviews in this area include Kabir et al.,³ providing a classification for degradation mechanisms and modes and briefly covering key experimental techniques; Hapuarachichi et al.,⁵ having a strong focus on in situ experimental techniques for assessing anode degradation; Woody et al.,⁶ drawing out implications for best practise in LIB use and Pender et al.,⁷ covering the degradation of electrode materials for the extended LIB family. This perspective provides a simple and consistent classification for the main mechanisms affecting lithium intercalation materials, draws out the link between degradation mechanisms and their triggering conditions and highlights the interconnection between various mechanisms, presenting the complexity through updated figures and tables in an accessible way.

The rapid market expansion for LIBs⁸ is driving down cost, but making LIBs last longer is just as important. This improves the lifetime economics, enables longer warranties⁴ and dilutes the environmental impacts associated with raw material extraction and manufacturing.^9,10 Understanding battery degradation is key to increasing operational lifetime. Being able to accurately predict battery end-of-life (EoL) enables the risks of thermal runaway to be minimised.¹¹

With time and use, the storage capacity of LIBs diminishes and the internal resistance increases,¹² due to a wide range of degradation mechanisms, some occurring simultaneously, or triggering further mechanisms. Some usage patterns and operating conditions lead to rapid degradation by one or more processes and the interplay between mechanisms is still not well understood.¹³ This perspective presents a state-of-the-art picture of the most prominent degradation processes, presenting the latest understanding of each mechanism, experimental techniques and conditions that can trigger and/or exacerbate the degradation caused by that mechanism and the models which have been proposed to simulate it.

From a user's perspective, there are three main external stress factors that influence degradation: temperature, state of charge (SoC) and load profile. The relative importance of each of these factors varies depending on the chemistry, form factor and historic use conditions, among others. Works such as Birkl et al.¹⁴ have highlighted how these stress factors can influence the underpinning physical degradation processes, with models such as those reviewed in Reniers et al.,¹³ showing how individual mechanisms can be described. In general, temperature is the most significant stress factor, where deviations from the typical 25 °C can lead to accelerated failure.¹⁵ Higher SoC operation accelerates degradation, due to the relationship between the electrode potentials and the rate of parasitic side reactions, while higher current operation increases the likelihood of failure, due to mechanical stresses developing in the battery during cycling, but also promotion of lithium plating during charge.

The magnitude of these influences is also dependent on secondary factors, such as subtle manufacturing defects. Harris et al.,¹⁶ for instance, demonstrated the variability in lifetime of 24 nominally identical pouch cells, all cycled with the same load profile. While the root cause of this variability is still debated, slight variations in manufacturing conditions are likely to have played a role, thus highlighting the need for statistically significant sample sizes. This is further amplified by sensitivity to testing conditions often not controlled nor measured, such as the application of external pressure to pouch cells or thermal gradients that build up, due to internal heat generation.

Recently,^17,18 attention has been drawn to the importance of path dependence,¹⁹i.e. the order in which the various degradation mechanisms are triggered through either calendar ageing, occurring while the battery is at rest, or cycle ageing, when the battery is in use or being charged. In real world usage patterns, periods of rapid (dis)charging may be interspersed with slower (dis)charging or periods of idleness, therefore investigations of this aspect are needed for more accurate lifetime prediction.

Given the topical nature of LIBs, many publications have presented models to describe their degradation. However, in the vast majority of cases, these are done in isolation of other mechanisms, ignoring their interplay. To date, the authors are not aware of any fully comprehensive model capturing all effects and their influences on each other. Some notable works have attempted to link mechanisms together, such as Yang et al.,²⁰ who showed how the growth of the solid–electrolyte interphase (SEI) layer leads to pore blockage and subsequently an increase in the rate of lithium plating, ultimately leading to a non-linear drop-off in cell capacity. Beyond the importance of coupling the interactions between the various degradation mechanisms, the importance of path-dependency – i.e. which mechanism was triggered first – is also often understated; with the sequence of events being an important factor in determining life, especially at higher current loads.¹⁷ These complex interactions often cannot be captured accurately with empirical or semi-empirical models, instead needing physics-based models.

In this perspective, we cover the main mechanisms occurring during normal operating conditions, within the safety limits defined by the manufacturer's specifications. The structure of the perspective has three main sections, starting with descriptions of the mechanisms, their consequences and interactions, followed by experimental techniques for characterising and triggering these mechanisms. The third section covers the state-of-the art in modelling these mechanisms, including a discussion on models which attempt to capture the interactions between them.

Clarification of nomenclature

There are six main components of a typical battery: two current collectors in contact with the two electrodes, between which redox reactions take place, allowing charge/discharge; a porous separator, preventing short circuiting between the two electrodes while allowing charged ions to migrate through; and the electrolyte, which enables facile charge transfer and is an additional source of lithium ions (Li⁺). Fig. 1 shows these components schematically.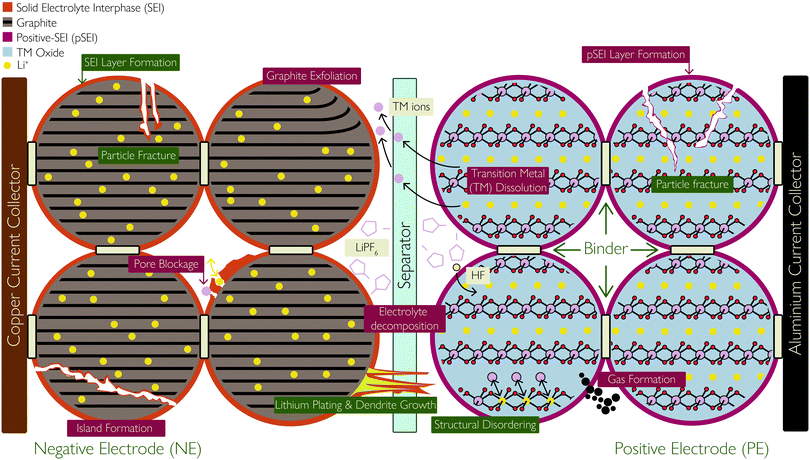

Fig. 1 Schematic showing the basic components of a lithium ion battery cell and the location and consequences of the degradation mechanisms covered in this review, with primary mechanisms labelled in green and secondary mechanisms labelled in dark red. Reprinted (adapted) with permission from Merla et al.²¹ Copyright (2015), Elsevier B.V.

Within some research domains, the electrodes in the LIB are referred to as the anode or cathode, defined from the electrodes’ role during the discharge process and then used absolutely. As both electrodes play the role of the anode or cathode, depending on whether the cell is charging or discharging, it is more accurate to define them by their relative electrode potentials. Hence, the electrode with the higher electrode potential, often referred to as the cathode, is herein referred to as the positive electrode (PE). It is typically a lithium transition metal (TM) oxide material, capable of undergoing reversible delithiation of Li⁺, and the limiting factor in determining the energy density of the battery. The other electrode – an intercalation material, usually graphite or a graphite hybrid material and sometimes lithium titanate (LTO)²² – is often referred to as the anode, but herein referred to as the negative electrode (NE).

Both the PE and NE are the active materials coated on metal foils (current collectors), which serve to facilitate electron transport to the active materials. As a cell is polarised for charging, the PE is oxidised, causing electrons to be released to the external circuit and Li⁺ to delithiate from the PE crystal structure. As the ions migrate across the cell and through the separator to intercalate between the layers of the NE material, electrons flow externally to the NE, reducing it and maintaining charge neutrality. Hence, both materials must undergo structural changes in order to accommodate Li⁺. During discharge, the reverse process takes place, where the NE is oxidised and the PE is reduced. Hence, the Li ions and electrons are shuttled back and forth in a ‘rocking chair’ fashion for charging and discharging the cell. This requires Li⁺ to be easily and reversibly extracted from the PE and is limited by the TM oxide crystal's ability to maintain a stable neutral crystal structure.

Mechanisms of battery degradation

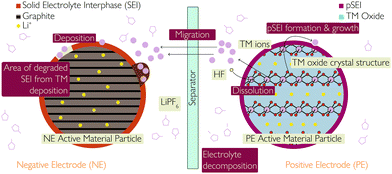
Battery degradation can be described using three tiers of detail. Degradation mechanisms describe the physical and chemical changes that have occurred within the cell. Mechanisms are the most detailed viewpoint of degradation but are also typically the most difficult to observe during battery operation. The directly observable effects of degradation are capacity fade and power fade. Capacity fade is a reduction in the usable capacity of the cell and power fade is a reduction of the deliverable power of the cell after degradation. These observable effects are the least detailed viewpoint of degradation but are the easiest to measure. As a result, many practical measures of cell degradation are of capacity fade and power fade.

Between degradation mechanisms and observable effects lie the degradation modes: a method of grouping degradation mechanisms, based on their overall impact on the cell's thermodynamic and kinetic behaviour. We would like to highlight four modes, all of which impact the thermodynamic behaviour of the cell, i.e. the shape of the open-circuit voltage (OCV) curve and the maximum theoretical capacity of the cell. Firstly, loss of active material (LAM), occurring in both positive and negative electrodes. This mode groups mechanisms which lead to a reduction in the material available for electrochemical activity. Secondly, loss of lithium inventory (LLI) groups mechanisms resulting in a reduction of the amount of cyclable lithium available for transport between electrodes. Thirdly, most often associated with LLI, is stoichiometric drift, where the electrodes become imbalanced relative to each other.²¹ Finally, impedance change groups those mechanisms affecting the kinetic behaviour of the cell. Various terms have been used in the literature to refer to this mode. Han et al.²³ use the term resistance increase, while Vetter et al.²⁴ use the term impedance rise. All of these terms lead to the same grouping of degradation mechanisms. This mode was further divided by Dubarry et al.,²⁵ who introduced two modes termed “ohmic resistance increase” and “faradaic rate degradation”. The former arises through degradation of the electronic conduction pathways in the cell, occurring through mechanisms such as current collector corrosion. faradaic rate degradation occurs primarily through electrodes not reacting with lithium ions at the same rate as had occurred at the beginning of life and is caused by mechanisms such as SEI growth and pore blockage. A notable cause of impedance increase is related to the loss of electrolyte (LE), taking place at the interface of both electrodes due to various mechanisms, such as SEI formation, high voltages, high temperature, lithium plating, or reaction with moisture contamination resulting in hydrofluoric acid (HF) formation. These are key degradation mechanisms and are discussed in detail below. In addition, as the volume of electrolyte reduces, drying of pores and local areas within both electrodes can take place, therefore LE leads to LAM, but also leads to an increased concentration of lithium salt.

Degradation of LIBs is evidently a complex issue and this perspective aims to provide a state-of-the-art overview of the principal degradation mechanisms afflicting both electrodes, illustrated in Fig. 1. We start by discussing SEI formation and lithium plating, which are exclusively associated with the NE. Then we cover a host of interlinked mechanisms affecting the structure and decomposition of positive electrodes, including the well-known formation of the cathode electrolyte interphase (CEI), herein referred to as positive solid electrolyte interface (pSEI) for consistency. Particle fracture is discussed next, affecting both electrodes, but the special case of silicon additives in negative electrodes is also described. The final subsection discusses the developing research area of the relationship between degradation mechanisms and how they either positively or negatively reinforce each other.

Although there are other mechanisms that exist, it is not the aim of this review to extensively cover all known processes, rather to provide the reader with a distillation of knowledge of the mechanisms that are generally considered to be the most important during normal operation. Other known degradation processes include: salt precipitation, current collector corrosion, binder decomposition, separator pore blockage, electrode-current collector delamination and electrolyte evaporation, to name but a few, and are covered well in other reviews.^11,23,24

SEI layer growth

Principles. The SEI is a passivation layer on most NE surfaces, having the properties of a solid electrolyte and formed when the liquid electrolyte comes into contact with the electron-conductive surface of the NE. This is usually operating at voltages below the electrochemical stability window of the electrolyte,^12,24 accelerating redox processes irreversibly breaking down the electrolyte, leading to electrolyte loss. Li metal electrodes develop this SEI layer, as well as graphite.^26,27 A variety of compounds have been observed within the SEI, for example: lithium fluoride (LiF), lithium carbonate (Li₂CO₃), lithium methyl carbonate (LiOCO₂CH₃), lithium ethylene dicarbonate (LiOCO₂CH₂)₂ and lithium oxide (Li₂O).²⁸

The SEI layer forms initially on the first cycle of the cell, resulting in ca. 10% reduction in capacity, but then serves to stop further reaction of the electrolyte at the NE. However, the thickness of the SEI layer increases (predominantly on the graphite NE) as the cell ages. The growth could be due to various reasons, including diffusion of solvent molecules through existing SEI, new exposed electrode surfaces which result from cracking and deposition of side reaction products, such as plated Li and TM ions dissolved from the PE, which react with the electrolyte to form SEI. The SEI growth rate approximately correlates with the square root of time;²⁹ as the SEI thickness increases, the rate of solvent molecule diffusion slows down.

Exacerbating and mitigating factors. The SEI begins to form as soon as the NE is lithiated and exposed to the electrolyte and will grow even if the battery is not then used.³⁰ However, high temperatures increase diffusion rates and hence also the SEI growth rate. High currents also lead to particle cracking and new SEI formation.³¹ Under normal conditions, LTO anodes do not form an SEI layer, due to LTO being within the stability limit of most organic electrolytes, however an SEI can form at potentials below 1 V.³²

Consequences. Capacity is irreversibly lost due to otherwise cyclable lithium being trapped within the SEI.³³ In addition, the SEI layer is less permeable to Li⁺ ions than the electrolyte, restricts electrolyte flow through pore blocking and consumes the electrolyte solvent. All of these effects increase the overall impedance of cells, leading to power fade. While the SEI layer itself is not thought to cause catastrophic failure, at elevated temperatures it can decompose and contribute to a thermal runaway event.¹¹ SEI growth consumes the electrolyte solvents, reducing both the amount and the conductivity of the electrolyte.

Links to other mechanisms. (i) TM ions dissolved from the PE are deposited on the NE, accelerating SEI growth.³⁴

(ii) Particle and SEI cracking, caused by high cycling rates, open up new surfaces for new SEI formation.

(iii) Plated Li can undergo additional side reactions with the electrolyte to form more SEI,³⁵ illustrated in Fig. 2.

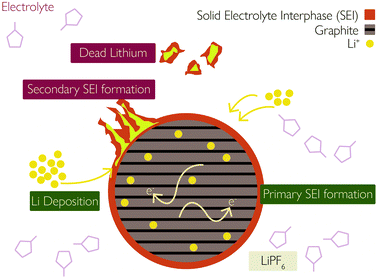Fig. 2 Interaction between solid–electrolyte interphase (SEI) and lithium plating. Reprinted (adapted) with permission from Zhao et al.³⁵ Copyright (2019) Elsevier B.V.

(iv) LLI from the NE causes the electrodes to become imbalanced relative to each other, stoichiometric drift²¹ which can lead to excessive de-lithiation and accelerated degradation of the PE at high SoCs.

Lithium plating

Principles. Li plating is a side reaction where metallic Li forms on the surface of the NE instead of intercalating into it. This can be caused by the NE surface becoming fully lithiated, in which the Li has nowhere else to go (thermodynamic plating),³⁶ or by fast charging, where the high electrolyte potential increases the rate of the side reaction relative to the main intercalation reaction (kinetic plating).³⁷ Even at moderate charge rates, below-freezing temperatures slow down the main intercalation reaction enough to cause plating.³⁸ As with any electroplating reaction, the Li metal can be recovered through the inverse reaction, known as stripping.³⁷

Exacerbating and mitigating factors. Low temperatures, high SoC, high (charge) current, high cell voltage and insufficient NE mass or electrochemically active surface area can all cause lithium plating. It is standard practice to put 10–20% spare capacity in the NE to prevent overcharge.³⁵ Local overcharge can also occur at the edges of the electrode, so spare surface area or “overhang” is included to minimise this.³⁸ However, these mitigating strategies are not enough to stop plating during fast charging, or at below-freezing temperatures, both of which the NE in Fig. 3 was subjected to.³⁸ Local defects in the separator or NE are also known to cause plating;³⁹ these can arise from either manufacturing defects⁴⁰ as shown in Fig. 3, or during use.⁴¹ Calendar ageing is slow at low temperatures, implying that Li plating does not occur when the battery is at equilibrium.⁴² However, rest periods immediately after fast charging will favour the reaction of the plated lithium with the electrolyte rather than its removal by stripping.⁴³

Fig. 3 Graphite electrode after extensive Li plating. Reprinted (adapted) with permission from Campbell et al.³⁸ Copyright (2019), The Electrochemical Society.

Consequences. The plated metallic Li quickly undergoes further side reactions with the electrolyte to form SEI.^20,35,38 This SEI growth can electrically isolate the remaining Li, forming “dead lithium” that cannot be recovered. Li plating therefore has both reversible and irreversible components. Both the additional SEI growth and dead lithium manifest as loss of lithium inventory and reduce conductivity through pore clogging.²⁰ The plating of metallic lithium can lead to dendrite growth, which can puncture the separator and cause an internal short circuit.¹¹

Links to other mechanisms. As already mentioned, Li plating results in further SEI growth and electrolyte solvent consumption.

Positive electrode structural change and decomposition

Principles. PE degradation is highly dependent on chemistry. Various TM oxide materials are currently used as positive electrodes in LIBs, including layered oxides (such as LiCoO₂ and LiNi_xMn_yCo_zO₂ (NMC)), spinel-type (LiMn₂O₄) and polyanion oxides (such as LiFePO₄).⁴⁴ To limit the scope of this perspective, we focus here on layered oxides, in particular NMC-based positive electrodes, since they currently provide one of the highest achievable energy densities and are one of the most prominent in current applications.

NMC materials themselves can vary significantly in their make-up, with different ratios of nickel, manganese and cobalt used in different cells. Each of these cations, with their unique properties, play a deciding role in the ageing and degradation of the PE. The main degradation mechanisms for NMC positive electrodes can be summarised as:

(i) Phase change: delithiated layered NMC structures, composed mainly of TM (Ni, Mn and Co) oxides, decompose into disordered spinel and rock salt phases, forming a passivation layer at the surface of the PE solid particles and releasing oxygen through the following process:⁴⁵

Li_xMO₂ (layered) → Li_xM₃O₄ (spinel) → Li_xMO (rock salt)

(i.e. metal/oxygen = 1 : 2 → 3 : 4 → 1 : 1, [O] releases in each step)

In summary: Li_xMO₂ → Li_xMO + [O]; [O] + [O] → O₂ (g)

where M represents TMs. The formation of spinel and rock salt phases are thermodynamically more favourable at increasingly delithiated states.⁴⁶ Release of lattice oxygen can lead to formation of O₂ and other gaseous products, through reaction with the electrolyte.

(ii) Oxidation of lattice oxygen: electrochemical oxidation of oxide anions within the lattice takes place, resulting in TM dissolution or formation of rock salt phases. LiCoO₂ can only be oxidised (delithiated) to Li_0.5CoO₂ before beginning to decompose, with loss of oxygen from the crystal lattice.⁴⁷

(iii) Electrolyte decomposition and loss: nickel is not known to be stable in high oxidation states and any highly oxidised nickel species will quickly react if in contact with the electrolyte. This leads to Ni²⁺ dissolved in the electrolyte (which will form surface films on either electrode) and electrolyte decomposition, with consequent LE.^45,48

(iv) TM/Li⁺ site exchange: the similar ionic radii of Li⁺ and Ni²⁺ can lead to site switching in the PE crystal lattice (also known as disordering), which can retard the diffusion of Li⁺ through the electrode due to reduced inter-slab space thickness, thereby increasing impedance.⁴⁹

(v) Acid attack: electrolytes tend to be fluoride-containing, non-aqueous organics that are highly reactive with moisture. The presence of moisture leads to the formation of acidic species such as HF and this leads to LE.^24,48 These acid species can then react with the PE material, resulting in the dissolution of TM ions from the electrode:⁴⁸

Acid attack: 2H⁺ + MO–R = M²⁺ + H₂O + R

Sources of H⁺:

I: Solvent → SL_o + H⁺ (SL⁺) + e⁻

II: LiPF₆ = LiF + PF₅; PF₅ + H₂O = POF₃ + 2HF; 2HF = 2H⁺ + 2F⁻

where M, R and SL_o/SL⁺ represent TMs, the residual composition of the host PE material and solvent oxidation products, respectively.

(i) pSEI formation: surface species form on either electrode due to the dissolution of TM ions during the above processes. The dissolute TM ions (Ni²⁺/Ni³⁺/Ni⁴⁺, Mn³⁺/Mn⁴⁺, Co³⁺/Co⁴⁺) react with the electrolyte to form MF₂ precipitates, where M represents TMs. The MF₂ species deposit onto the PE surface to form a layer of considerable thickness, in much the same way as the SEI forms on the NE, following this reaction:^48,50

2H⁺ + 2F⁻ + MO–R = MF₂ (pSEI) + H₂O + R

where M, R and SL_o/SL⁺ represent TMs, the residual composition of the host PE material and solvent oxidation products, respectively. This process usually happens during the first cycles. However, additional pSEI forms if the deposited layer is unstable and breaks,⁵¹ much like the SEI-layer on the NE side. The chemical composition of the pSEI strongly depends on the electrolyte composition as the pSEI formation reaction consumes the proton (H⁺) from the electrolyte with other solvent oxidation products (SL⁺). Thus, pSEI formation and growth also contributes to electrolyte decomposition and loss. Recent studies^48,50,51 show that, apart from TM fluoride (MF₂), TM carbonates, along with minor quantities of hydroxides and water, are the few other species that are present in the pSEI.

Exacerbating and mitigating factors. Mechanisms (i)–(iv) outlined above are all influenced by the chemical and structural stability of the material. Each of the constituent TMs impart different properties into the electrode material, with advantages and disadvantages for each. High cobalt content results in greater stability of the layered crystalline structure, but lower chemical stability. LiMnO₂ has a greater chemical stability due to its lower redox potential, but suffers from structural instability, undergoing a phase change from layered to spinel structure.²⁴ Pure LiNiO₂ electrodes are more unstable, but when mixed with Co and Mn to form NMC composites, their chemical and structural stabilities are intermediate to those of their cobalt and manganese analogues. They are less prone to phase change and are unlikely to decompose during oxidation (delithiation), due to the Ni^3+/4+ redox couple (which carries out the bulk of the redox work) sitting at a lower potential than that of Co^3+/4+ (and, crucially, the O²⁻ p band). However, high nickel content electrode materials can be prone to Li⁺–Ni²⁺ site exchange.⁴⁹ Furthermore, Ni⁴⁺ will react when in contact with the electrolyte, leading to dissolved nickel ions and electrolyte oxidation products.⁵²

High degrees of delithiation (Li_xMO₂ with x < 0.3), corresponding to high cell SoCs, cause NMC structures, especially Ni-rich positive electrodes such as NMC811, to become thermodynamically unstable.⁵³ High enough voltages can also lead to decomposition, due to oxidation of lattice oxygen.

Chemical and structural decomposition are both most likely to occur at the electrode surface. This is due to increased surface reactivity and the higher potentials experienced at the particle surface.⁵³ To mitigate degradation, protective surface films or coatings are used in some batteries to protect the PE from attack by the electrolyte.⁵⁴

High temperatures will accelerate the rate of degradation for all the mechanisms listed above.

Electrolytes tend to be non-aqueous organics and therefore highly reactive with water. Replacing these with non-organic analogues is an active area of research,⁵⁵ as a route to mitigating acid dissolution of the active material.

Consequences. Degradation due to any of these mechanisms results in the same outcomes: LAM and an increase in cell impedance. The formation of spinel and rock salt phases near the electrode surface not only reduces the amount of active material available for redox cycling, it can also increase cell impedance due to the retarded kinetics through these phases.

Reactive lattice oxygen ([O]) released during electrode decomposition or phase change converts into oxygen gas (O₂) or forms reactive peroxide species. The amount of O₂ released is largest in the first cycle and decreases in subsequent cycles, assumed to happen because O₂ releases from the surface-near regions only.^45,56 The released [O] also oxidise ethylene carbonate (EC) to produce gases like CO₂ and CO by the following reaction:

(CH₂O)₂CO (EC) + [O] → 2CO₂ (g) + CO (g) + 2H₂O

Recent studies^45,57,58 show the abovementioned mechanism is one of the possible ways of CO₂ and CO production within the cell, other than electrochemical oxidation of EC which happens when the cell is cycled above 5.0 V.

Formation of the pSEI layer and accelerated growth of the negative SEI layer due to TM dissolution will cause an increase in the cell impedance.

In one study carried out in 2017,⁵⁹ cell capacity loss, impedance increase and increase of TM content in the NE are all stated to be driven, to an extent, by the rate of TM dissolution from the PE. Another study, published in 2018,³⁴ details the specific effects at the PE and NE during Mn dissolution. On the PE side, the dissolution of Mn leads to the loss of the active material and increased impedance of the PE. However, the effect on the NE dominates.

Links to other mechanisms. TM deposits contribute to the formation of the pSEI layer and, similar to the behaviour seen at the NE, particle cracking on the PE can expose fresh surfaces to electrolyte, further promoting the degradation mechanisms listed in this section. Dissolved TM ions can migrate through the electrolyte to the NE,^60–62 forming deposits which can catalyse the formation of thicker, layered SEI structures, greatly increasing the NE impedance.^24,48 All of these interactions are shown schematically in Fig. 4.

Fig. 4 Schematic showing the various consequences and causes of transition metal dissolution, including the link with both SEI and pSEI formation and growth.

Particle fracture

Principles. Particle fracture occurs in both electrodes. It is caused by the substantial volume change of electrode materials and the resulting stress during electrochemical operation.⁶³ Local particle fragmentation has been found close to the separator because of higher local current densities causing larger stresses.^64,65 Particle fracture is a particular challenge for active materials with high theoretical specific capacity, e.g. silicon.

Effect of silicon additives. Silicon additives can greatly boost the specific capacity (mA h g⁻¹) of electrode materials. The specific capacity of a pure silicon electrode is over 11 times higher than a graphite electrode,⁶⁶ as seen in Table 1.

Table 1 Comparison of electrode materials and their specific capacities. Reprinted with permission from Zhang et al.⁶⁶ Copyright (2011), Elsevier B.V.

Materials	Li	C	Li4Ti5O12	Si
Density (g cm^−3)	0.53	2.25	3.5	2.33
Lithiated phase	Li	LiC6	Li7Ti5O12	Li4.4Si
Theoretical specific capacity (mA h g^−1)	3862	372	175	4200
Theoretical charge density (mA h cm^−3)	2047	837	613	9786
Volume change (%)	100	12	1	320
Potential vs. Li (∼V)	0	0.05	1.6	0.4

---

When lithium alloys with silicon, different Si–Li compounds form. These compounds have various unit cell volumes, with the unit cell of some of the largest compounds being almost four times larger than that of pure silicon with no alloyed lithium,⁶⁷ as observed in Table 2.

Table 2 Volumes of different Li–Si compounds observed in operando. Reprinted with permission from Boukamp et al.⁶⁷ Copyright (1981), The Electrochemical Society

Compound and crystal structure	Unit cell volume (Å^3)	Volume per silicon atom (Å^3)
Silicon, cubic	160.2	20.0
Li12Si7 (Li1.71Si), orthorhombic	243.6	58.0
Li14Si6 (Li2.33Si), rhombohedral	308.9	51.5
Li13Si4 (Li3.25Si), orthorhombic	538.4	67.3
Li22Si5 (Li4.4Si), cubic	659.2	82.4

---

The dramatic increase in size induces stress in the electrode and can lead to mechanical failure. Particle cracking is widely observed in silicon electrodes, even with a small amount of silicon,⁶⁸ and leads to very low cycle lifetimes.⁶⁶ As the electrode delithiates and tends towards pure silicon, the volume contracts and electronic contact between electrode particles becomes less effective, leading to increased contact and charge transfer resistances.⁶⁹ Some Li⁺ ions become trapped in the Si matrix, leading to irreversible capacity loss.

Alloying silicon with other metals, as well as dispersing the particles within a graphite matrix, has been shown to improve cycle life, but cycle lives are still low, compared with conventional electrodes. The cycle life of pure silicon is roughly 20 cycles, whereas the cycle life of Si–C composites is close to 70.⁶⁹ Form factors that inherently constrain the electrode stack (cylindrical, prismatic) will see better performance from silicon electrodes. The charge capacity lost due to trapping of Li⁺ ions in the contracting Si matrix can be overcome by applying pressure during delithiation.⁷⁰

Exacerbating and mitigating factors. Above room temperature, at around 45 °C, the cell generates larger thermal stress,⁷¹ accelerating fracture. At low temperatures, at or below 0 °C, graphite becomes more brittle and hence more susceptible to fracture.⁷² Particle cracking is worse for batteries with high Si content NEs, under deep discharge,⁷³ high currents and with large particle sizes.⁷⁴ Manufacturing processes, e.g. calendering, can lead to strain effects and particle cracking before a battery is even in use.⁷⁵ The pre-existing cracks cause stress concentration at the crack tips and accelerate particle fracture during normal battery operations.⁷⁶

Consequences. Cracks in electrode particles have a number of consequences:

(i) Disruption to electrical contact between active particles, conductive additives and current collector, therefore a loss in electronic/ionic conductivity and ultimately capacity fade,^64,73 as shown in Fig. 5;

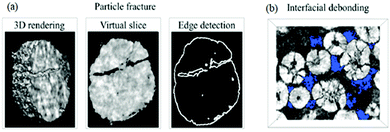Fig. 5 Images of the NMC cathode particles after cycling, with blue areas indicating the void regions. Reprinted with permission from Xu et al.⁶⁴ Copyright (2019) Elsevier B.V.

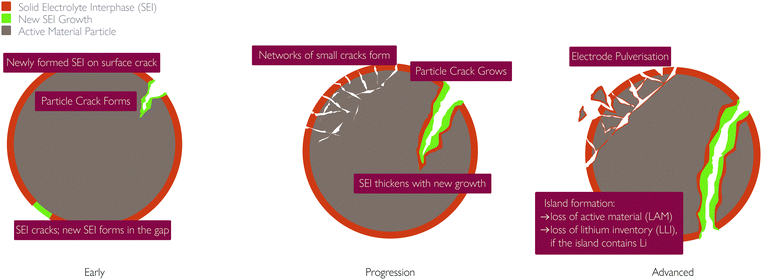
(ii) Particles beyond a certain critical size experience fracture, breaking into isolated islands;⁷⁷

(iii) Increased rate of SEI and pSEI formation, discussed below, in the subsection: “Links to other mechanisms”.

All three consequences cause capacity fade. Modelling work by Laresgoiti et al.⁷⁸ predicted a direct correlation between particle stress and rate of capacity loss, as shown in Fig. 6.

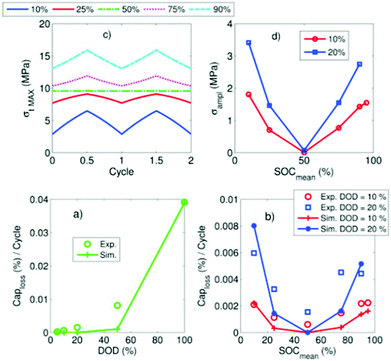Fig. 6 Correlation of particle stress and capacity loss rate. Reprinted with permission from Laresgoiti et al.⁷⁸ Copyright (2015), Elsevier B.V.

(iv) Electrode pulverisation, occurring when small cracks in the electrode join up and some of the active material becomes separated from the rest of the particle. This leads to a loss in active material and hence capacity fade.

Silicon additives. (i) The large volumetric changes during cycling caused by silicon additives will exacerbate⁶⁶ the particle fracture effect observed in the graphite anode, to the extent that it can lead to a more severe breakdown in the integrity of the cell structure, for example delamination⁷⁹ of the electrode from the current collector (which rarely happens in unalloyed graphite anodes).

(ii) Formation of solid electrolyte films – unlike the formation of a stable SEI film in graphite, the SEI formation on alloy NEs appears to be a dynamic process of breaking off and reforming, also caused by the large volume changes of the alloy particles during cycling.⁶⁶ This is illustrated in Fig. 7.

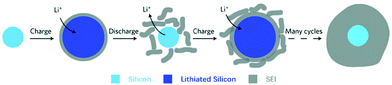Fig. 7 Schematic of constantly built-up SEI layer on silicon surfaces. The initial thin SEI layer cracks during contraction of a solid silicon particle and new SEI forms on the exposed surfaces, resulting in a very thick SEI layer after many cycles. Reprinted with permission from Wu et al.⁸⁰ Copyright (2012), Springer Nature.

Links to other mechanisms. Cracks in electrode particles expose new electron-conductive surfaces to liquid electrolytes for side reactions and trapping otherwise cyclable Li³³ within the extended SEI layer, as illustrated in Fig. 8. SEI layers, having different Young's moduli and fracture toughness than the active electrode materials, are likely to be more prone to cracking and the SEI shell may crack on its own, without the particle cracking.⁸¹ NEs with high Si content are subject to more extreme volume changes during cycling and are thus more prone to particle cracking and the associated extended SEI growth.⁸²

Fig. 8 Schematic showing links between particle fracture and SEI growth.

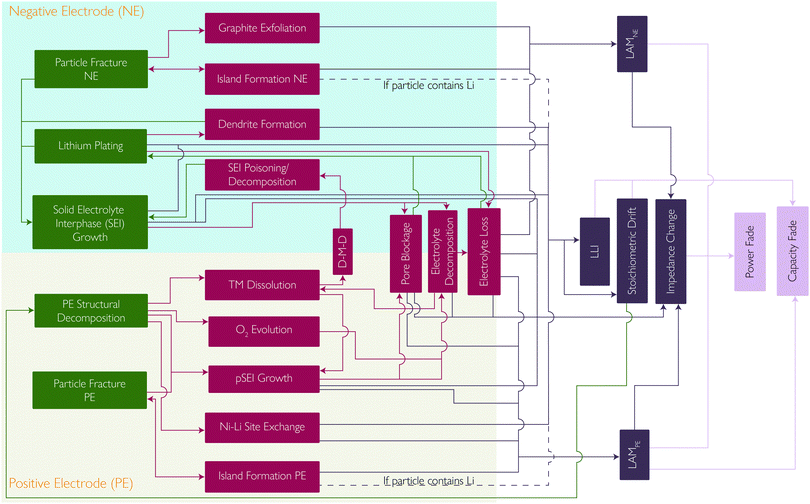
Coupling between mechanisms

Whilst extensive work has been done, with many studies describing each of these degradation mechanisms individually, the strong coupling, promotional or suppressive, between them is often neglected. Here we summarise some of the positive and negative feedback loops which have been identified. The mechanisms and their interplay are summarised in the flowchart in Fig. 9.

Fig. 9 The complex interplay between the primary and secondary mechanisms explained in this review, showing how each contributes to a degradation mode and how these in turn manifest in effects on cell performance.

Positive feedback. SEI layer growth is often quoted as one of the main degradation modes. Various models have been formulated since the seminal works by Peled⁸³ and Peled and Menkin's⁸⁴ more recent summary of the state-of-the-art, however, many of these models consider the SEI layer growth in isolation of other effects which can accelerate its growth. Mechanical fracture during cycling can release new surface area for SEI layer growth, which is often neglected, and TM dissolution from the cathode has been found to accelerate the rate of SEI layer growth.⁸⁵

Other degradation mechanisms are also vulnerable to positive feedback. TM dissolution and TM migration into the lithium layers of the layered oxide cathode can lead to a reduced lithium diffusivity. This can therefore lead to more severe concentration gradients and more mechanical fracture.

Mechanical fracture can also be self-reinforcing. Island formation causes the interfacial surface area of the island to become inactive, increasing the interfacial current density through the remaining active interfacial area. Increased current density results in increased concentration gradients, which in turn result in increased mechanical stress and further fracture.¹³

Lithium plating is highly sensitive to local electrolyte potential. SEI growth and TM deposition both cause pore blockage, decreasing the effective electrolyte conductivity and resulting in high electrolyte potentials close to the NE-separator interface, leading to lithium plating. Li plating also contributes to pore blockage, making it self-reinforcing.²⁰

Beyond pure mechanistic interactions, it is also important to consider the sensitivity of these mechanisms to scale, with effects such as thermal gradients having detrimental impacts on lifetime.⁸⁶ In this case, uneven temperature distribution, commonly found in commercial cells, can lead to heterogeneous current distributions amplifying these current and temperature sensitive degradation modes.^38–41

A reduction in the lithium content from the NE will lead to the SoC of that electrode decreasing whilst the PE remains the same. This is known as stoichiometric drift and leads to a reduction in the capacity but also an increase in the PE potential at the end of charge, accelerating the PE degradation mechanisms.

Negative feedback. Many of the conclusions made in the literature are generalisations and, in specific cases, opposing trends can also be proposed. For instance, the SEI layer growth causes LLI, which increases the NE potential with respect to Li,¹³ limiting the chance of lithium plating. SEI layer growth is evidently a key mechanism to consider, with many different models describing the nature of the cell degradation proposed. For instance, kinetically dominated models generally show a linear trend in cell capacity fade over time, however many researchers have shown that diffusion dominated models are a better representation of the behaviour of thicker SEI layers, indicating that as the SEI grows it presents greater resistance to solvent molecules diffusing to the surface of the graphite, thus limiting its own growth rate. However, this neglects the fresh surfaces exposed by cracks during battery cycling and the reality is likely to be a combination of kinetic and diffusion dominated behaviour.

Identifying and characterising degradation mechanisms

Whilst models are extremely useful for predicting future performance, their parameterisation and validation are equally essential. In much of the literature, electrochemical measurements form the foundations of characterisation, with galvanostatic methods being a key tool for establishing measurements of capacity, resistance and coulombic efficiency. Whilst relatively simple, these measurements can provide significant insight. A notable example is that of Harlow et al.⁸⁷ who extensively used high precision coulometry (HPC) and incremental capacity analysis (ICA) to probe the influences of different electrolytes of a NMC532-graphite cell towards an industrial benchmark.

Many variations of galvanostatic and potentiostatic methods exist, each providing different key insights. Electrochemical impedance spectroscopy (EIS), for instance, is a core technique for decoupling resistance contributions in battery electrodes. Other electrochemical techniques involving the OCV of the cell, such as analysing the curve itself,¹⁴ differential voltage analysis (DVA)⁶⁸ and ICA,⁸⁸ have been used to predict electrode capacities and their offset and, from this, the degradation modes of LAM and LLI. Slippage tracking is the process of monitoring the changing positions of IC or DV peaks as the battery is cycled, however this could be influenced by a range of degradation mechanisms.

Beyond electrical stimuli, a range of diffraction, spectroscopy and microscopy techniques have all been used to assess changes in electrode materials. For example, ex situ electron imaging or X-ray imaging is straightforward and hence carried out frequently, providing important parameters for models.⁶⁴

The highly coupled nature of many of these degradation effects, and their multiscale and multi-physical interactions, necessitates the use of multiple techniques to gain full insights into the underpinning processes. Furthermore, there is a need to both separate out the different contributions and capture their interactions. This is particularly important to consider in ex situ coin cell experiments, where a surrogate electrolyte is used. Since electrolyte volume and additives can have a significant impact on lifetime, as well as introduce cross talk between the negative and positive electrodes, this can lead to false conclusions due to experimental artefacts. In situ measurements can be used to overcome these challenges, however these often require modifications to the cell, which themselves bring about changes in the cell behaviour.

Validation of models should always include the use of real world drive cycles, to ensure that the interconnections between models as well as path dependence are fully represented.

The focus of this part of the perspective, however, is not to exhaustively review these techniques, but instead highlight the insights they provide in the context of developing more accurate battery models.

SEI layer growth

Experimental triggers. SEI grows more rapidly at high temperatures and high currents, but it grows even when the cell is at rest at high SoC, albeit at slower rates (this contributes to calendar ageing). Since particle cracking also enhances SEI growth, any conditions that cause particle cracking also cause increased SEI growth.

Characterisation. In situ experiments:

(i) HPC to identify irreversible capacity loss (most likely due to SEI growth).

(ii) EIS to monitor the impedance changes attributable to SEI growth.

(iii) Hybrid Pulse Power Characterisation (HPPC) tests, in lieu of EIS, are also possible.

Liu et al.²⁸ used an electrochemical quartz crystal microbalance (EQCM) to monitor how the mass of the SEI increased during formation. They confirmed these findings using in situ differential electrochemical mass spectroscopy (DEMS) and ex situ atomic force microscopy (AFM). They also found that (LiOCO₂CH₂)₂ could be re-oxidised to form Li₂O.

The mechanical properties (Young's moduli and fracture toughness) of the SEI layer would be useful properties, however, it is very challenging to measure these and, to our knowledge, no experimental study has been reported to have attempted this.

Lithium plating

Experimental triggers. The main experimental trigger for lithium plating is fast charging at low temperatures. The lower the temperature, the more Li is plated.³⁵ Higher charge currents and voltages also result in more Li plating.⁸⁹

Characterisation. Three different in situ methods for quantifying Li plating using cyclic capacity fade are proposed:⁸⁹

(i) Resistance–capacity plot – assuming that Li plating does not increase the cell's resistance, capacity loss due to plating is equal to the difference in capacity between the cell with plating and the cell without, for the same value of resistance.

(ii) Arrhenius plots – non-Arrhenius behaviour results from Li plating, while Arrhenius behaviour results from SEI growth. Capacity loss due to Li plating is found by extrapolating the Arrhenius behaviour from higher temperatures and subtracting extrapolated and measured capacity losses at the lower temperatures.

(iii) Conditions which trigger plating result in anomalously high capacity fade rates per cycle. Zhang et al.⁸⁹ assume that any capacity fade >0.024% per cycle is due to plating, but the exact value will vary between different cell types.

One proposed in situ method of quantifying plating resulting from a single charge is to detect the inverse stripping reaction through a tell-tale minimum in differential voltage (dV/dQ) plots,³⁷ but the large spread of values in the literature call the reliability of this method into question.^38,90 ICA (dQ/dV) has also been shown to have an additional minimum at high voltages when stripping occurs.⁹¹

Any of these methods can be used to parameterise a Li plating model, by adjusting the rate constant for the side reaction so that the model predicts the correct amount of Li to be plated.

Positive electrode structural change and decomposition

Experimental triggers. All six of the degradation mechanisms covered in the previous section on PE structural change and decomposition will be exacerbated at elevated temperatures.^58,92 With the exception of oxidation of the lattice oxygen, none of the mechanisms listed (phase change, cation site exchange, chemical oxidation of the electrolyte, acid attack, and pSEI formation) are direct electrochemical processes and so are not directly affected by varying the cell voltage or current. However, they are indirectly linked through the potential of the electrode (degree of lithiation) and the dynamics of the electrode–electrolyte interface, which are themselves functions of electrode potential and current.⁵⁸

Oxidation of lattice oxygen is an electrochemical process, happening when the electrode potential is greater than the edge of the O²⁻ p band.⁴⁴ Due to the oxidation potentials of the TM redox couples generally being below this value, oxidation of lattice oxygen will only happen in the extremely high SoC range.

Phase change from layered to spinel or rock salt structures is more favourable at low degrees of lithiation (high SoC), corresponding to high cell voltages. Higher ambient temperature favours the phase transformation from the layered NMC structure to the rock salt layer. The bulk materials undergo a two-phase transition from their layered structure to a spinel structure and eventually to a rock salt structure at around ∼170 °C.^92–94 Formation of more spinel/rock salt layer leads to [O] evolution, LAM and impedance rise.

Chemical oxidation of the electrolyte is primarily due to the presence of highly oxidised TM species (Ni⁴⁺), which also corresponds to high SoCs (and therefore high voltages).⁵¹ Due to this reaction taking place at the electrode–electrolyte interface, any conditions which lead to exposure of new electrode surfaces (e.g. particle cracking) will exacerbate this mechanism. Acid attack is due to the presence of contaminants in the electrolyte and can thus occur across the SoC range of the cell (full voltage range). Experimental studies^45,46,57,58 have found that high temperature and high voltage conditions should encourage TM dissolution and eventually encourage pSEI formation. This is likely due to the high voltage at higher SoCs (60–100%) exposing fresh electrode surfaces to the electrolyte. The result is spinel/rock salt phase transformation and O₂ evolution, with subsequent TM dissolution.⁵⁹

Characterisation. The effects of capacity fade and impedance increase should be visible through standard battery test methods. LAM at the PE will change the OCV profile of the battery, with peak depression, shift, or broadening in ICA an obvious sign. Direct in situ measurement of the mechanisms behind this performance drop are significantly more difficult, however, and often require specially instrumented cells.⁴⁵

The effects of these degradation mechanisms should be observable upon cell disassembly using structural and chemical analyses of the electrodes and electrolyte.⁵⁶ The electrode structure can be examined using techniques such as X-ray diffraction and spectroscopy (XRD and XAS), and electron microscopy and spectroscopy (TEM, SEM, EDX and EELS), giving information about the structural change of the electrode, any defects (e.g. Ni²⁺/Li⁺ site exchange) and surface films.⁵³ The chemical composition of the electrode could also be analysed using X-ray photoelectron spectroscopy (XPS), atomic emission spectroscopy (such as ICP-OES), or gas chromatography (GC).^50,95 This would also reveal if TMs have deposited onto the NE and the composition of surface films.⁹⁶

The presence of a spinel/rock salt phase at the PE particle surface and the O₂ evolution from the PE have been confirmed with the help of the following experiments:

(i) Reconstructed disordered layer upon phase transformation was visualised using the atomic resolution ADF-STEM imaging, as shown in Fig. 10.

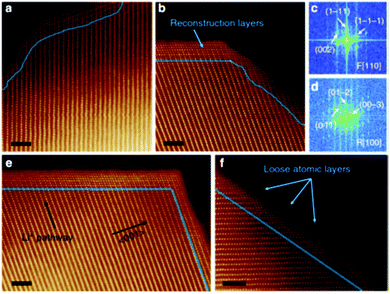Fig. 10 Atomic resolution ADF-STEM image of the spinel/rock salt phase. Reprinted with permission from Lin et al.⁵⁶ Copyright (2012), Springer Nature.

(ii) Online Electrochemical Mass Spectrometry (OEMS) has shown that at higher degrees of delithiation, all three NMC formulations (NMC111, NMC622 and NMC811) release O₂ at room temperature (25 °C) which eventually reacts with EC to produce CO and CO₂, as shown in Fig. 11.⁴⁵

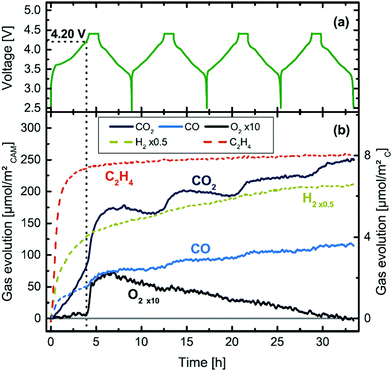Fig. 11 Cell voltage and gas evolution vs. time of a NMC811-graphite cell at 25 °C and 0.2 °C, over four charging/discharging cycles.⁴⁵

(iii) Phase changes in the NMC materials can be tracked by plotting ICA peaks at higher voltages (3.0–4.8 V)⁴⁵ and standard electrochemical characterisations at similar conditions can capture the capacity fade and impedance rise in the cell happening because of this particular degradation mechanism.

The thicknesses of both the spinel/rock salt phase and pSEI at different operating conditions reported in several publications are as follows:

(a) 15–100 nm spinel/rock salt layer thickness has been reported for different battery chemistries at different cycling, operating and storage conditions.^53,97,98

(b) Comparing gas chromatographs of fresh and calendar aged electrodes, stored for a year under ambient conditions, a surface layer (pSEI) of up to ∼10 nm thickness was found on the NMC811 positive electrodes.⁵⁰

Additionally, the electrolyte can be analysed for the presence of TM ions and any electrolyte degradation products using NMR, ICP-OES, UV/vis-spectroscopy and cyclic voltammetry.⁹⁵

Particle fracture

Experimental triggers. Operating at extreme temperatures, both above room temperature and sub-zero temperatures, accelerates electrode particle fracture. High current loading causes a larger concentration gradient, resulting in greater stress and a higher likelihood of fracture. Cycling across certain SoC windows, for example during graphite staging,⁷² can also accelerate fracture. From the material's perspective, electrodes with high silicon content and/or large electrode particle size exhibit greater degrees of fracture.

Silicon additives. Generally, different degrees of lithiation of the NE will cause different phases of Li–Si products to be formed, with the highest lithiated phase having a volume of 400% of a delithiated silicon lattice.⁶⁹ From the literature, there does not seem to be a “standard” SoC window that this occurs in; this will depend on the ratio of silicon in the electrode. Yao et al. carried out an in operando experiment on cycling behaviour of silicon–graphite blended electrodes, and the results revealed that the lithiation of silicon occurs throughout the whole range of voltage, while the lithiation of graphite starts when the potential dips below 0.2 V. The delithiation is carried out sequentially: Li extraction happens first from graphite particles and then from silicon particles, when the voltage exceeds 0.22 V. These experimental facts indicate that in a graphite anode composited with silicon, the large volume change of silicon should occur during more than one voltage (SoC) range.⁹⁹

Zhang⁶⁶ briefly mentions the effects of temperature on cycle life in silicon/matrix negative electrodes. The findings are that higher temperatures increased the capacity of the cells per cycle, but were detrimental to the cycle life of the cell. This could be attributed to the reduction in overpotential for cells at a higher temperature, allowing more of the lithium to be removed from the silicon in normal operating voltage windows, causing smaller particle size and hence increased tensile stresses in the electrode.

There seems to be no concrete evidence of the effects of C-rate on cycle life in electrodes with silicon additives.

Characterisation. In situ measurements include use of an acoustic emissions sensor,¹⁰⁰ where fractures return a characteristic waveform and in situ X-ray computed tomography (XCT) in snapshot mode, shown in Fig. 12.⁶³ These measurements validate the operating conditions at which fracture occurs, predicted by simulations. To determine the extent of particle cracking, studies use in situ and ex situ XRD to image the electrodes.^64,66,69 XCT information provides important parameters for models, including crack length, fragment particle size and particle volume changes. Fig. 13 shows an example of ex situ SEM, showing fracture of a Si–graphite anode.⁶⁸

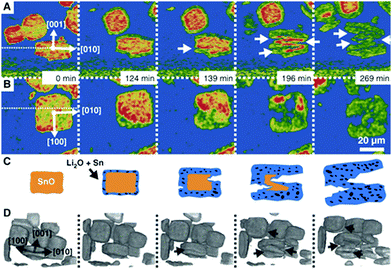Fig. 12 Particle fracture observed by in situ synchrotron X-ray in a model SnO system during lithiation. Reprinted with permission from Ebner et al.⁶³ Copyright (2013), American Association for the Advancement of Science.

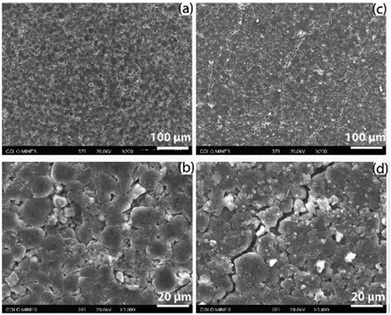Fig. 13 Fracture observed with SEM from the negative electrodes from an LGMJ1 18650 cell after degradation, (a and b) fresh and (c and d) aged. Reprinted with permission from Li et al.⁶⁸ Copyright (2019), Elsevier B.V.

Stress/strain measurements on stack level¹⁰¹ are highly relevant to failure analysis due to particle fracture, though they do not provide direct evidence of fracture. The stress/strain values are important parameters for fatigue models.

DVA (dV/dQ) is used to determine the LAM in the electrodes, which can be an indicator of particle fracture, the work of Li et al. being an example.⁶⁸ However, other mechanisms can lead to LAM too and some fractures may not be severe enough to cause LAM.

For particle fracture, the important parameters are (1) stress/strain and (2) intrinsic mechanical properties of the materials. In situ stress/strain measurement can be done by digital image correlations, curvature measurement methods and optical fibre sensor.¹⁰² Material properties including Young's modulus, hardness and fracture strength can be measured by indentation tests.¹⁰³

As a guide to designing experiments for investigating specific battery degradation mechanisms in isolation, where possible, or in concert, where required, Table 3 shows the experimental conditions which can be expected to trigger the primary and secondary degradation mechanisms covered in this perspective.

Table 3 Experimental conditions required to trigger a range of degradation mechanisms, as a guide to experiments

Degradation mechanism	Subsets	T dependence	V or SoC dependence	I dependence
Lithium plating	Reversible, irreversible, dendritic	Low T	High V	High I
SEI growth	Kinetic limited, diffusion limited	High T	High V	N/A
Particle fracture	Graphite	Low T	More than one SoC region	High I
	SiGr	Low T	More than one SoC region^99	High I
	NMC	Low T	High SoC^104	High I
PE structural change and decomposition	Phase change (layered to spinel to rock salt)	High T	Both high V and SoC	High I
	Electrochemical decomposition (oxidation of lattice oxygen)	High T	High V	High I
	Ni–Li site exchange (LiNiO2)	High T	High V	N/A
	Acid attack	High T	N/A	N/A
	Reaction with electrolyte	High T	High V	N/A

---

Models of battery degradation

The performance and behaviour of a battery depends on the integrity of its complex inner structure. At present, it is difficult to directly measure State of Health (SoH) of a battery, as sensors placed within the structure are expensive and could disrupt the function. Instead, battery models which accurately predict their long-term behaviour can act as a “digital twin” of the battery, running alongside it as it operates and ages and occasionally resynchronising, using input from the few measurements which can be obtained, such as cell voltage, temperature and current. The SoC of a battery, essential information for smart charging, is also difficult to measure and must be estimated by the digital twin. For both SoC and SoH monitoring, simulations need to be both accurate and very fast, providing results in real time.

By predicting the key performance parameters of a battery, such as capacity and lifetime, models can also be useful tools for designing electrodes, cells and packs, enabling the vast design space of batteries to be explored, where the constituent materials, electrode structure, thermal management and many more aspects can be varied and combined, without the need for expensive and potentially hazardous prototypes to be built.

Types of models

In general, there are essentially two approaches for modelling: empirical and physics-based. The former involves an incremental process of applying equations and parameters to achieve the best fit to experimental data, while the latter derives the simulated behaviour from equations known to represent the actual physical behaviour involved. In empirical models, the underlying equations may not have any real meaning, but rather attempt to emulate the behaviour of the battery, which is treated as a black box. There are also hybrid models employing simplifying techniques to achieve the speed of empirical models while harnessing the accuracy of a physics-based approach. Examples include the single particle model¹⁰⁵ and mechanistic models,²⁵ which use an inverse approach to estimate cell voltage and capacity for a given degradation mechanism and are becoming more widely used for machine learning (ML) and BMS.³⁶Fig. 14 shows the various scales involved in physical and empirical models.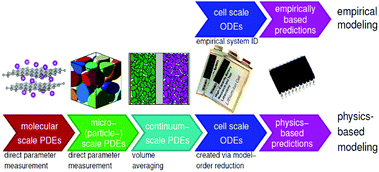

Fig. 14 Illustration of multiscale battery modelling, represented by physics-based and empirical models. Reproduced from ECE4710/5710: Modelling, Simulation, and Identification of Battery Dynamics, courtesy of G. J. Plett.¹⁰⁶

Empirical. One family of empirical models is equivalent-circuit models (ECM), describing the electrical behaviour of a battery using a set of circuit elements, such as resistors and capacitors. The elements in the model may not necessarily have direct relevance to the real device, but simulate its overall behaviour. Due to its computational efficiency in terms of speed, memory and numerical convergence, ECMs are widely used in BMS to predict the SoC and SoH of batteries for vehicle power management control.^88,107,108 In principle, this technique predicts the battery voltages based on current inputs, where different resistor–capacitor combinations are used to represent different time constants inherent in a battery.¹⁰⁹ Commonly studied equivalent-circuit models include Thévenin model, the Randles model and resistance–capacitance (RC) network based ECMs, such as first-order RC, second-order RC and third-order RC models.^108,110 Because the ECM is an empirical model, it is often limited by the underlying experimental data and cannot provide deep insights into the electrochemical interactions within the battery. A model developed for a particular scenario may therefore not be applicable to another. For example, empirical battery degradation models for EVs often assume a regular daily charging pattern. Obtaining an accurate empirical model of battery degradation therefore requires that operation-specific battery ageing experiments be performed for each new application. Such tests take months or even years and would have to be performed in advance, using expensive test facilities. Moreover, fitting an ECM to experimental datasets can be ambiguous, as different arrangements of the circuit elements can be fitted to obtain a similar impedance curve.¹¹¹ Therefore, proper assignment of the circuit elements can only be achieved when adequate information on the underlying electrochemical phenomena is available.

Physical. In contrast to empirical models, physics-based models use a set of coupled partial differential equations (PDEs), based on vector calculus and physical chemistry, to model the electrochemical and chemical interactions within a battery. The physics can be described at a range of scales, shown in Fig. 14, from the atomistic/molecular scale of materials, through to microscale structure of electrodes and continuum scale models representing whole cells. The values derived at each scale can provide input parameters for the models at higher scales. Typically, these models describe the charge and mass conservations in the homogeneous solid and electrolyte, as well as the lithium flux between the solid and electrolyte phases. Digital simulation of the physics-based models requires a discretisation in space and time. Three frequently used discretisation methods include (1) finite difference, where space and time are divided into small segments, and the derivatives are discretised using Euler's rule; (2) finite volume, in which time is divided into small segments and space into volumes; and (3) finite element, where time is divided into small segments but space is formulated as a summation over quadratic or linear basis function.¹⁰⁶

At the atomistic scale, no universal framework exists for simulating degradation mechanisms, but classical molecular dynamics (MD), mesoscopic modelling and ab initio density functional theory (DFT) have been used to investigate the origin and effects of cracking and stresses in Si anodes during charge¹¹² and techniques for understanding cathode degradation have been recently reviewed.¹¹³

Doyle, Fuller and Newman have developed the widely used electrochemical model including mass conservation, charge conservation and reaction kinetics.^114,115 As the model consists of a spatial variation along the thickness of the electrode and a pseudo radial dimension along the solid phase electrode particles, these models are commonly known as pseudo-two-dimensional (P2D) models. While this model can provide a comprehensive analysis of the internal dynamics of a battery,^114,115 discretising and solving a physics-based model in both dimensions often result in hundreds or even thousands of equations. Therefore, implementing a physics-based model for real-time BMS monitoring is computationally expensive.

Single-particle models (SPM). To bridge the gap between empirical and physics-based models, the SPM was developed, in which each electrode domain is simplified into a single spherical particle.^116–118 Unlike an electrochemical model, it is assumed that radial diffusion of lithium-ions in the electrode particle is the slowest process and, therefore, lithium concentration gradients in the particle occur only in the radial direction.¹¹⁸ Despite the reduced computational demand compared to a physics-based electrochemical model, one significant drawback of the SPM is that the model does not consider Li-ion distribution in the electrolyte phase. As a rule, SPMs are usually limited to low-current applications, which constrain the usage of such models for fast-charging in an electric vehicle.^119,120 Kemper and Kum showed that this limitation can be mitigated by extending the SPM to include the electrolyte dynamics, which could improve the prediction accuracy by 14%, compared with the standard SPM.¹²⁰ Recently, Li and co-workers¹²¹ have also extended a SPM with electrolyte dynamics to include SEI layer formation, in which crack propagation due to stress generated by the volume expansion of the particles are coupled to predict the effects of chemical and mechanical degradation. They showed that the effect of crack propagation depends strongly on temperature, current densities and particle sizes. By including the SEI layer formation and crack propagation, they were able to accurately predict battery capacity fade and voltage profile as a function of cycle number over a broad temperature range with an error of 10.3 × 10⁻³ root-mean-square error (RMSE), compared to experimental results.

SEI layer growth

Many P2D models of SEI growth exist, all of which are predominantly based on the pioneering work of Safari et al.,²⁹ who model solvent diffusion through the SEI layer, followed by electrochemical reactions governed by the Tafel equation, including both kinetic and diffusion limitations. Although the degradation mechanism of SEI is well captured by these physics-based models, their high computation cost is prohibitive for simulating degradation over hundreds or thousands of cycles. For this, semi-empirical and empirical models are preferred, where the fitted ageing laws capture resistance increase and capacity loss caused by SEI degradation. These ageing laws can be implemented on both physics-based and ECMs.

In a semi-empirical degradation model by Zhang et al.,¹²² SEI layer growth is expected to be the main cause of battery degradation at temperatures between 25 and 30 °C. Key parameters such as OCV, resistance, diffusion coefficient and electrochemical reaction rates, were extracted from cycling degradation tests. With these fundamental parameters expressed as a function of cycle number, cyclical ageing could be simulated by the P2D model, while the ageing simulation based on the original physics-based degradation model of Safari et al.²⁹ is unrealistic.

The empirical model is frequently combined with ECMs, due to their simplicity and ability to lump all the degradation physics into limited variables. In a study by Liaw et al.,¹²³ based on lumped ECM, empirical ageing laws of resistance and capacity loss, as a result of SEI degradation, are described. Cordoba-Arenas et al.¹²⁴ takes into account factors of SoC swing, current and temperature. The simplicity and proven accuracy of these models makes them suitable for battery SoH estimation. Moreover, due to the fact that the SoH Kalman filter algorithm is mostly based on equivalent circuits, SoH prediction can easily be combined with the empirical type degradation model.¹²⁵ The work of Fleckenstein et al.¹²⁶ introduces an SEI degradation distributed model by implementing empirical ageing laws into an electrothermal model of a large format cell. The SEI degradation inhomogeneity is represented by the distribution of impedance and capacity loss.

Above all, the physics-based model of SEI layer growth can capture the degradation behaviours with clear physical meanings. Based on the P2D model framework, the SEI degradation mode can be linked with other degradation mechanisms and there have been attempts to model the stress and fatigue behaviour with both the SEI and the electrode materials combined, where SEI properties were assumed.⁷⁸

Lithium plating

Li plating and the inverse process, Li stripping, can be incorporated into P2D models by adding an additional Butler–Volmer equation for the side reaction, as first proposed by Arora, Doyle and White in 1999.¹²⁷

The most mathematically rigorous model in the literature is that of Yang et al.,³⁷ illustrated in Fig. 15, as they explicitly consider dependence on both electrolyte and plated Li concentrations.

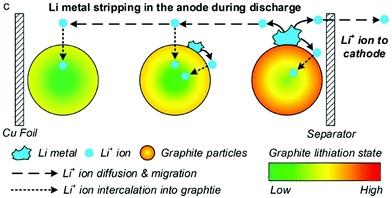Fig. 15 During stripping, Li metal is dissolved back into the electrolyte and then intercalated into both positive and negative electrodes. Reprinted with permission from Yang et al.³⁷ Copyright (2018), Elsevier B.V.

O’Kane et al.⁹⁰ build on Yang's model by incorporating a nonlinear diffusion model that accounts for phase transitions in the graphite NE. They show that nonlinear diffusion yields qualitatively different results.

Positive electrode structural change and decomposition

PE degradation is an ongoing area of research, with several publications available on the different mechanisms of positive electrodes. However, very few studies deal with the mechanisms individually.

(i) Phase change and oxygen evolution: oxygen evolution from the PE has been conventionally modelled as the oxidation of electrolyte at the PE side using a simple kinetically limited Tafel equation.^13,85,128 However, this approach does not include any physics to describe the source of the oxygen evolution. Ghosh et al.¹²⁹ have recently proposed the first model to include this, describing oxygen evolution from the bulk and diffusion through the rock salt layer using a shrinking core model. This model can reproduce the modes LLI and LAM, and the effects of capacity fade and power fade caused by this mechanism. Jana et al.¹²⁸ proposed that the capacity fade is a linear function of the oxidation current density, which they used in the Tafel equation to model the electrolyte oxidation at the PE. This oxidation reaction also produces H₂ which in turn enhances the TM dissolution.

(ii) TM dissolution and pSEI formation: TM dissolution at the PE is modelled using a first order chemical reaction, limited by concentration of H⁺ ions in the electrolyte.¹³⁰ H⁺ ions are generated from LiPF₆ salt dissociation in the electrolyte and solvent oxidation at the PE.¹³⁰ While LiPF₆ dissociation in the presence of H₂O is modelled using a chemical reaction rate, solvent oxidation is modelled using irreversible Butler–Volmer kinetics.¹³⁰ Lin et al.⁸⁵ provided detailed P2D model equations for Mn dissolution at the PE coupled with SEI layer formation at NE. The Mn deposition on the NE is also included in the model. The growth of the pSEI can be modelled as similar to any of the SEI layer growth models.

Particle fracture

The stress model in electrode particles has been developed as a function of current, particle size and partial molar volume.⁷⁴

The fatigue crack model (Paris’ law) has been incorporated into a single particle model for predicting battery capacity loss.¹²¹ Crack propagation is coupled with the SEI formation and growth (diffusion dominant), to account for the loss of lithium inventory.

Morphological effects from electrode microstructures have been studied by Xu et al.,⁶⁴ using finite element method in 3D. Cracks were handled by breaking the connection between two elements using a cohesive model.

Silicon additives. While silicon reacts electrochemically with lithium-ions to form lithium metal alloys, achieving high specific and volumetric capacities, large volume expansion occurs due to the alloying reactions. Otero and co-workers¹³¹ derived an analytical model to demonstrate the importance of the volume expansion factor and initial porosity in achieving high gravimetric and volumetric capacities, summarised in Fig. 16. Sethuraman et al.¹³² developed an electrochemical-mechanical model based on the Larché and Cahn chemical potential calculation, to study the effects of electrode mechanics on the potential hysteresis.

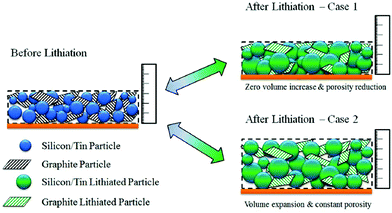Fig. 16 The analytical model developed to study the influence of volume expansion factor and porosity in a silicon–graphite composite electrode.¹³¹

Combined models

Fig. 17 shows the three main stages of battery degradation. The initial acceleration stage is thought to be caused by the initial SEI formation,^13,85 which rapidly reduces the capacity but also hinders further SEI growth. The causes of the stabilisation (linear ageing) and saturation (nonlinear ageing) stages are more debatable. Various models of two or more degradation mechanisms have been published, each proposing a different explanation as to what causes the switch from stabilisation to saturation stages.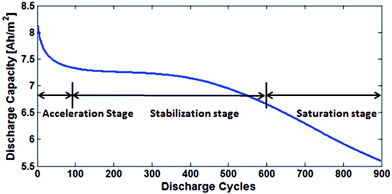

Fig. 17 The degradation is divided into three stages: acceleration, stabilisation and saturation. Reprinted with permission from Lin et al.⁸⁵ Copyright (2013), IOP Publishing.

The models of Arora, Doyle and White,¹²⁷ Yang et al.²⁰ and Zhao et al.³⁵ are notable for considering the coupling between Li plating and SEI growth, in different ways. Arora, Doyle and White¹²⁷ assume that a fraction of the plated Li immediately reacts to form SEI instead of forming Li metal, but the simplicity of their model means this SEI can be stripped, as if it was plated Li. Yang et al.²⁰ use two separate Tafel equations for the two reactions, in order to model a scenario where SEI-induced pore clogging causes rapid Li plating even at room temperature, causing the transition between the stabilisation and saturation stages of degradation. Zhao et al.³⁵ present an updated version of Arora, Doyle and White's model that allows them to model both reversible and irreversible plating at the same time.

Few attempts have been made to model more than two degradation mechanisms at a time. Lin et al.⁸⁵ presented a combined model of Mn dissolution, SEI formation and Mn deposition on the NE and analysed the combined effect of these degradation mechanisms. The model was able to qualitatively reproduce all three stages of degradation, but neither quantitative comparison with experiment nor temperature variation were included. A recent follow-up paper by Li, Landers and Park¹³³ added a semi-empirical model of SEI formation on cracks in particles and found that the majority of SEI was formed on cracks, as opposed to growing on top of existing SEI.

Jin et al.¹³⁴ combined Safari et al.'s²⁹ model of SEI growth on the NE, the same model applied to pSEI growth on the PE and an empirical model for loss of electrical contact due to particle cracking in both electrodes. The experiments did not last long enough to include the saturation stage, but the physics-based degradation model was found to be far superior to both equivalent circuit and purely empirical models in predicting capacity loss during an EV drive cycle.

Reniers, Mulder and Howey¹³ devised a SPM incorporating a NE SEI model valid in both the reaction-limited and diffusion-limited extremes, a Tafel equation for irreversible lithium plating on the NE, an empirical expression for loss of electrical contact in the NE and a Tafel equation for acid dissolution of the PE. Their model results in a good qualitative fit to experimental data at 25 °C and 45 °C, but not at 5 °C, which implies their model of lithium plating could be improved.

Keil and Jossen¹³⁵ presented a P2D model combining SEI growth, SEI formation on cracks and partially reversible Li plating. Like Yang et al.,²⁰ they found that Li plating could explain the transition from linear to nonlinear ageing, even at room temperature.

From these combined models, three different possible explanations for the transition between stabilisation and saturation stages emerge. Lin et al.'s 2013⁸⁵ model predicts that the stabilisation stage is dominated by SEI growth on the NE while the saturation stage is dominated by acid dissolution of the PE. Yang et al.²⁰ propose that the transition is caused by SEI-induced pore clogging, which in turn causes Li plating, neglecting the role of the PE completely. Keil and Jossen¹³⁵ also found that partially reversible Li plating could explain the transition. Reniers, Mulder and Howey¹³ argue that their empirical model of electrical contact loss also reproduces the saturation stage.

Prospective applications of machine learning

In recent years, ML techniques have become increasingly deployed at multiple length scales to aid researchers handle the increasing volumes of data and develop new underpinning insights. At the microstructural level, Wei et al.¹³⁶ demonstrated a supervised and unsupervised data mining approach to analyse larger XCT datasets for studying the effect of heterogeneous electrode particle degradation on cell level performance. Jiang et al.¹³⁷ also used ML approaches to aid their tomographic analysis of interfacial degradation effects between electrode particles and binders/conductive additives which are generally difficult to segment. Here, a convolutional neural network approach was used to aid with image segmentation. However, the real power of ML approaches come from not just automating analysis, but from developing deeper insights. Gayon-Lombardo et al.,¹³⁸ for instance, developed a deep convolutional generative adversarial network for the creation of synthetic microstructures. The power of these approaches further manifest themselves as these insights are integrated within a multiscale framework from atomistic length scales towards cell level control with the fusion of models, data and ML.^139,140

At the cell level, various authors have demonstrated the ability to provide accurate estimations of the remaining useful lifetime (RUL) by using techniques such as linear regression¹⁴¹ and different types of neural networks from input voltage and resistance data. Often these signals are transformed into differentials, with Severson et al.¹⁴² showing that differential capacity is a strong indicator of RUL. Extensions of these approaches which use spectroscopic information, such as EIS, have also demonstrated accurate RUL estimation from non-intuitive data sources. Zhang et al.¹⁴³ for instance combined EIS measurements of batteries aged in various modes with Gaussian process regression and an automatic feature identification approach to identify two specific frequencies (2 Hz and 17 Hz) which were particularly sensitive to degradation. Here the authors attribute this to changing interfacial properties, however further validation of this was needed.

Beyond these applications, text mining tools have also been developed, such as the work by Torayev et al.¹⁴⁴ which automatically scanned over 1800 articles and extracted key performance data for a LiO₂ system. Predicting battery catastrophic failure is also an emerging domain of interest for data-driven approaches as highlighted by Finegan et al.¹⁴⁵ However, whilst the frameworks are currently available, ensuring large enough volumes of high quality data and the fusion of multi-modal data types remains a challenge.

Conclusions

Understanding battery degradation is vital for developing high performance batteries that will meet the requirements for multiple applications. This perspective has identified five principal degradation mechanisms that are most commonly considered to be the cause of battery degradation during normal operation. These are SEI layer growth, lithium plating, PE decomposition and particle fracture at both electrodes. These five principal degradation mechanisms interact with each other and give rise to thirteen secondary degradation mechanisms, which are shown in Fig. 9, along with their interconnections. All of these degradation mechanisms result in 5 modes which are observable at the cell level. These are: LLI inventory, impedance change, stoichiometric drift, and LAM at both electrodes. These then result in operational effects such as capacity or power fade. Calendar or cycle ageing merely represent different pathways through the degradation space represented by these mechanisms.

Multiple interactions between degradation mechanisms have been identified and discussed, which in many cases require further study to properly understand. Multiple explanations to explain the transition between linear and non-linear degradation were found, also known as the knee point, cell drop-off, sudden failure, etc. Two examples of coupling found to explain this include SEI layer growth leading to pore blockage and subsequent lithium plating, and SEI layer growth leading to electrolyte loss and the cell drying out. However, we found no evidence for a universal explanation that applies in every case. We consider it to be far more likely that all reported explanations are possible, as well as many not proposed yet, and that the exact combination of degradation mechanisms that leads to end-of-life will be a function of cell chemistry and how a cell is used, simply resulting again in different pathways through the degradation space. Multiple other degradation mechanisms were considered, but were not included in this perspective, as they were not generally considered to be significant during normal operation.

Battery models need to be parameterised before they can be reliably applied to particular chemistries, applications or stages of the battery life. A variety of experimental and atomistic techniques exist for battery parameterisation, but these are not well understood and there is a need for a similar, concerted effort to be made to review parameterisation techniques for battery models.

We found that degradation at the PE is generally overlooked and the majority of previous work has been focused on the negative electrode. However, with the increased use of high nickel NMC electrodes, the thermodynamic stability of the electrode is lowered and positive electrode degradation is increasingly reported as significant.

The conditions that promote or attenuate the progression of each degradation mechanism are summarised, in a way that will help inform how to operate a cell to extend life, and also inform the design of accelerated degradation experiments. Understanding that only degradation modes and not the mechanisms themselves are observable at the cell level in situ, and which degradation mechanisms result in similar modes, will also help with the design of accelerated degradation experiments for which the effects of each degradation mechanism on its own are observable. The attempts to model each degradation mechanism and a limited number of examples of attempts to couple degradation mechanisms are also summarised, in a way that will help inform future modelling attempts.

We propose that the first universal cell degradation model that would be suitable for the majority of operating conditions would need to include the 5 principal and 13 secondary degradation mechanisms that we have identified and how they interact with each other. However, consensus has not yet been reached for the governing equations for many of these mechanisms and parameterisation will be difficult, requiring modellers and experimentalists to work closely together. However, achieving this ‘moonshot’ goal would significantly advance the field of lithium ion battery modelling and would provide industry with an extremely useful tool to extend battery lifetime and performance in multiple applications.

Author contributions

Jacqueline S. Edge: conceptualisation, funding & acquisition, methodology, project administration, visualisation, writing – original draft, writing – review and editing. Simon O’Kane: conceptualisation, investigation, writing – original draft. Ryan Prosser: conceptualisation, investigation, visualisation, writing – original draft. Niall D. Kirkaldy: investigation, methodology, visualisation, writing – original draft. Anisha N. Patel: conceptualisation, writing – review and editing. Alastair Hales: investigation, methodology, writing – original draft. Abir Ghosh, Weilong Ai, Jingyi Chen, Jiang Yang, Shen Li, Laura Bravo Diaz, Karthik N. Radhakrishnan: investigation, writing – original draft. Mei-Chin Pang: project administration, writing – original draft, Anna Tomaszewska, M. Waseem Marzook: writing – original draft. Huizhi Wang, Yatish Patel: supervision, writing – review and editing. Billy Wu, Gregory J. Offer: conceptualisation, funding & acquisition, supervision, writing – original draft, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially carried out with funding from the Faraday Institution (http://faraday.ac.uk; EP/S003053/1), grant number FIRG003. We would also like to thank Mr Amir Kosha Amiri for his graphical design expertise in constructing Fig. 1, 2, 4, 8 and 9.

Notes and references

1. D. Sanders, A. Hart, M. Ravishankar, J. Brunert, G. Strbac, M. Aunedi and D. Pudjianto, An analysis of electricity system flexibility for Great Britain, London, 2016.
2. G. E. Blomgren, The Development and Future of Lithium Ion Batteries, J. Electrochem. Soc., 2017, 164, A5019–A5025.
3. M. M. Kabir and D. E. Demirocak, Application of graphene and graphene-based materials in clean energy-related devices Minghui, Int. J. Energy Res., 2017, 41, 1963–1986.
4. J. C. Burns, A. Kassam, N. N. Sinha, L. E. Downie, L. Solnickova, B. M. Way and J. R. Dahn, Predicting and Extending the Lifetime of Li-Ion Batteries, J. Electrochem. Soc., 2013, 160, A1451–A1456.
5. S. N. S. Hapuarachchi, Z. Sun and C. Yan, Advances in In Situ Techniques for Characterization of Failure Mechanisms of Li-Ion Battery Anodes, Adv. Sustainable Syst., 2018, 2, 1–29.
6. M. Woody, M. Arbabzadeh, G. M. Lewis, G. A. Keoleian and A. Stefanopoulou, Strategies to limit degradation and maximize Li-ion battery service lifetime - Critical review and guidance for stakeholders, J. Energy Storage, 2020, 28, 101231.
7. J. P. Pender, G. Jha, D. H. Youn, J. M. Ziegler, I. Andoni, E. J. Choi, A. Heller, B. S. Dunn, P. S. Weiss, R. M. Penner and C. B. Mullins, Electrode Degradation in Lithium-Ion Batteries, ACS Nano, 2020, 14, 1243–1295.
8. M. Wörsdörfer, T. Gül, P. Cazzola, M. Gorner, T. Bunsen, L. D’Amore, S. Scheffer, R. Schuitmaker, H. Signollet, J. Tattini and J. Teter, Global EV Outlook 2019 to electric mobility, 2019.
9. C. P. Grey and J. M. Tarascon, Sustainability and in situ monitoring in battery development, Nat. Mater., 2017, 16, 45–56.
10. J. F. Peters, M. Baumann, B. Zimmermann, J. Braun and M. Weil, The environmental impact of Li-Ion batteries and the role of key parameters – A review, Renewable Sustainable Energy Rev., 2017, 67, 491–506.
11. C. Hendricks, N. Williard, S. Mathew and M. Pecht, A failure modes, mechanisms, and effects analysis (FMMEA) of lithium-ion batteries, J. Power Sources, 2015, 297, 113–120.
12. C. Lin, A. Tang, H. Mu, W. Wang and C. Wang, Aging mechanisms of electrode materials in lithium-ion batteries for electric vehicles, J. Chem., 2015, 104673,  DOI:10.1155/2015/104673.
13. J. M. Reniers, G. Mulder and D. A. Howey, Review and performance comparison of mechanical-chemical degradation models for lithium-ion batteries, J. Electrochem. Soc., 2019, 166, A3189–A3200.
14. C. R. Birkl, M. R. Roberts, E. McTurk, P. G. Bruce and D. A. Howey, Degradation diagnostics for lithium ion cells, J. Power Sources, 2017, 341, 373–386.
15. T. Waldmann, M. Wilka, M. Kasper, M. Fleischhammer and M. Wohlfahrt-Mehrens, Temperature dependent ageing mechanisms in Lithium-ion batteries – A Post-Mortem study, J. Power Sources, 2014, 262, 129–135.
16. S. J. Harris, D. J. Harris and C. Li, Failure statistics for commercial lithium ion batteries: A study of 24 pouch cells, J. Power Sources, 2017, 342, 589–597.
17. T. Raj, A. A. Wang, C. W. Monroe and D. A. Howey, Investigation of Path Dependent Degradation in Lithium-Ion Batteries, Batteries Supercaps, 2020, 3, 1377–1385.
18. M. Dubarry, N. Qin and P. Brooker, Calendar aging of commercial Li-ion cells of different chemistries – A review, Curr. Opin. Electrochem., 2018, 9, 106–113.
19. K. L. Gering, S. V. Sazhin, D. K. Jamison, C. J. Michelbacher, B. Y. Liaw, M. Dubarry and M. Cugnet, Investigation of path dependence in commercial lithium-ion cells chosen for plug-in hybrid vehicle duty cycle protocols, J. Power Sources, 2011, 196, 3395–3403.
20. X. G. Yang, Y. Leng, G. Zhang, S. Ge and C. Y. Wang, Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging, J. Power Sources, 2017, 360, 28–40.
21. Y. Merla, B. Wu, V. Yufit, N. P. Brandon, R. F. Martinez-Botas and G. J. Offer, Novel application of differential thermal voltammetry as an in-depth state-of-health diagnosis method for lithium-ion batteries, J. Power Sources, 2016, 307, 308–319.
22. N. Nitta, F. Wu, J. T. Lee and G. Yushin, Li-ion battery materials: Present and future, Mater. Today, 2015, 18, 252–264.
23. X. Han, L. Lu, Y. Zheng, X. Feng, Z. Li, J. Li and M. Ouyang, A review on the key issues of the lithium ion battery degradation among the whole life cycle, eTransportation, 2019, 1, 100005.
24. J. Vetter, P. Novák, M. R. Wagner, C. Veit, K.-C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, Ageing mechanisms in lithium-ion batteries, J. Power Sources, 2005, 147, 269–281.
25. M. Dubarry, C. Truchot and B. Y. Liaw, Synthesize battery degradation modes via a diagnostic and prognostic model, J. Power Sources, 2012, 219, 204–216.
26. P. Bai, J. Li, F. R. Brushett and M. Z. Bazant, Transition of lithium growth mechanisms in liquid electrolytes, Energy Environ. Sci., 2016, 9, 3221–3229.
27. G. Liu and W. Lu, A Model of Concurrent Lithium Dendrite Growth, SEI Growth, SEI Penetration and Regrowth, J. Electrochem. Soc., 2017, 164, A1826–A1833.
28. T. Liu, L. Lin, X. Bi, L. Tian, K. Yang, J. Liu, M. Li, Z. Chen, J. Lu, K. Amine, K. Xu and F. Pan, In situ quantification of interphasial chemistry in Li-ion battery, Nat. Nanotechnol., 2019, 14, 50–56.
29. M. Safari, M. Morcrette, A. Teyssot and C. Delacourt, Multimodal Physics-Based Aging Model for Life Prediction of Li-Ion Batteries, J. Electrochem. Soc., 2009, 156, A145.
30. E. Sarasketa-Zabala, I. Gandiaga, L. M. Rodriguez-Martinez and I. Villarreal, Calendar ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions, J. Power Sources, 2014, 272, 45–57.
31. P. M. Attia, S. Das, S. J. Harris, M. Z. Bazant and W. C. Chueh, Electrochemical Kinetics of SEI Growth on Carbon Black: Part I. Experiments, J. Electrochem. Soc., 2019, 166, E97–E106.
32. S. Wang, K. Yang, F. Gao, D. Wang and C. Shen, Direct visualization of solid electrolyte interphase on Li4Ti5O12 by: In situ AFM, RSC Adv., 2016, 6, 77105–77110.
33. S. Zhang, K. Zhao, T. Zhu and J. Li, Electrochemomechanical degradation of high-capacity battery electrode materials, Prog. Mater. Sci., 2017, 89, 479–521.
34. C. Zhan, T. Wu, J. Lu and K. Amine, Dissolution, migration, and deposition of transition metal ions in Li-ion batteries exemplified by Mn-based cathodes – a critical review, Energy Environ. Sci., 2018, 11, 243–257.
35. X. Zhao, Y. Yin, Y. Hu and S. Y. Choe, Electrochemical-thermal modeling of lithium plating/stripping of Li(Ni0.6Mn0.2Co0.2)O2/Carbon lithium-ion batteries at subzero ambient temperatures, J. Power Sources, 2019, 418, 61–73.
36. M. Dubarry and D. Beck, Big data training data for artificial intelligence-based Li-ion diagnosis and prognosis, J. Power Sources, 2020, 479, 228806.
37. X. G. Yang, S. Ge, T. Liu, Y. Leng and C. Y. Wang, A look into the voltage plateau signal for detection and quantification of lithium plating in lithium-ion cells, J. Power Sources, 2018, 395, 251–261.
38. I. D. Campbell, M. Marzook, M. Marinescu and G. J. Offer, How Observable Is Lithium Plating? Differential Voltage Analysis to Identify and Quantify Lithium Plating Following Fast Charging of Cold Lithium-Ion Batteries, J. Electrochem. Soc., 2019, 166, A725–A739.
39. Q. Liu, C. Du, B. Shen, P. Zuo, X. Cheng, Y. Ma, G. Yin and Y. Gao, Understanding undesirable anode lithium plating issues in lithium-ion batteries, RSC Adv., 2016, 6, 88683–88700.
40. X. M. Liu and C. B. Arnold, Effects of Current Density on Defect-Induced Capacity Fade through Localized Plating in Lithium-Ion Batteries, J. Electrochem. Soc., 2020, 167, 130519.
41. T. C. Bach, S. F. Schuster, E. Fleder, J. Müller, M. J. Brand, H. Lorrmann, A. Jossen and G. Sextl, Nonlinear aging of cylindrical lithium-ion cells linked to heterogeneous compression, J. Energy Storage, 2016, 5, 212–223.
42. M. Dubarry, N. Qin and P. Brooker, Calendar aging of commercial Li-ion cells of different chemistries – A review, Curr. Opin. Electrochem., 2018, 9, 106–113.
43. J. Keil, N. Paul, V. Baran, P. Keil, R. Gilles and A. Jossen, Linear and Nonlinear Aging of Lithium-Ion Cells Investigated by Electrochemical Analysis and In-Situ Neutron Diffraction, J. Electrochem. Soc., 2019, 166, A3908–A3917.
44. A. Manthiram, A reflection on lithium-ion battery cathode chemistry, Nat. Commun., 2020, 11, 1550.
45. R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, Oxygen Release and Its Effect on the Cycling Stability of LiNix MnyCozO2 (NMC) Cathode Materials for Li-Ion Batteries, J. Electrochem. Soc., 2017, 164, A1361–A1377.
46. M. D. Radin, S. Hy, M. Sina, C. Fang, H. Liu, J. Vinckeviciute, M. Zhang, M. S. Whittingham, Y. S. Meng and A. Van der Ven, Narrowing the Gap between Theoretical and Practical Capacities in Li-Ion Layered Oxide Cathode Materials, Adv. Energy Mater., 2017, 7, 1–33.
47. E. Billy, M. Joulié, R. Laucournet, A. Boulineau, E. De Vito and D. Meyer, Dissolution Mechanisms of LiNi1/3Mn1/3Co1/3O2 Positive Electrode Material from Lithium-Ion Batteries in Acid Solution, ACS Appl. Mater. Interfaces, 2018, 10, 16424–16435.
48. D. Li, H. Li, D. Danilov, L. Gao, J. Zhou, R. A. Eichel, Y. Yang and P. H. L. Notten, Temperature-dependent cycling performance and ageing mechanisms of C6/LiNi1/3Mn1/3Co1/3O2 batteries, J. Power Sources, 2018, 396, 444–452.
49. E. Zhao, L. Fang, M. Chen, D. Chen, Q. Huang, Z. Hu, Q. Yan, M. Wu and X. Xiao, New insight into Li/Ni disorder in layered cathode materials for lithium ion batteries: a joint study of neutron diffraction, electrochemical kinetic analysis and first-principles calculations, J. Mater. Chem. A, 2017, 5, 1679–1686.
50. R. Jung, R. Morasch, P. Karayaylali, K. Phillips, F. Maglia, C. Stinner, Y. Shao-Horn and H. A. Gasteiger, Effect of Ambient Storage on the Degradation of Ni-Rich Positive Electrode Materials (NMC811) for Li-Ion Batteries, J. Electrochem. Soc., 2018, 165, A132–A141.
51. E. M. Erickson, F. Schipper, T. R. Penki, J.-Y. Shin, C. Erk, F.-F. Chesneau, B. Markovsky and D. Aurbach, Review—Recent Advances and Remaining Challenges for Lithium Ion Battery Cathodes, J. Electrochem. Soc., 2017, 164, A6341–A6348.
52. T. Li, X.-Z. Yuan, L. Zhang, D. Song, K. Shi and C. Bock, Degradation Mechanisms and Mitigation Strategies of Nickel-Rich NMC-Based Lithium-Ion Batteries, Electrochem. Energy Rev., 2020, 3, 43–80.
53. S.-K. Jung, H. Gwon, J. Hong, K.-Y. Park, D.-H. Seo, H. Kim, J. Hyun, W. Yang and K. Kang, Understanding the Degradation Mechanisms of LiNi0.5Co0.2Mn0.3O2 Cathode Material in Lithium Ion Batteries, Adv. Energy Mater., 2014, 4, 1300787.
54. C. Li, H. P. Zhang, L. J. Fu, H. Liu, Y. P. Wu, E. Rahm, R. Holze and H. Q. Wu, Cathode materials modified by surface coating for lithium ion batteries, Electrochim. Acta, 2006, 51, 3872–3883.
55. N. Alias and A. A. Mohamad, Advances of aqueous rechargeable lithium-ion battery: A review, J. Power Sources, 2015, 274, 237–251.
56. F. Lin, I. M. Markus, D. Nordlund, T.-C. Weng, M. D. Asta, H. L. Xin and M. M. Doeff, Surface reconstruction and chemical evolution of stoichiometric layered cathode materials for lithium-ion batteries, Nat. Commun., 2014, 5, 3529.
57. R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, Chemical versus electrochemical electrolyte oxidation on NMC111, NMC622, NMC811, LNMO, and conductive carbon, J. Phys. Chem. Lett., 2017, 8, 4820–4825.
58. R. Jung, P. Strobl, F. Maglia, C. Stinner and H. A. Gasteiger, Temperature Dependence of Oxygen Release from LiNi 0.6 Mn 0.2 Co 0.2 O 2 (NMC622) Cathode Materials for Li-Ion Batteries, J. Electrochem. Soc., 2018, 165, A2869–A2879.
59. J. A. Gilbert, I. A. Shkrob and D. P. Abraham, Transition Metal Dissolution, Ion Migration, Electrocatalytic Reduction and Capacity Loss in Lithium-Ion Full Cells, J. Electrochem. Soc., 2017, 164, A389–A399.
60. S. Komaba, B. Kaplan, T. Ohtsuka, Y. Kataoka, N. Kumagai and H. Groult, Inorganic electrolyte additives to suppress the degradation of graphite anodes by dissolved Mn(II) for lithium-ion batteries, J. Power Sources, 2003, 119–121, 378–382.
61. A. Blyr, C. Sigala, G. Amatuc, D. Guyornard, Y. Chabre and J.-M. Tarascon, Self - Discharge of LiMn 2 O 4/C Li – Ion Cells in Their Discharged State: Understanding by Means of Three – Electrode Measurements Cells in Their Discharged State, J. Electrochem. Soc., 1998, 145, 194–209.
62. J. Cho and M. M. Thackeray, Structural Changes of LiMn2 O 4 Spinel Electrodes during Electrochemical Cycling, J. Electrochem. Soc., 1999, 146, 3577–3581.
63. M. Ebner, F. Marone, M. Stampanoni and V. Wood, Visualization and quantification of Electrochemical and Mechanical, Science, 2013, 342, 716–721.
64. R. Xu, Y. Yang, F. Yin, P. Liu, P. Cloetens, Y. Liu, F. Lin and K. Zhao, Heterogeneous damage in Li-ion batteries: Experimental analysis and theoretical modeling, J. Mech. Phys. Solids, 2019, 129, 160–183.
65. W. Ai, L. Kraft, J. Sturm, A. Jossen and B. Wu, Electrochemical thermal-mechanical modelling of stress inhomogeneity in lithium-ion pouch cells, J. Electrochem. Soc., 2020, 167, 013512.
66. W.-J. Zhang, A review of the electrochemical performance of alloy anodes for lithium-ion batteries, J. Power Sources, 2011, 196, 13–24.
67. B. A. Boukamp, G. C. Lesh, R. A. Huggins and J. E. Soc, All-Solid Lithium Electrodes with Mixed-Conductor Matrix, J. Electrochem. Soc., 1981, 128, 725–729.
68. X. Li, A. M. Colclasure, D. P. Finegan, D. Ren, Y. Shi, X. Feng, L. Cao, Y. Yang and K. Smith, Degradation mechanisms of high capacity 18650 cells containing Si-graphite anode and nickel-rich NMC cathode, Electrochim. Acta, 2019, 297, 1109–1120.
69. U. Kasavajjula, C. Wang and A. J. Appleby, Nano- and bulk-silicon-based insertion anodes for lithium-ion secondary cells, J. Power Sources, 2007, 163, 1003–1039.
70. J. H. Ryu, J. W. Kim, Y.-E. Sung and S. M. Oh, Failure Modes of Silicon Powder Negative Electrode in Lithium Secondary Batteries, Electrochem. Solid-State Lett., 2004, 7, A306.
71. S. Mohan, Y. Kim, J. B. Siegel, N. A. Samad and A. G. Stefanopoulou, A Phenomenological Model of Bulk Force in a Li-Ion Battery Pack and Its Application to State of Charge Estimation, J. Electrochem. Soc., 2014, 161, A2222–A2231.
72. T. Rauhala, K. Jalkanen, T. Romann, E. Lust, N. Omar and T. Kallio, Low-temperature aging mechanisms of commercial graphite/LiFePO4 cells cycled with a simulated electric vehicle load profile—A post-mortem study, J. Energy Storage, 2018, 20, 344–356.
73. F. P. McGrogan, S. N. Raja, Y.-M. Chiang and K. J. Van Vliet, Electrochemomechanical Fatigue: Decoupling Mechanisms of Fracture-Induced Performance Degradation in LiXMn2O4, J. Electrochem. Soc., 2018, 165, A2458–A2466.
74. J. Christensen and J. Newman, A Mathematical Model of Stress Generation and Fracture in Lithium Manganese Oxide, J. Electrochem. Soc., 2006, 153, A1019.
75. T. Günther, D. Schreiner, A. Metkar, C. Meyer, A. Kwade and G. Reinhart, Classification of Calendering-Induced Electrode Defects and Their Influence on Subsequent Processes of Lithium-Ion Battery Production, Energy Technol., 2020, 8, 1900026.
76. P. Zuo and Y.-P. Zhao, A phase field model coupling lithium diffusion and stress evolution with crack propagation and application in lithium ion batteries, Phys. Chem. Chem. Phys., 2015, 17, 287–297.
77. X. H. Liu, L. Zhong, S. Huang, S. X. Mao, T. Zhu and J. Y. Huang, Size-dependent fracture of silicon nanoparticles during lithiation, ACS Nano, 2012, 6, 1522–1531.
78. I. Laresgoiti, S. Käbitz, M. Ecker and D. U. Sauer, Modeling mechanical degradation in lithium ion batteries during cycling: Solid electrolyte interphase fracture, J. Power Sources, 2015, 300, 112–122.
79. J. P. Maranchi, A. F. Hepp, A. G. Evans, N. T. Nuhfer and P. N. Kumta, Interfacial Properties of the a-Si/Cu:Active–Inactive Thin-Film Anode System for Lithium-Ion Batteries, J. Electrochem. Soc., 2006, 153, A1246.
80. H. Wu, G. Chan, J. W. Choi, I. Ryu, Y. Yao, M. T. Mcdowell, S. W. Lee, A. Jackson, Y. Yang, L. Hu and Y. Cui, Stable cycling of double-walled silicon nanotube battery anodes through solid-electrolyte interphase control, Nat. Nanotechnol., 2012, 7, 310–315.
81. R. D. Deshpande and D. M. Bernardi, Modeling Solid-Electrolyte Interphase (SEI) Fracture: Coupled Mechanical/Chemical Degradation of the Lithium Ion Battery, J. Electrochem. Soc., 2017, 164, A461–A474.
82. S. Müller, P. Pietsch, B. E. Brandt, P. Baade, V. De Andrade, F. De Carlo and V. Wood, Quantification and modeling of mechanical degradation in lithium-ion batteries based on nanoscale imaging, Nat. Commun., 2018, 9, 1–8.
83. E. Peled, The Electrochemical Behavior of Alkali and Alkaline Earth Metals in Nonaqueous Battery Systems—The Solid Electrolyte Interphase Model, J. Electrochem. Soc., 1979, 126, 2047.
84. E. Peled and S. Menkin, Review—SEI: Past, Present and Future, J. Electrochem. Soc., 2017, 164, A1703,  DOI:10.1149/2.1441707jes.
85. X. Lin, J. Park, L. Liu, Y. Lee, W. Lu and A. M. Sastry, A Comprehensive Capacity Fade Model and Analysis for Li-Ion Batteries, J. Electrochem. Soc., 2013, 160, A1701–A1710.
86. I. A. Hunt, Y. Zhao, Y. Patel and J. Offer, Surface Cooling Causes Accelerated Degradation Compared to Tab Cooling for Lithium-Ion Pouch Cells, J. Electrochem. Soc., 2016, 163, A1846–A1852.
87. J. E. Harlow, X. Ma, J. Li, E. Logan, Y. Liu, N. Zhang, L. Ma, S. L. Glazier, M. M. E. Cormier, M. Genovese, S. Buteau, A. Cameron, J. E. Stark and J. R. Dahn, A Wide Range of Testing Results on an Excellent Lithium-Ion Cell Chemistry to be used as Benchmarks for New Battery Technologies, J. Electrochem. Soc., 2019, 166, A3031–A3044.
88. M. Dubarry, N. Vuillaume and B. Y. Liaw, From single cell model to battery pack simulation for Li-ion batteries, J. Power Sources, 2009, 186, 500–507.
89. Y. Zhang, X. Li, L. Su, Z. Li, B. Y. Liaw and J. Zhang, Lithium Plating Detection and Quantification in Li-Ion Cells from Degradation Behaviors, ECS Trans., 2017, 75, 37–50.
90. S. E. J. O’Kane, I. D. Campbell, M. W. J. Marzook, G. J. Offer and M. Marinescu, Physical Origin of the Differential Voltage Minimum Associated with Lithium Plating in Li-Ion Batteries, J. Electrochem. Soc., 2020, 167, 090540.
91. D. Anseán, M. Dubarry, A. Devie, B. Y. Liaw, V. M. García, J. C. Viera and M. González, Operando lithium plating quantification and early detection of a commercial LiFePO4 cell cycled under dynamic driving schedule, J. Power Sources, 2017, 356, 36–46.
92. H. Konishi, T. Yuasa and M. Yoshikawa, Thermal stability of Li1-yNixMn (1-x)/2Co(1-x)/2O2 layer-structured cathode materials used in Li-Ion batteries, J. Power Sources, 2011, 196, 6884–6888.
93. H. Arai, S. Okada, Y. Sakurai and J. I. Yamaki, Thermal behavior of Li1-yNiO2 and the decomposition mechanism, Solid State Ionics, 1998, 109, 295–302.
94. I. Belharouak, D. Vissers and K. Amine, Thermal Stability of the Li(Ni[sub 0.8]Co[sub 0.15]Al[sub 0.05])O[sub 2] Cathode in the Presence of Cell Components, J. Electrochem. Soc., 2006, 153, A2030.
95. H. Zheng, Q. Sun, G. Liu, X. Song and V. S. Battaglia, Correlation between dissolution behavior and electrochemical cycling performance for LiNi1/3Co1/3Mn1/3O2-based cells, J. Power Sources, 2012, 207, 134–140.
96. A. Banerjee, Y. Shilina, B. Ziv, J. M. Ziegelbauer, S. Luski, D. Aurbach and I. C. Halalay, On the oxidation state of manganese ions in li-ion battery electrolyte solutions, J. Am. Chem. Soc., 2017, 139, 1738–1741.
97. S. Muto, Y. Sasano, K. Tatsumi, T. Sasaki, K. Horibuchi, Y. Takeuchi and Y. Ukyo, Capacity-Fading Mechanisms of LiNiO2-Based Lithium-Ion Batteries, J. Electrochem. Soc., 2009, 156, A371.
98. D. P. Abraham, R. D. Twesten, M. Balasubramanian, I. Petrov, J. McBreen and K. Amine, Surface changes on LiNi0.8Co0.2O2 particles during testing of high-power lithium-ion cells, Electrochem. Commun., 2012, 4, 620–625.
99. K. P. C. Yao, J. S. Okasinski, K. Kalaga, J. D. Almer and D. P. Abraham, Operando Quantification of (De)Lithiation Behavior of Silicon–Graphite Blended Electrodes for Lithium-Ion Batteries, Adv. Energy Mater., 2019, 9, 1803380.
100. S. Kalnaus, K. Rhodes and C. Daniel, A study of lithium ion intercalation induced fracture of silicon particles used as anode material in Li-ion battery, J. Power Sources, 2011, 196, 8116–8124.
101. J. Cannarella and C. B. Arnold, State of health and charge measurements in lithium-ion batteries using mechanical stress, J. Power Sources, 2014, 269, 7–14.
102. X. Cheng and M. Pecht, In situ stress measurement techniques on li-ion battery electrodes: A review, Energies, 2017, 10, 1–19.
103. L. S. de Vasconcelos, N. Sharma, R. Xu and K. Zhao, In-Situ Nanoindentation Measurement of Local Mechanical Behavior of a Li-Ion Battery Cathode in Liquid Electrolyte, Exp. Mech., 2019, 59, 337–347.
104. J. M. Lim, T. Hwang, D. Kim, M. S. Park, K. Cho and M. Cho, Intrinsic Origins of Crack Generation in Ni-rich LiNi0.8Co0.1Mn0.1O2 Layered Oxide Cathode Material, Sci. Rep., 2017, 7, 2–11.
105. S. Atlung, K. West and T. Jacobsen, Dynamic Aspects of Solid Solution Cathodes for Electrochemical Power Sources, J. Electrochem. Soc., 1979, 126, 1311–1321.
106. G. J. Plett, ECE4710/5710: Modeling, Simulation, and Identification of Battery Dynamics, Colorado Springs, 2019.
107. Y. H. Chiang, W. Y. Sean and J. C. Ke, Online estimation of internal resistance and open-circuit voltage of lithium-ion batteries in electric vehicles, J. Power Sources, 2011, 196, 3921–3932.
108. X. Hu, S. Li and H. Peng, A comparative study of equivalent circuit models for Li-ion batteries, J. Power Sources, 2012, 198, 359–367.
109. W. He, M. Pecht, D. Flynn and F. Dinmohammadi, A physics-based electrochemical model for lithium-ion battery state-of-charge estimation solved by an optimised projection-based method and moving-window filtering, Energies, 2018, 11, 1–24.
110. D. D. MacDonald, Reflections on the history of electrochemical impedance spectroscopy, Electrochim. Acta, 2006, 51, 1376–1388.
111. D. Klotz, D. S. Ellis, H. Dotan and A. Rothschild, Empirical: In operando analysis of the charge carrier dynamics in hematite photoanodes by PEIS, IMPS and IMVS, Phys. Chem. Chem. Phys., 2016, 18, 23438–23457.
112. D. E. Galvez-Aranda, A. Verma, K. Hankins, J. M. Seminario, P. P. Mukherjee and P. B. Balbuena, Chemical and mechanical degradation and mitigation strategies for Si anodes, J. Power Sources, 2019, 419, 208–218.
113. R. Hausbrand, G. Cherkashinin, H. Ehrenberg, M. Gröting, K. Albe, C. Hess and W. Jaegermann, Fundamental degradation mechanisms of layered oxide Li-ion battery cathode materials: Methodology, insights and novel approaches, Mater. Sci. Eng. B, 2015, 192, 3–25.
114. M. Doyle, T. F. Fuller and J. Newman, Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell, J. Electrochem. Soc., 1993, 140, 1526–1533.
115. T. F. Fuller, M. Doyle and J. Newman, Simulation and Optimization of the Dual Lithium Ion Insertion Cell, J. Electrochem. Soc., 1994, 141, 1–10.
116. S. G. Marquis, V. Sulzer, R. Timms, C. P. Please and S. J. Chapman, An Asymptotic Derivation of a Single Particle Model with Electrolyte, J. Electrochem. Soc., 2019, 166, A3693–A3706.
117. G. Richardson, I. Korotkin, R. Ranom, M. Castle and J. M. Foster, Generalised single particle models for high-rate operation of graded lithium-ion electrodes: Systematic derivation and validation, Electrochim. Acta, 2020, 339, 135862.
118. D. Zhang, B. N. Popov and R. E. White, Modeling Lithium Intercalation of a Single Spinel Particle under Potentiodynamic Control, J. Electrochem. Soc., 2000, 147, 831.
119. E. Prada, D. Di Domenico, Y. Creff, J. Bernard, V. Sauvant-Moynot and F. Huet, Simplified Electrochemical and Thermal Model of LiFePO 4 -Graphite Li-Ion Batteries for Fast Charge Applications, J. Electrochem. Soc., 2012, 159, A1508–A1519.
120. P. Kemper and D. Kum, 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), IEEE, 2013, pp. 1–6.
121. J. Li, K. Adewuyi, N. Lotfi, R. G. Landers and J. Park, A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation, Appl. Energy, 2018, 212, 1178–1190.
122. L. Zhang, L. Wang, C. Lyu, J. Li and J. Zheng, Non-destructive analysis of degradation mechanisms in cycle-aged graphite/LiCoO2 batteries, Energies, 2014, 7, 6282–6305.
123. B. Y. Liaw, R. G. Jungst, G. Nagasubramanian, H. L. Case and D. H. Doughty, Modeling capacity fade in lithium-ion cells, J. Power Sources, 2005, 140, 157–161.
124. A. Cordoba-Arenas, S. Onori, Y. Guezennec and G. Rizzoni, Capacity and power fade cycle-life model for plug-in hybrid electric vehicle lithium-ion battery cells containing blended spinel and layered-oxide positive electrodes, J. Power Sources, 2015, 278, 473–483.
125. J. Kim and B. H. Cho, State-of-charge estimation and state-of-health prediction of a Li-Ion degraded battery based on an EKF combined with a per-unit system, IEEE Trans. Veh. Technol., 2011, 60, 4249–4260.
126. M. Fleckenstein, O. Bohlen and B. Bäker, Aging effect of temperature gradients in Li-ion cells experimental and simulative investigations and the consequences on thermal battery management, World Electr. Veh. J., 2012, 5, 322–333.
127. P. Arora, Mathematical Modeling of the Lithium Deposition Overcharge Reaction in Lithium-Ion Batteries Using Carbon-Based Negative Electrodes, J. Electrochem. Soc., 1999, 146, 3543.
128. A. Jana, G. M. Shaver and R. E. García, Physical, on the fly, capacity degradation prediction of LiNiMnCoO2-graphite cells, J. Power Sources, 2019, 422, 185–195.
129. A. Ghosh, J. M. Foster, G. J. Offer and A. Marinescu, Shrinking-Core Model for the Degradation of High-Nickel Cathodes (NMC811) in Li-Ion Batteries: Passivation Layer Growth and Oxygen Evolution, J. Electrochem. Soc., 2021, 168, 020509,  DOI:10.1149/1945-7111/abdc71.
130. Y. Dai, L. Cai and R. E. White, Capacity Fade Model for Spinel LiMn2O4 Electrode, J. Electrochem. Soc., 2013, 160, A182–A190.
131. M. Otero, C. Heim, E. P. M. Leiva, N. Wagner and A. Friedrich, Design-Considerations regarding Silicon/Graphite and Tin/Graphite Composite Electrodes for Lithium-Ion Batteries, Sci. Rep., 2018, 8, 1–10.
132. V. A. Sethuraman, V. Srinivasan, A. F. Bower and P. R. Guduru, In Situ Measurements of Stress-Potential Coupling in Lithiated Silicon, J. Electrochem. Soc., 2010, 157, A1253.
133. J. Li, R. G. Landers and J. Park, A comprehensive single-particle-degradation model for battery state-of-health prediction, J. Power Sources, 2020, 456, 227950,  DOI:10.1016/j.jpowsour.2020.227950.
134. X. Jin, A. Vora, V. Hoshing, T. Saha, G. Shaver, O. Wasynczuk and S. Varigonda, Applicability of available Li-ion battery degradation models for system and control algorithm design, Control Eng. Pract., 2018, 71, 1–9.
135. J. Keil and A. Jossen, Electrochemical Modeling of Linear and Nonlinear Aging of Lithium-Ion Cells, J. Electrochem. Soc., 2020, 167, 110535.
136. C. Wei, S. Xia, H. Huang, Y. Mao, P. Pianetta and Y. Liu, Mesoscale Battery Science: The Behavior of Electrode Particles Caught on a Multispectral X-ray Camera, Acc. Chem. Res., 2018, 51, 2484–2492.
137. Z. Jiang, J. Li, Y. Yang, L. Mu, C. Wei, X. Yu, P. Pianetta, K. Zhao, P. Cloetens, F. Lin and Y. Liu, Machine-learning-revealed statistics of the particle-carbon/binder detachment in lithium-ion battery cathodes, Nat. Commun., 2020, 11, 2310.
138. A. Gayon-Lombardo, L. Mosser, N. P. Brandon and S. J. Cooper, Pores for thought: generative adversarial networks for stochastic reconstruction of 3D multi-phase electrode microstructures with periodic boundaries, npj Comput. Mater., 2020, 6, 1–11.
139. X. Gao, X. Liu, R. He, M. Wang, W. Xie, N. P. Brandon, B. Wu, H. Ling and S. Yang, Designed high-performance lithium-ion battery electrodes using a novel hybrid model-data driven approach, Energy Storage Mater., 2021, 36, 435–458.
140. B. Wu, W. D. Widanage, S. Yang and X. Liu, Battery digital twins: Perspectives on the fusion of models, data and artificial intelligence for smart battery management systems, Energy and AI, 2020, 1, 100016.
141. S. J. Kwon, D. Han, J. H. Choi, J. H. Lim, S. E. Lee and J. Kim, Remaining-useful-life prediction via multiple linear regression and recurrent neural network reflecting degradation information of 20Ah LiNi_xMn_yCo_1−x−yO₂ pouch cell, J. Electroanal. Chem., 2020, 858, 113729.
142. K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring, D. Fraggedakis, M. Z. Bazant, S. J. Harris, W. C. Chueh and R. D. Braatz, Data-driven prediction of battery cycle life before capacity degradation, Nat. Energy, 2019, 4, 383–391.
143. Y. Zhang, Q. Tang, Y. Zhang, J. Wang, U. Stimming and A. A. Lee, Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning, Nat. Commun., 2020, 11, 6–11.
144. A. Torayev, P. C. M. M. Magusin, C. P. Grey, C. Merlet and A. A. Franco, Text mining assisted review of the literature on Li–O₂ batteries, J. Phys.: Mater., 2019, 2, 044004.
145. D. P. Finegan, J. Zhu, X. Feng, M. Keyser, M. Ulmefors, W. Li, M. Z. Bazant and S. J. Cooper, The Application of Data-Driven Methods and Physics-Based Learning for Improving Battery Safety, Joule, 2021, 5, 316–329.

---