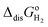The energetics of electron and proton transfer to CO2 in aqueous solution
Received
22nd June 2021
, Accepted 20th September 2021
First published on 21st September 2021
Abstract
The electrocatalytic reduction of CO2 is considered an effective method to reduce CO2 emissions and achieve electrical/chemical energy conversion. It is crucial to determine the reaction mechanism so that the key reaction intermediates can be targeted and the overpotential lowered. The process involves the interaction with the electrode surface and with species, including the solvent, at the electrode-electrolyte interface, and it is therefore not easy to separate catalytic contributions of the electrode from those of the electrolyte. We have used density functional theory-based molecular dynamics to calculate the Gibbs free energy of the proton and electron transfer reactions corresponding to each step in the electroreduction of CO2 to HCOOH in aqueous media. The results show thermodynamic pathways consistent with the mechanism proposed by Hori. Since electrodes are not included in this work, differences between the calculated results and the experimental observations can help determine the catalytic contribution of the electrode surface.
1. Introduction
CO2 is a linear and centrosymmetric molecule with two identical C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. The thermodynamic cell potentials for the decomposition of CO2 to CO and O2 (eqn (1)) and for its reaction with H2O to produce HCOOH and O2 (eqn (2)) are 1.33 and 1.43 V, respectively:
O bonds. The thermodynamic cell potentials for the decomposition of CO2 to CO and O2 (eqn (1)) and for its reaction with H2O to produce HCOOH and O2 (eqn (2)) are 1.33 and 1.43 V, respectively:| | | 2CO2 → 2CO + O2 (ECell = 1.33 V) | (1) |
| | | 2CO2 + 2H2O → 2HCOOH + O2 (ECell = 1.43 V) | (2) |
This implies that the equilibrium potential for the reduction of CO2 to either CO or HCOOH is only 0.1 and 0.2 V more negative, respectively, than that required for hydrogen evolution (ECell = 1.23 V).1 However, the onset potential of CO2 electroreduction in aqueous solution2 often requires very negative (>1 V) overpotentials, and it depends on the electrode material. The first electron transfer step:| | | CO2(aq) + e− → CO2−(aq) | (3) |
is currently believed to be the bottleneck in reducing CO2 to other chemicals, because the equilibrium potential of this reaction is very negative. ca. −1.9 V vs. SHE3 (although pH independent and therefore closer to hydrogen evolution in neutral or alkaline media as compared to acidic). An adequate electrode material can help stabilize the key intermediate CO2− and reduce the apparent energy barrier for the overall reaction.
The mechanism of the reduction of CO2 to HCOOH is still controversial after more than 40 years of study.4–15 Hori and co-workers1,2 suggested that CO2− adsorbs on the electrode surface through its carbon atom, and that whether CO or HCOOH is the final product of the 2-electron reduction depends on the corresponding adsorption energy. Fig. 1 is an illustration of these two reaction pathways. On the contrary, according to Koper and co-workers16 HCOOH is the product when CO2− is adsorbed through its two oxygen atoms, whereas CO would be produced if adsorption occurs through the carbon atom of CO2−. A related transformation mechanism of monodentate HCOO* (i.e., one oxygen atom bonds to the surface) to bidentate HCOO* (i.e., two oxygen atoms bond to the surface) was also proposed recently.8 Interestingly, this is reminiscent of the mechanism by which, as recently demonstrated,17–19 formic acid is dehydrated to adsorbed CO on Pt electrodes. However, despite considerable efforts using the most advanced experimental techniques, the challenging nature of characterizing interfaces at the atomic level makes a comprehensive understanding of reaction pathways based exclusively on experimental results a nearly impossible task.
 |
| | Fig. 1 Reaction mechanism of the electroreduction of CO2 in the bulk of an aqueous medium and at the metal/water interface. Proposed by Hori.1 | |
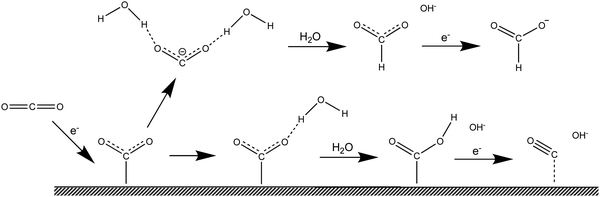
Computational simulations are a suitable alternative, and have proven to be able to successfully predict catalytic effects and reaction pathways.20–24 However, electrochemical reactions are complex, not least because they occur at the interface between a solid and a liquid, and, therefore, simulations require approximations. The common approach is to build a surface model and then add a solvation environment around the electrode, as illustrated in Fig. 2, steps 1 and 2. In Fig. 2 we have divided the process leading to the simulation of a complete electrochemical system into four stages, namely, (i) simulating the reaction in the gas phase, (ii) adding the electrode surface, (iii) adding the liquid phase and (iv) assembling of these elements together to simulate the electrochemical reaction. Simulating the reaction in the gas phase is obviously the simplest stage, but it differs enormously from the conditions under which electrochemical reactions proceed. Step 1 in Fig. 2 corresponds to adding a surface to stage-1 simulations to compute reactions at the solid gas interface, which allows to elucidate the surface catalytic effect. Step 2 involves additionally including the liquid phase, whereby solvation effects on the reactants, products and intermediates, as well as the effect of the interaction of solvent and, eventually, the supporting electrolyte, with the electrode surface can be included and analyzed. Alternatively, steps 3 and 4 allow to first isolate the effect of solvation and then estimate the surface effect in the electrocatalytic reaction. In computation, the surface effect in step 1 and the solvation effect in step 3 can be obtained more accurately than in steps 4 and 2, respectively. Because the conditions in steps 2 and 4 are introduced on the basis of the previous stages, the step 1–step 2 sequence is good at predicting reactions in which the surface effect is the main contribution to catalysis, whereas the step 3–step 4 sequence allows more accurate insight into the catalytic contribution of the solvent.
 |
| | Fig. 2 Schematic illustration of simulation protocols that can be employed in the study of electrochemical reactions. | |
Arguably, if our final goal is to screen electrode materials, it is better to use the step 3–step 4 sequence as the simulation protocol, because the result in step 3 is constant, and can be used as a reference state, which is consistent with the idea of a control experiment. Otherwise, when changing the electrode material both the free energy of step 1 and the solvation effect in step 2 will vary. Furthermore, the reference state when using the step 1–step 2 simulation protocol is the gas phase, much more distant from electrochemical conditions than the liquid phase. By comparison, if our goal is to screen the electrolyte, the simulation protocol composed of steps 1 and 2 would be preferred. The work by Kim and co-workers22 is a good example of the use of the step 1–step 2 sequence to screen the electrolyte medium. They calculated the free energies of adsorbed intermediates *CO2, *COOH and *CO in both aqueous solution and 1-ethyl-3-methylimidazolium tetrafluoroborate (EMIM-BF4)/water mixtures. Thus, the electrode surface is constant and so is the free energy of the surface effect in step 1. They found that in EMIM-BF4/water mixtures, the overpotential for the reduction of CO2 to CO can be decreased by 0.31 V compared with aqueous solutions.
Since the mechanism of the reduction of CO2 to HCOOH in aqueous medium is still controversial, we plan to study this reaction using the simulation protocol composed of steps 3 and 4. The first step is to obtain all reaction pathways in the liquid phase. Insight into the reaction pathway can be obtained from studying the energies associated to all the possible electron and proton transfer processes (i.e., their equilibrium potentials and pKa values, respectively) that can follow the formation of the CO2− radical. The experimental determination of the equilibrium potential and pKa values of electron and proton transfer events, respectively, that can occur after the formation of CO2− is extremely challenging, when not outright impossible, computation being therefore the most convenient approach.25–28
Computation methods based on continuum models, such as the polarizable continuum model (PCM)29 and the self-consistent continuum model (SCCS)27 to reproduce the liquid environment have successfully been employed to calculate equilibrium potentials and acidity constants in aqueous solutions.30,31 Alternatively, the solvent environment can be described by explicit solvent molecules, which can reproduce the hydrogen-bond network in solutions. This hydrogen-bond network plays an important role in stabilizing intermediates such as the CO2− radical, and adequately reproducing it is therefore crucial for the accurate computation of equilibrium potentials and acidity constants.22 It is common for this purpose to use density functional theory-based molecular dynamics (DFT-MD) under periodic boundary conditions (PBC) to reproduce accurate solvation structures.25,32–35 DFT-MD treats both the solute and solvent molecules at the same level of electronic structure theory, where energies and forces are calculated from first principles. The PBC replicates the unit cell periodically, such that sufficient solvent molecules are included to reproduce the solution environment in the simulation model. Accurate solvation free energies can be calculated with DFT-MD by using various free energy calculation schemes, such as thermodynamic integration (TI), which can calculate the free energy difference between the initial state and the final state (details are explained in the Methods section). TI can also be applied to compute ionization and deprotonation energies, however, the values obtained are different from the adiabatic ionization energies (AIP) and adiabatic deprotonation energies (ADP), because of the uncertainty of the electrostatic potential reference for the charged system in the standard Ewald summation under PBC. Cheng and Sprik25,35–38 developed a computational SHE method that can align the reference electrostatic potential to the SHE. The method was successfully applied to calculate equilibrium potentials and acidity constants using DFT-MD, including the CO2/CO2− equilibrium potential and the pKa of HCOOH. Equilibrium potentials were aligned to the SHE with a mean error of about 0.5 V, and the uncertainty of the acidity constants is 1–2 pKa units.35 The large error in the calculation of redox potentials is due to the delocalization error in DFT approximations using the GGA functional, and can be reduced to 0.2 V if the HSE06 functional is employed.
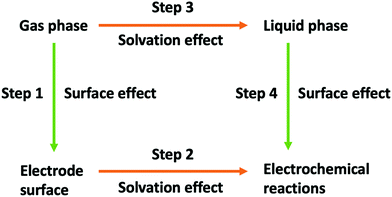
The aim of this work is to find the reaction pathway for the reduction of CO2 to HCOOH in the absence of any electrode catalytic effect. The conversion of CO2 to HCOOH involves two proton-coupled electron transfer (PCET) events. The possible reaction pathways studied in this work are presented in Fig. 3, which closely follows the mechanism proposed by Hori1 and illustrated in Fig. 1. We use Cheng et al.'s computational SHE method combining DFT-MD and TI to calculate the equilibrium potentials and acidity constants of each electron and proton transfer, respectively, in Fig. 3. Based on Hess's law, a self-consistency test is also introduced by comparing the difference between the sum of deprotonation and oxidation free energies with the calculated dehydrogenation free energies.
 |
| | Fig. 3 Possible reaction pathways for the electroreduction of CO2 to formic acid in aqueous solution. Red arrows correspond to the transfer of one electron, green arrows correspond to the transfer of a proton, and blue arrows correspond to the transfer of a hydrogen atom (i.e., to the simultaneous transfer of an electron and a proton). | |
2. Methods
2.1 Thermodynamic integration
The TI method is one of several computational schemes for the calculation of free energy differences between two states. In this method, two states are connected by a linear combination through a coupling parameter, η (η ∈ [0,1]). Thus, a thermodynamic path (η from 0 to 1) between two states is constructed, where the two ends of the path (η = 0 and 1) correspond to the initial and final states, respectively. A fictitious hybrid energy state can be defined as Eη = (1 − η)E0 + ηE1, with E0 and E1 the energy of the initial and final states, respectively. The derivative of Eη with respect to the coupling parameter corresponds to the energy difference between the final and initial states at a fixed configuration 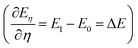 . ΔE is the vertical energy gap and can be obtained from the electronic structure calculation as a total energy difference. ΔE is then averaged over molecular dynamics (MD) runs for a sequence of values of η. Integration of the thermal average 〈ΔE〉η along the thermodynamic path (η from 0 to 1) converts vertical into adiabatic free energies:
. ΔE is the vertical energy gap and can be obtained from the electronic structure calculation as a total energy difference. ΔE is then averaged over molecular dynamics (MD) runs for a sequence of values of η. Integration of the thermal average 〈ΔE〉η along the thermodynamic path (η from 0 to 1) converts vertical into adiabatic free energies:| | 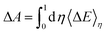 | (4) |
In practice, this ΔE is averaged over the MD trajectory corresponding to an η value. The numerical integration in eqn (4) is achieved by sampling a sequence of numerical integration points η. Simpson's rule gives a good approximation for three integration points (η = 0,0.5,1) calculations:| | 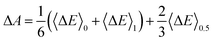 | (5) |
If the 〈ΔE〉0.5 significantly deviates from the midpoint between 〈ΔE〉0 and 〈ΔE〉1, more integration points are required and the general trapezium rule for the N point integration is employed:32–34,39| | 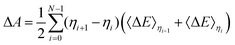 | (6) |
2.2 Free energy calculations
We use a generic redox couple X−/X in an aqueous solution to introduce the computation of electron-transfer free energies. Using the TI method, the free energy of oxidation (reduction) from X− to X can be obtained by reversibly removing (inserting) an electron from the DFT-MD simulation under PBC. However, directly inserting an electron in a PBC system charges the system and, due to the standard Ewald summation under PBC, renders the reference for the electrostatic potential uncertain. Please note that there is a field in the system due to the background charge,40 and this field can cause strong interactions with water molecules, because water molecules have a large dipole moment. The interaction can affect solvation structures during the simulation. However, the structural change caused by the field has little effect on the potential energy.32–34 The electrostatic potential of the charged system has a potential shift V0,X−/X compared to the neutral system.32 Therefore, the oxidation free energy ΔA obtained from eqn (4) does not correspond to the adiabatic ionization free energy (AIP), by a difference equal to qX−/X·V0,X−/X. The AIP can therefore be obtained from eqn (7), where qX−/X = −1 is the total charge difference between the initial and final states.| | 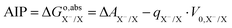 | (7) |
Please note that we are ignoring the difference between the Helmholtz and Gibbs free energies (ΔA and ΔG, respectively), which is negligible for condensed phases under ambient pressure.35
The computation of proton-transfer free energies is slightly more complicated. In this case, TI requires to reversibly insert or remove a proton in the system. The insertion of electrons in the simulation can be automatically localized in the lowest state thanks to the SCF convergence. However, protons cannot be automatically located in the simulation. Therefore, when conducting simulations for deprotonation reactions, the proton is not simply removed from the system in each MD step, but replaced by a classical dummy at the same location. The dummy has neither coulombic nor van der Waals interactions with other molecules, which implies that it can be anywhere within the system during the simulation. This can lead to unphysical configurations of the solute in the solvent, including overlap with other molecules, deeming computation impossible. A conventional approach to avoid this problem is to apply a harmonic restraining potential on the dummy.33 For example, to compute the solvation energy of a proton, the dummy is bonded with a water molecule in a hydronium-like structure.34
In summary, to calculate the free energy of moving a proton from HX molecule in the solution to the gas phase, we need four steps.35 First, TI is used to calculate the deprotonation energy, ΔAHX/X−. Here, the proton on the HX molecule is replaced with a dummy, and the new molecule is denoted as dX−. Then, we estimate the zero-point energy of the ground state H–X vibration (ΔEH(X)), and add the free energy of the proton in the gas phase, i.e., the translational energy (kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3), with Λ the thermal de Broglie wavelength of the proton, kB the Boltzmann constant, and T the temperature in Kelvin) of the monoatomic gas in equilibrium with a standard concentration in the solution (co = 1 M). Finally, as in eqn (7), the energy correction qHX/X−·V0,HX/X− needs to be included due to the uncertain reference of electrostatic potential in the charged system (the dX− molecule). Therefore, the free energy of transferring a proton from HX to the gas phase can be written as:
ln(coΛ3), with Λ the thermal de Broglie wavelength of the proton, kB the Boltzmann constant, and T the temperature in Kelvin) of the monoatomic gas in equilibrium with a standard concentration in the solution (co = 1 M). Finally, as in eqn (7), the energy correction qHX/X−·V0,HX/X− needs to be included due to the uncertain reference of electrostatic potential in the charged system (the dX− molecule). Therefore, the free energy of transferring a proton from HX to the gas phase can be written as:
| | 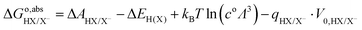 | (8) |
2.3 Computational SHE
The energy correction term q·V0 in eqn (7) and (8) is unknown. This term is a collective effect due to all molecules in the unit cell and therefore attains different values in different simulations but, for the same system, and as long as the same PBC is used, V0 is constant.41 If the hydronium ion (H3O+) is considered as the structure of solvated proton in the aqueous solution, the free energy to remove the proton from aqueous solution is:| | 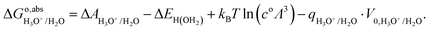 | (9) |
However, the solvated proton has many conformations and can transfer between water molecules. Using hydronium as the conformation of the solvated proton makes the solvated proton lose the translational energy. Here we closely follow Costanzo et al.'s34 theory of the actual work function of the proton, described by the process in eqn (10),| | | H2O(l) + H+(aq) → H3O+(aq) → H2O(l) + H+(g) | (10) |
is given by eqn (11):| | 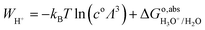 | (11) |
Replacing 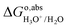 in eqn (11) by eqn (9), the term of proton translational energy, −kBT
in eqn (11) by eqn (9), the term of proton translational energy, −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3), is cancelled, yielding:
ln(coΛ3), is cancelled, yielding:| | | WH+ = ΔAH3O+/H2O − ΔEH(OH2) − qH3O+/H2O·V0,H3O+/H2O | (12) |
Here, qH3O+/H2O = 1 is the total charge difference between the H3O+ unit cell and H2O unit cell, and V0,H3O+/H2O has the same value as V0,HX/X− and V0,X−/X if the same system is employed.
The actual reaction of deprotonation free energy of HX in the aqueous solution is:34
| | | H2O(l) + HX(aq) → X−(aq) + H2O(l) + H+(aq) | (13) |
However,
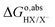
as calculated with
eqn (8) only includes the free energy of transferring the proton from aqueous HX to the gas phase. The full reaction can be achieved if we add the reverse of
eqn (10)–(13),
i.e., if we subtract from
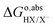
the work function of the proton:
35| | 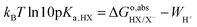 | (14) |
The equilibrium potential of the X
−/X couple with respect to the vacuum can be converted to the SHE scale by adding the reaction free energy of
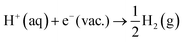
. The free energy of this reaction is the sum of the work function of the solvated proton (
eqn (10)) plus the reaction free energy of
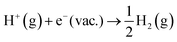
. The former can be calculated by using
eqn (11), and the latter is the sum of the negative ionization energy of hydrogen atom (−
EIE) plus the negative of half the dissociation energy of hydrogen
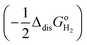
.
35 Therefore, the redox potential of X
−/X couple with respect to the SHE can be calculated as:
| | 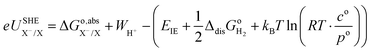 | (15) |
where the standard state compression term,
kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln(
RT·
co/
po), is added to the gas phase standard Gibbs free energies,
i.e.,
EIE and
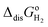
in
eqn (15). This correction term converts the free energy in standard pressure (1 bar) to the standard concentration (1 mol L
−1).
39
For the sake of clarity, thermodynamic calculation terms are not present explicitly in eqn (14) and (15). Their corresponding calculation steps are summarised in Fig. 4 as thermodynamic cycles. As can be seen in Fig. 4, the Vo terms in eqn (7)–(9) and (12) can be omitted, and the difference between zero-point energy of ground state H–X vibration (ΔEH(X)) and H–H2O vibration (ΔEH(OH2)) is ignored.39 Thus, redox potentials and acidity constants can be accurately obtained by using the following equations:
| | 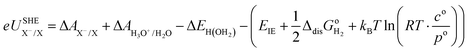 | (16) |
| | kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pKa,HX = ΔAHX/X− + kBT pKa,HX = ΔAHX/X− + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3) − ΔAH3O+/H2O ln(coΛ3) − ΔAH3O+/H2O | (17) |
To finalise this section, in the computation of a hydrogen atom transfer reaction the hydrogen atom is reversibly replaced with a dummy in the simulation model and placed in the gas phase. The calculation of Δ
AHX/X in this case is similar to the Δ
AHX/X− computation protocol, but without potential shift (
V0), because both the initial and final states are neutral (
qHX/X = 0). Hence, the Gibbs free energy of the hydrogen-atom transfer reaction is:
35| | 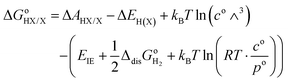 | (18) |
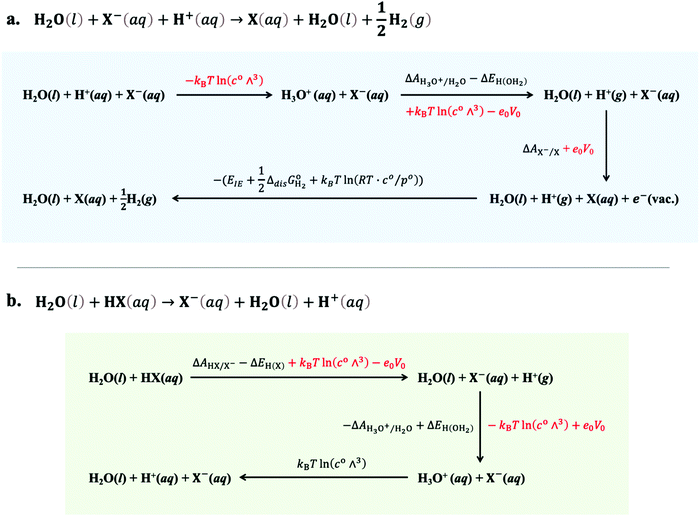 |
| | Fig. 4 Thermodynamic cycles used for the calculation of (a) the X/X− electron-transfer free energy with respect to SHE and (b) the HX/X− proton-transfer free energy in aqueous media. Energy terms in red colour are cancelled during the calculation. | |
2.4 Computational setup
All simulations were conducted using the BOMD approach, and the computational program employed was the open-source CP2K/quickstep computational chemistry package.42 The density functional implementation is based on the hybrid Gaussian plane wave scheme, which employs the Gaussian-type basis set to describe orbitals and an auxiliary plane wave basis to reexpand the electron density. The atomic basis set was a triple-ζ basis with two sets of polarization functions (TZV2P) standard basis set, and the plane wave density cut-off was set to 400 Ry. All quantum chemical calculations were performed with the Perdew–Burk–Ernzerhof (PBE) functional43 for the exchange correlation approximation, Goedecker–Teter–Hutter (GTH) pseudopotentials for the 1s electrons of O and C elements44,45 and the van der Waals correction with Grimme D3 method.46 The traditional matrix diagonalization method was replaced by the orbital transformation method for the wave function optimization.
The dimensions of the unit cell are 9.86 × 9.86 × 9.86 Å3, containing 31 water molecules and 1 reactant molecule corresponding to the ambient density. The Nose–Hoover thermostat is employed for generating the NVT ensembles, and the temperature of the system is 330 K. The time step is 0.5 fs for a good total energy conservation. The first two picoseconds are removed as the structures are not yet equilibrated, and the simulation ends when the averaged vertical energy difference, 〈ΔE〉η, is converged within 0.1 eV during the production period.
3. Results and discussion
3.1 Thermodynamic integrations
The Helmholtz free energies ΔA were obtained from eqn (4). The number of numerical integration points employed for the practical calculation depends on the position of the vertical energy gap ΔE when η = 0.5. Fig. 5 shows all results for the averaged vertical energy gap 〈ΔE〉η.
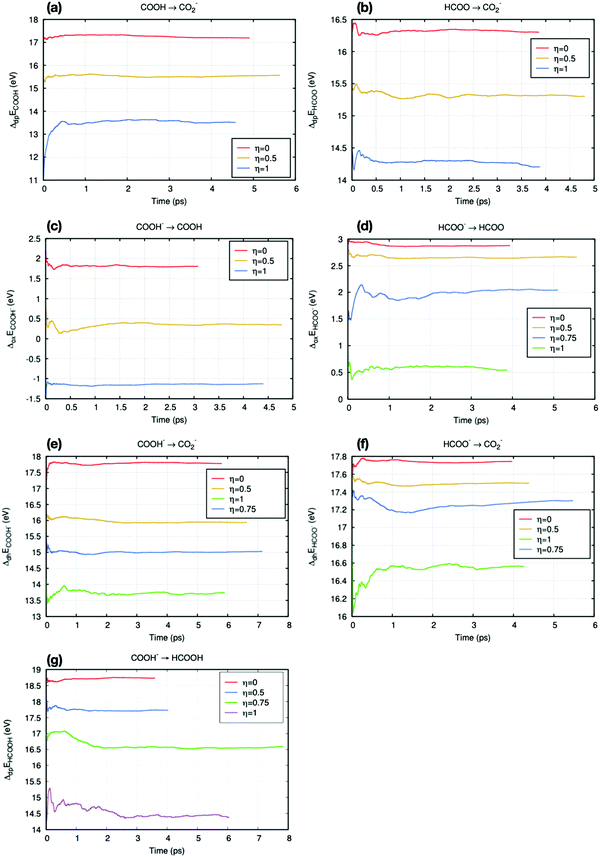 |
| | Fig. 5 Time accumulated averages of the vertical energies for all reactions in this work. (a) and (b) are deprotonation reactions. (c) and (d) are oxidation reactions. (e) and (f) are dehydrogenation reactions. All reactions involving the COOH radical (a, c and e) have been placed on the left column, while those on the right column involve the HCOO radical (b, d and f). (g) is the deprotonation reaction between formic acid and COOH−. | |
In Fig. 5(a), (c) and (d), the time accumulation averages 〈ΔE〉0.5 are close to their median value (average of two end-point values). Thus, in these reactions, Simpson's three points approximation (eqn (5)) can be employed to calculate the free energy. The other reactions, Fig. 5(b) and (e)–(g), require more numerical integration points. Thus, general trapezium rule (eqn (6)) is employed. Most vertical energy gaps were converged in 5 ps, and the fluctuation after equilibration is small (within 0.1 eV). However, some states took more than 5 ps to reach this standard, such as trajectories in Fig. 5(d) and (f). These slow convergences are mainly due to the large perturbation at the end-point of proton or electron insertion.
Some free energy results were adopted from Cheng et al.'s work35 to avoid repeating simulations and waste computational cost, such as the deprotonation free energy of hydronium (ΔAH3O+/H2O), the oxidation free energy of CO2− (ΔACO2−/CO2), and the deprotonation reaction of HCOOH/HCOO− (ΔAHCOOH/HCOO−).
3.2 Equilibrium potential and pKa results
The computed thermodynamic integrals ΔA are used to calculate oxidation (eqn (16)), deprotonation (eqn (17)), and dehydrogenation (eqn (18)) free energies. Some experimental values such as EIE and 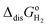 can be found in textbooks,47 and other results or correction terms like ΔEH(OH2) and kBT
can be found in textbooks,47 and other results or correction terms like ΔEH(OH2) and kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3) were adopted from Cheng et al.'s work.35 Values of all those terms together with the borrowed ΔA results are listed in Table 1, and free energy integrals ΔA for all half reactions and the corresponding thermodynamic data are summarized in Table 2.
ln(coΛ3) were adopted from Cheng et al.'s work.35 Values of all those terms together with the borrowed ΔA results are listed in Table 1, and free energy integrals ΔA for all half reactions and the corresponding thermodynamic data are summarized in Table 2.
Table 1 List of experimental results and correction terms used from other sources
| Energy terms |
Values (eV) |
Ref. |
| ΔAH3O+/H2O |
15.35 |
35
|
| ΔACO2−/CO2 |
−1.29 |
35
|
| ΔAHCOOH/HCOO− |
15.8 |
35
|
|
E
IE
|
13.62 |
47
|
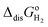
|
4.21 |
47
|
| ΔEH(OH2) |
0.35 |
35
|
k
B
T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3) ln(coΛ3) |
−0.19 |
35
|
k
B
T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(RT ln(RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) co/po) co/po) |
0.082 |
35
|
Table 2 Results of free energy integrals ΔA for all half reactions, followed by the corresponding full reaction Gibbs free energies ΔG and acidity constants pKa
| Half reactions |
ΔA (eV) |
ΔG (eV) |
pKa |
| COOH(aq) → CO2−(aq) + H+(g) |
15.49 |
−0.05 |
−0.7 |
| HCOO(aq) → CO2−(aq) + H+(g) |
15.29 |
−0.25 |
−3.9 |
| HCOOH(aq) → COOH−(aq) + H+(g) |
17.32 |
1.78 |
27.2 |
| COOH−(aq) → COOH(aq) + e−(vac.) |
0.35 |
−0.47 |
|
| HCOO−(aq) → HCOO(aq) + e−(vac.) |
2.30 |
1.49 |
|
| COOH−(aq) → CO2−(aq) + 1/2H2(g) |
15.90 |
−0.45 |
|
| HCOO−(aq) → CO2−(aq) + 1/2H2(g) |
17.40 |
1.04 |
|
A scheme illustrating the possible pathways for the reduction of CO2 to HCOOH is presented in Fig. 6. The scheme includes the equilibrium potentials for the electron transfer processes in the SHE scale and the pKa values for the proton transfer reactions. The performance of our computational SHE method can be evaluated by utilizing Hess's law to determine the free energies of the hydrogenation reactions from the computed equilibrium potentials and pKa's (values within brackets in Fig. 6) and comparing the result with the free energy of hydrogen transfer calculated using eqn (16) for self-consistency. As seen in Fig. 6, the results for the pathway from CO2− to COOH− are indeed self-consistent, the difference between the sum of the proton and electron transfer free energies, on one side, and the hydrogen-atom transfer free energy being only 0.1 eV. Regarding the pathway from CO2− to HCOO−, this difference is 0.2 eV. We attribute this difference to the statistical error in MD calculation. Since our statistical error in MD calculation is about 0.1 eV, the sum of the two results may cause the error to double. Other sources of error in this work, such as the finite size effect under PBC, the statistical error in MD calculation and the DFT error in calculating highly oxidant couples have been analysed in ref. 35, 38 and 48. Note that the DFT error in the reduction of HCOO/HCOO− could be significant compared to the redox potential of Cl− (underestimate about 0.9 V at GGA level) reported in Cheng et al.'s35 work.
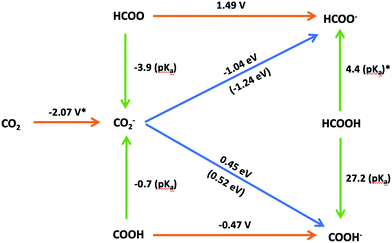 |
| | Fig. 6 Scheme of the possible reaction pathways for CO2 electroreduction to formic acid in aqueous media. The colour code for the arrows corresponding to electron, proton or hydrogen-atom transfer is the same used in Fig. 3. The equilibrium potentials for electron transfer reactions in the SHE scale are presented above the corresponding arrows. Similarly, the pKa values of proton transfer reactions and free energies in eV for hydrogen-atom reactions are presented next to the corresponding arrows. Values denoted with an asterisk (*) have been taken from ref. 35. | |
DFT-MD allows for a detailed investigation of the thermodynamic stability of the possible intermediates involved in the electroreduction of CO2 to formic acid. Interestingly, COOH is more stable in aqueous solutions than HCOO (pKa,HCOO = −3.9 < pKa,COOH = −0.7), which suggest that protonation of the CO2− radical on its carbon atom as proposed by Hori (Fig. 1) is unlikely in the absence of a catalytic effect from the electrode surface. However, if HCOO is formed it would be readily reduced, as suggested by the very positive equilibrium potential (1.49 V vs. SHE) of the HCOO/HCOO− couple. Since the CO2− radical and its conjugate acid (HCOO or COOH, denoted as HCO2) are difficult to observe in experiment, the pKa value of HCO2 is controversial.4,49–52 Considering errors in the computation, our calculated pKa,COOH is consistent with several experimental results, such as the pKa,HCO2 = −0.2 obtained by Jeevarajan et al.50 and pKa,HCO2 = 1.4 obtained by Buxton and Sellers.49 However, Janik and Tripathi52 measured a higher pKa,HCO2 value (ca. 3.4) than previous studies, which is nearly the same as the pKa of formic acid (experimental value of pKa,HCOO− is 3.7). Because the thermodynamic results in Fig. 6 suggest that, once formed HCOO can be readily reduced to formic acid, we speculate that what was actually measured in Janik and Tripathi's experiment was the acidity constant of HCOO−.
The results of this preliminary work suggest that, in the absence of a catalytic effect of the electrode surface, although protonation of the CO2− radical generated in the first reaction step on one of its oxygen atoms is preferred to protonation on its carbon atom, the very positive equilibrium potential of the HCOO/HCCO− couple makes this the thermodynamically preferred pathway to formate (eventually coupled to a proton transfer reaction to yield HCOOH if the solution pH is acidic enough), as initially proposed by Hori. As also proposed by Hori, generation of CO as the preferred product, or as the intermediate for further hydrogenation, probably requires sufficiently strong interaction of the CO2− radical with the electrode surface through the carbon atom to prevent its protonation (which would lead to formate, a dead end for further reduction). Although these conclusions had been reached in previous works, the internal and external consistency of our data prove the potential of our DFT-MD method for the calculation of free energies of electron and proton transfer reactions and, therefore, for the estimation of the most likely reaction pathways in the electrocatalytic reduction of CO2 beyond CO, as well as their potential dependence. Furthermore, because our computations have neglected any catalytic effect from the electrode, they provide an ideal starting point for screening candidates for possible electrocatalyst.
4. Summary and outlook
This work suggests an alternative approach to study catalytic effects in electrochemistry from both the electrode surface and the electrolyte. Reaction free energies in aqueous solution are obtained, which do not take into account any interaction with the electrode surface. This can be considered as a first step in trying to decompose catalytic effects among contributions of the solvent, the electrode surface and the components of the electrolyte that will then allow to screen electrode materials or the components of the electrolyte.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We are grateful for funding support from the National Natural Science Foundation of China (Grants No. 21861132015, 21991151, 21991150, 22021001 and 91745103). The support of the Leverhulme Trust (RPG-2015-0400) is gratefully acknowledged.
References
-
Y. Hori, in Modern Aspects of Electrochemistry, ed. C. G. Vayenas, R. E. White and M. E. Gamboa-Aldeco, Springer, New York, 2008, vol. 42, pp. 89–189 Search PubMed.
- Y. Hori, H. Wakebe, T. Tsukamoto and O. Koga, Electrocatalytic process of CO selectivity in electrochemical reduction of CO2 at metal electrodes in aqueous media, Electrochim. Acta, 1994, 39, 1833–1839 CrossRef CAS.
- P. S. Surdhar, S. P. Mezyk and D. A. Armstrong, Reduction potential of the carboxyl radical anion in aqueous solutions, J. Phys. Chem., 1989, 93, 3360–3363 CrossRef CAS.
- I. V. Chernyshova, P. Somasundaran and S. Ponnurangam, On the origin of the elusive first intermediate of CO2 electroreduction, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 201802256 CrossRef PubMed.
- D. C. Grills and S. V. Lymar, Radiolytic formation of the carbon dioxide radical anion in acetonitrile revealed by transient IR spectroscopy, Phys. Chem. Chem. Phys., 2018, 20, 10011–10017 RSC.
- M. Papasizza, X. Yang, J. Cheng and A. Cuesta, Electrocatalytic reduction of CO2 in neat and water-containing imidazolium-based ionic liquids, Curr. Opin. Electrochem., 2020, 23, 80–88 CrossRef CAS.
- Y. Y. Birdja, J. Shen and M. Koper, Influence of the metal center of metalloprotoporphyrins on the electrocatalytic CO2 reduction to formic acid, Catal. Today, 2017, 288, 37–47 CrossRef CAS.
- X.-G. Zhang, X. Jin, D.-Y. Wu and Z.-Q. Tian, Selective electrocatalytic mechanism of CO2 reduction reaction to CO on silver electrodes: a unique reaction intermediate, J. Phys. Chem. C, 2018, 122, 25447–25455 CrossRef CAS.
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nøskov, T. F. Jaramillo and I. Chorkendorff, Progress and perspectives of electrochemical CO2 reduction on copper in aqueous electrolyte, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed.
- A. Goyal, G. Marcandalli, V. A. Mints and M. T. M. Koper, Competition between CO2 reduction and hydrogen evolution on a gold electrode under well-defined mass transport conditions, J. Am. Chem. Soc., 2020, 142, 4154–4161 CrossRef CAS PubMed.
- S. Guo, Y. Li, L. Liu, L. Liu, X. Zhang and S. Zhang, Computational identification of a new adsorption site of CO2 on the Ag (211) surface, Chem, 2020, 5, 11503–11509 CAS.
- N. Umezawa, H. H. Kristoffersen, L. B. Vilhelmsen and B. Hammer, Reduction of CO2 with water on Pt-loaded rutile TiO2 (110) modeled with density functional theory, J. Phys. Chem. C, 2016, 120, 9160–9164 CrossRef CAS.
- A. J. Götle and M. T. M. Koper, Proton-coupled electron transfer in the electrocatalysis of CO2 reduction: prediction of sequential vs. concerted pathways using DFT, Chem. Sci., 2016, 8, 458–465 RSC.
- A. Wuttig, M. Yaguchi, K. Motobayashi, M. Osawa and Y. Surendranath, Inhibited proton transfer enhances Au-catalyzed CO2-to-fuels selectivity, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E4585–4593 CrossRef CAS PubMed.
- H. Liu, J. Xia, N. Zhang, H. Cheng, W. Bi, X. Zu, W. Chu, H. Wu, C. Wu and Y. Xie, Solid–liquid phase transition induced electrocatalytic switching from hydrogen evolution to highly selective CO2 reduction, Nat. Catal., 2021, 4, 202–211 CrossRef CAS.
- R. Kortlever, J. Shen, K. J. P. Schouten, F. Calle-Vallejo and M. T. M. Koper, Catalysts and reaction pathways for the electrochemical reduction of carbon dioxide, J. Phys. Chem. Lett., 2015, 6, 4073–4082 CrossRef CAS PubMed.
- A. Cuesta, G. Cabello, C. Gutiérrez and M. Osawa, Adsorbed formate: the key intermediate in the oxidation of formic acid on platinum electrodes, Phys. Chem. Chem. Phys., 2011, 13, 20091–20095 RSC.
- A. Cuesta, G. Cabello, M. Osawa and C. Gutiérrez, Mechanism of the electrocatalytic oxidation of formic acid on metals, ACS Catal., 2012, 2, 728–738 CrossRef CAS.
- A. Betts, V. Briega-Martos, A. Cuesta and E. Herrero, Adsorbed formate is the last common intermediate in the dual-path mechanism of the electrooxidation of formic acid, ACS Catal., 2020, 10, 8120–8130 CrossRef CAS.
- T. Cheng, H. Xiao and W. A. Goddard, Reaction mechanisms for the electrochemical reduction of CO2 to CO and formate on the Cu(100) surface at 298 K from quantum mechanics free energy calculations with explicit water, J. Am. Chem. Soc., 2016, 138, 13802–13805 CrossRef CAS PubMed.
- S. Xu and E. A. Carter, Theoretical insights into heterogeneous (photo)electrochemical CO2 reduction., Chem. Rev., 2018, 119, 6631–6669 CrossRef PubMed.
- H.-K. Lim, Y. Kwon, H. S. Kim, J. Jeon, Y.-H. Kim, J.-A. Lim, B.-S. Kim, J. Choi and H. Kim, Insight into the microenvironments of the metal–ionic liquid interface during electrochemical CO2 reduction, ACS Catal., 2018, 8, 2420–2427 CrossRef CAS.
- J. A. Gauthier, M. Fields, M. Bajdich, L. D. Chen, R. B. Sandberg, K. Chan and J. K. Nøskov, Facile electron transfer to CO2 during adsorption at the metal/solution interface, J. Phys. Chem. C, 2019, 123, 29278–29283 CrossRef CAS.
- J. Wang, T. Cheng, A. Q. Fenwick, T. N. Baroud, A. Rosas-Hernádez, J. H. Ko, Q. Gan, W. A. G. Iii and R. H. Grubbs, Selective CO2 electrochemical reduction enabled by a tricomponent copolymer modifier on a copper surface, J. Am. Chem. Soc., 2021, 143, 2857–2865 CrossRef CAS PubMed.
- J. Cheng, M. Sulpizi and M. Sprik, Redox potentials and pKa for benzoquinone from density functional theory based molecular dynamics, J. Chem. Phys., 2009, 131, 154504 CrossRef PubMed.
- S. C. L. Kamerlin, M. Haranczyk and A. Warshel, Progress in ab initio QM/MM free-energy simulations of electrostatic energies in proteins: accelerated QM/MM studies of pKa, redox reactions and solvation free energies, J. Phys. Chem. B, 2009, 113, 1253–1272 CrossRef CAS PubMed.
- O. Andreussi, I. Dabo and N. Marzari, Revised Self-Consistent Continuum solvation in electronic-structure calculations, J. Chem. Phys., 2012, 136, 064102 CrossRef PubMed.
- J. T. Feaster, C. Shi, E. R. Cave, T. Hatsukade, D. N. Abram, K. P. Kuhl, C. Hahn, J. K. Nøskov and T. F. Jaramillo, Understanding selectivity for the electrochemical reduction of carbon dioxide to formic acid and carbon monoxide on metal electrodes, ACS Catal., 2017, 7, 4822–4827 CrossRef CAS.
- C. Amovilli, V. Barone, R. Cammi, E. Cancès, M. Cossi, B. Mennucci, C. S. Pomelli and J. Tomasi, Recent advances in the description of solvent effects with the polarizable continuum model, Adv. Quantum Chem., 1998, 32, 227–261 CrossRef.
- H. R. Zare, M. Namazian and M. L. Coote, Experimental and theoretical studies of electrochemical characteristics of 3,4-dihydroxyphenylacetic acid (DOPAC), Electrochim. Acta, 2009, 54, 5353–5357 CrossRef CAS.
- Y. Wang, M. Hatakeyama, K. Ogata, M. Wakabayashi, F. Jin and S. Nakamura, Activation of CO2 by ionic liquid EMIM-BF4 in the electrochemical system: a theoretical study, Phys. Chem. Chem. Phys., 2015, 17, 23521–23531 RSC.
- J. VandeVondele, R. Ayala, M. Sulpizi and M. Sprik, Redox free energies and one-electron energy levels in density functional theory based ab initio molecular dynamics, J. Electroanal. Chem., 2007, 607, 113–120 CrossRef CAS.
- M. Sulpizi and M. Sprik, Acidity constants from vertical energy gaps: density functional theory based molecular dynamics implementation, Phys. Chem. Chem. Phys., 2008, 10, 5238 RSC.
- F. Costanzo, M. Sulpizi, R. G. D. Valle and M. Sprik, The oxidation of tyrosine and tryptophan studied by a molecular dynamics normal hydrogen electrode, J. Chem. Phys., 2011, 134, 244508 CrossRef PubMed.
- J. Cheng, X. Liu, J. VandeVondele, M. Sulpizi and M. Sprik, Redox potentials and acidity constants from density functional theory based molecular dynamics, Acc. Chem. Res., 2014, 47, 3522–3529 CrossRef CAS PubMed.
- J. Cheng and M. Sprik, Aligning electronic energy levels at the TiO2/H2O interface, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081406 CrossRef.
- J. Cheng and M. Sprik, Alignment of electronic energy levels at electrochemical interfaces, Phys. Chem. Chem. Phys., 2012, 14, 11245 RSC.
- J. Cheng and J. VandeVondele, Calculation of electrochemical energy levels in water using the random phase approximation and a double hybrid functional, Phys. Rev. Lett., 2016, 116, 086402 CrossRef PubMed.
- J. Cheng, M. Sulpizi and M. Sprik, Redox potentials and pKa for benzoquinone from density functional theory based molecular dynamics, J. Chem. Phys., 2009, 131, 154504 CrossRef PubMed.
- A. Y. Lozovoi, A. Alavi, J. Kohanoff and R. M. Lynden-Bell, Ab initio simulation of charged slabs at constant chemical potential, J. Chem. Phys., 2001, 115, 1661–1669 CrossRef CAS.
- J. Cheng and M. Sprik, Alignment of electronic energy levels at electrochemical interfaces, Phys. Chem. Chem. Phys., 2012, 14, 11245 RSC.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from H to Rn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
-
D. R. Lide, in CRC Handbook of Chemistry and Physics, ed. D. R. Lide, National Institute of Standards and Technology). CRC Press (an imprint of Taylor and Francis Group), Boca Raton, FL, 86th edn, 2005, p. 2544 $125.96. ISBN 0-8493-0486-5, 2006, vol. 128 Search PubMed.
- X.-H. Yang, A. Cuesta and J. Cheng, Computational Ag/AgCl reference electrode from density functional theory-based molecular dynamics, J. Phys. Chem. B, 2019, 123, 10224–10232 CrossRef CAS PubMed.
- G. V. Buxton and R. M. Sellers, Acid dissociation constant of the carboxyl radical. Pulse radiolysis studies of aqueous solutions of formic acid and sodium formate, J. Chem. Soc., Faraday Trans. 1, 1973, 69, 555 RSC.
- A. S. Jeevarajan, I. Carmichael and R. W. Fessenden, ESR measurement of the pKa of carboxyl radical and ab initio calculation of the carbon-13 hyperfine constant, J. Phys. Chem., 1990, 94, 1372–1376 CrossRef CAS.
- R. Flyunt, M. N. Schuchmann and C. von Sonntag, A common carbanion intermediate in the recombination and proton-catalysed disproportionation of the carboxyl radical anion, CO2˙−, in Aqueous Solution, Chem, 2001, 7, 796–799 CrossRef CAS.
- I. Janik and G. N. R. Tripathi, The nature of the CO2− radical anion in water, J. Chem. Phys., 2016, 144, 154307 CrossRef PubMed.
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *b and
Jun
Cheng
*b and
Jun
Cheng
 *a
*a
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. The thermodynamic cell potentials for the decomposition of CO2 to CO and O2 (eqn (1)) and for its reaction with H2O to produce HCOOH and O2 (eqn (2)) are 1.33 and 1.43 V, respectively:
O bonds. The thermodynamic cell potentials for the decomposition of CO2 to CO and O2 (eqn (1)) and for its reaction with H2O to produce HCOOH and O2 (eqn (2)) are 1.33 and 1.43 V, respectively:

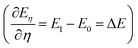 . ΔE is the vertical energy gap and can be obtained from the electronic structure calculation as a total energy difference. ΔE is then averaged over molecular dynamics (MD) runs for a sequence of values of η. Integration of the thermal average 〈ΔE〉η along the thermodynamic path (η from 0 to 1) converts vertical into adiabatic free energies:
. ΔE is the vertical energy gap and can be obtained from the electronic structure calculation as a total energy difference. ΔE is then averaged over molecular dynamics (MD) runs for a sequence of values of η. Integration of the thermal average 〈ΔE〉η along the thermodynamic path (η from 0 to 1) converts vertical into adiabatic free energies: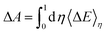
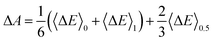
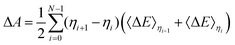
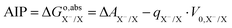
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3), with Λ the thermal de Broglie wavelength of the proton, kB the Boltzmann constant, and T the temperature in Kelvin) of the monoatomic gas in equilibrium with a standard concentration in the solution (co = 1 M). Finally, as in eqn (7), the energy correction qHX/X−·V0,HX/X− needs to be included due to the uncertain reference of electrostatic potential in the charged system (the dX− molecule). Therefore, the free energy of transferring a proton from HX to the gas phase can be written as:
ln(coΛ3), with Λ the thermal de Broglie wavelength of the proton, kB the Boltzmann constant, and T the temperature in Kelvin) of the monoatomic gas in equilibrium with a standard concentration in the solution (co = 1 M). Finally, as in eqn (7), the energy correction qHX/X−·V0,HX/X− needs to be included due to the uncertain reference of electrostatic potential in the charged system (the dX− molecule). Therefore, the free energy of transferring a proton from HX to the gas phase can be written as: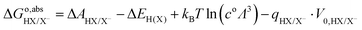
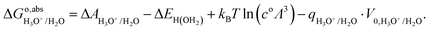
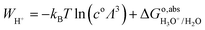
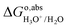 in eqn (11) by eqn (9), the term of proton translational energy, −kBT
in eqn (11) by eqn (9), the term of proton translational energy, −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3), is cancelled, yielding:
ln(coΛ3), is cancelled, yielding: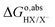 as calculated with eqn (8) only includes the free energy of transferring the proton from aqueous HX to the gas phase. The full reaction can be achieved if we add the reverse of eqn (10)–(13), i.e., if we subtract from
as calculated with eqn (8) only includes the free energy of transferring the proton from aqueous HX to the gas phase. The full reaction can be achieved if we add the reverse of eqn (10)–(13), i.e., if we subtract from 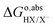 the work function of the proton:35
the work function of the proton:35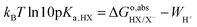
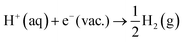 . The free energy of this reaction is the sum of the work function of the solvated proton (eqn (10)) plus the reaction free energy of
. The free energy of this reaction is the sum of the work function of the solvated proton (eqn (10)) plus the reaction free energy of 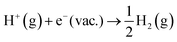 . The former can be calculated by using eqn (11), and the latter is the sum of the negative ionization energy of hydrogen atom (−EIE) plus the negative of half the dissociation energy of hydrogen
. The former can be calculated by using eqn (11), and the latter is the sum of the negative ionization energy of hydrogen atom (−EIE) plus the negative of half the dissociation energy of hydrogen 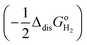 .35 Therefore, the redox potential of X−/X couple with respect to the SHE can be calculated as:
.35 Therefore, the redox potential of X−/X couple with respect to the SHE can be calculated as: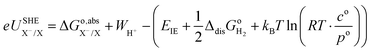
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(RT·co/po), is added to the gas phase standard Gibbs free energies, i.e., EIE and
ln(RT·co/po), is added to the gas phase standard Gibbs free energies, i.e., EIE and 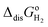 in eqn (15). This correction term converts the free energy in standard pressure (1 bar) to the standard concentration (1 mol L−1).39
in eqn (15). This correction term converts the free energy in standard pressure (1 bar) to the standard concentration (1 mol L−1).39
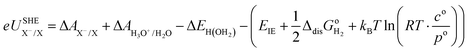
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pKa,HX = ΔAHX/X− + kBT
pKa,HX = ΔAHX/X− + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3) − ΔAH3O+/H2O
ln(coΛ3) − ΔAH3O+/H2O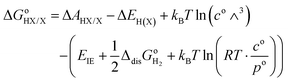
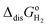 can be found in textbooks,47 and other results or correction terms like ΔEH(OH2) and kBT
can be found in textbooks,47 and other results or correction terms like ΔEH(OH2) and kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(coΛ3) were adopted from Cheng et al.'s work.35 Values of all those terms together with the borrowed ΔA results are listed in Table 1, and free energy integrals ΔA for all half reactions and the corresponding thermodynamic data are summarized in Table 2.
ln(coΛ3) were adopted from Cheng et al.'s work.35 Values of all those terms together with the borrowed ΔA results are listed in Table 1, and free energy integrals ΔA for all half reactions and the corresponding thermodynamic data are summarized in Table 2.