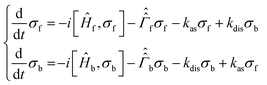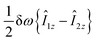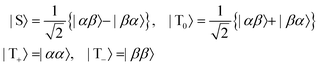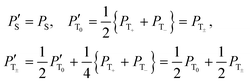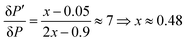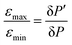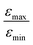Open Access Article
Open Access ArticleSinglet to triplet conversion in molecular hydrogen and its role in parahydrogen induced polarization†
Danil A.
Markelov‡
a,
Vitaly P.
Kozinenko‡
 a,
Stephan
Knecht
b,
Alexey S.
Kiryutin
a,
Alexandra V.
Yurkovskaya
a,
Stephan
Knecht
b,
Alexey S.
Kiryutin
a,
Alexandra V.
Yurkovskaya
 *a and
Konstantin L.
Ivanov§
*a and
Konstantin L.
Ivanov§
 a
a
aInternational Tomography Center and Novosibirsk State University, Russian Federation. E-mail: yurk@tomo.nsc.ru
bNVision-Imaging Technologies, Ulm, Germany
First published on 20th September 2021
Abstract
Detailed experimental and comprehensive theoretical analysis of singlet–triplet conversion in molecular hydrogen dissolved in a solution together with organometallic complexes used in experiments with parahydrogen (the H2 molecule in its nuclear singlet spin state) is reported. We demonstrate that this conversion, which gives rise to formation of orthohydrogen (the H2 molecule in its nuclear triplet spin state), is a remarkably efficient process that strongly reduces the resulting NMR (nuclear magnetic resonance) signal enhancement, here of 15N nuclei polarized at high fields using suitable NMR pulse sequences. We make use of a simple improvement of traditional pulse sequences, utilizing a single pulse on the proton channel that gives rise to an additional strong increase of the signal. Furthermore, analysis of the enhancement as a function of the pulse length allows one to estimate the actual population of the spin states of H2. We are also able to demonstrate that the spin conversion process in H2 is strongly affected by the concentration of 15N nuclei. This observation allows us to explain the dependence of the 15N signal enhancement on the abundance of 15N isotopes.
Introduction
Parahydrogen Induced Polarization (PHIP)1–5 is a well-established low-cost tool to significantly enhance intrinsically weak NMR signals. PHIP makes efficient use of the spin order of parahydrogen (pH2, the H2 molecule in its nuclear singlet spin state) which is converted into observable NMR signals. The possibility to enrich the pH2 component of hydrogen gas arises from the Pauli principle which dictates the total wave function of fermions to be antisymmetric under exchange. This couples the singlet (parahydrogen) and triplet (orthohydrogen) spin states of H2 with even numbered and odd numbered rotational states respectively. As a result, cooling down hydrogen gas in the presence of a catalyst to low temperatures where only the rotational ground state is populated allows to produce hydrogen gas where all molecules are in the singlet state. Once formed and removed from the interconversion catalyst parahydrogen is relatively stable to spin-reequilibration. However, since pH2 itself is NMR silent (as it has the zero magnetic moment) a suitable chemical processes must be harnessed to convert the spin order into an enhanced NMR signal. Such processes are given by catalytic hydrogenation reactions3 with pH2 or by reversible interactions of pH2 with an organometallic complex.5,6 In the first method, hydrogenative PHIP, pH2 is added to a substrate with an unsaturated C–C bond; when the “nascent” protons in the reaction product stemming from pH2 are non-equivalent (chemically or magnetically), one can obtain strong NMR signal enhancements. In the second method, termed Signal Amplification By Reversible Exchange (SABRE), pH2 and a to-be-polarized substrate bind to an Ir-based complex, where spin order transfer gives rise to polarization of the substrate. An advantage of the SABRE method is that the substrate and pH2 only bind to the complex transiently, i.e., they are not consumed, and dissociation of substrate from the complex results in the formation of hyperpolarized free substrate molecules in solution. Hence, the substrate can be re-polarized multiple times by supplying pH2 to the solution. The SABRE method can be used to enhance NMR signals of protons,6,7 and “insensitive” nuclei such as 15N and 13C8–15 and to polarize various molecules, notably, biomolecules,16–18 metabolites,19 oligopeptides,20 and drugs.21–23 The possibility to continuously repeat SABRE measurements with high level of reproducibility opens great perspectives for mixture analysis24 and reaction monitoring25 by means of SABRE.Both hydrogenative PHIP and SABRE have been successfully applied to hyperpolarize various compounds; however, the optimization of hyperpolarization experiments still remains challenging. Specifically, reaction conditions have to be optimized, as well as polarization transfer efficiency. In this work, we address one more issue, which turns out to be important in both PHIP and SABRE. Specifically, we address the question: “What is the spin order of H2 in PHIP/SABRE experiments?”. At the first glance, this question seems to make no sense, as we always introduce pH2, i.e., two protons in the nuclear singlet spin state, into the chemical reaction. However, this obvious answer holds only in the gas phase, where conversion between pH2 and triplet H2 (orthohydrogen, oH2) is a very slow process. For the actual PHIP and SABRE processes the answer is not so obvious because pH2 binds to a PHIP substrate or SABRE catalyst in such a way that the two protons occupy non-equivalent positions. In this situation, their magnetic or chemical equivalence is broken and singlet–triplet conversion in H2 becomes operative. It is important to note that the conversion is not equivalent to a simple decay of singlet spin order via relaxation, since hyperpolarized oH2 can be formed in a strongly non-equilibrium state, as has been confirmed by several groups.26–28
The aim of this work is to study in detail spin conversion of H2 and to characterize its actual spin state. Here we perform the study for a SABRE system (using an Ir-based catalyst) and measure the SABRE-derived enhancement of 15N spins. By introducing radio-frequency pulses on the proton channel (which have no effect pH2 since it is in a rotation-invariant singlet state, but modify the state of oH2) we are able to probe the amount of pH2 and to determine the state of non-thermally polarized oH2. Furthermore, we reveal the influence of the magnetic 15N isotope on the singlet–triplet conversion in complex-bound H2. This effect is conditioned by a weak symmetry breaking resulting in magnetic non-equivalence of the chemically equivalent pH2-nascent protons in the SABRE complex. The study presented here is driven not only by general interest and curiosity, but has important practical consequences for optimizing PHIP and SABRE experiments and for achieving the highest possible NMR signal enhancement. There are two reasons for this. First, the lifetime of the spin order of H2 (which is the source of NMR signal enhancement) is important to achieving maximal polarization. Second, some of the pulse sequences for transferring spin order from H2 have been designed assuming that the initial spin order of the two protons is a pure state of singlet order: such pulse sequences might become inefficient when the spin state of H2 is a mixture of pH2 and oH2. We clearly show in this work that the formation of hyperpolarized oH2 is an important factor in PHIP and SABRE, which has a strong influence on the resulting NMR signal enhancement.
Methods
Sample preparation
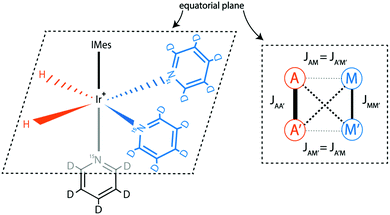
All experiments presented here were done for a SABRE system using the IrCl(COD)(IMes) complex,29 where IMes = 1,3-bis(2,4,6-trimethylphenyl)imidazole-2-ylidene and COD = cyclooctadiene; activation of this pre-catalyst by hydrogenation of COD and addition of pyridine forms the main dihydride Iridium complex [Ir(H)2(IMes)(Py)3]+, with Cl− as a counter ion (Py = pyridine). The structure of the SABRE complex is given in Fig. 1. The SABRE process in this system is due to exchange of H2 and Py between their free forms in solution and bound forms. It is important to note that in methanol solution there is also exchange30 between the main complex and two other complexes: one with a Cl− and one with an equatorial Py ligand replaced by a methanol solvent molecule. In these complexes the pH2-nascent protons are chemically non-equivalent, which strongly affects30 the spin conversion. To simplify the reacting system, we have replaced the Cl− counter-ion with PF6−, which does not bind to the complex. As previously described30 this can be achieved by adding AgPF6 and removing the resulting AgCl precipitate from the sample. As a SABRE substrate, we used either 15N-labelled Py-d5 or mixtures of 15N–Py-d5 and 14N–Py-d5, thus varying the abundance of the spin-1/2 15N isotopes. Using a deuterated substrate allowed to simplify the spin system and, hence, to ease the optimization and interpretation of SABRE experiments. In all experiments the sample temperature was 25 °C.The spin system of the main SABRE complex can be modelled as an AA′MM′ system, as shown in Fig. 1. Here the A-spins stand for the protons originating from pH2, while the M-spins are the 15N nuclei of the two equatorial Py ligands.
NMR experiments
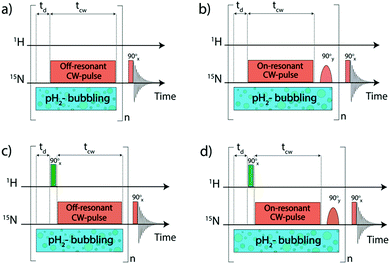
NMR experiments were mostly carried out at high magnetic fields using the protocols shown in Fig. 2. To polarize the 15N nuclei we used pulse sequences with radiofrequency (rf) pulses applied to the 15N channel. For transferring spin order from pH2 essentially a single long 15N pulse of a low intensity is used, hereafter called pseudo continuous-wave (“pseudo cw”) pulse.When the parameters of the rf field applied to the 15N channel are properly set, proton singlet spin order is transferred to 15N spins in the SABRE complex. Specifically, the effective field ωeff (given in the frequency units) should be matched9,31,32 to a certain combination of scalar J-couplings in the AA′MM′ system. The effective field is given by the vector sum of the transverse rf-field (in the rf-rotating frame) and the longitudinal field given by offset from resonance 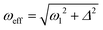 where ω1 is the rf-field strength and Δ the resonance offset. A more detailed discussion of the definition of Δ for the system under study is given below. In the case of single-resonance experiments (excitation only on the 15N channel) the source of polarization is given by the population difference of the singlet and central triplet states of H2. As we show below, this feature is critical for the performance of the pulse sequences.
where ω1 is the rf-field strength and Δ the resonance offset. A more detailed discussion of the definition of Δ for the system under study is given below. In the case of single-resonance experiments (excitation only on the 15N channel) the source of polarization is given by the population difference of the singlet and central triplet states of H2. As we show below, this feature is critical for the performance of the pulse sequences.
The magnetization transferred to the 15N nuclei is parallel to the effective field. Hence, it is a purely transverse magnetization when Δ = 0 (on-resonance excitation); whereas for Δ ≠ 0 the magnetization has a longitudinal component. In SABRE, one seeks to generate polarization of the free substrate molecule via chemical exchange. Upon exchange, longitudinal polarization of the bound species is transferred to the free substrate pool. Thus, in the case of resonant excitation, an additional 90° pulse should be inserted to convert transverse into longitudinal polarization; when Δ ≠ 0 this may be not necessary. To maximize 15N signal enhancement, the polarization transfer cycle is repeated n times.31 For this reason, the additional 90° pulse should be selective, exciting only the bound substrate, but not its free form in solution. Finally, after applying a 90° pulse, the 15N Free Induction Decay (FID) signal is acquired (its Fourier transform gives the NMR spectrum). Two of the pulse sequences shown in Fig. 2 exploit resonant rf-excitation (Fig. 2b and d), whereas the other two make use of off-resonant excitation (Fig. 2a and c). The sequence in Fig. 2b is known as LIGHT-SABRE (Low-Irradiation Generation of High Tesla-SABRE).31
Two of the pulse sequences (Fig. 2c and d) in Fig. 2 comprise a modification which would be meaningless if we were dealing only with pure rotation-invariant singlet order: this is a 90° pulse applied to the proton channel. It turns out that this pulse strongly affects the performance of the polarization transfer experiment if some hyperpolarized oH2 is generated. In this work, we analyse the effect of proton pulses with arbitrary nutation angles on the 15N NMR signal enhancement. The pulse sequences given in Fig. 2c and d are known9 as SLIC-SABRE (Spin-Locking Induced Crossing SABRE33).
In addition to high-field NMR experiments, we also performed field-cycling NMR studies, in which polarization was allowed to build up by SABRE at an ultralow magnetic field (in the range 10 nT < B0 < 1 μT). Subsequently the hyperpolarized sample is transferred to an 400 MHz NMR spectrometer (B0 = 9.4 T). To run such experiments, we used a home-built device for sample shuttling with a set of coils inside the magnetic shield, as described before.11,34
All NMR spectra were recorded using a 400 MHz Bruker NMR spectrometer. In all high-field SABRE experiments the para-component of H2 was enriched to 85% by using a commercial Bruker parahydrogen generator. In ultralow field experiments we have used 95% enriched pH2, obtained by cooling down H2 in a helium cryostat CFA-200-H2CELL (CryoPribor). The pH2 bubbling pressure was equal to 2 bar. The signal enhancement factor ε (ratio of the hyperpolarized 15N NMR signal and thermal signal both measured at 9.4 tesla) gives a measure of polarization.
Results and discussion
Theoretical analysis of singlet–triplet conversion
To analyse singlet–triplet conversion in H2 and to optimize the pulse sequences we used spin dynamics simulations and additionally took into account exchange of H2 or SABRE substrate.In order to consider spin conversion in molecular hydrogen, we introduce a set of equations for the spin density operators, σf and σb, of free and bound H2, respectively:
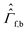 are the corresponding relaxation superoperators; kas is the rate of association of H2 to form the Ir-based complex and kdis is the dissociation rate of molecular hydrogen from the complex. Here, we choose the normalization Tr{σf} + Tr{σb} = 1. In this case, the total probability of finding H2 either in the free form (σf) or in the bound form (σb) is equal to unity, but not their individual traces.35 This model is sufficient to simulate singlet–triplet conversion, which gives rise to hyperpolarized oH2. To carry out these simulations, we introduce Ĥf,b in the rotating frame (this is done to ease numerical calculations and to get rid of the large nuclear Zeeman interaction with the B0 field, which is parallel to the z-axis). For simplicity, we take the frequency of the rotating frame equal to the NMR frequency of free H2, so that Ĥf = 0 and Ĥb = Ω1Î1z + Ω2Î2z (here Î1 and Î2 are the spin operators of the two non-equivalent bound protons, Ω1,2 are their NMR frequencies in the rotating frame). In fact, the only relevant parameter in Ĥb is the frequency difference δω = |Ω1 − Ω2|. Indeed, it is the term
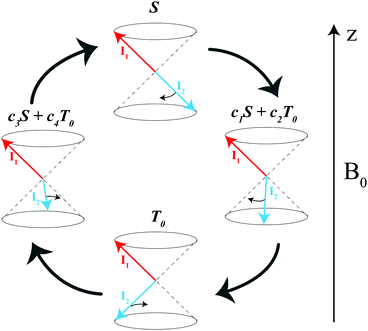
are the corresponding relaxation superoperators; kas is the rate of association of H2 to form the Ir-based complex and kdis is the dissociation rate of molecular hydrogen from the complex. Here, we choose the normalization Tr{σf} + Tr{σb} = 1. In this case, the total probability of finding H2 either in the free form (σf) or in the bound form (σb) is equal to unity, but not their individual traces.35 This model is sufficient to simulate singlet–triplet conversion, which gives rise to hyperpolarized oH2. To carry out these simulations, we introduce Ĥf,b in the rotating frame (this is done to ease numerical calculations and to get rid of the large nuclear Zeeman interaction with the B0 field, which is parallel to the z-axis). For simplicity, we take the frequency of the rotating frame equal to the NMR frequency of free H2, so that Ĥf = 0 and Ĥb = Ω1Î1z + Ω2Î2z (here Î1 and Î2 are the spin operators of the two non-equivalent bound protons, Ω1,2 are their NMR frequencies in the rotating frame). In fact, the only relevant parameter in Ĥb is the frequency difference δω = |Ω1 − Ω2|. Indeed, it is the termwhich is responsible for driving the transitions between the singlet state |S〉 and central triplet state |T0〉, as illustrated by the vector diagram36 in Fig. 3. Setting δω ≠ 0 we assume that the chemical equivalence of the two protons in the complex is broken, giving rise to a non-vanishing difference in their chemical shifts. Alternatively, symmetry breaking can be due to magnetic non-equivalence, i.e., caused by a difference in J-couplings with other spin-1/2 nuclei present in the complex. In both cases we achieve δω ≠ 0. The singlet–triplet states are introduced in the usual way:
where |α〉 and |β〉 are the states of a spin-1/2 particle with z-projections equal to
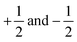 , respectively.
, respectively.
As far as relaxation effects are concerned, we merely consider the simplest case of relaxation driven by fluctuating local fields experienced by the two protons, ignoring the fluctuations of their mutual dipole–dipole coupling. We also assume that the local fields are almost completely correlated, which implies that they efficiently drive the transitions between the triplet states, but not the transitions between the singlet state and triplet states. Hence, in the absence of exchange, singlet–triplet conversion takes infinitely long (in experiments, conversion in the absence of a SABRE catalyst is indeed a very slow process). Precise details and parameters of the model are given in ESI,† as well as the method for numerical solution of the set of equations.
According to the model outlined above, singlet–triplet conversion in H2 occurs in the following way. When H2 binds to the complex, the chemical equivalence is lifted so that coherent transitions between the |S〉 and the central |T0〉 states become operative. As a result, the population is distributed between these two states. This gives rise to formation of oH2 in a non-equilibrium spin state. Subsequently, spin relaxation comes into play and tends to equalize the populations of the three triplet states; eventually, all four states acquire the same population. The rate of the first conversion step S → T0 critically depends on δω, kas and kdis. Simulations assuming an initial |S〉 state of H2 are shown in Fig. 4 for different δω values, presenting the time dependence of the populations of the |S〉, |T0〉 and |T±〉 states, and of the population imbalance δP = PS − PT0. When δω is small, the conversion process is very slow (just like the inefficient singlet–triplet relaxation in free H2). As δω increases, the populations of the |S〉 and |T0〉 states are redistributed in a coherent fashion via spin mixing in the complex and PT0 ≠ 0. As the central |T0〉 state gets populated, relaxation between the triplet states also populates the |T±〉 states, PT± ≠ 0. Hence, spin order conversion is a two-step process. With the parameters chosen in Fig. 3, the |S〉 and |T0〉 state populations are rapidly equilibrated and δP → 0, whereas the |T0〉 population remains different from that of the |T±〉 states for longer time. Moreover, introducing the spin–spin coupling constant between two hydrid protons JHH alters the described behavior, especially for the case of moderate δω values. This coupling induces the energy splitting between the singlet and the triplet manifolds, thus decreasing the rate of S → T0 transitions. However, when δω exceeds JHH, the process of δP reduction is very similar to the case of JHH = 0.
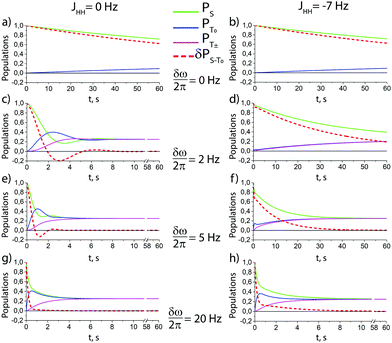 | ||
Fig. 4 Theoretical time dependence of the spin state populations of H2 and the population difference δP = PS − PT0 in the presence of exchange between bound and free hydrogen. Calculation parameters: kas = 6 s−1, kdis = 60 s−1, 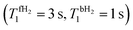 for all subplots; the δω/2π equal to 0 Hz (subplots a and b), 2 Hz (subplots c and d), 5 Hz (subplots e and f), and to 20 Hz (subplots g and h); the spin–spin coupling constant between two hydrid protons JHH = 0 Hz (left column), and JHH = −7 Hz (right column). The relaxation model considers only fluctuating local fields, experienced by the two spins, which are modelled as almost completely correlated, so that singlet–triplet relaxation transitions are slow, as compared to transitions within the triplet manifold (see ESI† for a detailed explanation). for all subplots; the δω/2π equal to 0 Hz (subplots a and b), 2 Hz (subplots c and d), 5 Hz (subplots e and f), and to 20 Hz (subplots g and h); the spin–spin coupling constant between two hydrid protons JHH = 0 Hz (left column), and JHH = −7 Hz (right column). The relaxation model considers only fluctuating local fields, experienced by the two spins, which are modelled as almost completely correlated, so that singlet–triplet relaxation transitions are slow, as compared to transitions within the triplet manifold (see ESI† for a detailed explanation). | ||
Optimization of the pulse sequence
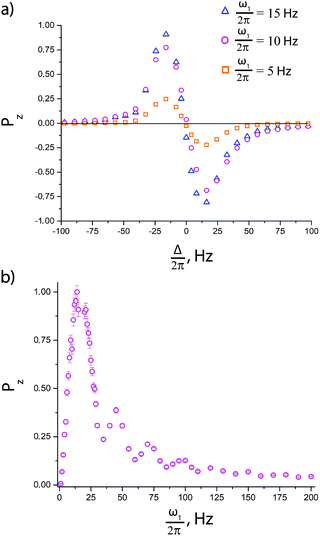
Before comparing the performance of the pulse sequences of interest, we optimized the experimental parameters, such as the delays td and tcw and the number of cycles n. The dependence of the enhancement on these parameters is presented in ESI.† In the experiments presented below we always set td = 500 ms, tcw = 39 ms and n = 50, which provide substantially improved signal enhancements.To optimize the performance of the pulse sequence, it is necessary to set the optimum resonance offset Δ for the pseudo cw pulse. As pointed out above, the optimization is different for a single pulse and for a pulse followed by an additional 90° pulse. This is indeed the case, see Fig. 5. When no extra pulses are used, the resulting longitudinal 15N polarization vanishes for Δ = 0 (the spins are polarized parallel to the effective field, and therefore do not have any longitudinal component). When an additional 90° pulse is used to convert the transverse polarization into longitudinal polarization, the resulting polarization is maximal for Δ = 0. The Δ-dependence of polarization shows positive and negative extrema, see Fig. 5a, corresponding to matching of the energy levels of the AA′MM′ spin system in the rotating frame, as explained before.9 To make the pulse sequences work one should also optimize the ω1 value:9 when ω1 is very small, spin mixing is inefficient, whereas if ω1 is much larger than the relevant J-couplings, the matching conditions can no longer be fulfilled (this is the reason for using a low-intensity cw rf pulse). In the experimental ω1 dependence of the enhancement, see Fig. 5b, the peak corresponds to the matching condition.
NMR signal enhancement
We have optimized the relevant experimental parameters for all four protocols shown in Fig. 2. One can see that using off-resonant excitation with a small Δ value one can achieve higher ε values, see Fig. 5. Although the theoretical treatment suggests that the efficiency of the scheme should be the same or even higher for resonant excitation (Δ = 0); this experiment is more difficult to optimize, in particular, when chemical exchange is constantly going on, as is the case in SABRE. The enhancements obtained by these two methods are moderate, ε ≈ 30 for resonant excitation and ε ≈ 150 for off-resonance excitation, for the experimental conditions used here. We attribute this to efficient S–T0 conversion, rendering δP small. Since this population imbalance is the source of non-thermal spin order, the signal enhancement factors become low.A simple way to re-introduce the δP population imbalance is to exploit the difference in populations between the |T0〉 and |T±〉 states. This can be done in different ways.9 Here we investigate the simple method of using a single 90° pulse on the proton channel. In this situation, the state populations change as follows (we assume that before applying the pulse PT+ = PT− = PT±):
To exploit this effect, we have run two more experiments (with on- and off-resonance excitation) using an additional 90° proton pulse prior to the polarization transfer sequence. As one can see from Fig. 6, the resulting enhancement dramatically increases for both transfer schemes, here approximately by a factor of 7. This is a clear indication that fast and efficient S–T0 conversion in H2 is indeed taking place in the studied sample. Comparison of the pulse sequences also shows that applying a 90° proton pulse is indeed an efficient way to re-establish the desired S–T0 population difference.
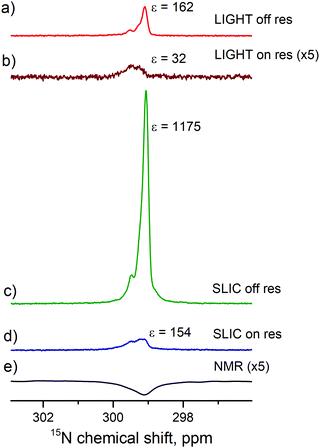 | ||
| Fig. 6 Comparison of the polarization transfer schemes shown in Fig. 2. LIGHT-SABRE scheme with off-resonant CW pulse followed by a selective 90° proton pulse (a) and on-resonant CW 15N pulse (b). SLIC-SABRE scheme (with an additional hard 90° proton pulse before polarization transfer) with off-resonant CW 15N pulse followed by a selective 90° 15N pulse (c) and an on-resonant CW 15N pulse (d). Thermal signal acquired with 256 transients is presented as a reference (e). Experimental parameters: [S] = 95 mM, [C] = 7 mM, ω1/2π = 10 Hz, n = 50, td = 500 ms, tcw = 39 ms, Δ/2π = −14 Hz (for off-resonant excitation). | ||
One should note that the resulting 15N spectra yield a broadened NMR signal with a non-Lorentzian lineshape. This is a result of exchange of deuterons in the ortho-positions of Py with dihydrogen protons, which leads to the formation of three isotopomers of free pyridine, with D–D, H–D and H–H nuclei in the ortho-positions.10 Since each isotopomer has its own spin system, the spectral pattern becomes more complex and contains several components. However, the signal of fully deuterated pyridine dominates over any other signal in the resulting 15N spectra,
The improvement of the enhancement ε by a factor of 7 allows one to calculate the populations of the spin states of H2. Here we do so assuming that (i) ε is proportional to δP and (ii) PT± = 0.05 (this corresponds to 85% of pH2 enrichment). Hence, if we set PS = x before the pulse is applied, we obtain that PT0 = 0.9 − x. After application of the pulse we obtain 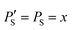 and
and 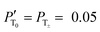 . Consequently,
. Consequently,
Singlet–triplet conversion
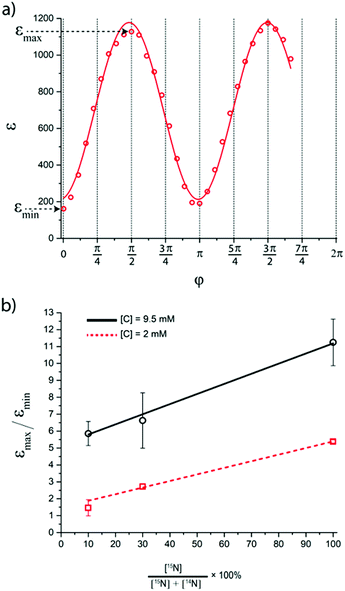
Inspired by the strong, approximately 7-fold, improvement of ε provided by the pulse applied to protons, we decided to look more closely at the singlet–triplet conversion efficiency. To this end, we have varied the length of the proton pulse and measured ε as a function of the flip angle φ of this pulse, see Fig. 7a. The experimental data were fitted by the periodic function ε(φ) = a1 − a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2φ), with the maxima at φ = (1/2 + m)π and the minima at φ = mπ (m is an integer number). The maximal value is εmax = a1 + a2 ∝ δP′ and the minimal value is εmin = a1 − a2 ∝ δP. The ratio
cos(2φ), with the maxima at φ = (1/2 + m)π and the minima at φ = mπ (m is an integer number). The maximal value is εmax = a1 + a2 ∝ δP′ and the minimal value is εmin = a1 − a2 ∝ δP. The ratiothus can be used to characterize the efficiency of the S–T0 conversion process, which is due to symmetry breaking in H2 bound to the SABRE complex. Symmetry breaking can be due to the chemical shift difference between the two protons and/or to subtler effects of J-couplings. In the SABRE complex, the 1H–15N J-couplings are sizeable; furthermore, there is a large difference in the couplings JAM = JA′M′ and JA′M = JAM′, so that it has been estimated that δJ = JAM−JA′M ≈ 20 Hz. As a consequence, the two pH2-nascent protons become magnetically non-equivalent and the effective δω value becomes non-zero.
We have studied the effect of symmetry breaking through magnetic non-equivalence by varying the enrichment of 15N nuclei, i.e., by using a mixture of 14N–Py and 15N–Py (the fast relaxing quadrupolar 14N nuclei do not alter the spin dynamics of the proton system).
In Fig. 7b, the ratio 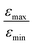 is plotted as a function of the fraction of 15N nuclei (we used three values, η15N = 10%, 30% and 100% of 15N–Py) and measured the dependence for two different concentrations [C] of the catalyst. We have set the total concentration of substrate (both 15N labelled and non-labelled) equal to 190 mM in order to achieve sufficient signal-to-noise ratio in cases where the SABRE signal was low, i.e. LIGHT-SABRE experiments with an 15N enrichment η15NZ = 10%. One can see that the effect of 15N spins is significant, in particular, at low [C] concentration, where the violation of magnetic equivalence of the protons in bound H2 is the dsominant mechanism. Note that
is plotted as a function of the fraction of 15N nuclei (we used three values, η15N = 10%, 30% and 100% of 15N–Py) and measured the dependence for two different concentrations [C] of the catalyst. We have set the total concentration of substrate (both 15N labelled and non-labelled) equal to 190 mM in order to achieve sufficient signal-to-noise ratio in cases where the SABRE signal was low, i.e. LIGHT-SABRE experiments with an 15N enrichment η15NZ = 10%. One can see that the effect of 15N spins is significant, in particular, at low [C] concentration, where the violation of magnetic equivalence of the protons in bound H2 is the dsominant mechanism. Note that 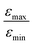 increases from 1 for η15N = 10% to approximately 5 for η15N = 100%. For higher concentrations [C] other conversion mechanisms come into play as well, most likely coming from other complexes with molecular hydrogen. This follows from the fact that
increases from 1 for η15N = 10% to approximately 5 for η15N = 100%. For higher concentrations [C] other conversion mechanisms come into play as well, most likely coming from other complexes with molecular hydrogen. This follows from the fact that 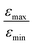 = 5 for η15N = 10%. Nonetheless, the contribution of magnetic non-equivalence to symmetry breaking is still significant in this case, as
= 5 for η15N = 10%. Nonetheless, the contribution of magnetic non-equivalence to symmetry breaking is still significant in this case, as 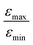 increases by roughly a factor of 2 for η15N = 100%. Remarkably,
increases by roughly a factor of 2 for η15N = 100%. Remarkably, 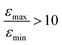 at high [C] and for η15N = 100%. Hence, the contribution of symmetry breaking driven by scalar 1H–15N couplings in the SABRE complex to overall conversion is significant. Furthermore, this contribution strongly affects the resulting enhancement.
at high [C] and for η15N = 100%. Hence, the contribution of symmetry breaking driven by scalar 1H–15N couplings in the SABRE complex to overall conversion is significant. Furthermore, this contribution strongly affects the resulting enhancement.
Ultra-low field experiments
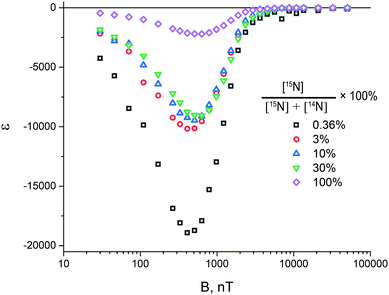
In this context, it is interesting to estimate how the resulting 15N enhancement depends on the abundance of 15N nuclei in the SABRE substrate. The experimental data shown in Fig. 7 do not give a complete and clear answer to this question: in this figure, only relative ε values are presented, but not the actual values of the enhancement. Furthermore, high-field experiments are not suitable for this purpose, because the pulse sequences have been optimized for a complex with two 15N nuclei, whereas at lower 15N abundance a fraction of the complexes have only one 15N nucleus (at low 15N abundance the fraction of the complexes with two 15N nuclei become negligible). The parameters of the complexes with one or two 15N nuclei are quite different; consequently, for such complexes optimal ε may be achieved for different ω1 and Δ values. As a result, direct comparison of ε values measured at different 15N abundance becomes problematic.To get around this problem, we have decided to measure ε at ultralow magnetic fields, where the 1H and 15N nuclei become strongly coupled and “spontaneous” polarization transfer without rf-excitation between them becomes efficient. This is the essence of the SABRE-SHEATH method.21,37,38 It is important to note that at ultralow fields the chemical shift difference of the protons bound to the SABRE complex is of no importance, so that symmetry breaking (and hence, singlet–triplet conversion) occurs solely due to magnetic non-equivalence. Furthermore, there is no need to analyse the spin dynamics in additional complexes, which strongly affect the para-to-ortho conversion at high field. Although at ultralow fields we are unable to run experiments to elucidate the relative populations of different spin states since we cannot apply any pulses to the protons, we can measure ε over a wide range of fields.
Comparison of the SABRE field dependences measured as a function of the 15N enrichment (at the same total concentration of 15N–Py and 14N–Py) is shown in Fig. 8. The measured signal enhancement indicates that the SABRE polarization efficiency at ultra-low field increases when the abundance of 15N nuclei is lowered. It is noteworthy that the position of the maximum of the field dependence also depends on the concentration of labelled substrate, which is due to the difference in the parameters of the spin system of the SABRE complex for each specific solution.
We attribute these results to conversion between different forms of H2, driven by the interaction with 15N spins. Such interactions not only give rise to spin order transfer to the nitrogen spins, but also to singlet-to-triplet conversion in bound H2, by perturbing the spin state of H2. As a consequence, at high concentration of 15N isotopes, pH2 is converted to thermally polarized H2, which can no longer provides any NMR enhancements. When the abundance of 15N nuclei is low, the source spin order survives for a longer period of time, giving rise to a stronger 15N signal enhancement. Our observations also explain why 15N-NMR enhancement factors are so high, of the order of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for natural isotopic abundance (which is only 0.365%).22 The absolute signal intensity, which is given by the product of the concentration (proportional to ηN, the fraction of 15N containing molecules) and the maximal enhancement εopt, is the highest for large η15N. The reason is that at low η15N15N containing molecules very seldom bind to the SABRE complex, resulting in slow polarization build-us and lower signal intensity.
000 for natural isotopic abundance (which is only 0.365%).22 The absolute signal intensity, which is given by the product of the concentration (proportional to ηN, the fraction of 15N containing molecules) and the maximal enhancement εopt, is the highest for large η15N. The reason is that at low η15N15N containing molecules very seldom bind to the SABRE complex, resulting in slow polarization build-us and lower signal intensity.
Another effect, which supports our conclusions, is the striking dependence of SABRE enhancement levels on the pH2 bubbling pressure. The results of SABRE experiments performed at bubbling pressures in a range from 5 to 25 bars are presented in ESI† (Fig. S3). The linear growth of SABRE enhancement with increasing bubbling pressure (which leads to an increasing pH2 concentration in the sample) demonstrates that the excess of fresh pH2 in the solution attenuates the negative effect of singlet–triplet conversion. However, it is noteworthy, that even at 25 bar with reasonable gas flow rates, the enhancement level does not reach saturation, which possibly indicates the substantial effect of singlet–triplet conversion even at ultra-low field conditions.
Conclusions
Our work gives a clear evidence that singlet–triplet conversion in bound H2 plays an important role in SABRE experiments. Due to the spin dynamics, this conversion becomes fast in the Iridium complex. An important feature of this conversion is that it favours one of the three triplet states, here to the central triplet state, producing polarized oH2 that does not obey a Boltzmann distribution. This can be unequivocally proven by running polarization transfer experiments with an additional pulse applied to the proton channel. Such experiments allow one to estimate the populations of the three spin states of oH2 experimentally. In the present case, the additional proton pulse giving rise to a strong additional gain in 15N signal, which is more than 10-fold in some cases. Hence, studying the conversion process is not a matter of pure curiosity, but it is of great practical importance for the performance of the SABRE method. In addition, we demonstrated that the conversion process is strongly affected by the presence of 15N nuclei, which make the pH2-nascent protons in the complex magnetically inequivalent. This effect is of great importance for polarization transfer experiments at ultralow fields, where the signal enhancement decreases when the isotopic abundance of 15N nuclei is increased. The reason is that the limited source of pH2-derived polarization is exhausted upon polarization transfer to 15N nuclei.Thus, we can conclude that spin order conversion processes from pH2 to oH2, and within the triplet manifold of oH2 are an important for the success of PHIP and SABRE experiments. We believe that consideration of these processes and corresponding optimization of experimental parameters (concentrations, extent of isotopic labelling, pH2 pressure, parameters of NMR pulse sequences) can significantly improve the signal enhancements that can be achieved by PHIP and SABRE.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support for the theoretical part by the Russian Science Foundation (grant No. 20-62-47038) is gratefully acknowledged. We acknowledge the Ministry of Science and Education of RF (contract No. 075-15-2021-580) for providing financial support for the experimental work at ITC. Prof. Geoffrey Bodenhausen (ENS, Paris) suggested several editorial changes. Prof. Konstantin L. Ivanov passed away on the 5th of March, 2021 at the age 44. In his early career, he made major contributions to the theory of chemical reaction kinetics in liquid phase. Later, he significantly contributed to unraveling the mechanisms of light-induced nuclear hyperpolarization in liquids and solid state using the concept of level anti-crossing (LAC). In recent years, his main research efforts, both theoretical and experimental, were concentrated on spin and chemical dynamics in PHIP and SABRE methods using LAC; for this, he was awarded the Günther Laukien Prize in 2020. He also was the scientific PhD adviser of two authors (DAM and VPK). Theoretical explanation of singlet to triplet conversion of nuclear spins molecular hydrogen and its experimental verification was his last project. He worked on this manuscript shortly before being deadly infected.References
- C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645–2648 CrossRef CAS PubMed.
- C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541–5542 CrossRef CAS.
- J. Natterer and J. Bargon, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 293–315 CrossRef.
- R. A. Green, R. W. Adams, S. B. Duckett, R. E. Mewis, D. C. Williamson and G. G. R. Green, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 67, 1–48 CrossRef CAS.
- D. A. Barskiy, S. Knecht, A. V. Yurkovskaya and K. L. Ivanov, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114–115, 33–70 CrossRef CAS PubMed.
- R. W. Adams, J. A. Aguilar, K. D. Atkinson, M. J. Cowley, P. I. P. Elliott, S. B. Duckett, G. G. R. Green, I. G. Khazal, J. López-Serrano and D. C. Williamson, Science, 2009, 323, 1708–1711 CrossRef CAS PubMed.
- E. B. Dücker, L. T. Kuhn, K. Münnemann and C. Griesinger, J. Magn. Reson., 2012, 214, 159–165 CrossRef PubMed.
- S. Knecht, A. S. Kiryutin, A. V. Yurkovskaya and K. L. Ivanov, J. Magn. Reson., 2018, 287, 10–14 CrossRef CAS PubMed.
- S. Knecht, A. S. Kiryutin, A. V. Yurkovskaya and K. L. Ivanov, Mol. Phys., 2018, 2018, 1–10 Search PubMed.
- A. N. Pravdivtsev, A. V. Yurkovskaya, H. Zimmermann, H. M. Vieth and K. L. Ivanov, RSC Adv., 2015, 5, 63615–63623 RSC.
- A. S. Kiryutin, A. V. Yurkovskaya, H. Zimmermann, H.-M. Vieth and K. L. Ivanov, Magn. Reson. Chem., 2018, 56, 651–662 CrossRef CAS PubMed.
- T. Theis, M. L. Truong, A. M. Coffey, R. V. Shchepin, K. W. Waddell, F. Shi, B. M. Goodson, W. S. Warren and E. Y. Chekmenev, J. Am. Chem. Soc., 2015, 137, 1404–1407 CrossRef CAS PubMed.
- J. F. P. Colell, M. Emondts, A. W. J. Logan, K. Shen, J. Bae, R. V. Shchepin, G. X. Ortiz, P. Spannring, Q. Wang, S. J. Malcolmson, E. Y. Chekmenev, M. C. Feiters, F. Rutjes, B. Blumich, T. Theis and W. S. Warren, J. Am. Chem. Soc., 2017, 139, 7761–7767 CrossRef CAS PubMed.
- R. V. Shchepin, B. M. Goodson, T. Theis, W. S. Warren and E. Y. Chekmenev, ChemPhysChem, 2017, 18, 1961–1965 CrossRef CAS PubMed.
- Z. J. Zhou, J. Yu, J. F. P. Colell, R. Laasner, A. Logan, D. A. Barskiy, R. V. Shchepin, E. Y. Chekmenev, V. Bum, W. S. Warren and T. Theis, J. Phys. Chem. Lett., 2017, 8, 3008–3014 CrossRef CAS PubMed.
- S. Glöggler, R. Müller, J. Colell, M. Emondts, M. Dabrowski, B. Blümich and S. Appelt, Phys. Chem. Chem. Phys., 2011, 13, 13759–13764 RSC.
- W. Iali, G. G. R. Green, S. J. Hart, A. C. Whitwood and S. B. Duckett, Inorg. Chem., 2016, 55, 11639–11643 CrossRef CAS PubMed.
- A. M. Olaru, M. J. Burns, G. G. R. Green and S. B. Duckett, Chem. Sci., 2017, 8, 2257–2266 RSC.
- W. Iali, S. S. Roy, B. J. Tickner, F. Ahwal, A. J. Kennerley and S. B. Duckett, Angew. Chem., Int. Ed., 2019, 58(30), 10271–10275 CrossRef CAS PubMed.
- T. Ratajczyk, T. Gutmann, P. Bernatowicz, G. Buntkowsky, J. Frydel and B. Fedorczyk, Chem. – Eur. J., 2015, 21, 12616–12619 CrossRef CAS PubMed.
- D. A. Barskiy, R. V. Shchepin, A. M. Coffey, T. Theis, W. S. Warren, B. M. Goodson and E. Y. Chekmenev, J. Am. Chem. Soc., 2016, 138, 8080–8083 CrossRef CAS PubMed.
- I. V. Skovpin, A. Svyatova, N. Chukanov, E. Y. Chekmenev, K. V. Kovtunov and I. V. Koptyug, Chem. – Eur. J., 2019, 25, 12694–12697 CrossRef CAS PubMed.
- H. Zeng, J. Xu, J. Gillen, M. T. McMahon, D. Artemov, J.-M. Tyburn, J. A. B. Lohman, R. E. Mewis, K. D. Atkinson, G. G. R. Green, S. B. Duckett and P. C. M. van Zijl, J. Magn. Reson., 2013, 237, 73–78 CrossRef CAS PubMed.
- N. Eshuis, B. J. van Weerdenburg, M. C. Feiters, F. P. Rutjes, S. S. Wijmenga and M. Tessari, Angew. Chem., 2015, 127, 1501–1504 CrossRef.
- B. J. Tickner, P. J. Rayner and S. B. Duckett, Anal. Chem., 2020, 92(13), 9095–9103 CrossRef CAS PubMed.
- S. Aime, R. Gobetto and D. Canet, J. Am. Chem. Soc., 1998, 120, 6770–6773 CrossRef CAS.
- S. Knecht, A. S. Kiryutin, A. V. Yurkovskaya and K. L. Ivanov, J. Magn. Reson., 2018, 287, 74–81 CrossRef CAS PubMed.
- A. S. Kiryutin, G. Sauer, A. V. Yurkovskaya, H.-H. Limbach, K. L. Ivanov and G. Buntkowsky, J. Phys. Chem. C, 2017, 121, 9879–9888 CrossRef CAS.
- M. J. Cowley, R. W. Adams, K. D. Atkinson, M. C. R. Cockett, S. B. Duckett, G. G. R. Green, J. A. B. Lohman, R. Kerssebaum, D. Kilgour and R. E. Mewis, J. Am. Chem. Soc., 2011, 133, 6134–6137 CrossRef CAS PubMed.
- S. Knecht, S. Hadjiali, D. A. Barskiy, A. Pines, G. Sauer, A. S. Kiryutin, K. L. Ivanov, A. V. Yurkovskaya and G. Buntkowsky, J. Phys. Chem. Lett., 2019, 123, 16288–16293 CrossRef CAS.
- T. Theis, M. Truong, A. M. Coffey, E. Y. Chekmenev and W. S. Warren, J. Magn. Reson., 2014, 248, 23–26 CrossRef CAS PubMed.
- T. Theis, N. M. Ariyasingha, R. V. Shchepin, J. R. Lindale, W. S. Warren and E. Y. Chekmenev, J. Phys. Chem. Lett., 2018, 9, 6136–6142 CrossRef CAS.
- S. J. DeVience, R. L. Walsworth and M. S. Rosen, Phys. Rev. Lett., 2013, 111, 173002 CrossRef PubMed.
- I. V. Zhukov, A. S. Kiryutin, A. V. Yurkovskaya, Y. A. Grishin, H.-M. Vieth and K. L. Ivanov, Phys. Chem. Chem. Phys., 2018, 20, 12396–12405 RSC.
- S. Knecht, A. N. Pravdivtsev, J. B. Hovener, A. V. Yurkovskaya and K. L. Ivanov, RSC Adv., 2016, 6, 24470–24477 RSC.
- P. Kating, A. Wandelt, R. Selke and J. Bargon, J. Phys. Chem., 1993, 97, 13313–13317 CrossRef CAS.
- M. L. Truong, T. Theis, A. M. Coffey, R. V. Shchepin, K. W. Waddell, F. Shi, B. M. Goodson, W. S. Warren and E. Y. Chekmenev, J. Phys. Chem. C, 2015, 119, 8786–8797 CrossRef CAS PubMed.
- R. V. Shchepin, D. A. Barskiy, A. M. Coffey, T. Theis, F. Shi, W. S. Warren, B. M. Goodson and E. Y. Chekmenev, ACS Sens., 2016, 1, 640–644 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Model of S–T conversion and optimization of experimental parameters. See DOI: 10.1039/d1cp03164c |
| ‡ These authors have contributed equally. |
| § Konstantin Ivanov deceased on March 5th 2021. |
| This journal is © the Owner Societies 2021 |