DOI:
10.1039/D0DT04198J
(Paper)
Dalton Trans., 2021,
50, 1465-1477
Utilization of a Pt(II) di-yne chromophore incorporating a 2,2′-bipyridine-5,5′-diyl spacer as a chelate to synthesize a green and red emitting d–f–d heterotrinuclear complex†
Received
9th December 2020
, Accepted 23rd December 2020
First published on 28th December 2020
Abstract
A new heterotrinuclear (d–f–d) complex [Eu(btfa)31c] (btfa = 4,4,4-trifluoro-1-phenyl-1,3-butanedione and 1c = [(Ph)(Et3P)2Pt–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl) has been synthesized by utilizing the N,N-donor sites of the organometallic chromophore. The complex was characterized by analytical and spectroscopic methods. Photophysical properties of the complex were analysed in detail using both steady-state and time-resolved emission and excitation spectroscopy. The optical absorption spectrum of the complex is dominated by the spin allowed π–π* transitions of the btfa and 1c units in the UV–visible region (200–418 nm) and thus is excitable over a wide range of wavelengths across the UV into the visible region of the electromagnetic spectrum. The complex displays typical red Eu(III) emission when excited at 345 nm. However, it also shows green emission when excited at 464 nm and, thus could be an interesting candidate for full colour display applications. The change in the colour could be a result of the high value of the energy back-transfer rate (6.73 × 105 s−1) from the triplet state of the organometallic chromophore to the 5D1 state of Eu(III). Judd–Ofelt (J–O) intensity parameters (Ω2 and Ω4), radiative (AR), non-radiative (AR) decay rates and intrinsic quantum yield (QEuEu) have been calculated.
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl) has been synthesized by utilizing the N,N-donor sites of the organometallic chromophore. The complex was characterized by analytical and spectroscopic methods. Photophysical properties of the complex were analysed in detail using both steady-state and time-resolved emission and excitation spectroscopy. The optical absorption spectrum of the complex is dominated by the spin allowed π–π* transitions of the btfa and 1c units in the UV–visible region (200–418 nm) and thus is excitable over a wide range of wavelengths across the UV into the visible region of the electromagnetic spectrum. The complex displays typical red Eu(III) emission when excited at 345 nm. However, it also shows green emission when excited at 464 nm and, thus could be an interesting candidate for full colour display applications. The change in the colour could be a result of the high value of the energy back-transfer rate (6.73 × 105 s−1) from the triplet state of the organometallic chromophore to the 5D1 state of Eu(III). Judd–Ofelt (J–O) intensity parameters (Ω2 and Ω4), radiative (AR), non-radiative (AR) decay rates and intrinsic quantum yield (QEuEu) have been calculated.
1. Introduction
Organo-transition metal complexes with triplet (T) and singlet (S) harvesting features have emerged as attractive materials for efficient optoelectronic (O-E) applications.1 The introduction of heavy transition metals such as rhenium (Re), ruthenium (Ru), osmium (Os) and platinum (Pt) into these systems, with their associated high spin–orbit coupling (SOC), facilitates intersystem-crossing (ISC) of the excited singlet state S1 to the lower-lying triplet state T1.2 As a result, highly efficient photoluminescence quantum yields (PLQY) approaching 100% efficiency at ambient temperature are achievable. Hence, in the electroluminescence experiments, Pt(II) complexes can exploit both the singlet and triplet excitons and produce light.1,3 Additionally, trivalent lanthanide [Ln(III)] ions provide a fascinating platform because of their atom-like emission spectra with very sharp emission bands (full width at half maxima (FWHM) less than 10 nm), long luminescence lifetimes and ion-specific emissions.4 Coordinating Ln(III) complex ions to organo-transition metal complexes could endow the resultant complexes with enhanced PL properties for many potential applications.5 The unique optical properties of the Ln(III) ions render them useful in a range of applications such as in lasers,5h,6 light-emitting sensors for hetero- and homogeneous fluoroimmunoassays,7 organic light-emitting diodes (OLEDs) used in display devices,5c,e,8 and biological imaging.9 Hetero-multimetallic d–f complexes have shown enhanced PL properties via energy transfer from the transition metals acting as an antenna triplet state for the Ln(III) ions.10 Compared to organic sensitizer chromophores, the metal-based chromophores possess both a low energy singlet state and a low triplet excited state and thus can be used to extend the excitation window of the luminescent lanthanide complexes.11 Hence, optimized and tuned photophysical properties of luminescent lanthanide complexes such as narrow emission bands, large Stokes’ shifts and long-lived excited state lifetimes can be easily enhanced. Moreover, 3d/5d coordination complexes can facilitate highly efficient Electronic Energy Transfer (EET) to the excited states of chelated 4f* cations.12 The latter process can be performed via two possible pathways: (a) 1MLCT–3MLCT intersystem crossing arising from the heavy-atom effect of the transition metals upon coordination to the lanthanide unit, (b) efficient 3MLCT–Ln* process that can compete with bimolecular quenching of the 3MLCT state by triplet oxygen.13 The coordination of 3d/5d metals containing appropriate ligands allows the excitation in the visible region.14 In addition, the inclusion of acetylide-functionalized chelating ligands allows light emission from the triplet excited state of the conjugated ligand.15 Moreover, introducing the acetylide unit may endow the complex with intriguing photophysical properties by additional intra-ligand and/or inter-ligand charge-transfer excited states (ILCT). Therefore, a strong sensitization of Eu(III) in the visible domain (up to 460 nm) by the use of a phosphorescent Pt(II) complex raises the overall luminescence QY of the complexes.12,13 We have recently4c reported a heterotrinuclear ‘Pt–Eu–Pt’ complex of a sterically hindered kinked/V-shaped Pt(II) di-yne antenna chromophore of the type trans-[(Ph)(Et3P)2Pt–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl) (1d) as shown in Chart 1 and described its photophysical properties. The complex displayed typical red emission of the Eu(III) centre; however, the excitation window was confined to the UV region. This can be attributed to conjugation interruption in the system due to ligand topology (presence of the ethynyl groups at 6,6′-positions of 2,2′-Bipy).16 A general strategy to shift the excitation window of a complex is to design and engineer the molecule(s) with extended/uninterrupted π-conjugation. We have previously reported that Pt(II) di-ynes and poly-ynes incorporating a variety of carbocyclic,15a,17 heterocyclic15a,18 and mixed heterocyclic15a,19 spacers with extended conjugation exhibit improved photophysical properties for various opto-electronic applications. We noted that 5,5′-bis(ethnyl)-2,2′-bipyridine is fully conjugated while its 6,6′-bis(ethynyl) counterpart has broken conjugation and that 2,2′-bipyridine-5,5′-diyl spacer imparts more desirable optical properties to the Pt(II) di-yne and poly-yne complexes.20 Based on this idea, in the present work, we have utilized the ‘rigid-rod’ Pt(II) di-yne chromophore incorporating 2,2′-bipyridine-5,5′-diyl chelating spacer to synthesize a new heterotrinuclear Pt–Eu–Pt complex (Chart 1). The photophysical properties of the heterotrinuclear complex have been investigated. The optical absorption spectrum of the present heterotrinuclear complex [Eu(btfa)31c] displays a red shift compared to its kinked counterpart [Eu(btfa)31d] [1d] = [(Ph)(Et3P)2Pt–C
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl) (1d) as shown in Chart 1 and described its photophysical properties. The complex displayed typical red emission of the Eu(III) centre; however, the excitation window was confined to the UV region. This can be attributed to conjugation interruption in the system due to ligand topology (presence of the ethynyl groups at 6,6′-positions of 2,2′-Bipy).16 A general strategy to shift the excitation window of a complex is to design and engineer the molecule(s) with extended/uninterrupted π-conjugation. We have previously reported that Pt(II) di-ynes and poly-ynes incorporating a variety of carbocyclic,15a,17 heterocyclic15a,18 and mixed heterocyclic15a,19 spacers with extended conjugation exhibit improved photophysical properties for various opto-electronic applications. We noted that 5,5′-bis(ethnyl)-2,2′-bipyridine is fully conjugated while its 6,6′-bis(ethynyl) counterpart has broken conjugation and that 2,2′-bipyridine-5,5′-diyl spacer imparts more desirable optical properties to the Pt(II) di-yne and poly-yne complexes.20 Based on this idea, in the present work, we have utilized the ‘rigid-rod’ Pt(II) di-yne chromophore incorporating 2,2′-bipyridine-5,5′-diyl chelating spacer to synthesize a new heterotrinuclear Pt–Eu–Pt complex (Chart 1). The photophysical properties of the heterotrinuclear complex have been investigated. The optical absorption spectrum of the present heterotrinuclear complex [Eu(btfa)31c] displays a red shift compared to its kinked counterpart [Eu(btfa)31d] [1d] = [(Ph)(Et3P)2Pt–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl) because of the uninterrupted conjugation present in the former complex. Moreover, the newly synthesized heterotrinuclear complex displays fascinating dual emissions i.e., typical red emission due to the Eu(III) ion occurs when excited at 345 nm while a strong green emission is observed when the complex is excited at 464 nm. Finally, DFT calculations have been carried out to understand the photophysical properties and the nature of the excited state. Furthermore, the results of the DFT in conjunction with the observed photophysical data were utilized to gain an insight into the IET processes with the help of the LUMPAC21 software package.
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl) because of the uninterrupted conjugation present in the former complex. Moreover, the newly synthesized heterotrinuclear complex displays fascinating dual emissions i.e., typical red emission due to the Eu(III) ion occurs when excited at 345 nm while a strong green emission is observed when the complex is excited at 464 nm. Finally, DFT calculations have been carried out to understand the photophysical properties and the nature of the excited state. Furthermore, the results of the DFT in conjunction with the observed photophysical data were utilized to gain an insight into the IET processes with the help of the LUMPAC21 software package.
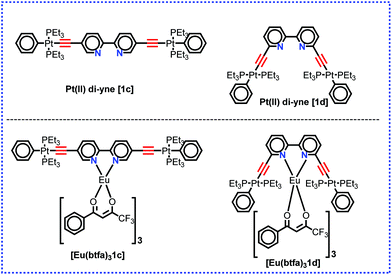 |
| | Chart 1 Structure of the present and previously4c designed Pt(II) di-yne organometallic chromophore and their heterotrinuclear (d–f–d) complex. | |
2. Experimental
2.1. General
All reactions were performed under a dry Argon (Ar) atmosphere using standard Schlenk line techniques. Solvents were pre-dried and distilled before use according to standard procedures. Europium chloride and gadolinium nitrate were purchased from Strem, USA. All other chemicals were obtained from Sigma Aldrich except 5,5′-dibromo-2,2′-bipyridine which was obtained from Tokyo Chemical Industry (TCI) and all were used as received. The compound trans-[Ph(Et3P)2PtCl] was prepared according to reported procedures.4c Column chromatography was performed either with Kieselgel 60 (230–400 mesh) silica gel or alumina (Brockman Grade I). Elemental analysis was performed in the Department of Chemistry, Sultan Qaboos University. Attenuated total-reflectance (ATR) infrared (IR) spectra were recorded on pure samples on diamond using a Cary 630 FT-IR spectrometer. Mass spectra were obtained using the Agilent 6530 Accurate-Mass Quadruple Time-of-Flight (Q-TOF) LC/MS.
2.2. Synthesis of hetero-trinuclear complex [Eu(btfa)31c]
5,5′-Bis(trimethylsilylethynyl)-2,2′-bipyridine (1a), 5,5′-bis(ethynyl)-2,2′-bipyridine (1b) and trans-[(Ph)(Et3P)2Pt–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl (1c) (Scheme 1) were synthesized as reported by us previously.16 A solution of 1c (0.073 g, 0.06 mmol) in MeOH/DCM (10 mL) was added to a solution of [Eu(btfa)3(H2O)2] (0.050 g, 0.06 mmol) in MeOH/DCM (10 mL). The reaction mixture was left overnight with stirring at RT. The solution was left for slow solvent evaporation, after which solid product was obtained as a yellow solid. The solid product was washed with cold ethanol and dried in vacuo to obtain a light yellow solid. IR: ν/cm−1 –C
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl (1c) (Scheme 1) were synthesized as reported by us previously.16 A solution of 1c (0.073 g, 0.06 mmol) in MeOH/DCM (10 mL) was added to a solution of [Eu(btfa)3(H2O)2] (0.050 g, 0.06 mmol) in MeOH/DCM (10 mL). The reaction mixture was left overnight with stirring at RT. The solution was left for slow solvent evaporation, after which solid product was obtained as a yellow solid. The solid product was washed with cold ethanol and dried in vacuo to obtain a light yellow solid. IR: ν/cm−1 –C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C– 2087 cm−1; C = O 1610 cm−1 (Fig. S1, ESI†). C80H94EuF9N2O6P4Pt2; calc. C, 47.65; H, 4.70; N, 1.39%; found: C, 47.63; H, 4.67; N, 1.36%. (Q-TOF) LC/MS = 2016.5935 m/z [M+] (Fig. S2, ESI†). 1H NMR (400 MHz, CDCl3): δ 12.45 (b, 2H); δ 9.34 (d, 2H, J = 7.2 Hz), 9.17 (d, 2H, J = 7.2 Hz), δ 8.60–6.0 (m, 25 H); δ 3.34 (ss, 3H); 1.95 (b, 24H), 1.24 (b, 36H) (Fig. S3, ESI†). 13C NMR (100.6 MHz, CDCl3): δ 187.48, 176.99, 155.10, 138.10, 132.48, 126.44, 125.92 125.70, 124.32, 120.43 121.89 (C
C– 2087 cm−1; C = O 1610 cm−1 (Fig. S1, ESI†). C80H94EuF9N2O6P4Pt2; calc. C, 47.65; H, 4.70; N, 1.39%; found: C, 47.63; H, 4.67; N, 1.36%. (Q-TOF) LC/MS = 2016.5935 m/z [M+] (Fig. S2, ESI†). 1H NMR (400 MHz, CDCl3): δ 12.45 (b, 2H); δ 9.34 (d, 2H, J = 7.2 Hz), 9.17 (d, 2H, J = 7.2 Hz), δ 8.60–6.0 (m, 25 H); δ 3.34 (ss, 3H); 1.95 (b, 24H), 1.24 (b, 36H) (Fig. S3, ESI†). 13C NMR (100.6 MHz, CDCl3): δ 187.48, 176.99, 155.10, 138.10, 132.48, 126.44, 125.92 125.70, 124.32, 120.43 121.89 (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C), 94.29, 57.82, 28.67, 14.08 (CH2), 7.39 (CH3) (Fig. S4, ESI†). NB. The NMR spectroscopic signals were broadened by the presence of the highly paramagnetic Eu(III) ion.
C), 94.29, 57.82, 28.67, 14.08 (CH2), 7.39 (CH3) (Fig. S4, ESI†). NB. The NMR spectroscopic signals were broadened by the presence of the highly paramagnetic Eu(III) ion.
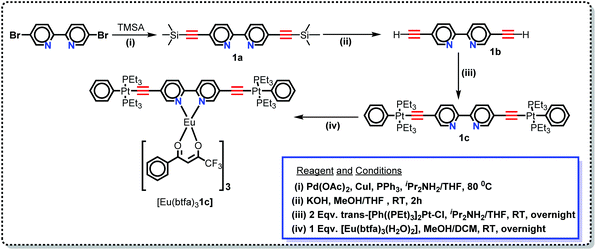 |
| | Scheme 1 Synthetic protocol for the Pt(II) di-yne organometallic chromophore and the heterotrinuclear (d–f–d) complex. | |
2.3. Spectrofluorimetric measurements
UV–visible spectra were recorded on a Varian Cary 50 spectrophotometer in the 200–600 nm range. Quartz cuvettes with 1 cm path length were used, and solvent background corrections were applied. The steady state emission spectrum of the Eu(III) complex and its phosphorescence lifetime in solution were recorded on an Edinburgh FS5 fluorimeter at room-temperature (RT). The measured time dependent emission signal intensity was fitted to exponential functions convoluted with the system response function. The goodness of the fit was judged by the value of the reduced chi-squared (χ2). In all the experiments, samples were contained in a 1 cm path length quartz cell, and the measurements were conducted at 24 ± 1 °C. Important photophysical parameters such as the Judd–Ofelt (Ω2 and Ω4), radiative (AR) and non-radiative (ANR) decay rates, radiative lifetime (τrad), and intrinsic quantum yield (QEuEu) of the heterotrinuclear complex was estimated with the help of the following equations and the details are discussed in our recent report.5c| | 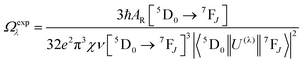 | (1) |
| | 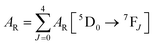 | (2) |
| | 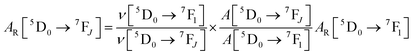 | (3) |
| | 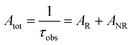 | (4) |
| | 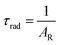 | (5) |
| | 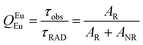 | (6) |
Photoluminescent quantum yield (PLQY) of the complex was measured using previously reported methods.22 Both the standard complex [Eu(btfa)3(H2O)2] and [Eu(btfa)31c] were dissolved in DCM and treated similarly in terms of absorption and emission measurements. The excitation wavelength was 360 nm and measurements were carried out at room temperature, with a slit width of 1.0 nm for the excitation, and 1.0 nm for the emission. The Φ of [Eu(btfa)31c] was measured relative to solution of [Eu(btfa)3(H2O)2].23
2.4. Cyclic voltammetry (CV)
Cyclic voltammetry (CV) was performed at room temperature at a scan rate of 100 mV s−1 using a standard three-electrode configuration employing (i) a Pt wire counter electrode, (ii) a 3.0 mm diameter glassy carbon working electrode (GCE) immersed in deaerated dichloromethane solution with approx. 1 mM concentration of redox active material and (iii) an Ag/AgCl non-aqueous reference electrode kit (all from BASi, USA). The Ag/AgCl non-aqueous reference electrode was filled with 0.1 M n-Bu4NPF6 containing ca. 10 mM AgCl in order to provide a constant reference potential; to allow comparison with theoretical calculations, this was subsequently corrected to the ferrocene/ferrocenium potential in the same electrolyte on the day of use.
2.5. Theoretical analysis
2.5.1. Elucidation of ground-state geometry and determination of singlet and triplet state.
The crystallographic structure of the organometallic chromophore 1c was obtained previously by us.5c This was utilized to aid the drawing of the starting geometry of the hetero-trinuclear complex [Eu(btfa)31c] and was first optimized with the semiempirical quantum mechanical Sparkle/PM6 model24 implemented in the MOPAC2016 software,25 without imposing any symmetry restrictions. The optimized Sparkle/PM6 geometry was used to finally elucidate the structure of [Eu(btfa)31c] by the DFT approach at the B3LYP level of theory with the help of the ORCA 4.2.1 software package.26 The SVP basis set27 was used to represent the electronic structure of the hydrogen (H) atom as (4s1p)/[2s1p], while the carbon (C), nitrogen (N), oxygen (O) and fluorine (F) atoms are treated as (7s4p1d)/[3s2p1d] by SVP. The electronic structure of the Eu and Pt atoms were represented by the MWB(52) and LANL(68)28 effective core potentials (ECP),28 respectively, which considered 52 and 68 electrons in each of the respective cores. For Eu and Pt atoms the remaining electrons were treated as (7s6p5d)/[5s4p3d] and (7s6p5d1f)/[6s3p2d1f], respectively. Finally, the phosphorus (P) atom was represented by the LANL(10)28 ECP with the remaining electrons being treated as (10s7p1d)/[4s3p1d].
Using the B3LYP geometry the singlet and triplet states of the coordinated ligands were determined with the time-dependent density functional theory (TD-DFT) approach, applying the CAM-B3LYP functional.28 The elements were represented by the same basis set and ECPs specified for the procedure of geometry optimization. As in a previous study5a the effect of the dichloromethane solvent was implicitly considered and did not promote change in the excited states energies, therefore such effect was not considered in the current work. The corresponding absorption spectrum was obtained from fitting to a Lorentzian function with a half-width at half maximum (HWHM) arbitrarily attributed as 10 nm.
2.5.2. Intermolecular energy transfer (IET) rate.
The most recent Malta's model29 implemented into LUMPAC 1.4.121 was employed in the ET rates calculation involving the main ET channels for [Eu(btfa)31c]. Such a model considers the contribution from two mechanisms, being the ligand–metal ET in view only of the direct coulombic interaction calculated by:| | 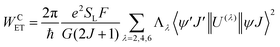 | (7) |
| | 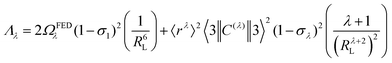 | (8) |
The ligand–metal ET rates considering only the exchange mechanism is given by:
| | 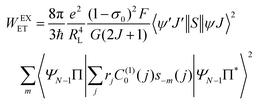 | (9) |
The 〈ψ′J′∥U(λ)∥ψJ〉2 and 〈ψ′J′∥S∥ψJ〉2 reduced matrix elements provide the selection rules for the direct coulombic interaction (CI) and exchange (Ex) mechanisms, respectively. As a consequence, the electronic excitation of the states 5D4 ← 7F0, 5G6 ← 7F0, and 5L6 ← 7F0 for the Eu(III) ion are governed by the multipolar mechanism, while the exchange mechanism dominates the 5D1 ← 7F0 and 5D0 ← 7F1 excitations. Reference21 presents the details of all terms contained in the eqn (7)–(9).
The (1 − σ0) shielding factor, from eqn (9), deserves particular mention and is estimated as a function of the distance from the Ln(III) ion nucleus to the electronic barycentre of the ligand donor (or acceptor) state,29 such distance is known as RL (eqn (11)).
| | 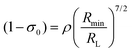 | (10) |
| | 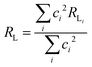 | (11) |
where
ci is a given molecular orbital coefficient of the
i atom that contributes to the ligand state,
RL,i is the distance from
i atom to the Ln(
III) ion, and
Rmin is the smallest distance between the atoms coordinated directly and the Ln(
III) ion. The
ρ overlap integral between the valence shells of the Ln(
III) ion and the ligating atom usually assumes a value equal to 0.05.
The F term, from eqn (7) and (9), corresponds to the energy mismatch spectral overlap and is approximately calculated by:
| | 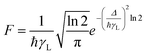 | (12) |
where the ligand bandwidth at half-height,
γL (in s
−1) is considered as being much larger than the widths of the 4f–4f transitions of Ln(
III) ions (
γLn). The
Δ quantity (in erg) is the energy difference between donor and acceptor energy states involved in the ligand–metal ET. Back ET rate is calculated multiplying the corresponding direct ET rate by the Boltzmann factor
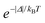
, where
kB stands for the Boltzmann constant and
T is assumed as being the environment temperature.
The ΩFEDλ corresponds to the forced electric dipole (FED) intensity parameters, which is derived from the Judd–Ofelt theory (eqn (13)), and is taken from the eqn (14) neglecting the contribution from the dynamic coupling (DC). The FED and DC contributions depend on the so-called odd-rank ligand field parameter (γtp) and Γtp, respectively.
| | 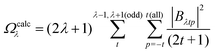 | (13) |
| | 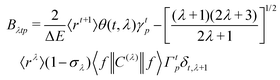 | (14) |
| | 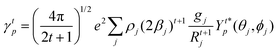 | (15) |
| | 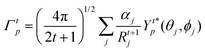 | (16) |
The j index runs over the atoms coordinated directly to the lanthanide ion, Rj corresponds to the distance between a given j atom and the lanthanide ion, θj and ϕj are the corresponding angular coordinates. The charge factors (gj) and polarizabilities (αj), present in eqn (15) and (16), respectively, were adjusted using the QDC model30 to reproduce the experimental values of Ωλ. QDC model is implemented into LUMPAC21 and postulates that the gj are obtained from the product between an adjustable parameter (Q) and each ZDO (Zero Differential Overlap) electronic density (qj) of each j atom (eqn (17)). As shown in eqn (18), the αj quantities are calculated by using the D and C adjustable parameters together with the electrophilic superdelocalizabilities (SE). The reference21 details all terms present in eqn (13)–(18).
From the energy of the occupied molecular orbital and the corresponding linear coefficients calculated with Sparkle/PM6, considering the B3LYP geometry of [Eu(btfa)31c], the qj and SEj quantities were obtained using LUMPAC.
2.5.3. Theoretical quantum yield.
The PLQY (q) is an important spectroscopic parameter and is defined as the ratio of the number of emitted photons by the lanthanide ion to the number of absorbed photons by the ligand. For the Eu(III) ion, q is calculated using the following equation:| | 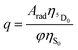 | (19) |
where φ is the absorption rate (s−1) from the fundamental singlet to the excited singlet of the ligand. ηS0 and 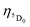 are the energetic population of the S0 fundamental state of the ligand and the 5D0 emitting state of the Eu3+, respectively.
are the energetic population of the S0 fundamental state of the ligand and the 5D0 emitting state of the Eu3+, respectively.
The radiative emission rate (Arad) depends on the theoretical intensity parameters (eqn (13)) and for the europium ion is calculated by:
| | 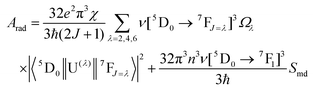 | (20) |
where
e is the elementary charge; 2
J + 1 is the degeneracy of the initial state, for Eu
3+ the
5D
0 emitting is considered (
J = 0). The energies of the barycentres of the respective transitions are represented by the
ν[
5D
0 →
7F
J] quantities.
χ is the Lorentz local-field correction term, and is given by
χ =
n(
n2 + 2)
2/9, where the
n refractive index was considered as equal to 1.424, regarding the DCM solvent. The magnetic dipole strength (
Smd) of the
5D
0 →
7F
1 transition is theoretically equals 9.6 × 10
−42 esu
2 cm
2.
30
From a system of equations in the steady-state condition the normalized population of a given a level considered in the ET modelling (ηj) is calculated analytically by:
| | 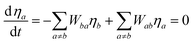 | (21) |
where
Wab is the transfer rate from level
a to level
b, and if
a =
b,
Wab = 0.
3. Results and discussion
3.1. Synthesis, characterization and elucidation of the ground state geometry
In this work, we have synthesized a new hetero-trinuclear complex (Scheme 1) bearing a rigid dinuclear Pt(II) di-yne chromophore. The chemical structure of the Pt(II) di-yne chromophore, heterotrinuclear (d–f–d) complex and their step-wise synthesis is depicted in Scheme 1. Trans-[(Ph)(Et3P)2Pt–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(PEt3)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl) was synthesized following our previously reported method.16 Briefly, 5,5′-dibromo-2,2′-bipyridine was protected with trimethylsilylethyne yielding 1a (Scheme 1) by a Sonogashira cross-coupling reaction.31 Smooth removal of trimethylsilyl groups with KOH/MeOH (Scheme 1) followed by dehydrohalogenation reaction of the diterminal alkyne 1b with trans-[Ph(Et3P)2PtCl] yielded the Pt(II) di-yne 1c (Scheme 1) as a yellow solid. The heterotrinuclear complex [Eu(btfa)31c] (Scheme 1) was synthesized in 74.0% yield by reacting [Eu(btfa)3(H2O)2] and Pt(II) di-yne (1c) in 1
C–Pt(PEt3)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl) was synthesized following our previously reported method.16 Briefly, 5,5′-dibromo-2,2′-bipyridine was protected with trimethylsilylethyne yielding 1a (Scheme 1) by a Sonogashira cross-coupling reaction.31 Smooth removal of trimethylsilyl groups with KOH/MeOH (Scheme 1) followed by dehydrohalogenation reaction of the diterminal alkyne 1b with trans-[Ph(Et3P)2PtCl] yielded the Pt(II) di-yne 1c (Scheme 1) as a yellow solid. The heterotrinuclear complex [Eu(btfa)31c] (Scheme 1) was synthesized in 74.0% yield by reacting [Eu(btfa)3(H2O)2] and Pt(II) di-yne (1c) in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. The formulation of [Eu(btfa)31c] was confirmed by elemental analysis, ESI-MS and IR spectroscopy. The elemental analysis shows satisfactory results and confirms the proposed formulation for the newly synthesized complex. The result of the elemental analysis was further confirmed by the ESI-MS. The spectrum of [Eu(btfa)31c] in positive ion mode was recorded in MeOH. The complex displayed a molecular ion peak at 2016.59 m/z [M+] (Fig. S2, ESI†) and thus confirms the proposed stoichiometry shown in Chart 1. The spectrum also displayed various peaks which could be due to fragmentation of the fluorinated β-diketonate ligands.32 The results of the elemental analysis and ESI† were further confirmed by IR spectroscopy. The IR spectra of [Eu(btfa)31c] together with those of [Eu(btfa)3(H2O)2] and 1c are shown in Fig. S1, ESI.† The spectrum of [Eu(btfa)31c] displayed a single, sharp –C
1 ratio. The formulation of [Eu(btfa)31c] was confirmed by elemental analysis, ESI-MS and IR spectroscopy. The elemental analysis shows satisfactory results and confirms the proposed formulation for the newly synthesized complex. The result of the elemental analysis was further confirmed by the ESI-MS. The spectrum of [Eu(btfa)31c] in positive ion mode was recorded in MeOH. The complex displayed a molecular ion peak at 2016.59 m/z [M+] (Fig. S2, ESI†) and thus confirms the proposed stoichiometry shown in Chart 1. The spectrum also displayed various peaks which could be due to fragmentation of the fluorinated β-diketonate ligands.32 The results of the elemental analysis and ESI† were further confirmed by IR spectroscopy. The IR spectra of [Eu(btfa)31c] together with those of [Eu(btfa)3(H2O)2] and 1c are shown in Fig. S1, ESI.† The spectrum of [Eu(btfa)31c] displayed a single, sharp –C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C– stretch at 2087 cm−1, consistent with a trans configuration of the ethynyl units around the Pt(II) centres.15b The presence of this stretching absorption clearly supports the formation of the hetero-trinuclear complex. Moreover, the IR spectra of the complex exhibits C
C– stretch at 2087 cm−1, consistent with a trans configuration of the ethynyl units around the Pt(II) centres.15b The presence of this stretching absorption clearly supports the formation of the hetero-trinuclear complex. Moreover, the IR spectra of the complex exhibits C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations at 1610 and 1571 cm−1, respectively, characteristics of the lanthanide chelate complexes containing β-diketone ligand.4c The appearance of (PCH2CH3)3 twisting and bending vibration bands in the spectrum also provide additional evidence of complex formation; however, the position of the peaks remain unaltered appearing at 3041, 2961 and 2871 cm−1 as observed in the Pt(II) di-yne chromophore. The results clearly provide unambiguous support for the formation of the heterotrinuclear complex [Eu(btfa)31c].
C stretching vibrations at 1610 and 1571 cm−1, respectively, characteristics of the lanthanide chelate complexes containing β-diketone ligand.4c The appearance of (PCH2CH3)3 twisting and bending vibration bands in the spectrum also provide additional evidence of complex formation; however, the position of the peaks remain unaltered appearing at 3041, 2961 and 2871 cm−1 as observed in the Pt(II) di-yne chromophore. The results clearly provide unambiguous support for the formation of the heterotrinuclear complex [Eu(btfa)31c].
Repeated attempts to obtain single crystals of the complex suitable for X-ray analysis failed. In fact, for predicting the photophysical properties of the given Eu complex, one needs to have the theoretical structure of the complex, even though the experimental structure is available.5a Given this fact, the ground state geometry of the present hetero-trinuclear complex was elucidated by the DFT method shown in Fig. 1, and the coordination geometry of EuN2O6 polyhedron is highlighted. The crystallographic structure of the 1c [EWOQEM Cambridge Structural Database (CSD) code]16 shows a linear orientation around the –C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C– triple bond. However, in the present case, we noted distortion when 1c is coordinated to the Eu(III) ion. Such a structural modification is observed in the literature when ligands comparable to 1c are coordinated to a given metal centre (e.g., ASUVER and KIRSOU CSD refcodes),33 and could be due to the interactions involving the peripheral substituents in the different ligands of 1c with the β-diketonate ligands. Spherical coordinates of coordination polyhedron are gathered in Table S1, ESI,† and, as can be seen, the Eu–N bonds predicted by the applied DFT approach are 2.684 and 2.647 Å, in line with literature values.34 On the other hand, the Eu–O bonds are in the ranges of 2.399–2.422 Å and plainly the coordination polyhedron is of low symmetry.
C– triple bond. However, in the present case, we noted distortion when 1c is coordinated to the Eu(III) ion. Such a structural modification is observed in the literature when ligands comparable to 1c are coordinated to a given metal centre (e.g., ASUVER and KIRSOU CSD refcodes),33 and could be due to the interactions involving the peripheral substituents in the different ligands of 1c with the β-diketonate ligands. Spherical coordinates of coordination polyhedron are gathered in Table S1, ESI,† and, as can be seen, the Eu–N bonds predicted by the applied DFT approach are 2.684 and 2.647 Å, in line with literature values.34 On the other hand, the Eu–O bonds are in the ranges of 2.399–2.422 Å and plainly the coordination polyhedron is of low symmetry.
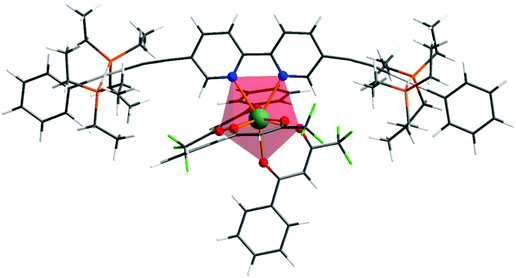 |
| | Fig. 1 Ground state geometry of the heterotrinuclear complex optimized at the B3LYP level of theory. | |
3.2. Optical absorption spectroscopy
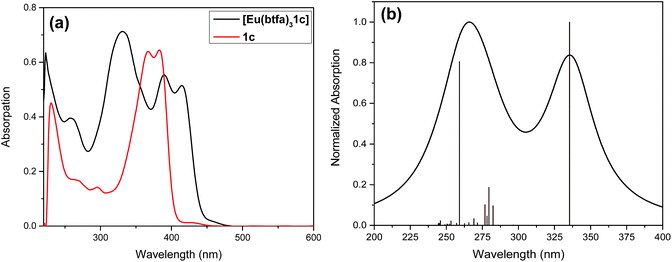
Fig. 2 shows the optical absorption spectra of the Pt(II) di-yne chromophore (1c) and of [Eu(btfa)31c]. The spectrum of the Pt(II) chromophore displays a strong split peak at 382 nm due to the π–π* transitions. It is important to emphasize that in the spectrum of 1c with the ethynyl groups at the 5,5′-positions there is a 50 nm red shift compared to 6,6′-ethynyl based Pt(II) chromophore. This shift is a result of uninterrupted conjugation along the chromophore and attests to our assumption as stated in the introduction. The absorption spectrum of [Eu(btfa)31c] is dominated by spin allowed π–π* transitions of the β-diketone ligand and 1c in the UV–visible region (200–418 nm) with three major absorption peaks at 331 nm, 389 nm and 416 nm. As noted in the organometallic chromophore 1c, the spectrum of the present heterotrinuclear complex displays a red shift and this extends into the visible region of the spectrum compared to previously reported [Eu(btfa)31d] [1d] = [(Ph)(Et3P)2Pt–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl)4c (Fig S4, ESI†). It is thus excitable across a wide range of wavelengths from UV to the visible. The spectral differences of the two systems encouraged us to study the photoluminescence (PL) of the new system further.
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl)4c (Fig S4, ESI†). It is thus excitable across a wide range of wavelengths from UV to the visible. The spectral differences of the two systems encouraged us to study the photoluminescence (PL) of the new system further.
 |
| | Fig. 2 (a) Optical absorption spectra of 1c and [Eu(btfa)31c] at RT. (b) Theoretical electronic spectrum calculated at the CAM-B3LYP level of theory using the B3LYP geometry for [Eu(btfa)31c]. | |
To underpin the optical absorption spectroscopy result and to clearly understand the origin of transition, we obtained the theoretical absorption spectrum of the present complex (Fig. 2b). As shown in Fig. 2b, the theoretical absorption spectrum is in qualitative agreement with the experimental spectrum. The aforementioned assigned electronic transition is further supported by the molecular orbital (MO) analysis. Table 1 shows that the electronic transition highest occupied molecule orbital (HOMO) → lowest unoccupied molecular orbital (LUMO) dominates the band located at the highest wavelengths, and such MOs are centred in the molecular fragment present in the 1c complex (Fig. 3). On the other hand, the band corresponding to the lowest wavelengths is dominated by electronic transitions involving MOs centred on the β-diketonate ligands.
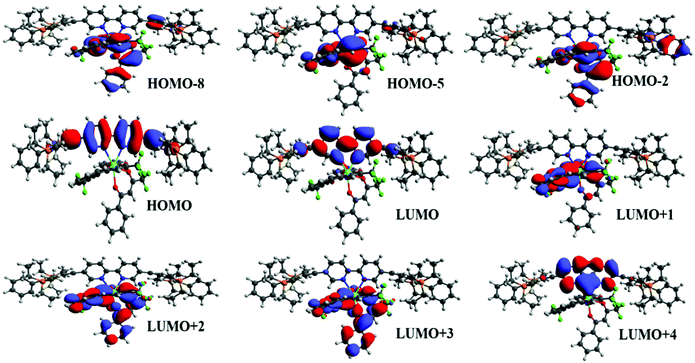 |
| | Fig. 3 Most relevant MOs calculated at the TD-DFT CAM-BLYP level of theory that explain the main electronic transitions. | |
Table 1 Electron transition configurations calculated at the TD-DFT CAM-B3LYP level of theory for the most relevant singlet states of [Eu(btfa)31c]
| Wavelength |
Ligand |
Oscillator strength |
Major contribution |
Total |
| 338.09 nm |
1c
|
1.79 |
HOMO → LUMO |
87.30% |
| 263.82 nm |
1c/btfa |
1.44 |
HOMO−2 → LUMO+3 (25.15%) |
60.91% |
| HOMO−5 → LUMO+1 (22.94%) |
| HOMO−8 → LUMO+2 (12.81%) |
| 277.85 nm |
1c/btfa |
0.34 |
HOMO → LUMO+1 (41.21%) |
71.54% |
| HOMO → LUMO+4 (30.33%) |
3.3. PL properties
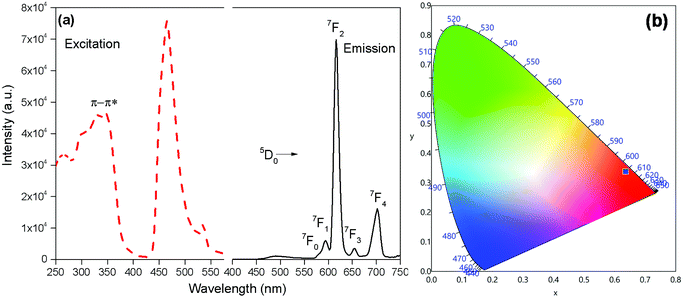
The PL and excitation spectrum of [Eu(btfa)31c] recorded in DCM at RT is shown in Fig. 4a. The excitation spectrum of the complex was recorded by monitoring the most intense emission transition 5D0 → 7F2 at 616 nm. The excitation spectrum contains a broad band in the region between 270–400 nm. Apart from this, the spectrum exhibits Eu(III) excitation transitions assigned to 7F0 → 5D2 (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 551 cm−1; 464 nm) and 7F0 → 5D1 (18
551 cm−1; 464 nm) and 7F0 → 5D1 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657cm−1; 536 nm). The intensity of the excitation transition is higher than the broad band suggesting that the heterotrinuclear complex could be excitable at the blue 464 nm wavelength.
657cm−1; 536 nm). The intensity of the excitation transition is higher than the broad band suggesting that the heterotrinuclear complex could be excitable at the blue 464 nm wavelength.
 |
| | Fig. 4 (a) Excitation (broken line) and emission (solid line) spectra (λex = 345 nm) (b) CIE-1931 chromaticity diagram demonstrating the calculated colour coordinate (x, y) values for [Eu(btfa)31c] in DCM at RT. | |
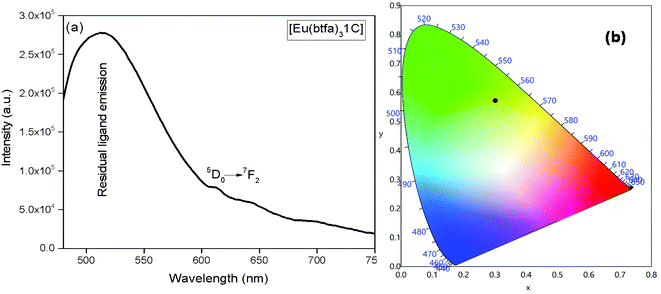
The emission spectrum of [Eu(btfa)31c] at RT was obtained by exciting it at λmax 345 nm (Fig. 4a). The spectrum displays typical well resolved sharp Eu(III) emission transitions at 579 nm, 594 nm, 616 nm, 653 nm and 701 nm, which corresponds to D0 → 7F0, 5D0 → 7F1, 5D0 → 7F2, 5D0 → 7F3 and 5D0 → 7F4, respectively. The spectrum is dominated by the narrow hypersensitive electric dipole 5D0 → 7F2 transitions (FWHM = 12.57 nm, Table 2). Moreover, the spectrum does show some residual ligand fluorescence in the region between 425–531 nm, suggesting less efficient energy transfer (ET) from the newly synthesized organometallic chromophore compared to [Eu(btfa)31d]. The 1931 CIE (Commission internationale de l’éclairage) colour coordinate of the heterotrinuclear complex calculated from the PL spectrum shows a typical red emission with colour coordinates (x = 0.6358; y = 0.3381, Table 2), which is very close to National Television System Committee (NTSC) and, thus, could be beneficial for the design of monochromatic red emitter for full colour displays.5a Moreover, as mentioned previously, we excited the complex at 464 nm. Interestingly, the complex displays a totally different PL spectrum with a broad band that covers a region between 475–750 nm (Fig. 5a). A close analysis of the spectrum shows that the broadband also comprises very faint Eu(III) emission transitions 5D0 → 7F2 at 613 nm. This could be caused by the back-energy transfer from the 5D0 state to the ligand triplet state leading to very severe quenching of the Eu(III) emission. Furthermore, the PL spectrum was utilized to calculate the CIE colour coordinates which is in green region with (CIE)x,y = 0.3011, 0.5726 (Fig. 5b). Thus, the dual emitting properties of the complex could be utilized in full colour display devices.3c,35
 |
| | Fig. 5 (a) Emission spectrum in DCM at RT at 464 nm, (b) CIE-1931 chromaticity diagram demonstrating the calculated color coordinate (x, y) values for [Eu(btfa)31c] complex. | |
Table 2 Experimental intensity parameters (Ω2 and Ω4), radiative (AR) and non-radiative (ANR) rates, Intensity ratio, observed luminescence lifetime (τobs), and intrinsic quantum yield (ΦEu) of [Eu(btfa)31c]
| Complex |
Ω
2
|
Ω
4
|
FWHM (nm) |
τ
obs
|
τ
rad
|
A
R
|
A
NR
|
Q
LEu (%) |
Q
EuEu (%) |
R
21
|
CIE(x,y) |
| ×10−20 cm2 |
(μs) |
(s−1) |
*Value in the square brackets are for [Eu(btfa)31d]4c1d = [(Ph)(Et3P)2Pt–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl). Calculated using eqn (1). Calculated using eqn (5). Calculated using eqn (2)–(4). Calculated using eqn (6). C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl). Calculated using eqn (1). Calculated using eqn (5). Calculated using eqn (2)–(4). Calculated using eqn (6). |
|
[Eu(btfa)31c]
|
20.61a [29.45]* |
14.80a [8.90]* |
12.57 |
τ
1 = 39.52 (6.91%) and τ2 = 519.86 (93.09%) |
1347b |
742.51c [912.81]* |
1184.28c [779.24] |
15.10 |
38.54d [53.95] |
11.65 [16.60] |
0.6358; 0.3381 [0.668; 0.324] |
| Theoretical |
20.61 |
14.79 |
— |
— |
— |
760.94 |
1162.66 |
19.8 |
39.56 |
— |
— |
A range of important photophysical parameters can be determined from the PL spectrum of Eu(IIII) coupled with the experimental decay lifetime. Firstly, the important parameter is intensity ratio ‘R21’ which is a measure of asymmetric environment around Eu(III) ion and can be estimated by the ratio of intensity of the electric dipole (ED) 5D0 → 7F2 transition to the magnetic dipole (MD) 5D0 → 7F1 transition.5a The high R21 = 11.65 value for the present complex indicates that it is not a centrosymmetric complex and the coordination sphere around Eu(III) is highly asymmetric. As mentioned above, and to evaluate important photophysical parameters such as AR, ANR, τrad, Ω2 and Ω4, we first determined the experimental decay lifetime (τobs) of the 5D0 excited state of the complex in solution by exciting it at λmaxEx and fitting the decay curves (Fig. S6, ESI† and Table 2). The decay curves fit with biexponential behaviour with τobs value τ1 = 39.52 (6.91%) and τ2 = 519.86 μs (93.09%) (Table 2). The AR and ANR decay rates of the complex were estimated utilizing the steady-state PL spectrum and τobs (the longer lifetime component was utilized for the calculation and refractive index 1.424) and are summarized in Table 2. The complex displayed a larger ANR = 1184.28 s−1 value compared to the reported 2,2′-bipyridine-6,6′-diyl based complex as shown in Chart 1. Despite the same chemical composition, interestingly, the larger ANR displayed by [Eu(btfa)31c] can be attributed to the linearity of the present chromophore compared to the bent shape of 2,2′-bipyridine-6,6′-diyl.4c Finally, Ω2 and Ω4 were calculated (Table 2); the high values of Ω2 = 20.61 × 10−20 cm2 suggest that the Eu(III) ion in the present complex is surrounded by a highly polarizable environment. The parameter Ω4 is related to the rigidity and long-range effects such as hydrogen bonding, π–π stacking and large value (Ω4 ≈ 14.80 × 10−20 cm2) is an indication of the presence of these effects.6 A comparison of the Ω2 parameter of the present complex suggests that 2,2′-bipyridine-5,5′-diyl unit is more symmetrical than the 2,2′-bipyridine-6,6′-diyl unit (Ω2 = 29.45 × 10−20 cm2)4c and results in less hypersensitivity of the ED 5D0 → 7F2 transition. This is further supported by the observed lower R21 = 11.65 value compared to that in the 2,2′-bipyridine-6,6′-diyl based complex (R21 = 16.60).4c The intrinsic quantum yield (QEuEu) is calculated by utilizing eqn (6) and the data is summarized in Table 3. The complex [Eu(btfa)31c] displayed high QEuEu = 38.45%, however, it is lower than [Eu(btfa)31d] QEuEu = 53.95%,4c which is due to the increased ANR value of the present complex.
Table 3 Energy of the singlet and triplet excited states most relevant, distance from energy donor to acceptor centre (RL), and electronic transition configurations calculated at the TD-DFT CAM-B3LYP level of theory for the corresponding triplet state of [Eu(btfa)31c]
| State |
Energy |
R
L
|
Major contribution |
Total |
| S1 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.5 cm−1 577.5 cm−1 |
5.49 Å |
HOMO → LUMO |
87.30% |
| T1 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2 cm−1 442.2 cm−1 |
4.98 Å |
HOMO → LUMO (79.55%) |
79.55% |
| T2 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.2 cm−1 664.2 cm−1 |
4.35 Å |
HOMO−2 → LUMO+2 (26.69%) |
62.03% |
| HOMO−2 → LUMO+3 (19.00%) |
| HOMO−8 → LUMO+3 (16.34%) |
The fitted Ω2 and Ω4 values using the QDC model are in perfect agreement with the corresponding experimental values. This procedure is important to obtain the forced electric dipole contribution for the intensity parameters, which are presented in Table S2, ESI† and are used to evaluate the energy transfer rates via the direct coulombic interaction mechanism.
3.4. Intermolecular energy transfer (IET) process
The energy of the most relevant triplet excited states, as well as the respective distance between donor and acceptor centre (RL), calculated at the TD-DFT CAM-B3LYP level of theory are shown in Table 3. In addition, the table presents the electronic transition configurations for each of the relevant triplet states of [Eu(btfa)31c]. The HOMO → LUMO transition is the one responsible for the lowest triplet state and as pictured in Fig. 4, such orbitals are centred on the ligands present in 1c. In this manner, the lowest triplet state (T1 = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2 cm−1) calculated at the CAM-B3LYP level of theory using the B3LPY geometry is characterized as involving MOs centred on the ligands present in the 1c molecular fragment. The energy of the next lowest triplet state (T2) is equal to 22
442.2 cm−1) calculated at the CAM-B3LYP level of theory using the B3LPY geometry is characterized as involving MOs centred on the ligands present in the 1c molecular fragment. The energy of the next lowest triplet state (T2) is equal to 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 cm−1 and the most relevant electronic transitions involve MOs centred mainly on the btfa ligands. RL values present in Table 3 show that the donor centre is more distant from the Eu(IIII) centre for T2 in comparison with T1 due to the contribution of the btfa ligands in T2.
664 cm−1 and the most relevant electronic transitions involve MOs centred mainly on the btfa ligands. RL values present in Table 3 show that the donor centre is more distant from the Eu(IIII) centre for T2 in comparison with T1 due to the contribution of the btfa ligands in T2.
In order to take account the effect of the distinct molecular groups (Table 3) in the modelling of the ligand – Eu(III) energy transfer, the diagram pictured in Fig. 6 was proposed, in which the ET rates were calculated applying the LUMPAC program. In the ET modelling, for Eu(III) only three states were considered, namely, 5D4 (ca. 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 586 cm−1), 5D1 (ca. 19
586 cm−1), 5D1 (ca. 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 cm−1), and 5D0 (ca. 17
027 cm−1), and 5D0 (ca. 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293 cm−1), with the energy values obtained from Carnall et al.36 To calculate the energetic population involving the states shown in Fig. 6, typical experimental values for the non-radiative rates in coordination compounds were considered.36
293 cm−1), with the energy values obtained from Carnall et al.36 To calculate the energetic population involving the states shown in Fig. 6, typical experimental values for the non-radiative rates in coordination compounds were considered.36
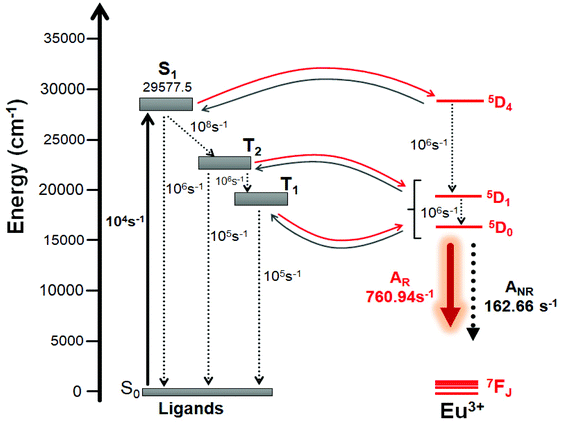 |
| | Fig. 6 Schematic energy-level diagram showing the most important ET channels for [Eu(btfa)31c]. Please see Table 5 for the corresponding values of ET rates. | |
For complexes containing β-diketonate ligands it is known that the ET channel is the one dominated by the exchange mechanism (Dexter mechanism), and the ET value the order of 108 s−1 (Table 4) calculated with the exchange mechanism confirms this. The triplet → (5D0, 5D1) channels are related to the 5D1 ← 7F0 and 5D0 ← 7F1 excitations, respectively, where the 7F1 state is considered as being thermally populated.5c By considering the schematic energy-level diagram postulated in Fig. 6 together the ET rates presented in Table 4, the populations of the S0 and 5D0 states were calculated (ηS0 = 0.28 and 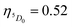 ), which provided a theoretical PLQY of 19.8% that is close to experimentally determined value 15.10%.
), which provided a theoretical PLQY of 19.8% that is close to experimentally determined value 15.10%.
Table 4 Energy transfer rates calculated by the Malta's model using LUMPAC for the [Eu(btfa)31c] complexes with the ligand state energies calculated at the TD-DFT CAM-B3LYP level of theory
| Ligand state (cm−1) |
|
4f state (cm−1) |
ET rate (s−1) |
Energy back-transfer rate (s−1) |
S1 (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.5) 577.5) |
→ |
5D4 (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 586) 586) |
1.60 × 104 |
1.14 × 101 |
T2 (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.2) 664.2) |
→ |
5D1 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027) 027) |
1.27 × 109 |
3.36 × 101 |
T2 (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.2) 664.2) |
→ |
5D0 (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293) 293) |
8.72 × 108 |
5.66 × 10−3 |
T1 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2) 442.2) |
→ |
5D1 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027) 027) |
5.96 × 108 |
6.73 × 105 |
T1 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2) 442.2) |
→ |
5D1 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027) 027) |
6.81 × 108 |
1.88 × 102 |
3.5. Electrochemical properties
Preliminary CV experiments were conducted with a glassy carbon disk, Pt wire, and Ag/AgCl electrode as the working electrode, counter electrode, and reference electrode, respectively, in deaerated DCM solution containing 0.1 M tetrabutylammonium hexafluorophosphate (Bu4NPF6) as the electrolyte and approx. 1 mM metal complex. The CV experiment was performed to investigate the electrochemical behaviour of [Eu(btfa)31c] and the related [Eu(btfa)3(H2O)2] in the −2.0 to 2.0 V range. Table 5 contains all the electrochemical parameters and data obtained. The protonated btfa ligand showed two reductions peaks with an initial broad shoulder in the region of −2.0 to 0.0 V and there was no oxidation peak in the positive potential region. Both [Eu(btfa)3(H2O)2] and [Eu(btfa)31c] show an oxidation signal and a complex sequence of reduction signals. We noted a considerable difference in reduction peaks between [Eu(btfa)3(H2O)2] and [Eu(btfa)31c]. New chemically irreversible oxidation peaks appear in positive region at 1.74 V and 1.57 V for [Eu(btfa)3(H2O)2] and for [Eu(btfa)31c] respectively. The latter complex shows a reduction peak at −0.77 V (Fig. 7), which we tentatively assign to the reduction peak of the Eu(III).37 The reduction peak of [Eu(btfa)3(H2O)2] was ca. 0.49 V less negative compared to [Eu(btfa)31c]. This observation suggests that primary ligands play a significant role in changing the electrochemical behaviour of Eu(III) complexes and the shift of reduction peak of Eu(III).38 The other peaks could correspond to the reduction/oxidation of the electrochemically active β-diketonate groups39 or further fragmentation products.
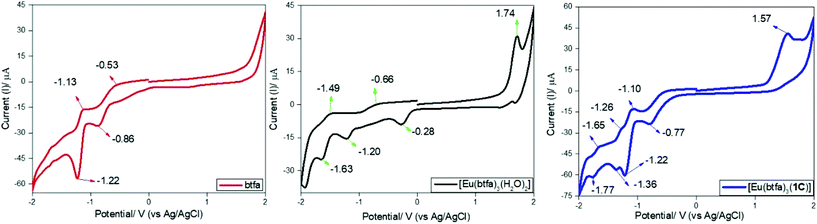 |
| | Fig. 7 Cyclic voltammograms of btfa (red), [Eu(btfa)3(H2O)2] (black) and [Eu(btfa)31c] (blue) in the region between −2.0 to 2.0 V on glassy carbon electrode in 0.1 M Bu4NPF6 solution in DCM at a scan rate of 100 mV s−1. | |
Table 5 Cyclic voltammetry data of btfa, [Eu(btfa)3(H2O)2] and [Eu(btfa)31c]
| Compound |
E
onsetOx (V) |
E
onsetred (V) |
E
OxP (V) |
E
REP (V) |
HOMO (eV) |
LUMO (eV) |
E
eleg (eV) |
E
optg (eV) |
|
E
onsetOx = the onset oxidation potentials; EonsetRe = the onset reduction potentials.
Anodic peak potential.
Cathodic peak potential.
HOMO energy level.
LUMO energy level.
Energy gap measured from electrochemical data according to the Eonset, Eeleg = EonsetOx − Eonsetred eV. The energy LUMO values were calculated by cyclic voltammogram and are displayed in parentheses.
|
| btfa |
−0.82a |
−0.67a |
−0.53b, −1.13b |
−0.86c, −1.22c |
— |
— |
— |
— |
| [Eu(btfa)3(H2O)2] |
1.44a |
−0.06a |
1.74b |
−0.28c, −1.20c, −1.63c |
−5.85d |
−2.49e (−4.35)e |
1.6f |
3.36 |
|
[Eu(btfa)31c]
|
1.19a |
−0.41a |
1.57b |
−0.77c, −1.22c, −1.36c, −1.77c |
−5.60d |
−3.03e (−4.00)e |
1.5f |
2.57 |
| Theoretical (B3LYP) |
— |
— |
— |
— |
−5.40 |
−2.18 |
— |
3.19 |
For calibration, the redox potential of ferrocene/ferrocenium (Fc/Fc+) was measured under the same experimental conditions, and it is located at 0.39 V vs. the Ag/AgCl electrode (Fig. S7. ESI†). HOMO energy values were calculated based on the value of −4.8 eV for Fc with respect to a zero vacuum level.40 The energy levels of the HOMO was estimated according to the following equation:41EHOMO = −(EonsetOx + 4.41) eV where EonsetOx is the onset oxidation potential vs. Ag/AgCl. The energy band gap (Eeleg) was calculated from the onset wavelength of the UV absorption (Eeleg = 1240/λ).42 The LUMO energy level was obtained from the HOMO energy and the energy bandgap (Eeleg = LUMO–HOMO) and ELUMO = −(EonsetRe + 4.41) eV where EonsetRe = onset reduction potential vs. Ag/AgCl. An important disparity was ascertained between the measured optical and electrochemical energy bandgap values. However, there is no contradiction between these values, since they refer to different processes. The optical absorption data provides an estimation of the energy difference of the HOMO–LUMO orbitals, while the electrochemical band gap is consistent with the energy required to form a tightly bound exciton with additional contributions from charging.43 The redox potentials measured by CV afford the absolute energetic positions of the HOMO and LUMO levels (assuming insignificant effects from charging), and the electrochemical or transport bandgap depicts the energy required to form free charge carriers.43,44 Moreover, the theoretically estimated HOMO and LUMO values are almost similar to the experimentally determined value (HOMO ≈ −5.60 eV, Table 5) especially at the B3LYP level (HOMO ≈ −5.40 eV, Table S3, ESI†).
4. Conclusion
In summary, we have utilized a Pt(II) di-yne chromophore incorporating a bipyridine-5,5′,-diyl spacer (1c) as a chelate to synthesize a novel hetero-trinuclear (d–f–d) complex [Eu(btfa)31c]. The structure of the complex was elucidated using DFT methods. The optical absorption spectrum of the complex exhibited transitions in the 200–418 nm range. Interestingly, the complex displayed a red shift compared to the analogous kinked hetero-trinuclear complex reported earlier by us.4c This shift is due to uninterrupted conjugation in the present complex (Chart 1). The PL studies revealed dual emissions, with a typical red emission (CIE; x = 0.6358; y = 0.3381) when excited at 345 nm and a green emission (CIEx,y = 0.3011, 0.5726 at 464 nm excitation. The dual emission could be due to two different triplet states centred at: (a) btfa 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.2 cm−1 with the ET rate 1.27 × 109 s−1 with the negligible energy back-transfer rate (Table 4) and (b) organometallic chromophore (20
664.2 cm−1 with the ET rate 1.27 × 109 s−1 with the negligible energy back-transfer rate (Table 4) and (b) organometallic chromophore (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2 cm−1) with an ET rate 5.96 × 108 s−1 with the energy back-transfer rate of 6.73 × 105 s−1 for the T1 → 5D1. The excited state lifetime of the present complex is in microsecond range typical for europium β-diketonate complexes. The intermolecular energy transfer in the complex on the basis of experimental results and DFT calculations is discussed in detail. Moreover, the calculated photophysical parameters are in excellent agreement with the experimentally observed results.
442.2 cm−1) with an ET rate 5.96 × 108 s−1 with the energy back-transfer rate of 6.73 × 105 s−1 for the T1 → 5D1. The excited state lifetime of the present complex is in microsecond range typical for europium β-diketonate complexes. The intermolecular energy transfer in the complex on the basis of experimental results and DFT calculations is discussed in detail. Moreover, the calculated photophysical parameters are in excellent agreement with the experimentally observed results.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
M. S. K. acknowledges the Research Council (TRC), Oman (Grant: RC/RG-SCI/CHEM/20/01) for funding. I. J. A. B. acknowledges the Ministry of Education, Oman for a Ph.D. scholarship. R. I. thanks HM's Trust Fund (Grant No. SR/SQU/SCI/CHEM/16/02) for a postdoctoral fellowship. W. F. O. thanks PIBIC/CNPq/UFS (02/2019 COPES/POSGRAP/UFS) for a scientific initiation fellowship. P. R. R. is grateful to the Engineering and Physical Sciences Research Council (EPSRC) for continued funding (Grant EP/K004956/1).
References
- A. Haque, R. A. Al-Balushi, I. J. Al-Busaidi, M. S. Khan and P. R. Raithby, Chem. Rev., 2018, 118, 8474–8597 CrossRef CAS.
-
(a)
A. F. Rausch, H. H. H. Homeier and H. Yersin, in Photophysics of Organometallics, ed. A. J. Lees, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 193–235 Search PubMed;
(b) I. J. Al-Busaidi, A. Haque, N. K. Al Rasbi and M. S. Khan, Synth. Met., 2019, 257, 116189 CrossRef CAS;
(c) C.-L. Ho, Z.-Q. Yu and W.-Y. Wong, Chem. Soc. Rev., 2016, 45, 5264–5295 RSC;
(d) W.-Y. Wong, Dalton Trans., 2007, 4495–4510 RSC;
(e)
J. Zhang, L. Xu, C.-L. Ho and W.-Y. Wong, in Polymer Synthesis Based on Triple-Bond Building Blocks, ed. B. Z. Tang and R. Hu, Springer International Publishing, Cham, 2018, pp. 157–189 Search PubMed;
(f) L. Xu, C.-L. Ho, L. Liu and W.-Y. Wong, Coord. Chem. Rev., 2018, 373, 233–257 CrossRef CAS;
(g) C.-L. Ho and W.-Y. Wong, Coord. Chem. Rev., 2013, 257, 1614–1649 CrossRef CAS.
-
(a)
H. Yersin, Highly Efficient Oleds with Phosphorescent Materials, John Wiley & Sons, 2008 Search PubMed;
(b) S. Wang, H. Zhang, B. Zhang, Z. Xie and W.-Y. Wong, Mater. Sci. Eng., R, 2020, 140, 100547 CrossRef;
(c) Z. Chen, C.-L. Ho, L. Wang and W.-Y. Wong, Adv. Mater., 2020, 32, 1903269 CrossRef CAS;
(d) G. Zhou, W.-Y. Wong and X. Yang, Chem. – Asian J., 2011, 6, 1706–1727 CrossRef CAS;
(e) X. Yang, G. Zhou and W.-Y. Wong, Chem. Soc. Rev., 2015, 44, 8484–8575 RSC.
-
(a) A. N. Al-Khalili, I. J. Al-Busaidi, R. Ilmi, M. Al-Mandhary, M. S. Khan and N. K. Al-Rasbi, Inorg. Chim. Acta, 2020, 501, 119226 CrossRef CAS;
(b) K. Binnemans, Coord. Chem. Rev., 2015, 295, 1–45 CrossRef CAS;
(c) R. Ilmi, A. Haque, I. J. Al-Busaidi, N. K. Al Rasbi and M. S. Khan, Dyes Pigm., 2019, 162, 59–66 CrossRef CAS.
-
(a) M. S. Khan, R. Ilmi, W. Sun, J. D. L. Dutra, W. F. Oliveira, L. Zhou, W.-Y. Wong and P. R. Raithby, J. Mater. Chem. C, 2020, 8, 5600–5612 RSC;
(b) R. Ilmi, W. Sun, J. D. L. Dutra, N. K. Al-Rasbi, L. Zhou, P.-C. Qian, W.-Y. Wong, P. R. Raithby and M. S. Khan, J. Mater. Chem. C, 2020, 8, 9816–9827 RSC;
(c) R. Ilmi, M. S. Khan, Z. Li, L. Zhou, W.-Y. Wong, F. Marken and P. R. Raithby, Inorg. Chem., 2019, 58, 8316–8331 CrossRef CAS;
(d) R. Ilmi, S. Kansız, N. K. Al-Rasbi, N. Dege, P. R. Raithby and M. S. Khan, New J. Chem., 2020, 44, 5673–5683 RSC;
(e) R. Ilmi, M. S. Khan, W. Sun, L. Zhou, W.-Y. Wong and P. R. Raithby, J. Mater. Chem. C, 2019, 7, 13966–13975 RSC;
(f) J. Li, J.-Y. Wang and Z.-N. Chen, J. Mater. Chem. C, 2013, 1, 3661–3668 RSC;
(g) M. D. Ward, Coord. Chem. Rev., 2007, 251, 1663–1677 CrossRef CAS;
(h) H.-B. Xu, L.-X. Shi, E. Ma, L.-Y. Zhang, Q.-H. Wei and Z.-N. Chen, Chem. Commun., 2006, 1601–1603 RSC.
- R. Ilmi, S. Anjum, A. Haque and M. S. Khan, J. Photochem. Photobiol., A, 2019, 383, 111968 CrossRef CAS.
- E. G. Moore, A. P. S. Samuel and K. N. Raymond, Acc. Chem. Res., 2009, 42, 542–552 CrossRef CAS.
- J. Kido and Y. Okamoto, Chem. Rev., 2002, 102, 2357–2368 CrossRef CAS.
-
(a)
S. Zhu and Z. Gu, in Lanthanide-Based Multifunctional Materials, ed. P. Martín-Ramos and M. Ramos Silva, Elsevier, 2018, pp. 381–410 Search PubMed;
(b) K. Y. Zhang, Q. Yu, H. Wei, S. Liu, Q. Zhao and W. Huang, Chem. Rev., 2018, 118, 1770–1839 CrossRef CAS.
-
(a) S. I. Klink, H. Keizer and F. C. van Veggel, Angew. Chem., 2000, 112, 4489–4491 CrossRef;
(b) T. J. Sørensen and S. Faulkner, Acc. Chem. Res., 2018, 51, 2493–2501 CrossRef;
(c) M. Pan, W.-M. Liao, S.-Y. Yin, S.-S. Sun and C.-Y. Su, Chem. Rev., 2018, 118, 8889–8935 CrossRef CAS.
-
(a) K.-J. Chen, H.-B. Xu, L.-Y. Zhang and Z.-N. Chen, Inorg. Chem. Commun., 2009, 12, 744–746 CrossRef CAS;
(b) O. J. Stacey, A. J. Amoroso, J. A. Platts, P. N. Horton, S. J. Coles, D. Lloyd, C. F. Williams, A. J. Hayes, J. J. Dunsford and S. J. A. Pope, Chem. Commun., 2015, 51, 12305–12308 RSC.
- I. M. Etchells, M. C. Pfrunder, J. A. G. Williams and E. G. Moore, Dalton Trans., 2019, 48, 2142–2149 RSC.
- R. Ziessel, S. Diring, P. Kadjane, L. Charbonnière, P. Retailleau and C. Philouze, Chem. – Asian J., 2007, 2, 975–982 CrossRef CAS.
- M. D. Ward, Coord. Chem. Rev., 2007, 251, 1663–1677 CrossRef CAS.
-
(a) J. S. Wilson, N. Chawdhury, M. R. A. Al-Mandhary, M. Younus, M. S. Khan, P. R. Raithby, A. Köhler and R. H. Friend, J. Am. Chem. Soc., 2001, 123, 9412–9417 CrossRef CAS;
(b) M. Jayapal, A. Haque, I. J. Al-Busaidi, R. Al-Balushi, M. K. Al-Suti, S. M. Islam and M. S. Khan, J. Organomet. Chem., 2017, 842, 32–38 CrossRef CAS.
- M. S. Khan, M. R. A. Al-Mandhary, M. K. Al-Suti, A. K. Hisahm, P. R. Raithby, B. Ahrens, M. F. Mahon, L. Male, E. A. Marseglia, E. Tedesco, R. H. Friend, A. Kohler, N. Feeder and S. J. Teat, J. Chem. Soc., Dalton Trans., 2002, 1358–1368 RSC.
-
(a) M. S. Khan, M. R. A. Al-Mandhary, M. K. Al-Suti, F. R. Al-Battashi, S. Al-Saadi, B. Ahrens, J. K. Bjernemose, M. F. Mahon, P. R. Raithby, M. Younus, N. Chawdhury, A. Köhler, E. A. Marseglia, E. Tedesco, N. Feeder and S. J. Teat, Dalton Trans., 2004, 2377–2385 RSC;
(b) R. A. Al-Balushi, A. Haque, M. Jayapal, M. K. Al-Suti, J. Husband, M. S. Khan, J. M. Skelton, K. C. Molloy and P. R. Raithby, Inorg. Chem., 2016, 55, 10955–10967 CrossRef CAS;
(c) M. S. Khan, M. R. A. Al-Mandhary, M. K. Al-Suti, T. C. Corcoran, Y. Al-Mahrooqi, J. P. Attfield, N. Feeder, W. I. F. David, K. Shankland, R. H. Friend, A. Köhler, E. A. Marseglia, E. Tedesco, C. C. Tang, P. R. Raithby, J. C. Collings, K. P. Roscoe, A. S. Batsanov, L. M. Stimson and T. B. Marder, New J. Chem., 2003, 27, 140–149 RSC;
(d) M. S. Khan, A. K. Kakkar, N. J. Long, J. Lewis, P. Raithby, P. Nguyen, T. B. Marder, F. Wittmann and R. H. Friend, J. Mater. Chem., 1994, 4, 1227–1232 RSC;
(e) M. S. Khan, M. K. Al-Suti, M. R. A. Al-Mandhary, B. Ahrens, J. K. Bjernemose, M. F. Mahon, L. Male, P. R. Raithby, R. H. Friend, A. Köhler and J. S. Wilson, Dalton Trans., 2003, 65–73 RSC.
-
(a) N. Chawdhury, A. Köhler, R. H. Friend, W. Y. Wong, J. Lewis, M. Younus, P. R. Raithby, T. C. Corcoran, M. R. A. Al-Mandhary and M. S. Khan, J. Chem. Phys., 1999, 110, 4963–4970 CrossRef CAS;
(b) L. Sudha Devi, M. K. Al-Suti, N. Zhang, S. J. Teat, L. Male, H. A. Sparkes, P. R. Raithby, M. S. Khan and A. Köhler, Macromolecules, 2009, 42, 1131–1141 CrossRef CAS;
(c) R. A. Al-Balushi, A. Haque, M. Jayapal, M. K. Al-Suti, J. Husband, M. S. Khan, O. F. Koentjoro, K. C. Molloy, J. M. Skelton and P. R. Raithby, Inorg. Chem., 2016, 55, 6465–6480 CrossRef CAS;
(d) J. S. Wilson, A. S. Dhoot, A. J. A. B. Seeley, M. S. Khan, A. Köhler and R. H. Friend, Nature, 2001, 413, 828–831 CrossRef CAS;
(e) M. Younus, A. Köhler, S. Cron, N. Chawdhury, M. R. A. Al-Mandhary, M. S. Khan, J. Lewis, N. J. Long, R. H. Friend and P. R. Raithby, Angew. Chem., Int. Ed., 1998, 37, 3036–3039 CrossRef CAS;
(f) P. Li, B. Ahrens, K.-H. Choi, M. S. Khan, P. R. Raithby, P. J. Wilson and W.-Y. Wong, CrystEngComm, 2002, 4, 405–412 RSC.
- M. S. Khan, M. R. A. Al-Mandhary, M. K. Al-Suti, N. Feeder, S. Nahar, A. Köhler, R. H. Friend, P. J. Wilson and P. R. Raithby, J. Chem. Soc., Dalton Trans., 2002, 2441–2448 RSC.
- M. S. Khan, M. R. A. Al-Mandhary, M. K. Al-Suti, A. K. Hisahm, P. R. Raithby, B. Ahrens, M. F. Mahon, L. Male, E. A. Marseglia, E. Tedesco, R. H. Friend, A. Köhler, N. Feeder and S. J. Teat, J. Chem. Soc., Dalton Trans., 2002, 1358–1368 RSC.
- J. D. Dutra, T. D. Bispo and R. O. Freire, J. Comput. Chem., 2014, 35, 772–775 CrossRef CAS.
- D. F. Eaton, J. Photochem. Photobiol., B, 1988, 2, 523–531 CrossRef CAS.
- N. B. Lima, S. M. Goncalves, S. A. Junior and A. M. Simas, Sci. Rep., 2013, 3, 2395 CrossRef.
- M. S. Khan, M. K. Al-Suti, B. Ahrens, P. R. Raithby and S. J. Teat, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, m735–m737 CrossRef CAS.
- R. O. Freire and A. M. Simas, J. Chem. Theory Comput., 2010, 6, 2019–2023 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
-
A. N. Carneiro Neto, E. E. S. Teotonio, G. F. de Sá, H. F. Brito, J. Legendziewicz, L. D. Carlos, M. C. F. C. Felinto, P. Gawryszewska, R. T. Moura, R. L. Longo, W. M. Faustino and O. L. Malta, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, 2019, vol. 56, pp. 55–162 Search PubMed.
- J. D. L. Dutra, N. B. D. Lima, R. O. Freire and A. M. Simas, Sci. Rep., 2015, 5, 13695 CrossRef.
- K. Sonogashira, Y. Tohda and N. Hagihara, Tetrahedron Lett., 1975, 16, 4467–4470 CrossRef.
- S. V. Eliseeva, O. V. Kotova, F. Gumy, S. N. Semenov, V. G. Kessler, L. S. Lepnev, J.-C. G. Bünzli and N. P. Kuzmina, J. Phys. Chem. A, 2008, 112, 3614–3626 CrossRef CAS.
-
(a) J. E. Barnsley, S. Ø. Scottwell, A. B. S. Elliott, K. C. Gordon and J. D. Crowley, Inorg. Chem., 2016, 55, 8184–8192 CrossRef CAS;
(b) F. Paul, S. Goeb, F. Justaud, G. Argouarch, L. Toupet, R. F. Ziessel and C. Lapinte, Inorg. Chem., 2007, 46, 9036–9038 CrossRef CAS.
- S. A. Cotton and P. R. Raithby, Coord. Chem. Rev., 2017, 340, 220–231 CrossRef CAS.
-
(a) F. Wu, H. Tong, Z. Li, W. Lei, L. Liu, W.-Y. Wong, W.-K. Wong and X. Zhu, Dalton Trans., 2014, 43, 12463–12466 RSC;
(b) X. Yang, G. Zhou and W.-Y. Wong, J. Mater. Chem. C, 2014, 2, 1760–1778 RSC.
-
W. T. Carnall, H. Crosswhite and H. M. Crosswhite, Energy Level Structure and Transition Probabilities in the Spectra of the Trivalent Lanthanides in Laf3, United States, 1978 Search PubMed.
- M. Gál, F. Kielar, R. Sokolová, Š. Ramešová and V. Kolivoška, Eur. J. Inorg. Chem., 2013, 2013, 3217–3223 CrossRef.
-
(a) E. L. Yee, R. J. Cave, K. L. Guyer, P. D. Tyma and M. J. Weaver, J. Am. Chem. Soc., 1979, 101, 1131–1137 CrossRef CAS;
(b) F. Murauer, L. Kišová, J. Komenda and G. Gritzner, J. Electroanal. Chem., 1999, 470, 1–8 CrossRef CAS.
- M. M. Richter and A. J. Bard, Anal. Chem., 1996, 68, 2641–2650 CrossRef CAS.
-
(a) M. Thelakkat and H.-W. Schmidt, Adv. Mater., 1998, 10, 219–223 CrossRef CAS;
(b) L. Dou, J. Gao, E. Richard, J. You, C.-C. Chen, K. C. Cha, Y. He, G. Li and Y. Yang, J. Am. Chem. Soc., 2012, 134, 10071–10079 CrossRef CAS.
- J. Yu, M. Xiao, H. Tan and W. Zhu, Thin Solid Films, 2016, 619, 1–9 CrossRef CAS.
- X. Zhang, Z. Chi, H. Li, B. Xu, X. Li, S. Liu, Y. Zhang and J. Xu, J. Mater. Chem., 2011, 21, 1788–1796 RSC.
- A. Bejan, S. Shova, M.-D. Damaceanu, B. C. Simionescu and L. Marin, Cryst. Growth Des., 2016, 16, 3716–3730 CrossRef CAS.
- Y. Takeda, T. L. Andrew, J. M. Lobez, A. J. Mork and T. M. Swager, Angew. Chem., Int. Ed., 2012, 51, 9042–9046 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0dt04198j |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Rashid
Ilmi
a,
Rashid
Ilmi
 *a,
José D. L.
Dutra
*a,
José D. L.
Dutra
 b,
Willyan F.
Oliveira
b,
Ashanul
Haque
b,
Willyan F.
Oliveira
b,
Ashanul
Haque
 ac,
Nawal K.
Al Rasbi
a,
Frank
Marken
ac,
Nawal K.
Al Rasbi
a,
Frank
Marken
 d,
Paul R.
Raithby
d,
Paul R.
Raithby
 *d and
Muhammad S.
Khan
*a
*d and
Muhammad S.
Khan
*a
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl) has been synthesized by utilizing the N,N-donor sites of the organometallic chromophore. The complex was characterized by analytical and spectroscopic methods. Photophysical properties of the complex were analysed in detail using both steady-state and time-resolved emission and excitation spectroscopy. The optical absorption spectrum of the complex is dominated by the spin allowed π–π* transitions of the btfa and 1c units in the UV–visible region (200–418 nm) and thus is excitable over a wide range of wavelengths across the UV into the visible region of the electromagnetic spectrum. The complex displays typical red Eu(III) emission when excited at 345 nm. However, it also shows green emission when excited at 464 nm and, thus could be an interesting candidate for full colour display applications. The change in the colour could be a result of the high value of the energy back-transfer rate (6.73 × 105 s−1) from the triplet state of the organometallic chromophore to the 5D1 state of Eu(III). Judd–Ofelt (J–O) intensity parameters (Ω2 and Ω4), radiative (AR), non-radiative (AR) decay rates and intrinsic quantum yield (QEuEu) have been calculated.
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl) has been synthesized by utilizing the N,N-donor sites of the organometallic chromophore. The complex was characterized by analytical and spectroscopic methods. Photophysical properties of the complex were analysed in detail using both steady-state and time-resolved emission and excitation spectroscopy. The optical absorption spectrum of the complex is dominated by the spin allowed π–π* transitions of the btfa and 1c units in the UV–visible region (200–418 nm) and thus is excitable over a wide range of wavelengths across the UV into the visible region of the electromagnetic spectrum. The complex displays typical red Eu(III) emission when excited at 345 nm. However, it also shows green emission when excited at 464 nm and, thus could be an interesting candidate for full colour display applications. The change in the colour could be a result of the high value of the energy back-transfer rate (6.73 × 105 s−1) from the triplet state of the organometallic chromophore to the 5D1 state of Eu(III). Judd–Ofelt (J–O) intensity parameters (Ω2 and Ω4), radiative (AR), non-radiative (AR) decay rates and intrinsic quantum yield (QEuEu) have been calculated.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl) (1d) as shown in Chart 1 and described its photophysical properties. The complex displayed typical red emission of the Eu(III) centre; however, the excitation window was confined to the UV region. This can be attributed to conjugation interruption in the system due to ligand topology (presence of the ethynyl groups at 6,6′-positions of 2,2′-Bipy).16 A general strategy to shift the excitation window of a complex is to design and engineer the molecule(s) with extended/uninterrupted π-conjugation. We have previously reported that Pt(II) di-ynes and poly-ynes incorporating a variety of carbocyclic,15a,17 heterocyclic15a,18 and mixed heterocyclic15a,19 spacers with extended conjugation exhibit improved photophysical properties for various opto-electronic applications. We noted that 5,5′-bis(ethnyl)-2,2′-bipyridine is fully conjugated while its 6,6′-bis(ethynyl) counterpart has broken conjugation and that 2,2′-bipyridine-5,5′-diyl spacer imparts more desirable optical properties to the Pt(II) di-yne and poly-yne complexes.20 Based on this idea, in the present work, we have utilized the ‘rigid-rod’ Pt(II) di-yne chromophore incorporating 2,2′-bipyridine-5,5′-diyl chelating spacer to synthesize a new heterotrinuclear Pt–Eu–Pt complex (Chart 1). The photophysical properties of the heterotrinuclear complex have been investigated. The optical absorption spectrum of the present heterotrinuclear complex [Eu(btfa)31c] displays a red shift compared to its kinked counterpart [Eu(btfa)31d] [1d] = [(Ph)(Et3P)2Pt–C
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl) (1d) as shown in Chart 1 and described its photophysical properties. The complex displayed typical red emission of the Eu(III) centre; however, the excitation window was confined to the UV region. This can be attributed to conjugation interruption in the system due to ligand topology (presence of the ethynyl groups at 6,6′-positions of 2,2′-Bipy).16 A general strategy to shift the excitation window of a complex is to design and engineer the molecule(s) with extended/uninterrupted π-conjugation. We have previously reported that Pt(II) di-ynes and poly-ynes incorporating a variety of carbocyclic,15a,17 heterocyclic15a,18 and mixed heterocyclic15a,19 spacers with extended conjugation exhibit improved photophysical properties for various opto-electronic applications. We noted that 5,5′-bis(ethnyl)-2,2′-bipyridine is fully conjugated while its 6,6′-bis(ethynyl) counterpart has broken conjugation and that 2,2′-bipyridine-5,5′-diyl spacer imparts more desirable optical properties to the Pt(II) di-yne and poly-yne complexes.20 Based on this idea, in the present work, we have utilized the ‘rigid-rod’ Pt(II) di-yne chromophore incorporating 2,2′-bipyridine-5,5′-diyl chelating spacer to synthesize a new heterotrinuclear Pt–Eu–Pt complex (Chart 1). The photophysical properties of the heterotrinuclear complex have been investigated. The optical absorption spectrum of the present heterotrinuclear complex [Eu(btfa)31c] displays a red shift compared to its kinked counterpart [Eu(btfa)31d] [1d] = [(Ph)(Et3P)2Pt–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl) because of the uninterrupted conjugation present in the former complex. Moreover, the newly synthesized heterotrinuclear complex displays fascinating dual emissions i.e., typical red emission due to the Eu(III) ion occurs when excited at 345 nm while a strong green emission is observed when the complex is excited at 464 nm. Finally, DFT calculations have been carried out to understand the photophysical properties and the nature of the excited state. Furthermore, the results of the DFT in conjunction with the observed photophysical data were utilized to gain an insight into the IET processes with the help of the LUMPAC21 software package.
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl) because of the uninterrupted conjugation present in the former complex. Moreover, the newly synthesized heterotrinuclear complex displays fascinating dual emissions i.e., typical red emission due to the Eu(III) ion occurs when excited at 345 nm while a strong green emission is observed when the complex is excited at 464 nm. Finally, DFT calculations have been carried out to understand the photophysical properties and the nature of the excited state. Furthermore, the results of the DFT in conjunction with the observed photophysical data were utilized to gain an insight into the IET processes with the help of the LUMPAC21 software package.

![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl (1c) (Scheme 1) were synthesized as reported by us previously.16 A solution of 1c (0.073 g, 0.06 mmol) in MeOH/DCM (10 mL) was added to a solution of [Eu(btfa)3(H2O)2] (0.050 g, 0.06 mmol) in MeOH/DCM (10 mL). The reaction mixture was left overnight with stirring at RT. The solution was left for slow solvent evaporation, after which solid product was obtained as a yellow solid. The solid product was washed with cold ethanol and dried in vacuo to obtain a light yellow solid. IR: ν/cm−1 –C
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl (1c) (Scheme 1) were synthesized as reported by us previously.16 A solution of 1c (0.073 g, 0.06 mmol) in MeOH/DCM (10 mL) was added to a solution of [Eu(btfa)3(H2O)2] (0.050 g, 0.06 mmol) in MeOH/DCM (10 mL). The reaction mixture was left overnight with stirring at RT. The solution was left for slow solvent evaporation, after which solid product was obtained as a yellow solid. The solid product was washed with cold ethanol and dried in vacuo to obtain a light yellow solid. IR: ν/cm−1 –C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C– 2087 cm−1; C = O 1610 cm−1 (Fig. S1, ESI†). C80H94EuF9N2O6P4Pt2; calc. C, 47.65; H, 4.70; N, 1.39%; found: C, 47.63; H, 4.67; N, 1.36%. (Q-TOF) LC/MS = 2016.5935 m/z [M+] (Fig. S2, ESI†). 1H NMR (400 MHz, CDCl3): δ 12.45 (b, 2H); δ 9.34 (d, 2H, J = 7.2 Hz), 9.17 (d, 2H, J = 7.2 Hz), δ 8.60–6.0 (m, 25 H); δ 3.34 (ss, 3H); 1.95 (b, 24H), 1.24 (b, 36H) (Fig. S3, ESI†). 13C NMR (100.6 MHz, CDCl3): δ 187.48, 176.99, 155.10, 138.10, 132.48, 126.44, 125.92 125.70, 124.32, 120.43 121.89 (C
C– 2087 cm−1; C = O 1610 cm−1 (Fig. S1, ESI†). C80H94EuF9N2O6P4Pt2; calc. C, 47.65; H, 4.70; N, 1.39%; found: C, 47.63; H, 4.67; N, 1.36%. (Q-TOF) LC/MS = 2016.5935 m/z [M+] (Fig. S2, ESI†). 1H NMR (400 MHz, CDCl3): δ 12.45 (b, 2H); δ 9.34 (d, 2H, J = 7.2 Hz), 9.17 (d, 2H, J = 7.2 Hz), δ 8.60–6.0 (m, 25 H); δ 3.34 (ss, 3H); 1.95 (b, 24H), 1.24 (b, 36H) (Fig. S3, ESI†). 13C NMR (100.6 MHz, CDCl3): δ 187.48, 176.99, 155.10, 138.10, 132.48, 126.44, 125.92 125.70, 124.32, 120.43 121.89 (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C), 94.29, 57.82, 28.67, 14.08 (CH2), 7.39 (CH3) (Fig. S4, ESI†). NB. The NMR spectroscopic signals were broadened by the presence of the highly paramagnetic Eu(III) ion.
C), 94.29, 57.82, 28.67, 14.08 (CH2), 7.39 (CH3) (Fig. S4, ESI†). NB. The NMR spectroscopic signals were broadened by the presence of the highly paramagnetic Eu(III) ion.

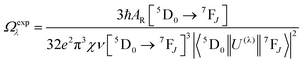
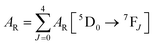
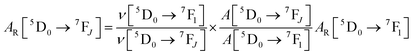
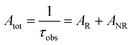
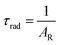
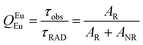
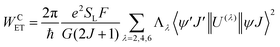
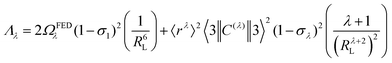
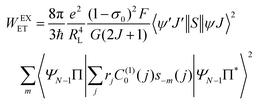
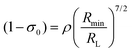
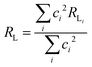
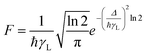
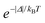 , where kB stands for the Boltzmann constant and T is assumed as being the environment temperature.
, where kB stands for the Boltzmann constant and T is assumed as being the environment temperature.
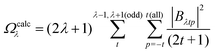
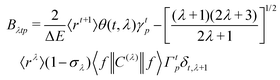
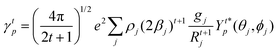
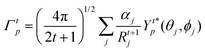
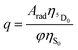
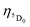 are the energetic population of the S0 fundamental state of the ligand and the 5D0 emitting state of the Eu3+, respectively.
are the energetic population of the S0 fundamental state of the ligand and the 5D0 emitting state of the Eu3+, respectively.
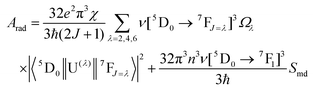
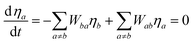
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(PEt3)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl) was synthesized following our previously reported method.16 Briefly, 5,5′-dibromo-2,2′-bipyridine was protected with trimethylsilylethyne yielding 1a (Scheme 1) by a Sonogashira cross-coupling reaction.31 Smooth removal of trimethylsilyl groups with KOH/MeOH (Scheme 1) followed by dehydrohalogenation reaction of the diterminal alkyne 1b with trans-[Ph(Et3P)2PtCl] yielded the Pt(II) di-yne 1c (Scheme 1) as a yellow solid. The heterotrinuclear complex [Eu(btfa)31c] (Scheme 1) was synthesized in 74.0% yield by reacting [Eu(btfa)3(H2O)2] and Pt(II) di-yne (1c) in 1
C–Pt(PEt3)2(Ph)] (R = 2,2′-bipyridine-5,5′-diyl) was synthesized following our previously reported method.16 Briefly, 5,5′-dibromo-2,2′-bipyridine was protected with trimethylsilylethyne yielding 1a (Scheme 1) by a Sonogashira cross-coupling reaction.31 Smooth removal of trimethylsilyl groups with KOH/MeOH (Scheme 1) followed by dehydrohalogenation reaction of the diterminal alkyne 1b with trans-[Ph(Et3P)2PtCl] yielded the Pt(II) di-yne 1c (Scheme 1) as a yellow solid. The heterotrinuclear complex [Eu(btfa)31c] (Scheme 1) was synthesized in 74.0% yield by reacting [Eu(btfa)3(H2O)2] and Pt(II) di-yne (1c) in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. The formulation of [Eu(btfa)31c] was confirmed by elemental analysis, ESI-MS and IR spectroscopy. The elemental analysis shows satisfactory results and confirms the proposed formulation for the newly synthesized complex. The result of the elemental analysis was further confirmed by the ESI-MS. The spectrum of [Eu(btfa)31c] in positive ion mode was recorded in MeOH. The complex displayed a molecular ion peak at 2016.59 m/z [M+] (Fig. S2, ESI†) and thus confirms the proposed stoichiometry shown in Chart 1. The spectrum also displayed various peaks which could be due to fragmentation of the fluorinated β-diketonate ligands.32 The results of the elemental analysis and ESI† were further confirmed by IR spectroscopy. The IR spectra of [Eu(btfa)31c] together with those of [Eu(btfa)3(H2O)2] and 1c are shown in Fig. S1, ESI.† The spectrum of [Eu(btfa)31c] displayed a single, sharp –C
1 ratio. The formulation of [Eu(btfa)31c] was confirmed by elemental analysis, ESI-MS and IR spectroscopy. The elemental analysis shows satisfactory results and confirms the proposed formulation for the newly synthesized complex. The result of the elemental analysis was further confirmed by the ESI-MS. The spectrum of [Eu(btfa)31c] in positive ion mode was recorded in MeOH. The complex displayed a molecular ion peak at 2016.59 m/z [M+] (Fig. S2, ESI†) and thus confirms the proposed stoichiometry shown in Chart 1. The spectrum also displayed various peaks which could be due to fragmentation of the fluorinated β-diketonate ligands.32 The results of the elemental analysis and ESI† were further confirmed by IR spectroscopy. The IR spectra of [Eu(btfa)31c] together with those of [Eu(btfa)3(H2O)2] and 1c are shown in Fig. S1, ESI.† The spectrum of [Eu(btfa)31c] displayed a single, sharp –C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C– stretch at 2087 cm−1, consistent with a trans configuration of the ethynyl units around the Pt(II) centres.15b The presence of this stretching absorption clearly supports the formation of the hetero-trinuclear complex. Moreover, the IR spectra of the complex exhibits C
C– stretch at 2087 cm−1, consistent with a trans configuration of the ethynyl units around the Pt(II) centres.15b The presence of this stretching absorption clearly supports the formation of the hetero-trinuclear complex. Moreover, the IR spectra of the complex exhibits C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations at 1610 and 1571 cm−1, respectively, characteristics of the lanthanide chelate complexes containing β-diketone ligand.4c The appearance of (PCH2CH3)3 twisting and bending vibration bands in the spectrum also provide additional evidence of complex formation; however, the position of the peaks remain unaltered appearing at 3041, 2961 and 2871 cm−1 as observed in the Pt(II) di-yne chromophore. The results clearly provide unambiguous support for the formation of the heterotrinuclear complex [Eu(btfa)31c].
C stretching vibrations at 1610 and 1571 cm−1, respectively, characteristics of the lanthanide chelate complexes containing β-diketone ligand.4c The appearance of (PCH2CH3)3 twisting and bending vibration bands in the spectrum also provide additional evidence of complex formation; however, the position of the peaks remain unaltered appearing at 3041, 2961 and 2871 cm−1 as observed in the Pt(II) di-yne chromophore. The results clearly provide unambiguous support for the formation of the heterotrinuclear complex [Eu(btfa)31c].
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C– triple bond. However, in the present case, we noted distortion when 1c is coordinated to the Eu(III) ion. Such a structural modification is observed in the literature when ligands comparable to 1c are coordinated to a given metal centre (e.g., ASUVER and KIRSOU CSD refcodes),33 and could be due to the interactions involving the peripheral substituents in the different ligands of 1c with the β-diketonate ligands. Spherical coordinates of coordination polyhedron are gathered in Table S1, ESI,† and, as can be seen, the Eu–N bonds predicted by the applied DFT approach are 2.684 and 2.647 Å, in line with literature values.34 On the other hand, the Eu–O bonds are in the ranges of 2.399–2.422 Å and plainly the coordination polyhedron is of low symmetry.
C– triple bond. However, in the present case, we noted distortion when 1c is coordinated to the Eu(III) ion. Such a structural modification is observed in the literature when ligands comparable to 1c are coordinated to a given metal centre (e.g., ASUVER and KIRSOU CSD refcodes),33 and could be due to the interactions involving the peripheral substituents in the different ligands of 1c with the β-diketonate ligands. Spherical coordinates of coordination polyhedron are gathered in Table S1, ESI,† and, as can be seen, the Eu–N bonds predicted by the applied DFT approach are 2.684 and 2.647 Å, in line with literature values.34 On the other hand, the Eu–O bonds are in the ranges of 2.399–2.422 Å and plainly the coordination polyhedron is of low symmetry.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl)4c (Fig S4, ESI†). It is thus excitable across a wide range of wavelengths from UV to the visible. The spectral differences of the two systems encouraged us to study the photoluminescence (PL) of the new system further.
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl)4c (Fig S4, ESI†). It is thus excitable across a wide range of wavelengths from UV to the visible. The spectral differences of the two systems encouraged us to study the photoluminescence (PL) of the new system further.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 551 cm−1; 464 nm) and 7F0 → 5D1 (18
551 cm−1; 464 nm) and 7F0 → 5D1 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657cm−1; 536 nm). The intensity of the excitation transition is higher than the broad band suggesting that the heterotrinuclear complex could be excitable at the blue 464 nm wavelength.
657cm−1; 536 nm). The intensity of the excitation transition is higher than the broad band suggesting that the heterotrinuclear complex could be excitable at the blue 464 nm wavelength.

![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–R–C
C–R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl).a Calculated using eqn (1).b Calculated using eqn (5).c Calculated using eqn (2)–(4).d Calculated using eqn (6).
C–Pt(Et3P)2(Ph)] (R = 2,2′-bipyridine-6,6′-diyl).a Calculated using eqn (1).b Calculated using eqn (5).c Calculated using eqn (2)–(4).d Calculated using eqn (6).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.5 cm−1
577.5 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2 cm−1
442.2 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.2 cm−1
664.2 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2 cm−1) calculated at the CAM-B3LYP level of theory using the B3LPY geometry is characterized as involving MOs centred on the ligands present in the 1c molecular fragment. The energy of the next lowest triplet state (T2) is equal to 22
442.2 cm−1) calculated at the CAM-B3LYP level of theory using the B3LPY geometry is characterized as involving MOs centred on the ligands present in the 1c molecular fragment. The energy of the next lowest triplet state (T2) is equal to 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 cm−1 and the most relevant electronic transitions involve MOs centred mainly on the btfa ligands. RL values present in Table 3 show that the donor centre is more distant from the Eu(IIII) centre for T2 in comparison with T1 due to the contribution of the btfa ligands in T2.
664 cm−1 and the most relevant electronic transitions involve MOs centred mainly on the btfa ligands. RL values present in Table 3 show that the donor centre is more distant from the Eu(IIII) centre for T2 in comparison with T1 due to the contribution of the btfa ligands in T2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 586 cm−1), 5D1 (ca. 19
586 cm−1), 5D1 (ca. 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 cm−1), and 5D0 (ca. 17
027 cm−1), and 5D0 (ca. 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293 cm−1), with the energy values obtained from Carnall et al.36 To calculate the energetic population involving the states shown in Fig. 6, typical experimental values for the non-radiative rates in coordination compounds were considered.36
293 cm−1), with the energy values obtained from Carnall et al.36 To calculate the energetic population involving the states shown in Fig. 6, typical experimental values for the non-radiative rates in coordination compounds were considered.36
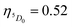 ), which provided a theoretical PLQY of 19.8% that is close to experimentally determined value 15.10%.
), which provided a theoretical PLQY of 19.8% that is close to experimentally determined value 15.10%.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577.5)
577.5)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 586)
586)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.2)
664.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027)
027)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.2)
664.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 293)
293)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2)
442.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027)
027)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2)
442.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027)
027)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.2 cm−1 with the ET rate 1.27 × 109 s−1 with the negligible energy back-transfer rate (Table 4) and (b) organometallic chromophore (20
664.2 cm−1 with the ET rate 1.27 × 109 s−1 with the negligible energy back-transfer rate (Table 4) and (b) organometallic chromophore (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.2 cm−1) with an ET rate 5.96 × 108 s−1 with the energy back-transfer rate of 6.73 × 105 s−1 for the T1 → 5D1. The excited state lifetime of the present complex is in microsecond range typical for europium β-diketonate complexes. The intermolecular energy transfer in the complex on the basis of experimental results and DFT calculations is discussed in detail. Moreover, the calculated photophysical parameters are in excellent agreement with the experimentally observed results.
442.2 cm−1) with an ET rate 5.96 × 108 s−1 with the energy back-transfer rate of 6.73 × 105 s−1 for the T1 → 5D1. The excited state lifetime of the present complex is in microsecond range typical for europium β-diketonate complexes. The intermolecular energy transfer in the complex on the basis of experimental results and DFT calculations is discussed in detail. Moreover, the calculated photophysical parameters are in excellent agreement with the experimentally observed results.


