DOI:
10.1039/D1DT02346B
(Communication)
Dalton Trans., 2021,
50, 14130-14138
Assessment of minimal active space CASSCF-SO methods for calculation of atomic Slater–Condon and spin–orbit coupling parameters in d- and f-block ions†
Received
14th July 2021
, Accepted 1st October 2021
First published on 1st October 2021
Abstract
Slater–Condon parameters and the spin–orbit (SO) coupling constants for various oxidation states of transition metal ions (3d/4d/5d) and trivalent f-block ions were calculated using minimal active space complete active space self-consistent field (CASSCF)-SO methods in OpenMolcas. The SO coupling constants have a quadratic relationship to atomic number Z for a fixed dn configuration, as do those for the trivalent lanthanides where configuration also changes as a function of Z. Compared to experimentally-derived values, minimal active space CASSCF-SO approximates SO coupling constants within ca. 200 cm−1, which is usually <10% error for 4dn, 5dn and 4fn configurations, but up to 30% error for 3dn configurations. Slater–Condon parameters are usually overestimated on the order of 10–50%, arising from a lack of dynamic correlation in the method, and thus we do not recommend minimal active space CASSCF-SO methods where accurate term excitation energies are required. However, the error in the Slater–Condon parameters appears to be systematic for divalent 4d and trivalent 4f ions such that scaling may be a useful approach where computational resources are limited, but this is not the case for 3d ions. Hence, caution is advised when using CASSCF-SO methods for comparisons with spectroscopic data, wherein only qualitative results can be expected, and methods accounting for dynamic correlation effects (such as CASPT2 or NEVPT2) should be employed if more quantitative results are required.
Introduction
Computational chemistry has been an integral part of chemistry since the early 1950s, following the invention of digital computers in the 1940s. Computational chemistry methods were developed based on theoretical methods prevalent since the early 1900s. Nowadays, real chemical systems can mostly be solved to a very good degree of accuracy compared to experimental methods. However, there are still advantages in using simplified theoretical models as these often provide more clarity in explaining molecular properties or provide a flexible parameter-based framework in which to refine against experimental data, which is not possible with numerical-based solutions to many-body quantum problems.
Of the many theoretical methods for studying spectroscopic and magnetic properties in metal complexes, the methods of Condon and Shortley,1 and later recast in spherical tensor formalisms by Racah,2 have continued to find common application. In these methods, the quantum states are usually simplified to considering those of only the metal atom or ion valence electrons, where the angular parts of the atomic or ionic wavefunction are treated exactly and integrals over radial part of the wavefunction Rnl(r) are treated as parameters (see eqn (1)). For instance, this allows one to consider the manifold of states arising from dn or fn configurations (and indeed including excited configurations such as fn−1d1, etc.) and transition moments between them, with the Hamiltonian equation (2) (here the first term describes the interelectronic Coulomb repulsion and the second term is the spin–orbit (SO) coupling). In such cases, the Coulomb-repulsion between electrons in these manifolds, which gives rise to the separations of 2S+1L electronic terms, are described by the Slater–Condon parameters Fk (eqn (3), which enter into the first term of Hamiltonian equation (2) by means of exact solution to the angular part of the operator1) for the single configuration approximation, which are sometimes expressed as Slater integrals Fk (eqn (3) and Table 1), or as Racah parameters for dn configurations (eqn (5) and (6));3 the difference between Slater–Condon parameters Fk and Slater integrals Fk is merely one of convention, where the latter avoid occurrence of fractional coefficients arising from integrals of spherical harmonics.1 A single Slater–Codon parameter F2 is sufficient in describing a pn-system, whereas F2 and F4 are required to describe a dn-system and all three F2, F4 and F6 are required for fn-systems.4
| | 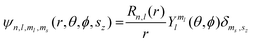 | (1) |
| | 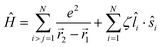 | (2) |
| | 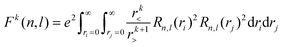 | (3) |
| | 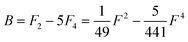 | (5) |
| | 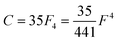 | (6) |
Table 1 Dk parameters for s, p and d orbitals
| |
D
2
|
D
4
|
D
6
|
| p |
25 |
|
|
| d |
49 |
441 |
|
| f |
225 |
1089 |
7361.64 |
Moving beyond simulations of free atoms and ions, the environment is parameterised using the crystal field (CF) formalism, of which there are many varieties,5 and are of great utility in interpreting spectral data of complexes.6,7 While such model Hamiltonians do not account for metal–ligand covalency, polarisation, screening, etc., the parameters are amenable to optimisation compared to experimental observations (for instance via spectroscopy), and hence “experimental” wavefunctions can in principle be determined. These methods form a super-set encompassing spin Hamiltonian methods, such as those used to model molecular magnetic data8 and electron paramagnetic resonance spectroscopy.9 The utility of moving beyond spin Hamiltonians, which consider only low-lying electronic states, to explicit dn or fn configurations is that higher-order effects, such as deviations from the Landé interval rule10 and J-mixing,11 are implicitly included.12
Multi-configurational complete active space self-consistent field (CASSCF) methods, pioneered by Roos and co-workers,13 have seen an enormous rise in use recently for calculation of magnetic and spectroscopic properties of metal complexes, owing to the simple choice of active space of the dn or fn manifolds (the so-called “minimal active space”), and the availability of the single_aniso module14,15 in (Open)Molcas,16 and the ab initio ligand field theory (AILFT) module17 in Orca.18 The most-common implementations of CASSCF methods use scalar-relativistic Hamiltonians in a spin-free formalism,19 where a decoupling method is employed to transform the four-component Dirac Hamiltonian into a two-component method.20 This allows orbital optimisation with CASSCF in a spin-free formalism, where spin (and hence SO coupling) is introduced in a state-interaction picture after variational orbital optimisation.21 While such CASSCF calculations account for the static correlation of (near-)degenerate orbitals, often found in metal complexes which make single-determinant methods such as Hartree–Fock and density-functional theory inappropriate, and hence these calculations provide excellent qualitative results,22 CASSCF calculations lack the dynamic correlation of the exact configuration interaction (CI) solution.23 Dynamic correlation can, in principle, by introduced using perturbative methods such as CASPT224 or NEVPT2,25–27 however these are extremely costly methods. Hence, it is commonplace to simply perform CASSCF calculations without such corrections.
Given the prominent use of minimal active space CASSCF-SO calculations with OpenMolcas for predicting electronic structure of coordination complexes, we decided to systematically explore the performance of this approach in predicting the electronic structure of metal ions. We employ minimal active space calculations for metal ions of varying oxidation states across the periodic table, accounting for all possible spin states in each dn or fn configuration, then recast the results into Slater–Condon and SO coupling parameters, and compare these to experimentally-determined parameters where possible, as well as results from the similar methods of AILFT and ligand field density-functional theory (LF-DFT). Compared to experiment, we find that minimal active space CASSCF-SO calculations generally overestimate the Slater–Condon parameters on the order of 20–50% (with some outliers in the 3d dataset which are underestimated by 1–20%), while SO parameters are overestimated by 5–30% for 3d ions, generally predicted within ±10% for 4d and 5d ions, and usually overestimated by 2–10% for trivalent 4f ions. Thus, we urge caution on the use of minimal active space CASSCF-SO calculations for the prediction of high-energy spectroscopic data and argue that dynamic correlation must be accounted for.
Methods
We employed the OpenMolcas program16,28 to perform CASSCF-SO calculations on each of the metal ions herein. We used ANO-RCC-VQZP basis sets29 and atomic mean-field integrals (AMFI) to obtain the SO coupling Hamiltonian.30 We used the “ATOM” supersymmetry keyword to enforce spherical symmetry for the optimised atomic orbitals. State-averaged CASSCF (SA-CASSCF) optimisations with an n in 5 (d-block) or n in 7 (f-block) active space were performed for all possible roots for a given configuration and spin multiplicity (Tables 2 and 3); owing to computational limitations we have not explored Eu(III), Gd(III) and Tb(III). Additionally, we have performed multi-state CASPT2 (MS-CASPT2)31 and extended multi-state CASPT2 (XMS-CASPT2)32,33 calculations for Co(II) and Pr(III), to illustrate the effects of corrections for dynamic correlation, using all roots from SA-CASSCF and an imaginary shift of 0.1. Following either SA-CASSCF or (X)MS-CASPT2, all roots were mixed with SO coupling. The resulting SO eigenstates were transformed into the Russell–Saunders basis with well-defined spin, orbital and total angular momenta as follows: (i) the matrix representation of Ŝ2 in the SO eigenbasis was diagonalised to obtain the SO → Ŝ2 unitary transformation 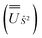 and blocks of different Ŝ2 eigenstates were identified; (ii) the matrix representation of
and blocks of different Ŝ2 eigenstates were identified; (ii) the matrix representation of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2 in the SO eigenbasis was transformed into the Ŝ2 eigenbasis with
2 in the SO eigenbasis was transformed into the Ŝ2 eigenbasis with 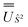 and diagonalised within each eigenblock of Ŝ2, where the resulting eigenvectors were used to construct the SO → Ŝ2,
and diagonalised within each eigenblock of Ŝ2, where the resulting eigenvectors were used to construct the SO → Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2 unitary transformation
2 unitary transformation 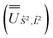 ; (iii) the matrix representation of Ĵ2 in the SO eigenbasis was transformed into the Ŝ2,
; (iii) the matrix representation of Ĵ2 in the SO eigenbasis was transformed into the Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2 eigenbasis with
2 eigenbasis with 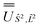 , and diagonalised within each eigenblock of Ŝ2,
, and diagonalised within each eigenblock of Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2, where the resulting eigenvectors were used to construct the SO → Ŝ2,
2, where the resulting eigenvectors were used to construct the SO → Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2, Ĵ2 unitary transformation
2, Ĵ2 unitary transformation 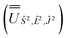 ; (iv) the SO Hamiltonian of the electronic structure calculation (which is diagonal in the SO eigenbasis) was transformed into the Ŝ2,
; (iv) the SO Hamiltonian of the electronic structure calculation (which is diagonal in the SO eigenbasis) was transformed into the Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2, Ĵ2 basis with
2, Ĵ2 basis with 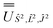 and then diagonalised to return the original SO eigenstates and their composition in terms of the Russell–Saunders basis. Then, the Slater–Condon and SO parameters were first estimated from the average SO eigenvalues of each 2S+1LJ term, and subsequently refined by fitting the entire energy spectrum of the model Hamiltonian (eqn (2)) to the entire energy spectrum from CASSCF-SO. We note that this method is not restricted to minimal active space calculations and thus is broadly applicable beyond the scope of the present work. This code is under preparation and will soon be released as an open-source package.
and then diagonalised to return the original SO eigenstates and their composition in terms of the Russell–Saunders basis. Then, the Slater–Condon and SO parameters were first estimated from the average SO eigenvalues of each 2S+1LJ term, and subsequently refined by fitting the entire energy spectrum of the model Hamiltonian (eqn (2)) to the entire energy spectrum from CASSCF-SO. We note that this method is not restricted to minimal active space calculations and thus is broadly applicable beyond the scope of the present work. This code is under preparation and will soon be released as an open-source package.
Table 2 Spin multiplicities and roots included in the SA-CASSCF and SO coupling steps for d-block ions
| dn |
Spin multiplicity |
Roots |
| 1 |
2 |
|
|
5 |
|
|
| 2 |
3 |
1 |
|
10 |
15 |
|
| 3 |
4 |
2 |
|
10 |
40 |
|
| 4 |
5 |
3 |
1 |
5 |
45 |
50 |
| 5 |
6 |
4 |
2 |
1 |
24 |
75 |
| 6 |
5 |
3 |
1 |
5 |
45 |
50 |
| 7 |
4 |
2 |
|
10 |
40 |
|
| 8 |
3 |
1 |
|
10 |
15 |
|
| 9 |
2 |
|
|
5 |
|
|
| 10 |
1 |
|
|
1 |
|
|
Table 3 Spin multiplicities and roots included in the SA-CASSCF and SO coupling steps for f-block ions
| fn |
Spin multiplicity |
Roots |
| 1 |
2 |
|
|
|
7 |
|
|
|
| 2 |
3 |
1 |
|
|
21 |
28 |
|
|
| 3 |
4 |
2 |
|
|
35 |
112 |
|
|
| 4 |
5 |
3 |
1 |
|
35 |
210 |
196 |
|
| 5 |
6 |
4 |
2 |
|
21 |
224 |
490 |
|
| 9 |
6 |
4 |
2 |
|
21 |
224 |
490 |
|
| 10 |
5 |
3 |
1 |
|
35 |
210 |
196 |
|
| 11 |
4 |
2 |
|
|
35 |
112 |
|
|
| 12 |
3 |
1 |
|
|
21 |
28 |
|
|
| 13 |
2 |
|
|
|
7 |
|
|
|
| 14 |
1 |
|
|
|
1 |
|
|
|
Results and discussion
Performing CASSCF-SO calculations accounting for all spin states (see Method) for a range of 3d, 4d and 4f ions and oxidations states, and mapping onto a free-ion Slater–Condon Hamiltonian (eqn (2)), we obtain the SO coupling and Slater–Condon Fk parameters (Tables S1–S4†). Note that the single-electron SO coupling parameter can be related to the multi-electron SO coupling parameter viaeqn (7).34 We find smooth variation in the SO coupling parameters, ζ, as a function of atomic number, Z (Fig. 1 and 4), which can be well-described as a quadratic function in Z (Tables S5 and S7†); similar trends have been seen previously.35,36| | 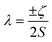 | (7) |
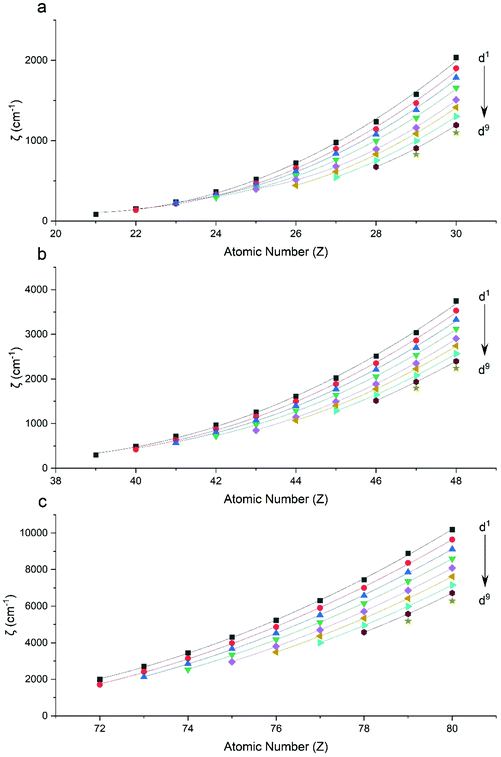 |
| | Fig. 1 CASSCF-SO-calculated SO coupling parameters (points) for free ions (a) 3d, (b) 4d, (c) 5d. Lines are second-order polynomial fits, with parameters given in Table S5.† | |
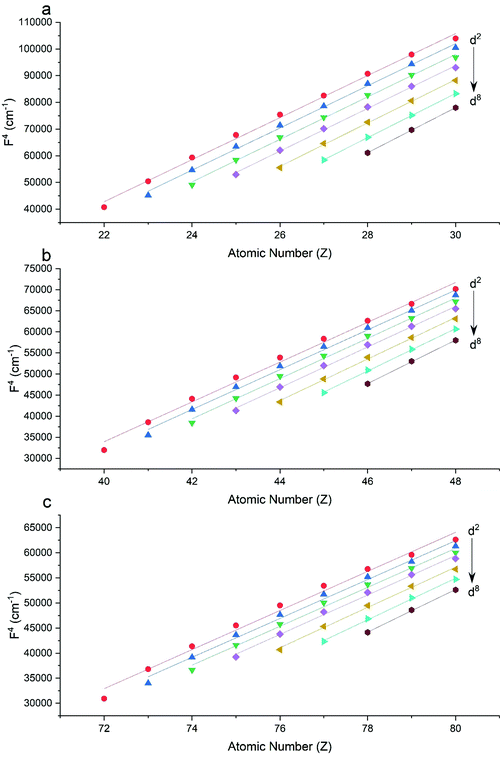
The Slater–Condon parameters, on the other hand, show linear variation with Z for isoelectronic series (Fig. 2, 3 and Tables S6, S7†), a feature that has been observed before;37 however, there is a slight deviation from linearity that is most noticeable for the d2 configurations. We also find a linear trend in the Slater–Condon parameters for the trivalent 4f series where the configuration also changes as a function of Z(Fig. 5).
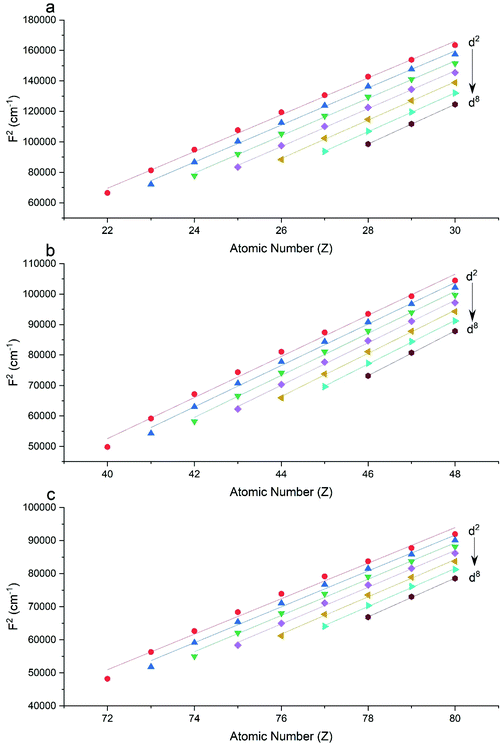 |
| | Fig. 2 CASSCF-SO-calculated F2 parameters (points) for free ions (a) 3d, (b) 4d, (c) 5d. Lines are second-order polynomial fits, with parameters given in Table S6.† | |
 |
| | Fig. 3 CASSCF-SO-calculated F4 parameters (points) for free ions (a) 3d, (b) 4d, (c) 5d. Lines are second-order polynomial fits, with parameters given in Table S6.† | |
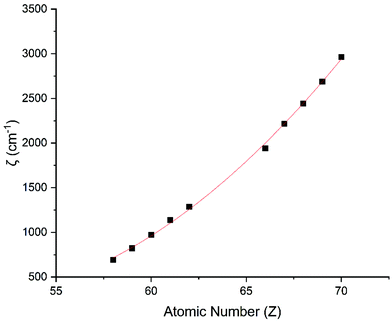 |
| | Fig. 4 CASSCF-SO-calculated SO coupling parameters (points) for trivalent lanthanide ions. Note here that the configuration 4fn is changing with Z as all ions are trivalent. Line is best fit with parameters in Table S7.† | |
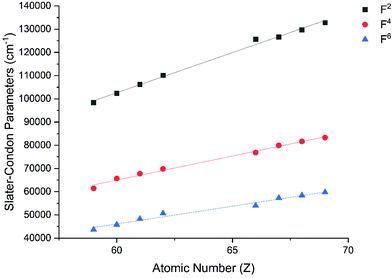 |
| | Fig. 5 CASSCF-SO-calculated Slater–Condon (F2, F4, F6) parameters (points) for trivalent lanthanide ions. Note here that the configuration 4fn is changing with Z as all ions are trivalent. Lines are best fits with parameters in Table S7.† | |
Compared to experiment, we find that SO coupling parameters for 3d ions are generally estimated with an error of ca. −20 to 60 cm−1 (Table S1†), with absolute relative errors on the order of 5–30% (Fig. S1†). For 4d ions, the SO coupling parameters are usually accurate within 100 cm−1 (with an outlier of ca. −200 cm−1 for Tc(VI)), corresponding to absolute relative errors within ca. 10% (Fig. S1†). The errors tend to be lower for 3d ions nearer empty or full d-shell configurations, which is likely due to averaging over fewer states in CASSCF compared to nearer half-filled configurations where there are more excited states. However, the same trend is not as clear for 4d ions, most probably because these effects are hidden in the larger absolute errors for these heavier elements. For 5d ions, the SO parameters are accurately calculated within about 200 cm−1 (Table S1†) which corresponds to relative errors within 10% (Fig. S1†). For trivalent 4f ions, the calculated SO coupling parameters are always overestimated by ca. 20–150 cm−1 (Table S1†) and the absolute relative errors are on the order of 1–10% (Fig. S2†), except for an outlier of Ce(III) which is overestimated by around 20%. From these data, we can conclude that dn and fn SO coupling parameters are predicted to within ca. 200 cm−1 by the minimal CASSCF-SO method, which corresponds to a relatively low percentage error, usually <10% for 4dn, 5dn and 4fn configurations owing to the larger SO constants in the heavier elements, compared to the larger percentage error up to 30% in 3dn configurations.
Examination of the Slater–Condon parameters show that these are subject to larger errors compared to experiment than the SO coupling parameters (Tables S2 and S3†); this is because these parameters are hugely sensitive to electron correlation, while the SO parameters are less so. Considering 3d ions, most cases, excepting a handful of F4 parameters and the F2 parameter for Co(VII), show that minimal CASSCF-SO calculations overestimate both F2 and F4 by ca. 2000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which amounts to around 10–40% relative error in F2 (Fig. S3a†). For F4 the relative errors are larger for the underestimated values which generally occur for d2 configurations, whereas most values are overestimated around 5–45%. For 4d ions, for which we only have data for the divalent series, we find all the Slater–Condon parameters are overestimated, and that there appears to be a systematic error owing to the smooth trend in error (Fig. S3†). For the trivalent 4f ions, all F2, F4 and F6 parameters are overestimated by ca. 6000–30
000 cm−1, which amounts to around 10–40% relative error in F2 (Fig. S3a†). For F4 the relative errors are larger for the underestimated values which generally occur for d2 configurations, whereas most values are overestimated around 5–45%. For 4d ions, for which we only have data for the divalent series, we find all the Slater–Condon parameters are overestimated, and that there appears to be a systematic error owing to the smooth trend in error (Fig. S3†). For the trivalent 4f ions, all F2, F4 and F6 parameters are overestimated by ca. 6000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which corresponds to around 25–30% error for F2 (Table S2†), 15–20% error for F4 (Table S3†) and 12–26% error for F6 (Table S4†). We see a similar decrease in error in the Slater–Condon parameters for the trivalent 4f ions as observed for the divalent 4d ions, although there is more scatter in the 4f data (Fig. S3†), again suggesting that there is a systematic error in the estimation of the interelectronic repulsion in minimal CASSCF-SO calculations.
000 cm−1, which corresponds to around 25–30% error for F2 (Table S2†), 15–20% error for F4 (Table S3†) and 12–26% error for F6 (Table S4†). We see a similar decrease in error in the Slater–Condon parameters for the trivalent 4f ions as observed for the divalent 4d ions, although there is more scatter in the 4f data (Fig. S3†), again suggesting that there is a systematic error in the estimation of the interelectronic repulsion in minimal CASSCF-SO calculations.
Given the relatively large errors in calculated Slater–Condon parameters we can hardly recommend the use of minimal active space CASSCF-SO calculations for modelling spectroscopic data. However, as the errors appear systematic for both Slater–Condon and SO parameters for trivalent 4f ions and the Slater–Condon parameters for divalent 4d, if minimal CASSCF-SO calculations are the only viable option due to computational limitations, it appears that an appropriate scaling factor on the order of 0.7–0.9 (Tables S8 and S9†) may lead to useful results, which indeed is a common approach in some communities.38,39 However, we do not recommend such an approach for complexes of 3d ions given that the data show rather large variations in relative error. In all cases, the errors in the calculation of the Slater–Condon parameters are due to the poor treatment of dynamic correlation in CASSCF, and as such the results can be improved if dynamic correlation can be approximated. While the accurate calculation of ionic Slater–Condon parameters is not the goal of this work, and hence we do not perform a systematic study of dynamic correlation methods here, we have performed multistate CASPT2 (MS-CASPT2)31 and extended multistate CASPT2 (XMS-CASPT2)32,33 calculations for 3d7 Co(II) and 4f2 Pr(III) to illustrate how the addition of corrections for dynamic correlation affects the resulting parameters (Table 4). Both MS-CASPT2 and XMS-CASPT2 are perturbative treatments to include dynamic correlation effects, however, they differ in how they are applied. MS-CASPT2 employs a state-specific Fock operator in generating the zeroth-order Hamiltonian, while XMS-CASPT2 uses a state-average Fock operator to render the zeroth-order states invariant to unitary transformations, making the XMS approach more robust in the vicinity of low-lying excitations at the cost of accuracy in cases where states are well separated; an excellent overview can be found in the discussion of a hybrid method, extended dynamically-weighted CASPT2 (XDW-CASPT2), of Battaglia and Lindh.40
Table 4 Comparison of Slater–Condon and SO parameters calculated with CASSCF, MS-CASPT2 and XMS-CASPT2 to experimental results
| Parameter |
Experiment (cm−1) |
CASSCF (cm−1) |
MS-CASPT2 (cm−1) |
XMS-CASPT2 (cm−1) |
AILFT-NEVPT242 (cm−1) |
|
Co(II)
|
|
F
2
|
79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 037 |
93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 743 743 |
79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602 602 |
— |
|
F
4
|
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889 889 |
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407 407 |
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227 227 |
53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 543 543 |
— |
|
ζ
|
515 |
545 |
662 |
771 |
— |
|
Pr(III)
|
|
F
2
|
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 323 |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391 391 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 429 429 |
84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 486 |
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 980 |
|
F
4
|
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 979 979 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 439 439 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971 971 |
51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
|
F
6
|
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 589 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 365 365 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181 181 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 686 686 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126 126 |
|
ζ
|
747 |
822 |
823 |
883 |
800 |
The results for Pr(III) show that the electronic-repulsion is much more accurately modelled when dynamic correlation is accounted for, reducing the absolute error in F2, F4 and F6 from 44, 23 and 33%, respectively, for CASSCF, to 21, 4 and 2% for MS-CASPT2 and 24, 3 and 10% for XMS-CASPT2. However, both CASPT2 variants fail to maintain the degeneracy of SO eigenstates (each 2S+1LJ term should be (2J + 1)-fold degenerate in spherical symmetry), and hence this can have a detrimental effect on the prediction of the SO coupling parameter; the 10% error at the CASSCF level is maintained at 10% for MS-CASPT2, but increases to 18% for XMS-CASPT2. There are similar improvements for Co(II): the absolute error in F2 and F4 changes from 19 and 3%, respectively, for CASSCF, to <1% and 8% for MS-CASPT2 and <1% and 6% for XMS-CASPT2. However, in this case the error in the prediction of the SO parameter increases from 6% at the CASSCF level to 29% and 50% for MS-CASPT2 and XMS-CASPT2, respectively. It is expected that CASPT2 variants will be more reliable in molecular systems where the CF removes the high degeneracy of ionic electronic terms, and thus perturbation methods are more reliable, however extreme care must be taken in the case of near-degenerate states.
We now compare our results to those obtained using the related methods of AILFT and LF-DFT. AILFT as developed by Atanasov, Ganyushin, Sivalingam and Neese,17 is a module of the Orca program that is able to re-cast a minimal active space CASSCF calculation into a ligand field (a.k.a. crystal field) model Hamiltonian. This method partitions the configuration state functions (CSF) of a CASSCF calculation into those arising from a dn or fn configuration, and the remaining ones (the “outer space”), and then approximates an effective Hamiltonian in the dn or fn CSF space which can be mapped in a one-to-one fashion with a model Hamiltonian (such as eqn (2)) in order to extract the Slater–Condon and spin–orbit coupling parameters (and crystal or ligand field parameters). The main difference between AILFT and the present method is that AILFT approximates the effective ab initio Hamiltonian in the restricted CSF space before projecting onto a model Hamiltonian, while the present method directly projects the ab initio states onto a model Hamiltonian, and thus it is in the alignment between the ab initio and the model states where the approximation is made in the present case. Each approach has its advantages and disadvantages: while the present method makes no approximations in the construction of the effective Hamiltonian (subject to the premise that the ab initio Hamiltonian can be approximated by a model Hamiltonian at all), it is not as simple to perform the projection when the ab initio states are polluted by states outside the proposed model space. AILFT has no such problems as the model space is always well defined, however it requires approximation of the effective Hamiltonian. Thus, despite both AILFT and the present method deriving from CASSCF wavefunctions, they take rather different approaches to obtain the model parameters. None-the-less, the two methods provide very similar results: the AILFT-calculated F2 and F4 parameters for Cr(III), Mo(III) and W(III) are within 1% of those from the present method,41 and the F2, F4 and F6 parameters for the series of trivalent 4f ions agree within 4% to the present method (average discrepancy is <1%).42 We have shown that our minimal CASSCF-SO calculations significantly overestimate the interelectronic repulsion and hence the Slater–Condon parameters, which can be improved by perturbative corrections for dynamic correlation, and the AILFT method is no different; addition of NEVPT2 corrections to the reference wavefunction improves the predicted parameters for the Pr(III) free ion (Table 4), where the calculated value of F2 is the closest of all methods to the experimental one, however the present calculations with MS-CASPT2 corrections appear to have an edge over NEVPT2 when it comes to the F4 and F6 parameters. We have found that the SO parameters obtained herein (which employs the AMFI method30 to obtain the SO Hamiltonian) are accurate to within ca. 10% of the experimental data, while it is reported that the SO parameters obtained from AILFT using the SO mean-field (SOMF) method are accurate to within 5% of experiment;42 this suggests that the latter method is more accurate for SO coupling in the 4f ions.
The second method LF-DFT, developed by Atanasov, Daul and Rauzy,43,44 is rather different to AILFT and the method used herein because it is based on DFT calculations. Simply, the LF-DFT method determines a set of d- or f-based Kohn–Sham orbitals using a spin-restricted average-of-configuration calculation (where each d or f orbital carries n/5 or n/7, respectively, electrons), and subsequently calculates the energies of all possible Slater determinants in these d or f orbitals using a spin-unrestricted formalism.43,44 From these energies, the Slater–Condon and SO coupling45 parameters (and crystal or ligand field parameters) can be extracted. Most comparisons of this method have been made on complexes of metal ions rather than free ions, however one of the early papers presents data for Cr(IV), Mn(V) and Fe(VI) using the LDA density-functional. The LF-DFT(LDA)-calculated Slater–Condon parameters are very good for Cr(IV), coming within 3% for both F2 and F4 compared to experiment, however the method underestimates the parameters for Mn(V) and Fe(VI) by 10–20%. In contrast, the calculations herein overestimate F2 and F4 by 10–20% for Cr(IV), while overestimating F2 and underestimating F4 by around 10% and 20%, respectively, for both Mn(V) and Fe(VI). Thus, overall, the results of LF-DFT(LDA) are of a similar quality to those obtained with minimal CASSCF-SO, with the caveat that LF-DFT will be subject to a user choice of density-functional which does not offer systematic improvement, unlike the ability to add dynamic correlation with CASSCF methods via perturbation theory. However, it should be noted that in real applications LF-DFT will almost certainly always outperform CASSCF methods in efficiency. Indeed, the LF-DFT method has recently been shown to outperform the accuracy of commonplace time-dependent DFT (TD-DFT) calculations for d–d optical spectra, and approaches the accuracy of more advanced multiconfigurational methods.46
Conclusions
Herein we have performed minimal active space CASSCF-SO calculations with OpenMolcas to determine Slater–Condon and SO coupling parameters for metal ions from across the periodic table. We find that the variance of SO coupling parameters as a function of atomic number for a given dn configuration is well-described by a quadratic function, while the Slater–Condon parameters show a linear variation. Comparison to experimentally-derived parameters show that the SO coupling is predicted to within ca. 200 cm−1 by the minimal CASSCF-SO method, corresponding usually to <10% error for 4dn, 5dn and 4fn configurations, but the relative error is larger in the case of 3dn configurations, up to 30%, owing to the smaller SO coupling. On the other hand, Slater–Condon parameters are usually overestimated with larger relative errors on the order of 10–50%. These significant errors arise due to the well-known lack of dynamic correlation in CASSCF calculations, and as such we cannot recommend minimal active space CASSCF-SO for applications where high-energy spectroscopic data are concerned. However, there are systematic errors in the calculated Slater–Condon for divalent 4d and trivalent 4f ions, such that scaling may lead to useful results in cases where minimal CASSCF-SO calculations are the only viable option. We show that (X)MS-CASPT2 corrections can substantially improve the calculated Slater–Condon parameters, but that the calculated SO parameters are detrimentally affected, and observe significant symmetry breaking of the SO manifolds, so care should be taken using such methods in cases of high symmetry.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We acknowledge funding from The University of Manchester, The Royal Society (URF to NFC) and the European Research Council (ERC-2019-STG-851504).
References
-
E. U. Condon and G. H. Shortley, The theory of atomic spectra, Cambridge University Press, 1935 Search PubMed.
-
U. Fano and G. Racah, Irreducible tensorial sets, Academic Press, 1959, vol. 4 Search PubMed.
-
F. E. Mabbs and D. J. Machin, Magnetism and Transition Metal Complexes, 2008 Search PubMed.
-
C. K. Jørgensen, in Absorption Spectra and Chemical Bonding in Complexes, 1962 Search PubMed.
-
J. Mulak and Z. Gajek, The effective crystal field potential, Elsevier, 2000 Search PubMed.
- J. S. Griffith and L. E. Orgel, Q. Rev., Chem. Soc., 1957, 11, 381–393 RSC.
-
D. S. McClure, Solid State Physics, ed. F. Seitz and D. Turnbull, Academic Press, 1959, vol. 9, pp. 399–525 Search PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
-
A. Bencini and D. Gatteschi, EPR of exchange coupled systems, Courier Corporation, 2012 Search PubMed.
- N. Karayianis, J. Chem. Phys., 1970, 53, 2460–2469 CrossRef CAS.
- A. S. Souza and M. A. Couto dos Santos, Chem. Phys. Lett., 2012, 521, 138–141 CrossRef CAS.
- M. Speldrich, J. van Leusen and P. Kögerler, J. Comput. Chem., 2018, 39, 2133–2145 CrossRef CAS PubMed.
- B. Roos and P. R. Taylor, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. Manuel Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. Pedro Malhado, P.-A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. Manh Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. Kragh Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. Patrick Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
-
M. Atanasov, D. Ganyushin, K. Sivalingam and F. Neese, in Molecular Electronic Structures of Transition Metal Complexes II, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, vol. 143, pp. 149–220 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- T. Fleig and L. Visscher, Chem. Phys., 2005, 311, 113–120 CrossRef CAS.
-
M. Barysz, in Theoretical Chemistry and Physics of Heavy and Superheavy Elements, ed. U. Kaldor and S. Wilson, Springer, Dordrecht, 2003, pp. 349–397 Search PubMed.
- G. Levi, A. V. Ivanov and H. Jónsson, Faraday Discuss., 2020, 224, 448–466 RSC.
- A. Lunghi and F. Totti, Inorganics, 2016, 4(4), 28 CrossRef.
-
C. D. Sherrill and H. F. Schaefer, The Configuration Interaction Method: Advances in Highly Correlated Approaches, Elsevier Masson SAS, 1999, vol. 34 Search PubMed.
- D. Reta, F. Ortu, S. Randall, D. P. Mills, N. F. Chilton, R. E. P. Winpenny, L. Natrajan, B. Edwards and N. Kaltsoyannis, J. Organomet. Chem., 2018, 857, 58–74 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. Fdez. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS PubMed.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106 CrossRef PubMed.
-
B. N. Figgis and M. A. Hitchman, Ligand Field Theory and Its Applications, Wiley, 2000 Search PubMed.
- S. Koseki, N. Matsunaga, T. Asada, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 2019, 123, 2325–2339 CrossRef CAS PubMed.
- T. M. Dunn, Trans. Faraday Soc., 1961, 57, 1441–1444 RSC.
- T. Anno and H. Teruya, Theor. Chim. Acta, 1971, 21, 127–142 CrossRef CAS.
- S. M. Butorin, Inorg. Chem., 2020, 59, 16251–16264 CrossRef CAS PubMed.
- D. W. Lynch and R. D. Cowan, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 9228 CrossRef CAS PubMed.
- S. Battaglia and R. Lindh, J. Chem. Theory Comput., 2020, 16, 1555–1567 CrossRef CAS PubMed.
- S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25 CrossRef CAS.
- D. Aravena, M. Atanasov and F. Neese, Inorg. Chem., 2016, 55, 4457–4469 CrossRef CAS PubMed.
- M. Atanasov, C. A. Daul and C. Rauzy, Chem. Phys. Lett., 2003, 367, 737–746 CrossRef CAS.
-
M. Atanasov, C. A. Daul and C. Rauzy, in Optical Spectra and Chemical Bonding in Inorganic Compounds, ed. D. M. P. Mingos and T. Schönherr, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, vol. 106, pp. 97–125 Search PubMed.
- M. Atanasov and C. A. Daul, C. R. Chim., 2005, 8, 1421–1433 CrossRef CAS.
- F. Vlahović, M. Perić, M. Gruden-Pavlović and M. Zlatar, J. Chem. Phys., 2015, 142, 214111 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1dt02346b |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Nicholas F.
Chilton
and
Nicholas F.
Chilton
 *
*
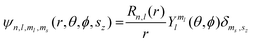
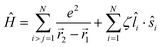
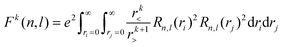
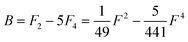
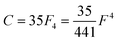
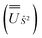 and blocks of different Ŝ2 eigenstates were identified; (ii) the matrix representation of
and blocks of different Ŝ2 eigenstates were identified; (ii) the matrix representation of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2 in the SO eigenbasis was transformed into the Ŝ2 eigenbasis with
2 in the SO eigenbasis was transformed into the Ŝ2 eigenbasis with 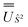 and diagonalised within each eigenblock of Ŝ2, where the resulting eigenvectors were used to construct the SO → Ŝ2,
and diagonalised within each eigenblock of Ŝ2, where the resulting eigenvectors were used to construct the SO → Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2 unitary transformation
2 unitary transformation 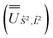 ; (iii) the matrix representation of Ĵ2 in the SO eigenbasis was transformed into the Ŝ2,
; (iii) the matrix representation of Ĵ2 in the SO eigenbasis was transformed into the Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2 eigenbasis with
2 eigenbasis with 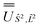 , and diagonalised within each eigenblock of Ŝ2,
, and diagonalised within each eigenblock of Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2, where the resulting eigenvectors were used to construct the SO → Ŝ2,
2, where the resulting eigenvectors were used to construct the SO → Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2, Ĵ2 unitary transformation
2, Ĵ2 unitary transformation 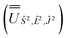 ; (iv) the SO Hamiltonian of the electronic structure calculation (which is diagonal in the SO eigenbasis) was transformed into the Ŝ2,
; (iv) the SO Hamiltonian of the electronic structure calculation (which is diagonal in the SO eigenbasis) was transformed into the Ŝ2, ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) 2, Ĵ2 basis with
2, Ĵ2 basis with 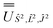 and then diagonalised to return the original SO eigenstates and their composition in terms of the Russell–Saunders basis. Then, the Slater–Condon and SO parameters were first estimated from the average SO eigenvalues of each 2S+1LJ term, and subsequently refined by fitting the entire energy spectrum of the model Hamiltonian (eqn (2)) to the entire energy spectrum from CASSCF-SO. We note that this method is not restricted to minimal active space calculations and thus is broadly applicable beyond the scope of the present work. This code is under preparation and will soon be released as an open-source package.
and then diagonalised to return the original SO eigenstates and their composition in terms of the Russell–Saunders basis. Then, the Slater–Condon and SO parameters were first estimated from the average SO eigenvalues of each 2S+1LJ term, and subsequently refined by fitting the entire energy spectrum of the model Hamiltonian (eqn (2)) to the entire energy spectrum from CASSCF-SO. We note that this method is not restricted to minimal active space calculations and thus is broadly applicable beyond the scope of the present work. This code is under preparation and will soon be released as an open-source package.
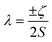





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which amounts to around 10–40% relative error in F2 (Fig. S3a†). For F4 the relative errors are larger for the underestimated values which generally occur for d2 configurations, whereas most values are overestimated around 5–45%. For 4d ions, for which we only have data for the divalent series, we find all the Slater–Condon parameters are overestimated, and that there appears to be a systematic error owing to the smooth trend in error (Fig. S3†). For the trivalent 4f ions, all F2, F4 and F6 parameters are overestimated by ca. 6000–30
000 cm−1, which amounts to around 10–40% relative error in F2 (Fig. S3a†). For F4 the relative errors are larger for the underestimated values which generally occur for d2 configurations, whereas most values are overestimated around 5–45%. For 4d ions, for which we only have data for the divalent series, we find all the Slater–Condon parameters are overestimated, and that there appears to be a systematic error owing to the smooth trend in error (Fig. S3†). For the trivalent 4f ions, all F2, F4 and F6 parameters are overestimated by ca. 6000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which corresponds to around 25–30% error for F2 (Table S2†), 15–20% error for F4 (Table S3†) and 12–26% error for F6 (Table S4†). We see a similar decrease in error in the Slater–Condon parameters for the trivalent 4f ions as observed for the divalent 4d ions, although there is more scatter in the 4f data (Fig. S3†), again suggesting that there is a systematic error in the estimation of the interelectronic repulsion in minimal CASSCF-SO calculations.
000 cm−1, which corresponds to around 25–30% error for F2 (Table S2†), 15–20% error for F4 (Table S3†) and 12–26% error for F6 (Table S4†). We see a similar decrease in error in the Slater–Condon parameters for the trivalent 4f ions as observed for the divalent 4d ions, although there is more scatter in the 4f data (Fig. S3†), again suggesting that there is a systematic error in the estimation of the interelectronic repulsion in minimal CASSCF-SO calculations.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037
037![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 743
743![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400
400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602
602![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889
889![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407
407![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227
227![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 543
543![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323
323![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391
391![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 429
429![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486
486![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980
980![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 979
979![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 439
439![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971
971![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707
707![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740
740![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589
589![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 365
365![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181
181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 686
686![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126
126