Formation of atmospheric molecular clusters from organic waste products and sulfuric acid molecules: a DFT study

Abstract

The interaction of one or two sulfuric acid molecules with the indole (C₈H₇N) molecule and with the skatole (C₉H₉N) molecule and two of its oxidation products (C₉H₉NO₂ and C₉H₉NO₃) has been investigated by means of computational methods at the quantum level. Gibbs free energies of formation have been calculated using the ωB97X-D exchange-correlation functional with three different basis sets to characterize the stability of the corresponding hetero-molecular clusters. The careful examination of the cluster geometries shows the key role of the hydrogen bonding in the stabilization of the critical nucleus that these organics can form with the sulfuric acid molecules. However, the thermodynamic results demonstrate that the interaction between indole/skatole and one or two sulfuric acid molecules remains quite weak in atmospheric conditions and may likely compete with the formation of sulfuric acid dimers. By contrast, the oxidized C₉H₉NO₃ and C₉H₉NO₂ species appear to be much better candidates for the formation of critical nuclei with sulfuric acid molecules than their parent compounds, indole or skatole. This supports the conclusions of recent experimental observations on the ability of molecules issued from organic waste products to form nuclei with sulfuric acid molecules and emphasizes the potential role of agricultural recycling of sewage sludge as an unaccounted source of nucleation precursors in the atmosphere.

---

Environmental significance

Secondary organic aerosols represent one of the main sources of uncertainty in the current understanding of the Earth's climate. Predicting their formation from various sources is thus essential for evaluating their real impact. Recent experiments have shown that spreading of sewage sludge may lead to intensive new particle formation. Here, we use DFT calculations to characterize the molecular clusters that may be formed by addition of H₂SO₄ on the indole and skatole molecules and on two of their oxidation products. We show that the key point for the particle formation is the optimization of the hydrogen bond network between these species, and that skatole oxidation products may initiate nucleation events more likely than the skatole molecule itself.

1 Introduction

Atmospheric aerosols are ubiquitous liquid or solid particles suspended in the atmosphere. In addition to their negative effect on human health,^1,2 they also impact atmospheric chemistry and Earth's radiative balance, directly via absorption/scattering of the incoming radiation and indirectly through their influence on cloud properties.^3–5 Therefore, this recent recognition of aerosols as major players of the Earth's atmosphere has led to the emergence of numerous research studies aiming at better characterizing their physico-chemical properties. However, despite all the efforts undertaken in recent years, the exact role of aerosols still remains poorly understood, mainly because of the great diversity of their sources and also of their atmospheric fate.⁶ This is especially true for organic aerosols (OAs),⁷ since most of them are directly formed in the atmosphere through complex nucleation processes.⁵ Indeed, while a lot of atmospheric aerosols are directly emitted from natural and anthropogenic sources as particles such as, for example, marine aerosols, mineral dusts (volcano and desert dust), combustion emitted particles (soot), etc., a significant fraction of OAs comes from the recombination of gas phase species, thus forming what is named secondary organic aerosols (SOAs).⁸

Atmospheric formation of new particles is a complex process, initiated by the clustering of gas phase molecules via strong inter-molecular interactions such as hydrogen bonding or coulombic interactions.^9–11 Strongly bonded clusters may thus grow and reach a critical size where they become stable against the evaporation of their own constituents.¹² Then, these nuclei may spontaneously grow to detectable sizes via additional uptake of gases.⁹ On the contrary, they may be scavenged by various processes including coagulation with pre-existing particles.¹⁰

Although the conversion process from small nuclei to larger stable aerosol particles remains elusive, our knowledge on the first steps of the clustering have been deeply improved thanks to the development of cutting edge experimental and theoretical approaches.^10,13 New-particle formation often involves sulfuric acid, ions, ammonia, and among other possible candidates, highly oxidized organic compounds.^9,14–18 Both the chemical composition of the critical nucleus and the gaseous concentration of the nucleating species are key factors impacting the rate at which nucleation may occur. Moreover, it has been inferred from atmospheric measurements and laboratory experiments, that only very few sulfuric acid molecules (typically one or two) might be involved in the formation of a critical nucleus, especially if other sulfuric acid-stabilizing species like organic acids are simultaneously present.^9,10,19,20 Thus, critical molecular clusters relevant for atmospheric nucleation may be surprisingly small.¹⁰ This allows a molecular-level understanding of their formation on the basis of advanced quantum chemistry methods,²¹ as an alternative to classical nucleation theory that rather uses bulk properties to simulate aerosol growth.¹⁰

Among all the available quantum chemistry approaches, density functional theory (DFT) has been the dominant method in the last decade because of its versatility and relatively low computational cost, although higher-level wavefunction-based methods have also been used.²¹ Because it has been shown that, in usual atmospheric conditions, only hetero-molecular pre-nucleation clusters may lead to subsequent new particle formation,¹⁰ computational models of pre-nucleation have focused on the properties of clusters made of different species.^{11,12,21–26} However, although a recent compiled database has been published consisting of more than 630 atmospherically relevant clusters containing sulfuric acid, bases, various oxidized organic compounds and water,²⁵ it does not entirely cover the huge diversity of atmospheric organic compounds and complementary studies are thus needed, in many situations.

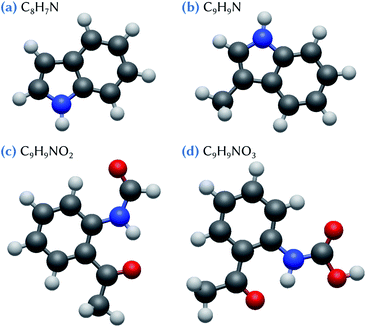
For example, very recent reaction chamber experiments have shown that agricultural recycling of sewage sludge is an unaccounted source of nucleation precursors, involving especially indole and skatole molecules and some of their oxidation products.²⁷ Thus, here, we make use of quantum chemistry methods to characterize the critical nucleus formed by one or two sulfuric acid molecules and these species issued from organic waste products. On the basis of the experimental conclusions,²⁷ we particularly focus on the C₈H₇N (indole), C₉H₉N (skatole), C₉H₉NO₂, and C₉H₉NO₃ molecules (Fig. 1). Notice that, among the intermediate reaction products that have been detected in the experiments,²⁷ we limit our theoretical study to those that are the most likely candidates to be involved in nucleation process, based on their high O content.

Fig. 1 Snapshots of (a) indole, (b) skatole and (c, d) two oxidized derivatives which are considered in this work. Hydrogen atoms are represented in white, carbon atoms in dark gray, nitrogen atoms in blue and oxygen atoms in red.

We follow a numerical procedure similar to the one used in preceding studies,^23–25 that involves preliminary optimization of the molecular clusters at a semi-empirical level, followed by subsequent DFT optimizations performed on selected configurations. This study aims at determining the most stable structures and the underlying thermochemistry of the pre-nucleation clusters, to decipher which species among skatole and its oxidation products is the most favorable to nucleation. We also consider the case of the indole molecule, for comparison with the skatole one.

2 Computational details

All calculations are performed using the Gaussian 09 quantum chemistry software.²⁸ Energy optimizations are carried out with the ωB97X-D exchange-correlation functional, a long-range corrected hybrid functional with dispersion corrections.²⁹ Three Gaussian-type atomic orbital basis sets, of the split valence double-ζ quality with additional polarization and diffuse functions, are used, namely the old but still widely-used Pople 6-31++G(d,p)^30–36 and the more recent Jensen aug-pcseg-1 ³⁷ and Karlsruhe def2-SVPD.^38,39 Note that the Jensen and Karlsruhe basis sets used in this work, which are not implemented by default in Gaussian 09, have been retrieved from the Basis Set Exchange online database.⁴⁰ Production calculations are performed with a dense integration grid (ultra-fine) and tight convergence criteria, together with a vibrational frequency analysis. Atomic partial charges are computed using the natural population analysis (NPA) part of the natural bond orbital (NBO) method.⁴¹

To determine the lowest energy clusters involving one organic and one or two sulfuric acid molecules, the following methodology is used. First, a set of initial conformers are randomly generated by placing one sulfuric acid molecule in predetermined regions around the organic molecule under consideration. These regions have been chosen because of their strong electrostatic charge, as identified on the electrostatic potential maps generated using the NPA method. This ensured that only the regions of the configuration space that are the most likely to lead to strong binding are sampled. For each system considered in this study, between 20 to 80 configurations are generated this way and pre-optimized at the semi-empirical PM6 level of theory. All redundant configurations, discriminated by their identical electronic energy, within 6 × 10⁻³ kcal mol⁻¹, are discarded and the remaining configurations are optimized at the PW91/6-31G(d,p) level. The resulting conformers are then sorted by their electronic energy and the lowest energy configurations, within 6 kcal mol⁻¹, are selected for production calculations using the ωB97X-D functional and various basis sets, as described above. This procedure is then reused when considering the adsorption of an additional sulfuric acid molecule on the optimized cluster formed by one organic and one sulfuric acid molecule.

Three thermodynamic quantities are computed, namely the binding energy ΔE, the enthalpy of formation ΔH and the Gibbs energy of formation ΔG. They are calculated using the following formula:

ΔΘ = Θ[OM + nSA] − Θ[OM] − nΘ[SA] (1)

where OM refers to the organic molecule under consideration, n = {1, 2} is the number of sulfuric acid molecules (SA), and Θ denotes either the energy E, the enthalpy H or the Gibbs energy G. The energy E is corrected by the zero-point vibration energy. The enthalpy H and the entropy S are calculated at standard conditions (i.e., T = 298.15 K and P = 1 atm) using the rigid-rotor harmonic oscillator approximation, with a quasi-harmonic treatment for the low-lying frequency modes.^42,43 For clusters involving two sulfuric acid molecules, two alternative definitions of the binding energy and of the enthalpy and Gibbs energy of formation are also used, with two different reference points for the calculations:

ΔΘ^* = Θ[OM + 2SA] − Θ[OM] − Θ[2SA] (2)

ΔΘ^†= Θ[OM+2SA] − Θ[OM + SA] − Θ[SA] (3)

indeed, eqn (2) considers the separated organic molecule and gaseous H₂SO₄ dimer as the reference, while in eqn (3) the reference is the optimized cluster formed by the organic molecule and the first attached sulfuric acid molecule. Note that for the latter, when several conformers have been found for the cluster, always the one with the lowest Gibbs energy configuration is used as a reference.

3 Results and discussion

3.1 Indole/skatole and sulfuric acid clusters

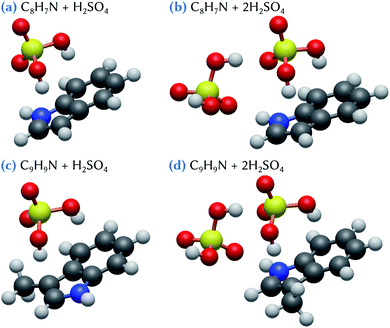
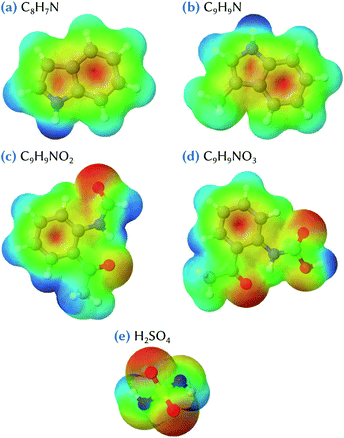
The structures of the lowest energy clusters composed of indole or skatole and one or two sulfuric acid molecules are shown in Fig. 2. Both indole and skatole have a –NH group that can form a strong hydrogen bond with an incoming gas phase molecule. Moreover, as can be seen in the electrostatic potential (ESP) maps calculated for these molecules and shown in Fig. 3, the centers of the benzene and pentagonal cycles exhibit a negative charge which may also attract the –OH groups of sulfuric acid. This allows the stabilization of the indole/skatole and sulfuric acid cluster in configurations where the two –OH groups of H₂SO₄ point toward the centers of the two cycles of the organic molecule. In addition, one oxygen atom of the acid molecule can also point to the –CH₃ or the –NH group of the skatole or indole molecules, respectively. Then, when approaching a second H₂SO₄ molecule, it can interact with this small cluster by forming two hydrogen bonds, the first one with the already attached sulfuric acid molecule and the second one with the –NH group of the organic molecule. Because the number of attractive groups for H₂SO₄ in both indole and skatole species is limited, these systems are quite easily optimized and, thus, no other conformer was found in our investigations.

Fig. 2 Snapshots of (a, b) indole and sulfuric acid clusters and (c, d) skatole and sulfuric acid clusters. Hydrogen atoms are represented in white, carbon atoms in dark gray, nitrogen atoms in blue, oxygen atoms in red and sulfur atoms in yellow.

Fig. 3 Electrostatic potential maps of (a) indole, (b) skatole, (c, d) two oxidized derivatives and (e) sulfuric acid. Negative potential values are rendered in red, neutral values in green and positive values in blue.

The corresponding energetic data are given in Table 1 for calculations performed at the ωB97X-D/6-31++G(d,p) level of theory. In the following, and until stated otherwise, we will only discuss the results obtained at this level of theory. The influence of the basis set, which do not change the discussions that follow, will be discussed later. As expected due to their similarity, indole and skatole molecules exhibit similar behavior with respect to their binding with sulfuric acid molecules. Indeed, the corresponding values of the Gibbs energy of formation are equal to −2.3 kcal mol⁻¹ for C₈H₇N + H₂SO₄ and −2.4 kcal mol⁻¹ for C₉H₉N + H₂SO₄ clusters, and are equal to −7.5 and −7.8 kcal mol⁻¹ for C₈H₇N + 2H₂SO₄ and C₉H₉N + 2H₂SO₄ clusters, respectively. It is worth mentioning that, in the atmosphere, the formation of a cluster made of one organic and one H₂SO₄ molecules may compete with the direct formation of sulfuric acid dimers. Indeed, when compared to the Gibbs energy of formation of this dimer (−6.4 kcal mol⁻¹), the clustering of one sulfuric acid molecule with both indole and skatole molecules appears rather unlikely, at least from a thermodynamic point of view. By contrast, the direct binding of one sulfuric acid dimer with one indole or skatole molecule could represent a favored pathway for the formation of the corresponding tri-molecular cluster. Indeed, by using eqn (2), the Gibbs energy of formation for the corresponding clusters is equal to −1.1 and −1.4 kcal mol⁻¹ for C₈H₇N + 2H₂SO₄ and C₉H₉N + 2H₂SO₄, respectively. This weak stabilization with respect to the sulfuric acid dimer in the gas phase can be related to the formation of the hydrogen bonds discussed above, i.e., one between the attached sulfuric acid molecules themselves, and three between these acid molecules and the organic one (Fig. 2). But, overall, these results show that the interaction between indole/skatole and one or two sulfuric acid molecules is quite weak, thus questioning the stability of the resulting clusters in the atmospheric environment. As a consequence, this may hinder the ability of indole and skatole to act as efficient aerosol nuclei with sulfuric acid.

Table 1 Energetic data of cluster formation calculated at the ωB97X-D/6-31++G(d,p) level of theory. All values are given in kcal mol⁻¹

Configurations	ΔE	ΔH	ΔG	ΔE*	ΔG*	ΔE^†	ΔG^†
C8H7N + H2SO4	−13.6	−14.5	−2.3	—	—	—	—
C8H7N + 2H2SO4	−30.7	−32.7	−7.5	−13.1	−1.1	−17.1	−5.2
C9H9N + H2SO4	−14.0	−15.1	−2.4	—	—	—	—
C9H9N + 2H2SO4	−31.2	−33.2	−7.8	−13.6	−1.4	−17.1	−5.4
C9H9NO2 + H2SO4 (1)	−15.5	−16.3	−3.7	—	—	—	—
C9H9NO2 + H2SO4 (2)	−13.6	−14.6	−2.8	—	—	—	—
C9H9NO2 + H2SO4 (3)	−12.3	−13.3	−1.4	—	—	—	—
C9H9NO2 + 2H2SO4 (1)	−39.5	−41.6	−14.1	−21.9	−7.8	−24.1	−10.4
C9H9NO2 + 2H2SO4 (2)	−37.5	−39.7	−12.8	−19.9	−6.4	−22.1	−9.1
C9H9NO3 + H2SO4 (1)	−19.6	−20.6	−7.9	—	—	—	—
C9H9NO3 + H2SO4 (2)	−15.2	−16.1	−3.2	—	—	—	—
C9H9NO3 + 2H2SO4 (1)	−39.6	−41.7	−13.6	−22.0	−7.3	−20.0	−5.8
C9H9NO3 + 2H2SO4 (2)	−36.4	−38.7	−13.0	−18.8	−6.6	−16.9	−5.1
C9H9NO3 + 2H2SO4 (3)	−37.9	−40.1	−12.7	−20.3	−6.4	−18.3	−4.8
C9H9NO3 + 2H2SO4 (4)	−36.4	−38.4	−10.7	−18.8	−4.4	−16.8	−2.9
C9H9NO3 + 2H2SO4 (5)	−35.7	−37.9	−10.4	−18.1	−4.1	−16.2	−2.6
2H2SO4	−17.6	−18.6	−6.4	—	—	—	—
3H2SO4	−35.8	−37.9	−11.7	−18.2	−5.4	—	—

---

3.2 Oxidized derivatives of skatole and sulfuric acid clusters

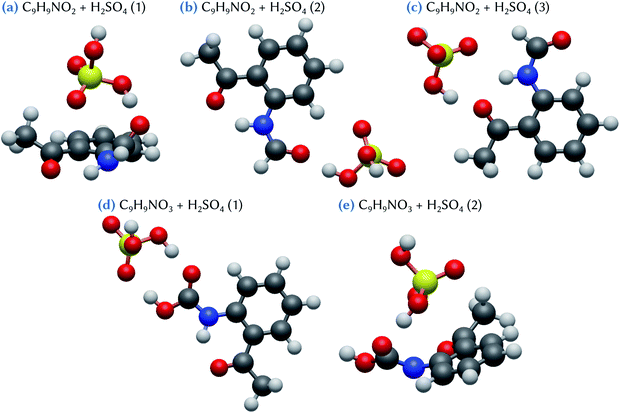
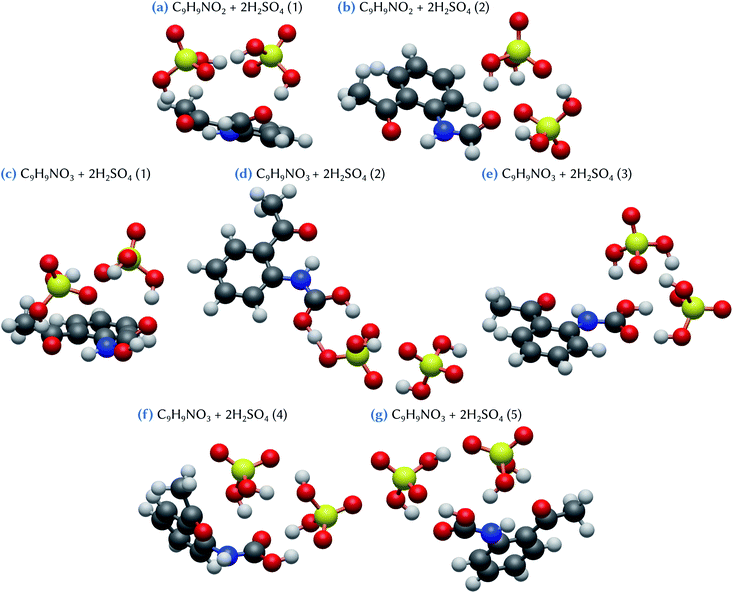
Three minimum energy configurations are found for the C₉H₉NO₂ + H₂SO₄ clusters, as shown in Fig. 4. The lowest energy conformer (Table 1), C₉H₉NO₂ + H₂SO₄ (1), is characterized by a bending of the organic molecule, which thus becomes non-planar, allowing for the sulfuric acid molecule to form a bridge between the –COOH and the –CH₃ groups of the organic molecule. This configuration has a Gibbs energy of formation of −3.7 kcal mol⁻¹. By contrast, in the two other conformers, C₉H₉NO₂ + H₂SO₄ (2) and (3), the organic molecule remains flat, and an acceptor hydrogen bond between one of its oxidized groups and the H₂SO₄ molecule is formed. Meanwhile, an oxygen atom of this sulfuric acid molecule points toward the two nearest hydrogen atoms belonging either to the benzene ring (conformer 2) or to the –NHCOH group of the C₉H₉NO₂ molecule (conformer 3). These two configurations are characterized by Gibbs energies of formation equal to −2.8 and −1.4 kcal mol⁻¹ for conformers 2 and 3, respectively. Note that, whereas the conformer C₉H₉NO₂ + H₂SO₄ (1) has a binding energy which is lower than the two others, by at least 2 kcal mol⁻¹, this difference is significantly reduced when considering the Gibbs energy of formation. This can be related to the entropic effects coming from the deformation of the organic molecule in conformer 1, that may hinder the stability of this cluster at standard conditions. When compared to the indole and skatole molecules, which do not have any oxidized groups able to form additional hydrogen bonds with sulfuric acid, as for the C₉H₉NO₂ species, the energy values given in Table 1 show that the stability of the C₉H₉NO₂ + H₂SO₄ clusters is slightly reinforced, but only for conformers 1 and 2. In addition, the Gibbs energy values remain overall quite weak, with only a maximum decrease of 1.4 kcal mol⁻¹ with respect to the corresponding indole and skatole analogues. This emphasizes the quite subtle energetic balance between the various hydrogen bonds that may be formed in the corresponding clusters. Indeed, indole and skatole molecules are tied to the sulfuric acid molecule by two acceptor hydrogen bonds, whereas one donor and one acceptor hydrogen bonds are formed in the case of the C₉H₉NO₂ molecule.

Fig. 4 Snapshots of clusters formed between oxidized skatole derivatives and one sulfuric acid molecule. The structures of the clusters have been optimized at the ωB97X-D/6-31++G(d,p) level of theory. Hydrogen atoms are represented in white, carbon atoms in dark gray, nitrogen atoms in blue, oxygen atoms in red and sulfur atoms in yellow.

Two low energy configurations are found for the C₉H₉NO₃ + H₂SO₄ clusters (Fig. 4). In one of these structures, the conformer, C₉H₉NO₃ + H₂SO₄ (2), is similar to that of C₉H₉NO₂ + H₂SO₄ (1), exhibiting the same bridge structure due to the strong deformation of the geometry of the organic molecule (i.e., loss of flatness). This conformer has a Gibbs energy of formation equal to −3.2 kcal mol⁻¹. The most stable conformer (Table 1), C₉H₉NO₃ + H₂SO₄ (1), is characterized by the formation of two hydrogen bonds, one donor and one acceptor, with the –COOH group of C₉H₉NO₃. Its Gibbs energy of formation is equal to −7.9 kcal mol⁻¹, which is in fact the lowest value for all the clusters involving one sulfuric acid molecule considered in this work. It is also the only one which is lower than the value of −6.4 kcal mol⁻¹ corresponding to the formation of the H₂SO₄ dimer in the gas phase, thus demonstrating the strong stabilizing role of the formation of double hydrogen bonds for such atmospheric clusters.

When considering the C₉H₉NO₂ + 2H₂SO₄ and the C₉H₉NO₃ + 2H₂SO₄ clusters, respectively two and five stable configurations are found, as shown in Fig. 5. The lowest energy conformer for the first system, C₉H₉NO₂ + 2H₂SO₄ (1), exhibits a bridged structure with an out-of-the-plane deformation of the C₉H₉NO₂ molecule, thus allowing the formation of two acceptor hydrogen bonds, one with each sulfuric acid molecules. In addition, these two H₂SO₄ molecules are strongly tied together by two hydrogen bonds, as in an optimized H₂SO₄ dimer. The corresponding Gibbs energy of formation is equal to −14.1 kcal mol⁻¹ with respect to the separated species, or to −7.8 and −10.4 kcal mol⁻¹ using the references of eqn (2) and (3), respectively. This means that a substantial increase of stability is achieved when compared to the corresponding separated systems. By contrast, in the case of the second slightly less stable conformer, C₉H₉NO₂ + 2H₂SO₄ (2), only the oxygen atom of the –NHCOH group of the organic molecule is involved in the bonding with the two sulfuric acid molecules, that also attachtogether via hydrogen bonding. In this case, the Gibbs energy of formation is equal to −12.8 kcal mol⁻¹ with respect to the separated species, or to −6.4 and −9.1 kcal mol⁻¹ using eqn (2) and (3), respectively. As evidenced by these results, the addition of a second sulfuric acid molecule leads to the formation of much more stable clusters than those formed with only one H₂SO₄. This may indicate that, in atmospheric conditions, the formation pathway involving a sulfuric acid dimer and the C₉H₉NO₂ molecule is likely to have a dominant role with respect to the one involving the successive addition of sulfuric acid molecules on the organic.

Fig. 5 Snapshots of clusters formed between oxidized skatole derivatives and two sulfuric acid molecules. The structures of the clusters have been optimized at the ωB97X-D/6-31++G(d,p) level of theory. Hydrogen atoms are represented in white, carbon atoms in dark gray, nitrogen atoms in blue, oxygen atoms in red and sulfur atoms in yellow.

For the C₉H₉NO₃ + 2H₂SO₄ system, the conformer with the lowest Gibbs energy of formation, C₉H₉NO₃ + 2H₂SO₄ (1), exhibits a bridged structure similar to that obtained for C₉H₉NO₂ + 2H₂SO₄ (1). Indeed, it is characterized by the bending of the organic molecule to optimize hydrogen bonding with the two sulfuric acid molecules, these molecules being themselves attached by two hydrogen bonds. The Gibbs energy of formation of this conformer is equal to −13.6 kcal mol⁻¹. This value is 0.9 kcal mol⁻¹ lower than the one calculated for the C₉H₉NO₃ + 2H₂SO₄ (3) conformer (−12.7 kcal mol⁻¹), which has a structure similar to C₉H₉NO₂ + 2H₂SO₄ (2), with a hydrogen bond network between the two H₂SO₄ themselves and the –COOH group of C₉H₉NO₃. Note that the difference in the corresponding binding energy between these two configurations is larger, conformer 3 having a ΔE value 2 kcal mol⁻¹ higher than conformer 1. Again, this originates from a strong entropic effect that appears unfavorable to the bridged structure of C₉H₉NO₃ + 2H₂SO₄ (1). Likewise, the second less stable conformer, C₉H₉NO₃ + 2H₂SO₄ (2), despite exhibiting a binding energy 3.2 kcal mol⁻¹ higher than conformer (1), has only a slightly higher Gibbs energy of formation at a value of −13.0 kcal mol⁻¹. This configuration can be viewed as the hetero-dimer of C₉H₉NO₃ + H₂SO₄ (1) (Fig. 4d) to which a second H₂SO₄ molecule has been added, forming two hydrogen bonds with the already attached sulfuric acid molecule. Interestingly, the hydrogen atom of the first H₂SO₄ is located just in between the two surrounding oxygen atoms, at a distance of 1.06 Å from the oxygen atom of C₉H₉NO₃ and at 1.39 Å from the one of H₂SO₄, suggesting a proton exchange between the two molecules that can thus be viewed as forming a zwitterion-like configuration. Note that this behavior is not observed with the smaller C₉H₉NO₃ + H₂SO₄ (1), although its configuration exhibits the same double hydrogen bonds between the organic and the sulfuric acid molecules. Thus, the zwitterion formation clearly appears as the consequence of the addition of the second sulfuric acid molecule. The two remaining stable conformers, C₉H₉NO₃ + 2H₂SO₄ (4) and (5), both exhibit hydrogen bonding between one H₂SO₄ molecule and the –COOH group of C₉H₉NO₃ but, in these configurations, the organic molecule is slightly distorted to allow for the formation of an additional hydrogen bond with the –CH₃ group (conformer 4) or the oxygen atom of the –COCH₃ group (conformer 5). The corresponding Gibbs energies of formation are equal to −10.7 and −10.4 kcal mol⁻¹, respectively. These results indicate that, overall, both C₉H₉NO₃ and C₉H₉NO₂ molecules have a similar ability to form clusters with two sulfuric acid molecules, despite the fact that the C₉H₉NO₃ species appear more likely to form clusters with one H₂SO₄ molecule than C₉H₉NO₂ does. The three most stable C₉H₉NO₃ + 2H₂SO₄ clusters show Gibbs energies of formation ranging from −7.3 to −6.4 kcal mol⁻¹ with respect to the addition of a sulfuric acid dimer; these values are equivalent or lower than the corresponding value for the formation of the H₂SO₄ dimer (−6.4 kcal mol⁻¹). These results emphasize the strong stabilizing effect of the binding of a sulfuric acid dimer with the C₉H₉NO₃ molecule.

Finally, as evidenced by the present thermodynamic results obtained at the quantum level, the oxidized C₉H₉NO₂ and C₉H₉NO₃ species appear overall to be much better candidates for the formation of critical nuclei with sulfuric acid molecules in the atmosphere than their parent compounds, indole and skatole.

3.3 Influence of the basis set

In the previous parts of this work, the results obtained with the Pople 6-31++G(d,p) basis set together with the ωB97X-D functional have been discussed, aiming at providing data which are comparable with previously published results such as the ones reported in the atmospheric cluster database.²⁵ In addition, as mentioned in the computational section, we have performed calculations with the aug-pcseg-1 and def2-SVPD basis sets, to quantify the influence of changing the level of calculations on the results presented above. The corresponding energetic data are given in Tables S1 and S2 (ESI†) for ωB97X-D/aug-pcseg-1 and ωB97X-D/def2-SVPD calculations, respectively. As expected, quantitative differences in the computed thermodynamic data are obtained when using different basis sets. However, overall, these new results do not fundamentally change the conclusions of the previous discussion based on the results obtained at the ωB97X-D/6-31++G(d,p) level. In particular, it should be emphasized that the geometries of the different clusters remain very similar, exhibiting only a few slight changes in the bond lengths, including hydrogen bonds, accounting for less than 1 × 10⁻² Å in average. The corresponding thermodynamic data show a bit more differences, being characterized by lower Gibbs energies of formation with the new basis sets. Nevertheless, the ordering of the configurations based on their relative stability remains almost unchanged. Thus, the present results do not exhibit any significant influence of the choice of the basis set on the cluster formation between sulfuric acid molecules and the organics considered in this work.

4 Conclusion

The interaction of one or two sulfuric acid molecules with indole (C₈H₇N) and skatole (C₉H₉N) molecules and two of its oxidation products (C₉H₉NO₂ and C₉H₉NO₃) has been investigated by means of computational methods at the DFT level. Thermodynamic quantities such as binding energy, enthalpy of formation, and Gibbs free energies of formation have been calculated using the ωB97X-D exchange-correlation functional to characterize the stability of the corresponding hetero-molecular clusters. Using three different basis sets does not significantly change the conclusions of the quantum results and it is thus found that the sulfuric acid molecules are able to attach to the organics via hydrogen bonding, with Gibbs energy of formation that are lower for the oxidized molecules than for their indole or skatole parents. However, in most of the systems considered here, it is found that the formation of the sulfuric acid dimer in the gas phase may compete with the attachment of the first sulfuric acid molecule to the organic one, at least from a thermodynamic point of view, with the exception of the C₉H₉NO₃ molecule, for which the presence of the –COOH group strongly favors the attachment of the first sulfuric acid molecule, through the formation of two hydrogen bonds between these molecules. By contrast, the bonding of two sulfuric acid molecules on the organics considered here is found to be a strongly exothermic process, irrespective of the corresponding pathway (i.e., attachment of a second H₂SO₄ molecule on the already attached first one or direct attachment of one sulfuric acid dimer). Moreover, the values of ΔG* given in Tables 1, S1 and S2 (ESI†) clearly show that the addition of the skatole oxidation products to the sulfuric acid dimer is also energetically favored with respect to the formation of the sulfuric acid trimer, thus emphasizing the role that these oxidized molecules may play in the nucleation events of atmospheric nanoparticles. Overall, the present results evidence the strong competition that exists between, on the one hand, the optimization of the hydrogen bonds formed between the sulfuric acid molecules and, on the other hand, the optimization of the hydrogen bonds that these molecules are able to form with the organics considered here, as previously evidenced for other organic species interacting with various atmospheric nucleation precursors.^22–25,44 Moreover, although the present calculations have been limited to hetero-clusters made of at most three molecules because of the corresponding computational cost, we may infer from the results, that the availability of sites able to form hydrogen bonding with additional molecules could be a key point for cluster growing and the subsequent nucleation of larger particles.²⁴

Finally, the present findings indicate that agricultural recycling of sewage sludge could play an important role in aerosol formation, in accordance with recent experimental conclusions.²⁷ More precisely, our results emphasize that the skatole oxidation products may initiate the nucleation events more likely than the skatole molecule does. Notice that the subsequent impact on climate and/or health of the particles formed this way will depend on their atmospheric fate, especially on their interaction with water and other molecular atmospheric species, which is clearly out of the scope of the present theoretical calculations at the quantum level.

Anyway, the main contributions of the present work are (i) the identification of some of the molecular species that might be relevant on a new mechanism of particle formation from agricultural recycling of organic waste products, (ii) the demonstration of the nice complementarity of experimental and quantum chemistry approaches to achieve a deeper understanding of atmospheric nucleation processes. Indeed, the experiments were able to measure particle formation from skatole, and identify that sulfuric acid was involved. However, although they characterized the oxidation products of skatole, they couldn't determine which one of those where directly involved in the nucleation process. The results of our calculations clearly show how most likely the C₉H₉NO₃ molecule is behind the observed events.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the UNREAL ANR-18-CE22-0019-03 project funded by the French ANR “Agence Nationale de la Recherche”. Discussions with Prof. C. Focsa are gratefully acknowledged. Calculations have been performed using the computing resources of the Mésocentre de Calcul, a regional computing center at Université de Franche-Comté.

References

1. J. L. Mauderly and J. C. Chow, Inhalation Toxicol., 2008, 20, 257–288.
2. K. H. Kim, E. Kabir and S. Kabir, Environ. Int., 2015, 74, 136–143.
3. U. Pöschl, Angew. Chem., Int. Ed., 2005, 44, 7520–7540.
4. M. Kanakidou, J. H. Seinfeld, S. N. Pandis, I. Barnes, F. J. Dentener, M. C. Facchini, R. V. Dingenen, B. Ervens, A. Nenes, C. J. Nielsen, E. Swietlicki, J. P. Putaud, Y. Balkanski, S. Fuzzi, J. Horth, G. K. Moortgat, R. Winterhalter, C. E. L. Myhre, K. Tsigaridis, E. Vignati, E. G. Stephanou and J. Wilson, Atmos. Chem. Phys., 2005, 5, 1053–1123.
5. S. Fuzzi, M. O. Andreae, B. J. Huebert, M. Kulmala, T. C. Bond, M. Boy, S. J. Doherty, A. Guenther, M. Kanakidou, K. Kawamura, V.-M. Kerminen, U. Lohmann, L. M. Russell and U. Pöschl, Atmos. Chem. Phys., 2006, 6, 2017–2038.
6. K. S. Carslaw, O. Boucher, D. V. Spracklen, G. W. Mann, J. G. L. Rae, S. Woodward and M. Kulmala, Atmos. Chem. Phys., 2010, 10, 1701–1737.
7. K. Kawamura and S. Bikkina, Atmos. Res., 2016, 170, 140–160.
8. R. Volkamer, J. L. Jimenez, F. S. Martini, K. Dzepina, Q. Zhang, D. Salcedo, L. T. Molina, D. R. Worsnop and M. J. Molina, Geophys. Res. Lett., 2006, 33, L17811.
9. R. Zhang, Science, 2010, 328, 1366–1367.
10. R. Zhang, A. Khalizov, I. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011.
11. N. Myllys, T. Olenius, T. Kurtén, H. Vehkamäki, I. Riipinen and J. Elm, J. Phys. Chem. A, 2017, 121, 4812–4824.
12. J. Elm, J. Phys. Chem. A, 2021, 125, 895–902.
13. M. Kulmala, T. Petäjä, M. Ehn, J. Thornton, M. Sipilä, D. R. Worsnop and V.-M. Kerminen, Annu. Rev. Phys. Chem., 2014, 65, 21–37.
14. D. L. Yue, M. Hu, R. Y. Zhang, Z. B. Wang, J. Zheng, Z. J. Wu, A. Wiedensohler, L. Y. He, X. F. Huang and T. Zhu, Atmos. Chem. Phys., 2010, 10, 4953–4960.
15. J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagné, L. Ickes, A. Kürten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreiss, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkilä, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petäjä, R. Schnitzhofer, J. H. Seinfeld, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tomé, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Nature, 2011, 476, 429–433.
16. F. Riccobono, S. Schobesberger, C. E. Scott, J. Dommen, I. K. Ortega, L. Rondo, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, A. Downard, E. M. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, A. Hansel, H. Junninen, M. Kajos, H. Keskinen, A. Kupc, A. Kürten, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, T. Nieminen, A. Onnela, T. Petäjä, A. P. Praplan, F. D. Santos, S. Schallhart, J. H. Seinfeld, M. Sipilä, D. V. Spracklen, Y. Stozhkov, F. Stratmann, A. Tomé, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, D. Wimmer, K. S. Carslaw, J. Curtius, N. M. Donahue, J. Kirkby, M. Kulmala, D. R. Worsnop and U. Baltensperger, Science, 2014, 344, 717–721.
17. S. Schobesberger, A. Franchin, F. Bianchi, L. Rondo, J. Duplissy, A. Kürten, I. K. Ortega, A. Metzger, R. Schnitzhofer, J. Almeida, A. Amorim, J. Dommen, E. M. Dunne, M. Ehn, S. Gagné, L. Ickes, H. Junninen, A. Hansel, V.-M. Kerminen, J. Kirkby, A. Kupc, A. Laaksonen, K. Lehtipalo, S. Mathot, A. Onnela, T. Petäjä, F. Riccobono, F. D. Santos, M. Sipilä, A. Tomé, G. Tsagkogeorgas, Y. Viisanen, P. E. Wagner, D. Wimmer, J. Curtius, N. M. Donahue, U. Baltensperger, M. Kulmala and D. R. Worsnop, Atmos. Chem. Phys., 2015, 15, 55–78.
18. J. Kirkby, J. Duplissy, K. Sengupta, C. Frege, H. Gordon, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Tröst, T. Nieminen, I. K. Ortega, R. Wagner, A. Adamov, A. Amorim, A. K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. Craven, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, M. Krapf, A. Kürten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, A. Onnela, O. Peräkylä, F. Piel, T. Petäjä, A. P. Praplan, K. Pringle, A. Rap, N. A. D. Richards, I. Riipinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, M. Sipilä, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tomé, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, K. S. Carslaw and J. Curtius, Nature, 2016, 533, 521–526.
19. R. Zhang, I. Suh, J. Zhao, D. Zhang, E. C. Fortner, X. Tie, L. T. Molina and M. J. Molina, Science, 2004, 304, 1487–1490.
20. V.-M. Kerminen, X. Chen, V. Vakkari, T. Petäjä, M. Kulmala and F. Bianchi, Environ. Res. Lett., 2018, 13, 103003.
21. A. Leonardi, H. M. Ricker, A. G. Gale, B. T. Ball, T. T. Odbadrakh, G. C. Shields and J. G. Navea, Int. J. Quantum Chem., 2020, 120, e26350.
22. W. Xu and R. Zhang, J. Phys. Chem. A, 2012, 116, 4539–4550.
23. J. Elm, M. Fard, M. Bilde and K. V. Mikkelsen, J. Phys. Chem. A, 2013, 117, 12990–12997.
24. J. Elm, N. Myllys, T. Olenius, R. Halonen, T. Kurtén and H. Vehkamäki, Phys. Chem. Chem. Phys., 2017, 19, 4877–4886.
25. J. Elm, ACS Omega, 2019, 4, 10965–10974.
26. V. Besel, J. Kubeĉka, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2020, 124, 5931–5943.
27. R. Ciuraru, J. Kammer, C. Decuq, M. Vijkovic, K. Haider, Y. Carpentier, F. Lafouge, C. Berger, M. Bourdat-Deschamps, I. K. Ortega, F. Levavasseur, S. Houot, B. Loubet, D. Petitprez and C. Focsa, npj Clim. Atmos. Sci., 2021, 4, 5.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
29. J.-D. Chai and H.-G. Martin, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
30. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
31. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
32. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
33. M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803.
34. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. De Frees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
35. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. von Ragué Schleyer, J. Comput. Chem., 1983, 4, 294–301.
36. G. W. Spitznagel, T. Clark, P. von Ragué Schleyer and W. J. Hehre, J. Comput. Chem., 1987, 8, 1109–1116.
37. F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085.
38. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
39. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
40. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820.
41. E.D. Glendening, A.E. Reed, J.E. Carpenter and F. Weinhold, NBO Version 3.1, Gaussian Inc., Pittsburgh, 2003.
42. S. Grimme, Chem. - Eur. J., 2012, 18, 9955–9964.
43. Y.-P. Li, J. Gomes, S. Mallikarjun Sharada, A. T. Bell and M. Head-Gordon, J. Phys. Chem. C, 2015, 119, 1840–1850.
44. H. Wang, X. Zhao, C. Zuo, X. Ma, F. Xu, Y. Sun and Q. Zhang, RSC Adv., 2019, 9, 36171–36181.

---

Footnote

† Electronic supplementary information (ESI) available: energetic data at the ωB97X-D/aug-pcseg-1 and ωB97X-D/def2-SVPD levels of theory, and coordinates of the optimized clusters in XYZ format. See DOI: 10.1039/d1ea00023c

---