Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamic baselines for the detection of water quality impacts – the case of shale gas development†
Fred
Worrall
 *a,
Richard J.
Davies
b and
Alwyn
Hart
c
*a,
Richard J.
Davies
b and
Alwyn
Hart
c
aDepartment of Earth Sciences, Science Labs, Durham University, Durham DH1 3LE, UK. E-mail: Fred.Worrall@durham.ac.uk; Fax: +44 (0)191 334 2301; Tel: +44 (0)191 334 2295
bSchool of Natural and Environmental Sciences, Newcastle University, Newcastle, NE1 7RU, UK
cEnvironment Agency, Research Assessment and Evaluation, Sapphire East, Streetsbrook Road, Solihull, B91 1QT, UK
First published on 18th June 2021
Abstract
There is a need for the development of effective baselines against which the water quality impacts of new developments can be assessed. The specific conductance of flowback water from shale gas operations is typically many times the specific conductance of surface water and near-surface groundwater. This contrast in specific conductance means that specific conductance could be the ideal determinand for detecting water quality impacts from shale gas extraction. If specific conductance is to be used for detecting the impacts of shale gas operations, then a baseline of specific conductance in water bodies is required. Here, Bayesian hierarchical modelling of specific conductance was applied across English groundwater. The modelling used existing, spot-sampled data from the years 2000 to 2018 from 537 unique borehole locations. When the differences between boreholes was considered, then the approach was sufficiently sensitive to detect 1% mixing of fracking fluid in groundwater at a 95% confidence interval. The Bayesian hierarchical modelling maximises the return on public investment and provides a means by which future observations can be judged.
Environmental significance“Dynamic baselines for the detection of water quality impacts – the case of shale gas development”. This paper describes a new approach to defining environmental baselines. Environmental baselines are needed so as to be able to define whether an impact has, or has not, occurred with acceptable confidence. What is required is a probabilistic baseline which can predict the expected distribution at a monitoring location and so it is possible to judge whether a new observation is “unusual” at a given probability. In this study we use a Bayesian hierarchical analysis of the specific conductance of English groundwater to develop a baseline against which the impact of shale gas exploitation could be judged. The approach could detect 1% fracking fluid in groundwater at a 95% confidence. |
1. Introduction
Many developed countries have extensive water quality monitoring networks that have been active for many years and so generating a large resource of water quality monitoring data, earliest river water quality monitoring starts in the nineteenth century;1 and in the developed world this monitoring is now spatially extensive. However, monitoring data has often been acquired for very specific, sometimes local, purposes, and in the European Union this has often been focused upon the “good ecological status” dictated by the Water Framework Directive.2,3 The use of these data in ways beyond those originally intended is attractive but can be problematic.4 Our aim was to determine whether this considerable quantity of data can be used not only to meet its original purpose but also aid in the protection and improvement of water resources from new challenges such as the development of a new onshore shale gas industry. One of the purposes of water quality monitoring is to assess whether activities have an adverse impact on a water body. To assess whether a human activity has an adverse impact or conversely demonstrate that no adverse impact has occurred, within an acceptable level of uncertainty, it is necessary to demonstrate that the activity (in this case shale gas exploitation) has changed the water quality above an acceptable limit or above a value that would have been expected without the activity present. In many cases, when the presence of pollutants is not overwhelming, then to demonstrate the presence or absence of an impact an effective baseline must exist, but such a baseline is not commonly available.For a baseline, or indicator or change, to be of use in detecting and apportioning change or adverse impact there are a number of properties that a robust baseline should have. First, the monitored parameter should be related to the activities of concern, or provide an unrelated comparison for assurance purposes (e.g. a conservative marker), and the monitored parameter should be not related to other pollution sources. Second, the monitored parameter should be sensitive to the change with a large change in the magnitude for a small change in the activity. Third, any chosen water quality parameter should be a lead indicator of change, and in the case of water quality this may mean a determinand with little attenuation in its environment. It would be preferable that monitoring could provide early warning of any impact so that measures could be deployed in time to mitigate or avoid a problem. Finally, a larger sample size is preferable and that is more easily achieved if the measurement cost is low and readily deployable.
Shale gas exploitation is in its infancy in England and the potential impact on ground and surface water quality is a public concern.5,6 Extensive monitoring campaigns have been undertaken around a shale gas exploration site in Lancashire including the determination of baseline conditions for a wide variety of determinands.7 A number of technologies have been proposed directed at indicator substances for the monitoring of shale gas impacts on water resources, for example, measurement of dissolved CH4;8 radium;9 barium and sulphate;10 strontium isotopes11). However, by far the greatest contrast between flowback or produced water (i.e. water returning from shale gas operations) and shallow ground or surface water is their salinity, where salinity could be measured as total dissolved solids (TDS) or electrical conductivity. A review of the total dissolved solids (TDS) of shale gas flowback water from US shale gas operations showed that its salinity was between 0.67 and 10 times the TDS of seawater TDS (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TDS seawater < 4.6) and far larger than the TDS of freshwater (log
TDS seawater < 4.6) and far larger than the TDS of freshwater (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TDS of freshwater ∼ 2.6).12 So far only one fracking operation has been conducted in the UK, for which flowback fluid composition has been measured (Preese Hall, Lancashire). The conductivity of the flowback fluid from the Preese Hall well was between 133
TDS of freshwater ∼ 2.6).12 So far only one fracking operation has been conducted in the UK, for which flowback fluid composition has been measured (Preese Hall, Lancashire). The conductivity of the flowback fluid from the Preese Hall well was between 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 and 150
730 and 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 μS cm−1.13 Measuring salinity, as electrical conductivity, requires no special equipment and is commonly and frequently measured in freshwater. Furthermore, the UK has been monitoring specific conductance (electrical conductivity of water corrected to a known temperature) across its range of fresh water bodies for decades. The availability and ease of collecting conductivity data are in contrast with some of the other indicators proposed for assessing shale gas, for example, the availability of strontium isotope data14 and the expense and facility required to collect further data.
614 μS cm−1.13 Measuring salinity, as electrical conductivity, requires no special equipment and is commonly and frequently measured in freshwater. Furthermore, the UK has been monitoring specific conductance (electrical conductivity of water corrected to a known temperature) across its range of fresh water bodies for decades. The availability and ease of collecting conductivity data are in contrast with some of the other indicators proposed for assessing shale gas, for example, the availability of strontium isotope data14 and the expense and facility required to collect further data.
These idealised characteristics for a good baseline indicator parameter mean that salinity, and its allied measures, specific conductance and TDS, are excellent prospects for detecting change in water quality from any developing shale gas industry. Measures of salinity show a high contrast between flowback fluids and freshwater environments and that this contrast is highly specific to shale gas. The high specificity and contrast between the salinity of the flowback fluids and the salinity of freshwater means that salinity could be a lead indicator of pollution incidents. What is more, high salinity water from hydrocarbon exploitation has been shown to be toxic to exposed organisms.15,16 Shale gas sites would be expected to have a range of mitigation measures in place; however, Davies et al.17 showed that 6% of active, onshore oil wells in the UK have reported a pollution incident in the last decade. Clancy et al.18 showed, for Colorado, that for conventional oil exploitation sites, 0.02% of the produced water was spilt. Meanwhile in Alberta, Canada, in 2015 there were 113 incidents of spills of flowback and produced water documented.19 Boothroyd et al.20 showed that 30% of decommissioned oil and gas wells showed significant CH4 leaks even within 10 years of their decommissioning.
Although there are considerable numbers of specific conductance measurements available, these measurements were not collected with the purpose of creating a baseline for judging the impacts of a new industry. The government bodies responsible for water quality monitoring in England (The Environment Agency) are testing a range of statistical tools to use with monitoring data from shale sites but as yet they make no recommendations for indicator substances. Moreover, a simple, coherent method is required for the objective and transparent assessment of water quality monitoring. Worrall et al.21 proposed to use existing riverwater specific conductance data to develop a baseline against which the impacts of shale gas exploitation could be assessed using Bayesian generalised linear modelling. The proposed method had several innate advantages; the method was data-driven; flexible with respect to how the specific conductance data are represented; can use factorial (e.g. month of sampling) and include covariate information (e.g. land-use). Creating the statistical modelling within a Bayesian approach means that the approach creates a framework whereby all information has value. Equally, within this framework, new information can be added to update estimates and model outputs are a probability distribution which means that risk can be considered at all stages. The approach developed by Worrall et al.,21 creates a baseline which is dynamic in time and space as it predicts values for sites but updates with each new observation. However, the analysis of Worrall et al.21 showed that for river water the sampling frequency and the in-stream residence time compared to the likely volume spilt in acute incidents would mean that monitoring would be unlikely to detect all but the most catastrophic spills. Bayesian modelling approaches have been successfully developed and applied elsewhere for environmental management: for detecting dissolved CH4;22 ecological risk assessment;23 stream water quality;24 impacts of climate change.25
Therefore, the objective of this study was to develop a dynamic baseline for groundwater which is dynamic as it adapts in time and space as new data become available. Furthermore, the baseline, obtained by means of calculating the expected distribution of specific conductance in groundwater, will provide a probabilistic risk assessment of a pollution event. The approach of this study was to consider specific conductance in groundwater and use hierarchical Bayesian generalised linear modelling to predict the expected distribution at the time of sampling. Any sampled value can be compared to its predicted distribution to estimate the probability that an unusual event has occurred, i.e. there has been a pollution incident.
2. Methodology
2.1. Study sites
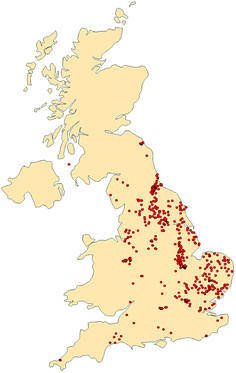
The study considered all the specific conductance at 25 °C measured in English groundwater wells and boreholes between the years 2000 and 2018 – no springs were included in this analysis. Only measurements that were from routine monitoring were included and data listed as being from pollution incidents were excluded as they will represent additional sampling at a higher frequency of times when higher specific conductance might be expected. Any boreholes that were listed as being part of or adjacent to landfill sites were removed. The data distribution of specific conductance was examined and values reported as having specific conductance lower than 40 μS cm−1 were removed as these had specific conductance lower than that of rainfall26 and such entries therefore were removed as being mis-entered data. Similarly, a QQ′ plot was used to assess the distribution of the data and values above 6000 μS cm−1 were excluded as being outliers – this represented the data from one site. The analytical methodology for specific conductance is outlined and controlled by the UK government's Standing Committee of Analysts (http://standingcommitteeofanalysts.co.uk/). Sites were retained within the study if they were sampled in at least two years during the period 2000 to 2018. This condition was used in part to restrict the number of sample sites that had to be considered and also to facilitate the estimation of interaction terms. Given the criteria for selection, there were 3370 observations from 537 unique locations that could be included in this analysis (Fig. 1).2.2. Bayesian hierarchical generalised linear modelling
The estimation was based upon Bayesian hierarchical generalised linear modelling. Each data point (i.e., specific conductance measurement – κ) within a generalised linear modelling approach is assumed to be generated from a specific distribution within the exponential family of distribution. For the prediction of groundwater specific conductance (κ – μS cm−1), the generalised linear model for the prediction of κ for site x at time t given a gamma distribution would be: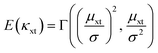 | (i) |
| μxt = (αxt(site, month) + βxt(site, month)Δ[year]xt) | (ii) |
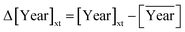 | (iii) |
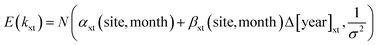 | (iv) |
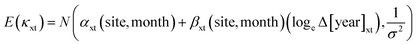 | (v) |
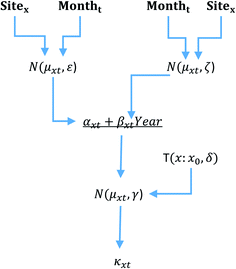
The approach given in eqn (i) through (v) is hierarchical because the model is established with a prior distribution on a prior distribution. In this case, the prior distribution on the terms α and β depends on the factors and each of these factors has its own prior distribution. The conceptual structure of the model is illustrated in Fig. 2.
Eqn (i) to (v) are expressed in terms of site and month as factors and year as a covariate. Year was considered as a covariate, which meant that for each of the factors (e.g. the difference between the months of sampling), the value of α and β could be estimated for each factor level included in a particular model. Furthermore, the inclusion of year as a covariate meant that predictions for future years could also be made for each of the factor level combinations. The site factor considers the difference between the monitoring sites and sites were included in the analysis if they were sampled in two or more years. Only sites with two or more years of sampling were retained as this facilitated the estimation of interaction terms, i.e. those terms that are the combination of factors. The month factor had 12 levels which is one for each calendar month.
As an alternative to the site factor, the aquifer class and aquifer type were considered. The aquifer class had seven classes defined by the British Geological Survey (BGS) and the classes are: 1A, 1B, 1C, 2A, 2B, 2C, and 3, where: 1 = inter-granular aquifer; 2 = fractured aquifer; 3 – rocks with essentially no groundwater; furthermore, with A = highly productive aquifer; B = moderately productive; C = low productive aquifer.27 The aquifer type is based on the geology that the borehole penetrates. The aquifer type was established from the British Geological Survey (BGS) aquifer designation map and the aquifer type was included if two of more sites sampled that particular aquifer geology; in all it was possible to include 27 different aquifer types (https://www.bgs.ac.uk/products/hydrogeology/aquiferDesignation.html – the dataset summarised by the aquifer class and type is given in Table S1†). The approach is hierarchical because the model is established with a prior distribution on a prior distribution. In this case the prior distribution on the trend over time, e.g. the terms α and β (eqn (i)), depends on the factors site, month, etc., and each of these terms has its own prior distribution.
Markov Chain Monte Carlo (MCMC) simulation was used for the Bayesian analysis. The posterior distribution of the specific conductance was calculated using the Jags code called from R (version 4.0) using the R2Jags (version 0.6–1) library (R and JAGS code for the most complex model is included in the ESI†). An MCMC chain of length 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations after a 2000 burn was used with samples saved every 10 cycles and with 3 chains.
000 iterations after a 2000 burn was used with samples saved every 10 cycles and with 3 chains.
The prior distribution for the values of β were set as normal distributions with a mean of zero so that both positive and negative trends in time were equally favoured at the outset, and standard deviation of the priors was set to be an uninformative prior and the likely small value of values of β, e.g. N(0, 1000). The prior distributions for the values of α were also set as a normal distribution but with the mean set to be the mean of all the dataset and a standard deviation chosen to make negative values unlikely, e.g. N(6, 0.25). The choice of such a distribution is justified because if values of β are small (e.g. influence of factors is weak), then α is the prediction of the specific conductance and thus should approximate the expected value of the distribution of the data as a whole. A half-t distribution was used for the prior distributions of the standard deviations for all terms as half-t distributions mean that a negative value of the standard deviation cannot occur, e.g. halft(0, 5, 1)T(0).
The fit of model was tested by a number of approaches. Firstly, the adequacy of the MCMC process was assessed using ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) , the convergence statistic, and values of
, the convergence statistic, and values of ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) < 1.1 were considered acceptable. If
< 1.1 were considered acceptable. If ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) > 1.1, then the burn in process and number of iterations were increased. Second, for any factor, the 95% credible interval does not include zero, and going forward this is referred to as being a 95% probability of being significantly different from zero. Third, when a factor, interaction, or covariate is included, this caused total model deviance to decrease – deviance is a goodness of fit measure and is a generalization of the idea of using the sum of squares of residuals in ordinary least squares. Fourth, when an additional factor, interaction or covariate is included, there is a resulting decrease in the deviance information criterion (DIC). Because the inclusion of additional factors, covariates or interactions will increase the degrees of freedom of a model such inclusion would lead to a decrease in the total deviance of a model, and hence the need for another measure rather than just total deviance. The DIC accounts for the trade-off between the inclusion of more fitting parameters against the additional fit of the model and penalises for additional parameters relative to the fit of the model – DIC is the general case of the Akaike Information Criterion. Finally, the effective number of parameters (pD) was monitored, and it would be expected that as a factor or covariate was added to the model, then the number of effective parameters would likewise increase, and if pD did not increase with the inclusion of a factor or covariate then that parameter has no effect on the model and could be removed. Furthermore, that pD should be close to the ideal case if all parameters are contributing, and so therefore the calculated pD can be expressed as a percentage of that maximum possible – this value can never be greater than 100%. Finally, the fit of any model was judged using a posterior prediction check, i.e. the output of the model was plotted against the observed values and the fitted line between these two examined – it would be expected that a good fit model would give a 1
> 1.1, then the burn in process and number of iterations were increased. Second, for any factor, the 95% credible interval does not include zero, and going forward this is referred to as being a 95% probability of being significantly different from zero. Third, when a factor, interaction, or covariate is included, this caused total model deviance to decrease – deviance is a goodness of fit measure and is a generalization of the idea of using the sum of squares of residuals in ordinary least squares. Fourth, when an additional factor, interaction or covariate is included, there is a resulting decrease in the deviance information criterion (DIC). Because the inclusion of additional factors, covariates or interactions will increase the degrees of freedom of a model such inclusion would lead to a decrease in the total deviance of a model, and hence the need for another measure rather than just total deviance. The DIC accounts for the trade-off between the inclusion of more fitting parameters against the additional fit of the model and penalises for additional parameters relative to the fit of the model – DIC is the general case of the Akaike Information Criterion. Finally, the effective number of parameters (pD) was monitored, and it would be expected that as a factor or covariate was added to the model, then the number of effective parameters would likewise increase, and if pD did not increase with the inclusion of a factor or covariate then that parameter has no effect on the model and could be removed. Furthermore, that pD should be close to the ideal case if all parameters are contributing, and so therefore the calculated pD can be expressed as a percentage of that maximum possible – this value can never be greater than 100%. Finally, the fit of any model was judged using a posterior prediction check, i.e. the output of the model was plotted against the observed values and the fitted line between these two examined – it would be expected that a good fit model would give a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line between observed and posterior predicted values. Given the purpose of the model the balance of these criteria would be for a model that includes significant factors and gives the best possible fit as described by the lowest deviance given a reasonable fit across the range of observations shown in the posterior probability plots.
1 line between observed and posterior predicted values. Given the purpose of the model the balance of these criteria would be for a model that includes significant factors and gives the best possible fit as described by the lowest deviance given a reasonable fit across the range of observations shown in the posterior probability plots.
2.3. Model types
Three models were fitted(i) Year, month and site factors – this model was used to give prediction at individual sites and was designed to understand the temporal trend at each site and assess the capacity for prediction and baseline development.
(ii) Year, month and aquifer class factors – the primary purpose of this model was to predict specific conductance for a previously unknown site. The aquifer into which any borehole will penetrate could be known before drilling, and so even if any previous sampling has not been included in the model development the question is whether it would be possible to predict specific conductance at sites not included in the analysis.
(iii) Year, month and aquifer type factors – as with the aquifer class we can consider a model based on the aquifer type as a means of predicting a specific conductance baseline for a site not previously sampled or not included in the model development.
2.4. Model verification and application
The data used for this study were groundwater data collected from the year 2000 to 2019. The models were developed on the groundwater data collected between 2000 and 2018, and to verify and further test the models, the models were used to predict the specific conductance for 2019. Given the factors included in the model, this prediction could be done for each borehole, aquifer class and aquifer type and for every month. These predictions were compared to the results of specific conductance in groundwater available for 2019.As an example, the models were applied to the most and the least sampled sites and results shown over the study period.
2.5. The problem of the depth of sampling
The specific conductance of groundwater is expected to increase with the depth below the surface and therefore, any variation modelled could be due to variation in the depth that the sample came from. The depth of sampling is not recorded as part of the Environment Agency's monitoring; however, as part of separate investigations into the potential for geothermal energy in the UK a catalogue of depth constrained monitoring is available from Burley et al.28 These data were used to test how much of the observed variation in specific conductance could be explained by the change in the depth of sampling. It should be noted that no groundwater body is delimited for water supply below 400 m in the UK.29 No specific conductivity was reported within the available geothermal database but a standard relationship between salinity and specific conductance was used for the conversion.30The relationship between the specific conductance and depth for English groundwater was used to examine whether variation in specific conductance observed between sites within this study could simply be ascribed to variation in the depth of sampling.
2.6. Comparative data
To give context to the specific conductance of English groundwater, the Environment Agency database was examined for the same time period to give the distribution of specific conductance for English river water, lake water and sewage treatment discharge. For English rainfall records from UK Precip-NET were used (https://uk-air.defra.gov.uk/networks/network-info?view=precipnet).3. Results
Because the aquifer type was not defined for every borehole, the dataset when considering the aquifer type was slightly smaller with 3315 observations at 535 unique locations with 27 different aquifer types. The data have a median of 772.5 μS cm−1 and a 95% percentile range of 221 to 2350 μS cm−1. The comparative data for English river water, lake water, rain water and final sewage effluent (Table 1) show that groundwater does have a higher specific conductance| Type | Expected value | 95% interval | N | Source |
|---|---|---|---|---|
| Groundwater | 772.5 | 221–2350 | 3370 | This study |
| Riverwater | 633.5 | 95–1117 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 495 495 |
Worrall et al. (2019) |
| Lakewater | 1243 | 45–7465 | 6967 | EA WIMS |
| Rainwater | 33 | 6–82 | 1484 | UK PRECIP-NET |
| Final sewage effluent | 1103.5 | 360–3739 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 245 245 |
EA WIMS |
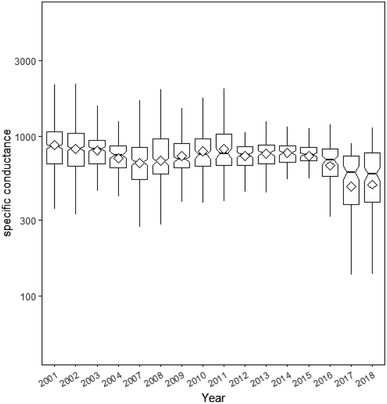
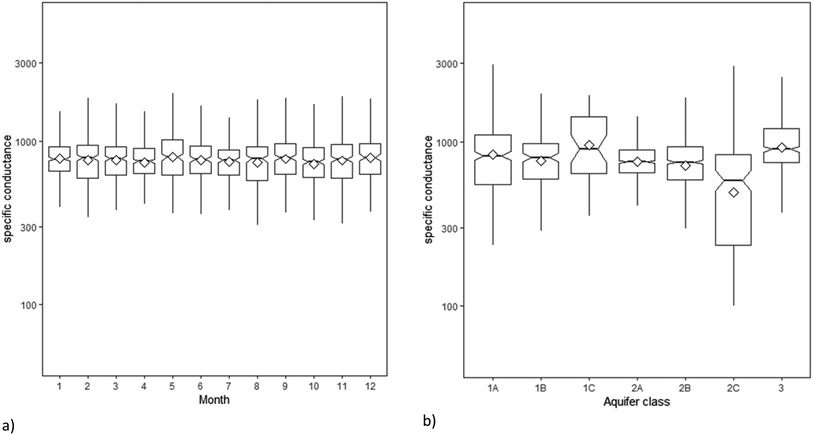
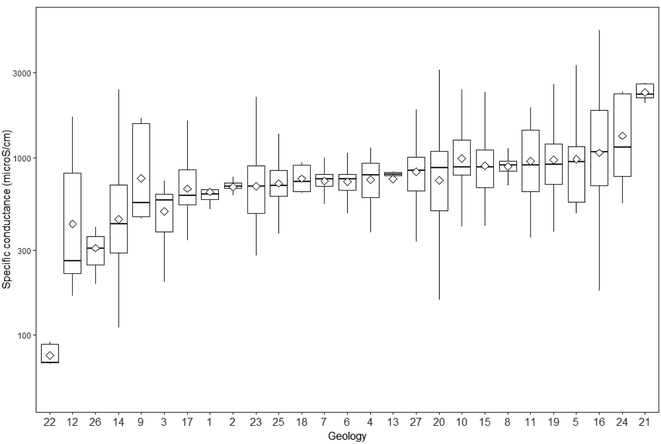
The distribution of the data by covariates and factors shows that there is a decline in the specific conductance of groundwater over time since 2000 (Fig. 3). Patterns of difference are less clear for the month and aquifer class factors (Fig. 4). For the geology, there are some clear distinctions with the lowest values in the Upper Greensand and highest in the Upper Devonian formations, although both of these aquifers had sample size of less than 6 samples (Table S1† – Fig. 5).
3.1. Statistical modelling
For all models the![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) < 1.01 and so the fitting process for all models was deemed adequate. In all cases the best fit model was log normal for each model and the results of model fit relative to covariates and factors are detailed in Table 2. The pD will increase with the number of parameters included in the model, but the percentage of the expected pD may decrease as more parameters are included. The model with the most possible parameters (year + month + site) was the one with the lowest percentage of the expected pD. This low value of the percentage of the expected pD can be interpreted as that there being strong inter- and intra-annual relationships at some sites but by no means at all sites. The DIC value is at a minimum for the year + site model but increases for the model with the most parameters, i.e. year + month + site, implying that the most efficient model was year + site. However, model efficiency, as defined by DIC, may not be the most important criterion in terms of predicting specific conductance and the ability to fit the data accurately would be more important. With respect to deviance the best-fit model was the year + month + site model. The final test to be considered is the posterior prediction comparison (Fig. 6) and this suggests that the model year + month + site was the best predictor.
< 1.01 and so the fitting process for all models was deemed adequate. In all cases the best fit model was log normal for each model and the results of model fit relative to covariates and factors are detailed in Table 2. The pD will increase with the number of parameters included in the model, but the percentage of the expected pD may decrease as more parameters are included. The model with the most possible parameters (year + month + site) was the one with the lowest percentage of the expected pD. This low value of the percentage of the expected pD can be interpreted as that there being strong inter- and intra-annual relationships at some sites but by no means at all sites. The DIC value is at a minimum for the year + site model but increases for the model with the most parameters, i.e. year + month + site, implying that the most efficient model was year + site. However, model efficiency, as defined by DIC, may not be the most important criterion in terms of predicting specific conductance and the ability to fit the data accurately would be more important. With respect to deviance the best-fit model was the year + month + site model. The final test to be considered is the posterior prediction comparison (Fig. 6) and this suggests that the model year + month + site was the best predictor.
| Factors and covariates | pD (% expected) | DIC | Deviance |
|---|---|---|---|
| Year + month | 21.5 (90) | 4767 | 4745 |
| Year + aquifer class | 15.3 (95) | 4318 | 4303 |
| Year + month + aquifer class | 201.9 (70) | 4328 | 4126 |
| Year + geology | 60.2 (54) | 3690 | 3630 |
| Year + month + geology | 545 (56) | 4145 | 3600 |
| Year + site | 948 (59) | 487 | 457 |
| Year + month + site | 4980 (38) | 5344 | 364 |
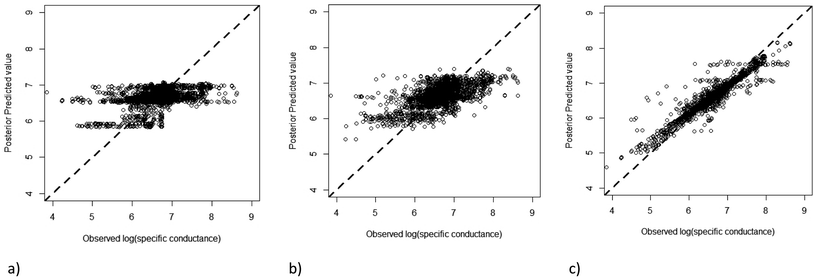 | ||
| Fig. 6 Posterior prediction comparison for: (a) year + month + aquifer class; (b) year + month + aquifer type; (c) year + month + site. | ||
The slopes (β) estimated for each site shows that the mean slope estimates were negative for 497 out of the 535 sites with the remainder having positive estimates of the slope (Fig. 7). When the uncertainty in those estimates is considered, then it is possible to consider the chance that each of the slope estimates is zero, in which case at the 95% probability no site showed a positive slope and 7 showed a negative slope. The spatial distribution of the sites with significant slope, and indeed negative, slopes are all relatively coastal when compared to the distribution of all the boreholes in the study (Fig. 7). The site with the greatest significant slope would have a specific conductance decrease from 1685 μS cm−1 in the year 2000 to 572 μS cm−1 in 2018.
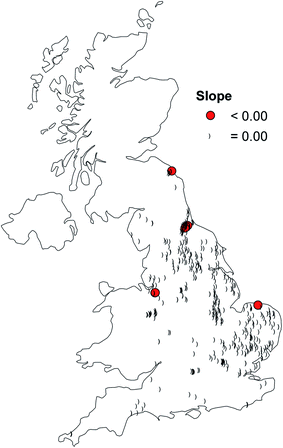 | ||
| Fig. 7 The distribution of sites with significant mean slopes in comparison to the location of every monitored site in the study. | ||
The slopes (β) estimated for each aquifer type shows that the mean slope estimates were negative for 20 out of the 27 aquifer types with the remainder having positive estimates of the slope. When the uncertainty in those estimates was considered. then 11 out of the 27 aquifer types had a 95% probability, while four aquifer types showed a significantly positive slope. The largest decline was for the Lias clay group and the greatest increase was for the Millstone Grit group.
The slopes estimated (β) for the aquifer classes showed that all seven aquifer classes had slopes significantly different from zero with five out seven aquifer classes showing a negative slope (aquifer classes: 1A, 1B, 1C, 2A and 2C), while two aquifer classes showed positive trends (aquifer classes: 2B and 3). The greatest increase was observed in aquifer class 3 and the largest decrease was estimated for aquifer class 2C.
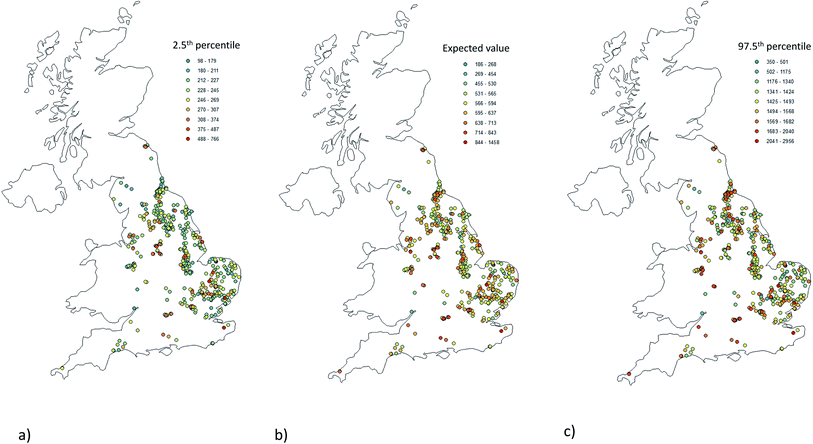
The prediction of the model can be plotted both in terms of the expected value (the arithmetic mean as the fitted distribution was normal) and measures of the distribution across the UK (Fig. 8). The distribution of expected values across the UK shows no distinctive patterns with no apparent pattern contrasting coastal with inland sites; no geographical trend (e.g. west vs. east); or upland vs. lowland sites. The pattern does indeed reflect the result in Fig. 6, i.e. the aquifer class and type are not as good predictors of groundwater specific conductance as site specific prediction.
3.2. Model verification application
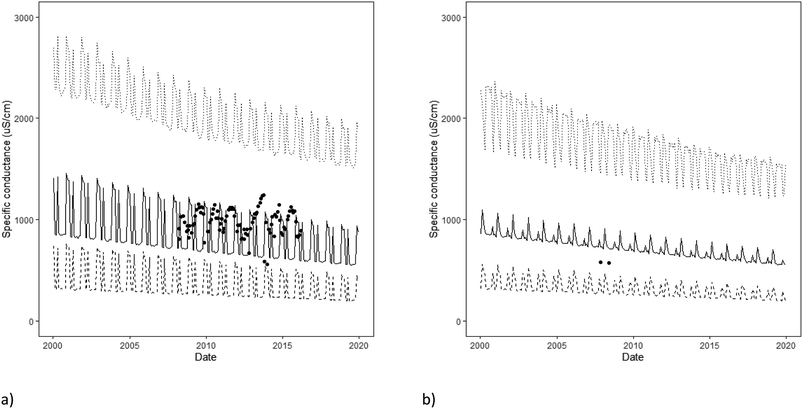
The results for the most and the least sampled sites (Fig. 9) shows that in both cases the observed data are well within the envelope of the 95th percentile confidence interval predicted from the statistical modelling. Further, verification of the model comes from the comparison between the predicted and observed values for 2019, and this shows that all but 4 out of 29 possible observations were as predicted (Fig. 10). It is of course possible that the predicted distribution does not fit the observed because an unusual event has occurred at one of the sites. In each of the cases that could be considered in this study where the observed was outside the predicted distribution the observed was lower than the predicted distribution – therefore the modelling may be over-predicting values.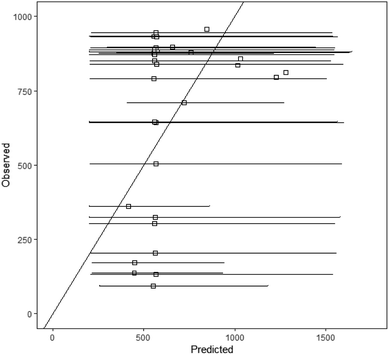 | ||
| Fig. 10 The comparison of the predicted and observed specific conductance, which could be included in the modelling and for which measurements had been made in 2019. | ||
3.3. Problem of depth
From the Geothermal catalogue, the specific conductance is often greater at depth than at the surface (Fig. 10). At the greatest depth sampled (2059 m) the specific conductance was 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108 μS cm−1 which is a TDS = 128
108 μS cm−1 which is a TDS = 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714 mg L−1 (Weyl equation30). However, the sites in this study only show specific conductance in the box illustrated within Fig. 10 and in this box it would be difficult to suggest any relationship between the depth and specific conductance. Within the box drawn (as defined by the specific conductance within the dataset of this study), the depths of the samples from the UK Geothermal catalogue were up to 451 m below the surface. The lower extent of groundwater for water supply in the UK is often considered as 400 mbgl.29
714 mg L−1 (Weyl equation30). However, the sites in this study only show specific conductance in the box illustrated within Fig. 10 and in this box it would be difficult to suggest any relationship between the depth and specific conductance. Within the box drawn (as defined by the specific conductance within the dataset of this study), the depths of the samples from the UK Geothermal catalogue were up to 451 m below the surface. The lower extent of groundwater for water supply in the UK is often considered as 400 mbgl.29
Over the entire range of depths sampled the best-fit equation was:
loge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ = 1.64 κ = 1.64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) loge(depth) n = 131, r2 = 0.51 (0.14) loge(depth) n = 131, r2 = 0.51 (0.14) | (vi) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895 μS cm−1 (TDS = 228
895 μS cm−1 (TDS = 228![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728 mg L−1) was ever observed.
728 mg L−1) was ever observed.
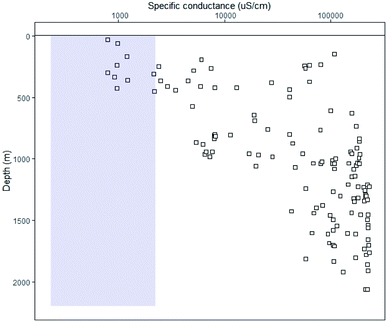 | ||
| Fig. 11 The variation of specific conductance with the depth for data derived from Burley et al. (1984). The shaded box represents the values observed for surface water in England. | ||
For the range of specific conductance observed in this study (up to 2350 μS cm−1), the relationship with the depth was not significant at a 95% probability of being different from zero, i.e. the inability to include the depth of sampling in this analysis was not critical to the result.
4. Discussion
Fig. 11 illustrates why analysing the specific conductance of groundwater will be useful for detecting water from depth. There have only been two fracking operations conducted in the UK at Preese Hall and Preston New Road, both in Lancashire, for which the conductivity of flowback fluid is known. The conductivity (not specific conductance) from the Preese Hall well varied from 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 and 150
730 and 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 μS cm−1.13,31 At the depth of fracking at Preese Hall, it would be expected that the specific conductance of the groundwater would be 450
614 μS cm−1.13,31 At the depth of fracking at Preese Hall, it would be expected that the specific conductance of the groundwater would be 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μS cm−1 or even if Fig. 11 is viewed in linear as opposed to log–log space the predicted specific conductance would be 285
000 μS cm−1 or even if Fig. 11 is viewed in linear as opposed to log–log space the predicted specific conductance would be 285![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μS cm−1, i.e. this would suggest that there is mixing of the deep groundwater with either the fracking fluid itself or less saline water as the water raised back to the surface. The fracking fluid used at Preese Hall was a “slick water” fluid,32 a fluid that is predominantly composed of water and 1–2 additives (Table 3), usually a friction reducer and a chemical tracer.33 At Preese Hall, 425 g of a “sodium salt” were used in 8399 m3 of tap water, which would suggest that the TDS of the fracking fluid would be of the order of 400 mg L−1 or 1122 μS cm−1. Therefore, given the measured conductivity of the Preese Hall flowback fluid; the predicted specific conductance of the groundwater at the depth of fracking; and the specific conductance of the fracking fluids; this would suggest that fracking fluid mixes with the groundwater at depth in 1
000 μS cm−1, i.e. this would suggest that there is mixing of the deep groundwater with either the fracking fluid itself or less saline water as the water raised back to the surface. The fracking fluid used at Preese Hall was a “slick water” fluid,32 a fluid that is predominantly composed of water and 1–2 additives (Table 3), usually a friction reducer and a chemical tracer.33 At Preese Hall, 425 g of a “sodium salt” were used in 8399 m3 of tap water, which would suggest that the TDS of the fracking fluid would be of the order of 400 mg L−1 or 1122 μS cm−1. Therefore, given the measured conductivity of the Preese Hall flowback fluid; the predicted specific conductance of the groundwater at the depth of fracking; and the specific conductance of the fracking fluids; this would suggest that fracking fluid mixes with the groundwater at depth in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 volume ratio.
3 volume ratio.
| Additive | Type | Quantity | % by volume |
|---|---|---|---|
| Water | Local mains tap water | 8399 m3 | 97.93 |
| Proppant | Glacial outwash sand | 462.7 tonnes | 2.02 |
| Friction reducer | Polyacrylamide emulsion | 3.7 m3 | 0.043 |
| Chemical tracer | Sodium salt | 425 g | 0.00043 |
Given the likely conductance of flowback fluid (for Preese Hall: 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 and 150
730 and 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 μS cm−1) and the predicted specific conductance of each monitored site (median = 696 μS cm−1, 95th percentile range of 404 to 1158 μS cm−1), it is possible to assess what amount of mixing of the flowback fluid would be sufficient to increase the specific conductance of the local shallow groundwater to a value greater than would be expected at a given probability, for example:
614 μS cm−1) and the predicted specific conductance of each monitored site (median = 696 μS cm−1, 95th percentile range of 404 to 1158 μS cm−1), it is possible to assess what amount of mixing of the flowback fluid would be sufficient to increase the specific conductance of the local shallow groundwater to a value greater than would be expected at a given probability, for example:
| κ97.5 < ϕκflowback + (1 − ϕ)κ2.5 | (vii) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3, whilst Jiang et al.34 noted that an average Marcellus well consumed 20
000 m3, whilst Jiang et al.34 noted that an average Marcellus well consumed 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3 (with a range from 6700 to 33
000 m3 (with a range from 6700 to 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3) of freshwater per well over its lifetime. The single well drilled in the UK at Preese Hall (Lancashire) required 8400 m3 of water.35 Therefore, for 8400 m3 of flowback fluid and the median ϕ value predicted from eqn (vii), this volume would be sufficient to bring 906
000 m3) of freshwater per well over its lifetime. The single well drilled in the UK at Preese Hall (Lancashire) required 8400 m3 of water.35 Therefore, for 8400 m3 of flowback fluid and the median ϕ value predicted from eqn (vii), this volume would be sufficient to bring 906![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3 of groundwater above the 97.5th percentile. Of course, it unlikely that all 8400 m3 of flowback would be released. Clancy et al.18 considered the water spill records kept by the Texas Railroad commission and the Colorado Oil and Gas Commission that the spill rate from produced waters was 0.1% per well per year meaning that nearer 906 m3 of groundwater would be under threat, but this would be the volume under threat each year. In 2017 there were 18
000 m3 of groundwater above the 97.5th percentile. Of course, it unlikely that all 8400 m3 of flowback would be released. Clancy et al.18 considered the water spill records kept by the Texas Railroad commission and the Colorado Oil and Gas Commission that the spill rate from produced waters was 0.1% per well per year meaning that nearer 906 m3 of groundwater would be under threat, but this would be the volume under threat each year. In 2017 there were 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 655 licensed groundwater abstractions and the total groundwater abstracted was 2 × 109 m3, i.e. the average volume per abstraction is of the order of 1 × 105 m3 per year.
655 licensed groundwater abstractions and the total groundwater abstracted was 2 × 109 m3, i.e. the average volume per abstraction is of the order of 1 × 105 m3 per year.
There is still little evidence that shale gas exploitation has actual significant impacts on groundwater resources. Fontenot et al.36 did not find any significant increase in TDS in well water within 3 km of shale gas operations in the Barnett shale basin, Texas. Similarly, Warner et al.37 found that the shallow groundwater composition in 127 boreholes of the Fayetteville shale gas basin, Arkansas, did not reflect the composition of the flowback and produced water from the shale gas operations. Harkness et al.38 and Warner et al.37 did suggest that there was evidence of contamination from leaks and spills originating on shale gas well pads. Wen et al.,39 considered samples from 1384 boreholes and found that the higher dissolved CH4 in 7 out of the 1384 boreholes could be associated with shale gas. Therefore, there is little published evidence that fluids injected at depth are actually causing a threat to shallow groundwater aquifers.
A simple approach to analyzing these data would have been to observe the distribution at one site and simply compare the newest observation with that distribution. Such a comparison would be limited by the size of the sample set at each site and for the sites used in this study the average sample size was only 6 samples. But such a comparison would not be fair as all the samples at the site might have been taken in summer months or perhaps at the beginning of the sampling period rather than in the most recent years. It would be better to compare the most recent observations with observations for the current year, even better with the most recent time step, i.e. for the same year, month, day of the month or hour of the day. Of course it is unlikely that there will be sufficient observations to give such a reasonable distribution for any month for any year at any site. So it would be useful if information from other sites could be drawn upon to make the most appropriate comparison possible; this then is what the approach of this study has achieved. By using all available information, the approach of this study could estimate a distribution of observations for every month and for every year at each site. An analogous, non-Bayesian approach might be weighted regression analysis.40,41 The Bayesian approach uses all available data to predict distributions at the sites of interest. The approach is a systematic and transparent approach to analysing data and provides a probability, with uncertainty, as to the nature of any observed data. Thus in turn the probability that any pollution has, or has not, occurred can be assessed. All risk assessment is actual a probability statement and the tools here use Bayesian approaches so all results will be a probability with an uncertainty. The Bayesian framework means that not only does the tool use all available data it also automatically updates as new information becomes available. A physical modelling approach would require more extensive data and observations to parameterise, calibrate and validate the physical model and so is not well suited to the type of dispersed data set that commonly arises from water quality monitoring. Conversely, the Bayesian approach developed here uses all the information and can return a result with clear uncertainty estimation.
For determinands such as specific conductance no specific legal standard exists within the UK or EU. For operators of works such as shale gas sites the review period for water quality monitoring is dictated in their license to operate, but, are data reviewed each time new data are produced and is the regulator informed if there is an issue? The regulator in the UK may be asked to report at any time to the secretary of state at the highest government level, although it is not clear how often this might occur. The approach presented here could be used for each new datapoint, i.e. the calculation and method presented would give the probability that a new observation is exceptional and not what should be expected.
Could it be possible to improve on the current approach? It is possible to include covariates and other factors within the analysis. This study has already included the aquifer class and type, but there could be a spatial correlation within the monitoring that could relate boreholes between aquifers. Such a spatial correlation in the observations is not included in this modelling approach. Qian et al.42 have developed a Bayesian hierarchical model for the calculation of nutrient loads in rivers that incorporated spatial correlation, but the spatial correlation was based on the flow through the river network which provides for one dimensional and directional correlation not appropriate for the three dimensions of the aquifers considered here.
Specific conductance could be expected to co-vary with some cations and anions and indeed different sources of water may have a similar range of specific conductance but a very diffident set of cations and anions that constitute that ionic strength. Other studies have considered other chemical indicators of pollution from unconventional hydrocarbons: Cl/Br;43 Sr isotopes;14 or the ratio (Ba + Sr)/Mg. Indeed, Wilson and Van Briesen44 used Cl/Br ratios to detect shale gas fluids in surface water of the Monongahela river in Pennsylvania. However, a particular advantage of specific conductance is that it is regularly monitored whereas other determinands proposed in the literature have been far less frequently monitored.
This study has shown that between 2000 and 2018, specific conductance in English groundwater declined. Although only seven sites showed a significant decline the distribution of the slopes showed that 93% of sties had a negative slope and no sites had a significant increase. The salinisation of aquifers has been commonly reported across the globe, typically in coastal aquifers45 and this can be due to overexploitation46 or rising sea levels.47 Not all salinification has occurred in coastal aquifers and Rivett et al.48 have noted that in the UK we use between 1 and 3 Mtonnes of salt every year for road deicing and that this can be traced into aquifers. Indeed, many countries have noted deicing salt accumulating in aquifers (e.g. Canada49) and Perera et al.50 estimated that 19% of the applied road salt accumulated in the aquifer. These studies would suggest to expect salinisation in a country such as the UK where coastal aquifers are common and where there is an increasing demand for water with an expanding population. However, desalinisation was observed and never salinization. Han et al.46 ascribed desalinisation in coastal karst aquifers to return flows from irrigation. Cloutier et al.51 gave an example of desalinisation as a recovery from a period of a high sea level during a glacial period as modern recharge flushes the seawater out. We would propose that the decline in groundwater specific conductance observed in this study could be due to changes in recharge patterns driven by climate change. If wetter winters caused an increase in the recharge of meteoritic water, then the specific conductance of the groundwater would decrease. Wen et al.39 found significant declines in TDS since 1990 across 1384 in Pennsylvania and they ascribed these declines to declining atmospheric deposition and decreased inputs from the coal and steel industry.
5. Conclusions
This study has developed a Bayesian hierarchical model for determining the specific conductance of English groundwater. The model is able to estimate the distribution of specific conductance for any aquifer type, aquifer class or borehole that was included in the monitoring dataset. This estimation could be projected forward to predict distributions in the future, and furthermore, the Bayesian framework means that the probability estimation will continue to improve with all ongoing monitoring. The method was sensitive enough such that it could detect mixing of 1% of shale gas produced water into shallow groundwater.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded as part of the NERC-funded Equipt4risk project which in turn is part of the United Kingdom Unconventional Hydrocarbon (UKUH) Programme.References
- V. Noacco, T. Wagener, F. Worrall, T. P. Burt and N. J. K. Howden, Human impact on long-term organic carbon export to rivers, J. Geophys. Res.: Biogeosci., 2017, 122(4), 947–965 CrossRef CAS.
- European Commission, Directive2000/60/EC of the European Parliament and of the council of 23rd October 2000 establishing a framework for community action in the field of water policy, Off. J. Eur. Communities: Legis., 2000, 327/1 Search PubMed , Brussels, European Commission..
- L. Carvalho, E. B. Mackay, A. C. Cardoso, A. Baattrup-Pedersen, S. Birk, K. L. Blackstock, G. Borics, A. Borja, C. K. Feld, M. T. Ferreira, L. Globevnik, B. Grizzetti, S. Hendry, D. Hering, M. Kelly, S. Langaas, K. Meissner, Y. Panagopoulos, E. Penning, J. Rouillard, S. Sabater, U. Schmedtje, B. M. Spears, M. Venohr, W. van de Bund and A. L. Solheim, Protecting and restoring Europe's waters: An analysis of the future development needs of the Water Framework Directive, Sci. Total Environ., 2019, 658, 1228–1238 CrossRef CAS PubMed.
- Á. Borja, G. Chust, J. G. Rodríguez, J. Bald, M. J. Belzunce-Segarra, J. Franco, J. M. Garmendia, J. Larreta, I. Menchaca, I. Muxika, O. Solaun, M. Revilla, A. Uriarte, V. Valencia and I. Zorita, The past is the future of the present: learning from long-time series of marine monitoring, Sci. Total Environ., 2016, 566–567, 698–711 CrossRef PubMed.
- G. A. Kahrilas, J. Blotevogel, P. S. Stewart and T. Borch, Biocides in hydraulic fracturing fluids: A critical review of their usage, mobility, degradation, and toxicity, Environ. Sci. Technol., 2014, 49(1), 16–32 CrossRef PubMed.
- A. Vengosh, R. B. Jackson, N. Warner, T. H. Darrah and A. Kondash, A critical review of the risks to water resources from unconventional shale gas development and hydraulic fracturing in the United States, Environ. Sci. Technol., 2014, 48(15), 8334–8348 CrossRef CAS PubMed.
- R. S. Ward, P. L. Smedley, G. Allen, B. J. Baptie, Z. Daraktchieva, A. Horleston, D. G. Jones, C. J. Jordan, A. Lewis, D. Lowry, R. M. Purvis and M. O. Rivett, Environmental Baseline Monitoring Project, Phase II, Final Report, British Geological Survey, 2017, p. 163, OR/17/049 Search PubMed.
- C. J. Teasdale, J. A. Hall, J. P. Martin and D. A. C. Manning, Ground Gas Monitoring: Implications for Hydraulic Fracturing and CO2 Storage, Environ. Sci. Technol., 2014, 48(23), 13610–13616 CrossRef CAS PubMed.
- F. Lagace, D. Foucher, C. Surette and O. Clarisse, Radium geochemical monitoring in well waters at regional and local scales: an environmental impact indicator-based approach, Chemosphere, 2018, 205, 627–634 CrossRef CAS PubMed.
- X. Z. Niu, A. Wendt, Z. H. Li, A. Agarwal, L. Z. Xue, M. Gonzales and S. L. Brantley, Detecting the effects of coal mining, acid rain, and natural gas extraction in Appalachian basin streams in Pennsylvania (USA) through analysis of barium and sulfate concentrations, Environ. Geochem. Health, 2018, 40(2), 865–885 CrossRef CAS PubMed.
- C. A. K. Kohl, R. C. Capo, B. W. Stewart, A. J. Wall, K. T. Schroeder, R. W. Hammack and G. D. Guthrie, Strontium Isotopes Test Long-Term Zonal Isolation of Injected and Marcellus Formation Water after Hydraulic Fracturing, Environ. Sci. Technol., 2014, 48(16), 9867–9873 CrossRef PubMed.
- E. L. Rowan, M. A. Engle, C. S. Kirby and T. F. Kraemar, Radium Content of Oil- and Gas-Field Produced Waters in the Northern Appalachian Basin (USA): Summary and Discussion of Data. Scientific Investigations Report 2011-5135, US Geological Survey, 2011 Search PubMed.
- J. Broderick, R. Wood, P. Gilbert, M. Sharmina, K. Anderson, A. Footitt, S. Glynn and F. Nicholls, Shale Gas: an Updated Assessment of Environmental and Climate Change Impacts, A Report Commissioned by the Co-operative and Undertaken by Researchers at the Tyndall Centre, University of Manchester, 2011 Search PubMed.
- L. A. Neymark, W. R. Premo and P. Emsbo, Combined radiogenic (Sr-87/Sr-86, U-234/U-238) and stable (delta Sr-88) isotope systematics as tracers of anthropogenic groundwater contamination within the Williston Basin, USA, Appl. Geochem., 2018, 96, 11–23 CrossRef CAS.
- Y. He, S. L. Flynn, E. J. Folkerts, Y. Zhang, D. L. Ruan, D. S. Alessi, J. W. Martin and G. G. Goss, Chemical and toxicological characterizations of hydraulic fracturing flowback and produced water, Water Res., 2017, 114, 78–87 CrossRef CAS PubMed.
- T. A. Blewett, P. L. M. Delompre, Y. H. He, E. J. Folkerts, S. L. Flynn, D. S. Alessi and G. G. Goss, Sublethal and Reproductive Effects of Acute and Chronic Exposure to Flowback and Produced Water from Hydraulic Fracturing on the Water Flea Daphnia magna, Environ. Sci. Technol., 2017, 51(5), 3032–3039 CrossRef CAS PubMed.
- R. J. Davies, S. Almond, R. S. Ward, R. B. Jackson, C. Adams, F. Worrall, L. G. Herringshaw, J. G. Gluyas and M. A. Whitehead, Oil and gas wells and their integrity: Implications for shale and unconventional resource exploitation, Mar. Pet. Geol., 2014, 56, 239–254 CrossRef.
- S. A. Clancy, F. Worrall, R. J. Davies and J. G. Gluyas, The potential for spills and leaks of contaminated liquids from shale gas developments, Sci. Total Environ., 2018, 626, 1463–1473 CrossRef CAS PubMed.
- D. S. Alessi, A. Zlofarghari, S. Kletke, J. Gehman, D. M. Allen and G. G. Goss, Comparative analysis of hydraulic fracturing wastewater practices in unconventional shale development: water sourcing, treatment and disposal practices, Canadian Water Resources Journal, 2016, 42(2), 122–137 Search PubMed.
- I. M. Boothroyd, S. Almond, S. M. Qassim, F. Worrall and R. J. Davies, Fugitive emissions of methane from abandoned, decommissioned oil and gas wells, Sci. Total Environ., 2016, 547, 461–469 CrossRef CAS PubMed.
- F. Worrall, A. J. Wade, R. J. Davies and A. Hart, Setting the baseline for shale gas - Establishing effective sentinels for water quality impacts of unconventional hydrocarbon development, J. Hydrol., 2019, 571, 516–527 CrossRef.
- M. P. Wilson, F. Worrall, R. J. Davies and A. Hart, A dynamic baseline for dissolved methane in English groundwater, Sci. Total Environ., 2020, 711, 134854 CrossRef CAS PubMed.
- K. S. McDonald, D. S. Ryder and M. Tighe, Developing best-practice Bayesian Belief Networks in ecological risk assessments for freshwater and estuarine ecosystems: A quantitative review, J. Environ. Manage., 2015, 154, 190–200 CrossRef CAS PubMed.
- R. Wan, S. Cai, H. Li, G. Yang, Z. Li and X. Nie, Inferring land use and land cover impact on stream water quality using a Bayesian hierarchical modeling approach in the Xitiaoxi River Watershed, China, J. Environ. Manage., 2014, 133, 1–14 CrossRef CAS PubMed.
- B. F. Hobbs, Bayesian Methods for Analysing Climate Change and Water Resource Uncertainties, J. Environ. Manage., 1997, 49(1), 53–72 CrossRef.
- F. Worrall, T. P. Burt and J. K. Adamson, Controls on the chemistry of runoff from an upland peat catchment, Hydrol. Processes, 2003, 17(10), 2063–2083 CrossRef.
- R. C. Palmer, I. P. Holman, N. S. Robins and M. A. Lewis, Guide to Groundwater Vulnerability Mapping in England and Wales, National Rivers Authority Publication, 1995, ISBN 0113101031 Search PubMed.
- A. J. Burley, W. M. Edmunds and I. N. Gale. Catalogue of Geothermal Data for the Land Area of the United Kingdom, Second Revision April 1984, Investigation of the Geothermal Potential of the UK, British Geological Survey, Keyworth, 1984, p. 26 Search PubMed.
- UK Technical Advisory Group (UKTAG), Defining & Reporting on Groundwater Bodies, 2011 Search PubMed.
- P. K. Weyl, On the change in electrical conductance of seawater with temperature, Limnol. Oceanogr., 1964, 9(1), 75–78 CrossRef.
- S. Almond, S. A. Clancy, R. J. Davies and F. Worrall, The flux of radionuclides in flowback fluid from shale gas exploitation, Environ. Sci. Pollut. Res., 2014, 21(21), 12316–12324 CrossRef CAS PubMed.
- P. B. Kaufman, G. S. Penny and J. Paktinat, Critical Evaluation of Additives Used in Shale Slickwater Fracs, Presented at the SPE Shale Gas Production Conference, Society of Petroleum Engineers, 2008, DOI:10.2118/119900-MS.
- T. T. Palisch, M. Vincent and P. J. Handren, Slickwater Fracturing: Food for Thought, SPE Prod. Oper., 2010, 25, 327–344 Search PubMed.
- M. Jiang, C. T. Hendrickson and J. M. Van Briesen, Life cycle water consumption and wastewater generation impacts of a Marcellus shale gas well, Environ. Sci. Technol., 2014, 48(4), 1911–1920 CrossRef CAS PubMed.
- C. Taylor, D. Lewis and D. Byles, Institute of Directors (Infrastructure for Business) Report: Getting Shale Gas Working, Institute of Director, London, UK, 2013 Search PubMed.
- B. E. Fontenot, L. R. Hunt, Z. L. Hildenbrand, D. D. Carlton, H. Oka, J. L. Walton, D. Hopkins, A. Osorio, B. Bjorndal, Q. H. H. Hu and K. A. Schug, An Evaluation of Water Quality in Private Drinking Water Wells Near Natural Gas Extraction Sites in the Barnett Shale Formation, Environ. Sci. Technol., 2013, 47, 10032–10040 CrossRef CAS PubMed.
- N. R. Warner, T. M. Kresse, P. D. Hays, A. Down, J. D. Karr, R. B. Jackson and A. Vengosh, Geochemical and isotopic variations in shallow groundwater in areas of the Fayetteville Shale development, north-central Arkansas, Appl. Geochem., 2013, 35, 207–220 CrossRef CAS.
- J. S. Harkness, T. H. Darrah, N. R. Warner, C. J. Whyte, M. T. Moore, R. Millot, W. Kloppmann, R. B. Jackson and A. Vengosh, The geochemistry of naturally occurring methane and saline groundwater in an area of unconventional shale gas development, Geochim. Cosmochim. Acta, 2017, 208, 302–334 CrossRef CAS.
- T. Wen, X. Z. Niu, M. Gonzales, G. J. Zheng, Z. H. Li and S. L. Brantley, Big Groundwater Data Sets Reveal Possible Rare Contamination Amid Otherwise Improved Water Quality for Some Analytes in a Region of Marcellus Shale Development, Environ. Sci. Technol., 2018, 52, 7149–7159 CrossRef CAS PubMed.
- R. M. Hirsch, D. L. Moyer and S. A. Archfield, Weighted regression on time, discharge and season (WRTDS), with application to Chesapeake Bay river inputs, J. Am. Water Resour. Assoc., 2010, 46(5), 857–880 CrossRef PubMed.
- R. M. Hirsch, S. A. Archfield and L. A. De Cicco, A bootstrap method for estimating uncertainty of water quality trends, Environmental Modelling & Software, 2015, 73, 148–166 Search PubMed.
- S. S. Qian, K. H. Reckhow, J. Zhai and G. McMahon, Nonlinear regression modeling of nutrient loads in streams: A Bayesian approach, Water Resour. Res., 2005, 41, W07012 CrossRef.
- J. D. Johnson, J. R. Graney, R. C. Capo and B. W. Stewart, Identification and quantification of regional brine and road salt sources in watersheds along the New York/Pennsylvania border, USA, Appl. Geochem., 2015, 60, 37–50 CrossRef CAS.
- J. M. Wilson and J. M. Van Briesen, Source Water Changes and Energy Extraction Activities in the Monongahela River, 2009-2012, Environ. Sci. Technol., 2013, 47(21), 12575–12582 CrossRef CAS PubMed.
- P. Fleury, M. Bakalowicz and G. de Marsily, Submarine springs and coastal karst aquifers, a review, J. Hydrol., 2007, 339, 79–92 CrossRef.
- D. Han, V. E. A. Post and X. Song, Groundwater salinization processes and reversibility of seawater intrusion in coastal carbonate aquifers, J. Hydrol., 2015, 531, 1067–1080 CrossRef CAS.
- P. Pauw, P. G. B. de Louw and G. H. P. Oude-Essink, Groundwater salinization in the Wadden Sea area of the Netherlands: quantifying the effects of climate change, sea-level rise and anthropogenic interferences, Neth. J. Geosci., 2012, 91–93, 373–383 Search PubMed.
- M. O. Rivett, M. O. Cuthbert, R. Gamble, L. E. Connon, A. Pearson, M. G. Shepley and J. Davis, Highway deicing salt dynamic runoff to surface water and subsequent infiltration to groundwater during severe UK winters, Sci. Total Environ., 2016, 565, 324–338 CrossRef CAS PubMed.
- K. W. F. Howard and H. Maier, Road de-icing salt as a potential constraint on urban growth in the Greater Toronto area, J. Contam. Hydrol., 2007, 91, 146–170 CrossRef CAS PubMed.
- N. Perera, B. Gharabaghi and K. Howard, Groundwater chloride response in the Highland Creek watershed due to road salt applications: a re-assessment after 20 years, J. Hydrol., 2013, 479, 159–168 CrossRef CAS.
- V. Cloutier, R. Lefebvre, M. M. Savard and R. Therrien, Desalination of a sedimentary rock aquifer system invaded by Pleistocene Champlain Sea water and processes controlling groundwater geochemistry, Environ. Earth Sci., 2010, 59, 977–994 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0em00440e |
| This journal is © The Royal Society of Chemistry 2021 |